Accuracy Analysis of Slurry Characterization in a Rectifying Liquid Concentration Detection System
Abstract
1. Introduction
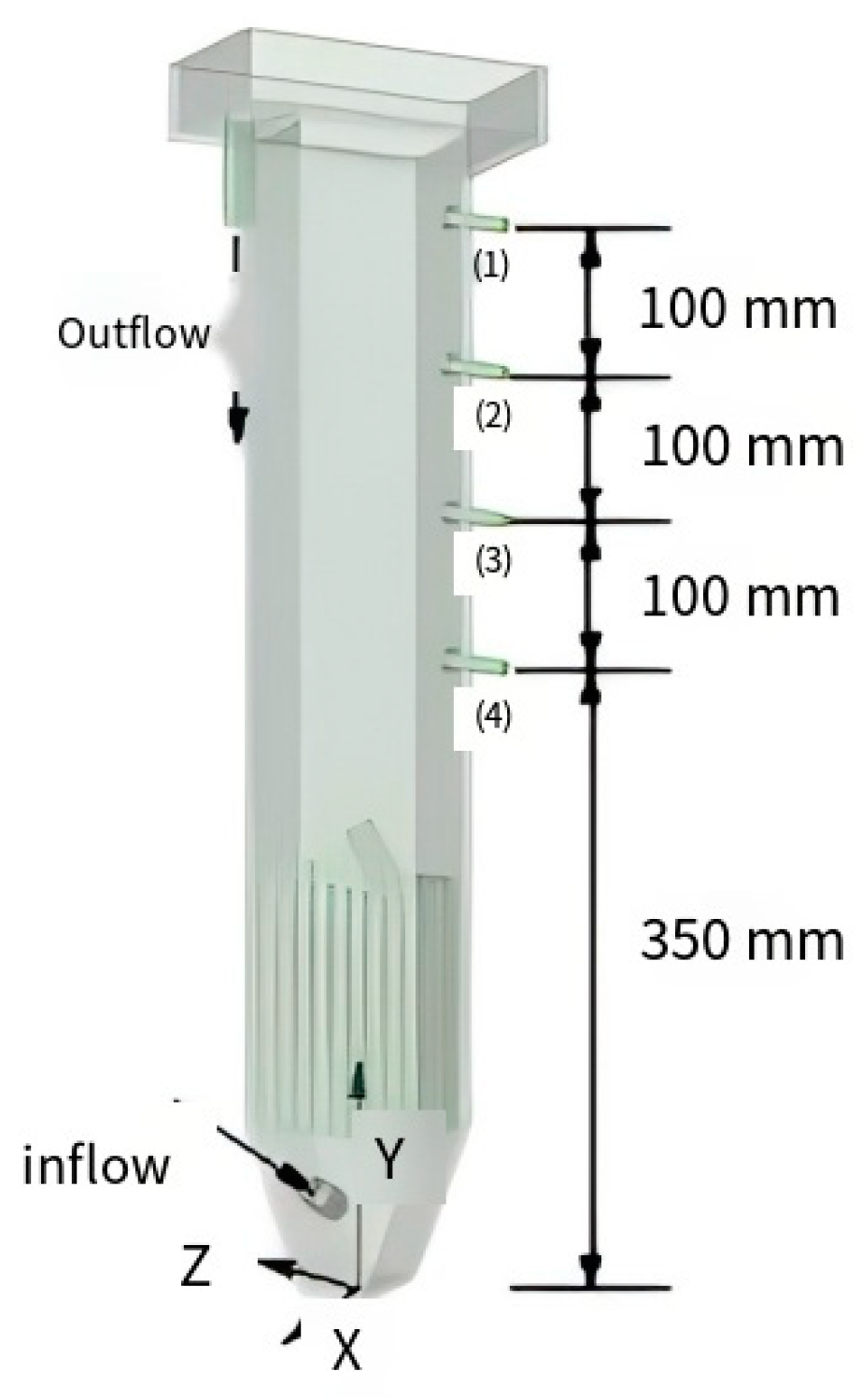
2. Experimental System and the Detection Principle
2.1. Experimental Equipment
Description of the Experimental System
2.2. Experimental Principle and Process
2.3. Experimental Scheme Design
3. Numerical Simulation
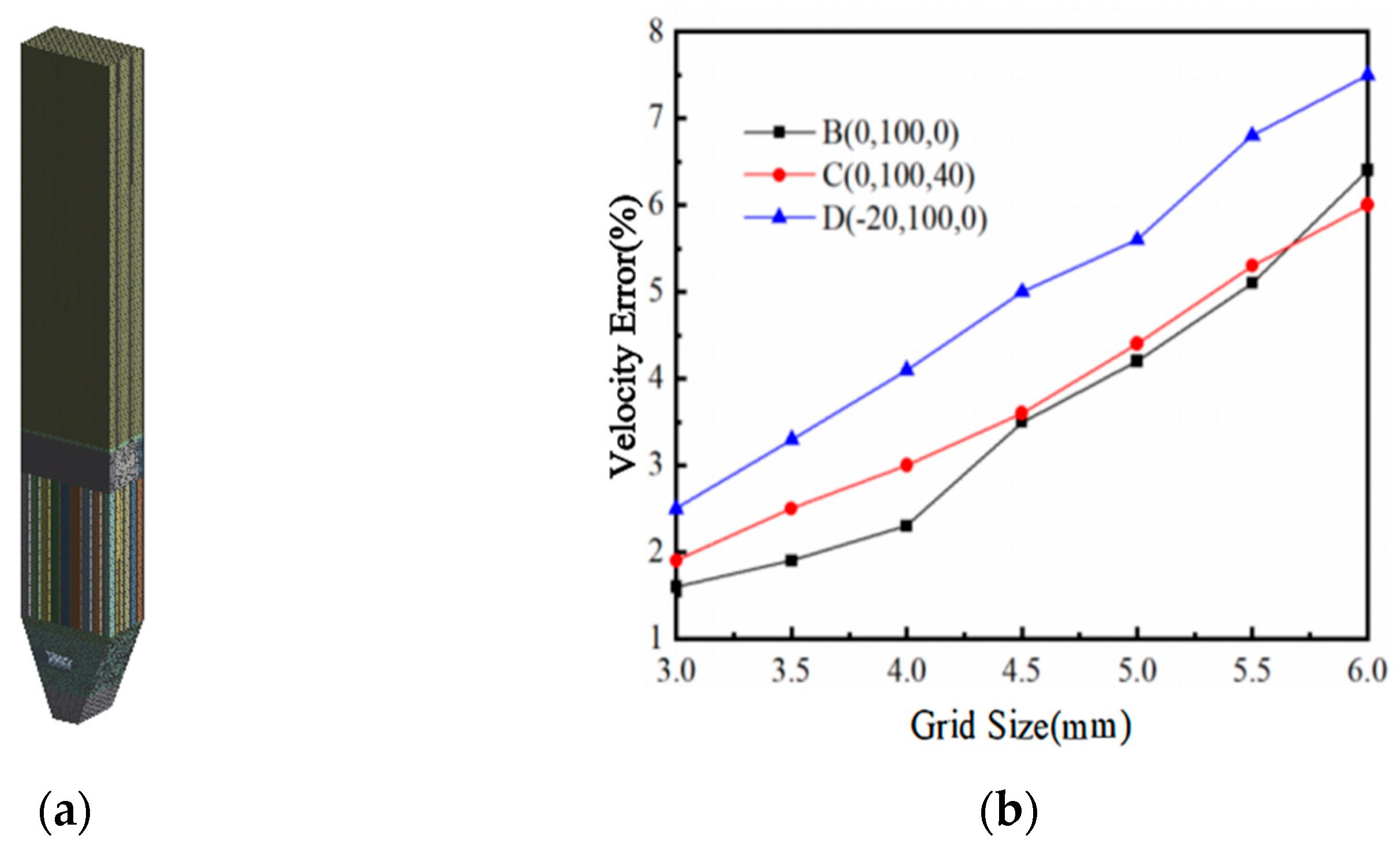
3.1. Establishing Turbulence Dissipation Measurement Tank Model
3.2. Numerical Model Settings
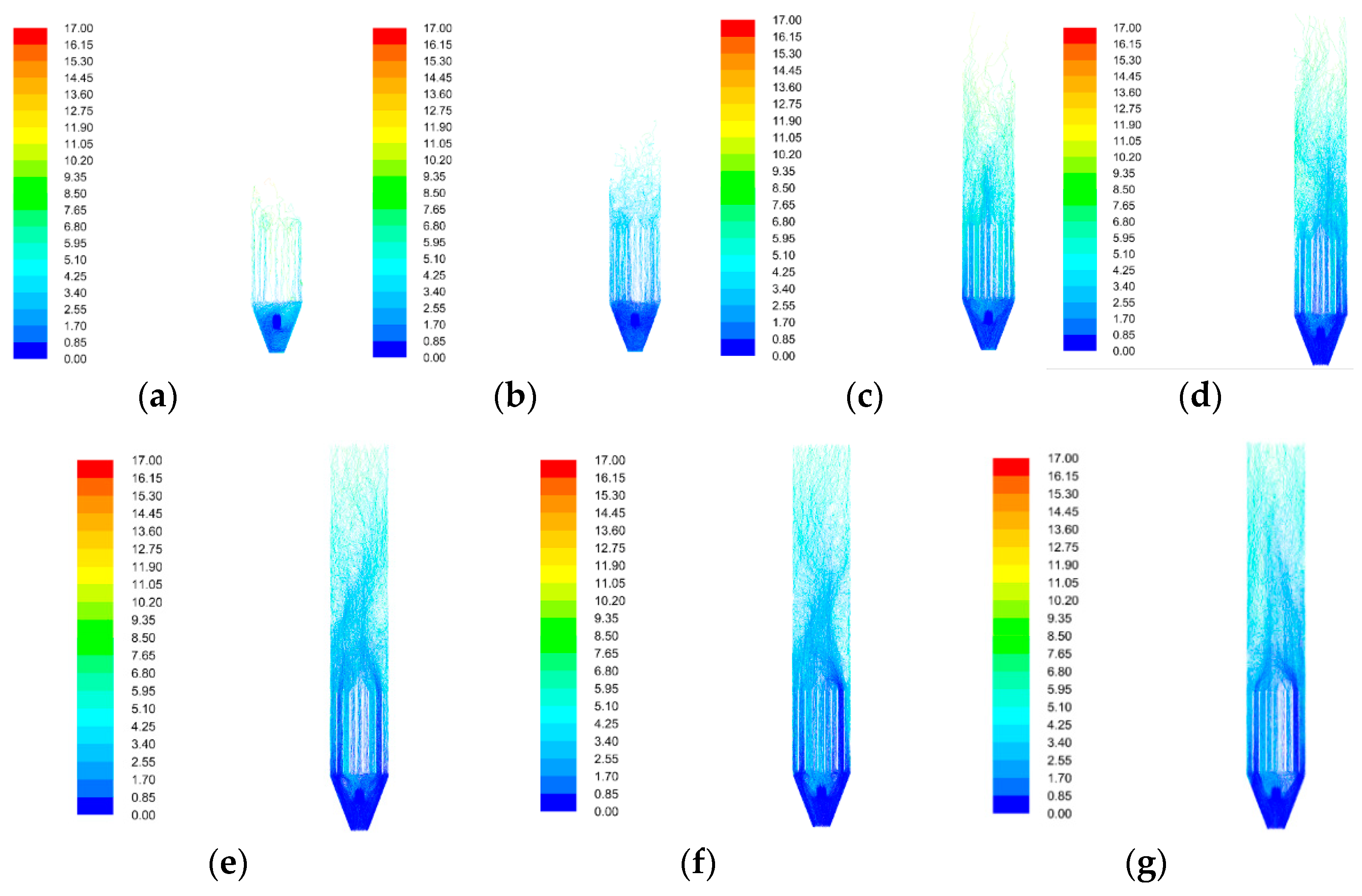
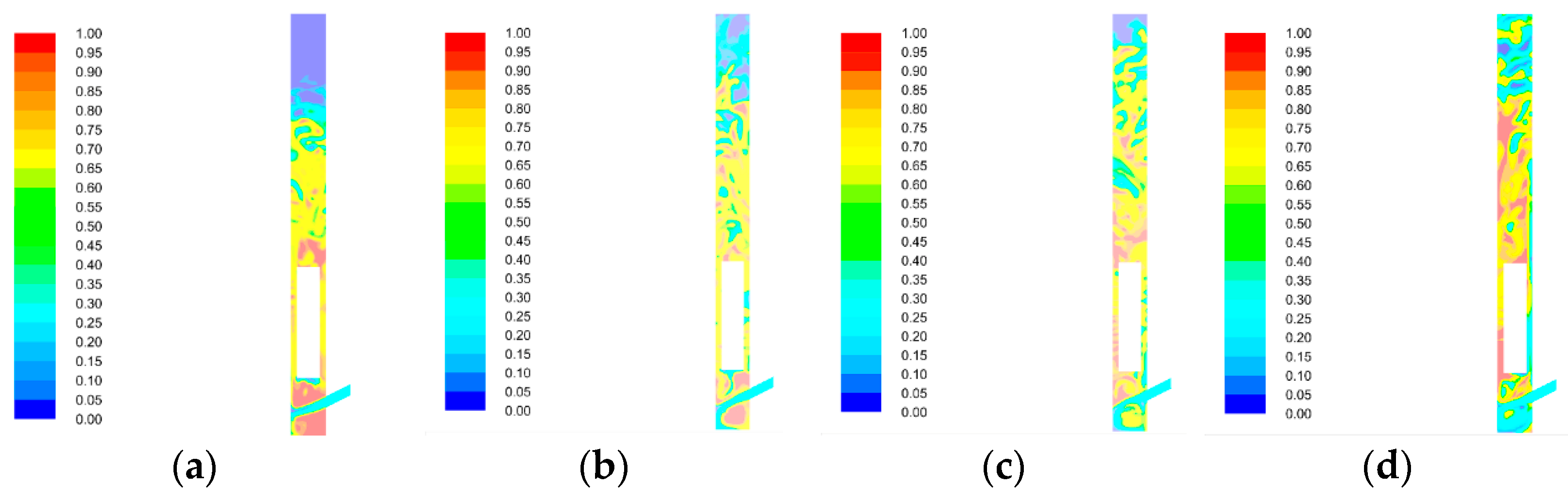
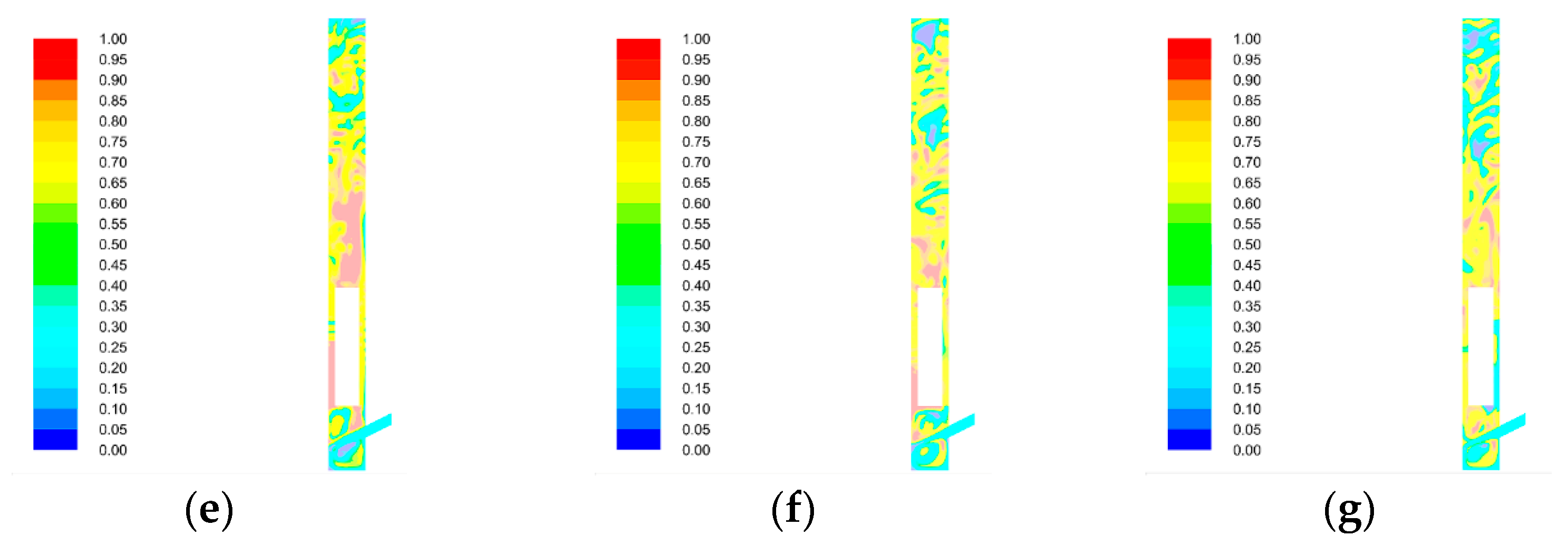
4. Numerical Simulation
Influence of Particle Content on Detecting the Flow Field
5. Analysis of the Experimental Results
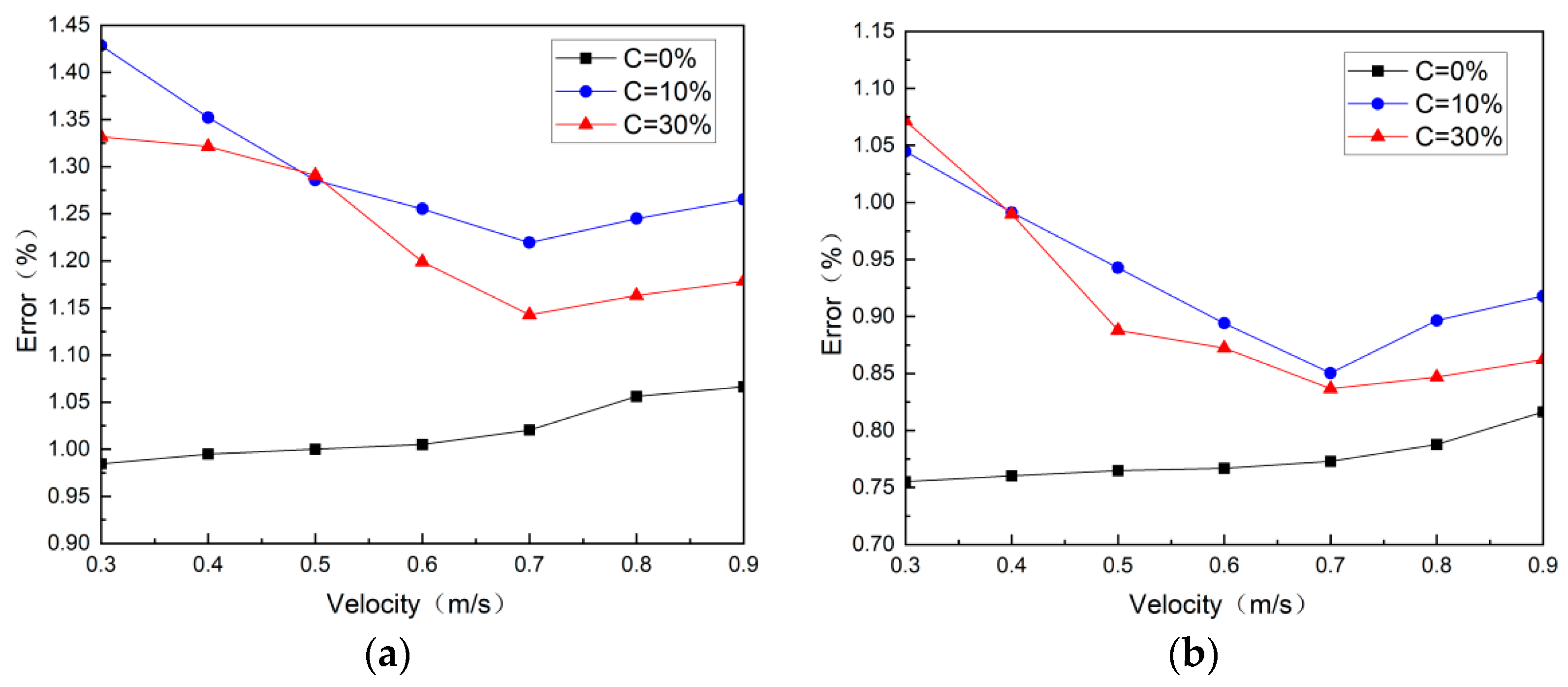
5.1. Research on the Measurement Accuracy of the Detection Device Under Different Pulp Concentrations
5.2. Research on the Measurement Accuracy of Particle Flow to the Detection Device
5.3. Error Analysis and Discussion of Discrepancies
6. Conclusions
- (1)
- The combined fluid simulation and the experimental results confirm that inflow characteristics notably influence the accuracy of pulp concentration measurements. By integrating CFD modeling with a novel interference rectification structure, this study systematically reveals the nonlinear coupling mechanism between flow velocity and turbulence suppression. Numerical simulations indicate that as inflow velocity increases, turbulence in the observation measurement tank decreases, leading to greater particle dispersion and a more uniform distribution. The experimental results further demonstrate that increased inflow velocity enhances dispersion uniformity, thereby reducing measurement error. However, further increases in the flow rates reduce flow field stability and increase dynamic pressure, resulting in higher measurement errors.
- (2)
- The numerical simulations demonstrate that achieving a uniform suspension of solid particles in high-concentration slurries (C = 30%) requires significantly greater inflow velocities (≥0.8 m/s) compared to low-concentration systems. The optimized sensor configuration (No. 2 and No. 4) minimizes boundary turbulence interference by leveraging flow field stability in central regions. The experimental results confirm that higher concentrations lead to lower measurement errors, while fluctuations remain within a reasonable range of approximately 1%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Meng, L.; Shen, X. Study on ultrasonic-electrochemical treatment for difficult-to-settle slime water. Ultrason. Sonochemistry 2020, 64, 104978. [Google Scholar] [CrossRef]
- Ding, S.; Pan, F.; Zhou, S.; Bu, X.; Alheshibri, M. Ultrasonic-assisted flocculation and sedimentation of coal slime water using the Taguchi method. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 10523–10536. [Google Scholar] [CrossRef]
- M, E.V.; M, S.O.; T, M.A. Study of concentrating plants’ coal slurry dewatering. J. Min. Geotech. Eng. 2024, 24. [Google Scholar]
- Муркo, Е.В.; Маркoв, С.О. Тюленев, М.А. ИССЛЕДОВАНИЕ ОБЕЗВОЖИВАНИЯ УГОЛЬНОГО ШЛАМА ОБОГАТИТЕЛЬНЫХ ФАБРИК. ТЕХНИКА 2024, 1, 58–76. [Google Scholar]
- Wu, W.-J.; Zheng, Q.-J.; Liang, J.-W.; Zhao, H.-M.; Liu, B.-L.; Li, Y.-W.; Feng, N.-X.; Cai, Q.-Y.; Xiang, L.; Mo, C.-H.; et al. Mining flotation reagents: Quantitative and robust analysis of metal-xanthate complexes in water. J. Hazard. Mater. 2024, 476, 134873. [Google Scholar] [CrossRef] [PubMed]
- Burdonov, A.E.; Verochkina, E.A.; Rozentsveig, I.B.; Vchislo, N.V. Xanthates and Dithiocarbamates: Synthesis, Characterization and Application in Flotation Processes. Mini-Rev. Org. Chem. 2024, 22, 44–53. [Google Scholar]
- Taşdemir, T.; Taşdemir, A. Modeling and optimization of reagent dosages and pH for efficient floc-flotation of suspended particles in Jameson flotation cell by CCD. J. Water Process Eng. 2023, 55, 104243. [Google Scholar] [CrossRef]
- Duchnowska, M.; Bakalarz, A.; Luszczkiewicz, A. Influence of reagent dose on the flotation selectivity of copper ore from LGOM area (SW Poland). IOP Conf. Ser. Mater. Sci. Eng. 2019, 641, 012016. [Google Scholar] [CrossRef]
- Cao, B.F.; Xie, Y.F.; Yang, C.H.; Gui, W.H.; Li, J.Q. Reagent Dosage Control for the Antimony Flotation Process Based On Froth Size Pdf Tracking and an Index Predictive Model. J. Min. Sci. 2020, 55, 452–468. [Google Scholar] [CrossRef]
- Sun, B.; Chen, S.; Liu, Q.; Lu, Y. Review of sewage flow measuring instruments. Ain Shams Eng. J. 2020, 12, 2089–2098. [Google Scholar] [CrossRef]
- Li, Y.; Peng, S.; Song, Z.; Wang, F. Measurement of two phase flow concentration with a novel pressure difference method. I: Principle. Flow Meas. Instrum. 2024, 97, 102591. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Zhang, J.; Zhou, F.; Chen, A. Measurement of the phosphorite ore pulp density based on the image recognition method. Int. J. Min. Miner. Eng. 2022, 13, 64–75. [Google Scholar] [CrossRef]
- de Aquino, G.S.; Martins, R.S.; Martins, M.F.; Ramos, R. An Overview of Computational Fluid Dynamics as a Tool to Support Ultrasonic Flow Measurements. Metrology 2025, 5, 11. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ.-Sci. A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]
- Tang, H.; Fan, Y.; Ma, X.; Dong, X.; Chang, M.; Li, N. Modelling Flocculation in a Thickener Feedwell Using a Coupled Computational Fluid Dynamics–Population Balance Model. Minerals 2023, 13, 309. [Google Scholar] [CrossRef]
- De Castro, B.; Benzaazoua, M.; Chopard, A.; Plante, B. Automated mineralogical characterization using optical microscopy: Review and recommendations. Miner. Eng. 2022, 189, 107896. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Tang, F.H.; Maggi, F. Optical Measurement of Cell Colonization Patterns on Individual Suspended Sediment Aggregates. J. Geophys. Res. Earth Surf. 2017, 122, 1794–1807. [Google Scholar] [CrossRef]
- Zhang, X.R.; Zhu, Y.G.; Zheng, G.B.; Han, L.; McFadzean, B.; Qian, Z.B.; Piao, Y.C.; O'Connor, C. An investigation into the selective separation and adsorption mechanism of a macromolecular depressant in the galena-chalcopyrite system. Miner. Eng. 2019, 134, 291–299. [Google Scholar] [CrossRef]
- Fu, L.; Bai, H.; Bai, D.; Xu, G. Hydrodynamics of gas-solid fluidization at ultra-high temperatures. Powder Technol. 2022, 406, 117552. [Google Scholar] [CrossRef]
- Dontsov, E.V. A model for proppant dynamics in a perforated wellbore. Int. J. Multiph. Flow 2023, 167, 104552. [Google Scholar] [CrossRef]
- Zhou, H.; Guo, J.; Zhang, T.; Li, M.; Tang, T.; Gou, H. Eulerian multifluid simulations of proppant transport with different sizes. Phys. Fluids 2023, 35, 043314. [Google Scholar]
- Liu, H.; Li, Z.; Wang, C.; Zhang, Q. Impacts of inflow conditions on the measurement stability of a turbulence-mitigation based liquid concentration detection system. Flow Meas. Instrum. 2023, 90, 102337. [Google Scholar] [CrossRef]
- Kawakita, R.; Strobel, S.; Soares, B.; Scher, H.B.; Becker, T.; Dale, D.; Jeoh, T. Fluidized bed spray-coating of enzyme in a cross-linked alginate matrix shell (CLAMshell). Powder Technol. 2021, 386, 372–381. [Google Scholar] [CrossRef]

| Inflow Velocity (m/s) | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|
| ΔP1 | 1.941 | 1.941 | 1.940 | 1.940 | 1.940 | 1.939 | 1.939 |
| ΔP2 | 1.945 | 1.945 | 1.945 | 1.945 | 1.945 | 1.945 | 1.944 |
| Inflow Velocity (m/s) | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|
| ΔP1 | 2.030 | 2.032 | 2.033 | 2.033 | 2.034 | 2.034 | 2.033 |
| ΔP2 | 2.037 | 2.038 | 2.039 | 2.040 | 2.041 | 2.040 | 2.039 |
| Inflow Velocity (m/s) | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|
| ΔP1 | 2.228 | 2.228 | 2.229 | 2.231 | 2.232 | 2.231 | 2.231 |
| ΔP2 | 2.233 | 2.235 | 2.237 | 2.237 | 2.238 | 2.237 | 2.237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Song, P.; Li, Z.; Yang, D. Accuracy Analysis of Slurry Characterization in a Rectifying Liquid Concentration Detection System. Processes 2025, 13, 1421. https://doi.org/10.3390/pr13051421
Wang C, Song P, Li Z, Yang D. Accuracy Analysis of Slurry Characterization in a Rectifying Liquid Concentration Detection System. Processes. 2025; 13(5):1421. https://doi.org/10.3390/pr13051421
Chicago/Turabian StyleWang, Chao, Pengfei Song, Zhiyang Li, and Dong Yang. 2025. "Accuracy Analysis of Slurry Characterization in a Rectifying Liquid Concentration Detection System" Processes 13, no. 5: 1421. https://doi.org/10.3390/pr13051421
APA StyleWang, C., Song, P., Li, Z., & Yang, D. (2025). Accuracy Analysis of Slurry Characterization in a Rectifying Liquid Concentration Detection System. Processes, 13(5), 1421. https://doi.org/10.3390/pr13051421





