Macroscopic Simulation Study on Inhomogeneity of Small Billet Continuous Casting Mold
Abstract
1. Introduction
2. Model Development
3. Results and Discussions
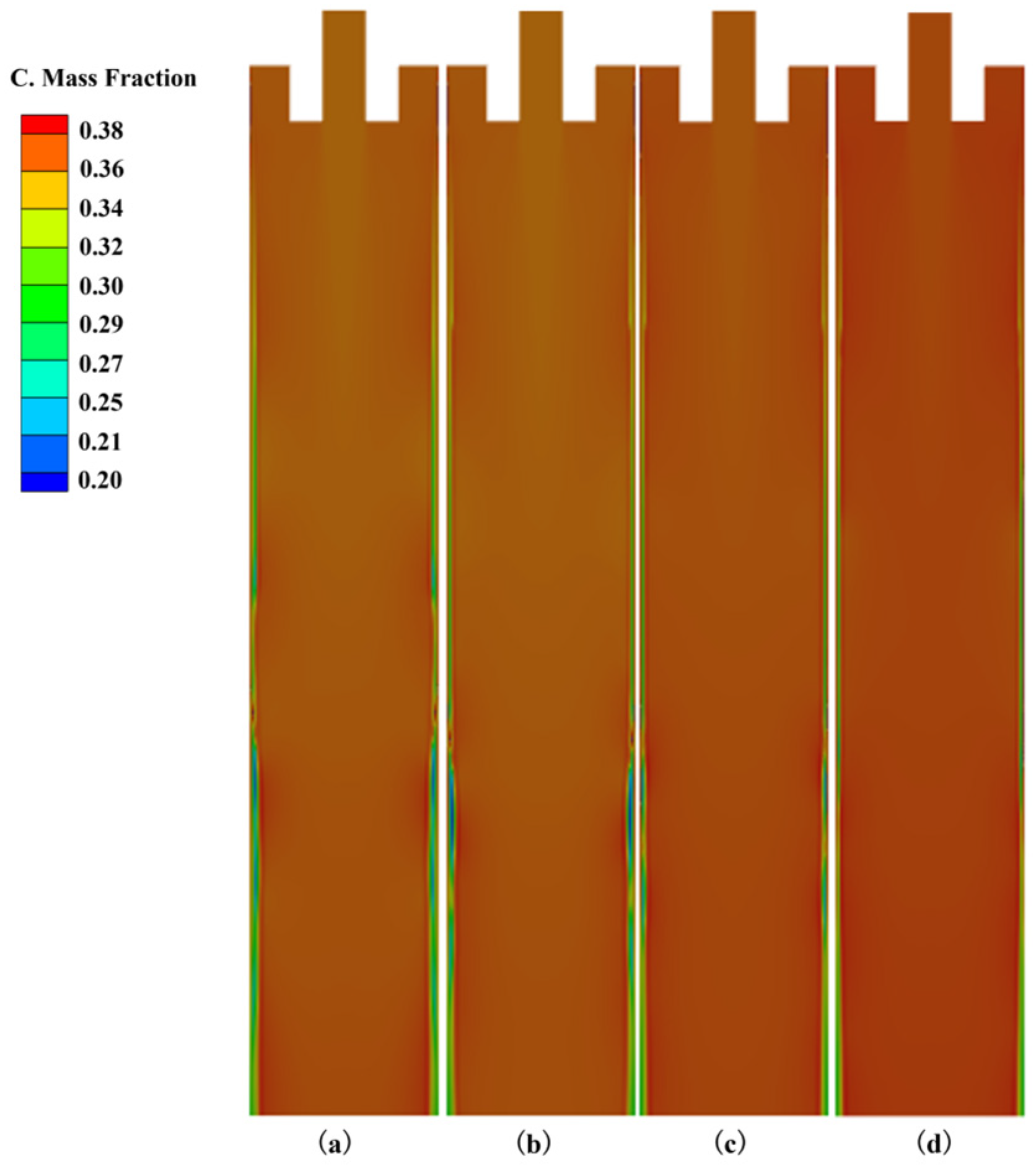
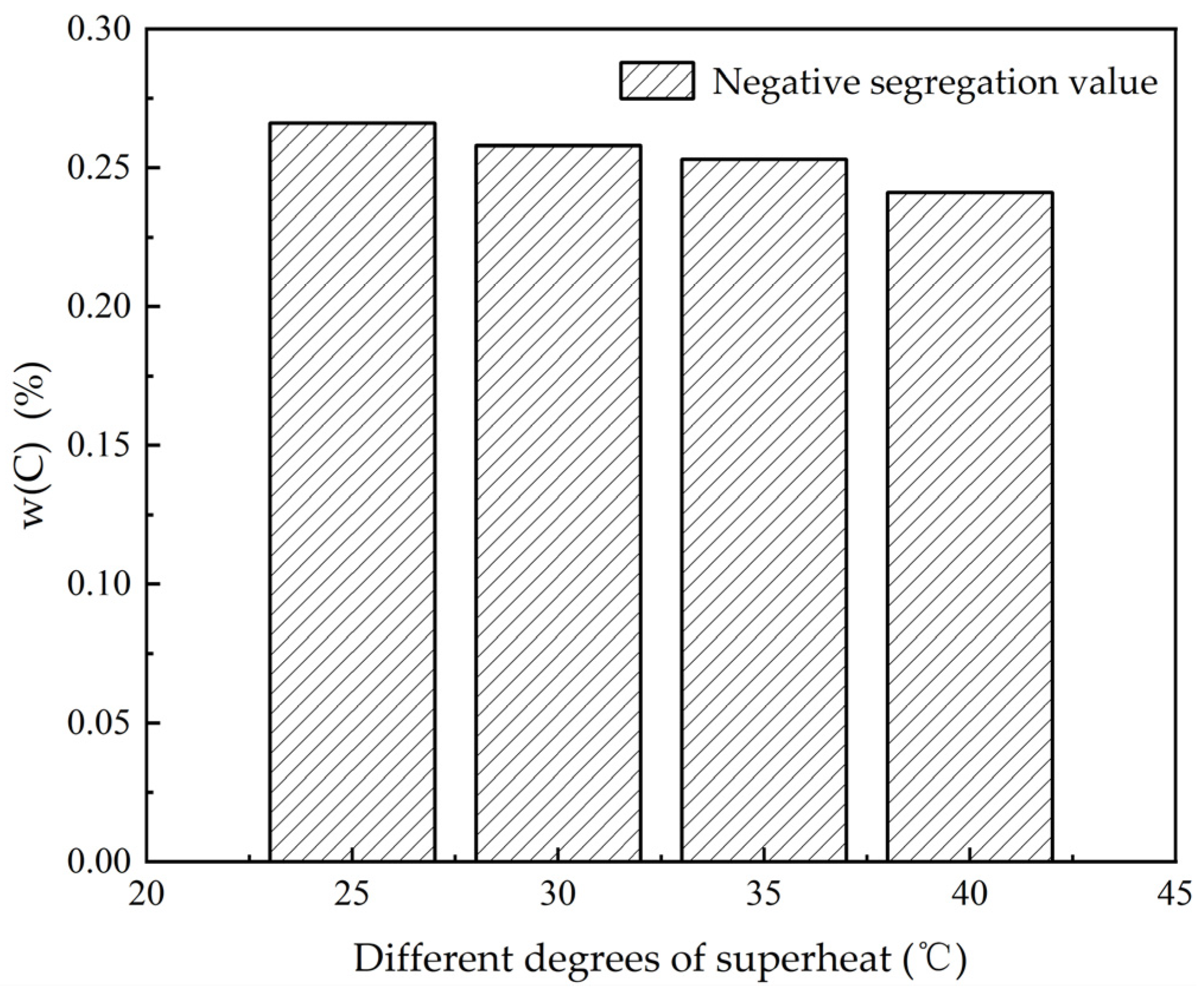
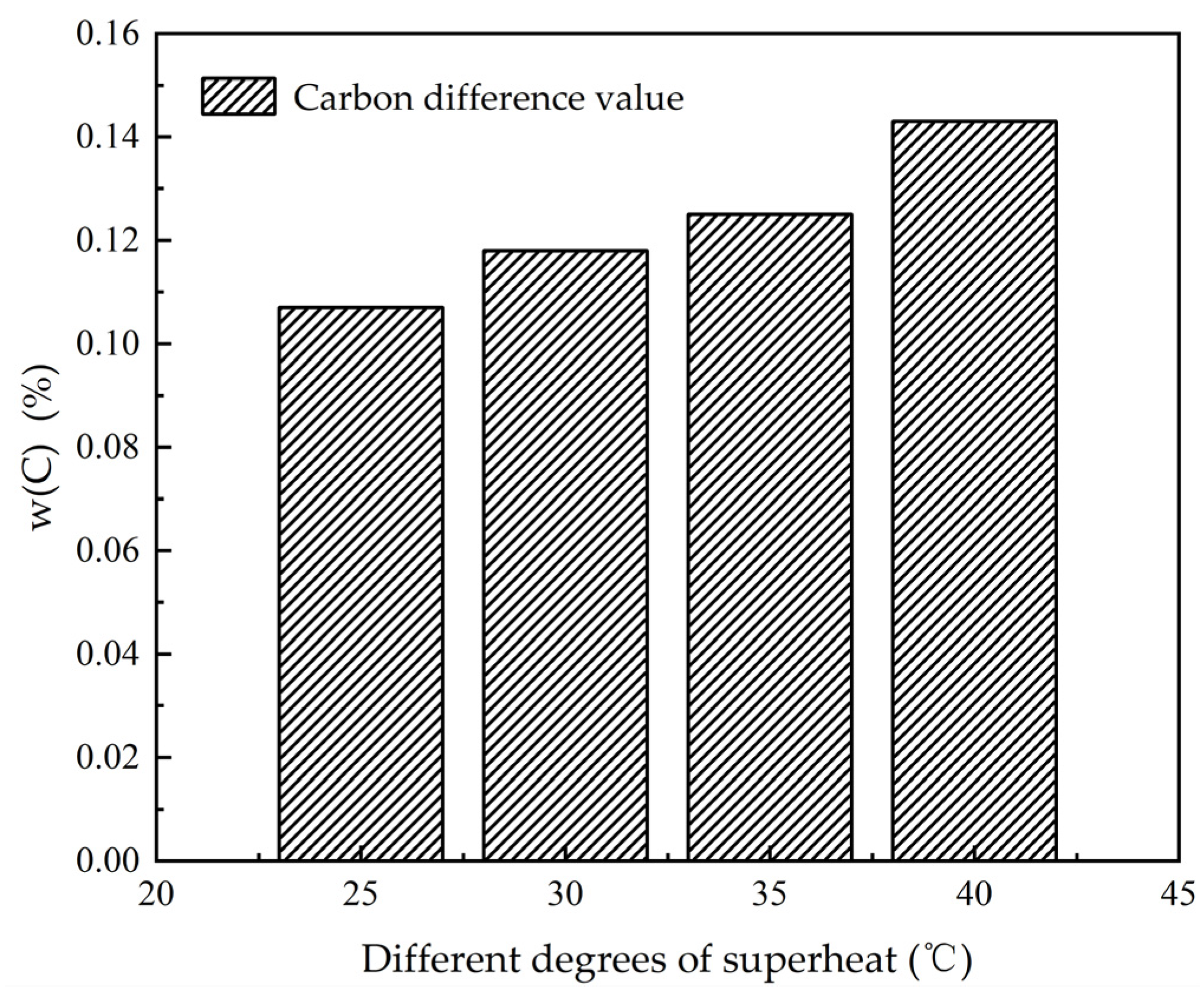
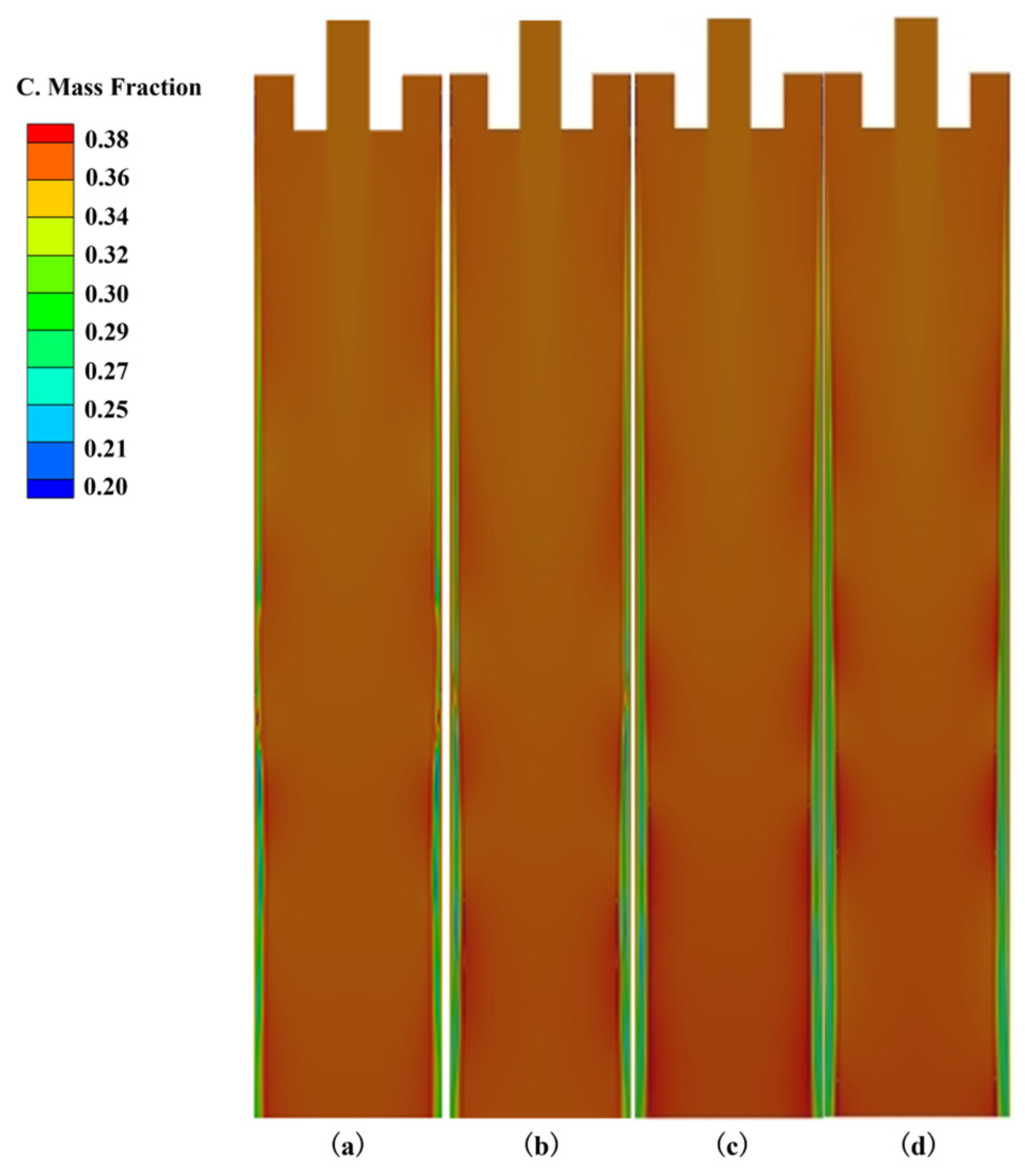
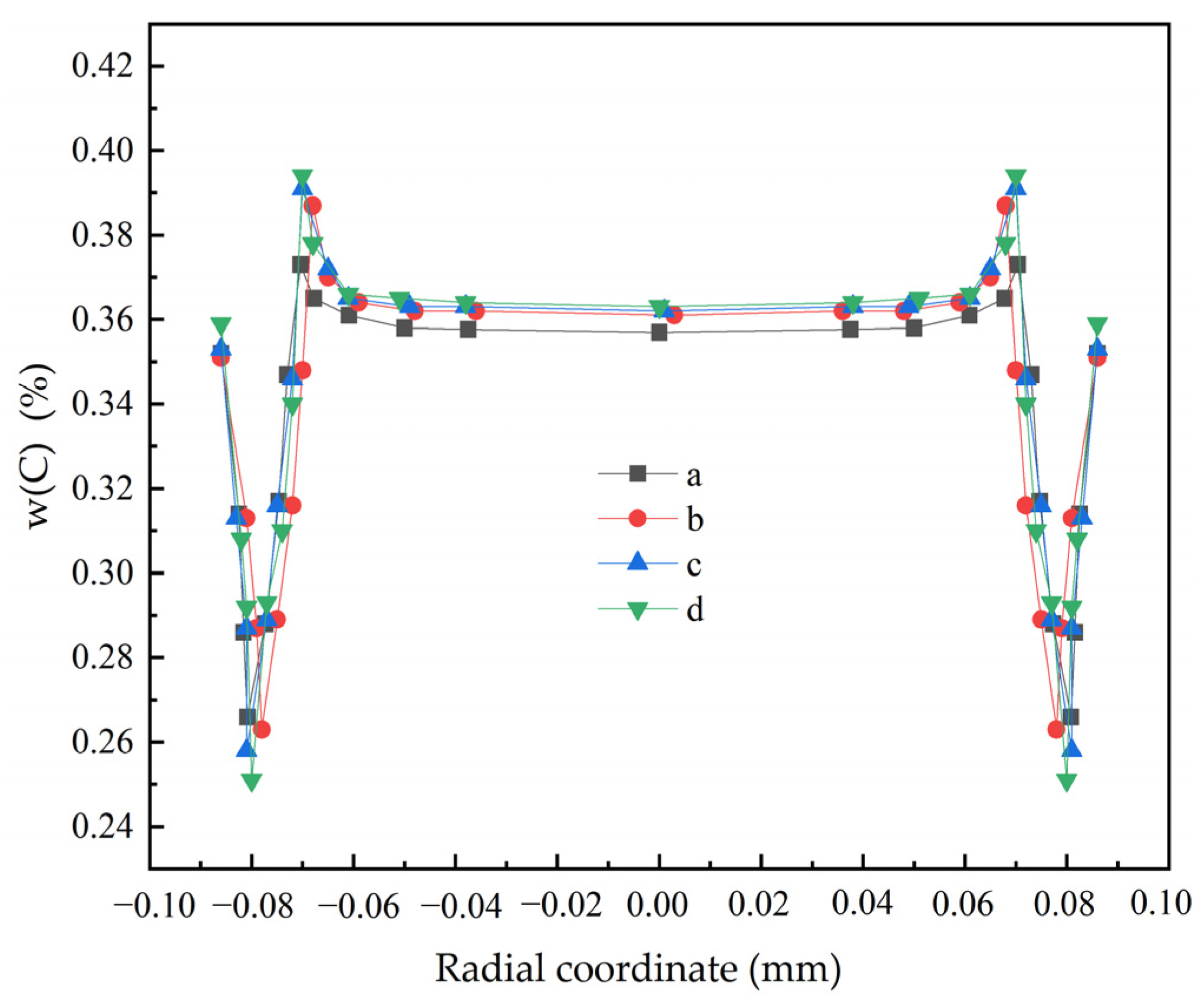
3.1. The Influence of Superheat Degree on Heat Transfer, Solidification and Macroscopic Segregation Phenomena
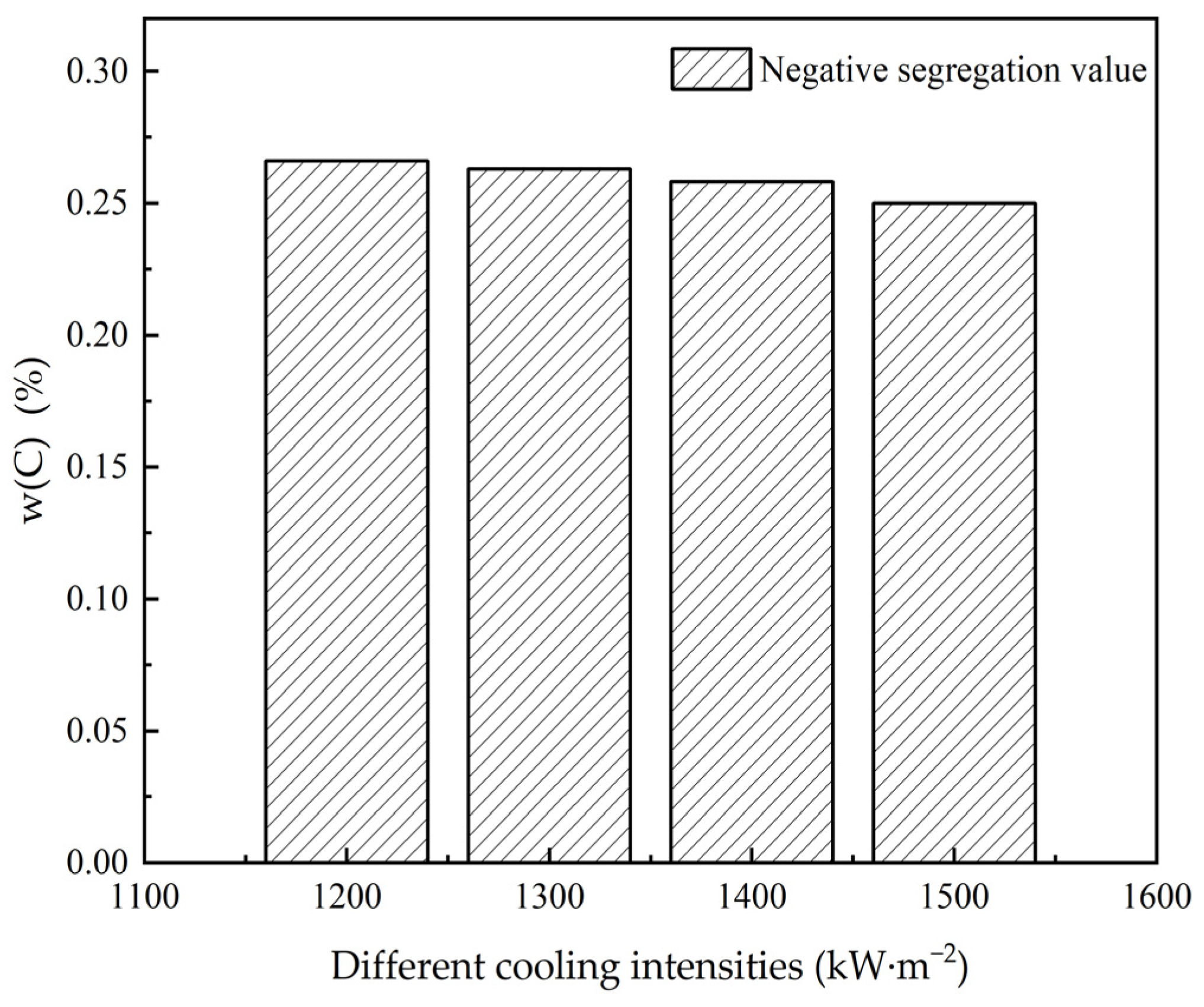
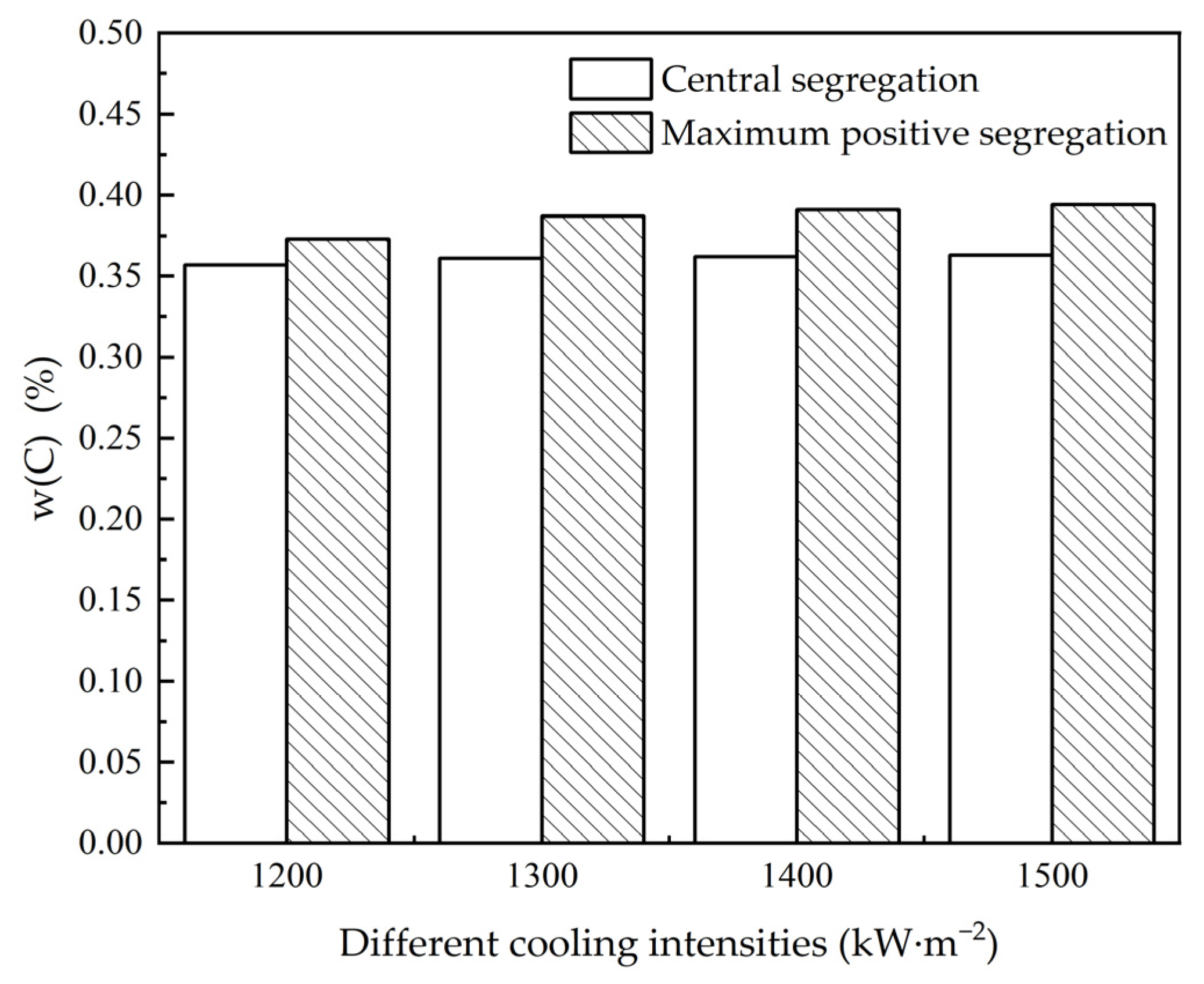
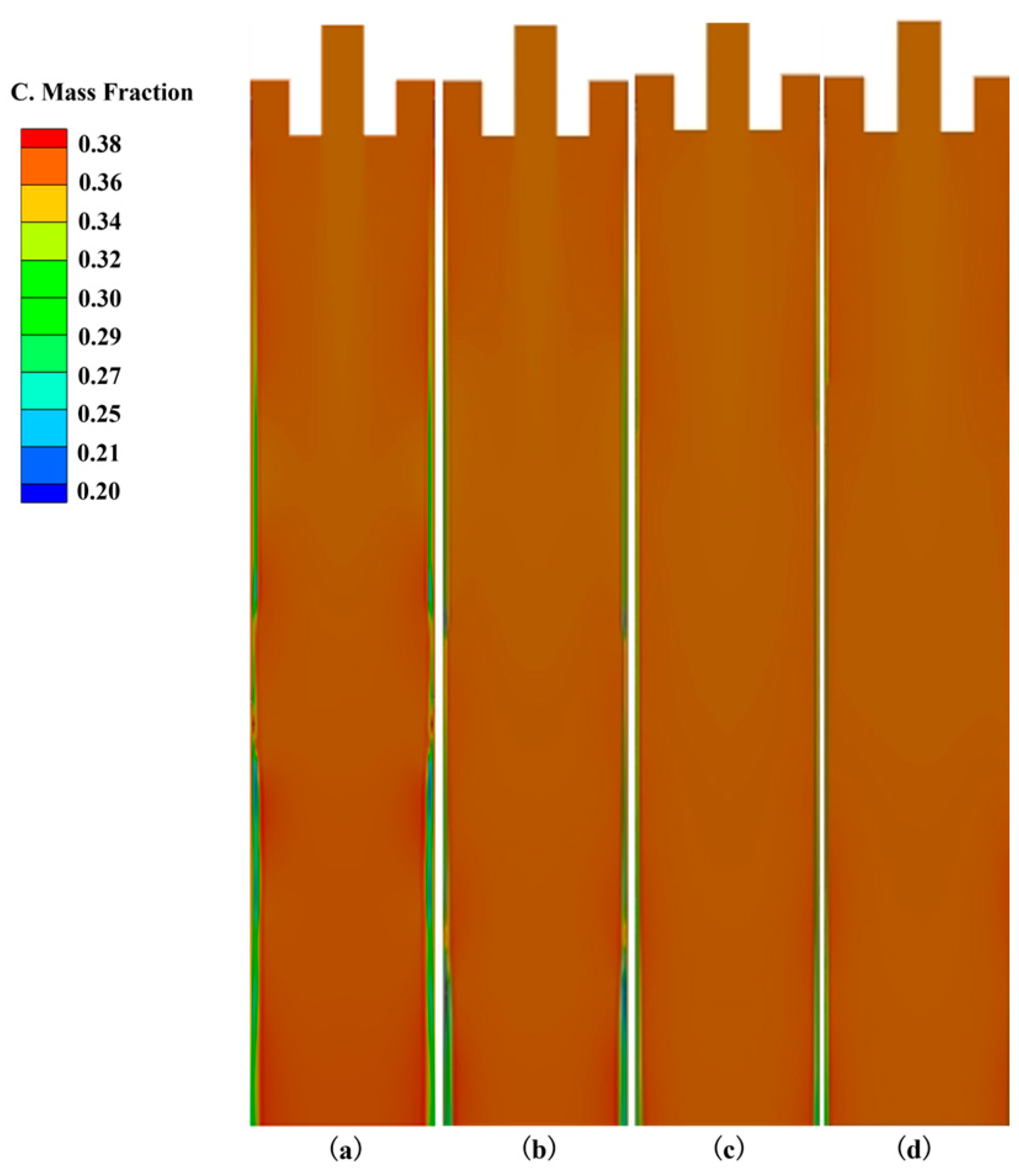
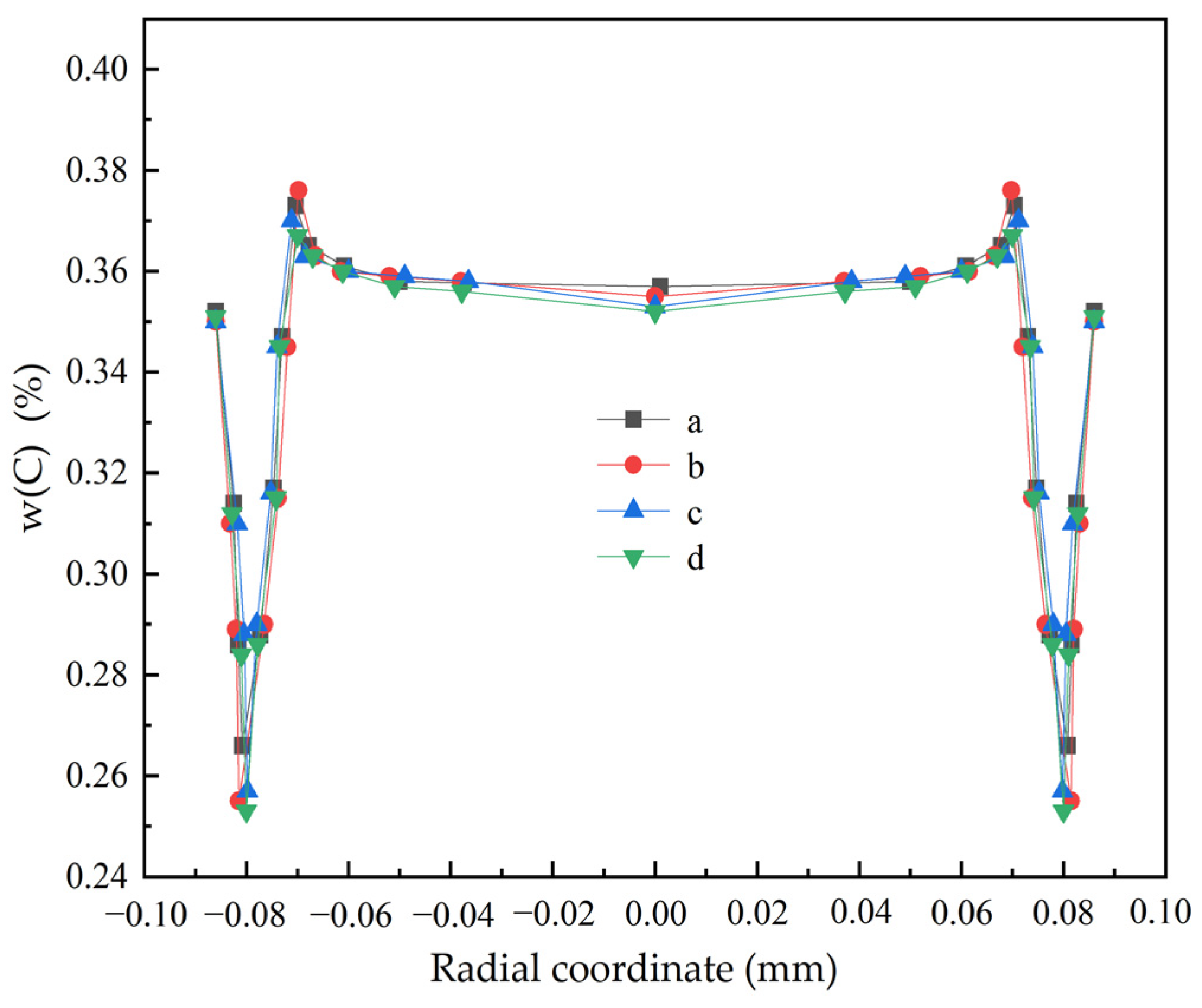
3.2. The Influence of Cooling Intensity on Heat Transfer, Solidification and Macroscopic Segregation Phenomena
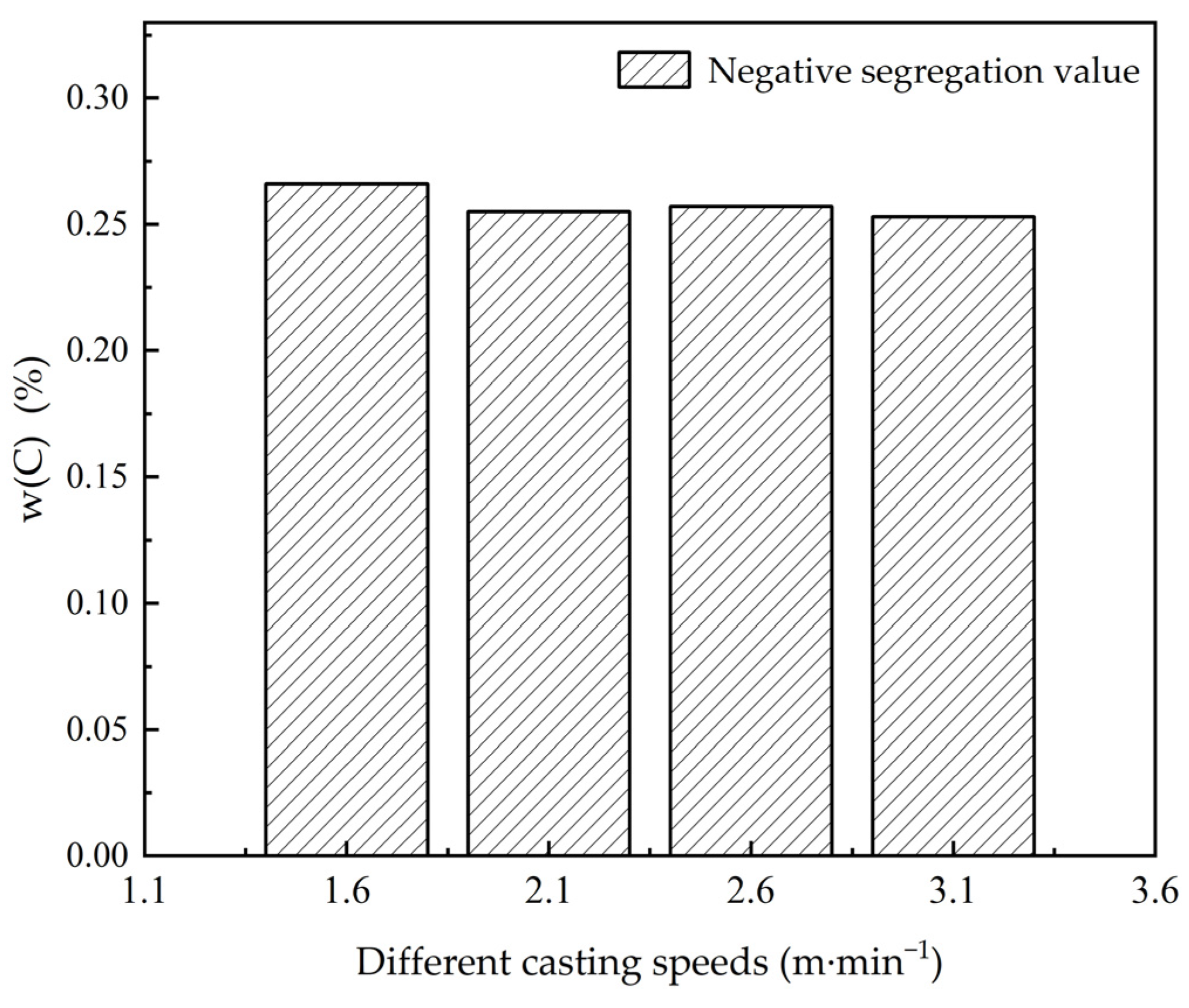
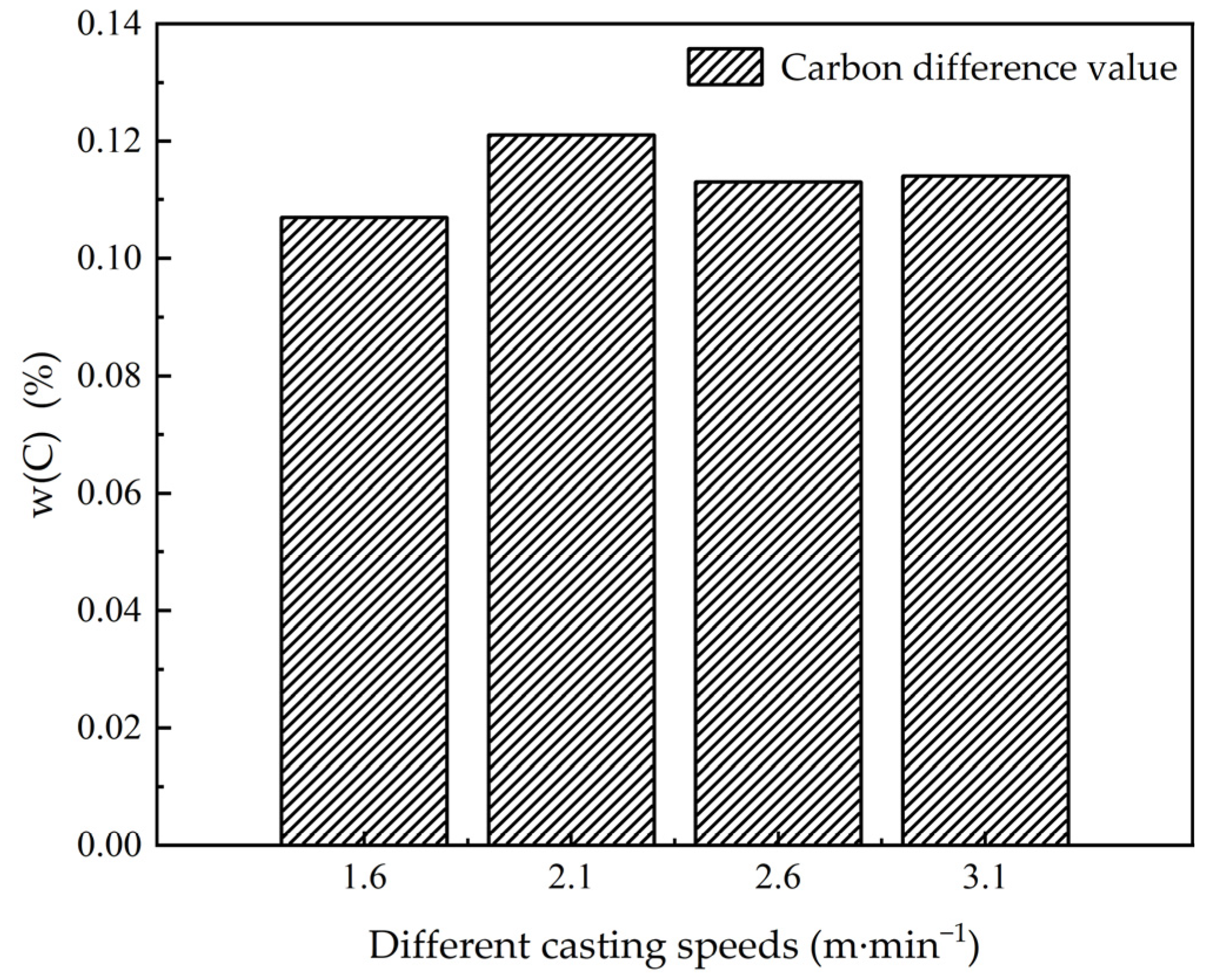
3.3. The Influence of the Casting Speed on Macroscopic Segregation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nian, Y.; Zhang, L.; Zhang, C.; Ali, N.; Chu, J.; Li, J.; Liu, X. Application Status and Development Trend of Continuous Casting Reduction Technology: A Review. Processes 2022, 10, 2669. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Cheng, C.; Lan, P.; Wu, W. Study on Parameter Optimization of Diversion Wall in an Eight-Strand Tundish during Continuous Casting of Billet with High Casting Speed. Processes 2022, 10, 555. [Google Scholar] [CrossRef]
- Pang, X.; Li, H.; Wang, J.; Zhu, L.; Sun, L. Optimization of Billet Tube Mold Designs for High-Speed Continuous Casting. Processes 2023, 11, 3367. [Google Scholar] [CrossRef]
- Wang, G.; Chu, M. Green Steel Metallurgy Technology for Low Carbon Emission Reduction. Sci. Bull. 2020, 38, 68–76. [Google Scholar]
- Xu, L.; Pei, Q.W.; Han, Z.F.; Cui, J.; Pan, H.G.; Yao, Y.T. Influences of the Braking Effect of Ruler EMBr on Molten Steel Flow and Steel–Slag Interface Fluctuation in a Continuous Casting Mold. Processes 2023, 11, 33. [Google Scholar] [CrossRef]
- Paweł, K.; Paweł, S.; Grzegorz, K.; Szymon, K.; Krystian, F.; Michał, S.; Wojciech, Ś.; Anna, B.; Joanna, K.; Barbara, J.; et al. External Surface Quality of the Graphite Crystallizer as a Factor Influencing the Temperature of the Continuous Casting Process of ETP Grade Copper. Materials 2021, 14, 6309. [Google Scholar] [CrossRef]
- Dong, X.; Li, L.; Tang, Z.; Huang, L.; Liu, H.; Liao, D.; Yu, H. The Effect of Continuous Casting Cooling Process on the Surface Quality of Low-Nickel Austenitic Stainless Steel. Steel Res. Int. 2025, 2400957, Early View. [Google Scholar]
- Cho, S.; Thomas, G.B. Thomas. Electromagnetic Forces in Continuous Casting of Steel Slabs. Metals 2019, 9, 471. [Google Scholar] [CrossRef]
- Aboutaleb, M.M.; Lapointe, F.; D’Amours, J.; Isac, M.M.; Guthrie, R. Effects of Angle of Rotation of Submerged Entry Nozzle on Fluid Flows in a Square Billet Casting Mold. J. Met. 2018, 70, 2088–2095. [Google Scholar] [CrossRef]
- Bai, L.; Wang, B.; Zhong, H.G.; Ni, J.; Zhai, Q.J.; Zhang, J.Y. Experimental and Numerical Simulations of the Solidification Process in Continuous Casting of Slab. Metals 2016, 6, 53. [Google Scholar] [CrossRef]
- Ren, L.; Liu, W.; Ling, H.; Yang, J. Study on Multiphase Flow in a Wide-Width Continuous Casting Mold. Processes 2022, 10, 1269. [Google Scholar] [CrossRef]
- Yang, L. “13th Five-Year” key technology progress and thinking of steelmaking in China. Steel 2022, 57, 1–10. [Google Scholar]
- Gao, X.Z.; Yang, S.F.; Li, J.S.; Liao, H. Numerical Simulation on Optimization of Center Segregation for 50CrMo Structural Alloy Steel. High Temp. Mater. Processes. 2016, 35, 583–589. [Google Scholar] [CrossRef]
- Zeng, Q.; Xiao, C.; Li, J.L. Analysis of Micro-Segregation of Solute Elements on the Central Cracking of Continuously Cast Bloom. Metals 2021, 11, 382. [Google Scholar] [CrossRef]
- Song, S.C.; Sun, Y.H.; Wei, Y.H.; Liu, C.L. Control of macrosegregation at the steel gradient transition by submerged entry nozzle and mold electromagnetic stirring. Ironmak. Steelmak. 2024, 51, 675–691. [Google Scholar] [CrossRef]
- Dong, Q.P.; Zhang, J.M.; Liang, Q.; Yin, Y.B. Numerical Modeling of Macrosegregation in Round Billet with Different Microsegregation Models. ISIJ Int. 2017, 57, 814–823. [Google Scholar] [CrossRef]
- Yang, Y.W.; Luo, S.; Wang, W.L.; Zhu, M.Y. Multiphase Solidification Modeling of Solidification Structure Evolution and Macrosegregation of Round Bloom Continuous Casting Process with Mold Electromagnetic Stirring and Final Electromagnetic Stirring. Steel Res. Int. 2023, 95, 2300446. [Google Scholar] [CrossRef]
- Wu, C.L.; Liu, X.M.; Wang, Q.; He, M.; Zhu, X.W.; Li, D.W.; Zhao, J.L.; Hong, L. Macrosegregation Prediction by Evaluating Liquid Level Fluctuation in Round Billet Continuous Casting with Electromagnetic Nozzle Swirling Flow. Metall. Mater. Trans. B 2021, 52, 3571–3575. [Google Scholar] [CrossRef]
- Kengo, K.; Nobuhiro, O.; Shun, S.; Kento, K. Numerical Simulation of Macrosegregation in a Continuous Casting Mold with Electromagnetic Stirring. ISIJ Int. 2022, 62, 1862–1873. [Google Scholar]
- Guan, R.; Cheng, J.; Zhu, M.Y.; Deng, S.M. Numerical simulation of v-shaped segregation in continuous casting blooms based on a microsegregation model. Metall. Mater. Trans. B 2018, 49, 2571–2583. [Google Scholar] [CrossRef]
- Zhang, C.P.; Loucif, A.; Jahazi, M.; Morin, J.B. FEM Simulation of the Effect of Mold Initial Temperature on Carbon Macrosegregation in Large-Size Steel Ingots. Mater. Sci. Forum. 2022, 6351258–6351263. [Google Scholar] [CrossRef]
- Ma, H.T.; Zhang, J.M.; Yin, Y.B.; Yan, Z.Z.; Liu, H.Y. Numerical simulation on the centre macrosegregation during Billet continuous casting with the soft reduction. Ironmak. Steelmak. 2022, 49, 887–897. [Google Scholar] [CrossRef]
- Zhao, X.K.; Zhang, J.M.; Lei, S.W.; Wang, Y.N. The position study of heavy reduction process for improving centerline segregation or porosity with extra-thickness slabs. Steel Res. Int. 2014, 85, 645–658. [Google Scholar] [CrossRef]
- Chen, H.B.; Long, M.J.; Chen, D.F.; Liu, T.; Duan, H.M. Numerical study on the characteristics of solute distribution and the formation of centerline segregation in continuous casting (CC) slab. Int. J. Heat Mass Transf. 2018, 126, 843–853. [Google Scholar] [CrossRef]
- Qiao, T.H.; Wang, S.; Guan, R.; Zhu, X.L.; Ai, X.G.; Ji, Y.; Li, S.L. A Numerical Investigation into the Effect of Thermal Shrinkage and Solidification Shrinkage on the Microstructure and Macrosegregation for Continuous Casting Billet. Metall. Mater. Trans. B 2024, 55, 3663–3678. [Google Scholar] [CrossRef]
- Xu, L.; Pei, Q.W.; Han, Z.F.; Yang, S.; Wang, J.Y.; Yao, Y.T. Modeling Study on Melt Flow, Heat Transfer, and Inclusion Motion in the Funnel-shaped Molds for Two Thin-Slab Casters. Processes 2022, 10, 2738. [Google Scholar] [CrossRef]
- Dong, Q.D.; Zhang, J.M.; Yin, Y.B.; Wang, B. Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets. Metals 2017, 7, 209. [Google Scholar] [CrossRef]
- Gao, Y.B.; Bao, Y.P.; Wang, M.; Zhang, M.Y. On the Macrosegregation of Continuous Casting of High Carbon Steel Billet with Strand Reduction Process. Metals 2024, 14, 157. [Google Scholar] [CrossRef]
- Peng, J.; Yang, J.; Zhang, T.; Xu, G.J.; Liu, H.J.; Zhou, J.J.; Qin, W. Optimization of Flow Field in Slab Continuous Casting Mold with Medium Width Using High Temperature Measurement and Numerical Simulation for Automobile Exposed Panel Production. Metals 2019, 10, 9. [Google Scholar] [CrossRef]
- Li, X.L.; Li, B.K.; Liu, Z.Q.; Niu, R.; Liu, Y.Q.; Zhao, C.L.; Huang, C.D.; Qiao, H.S.; Yuan, T.X. Large Eddy Simulation of Multi-Phase Flow and Slag Entrapment in a Continuous Casting Mold. Metals 2018, 9, 7. [Google Scholar] [CrossRef]
- Qiu, D.J.; Zhang, Z.H.; Li, X.T.; Lv, M.; Xi, X.F. Numerical Simulation of the Flow Field in an Ultrahigh-Speed Continuous Casting Billet Mold. Metals 2023, 13, 964. [Google Scholar] [CrossRef]
- Wang, W.; Hou, Z.B.; Chang, Y.; Cao, J.H. Effect of superheat on quality of central equiaxed grain zone of continuously cast bearing steel billet based on two-dimensional segregation ratio. J. Iron Steel Res. Int. 2018, 25, 9–18. [Google Scholar] [CrossRef]
- Zhang, C.; Jahazi, M.; Tremblay, R. Simulation and experimental validation of the effect of superheat on macrosegregation in large-size steel ingots. Int. J. Adv. Manuf. Technol. 2020, 107, 167–175. [Google Scholar] [CrossRef]
- Pan, D.; Zhong, H.G.; Guo, Q.T.; Li, Y.T.; Xiao, Y.B.; Zhang, K.L. Research on solidification behavior of a high Mn steel during continuous casting based on solidification characteristic unit analysis. Mater. Lett. 2022, 327, 133028. [Google Scholar] [CrossRef]
- Jiang, D.B.; Zhang, L.F.; Wang, Y.D. Effect of mold electromagnetic stirring on solidification structure and solute segregation in continuous casting bloom. J. Iron Steel Res. Int. 2022, 29, 124–131. [Google Scholar] [CrossRef]
- Ma, H.T.; Zhang, J.M.; Cheng, R.; Wang, S.X. Numerical Simulation Study on Quality Control of the Center Macroscopic Segregation in the Continuous Casting Slab. Trans. Indian Inst. Met. 2019, 72, 825–835. [Google Scholar] [CrossRef]
- Zhong, H.G.; Wang, R.J.; Han, Q.Y.; Fang, M.T.; Yuan, H.Z.; Song, L.X.; Xie, X.; Zhai, Q.J. Solidification structure and central segregation of 6Cr13Mo stainless steel under simulated continuous casting conditions. J. Mater. Res. Technol. 2022, 20, 3408–3419. [Google Scholar] [CrossRef]
- Fang, X.; Yang, Y.G.; Mu, W.Z.; Yang, X.Y.; Zhang, H.L.; Mi, Z.L. Effects of the superheating degree and cooling intensity on the as-cast microstructure of CP780 thin slab. Int. J. Cast Met. Res. 2023, 36, 9–17. [Google Scholar] [CrossRef]
- Wang, F.K.; He, H.; Wang, W.L.; Zhang, L.; Chen, J.X.; Du, J.; Zeng, J. Effect of mold cooling intensity on the depression-type crack formation and mold flux infiltration during continuous casting process. Metall. Mater. Trans. B 2023, 54, 9. [Google Scholar] [CrossRef]
- Chen, G.; Li, J.T.; Yin, Z.K.; Xu, G.M. Improvement of microstructure and properties in twin-roll casting 7075 sheet by lower casting speed and compound field. Ceram. Mater. 2017, 127, 325–332. [Google Scholar] [CrossRef]
- An, H.H.; Bao, Y.P.; Wang, M.; Yang, Q.; Dang, Y.Y. Numerical and experimental investigation of solidification structure evolution and reduction of centre segregation in continuously cast GCr15 bloom. Ironmak. Steelmak. 2020, 47, 1063–1077. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, J.Q.; Yao, Z.W.; Liu, F.Z.; Dong, Q.P.; Nagaumi, H. Effect of casting speed on floating grains in direct-chill casting of aluminum alloys. Mater. Trans. 2023, 64, 2039–2314. [Google Scholar] [CrossRef]
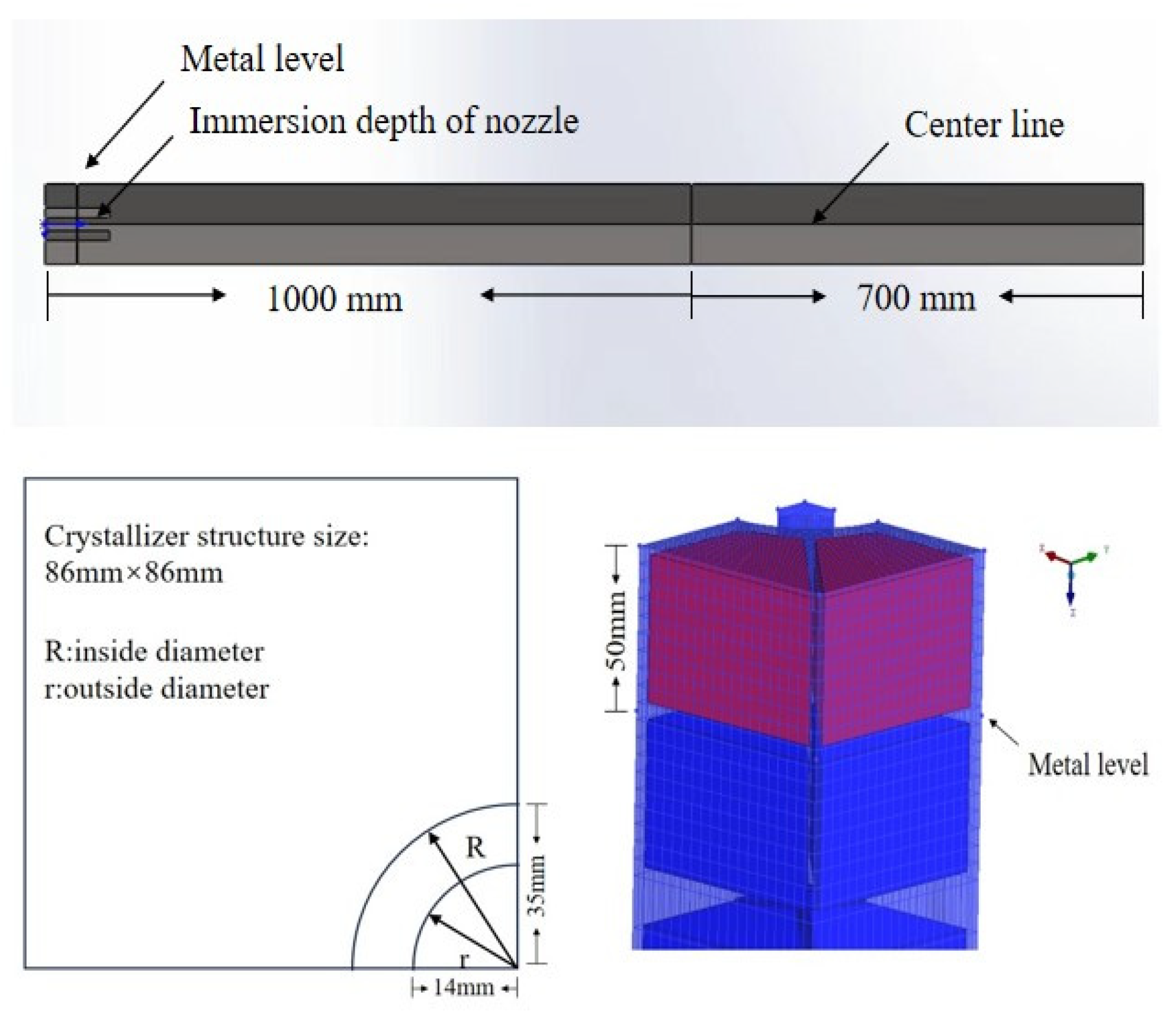

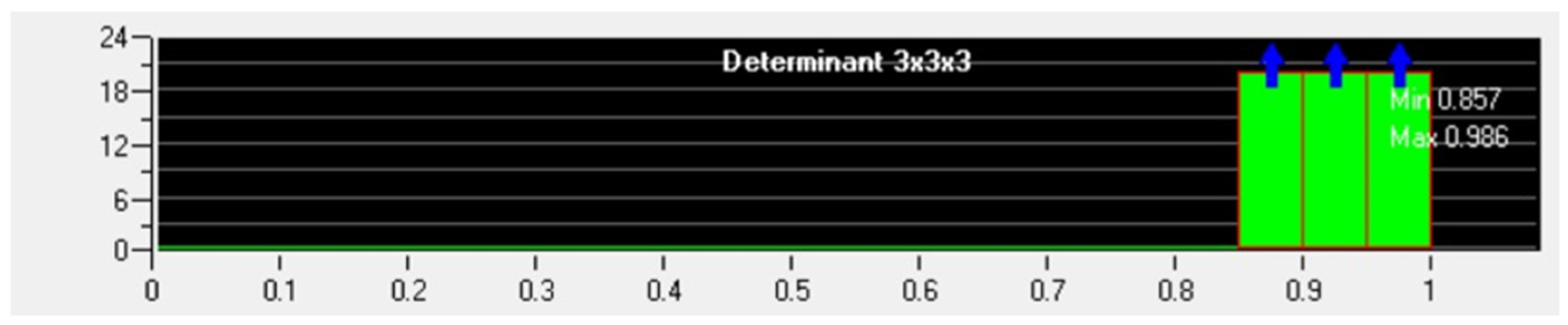

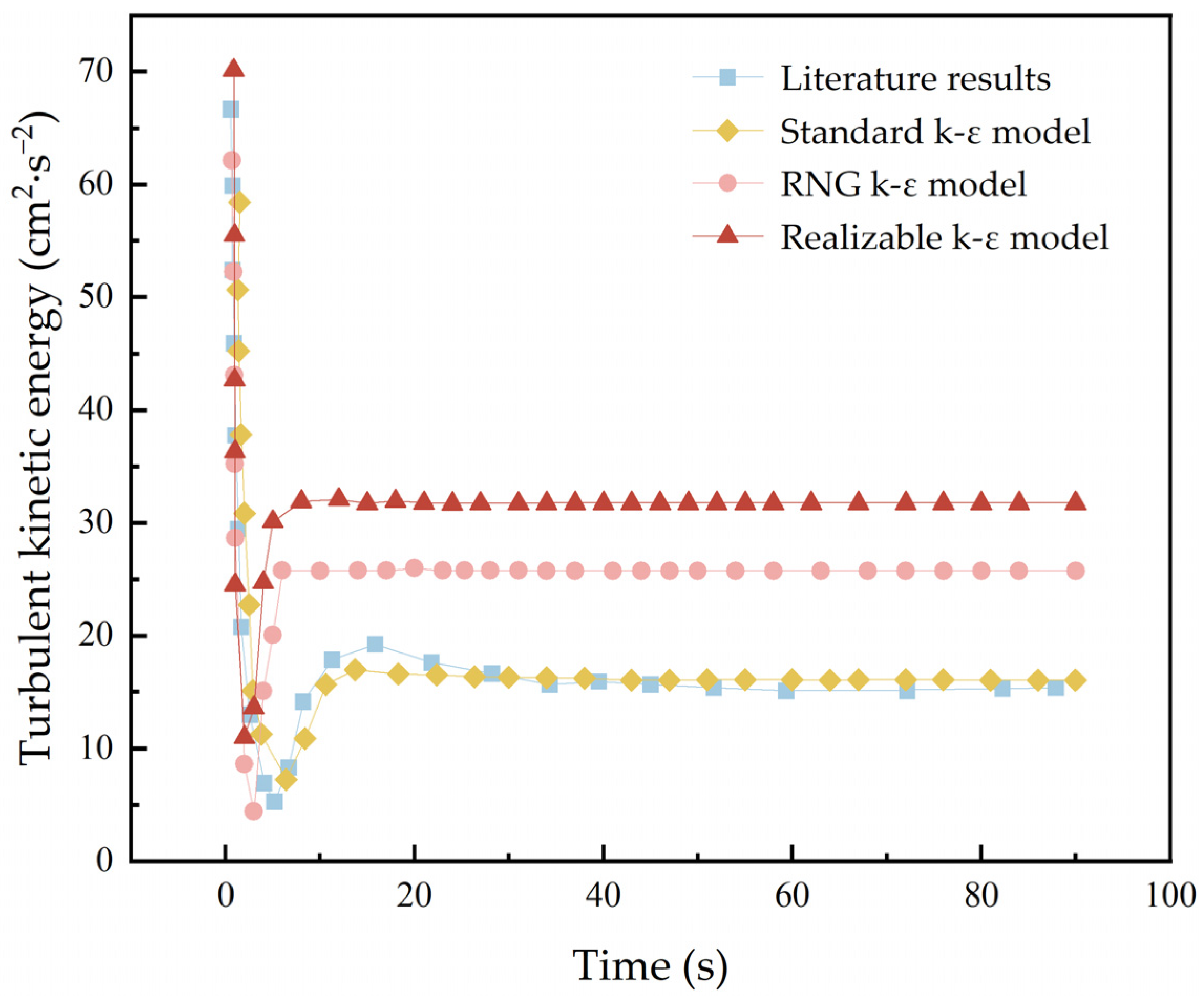




| Simulation Parameters | Values |
|---|---|
| Mold dimension | 172 mm × 172 mm |
| Mold length | 1000 mm |
| The inner diameter | 14 mm |
| Extended length | 700 mm |
| Viscosity | 0.0065 Pa·s |
| Density | 7050 kg·m−3 |
| Specific heat | 700 J·(kg−1·K−1) |
| Latent heat of solidification | 270,000 J·kg |
| Solidus temperature | 1703 K |
| Liquidus temperature | 1754 K |
| Case | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Maximum size/mm | 4 | 6 | 8 | 10 | 12 |
| Gird number/10,000 | 100 | 61 | 30 | 24 | 19 |
| Superheat Degrees (°C) | Cooling Intensities (kW·m−2) | Casting Speeds (m·min−1) | Negative Segregation Value (%) | Central Segregation Value (%) | Maximum Positive Segregation Value (%) | Carbon Difference Value (%) | Cn/Co | Cc/Co | Cm/Co |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 1200 | 1.6 | 0.266 | 0.357 | 0.373 | 0.107 | 0.76 | 1.02 | 1.07 |
| 30 | 1200 | 1.6 | 0.258 | 0.359 | 0.374 | 0.118 | 0.74 | 1.03 | 1.07 |
| 35 | 1200 | 1.6 | 0.253 | 0.360 | 0.3745 | 0.125 | 0.72 | 1.03 | 1.07 |
| 40 | 1200 | 1.6 | 0.241 | 0.364 | 0.375 | 0.143 | 0.69 | 1.04 | 1.07 |
| Superheat Degrees (°C) | Cooling Intensities (kW·m−2) | Casting Speeds (m·min−1) | Negative Segregation (%) | Central Segregation Value (%) | Maximum Positive Segregation Value (%) | Carbon Difference Value (%) | Cn/Co | Cc/Co | Cm/Co |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 1200 | 1.6 | 0.266 | 0.357 | 0.373 | 0.107 | 0.76 | 1.02 | 1.07 |
| 25 | 1300 | 1.6 | 0.263 | 0.361 | 0.387 | 0.124 | 0.75 | 1.03 | 1.11 |
| 25 | 1400 | 1.6 | 0.258 | 0.362 | 0.391 | 0.133 | 0.74 | 1.03 | 1.12 |
| 25 | 1500 | 1.6 | 0.250 | 0.363 | 0.394 | 0.144 | 0.71 | 1.04 | 1.13 |
| Superheat Degrees (°C) | Cooling Intensities (kW·m−2) | Casting Speeds (m·min−1) | Negative Segregation (%) | Central Segregation Value (%) | Maximum Positive Segregation Value (%) | Carbon Difference Value (%) | Cn/Co | Cc/Co | Cm/Co |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 1200 | 1.6 | 0.266 | 0.357 | 0.373 | 0.107 | 0.76 | 1.02 | 1.07 |
| 25 | 1200 | 2.1 | 0.255 | 0.355 | 0.376 | 0.121 | 0.73 | 1.01 | 1.07 |
| 25 | 1200 | 2.6 | 0.257 | 0.353 | 0.370 | 0.113 | 0.73 | 1.01 | 1.06 |
| 25 | 1200 | 3.1 | 0.253 | 0.370 | 0.367 | 0.114 | 0.72 | 1.06 | 1.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Li, Z.; Han, S.; Kou, H.; Huang, X.; Liang, J.; Xue, Y.; Wang, S.; Yao, X. Macroscopic Simulation Study on Inhomogeneity of Small Billet Continuous Casting Mold. Processes 2025, 13, 1415. https://doi.org/10.3390/pr13051415
Ding Z, Li Z, Han S, Kou H, Huang X, Liang J, Xue Y, Wang S, Yao X. Macroscopic Simulation Study on Inhomogeneity of Small Billet Continuous Casting Mold. Processes. 2025; 13(5):1415. https://doi.org/10.3390/pr13051415
Chicago/Turabian StyleDing, Zhijun, Zisheng Li, Shaohui Han, Hanwen Kou, Xing Huang, Jiabao Liang, Yuekai Xue, Shuhuan Wang, and Xin Yao. 2025. "Macroscopic Simulation Study on Inhomogeneity of Small Billet Continuous Casting Mold" Processes 13, no. 5: 1415. https://doi.org/10.3390/pr13051415
APA StyleDing, Z., Li, Z., Han, S., Kou, H., Huang, X., Liang, J., Xue, Y., Wang, S., & Yao, X. (2025). Macroscopic Simulation Study on Inhomogeneity of Small Billet Continuous Casting Mold. Processes, 13(5), 1415. https://doi.org/10.3390/pr13051415






