1. Introduction
In robotic manufacturing systems, the absolute positioning accuracy of industrial robots plays a critical role in the implementation of offline programming. However, due to inherent kinematic errors in the robot body, discrepancies often arise between the theoretical kinematic model and the actual robot behavior [
1]. These errors may result from various sources, such as geometric machining inaccuracies during production, misalignments during assembly, and component wear or deformation over extended periods of operation [
2]. Collectively, these factors contribute to positional deviations during task execution, thereby compromising the overall precision and stability of the robotic system. To improve the positioning accuracy of industrial robots in real-world working environments, kinematic parameter calibration has emerged as a key approach [
3]. This process typically involves four main steps: (1) establishing a mathematical model of the robot’s kinematics; (2) acquiring actual end-effector pose data using sensors or external measurement systems; (3) identifying parameter errors, often by applying optimization algorithms to estimate a parameter set that best matches the observed kinematic; and (4) compensating for the identified model errors to enhance the accuracy of the kinematic model [
4].
Based on the established error model, parameter identification typically involves constructing a multi-parameter optimization objective function, which can be solved using either traditional optimization methods or intelligent optimization algorithms [
5]. Conventional approaches, such as the Least Squares Method [
6], Levenberg–Marquardt (LM) algorithm [
7], extended Kalman filter (EKF) [
8], and maximum likelihood estimation [
9], are often affected by the singularity of the Jacobian matrix and the sensitivity to initial values [
10]. Moreover, their performance deteriorates significantly when dealing with nonlinear, high-dimensional, and ill-conditioned calibration problems, which are common in industrial robot applications. In contrast, intelligent optimization algorithms offer effective solutions to these limitations. In recent years, an increasing number of researchers have employed such algorithms for kinematic parameter calibration of industrial robots, demonstrating promising results. Khanesar et al. [
11] used intelligent swarm algorithms, such as the artificial bee colony, to calibrate industrial robot DH parameters, improving forward kinematics accuracy by 20.3%. Bastl et al. [
12] proposed a robot calibration method using a multi-objective deep-learning evolutionary algorithm optimized by cRVEA, demonstrating improved robustness to measurement noise. Chen et al. [
13] developed an improved beetle swarm optimization algorithm with a preference random substitution strategy for kinematic calibration of industrial robots, enhancing positioning accuracy by over 60% compared to traditional methods. Chen et al. [
14] utilized a hybrid evolutionary scheme (HOEs) combining multiple evolutionary computing algorithms with a sequential ensemble strategy, memory mechanism, and punishment system, achieving superior performance in industrial robot kinematic calibration. Fan et al. [
15] adopted a combined Levenberg–Marquardt and beetle antennae search algorithm to calibrate kinematic parameter errors, significantly enhancing the positioning accuracy of industrial robots. Each intelligent optimization algorithm employs its own unique optimization mechanism. However, existing methods still face limitations such as slow convergence and vulnerability to local optima. Therefore, it is necessary to propose an improved intelligent optimization algorithm to further enhance the accuracy and robustness of industrial robot kinematic parameter calibration.
In 2024, Tian et al. [
16] proposed the snow geese algorithm (SGA), demonstrating superior performance over classical algorithms such as particle swarm optimization (PSO) and differential evolution (DE) in terms of solution accuracy and convergence speed for benchmark optimization problems, and successfully applied it to practical engineering problems including tubular column design, piston lever optimization, reinforced concrete beam design, and car side impact design. However, when applied to the kinematic calibration of industrial robots, the Snow Geese Algorithm (SGA) suffers from a significant imbalance between global exploration and local exploitation capabilities. This imbalance leads to a rapid reduction in the effective search space, causing premature convergence and trapping the kinematic parameter estimation in local optima. As a result, the calibration accuracy and robustness are severely compromised, highlighting the need for enhanced optimization strategies.
Although intelligent optimization algorithms have significantly improved the calibration performance of industrial robots, several key challenges remain unresolved. First, most existing methods rely on fixed heuristic strategies for agent movement, limiting their adaptability when facing high-dimensional, nonlinear, and dynamically changing calibration tasks. Second, traditional algorithms often exhibit an imbalance between global exploration and local exploitation, leading to premature convergence and suboptimal calibration accuracy. Third, while emerging algorithms like SGA have demonstrated competitive performance, they still suffer from the rapid shrinkage of search space during optimization, causing the solutions to fall into local optima when applied to complex calibration problems.
Motivated by these challenges, this paper introduces a deep reinforcement learning-enhanced snow geese optimizer (RLSGA) for robot calibration. The main novelty of this research lies in integrating a deep policy network into the Snow Geese Algorithm framework to enable adaptive migration strategies for robot calibration. Key innovations include:
(a) adaptive policy models using deep neural networks to replace traditional heuristic velocity updates, enhancing global search capability and robustness;
(b) a “behavior–learning–perturbation” update mechanism integrating SGA migration behaviors with policy network predictions. This approach significantly improves convergence speed, stability, and accuracy, making RLSGA ideal for calibrating robots with complex or nonlinear error models.
Section 2 describes the kinematic and error modeling methods.
Section 3 presents the proposed identification strategy. Experimental results are discussed in
Section 4, followed by concluding remarks in
Section 5.
2. Kinematic and Error Model
As illustrated in
Figure 1, the kinematic structure of an ABB IRB120 robot is developed using the Denavit–Hartenberg (DH) method, a standard approach widely utilized in industrial robot modeling. The figure further illustrates the transformation matrix linking the robot’s base frame to its end-effector frame. The measurement system consists of an ABB IRB120 robot, a nylon cable, and a draw-wire encoder. The calibration procedure focuses on kinematic parameters within the homogeneous transformation matrix that connects the base coordinate system with the end-effector coordinate system. Here,
Pi denotes the measurement points (
i = 1, 2, …,
n), and
PW indicates the draw-wire anchor point. By positioning the robot’s end-effector at various
Pi points, different lengths of the draw wire are obtained. The positioning error is the measured distance between each point
Pi and the anchor point
PW. Consequently, the calibration of the end position transforms the problem of reducing positioning errors into minimizing discrepancies in draw-wire length measurements.
The DH parameters of the robot are summarized in
Table 1. The homogeneous transformation matrix that maps coordinates from link
i − 1 to link
i is provided as follows:
where
i is the index of the joint angle,
i = 1, 2, 3, 4, 5, 6.
θi represents the joint angle;
di denotes the link offset.
ai is the link length.
αi indicates the link twist angle;
c stands for the cosine function (cos).
s stands for the sine function (sin).
The nominal end-effector pose matrix
T of the robot can be expressed as:
where
R and
P denote the nominal orientation matrix and the nominal position matrix, respectively.
R∈ℜ
3×3,
P∈ℜ
3×1.
θ,
d,
a, and
α are related to the end-effector pose and have an influence on the robot’s end-effector position and orientation. Assuming that the four parameters contain errors denoted as Δ
ai, Δ
di, Δ
αi, and Δ
θi, the actual end-effector pose of the robot can be represented as
T*:
The pose variation matrix of the robot end-effector, denoted as
dT, can be expressed as:
where
ω is the differential transformation matrix relative to the base frame.
where
δ denotes the deviation in the rotation matrix;
d = [
dx,
dy,
dz]
T is the differential translation vector;
δx,
δy, and
δz correspond to the orientation errors between the robot’s actual and nominal pose.
Substituting Equations (2) into (4) and rearranging yields:
where Δ
P represents the position error between the robot’s actual position and its nominal position.
J is the Jacobian matrix and Δ
D denotes the kinematic error vector; they are respectively expressed as:
Hence, the fundamental objective of robot geometric parameter calibration is to identify the discrepancies between the nominal and actual end-effector poses under various joint configurations (θ1j, θ2j, θ3j, θ4j, θ5j, θ6j), and to determine the optimal set of geometric parameter deviations (Δai, Δdi, Δαi, Δθi) by means of an optimization algorithm, thereby minimizing the pose error.
When using a cable encoder for robot calibration, orientation errors are neglected, and only positional deviations are considered. Let
L denote the measured cable length and
L* represent the theoretical length computed based on the kinematic model. In accordance with the calibration principles, a corresponding loss function can be constructed to optimize the D-H parameters.
where
N is the number of measurement samples, and the expression for
Li is provided as follows:
where
PW represents the fixed position of the cable encoder, which is directly acquired through the measurement software.
Accordingly, based on the formulated objective function, the problem can be characterized as a typical complex, high-dimensional, and nonlinear equation-solving task.
3. Kinematic Parameter Error Identification
3.1. SGA Algorithm for Identification
The SGA algorithm is primarily divided into three phases: the Initialization Phase, the Exploration Phase, and the Exploitation Phase.
In the Initialization Phase, the positions of individuals are initialized. Candidate solutions
X for kinematic parameter errors are randomly generated within the search space. The initial positions are determined based on the population size, the boundaries of the solution space, and the problem dimension. The initialization formula is expressed as follows:
During the initialization of the SGA optimization process, the deviations in link lengths and offsets (ai and di) were constrained within ±8 mm, and the deviations in joint angles and twist angles (θi and αi) were constrained within ±8°, based on the mechanical design tolerances of the ABB IRB120 robot. This ensured that the optimization process remained within physically meaningful bounds and prevented parameter drift due to redundant parameterizations.
Exploration phase-velocity update: In the exploration phase, individuals update their velocities to search for promising regions in the solution space. The velocity-update mechanism enables the algorithm to explore diverse areas and avoid premature convergence. The velocity of each individual is typically influenced by its current state, the positions of other individuals, and specific control parameters. The velocity update formula is provided as:
where
Vt and
Vt+1 denote the velocities at the
t-th and (
t + 1)-th iterations, respectively. Here,
c is the weighting factor, and
a represents the acceleration coefficient. They are calculated as follows:
where
T is the maximum iteration number,
represents the global best solution at the
t-th iteration,
denotes the
i-th candidate solution at the
t-th iteration, and
θ refers to the fight angle.
Position update (exploration phase): In the exploration phase, individuals update their positions based on their current velocities. This update guides individuals to move through the search space and discover new potential solutions. The position update formula is typically expressed as:
where
b is the weighting factor.
Exploitation Phase: In the exploitation phase, the algorithm simulates the “linear” flight pattern of snow geese to perform intensive local search around promising regions. This strategy enhances the exploitation capability of the algorithm by focusing on refining the current best solutions. The position update in this phase is governed by the following formula:
where
γ is a random number within the range [0, 1], ⊕ denotes element-wise multiplication, and Brownian(
d) represents Brownian motion in d-dimensional space.
3.2. Enhancing Snow Geese Algorithm with Deep Neural Networks
To further improve the identification accuracy of the SGA and to avoid premature convergence to local optima, a policy network
πθ(·) is introduced to replace the traditional velocity update formula of the standard SGA. The network takes as input the current position of the individual, the current velocity, the current global best position, and the current global center position. It outputs the updated velocity for the next iteration. As shown in
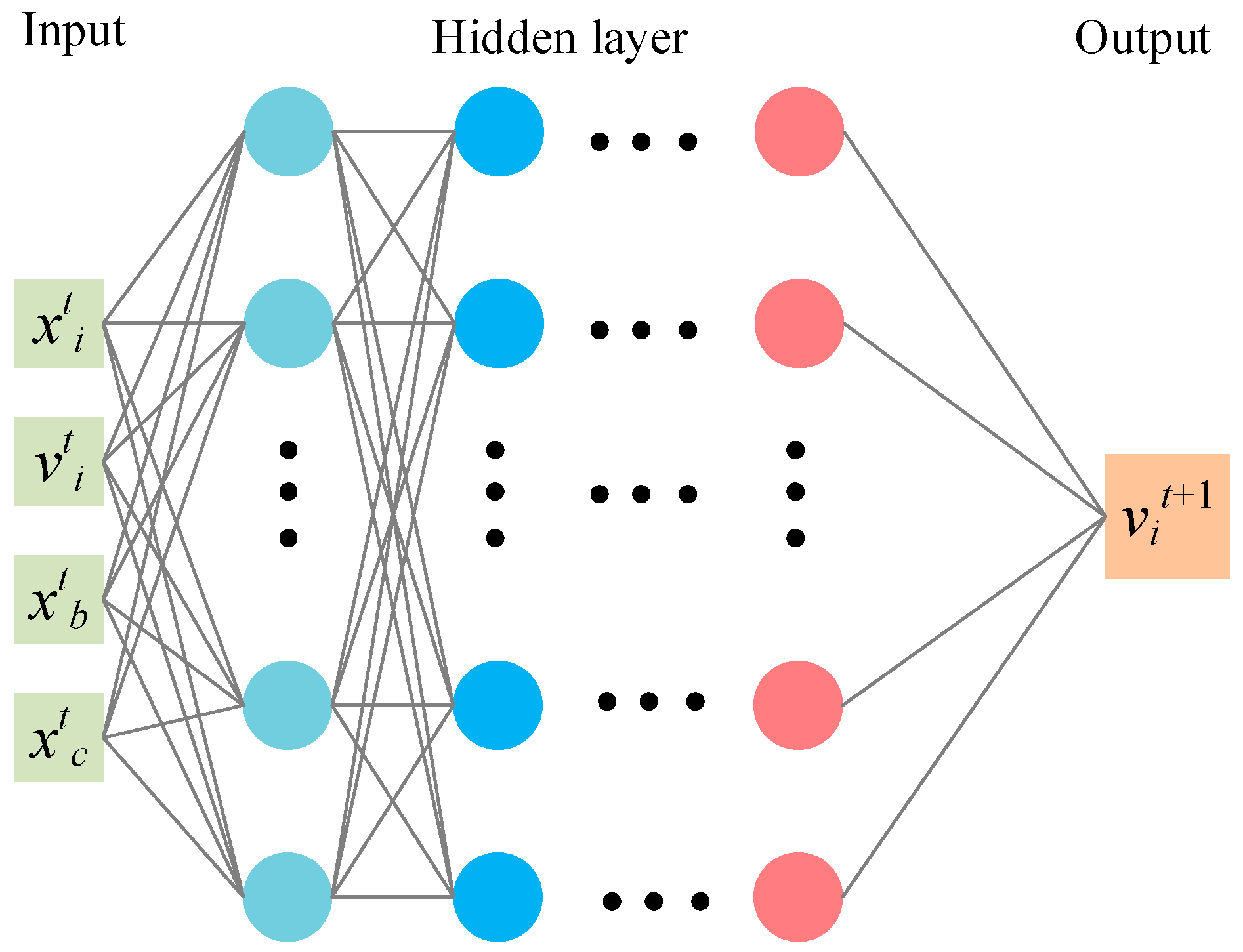
Figure 2, a fully connected neural network is designed to capture the nonlinear relationship between the input features and the updated velocity. The neural network structure (4-30-30-30-30-30-1) comprises five hidden layers, offering sufficient depth to model complex dynamics during the optimization process.
The state vector is constructed for each individual, representing its status at the t-th iteration. The state vector for an individual at iteration t is defined as:
where:
represents the current estimated kinematic parameter error of the individual,
denotes the current adjustment velocity, corresponding to the step size and direction of parameter correction,
refers to the current global best estimated kinematic parameter error among all individuals, serving as the best-known calibration solution so far,
is the current global center position of the population, reflecting the collective search status.
The policy network takes this state vector as input and outputs a new adjustment velocity
. This predicted velocity represents the next movement direction and step size for updating the estimated kinematic parameters, aiming to minimize the overall calibration residuals. The policy network is defined as:
The output vit+1 corresponds to the velocity update for the next iteration.
The training objective of the policy network is formulated as a supervised learning task. Training samples (
,
vit+1) are collected by observing the actual behavior of the standard SGA. The loss function is defined as:
where
M denotes the number of training samples.
In the context of robot calibration, the input state vector elements correspond to the estimated kinematic parameter deviations and their dynamic adjustment behaviors, while the output velocity adjustment guides the refinement of the calibration parameter estimates to achieve higher positioning accuracy.
The position update is performed using the updated velocity according to the following formula:
where
is a perturbation term derived from the modeling of snow geese migration behavior, including V-formation, linear flight, and Brownian motion.
A convergence-checking mechanism was incorporated into the RLSGA implementation, where convergence is confirmed based on objective function improvement thresholds, and a convergence alarm is triggered if the convergence condition is not satisfied within the maximum allowable iterations.
In each iteration, the state vector of each agent is processed by the policy network to infer the new adjustment velocity, which is subsequently combined with SGA migration updates for position refinement. The updated position is then evaluated for calibration accuracy, completing one cycle of interaction between the learning and optimization components.
Algorithm 1 presents the pseudo-code of the proposed RLSGA algorithm for solving the robot calibration problem. RLSGA builds upon the conventional SGA by integrating a deep policy network to model individual migration behaviors adaptively. Instead of relying on fixed-velocity update formulas, the algorithm leverages learned state-action mappings to predict individual movement directions, thereby enhancing its adaptability and convergence efficiency in high-dimensional and nonlinear optimization scenarios. Meanwhile, the inherent biological behaviors of SGA—namely, the V-formation and straight-line flight—are preserved and combined with the learned strategy to form a collaborative search mechanism. This hybrid approach makes SGA-RL particularly suitable for complex robot calibration tasks involving multi-source uncertainties and nonlinear parameter dependencies.
Unlike conventional gradient-based methods that require explicit Jacobian and Hessian computations, the proposed RLSGA operates through population-based stochastic updates guided by a deep policy network, thereby avoiding numerical instabilities associated with near-singular configurations and heterogeneous constraint conditions.
3.3. Performance Evaluation of RLSGA
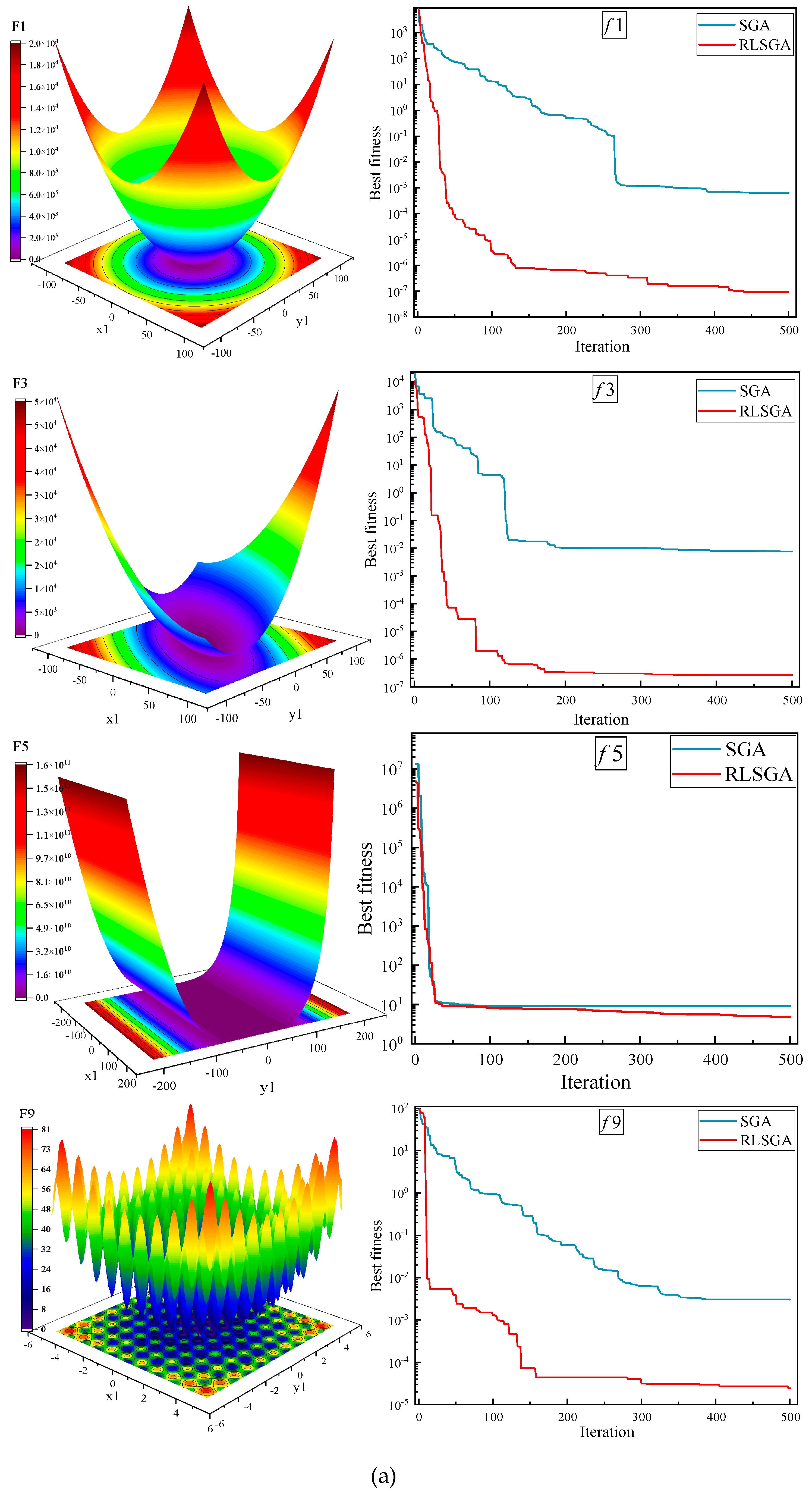
To validate the performance improvement introduced by RLSGA, several representative benchmark functions (f1, f3, f5, f9, f13, f15, f16, f20, f22) from the CEC2005 test suite are selected for evaluation. The original SGA is used as a baseline for comparison.
Figure 3 presents the experimental results, illustrating the convergence behavior of both algorithms across the selected test functions. As shown in
Figure 3, the improved RLSGA demonstrates significantly better performance than the original SGA in terms of both convergence speed and solution accuracy. Specifically, RLSGA converges faster and reaches lower final objective values on most functions, indicating its superior optimization capability. These results confirm the effectiveness of incorporating deep reinforcement learning into the optimization process. The learning-guided strategy enables RLSGA to dynamically adapt its search direction, enhancing global exploration and local exploitation abilities in complex, high-dimensional search spaces.
5. Conclusions
To enhance the calibration accuracy of industrial robots, this paper proposed a novel RLSGA algorithm, which integrates deep reinforcement learning with a biologically inspired metaheuristic framework. A series of benchmark function tests and robot calibration experiments were conducted to verify the effectiveness and superiority of the proposed method. The main conclusions are summarized as follows:
(1) In comparison with the original SGA, the proposed RLSGA demonstrates significantly improved performance on the CEC2005 benchmark functions in terms of convergence speed and solution accuracy. By introducing a learned policy network to adaptively guide the optimization process, RLSGA effectively overcomes the limitations of premature convergence and local optima, enhancing both global exploration and local exploitation capabilities.
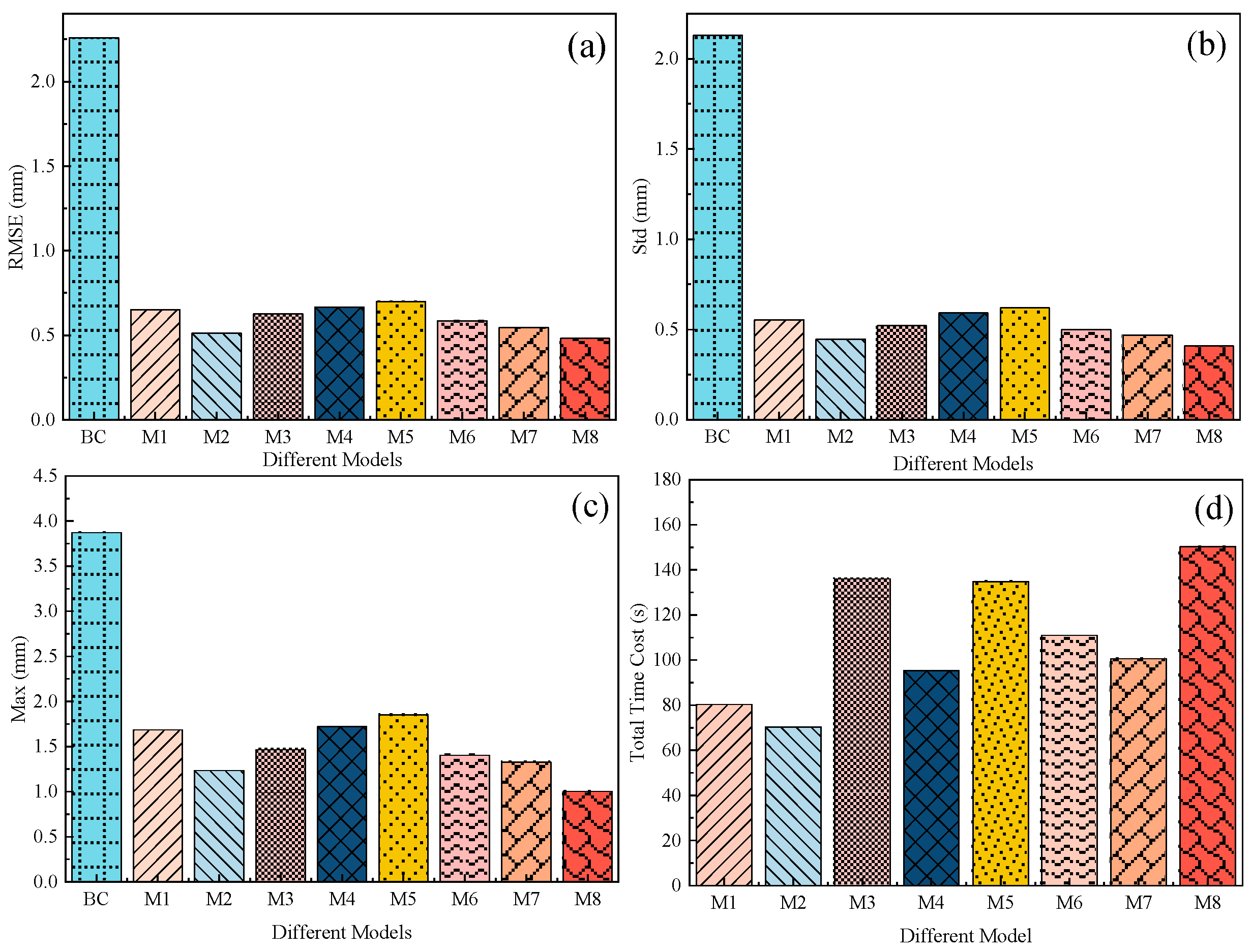
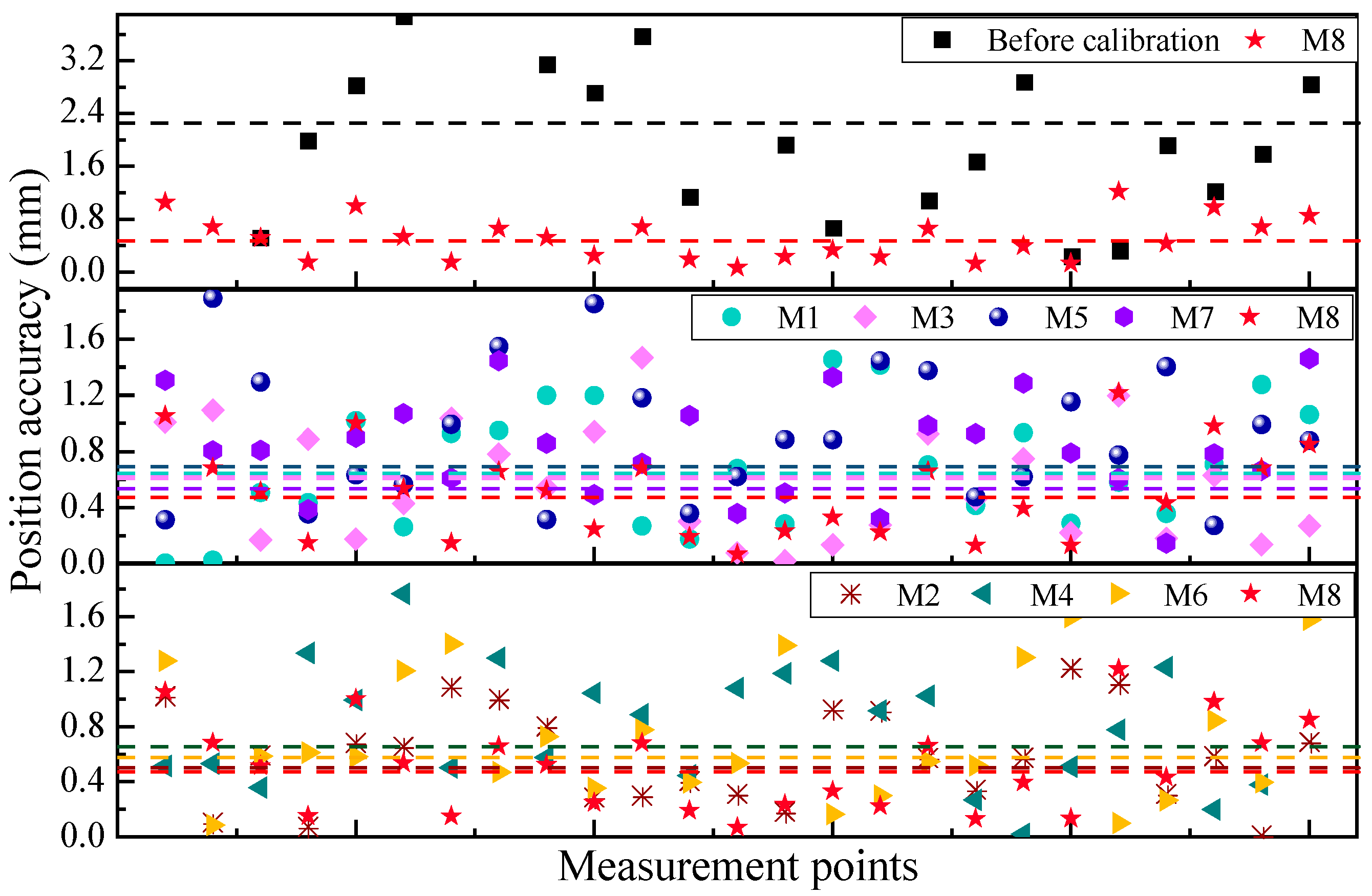
(2) In industrial robot calibration tasks, RLSGA achieves the highest calibration accuracy among eight representative methods, including both classical optimization algorithms (e.g., PSO, DE) and advanced heuristics (e.g., BAS, ABC). Specifically, RLSGA reduces the RMSE, Std, and Max to 0.481 mm, 0.408 mm, and 1.002 mm, respectively, representing the best performance across all evaluated metrics. Moreover, its convergence curves are smoother and faster than those of the baseline methods, confirming the robustness and learning efficiency of the proposed strategy.
(3) Although RLSGA incurs higher computational cost due to the training and inference procedures of the deep policy network, this trade-off is acceptable in high-precision applications where calibration accuracy is of critical importance. Overall, the proposed RLSGA provides a promising solution for robot calibration tasks with complex, nonlinear error models and offers potential for broader applications in intelligent manufacturing and adaptive robotics.
In future work, several promising research directions can be explored to further enhance the effectiveness and applicability of the proposed RLSGA method. First, developing online learning strategies could enable real-time adaptation of the calibration model during robot operation, improving dynamic accuracy under changing conditions. Second, extending the kinematic error modeling to incorporate thermal effects, payload variations, and other environmental factors could further improve calibration robustness. Third, applying the RLSGA framework to different types of robots, such as collaborative or redundant robots, would validate its generalization capability across various robotic platforms. These potential extensions will be the focus of our subsequent research.