Dynamic Risk Assessment of Gas Accumulation During Coal and Gas Outburst Catastrophes Based on Analytic Hierarchy Process and Information Entropy

Abstract

Gas accumulation triggered by coal and gas outbursts is the core cause of secondary disasters in coal mines. This study focuses on the risk assessment of gas accumulation during disaster scenarios, proposing a multidimensional evaluation method integrating the analytic hierarchy process (AHP), information entropy theory, kernel density estimation, and dynamic risk propagation modeling. A unified intelligent prevention system encompassing “monitoring–prediction–decision making” is established. Leveraging the TFIM3D simulation platform and case studies from the Qunli Coal Mine accident, this research reveals spatiotemporal evolution patterns of gas concentration and explosion risk thresholds. A ventilation optimization strategy based on risk classification is proposed. The results demonstrate that the dynamic risk index (DRI), derived from the coupling of the roadway air volume stability coefficient and gas concentration information entropy, can accurately identify high-risk zones. The findings provide theoretical foundations and practical pathways for dynamic risk management in ventilation systems during coal and gas outburst disasters.

1. Introduction

As its mainstay of energy, coal secures a vital strategic place in the national economy. It is expected that by 2030, when carbon dioxide emissions peak, the proportion of coal in the energy consumption structure will still be higher than 43% [1,2]. However, as the coal mining depth increases, high ground temperature, high ground pressure, and other factors have posed greater risks and aggravated disasters. Mine gas prevention and control are facing new problems and challenges [3,4,5]. Coal and gas outbursts, among the most severe dynamic disasters in coal mining, are often accompanied by instantaneous, massive gas emissions, resulting in a sharp increase in gas concentration in local areas, thereby creating explosion or asphyxiation risks [6,7,8]. The gas–solid mixed flow of coal and gas can disrupt mine ventilation systems while destroying underground equipment and facilities. Furthermore, the reduction in oxygen levels not only threatens personnel safety but may also trigger mine fires and gas explosions. Additionally, such incidents can induce secondary disasters, leading to cascading catastrophic events [9,10].

In recent years, many researchers have thoroughly examined the impact of gas on mine ventilation systems, particularly in response to coal and gas outbursts. Wang et al. [11,12] utilized both experimental and numerical simulation methods to investigate how gas accumulation affects airflow oscillations in the inclined roadways of outburst-prone mines. They developed a quantitative model that links the angles of roadway inclinations to the intensity of airflow disturbances. Meanwhile, Zhang [13] provided a comprehensive overview of the research landscape concerning outburst two-phase flow, highlighting five key aspects: the visualization of outburst dynamics, the structural complexity of roadways, multi-source data acquisition, a wide range of influencing factors, and diverse research methodologies. Yang [14] designed a physical test system to simulate the outburst process and conducted experiments with it to explore the formation and propagation of outburst shock waves and the backflow of gas. The coal powder flow and methane–air mixture are intrinsically coupled in coal and gas outburst processes. Experimental and field investigations have demonstrated a characteristic gas-leading powder-lag phenomenon in post-outburst roadways, where high-pressure gas flow precedes pulverized coal migration during dynamic discharge phases [15,16,17].

Driven by evolving coal mining practices and emerging safety demands in China’s new era, the prevention and dynamic early warning of coal and gas outburst disasters have entered a transformative stage. Academician Yuan Liang [18,19] pioneered a tri-parameter early warning index system based on the outburst hazard probability, energy release rate, and system stability rate. This system established China’s first cloud-based platform for coal mine dynamic disaster monitoring. Building upon quantitative outburst risk assessment and dynamic warning frameworks, Zhang et al. [20] proposed an integrated risk evaluation method combining variable weight theory and uncertainty theory. To enhance the prediction accuracy of coal and gas outburst dynamics, Shao et al. [21] developed a novel hybrid framework integrating a Markov chain Monte Carlo (MCMC) data imputation algorithm with an improved sparrow search algorithm (ISSA)–optimized support vector machine (SVM), achieving a breakthrough in multi-phase risk quantification. Zhang et al. [22] proposed a coal and gas outburst risk assessment methodology based on an enhanced comprehensive weighting system and cloud theory. This approach effectively addresses issues of fuzziness and randomness in risk evaluation, deviations in indicator weighting, and inter-indicator correlations. Jiang et al. [23] employed a multi-weight combination optimization model utilizing the Gram–Schmidt orthogonalization method to eliminate inter-factor correlations. This optimized weighted comprehensive evaluation model assessed outburst pressure risks in coal seams at the Liangjia Coal Mine.

Generally speaking, machine learning models are trained on static data and cannot provide highly real-time responses to coal and gas outburst accidents in coal mines. To address this limitation in risk assessment methods, some scholars have proposed solutions. For instance, Zhang et al. [24] introduced a dynamic probabilistic risk assessment method based on a dynamic Bayesian network (DBN) for emergency response in smart coal mines. This approach was validated through practical case studies in gas overlimit scenarios, effectively enhancing risk prediction capabilities and enabling bidirectional risk analysis. Du et al. [25] implemented rapid detection techniques and multi-source dynamic monitoring technologies specific to mining operations to classify risk zones of typical dynamic hazards. They concurrently developed an early warning software platform capable of automated evaluation and practical three-dimensional visualization in coal mining areas. Zhu et al. [26] conducted a dynamic assessment and simulation of coal mine safety risk using ANP, fuzzy comprehensive evaluation, and a system dynamics model.

However, current research on risk assessment throughout the entire disaster process of coal and gas outbursts remains limited. This study employed the information entropy method to evaluate the hazard of gas concentration accumulation following outbursts. As a technical approach that integrates data analysis and system modeling, it provides a scientific basis for gas accident early warning, mine ventilation optimization, mine monitoring, and the implementation of disaster prevention and control measures.

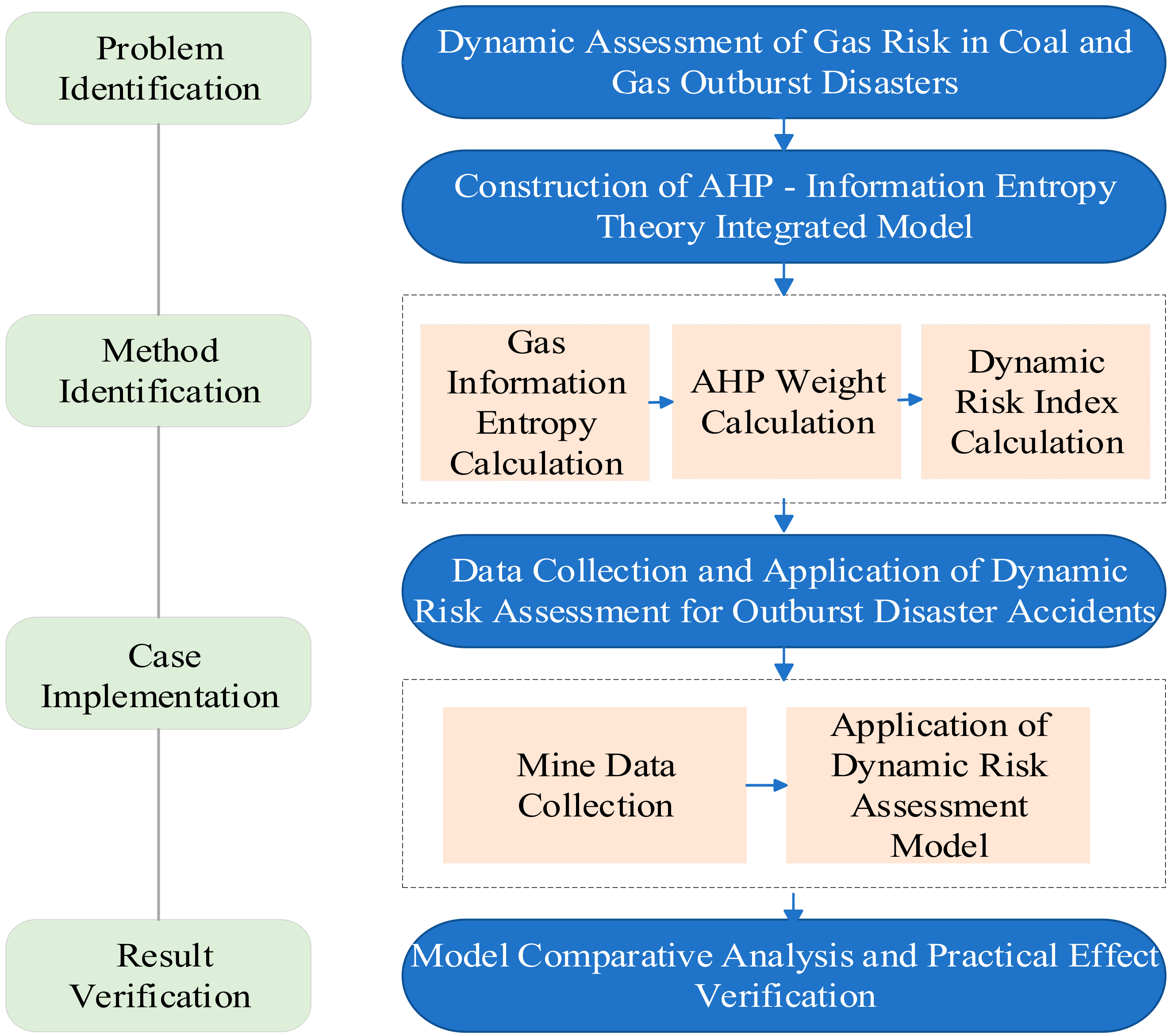
The accurate identification of spatiotemporal evolution patterns of coal–gas dynamic disasters (e.g., coal and gas outbursts) in underground mining environments constitutes a critical scientific foundation for precise gas hazard management and disaster risk mitigation. Recent advancements in computational geomechanics have established numerical simulation as a powerful methodology for predicting gas migration behavior and characterizing high-risk accumulation zones. This study developed a coupled multi-physics model integrating gas adsorption–desorption dynamics, fracture network evolution, and stress redistribution mechanisms to systematically investigate gas concentration field evolution during catastrophic outburst processes. The simulation results generated a high-resolution spatial–temporal dataset that quantitatively delineates hazardous gas distribution patterns, which serves as the scientific basis for establishing a dynamic risk assessment system that integrates monitoring and early warning mechanisms. A systematic workflow detailing the methodology framework is presented in the graphical abstract (Figure 1), encompassing numerical modeling, risk factor extraction, and decision-support applications.

2. Materials and Methods

Based on the gas migration characteristics during the entire coal and gas outburst disaster process, the regularity of gas concentration variations in mine roadways during the disaster period and their influencing factors exhibit uncertainty characteristics. The information entropy method can, therefore, be employed to assess the hazard of gas accumulation in roadways during coal and gas outburst disasters [27].

Information entropy (IE) measures uncertainty represented by a probability distribution function. The amount of information (attributes, features) directly correlates with its degree of uncertainty; more significant uncertainty corresponds to a more extensive information quantity. Depending on the logarithmic base (2, e, or 10), the units are expressed as bits, nats, or Hartleys, respectively.

The gas concentration is influenced by the gas emission/flow rate and roadway airflow for gas accumulation. These two factors are independent random variables in ventilated roadways. After the outburst process concludes, the migration and dispersion of gas within the roadway are predominantly governed by airflow, with relatively minor impacts from other uncertain factors [28]. Therefore, this study focuses on the influence of roadway airflow during the disaster period on gas accumulation. Precisely, the airflow stability coefficient and the information entropy of gas concentration are calculated to quantify these effects.

2.1. Information Entropy of Gas Concentration

The information entropy H(x) of a continuous random variable is as follows: For a one-dimensional continuous random variable x, if its probability density function is f(x), then the information entropy of x over the integration interval is given by Formula (1).

$$H\left(x\right)=-\int f(x)\mathit{ln}f\left(x\right)dx$$

(1)

The information entropy of gas concentration H_gc(i) can be expressed by Formula (2).

$$H_{gc}\left(i\right)=-\int f_i\left(x\right)\mathit{ln}{f}_i\left(x\right)dx$$

(2)

The dimensionless probability density function f_i(x) describes the gas concentration distribution in the ii-th tunnel, while H_gc(i) quantifies its corresponding dimensionless information entropy.

The change in gas concentration in roadways has the characteristic of uncertainty. The more complex the mine is, the more complicated the gas concentration change in roadways across the network will be. Mathematical statistics methods can be used to analyze roadway branches’ gas concentration density function. Solving the distribution density function of a random variable from a given sample set is one of the fundamental problems in probability and statistics. The methods to solve this problem include parametric and non-parametric estimations. Kernel density estimation is a non-parametric estimation method. It was proposed by Rosenblatt (1955) and Emanuel Parzen (1962) and is also known as the Parzen window. Ruppert and Cline proposed a revised kernel density estimation method based on the clustering algorithm of the dataset density function [29].

Kernel density estimation (KDE) employs smooth peak functions (“kernels”) to fit observed data points, thereby approximating the true probability distribution curve. Consider n independent and identically distributed (i.i.d.) samples drawn from a distribution F(x), where the probability density function (PDF) is denoted as f(x). To estimate the density value at X = x, a histogram-like approach can be adopted: select a small neighborhood around xx, count the number of samples falling within this interval, and divide by the total number of samples to obtain a robust estimate. Mathematically, by leveraging the definition of the derivative, the density function can be formulated as Equation (3):

$$f(x)=\underset{h\to 0}{\lim }{\displaystyle \frac{F\left(x+h\right)-F\left(x-h\right)}{2h}}$$

(3)

To estimate the density function value at a point x, let h denote the bandwidth parameter. By defining a neighborhood [x − h, x + h] around xx, the density value within this interval converges to the true density at xx as h approaches zero. Mathematically, this is expressed as Equation (4):

$$\stackrel{\wedge }{f}\left(x\right)={\displaystyle \frac{1}{2h}}\underset{h\to 0}{\lim }{\displaystyle \frac{N_{xi\in \left[x-h,x+h\right]}}{n}}$$

(4)

$N_{xi\in \left[x-h,x+h\right]}$ denotes the number of sample points within the neighborhood [x − h, x + h], where n is the total number of samples in the dataset, and f(x) represents the estimated probability density function. By averaging the density values over this neighborhood, the density function value at xx, denoted as f(x), is obtained. Rewriting the expression in Equation (4) yields Equation (5):

$$\stackrel{\wedge }{f}\left(x\right)={\displaystyle \frac{1}{2hn}}{\displaystyle \sum _{i=x-h}^{x+h}{x}_i}={\displaystyle \frac{1}{hn}}{\displaystyle \sum _i\frac{\left|x-x_i\right|}{2h}}<1,h\to 0$$

(5)

where $K\left(x\right)={\displaystyle \frac{1}{2}}·1\{x<1\}$, and K(•) is the kernel function. The integral of the density function is given by Equation (6):

$$\stackrel{\wedge }{f}\left(x\right)={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^{n}K\left(x-x_i\right)}={\displaystyle \frac{1}{nh}}{\displaystyle \sum _{i=1}^{n}K\left(\frac{\left|x-x_i\right|}{h}\right)}$$

(6)

This leads to the property described by Equation (7):

$${\displaystyle \int \stackrel{\wedge }{f}\left(x\right)}={\displaystyle \frac{1}{n}}{\displaystyle \sum _i{\displaystyle \int K\left(\frac{\left|x-x_i\right|}{h}\right)dx}=}{\displaystyle \frac{1}{n}}{\displaystyle \sum _i{\displaystyle \int K\left(t\right)dt}=}{\displaystyle \int K\left(t\right)dt}$$

(7)

Therefore, as long as the integral of K(x) equals 1, the estimated density function f(x) is guaranteed to satisfy the normalization condition ∫f(x)dx = 1. Given a sample set, the problem of estimating the density function of a random variable is reduced to the selection of an appropriate kernel function K (·). The performance of the kernel density estimation—its accuracy and smoothness—depends critically on two factors: (1) the choice of the kernel function K (·), and (2) the optimal determination of the bandwidth parameter h.

For kernel density estimation (KDE) curves involving multiple data points, the final shape of the KDE curve is largely independent of the specific choice of the kernel function due to the superposition of adjacent waveform peaks. For computational convenience in waveform synthesis, the Gaussian curve (normal distribution curve) is commonly adopted as the kernel function in KDE. In this context, we apply the Gaussian kernel function to the kernel density estimation model, transforming Equation (6) into Equation (8):

$$\stackrel{\wedge }{f}\left(x\right)={\displaystyle \frac{1}{nh}}{\displaystyle \sum _{i=1}^n\frac{1}{\sqrt{2\pi }}\exp (-\frac{{\left(x-x_i\right)}^2}{2h^2})}$$

(8)

The accuracy of the kernel density estimator is determined by two factors: the choice of the kernel function and the bandwidth parameter h. When the bandwidth is fixed, different kernel functions exhibit comparable influence on the estimation results. However, once the kernel function is specified, the selection of h critically governs the smoothness of the estimated density curve. To optimize the trade-off between bias and variance, the mean integrated squared error (MISE) criterion is employed to derive the optimal bandwidth h. This is achieved by minimizing the following expression:

$$MISE(\stackrel{\wedge }{f(x)})=E\left[{\displaystyle \int {\{\stackrel{\wedge }{f(x)}-f(x)\}}^{2}dx}\right]$$

(9)

Let f(x) denote the true population density. The mean integrated squared error (MISE), defined as a function of the bandwidth h, is minimized to derive the optimal bandwidth estimate.

Under the Gaussian kernel assumption, if the unknown probability density function f(x) is also hypothesized to follow a Gaussian distribution, the bandwidth h can be analytically determined.

$$h={\left({\displaystyle \frac{4}{3}}\right)}^{{\displaystyle \frac{1}{5}}}\sigma n^{-{\displaystyle \frac{1}{5}}}\approx 1.06\sigma n^{-{\displaystyle \frac{1}{5}}}$$

(10)

Once the kernel function is selected, the kernel density estimation (KDE) model is fully defined. By substituting h into Equation (8), the estimation error of the model can be quantified.

For gas explosion risk assessment, the gas concentration is constrained to the interval [0.05, 0.15], corresponding to the gas explosion limits. Under the premise of a coal and gas outburst disaster, the probability of the gas concentration falling within the regulatory range [Cmin,Cmax] can be calculated using the KDE model. Specifically, the probability is given by

$$P_i\left(c_i(t)\right)={\displaystyle {\int }_{C\min }^{C\max }{f}_i(c_i(t))}d{c}_i(t)$$

(11)

2.2. Roadway Air Volume Stability Coefficient

The mine ventilation system can be represented as a network structure G(V,E) [30], where the node set of the system is V = {v₁, v₂,…, v_m}, and the branch set is E = {e₁, e₂,…, e_n}. Here, m denotes the number of nodes, and n represents the number of roadway branches. Changes in the network structure of the ventilation system, along with variations in roadway air resistance, collectively reflect unstable factors in the system. During a coal and gas outburst disaster, numerical simulations can obtain the airflow variations in all roadway branches within the ventilation system over the disaster duration. For the i-th roadway, the airflow during the entire coal and gas outburst disaster is denoted as q_i = {q_i1, q_i2, q_ik…, q_im}, where m represents the simulation duration of the disaster. Consequently, the total airflow in the ventilation system is the collection of airflow from all roadways. The roadway airflow stability coefficient represents the airflow ratio before and after air resistance changes to represent the airflow deviation. Therefore, during a coal and gas outburst disaster, the airflow deviation of the i-th roadway at time k is given by Equation (12).

$${{\delta }_i}_k(q)={\displaystyle \frac{q_{ik}}{q_{i0}}}$$

(12)

In the formula,

q_ik is the airflow in the i-th roadway at time k, in m³/s;

q_i0 is the initial airflow in the i-th roadway (i.e., under normal ventilation conditions), in m³/s;

δik(q) is the dimensionless airflow deviation of the i-th roadway at time k.

Therefore, the airflow stability of each roadway is determined by its stability at any given moment. Numerical simulation analysis revealed that during a disaster, airflow variations in the branches of the ventilation system are highly complex. The airflow stability coefficients of each roadway across all time steps often fall outside the interval [0, 1]. To perform unified data analysis on the airflow of all roadways and derive the airflow stability coefficient for each roadway over the disaster period, the following approach is adopted: (1) Independent variable treatment: Roadway branches in the ventilation system are treated as independent variables. (2) Fuzzy clustering analysis: A fuzzy clustering analysis method is applied to process the dataset.

Dimensionless normalization: The data are normalized to eliminate dimensional differences.

Unified dimensional framework: The influence of roadway airflow on gas concentration accumulation is analyzed under consistent metrics.

For a ventilation system with n classified roadway branches, each branch feature δi (e.g., airflow deviation) comprises m raw data points: δi = {δi1, δi2, δik, …, δim}, where these data points are referred to as the elements of this feature.

To statistically characterize these data, compute the mean value of the dataset, as shown in Equation (13). The standard deviation of the dataset is calculated as shown in Equation (14).

$$\overline{{\delta }_i}={\displaystyle \frac{1}{m}}{\displaystyle \sum _{k=1}^m{\delta }_{ik}}$$

(13)

$$S_i^2={\displaystyle \frac{1}{m}}{{\displaystyle \sum _{k=1}^m\left({\delta }_{ik}-\overline{{\delta }_{\mathit{ik}}}\right)}}^2$$

(14)

Using Equation (15), compute the standardized value of the data:

$${\delta }_{ik}\prime ={\displaystyle \frac{{\delta }_{ik}-\overline{{\delta }_{\mathit{ik}}}}{S_i}}$$

(15)

Next, apply extremum normalization to the above result using Equation (16):

$${\delta }_{ik}″={\displaystyle \frac{{\delta }_{ik}\prime -{\delta }_i{\prime }_{\min }}{{\delta }_i{\prime }_{\max }-{\delta }_i{\prime }_{\min }}}$$

(16)

In the equations,

$\overline{{\delta }_i}$ is the mean value of airflow deviation for the i-th roadway branch, dimensionless;

S_i is the standard deviation of airflow deviation for the i-th roadway branch, dimensionless;

δ_ik is the dimensionless standardized value of airflow deviation for the i-th roadway at time k, dimensionless;

δ_ik′′ is the extremum-normalized value of airflow deviation for the i-th roadway at time k, dimensionless;

δ_i′_min is the minimum value of airflow deviation for the i-th roadway, dimensionless;

δ_i′_max is the maximum value of airflow deviation for the i-th roadway, dimensionless.

Therefore, during a coal and gas outburst disaster, the influence of airflow in the underground ventilation system on gas accumulation risk, i.e., the airflow stability coefficient θ_i(q), is expressed by Equation (17):

$${\theta }_i\left(q\right)=\sqrt{{\displaystyle \frac{1}{m}}{\sum }_{k=1}^m{\left({\delta }_{ik}″-E\left({\delta }_i″\right)\right)}^2}$$

(17)

In the equation,

E(δ_i″) is the expected value (mean) of the extremum-normalized airflow deviation for the i-th roadway, dimensionless;

θi(q) is the airflow stability coefficient of the i-th roadway, dimensionless.

During a coal and gas outburst disaster, θ_i(q) serves as the impact factor reflecting how roadway airflow variations influence gas concentration. The larger the value of θ_i(q), the more turbulent the airflow changes in the roadway, indicating heightened instability and potential gas accumulation hazards.

2.3. Analysis of Gas Accumulation Risk in Roadways Based on Analytic Hierarchy Process

Although information entropy can characterize uncertainty, its independence assumption exhibits limitations in practical complex systems. It is necessary to integrate multi-factor weight allocation methods. This study employs the analytic hierarchy process (AHP) to construct a dynamic risk assessment model. The AHP has been widely applied in engineering risk evaluation fields as a multi-criteria decision-making tool. Establishing hierarchical structure models and conducting consistency checks effectively addresses multi-objective weight allocation issues [31]. Meanwhile, information entropy theory demonstrates unique advantages in uncertainty quantification and data dispersion analysis, which can compensate for the limitations of subjective weighting.

Based on the disaster mechanism of coal and gas outbursts, the air volume stability coefficient and gas concentration information entropy are key factors leading to disasters.

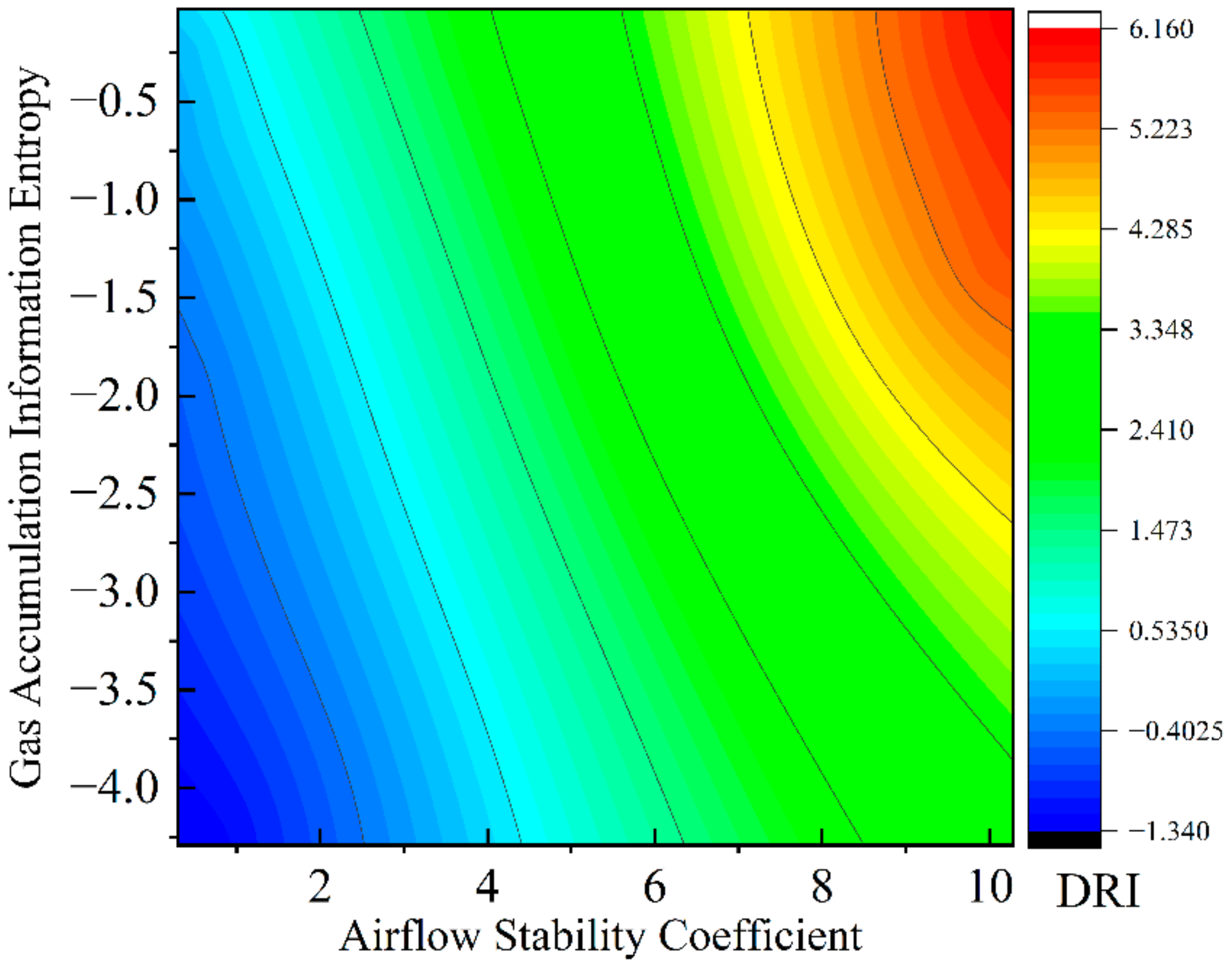
By integrating AHP weights with information entropy methods and extracting indicator data from disaster simulation results at different time points, the dynamic risk index (DRI) formula is established as follows:

$$DRI=\alpha ·{\theta }_i\left(q\right)+\beta ·H_{gc}\left(i\right)$$

(18)

In the formula, α and β denote the weight coefficients of the airflow stability coefficient and gas concentration information entropy, respectively, which are defined as dimensionless parameters.

To facilitate further analysis, the risk levels are categorized based on DRI values, as shown in

Table 1. Risk classification criteria.

DRI	Risk Level
DRI < 0	Low Risk
0 ≤ DRI < 2	Medium Risk
DRI ≥ 2	High Risk

below.

The analytic hierarchy process (AHP) is employed to determine the weight coefficients, with the following specific steps:

Step 1: Construct the judgment matrix.

Based on expert judgment, pairwise comparisons are conducted to evaluate the relative importance between the airflow stability coefficient θi(q) and the gas concentration information entropy H_gc(i), thereby forming the following judgment matrix:

$$\mathrm{A}=\left[\begin{array}{cc}1& 1.5\\ 0.67& 1\end{array}\right]$$

Step 2: Calculate the weight vector.

The weight vector is derived using the following geometric mean method:

(1) Compute the geometric mean of elements in each row:

$$g_1=\sqrt{1\times 1.5}\approx 1.2247, g_2=\sqrt{0.67\times 1}\approx 0.8185$$

(2) Normalize the geometric means to obtain subjective weights:

$$w_{AHP}=\left[{\displaystyle \frac{1.2247}{1.2247+0.8185}},{\displaystyle \frac{0.8185}{1.2247+0.8185}}\right]\approx \left[\mathrm{0.6,0.4}\right]$$

After calculation, the weight coefficients are determined as α = 0.6, β = 0.4.

(3) Calculate the consistency ratio (CR).

The order of the matrix is n = 2. According to the formula CI = ${\displaystyle \frac{{\lambda }_{max}-n}{n-1}}=0.0025$, find the average random consistency index (RI). When n = 2, RI = 0.

According to the formula CR = ${\displaystyle \frac{CI}{RI}}$, we obtain CR = ${\displaystyle \frac{0.0025}{0}}$. Since the denominator is 0, which is meaningless, in practical applications, when n = 2, the judgment matrix always has perfect consistency. In this case, since CR = 0 is less than 0.1, it indicates that the judgment matrix has satisfactory consistency. So, the consistency ratio (CR) calculated according to the given judgment matrix meets the consistency requirements.

We used the analytic hierarchy process (AHP) to determine the separation values of the weighting factors. Firstly, a team of experts with rich experience in this field was formed, consisting of five professors in mining safety and three chief field engineers. Subsequently, according to their professional knowledge and experience, pairwise comparisons of different factors were conducted, and scores were assigned using the 1–9 scale method. Then, we constructed the judgment matrix and determined the weights of each factor by calculating the eigenvectors and eigenvalues of the matrix. After the consistency check (the consistency ratio was CR = 0 < 0.1, indicating good consistency), the following separation values for the weighting factors were finally determined: the weight of the air volume stability coefficient was 0.6, and the weight of the gas concentration information entropy was 0.4. This division not only conforms to the coupled roles of the two in disaster dynamics (the former represents gas dilution efficiency, while the latter represents the degree of disaster escalation), but also verifies the predictive effectiveness of the weighting system using historical field data.

2.4. Case Study Overview

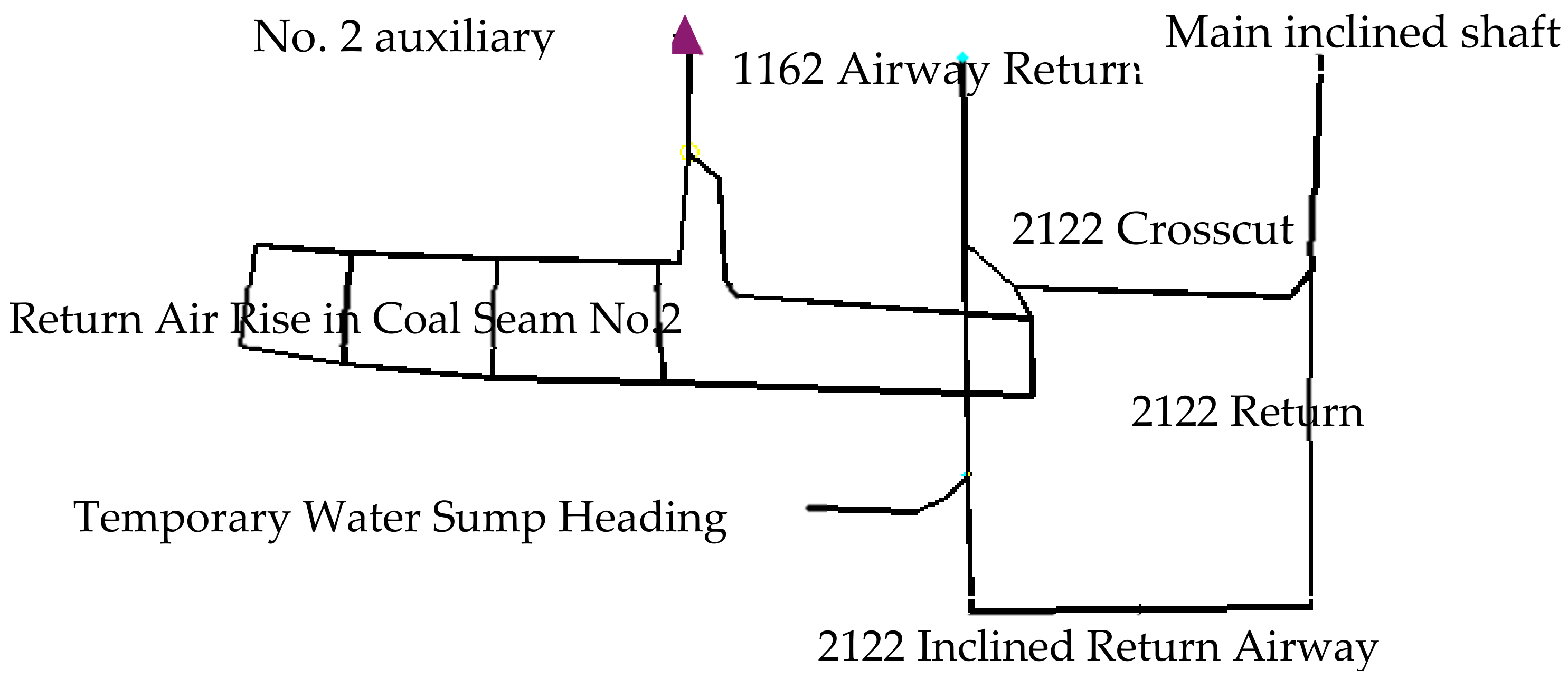
This study took the coal and gas outburst accident at the Qunli Coal Mine in Nayong County, Guizhou Province on 8 November 2007, as a case study [32]. In Xiongbi Town, Shizong County, Qujing City, Yunnan Province, the Qunli Coal Mine employed inclined shaft development with three mining levels and two mining districts (south and north wings) connected via the 1780-level haulage roadway. As shown in Figure 2, the mine adopted a central boundary ventilation system, with air intake through the No. 2 Auxiliary Shaft and Main Inclined Shaft and return airflow via the South Wing Boundary Ventilation Shaft using exhaust ventilation. The BD-II-6-No18 fan, operated at 740 r/min, delivered a 19.48 m³/s airflow with 2.18 m³/s external leakage, generating 211.23 Pa ventilation pressure against a natural ventilation pressure of −32.63 Pa. 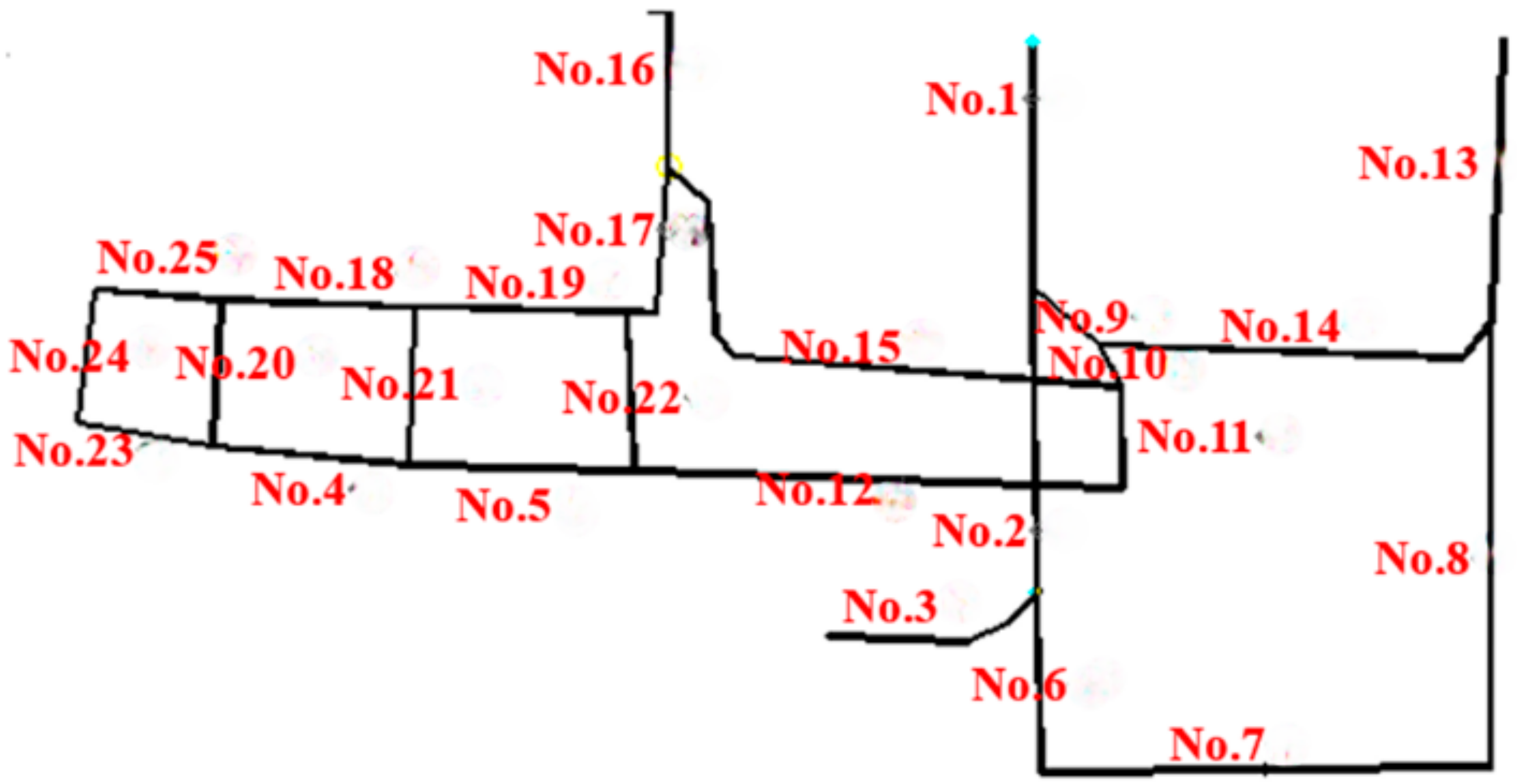Figure 3 presents a simplified ventilation network diagram of the mine.

At 13:43 on 8 November 2007, a coal and gas outburst occurred at the temporary sump excavation face in the central section of the Second Mining District, ejecting approximately 500 tons of coal and 49,000 m³ of gas. The accident resulted in 35 fatalities and 7 injuries. This privately owned mine, designed with an annual production capacity of 300,000 tons, commenced construction in early 2001 and began operation in March 2005. Preliminary analysis indicated that the direct cause was outburst induction by blasting operations during the 7 m advancement of the temporary sump. The post-accident investigation revealed gas backflow phenomena extending approximately 600 m along the main adit. The backflow forced open two airlock doors in the 2122 crosscut and reached intake shaft openings. As the outburst intensity diminished and gas emission decreased due to gradual desorption from surrounding coal seams, the backflow velocity reduced from 14.98 m/s to 13 m/s.

The fundamental roadway dimensions and ventilation parameters (friction resistance coefficients) of the Qunli Coal Mine were systematically measured, as detailed in

Table 2. Measurements of main roadway size and ventilation parameters in Xinxing Mine.

Roadway Number	Roadway Shape	Roadway Cross-Sectional Area/m2	Roadway Perimeter/m	Roadway Length/m	Atkinson Resistance Coefficient (N·s2/m4)
North Main Entry Return	Semicircular arch	11.3	11.3	246.2	0.01106
2122 Cutting Eye Return	Semicircular arch	13.9	12.8	129.8	0.03
2122 Cutting Eye Face	Semicircular arch	10.9	9.78	50.5	0.00167
Mine Total Return	Semicircular arch	14.7	13.9	65.9	0.058
2121 Mining Face	Rectangle	11.4	13.5	95.1	0.01583
1162 Airway Face	Rectangle	12.8	13.9	63.6	0.0098
1162 Machine Roadway Face	Rectangle	13.3	14.3	44.7	0.0657
2121 Mining Face Return	Semicircular arch	9	9	227.2	0.0067
1162 Airway Return	Rectangle	9.3	9	43.2	0.0067
1162 Machine Roadway Return	Semicircular arch	13.6	14.2	14.1	0.0067

. The table comprehensively documents critical parameters, including the roadway name, geometry type (cross-sectional shape), support structure, cross-sectional area (m²), perimeter (m), length (m), and the Atkinson resistance coefficient (N·s²/m⁴).

Following the coal and gas outburst at the Qunli Coal Mine, which propagated throughout the entire mining system, a comprehensive statistical analysis of gas concentration dynamics across all operational zones was conducted, with the quantified results systematically presented in

Table 3. Gas concentration changes in ventilation system roadways.

Location	Normal Gas Concentration	Gas First Arrival Time	Initial Gas Concentration	Peak Gas Concentration	Peak Gas Time
North Main Entry Return	0.23	13:44:08	1.1	7.05	13:44:21
2122 Cutting Eye Return	0.3	13:44:25	0.46	4.8	13:44:45
2122 Cutting Eye Face	0.33	13:45:06	0.5	3.95	13:45:22
Mine Total Return	0.35	13:44:47	0.4	5.71	13:45:04
2121 Mining Face	0.47	13:44:12	0.55	7.05	13:44:21
1162 Airway Face	0.57	13:45:09	0.7	7.88	13:46:36
1162 Machine Roadway Face	0.66	13:46:40	0.76	4	13:48:54
2121 Mining Face Return	0.66	13:46:28	0.74	6.71	13:47:33
1162 Airway Return	0.57	13:47:29	0.7	10	13:47:49
1162 Machine Roadway Return	0.57	13:58:16	0.8	1.5	13:58:49

.

3. Results

3.1. Visualized Construction of Coal and Gas Outburst Disaster Process

Coal, from a petrographic perspective, is a heterogeneous material composed of various macerals. Among them, vitrinite is the predominant maceral, which is closely related to the coking characteristics of coal [33]. To classify coal as prone to outbursts or not, a combination of factors should be considered. One widely accepted method is based on the gas content in the coal seam and the coal firmness coefficient. If the gas content in the coal seam exceeds 8 m³/t and the coal firmness coefficient is less than 0.5, the coal is generally considered to be at a higher risk of outbursts [34,35]. Other factors, such as geological structures and gas pressure, also play important roles in determining the outburst potential of coal.

The coal and gas outburst disaster process in coal mines is a complex dynamic phenomenon. Considering the characteristic analysis of mine network domain model factors during gas outburst disasters, this study employed numerical simulation based on active ventilation networks [10] to achieve a three-dimensional visualization reconstruction of the coal and gas outburst process. Using the TF1M3D [10] simulation platform, a coal and gas outburst accident was simulated and analyzed to determine the disaster-affected areas post-incident. The specific simulation workflow on the TF1M3D platform is illustrated in Figure 3.

Based on mine information and the influencing factors of coal and gas outbursts, the constructed mine gas disaster network domain model is a sophisticated system composed of multi-dimensional details and attributes. The gas outburst disaster network domain model incorporates three key parameter categories: spatial–geometric network parameters, physical property network parameters, and environmental attribute network parameters [36,37]. Through characteristic analysis of these network domain parameters, the gas outburst disaster process demonstrates differentiated network domain behaviors across distinct phases, as visually represented in Figure 4.

3.2. Simulation Results Analysis

3.2.1. Gas Dispersion Simulation Results

Following a coal and gas outburst dynamic disaster, gas dispersion across the mine network typically progresses through three distinct phases: the source dynamic influence phase, the post-outburst natural flow phase, and the ventilation restoration phase. The TF1M3D software (first version) mentioned previously was used to conduct numerical simulations of the Qunli Coal Mine, and relevant parameter data, such as gas and air volume during the coal and gas outburst disaster process, were obtained. The main parameters adopted include the following: the gas outburst volume was set to 49,000 m³, the temperature was 293 K, the initial pressure was 2.8 MPa, and the diffusion coefficient was set to 0.021 m²/s.

Figure 5 illustrates the gas concentration contour maps within the mine during these disaster simulation phases. Critical temporal nodes at 2 s, 122 s, 527 s, and 1127 s were selected to analyze the gas distribution patterns. The results demonstrate that gas rapidly propagated from the outburst epicenter (the temporary sump excavation face) throughout the mine network. The key findings include the following: At 122 s post-outburst, adjacent roadways reached gas concentrations exceeding 90%, accompanied by gas backflow in the main adit. Following ventilation system reactivation (527–1127 s), gas concentrations exhibited progressive attenuation, though residual concentrations (15–25%) persisted in localized zones before complete dissipation.

3.2.2. Dynamic Risk Assessment Results

For computational and analytical clarity, all roadways were systematically numbered, with the simplified network comprising 25 representative roadways, as depicted in Figure 6. Computational analysis of the ventilation system yielded key ventilation parameters for each roadway, with the comprehensive quantitative dataset tabulated in

Table 4. Disaster simulation data.

Tunnel Number	Airflow Stability Coefficient	Gas Concentration Information Entropy	Probability	DRI	Risk Level
1	1.6567	−0.2788	0.089783	0.8825	Medium Risk
2	3.5945	−0.2788	0.089783	2.04518	High Risk
3	10.2806	−0.0291	0.094323	6.15672	High Risk
4	0.4003	−0.3582	0.075327	0.0969	Medium Risk
5	0.5386	−0.3402	0.082779	0.18708	Medium Risk
6	5.5651	−0.671	0.019506	3.07066	High Risk
7	5.5651	−0.6821	0.019506	3.06622	High Risk
8	5.5651	−0.6931	0.019506	3.06182	High Risk
9	0.5019	−0.2168	0.089783	0.21442	Medium Risk
10	0.3921	−0.3008	0.08763	0.11494	Medium Risk
11	0.3616	−0.3074	0.087306	0.094	Medium Risk
12	0.3616	−0.3136	0.086662	0.09152	Medium Risk
13	9.9862	−1.3781	0.009874	5.44048	High Risk
14	0.8178	−0.6631	0.019506	0.22544	Medium Risk
15	0.7457	−4.291	0.052839	−1.26898	Low Risk
16	0.4124	−0.5611	0.018373	0.023	Medium Risk
17	0.361	−0.5203	0.027802	0.00848	Medium Risk
18	0.2948	−0.4844	0.044202	−0.01688	Low Risk
19	0.4232	−0.4791	0.043793	0.06228	Medium Risk
20	0.3966	−0.4386	0.060508	0.06252	Medium Risk
21	0.4419	−0.3582	0.075327	0.12186	Medium Risk
22	0.7186	−0.3402	0.082779	0.29508	Medium Risk
23	0.428	−1.2906	0.001971	−0.25944	Low Risk
24	0.428	−1.9191	0.010308	−0.51084	Low Risk
25	0.428	−0.4386	0.060508	0.08136	Medium Risk

.

According to the simulation results, the outburst volume was 49,000 m³, and the air volume stability coefficient values ranged widely from 0.2948 to 10.2806. Among them, two high values were observed in Roadway 3 (10.2806) and Roadway 13 (9.9862), indicating potential risks of extreme fluctuations. Roadway 3 is located at the outburst point and experienced the highest dynamic force from the coal and gas outburst, with the most changes. Roadway 13 is the main intake airway of the main adit, which experienced reverse airflow with high velocity during the entire disaster process. All gas concentration accumulation information entropy values for all mine roadways obtained from the disaster process simulation were negative, ranging from −4.2910 to −0.0291. The extreme value occurred in Roadway 15 (−4.2910), indicating a significant increase in information chaos of gas concentration in this roadway.

The probability of gas explosion within the mine ventilation network in the [0.05, 0.15] interval ranged from 0.001971 to 0.094323, with most values concentrated between 0.01 and 0.09. The overall low probabilities suggest that the gas concentration distribution within the [0.05, 0.15] interval is relatively rare, possibly related to actual safety thresholds. The dynamic risk index ranged from −0.9955 (Roadway 15) to 6.1356 (Roadway 3). High values were dominated by air volume stability (e.g., Roadways 3 and 13), while low values were dominated by gas concentration accumulation information entropy (e.g., Roadway 15).

The air volume stability coefficient, gas accumulation information entropy, and dynamic risk index were plotted as a heatmap (Figure 7). Observations from the figure include the following: Higher air volume stability coefficients indicate greater instability and fluctuations in the mine ventilation system. Lower gas concentration information entropy values reflect chaotic and severe variations in gas concentration distribution within the roadways. The dynamic risk index appeared in areas with high air volume stability coefficients, where gas concentration accumulation information entropy was not necessarily maximal. The dynamic risk index quantifies the overall dynamic hazard intensity of the mine ventilation system, with high values indicating significant system fluctuations or intense responses. The dynamic risk index was concentrated in regions with relatively high air volume stability coefficients and gas concentration information entropy.

Table 5. Catastrophe simulation data under varying outburst intensities.

Outburst Volume/m3	Tunnel Number	Airflow Stability Coefficient	Gas Concentration Information Entropy	Probability	DRI	Risk Level
100,000	3	12.0115	−0.3143	0.094692	7.08118	High
	13	8.1915	−0.6645	0.028025	4.6491	High
	2	3.3352	−0.5704	0.053568	1.77296	Medium
	6	7.6507	−0.8561	0.032465	4.24798	High
49,000	3	10.2806	−0.0291	0.094323	6.15672	High
	13	9.9862	−1.3781	0.0098736	5.44048	High
	2	3.5945	−0.2788	0.089783	2.04518	High
	6	5.5651	−0.671	0.019506	3.07066	High
10,000	3	6.2226	−0.6287	0.093295	3.48208	High
	13	0.6638	−0.9736	0.020664	0.00884	Medium
	2	2.2881	−0.7283	0.000022512	1.08154	Medium
	6	0.5349	−0.8654	0.022465	−0.02522	Low
1000	3	0.9532	−0.8567	0.08739	0.22924	Medium
	13	0.3186	−0.4277	0.000021982	0.02008	Medium
	2	0.4133	−0.5179	0.000019983	0.04082	Medium
	6	0.1618	−0.6132	0.000018167	−0.1482	Low

presents the parameters, including the air volume stability coefficient, gas concentration entropy, probability, dynamic risk index, and risk level, obtained from four experiments with varying coal and gas outburst intensities: 100,000 m³, 10,000 m³, 1000 m³, and the previously simulated 49,000 m³. Four representative roadways (13, 3, 2, and 6) were selected to analyze the variations in the gas concentration entropy and other parameters under different outburst intensities.

As the outburst intensity decreased, the proportion of high-risk levels in these roadways decreased, while medium and low risks increased. A significant positive correlation trend was observed between the air volume stability coefficient and the dynamic risk index (e.g., for an outburst volume of 100,000 m³, an air volume stability coefficient of 12.01 corresponded to a dynamic risk of 7.08; a coefficient of 0.95 corresponded to a risk of 0.23). More negative gas concentration entropy values (e.g., −1.3781) correlated with lower probabilities of gas accumulation within the explosion limit (0.0098), indicating reduced system uncertainty.

4. Discussion

As a complex dynamic disaster, coal and gas outburst has seen, in recent years, data-driven approaches—especially machine learning methods—emerge as powerful tools for nonlinear systems [38,39]. Wu et al. [40] designed a coal mine safety risk index analysis system based on big data. Through multisource data fusion, this system implements a safety situation awareness and analysis platform for coal mines and establishes a risk assessment indicator system and a two-level risk assessment model. Li Shuang et al. [41] proposed a prediction model based on the improved grey wolf optimizer–support vector machine (IGWO-SVM), aiming to improve the accuracy of coal and gas outburst risk prediction. This study introduces a new dynamic risk assessment framework by integrating the analytic hierarchy process (AHP) and information entropy, addressing the limitations of static methods in coal and gas outburst accidents. The framework is elaborated in the three following aspects:

(1) Comparison with Actual Disaster Data

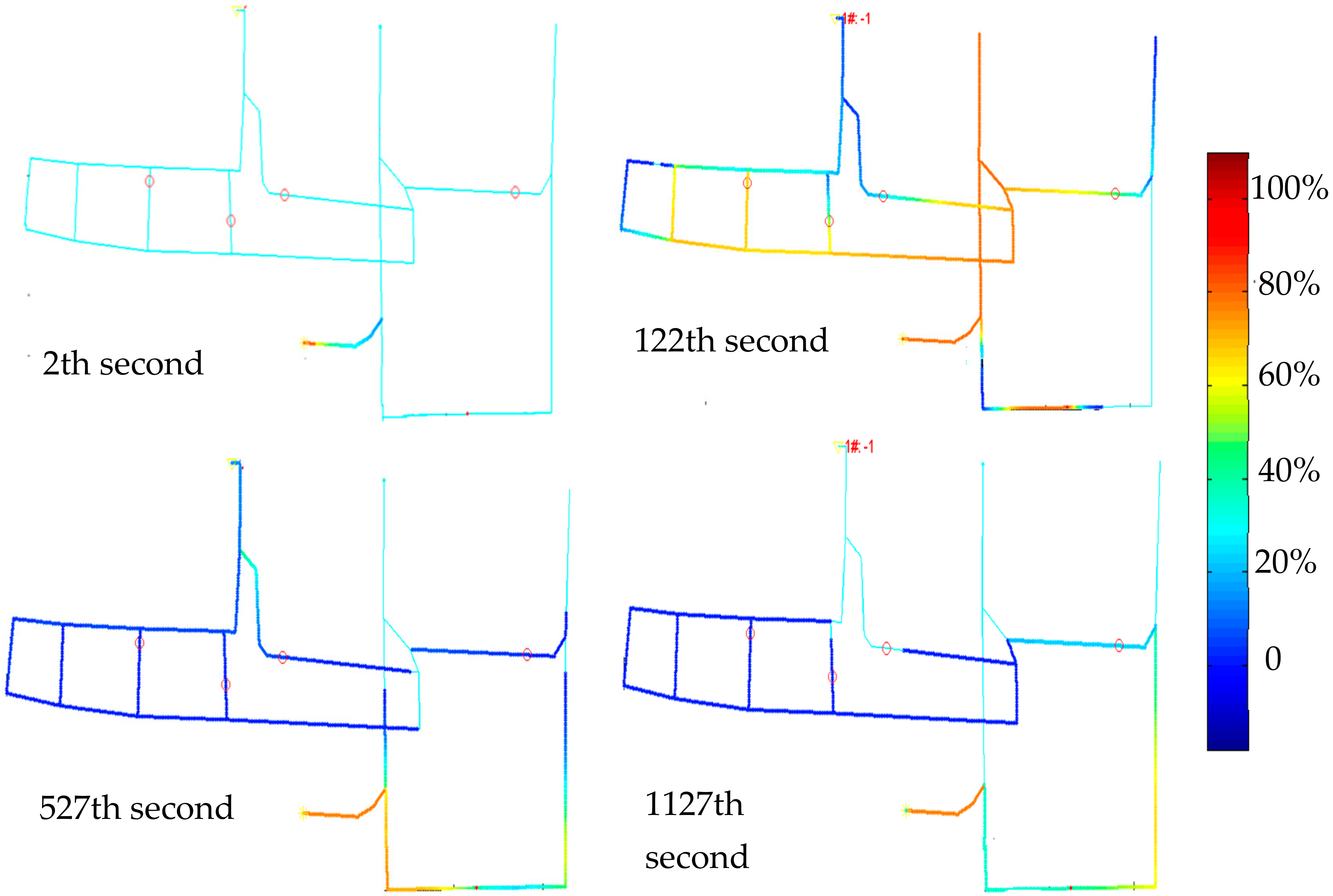
According to experimental records, Table 3 lists gas concentration data from Qunli Coal Mine roadways after the accident. The accident involved gas reverse flow primarily in the main adit, with a reverse flow distance of approximately 600 m. As shown in the figure below, the roadway experienced negative wind speed at 2 s, which ceased after ventilation resumed at 44 s. The concentration variation curve indicates that during the simulation, gas diffused into the roadway, reaching a maximum concentration of 41.4729% at 1526 s. This demonstrates that the accident simulation accurately reproduced the actual accident scenario.

(2) Correlation Analysis of Air Volume Stability Coefficient and Gas Accumulation Information Entropy

To further analyze whether the air volume stability coefficient and gas accumulation information entropy independently affect the dynamic risk index during disaster periods, a correlation verification between the two factors was conducted. Pearson’s correlation coefficient was used to determine their linear relationship. Pearson’s correlation coefficient (Pearson’s r) is a statistical measure quantifying the strength of linear correlation between two variables, ranging from −1 to 1. A value of 1 indicates perfect positive correlation, −1 indicates perfect negative correlation, and 0 indicates no linear correlation. The Pearson’s r was calculated as follows:

$$r={\displaystyle \frac{\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum _{i=1}^n{(x_i-\overline{x})}^2{(y_i-\overline{y})}^2}}}$$

(19)

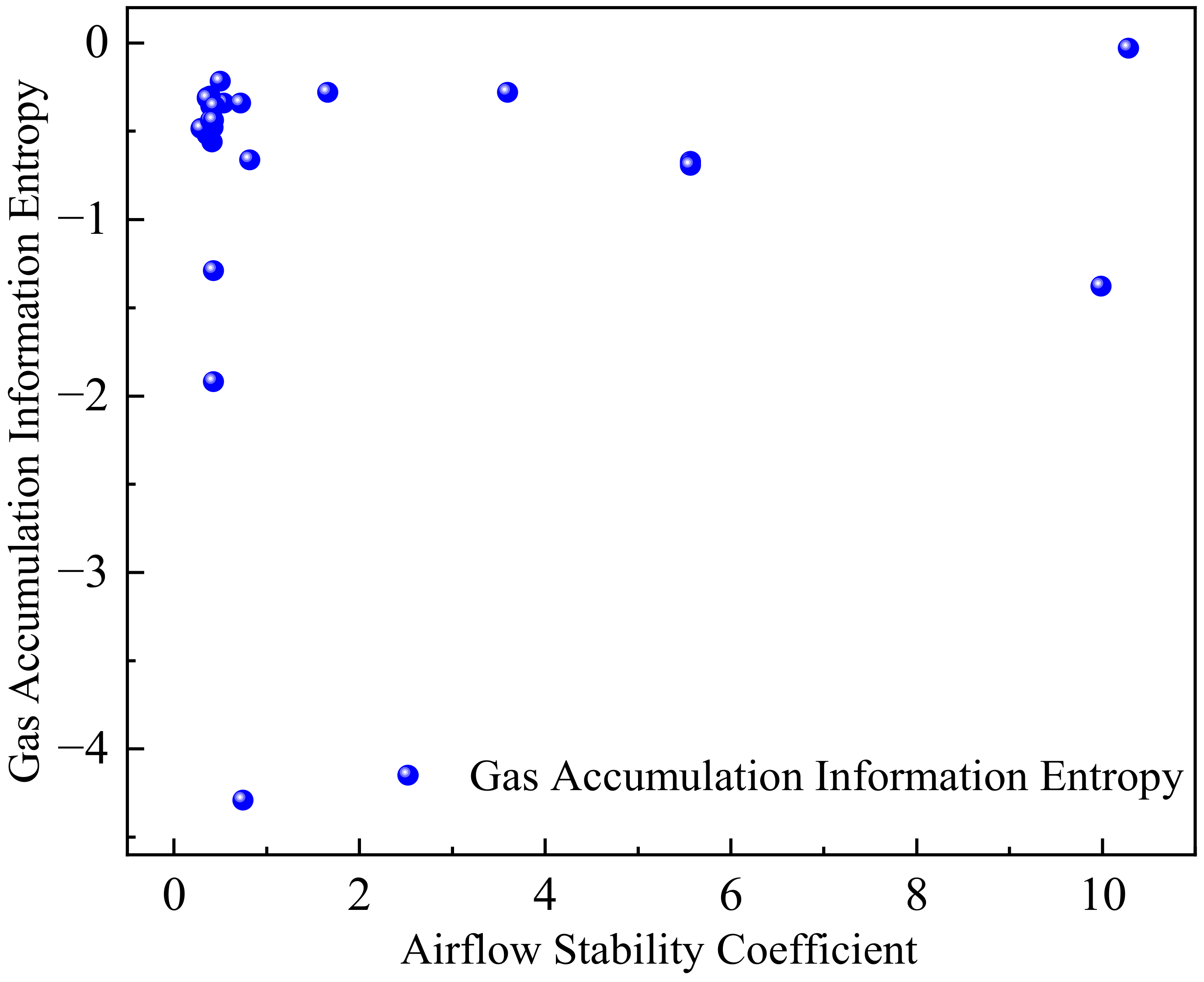
The air volume stability coefficient and gas accumulation information entropy data from Table 5 were substituted into the formula, resulting in a Pearson’s correlation coefficient of 0.215. Given that Pearson’s r ≈ 0.215 (close to 0), the results indicate a very weak linear correlation between the two variables. With 23 degrees of freedom and a significance level of 0.05, the critical value from the table is approximately 0.396. Since |r| = 0.215 < 0.396, there is no significant correlation between the air volume stability coefficient and gas accumulation information entropy. Furthermore, a scatter plot (Figure 8) was generated, with the horizontal axis representing the air volume stability coefficient and the vertical axis representing gas accumulation information entropy. The data points exhibit a random distribution, ruling out any nonlinear relationship.

(3) Application of Analytic Hierarchy Process-Information Entropy Method in Mine Monitoring

The analytic hierarchy process (AHP)–information entropy method can be applied to dynamically assess gas accumulation during disaster periods. Based on the dynamic risk index, preset thresholds for the ventilation system are established and integrated with mine monitoring systems to optimize early warning measures. Changes in information entropy can reflect real-time dynamic characteristics of gas concentration in mines, providing mine managers with real-time risk assessment data to facilitate timely prevention and control actions. Through data collection, accident simulation, information entropy calculation, and hazard assessment, mines can achieve real-time monitoring and accurate prediction of gas concentration variations, enabling timely early warnings and optimized prevention measures.

5. Conclusions

Using information entropy analysis theory to evaluate gas concentration accumulation hazards in roadways during disaster periods, a calculation method for roadway stability coefficients during coal and gas outbursts was proposed. The kernel density method was applied to estimate the gas concentration density function, and a calculation approach for gas accumulation hazard information entropy in roadways during disasters was established. By adopting gas concentration and airflow variations as indicators for assessing gas accumulation hazards, a dynamic risk index was introduced to quantify risk levels, enabling a transition from static thresholds to dynamic early warnings. Additionally, the probability of gas accumulation within the explosion limit [0.05, 0.15] was determined, achieving quantitative evaluation of gas accumulation hazards. Furthermore, gas concentration locations derived from numerical modeling provide critical spatial context for the dynamic risk assessment framework, enabling more precise identification of high-risk zones where gas accumulation may exacerbate outburst hazards. This contributes to optimizing real-time risk assessment in mine monitoring and early warning systems, providing a more scientific and effective approach for coal mine gas disaster prevention and control.