Nondestructive Detection of Submillimeter Air Cavities in Alumina-Doped Epoxy Resin Composites Using the Infrared Thermography
Abstract
1. Introduction
2. Materials and Methods
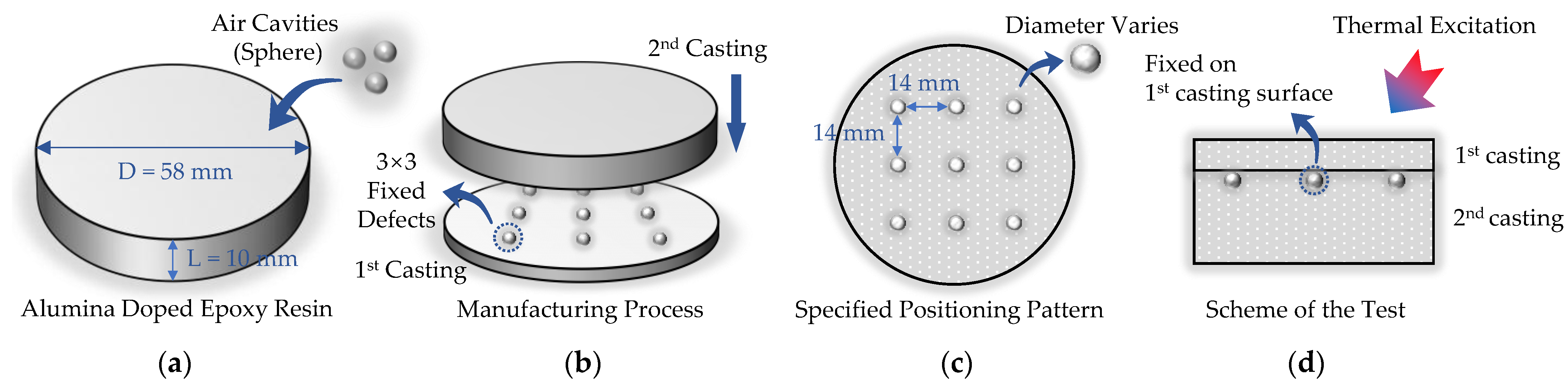
2.1. Material Description and Test Details
2.2. Experimental Details of Long Pulse Thermography
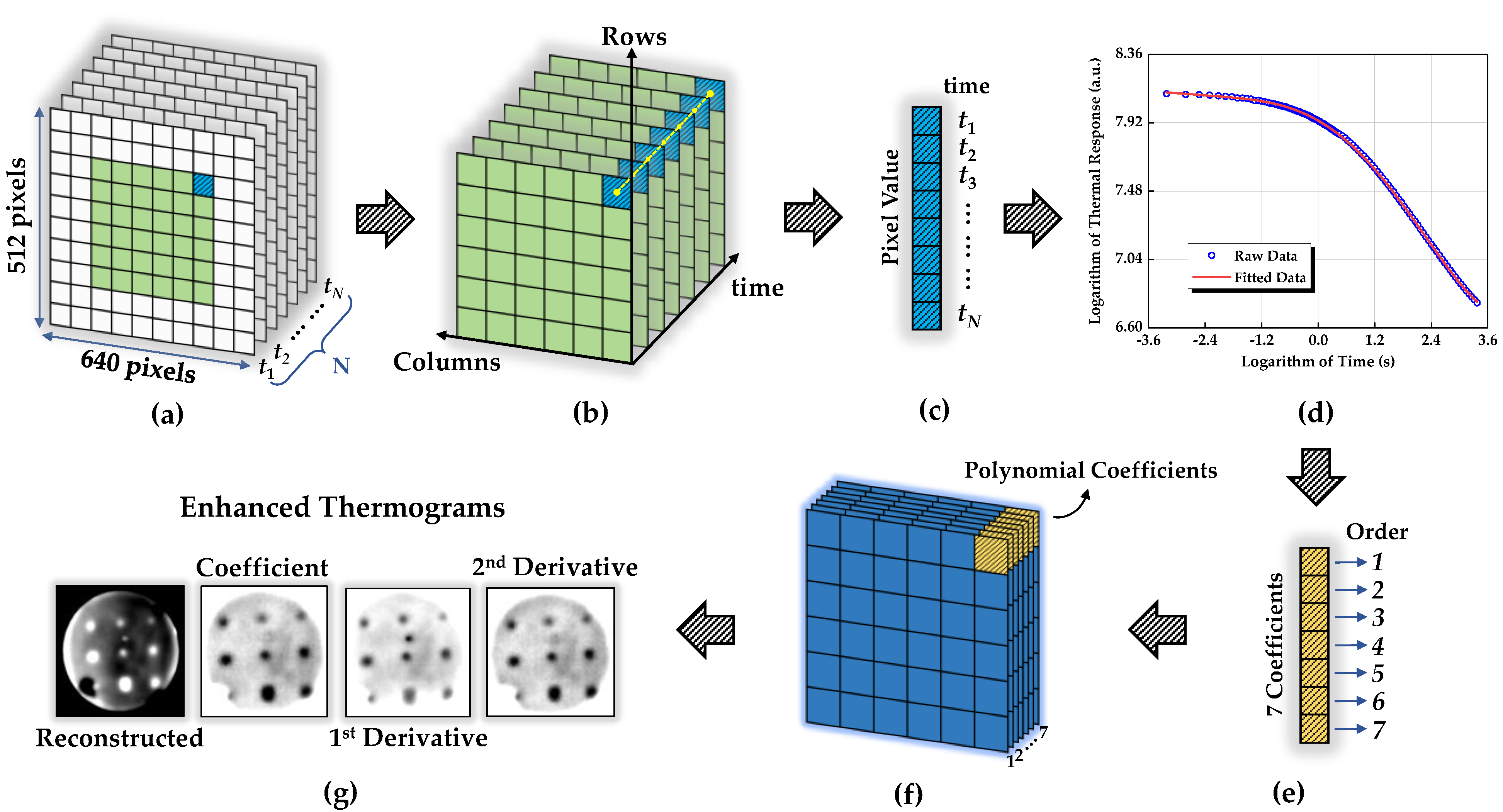
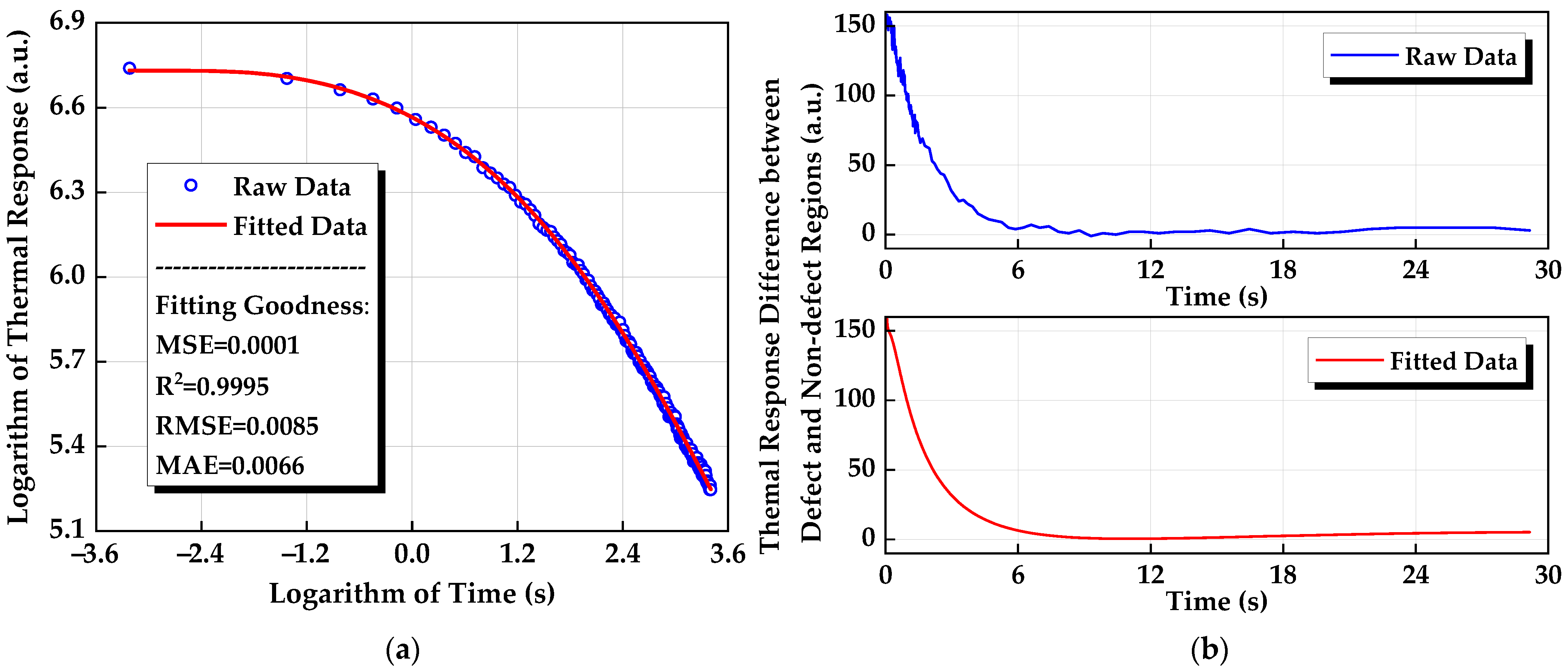
2.3. Data Processing Techniques
3. Results
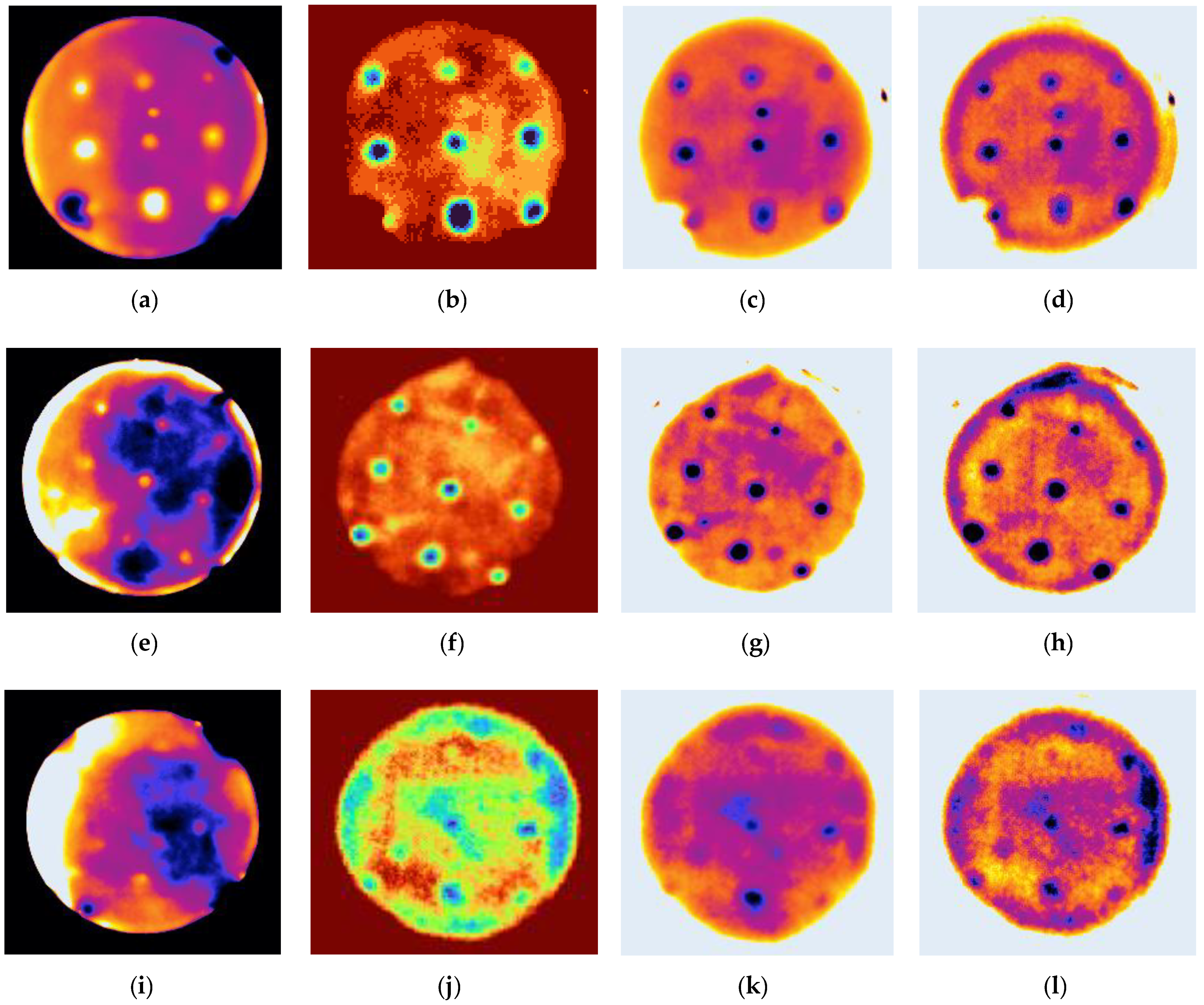
3.1. Thermal Images and Processed Results
3.2. Defect Detection
3.3. Quantitative Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tayseer, M.; Talaat, M.; Farahat, M.A. Optimum design of spacer material of gas-insulated switchgear by utilizing the technology of functionally graded material using different artificial optimization techniques. Surf. Coat Tech. 2024, 479, 130530. [Google Scholar] [CrossRef]
- Sarthak, S.; Ashok, M.; Shardul, J. Structural and modal analysis of gas insulated switchgear structure made up of glass-epoxy and carbon-epoxy composite materials for seismic application. Mater. Today Proc. 2023, 78, 501–507. [Google Scholar] [CrossRef]
- Han, X.; Zhang, X.; Guo, R.; Wang, H.; Li, J.; Li, Y. Partial discharge detection in Gas-Insulated Switchgears using sensors integrated with UHF and optical sensing methods. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 2026–2033. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, J.; Yang, Z.; Qi, Z.; Wang, J.; Geng, Y. Gas-Insulated Switchgear insulation defect diagnosis via a novel domain adaptive graph convolutional network. IEEE Trans. Instrum. Meas. 2022, 71, 3508910. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, Y.; Zhang, B.; He, J. Measurement of multipath transients in secondary cables near a 500 kV Gas-Insulated Switchgear during operations. IEEE Trans. Power Deliv. 2022, 38, 917–925. [Google Scholar] [CrossRef]
- Hao, Y.; Zheng, Y.; He, W.; Liang, X.; Zhang, Z.; Liu, L. A measurement method of ultrasonic critical refraction longitudinal wave for thermal stress in GIS basin-type insulators. IEEE Trans. Instrum. Meas. 2021, 71, 6001009. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Ding, H.; Jia, B.; Zhou, W.; Lu, W. Modeling of surface trapping effect on charge accumulation pattern at gas–solid interface in DC GIL. IEEE Trans. Dielectr. Electr. Insul. 2023, 31, 466–476. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, Z.; Liu, L. Defects and failure types of solid insulation in gas-insulated switchgear: In situ study and case analysis. High Volt. 2022, 7, 158–164. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, Y.; Shen, Z.; Liu, L.; Yao, C.; Huang, S. Ultrasonic longitudinal wave reflection propagation model and defect detection method for the cone of 126-kV three-phase basin insulators. IEEE Trans. Dielectr. Electr. Insul. 2024, 73, 9004608. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Yang, S.; Li, H.; Wang, B.; Qiao, S. Detection of intense partial discharge of epoxy insulation in sf6 insulated equipment using carbonyl sulfide. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2942–2948. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, W.; Zhao, H. Defect detection on operating insulation spacer of GIS based on 3D X⁃ray digital imaging technology. High Volt. Appar. 2022, 58, 230–236. [Google Scholar] [CrossRef]
- Muhammet, E.T.; Argyrios, Z.; Nicolas, P.A.; Muflih, A.; Clemente, I.; Maldague, X.P. A complementary fusion-based multimodal non-destructive testing and evaluation using phased-array ultrasonic and pulsed thermography on a composite structure. Materials 2024, 17, 3435. [Google Scholar] [CrossRef] [PubMed]
- Pan, P.; Zhang, R.; Yi Zhang, Y.; Li, H. Detecting internal defects in FRP-reinforced concrete structures through the integration of infrared thermography and deep learning. Materials 2024, 17, 3350. [Google Scholar] [CrossRef] [PubMed]
- Malgorzata, C.; Adam, S.; Marek, B.; Marcin, A. Evaluation and defect detection in L-Shaped GFRP laminates by infrared thermography. Materials 2024, 17, 2830. [Google Scholar] [CrossRef]
- Xiaoli Li, X.; Zhi Zeng, Z.; Shen, J.; Zhang, C.; Zhao, Y. Rectification of depth measurement using pulsed thermography with logarithmic peak second derivative method. Infrared Phys. Tech. 2018, 89, 1–7. [Google Scholar] [CrossRef]
- Zou, X.; Li, M.; Xu, H.; Lu, X. Array infrared thermography for visualization of defects in bonded fiber reinforced polymer joints. Compos. Sci. Technol. 2024, 259, 110930. [Google Scholar] [CrossRef]
- Shepard, S.M. Reconstruction and enhancement of active thermographic image sequences. Opt. Eng. 2003, 42, 1337–1342. [Google Scholar] [CrossRef]
- Maldague, X.; Marinetti, S. Pulse Phase Thermography. J. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Liu, L.; Wang, L.; Guo, C.; Mei, H.; Zhao, C. Detecting defects in porcelain post insulator coated with room temperature vulcanized silicone rubber by pulsed thermography. IEEE Trans. Instrum. Meas. 2019, 68, 225–233. [Google Scholar] [CrossRef]
- Liu, L.; Mei, H.; Guo, C.; Tu, Y.; Wang, L.; Liu, J. Remote optical thermography detection method and system for silicone polymer insulating materials used in power industry. IEEE Trans. Instrum. Meas. 2020, 69, 5782–5790. [Google Scholar] [CrossRef]
- Guo, C.; Liu, L.; Mei, H.; Tu, Y.; Wang, L. Nondestructive Evaluation of Composite Bonding Structure Used in Electrical Insulation Based on Active Infrared Thermography. Polymers 2022, 14, 3373. [Google Scholar] [CrossRef] [PubMed]
- Rezazadeh, N.; Annaz, F.; Jabbar, W.A.; Vieira Filho, J.; De Oliveira, M. A transfer learning approach for mitigating temperature effects on wind turbine blades damage diagnosis. Struct. Health Monit. 2025. [Google Scholar] [CrossRef]
- Vavilov, V.; Burleigh, D. Infrared Thermography and Thermal Nondestructive Testing; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Lopez, F.; Ibarra-Castanedo, C.; Maldague, X.; de Paulo Nicolau, V. Analysis of signal processing techniques in pulsed thermography. In Proceedings of the Thermosense: Thermal Infrared Applications XXXV, Baltimore, MA, USA, 29 April–3 May 2013; Volume 8705. [Google Scholar] [CrossRef]
- Vavilov, P.V.; Burleigh, D.D. Review of pulsed thermal NDT: Physical principles, theory and data processing. NDT E Int. 2015, 73, 28–52. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, G.; Meo, M.; Ciampa, F. Image processing based quantitative damage evaluation in composites with long pulse thermography. NDT E Int. 2018, 99, 93–104. [Google Scholar] [CrossRef]




| Sample No. | Defect Depth z (mm) | Defect Diameter d (mm) | Defect Naming | ||||
|---|---|---|---|---|---|---|---|
| Sample 1 | 0.6 | 0.5 | 0.3 | 0.2 | R1C1 | R1C2 | R1C3 |
| 1.1 | 0.7 | 0.9 | |||||
| 1.4 | 1.8 | 1.2 | |||||
| Sample 2 | 0.8 | 0.5 | 0.3 | 0.2 | R2C1 | R2C2 | R2C3 |
| 1.1 | 1.4 | 0.7 | |||||
| 1.8 | 2.0 | 1.6 | |||||
| Sample 3 | 1.2 | 0.3 | 0.6 | 0.8 | R3C1 | R3C2 | R3C3 |
| 1.0 | 1.8 | 1.5 | |||||
| 2.5 | 3.0 | 2.0 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Fan, L.; Bai, J.; Zheng, R.; Wei, L.; Yang, W.; Yang, Y.; Guo, Z.; Zhao, X. Nondestructive Detection of Submillimeter Air Cavities in Alumina-Doped Epoxy Resin Composites Using the Infrared Thermography. Processes 2025, 13, 1304. https://doi.org/10.3390/pr13051304
Li B, Fan L, Bai J, Zheng R, Wei L, Yang W, Yang Y, Guo Z, Zhao X. Nondestructive Detection of Submillimeter Air Cavities in Alumina-Doped Epoxy Resin Composites Using the Infrared Thermography. Processes. 2025; 13(5):1304. https://doi.org/10.3390/pr13051304
Chicago/Turabian StyleLi, Bo, Lei Fan, Jie Bai, Ruifeng Zheng, Liangliang Wei, Wenhao Yang, Yantao Yang, Zhengwei Guo, and Xuetong Zhao. 2025. "Nondestructive Detection of Submillimeter Air Cavities in Alumina-Doped Epoxy Resin Composites Using the Infrared Thermography" Processes 13, no. 5: 1304. https://doi.org/10.3390/pr13051304
APA StyleLi, B., Fan, L., Bai, J., Zheng, R., Wei, L., Yang, W., Yang, Y., Guo, Z., & Zhao, X. (2025). Nondestructive Detection of Submillimeter Air Cavities in Alumina-Doped Epoxy Resin Composites Using the Infrared Thermography. Processes, 13(5), 1304. https://doi.org/10.3390/pr13051304







