Adaptive Differential Evolution Integration: Algorithm Development and Application to Inverse Heat Conduction
Abstract
1. Introduction
2. The Adaptive Differential Evolution Integrated Optimization Algorithm Based on a Dynamic Tracking Strategy
2.1. The Basic Idea of the Dynamic Following Integrated Strategy
2.2. The DE-Based Leadership Population
2.3. The PSO-Based Mass Population
| Algorithm 1: Principle of ACDE algorithm. |
 |
- 1.
- Initialize the maximum number of fitness evaluations , the dimensionality D of the search space for the optimization problem, the size N of the leader population, the size P of the mass population, the reserve values of the control parameters F and for the leading particles, the learning factors , , and for the mass population particles, the inertia weight , and the influence radius scaling factor d. Randomly initialize the positions of the particles in the leader population within the search space, randomly initialize the positions and velocities of the particles in the mass population, and randomly initialize the conformity thresholds of the mass population particles. To keep track of the number of fitness evaluations, set a counter .
- 2.
- Calculate the fitness values of all particles, and during the iterative calculation process, record the optimal particle of the leading group and the optimal particle of the mass population based on the fitness values. Select the one with smaller fitness as the global optimal particle . Update the counter .
- 3.
- Calculate the influence radius R of the global optimal particle according to (1). Compute the distances between all crowd particles and the global optimal particle, select all particles within the influence radius, and divide the affected particles into three sub-populations based on their conformity thresholds. Update the velocities and positions of the particles in these sub-populations according to Equations (11) to (13), and calculate the fitness values of the obtained mass population particles to obtain the new optimal particle of the mass population. Update the counter .
- 4.
- is utilized to replace a randomly selected non-optimal solution within the leader population. Generate the trial vectors according to the ACDE in Algorithm 1, calculate the fitness values of all of the trial vectors, update the leader population from the previous generation, and select the optimal particle of the leader population. Update the counter .
- 5.
- Compare the fitness values of the optimal particle of the leader population and the optimal particle of the crowd group, and update the global optimal particle .
- 6.
- Check whether the maximum number of fitness evaluations has been reached. If , terminate the optimization and output the vector value of the global optimal particle as the global optimal solution. Otherwise, go to Step 3 and continue the optimization process.
3. Experiments
3.1. Benchmark Function Experiments
- (1)
- An Ablation Experiment
- (2)
- Comparison with State-of-the-Art Algorithms
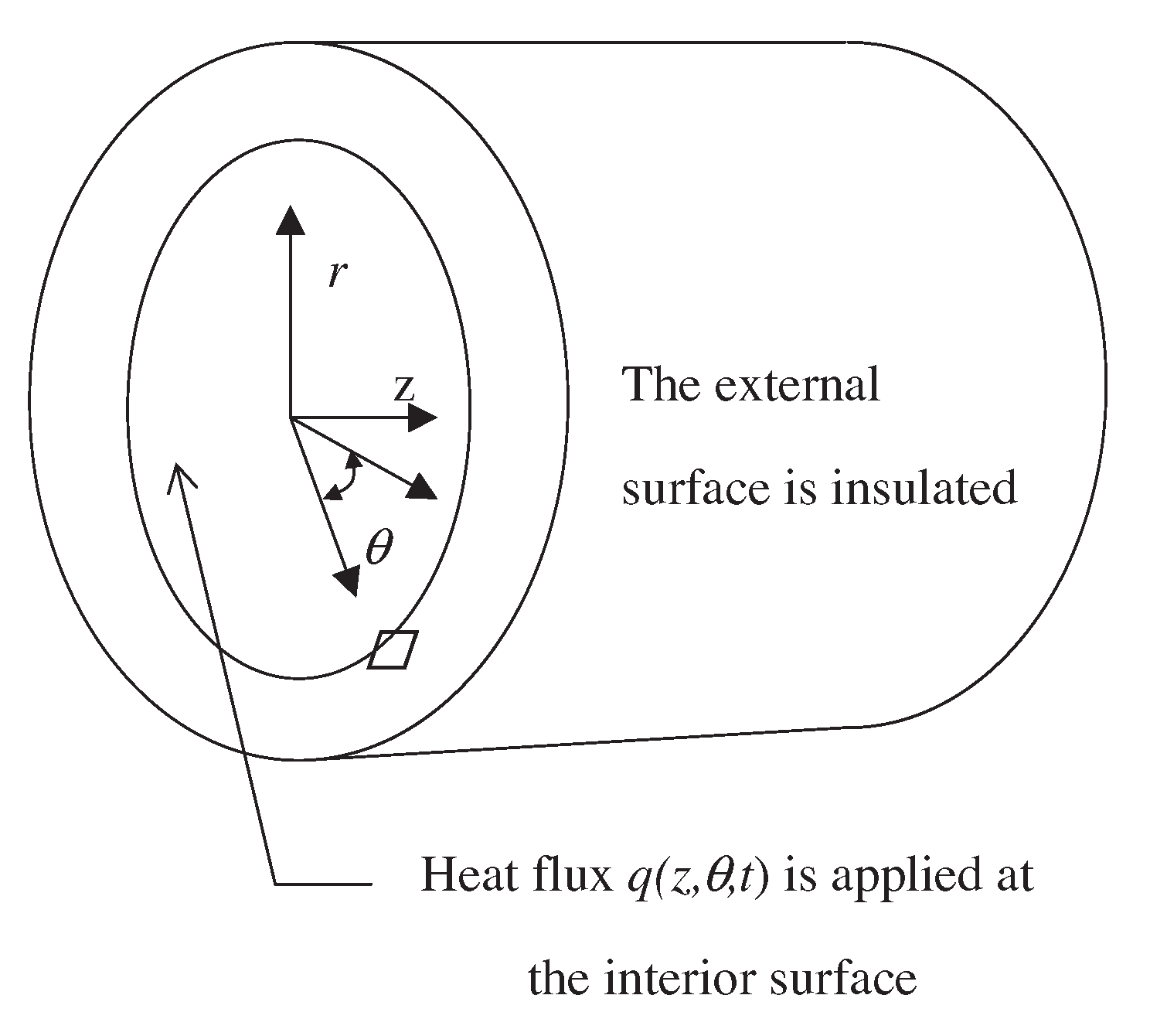
3.2. Three-Dimensional Inverse Heat Conduction Problem Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, Y.; Zhang, C.; Gharehchopogh, F.S.; Mirjalili, S. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems. Expert Syst. Appl. 2023, 215, 119269. [Google Scholar] [CrossRef]
- Teekaraman, Y.; Manoharan, H.; Basha, A.R.; Manoharan, A. Hybrid optimization algorithms for resource allocation in heterogeneous cognitive radio networks. Neural Process. Lett. 2023, 55, 3813–3826. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Yin, X. Precast production scheduling in off-site construction: Mainstream contents and optimization perspective. J. Clean. Prod. 2023, 405, 137054. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Ahmad, M.F.; Isa, N.A.M.; Lim, W.H.; Ang, K.M. Differential evolution: A recent review based on state-of-the-art works. Alex. Eng. J. 2022, 61, 3831–3872. [Google Scholar] [CrossRef]
- Papazoglou, G.; Biskas, P. Review and comparison of genetic algorithm and particle swarm optimization in the optimal power flow problem. Energies 2023, 16, 1152. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, S.; Jia, W. A hybrid optimization algorithm based on cuckoo search and differential evolution for solving constrained engineering problems. Eng. Appl. Artif. Intell. 2019, 85, 254–268. [Google Scholar] [CrossRef]
- Rosić, M.B.; Simić, M.I.; Pejović, P.V. An improved adaptive hybrid firefly differential evolution algorithm for passive target localization. Soft Comput. 2021, 25, 5559–5585. [Google Scholar] [CrossRef]
- Khan, A.; Hizam, H.; bin Abdul Wahab, N.I.; Lutfi Othman, M. Optimal power flow using hybrid firefly and particle swarm optimization algorithm. PLoS ONE 2020, 15, e0235668. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Eltaeib, T.; Dichter, J. Data optimization with differential evolution strategies: A survey of the state-of-the-art. In Proceedings of the 2017 IEEE International Conference on Power, Control, Signals and Instrumentation Engineering (ICPCSI), Chennai, India, 21–22 September 2017; pp. 17–23. [Google Scholar]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Faris, H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Lynn, N.; Suganthan, P.N. Ensemble particle swarm optimizer. Appl. Soft Comput. 2017, 55, 533–548. [Google Scholar] [CrossRef]
- Hui, S.; Suganthan, P.N. Ensemble and arithmetic recombination-based speciation differential evolution for multimodal optimization. IEEE Trans. Cybern. 2015, 46, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Tang, K.; Li, Z.; Luo, L.; Liu, B. Multi-strategy adaptive particle swarm optimization for numerical optimization. Eng. Appl. Artif. Intell. 2015, 37, 9–19. [Google Scholar] [CrossRef]
- Meng, Z.; Zhong, Y.; Mao, G.; Liang, Y. PSOsono: A novel PSO variant for single-objective numerical optimization. Inf. Sci. 2022, 586, 176–191. [Google Scholar] [CrossRef]
- El-Mihoub, T.A.; Hopgood, A.A.; Nolle, L.; Battersby, A. Hybrid Genetic Algorithms: A Review. Eng. Lett. 2006, 13, 124–137. [Google Scholar]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An enhanced hybrid arithmetic optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Spears, R. Social influence and group identity. Annu. Rev. Psychol. 2021, 72, 367–390. [Google Scholar] [CrossRef]
- Melamed, D.; Savage, S.V.; Munn, C. Uncertainty and social influence. Socius 2019, 5, 2378023119866971. [Google Scholar] [CrossRef]
- Liu, X.; Huang, C.; Dai, Q.; Yang, J. The effects of the conformity threshold on cooperation in spatial prisoner’s dilemma games. Europhys. Lett. 2019, 128, 18001. [Google Scholar] [CrossRef]
- Zhou, T.; Hu, Z.; Su, Q.; Xiong, W. A clustering differential evolution algorithm with neighborhood-based dual mutation operator for multimodal multiobjective optimization. Expert Syst. Appl. 2023, 216, 119438. [Google Scholar] [CrossRef]
- Liang, J.J.; Qu, B.; Suganthan, P.N.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2013; Volume 201212, pp. 281–295. [Google Scholar]
- Wang, X.; Zhao, H.; Han, T.; Zhou, H.; Li, C. A grey wolf optimizer using Gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem. Appl. Soft Comput. 2019, 78, 240–260. [Google Scholar] [CrossRef]
- Tu, Q.; Chen, X.; Liu, X. Multi-strategy ensemble grey wolf optimizer and its application to feature selection. Appl. Soft Comput. 2019, 76, 16–30. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Cleghorn, C.W.; Engelbrecht, A.P. Fitness-distance-ratio particle swarm optimization: Stability analysis. In Proceedings of the Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017; pp. 12–18. [Google Scholar]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Qu, B.Y.; Suganthan, P.N.; Das, S. A distance-based locally informed particle swarm model for multimodal optimization. IEEE Trans. Evol. Comput. 2012, 17, 387–402. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Q.; Mao, W.; Liu, S.; Dou, Z.; Liu, G. Hybrid Particle Swarm and Grey Wolf Optimizer and its application to clustering optimization. Appl. Soft Comput. 2021, 101, 107061. [Google Scholar] [CrossRef]
- Liu, F.B. Particle swarm optimization-based algorithms for solving inverse heat conduction problems of estimating surface heat flux. Int. J. Heat Mass Transf. 2012, 55, 2062–2068. [Google Scholar] [CrossRef]
- Udayraj; Mulani, K.; Talukdar, P.; Das, A.; Alagirusamy, R. Performance analysis and feasibility study of ant colony optimization, particle swarm optimization and cuckoo search algorithms for inverse heat transfer problems. Int. J. Heat Mass Transf. 2015, 89, 359–378. [Google Scholar]




| DE | CoDE | DE-PSO | ADEI | |
|---|---|---|---|---|
| f1 | 1.15 ± 6.68 | ± | 1.14 ± 1.14 | ± |
| f2 | 2.02 ± 8.01 | 2.96 ± 1.74 | 5.14 ± 1.72 | ± |
| f3 | 4.29 ± 2.05 | ± | 1.12 ± 2.17 | 1.84 ± 2.87 |
| f4 | 3.95 ± 6.68 | 3.91 ± 5.08 | 3.12 ± 1.47 | ± |
| f5 | 2.34 ± 6.91 | ± | 1.36 ± 4.55 | ± |
| f6 | 1.79 ± 1.27 | 5.61 ± 6.89 | 1.21 ± 7.17 | ± |
| f7 | 5.61 ± 9.13 | 9.56 ± 6.23 | 6.23 ± 5.19 | ± |
| f8 | 2.10 ± 2.81 | 2.09 ± 4.62 | 2.10 ± 4.31 | ± |
| f9 | 3.97 ± 7.46 | ± | 2.38 ± 9.17 | 1.32 ± 3.27 |
| f10 | 5.31 ± 1.66 | 1.48 ± 1.10 | ± | 3.19 ± 2.22 |
| f11 | 1.40 ± 3.99 | 4.54 ± 6.27 | 2.78 ± 5.43 | ± |
| f12 | 2.44 ± 1.02 | ± | 1.58 ± 7.07 | 3.62 ± 1.06 |
| f13 | 2.42 ± 1.79 | ± | 2.09 ± 1.06 | 8.33 ± 2.85 |
| f14 | 4.98 ± 9.12 | 5.68 ± 9.21 | 1.11 ± 2.39 | ± |
| f15 | 7.50 ± 2.53 | 5.96 ± 1.02 | 7.39 ± 3.22 | ± |
| f16 | 1.03 ± 3.18 | 1.02 ± 3.24 | 1.02 ± 2.93 | ± |
| f17 | 2.65 ± 2.28 | 1.42 ± 1.24 | 1.70 ± 9.08 | ± |
| f18 | 3.73 ± 1.02 | 3.02 ± 7.46 | 3.31 ± 1.79 | ± |
| f19 | 1.19 ± 1.84 | 1.07 ± 3.07 | 1.03 ± 8.46 | ± |
| f20 | 1.13 ± 2.67 | 1.12 ± 1.60 | 1.13 ± 1.72 | ± |
| f21 | 3.88 ± 4.07 | 4.37 ± 9.40 | ± | 4.47 ± 8.36 |
| f22 | 4.76 ± 1.51 | 1.51 ± 2.39 | 1.13 ± 3.05 | ± |
| f23 | 7.46 ± 1.92 | 6.63 ± 6.19 | 7.33 ± 3.25 | ± |
| f24 | 3.66 ± 1.17 | ± | 3.31 ± 6.65 | 3.23 ± 9.64 |
| f25 | 3.66 ± 7.98 | ± | 3.50 ± 5.07 | 3.53 ± 7.71 |
| f26 | 3.02 ± 6.61 | ± | 3.26 ± 5.26 | 3.12 ± 3.62 |
| f27 | 1.32 ± 1.27 | ± | 6.58 ± 6.21 | 6.65 ± 1.20 |
| f28 | 4.16 ± 6.22 | 4.00 ± 2.93 | 4.00 ± 2.91 | ± |
| +/−/= | 1/27/0 | 10/17/1 | 4/24/0 | -/-/- |
| FDR-PSO | GWO | EPSO | ADEI | ||||||||||||
| Mean | Std. | Rank | Mean | Std. | Rank | Mean | Std. | Rank | Mean | Std. | Rank | ||||
| f1 | 9.69 | 2.92 | 7 | 8.47 | 7.47 | 7 | 2.04 | 6.62 | 3 | 0.00 | 0.00 | 1 | |||
| f2 | 1.87 | 5.96 | 7 | 2.07 | 1.00 | 7 | 2.61 | 7.82 | 4 | 5.14 | 1.47 | 1 | |||
| f3 | 4.76 | 3.18 | 7 | 2.71 | 2.56 | 7 | 9.79 | 1.34 | 4 | 1.84 | 2.87 | 1 | |||
| f4 | 3.90 | 6.12 | 6 | 2.90 | 7.59 | 7 | 6.01 | 2.12 | 6 | 8.44 | 1.31 | 1 | |||
| f5 | 2.07 | 7.54 | 7 | 6.69 | 3.83 | 7 | 2.05 | 6.83 | 3 | 1.14 | 0.00 | 2 | |||
| f6 | 5.08 | 2.46 | 6 | 1.18 | 2.50 | 7 | 1.89 | 1.61 | 3 | 3.35 | 6.19 | 1 | |||
| f7 | 3.38 | 9.60 | 6 | 4.14 | 1.43 | 7 | 1.68 | 3.83 | 2 | 9.54 | 5.42 | 1 | |||
| f8 | 2.09 | 6.81 | 3 | 2.09 | 5.79 | 6 | 2.09 | 4.54 | 2 | 2.08 | 1.08 | 1 | |||
| f9 | 2.20 | 3.62 | 7 | 1.84 | 2.48 | 3 | 1.61 | 2.52 | 2 | 1.32 | 3.27 | 1 | |||
| f10 | 3.02 | 1.11 | 7 | 2.25 | 1.29 | 7 | 9.17 | 7.62 | 4 | 3.19 | 2.22 | 1 | |||
| f11 | 8.38 | 1.84 | 7 | 8.78 | 3.20 | 7 | 1.39 | 7.67 | 3 | 5.68 | 1.71 | 1 | |||
| f12 | 1.73 | 1.31 | 8 | 1.23 | 5.78 | 5 | 1.47 | 4.13 | 6 | 3.62 | 1.06 | 2 | |||
| f13 | 1.78 | 2.26 | 7 | 1.65 | 4.21 | 5 | 1.83 | 1.07 | 7 | 8.33 | 2.85 | 1 | |||
| f14 | 2.61 | 4.40 | 6 | 2.74 | 4.98 | 7 | 4.94 | 3.73 | 3 | 1.49 | 1.62 | 1 | |||
| f15 | 6.07 | 5.32 | 7 | 3.41 | 1.26 | 2 | 6.56 | 3.96 | 7 | 3.25 | 3.91 | 1 | |||
| f16 | 1.02 | 4.18 | 7 | 2.46 | 3.01 | 4 | 1.03 | 2.77 | 7 | 1.00 | 2.17 | 5 | |||
| f17 | 3.19 | 3.12 | 7 | 1.50 | 4.47 | 5 | 3.31 | 1.77 | 7 | 1.30 | 4.78 | 4 | |||
| f18 | 3.48 | 2.14 | 7 | 2.44 | 1.97 | 5 | 3.50 | 1.28 | 7 | 1.60 | 1.34 | 4 | |||
| f19 | 1.15 | 1.97 | 8 | 4.95 | 2.22 | 4 | 1.14 | 2.67 | 6 | 1.02 | 3.93 | 5 | |||
| f20 | 1.14 | 1.23 | 8 | 1.19 | 1.24 | 4 | 1.12 | 4.04 | 6 | 1.11 | 5.01 | 5 | |||
| f21 | 5.38 | 5.32 | 7 | 7.50 | 2.33 | 7 | 3.99 | 8.45 | 4 | 4.47 | 8.36 | 5 | |||
| f22 | 2.49 | 1.10 | 5 | 2.78 | 6.04 | 6 | 4.25 | 9.64 | 3 | 2.16 | 5.11 | 1 | |||
| f23 | 6.28 | 3.39 | 8 | 3.91 | 1.33 | 3 | 5.78 | 6.47 | 6 | 3.44 | 5.89 | 1 | |||
| f24 | 3.44 | 1.14 | 8 | 2.48 | 1.14 | 2 | 3.43 | 6.42 | 6 | 3.23 | 9.64 | 5 | |||
| f25 | 3.59 | 2.08 | 7 | 2.72 | 7.30 | 2 | 3.66 | 2.14 | 7 | 3.53 | 7.71 | 5 | |||
| f26 | 3.50 | 7.41 | 8 | 2.86 | 7.20 | 3 | 3.15 | 4.15 | 6 | 3.12 | 3.62 | 5 | |||
| f27 | 9.02 | 8.73 | 8 | 7.69 | 8.22 | 3 | 8.05 | 1.06 | 4 | 6.65 | 1.20 | 1 | |||
| f28 | 6.67 | 1.30 | 7 | 1.06 | 2.86 | 7 | 3.60 | 8.00 | 2 | 4.00 | 1.37 | 5 | |||
| +/−/= | 0/28/0 | 6/22/0 | 2/26/0 | -/-/- | |||||||||||
| MEGWO | GEDGWO | PSO-sono | ADEI | ||||||||||||
| Mean | Std. | Rank | Mean | Std. | Rank | Mean | Std. | Rank | Mean | Std. | Rank | ||||
| f1 | 3.66 | 1.14 | 6 | 3.85 | 6.93 | 4 | 0.00 | 0.00 | 1 | 0.00 | 0.00 | 1 | |||
| f2 | 3.15 | 1.60 | 3 | 3.22 | 2.52 | 3 | 7.72 | 8.08 | 5 | 5.14 | 1.47 | 1 | |||
| f3 | 1.40 | 1.41 | 3 | 2.61 | 2.55 | 5 | 8.59 | 1.32 | 3 | 1.84 | 2.87 | 1 | |||
| f4 | 8.29 | 4.31 | 5 | 7.56 | 7.07 | 3 | 1.63 | 1.25 | 2 | 8.44 | 1.31 | 1 | |||
| f5 | 4.71 | 1.23 | 6 | 1.05 | 3.27 | 4 | 2.01 | 5.43 | 1 | 1.14 | 0.00 | 2 | |||
| f6 | 1.44 | 2.26 | 3 | 2.78 | 2.72 | 4 | 7.59 | 3.38 | 6 | 3.35 | 6.19 | 1 | |||
| f7 | 2.37 | 1.06 | 4 | 3.43 | 1.03 | 6 | 3.30 | 1.53 | 4 | 9.54 | 5.42 | 1 | |||
| f8 | 2.09 | 6.03 | 5 | 2.10 | 5.25 | 7 | 2.09 | 6.06 | 5 | 2.08 | 1.08 | 1 | |||
| f9 | 1.95 | 3.56 | 5 | 2.02 | 3.54 | 5 | 2.70 | 3.77 | 7 | 1.32 | 3.27 | 1 | |||
| f10 | 5.16 | 1.06 | 6 | 7.92 | 7.14 | 3 | 7.42 | 6.25 | 2 | 3.19 | 2.22 | 1 | |||
| f11 | 2.00 | 1.40 | 3 | 4.69 | 1.15 | 5 | 2.78 | 8.22 | 4 | 5.68 | 1.71 | 1 | |||
| f12 | 7.40 | 1.91 | 5 | 4.71 | 1.28 | 3 | 3.59 | 1.44 | 1 | 3.62 | 1.06 | 2 | |||
| f13 | 1.03 | 2.51 | 4 | 1.17 | 2.93 | 4 | 9.01 | 2.79 | 2 | 8.33 | 2.85 | 1 | |||
| f14 | 2.18 | 9.83 | 3 | 2.27 | 6.29 | 4 | 2.66 | 4.81 | 6 | 1.49 | 1.62 | 1 | |||
| f15 | 3.78 | 5.28 | 5 | 4.09 | 9.65 | 5 | 3.53 | 7.72 | 3 | 3.25 | 3.91 | 1 | |||
| f16 | 1.93 | 3.72 | 2 | 2.36 | 3.04 | 3 | 1.57 | 5.61 | 1 | 1.00 | 2.17 | 5 | |||
| f17 | 4.03 | 1.14 | 1 | 7.30 | 1.80 | 3 | 5.91 | 1.09 | 2 | 1.30 | 4.78 | 4 | |||
| f18 | 1.29 | 2.46 | 3 | 1.20 | 4.41 | 2 | 5.95 | 1.02 | 1 | 1.60 | 1.34 | 4 | |||
| f19 | 3.13 | 5.60 | 1 | 7.85 | 3.58 | 3 | 3.27 | 9.23 | 2 | 1.02 | 3.93 | 5 | |||
| f20 | 1.10 | 7.51 | 3 | 1.10 | 8.70 | 2 | 1.10 | 5.29 | 1 | 1.11 | 5.01 | 5 | |||
| f21 | 2.01 | 1.53 | 1 | 3.13 | 6.43 | 2 | 3.15 | 6.23 | 3 | 4.47 | 8.36 | 5 | |||
| f22 | 2.71 | 1.17 | 3 | 2.53 | 6.81 | 5 | 2.79 | 5.56 | 7 | 2.16 | 5.11 | 1 | |||
| f23 | 4.42 | 5.73 | 6 | 4.07 | 7.52 | 4 | 3.64 | 7.31 | 2 | 3.44 | 5.89 | 1 | |||
| f24 | 2.52 | 1.13 | 3 | 2.42 | 6.48 | 1 | 2.61 | 1.30 | 4 | 3.23 | 9.64 | 5 | |||
| f25 | 2.71 | 1.04 | 1 | 2.80 | 1.15 | 3 | 2.84 | 8.82 | 4 | 3.53 | 7.71 | 5 | |||
| f26 | 2.00 | 3.75 | 1 | 2.65 | 6.92 | 2 | 3.05 | 7.84 | 4 | 3.12 | 3.62 | 5 | |||
| f27 | 8.10 | 8.27 | 6 | 6.89 | 7.32 | 2 | 8.76 | 1.35 | 6 | 6.65 | 1.20 | 1 | |||
| f28 | 2.80 | 6.15 | 1 | 3.70 | 3.24 | 3 | 3.72 | 2.90 | 4 | 4.00 | 1.37 | 5 | |||
| +/−/= | 10/18/0 | 10/18/0 | 12/15/1 | -/-/- | |||||||||||
| Parameter | Symbol | Value | Unit | Description |
|---|---|---|---|---|
| Density | 2200 | kg/m³ | Material density | |
| Thermal conductivity | k | 1.4 | W/m·K | Thermal conductivity |
| Specific heat capacity | 670 | J/kg·K | Specific heat capacity | |
| Cylinder length | L | 0.3 | m | Length of the cylindrical channel |
| Inner radius | 0.045 | m | Inner surface radius | |
| Outer radius | 0.0475 | m | Outer surface radius |
| Algorithm | Heat Flux Type | MAE (W/m²) | RMSE (W/m²) | MaxAE (W/m²) |
|---|---|---|---|---|
| PSO | Step | 2156.85 | 1778.55 | 4720.34 |
| Ramp | 2054.21 | 1652.56 | 4865.13 | |
| DE | Step | 1736.24 | 1367.51 | 3873.64 |
| Ramp | 1711.85 | 1285.38 | 3765.44 | |
| CoDE | Step | 1655.81 | 1313.26 | 3317.69 |
| Ramp | 1152.26 | 1289.45 | 3647.66 | |
| ADEI | Step | 1061.42 | 872.16 | 2325.19 |
| Ramp | 987.65 | 785.13 | 2763.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Li, Z.; Luan, H.; Shi, Y. Adaptive Differential Evolution Integration: Algorithm Development and Application to Inverse Heat Conduction. Processes 2025, 13, 1293. https://doi.org/10.3390/pr13051293
Zhao Z, Li Z, Luan H, Shi Y. Adaptive Differential Evolution Integration: Algorithm Development and Application to Inverse Heat Conduction. Processes. 2025; 13(5):1293. https://doi.org/10.3390/pr13051293
Chicago/Turabian StyleZhao, Zhibiao, Zhen Li, Hao Luan, and Yan Shi. 2025. "Adaptive Differential Evolution Integration: Algorithm Development and Application to Inverse Heat Conduction" Processes 13, no. 5: 1293. https://doi.org/10.3390/pr13051293
APA StyleZhao, Z., Li, Z., Luan, H., & Shi, Y. (2025). Adaptive Differential Evolution Integration: Algorithm Development and Application to Inverse Heat Conduction. Processes, 13(5), 1293. https://doi.org/10.3390/pr13051293





