Doubly Fed Induction Generator Frequency Regulation Enhancement Using Combined Inertia and Proportional Resonant Controller
Abstract
1. Introduction
- (a)
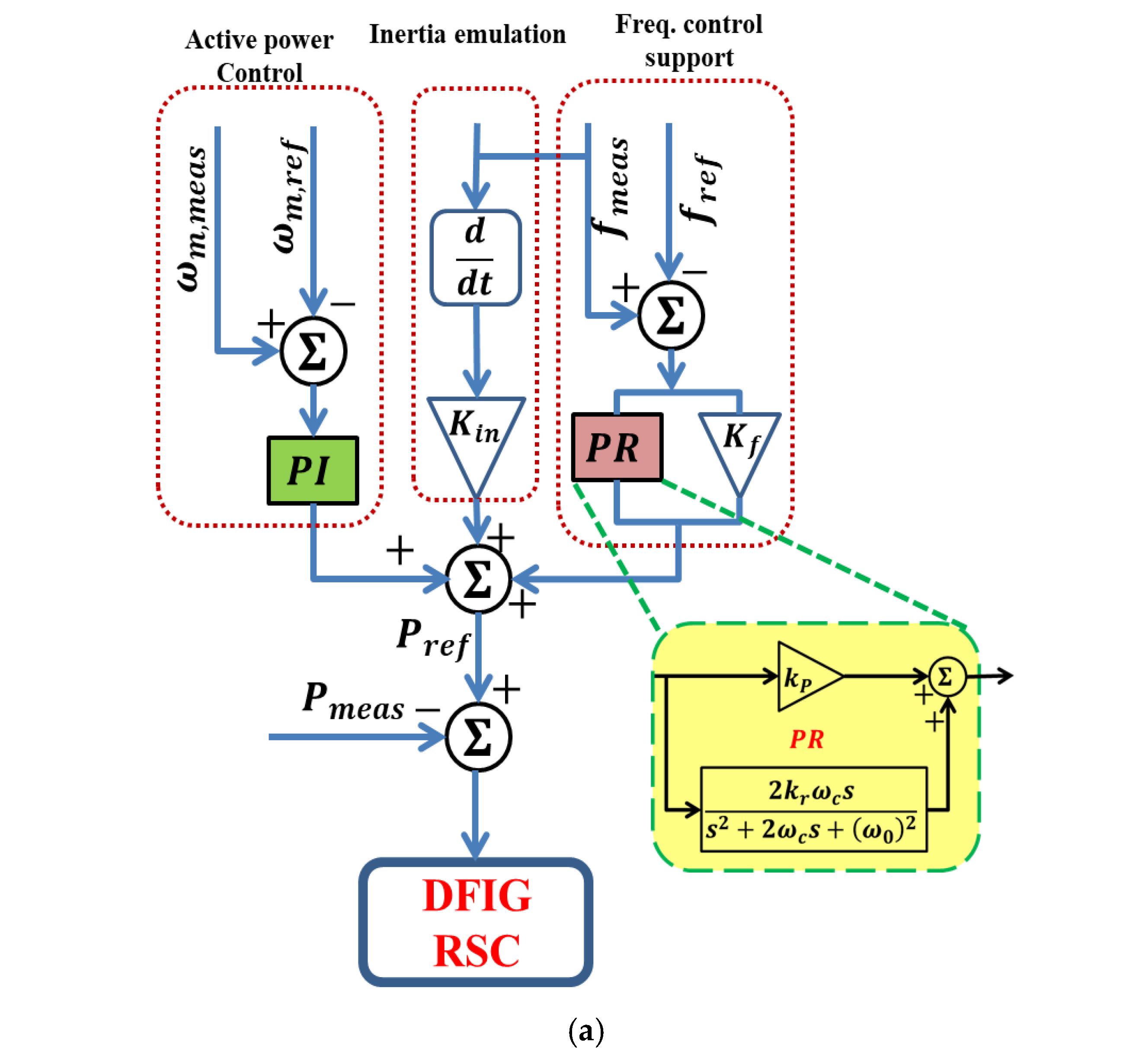
- The PR controller is proposed to be added to the inertial controller to achieve better frequency regulation.
- (b)
- The influence of the PR controller’s parameters on the frequency deviation, overshoot, settling time, and system stability is investigated to select the optimal values.
- (c)
- The proposed method is tested at increasing or decreasing the load, and multi-step load perturbation.
- (d)
- The simplified settings of the presented approach make it straightforward to execute in practice.
2. Modelling of the Studied System
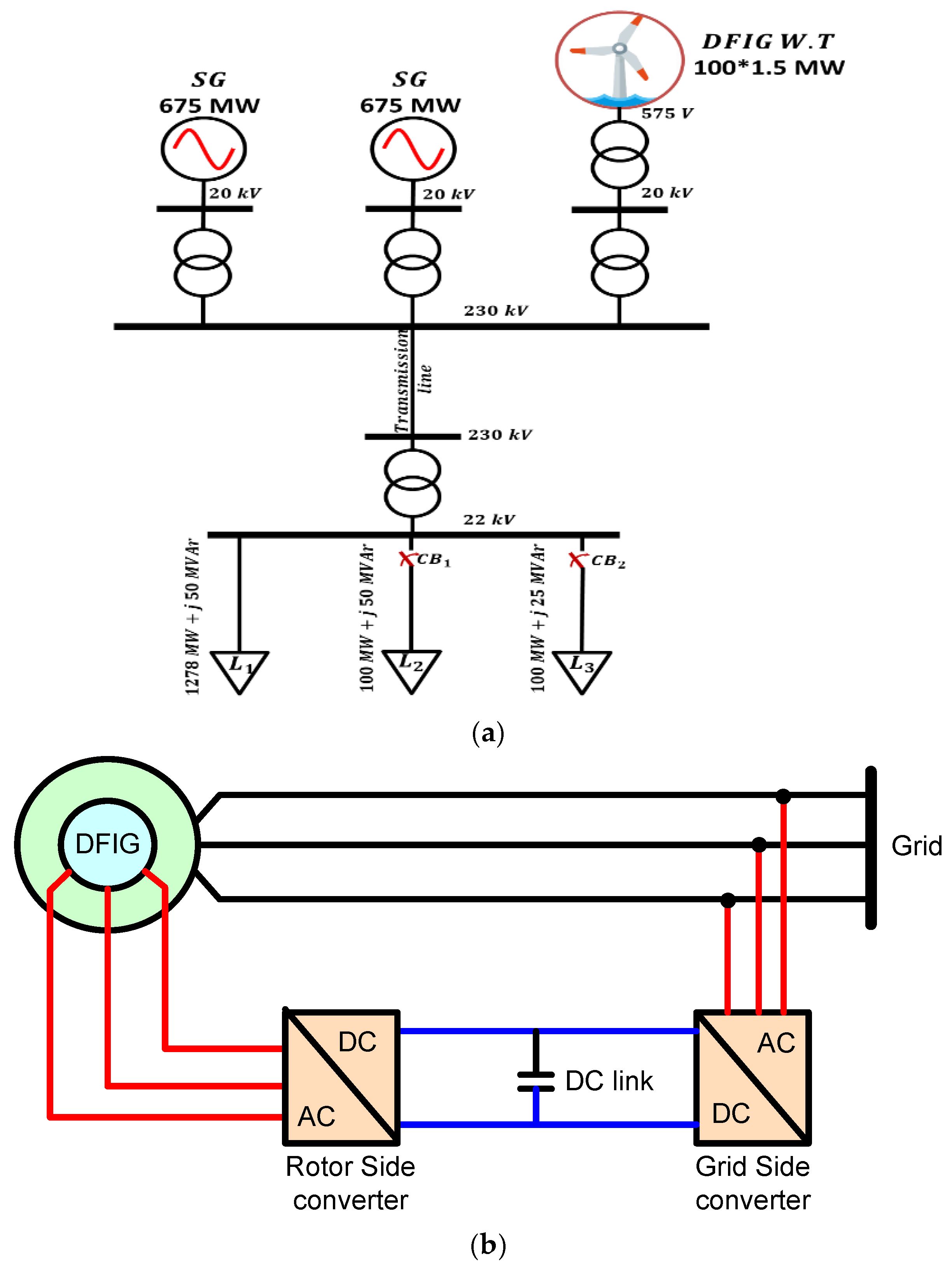
2.1. Test System
2.2. DFIG Modelling
2.3. Wind Turbine Modelling
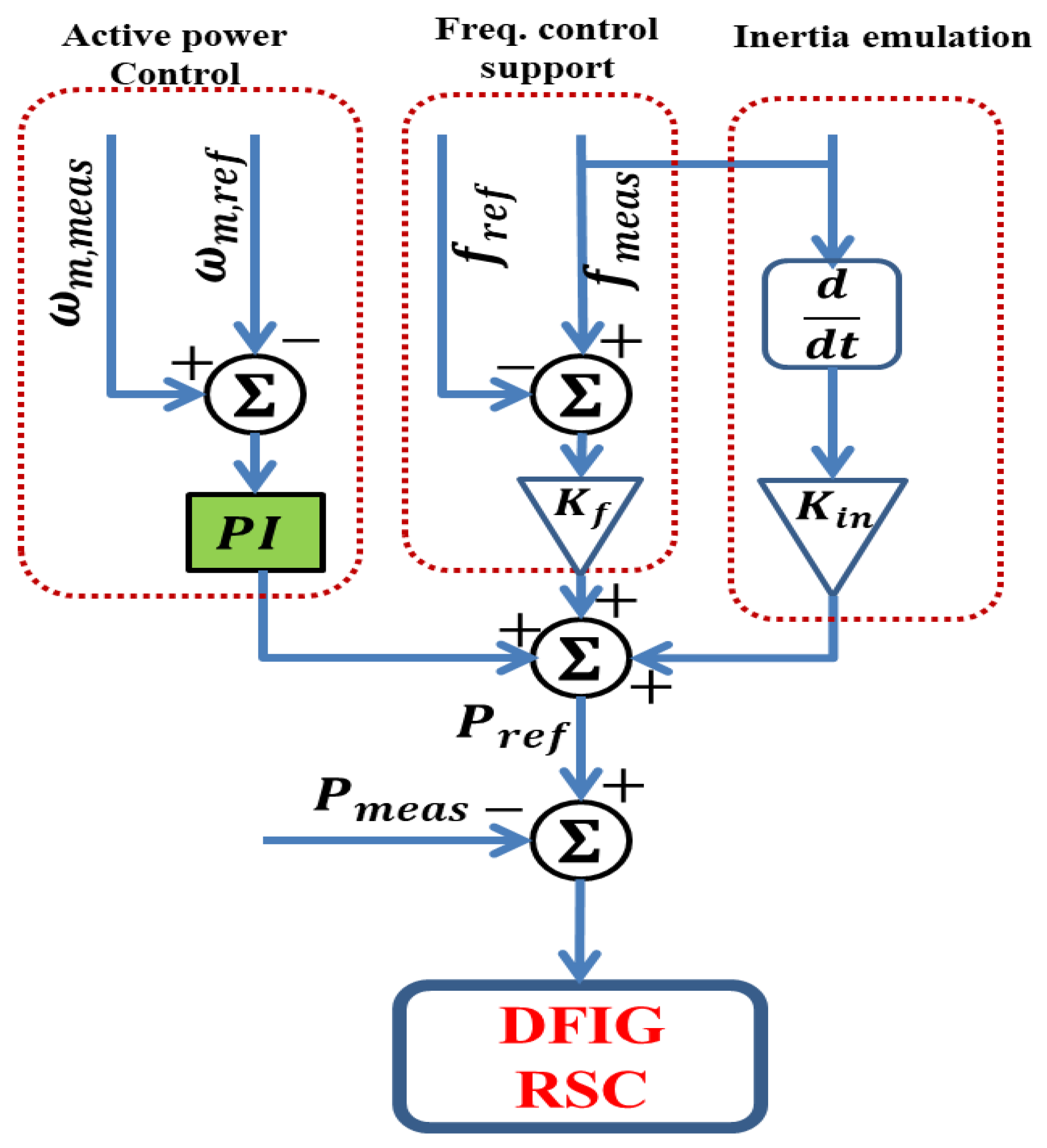
3. Frequency Regulation Proposed Solution
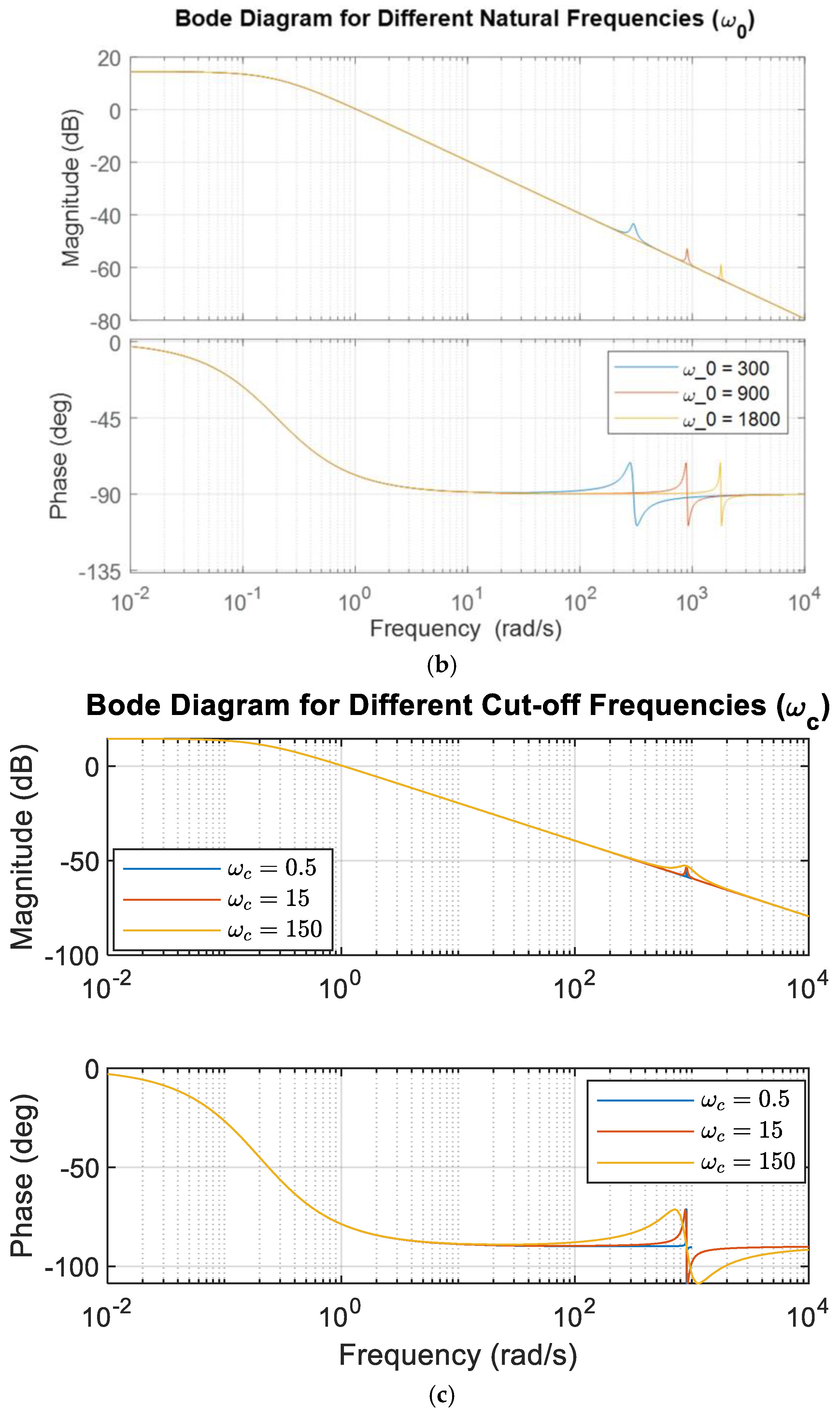
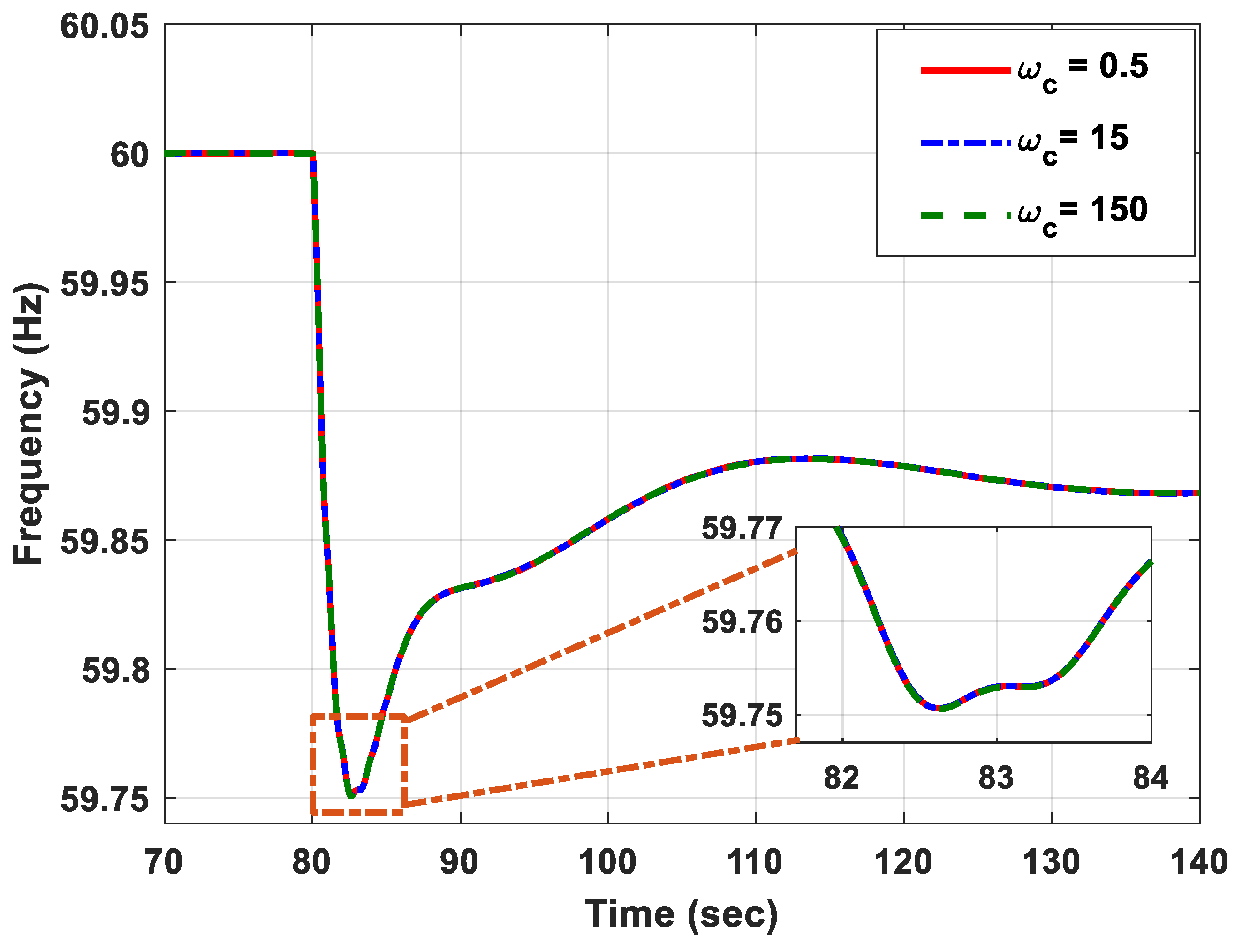
3.1. Impact of the PR Controller’s Cut-Off Frequency
3.2. Impact of the PR Controller’s Resonant Factor
3.3. Impact of the PR Controller’s Resonant Frequency
3.4. Impact of the PR Controller’s Proportional Gain
4. Results and Discussion
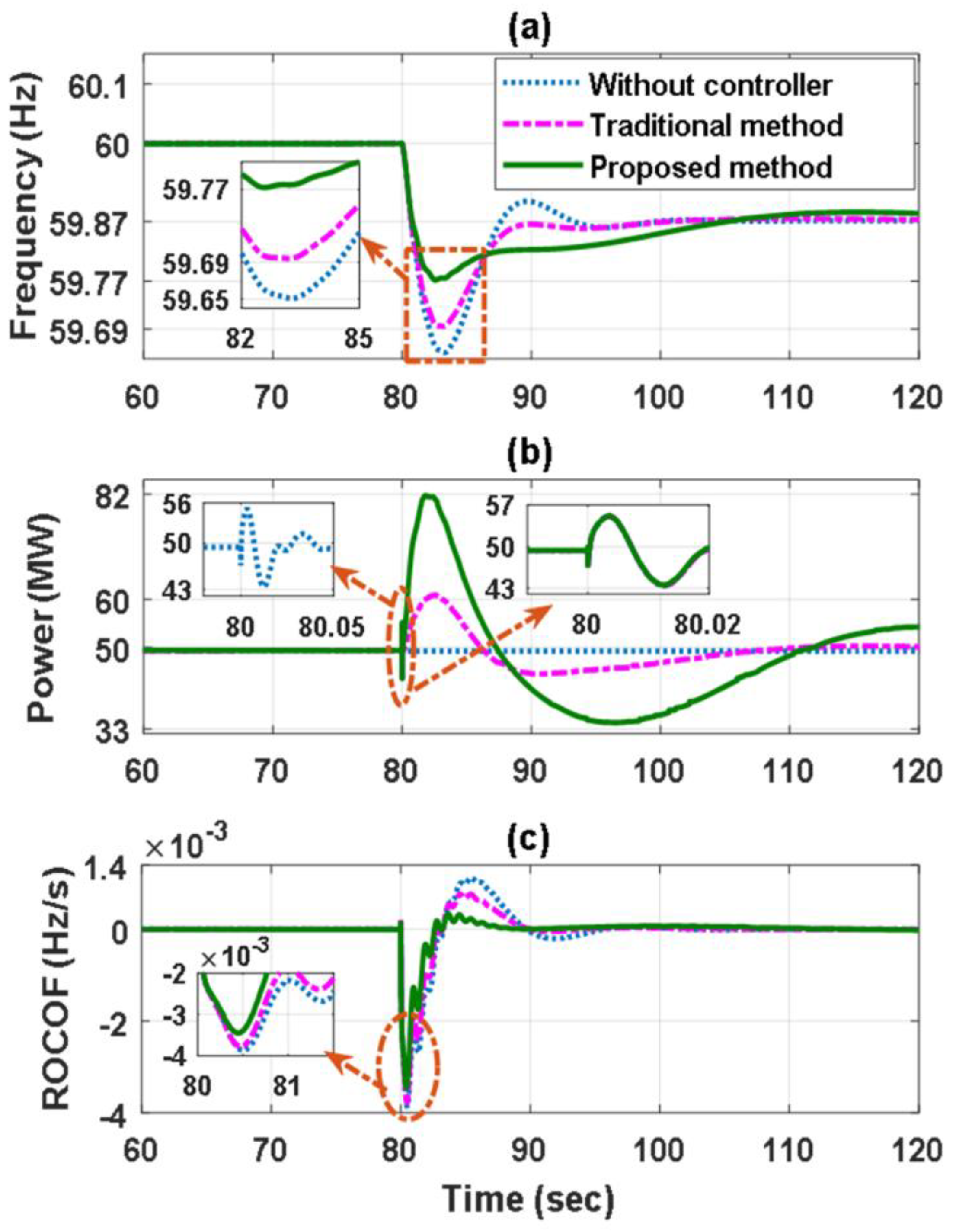
4.1. Impact of Increasing the Load
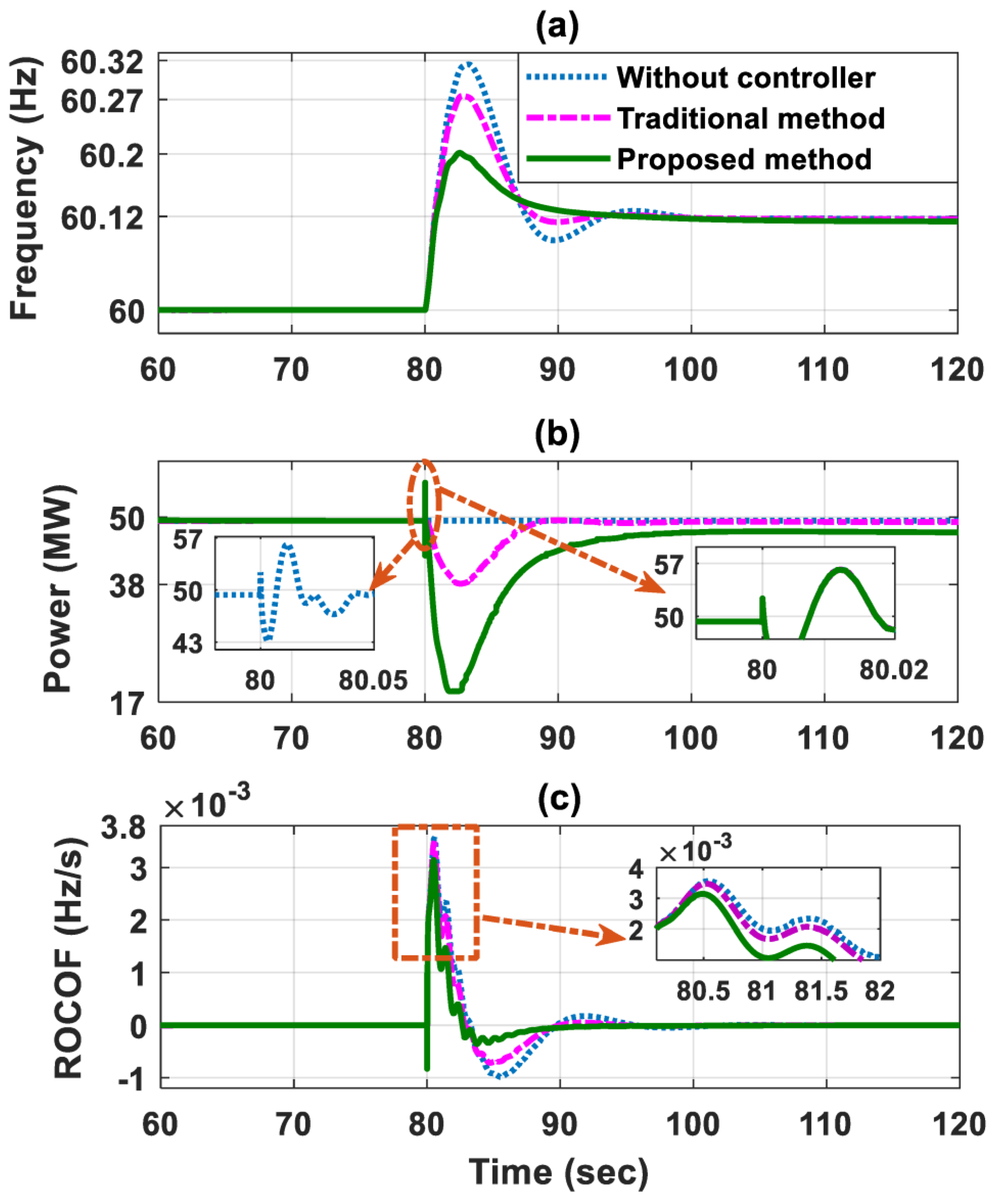
4.2. Impact of Reducing the Load
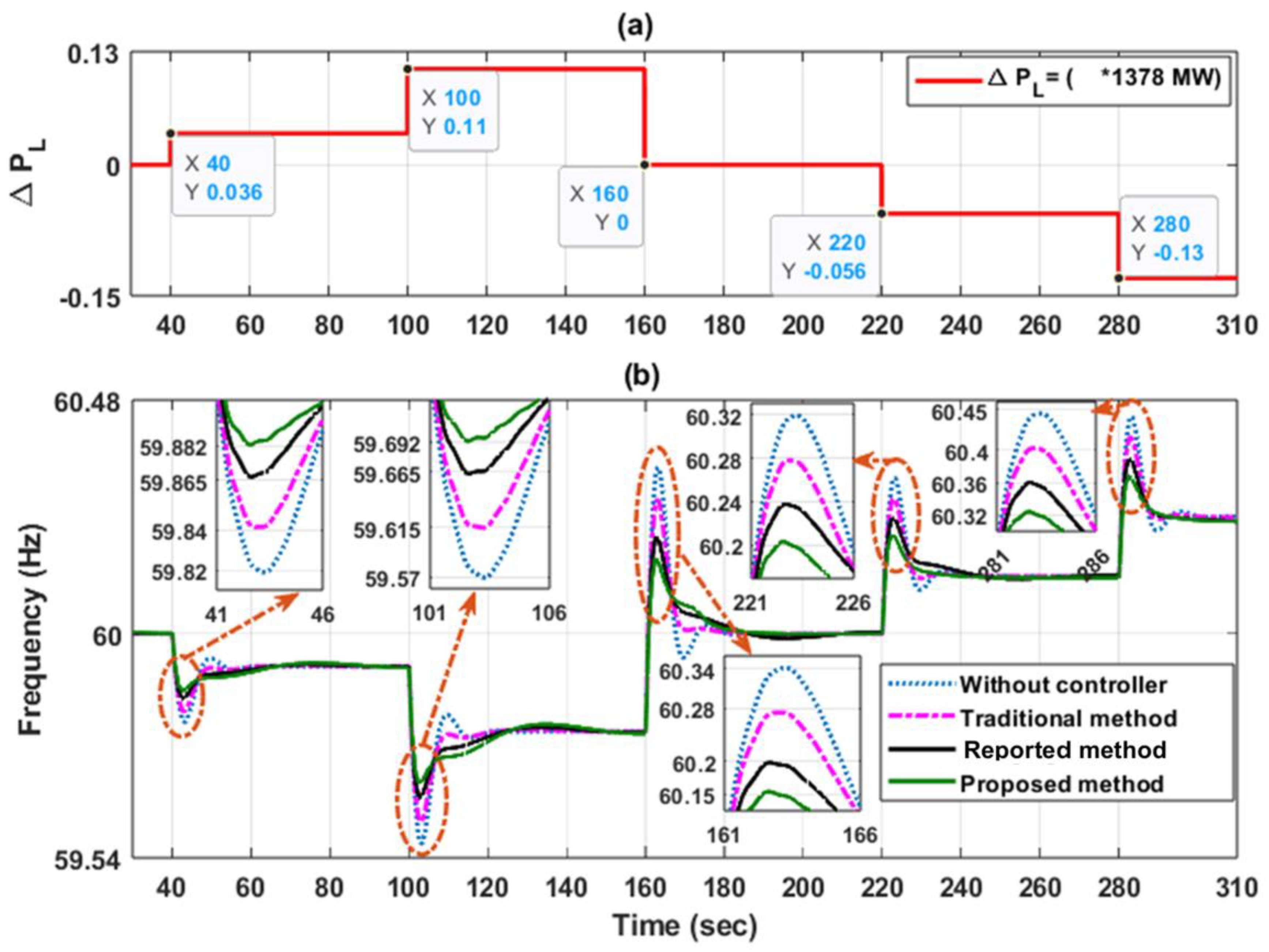
4.3. Impact of Multi-Step Load Perturbation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Rated power | 1.5 MW |
| Number of wind turbines | 100 |
| Rated voltage | 575 V |
| Rated frequency | 60 Hz |
| 0.007 p.u. | |
| 0.005 p.u. | |
| 0.171 p.u. | |
| 0.156 p.u. | |
| 2.9 p.u. | |
| DC-link voltage | 1200 V |
| DC-bus capacitor | 10,000 μF × 100 |
| Rated power | 675 MW |
| Rated voltage | 20 kV |
| Rated frequency | 60 Hz |
| Armature resistance | 0.0025 p.u. |
| Pole pairs | 4 |
| Inertia coefficient | 6.5 s |
| 1.8 p.u. | |
| 0.3 p.u. | |
| 8 s | |
| 0.25 p.u. | |
| 0.03 s | |
| 1.7 p.u. | |
| 0.55 p.u. | |
| 0.4 s | |
| 0.25 p.u. | |
| 0.05 s |
References
- Xue, Y.; Tai, N. Review of contribution to frequency control through variable speed wind turbine. Renew. Energy 2011, 36, 1671–1677. [Google Scholar] [CrossRef]
- Makolo, P.; Zamora, R.; Lie, T.-T. The role of inertia for grid flexibility under high penetration of variable renewables-A review of challenges and solutions. Renew. Sustain. Energy Rev. 2021, 147, 111223. [Google Scholar] [CrossRef]
- Ochoa, D.; Martinez, S. Fast-frequency response provided by DFIG-wind turbines and its impact on the grid. IEEE Trans. Power Syst. 2016, 32, 4002–4011. [Google Scholar] [CrossRef]
- Ma, C.; Sun, J.; Huang, J.; Wang, K. Transient Stability Enhancement Strategy for Islanded Microgrids Based on Energy Storage–Virtual Synchronous Machine Control. Energies 2023, 16, 6390. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, H.; Yang, D. An enhanced frequency response strategy of a DFIG based on over-speed de-loaded curve. Appl. Sci. 2021, 11, 9324. [Google Scholar] [CrossRef]
- Prasad, R.; Padhy, N.P. Synergistic frequency regulation control mechanism for DFIG wind turbines with optimal pitch dynamics. IEEE Trans. Power Syst. 2020, 35, 3181–3191. [Google Scholar] [CrossRef]
- Hu, Y.-L.; Wu, Y.-K. Approximation to frequency control capability of a DFIG-based wind farm using a simple linear gain droop control. IEEE Trans. Ind. Appl. 2018, 55, 2300–2309. Available online: http://ieeexplore.ieee.org/document/8579184/ (accessed on 10 March 2025). [CrossRef]
- Attya, A.B.; Hartkopf, T. Wind turbines support techniques during frequency drops—Energy utilization comparison. AIMS Energy 2014, 2, 260–275. [Google Scholar] [CrossRef][Green Version]
- Attya, A.; Dominguez-Garcia, J.L.; Anaya-Lara, O. A review on frequency support provision by wind power plants: Current and future challenges. Renew. Sustain. Energy Rev. 2018, 81, 2071–2087. [Google Scholar] [CrossRef]
- Sun, M.; Sun, Y.; Chen, L.; Zou, Z.; Min, Y.; Liu, R.; Xu, F.; Wu, Y. Novel temporary frequency support control strategy of wind turbine generator considering coordination with synchronous generator. IEEE Trans. Sustain. Energy 2022, 13, 1011–1020. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Zhang, Y. Electronically controlled broadband terahertz amplitude modulator based on Ionic Liquid/PEDOT: PSS: DMSO composite structure. J. Opt. Photonics Res. 2024. [Google Scholar] [CrossRef]
- Khaki-Sedigh, A.; Nasrollahi, S. A review of data-driven control systems design: Concepts and methods. J. Control 2023, 17, 81–111. Available online: http://joc.kntu.ac.ir/article-1-1007-en.html (accessed on 10 March 2025). [CrossRef]
- Nematov, D. Analysis of the optical properties and electronic structure of semiconductors of the Cu2NiXS4 (X = Si, Ge, Sn) family as new promising materials for optoelectronic devices. J. Opt. Photonics Res. 2024, 1, 91–97. [Google Scholar] [CrossRef]
- Alam, M.K.; Afsary, N.; Islam, M.Z.; Rasel, M.O.F. Investigation of polymer-based 1× 2 all-optical switches at C-band wavelength. J. Opt. Photonics Res. 2024, 1, 59–66. [Google Scholar] [CrossRef]
- Hu, Z.; Ren, Y.; Meng, Q.; Yun, P.; Fang, C.; Pan, Y. Improvement of frequency support for a DFIG using a virtual synchronous generator strategy at large power angles. Energies 2023, 16, 914. [Google Scholar] [CrossRef]
- Wang, S.; Tomsovic, K. A novel active power control framework for wind turbine generators to improve frequency response. IEEE Trans. Power Syst. 2018, 33, 6579–6589. [Google Scholar] [CrossRef]
- Li, Y.; He, L.; Liu, F.; Tan, Y.; Cao, Y.; Luo, L.; Shahidehpour, M. A dynamic coordinated control strategy of WTG-ES combined system for short-term frequency support. Renew. Energy 2018, 119, 1–11. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, J.; Hung, W.; Wang, C.; Zhang, X.; Bu, S.; Li, Q.; Urdal, H.; Booth, C.D. Synthetic inertia control strategy for doubly fed induction generator wind turbine generators using lithium-ion supercapacitors. IEEE Trans. Energy Convers. 2017, 33, 773–783. [Google Scholar] [CrossRef]
- Cui, S.; Yan, X.; Siddique, A. Inertia and primary frequency modulation strategy for a doubly fed induction generator based on supercapacitor energy storage control. Int. J. Green Energy 2022, 19, 941–955. [Google Scholar] [CrossRef]
- Sun, D.; Yu, J.; Zheng, W.; Ruan, J.; Zu, G. Multi-energy cooperative primary frequency regulation analysis of a hybrid plant station for wind power and hydrogen production based on ensemble empirical-mode decomposition algorithm. Appl. Sci. 2023, 13, 12394. [Google Scholar] [CrossRef]
- Sun, D.; Long, H.; Zhou, K.; Lv, Y.; Zheng, J.; Chen, Q. Research on SCESS-DFIG DC bus voltage fluctuation suppression strategy for frequency inertia regulation of power grid. IEEE Access 2020, 8, 173933–173948. [Google Scholar] [CrossRef]
- Okedu, K.E. A variable speed wind turbine flywheel based coordinated control system for enhancing grid frequency dynamics. Int. J. Smart Grid 2018, 2, 123–134. [Google Scholar] [CrossRef]
- Díaz-González, F.; Hau, M.; Sumper, A.; Gomis-Bellmunt, O. Coordinated operation of wind turbines and flywheel storage for primary frequency control support. Int. J. Electr. Power Energy Syst. 2015, 68, 313–326. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual inertia control application to enhance frequency stability of interconnected power systems with high renewable energy penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Guggilam, S.S.; Zhao, C.; Dall’Anese, E.; Chen, Y.C.; Dhople, S.V. Optimizing power–frequency droop characteristics of distributed energy resources. IEEE Trans. Power Syst. 2017, 33, 3076–3086. [Google Scholar] [CrossRef]
- Tian, X.; Wang, W.; Chi, Y.; Li, Y.; Liu, C. Virtual inertia optimisation control of DFIG and assessment of equivalent inertia time constant of power grid. IET Renew. Power Gener. 2018, 12, 1733–1740. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, J.; He, W. Synchronization mechanism between power-synchronized VS and PLL-controlled CS and the resulting oscillations. IEEE Trans. Power Syst. 2022, 37, 4129–4132. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y.; Mao, W.; Zhao, T.; Wang, M.; Liu, F.; Cao, R. A grid-supporting strategy for cascaded H-bridge PV converter using VSG algorithm with modular active power reserve. IEEE Trans. Ind. Electron. 2020, 68, 186–197. [Google Scholar] [CrossRef]
- Deng, J.; Wang, J.; Li, S.; Zhang, H.; Peng, S.; Wang, T. Adaptive damping design of PMSG integrated power system with virtual synchronous generator control. Energies 2020, 13, 2037. [Google Scholar] [CrossRef]
- Abdeen, M.; Sayyed, M.; Domínguez-García, J.L.; Kamel, S. Supplemental control for system frequency support of DFIG-based wind turbines. IEEE Access 2022, 10, 69364–69372. [Google Scholar] [CrossRef]
- Morren, J.; De Haan, S.W.; Kling, W.L.; Ferreira, J. Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Z.; Yu, J.; Huang, J.; Li, W. Coordinated control parameter setting of DFIG wind farms with virtual inertia control. Int. J. Electr. Power Energy Syst. 2020, 122, 106167. [Google Scholar] [CrossRef]
- Kazemi, M.V.; Sadati, S.J.; Gholamian, S.A. Adaptive frequency control support of a DFIG based on second-order derivative controller using data-driven method. Int. Trans. Electr. Energy Syst. 2020, 30, e12424. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, L.; Smith, J.S.; Wu, Q. Primary frequency control of DFIG-WTs using bang-bang phase angle controller. IET Gener. Transm. Distrib. 2018, 12, 2670–2678. [Google Scholar] [CrossRef]
- Ouyang, J.; Pang, M.; Li, M.; Zheng, D.; Tang, T.; Wang, W. Frequency control method based on the dynamic deloading of DFIGs for power systems with high-proportion wind energy. Int. J. Electr. Power Energy Syst. 2021, 128, 106764. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Synthesis of Robust Virtual Inertia Control. In Power Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 203–226. [Google Scholar]
- Cheng, P.; Wu, C.; Ma, J.; Blaabjerg, F. Coordinated derived current control of DFIG’s RSC and GSC without PLL under unbalanced grid voltage conditions. IEEE Access 2020, 8, 64760–64769. [Google Scholar] [CrossRef]
- Hamon, C.; Elkington, K.; Ghandhari, M. Doubly-fed induction generator modeling and control in DigSilent PowerFactory. In Proceedings of the 2010 International Conference on Power System Technology, Zhejiang, China, 24–28 October 2010; pp. 1–7. [Google Scholar]
- Li, H.; Abdeen, M.; Chai, Z.; Kamel, S.; Xie, X.; Hu, Y.; Wang, K. An improved fast detection method on subsynchronous resonance in a wind power system with a series compensated transmission line. IEEE Access 2019, 7, 61512–61522. [Google Scholar] [CrossRef]
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Chen, R.; Wu, W.; Sun, H.; Hu, Y.; Zhang, B. Supplemental control for enhancing primary frequency response of DFIG-based wind farm considering security of wind turbines. In Proceedings of the 2014 IEEE PES General Meeting| Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Castilla, M.; Miret, J.; Matas, J.; de Vicuña, L.G.; Guerrero, J.M. Linear current control scheme with series resonant harmonic compensator for single-phase grid-connected photovoltaic inverters. IEEE Trans. Ind. Electron. 2008, 55, 2724–2733. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame. IEEE Trans. Power Electron. 2006, 21, 836–841. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc. -Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Lee, R.; Pillay, P.; Harley, R. Q reference frames for the simulation of induction motors. Electr. Power Syst. Res. 1984, 8, 15–26. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F. Flexible control of small wind turbines with grid failure detection operating in stand-alone and grid-connected mode. IEEE Trans. Power Electron. 2004, 19, 1323–1332. [Google Scholar] [CrossRef]
- Amini, B.; Rastegar, H.; Pichan, M. An optimized proportional resonant current controller based genetic algorithm for enhancing shunt active power filter performance. Int. J. Electr. Power Energy Syst. 2024, 156, 109738. [Google Scholar] [CrossRef]
- Haro-Larrode, M.; Santos-Mugica, M.; Eguia, P.; Rodriguez-Sanchez, R.; Gil-de-Muro, A. Impact of proportional resonant controller parameters of VSC connected to AC grids with variable X/R characteristic on the small signal stability. Int. J. Electr. Power Energy Syst. 2020, 118, 105746. [Google Scholar] [CrossRef]
- Aragon, D.A.; Unamuno, E.; de Muro, A.G.; Ceballos, S.; Barrena, J.A. Second-Order Filter-Based Inertia Emulation (SOFIE) for Low Inertia Power Systems. IEEE Trans. Power Deliv. 2024, 39, 530–541. [Google Scholar] [CrossRef]
- Alam, M.S.; Al-Ismail, F.S.; Salem, A.; Abido, M.A. High-Level Penetration of Renewable Energy Sources Into Grid Utility: Challenges and Solutions. IEEE Access 2020, 8, 190277–190299. [Google Scholar] [CrossRef]



| Proportional Gain () | Frequency Drop | Frequency Deviation | Overshoot |
|---|---|---|---|
| 0.1 | 59.705 | 0.295 | 59.876 |
| 0.5 | 59.742 | 0.258 | 59.88 |
| 1.0 | 59.776 | 0.224 | 59.886 |
| 1.5 | 59.808 | 0.192 | 59.893 |
| 2.0 | 59.795 | 0.205 | 59.9 |
| 4.0 | 59.746 | 0.254 | 59.905 |
| 8.0 | The system becomes unstable | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdeen, M.; Al Dawsari, S.; El-Dabah, M.A.; Ahmed, M.K.; Touti, E.; Diab, A.A.Z.; Abo El-Magd, A.G. Doubly Fed Induction Generator Frequency Regulation Enhancement Using Combined Inertia and Proportional Resonant Controller. Processes 2025, 13, 1284. https://doi.org/10.3390/pr13051284
Abdeen M, Al Dawsari S, El-Dabah MA, Ahmed MK, Touti E, Diab AAZ, Abo El-Magd AG. Doubly Fed Induction Generator Frequency Regulation Enhancement Using Combined Inertia and Proportional Resonant Controller. Processes. 2025; 13(5):1284. https://doi.org/10.3390/pr13051284
Chicago/Turabian StyleAbdeen, Mohamed, Saleh Al Dawsari, Mahmoud A. El-Dabah, Mamdouh K. Ahmed, Ezzeddine Touti, Ahmed A. Zaki Diab, and Ayat G. Abo El-Magd. 2025. "Doubly Fed Induction Generator Frequency Regulation Enhancement Using Combined Inertia and Proportional Resonant Controller" Processes 13, no. 5: 1284. https://doi.org/10.3390/pr13051284
APA StyleAbdeen, M., Al Dawsari, S., El-Dabah, M. A., Ahmed, M. K., Touti, E., Diab, A. A. Z., & Abo El-Magd, A. G. (2025). Doubly Fed Induction Generator Frequency Regulation Enhancement Using Combined Inertia and Proportional Resonant Controller. Processes, 13(5), 1284. https://doi.org/10.3390/pr13051284









