Size-Induced Segregation Characteristics and Phase Transition Processes of Binary Particles in Non-Cylindrical Long Rotary Drums
Abstract
1. Introduction
2. Numerical Method and Model Validation
2.1. Numerical Method
2.2. Statistical Methods
2.3. Model Verification
3. Results and Discussion
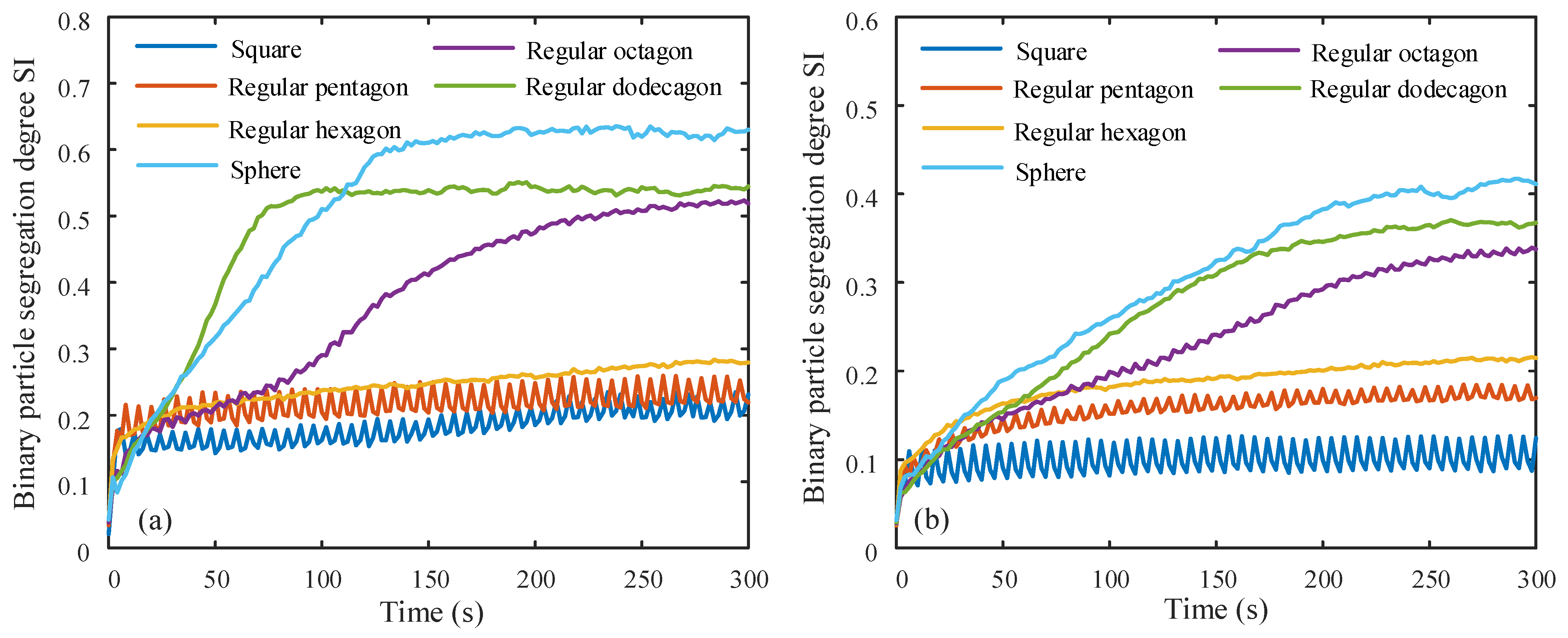
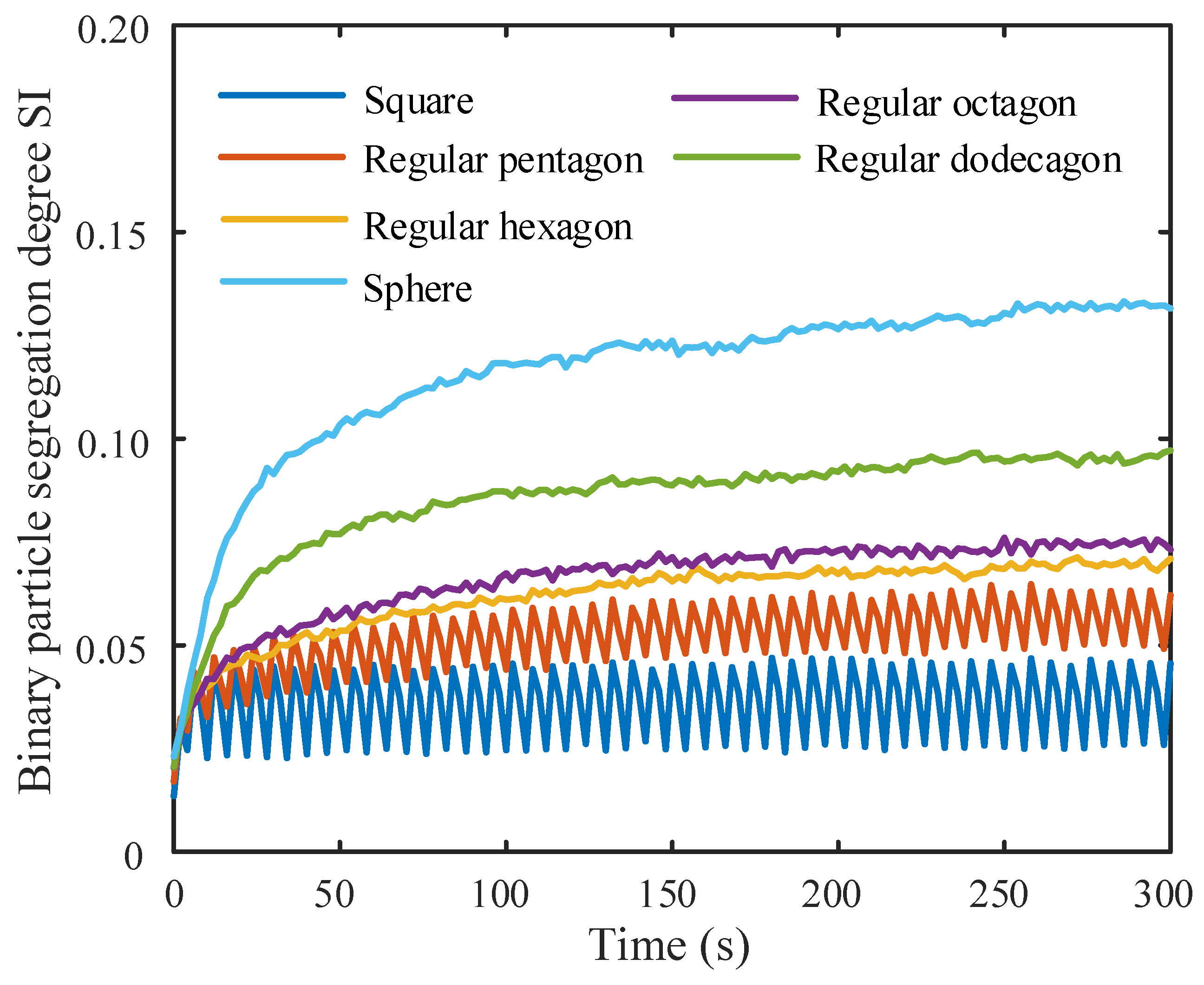
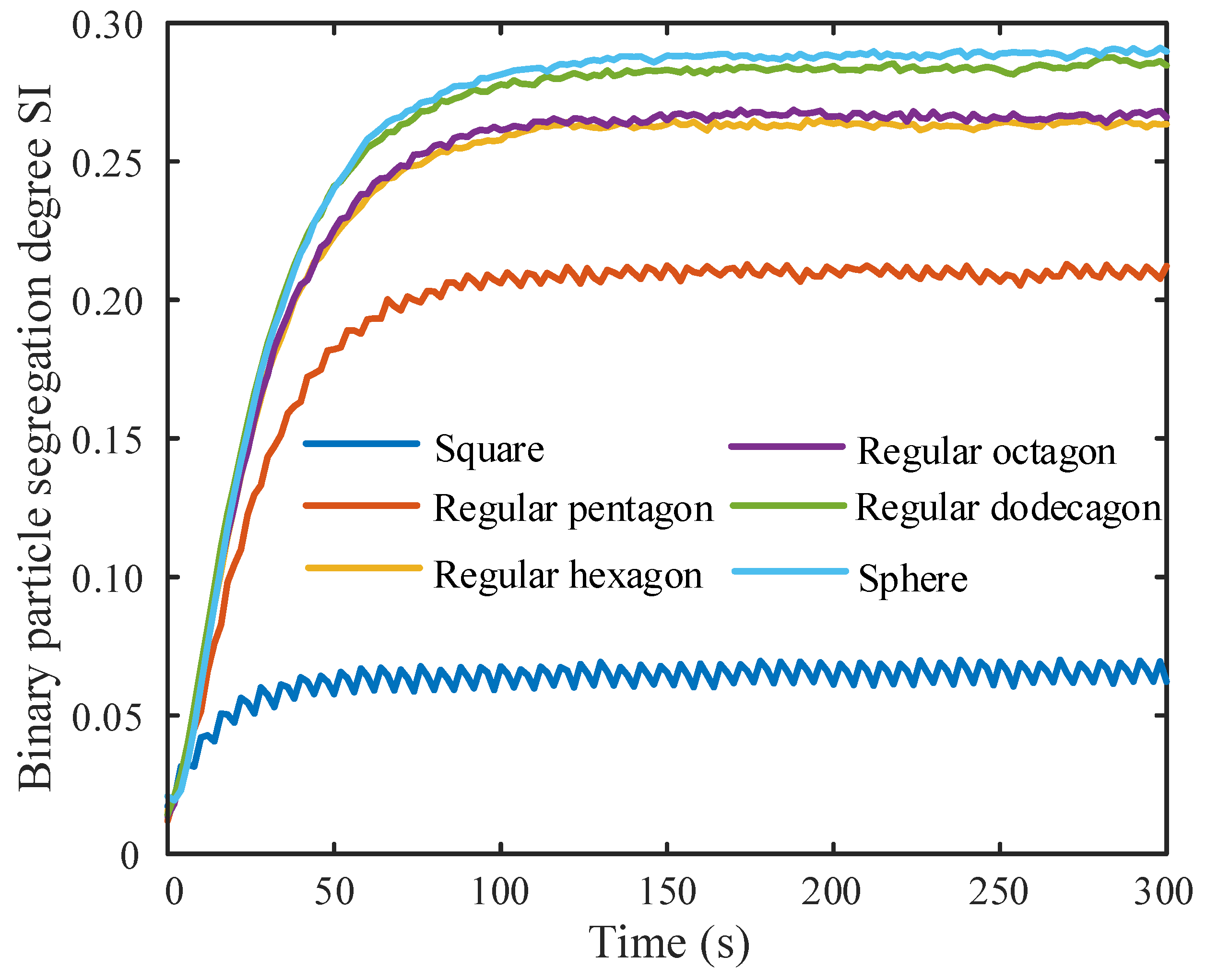
3.1. Influence of Drum Shape Parameters with Low Filling Rate
3.2. Influence of Drum Shape Parameters with Medium Filling Rate
3.3. Influence of Drum Shape Parameters with High Filling Rate
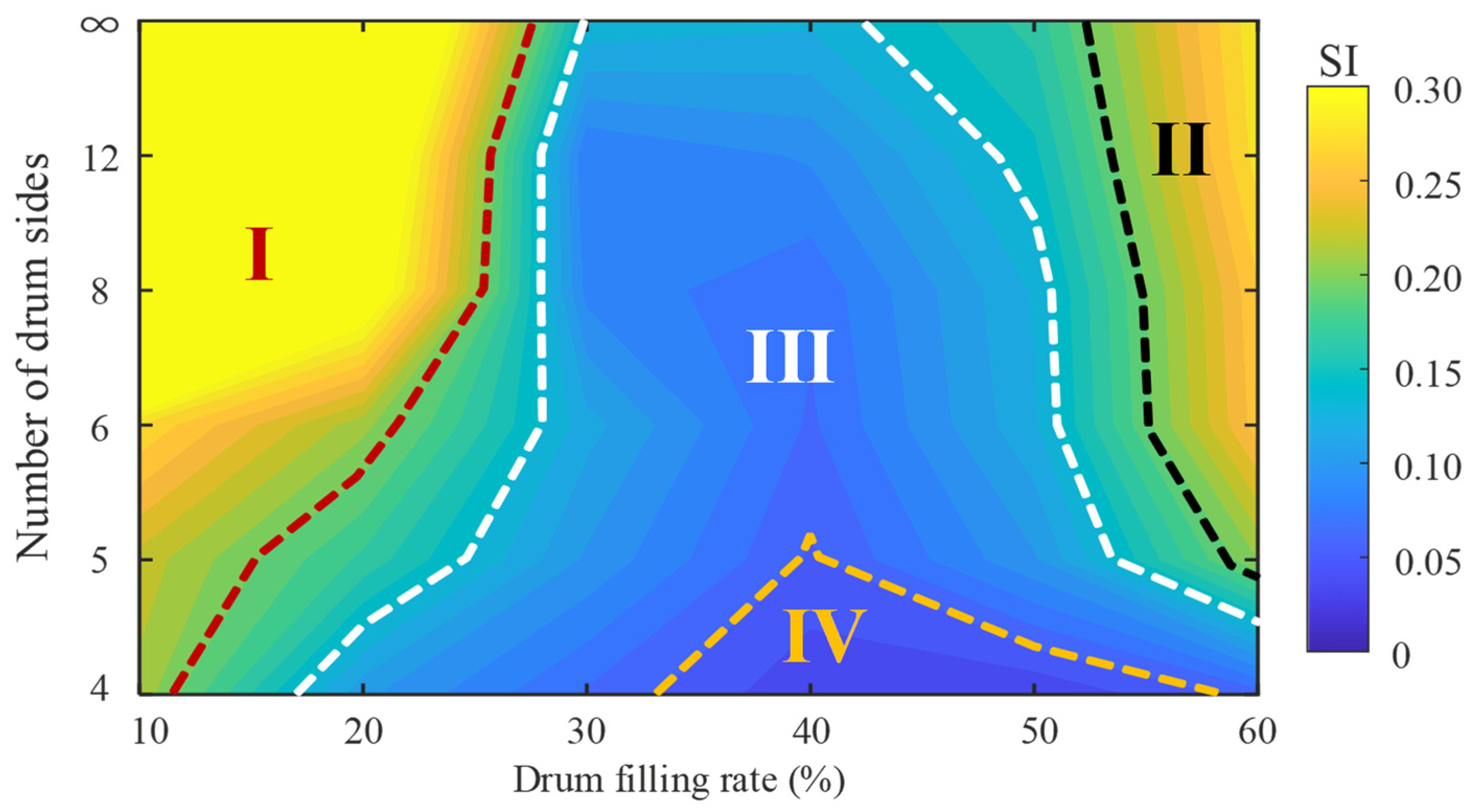
3.4. Combined Effect of Drum Shape Parameters and Drum Filling Rate
4. Conclusions
- (1)
- In low drum filling rate conditions, once the drum shapes are changed, the binary particles suffer from the formation, inversion, splitting, merging, and replication of axial banded segregation characteristics.
- (2)
- With the increase in the drum filling rates, the final stead segregation index of binary particles shows the first decreasing and then increasing characteristics. In particular, axial band segregation characteristics with alternating intervals are gradually formed in drums with medium filling rates, whereas axial-through core band characteristics are gradually formed in drums with high filling rates.
- (3)
- With the increase in the number of drum sides, the axial inclined seepage effect gradually plays a key role, which is characterized by a continuous increase in the final steady segregation index of binary particles.
- (4)
- With the combined effect of drum shapes and drum filling rates, the flow segregation of binary particles in rotary drums can be characterized by four phase transitions corresponding to the different mixing and segregation regions in the segregation index phase diagram, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Zhang, H.; Ye, X.; Su, Y.; Yu, A.; Tan, Y. Numerical Investigation on Thermal Drying Process of Sludges Based on CFD-DEM. Ind. Eng. Chem. Res. 2023, 62, 16990–17007. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Song, C.; Li, W.; Qin, H.; Wang, Q. Numerical Simulations of Particle Motions at Continuous Rotational Speed Changes in Horizontal Rotating Drums. Processes 2023, 11, 47. [Google Scholar] [CrossRef]
- Kreesaeng, S.; Chalermsinsuwan, B.; Piumsomboon, P. Effect of Inserting Baffles on the Solid Particle Segregation Behavior in Fluidized Bed Reactor: A Computational Study. ChemEngineering 2024, 8, 7. [Google Scholar] [CrossRef]
- Adepu, M.; Chen, S.; Jiao, Y.; Gel, A.; Emady, H. Wall to Particle Bed Contact Conduction Heat Transfer in a Rotary Drum Using DEM. Comp. Part. Mech. 2021, 8, 589–599. [Google Scholar] [CrossRef]
- He, S.; Wang, Y.; Zhou, Z.; Gan, J.; Yu, A.; Pinson, D. Size-Induced Axial Segregation of Ellipsoids in a Rotating Drum. Powder Technol. 2023, 422, 118490. [Google Scholar] [CrossRef]
- Li, M.; An, X.; Wu, Y. Segregation Behavior of Particles with Gaussian Distributions in the Rotating Drum with Rolling Regime. Adv. Powder Technol. 2023, 34, 103953. [Google Scholar] [CrossRef]
- Ahmed, E.M.E.; Govender, I.; Mainza, A.N. Axial Segregation of Polydisperse Granular Mixtures in Rotating Drum Flows. Minerals 2021, 11, 915. [Google Scholar] [CrossRef]
- Mesnier, A.; Peczalski, R.; Mollon, G.; Vessot-Crastes, S. Mixing of Bi-Dispersed Milli-Beads in a Rotary Drum. Mechanical Segregation Analyzed by Lab-Scale Experiments and DEM Simulation. Processes 2020, 8, 1166. [Google Scholar] [CrossRef]
- Yang, L.Y.M.; Zheng, Q.J.; Bai, L.; Yu, A.B. Continuum Modelling of Granular Segregation by Coupling Flow Rheology and Transport Equation. Powder Technol. 2021, 378, 371–387. [Google Scholar] [CrossRef]
- Naji, L.; Stannarius, R. Axial and Radial Segregation of Granular Mixtures in a Rotating Spherical Container. Phys. Rev. E 2009, 79, 031307. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Tsutsumi, K.; Tsuji, Y. MRI Measurement of Granular Motion in a Rotating Drum. In Proceedings of the Particle and Particle Systems Characterization; Wiley Online Library: Hoboken, NJ, USA, 2006; Volume 23, pp. 266–271. [Google Scholar]
- Turner, J.L.; Nakagawa, M. Particle Mixing in a Nearly Filled Horizontal Cylinder through Phase Inversion. Powder Technol. 2000, 113, 119–123. [Google Scholar] [CrossRef]
- Pereira, G.G.; Sinnott, M.D.; Cleary, P.W.; Liffman, K.; Metcalfe, G.; Šutalo, I.D. Insights from Simulations into Mechanisms for Density Segregation of Granular Mixtures in Rotating Cylinders. Granul. Matter 2011, 13, 53–74. [Google Scholar] [CrossRef]
- Jain, N.; Ottino, J.M.; Lueptow, R.M. Regimes of Segregation and Mixing in Combined Size and Density Granular Systems: An Experimental Study. Granul. Matter 2005, 7, 69–81. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X.; Xiao, Y.; Liu, Y.; Liu, Y. Radial Mixing and Segregation of Granular Bed Bi-Dispersed Both in Particle Size and Density within Horizontal Rotating Drum. Trans. Nonferrous Met. Soc. China 2016, 26, 527–535. [Google Scholar] [CrossRef]
- Cleary, P.W.; Morrison, R.D. Comminution Mechanisms, Particle Shape Evolution and Collision Energy Partitioning in Tumbling Mills. Miner. Eng. 2016, 86, 75–95. [Google Scholar] [CrossRef]
- Jo, S.-A.; Kim, E.-K.; Cho, G.-C.; Lee, S.-W. Particle Shape and Crushing Effects on Direct Shear Behavior Using DEM. Soils Found. 2011, 51, 701–712. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, J.; Wu, X.; Gong, S.; Zhang, J.; Lu, X. Segregation Dynamics of the Binary-Size Granular System in a Split Rotary Drum. Powder Technol. 2022, 404, 117480. [Google Scholar] [CrossRef]
- Zuo, Z.; Wang, J.; Chen, X.; Gong, S.; Lu, H. Numerical Study of Forced Axial Segregation of Binary Density Granular System in a Split Rotary Drum. Adv. Powder Technol. 2022, 33, 103831. [Google Scholar] [CrossRef]
- Das Gupta, S.; Khakhar, D.V.; Bhatia, S.K. Axial Segregation of Particles in a Horizontal Rotating Cylinder. Chem. Eng. Sci. 1991, 46, 1513–1517. [Google Scholar] [CrossRef]
- Chen, P.; Lochman, B.J.; Ottino, J.M.; Lueptow, R.M. Inversion of Band Patterns in Spherical Tumblers. Phys. Rev. Lett. 2009, 102, 148001. [Google Scholar] [CrossRef]
- Chen, P.; Ottino, J.M.; Lueptow, R.M. Onset Mechanism for Granular Axial Band Formation in Rotating Tumblers. Phys. Rev. Lett. 2010, 104, 188002. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Zhao, Y.; Chen, Y.; Liu, X.; Hua, Z.; Zhou, C.; Zheng, J. Transition of Axial Segregation Patterns in a Long Rotating Drum. Particuology 2014, 13, 128–133. [Google Scholar] [CrossRef]
- Arntz, M.M.H.D.; den Otter, W.K.; Beeftink, H.H.; Boom, R.M.; Briels, W.J. The Influence of End Walls on the Segregation Pattern in a Horizontal Rotating Drum. Granul. Matter 2013, 15, 25–38. [Google Scholar] [CrossRef]
- Arntz, M.M.H.D.; Beeftink, H.H.; den Otter, W.K.; Briels, W.J.; Boom, R.M. Segregation of Granular Particles by Mass, Radius, and Density in a Horizontal Rotating Drum. AIChE J. 2014, 60, 50–59. [Google Scholar] [CrossRef]
- Huang, P.; Miao, Q.; Ding, Y.; Sang, G.; Jia, M. Research on Surface Segregation and Overall Segregation of Particles in a Rotating Drum Based on Stacked Image. Powder Technol. 2021, 382, 162–172. [Google Scholar] [CrossRef]
- Miao, Q.; Zhu, W.; Cao, Y.; Huang, P.; Hu, C.; Jia, M. Axial Segregation Characteristics and Size-Induced Flow Behavior of Particles in a Novel Rotary Drum with Curved Sidewalls. Particuology 2024, 87, 1–19. [Google Scholar] [CrossRef]
- Ayeni, O.O.; Wu, C.L.; Joshi, J.B.; Nandakumar, K. A Discrete Element Method Study of Granular Segregation in Non-Circular Rotating Drums. Powder Technol. 2015, 283, 549–560. [Google Scholar] [CrossRef]
- Windows-Yule, C.R.K.; van der Horn, A.J.; Tunuguntla, D.R.; Parker, D.J.; Thornton, A.R. Inducing Axial Banding in Bidisperse-by-Density Granular Systems Using Noncylindrical Tumbler Geometries. Phys. Rev. Appl. 2017, 8, 024010. [Google Scholar] [CrossRef]
- Cleary, P.W. Predicting Charge Motion, Power Draw, Segregation and Wear in Ball Mills Using Discrete Element Methods. Miner. Eng. 1998, 11, 1061–1080. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, Y.; Song, T.; Zhao, Y. Investigation of the Effect of Filling Level on the Wear and Vibration of a SAG Mill by DEM. Particuology 2022, 63, 24–34. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, S.; Zhou, G.; Zhang, Y.; Ge, W. Geometrically Exact Discrete-Element-Method (DEM) Simulation on the Flow and Mixing of Sphero-Cylinders in Horizontal Drums. Powder Technol. 2018, 336, 415–425. [Google Scholar] [CrossRef]
- Rong, W.; Li, B.; Feng, Y. The Development and Application of a TFM for Dense Particle Flow and Mixing in Rotating Drums. Processes 2022, 10, 234. [Google Scholar] [CrossRef]
- Miao, Q.; Huang, P.; Ding, Y.; Guo, J.; Jia, M. Particle mixing and segregation behaviors in the rotating drums with adjacent axial segmentations in different speed directions. Powder Technol. 2022, 405, 117534. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Wright, B.D.; Yang, R.Y.; Xu, B.H.; Yu, A.B. Rolling Friction in the Dynamic Simulation of Sandpile Formation. Phys. A Stat. Mech. Its Appl. 1999, 269, 536–553. [Google Scholar] [CrossRef]
- Ai, J.; Chen, J.-F.; Rotter, J.M.; Ooi, J.Y. Assessment of Rolling Resistance Models in Discrete Element Simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Lacey, P.M.C. The Mixing of Solid Particles. Chem. Eng. Res. Des. 1997, 75, S49–S55. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Z.; Ji, S. Radial Segregation of a Gaussian-Dispersed Mixture of Superquadric Particles. Powder Technol. 2021, 394, 813–824. [Google Scholar] [CrossRef]
- Jain, A.; Evrard, F.; van Wachem, B. The Effect of Side Walls on Particles Mixing in Rotating Drums. Particuology 2023, 72, 112–121. [Google Scholar] [CrossRef]
- Huang, P.; Miao, Q.; Sang, G.; Zhou, Y.; Jia, M. Research on Quantitative Method of Particle Segregation Based on Axial Center Nearest Neighbor Index. Miner. Eng. 2021, 161, 106716. [Google Scholar] [CrossRef]
- Miao, Q.; Cao, Y.; Zhu, W.; Huang, P.; Huang, L.; Yu, A.; Kuang, S. Segregation Flow Behavior of Polydisperse Particle Mixture with Skewed Distribution in a Rotating Drum. Powder Technol. 2024, 444, 120041. [Google Scholar] [CrossRef]
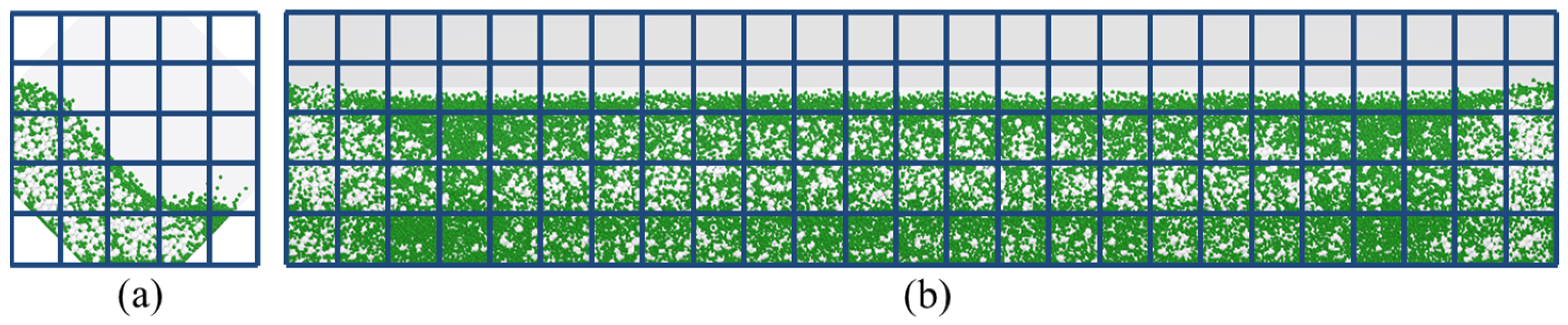

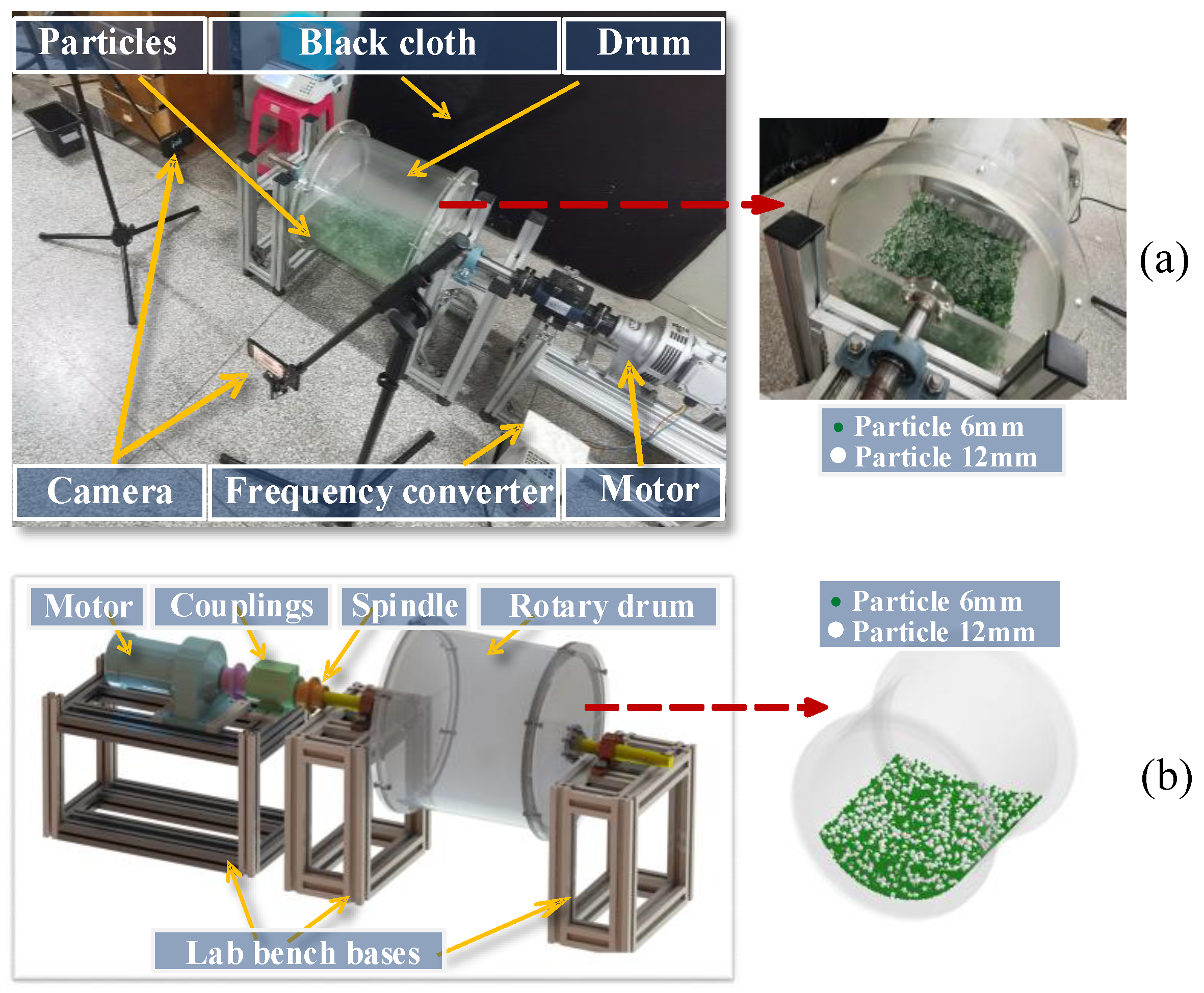





| Drum Shape |  |  |  |  |  |  |
|---|---|---|---|---|---|---|
| Internal angle (°) | 90 | 108 | 120 | 135 | 150 | - |
| Side length (mm) | 354.49 | 270.26 | 219.93 | 161.33 | 105.94 | - |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Drum diameter D (mm) | 400 | Drum shear modulus G (GPa) | 3 |
| Drum length | 2000 | Particle poisson’s ratio v | 0.25 |
| Drum speed n (rpm) | 40 | Drum Poisson’s ratio v | 0.35 |
| Drum filling rate (%) | 10~60 | Restitution coefficient. particle-particle | 0.91/0.727 |
| Particle volume ratio | 1 | Restitution coefficient. wall-particle | 0.90/0.722 |
| Particle diameter d (mm) | 6/12 | Static friction coeff. particle-particle | 0.435 |
| Particle density (kg/m3) | 2, 500 | Static friction coeff. wall-particle | 0.50 |
| Drum density (kg/m3) | 1, 250 | Rolling friction coeff. particle-particle | 0.01 |
| Particle shear modulus G (GPa) | 22 | Rolling friction coeff. wall-particle | 0.055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Miao, Q.; Huang, P. Size-Induced Segregation Characteristics and Phase Transition Processes of Binary Particles in Non-Cylindrical Long Rotary Drums. Processes 2025, 13, 971. https://doi.org/10.3390/pr13040971
Hu C, Miao Q, Huang P. Size-Induced Segregation Characteristics and Phase Transition Processes of Binary Particles in Non-Cylindrical Long Rotary Drums. Processes. 2025; 13(4):971. https://doi.org/10.3390/pr13040971
Chicago/Turabian StyleHu, Chaobin, Qiuhua Miao, and Peng Huang. 2025. "Size-Induced Segregation Characteristics and Phase Transition Processes of Binary Particles in Non-Cylindrical Long Rotary Drums" Processes 13, no. 4: 971. https://doi.org/10.3390/pr13040971
APA StyleHu, C., Miao, Q., & Huang, P. (2025). Size-Induced Segregation Characteristics and Phase Transition Processes of Binary Particles in Non-Cylindrical Long Rotary Drums. Processes, 13(4), 971. https://doi.org/10.3390/pr13040971







