The Effect of Pore Channel Structure Uniformity on the Performance of a Membrane Adsorber Determined by Flow Distribution Analysis Using Computational Fluid Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometrical Structure
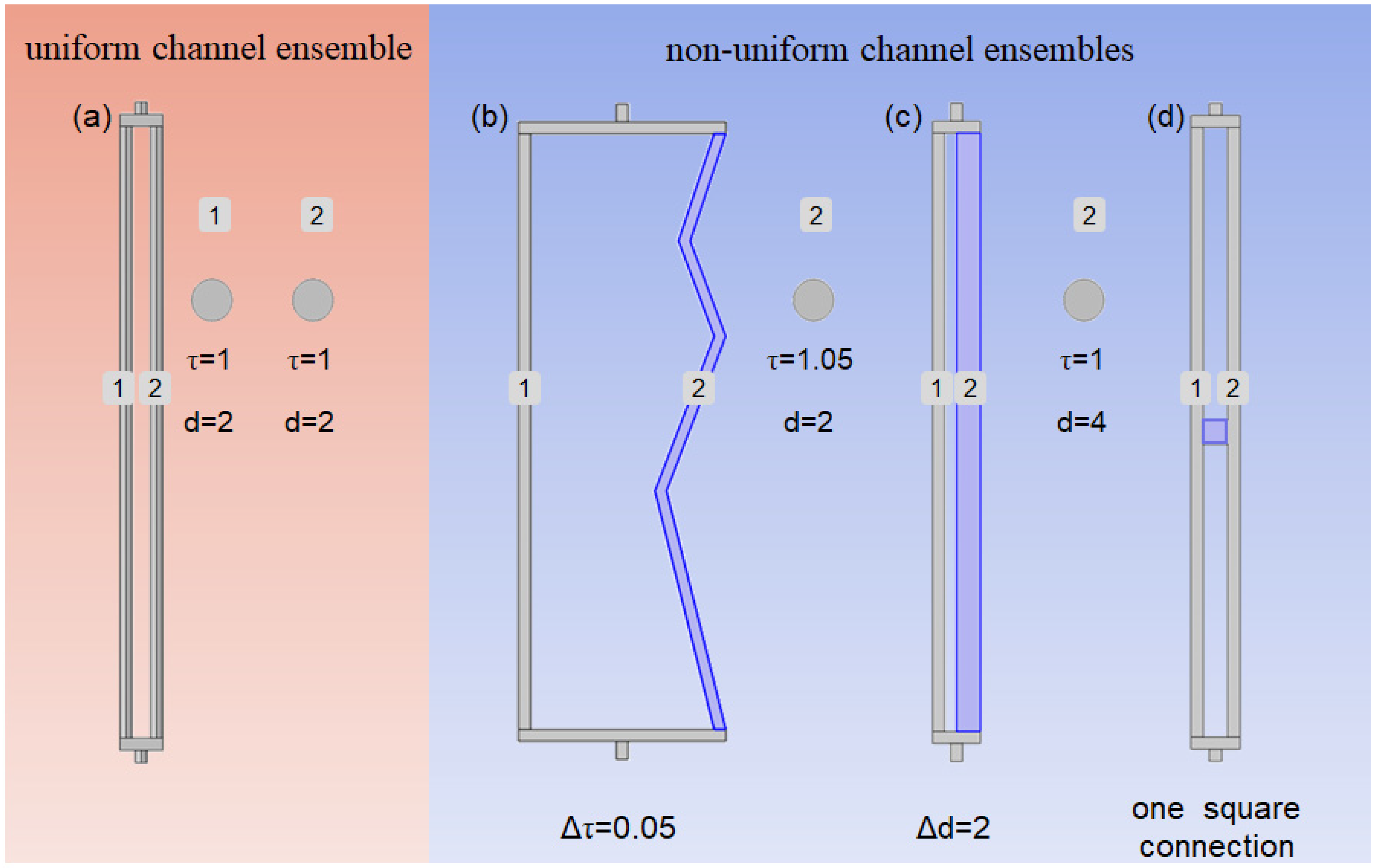
2.1.1. Geometric Structure of the Microscopic Channel
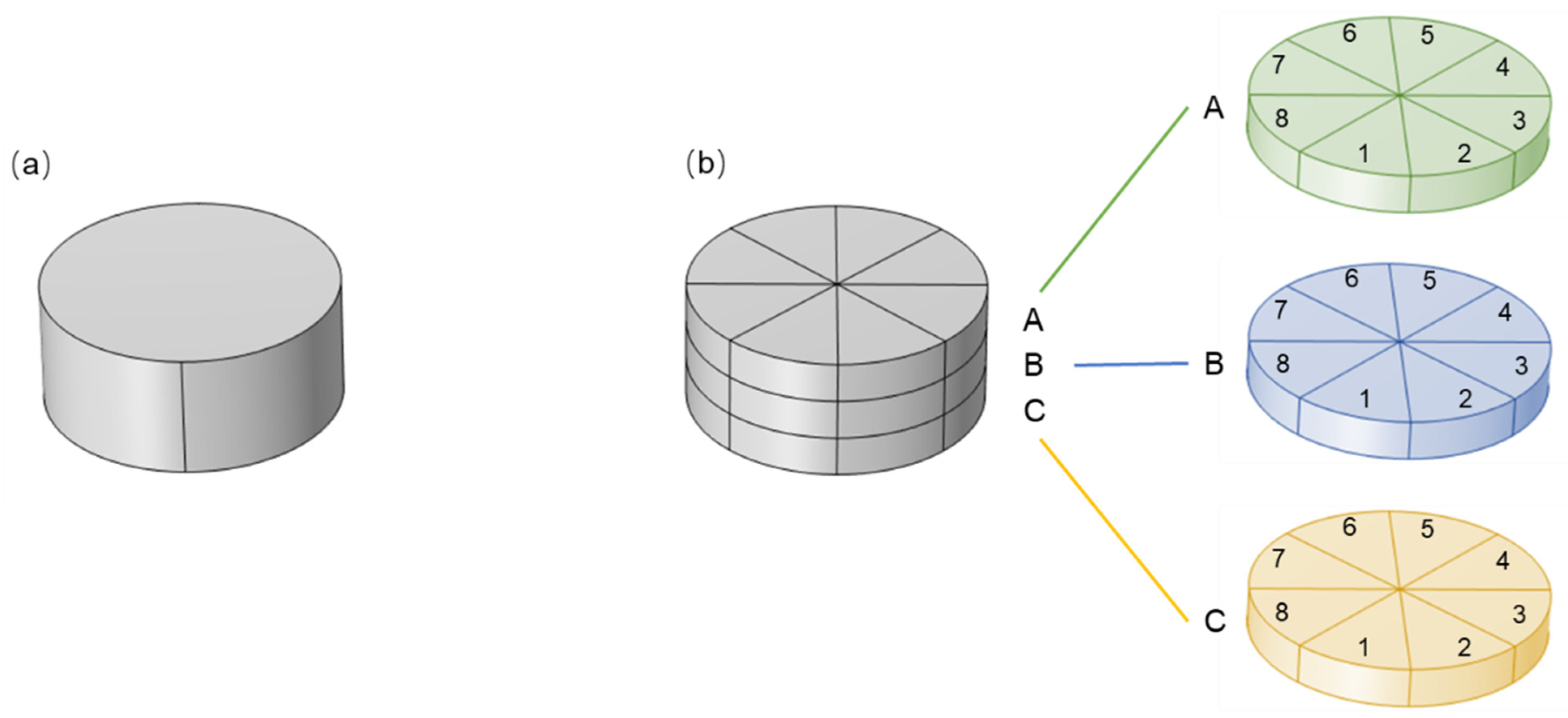
2.1.2. Geometry of the Macroscopic Membrane
2.2. Solving Methods
2.2.1. Momentum Conservation Equation
2.2.2. Mass Conservation Equation
2.2.3. Convection-Diffusion Equation
2.2.4. BSA Elution Equilibrium Equation
2.3. Model Setup
2.3.1. NaCl Tracer Process in Microscopic Channels
2.3.2. BSA Elution Process in Microscopic Channels
2.3.3. NaCl Tracer Process in Macroscopic Membranes
2.3.4. Mesh Generation
2.3.5. Convergence History
3. Results and Discussions
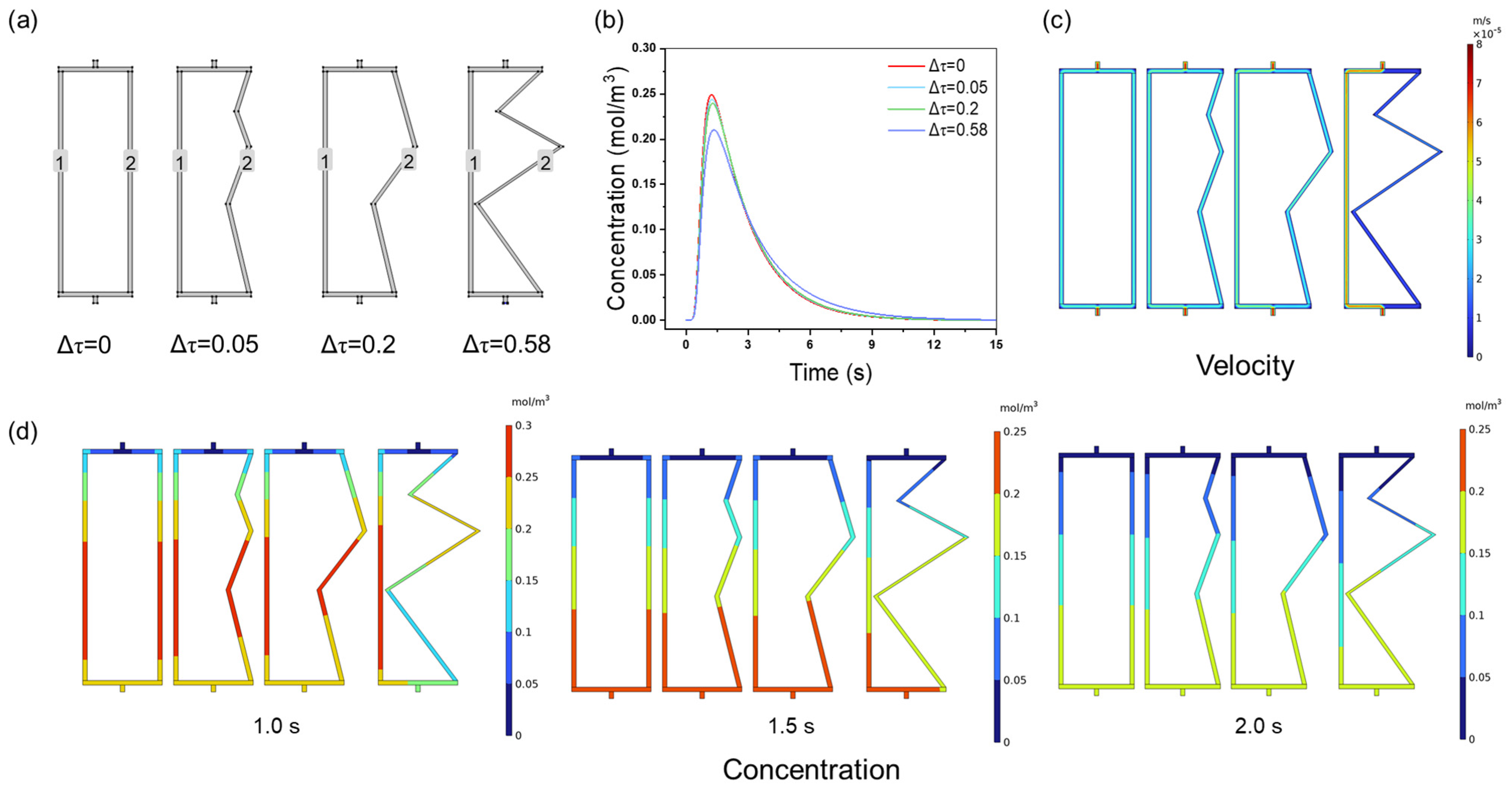
3.1. The Effect of Channel Tortuosity on Membrane Chromatography Performance
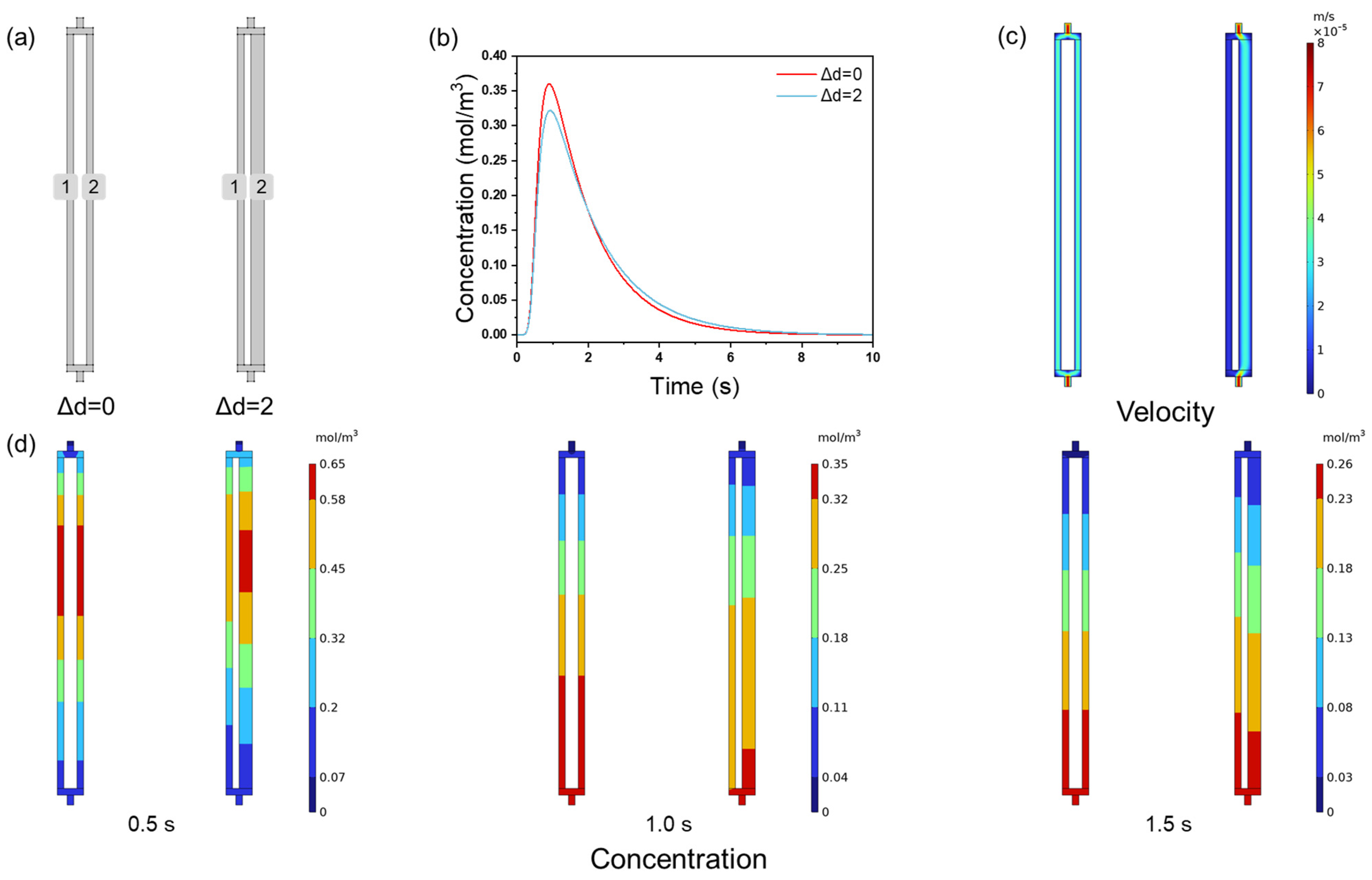
3.2. Effect of Channel Size Variation on Membrane Chromatography Performance
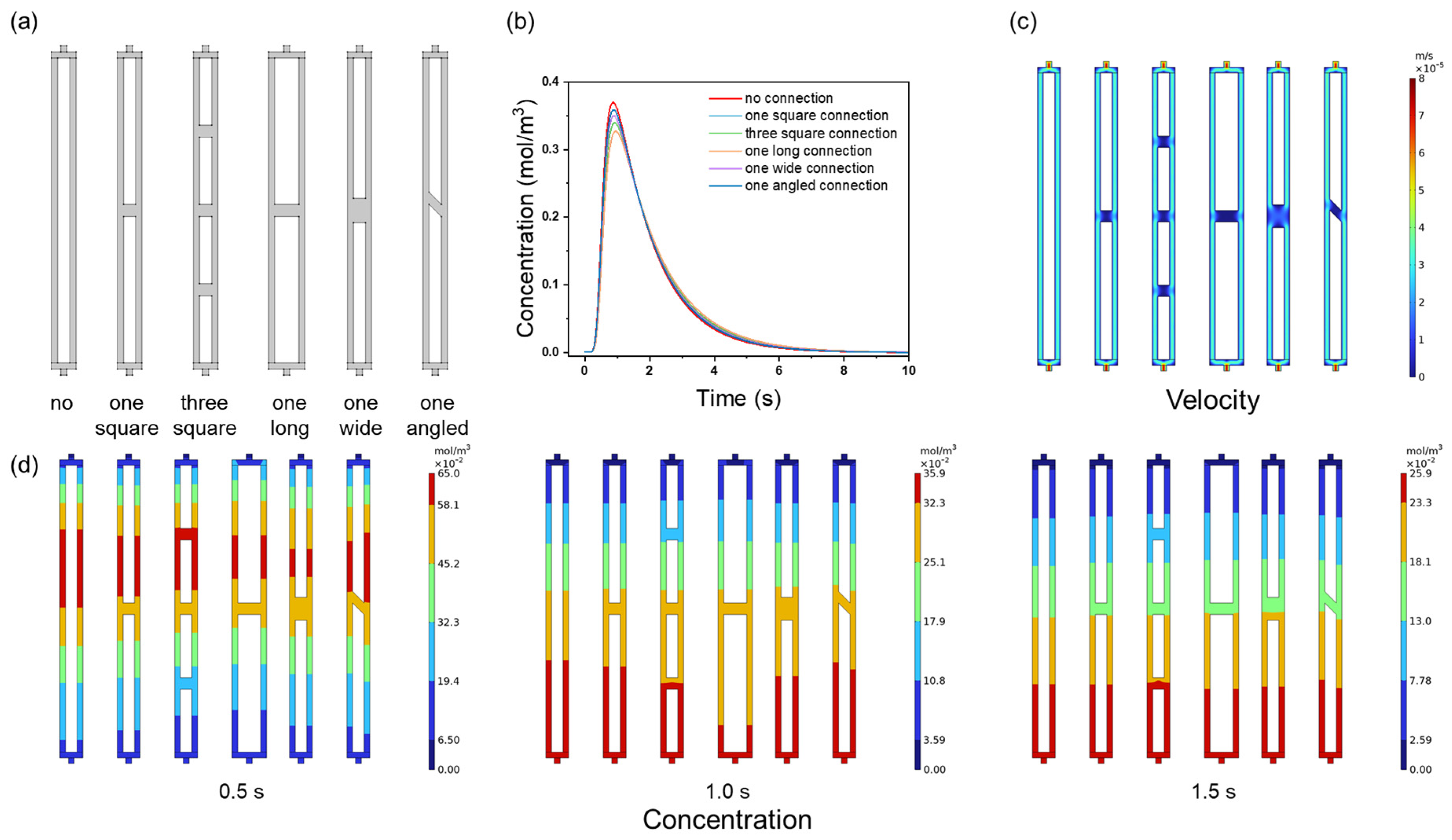
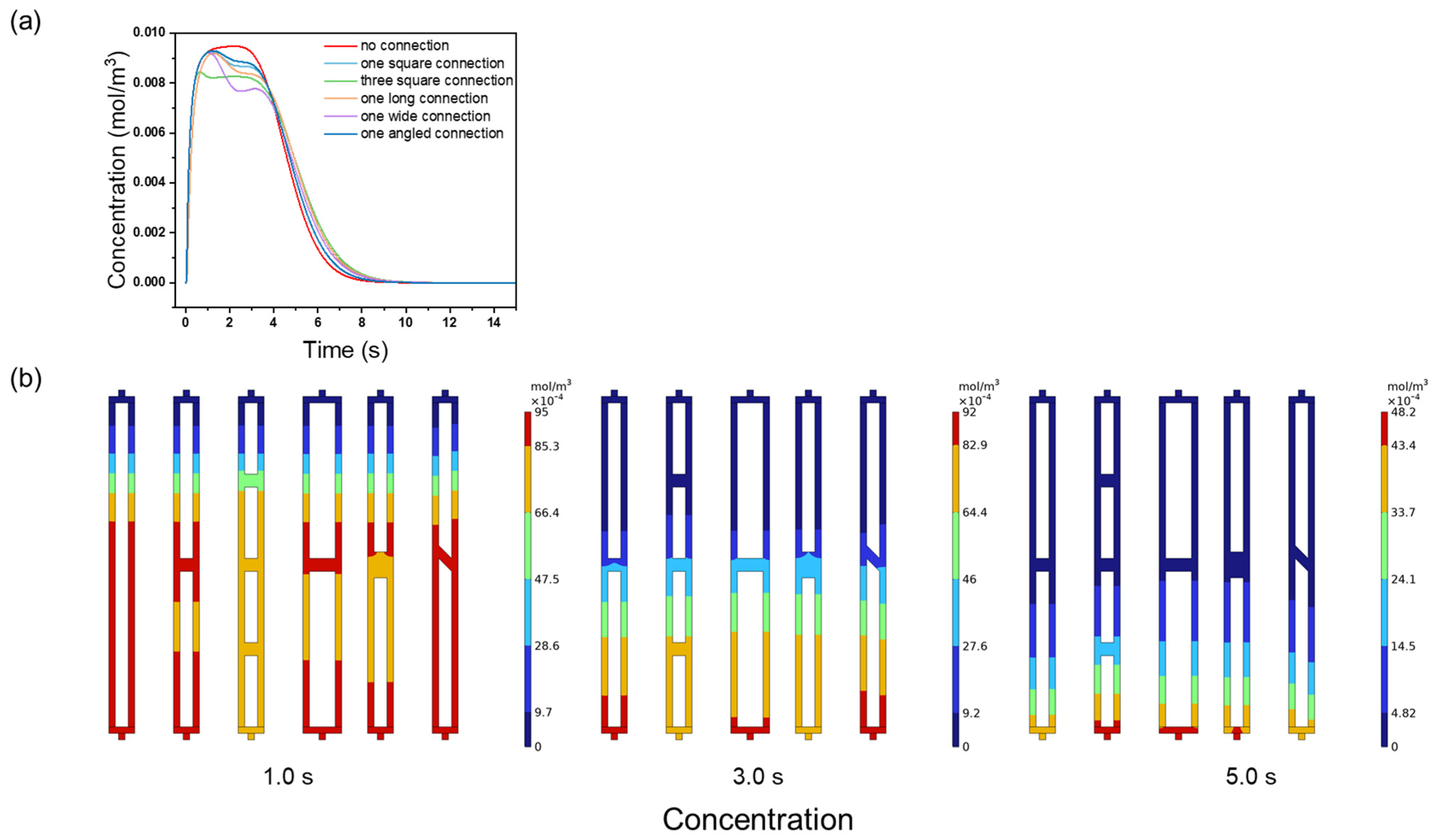
3.3. Effect of Channel Connectivity on Membrane Chromatography Performance
3.4. Effect of Membrane Uniformity on Membrane Chromatography Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rasmussen, A.S.B.; Hammou, A.; Poulsen, T.F.; Laursen, M.C.; Hansen, S.F. Definition, categorization, and environmental risk assessment of biopharmaceuticals. Sci. Total Environ. 2021, 789, 147884. [Google Scholar] [CrossRef] [PubMed]
- Makurvet, F.D. Biologics vs. small molecules: Drug costs and patient access. Med. Drug Discov. 2021, 9, 100075. [Google Scholar] [CrossRef]
- Lavoie, J.; Fan, J.; Pourdeyhimi, B.; Boi, C.; Carbonell, R.G. Advances in high-throughput, high-capacity nonwoven membranes for chromatography in downstream processing: A review. Biotechnol. Bioeng. 2024, 121, 2300–2317. [Google Scholar] [CrossRef]
- Ngo, H.X.; Garneau-Tsodikova, S. What are the drugs of the future? Med. Chem. Comm. 2018, 9, 757–758. [Google Scholar] [CrossRef]
- Rathore, A.S.; Kumar, D.; Kateja, N. Recent developments in chromatographic purification of biopharmaceuticals. Biotechnol. Lett. 2018, 40, 895–905. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Merenda, A.; Al-Attabi, R.; Dumée, L.F.; Zhang, X.; Thang, S.H.; Pham, H.; Kong, L. Towards next generation high throughput ion exchange membranes for downstream bioprocessing: A review. J. Membr. Sci. 2022, 647, 120325. [Google Scholar] [CrossRef]
- Ghosh, R. Protein separation using membrane chromatography: Opportunities and challenges. J. Chromatogr. A 2002, 952, 13–27. [Google Scholar] [CrossRef]
- Ghosh, R. Ultrahigh-speed, ultrahigh-resolution preparative separation of protein biopharmaceuticals using membrane chromatography. J. Sep. Sci. 2022, 45, 2024–2033. [Google Scholar] [CrossRef]
- Chen, G.; Wan, Y.; Ghosh, R. Bioseparation using membrane chromatography: Innovations, and challenges. J. Chromatogr. A 2025, 1744, 465733. [Google Scholar] [CrossRef]
- Orr, V.; Zhong, L.; Moo-Young, M.; Chou, C.P. Recent advances in bioprocessing application of membrane chromatography. Biotechnol. Adv. 2013, 31, 450–465. [Google Scholar] [CrossRef]
- Eon, C.H. Comparison of broadening patterns in regular and radially compressed large-diameter columns. J. Chromatogr. A 1978, 149, 29–42. [Google Scholar] [CrossRef]
- Hagemann, F.; Wypysek, D.; Baitalow, K.; Adametz, P.; Thom, V.; Wessling, M. Why device design is crucial for membrane adsorbers. J. Chromatogr. Open 2022, 2, 100029. [Google Scholar] [CrossRef]
- Camenzuli, M.; Ritchie, H.J.; Shalliker, R.A. Improving HPLC separation performance using parallel segmented flow chromatography. Microchem. J. 2013, 111, 3–7. [Google Scholar] [CrossRef]
- Camenzuli, M.; Ritchie, H.J.; Shalliker, R.A. Gradient elution chromatography with segmented parallel flow column technology: A study on 4.6 mm analytical scale columns. J. Chromatogr. A 2012, 1270, 204–211. [Google Scholar] [CrossRef]
- Ghosh, R.; Chen, G. Mathematical modelling and evaluation of performance of cuboid packed-bed devices for chromatographic separations. J. Chromatogr. A 2017, 1515, 138–145. [Google Scholar] [CrossRef]
- Janson, J.-C.; Hedman, P. Large-Scale Chromatography of Proteins. In Chromatography; Springer: Berlin/Heidelberg, Germany, 2005; pp. 43–99. [Google Scholar]
- Marchal, L.; Foucault, A.; Patissier, G.; Rosant, J.M.; Legrand, J. Influence of flow patterns on chromatographic efficiency in centrifugal partition chromatography. J. Chromatogr. A 2000, 869, 339–352. [Google Scholar] [CrossRef] [PubMed]
- Dorn, M.; Eschbach, F.; Hekmat, D.; Weuster-Botz, D. Influence of different packing methods on the hydrodynamic stability of chromatography columns. J. Chromatogr. A 2017, 1516, 89–101. [Google Scholar] [CrossRef] [PubMed]
- Horváth, K.; Lukács, D.; Sepsey, A.; Felinger, A. Effect of particle size distribution on the separation efficiency in liquid chromatography. J. Chromatogr. A 2014, 1361, 203–208. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, F.; Zhang, G. Mathematical analysis of affinity membrane chromatography. J. Chromatogr. A 2005, 1081, 156–162. [Google Scholar] [CrossRef]
- De Smet, J.; Gzil, P.; Vervoort, N.; Verelst, H.; Baron, G.V.; Desmet, G. On the optimisation of the bed porosity and the particle shape of ordered chromatographic separation media. J. Chromatogr. A 2005, 1073, 43–51. [Google Scholar] [CrossRef]
- Dolamore, F.; Dimartino, S.; Fee, C.J. Numerical Elucidation of Flow and Dispersion in Ordered Packed Beds: Nonspherical Polygons and the Effect of Particle Overlap on Chromatographic Performance. Anal. Chem. 2019, 91, 15009–15016. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.M.; Krühne, U. Computational Fluid Dynamics Modeling of Pressure-Retarded Osmosis: Towards a Virtual Lab for Osmotic-Driven Process Simulations. Membranes 2024, 14, 236. [Google Scholar] [CrossRef] [PubMed]
- Farzadfard, A.; Kunka, A.; Mason, T.O.; Larsen, J.A.; Norrild, R.K.; Dominguez, E.T.; Ray, S.; Buell, A.K. Thermodynamic characterization of amyloid polymorphism by microfluidic transient incomplete separation. Chem. Sci. 2024, 15, 2528–2544. [Google Scholar] [CrossRef]
- Ladd Effio, C.; Hahn, T.; Seiler, J.; Oelmeier, S.A.; Asen, I.; Silberer, C.; Villain, L.; Hubbuch, J. Modeling and simulation of anion-exchange membrane chromatography for purification of Sf9 insect cell-derived virus-like particles. J. Chromatogr. A 2016, 1429, 142–154. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Yao, S.-J.; Lin, D.-Q. Parameter-by-parameter method for steric mass action model of ion exchange chromatography: Theoretical considerations and experimental verification. J. Chromatogr. A 2022, 1680, 463418. [Google Scholar] [CrossRef]
- van Beijeren, P.; Kreis, P.; Zeiner, T. Ion exchange membrane adsorption of bovine serum albumin—Impact of operating and buffer conditions on breakthrough curves. J. Membr. Sci. 2012, 415–416, 568–576. [Google Scholar] [CrossRef]
- Vicente, T.; Sousa, M.F.Q.; Peixoto, C.; Mota, J.P.B.; Alves, P.M.; Carrondo, M.J.T. Anion-exchange membrane chromatography for purification of rotavirus-like particles. J. Membr. Sci. 2008, 311, 270–283. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in Porous Media: A Critical Review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Pápai, Z.; Pap, T.L. Analysis of peak asymmetry in chromatography. J. Chromatogr. A 2002, 953, 31–38. [Google Scholar] [CrossRef]
- Danielson, R.E.; Sutherland, P.L. Porosity. In Methods of Soil Analysis; American Society for Agronomy: Madison, WI, USA, 1986; pp. 443–461. [Google Scholar]
- Renard, P.; de Marsily, G. Calculating equivalent permeability: A review. Adv. Water Resour. 1997, 20, 253–278. [Google Scholar] [CrossRef]
- Temam, R. Navier–Stokes Equations: Theory and Numerical Analysis; American Mathematical Society: Providence, RI, USA, 2024; Volume 343. [Google Scholar]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 1987, 30, 3329–3341. [Google Scholar] [CrossRef]
- Constantin, P.; Foiaş, C. Navier-Stokes Equations; University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Stynes, M. Steady-state convection-diffusion problems. Acta Numer. 2005, 14, 445–508. [Google Scholar] [CrossRef]
- Karkov, H.S.; Sejergaard, L.; Cramer, S.M. Methods development in multimodal chromatography with mobile phase modifiers using the steric mass action model. J. Chromatogr. A 2013, 1318, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Dimartino, S.; Boi, C.; Sarti, G.C. A validated model for the simulation of protein purification through affinity membrane chromatography. J. Chromatogr. A 2011, 1218, 1677–1690. [Google Scholar] [CrossRef]




| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| A | 0.19 | 0.63 | 0.22 | 0.37 | 0.28 | 0.81 | 0.37 | 0.48 |
| B | 0.22 | 0.81 | 0.37 | 0.63 | 0.37 | 0.48 | 0.28 | 0.19 |
| C | 0.37 | 0.28 | 0.19 | 0.22 | 0.48 | 0.37 | 0.81 | 0.63 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| A | 0.0096 | 30 | 0.048 | 1.2 | 0.24 | 150 | 1.2 | 6 |
| B | 0.0480 | 150 | 1.2 | 30 | 1.2 | 6 | 0.24 | 0.0096 |
| C | 1.2 | 0.24 | 0.0096 | 0.048 | 6 | 1.2 | 150 | 30 |
| Parameters | Value | |
|---|---|---|
| Keq | Desorption reaction equilibrium constant | 5 |
| Csmax-inlet | Maximum NaCl concentration at the inlet (mol/m3) | 0.05 |
| CS0surf | Initial surface concentration of NaCl (mol/m3) | 9.9 × 10−9 |
| G0 | Initial site density on the reactive surface (mol/m2) | 1 × 10−8 |
| MA | Molar mass of BSA (kg/mol) | 66 |
| μ | Dynamic viscosity of water (Pa·s) | 1 × 10−3 |
| ρ | Density of water (kg/m3) | 1000 |
| Models | Nodes | Average Unit Qualities |
|---|---|---|
| Channel tortuosity | 14,758 | 0.774 |
| Channel size | 12,644 | 0.798 |
| Channel connectivity | 15,133 | 0.789 |
| Membrane | 331,245 | 0.556 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Tao, L.; Li, Y.; Liu, Q.; Zhou, H.; Wan, Y.; Chen, G. The Effect of Pore Channel Structure Uniformity on the Performance of a Membrane Adsorber Determined by Flow Distribution Analysis Using Computational Fluid Dynamics. Processes 2025, 13, 956. https://doi.org/10.3390/pr13040956
Yang X, Tao L, Li Y, Liu Q, Zhou H, Wan Y, Chen G. The Effect of Pore Channel Structure Uniformity on the Performance of a Membrane Adsorber Determined by Flow Distribution Analysis Using Computational Fluid Dynamics. Processes. 2025; 13(4):956. https://doi.org/10.3390/pr13040956
Chicago/Turabian StyleYang, Xu, Lu Tao, Yumeng Li, Qi Liu, Haoli Zhou, Yinhua Wan, and Guoqiang Chen. 2025. "The Effect of Pore Channel Structure Uniformity on the Performance of a Membrane Adsorber Determined by Flow Distribution Analysis Using Computational Fluid Dynamics" Processes 13, no. 4: 956. https://doi.org/10.3390/pr13040956
APA StyleYang, X., Tao, L., Li, Y., Liu, Q., Zhou, H., Wan, Y., & Chen, G. (2025). The Effect of Pore Channel Structure Uniformity on the Performance of a Membrane Adsorber Determined by Flow Distribution Analysis Using Computational Fluid Dynamics. Processes, 13(4), 956. https://doi.org/10.3390/pr13040956







