Abstract
This study develops a novel Lyrebird Optimization Algorithm (LOA), a technique inspired by the wild behavioral strategies of lyrebirds in response to potential threats. In a two-area interconnected power system that includes non-reheat thermal stations, this algorithm is applied to handle load frequency control (LFC) by optimizing the parameters of a Proportional–Integral–Derivative controller with a filter (PIDn). This study incorporates generation rate constraints (GRCs). The efficiency of the provided LOA-PIDn is evaluated through simulations under various disturbance scenarios and is compared against other well-established optimization techniques, including the Ziegler–Nichols (ZN), genetic algorithm (GA), Bacteria Foraging Optimization Algorithm (BFOA), Firefly Approach (FA), hybridized FA and pattern search (hFA–PS), self-adaptive multi-population elitist Jaya (SAMPE-Jaya)-based PI/PID controllers, and Teaching–Learning-Based Optimizer (TLBO) IDD/PIDD controllers. The results demonstrate the LOA’s ability to minimize the integral of time multiplied by absolute error (ITAE) and achieve significantly lower settling times for the two-area frequencies and transferred power variances in comparison with other methods. The comprehensive comparison and the inclusion of real-world constraints validate the LOA as a robust and effective tool for addressing complex optimization challenges in modern power systems.
1. Introduction
In both standalone and interconnected power systems, LFC plays a vital role in maintaining stability and reliability by ensuring that transferred power and frequencies remain at their permissible levels [1]. Any imbalance between electricity generation and demand caused by abrupt load changes or other disturbances leads to deviations in system frequency [2]. Such deviations are undesirable, as they can compromise the stability and performance of the power network. LFC is designed to quickly mitigate these frequency variations and restore tie-line power to its scheduled levels, ensuring smooth operation across the network. However, the inherent limitations of speed governors alone make them insufficient in achieving steady-state frequency regulation. This necessitates the use of an effective control mechanism capable of addressing these challenges by maintaining preferrable frequency operation and counteracting the effects of sudden load fluctuations [3,4].
The LFC problem is being studied by researchers worldwide, utilizing a variety of optimization and control tactics. A significant amount of research is being conducted to develop improved AGC systems based on different machine [5], deep [6], and reinforcement [7] learning methods. But unfortunately, these sophisticated methods are difficult to apply and need users to be familiar with them, which limits their application. As an alternative, engineers continue to select traditional PID controllers and their equivalents because of their structural simplicity, dependability, and advantageous cost–performance ratios. Also, they do not need high levels of user skill, require a minimum development time, and enable easier dynamic modeling. Many EA-based methods were applied to tune PI/PID controller knobs for AGC systems. In [8], a BFOA was used to optimize the PID parameters in a two-area system that has thermal plants, considering non-reheat types, demonstrating superior efficiency compared to the conventional ZN and GA methods. In [9], GSO was applied in an attempt to optimize the PI/PIDF settings in interconnected power grids with and without considering GRCs and GBD nonlinearity. In [10], the FA and hFA–PS-based PID controller techniques were employed twice for a simple and multi-source two-area system comprising nonlinearities. In [11], a PIDD controller was designed based on a TLBO for multi-area electrical infrastructures that use a variety of sources such as thermal sources that consider boiler dynamics, hydro, renewable and diesel units. In [12], a PID controller was optimally tuned based on an improved version of the Jaya algorithm known as the SAMPE-Jaya algorithm for thermal power systems presenting nonlinearity constraints, while the PID and PI controllers’ settings were optimized using the DE approach in [13]. The idea of regulating the load frequency while accounting for time delay was presented in [14]. To address load frequency fluctuations, a cascaded PD with a filter (n)-PI controller implemented the COA in [15]. Also, the CIO-based controller design of the PID/(1 + PID) PID controller cascaded for isolated and interconnected thermal power in [16], whereas CIO was applied to an FOPID-based secondary LFC for single-area and dual-area microgrids in [17]. In addition, an NNA based on biological nervous systems and ANNs was developed in designing a FOPID Controller for Power Systems LFC [18]. The finest address in every iteration acts as the desired level, and other responses adapt to minimize their error in relation to this goal. This is how the NNA uses linked neurons. The potential solutions mirror how neurons modify individual synaptic links and intensities through dynamic communication and updating. Since NNA tests and improves solutions iteratively, feedback methods are essential.
In order to improve the PID controller’s effectiveness at reducing frequency fluctuations, an MHABC-PSO has been suggested [19]. In [20], an IPD (1 + I) control scheme for a multi-area network based on renewable energies was designed using a TSA. In [21], an HBA was utilized to optimize a PI/PID configuration to address LFC in electrical systems with embedded environmentally friendly clean energy. Also, an MVO and a GWA have been proposed based on classical LFC design for an interconnected electrical system in [22] and [23,24], respectively. Furthermore, an LOA showed magnificent performance based on PI/PID controllers in [25,26]. In [27], a PID controller was applied to the LFC in a two-area power system, where the parameters were optimized using a PSO and HHO, and its performance was assessed using the ITAE metric. Nevertheless, the validation of the HHO was solely presented in relation to the PSO, lacking comparisons with established results. In another study [28], a PID controller was configured with optimized gains through a GA and PSO to manage LFC in deregulated systems with multiple sources and stakeholders. The aim of this research was to stabilize frequency, reduce uncontracted power flows in tie-lines, and fulfill load-balancing agreements. However, the comparative analyses were limited to the GA and PSO, neglecting comparisons with other contemporary methods or existing findings. In [29], the LFC in multi-area interconnected power systems was handled via a PID controller optimized using the POA. Four interconnected areas in the studied system in [29] included thermal, hydroelectric, and gas turbine units. Also, a sensitivity analysis under various load perturbations was conducted with significant improvements in the ITAE compared to the PSO and GWO. Through a three-area interconnected power system, a model-free adaptive control algorithm for LFC was developed and modeled in [30] as a switching system with dynamic linear subsystems to ensure stability under DoS attack conditions.
In [31], a study was conducted to optimize the LFC in a single-area power grid using a PID controller, with a PSO employed to set the controller parameters. However, this study only compared the performance of the traditional PID controllers and did not explore other contemporary optimization techniques or controllers. As a result, the findings lacked broader applicability, and the robustness of the controller across various operating conditions needed further validation through additional research. The study in [32] focused on LFC within a standalone single-area system that included gas, hydroelectric, and thermal power generation units. Here, the PID controller was tuned using the PSO algorithm. Although the research provided valuable insights into the system’s performance, the comparison was restricted to PID controllers. It did not include more advanced or contemporary control strategies, leaving a gap in performance evaluation against other modern optimization techniques. As a result, the study did not fully explore the potential improvements that could be achieved using advanced algorithms. In [33], a similar approach was taken to optimize the LFC in a stand-alone single-area system with gas, hydropower, and thermal equipment, again using the PID controller tuned using the PSO. Much like the previous study, the focus was solely on PID controllers, and there were no additional benchmarks or comparisons made with more recent or advanced strategies. This limits the ability to assess how well the system might perform when compared to newer control techniques or more complex optimization algorithms. Lastly, in [34], the study investigated LFC in a single-area thermal power station using both PI and PID controllers, optimized using GNO. The research was specifically limited to a single-area network, which restricted its relevance and applicability to larger, more complex power systems. Consequently, the results may not be generalizable to multi-area systems or broader applications in the field of LFC, highlighting the need for further research in more extensive power grid configurations.
In [35], an intelligent approach utilizing AO to fine-tune a FOPID controller was presented to enhance the stability of a multi-source power system comprising a thermal plant, hydroelectric infrastructure, gas turbine, and wind energy inputs. Another study, [36], addressed the challenges of wind power integration into hydropower networks by stabilizing grid operations disrupted by disturbances. It leveraged the GSO enhanced with the convergence factor of the PSO to resolve local convergence issues and mitigate wind power grid connection interference, offering an effective solution for hydropower systems with integrated renewable energy sources. In [37], an SMC was tuned using the Arctic Puffin optimizer in electrical power distribution systems and was compared to PI controllers. In this work, a voltage restorer was controlled with the primary objective of mitigating voltage dips due to nonlinear converter operation. Squirrel searching optimization was demonstrated in [38] for interconnected power systems, underlining a need for sophisticated control and demonstrating the versatility of designed algorithms in LFC. Kalyan et al. looked into FO fuzzy controllers for handling a range of sources with constraints that were optimized using the seagull optimization method [39]. These methods were employed to adjust the control system parameters in multi-area power systems in order to obtain optimal LFC. In [40], the LFC issues of a microgrid were optimized using an integrated trained artificial neural network and the PSO technique.
Biologically inspired algorithms derive their principles from natural processes such as adaptation, selection, and collective behavior. Their robustness and adaptability make them powerful tools for solving complex problems in various fields, including engineering optimization, resource allocation, feature selection, artificial intelligence, and machine learning. Figure 1 provides an overview of the classification of biologically inspired algorithms, illustrating some of the most frequently used techniques and their respective applications [41]. These algorithms can be broadly classified into two main categories: EAs and swarm-based algorithms, with the latter further divided into animal-inspired and plant-inspired approaches.
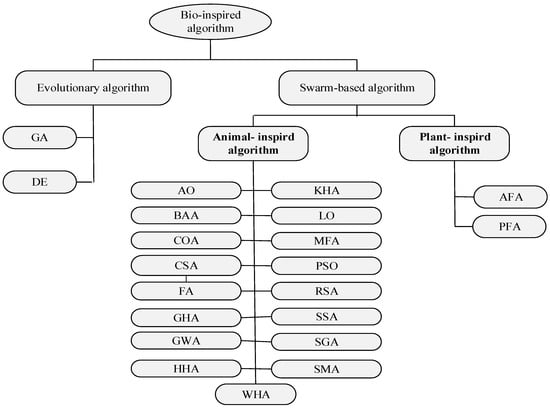
Figure 1.
Classification of bio-inspired algorithms.
EAs, inspired by natural evolution, refine solutions iteratively to achieve optimal performance. Examples include the GA, DE, and evolutionary strategies. Swarm-based algorithms take inspiration from collective intelligence observed in biological groups, where individual agents interact locally to achieve a globally optimal solution. This category can be further divided into animal-inspired algorithms, which replicate behaviors such as flocking, foraging, and hunting, and plant-inspired algorithms, which draw from growth patterns, nutrient distribution, and reproduction strategies. Animal-inspired algorithms like the PSO, the GWA, whale optimization, and the ABC are widely used in various fields.
Plant-inspired algorithms, inspired by plant behaviors like root growth and pollination, are a new branch of biological optimization methods. Examples include rooted tree optimization, the forest optimization algorithm, and pollination-based optimization.
The LOA is a new bio-inspired optimizer which mimics the distinctive protective behavior of lyrebirds in their natural environment when threatened [42]. These birds use a dual-phase strategy: first, they assess their environment for possible hazards, and then they adapt by fleeing to a safe region (exploration) or concealing in an appropriate spot (exploitation). The LOA uses this behavioral motivation to strike a balance between global searching and local refining in optimization tasks. The technique theoretically represents these phases, featuring the exploration phase, boosting variety through promoting broad scans, and the exploitation phase, focusing on fine-tuning solutions near optimal areas. In tackling real-world limited optimization issues, the LOA outperforms numerous well-established methods. This study expands the applicability of the LOA by employing it to optimize PIDn controllers in load frequency control systems, proving its capacity to efficiently deal with nonlinearities and physical restrictions. The LOA is used to formulate the suggested controller’s design as an optimization task that considers fluctuations in transferred power and area frequencies. The efficiency of the suggested technique is evaluated, contrasting with several previously published techniques, and its superiority is substantially demonstrated. Therefore, the key findings of the study are as follows:
- This study proposes the development of the LOA, inspired by the behavior of lyrebirds, for parameter optimization of nonlinear load frequency controllers.
- This research demonstrates the effectiveness of the LOA in designing a PID controller with a filter (PIDn) to address power system oscillations.
- This study compares the performance of LOA-tuned PIDn controllers against several advanced algorithms, including the ZN, GA, BFOA, FA, and hybrid approaches.
- Simulation results reveal that the LOA-tuned PIDn controller outperforms existing methods in terms of settling times and the ITAE, providing better dynamic and damping performance.
- This study incorporates real-world constraints like GRCs to make the results practical and applicable to real systems.
2. System Model: Generation-Rate-Constrained LFC in Multi-Area Systems
2.1. Framework for the System Model: A Comprehensive Overview of the Design Approach
To provide a structured understanding of the LFC system model and the application of the LOA, the following framework outlines the design approach. The model ensures effective frequency regulation in a multi-area power system, incorporating GRCs and optimized PIDn controllers. The system under consideration consists of two interconnected power areas, each with non-reheat thermal power plants; each area has a dedicated LFC to maintain frequency stability, and tie-line power exchange between the areas is considered to regulate deviations. The framework of the power system model is depicted in the next subsection. Also, in this section, the LFC mechanism is illustrated, where PIDn controllers are implemented in both areas and each ACE serves as the input for the controllers. In addition, the ITAE is used as the fitness function to minimize frequency deviations and improve transient response.
In Section 3, the LOA framework is depicted as optimizing the PIDn controller parameters to enhance system response under different disturbance scenarios. The LOA starts with an initial population of solutions, where each solution represents a set of PIDn controller gains. The fitness function (ITAE minimization) is evaluated for each solution. The LOA mimics the lyrebird’s searching behavior, where candidate solutions explore the search space to identify better control parameters. After identifying promising solutions, local refinement is performed to finetune controller gains. The best solution is to update iteratively until the stopping criteria are met. In Section 4, the proposed LOA-PIDn approach is validated through simulation studies under various conditions with comparisons against the ZN, GA, BFOA, FA, and SAMPE-Jaya approaches. Different key performance metrics are estimated, such as the settling time, frequency deviation, and tie-line power response.
2.2. Power System Model Under Investigation
As shown in Figure 2, the investigated structure includes two interconnecting electrical networks comprising non-reheat thermal plants. The frequency of each area is governed by the swing equation, where deviations arise due to load disturbances. The power system dynamics are represented using state-space modeling, incorporating governor, turbine, and system inertia effects. The GRC limits the rate at which thermal generators can adjust power output, which is typically 2–5% per minute. This framework is widely used in the scientific literature for the development and investigation of automated load frequency problems of linked regions [8,9,10,11,12]. The remaining parameters of system are the same as those mentioned in Appendix A [8,9,10,11,12].
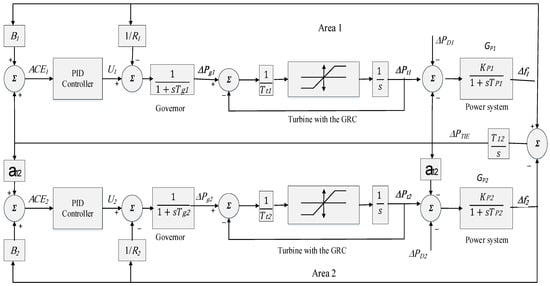
Figure 2.
Two-area power system under investigation.
Under dynamically changing system states, PID controllers are among the most effective controllers [10,11,12]. PID controllers are, therefore, used for both of the regions of the model under consideration. Figure 3 provides a description of the PID structure. The derivative term is filtered in order to reduce the input signal’s noise effect. Equations (1) and (2), correspondingly, could be used to characterize the transfer functions of PI and PIDn.
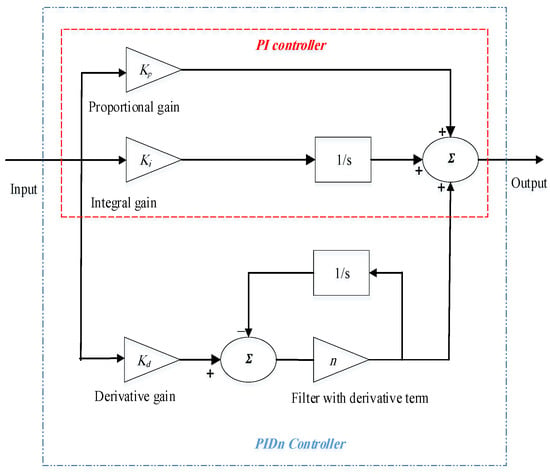
Figure 3.
PI/PIDn controller diagram.
The controllers receive as inputs the corresponding errors (ACE1 and ACE2), which are provided by [43]:
The performance index can be explained using the ITAE, since it offers rapid settling, which is widely utilized in LFC research [44]. As a result, it is regarded as a potent fitness function that can be used to achieve the best gains of the suggested PID controller, and it can be expressed as follows:
In LFC studies, a function’s fitness is assessed based on how effectively it keeps the system frequency and tie-line power within reasonable bounds while accounting for overshoot/undershoot and settling time. The appreciated ITAE must be as minimal as feasible in order to improve the system responsiveness. With the exclusion of the PID controller, which has a filter parameter n border set between 1 and 200, all of the parameters of the different prospective controllers, PI/PIDn, are tuned between 4 and −4 [15].
3. LOA
The LOA is an optimization algorithm influenced by nature; the algorithm is inspired by the behavioral characteristics of an Australian bird when it is primed to detect any possible threat. In such a scenario, the bird looks around before escaping or hiding in a suitable location. The creation of the proposed LOA optimization procedure was based on the lyrebird’s danger-avoidance tactics [42].
3.1. Population Initialization
In this step, the lyrebird population and the maximum number of iterations are initialized. Each lyrebird indicates a position vector that, according to Equation (6), indicates the current position of the specified lyrebird:
Here, La denotes the total number of lyrebirds that are present in the search space, which ranges from 1 to p, and Lj is the jth search agent. As is the case of every population-based metaphor [45,46,47], each seeking lyrebird is initially randomly determined. The fitness of each lyrebird is recorded in a vector as Equation (7):
The above description is used to store each lyrebird’s value; the best candidate solution is determined by the goal function’s best value, and vice versa.
3.2. Updating of Position
The exploration phase and exploitation phase are the two processes that can be employed to alter the position of the lyrebirds. The algorithm’s exploration phase involves the lyrebirds’ escape to safer areas, causing changes in their position, necessitating scanning different search areas to ensure safety. This is the exploration capability of the LOA in global optimum searching. According to this concept, the locations of the lyrebirds with superior fitness functions are also regarded as safe zones for each individual lyrebird. As a result, each LOA member has an assortment of safe areas that may be identified as follows:
Here, SAi is the assortment of safe areas for the ith lyrebird and Lk is the kth row of the L vector, which includes the best value of fitness function (i.e., Fk) compared to the other ith LOA members (i.e., Fk < Fi).
Each LOA member’s new position can be determined using Equation (9). Then, if the value of the objective function is improved, this new position replaces the previous position of the corresponding member according to Equation (10), as follows:
Here, the chosen safe area at the ith position is represented by SSAi, SSAi,j is its jth position, is the new proposed position determined for the ith lyrebird based on escape tactics, is its jth dimension, is the fitness function value, ri,j are the random numbers in the interval [0, 1], and Ii,j are the numbers that are arbitrarily selected as either 1 or 2.
Furthermore, each lyrebird’s value is updated in space throughout the exploitation phase (hiding strategy), which is based on the lyrebird’s survival strategy of hiding in its safe surroundings. Using Equations (11) and (12), the new position can be determined for every LOA member. Additionally, it can only be substituted if it is superior to the previous one and if the given position enhances the value of the fitness function.
Here, t is the present iteration, is the new position that is determined for the ith lyrebird that is totally reliant on the strategy proposed by the LOA optimization approach, is its jth dimension, is its fitness function’s value, and “t” is called the iteration counter. The LOA steps are illustrated in Figure 4. The LOA was employed in this study to optimize PIDn controller parameters for LFC in a multi-area power system. The primary objective of the optimization process was to minimize frequency deviations and improve the dynamic response of the power system following disturbances. The ITAE was chosen as the objective function as formulated in Equation (5) because it effectively penalizes larger deviations over extended time periods, ensuring a faster and smoother system response.
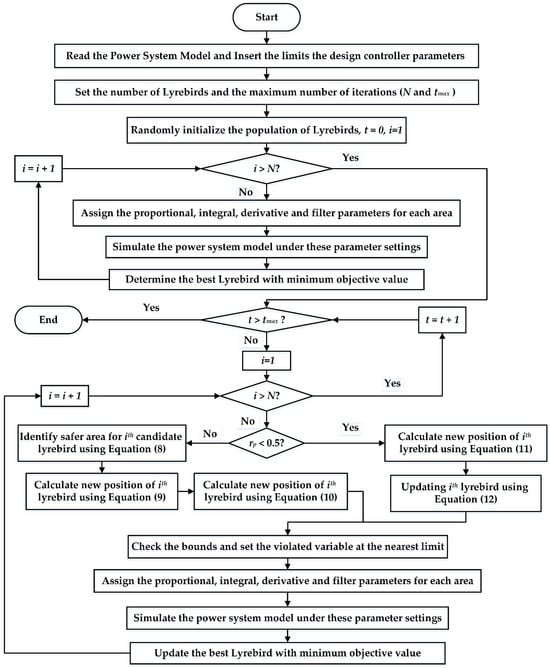
Figure 4.
LOA flowchart.
Minimizing the ITAE leads to a control system that not only reduces steady-state errors but also ensures minimal overshoot and a faster settling time. The LOA must adhere to several constraints that reflect the physical and operational limits of the power system. The PIDn controller gains are bounded to prevent excessive control effort:
where KP, Ki, Kd, and n are the proportional, integral, and derivative gains and filter parameter for the derivative term. The filter parameter is constrained to ensure numerical stability and prevent excessive noise amplification.
The minimum ITAE value is determined through an iterative optimization process using the LOA.
The LOA, like most metaheuristic algorithms, begins with randomly generated initial solutions. This randomness introduces variability in the results across multiple optimization runs, potentially leading to different optimized PIDn controller settings in each execution. However, this is a common characteristic of all metaheuristic optimization techniques, where exploration–exploitation trade-offs and convergence behavior determine the quality of the final solution. Since metaheuristic algorithms do not rely on a deterministic gradient-based search, their initial population is randomly distributed across the search space. This helps avoid local optima by diversifying the starting solutions; enables the algorithm to explore different regions of the search space, increasing robustness; and prevents bias toward the preselected parameter values, allowing a global search for optimal control gains. However, this also means that each optimization run may yield slightly different results, which can raise concerns regarding the repeatability and reliability of the optimization process. To mitigate the impact of random initialization and ensure reproducible and stable optimization results, multiple runs are implemented and instead of relying on a single optimization run, the LOA is executed multiple times. The optimization proceeds as follows:
- Initialization: a population of candidate solutions (i.e., different sets of PIDn gains) is randomly initialized.
- Evaluation: each candidate solution is simulated in the LFC model, and the ITAE value is computed.
- Exploration and exploitation: The LOA search mechanism guides the solutions toward better PIDn gain settings. Safe zones are identified and candidate solutions are adjusted iteratively.
- Convergence check: The algorithm stops when the maximum iterations are maintained. For every subsequent iteration, the best solution (i.e., the set of PIDn gains yielding the lowest ITAE) is selected.
In this study, the filter parameter (n) in the PIDn controller was treated as an additional control variable and optimized using the LOA. Unlike traditional PID controllers, where the derivative action can amplify high-frequency noise, the inclusion of a filter term helps to mitigate these effects. However, rather than manually selecting a filter coefficient, the optimization algorithm dynamically determines its optimal value alongside the PID gains to achieve a balance between controller responsiveness and noise suppression. By adjusting n optimally, the controller achieves smoother control action, reducing excessive oscillations and minimizing noise amplification. The evolutionary search ensures that the solution is not biased toward an arbitrarily chosen filter parameter but instead adapts dynamically based on system conditions. Since the optimized filter setting inherently reduces noise effects, the test cases presented in this study appear to deal with clean signals. This is a direct result of the LOA algorithm selecting an optimal n.
4. Simulation Results and Discussion
The efficiency of the suggested LOA for optimizing control parameters is demonstrated in this part through the examination of several comparative situations. The ideal controller PI/PIDn parameter values for the LOA approach with a considered GRC value of 0.05 for case (1) and (2) is outlined. The LOA and the LFC simulations were implemented using MATLAB software, version 2017b.
4.1. Case 1: SLI in Area 1
In this instance, a 5% SLI in area 1 is considered without change in area 2. Table 1 displays the optimal values of LOA-specific parameters for PI and PIDn controllers at both areas considering GRC of ±0.05. Also, the performance of the suggested LOA-tuned PIDn technique is contrasted with that of the LOA-tuned PI technique as well as other previously published heuristic and conventional approaches indicated in Table 2. With the same objective function (the ITAE) and saturation limit (GRC = ±0.05), Table 2 makes it evident that the LOA-tuned PIDn yields the lowest ITAE value of 0.2048 in contrast to the results of the ZN, GA, BFOA, FA, hFA–PS and SAMPE-Jaya approaches of 0.6040, 0.5513, 0.4788, 0.3240, 0.2782, 0.2078, respectively. Also, it is better than the LOA-tuned PI of 0.4231.

Table 1.
Values of LOA-specific parameters for GRC = ±0.05.

Table 2.
Comparing ITAE and settling time performance of several methods (case 1).
In addition, it achieves excellent results for transferred power variances and the overall settling time of area frequency results over other prior optimizations. Moreover, the dynamic responses corresponding to these optimum gains of the PI and PIDn controllers were compared (Figure 5, under the ITAE). Figure 5a,b depict the responses for frequency variations in each jurisdiction, while Figure 5c shows the tie-line power deviation between areas. It can be inferred from Figure 5 that at the instant of load change, the PIDn controller outperforms the PI controller in terms of dynamic performance, due to how it offers a very quick and steady response together with outstanding system damping characteristics.
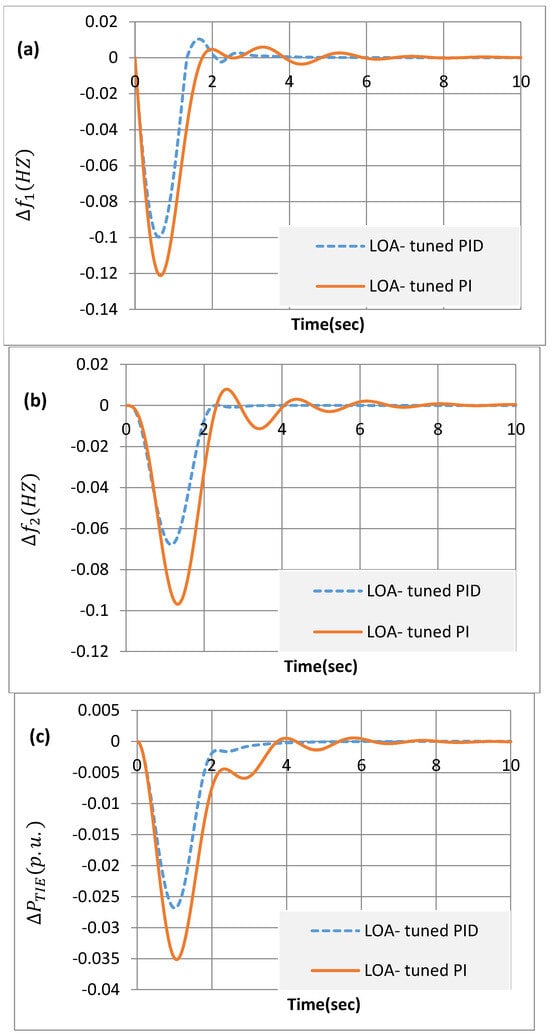
Figure 5.
Comparison of dynamic responses to 5% disturbance in area 1 with GRC = ±0.05 (a–c).
4.2. Case 2: SLI in Areas 1 and 2
Here, a 5% SLI in area 1 with a concurrent 2% SLI in area 2 and a GRC = ±0.05 were addressed. Table 3 illustrates the related outcomes of the LOA-based PI/PID controllers regarding the settling times’ optimum control for each area and the ITAE. The table indicates the improved capabilities of the suggested LOA-tuned PIDn controller since it gives a minimal ITAE reading of 0.2245 and settling frequency times and transferred power changes of 2.2573, 2.7583, and 2.7862, respectively, in contrast to the LOA-tuned PI controller with an ITAE of 0.5442 and settling frequency times and transferred power changes of 4.7414, 7.2896, and 7.6936, respectively. Additionally, the responses for the deviations in area frequencies and transmitted power are demonstrated in Figure 6. The proposed LOA-tuned PIDn controller is in fact more effective at enhancing the power system’s damping characteristics than the LOA-tuned PI controller in terms of area frequencies and transmitted power.

Table 3.
Performance comparison under case 2.
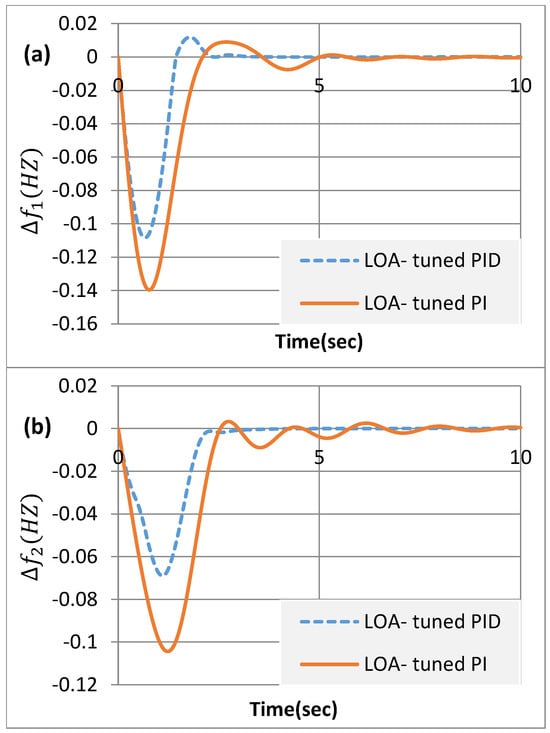
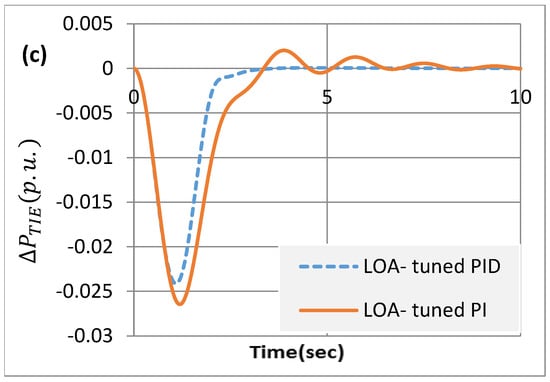
Figure 6.
Dynamic responses of LOA-PI and PID controls to 5% and 2% SLI in areas 1 and 2 with GRC = ±0.05 (a–c).
4.3. Case 3: Impact of Saturation Limit on System Response (GRC = ±0.025)
In this case, a 5% SLI in the domain of the first area with a GRC = ±0.025 was applied. The optimal controller PI/PIDn parameter settings for the LOA technique are illustrated in Table 4. The performance comparison between the suggested LOA-tuned PI/PIDn technique and other heuristic and traditional approaches that have been previously published is displayed in Table 5.

Table 4.
Values of LOA-specific parameters for GRC = ±0.025.

Table 5.
Comparing ITAE and settling time performance of several methods (case 3).
The tabulated results confirm the superiority of the LOA-tuned PID since it achieves a minimum ITAE value of 0.5841 as opposed to the ZN, GA, BFOA, FA, hFA–PS and TLBO-tuned IDD/PIDD results of 3.4972, 2.4668, 1.5078, 0.8023, 0.7405, 0.7400 and 0.6798, respectively. Additionally, the LOA-tuned PI controller achieves an ITAE value of 0.732. Furthermore, it outperforms other prior optimization methods in terms of settling time for frequencies and tie-line power deviations. The dynamic responses for tie-line power under the ITAE and frequency fluctuations in each jurisdiction are also displayed in Figure 7. The suggested LOA-tuned PIDn controller behaves better in terms of frequency deviations in each area and its tie-line power dynamic performance than the LOA-tuned PI controller, as illustrated in Figure 7.
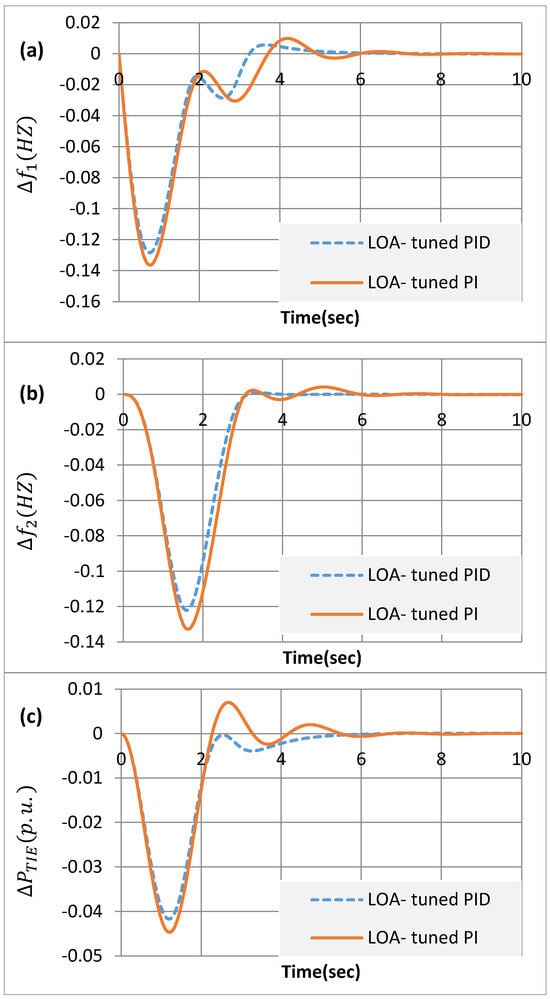
Figure 7.
Comparison of dynamic responses to 5% disturbance in area 1 with GRC = ±0.025 (a–c).
4.4. Discussion of Generalization of LOA to Different Power System Configurations
The LOA has demonstrated effectiveness at optimizing LFC for a two-area thermal power system. While the current study focuses on a thermal-based power system, modern grids increasingly rely on a mix of hydropower, wind power, solar power, gas turbines, and nuclear power plants. Renewable energy sources introduce higher frequency fluctuations, making frequency regulation complex. The LOA must dynamically adjust PIDn controller gains in wind- and solar-integrated power systems, incorporate hybrid energy storage, and test performance in multi-source energy systems. Testing the LOA’s performance in multi-source energy systems would validate its effectiveness at managing frequency deviations under diverse operating conditions. Further investigation is needed to understand the performance of the LOA in isolated microgrids and large interconnected grids, as microgrids require highly adaptive controllers for real-time frequency stabilization, and its scalability for national or regional grids.
One of the key considerations in power system optimization is the presence of nonlinear constraints, such as GRCs, governor dead bands, and communication delays. The current study evaluates the LOA under GRC limits of ±0.05 and ±0.025, which are typical for thermal power plants. However, in hydroelectric and nuclear power plants, GRC values differ significantly. Investigating the LOA’s applicability to power generation systems could enhance its ability to handle varying physical constraints and stochastic load variations, allowing controllers to dynamically adjust parameters for improved frequency stability.
Moreover, smart grids require real-time monitoring and demand response mechanisms and cyber-physical security. The LOA’s effectiveness should be tested under communication delays, cyber-attacks, and distributed control architectures, integrating IoT and blockchain.
5. Conclusions
The LOA was used in this research to optimize the PIDn controller’s parameters for LFC in nonlinear multi-area power systems. The nonlinearity characteristics of the GRC with its real physical restrictions were adopted in the nonlinear model. Using the ITAE as a fitness function, three distinct scenarios with different sets of disturbances were taken into consideration. A comparison between the suggested PIDn based on the LOA and the PI-controller-optimized LOA was conducted. Also, other previous reported methods using GA, FA, ZN, BFOA, hFA–PS, and SAMPE-Jaya based PI/PID controllers and TLBO-based IDD/PIDD controllers were mentioned. This comparison demonstrated the suggested LOA’s efficacy and capabilities in terms of PID controller design. The suggested method outperformed the others in terms of system performance indicators like settling times and the ITAE. Moreover, simulation results showed a notable improvement with the suggested PIDn-controller-tuned LOA, which offers a significantly better dynamic performance than the LOA-tuned PI controller. This study does not consider communication delays, cyber-security issues, the resilience of the suggested technique in the presence of uncertainty, or the complex characteristics of thermal plants with RESs, all of which can be considered limitations in the present work and which remain subjects of future investigations. Also, the LOA applications can be extended to electrical system optimizations, including PV parameter estimation [48,49,50], wireless systems [51], optimal power flow [52,53,54], relay coordination in power systems [55], and PV penetration in distribution systems [56].
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed at the corresponding author.
Conflicts of Interest
The author declares no conflict of interest. There are no financial competing interests.
Nomenclature
| List of Abbreviations | |
| AGC | Automatic Generation Control |
| MGs | microgrid systems. |
| AO | Aquila Optimization |
| BFOA | Bacterial Forage Optimization Approach |
| COA | Coyote Optimization Approach |
| DoS | Denial-of-Service |
| DE | Differential Evolution |
| EAs | evolutionary algorithms |
| FA | Firefly Algorithm |
| KHA | krill-herd algorithm |
| LO | lion optimizer |
| MFA | moth–flame algorithm |
| RSA | reptile search algorithm |
| SSA | salp swarm algorithm |
| SGA | seagull algorithm |
| SMA | spider monkey algorithm |
| BAA | bat-inspired algorithm |
| CSA | cuckoo search algorithm |
| GHA | grasshopper algorithm |
| HHA | Harris hawks algorithm |
| AFA | artificial flora algorithm |
| PFA | paddy field algorithm |
| WHA | whale-inspired algorithm |
| GA | genetic algorithm |
| GNO | Global Neighborhood Optimization |
| GSO | Gravity Search Optimisation |
| GWO | Grey Wolf Optimizer |
| CIO | cohort intelligence optimization |
| GBD | governor dead band |
| GRC | generation rate constraint |
| hFA–PS | hybridized Firefly Algorithm pattern search |
| HBA | Honey Badger Algorithm |
| LFC | Load Frequency Control |
| LOA | Lyrebird Optimization Algorithm |
| MVO | Multi-Verse Optimizer |
| MHABC-PSO | Modified Artificial Bee Colony and Particle Swarm Optimizer |
| PI | Proportional–Integral |
| PID | Proportional–Integral–Double |
| PIDD | Proportional–Integral–Double Derivative |
| SAMPE | self-adaptive multi-population elitist |
| SLI | Step Load Increase |
| SMC | Sliding Mode Controller |
| TSA | Tunicate Searching Algorithm |
| TLBO | Teaching–Learning-Based Optimizer |
| ZN | Ziegler–Nichols |
| List of Symbols | |
| j | Subscript regarding areas (j = 1, 2) |
| ACE | area control error |
| R | droop characteristics of governor speed |
| B | frequency bias factors |
| u | control inputs to the governor as well as the output of controllers |
| Tg | governor time constant (second) |
| ∆Pg | changes in governor valve positions (p.u.) |
| Tt | turbine time constant (second) |
| ∆Pt | changes in turbine output powers (p.u.) |
| kp | power system gains |
| Tp | time constant of power system (second) |
| ∆PD | changes in the power demands (p.u.) |
| ∆PTIE | change in transferred power via tie-line (p.u.) |
| T12 | synchronisation coefficient between both areas |
| ∆f | frequency deviations of the system (Hz) |
| PRg | each area capacity in MW where g = 1 or 2 |
| Kp | proportional gain |
| Ki | integral gain |
| Kd | derivative gains |
| ITAE | integral of time multiplied by absolute error |
| tsim | time range of simulation |
Appendix A
The nominal parameters for the system investigated are as follows:
PR = 2000 MW (rating); PL = 1000 MW (nominal loading); f = 60 Hz; R1 = R2 = 2.4 Hz/pu; B1 = B2 = 0.045 pu MW/Hz; Tg1 = Tg2 = 0.08 s; Tt1 = Tt2 = 0.3 s; KP1 = KP2 = 120 Hz/pu MW; TP1 = TP2 = 20 s; T12 = 0.545 pu; and a12 = −1.
References
- Ibrahim, N.M.A.; Talaat, H.E.A.; Shaheen, A.M.; Hemade, B.A. Optimization of Power System Stabilizers Using Proportional-Integral-Derivative Controller-Based Antlion Algorithm: Experimental Validation via Electronics Environment. Sustainability 2023, 15, 8966. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, A.E.G. Enhanced Coyote Optimizer-Based Cascaded Load Frequency Controllers in Multi-Area Power Systems with Renewable. Neural Comput. Appl. 2021, 33, 8459–8477. [Google Scholar] [CrossRef]
- Saadatmand, M.; Gharehpetian, G.B.; Siano, P.; Alhelou, H.H. PMU-Based FOPID Controller of Large-Scale Wind-PV Farms for LFO Damping in Smart Grid. IEEE Access 2021, 9, 94953–94969. [Google Scholar] [CrossRef]
- El-Sehiemy, R.; Shaheen, A.; Ginidi, A.; Al-Gahtani, S.F. Proportional-Integral-Derivative Controller Based-Artificial Rabbits Algorithm for Load Frequency Control in Multi-Area Power Systems. Fractal Fract. 2023, 7, 97. [Google Scholar] [CrossRef]
- Al-Majidi, S.D.; Al-Nussairi, M.K.; Mohammed, A.J.; Dakhil, A.M.; Abbod, M.F.; Al-Raweshidy, H.S. Design of a Load Frequency Controller Based on an Optimal Neural Network. Energies 2022, 15, 6223. [Google Scholar] [CrossRef]
- Rashidi, M.; Rashidi, F.; Arjomand, A.S.; Sahragard, J. Design of a Robust and Adaptive Load Frequency Controller for Multi-Area Power Networks with System Parametric Uncertainties Using TDMLP Neural Network. In Proceedings of the Conference Proceedings—IEEE International Conference on Systems, Man and Cybernetics, The Hague, The Netherlands, 10–13 October 2004; Volume 4. [Google Scholar]
- Yan, Z.; Xu, Y. A Multi-Agent Deep Reinforcement Learning Method for Cooperative Load Frequency Control of a Multi-Area Power System. IEEE Trans. Power Syst. 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd-Elazim, S.M. BFOA Based Design of PID Controller for Two Area Load Frequency Control with Nonlinearities. Int. J. Electr. Power Energy Syst. 2013, 51, 224–231. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. Optimal Gravitational Search Algorithm for Automatic Generation Control of Interconnected Power Systems. Ain Shams Eng. J. 2014, 5, 721–733. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. A Hybrid Firefly Algorithm and Pattern Search Technique for Automatic Generation Control of Multi Area Power Systems. Int. J. Electr. Power Energy Syst. 2015, 64, 9–23. [Google Scholar] [CrossRef]
- Sahu, R.K.; Gorripotu, T.S.; Panda, S. Automatic Generation Control of Multi-Area Power Systems with Diverse Energy Sources Using Teaching Learning Based Optimization Algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 113–134. [Google Scholar] [CrossRef]
- Adel, A.A.E.E.; Ragab, A.E.S.; Abdullah, M.S.; Abd El Galil, D. Optimal Design of PID Controller Based Sampe-Jaya Algorithm for Load Frequency Control of Linear and Nonlinear Multi-Area Thermal Power Systems. Int. J. Eng. Res. Afr. 2020, 50, 79–93. [Google Scholar] [CrossRef]
- Salman, G.A.; Jafar, A.S.; Ismael, A.I. Application of Artificial Intelligence Techniques for LFC and AVR Systems Using PID Controller. Int. J. Power Electron. Drive Syst. 2019, 10, 1694–1704. [Google Scholar] [CrossRef]
- Sharma, J.; Hote, Y.V.; Prasad, R. PID Controller Design for Interval Load Frequency Control System with Communication Time Delay. Control Eng. Pract. 2019, 89, 154–168. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Diab, A.E.G. Design of Cascaded Controller Based on Coyote Optimizer for Load Frequency Control in Multi-Area Power Systems with Renewable Sources. Control Eng. Pract. 2022, 121, 105058. [Google Scholar] [CrossRef]
- Murugesan, D.; Shah, P.; Jagatheesan, K.; Sekhar, R.; Kulkarni, A.J. Cohort Intelligence Optimization Based Controller Design of Isolated and Interconnected Thermal Power System for Automatic Generation Control. In Proceedings of the 2022 2nd International Conference on Computer Science, Engineering and Applications, ICCSEA 2022, Gunupur, India, 8 September 2022. [Google Scholar]
- Murugesan, D.; Jagatheesan, K.; Shah, P.; Sekhar, R. Fractional Order PIλDμ Controller for Microgrid Power System Using Cohort Intelligence Optimization. Results Control Optim. 2023, 11, 100218. [Google Scholar] [CrossRef]
- El-Rifaie, A.M.; Abid, S.; Ginidi, A.R.; Shaheen, A.M. Fractional Order PID Controller Based-Neural Network Algorithm for LFC in Multi-Area Power Systems. Eng. Rep. 2025, 7, e70028. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Limon, M.F.A.; Kabir, M.M.; Rabby, M.K.M.; Soeb, M.J.A.; Jubayer, M.F. A Hybrid Optimization Algorithm for Improving Load Frequency Control in Interconnected Power Systems. Expert Syst. Appl. 2024, 249, 123702. [Google Scholar] [CrossRef]
- Saha, A.; Bhaskar, M.S.; Almakhles, D.J.; Elmorshedy, M.F. Employment of Renewable Based Sources in Amalgamated Frequency-Voltage Control Restructured System with TSA Trained IPD(1+I) Controller. Renew. Energy 2024, 222. [Google Scholar] [CrossRef]
- Ozumcan, S.; Ozturk, A.; Varan, M.; Andic, C. A Novel Honey Badger Algorithm Based Load Frequency Controller Design of a Two-Area System with Renewable Energy Sources. Energy Rep. 2023, 9, 272–279. [Google Scholar] [CrossRef]
- Mudi, J.; Shiva, C.K.; Mukherjee, V. Multi-Verse Optimization Algorithm for LFC of Power System with Imposed Nonlinearities Using Three-Degree-of-Freedom PID Controller. Iran. J. Sci. Technol.-Trans. Electr. Eng. 2019, 43, 837–856. [Google Scholar] [CrossRef]
- Sharma, Y.; Saikia, L.C. Automatic Generation Control of a Multi-Area ST—Thermal Power System Using Grey Wolf Optimizer Algorithm Based Classical Controllers. Int. J. Electr. Power Energy Syst. 2015, 73, 853–862. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Boopathi, D.; Samanta, S.; Anand, B.; Dey, N. Grey Wolf Optimization Algorithm-Based PID Controller for Frequency Stabilization of Interconnected Power Generating System. Soft Comput. 2024, 28, 5057–5070. [Google Scholar] [CrossRef]
- Akila, P.; Kumari, P.K.J.; Swetha, B.; Kavitha, E.; Mahesh, K.; Kumar, V.R. Lyrebird-Optimized PI Regulator for Enhanced Load Frequency Control in Two-Area Systems. In Proceedings of the 2024 IEEE International Conference on Information Technology, Electronics and Intelligent Communication Systems (ICITEICS), Bangalore, India, 28–29 June 2024. [Google Scholar]
- Sharma, A.; Singh, N. Load Frequency Control of Connected Multi-Area Multi-Source Power Systems Using Energy Storage and Lyrebird Optimization Algorithm Tuned PID Controller. J. Energy Storage 2024, 100, 113609. [Google Scholar] [CrossRef]
- Moras, A.; Sridhar, S.; Vernekar, M.M.; Debnath, U. Load Frequency Control of a Two Area Power System Using Different Optimization Techniques. In Proceedings of the Lecture Notes in Electrical Engineering, Chongqing, China, 3–5 April 2024; Volume 1098. [Google Scholar]
- Jain, D.; Bhaskar, M.K.; Parihar, M. Optimization of Controller Parameters for Load Frequency Control Problem of Two-Area Deregulated Power System Using Soft Computing Techniques. In Proceedings of the Smart Innovation, Systems and Technologies, Matsue City, Japan, 4–6 October 2024; Volume 364. [Google Scholar]
- Sagor, A.R.; Talha, M.A.; Ahmad, S.; Ahmed, T.; Alam, M.R.; Hazari, M.R.; Shafiullah, G.M. Pelican Optimization Algorithm-Based Proportional–Integral–Derivative Controller for Superior Frequency Regulation in Interconnected Multi-Area Power Generating System. Energies 2024, 17, 3308. [Google Scholar] [CrossRef]
- Tian, G.; Wang, F. Data-Driven Load Frequency Control for Multi-Area Power System Based on Switching Method under Cyber Attacks. Algorithms 2024, 17, 233. [Google Scholar] [CrossRef]
- Kumarakrishnan, V.; Vijayakumar, G.; Boopathi, D.; Jagatheesan, K.; Saravanan, S.; Anand, B. Optimized PSO Technique Based PID Controller for Load Frequency Control of Single Area Power System. Solid State Technol. 2020, 63, 7979–7990. [Google Scholar]
- Kumarakrishnan, V.; Vijayakumar, G.; Jagatheesan, K.; Boopathi, D.; Anand, B.; Kanendra Naidu, V. PSO Optimum Design-PID Controller for Frequency Management of Single Area Multi-Source Power Generating System. In Proceedings of the Lecture Notes in Networks and Systems, Amsterdam, The Netherlands, 1–2 September 2022; Volume 281. [Google Scholar]
- Dhanasekaran, B.; Kaliannan, J.; Baskaran, A.; Dey, N.; Tavares, J.M.R.S. Load Frequency Control Assessment of a PSO-PID Controller for a Standalone Multi-Source Power System. Technologies 2023, 11, 22. [Google Scholar] [CrossRef]
- Choudhary, R.; Rai, J.N.; Arya, Y. Automatic Generation Control for Single Area Power System Using GNA Tuned PID Controller. In Proceedings of the Journal of Physics: Conference Series, Taiwan, 21–23 May 2020; Volume 1478. [Google Scholar]
- Gupta, D.K.; Dei, G.; Soni, A.K.; Jha, A.V.; Appasani, B.; Bizon, N.; Srinivasulu, A.; Nsengiyumva, P. Fractional Order PID Controller for Load Frequency Control in a Deregulated Hybrid Power System Using Aquila Optimization. Results Eng. 2024, 23, 102442. [Google Scholar] [CrossRef]
- Song, T. Optimization Technology of Hydroelectric Power Plant Unit Speed Control Based on the Constriction Coefficient-Based Particle Swarm Gravitational Search Algorithm Fusion Model. Results Eng. 2024, 22, 102313. [Google Scholar] [CrossRef]
- Abdelaal, A.K.; Shaheen, A.M.; El-Fergany, A.A.; Alqahtani, M.H. Sliding Mode Control Based Dynamic Voltage Restorer for Voltage Sag Compensation. Results Eng. 2024, 24, 102936. [Google Scholar] [CrossRef]
- Kalyan, C.N.S.; Goud, B.S.; Kumar, M.K.; Thakur, P.; Bajaj, M.; Bansal, R.C. Squirrel search algorithm based intelligent controller for interconnected power system. Int. J. Model. Simul. 2023, 1–21. [Google Scholar] [CrossRef]
- Naga Sai Kalyan, C.H.; Goud, B.S.; Reddy, C.R.; Udumula, R.R.; Bajaj, M.; Sharma, N.K.; Elgamli, E.; Shouran, M.; Kamel, S. Seagull Optimization Algorithm–Based Fractional-Order Fuzzy Controller for LFC of Multi-Area Diverse Source System with Realistic Constraints. Front. Energy Res. 2022, 10, 921426. [Google Scholar] [CrossRef]
- Irfan, M.; Deilami, S.; Huang, S.; Tahir, T.; Veettil, B.P. Optimizing Load Frequency Control in Microgrid with Vehicle-to-Grid Integration in Australia: Based on an Enhanced Control Approach. Appl. Energy 2024, 366, 123317. [Google Scholar] [CrossRef]
- Pham, T.H.; Raahemi, B. Bio-Inspired Feature Selection Algorithms With Their Applications: A Systematic Literature Review. IEEE Access 2023, 11, 43733–43758. [Google Scholar] [CrossRef]
- Dehghani, M.; Bektemyssova, G.; Montazeri, Z.; Shaikemelev, G.; Malik, O.P.; Dhiman, G. Lyrebird Optimization Algorithm: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 507. [Google Scholar] [CrossRef]
- Abid, S.; El-Rifaie, A.M.; Elshahed, M.; Ginidi, A.R.; Shaheen, A.M.; Moustafa, G.; Tolba, M.A. Development of Slime Mold Optimizer with Application for Tuning Cascaded PD-PI Controller to Enhance Frequency Stability in Power Systems. Mathematics 2023, 11, 1796. [Google Scholar] [CrossRef]
- Alqahtani, M.H.; Almutairi, S.Z.; Aljumah, A.S.; Shaheen, A.M.; Moustafa, G.; El-Fergany, A.A. A Proportional-Integral-One Plus Double Derivative Controller-Based Fractional-Order Kepler Optimizer for Frequency Stability in Multi-Area Power Systems with Wind Integration. Fractal Fract. 2024, 8, 323. [Google Scholar] [CrossRef]
- Moustafa, G.; El-Rifaie, A.M.; Smaili, I.H.; Ginidi, A.; Shaheen, A.M.; Youssef, A.F.; Tolba, M.A. An Enhanced Dwarf Mongoose Optimization Algorithm for Solving Engineering Problems. Mathematics 2023, 11, 3297. [Google Scholar] [CrossRef]
- El-Rifaie, A.M.; Shaheen, A.M.; Tolba, M.A.; Smaili, I.H.; Moustafa, G.; Ginidi, A.R.; Elshahed, M.A. Modified Gradient-Based Algorithm for Distributed Generation and Capacitors Integration in Radial Distribution Networks. IEEE Access 2023, 11, 120899–120917. [Google Scholar] [CrossRef]
- Moustafa, G.; Tolba, M.A.; El-Rifaie, A.M.; Ginidi, A.; Shaheen, A.M.; Abid, S. A Subtraction-Average-Based Optimizer for Solving Engineering Problems with Applications on TCSC Allocation in Power Systems. Biomimetics 2023, 8, 332. [Google Scholar] [CrossRef]
- Alsaggaf, W.; Gafar, M.; Sarhan, S.; Shaheen, A.M.; Ginidi, A.R. Chemical-Inspired Material Generation Algorithm (MGA) of Single- and Double-Diode Model Parameter Determination for Multi-Crystalline Silicon Solar Cells. Appl. Sci. 2024, 14, 8549. [Google Scholar] [CrossRef]
- Chaib, L.; Tadj, M.; Choucha, A.; El-Rifaie, A.M.; Shaheen, A.M. Hybrid Brown-Bear and Hippopotamus Algorithms with Fractional Order Chaos Maps for Precise Solar PV Model Parameter Estimation. Processes 2024, 12, 2718. [Google Scholar] [CrossRef]
- Moustafa, G.; Alnami, H.; Ginidi, A.R.; Shaheen, A.M. An Improved Kepler Optimization Algorithm for Module Parameter Identification Supporting PV Power Estimation. Heliyon 2024, 10, e39902. [Google Scholar] [CrossRef] [PubMed]
- Alwakeel, A.S.; El-Rifaie, A.M.; Moustafa, G.; Shaheen, A.M. Newton Raphson Based Optimizer for Optimal Integration of FAS and RIS in Wireless Systems. Results Eng. 2025, 25, 103822. [Google Scholar] [CrossRef]
- De Mel, I.; Klymenko, O.V.; Short, M. Complementarity Reformulations for the Optimal Design of Distributed Energy Systems with Multiphase Optimal Power Flow. Int. J. Electr. Power Energy Syst. 2024, 155, 109610. [Google Scholar] [CrossRef]
- Gao, M.; Yu, J.; Yang, Z.; Zhao, J. A Physics-Guided Graph Convolution Neural Network for Optimal Power Flow. IEEE Trans. Power Syst. 2024, 39, 380–390. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Hasanien, H.M.; Ginidi, A. An Enhanced Optimizer of Social Network Search for Multi-Dimension Optimal Power Flow in Electrical Power Grids. Int. J. Electr. Power Energy Syst. 2024, 155, 109572. [Google Scholar] [CrossRef]
- Alqahtani, M.H.; Draz, A.; Shaheen, A.M.; El-Fergany, A.A. Advanced Relay Coordination in Power Networks Considering Transformer Inrush and Motor Starting Currents via Weighted Mean Variance Optimizer. IEEE Access 2024, 12, 184953–184975. [Google Scholar] [CrossRef]
- Nasef, A.F.; Alqahtani, M.H.; Shaheen, A.M. Technical and Optimization Insights into PV Penetration in Power Distribution Systems-Based Wild Horse Algorithm: Real Cases on Egyptian Networks. Results Eng. 2025, 25, 104603. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).