Modeling and Optimization of p-Benzoquinone Degradation via Flow-By Electro-Oxidation on Boron-Doped Diamond Electrodes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents
2.2. Equipment
2.3. Analytical Procedures
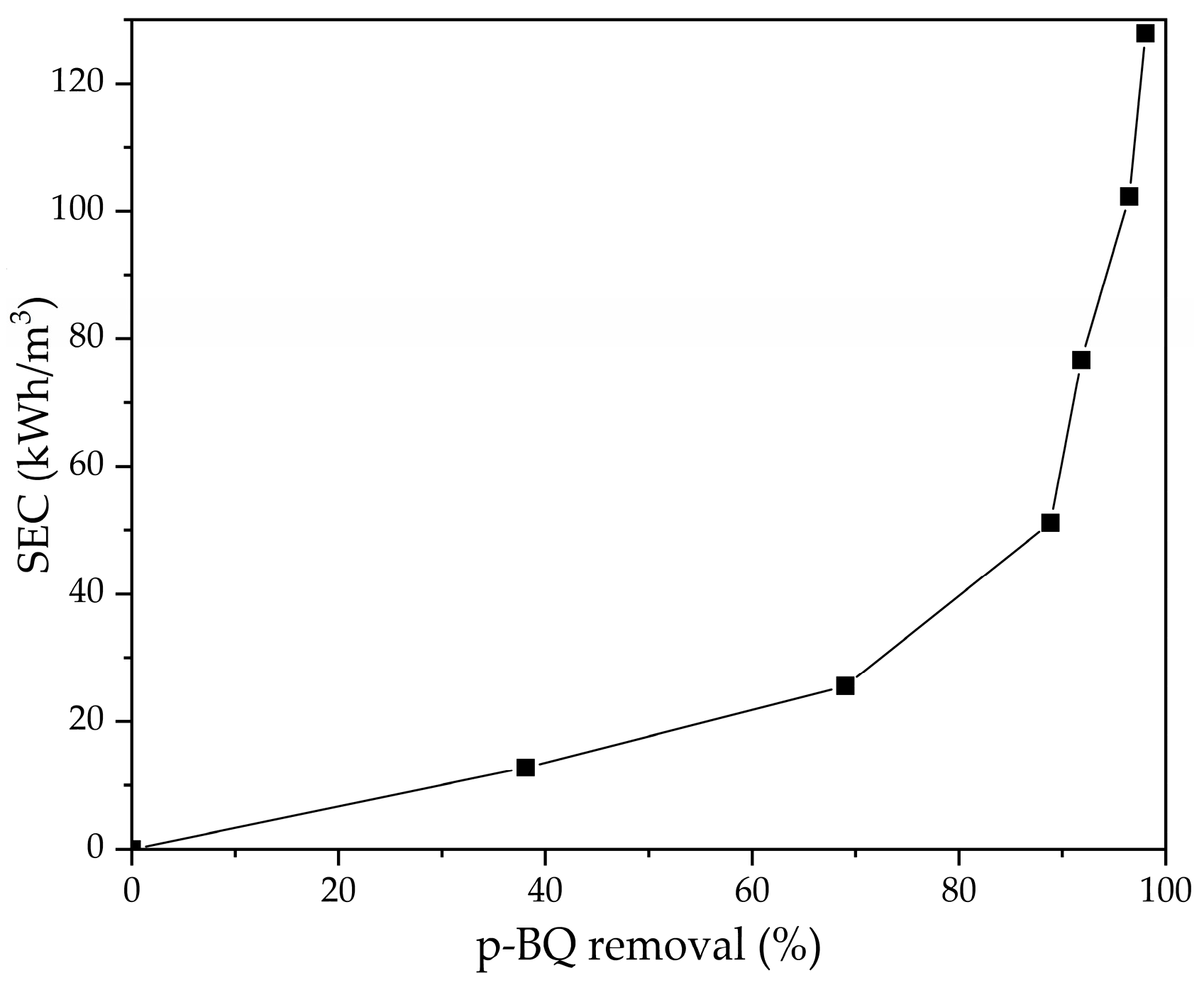
2.4. Operating Cost
2.5. Experimental Design
2.6. Modeling and Optimization Process
3. Results and Discussion
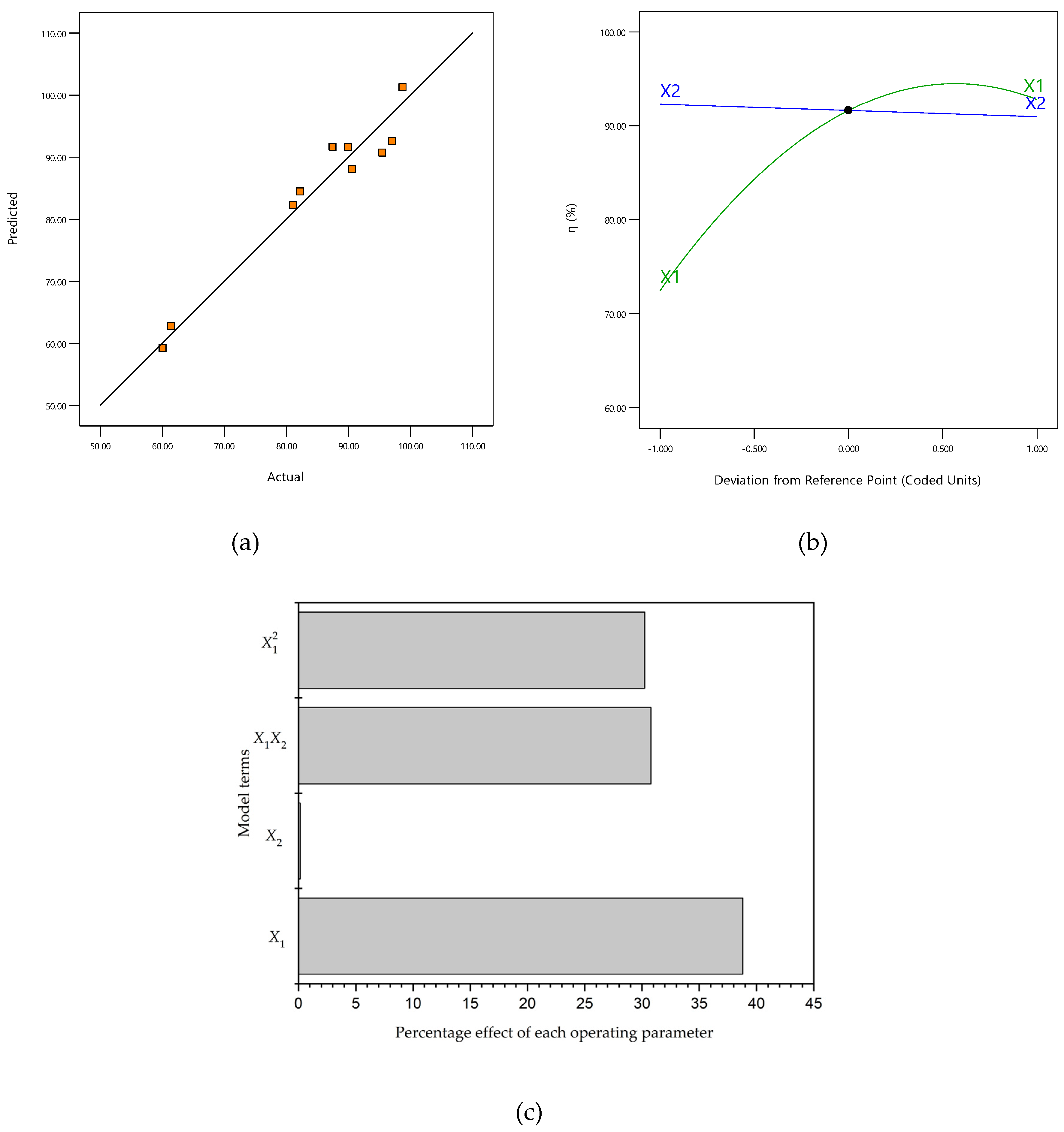
3.1. Polynomial Model
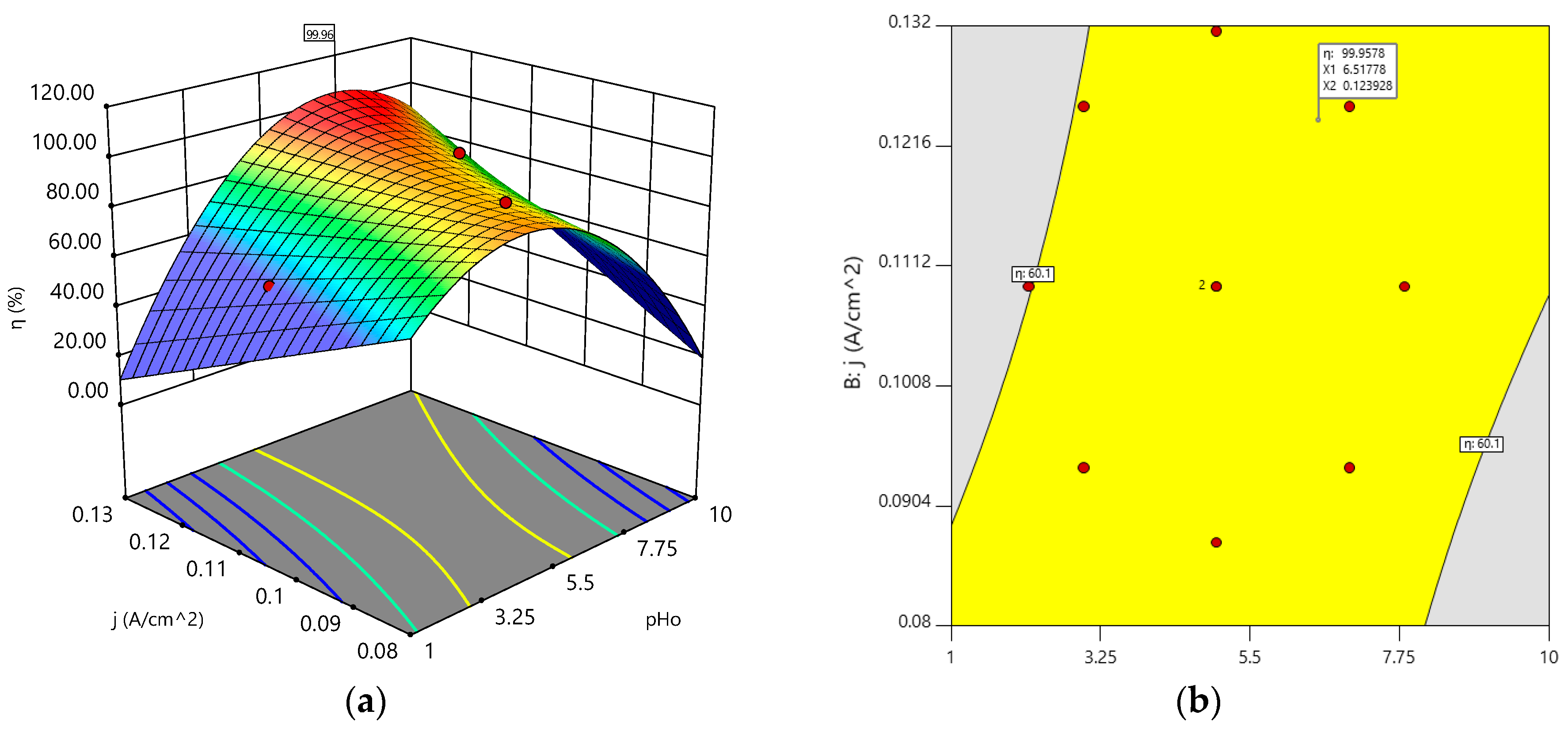
3.2. Interaction Effect Between Variables
3.3. ANOVA Test
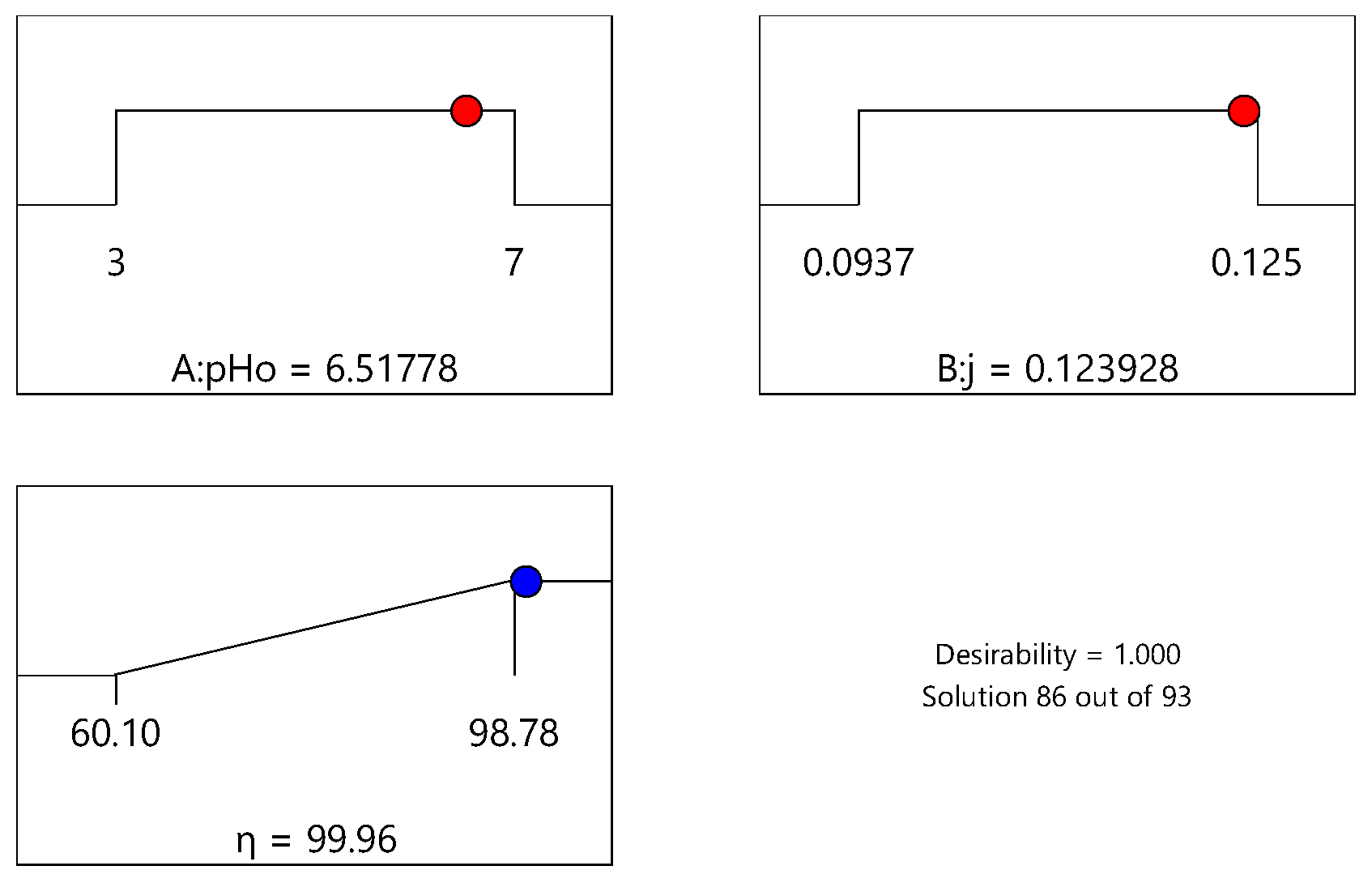
3.4. Optimization of p-BQ Removal (η)
3.5. Model Validation
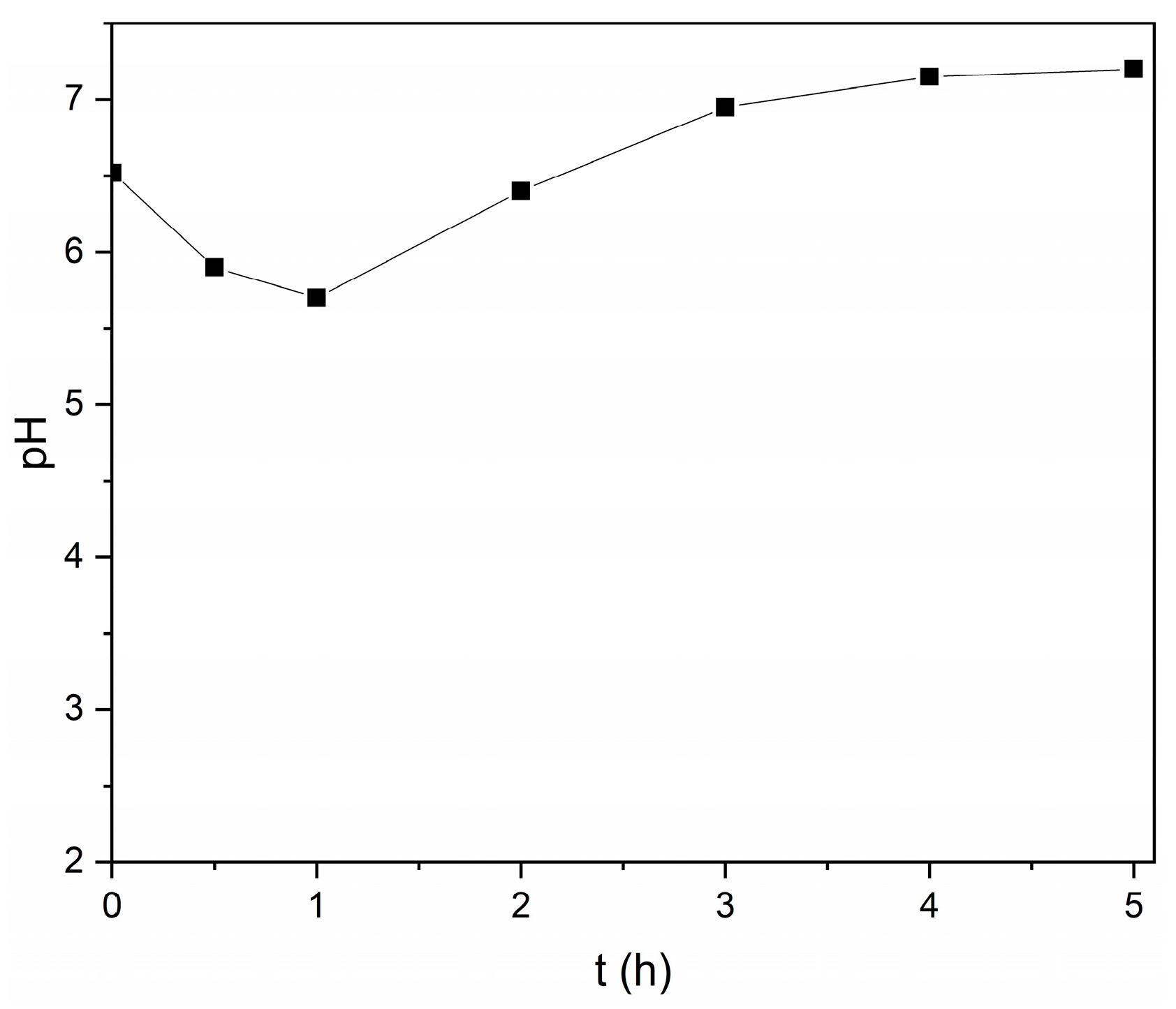
3.6. Kinetic Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nicklisch, S.C.T.; Rees, S.D.; McGrath, A.P.; Gökirmak, T.; Bonito, L.T.; Vermeer, L.M.; Cregger, C.; Loewen, G.; Sandin, S.; Chang, G.; et al. Global Marine Pollutants Inhibit P-Glycoprotein: Environmental Levels, Inhibitory Effects, and Cocrystal Structure. Sci. Adv. 2016, 2, e1600001. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Zhang, Y.; Guliaev, A.B.; Shen, H.; Hang, B.; Singer, B.; Wang, Z. The P-Benzoquinone DNA Adducts Derived from Benzene Are Highly Mutagenic. DNA Repair 2005, 4, 1399–1409. [Google Scholar] [CrossRef] [PubMed]
- Panizza, M. Anodic Oxidation of Benzoquinone Using Diamond Anode. Environ. Sci. Pollut. Res. 2014, 21, 8451–8456. [Google Scholar]
- Ajeel, M.A.; Aroua, M.K.; Daud, W.M.A.W. P-Benzoquinone Anodic Degradation by Carbon Black Diamond Composite Electrodes. Electrochim. Acta 2015, 169, 46–51. [Google Scholar] [CrossRef]
- Kiss, V.; Kecskeméti, Á.; Hülvely, B.M.; Tarczali Sarudi, P.; Csépes-Ruzicska, L.J.; Mercs, F.; Tóth, Á.; Fábián, I.; Ősz, K. Reductive Dehalogenation and Formation of Sulfonated Quinones in the Aqueous Reactions between Various Chloro-1,4-Benzoquinones and Sulfur(IV). J. Sulfur Chem. 2023, 44, 646–665. [Google Scholar] [CrossRef]
- Yu, Z.; Jin, X.; Guo, Y.; Liu, Q.; Xiang, W.; Zhou, S.; Wang, J.; Yang, D.; Wu, H.B.; Wang, J. Decoupled Oxidation Process Enabled by Atomically Dispersed Copper Electrodes for In-Situ Chemical Water Treatment. Nat. Commun. 2024, 15, 1186. [Google Scholar] [CrossRef]
- Martínez-Huitle, C.A.; Ferro, S. Electrochemical Oxidation of Organic Pollutants for the Wastewater Treatment: Direct and Indirect Processes. Chem. Soc. Rev. 2006, 35, 1324–1340. [Google Scholar] [CrossRef]
- Comninellis, C. Electrocatalysis in the Electrochemical Conversion/Combustion of Organic Pollutants for Waste Water Treatment. Electrochim. Acta 1994, 39, 1857–1862. [Google Scholar] [CrossRef]
- Iqbal, A.; Bokhari, T.H.; Usman, M.; Yusaf, A.; Mansha, A.; Saeed, M.; Khan, S.; Iqbal, M.; Bhatti, M.A.; Shafqat, S.S.; et al. Methodological Optimization for Efficient Degradation of Acid Violet 49 Using Advanced Oxidation Processes and Varied Photocatalyst Combinations. Sci. Rep. 2024, 14, 30339. [Google Scholar] [CrossRef]
- Yu, F.; Jia, C.; Wu, X.; Sun, L.; Shi, Z.; Teng, T.; Lin, L.; He, Z.; Gao, J.; Zhang, S.; et al. Rapid Self-Heating Synthesis of Fe-Based Nanomaterial Catalyst for Advanced Oxidation. Nat. Commun. 2023, 14, 4975. [Google Scholar] [CrossRef]
- Zuo, S.; Jin, X.; Wang, X.; Lu, Y.; Zhu, Q.; Wang, J.; Liu, W.; Du, Y.; Wang, J. Sandwich Structure Stabilized Atomic Fe Catalyst for Highly Efficient Fenton-like Reaction at All PH Values. Appl. Catal. B 2021, 282, 119551. [Google Scholar] [CrossRef]
- Shang, Y.; Xu, X.; Gao, B.; Wang, S.; Duan, X. Single-Atom Catalysis in Advanced Oxidation Processes for Environmental Remediation. Chem. Soc. Rev. 2021, 50, 5281–5322. [Google Scholar] [CrossRef]
- Neta, P.; Huie, R.E.; Ross, A.B. Rate Constants for Reactions of Inorganic Radicals in Aqueous Solution. J. Phys. Chem. Ref. Data 1988, 17, 1027–1284. [Google Scholar] [CrossRef]
- Hajalifard, Z.; Mousazadeh, M.; Khademi, S.; Khademi, N.; Jamadi, M.H.; Sillanpää, M. The Efficacious of AOP-Based Processes in Concert with Electrocoagulation in Abatement of CECs from Water/Wastewater. NPJ Clean Water 2023, 6, 30. [Google Scholar] [CrossRef]
- Ozge, T.; Sibel, B.; Hazal, Ö.; Bahar, Ö.; Gül, Ş.M. Toxicological Profile of 1,4-Benzoquinone and Its Degradation By-Products during Electro-Fenton, Electrocoagulation, and Electrosynthesized Fe(VI) Oxidation. J. Environ. Eng. 2018, 144, 04018124. [Google Scholar] [CrossRef]
- Yu, L.; Xue, J.; Zhang, L.; Tang, C.; Guo, Y. Fabrication of a Stable Ti/Pb-TiOxNWs/PbO2 Anode and Its Application in Benzoquinone Degradation. Electrochim. Acta 2021, 368, 137532. [Google Scholar] [CrossRef]
- Yoon, J.; Yang, J.; Shim, Y.; Won, M.S. Electrochemical Degradation of Benzoquinone in a Flow through Cell with Carbon Fibers. Bull. Korean Chem. Soc. 2007, 28, 403–407. [Google Scholar] [CrossRef]
- Espinoza-Montero, P.J.; Vasquez-Medrano, R.; Ibanez, J.G.; Frontana-Uribe, B.A. Efficient Anodic Degradation of Phenol Paired to Improved Cathodic Production of H2O2 at BDD Electrodes. J. Electrochem. Soc. 2013, 160, G3171. [Google Scholar] [CrossRef]
- Espinoza-Montero, P.J.; Alulema-Pullupaxi, P.; Frontana-Uribe, B.A.; Barrera-Diaz, C.E. Electrochemical Production of Hydrogen Peroxide on Boron-Doped Diamond (BDD) Electrode. Curr. Opin. Solid State Mater. Sci. 2022, 26, 100988. [Google Scholar] [CrossRef]
- Cisneros-León, D.G.; Espinoza-Montero, P.J.; Bolaños-Mendez, D.; Alvarez-Paguay, J.; Fernández, L.; Saavedra-Alulema, P.F.; Lopez, K.; Astorga, D.; Piñeiros, J.L. Electrochemical Degradation of Surfactants in Domestic Wastewater Using a DiaClean® Cell Equipped with a Boron-Doped Diamond Electrode. Front. Chem. 2023, 11, 900670. [Google Scholar] [CrossRef]
- Kapałka, A.; Fóti, G.; Comninellis, C. Kinetic Modelling of the Electrochemical Mineralization of Organic Pollutants for Wastewater Treatment. J. Appl. Electrochem. 2008, 38, 7–16. [Google Scholar] [CrossRef]
- Takagi, K.; Natsui, K.; Watanabe, T.; Einaga, Y. Increasing the Electric Double-Layer Capacitance in Boron-Doped Diamond Electrodes. ChemElectroChem 2019, 6, 1683–1687. [Google Scholar] [CrossRef]
- Qi, X.; Wang, T.; Long, Y.; Ni, J. Synergetic Antibacterial Activity of Reduced Graphene Oxide and Boron Doped Diamond Anode in Three Dimensional Electrochemical Oxidation System. Sci. Rep. 2015, 5, 10388. [Google Scholar] [CrossRef]
- Ganiyu, S.O.; Martínez-Huitle, C.A. Nature, Mechanisms and Reactivity of Electrogenerated Reactive Species at Thin-Film Boron-Doped Diamond (BDD) Electrodes During Electrochemical Wastewater Treatment. ChemElectroChem 2019, 6, 2379–2392. [Google Scholar] [CrossRef]
- Garcia-Segura, S.; Keller, J.; Brillas, E.; Radjenovic, J. Removal of Organic Contaminants from Secondary Effluent by Anodic Oxidation with a Boron-Doped Diamond Anode as Tertiary Treatment. J. Hazard. Mater. 2015, 283, 551–557. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Huitle, C.A.; dos Santos, E.V.; de Araújo, D.M.; Panizza, M. Applicability of Diamond Electrode/Anode to the Electrochemical Treatment of a Real Textile Effluent. J. Electroanal. Chem. 2012, 674, 103–107. [Google Scholar] [CrossRef]
- Ganiyu, S.O.; Gamal El-Din, M. Insight into In-Situ Radical and Non-Radical Oxidative Degradation of Organic Compounds in Complex Real Matrix during Electrooxidation with Boron Doped Diamond Electrode: A Case Study of Oil Sands Process Water Treatment. Appl. Catal. B 2020, 279, 119366. [Google Scholar] [CrossRef]
- Nava, J.L.; Sirés, I.; Brillas, E. Electrochemical Incineration of Indigo. A Comparative Study between 2D (Plate) and 3D (Mesh) BDD Anodes Fitted into a Filter-Press Reactor. Environ. Sci. Pollut. Res. 2014, 21, 8485–8492. [Google Scholar] [CrossRef]
- Yoon, J.; Shim, Y.; Lee, B.-S.; Choi, S.; Won, M.S. Electrochemical Degradation of Phenol and 2-Chlorophenol Using Pt/Ti and Boron-Doped Diamond Electrodes. Bull Korean Chem. Soc. 2012, 33, 2274–2278. [Google Scholar] [CrossRef]
- Nidheesh, P.V.; Divyapriya, G.; Oturan, N.; Trellu, C.; Oturan, M.A. Environmental Applications of Boron-Doped Diamond Electrodes: 1. Applications in Water and Wastewater Treatment. ChemElectroChem 2019, 6, 2124–2142. [Google Scholar] [CrossRef]
- Peralta-Reyes, E.; Natividad, R.; Castellanos, M.; Mentado-Morales, J.; Cordero, M.E.; Amado-Piña, D.; Regalado-Méndez, A. Electro-Oxidation of 2-Chlorophenol with BDD Electrodes in a Continuous Flow Electrochemical Reactor. J. Flow Chem. 2020, 10, 437–447. [Google Scholar] [CrossRef]
- Lupa, L.; Cocheci, L.; Trica, B.; Coroaba, A.; Popa, A. Photodegradation of Phenolic Compounds from Water in the Presence of a Pd-Containing Exhausted Adsorbent. Appl. Sci. 2020, 10, 8440. [Google Scholar] [CrossRef]
- Regalado-Méndez, A.; Ramos-Hernández, G.; Natividad, R.; Cordero, M.E.; Zárate, L.; Robles-Gómez, E.E.; Pérez-Pastenes, H.; Peralta-Reyes, E. Parametric Mathematical Model of the Electrochemical Degradation of 2-Chlorophenol in a Flow-by Reactor under Batch Recirculation Mode. Water 2023, 15, 4276. [Google Scholar] [CrossRef]
- Brillas, E.; Sirés, I.; Oturan, M.A. Electro-Fenton Process and Related Electrochemical Technologies Based on Fenton’s Reaction Chemistry. Chem. Rev. 2009, 109, 6570–6631. [Google Scholar] [CrossRef] [PubMed]
- Stat-Ease. Design Espert 10; Stat-Ease Inc.: Minneapolis, MN, USA, 2010. [Google Scholar]
- Regalado-Méndez, A.; Ruiz, M.; Hernández-Servín, J.A.; Natividad, R.; Romero, R.; Cordero, M.E.; Estrada-Vázquez, C.; Peralta-Reyes, E. Electrochemical Mineralization of Ibuprofen on BDD Electrodes in an Electrochemical Flow Reactor: Numerical Optimization Approach. Processes 2020, 8, 1666. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, M.; Li, J.; Zhao, W. Optimization of Preparation Conditions for Biochar Derived from Water Hyacinth by Using Response Surface Methodology (RSM) and Its Application in Pb2+ Removal. J. Env. Chem. Eng. 2020, 8, 104198. [Google Scholar] [CrossRef]
- Dixit, S.; Yadav, V.L. Optimization of Polyethylene/Polypropylene/Alkali Modified Wheat Straw Composites for Packaging Application Using RSM. J. Clean Prod. 2019, 240, 118228. [Google Scholar] [CrossRef]
- Rheem, S.; Rheem, I.; Oh, S. Response Surface Methodology Using a Fullest Balanced Model: A Re-Analysis of a Dataset in the Korean Journal for Food Science of Animal Resources. Korean J. Food Sci. Anim. Resour. 2017, 37, 139–146. [Google Scholar] [CrossRef]
- Javed, S.; Fisse, J.; Vogt, D. Optimization and Kinetic Evaluation for Glycolytic Depolymerization of Post-Consumer PET Waste with Sodium Methoxide. Polymer 2023, 15, 687. [Google Scholar] [CrossRef]
- Korde, S.; Deshmukh, S.; Tandekar, S.; Jugade, R. Implementation of Response Surface Methodology in Physi-Chemisorption of Indigo Carmine Dye Using Modified Chitosan Composite. Carbohydr. Polym. Technol. Appl. 2021, 2, 100081. [Google Scholar] [CrossRef]
- Chamoli, S. ANN and RSM Approach for Modeling and Optimization of Designing Parameters for a V down Perforated Baffle Roughened Rectangular Channel. Alex. Eng. J. 2015, 54, 429–446. [Google Scholar] [CrossRef]
- Elaoud, S.C.; Panizza, M.; Cerisola, G.; Mhiri, T. Electrochemical Degradation of Sinapinic Acid on a BDD Anode. Desalination 2011, 272, 148–153. [Google Scholar] [CrossRef]
- do Vale-Júnior, E.; dos Santos, A.J.; da Silva, D.R.; Fajardo, A.S.; Martínez-Huitle, C.A. Electrochemical Technologies for Detecting and Degrading Benzoquinone Using Diamond Films. ChemElectroChem 2019, 6, 4383–4390. [Google Scholar] [CrossRef]
- Vasilie, S.; Manea, F.; Baciu, A.; Pop, A. Dual Use of Boron-Doped Diamond Electrode in Antibiotics-Containing Water Treatment and Process Control. Process Saf. Environ. Prot. 2018, 117, 446–453. [Google Scholar] [CrossRef]
- da Silva, S.W.; Navarro, E.M.O.; Rodrigues, M.A.S.; Bernardes, A.M.; Pérez-Herranz, V. Using P-Si/BDD Anode for the Electrochemical Oxidation of Norfloxacin. J. Electroanal. Chem. 2019, 832, 112–120. [Google Scholar] [CrossRef]
- Maldonado Domínguez, S.M.; Barrera-Díaz, C.E.; Balderas Hernández, P.; Amado-Piña, D.; Torres-Blancas, T.; Roa-Morales, G. Metronidazole Electro-Oxidation Degradation on a Pilot Scale. Catalysts 2025, 15, 29. [Google Scholar] [CrossRef]
- Martín de Vidales, M.J.; Sáez, C.; Cañizares, P.; Rodrigo, M.A. Metoprolol Abatement from Wastewaters by Electrochemical Oxidation with Boron Doped Diamond Anodes. J. Chem. Technol. Biotechnol. 2012, 87, 225–231. [Google Scholar] [CrossRef]
- Isarain-Chávez, E.; Rodríguez, R.M.; Cabot, P.L.; Centellas, F.; Arias, C.; Garrido, J.A.; Brillas, E. Degradation of Pharmaceutical Beta-Blockers by Electrochemical Advanced Oxidation Processes Using a Flow Plant with a Solar Compound Parabolic Collector. Water Res. 2011, 45, 4119–4130. [Google Scholar] [CrossRef]
- Regalado-Méndez, A.; Vizarretea-Vásquez, D.; Robles-Gómez, E.E.; Natividad, R.; Escudero, C.J.; Peralta-Reyes, E. Data-Based Modeling, Multi-Objective Optimization, and Multi-Criterion Decision-Making to Maximize the Electro-Oxidation of Metoprolol over Boron-Doped Diamond Electrodes in a Flow-By Reactor. Processes 2024, 12, 1958. [Google Scholar] [CrossRef]
- Regalado-Méndez, A.; Zavaleta-Avendaño, J.; Alanis-Ramírez, C.; Amado-Piña, D.; Ramírez Serrano, A.; Peralta-Reyes, E. Electrochemical Mineralization of Chloroquine in a Filter-Press-Type Flow Reactor in Batch Recirculation Mode Equipped with Two Boron-Doped Diamond Electrodes: Parametric Optimization, Total Operating Cost, Phytotoxicity Test, and Life Cycle Assessment. Catalysts 2024, 14, 918. [Google Scholar] [CrossRef]


| Operating Variables | Levels | ||||
|---|---|---|---|---|---|
| −α | −1 | 0 | +1 | +α | |
| X1: pH0 | 2.71 | 3.00 | 5.00 | 7.00 | 7.83 |
| X2: j (A/cm2) | 0.0872 | 0.0937 | 0.1094 | 0.1250 | 0.1315 |
| Run | Factor | Response | |
|---|---|---|---|
| pH0 | j (A/cm2) | η (%) | |
| 1 | 7.00 | 0.0937 | 82.22 |
| 1 | 7.00 | 0.1250 | 98.78 |
| 3 | 5.00 | 0.0872 | 97.04 |
| 4 | 2.17 | 0.1094 | 60.10 |
| 5 | 3.00 | 0.0937 | 81.17 |
| 6 | 5.00 | 0.1094 | 89.97 |
| 7 | 5.00 | 0.1315 | 95.49 |
| 8 | 5.00 | 0.1094 | 87.49 |
| 9 | 3.00 | 0.1250 | 61.50 |
| 10 | 7.83 | 0.1094 | 90.63 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 1615.09 | 4 | 403.77 | 24.11 | 0.0018 | Significant |
| X1 | 828.07 | 1 | 828.07 | 49.45 | 0.0009 | |
| X2 | 3.52 | 1 | 3.52 | 0.2104 | 0.6257 | |
| X1X2 | 328.29 | 1 | 328.29 | 19.60 | 0.0068 | |
| X12 | 452.82 | 1 | 452.82 | 27.04 | 0.0035 | |
| Residual | 83.73 | 5 | 16.75 | |||
| Lack of Fit | 80.66 | 4 | 20.16 | 6.56 | 0.2839 | Not significant |
| Pure Error | 3.08 | 1 | 3.08 | |||
| Cor Total | 1698.83 | 9 | ||||
| ; adequate precision = 14.516; coefficient of variance = 4.85 | ||||||
| Response | Objective | Limits | |||
|---|---|---|---|---|---|
| Min | Max | Unit | Importance | ||
| pH0 | Within range | 3 | 7 | Dimensionless | +++ |
| j | Within range | 0.0937 | 0.125 | A/cm2 | +++ |
| η | Maximized | 60.1 | 98.78 | % | +++ |
| Orders (n) | kapp | Unit | R2 |
|---|---|---|---|
| Pseudo-zero-order | 1.7307 × 10−4 | M/h | 0.7179 |
| Pseudo-first-order | 0.9660 | 1/h | 0.9737 |
| Pseudo-second-order | 18879.4745 | 1/(M h) | 0.8465 |
| Op | NOp | An/Cat | V (L) | DE (%) | DQO (%) | SEC (kWh/m3) | OC (USD/L) | Ref. |
|---|---|---|---|---|---|---|---|---|
| Q = 1.0 L/min, [C6H4O2]0 = 0.001 M, pH0 = 6.52, j = 0.124 A/cm2, t = 5 h | BDD/BDD | 2.500 | 97.32 | --- | 127.85 | 3.07 | This work | |
| Q = 0.0016 L/min, [C6H4O2]0 = 0.01 M, [H2SO4] = 0.5 M, i = 0.124 A, pH = 7, t = 12 h | Pt/Carbon fiber | 0.025 | 99.23 | --- | --- | --- | [17] | |
| Q = 5 L/min, [C6H4O2]0 = 0.0092 M [HClO4] = 0.5 M, j = 0.02 A/cm2, t = 2.5 h | BDD/stainless steel | 0.400 | 100.00 | 80 | 49.50 | --- | [3] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peralta-Reyes, E.; Regalado-Méndez, A.; Robles, F.A.; Méndez-Durazno, C.; Espinoza-Montero, P.J. Modeling and Optimization of p-Benzoquinone Degradation via Flow-By Electro-Oxidation on Boron-Doped Diamond Electrodes. Processes 2025, 13, 942. https://doi.org/10.3390/pr13040942
Peralta-Reyes E, Regalado-Méndez A, Robles FA, Méndez-Durazno C, Espinoza-Montero PJ. Modeling and Optimization of p-Benzoquinone Degradation via Flow-By Electro-Oxidation on Boron-Doped Diamond Electrodes. Processes. 2025; 13(4):942. https://doi.org/10.3390/pr13040942
Chicago/Turabian StylePeralta-Reyes, Ever, Alejandro Regalado-Méndez, Frida A. Robles, Carlos Méndez-Durazno, and Patricio J. Espinoza-Montero. 2025. "Modeling and Optimization of p-Benzoquinone Degradation via Flow-By Electro-Oxidation on Boron-Doped Diamond Electrodes" Processes 13, no. 4: 942. https://doi.org/10.3390/pr13040942
APA StylePeralta-Reyes, E., Regalado-Méndez, A., Robles, F. A., Méndez-Durazno, C., & Espinoza-Montero, P. J. (2025). Modeling and Optimization of p-Benzoquinone Degradation via Flow-By Electro-Oxidation on Boron-Doped Diamond Electrodes. Processes, 13(4), 942. https://doi.org/10.3390/pr13040942








