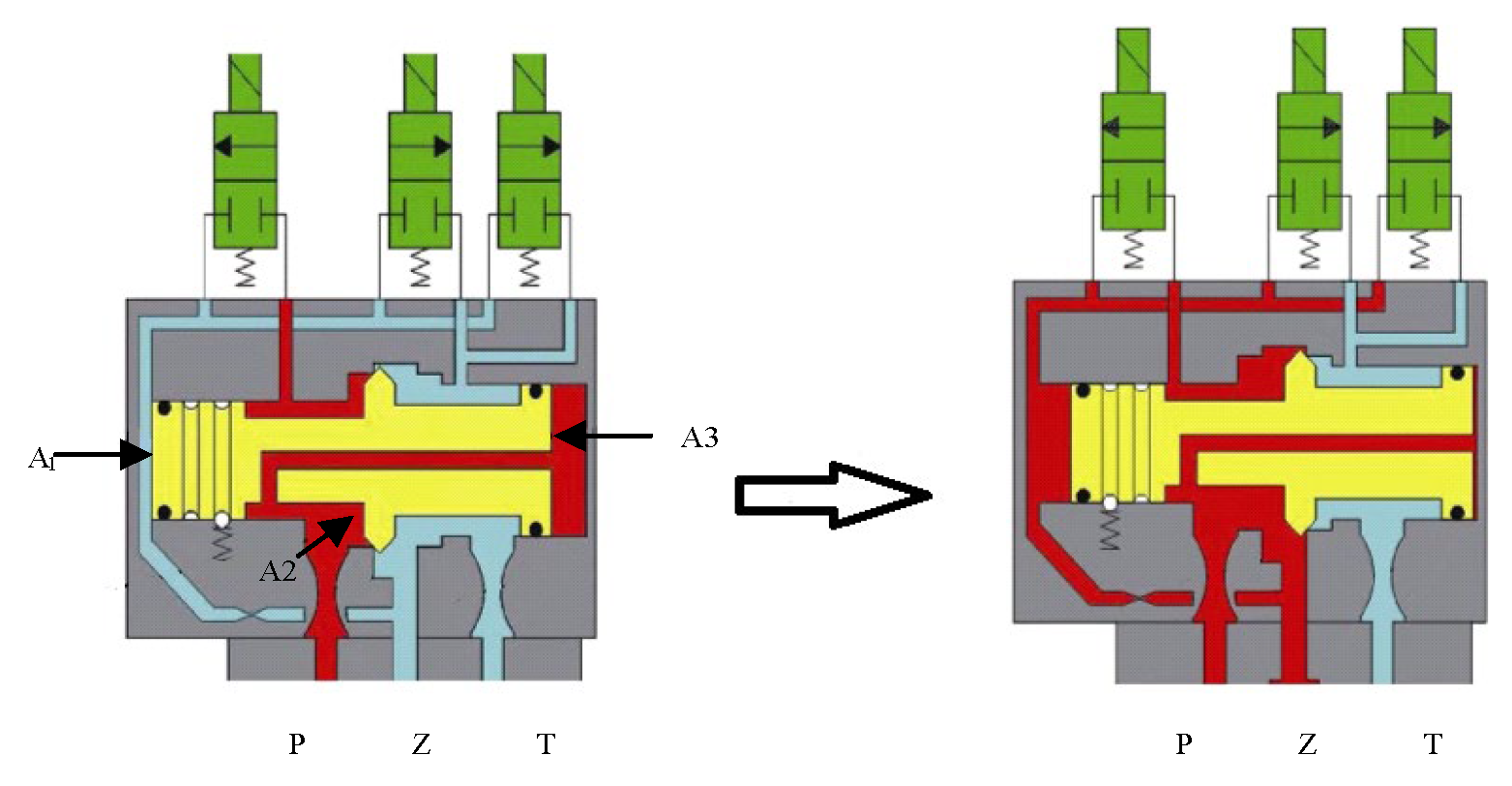
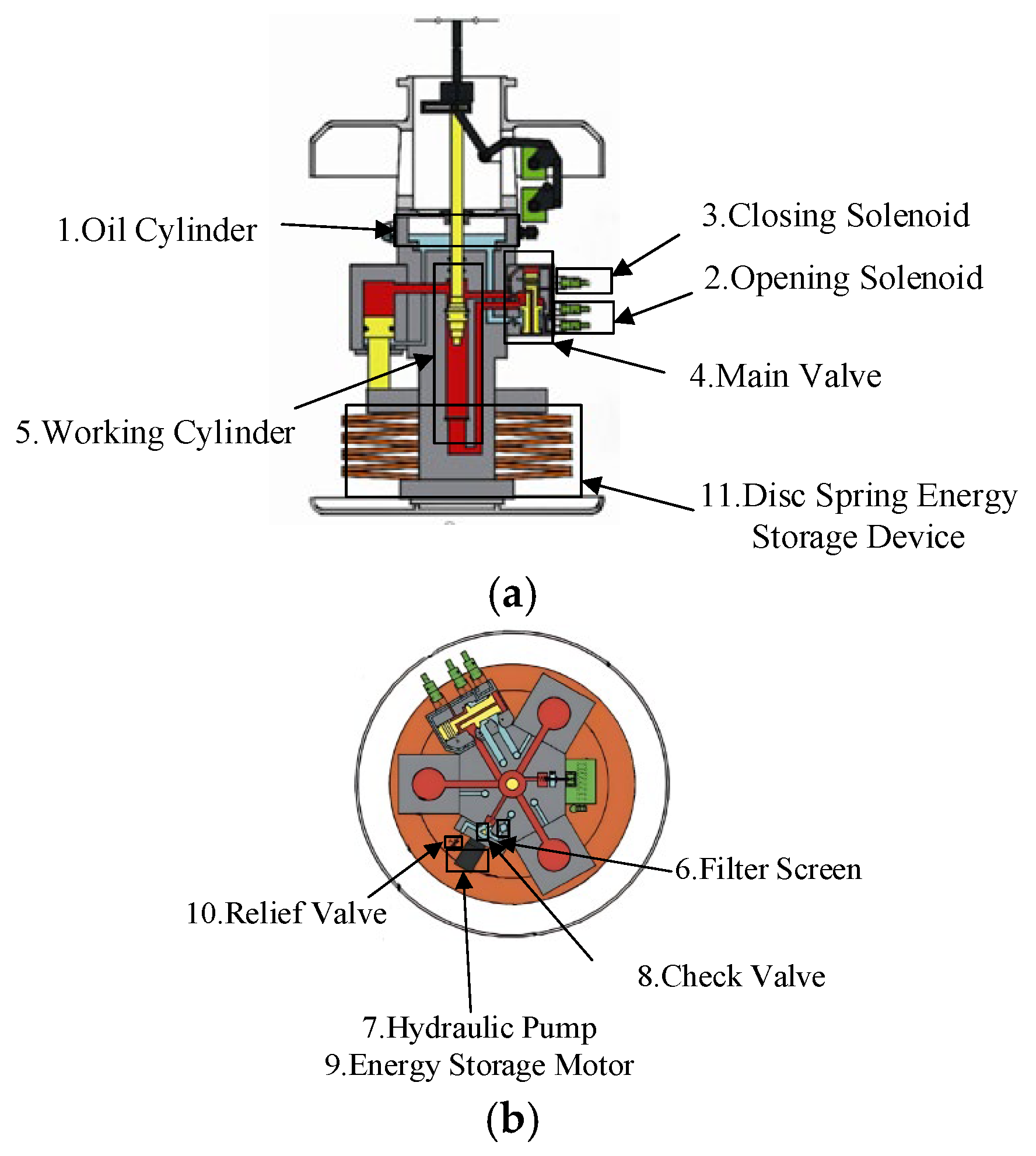
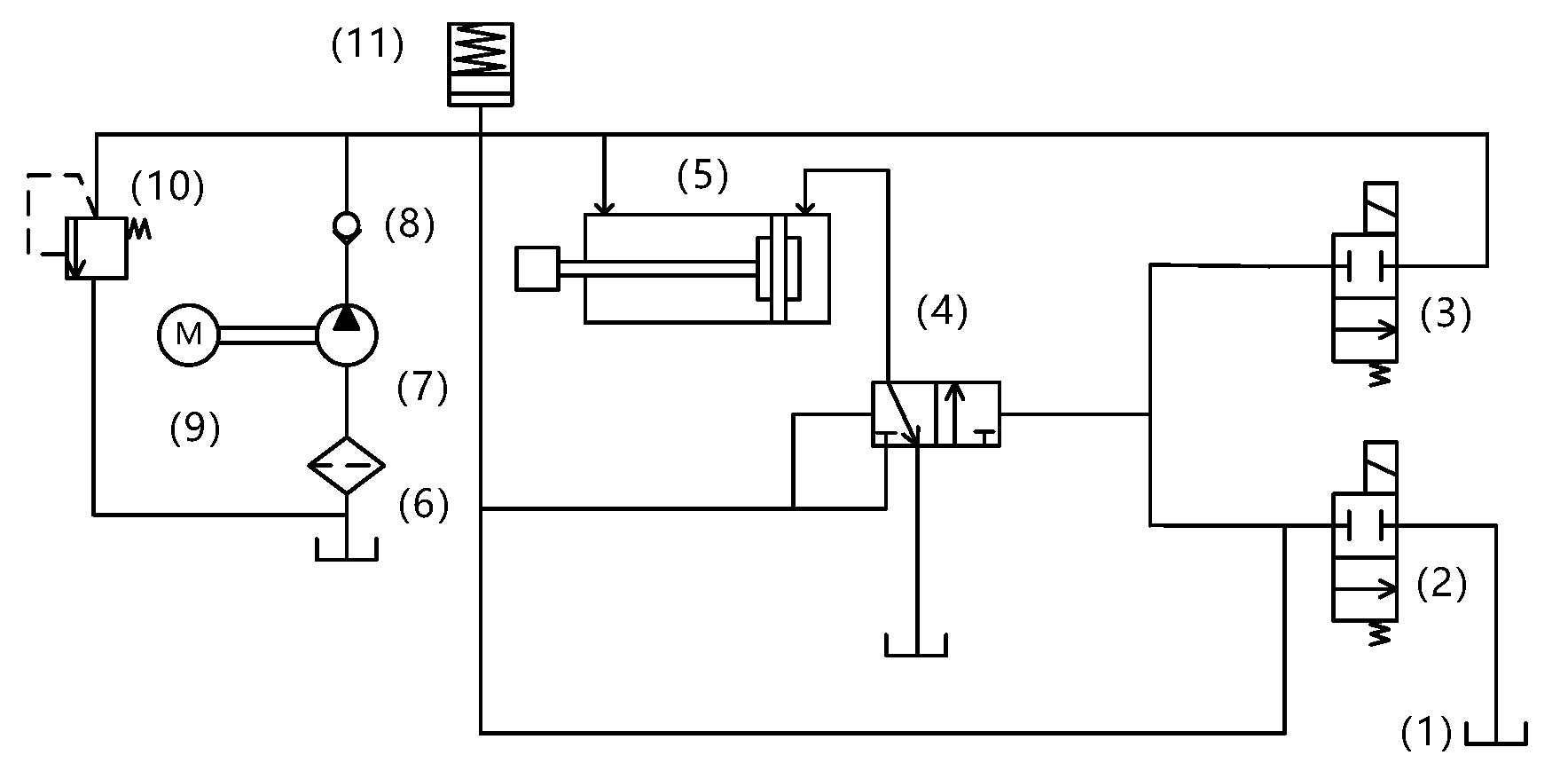
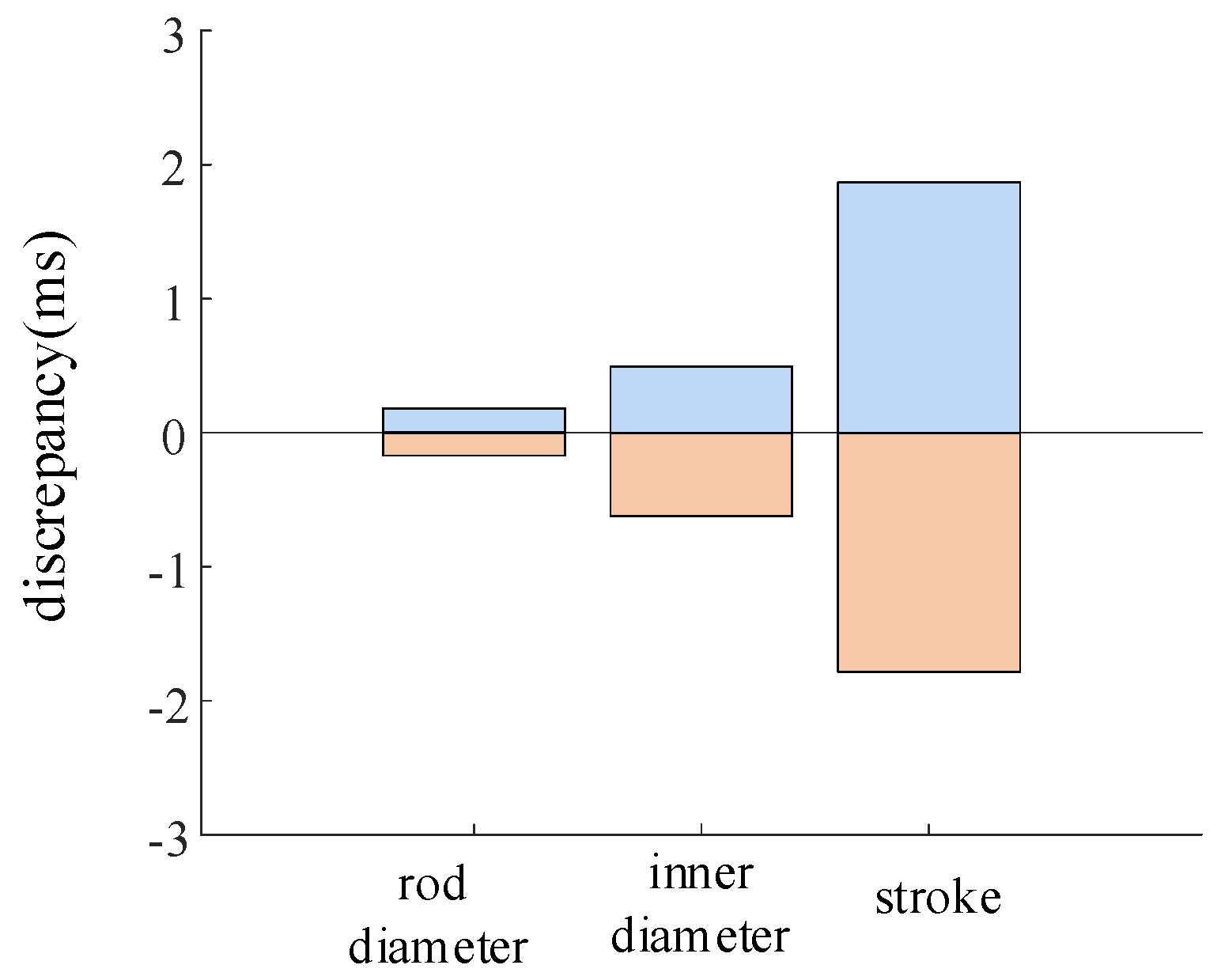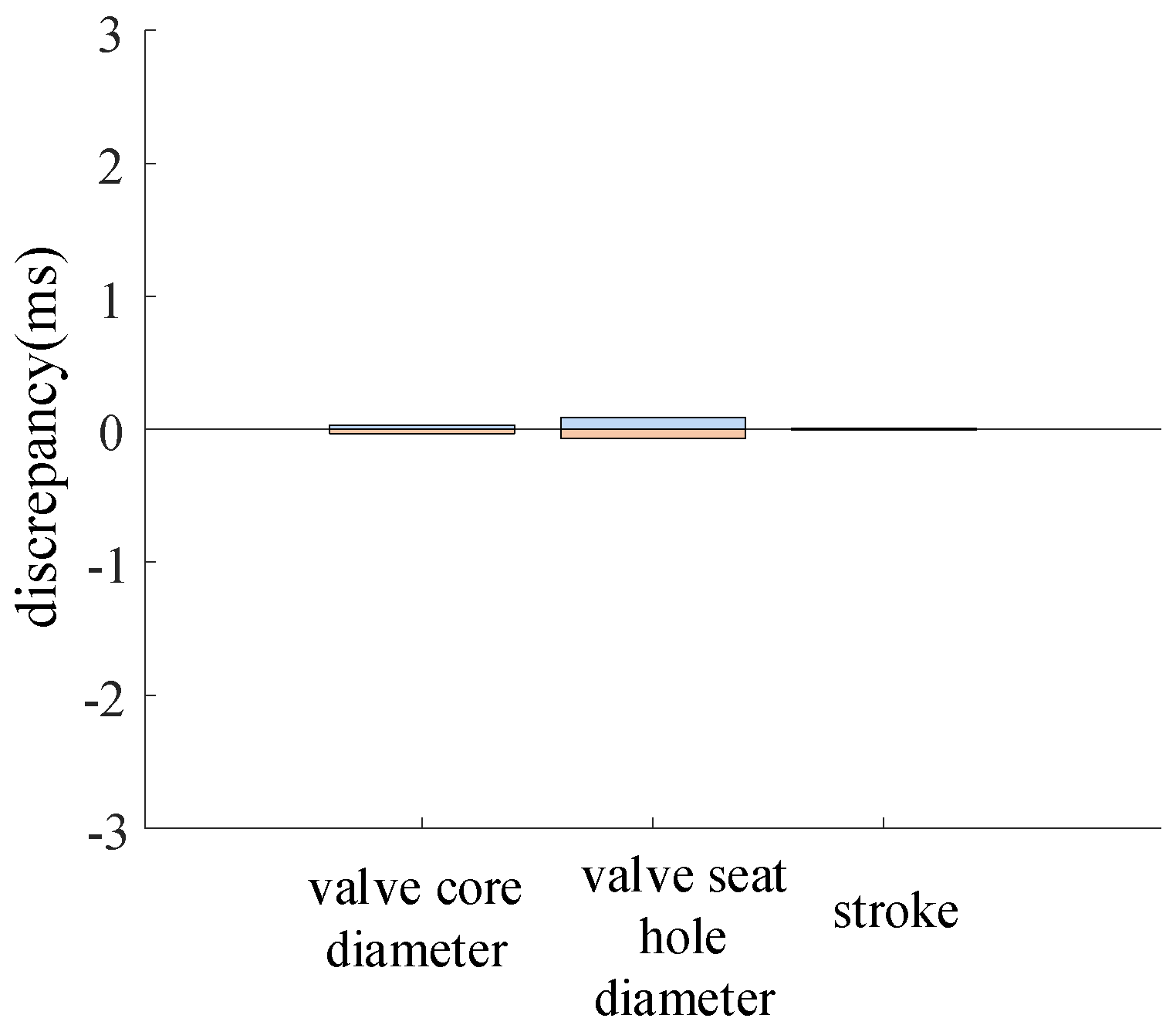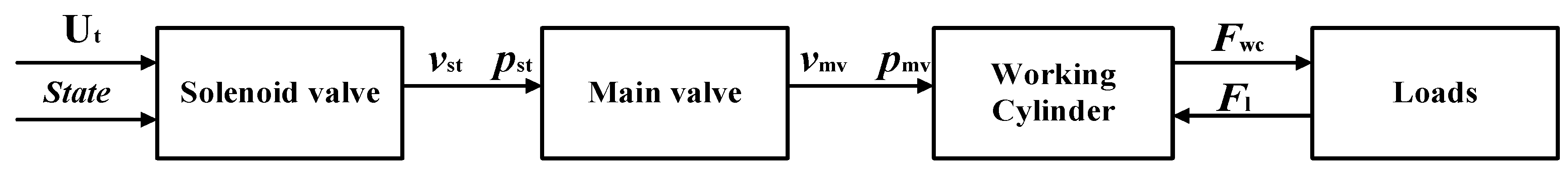1. Introduction
High-voltage circuit breakers, as critical primary equipment in power systems, are mainly composed of three parts: the interrupting section, transmission section, and insulation section [
1,
2,
3,
4]. Disc spring hydraulic operating mechanisms are widely applied in the 500–1100 kV extra-high voltage field due to their compact structure and large and stable output force [
5,
6,
7,
8]. As the number of circuit breaker operations increases, the continuous accumulation of plastic deformation caused by low-cycle fatigue in its internal structure leads to structural parameter changes, indirectly affecting the closing time of the circuit breaker. This results in reduced phase-controlled closing accuracy and endangers the stable operation of high-voltage lines and power equipment [
9,
10,
11,
12].
Currently, there are few studies on the stability degradation of ultra-high voltage circuit breaker operating mechanisms caused by structural parameter changes. Traditional ultra-high voltage circuit breakers have long operation times and poor stability, leading to a closing time dispersion of up to ±10 ms [
13]. With the upgrading of operating mechanisms, the use of mechanisms with higher energy density can reduce mechanical dispersion to approximately ±1 ms [
14,
15]. Current research mainly focuses on improving the stability of key components to enhance overall mechanism stability. Reference [
16] studies mechanical characteristics through the cross-verification of experimental and simulation results, then locates fault positions by comparing fault opening waveforms. In Reference [
17], structural optimization was performed by studying the fatigue life of the mechanism’s buffer, improving product quality. Reference [
18] investigates stress relaxation and fault identification in operating mechanisms, validates the accuracy of dynamic models through experimental comparison, and proposes a remaining fatigue prediction model. Reference [
19] integrates electrical, magnetic, dynamic operation, fluid, mechanical, pneumatic, and thermal models into a multi-physics coupling model, conducting simulations and experimental verification on a 550 kV high-voltage circuit breaker to accurately predict and optimize the dynamic characteristics of hydraulic operating mechanisms. Studies in References [
20,
21,
22,
23] focus on electric field and gas flow distribution in arc extinguishers under a given output pressure and velocity of operating mechanisms, or investigate hydraulic operating mechanism performance under specified loads [
24].
Scholars have made significant achievements in quantitative methods for analyzing the stability of hydraulic systems. Bošnjak et al. [
25] studied microstructural changes in stress-concentrated regions of hydraulic systems through finite element analysis, revealing the dominant factors in fatigue failure. Arsic et al. [
26] conducted three-point bending tests on wheel loader booms, deeply characterizing fatigue crack propagation processes. Their research provided a new experimental approach for fatigue analysis of welded structures and highlighted the critical impact of welding material selection on mechanical performance. Liu et al. [
27] investigated excavator digging processes under different working conditions, considering eccentric loads, impacts, and other factors to provide experimental data for constructing hinge point load spectra. They further predicted boom fatigue life using the discrete element method. This fatigue analysis not only explored excavator performance under real operational conditions but also evaluated the influence of different design parameters on fatigue life. Mohammad et al. [
28] applied Monte Carlo simulation to quantify uncertain loads on EC460 excavator working devices under complex conditions, optimizing dipper stick structures based on these results. The optimized dipper stick demonstrated significant improvements in both mass and stress performance, further enhancing structural stability and reliability.
Although numerous studies have been conducted on disc spring hydraulic operating mechanisms, most focus on model establishment and design optimization. There is a lack of quantitative research on the low-cycle fatigue of operating mechanisms caused by frequent operations in long-term running circuit breakers, which affects the stability of closing time and hinders the implementation of phase-controlled closing. Therefore, it is critical to establish an accurate and efficient stability calculation model for operating mechanisms. Based on this, this paper first constructs a mathematical model capable of accurately describing the dynamic performance of the mechanism to analyze the operational characteristics of disc spring hydraulic operating mechanisms. Then, a stability analysis limit state function based on time-threshold judgment is established, combining the Adaptive Kriging (Adaptive Kriging, AK) surrogate model with Directional Importance Sampling (Directional Importance Sampling, DIS) to develop an efficient and accurate stability assessment method. Finally, under different mechanical dispersion requirements, the influence weight changes of each component are analyzed, constructing a closing time prediction model and comparing it with actual experimental data.
3. Reliability Analysis of Disc Spring Hydraulic Operating Mechanism
To quantitatively describe the impact of changes in the internal structure of the circuit breaker on the stability of the closing time, the influence weights under different mechanical dispersity requirements are analyzed. A stability analysis model needs to be established based on the simulation data of the closing time for the disc spring hydraulic operating mechanism.
3.1. Limit State Functions
In the closing process of the disc spring hydraulic operating mechanism, the closing time is a key indicator, which affects the accuracy of phase-controlled operations and the safe and stable operation of the power line. The closing time is defined as the time from when the circuit breaker receives the closing signal to when the contacts close, with the closing action being considered complete when the piston of the working cylinder reaches the rated stroke. In phase-controlled closing operations, the mechanical dispersity of the circuit breaker is defined as the difference between the actual action time and the rated action time. In reliability analysis, the system’s state is described by the limit state function g. The limit state function for the reliability of the operating mechanism’s closing time can be defined as the difference between the actual closing time and the rated closing time being less than the specified mechanical dispersity.
where
Tσ = 3σ represents the specified mechanical dispersity;
T(
X) is the closing time during the fluctuation process of the circuit breaker’s structural parameters;
X denotes the parameters; and
Tμ is the rated action time of the circuit breaker.
3.2. Adaptive Kriging Surrogate Model
The key to the closing time stability of the disc spring hydraulic operating mechanism studied in this paper lies in estimating the structural failure probability, as shown in the following equation.
In the equation, denotes the distribution parameters of input variables, i.e., the dimensions of critical components in the operating mechanism; represents the distribution parameters of input variables; describes the uncertainties and probability density function of input variables, reflecting their stochastic sampling law; is the failure threshold, indicating that the system’s response does not meet the threshold requirement; and is the limit state function.
The numerical simulation method is a relatively general approach for estimating the failure probability. Based on the law of large numbers, this method uses the sample mean to estimate the population mean. That is, it transforms the integral for solving the failure probability in the above Formula (10) into the form of the mean. In other words, it estimates the failure probability using the frequency of failure. As long as there are a sufficient number of samples, the obtained estimated value will converge to the true failure probability. The most basic numerical simulation method is the Monte Carlo simulation method. This method first generates a set of samples of input variables according to the joint probability density function of the input variables. Then, it approximately estimates the failure probability through the ratio of the number of samples within the failure domain to the total number of samples. In contrast to the real and complex physical models, surrogate models have lower computational costs, so they can effectively improve the computational efficiency of the failure probability.
As an unbiased estimator with minimal estimation variance, the traditional Kriging surrogate model combines global approximation with local stochastic errors. Its effectiveness does not rely on the presence of random errors, and it demonstrates excellent fitting performance for highly nonlinear problems and local response discontinuities. Therefore, Kriging surrogate models can be employed to approximate both global and local function behaviors. The Kriging model can be expressed as the sum of a random distribution function and a polynomial [
35,
36]:
In the equation,
is the unknown Kriging model;
is the basis function of the random vector
providing a global approximation model within the design space;
are the regression coefficients to be determined, whose values can be estimated from known response values; p denotes the number of basis functions;
is a stochastic process modeling local deviations with 0 mean and variance
on top of the global approximation. The components of its covariance matrix can be expressed as follows:
In the equation,
represents the correlation function between any two sample points, which serves as a component of the correlation matrix R,
and m is the number of data points in the training sample set. Multiple functional forms are available for the
, with the Gaussian correlation function expressed as
In the equation,
represents the unknown correlation parameter. According to Kriging theory, the response estimate at an unknown point x is given by the following:
In the equation,
is the estimate of
,
g is a column vector composed of response values from training samples,
F is an
dimensional matrix formed by regression models at m sample points, and
is the correlation function vector between training samples and the prediction point, which can be expressed as follows:
In the equation,
and variance estimate
are given by the following:
The correlation parameter
can be obtained by maximizing the likelihood function
The Kriging model constructed using the parameter obtained via maximum likelihood estimation is the surrogate model with optimal fitting accuracy.
Therefore, for any unknown
follows a Gaussian distribution,
, where the mean and variance are calculated as follows:
The Kriging surrogate model is an exact interpolation method. At training points , the model satisfies and . indicates the minimum mean squared error between and . The performance function values at initial sample points have zero error, while the variances of performance function predictions for other input variable samples are generally non-zero. When is large, it indicates that the estimate at point x is unreliable. Therefore, the predicted variance can be used to quantify the estimation accuracy of the surrogate model at location x, thereby providing an effective indicator for updating the Kriging surrogate model.
Traditional Kriging relies on fixed covariance functions and parameters, making it less adaptable to non-stationary data or dynamically changing environments. It cannot automatically update the model to accommodate new data, and parameters must be manually set, which may compromise results. In contrast, the adaptive Kriging model automatically optimizes covariance function parameters based on data characteristics, incorporates new data in real time, and updates the model dynamically.
The adaptive Kriging model is an improved spatial statistical model based on the traditional Kriging method. Its core idea is to enhance the fitting capability for complex data and prediction accuracy by dynamically adjusting model parameters or structures.
The framework for constructing an adaptive Kriging surrogate model is as follows: 1. Initial model construction: Build a coarse Kriging surrogate model using a small number of training samples. 2. Adaptive sampling: Select candidate samples that meet specified criteria from a pool of potential points via an adaptive learning function, and update the Kriging model iteratively until convergence criteria are satisfied. 3. Stability analysis: Conduct a stability analysis using the final updated Kriging surrogate model. Sample points added to the Kriging training set for model updating must satisfy two criteria: 1. They are located in regions with a high probability density of random input variables. 2. They are close to the failure surface where the performance function equals zero and where the risk of misclassifying the sign is high. Sample points with high risk of sign misclassification exhibit the following characteristics: 1. they are located near the limit state surface (i.e., small
); 2. they have high prediction variance
from the current Kriging surrogate model; or 3. both conditions above simultaneously. The adaptive learning function selected here is the U-learning function [
37].
The U-learning function considers both the distance of the Kriging surrogate model’s predicted value to the failure surface and the standard deviation of the estimate. Specifically, when predicted values are equal, larger standard deviations result in smaller U-learning function values; when standard deviations are equal, predicted values closer to zero yield smaller U-learning function values. Points near the failure surface with larger standard deviations of estimates should be added to the training dataset to update the Kriging model. Specifically, from the candidate sample pool, select the sample point with the smallest U-value and add this sample point along with its corresponding true performance function value to the training dataset to update the current Kriging model. Reference [
37] indicates that using
as the termination condition for the adaptive updating process of the Kriging surrogate model with the U-learning function is appropriate.
3.3. Directionally Important Sampling
For engineering problems involving extremely low failure probabilities under specific conditions, the Monte Carlo method requires a vast number of samples to achieve convergent results, leading to inefficient sampling. Therefore, improved mathematical modeling methods are proposed, with importance sampling being the most common approach. Importance sampling has gained extensive application due to its high sampling efficiency and small computational variance.
The basic concept of importance sampling is to replace the original sampling density function with an importance sampling density function, thereby increasing the probability of samples falling into the failure region and achieving higher sampling efficiency and faster convergence. The fundamental principle for selecting the importance sampling density function is to ensure that samples contributing significantly to the failure probability are sampled with higher probability, which reduces the variance of the estimate.
Compared to traditional Monte Carlo simulation in Cartesian coordinate systems, directional importance sampling offers superior efficiency and accuracy for failure probability problems involving a single limit state. By solving nonlinear equations instead of performing univariate random sampling, it reduces the dimension of the original random variable space to one.
The component dimensions of the hydraulic operating mechanism with disc springs are mutually independent normal variables. The directional sampling method analyzes structural stability through random sampling in the standard normal space under polar coordinates, utilizing the distribution properties of directional vectors
. In the standard normal space, any random vector
in Cartesian coordinates can be represented in polar coordinates as
, where R is the polar radius and A is the unit directional vector of x. Under polar coordinates, the failure probability formula for the performance function
can be expressed as follows:
In the equation,
is the joint probability density function of the random vector
x,
is the joint probability density function of
R and
A.
is the probability density function of the unit directional vector
A. Since x follows an n-dimensional independent standard normal distribution,
follows a uniform distribution on the unit sphere.
is the conditional probability density function of the random variable R in the sampling direction
A =
a.
defines the failure threshold when
A =
a, assuming the distance from the origin to the failure surface in the sampling direction
A =
a is
r(a). The failure probability
in the direction
A =
a can be obtained from the cumulative distribution function of a chi-squared
distribution with n degrees of freedom, expressed as follows:
Thus, the unbiased estimator of structural failure probability
and its variance
are calculated as follows:
As an improved method of the directional sampling method, the basic idea of the directional importance sampling method is as follows: By establishing an important sampling density function to replace the original sampling density function, more sampling directions are directed towards the regions that make a greater contribution to the structural failure probability. This approach can improve the sampling efficiency and accelerate the convergence speed of the simulation process.
For the problem of failure probability in the limit state, the directional importance sampling method establishes an importance sampling density function
in the polar coordinate system, and the failure probability is given by the following equation:
The directional importance sampling density function is given by the following:
In the equation, represents the stability index, is the indicator function, which equals 1 if and 0 otherwise. The control parameter p ranges within [0, 1]. When p = 1, the directional importance sampling density function degenerates into the directional sampling density function . When p = 0, directional importance sampling will only sample on one side of the failure domain of the limit plane. The closer the limit state surface approaches a planar surface, the closer the value of p can be chosen to 0; the closer the limit state surface approaches a spherical surface, the closer the value of p can be chosen to 1. The value of p can be appropriately selected between 0 and 1 to ensure that directional importance sampling effectively reflects the actual failure domain.
The unbiased estimate of the structural failure probability and the calculation formula for its variance are presented as follows:
3.4. Calculation Process
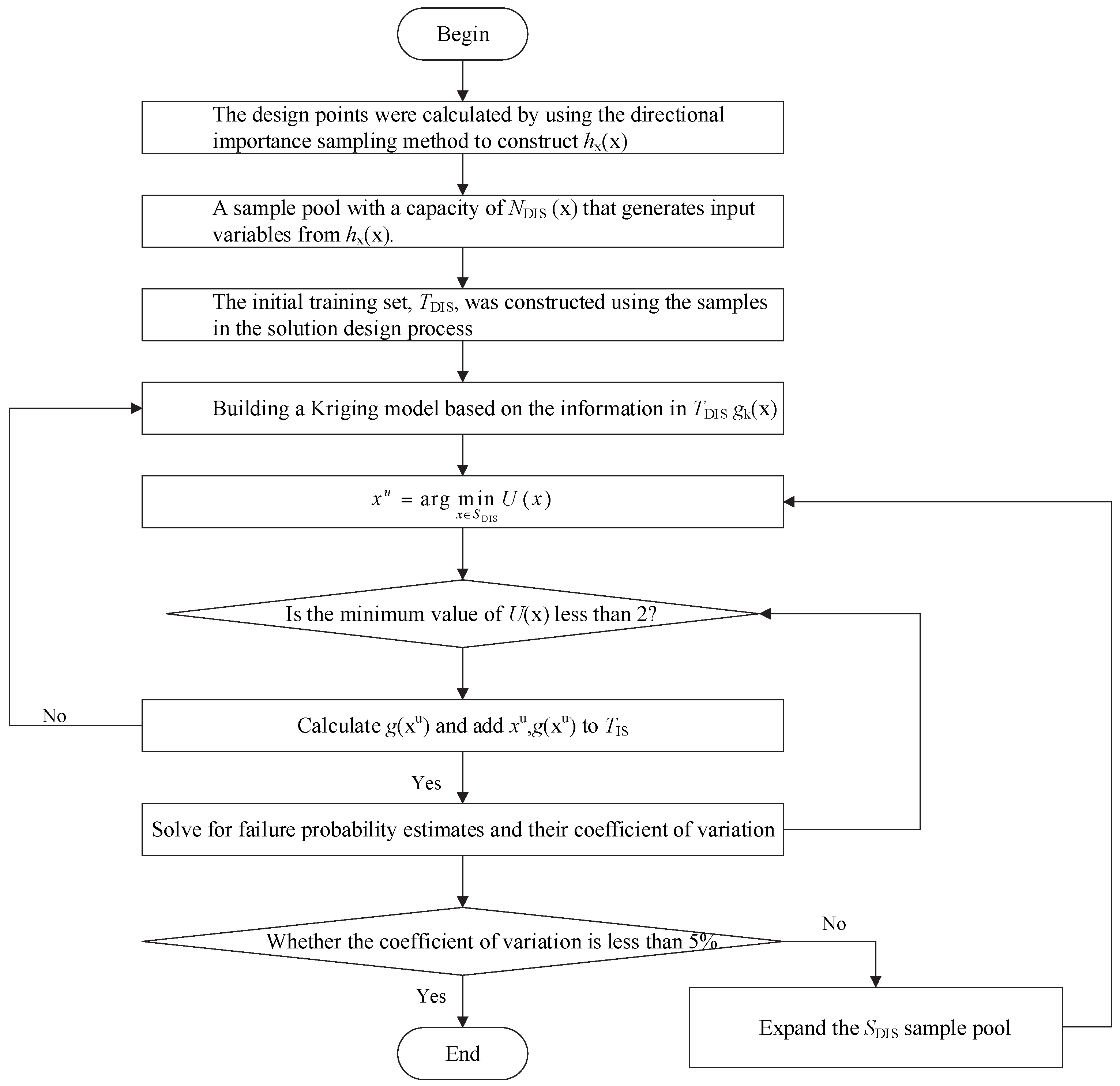
The main approach of the AK-DIS method for reliability analysis is as follows: First, the corresponding design point is obtained using the single-mode directional sampling method, and the sampling center of the original density function is shifted to the new design point. An importance sampling probability density function is constructed, and the single-mode sampling method is used to solve the input–output model data at the design point in order to build the original Kriging model. Next, the importance sampling density function is used to generate an importance sampling sample pool, and the U-learning function is employed to select the updated sample points that meet the requirements from the sample pool. The true function values are calculated for these points and added to the training sample set to iteratively update the Kriging model. Finally, the updated and converged Kriging model is used for reliability analysis. The process of solving reliability using the AK-DIS method is shown in
Figure 15, with the specific calculation steps as follows:
- (1)
The unimodal directional sampling density function is constructed by solving the design point P* using the unimodal directional method. The sampling center of the original sampling density function is shifted to P*, and the unimodal directional sampling density function hx(x) is constructed.
- (2)
Construct a single-mode directional sampling sample pool and initial training set TIS: hx(x) is used to extract the sample pool SDIS with a sample size of NDIS, and the input–output samples in the process of solving the design points are used to form the initial training sample set TDIS.
- (3)
Construct the Kriging model gk(x) based on the information in TDIS.
- (4)
Select the update sample point xu in SDIS; then, there is the following:
- (5)
Determine whether the self-learning process has converged: if the U-learning function is greater than 2, stop the adaptive learning process and proceed to step 6; otherwise, calculate g(xu), and add {xu, g(xu)} to the training samples in TDIS, and then return to step 3 to continue updating the Kriging model gk(x).
- (6)
Use the current Kriging surrogate model to estimate the failure probability: use the Kriging surrogate model to calculate the failure domain indicator function value corresponding to each sample point in SDIS, and obtain the estimated value of the failure probability.
- (7)
Calculate the coefficient of variation of the failure probability estimate to determine the convergence of AK-DIS reliability. When the coefficient of variation is less than 5%, the algorithm stops running.
Figure 15.
AK-DIS algorithm process.
Figure 15.
AK-DIS algorithm process.
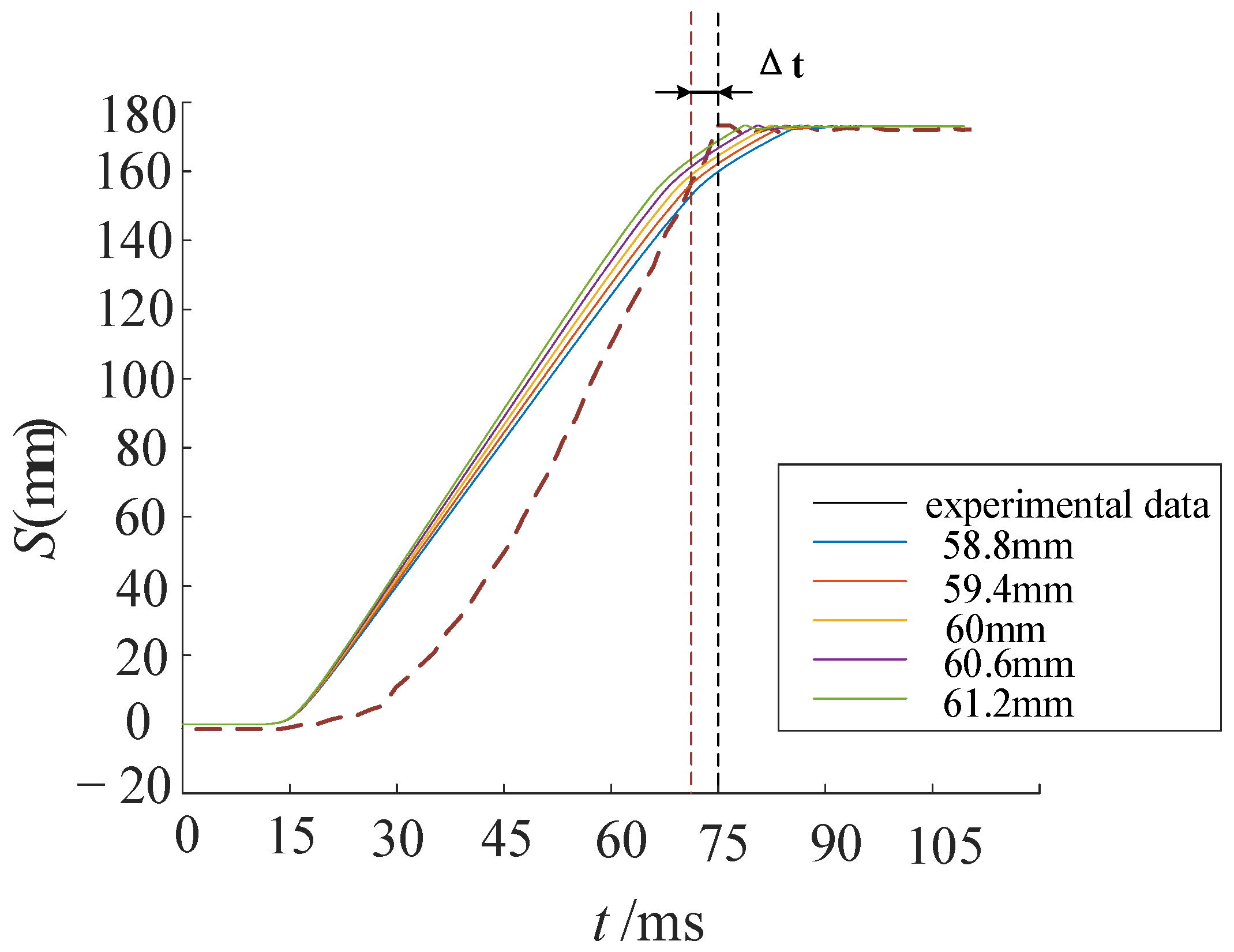
4. Closing Time Prediction Model
By setting structural parameters to randomly vary 1000 times within the low-cycle fatigue deformation range, 9000 combinations of nine variables and corresponding data for switching time and variable values are obtained. These are then input into the AK-DIS reliability algorithm, with mechanical dispersion set at 3σ = ±1 ms, yielding global and local stability results. Monte Carlo Simulation (MCS) is employed to numerically simulate the simulation data and provide the exact solution. The Importance Sampling (IS) method and the Adaptive Kriging surrogate model combined with Monte Carlo Simulation (AK-MCS) are used for comparison. The reliability analysis results are shown in
Table 5. In the table,
Nd represents the number of real model calls, and
n denotes the size of the alternative sample pool;
Cov is the coefficient of variation.
It can be observed that the failure probability estimates of the four methods are quite close, but the AK-DIS method exhibits the highest computational efficiency with the smallest error in failure probability Pf. From the perspective of a synchronized closing angle, when structural parameters experience low-cycle fatigue due to an increased number of actions, the failure probability is higher, making it difficult to meet the requirement within the mechanical dispersion of ±1 ms. In other words, the actual closing time of the high-voltage circuit breaker deviates significantly from the rated value.
To investigate the relationship between the accuracy and computational cost of the AK-DIS method, we analyzed the variations in computational time and accuracy by adjusting the candidate sample size as a proxy for computational cost, as shown in
Figure 16. The results indicate that when the candidate sample pool ranges from 104 to 20 × 104, a better balance between accuracy and computational cost is achieved.
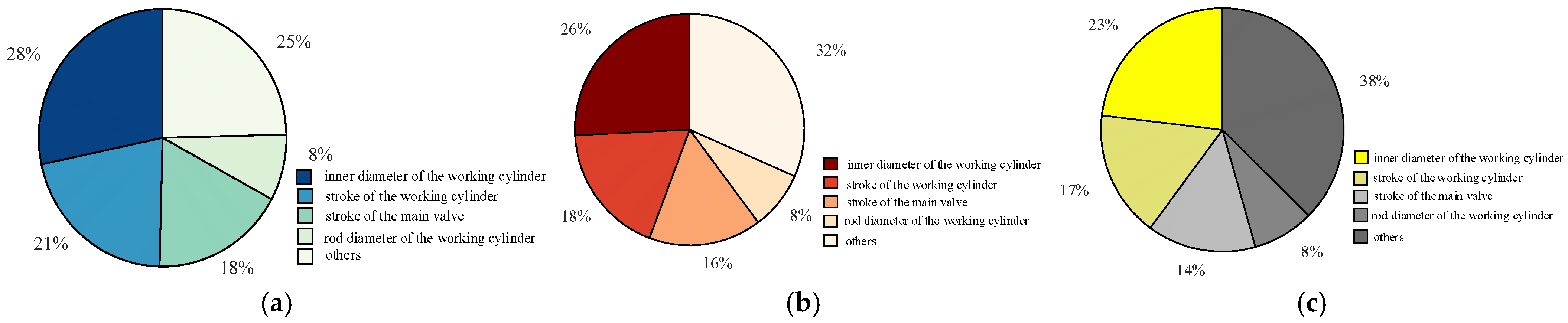
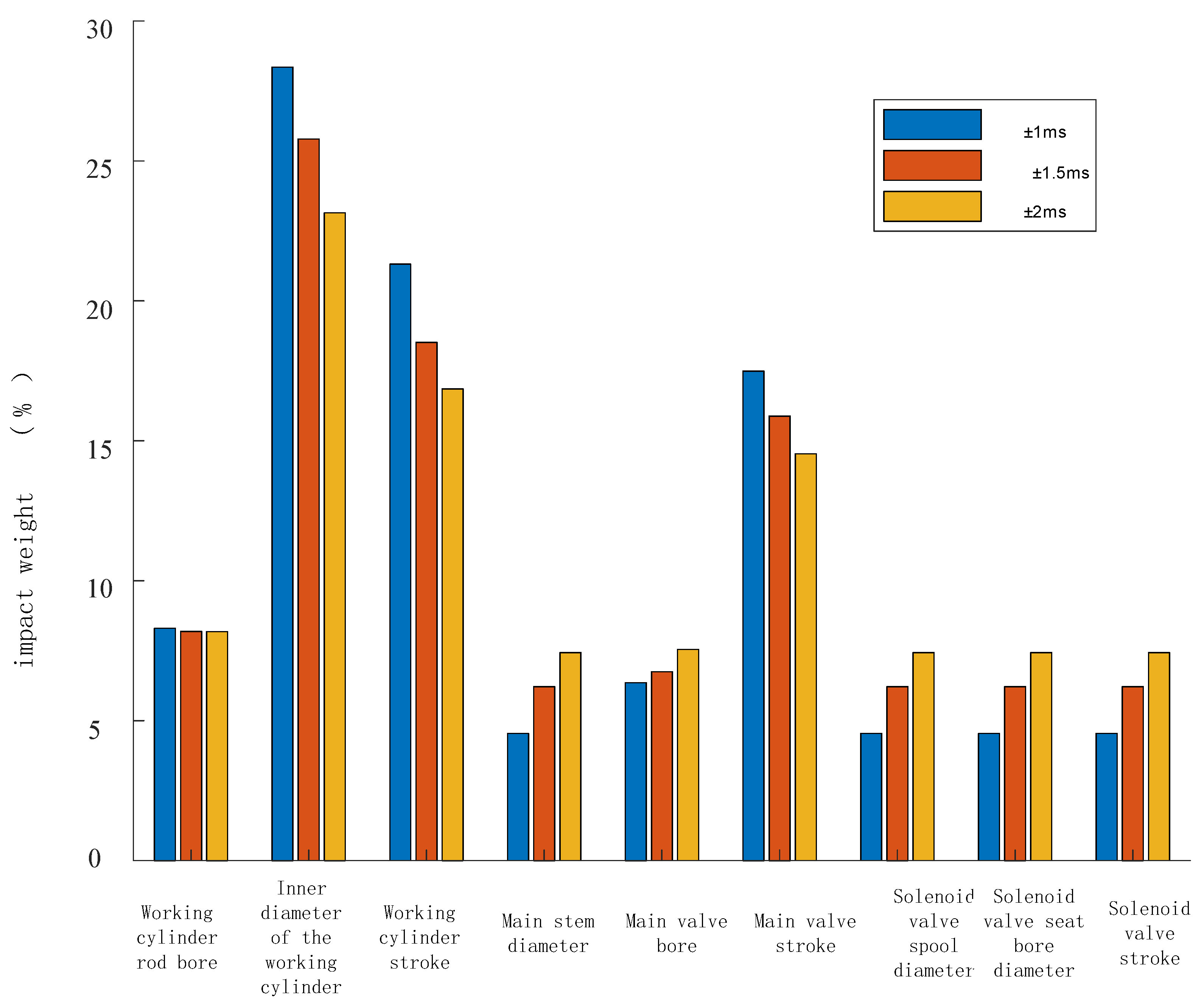
To facilitate the analysis of the influence weights of various parameters under different mechanical dispersions, the sensitivity is obtained by taking the partial derivative of the failure probability with respect to the mean value of each component. By comparing the sensitivity of individual variables with the sum of the sensitivities of all variables, the normalized stability impact weight of a single variable on the circuit breaker operation time is determined.
Figure 17 illustrates the stability impact weights of parameters under different mechanical dispersions, while
Figure 18 presents the stability impact weights of different parameters under different mechanical dispersion requirements.
From
Figure 17 and
Figure 18, it can be observed that under different mechanical dispersion conditions, the degree of influence on the circuit breaker closing time, i.e., the parameters with a higher proportion of reliability impact weight on the circuit breaker, are listed in descending order as follows: working cylinder bore diameter, working cylinder stroke, main valve stroke, and working cylinder rod diameter, totaling four parameters. As the mechanical dispersion requirement gradually decreases, the proportion of the stability impact weight of these four variables also gradually decreases.
For switch manufacturers, in order to reduce the low-cycle fatigue caused by excessive opening and closing cycles, materials with high fatigue strength and good ductility should be selected. Stress concentration should be avoided, and all connection points should be designed reasonably. Optimizing the geometry can effectively disperse stress. Coatings or surface plating should be used to protect surfaces from corrosion, and regular inspections of critical components should be carried out to detect and repair early-stage damage in a timely manner.
Due to the compact structure of the disc spring hydraulic operating mechanism, which makes it difficult to disassemble and replace, a closing time prediction model is established based on the weight coefficients under different mechanical dispersions. The prediction results are compared with the no-load test results of the ultra-high voltage circuit breaker to verify the accuracy of the weight analysis. The closing time prediction model is shown in the following formula.
In the formula, T is the predicted closing time; is the weight coefficient of different components under different mechanical dispersions; is the life state of different components under different mechanical dispersions, that is, the ratio of the number of actuations to the total designed number of actuations; and is the closing time offset caused by the low-cycle fatigue of different components throughout their entire life cycle.
Since the components with a relatively large weight in the disc spring hydraulic operating mechanism are, respectively, the inner diameter of the working cylinder, the stroke of the working cylinder, the stroke of the main valve, and the diameter of the working cylinder rod, these four components are taken as the analysis basis for the closing time prediction model. The design of the no-load closing test is as follows: 250 no-load closing tests are carried out in the initial state after the circuit breaker leaves the factory. The closing time is recorded every 50 times to obtain five groups of data, so as to obtain the initial closing time of the operating mechanism. Then, 2000 closing tests are carried out, and the closing time is measured every 50 times to obtain 40 groups of data. Therefore, a total of 45 groups of data are obtained.
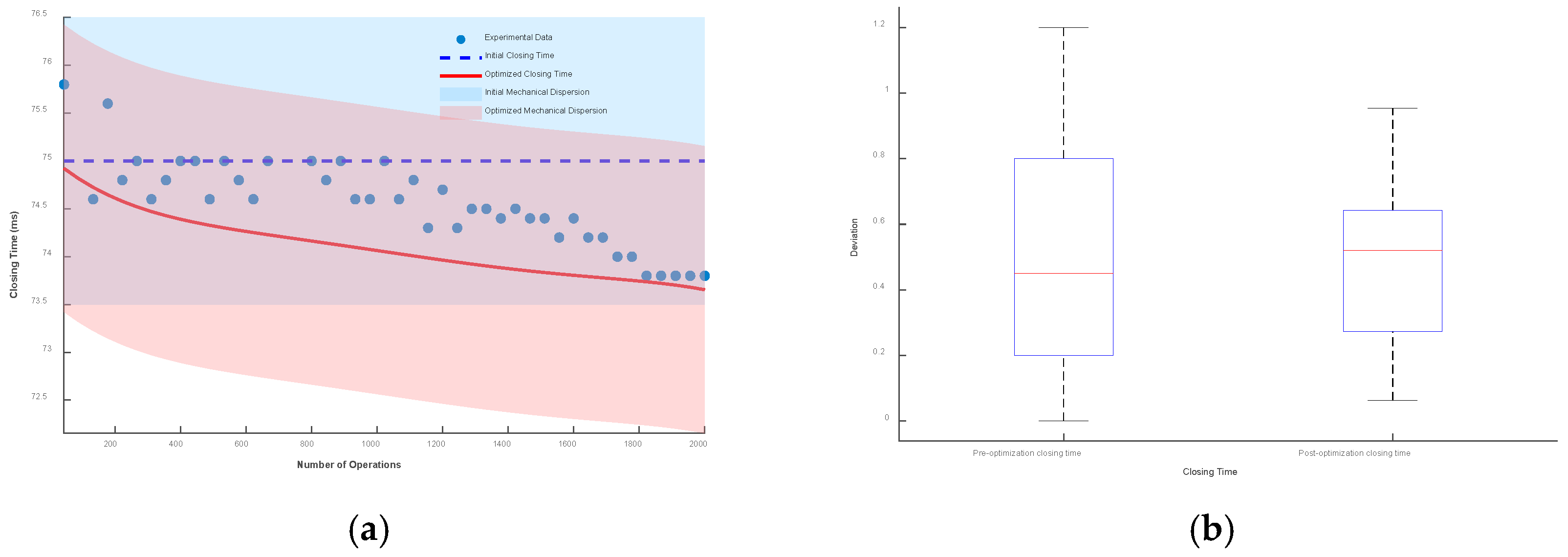
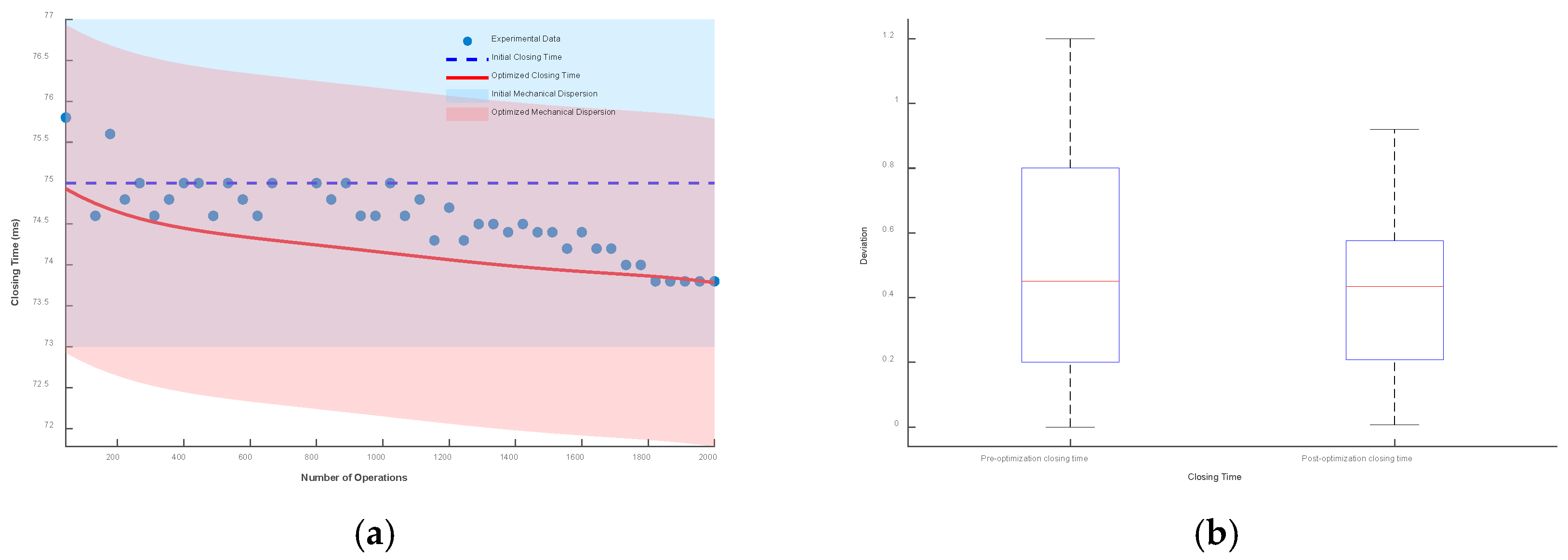
Taking the initial closing time as the reference, the envelope line composed of mechanical dispersion is drawn. Then, the closing time prediction model considering low-cycle fatigue is drawn, and the envelope line composed of its mechanical dispersion is also drawn. The results and box plots under different mechanical dispersions are shown in
Figure 19,
Figure 20 and
Figure 21.
It can be seen from the figures that when the mechanical dispersion is ±1 ms, after the number of operations is greater than 1750 times, the actual closing time has exceeded the boundary of the initial mechanical dispersion, which seriously affects the control of the circuit breaker and the stability of the power system. When the mechanical dispersions are ±1.5 ms and ±2 ms, although the actual operating time will not exceed the set mechanical dispersion, the deviation between the optimized closing time prediction model and the actual operating time is smaller.
The box plot represents the deviation between the optimized closing time model, the unoptimized model, and the test data. Under the mechanical dispersions of ±1 ms, ±1.5 ms, and ±2 ms, the maximum deviation values of the optimized closing time prediction model are reduced by 12.8%, 20.4%, and 23.3%, respectively, and the fluctuation ranges are reduced by 37%, 38.3%, and 38.6%, respectively.
Figure 19.
Mechanical dispersion of ±1 ms: (a) deviation plot and (b) box plot.
Figure 19.
Mechanical dispersion of ±1 ms: (a) deviation plot and (b) box plot.
Figure 20.
Mechanical dispersion of ±1.5 ms: (a) deviation plot and (b) box plot.
Figure 20.
Mechanical dispersion of ±1.5 ms: (a) deviation plot and (b) box plot.
Figure 21.
Mechanical dispersion of ±2 ms: (a) deviation plot and (b) box plot.
Figure 21.
Mechanical dispersion of ±2 ms: (a) deviation plot and (b) box plot.