Open Switch Fault Diagnosis in Three-Phase Voltage Source Inverters Using Single Neuron Implementation
Abstract
1. Introduction
1.1. Problem Statements and Research Gap
- PVT has been commonly adopted for OCF diagnosis because of its capability to normalize current measurements. However, implementations using DSPs need extra processing power and time [10].
- Artificial Intelligence-based Methods like ANNs, FL Systems and Deep Neural Networks have been adopted for fault classification. However, although these techniques provide high accuracy, they need considerable computational resources, increasing complexity in real-time execution [20,21,22,23,24,25].
1.2. Proposed Approach
1.3. Contributions of the Work
- Removal of DSP/Controller Dependence: In contrast to traditional methods requiring DSPs or microcontrollers, this technique depends on hardware-based computation, minimizing cost and operational complexity.
- Real-Time Fault Diagnosis: The addition of a single processing neuron with a high-speed multiplier and adder enables fast diagnosis of OCFs, making it appropriate for real-time applications.
- Robustness Under Variable Load Conditions: The suggested method maintains high accuracy and stability in OCF diagnosis despite fluctuating load conditions, confirming consistency in practical implementations.
2. Fault Diagnostic Method
3. Implementation
- Step 1.
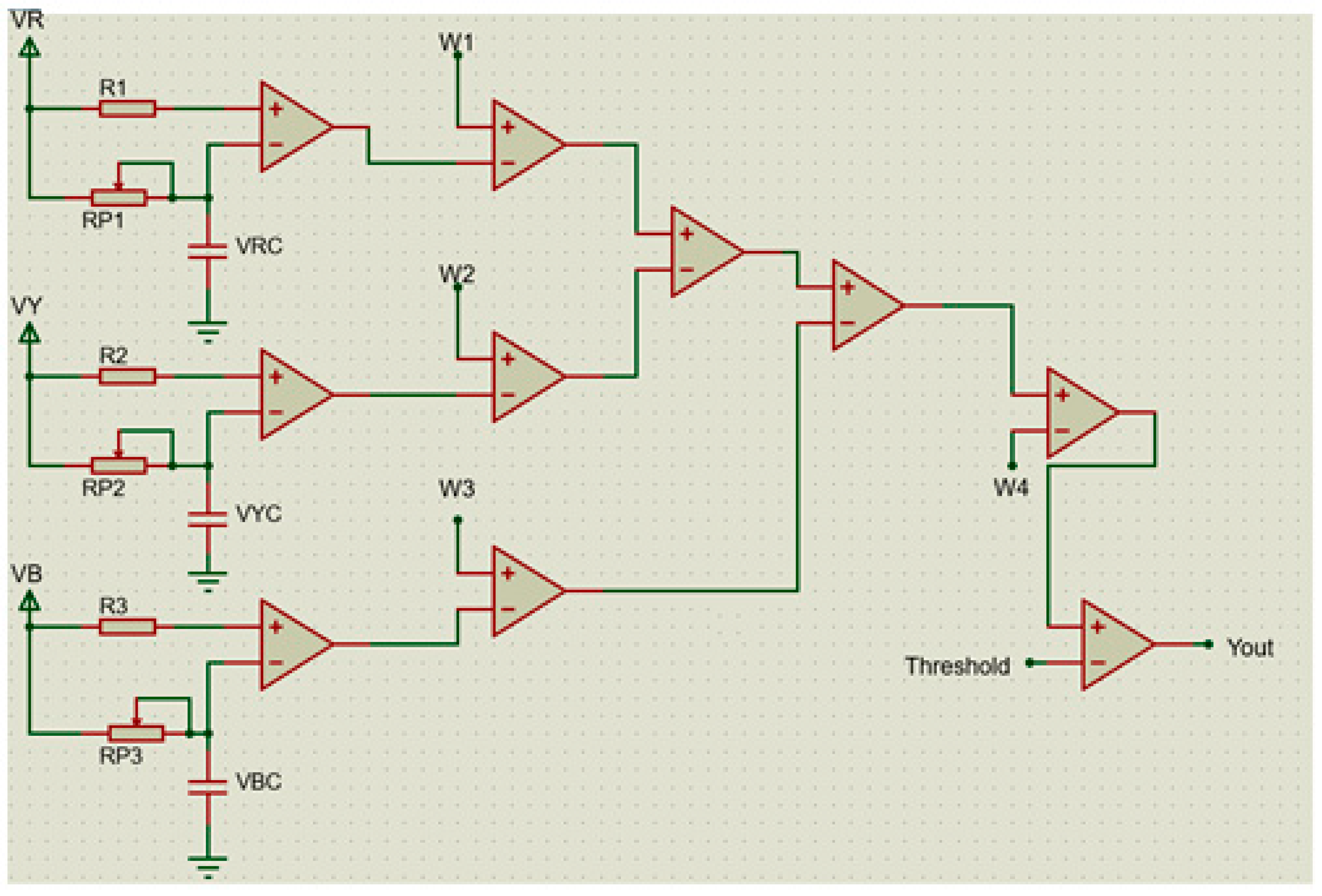
- Current normalization: For the diagnosis of faults under variable load conditions, 3ϕ currents are normalized within the range of ±1. The peak voltage Vm is stored as VRC, VYC and VBC in the capacitor, as shown in Figure 2. The input voltages VR, VY and VB are divided by VRC, VYC and VBC, respectively, and normalized like VRN, VYN and VBN within the range of ±1.
- Step 2.
- Data Collection: The 3ϕ current waveforms are collected under healthy and different faulty conditions. An open circuit fault in the VSI is introduced by the opening collector terminal. Such a facility is generated in the test box. A protection circuit is provided to avoid the damage to the IGBTs caused by the various faulty conditions. A data packet consists of an accumulation of samples for the angular frequency of 360° or one fundamental period of the current cycle. The training data set consists of 5000 samples for healthy and faulty conditions. Such samples are separately collected for six processing units, which are shown in Figure 1. The testing data set consists of 1250 samples.
- Step 3.
- Weight Calculations: The collected data samples for every processing unit are used to calculate the weights of that processing unit using MATLAB. For every processing unit weight () and bias () are calculated using Equations (5) and (6).
- Step 4.
- Multiplier: The normalized voltages, like VRN, VYN and VBN, are multiplied by their respective weights that are calculated in Step 4.
- Step 5.
- Adder: The result of the multiplication in step 4 is added using adder circuitry, as shown in Figure 2.
- Step 6.
- Comparator: The processed value in step 5 is converted into the decision of whether the IGBT is healthy or faulty. Such a decision is taken by comparing the processed value with the threshold value as given in Equation (7). By observing the waveforms in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, the threshold value (θ) is decided as 0.86. The threshold values, i.e., in this application of fault diagnosis the normalized signals, are used; hence, it is not required to change the threshold value (θ) as per load variation.
4. Results and Discussion
- A.
- Single switch open circuit fault (T1):
- B.
- Double switch OCF in the upper part of different legs (T1-T3):
- C.
- Double switch OCF in the same phase (T1 and T4):
- D.
- Double switch OCF in different legs (T1 and T6):
- E.
- OCF diagnosis under variable load conditions:
| Methods | Effectiveness | Resistivity | Detection Time | Implementation Effort | Tuning Effort | Threshold Dependence |
|---|---|---|---|---|---|---|
| Park’s Vector method [10] | Ambiguous at small currents | Poor at small currents | 20.00 ms | Medium | High | High |
| Phase current-based diagnostic algorithm [33] | Poor at small current | Poor | maximum of 63.5% | Low | High | High |
| Wavelet fuzzy Method [34] | Good if the fuzzy rules are carefully designed | Good | 75.19 ms | High | Medium | Low |
| Wavelet-Neural Network [35] | Diagnosis error < 5% | Good if NN is thoroughly trained | - | High due to NN training | Low | N/A |
| Hybrid Approach (Park’s Vector method and Wavelet-Neural N/w) [17] | Good | Good | 1 Cycle | High | - | N/A |
| Proposed HISNA system | Good | Good | Less than 1 Cycle | Low | - | N/A |
| Method | Accuracy (%) | Precision (%) | Recall (%) | False Positive Rate (%) |
|---|---|---|---|---|
| Wavelet-Fuzzy Method [36] | 92 | 90 | 89 | 7 |
| Wavelet-Neural Network [35] | 95 | 93 | 91 | 5 |
| Hybrid Approach (Park’s Vector + Wavelet-NN) [17] | 96 | 94 | 92 | 4 |
| Proposed HISNA System | 98 | 96 | 95 | 2 |
| Paper/Study | Processor or Controller Used | Remarks |
|---|---|---|
| FPGA Implementation of AI-Based Inverter IGBT Open Circuit Fault Diagnosis of IM Drives (2022) [30] | FPGA (Xilinx Zynq-7000 SoC) | FPGA-based implementation for AI-driven fault diagnosis, reducing reliance on DSPs. |
| Joint Fault Diagnosis of IGBT and Current Sensor in LLC Resonant Converter Module Based on Reduced Order Interval Sliding Mode Observer (2024) [31] | DSP (Texas Instruments TMS320F28335) | DSP-based implementation; requires additional processing time and power. |
| Two-Step Process-Based OCF Diagnosis for Three-Level NPC Converters (2025) [32] | DSP (Texas Instruments TMS320F28335) | Higher processing time, power consumption, complex implementation, limited scalability, making it less efficient for real-time, low-cost fault diagnosis. |
| Proposed Hardware-Based Approach | No DSP or Controller Used | Uses a single neuron-based processing circuit, eliminating DSP/controller dependency for cost and speed benefits. |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Ji, S. Benefits of High-voltage SiC-based Power Electronics in Medium-voltage Power-distribution Grids. Chin. J. Electr. Eng. 2021, 7, 1–26. [Google Scholar]
- Kumar, G.K.; Elangovan, D. Review on fault-diagnosis and fault-tolerance for DC-DC converters. IET Power Electron. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Jing, M.; Du, C.; Xing, X.; Chen, Z.; Wen, C. The switching decomposition pulse width modulation with reduced common mode voltage for reduced switch counts neutral point clamped inverter. IET Power Electron. 2023, 16, 612–630. [Google Scholar] [CrossRef]
- Adamczyk, M.; Orlowska-Kowalska, T. Post-Fault Direct Field-Oriented Control of Induction Motor Drive using Adaptive Virtual Current Sensor. IEEE Trans. Ind. Electron. 2021, 69, 3418–3427. [Google Scholar] [CrossRef]
- Chikondra, B.; Member, S.; Muduli, U.R.; Member, S. An Improved Open-Phase Fault-Tolerant DTC Technique for Five-Phase Induction Motor Drive Based on Virtual Vectors Assessment. IEEE Trans. Ind. Electron. 2021, 68, 4598–4609. [Google Scholar]
- Lu, Y.; Zhang, Y. Toward a Stakeholder Perspective on Safety Risk Factors of Metro Construction: A Social Network Analysis. Complexity 2020, 1–12. [Google Scholar] [CrossRef]
- Wang, B.; Member, S.; Li, Z.; Bai, Z.; Krein, P.T. A Voltage Vector Residual Estimation Method Based on Current Path Tracking for T-type Inverter Open-Circuit Fault Diagnosis. IEEE Trans. Power Electron. 2021, 36, 13460–13477. [Google Scholar] [CrossRef]
- Kumar, M. Characterization and Detection of Open Switch Faults for H-Bridge Inverter. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 16–19 December 2020; Volume 2. [Google Scholar]
- Wen, H.; Li, J.; Shi, H.; Hu, Y.; Yang, Y. Fault Diagnosis and Tolerant Control of Dual-Active-Bridge Converter with Triple-Phase Shift Control for Bidirectional EV Charging Systems. IEEE Trans. Transp. Electrif. 2021, 7, 287–303. [Google Scholar]
- Guo, H.; Guo, S.; Ph, D.; Xu, J. Power Switch Open-Circuit Fault Diagnosis of Six-Phase Fault Tolerant Permanent Magnet Synchronous Motor System under Normal and Fault-Tolerant Operation Conditions Using the Average Current Park’s Vector Approach. IEEE Trans. Power Electron. 2020, 36, 2641–2660. [Google Scholar] [CrossRef]
- Hu, K.; Member, S.; Liu, Z.; Member, S.; Yang, Y. Ensuring a Reliable Operation of Two-Level IGBT-Based Power Converters: A Review of Monitoring and Fault-Tolerant Approaches. IEEE Access 2020, 8, 89988–90022. [Google Scholar] [CrossRef]
- Wu, J.; Yue, X.; Li, W. Short Papers. IEEE/ASME Trans. Mechatron. 2016, 21, 576–583. [Google Scholar] [CrossRef]
- Xu, C.; Wu, Y.; Dai, S. What are the critical barriers to the development of hydrogen refueling stations in China? A modified fuzzy DEMATEL approach. Energy Policy 2020, 142, 111495. [Google Scholar] [CrossRef]
- Kong, J.W.; Wang, K.; Ieee, S.M.; Zhang, J.Y.; Zhang, H. Multiple Open-Switch Fault Diagnosis for Five-Phase Permanent Magnet Machine Utilizing Currents in Stationary Reference Frame. IEEE Trans. Energy Convers. 2020, 36, 314–324. [Google Scholar] [CrossRef]
- Yang, C.; Gui, W.; Chen, Z.; Zhang, J.; Peng, T.; Yang, C.; Karimi, H.R.; Ding, S.X. Voltage Difference Residual-Based Open-Circuit Fault Diagnosis Approach for Three-Level Converters in Electric Traction Systems. IEEE Trans. Power Electron. 2020, 35, 3012–3028. [Google Scholar] [CrossRef]
- Dhumale, R.B.; Lokhande, S.D. Diagnosis of multiple open switch faults in three phase voltage source inverter. J. Intell. Fuzzy Syst. 2016, 30, 2055–2065. [Google Scholar] [CrossRef]
- Dhumale, R.B.; Lokhande, S.D. Neural Network Fault Diagnosis of Voltage Source Inverter under variable load conditions at different frequencies. Meas. J. Int. Meas. Confed. 2016, 91, 565–575. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; He, M.; Zhou, Q.; Liu, X.; Meng, X. Fault-Tolerant Control of Dual Three-Phase PMSM Drives with Minimized Copper Loss. IEEE Trans. Power Electron. 2021, 36, 12938–12953. [Google Scholar] [CrossRef]
- Ibem, C.N.; Farrag, M.E.; Aboushady, A.A. New Fuzzy Logic Based Switch-Fault Diagnosis in Three Phase Inverters. In Proceedings of the 2020 55th International Universities Power Engineering Conference (UPEC), Torino, Italy, 1–4 September 2020. [Google Scholar] [CrossRef]
- Reyes-Malanche, J.A.; Villalobos-Pina, F.J.; Cabal-Yepez, E.; Alvarez-Salas, R.; Rodriguez-Donate, C. Open-Circuit Fault Diagnosis in Power Inverters through Currents Analysis in Time Domain. IEEE Trans. Instrum. Meas. 2021, 70, 3517512. [Google Scholar] [CrossRef]
- Du, B.; He, Y.; Zhang, Y. Open-circuit fault diagnosis of three-phase pwm rectifier using beetle antennae search algorithm optimized deep belief network. Electronics 2020, 9, 1570. [Google Scholar] [CrossRef]
- Cherif, B.D.E.; Bendiabdellah, A.; Tabbakh, M. An Automatic Diagnosis of an Inverter IGBT Open-Circuit Fault Based on HHT-ANN. Electr. Power Compon. Syst. 2020, 48, 589–602. [Google Scholar] [CrossRef]
- Chao, K.H.; Chang, L.Y.; Xu, F.Q. Three-Level T-Type Inverter Fault Diagnosis and Tolerant Control Using Single-Phase Line Voltage. IEEE Access 2020, 8, 44075–44086. [Google Scholar] [CrossRef]
- Yang, P.; Liu, J.; Dong, H.; Liu, C.; Li, X.; Jiang, B. Research on output power quality and fault characteristics of train traction inverter. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijón, Spain, 18 November–16 December 2020. [Google Scholar] [CrossRef]
- Bandyopadhyay, I.; Purkait, P.; Koley, C. Performance of a Classifier Based on Time-Domain Features for Incipient Fault Detection in Inverter Drives. IEEE Trans. Ind. Inform. 2019, 15, 3–14. [Google Scholar] [CrossRef]
- Wang, B.; Feng, X.; Wang, R. Open-Circuit Fault Diagnosis for Permanent Magnet Synchronous Motor Drives Based on Voltage Residual Analysis. Energies 2023, 16, 5722. [Google Scholar] [CrossRef]
- Liang, M.; Guan, Y.; Wang, F.; Wang, H.; Yang, L.; Deng, F.; Wang, Z. Research on compound fault diagnosis of inverter based on PCA current trace. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 715–719. [Google Scholar] [CrossRef]
- Lounici, Y.; Touati, Y.; Adjerid, S.; Touzout, W.; Benazzouz, D. Inverse bond graph model-based active fault tolerant control for health monitoring of electric vehicle path tracking. In Proceedings of the 2020 1st International Conference on Communications, Control Systems and Signal Processing (CCSSP), El Oued, Algeria, 16–17 May 2020; Volume 1, pp. 334–339. [Google Scholar] [CrossRef]
- Khater, F.; Abu El-Sebah, M.I.; Osama, M. Fault diagnostics in an inverter feeding an induction motor using fuzzy logic. J. Electr. Syst. Inf. Technol. 2017, 4, 10–17. [Google Scholar] [CrossRef]
- Rajeswaran, N.; Thangaraj, R.; Mihet-popa, L.; Vamsi, K.; Vajjala, K.; Özer, Ö. FPGA Implementation of AI-Based Inverter IGBT Open Circuit Fault Diagnosis of Induction Motor Drives. Micromachines 2022, 13, 663. [Google Scholar] [CrossRef]
- Zha, X.; Feng, W.; Zhang, X.; Cao, Z.; Chen, X. Joint Fault Diagnosis of IGBT and Current Sensor in LLC Resonant Converter Module Based on Reduced Order Interval Sliding Mode Observer. Sensors 2024, 24, 8077. [Google Scholar] [CrossRef]
- Zhang, W.; Guan, B.; Chang, Y. Two-Step Process-Based Open-Circuit Fault Diagnosis for Three-Level NPC Converters. Electronics 2025, 14, 542. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Y.; Yu, L.; Zhang, M.; Teffah, K. A new diagnostic algorithm for multiple IGBTs open circuit faults by the phase currents for power inverter in electric vehicles. Energies 2018, 11, 1508. [Google Scholar] [CrossRef]
- Kalong, T.; Jejawi, J.K. Fault Detection of 3-Phase VSI using Wavelet-Fuzzy Algorithm Terengganu Advanced Technical Institute (TATI), Jalan Panchor School of Mechatronics Engineering, Kolej Universiti Kejuruteraan Utara Malaysia Department of Electrical and Electronic Engineer. Am. J. Appl. Sci. 2006, 3, 1642–1648. [Google Scholar]
- Charfi, F.; Sellami, F.; Al-Haddad, K. Fault diagnostic in power system using wavelet transforms and neural networks. IEEE Int. Symp. Ind. Electron. 2006, 2, 1143–1148. [Google Scholar] [CrossRef]
- Dhumale, R.B.; Lokhande, S.D. Comparative Study of Fault Diagnostic Methods in Voltage Source Inverter Fed Three Phase Induction Motor Drive. IOP Conf. Ser. Mater. Sci. Eng. 2017, 197, 012006. [Google Scholar] [CrossRef]







| Parameters | Values |
|---|---|
| DC Link Electrolytic Capacitor | 5000 µF |
| Load Inductance | 10 mH |
| Load Resistor | 0.20 Ω |
| Output AC Voltage | 230 Vp |
| Output Current | 3.0630 Amp |
| Output Frequency | 40–70 Hz |
| Load Power (Variable) | 500 W–1.5 kW |
| Switch | WR | WY | WB | W0 | Cf (%) |
|---|---|---|---|---|---|
| T1 | 0.36 | 0.10 | 0.09 | 0.58 | 0.89 |
| T4 | 0.34 | 0.06 | 0.08 | 0.65 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dale, M.; Kamble, V.H.; Dhumale, R.B.; Nanthaamornphong, A. Open Switch Fault Diagnosis in Three-Phase Voltage Source Inverters Using Single Neuron Implementation. Processes 2025, 13, 1070. https://doi.org/10.3390/pr13041070
Dale M, Kamble VH, Dhumale RB, Nanthaamornphong A. Open Switch Fault Diagnosis in Three-Phase Voltage Source Inverters Using Single Neuron Implementation. Processes. 2025; 13(4):1070. https://doi.org/10.3390/pr13041070
Chicago/Turabian StyleDale, Manisha, Vaishali H. Kamble, R. B. Dhumale, and Aziz Nanthaamornphong. 2025. "Open Switch Fault Diagnosis in Three-Phase Voltage Source Inverters Using Single Neuron Implementation" Processes 13, no. 4: 1070. https://doi.org/10.3390/pr13041070
APA StyleDale, M., Kamble, V. H., Dhumale, R. B., & Nanthaamornphong, A. (2025). Open Switch Fault Diagnosis in Three-Phase Voltage Source Inverters Using Single Neuron Implementation. Processes, 13(4), 1070. https://doi.org/10.3390/pr13041070






