A Similarity Theory-Based Study on Natural Convection Condensation Boundary Layer Characteristics of Vertical Walls
Abstract
1. Introduction
2. Model Establishment
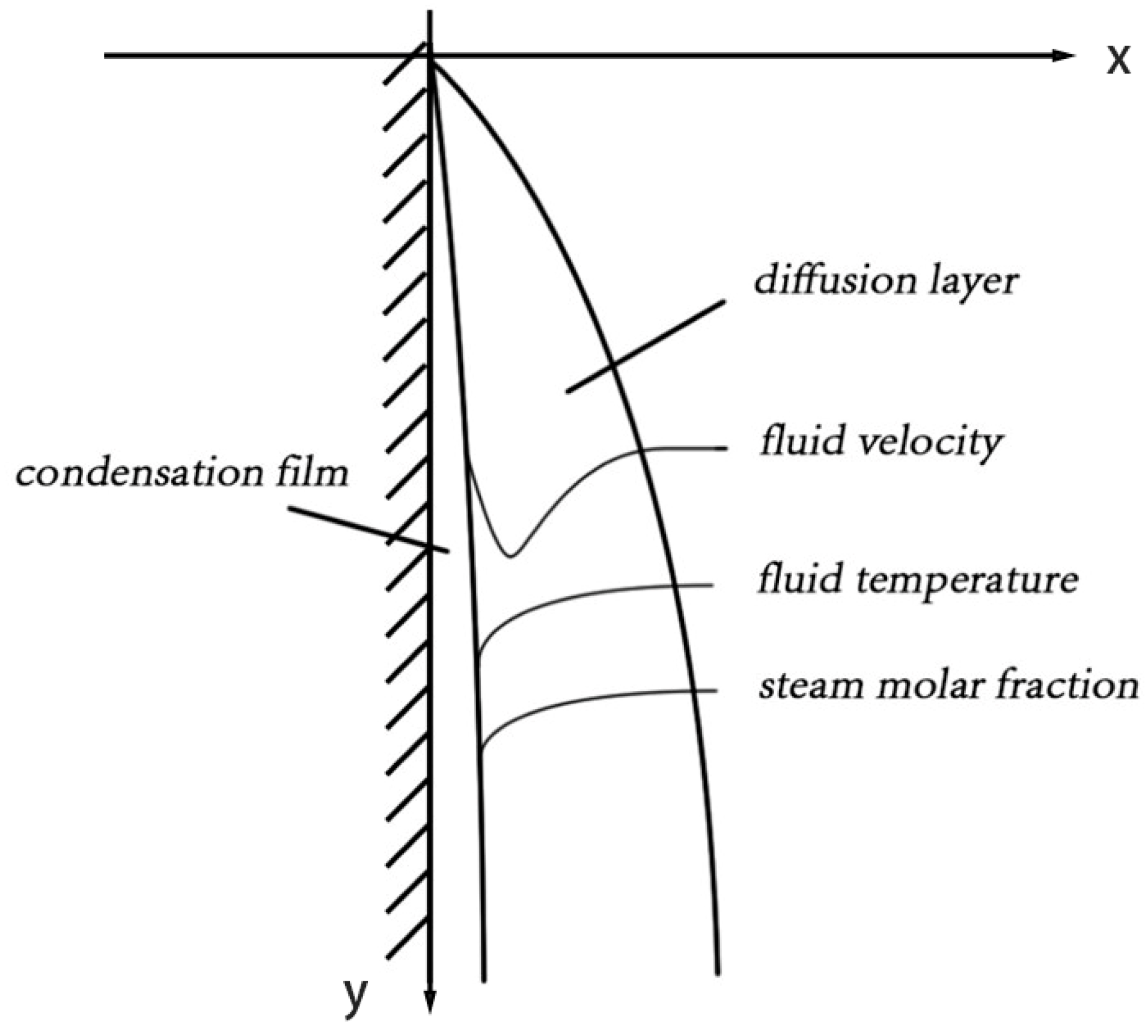
2.1. Basic Assumptions
2.2. Differential Equations of Convective Heat Transfer
2.3. Determination of Boundary Conditions
3. Model Solution and Verification
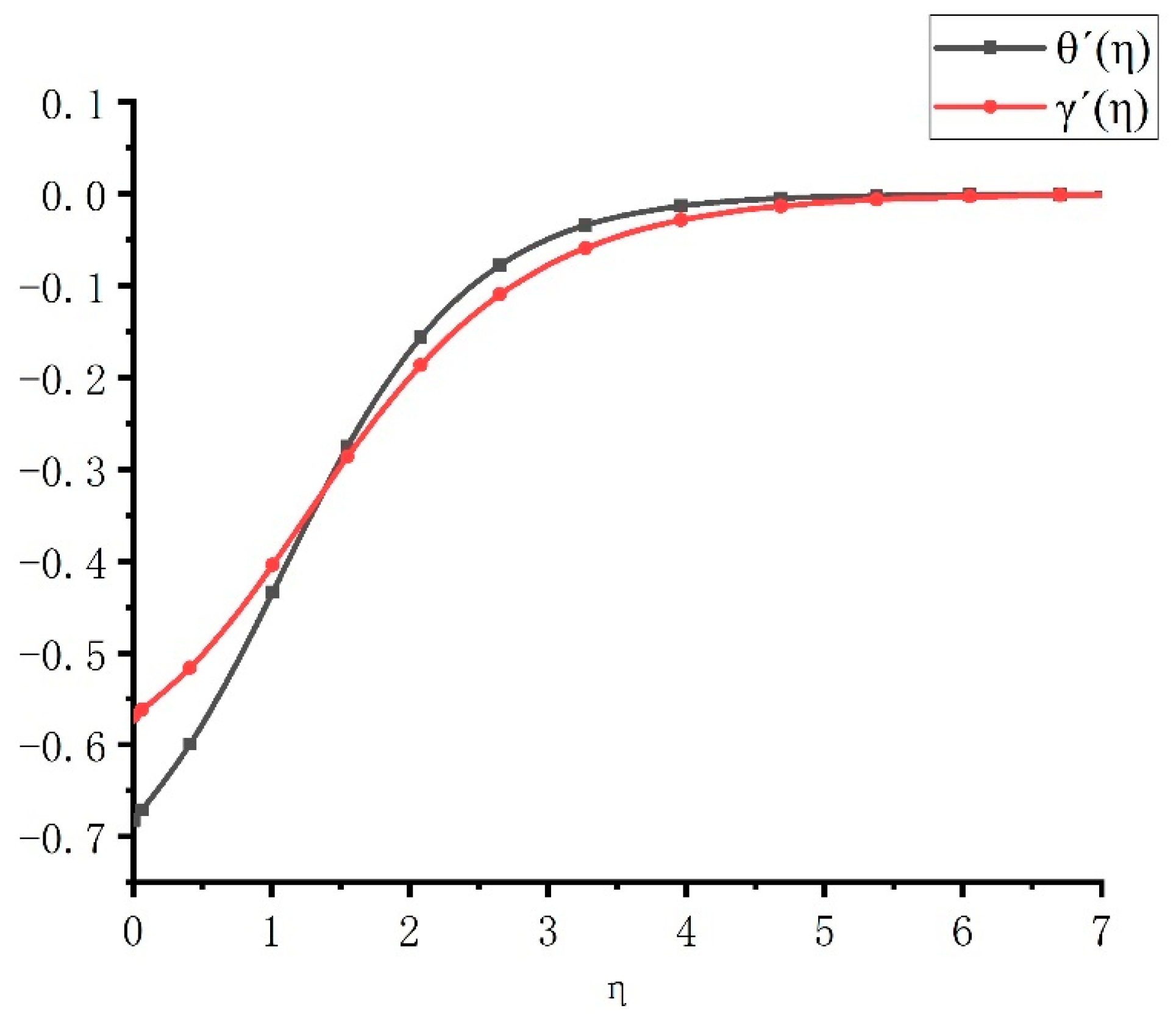
3.1. Model Solution
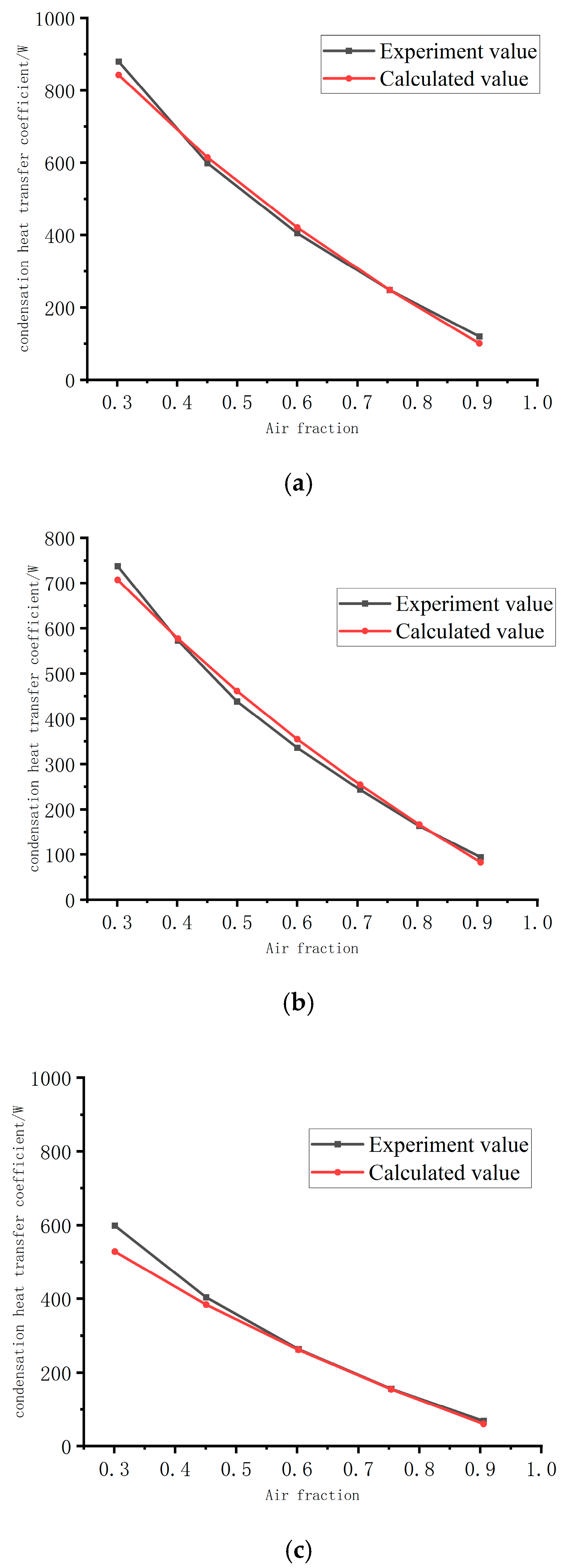
3.2. Experimental Verification
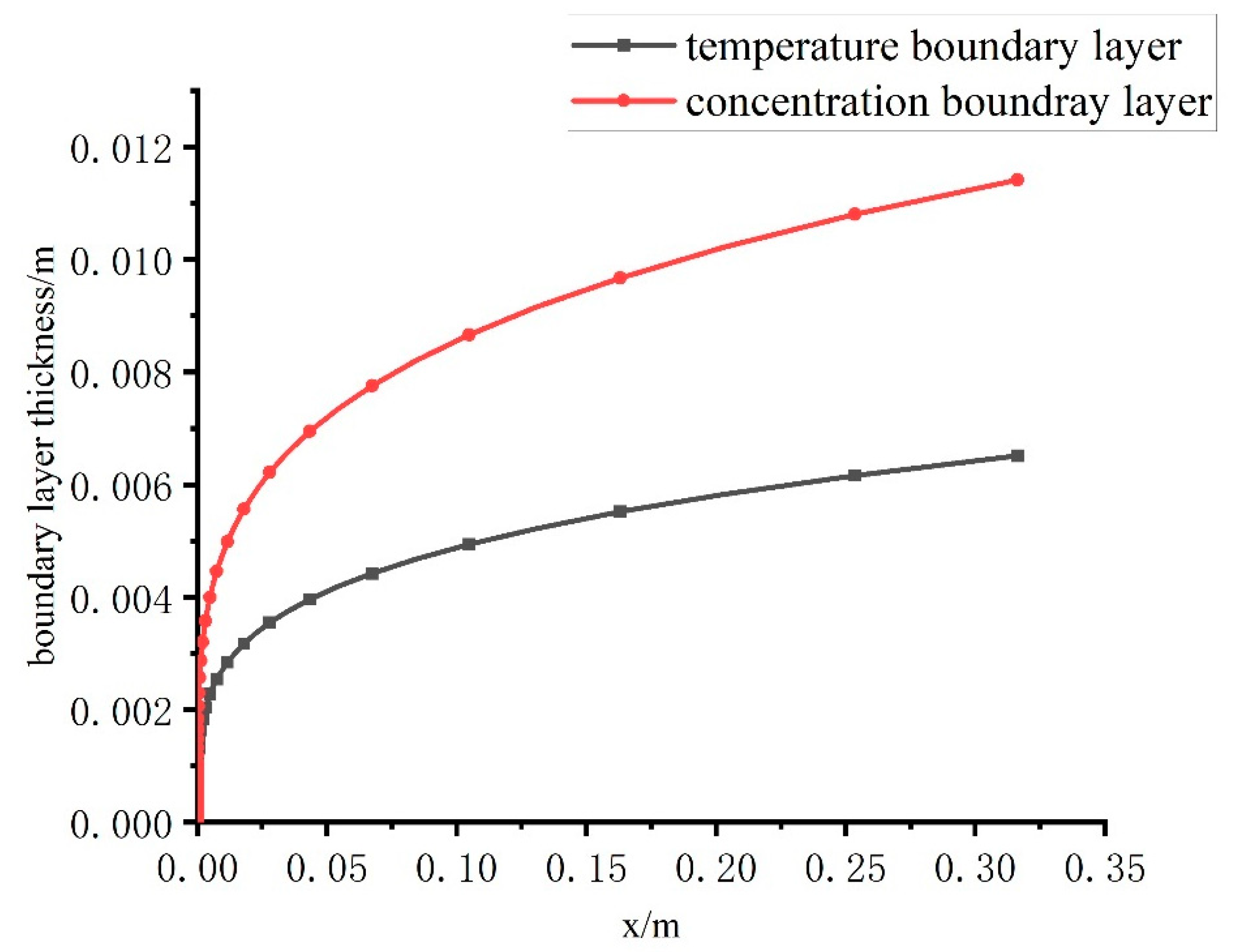
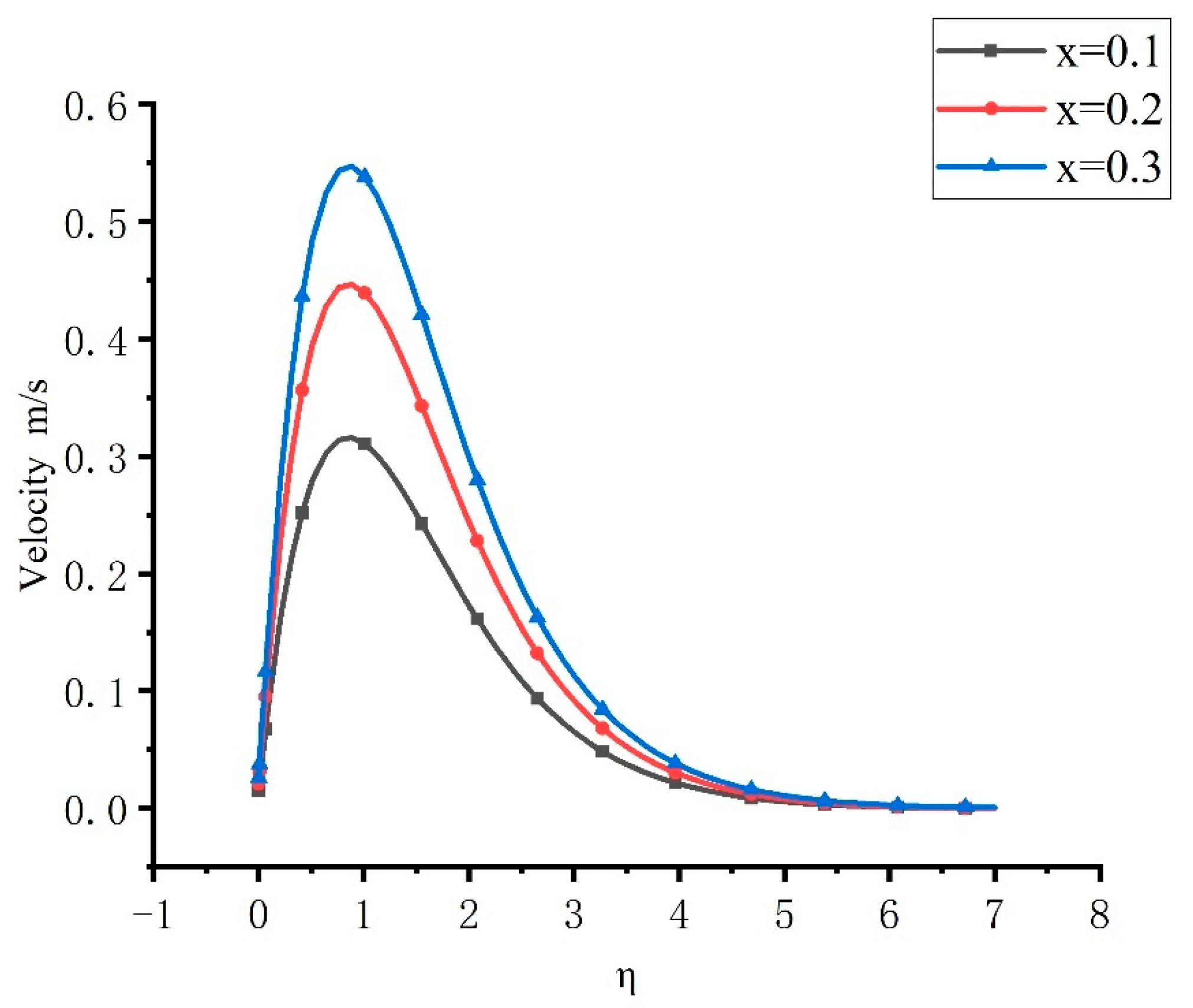
4. Analysis of Boundary-Layer Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Main Terms | ||
| Term | Definition | |
| Boundary Layer | Thin fluid region near walls with significant gradients in velocity, temperature, or concentration. | |
| Suction Effect | Enhanced mass transfer phenomenon where condensation-induced pressure drop drives gas–vapor mixtures toward walls. | |
| Liquid Film Drag Effect | Viscous interaction between condensate film flow and gas boundary layer, altering gas-phase velocity distribution. | |
| Similarity Theory | Analytical method converting partial differential equations to ordinary differential equations via similarity variables for boundary layer problems. | |
| Particle swarm optimization (PSO) | Bio-inspired optimization algorithm mimicking bird flocking behavior, used to solve differential equations with infinite boundary conditions. | |
| Mathematical Symbols | ||
| Symbol | Definition | |
| η | Similarity variable representing dimensionless normal coordinate in boundary layers. | |
| θ(η) | Dimensionless temperature profile: . | |
| γ(η) | Dimensionless concentration profile: . | |
| f(η) | Dimensionless stream function describing velocity boundary layer characteristics. | |
| Abbreviations | ||
| PSO | Particle swarm optimization | |
| Dimensionless Numbers | ||
| Symbol | Name | Physical Meaning |
| Gr | Grashof Number | Buoyancy-to-viscous force ratio, characterizing natural convection intensity: . |
| Pr | Prandtl Number | Momentum-to-thermal diffusivity ratio: Pr = ν/α, reflecting fluid heat transfer properties. |
| Sc | Schmidt Number | Momentum-to-mass diffusivity ratio: Sc = ν/D, reflecting fluid mass transfer characteristics. |
| Nu | Nusselt Number | Convective-to-conductive heat transfer ratio: . |
| Sh | Sherwood Number | Convective-to-diffusive mass transfer ratio: . |
References
- Wang, L.; Sundén, B.; Manglik, R.M. Enhanced Heat Transfer in Forced Convection Laminar Flow through Microfin Tubes. J. Heat Transf. 2021, 143, 071801. [Google Scholar]
- Xu, H.; Gu, H.; Sun, Z. Forced convection condensation of steam in the presence of multicomponent noncondensable gases inside a horizontal tube. Int. J. Heat Mass Transf. 2017, 104, 1110–1119. [Google Scholar]
- Muñoz-Cobo, J.L.; Chiva, S.; Corberán, J.M.; Escriva, A. Interaction between natural convection and condensation heat transfer in the passive containment cooling condensers of the ESBWR reactor. Ann. Nucl. Energy 1999, 26, 277–300. [Google Scholar]
- Senjaya, R.; Inoue, T. Effects of non-condensable gas on the performance of oscillating heat pipe, part I: Theoretical study. Appl. Therm. Eng. 2014, 73, 1387–1392. [Google Scholar]
- Kang, J.; Kim, H.; Bak, J.; Lim, S.-G.; Yun, B. Condensation of steam mixed with non-condensable gas on vertical heat exchanger tubes in circumstances with free convection. Int. J. Heat Mass Transf. 2021, 169, 120925. [Google Scholar]
- Kim, S.; Mudawar, I.; Kizito, J.P. Condensation heat transfer on downward-facing flat surfaces subjected to natural convection-driven flow. Int. J. Heat Mass Transf. 2022, 183, 122163. [Google Scholar]
- Zhang, T.-Y.; Mou, L.-W.; Zhang, J.-Y.; Fan, L.-W.; Li, J.-Q. A visualized study of enhanced steam condensation heat transfer on a honeycomb-like microporous superhydrophobic surface in the presence of a non-condensable gas. Int. J. Heat Mass Transf. 2020, 150, 119352. [Google Scholar]
- Uchida, H.; Oyama, A.; Togo, Y. Evaluation of Post-incident Cooling Systems of Light-Water Power Reactors. In Proceedings of the Third International Conference on the Peaceful Uses of Atomic Energy, Geneva, Switzerland, 31 August–9 September 1964; Volume 13, pp. 93–104. [Google Scholar]
- Tagami, T. Interim Report on Safety Assessments and Facilities Establishment Project for June 1965; Japanese Atomic Energy Research Agency: Tōkai Mura, Japan, 1965.
- Dehbi, A.A. The Effects of Noncondensable Gases on Steam Condensation Under Turbulent Natural Convection Conditions; Massachusetts Institute of Technology: Cambridge, MA, USA, 1991. [Google Scholar]
- Seungmin, O.; Shripad, T. Revankar. Experimental and theoretical investigation of film condensation with noncondensable gas. Int. J. Heat Mass Transf. 2006, 49, 2523–2534. [Google Scholar]
- Lee, K.-Y.; Kim, M.H. Experimental and empirical study of steam condensation heat transfer with a noncondensable gas in a small-diameter vertical tube. Nucl. Eng. Des. 2008, 238, 207–216. [Google Scholar]
- Su, J.; Sun, Z.; Fan, G.; Ding, M. Experimental study of the effect of non-condensable gases on steam condensation over a vertical tube external surface. Nucl. Eng. Des. 2013, 262, 201–208. [Google Scholar] [CrossRef]
- Gu, H.F.; Chen, Q.; Wang, H.J.; Zhang, H.Q. Condensation of a hydrocarbon in the presence of a non-condensable gas: Heat and mass transfer. Appl. Therm. Eng. 2015, 91, 938–945. [Google Scholar]
- Chen, J.; Gao, P.; Gu, H.; Chen, Y.; Xinnuo, E.; Yu, J. Experimental study of the natural deposition of submicron aerosols on the surface of a vertical circular tube with non-condensable gases. Nucl. Eng. Des. 2024, 417, 112863. [Google Scholar] [CrossRef]
- Lee, J.; Park, H.; Kim, M.H. Modified heat and mass transfer analogy for turbulent condensation with non-condensable gases under high-pressure conditions. Int. J. Heat Mass Transf. 2021, 165, 120678. [Google Scholar]
- Kim, J.-W.; Lee, Y.-G.; Ahn, H.-K.; Park, G.-C. Condensation heat transfer characteristic in the presence of noncondensable gas on natural convection at high pressure. Nucl. Eng. Des. 2009, 239, 688–698. [Google Scholar]
- Peterson, P.F. Theoretical basis for the Uchida correlation for condensation in reactor containments. Nucl. Eng. Des. 1996, 162, 301–306. [Google Scholar]
- Liao, Y.; Vierow, K. A Generalized Diffusion Layer Model for Condensation of Vapor with Noncondensable Gases. J. Heat Transf. 2007, 129, 988–994. [Google Scholar]
- Hwang, J.-H.; Jerng, D.-W. A condensation heat transfer model with light gas effects in non-condensable gas mixtures. Int. Commun. Heat Mass Transf. 2022, 130, 105765. [Google Scholar]
- Lu, J.; Cao, H.; Li, J. Diffusion layer model for condensation of vapor with the presence of noncondensable gas under natural convective condensation. Prog. Nucl. Energy 2020, 118, 103078. [Google Scholar]
- Sparrow, E.M.; Lin, S.H. Condensation Heat Transfer in the Presence of a Noncondensable Gas. J. Heat Transf. 1964, 86, 430–436. [Google Scholar]
- Oh, S.; Revankar, S.T. Quantitative analysis of gas-side resistance dominance in steam condensation with air under natural convection. Appl. Therm. Eng. 2019, 157, 113696. [Google Scholar]
- Zhang, Y.; Liu, C.; Chen, Q. Dominance of gas-phase resistance in condensation with non-condensable gases: A CFD study based on species transport model. Int. J. Heat Mass Transf. 2020, 153, 119563. [Google Scholar]
- Welty, J.R.; Charles, E.W.; Robert, E.W.; Gregory, L.R. Fundamentals of Momentum, Heat, and Mass Transfer, 4th ed; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Peterson, P.F. Diffusion Layer Theory for Turbulent Vapor Condensation with Non-condensable Gases. J. Heat Transf. 1993, 115, 998–1003. [Google Scholar] [CrossRef]

| Researcher and Reference | Solution Method | Considered Factors | Boundary Condition Treatment | Solution Technique |
|---|---|---|---|---|
| Sparrow & Lin (1964) [22] | Similarity theory | Temperature gradient driven | No suction effect | Analytical integration |
| Peterson (1996) [18] | Heat-mass transfer analogy | Dominant concentration diffusion | Simplified suction velocity | Finite difference |
| Liao et al. (2007) [19] | Integral approximation | Liquid film drag effect | Fixed interface velocity | Iterative method |
| Lu (2020) [21] | Modified similarity solution | Suction effect correction | Empirical correlations | Shooting method |
| This work | Similarity theory + PSO algorithm | Dual driving forces (temperature and concentration), coupled suction–drag effects | Asymmetric boundary conditions | Particle swarm optimization |
| Condition | Boundary Conditions |
|---|---|
| When η = 0 | f = f′ = 0, θ = 1, γ = 1 |
| When | , , |
| Condition | Boundary Conditions |
|---|---|
| When η = 0 | f = f (0), f′ = f ′(0), θ = 1, γ = 1 |
| When η→∞ | f′ = 0, θ = 0, γ = 0 |
| Data Point | Sub-Cooling (°C) | Air-Mass Fraction | Heat Transfer Coefficient (Experimental Value) [W/(m2·K)] | Calculated Relative Error |
|---|---|---|---|---|
| 1 | 14.4 | 0.306 | 1041 | 1.1% |
| 2 | 20.4 | 0.521 | 550 | 2.13% |
| 3 | 26.5 | 0.349 | 801 | 1.6% |
| 4 | 31.1 | 0.618 | 323 | −2.2% |
| 5 | 36 | 0.862 | 148 | −15.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Chen, Y.; Gu, H.; Zhang, Y.; Wang, W.; Xiao, H. A Similarity Theory-Based Study on Natural Convection Condensation Boundary Layer Characteristics of Vertical Walls. Processes 2025, 13, 1050. https://doi.org/10.3390/pr13041050
Liu J, Chen Y, Gu H, Zhang Y, Wang W, Xiao H. A Similarity Theory-Based Study on Natural Convection Condensation Boundary Layer Characteristics of Vertical Walls. Processes. 2025; 13(4):1050. https://doi.org/10.3390/pr13041050
Chicago/Turabian StyleLiu, Jialei, Yuqing Chen, Haifeng Gu, Yinxing Zhang, Wei Wang, and Hongguang Xiao. 2025. "A Similarity Theory-Based Study on Natural Convection Condensation Boundary Layer Characteristics of Vertical Walls" Processes 13, no. 4: 1050. https://doi.org/10.3390/pr13041050
APA StyleLiu, J., Chen, Y., Gu, H., Zhang, Y., Wang, W., & Xiao, H. (2025). A Similarity Theory-Based Study on Natural Convection Condensation Boundary Layer Characteristics of Vertical Walls. Processes, 13(4), 1050. https://doi.org/10.3390/pr13041050





