Enhanced Prediction of Muscle Activity Using Wearable Textile Stretch Sensors and Multi-Layer Perceptron
Abstract
1. Introduction
2. Experiment Method
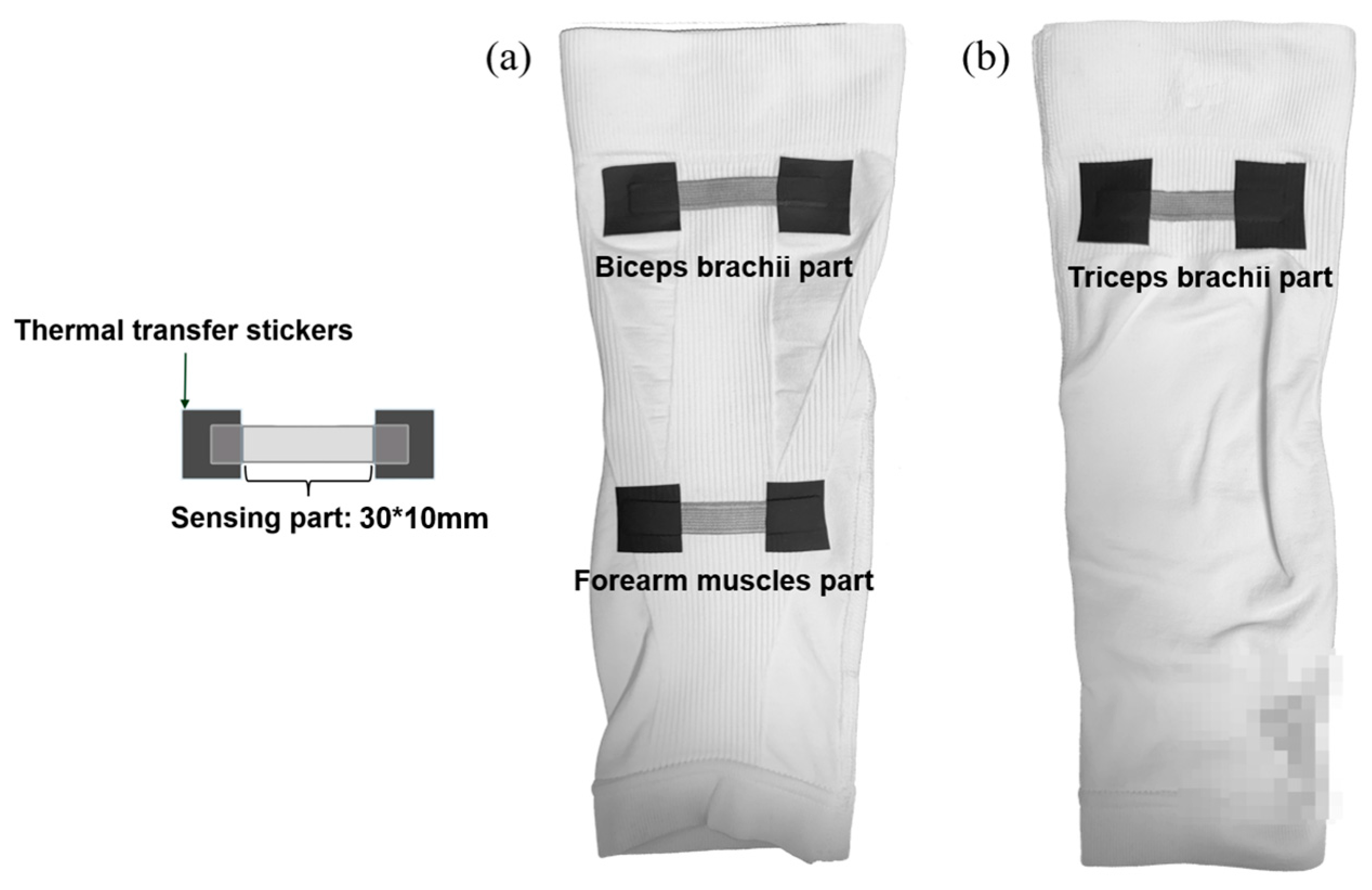
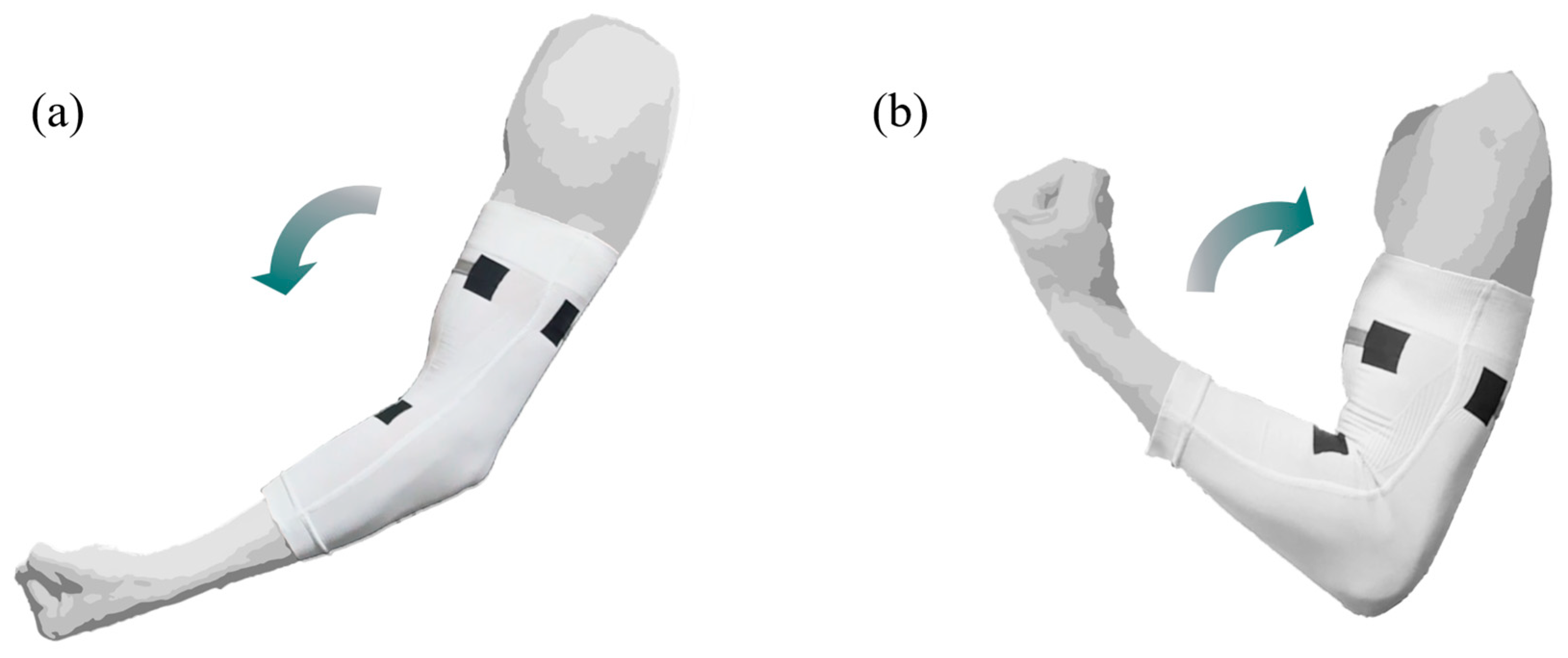
2.1. Fabrication of Textile Stretch Sensors and Application to Arm Sleeve
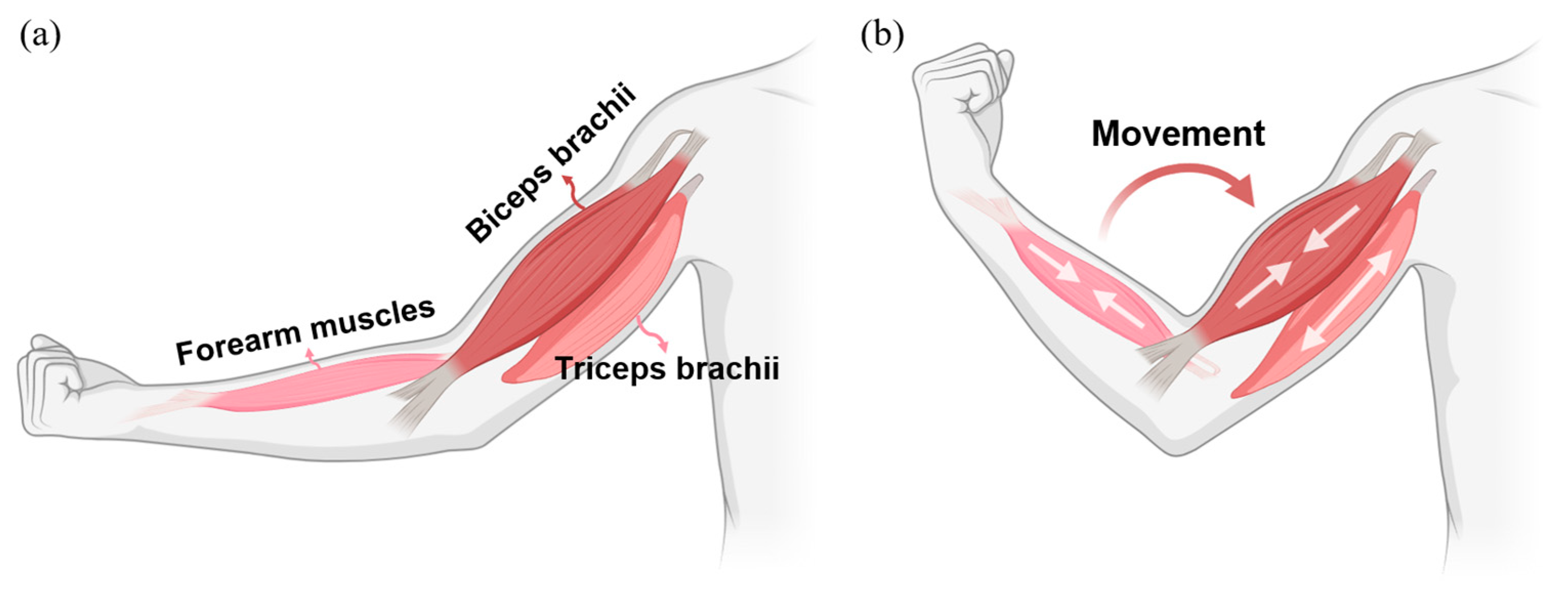
2.2. sEMG Data Collection
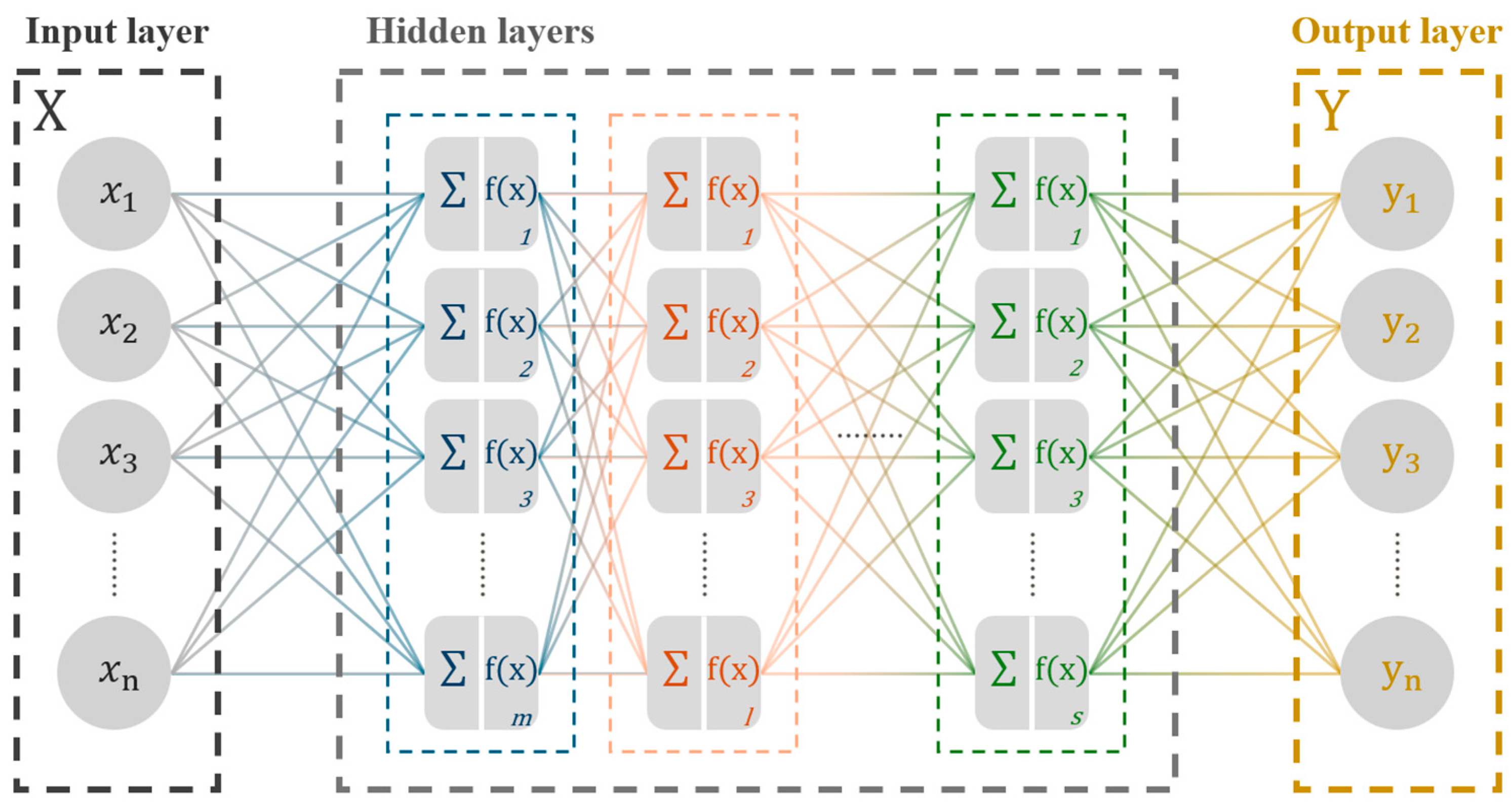
2.3. MLP Learning Process with Causal Relationship Data
2.3.1. First Stage: Effect of Low-Pass FIR Filter
2.3.2. Second Stage: Integration with Tensile Velocity Data
2.3.3. Third Stage: Expanding Dataset for Mapping Accuracy Comparison
3. Results
3.1. Textile Stretch Sensor Data Results
3.2. sEMG Data Results
3.3. MLP: Mapping Accuracy Results
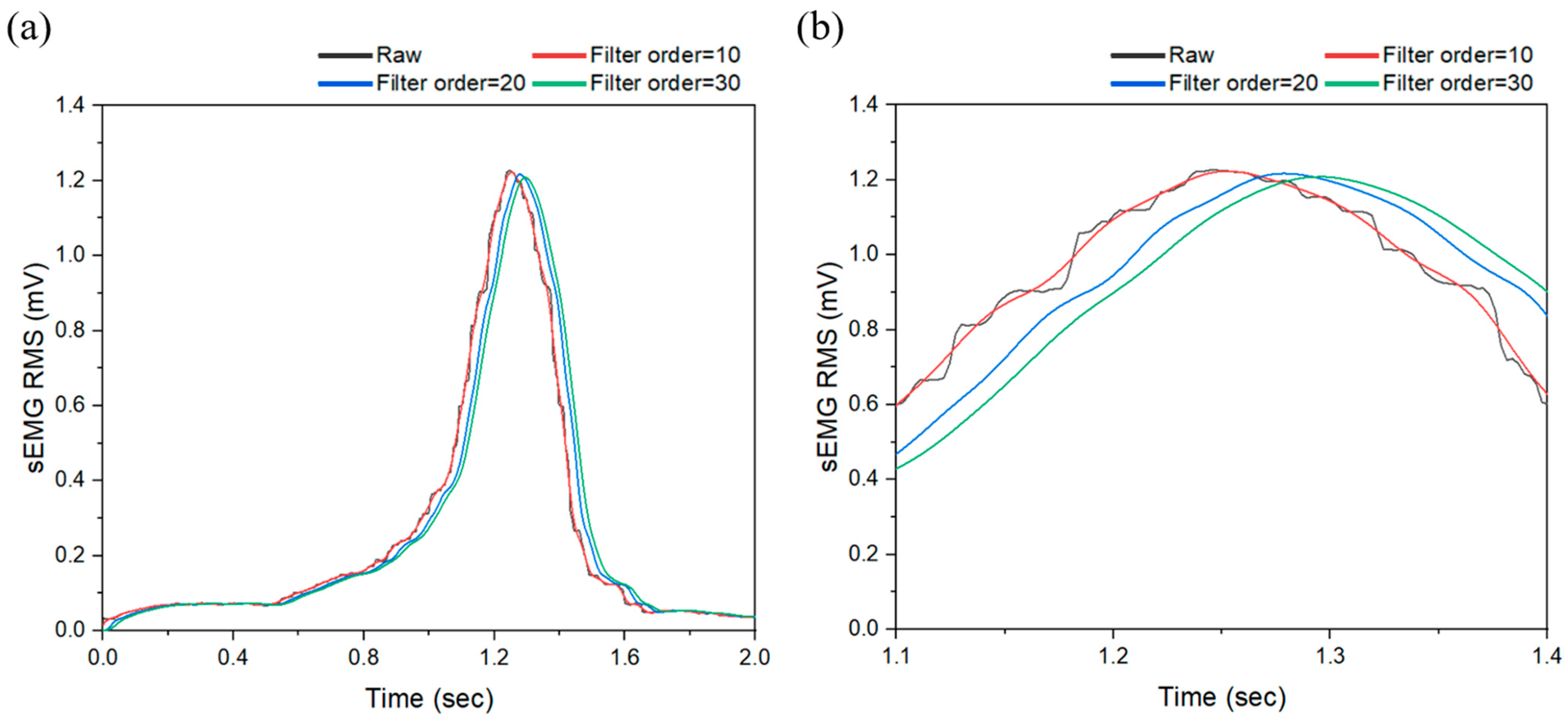
3.3.1. Result of First Stage: Low-Pass FIR Filter Application
3.3.2. Result of Second Stage: Effect of Tensile Velocity Data
3.3.3. Result of Third Stage: Effect of Multi-Muscle Data Integration
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luczak, T.; Saucier, D.; Burch, V.R.F.; Ball, J.E.; Chander, H.; Knight, A.; Wei, P.; Iftekhar, T. Closing the wearable gap: Mobile systems for kinematic signal monitoring of the foot and ankle. Electronics 2018, 7, 117. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.C. Wearable sensors for human activity monitoring: A review. IEEE Sens. J. 2014, 15, 1321–1330. [Google Scholar]
- Korhonen, I.; Parkka, J.; Van Gils, M. Health monitoring in the home of the future. IEEE Eng. Med. Biol. Mag. 2003, 22, 66–73. [Google Scholar]
- Trung, T.Q.; Lee, N.E. Flexible and stretchable physical sensor integrated platforms for wearable human-activity monitoringand personal healthcare. Adv. Mater. 2016, 28, 4338–4372. [Google Scholar] [PubMed]
- Yao, S.; Swetha, P.; Zhu, Y. Nanomaterial-enabled wearable sensors for healthcare. Adv. Healthc. Mater. 2018, 7, 1700889. [Google Scholar]
- Wang, M.; Wang, T.; Luo, Y.; He, K.; Pan, L.; Li, Z.; Cui, Z.; Liu, Z.; Tu, J.; Chen, X. Fusing stretchable sensing technology with machine learning for human–machine interfaces. Adv. Funct. Mater. 2021, 31, 2008807. [Google Scholar]
- Kwon, S.H.; Dong, L. Flexible sensors and machine learning for heart monitoring. Nano Energy 2022, 102, 107632. [Google Scholar]
- Liao, X.; Song, W.; Zhang, X.; Huang, H.; Wang, Y.; Zheng, Y. Directly printed wearable electronic sensing textiles towards human–machine interfaces. J. Mater. Chem. C 2018, 6, 12841–12848. [Google Scholar]
- Chun, S.; Kim, J. Textile smart sensors based on a biomechanical and multi-layer perceptron hybrid method. J. Ind. Text. 2023, 53, 15280837231208226. [Google Scholar]
- Shen, C.-L.; Kao, T.; Huang, C.-t.; Lee, J.-h. Wearable band using a fabric-based sensor for exercise ecg monitoring. In Proceedings of the 2006 10th IEEE International Symposium on Wearable Computers, Montreux, Switzerland, 11–14 October 2006; pp. 143–144. [Google Scholar]
- Thu, N.T.H.; Han, D.S. An Investigation on Deep Learning-Based Activity Recognition Using IMUs and Stretch Sensors. In Proceedings of the 2022 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Republic of Korea, 21–24 February 2022; pp. 377–382. [Google Scholar]
- Siu, H.C.; Arenas, A.M.; Sun, T.; Stirling, L.A. Implementation of a surface electromyography-based upper extremity exoskeleton controller using learning from demonstration. Sensors 2018, 18, 467. [Google Scholar] [CrossRef]
- Baek, J.-Y.; An, J.-H.; Choi, J.-M.; Park, K.-S.; Lee, S.-H. Flexible polymeric dry electrodes for the long-term monitoring of ECG. Sens. Actuators A Phys. 2008, 143, 423–429. [Google Scholar]
- Wang, C.; Cai, M.; Hao, Z.; Nie, S.; Liu, C.; Du, H.; Wang, J.; Chen, W.; Song, J. Stretchable, multifunctional epidermal sensor patch for surface electromyography and strain measurements. Adv. Intell. Syst. 2021, 3, 2100031. [Google Scholar]
- Yamagami, M.; Peters, K.M.; Milovanovic, I.; Kuang, I.; Yang, Z.; Lu, N.; Steele, K.M. Assessment of dry epidermal electrodes for long-term electromyography measurements. Sensors 2018, 18, 1269. [Google Scholar] [CrossRef] [PubMed]
- Merlo, A.; Bò, M.C.; Campanini, I. Electrode size and placement for surface emg bipolar detection from the brachioradialis muscle: A scoping review. Sensors 2021, 21, 7322. [Google Scholar] [CrossRef] [PubMed]
- Etana, B.B.; Malengier, B.; Timothy, K.; Wojciech, S.; Krishnamoorthy, J.; Van Langenhove, L. A review on the recent developments in design and integration of electromyography textile electrodes for biosignal monitoring. J. Ind. Text. 2023, 53, 15280837231175062. [Google Scholar]
- Chun, S.; Kim, S.; Kim, J. Human arm workout classification by arm sleeve device based on machine learning algorithms. Sensors 2023, 23, 3106. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Lahmiri, S. A comparative study of backpropagation algorithms in financial prediction. Int. J. Comput. Sci. Eng. Appl. (IJCSEA) 2011, 1, 15–21. [Google Scholar]
- Liu, J.; Zhang, J.; Zhao, Z.; Liu, Y.; Tam, W.C.; Zheng, Z.; Wang, X.; Li, Y.; Liu, Z.; Li, Y. A negative-response strain sensor towards wearable microclimate changes for body area sensing networks. Chem. Eng. J. 2023, 459, 141628. [Google Scholar]
- Zhang, J.; Liu, J.; Zhao, Z.; Sun, W.; Zhao, G.; Liu, J.; Xu, J.; Li, Y.; Liu, Z.; Li, Y. Calotropis gigantea fiber-based sensitivity-tunable strain sensors with insensitive response to wearable microclimate changes. Adv. Fiber Mater. 2023, 5, 1378–1391. [Google Scholar]
- Webster, J.B.; Darter, B.J. Principles of normal and pathologic gait. In Atlas of Orthoses and Assistive Devices; Elsevier: Amsterdam, The Netherlands, 2019; pp. 49–62.e41. [Google Scholar]
- Rafiq, M.; Bugmann, G.; Easterbrook, D. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar]
- Gavin, H.P. The Levenberg-Marquardt algorithm for nonlinear least squares curve-fitting problems. Dep. Civ. Environ. Eng. Duke Univ. August 2019, 3, 1–23. [Google Scholar]
- Goodfellow, I. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 196. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Garimella, R.M. Finite impulse response (FIR) filter model of synapses: Associated neural networks. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 25–27 August 2008; pp. 370–374. [Google Scholar]
- Kaur, H.; Dhaliwal, B. Design of Low Pass FIR Filter Using Artificial NeuralNetwork. Int. J. Inf. Electron. Eng. 2013, 3, 204. [Google Scholar]
- Delao, K.O. Improving EMG Movement Classification Accuracy with Relative Entropy; California State University: Los Angeles, CA, USA, 2020. [Google Scholar]
- Atzori, M.; Gijsberts, A.; Kuzborskij, I.; Elsig, S.; Hager, A.-G.M.; Deriaz, O.; Castellini, C.; Müller, H.; Caputo, B. Characterization of a benchmark database for myoelectric movement classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 73–83. [Google Scholar]
- d’Avella, A.; Saltiel, P.; Bizzi, E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 2003, 6, 300–308. [Google Scholar]
- Sanger, T.D. Human arm movements described by a low-dimensional superposition of principal components. J. Neurosci. 2000, 20, 1066–1072. [Google Scholar]


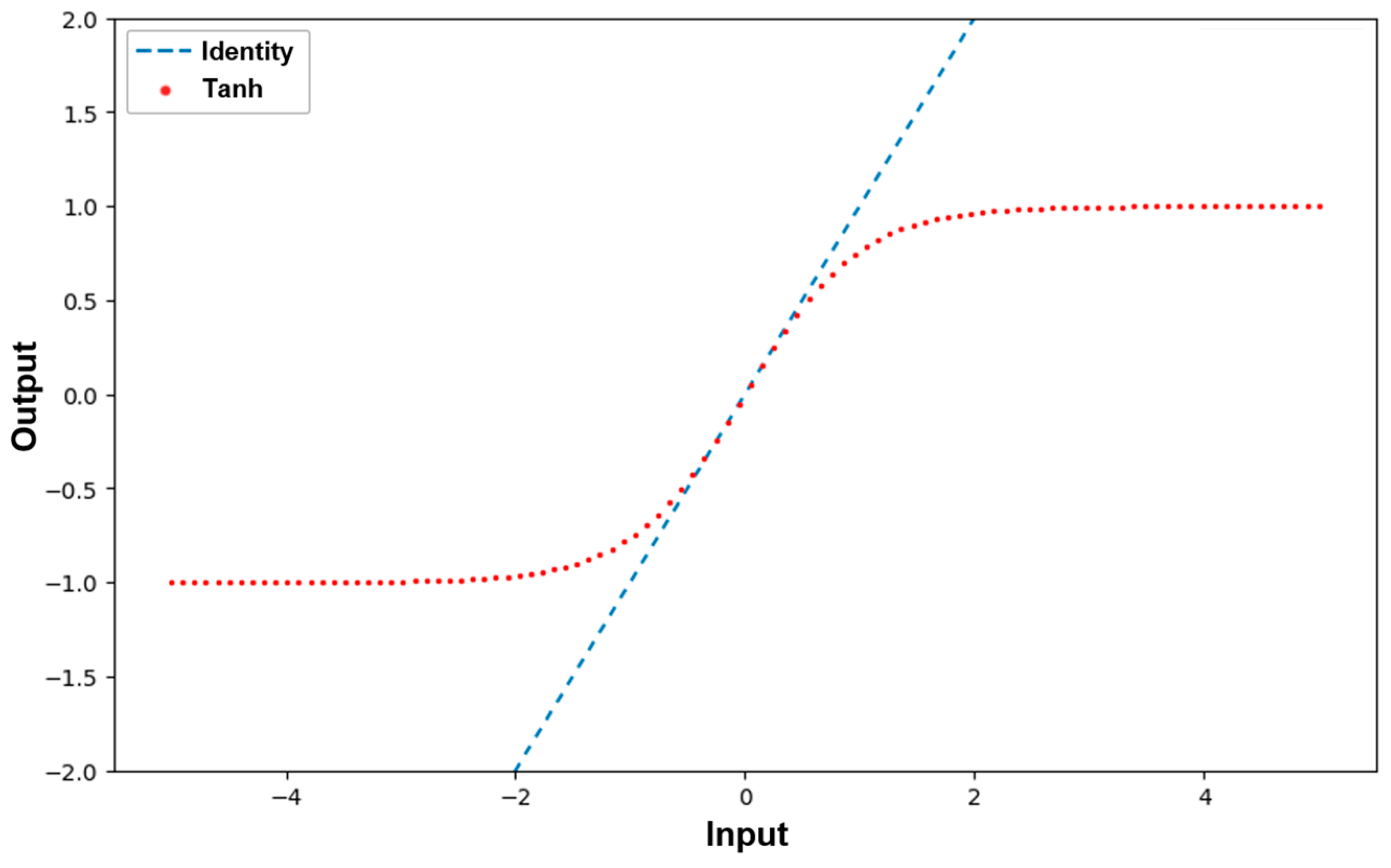
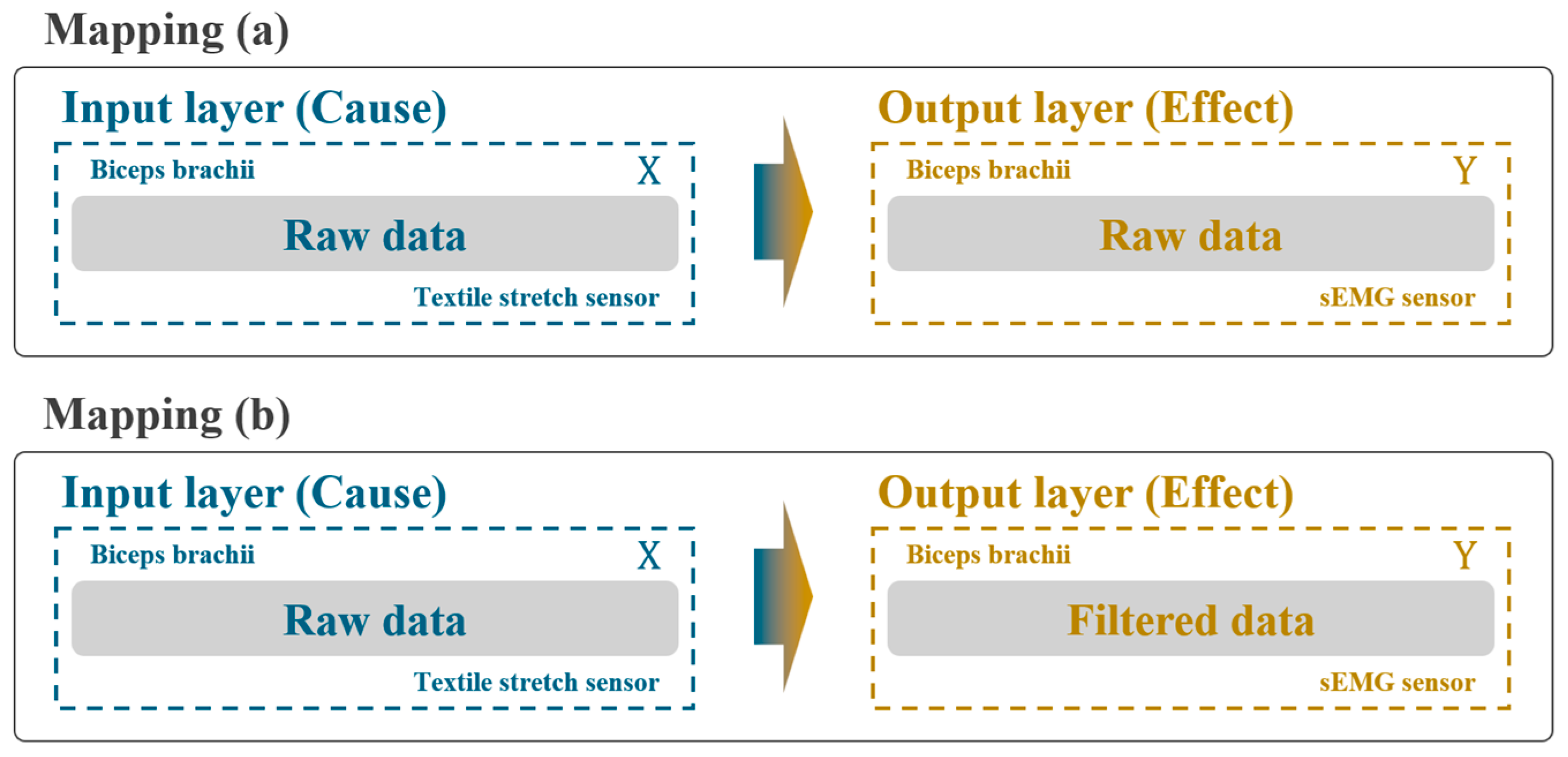
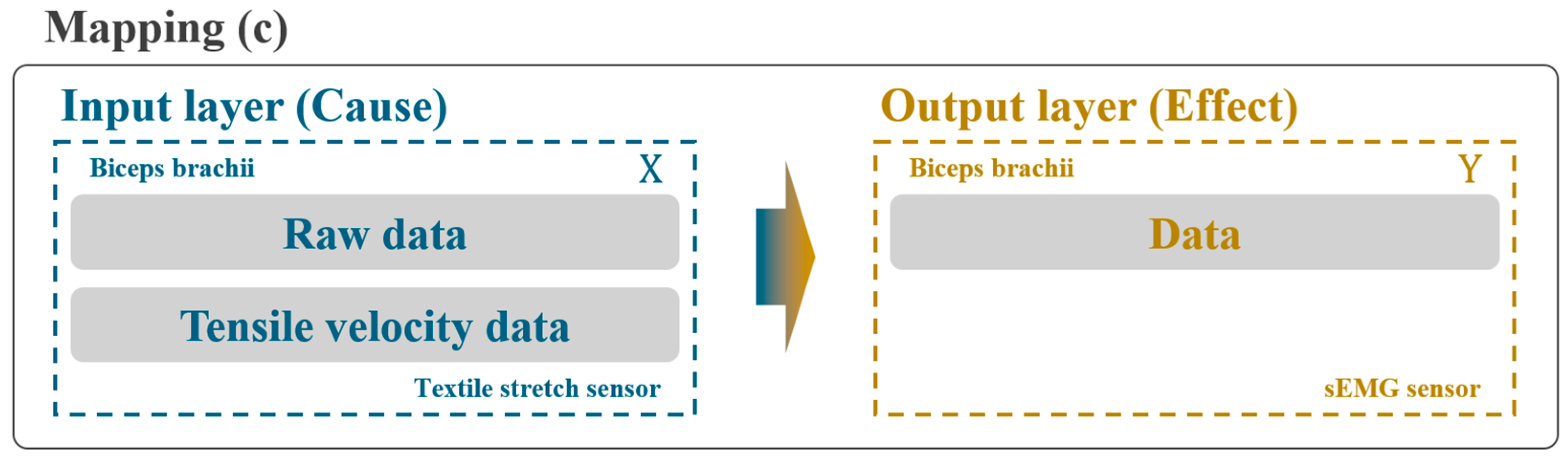
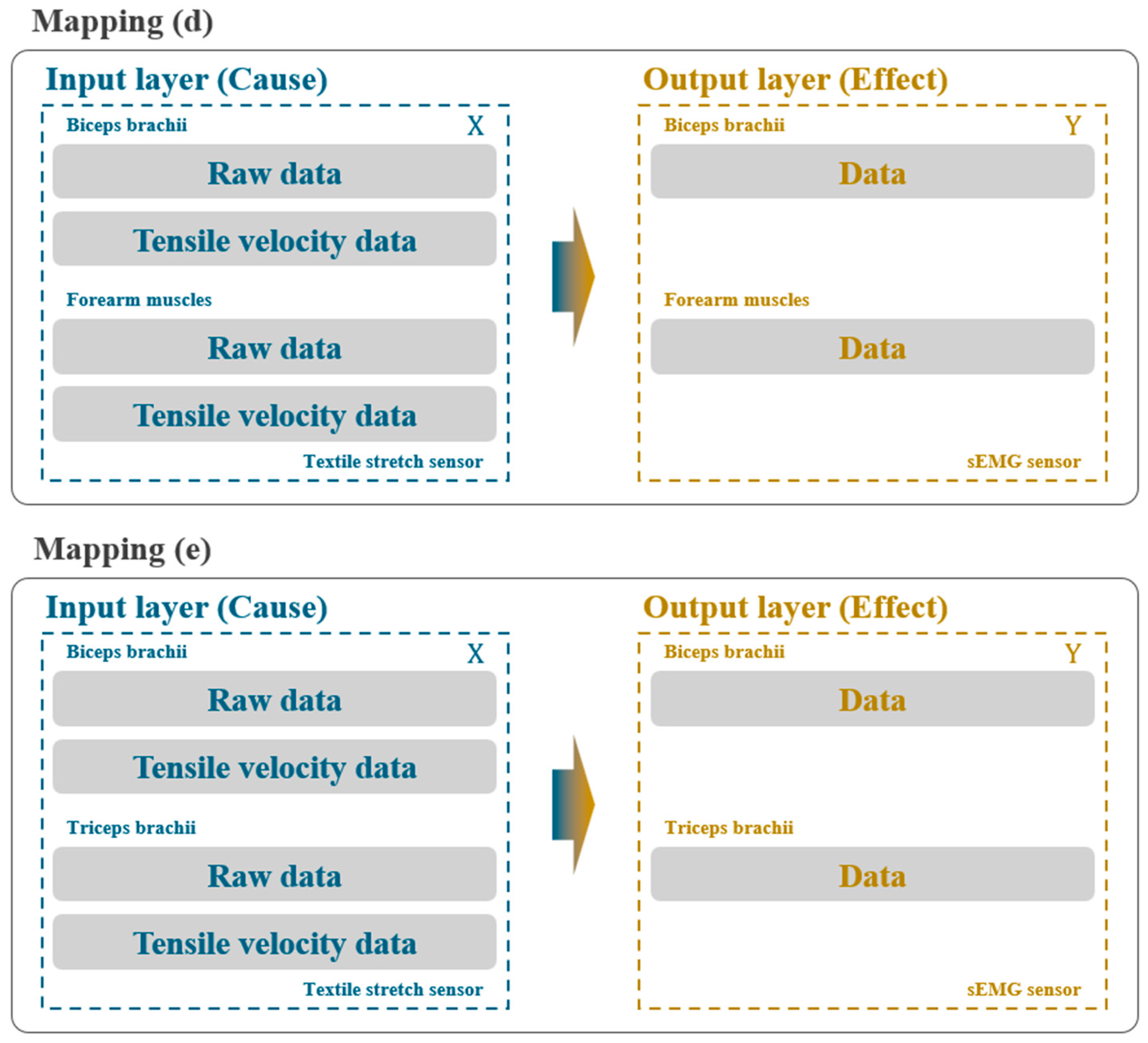



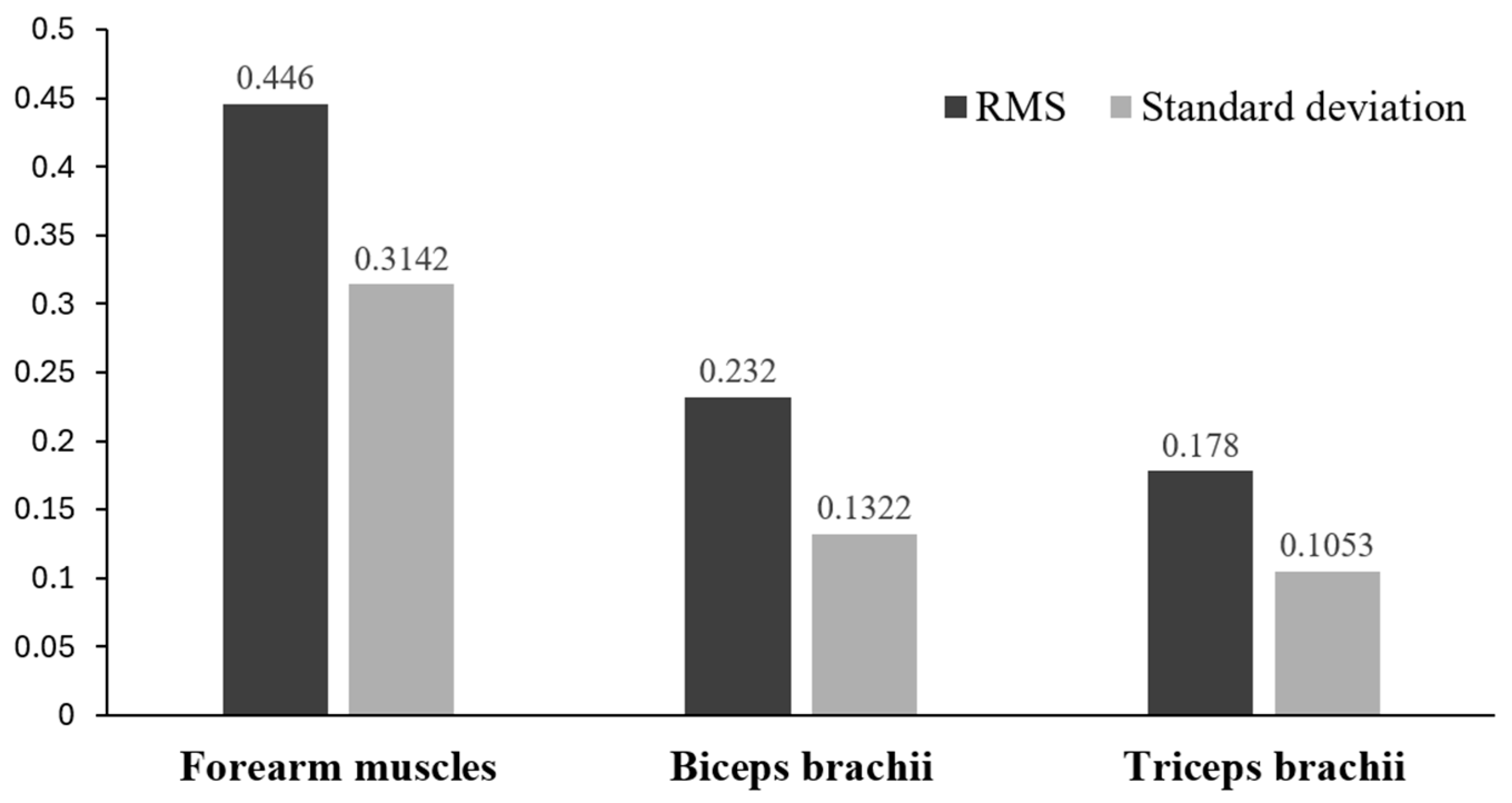
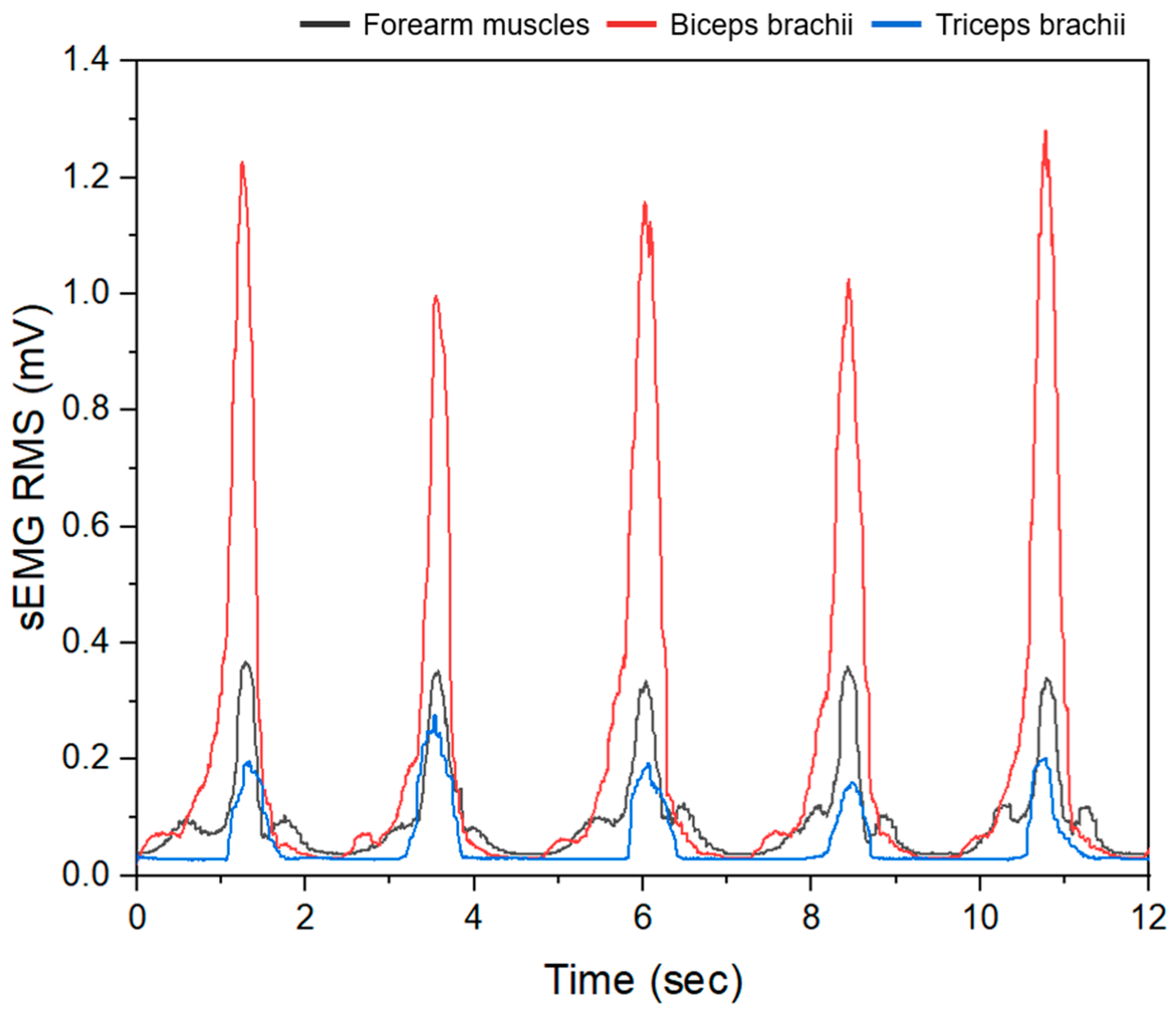
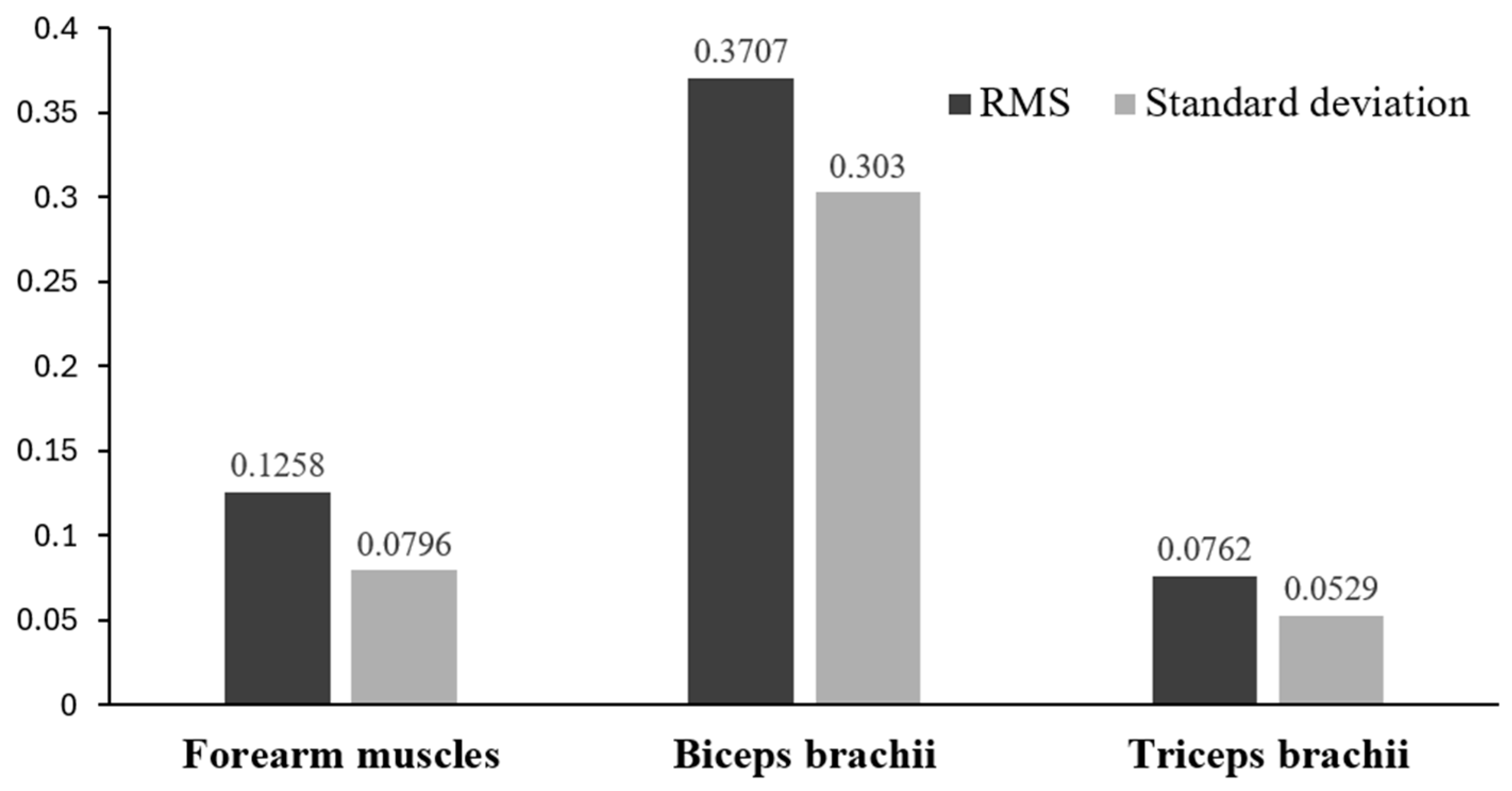

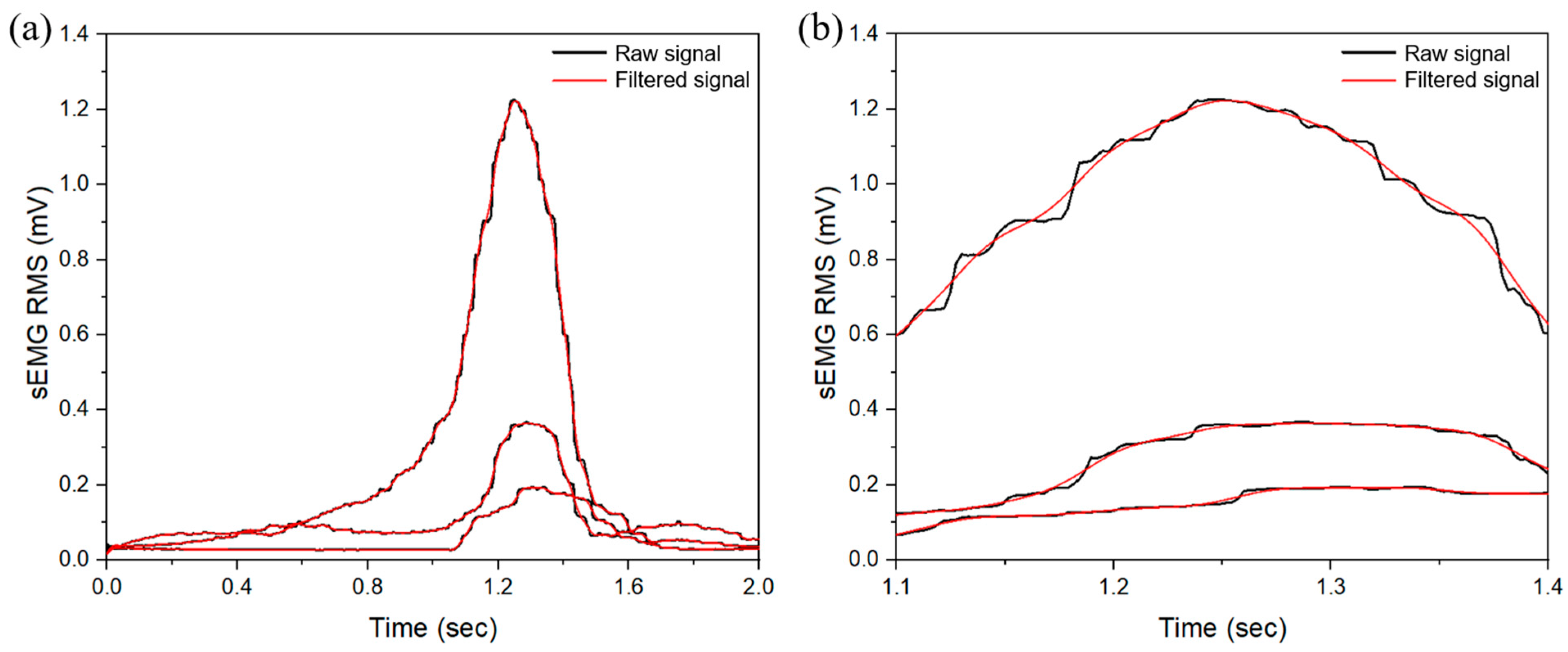

| Muscle | Peak Frequency (Hz) | Peak Amplitude (Arb. Units) | PSD at Peak (dB/Hz) | Total PSD (dB/Hz) |
|---|---|---|---|---|
| Forearm muscles | 0.417 | 0.082 | 0.0411 | 0.0158 |
| Biceps brachii | 0.417 | 0.301 | 0.5254 | 0.1374 |
| Triceps brachii | 0.417 | 0.047 | 0.0134 | 0.0058 |
| Mapping | Cutoff Frequency (Hz) | Training () | Validation () | Test () |
|---|---|---|---|---|
| a | - | 0.77947 | 0.77125 | 0.77233 |
| b | 3 | 0.77274 | 0.78957 | 0.78824 |
| 2.5 | 0.76703 | 0.75108 | 0.74565 | |
| 2 | 0.76198 | 0.74913 | 0.77064 | |
| 1.5 | 0.76829 | 0.73518 | 0.74350 | |
| 1.0 | 0.76244 | 0.75156 | 0.76698 | |
| 0.5 | 0.75180 | 0.75726 | 0.79812 | |
| 0.1 | 0.76282 | 0.79705 | 0.72023 |
| Mapping | Training () | Validation () | Test ( ) |
|---|---|---|---|
| (c) | 0.80277 | 0.79654 | 0.80695 |
| (d) | 0.92519 | 0.92841 | 0.91593 |
| (e) | 0.92881 | 0.89670 | 0.92058 |
| (f) | 0.94012 | 0.93919 | 0.94108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.; Kim, S.; Kim, J. Enhanced Prediction of Muscle Activity Using Wearable Textile Stretch Sensors and Multi-Layer Perceptron. Processes 2025, 13, 1041. https://doi.org/10.3390/pr13041041
Lee G, Kim S, Kim J. Enhanced Prediction of Muscle Activity Using Wearable Textile Stretch Sensors and Multi-Layer Perceptron. Processes. 2025; 13(4):1041. https://doi.org/10.3390/pr13041041
Chicago/Turabian StyleLee, Gyubin, Sangun Kim, and Jooyong Kim. 2025. "Enhanced Prediction of Muscle Activity Using Wearable Textile Stretch Sensors and Multi-Layer Perceptron" Processes 13, no. 4: 1041. https://doi.org/10.3390/pr13041041
APA StyleLee, G., Kim, S., & Kim, J. (2025). Enhanced Prediction of Muscle Activity Using Wearable Textile Stretch Sensors and Multi-Layer Perceptron. Processes, 13(4), 1041. https://doi.org/10.3390/pr13041041








