Radiated Free Convection of Dissipative and Chemically Reacting Flow Suspension of Ternary Nanoparticles
Abstract
1. Introduction
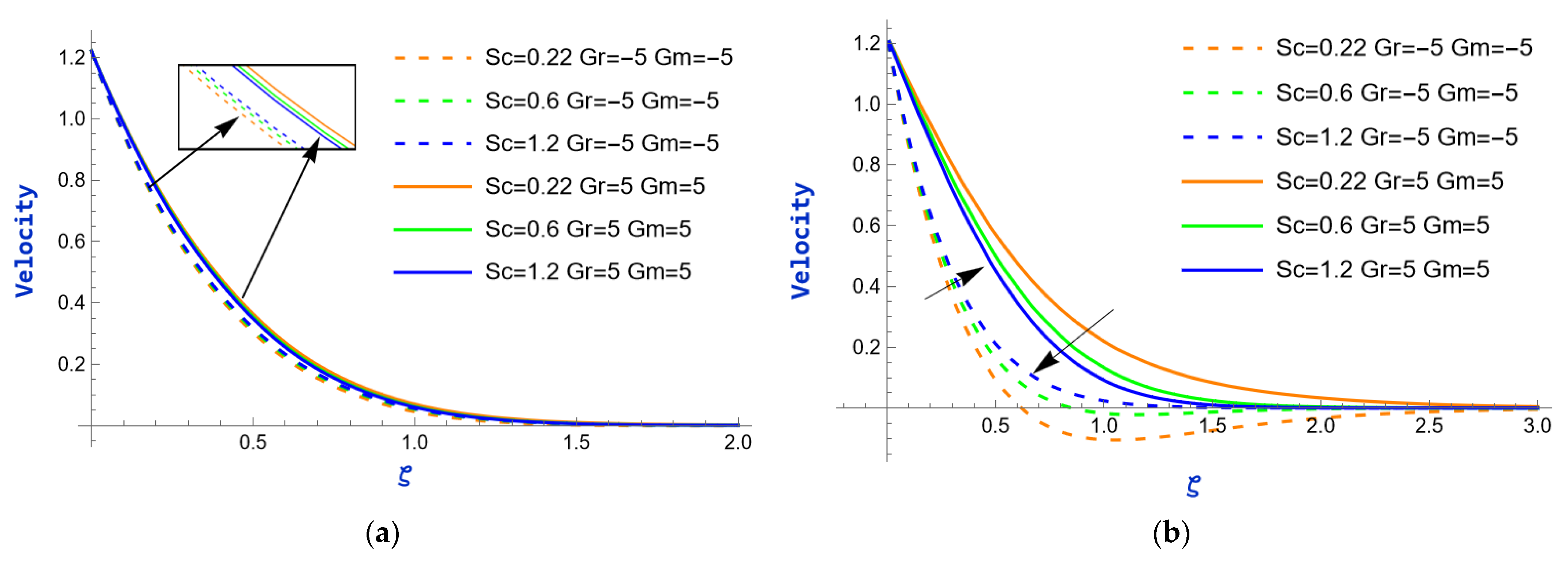
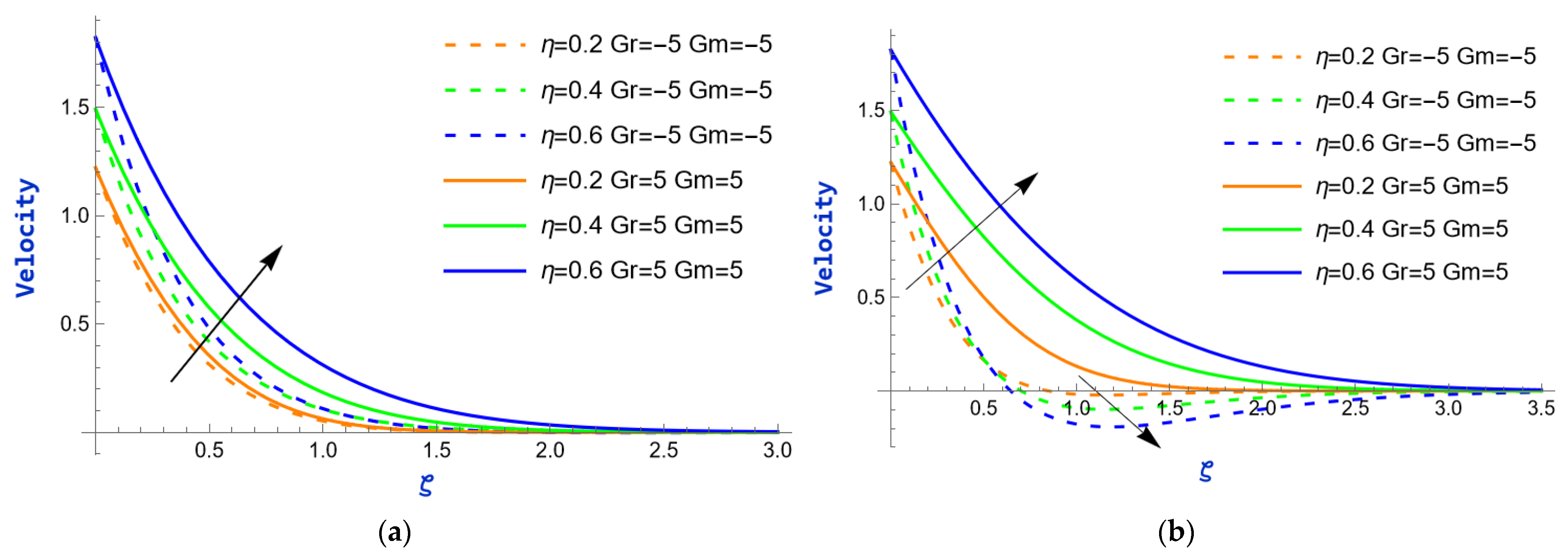
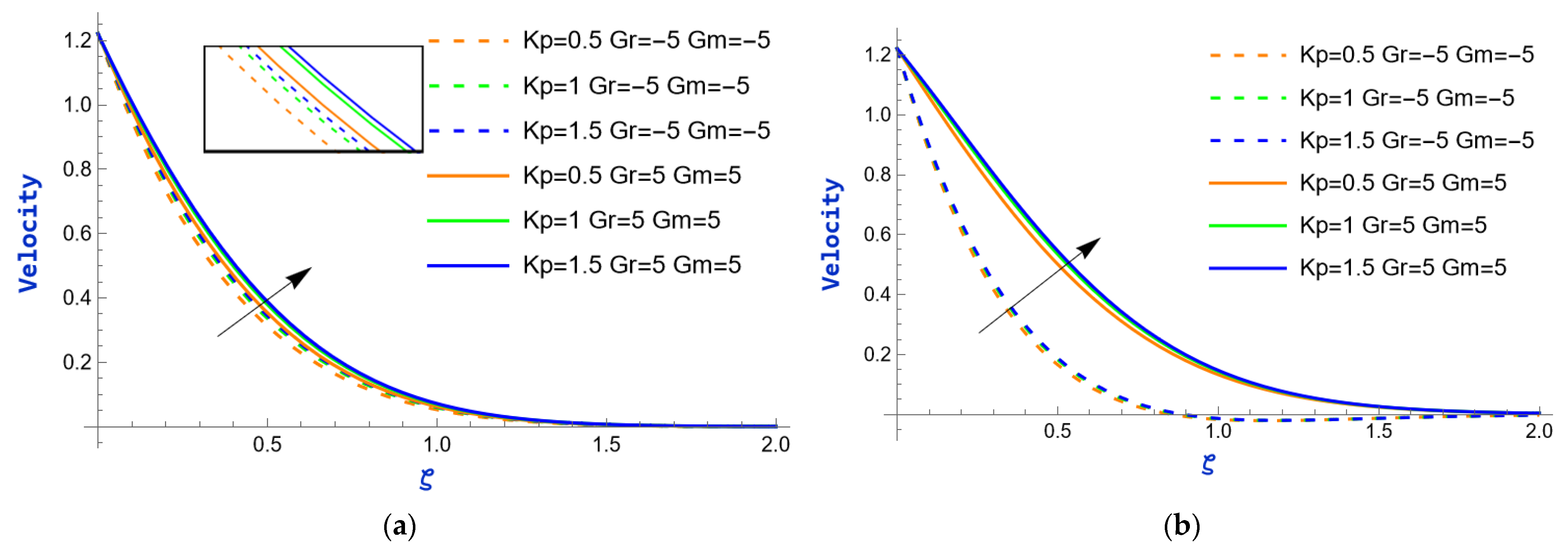
- How do flow parameters, such as Grashof numbers and the porosity parameter, affect the velocity profiles of water-based ternary hybrid nanofluid?
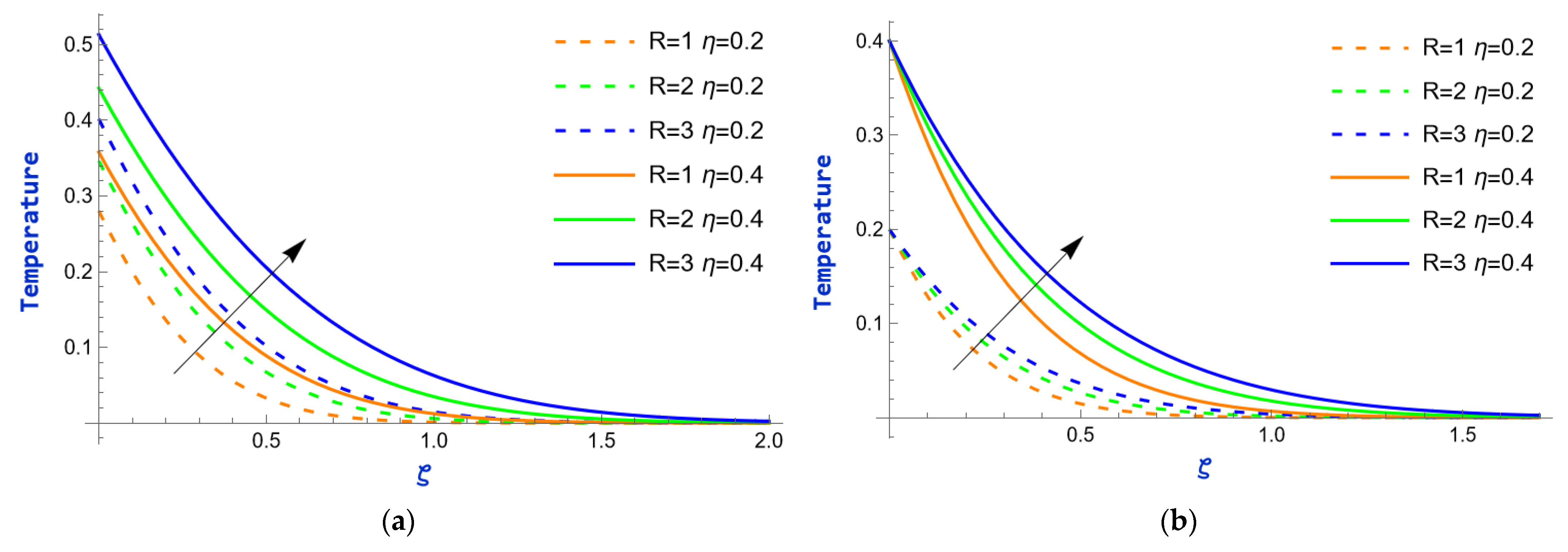
- What is the impact of increasing thermal radiation on temperature profiles?
- How does the heat absorption parameter influence the rate of heat transfer?
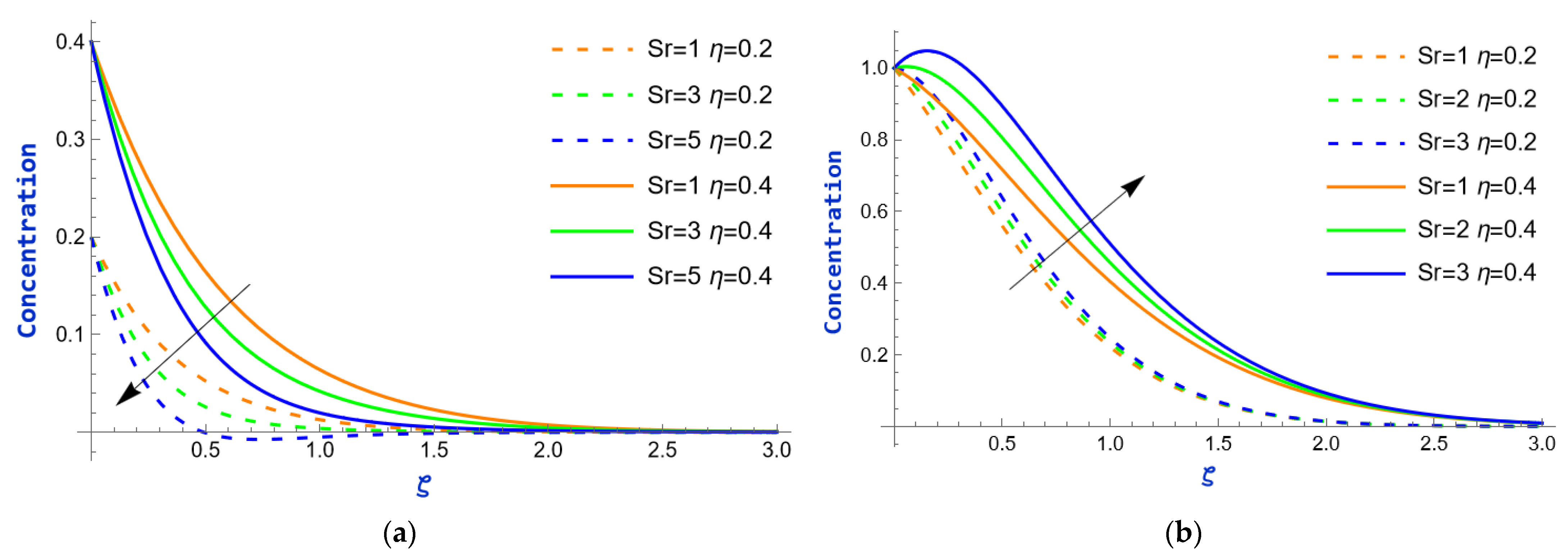
- What role does thermo-diffusion play in mass transfer rates?
- What are the unique findings and contributions of this research?
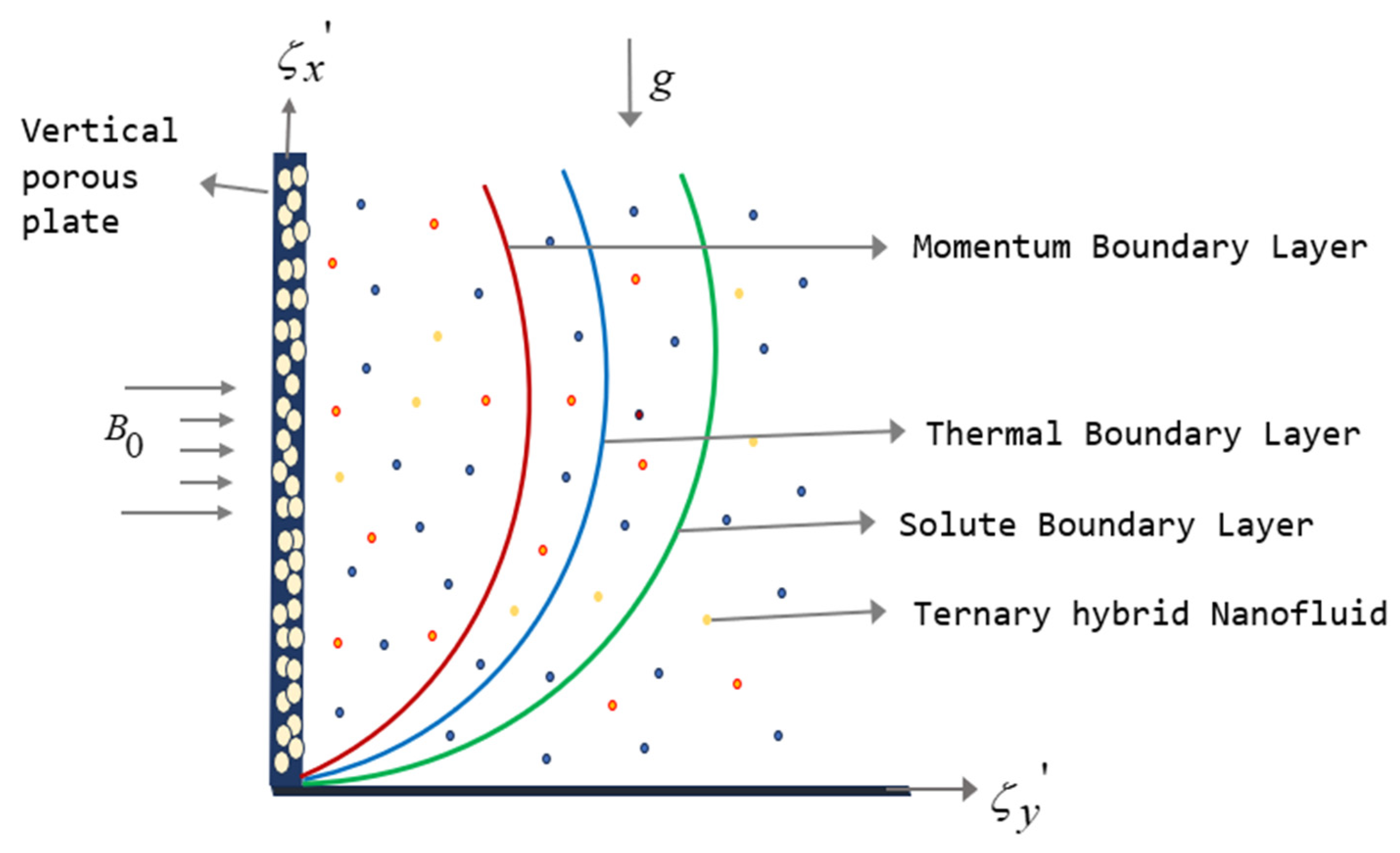
2. Mathematical Model
3. Methodology
- (i)
- Take the Laplace transform of the equation.
- The Laplace transform of a function is as follows:
- Where is the Laplace parameter
- (ii)
- Transform the differential equation into an algebraic equation.
- Convert the differential equation into an algebraic equation in terms of
- (iii)
- Solve for in the Laplace Domain.
- The inverse Laplace transform is applied to retrieve the physical solutions in the time domain =
4. Results and Discussions
4.1. Skin Friction Coefficient, Nusselt Number, and Sherwood Number
4.2. Finite Difference Method
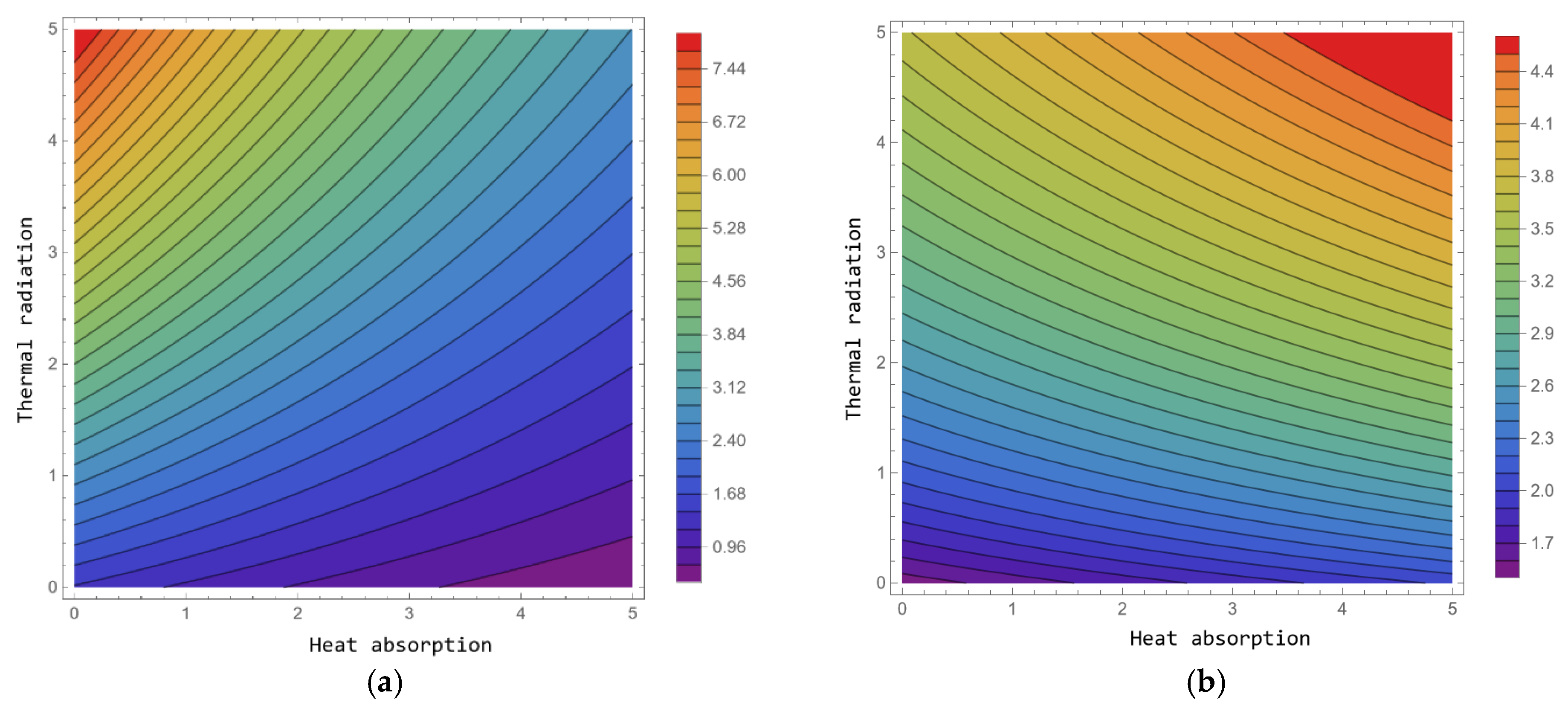
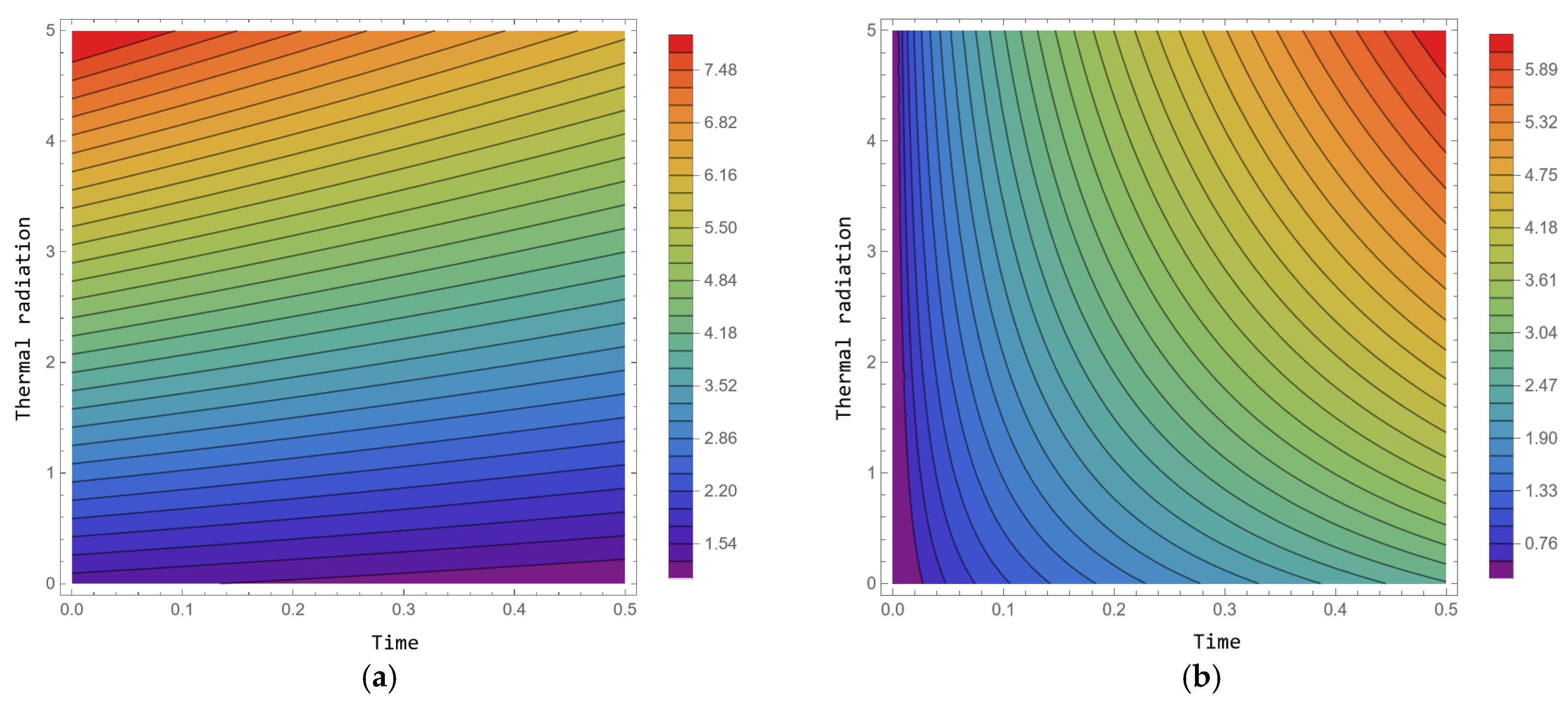
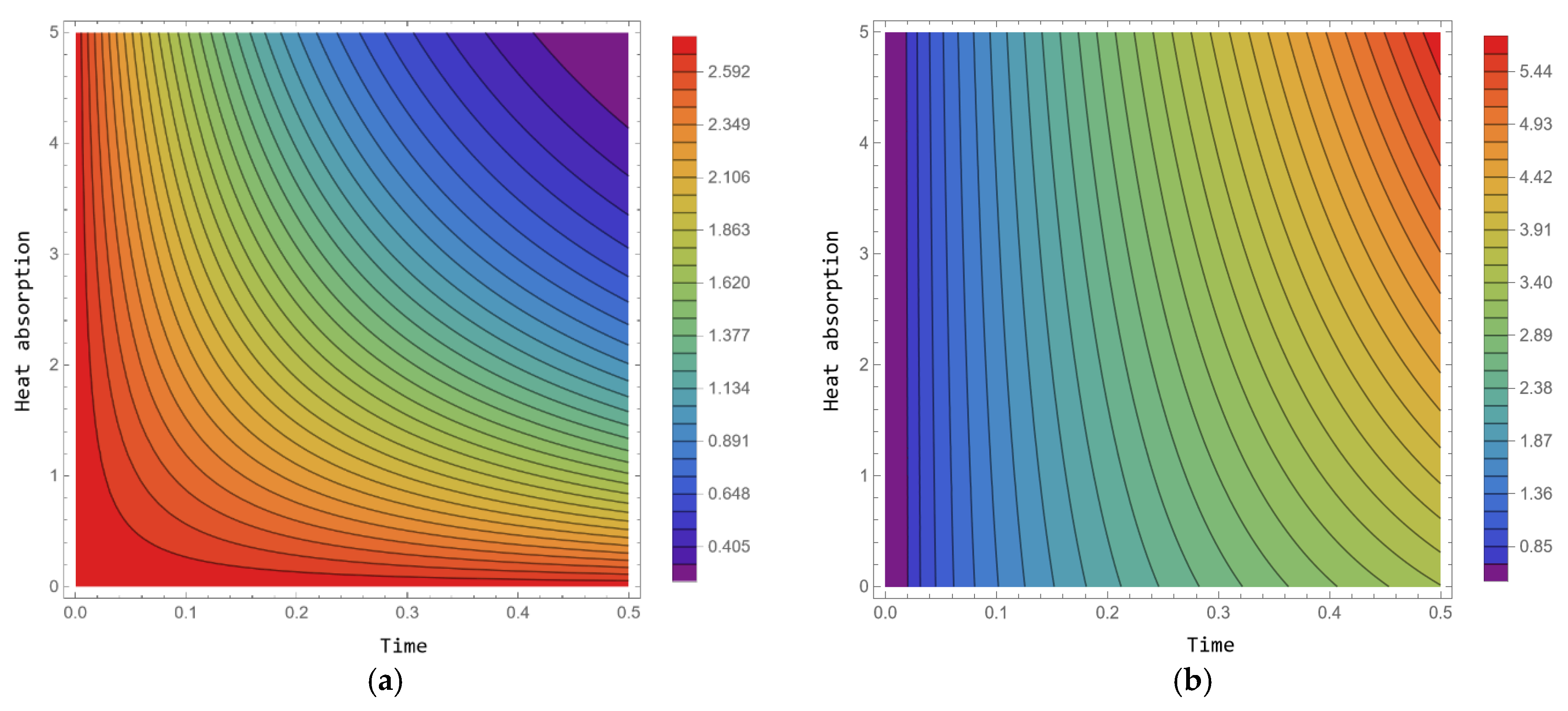
4.3. Contour Plots
5. Conclusions
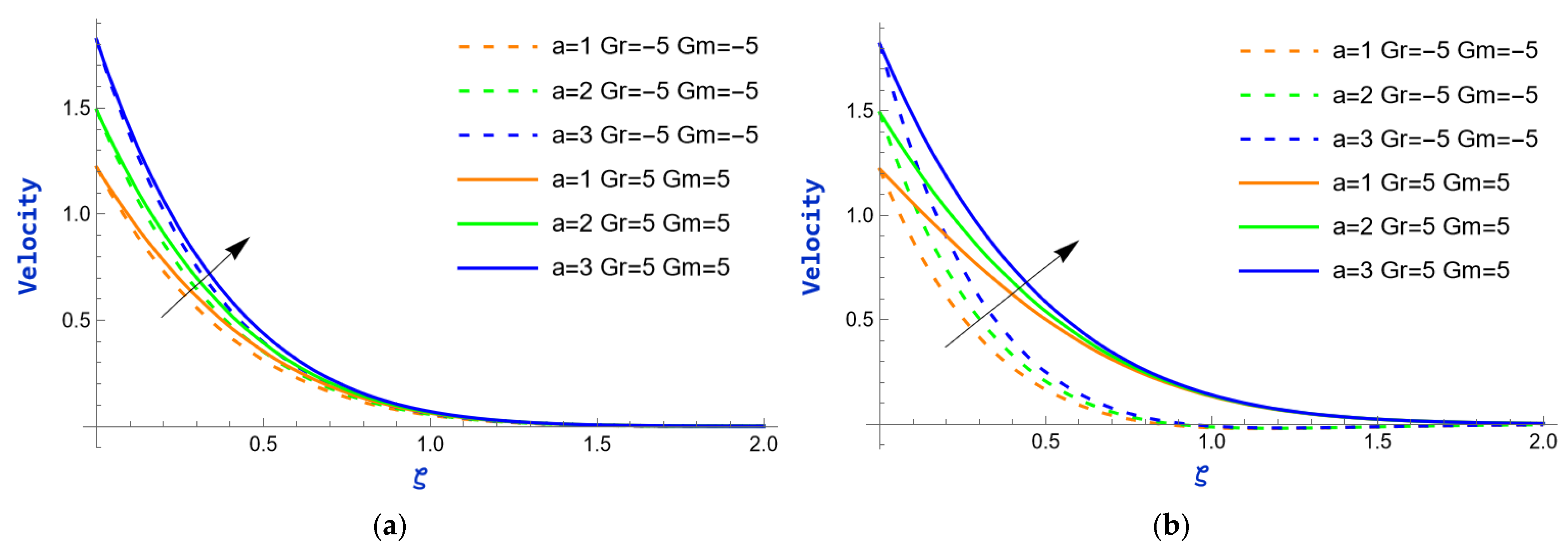
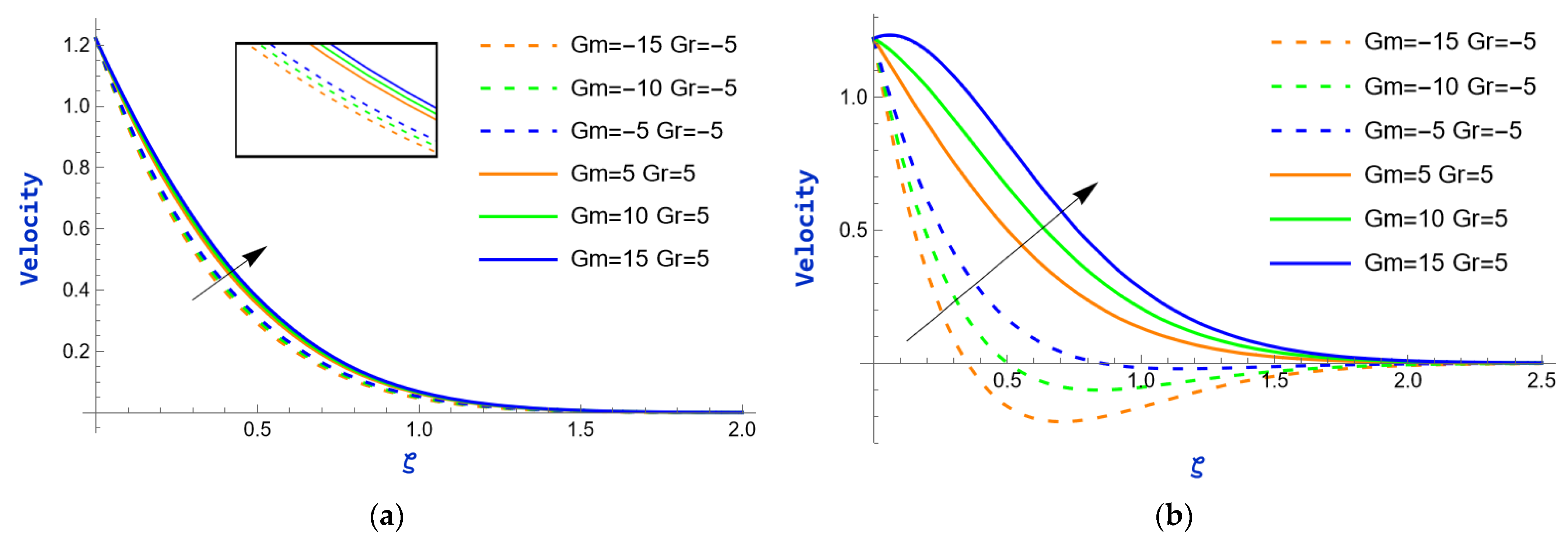
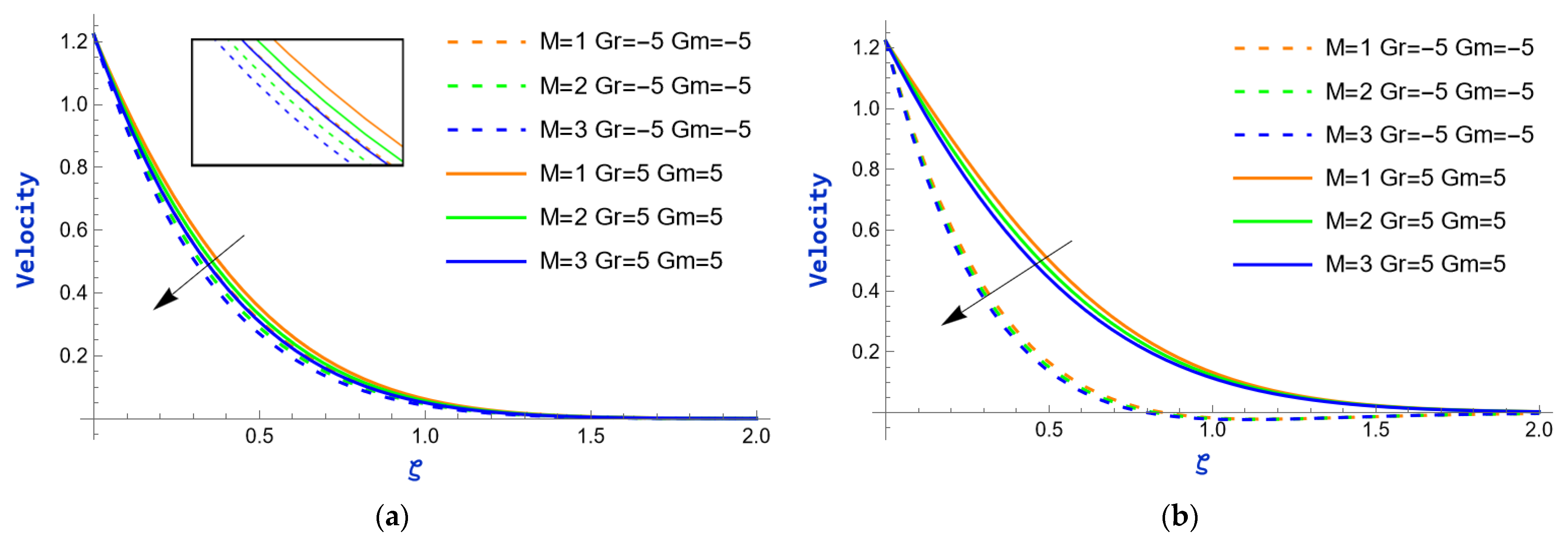
- The flow field increases with a rise in the exponential parameter, as well as with the thermal and mass Grashof numbers. However, an increase in the magnetic parameter has a detrimental effect on the flow.
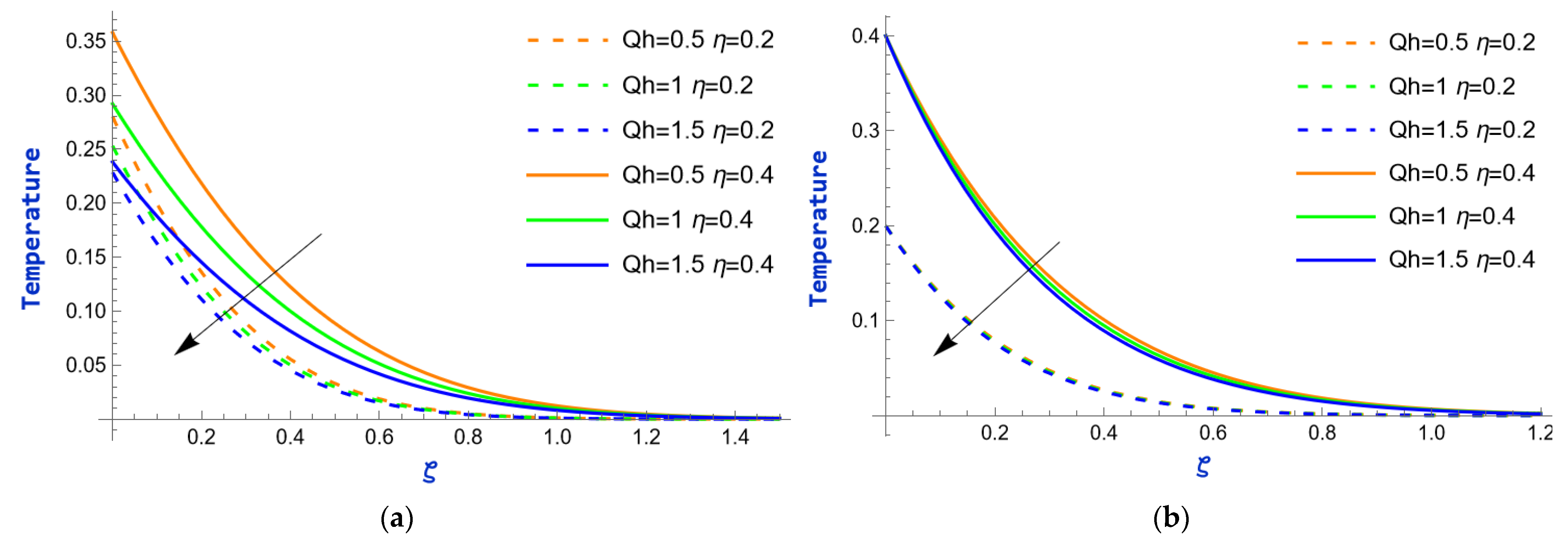
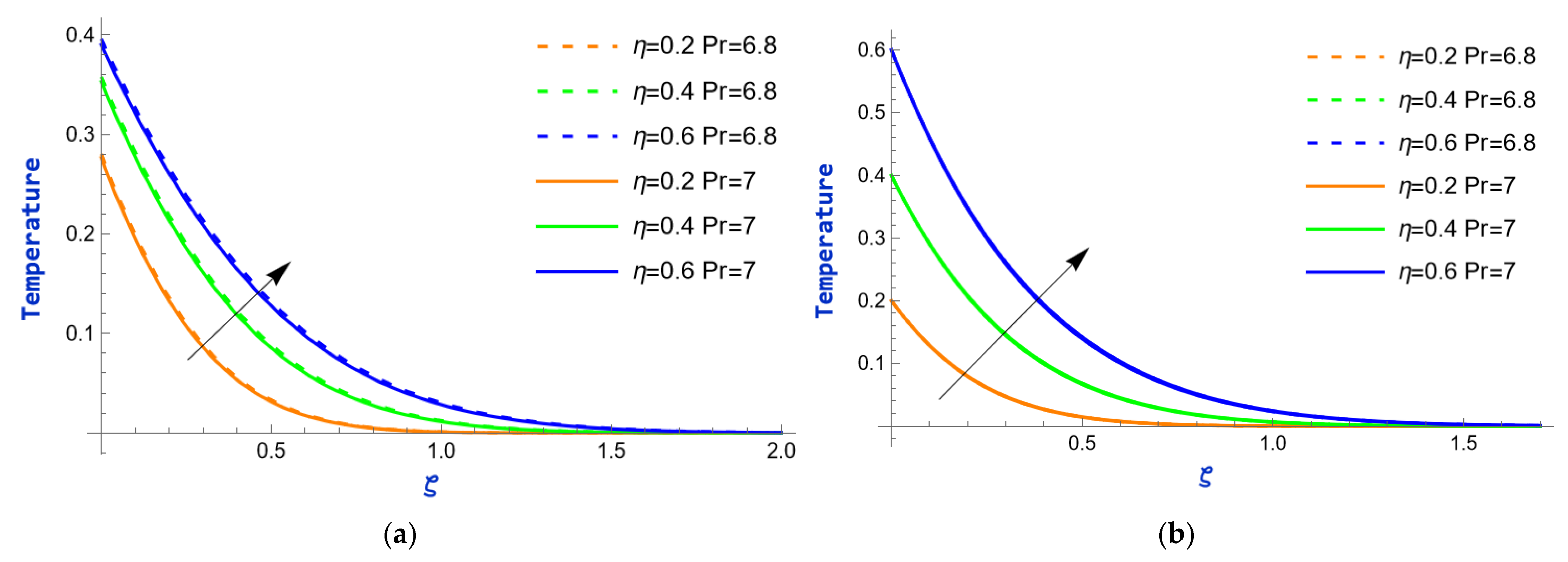
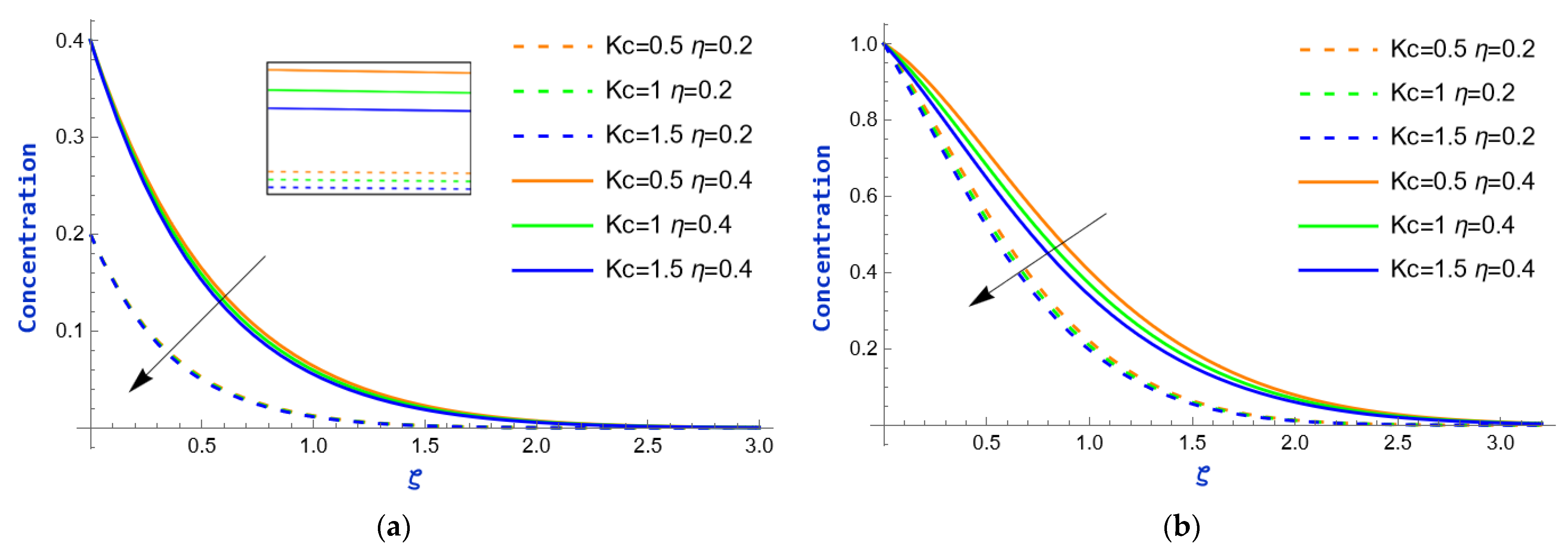
- The temperature field increases with the thermal radiation parameter but decreases as the heat absorption parameter rises. In contrast, the concentration field decreases with higher values of the chemical reaction parameter.
- Both the thermal and mass Grashof numbers significantly impact the skin friction coefficient, leading to a reduction in shear stress rates within fluid flows.
- The heat transfer rate is enhanced by the presence of thermal radiation, while the heat sink causes a considerable reduction in fluid temperature.
- The Soret effect has a varying influence on the rate of mass transfer, depending on specific conditions. In Case I, it causes an increase in the Sherwood number, while in Case II, it leads to a decreasing trend.
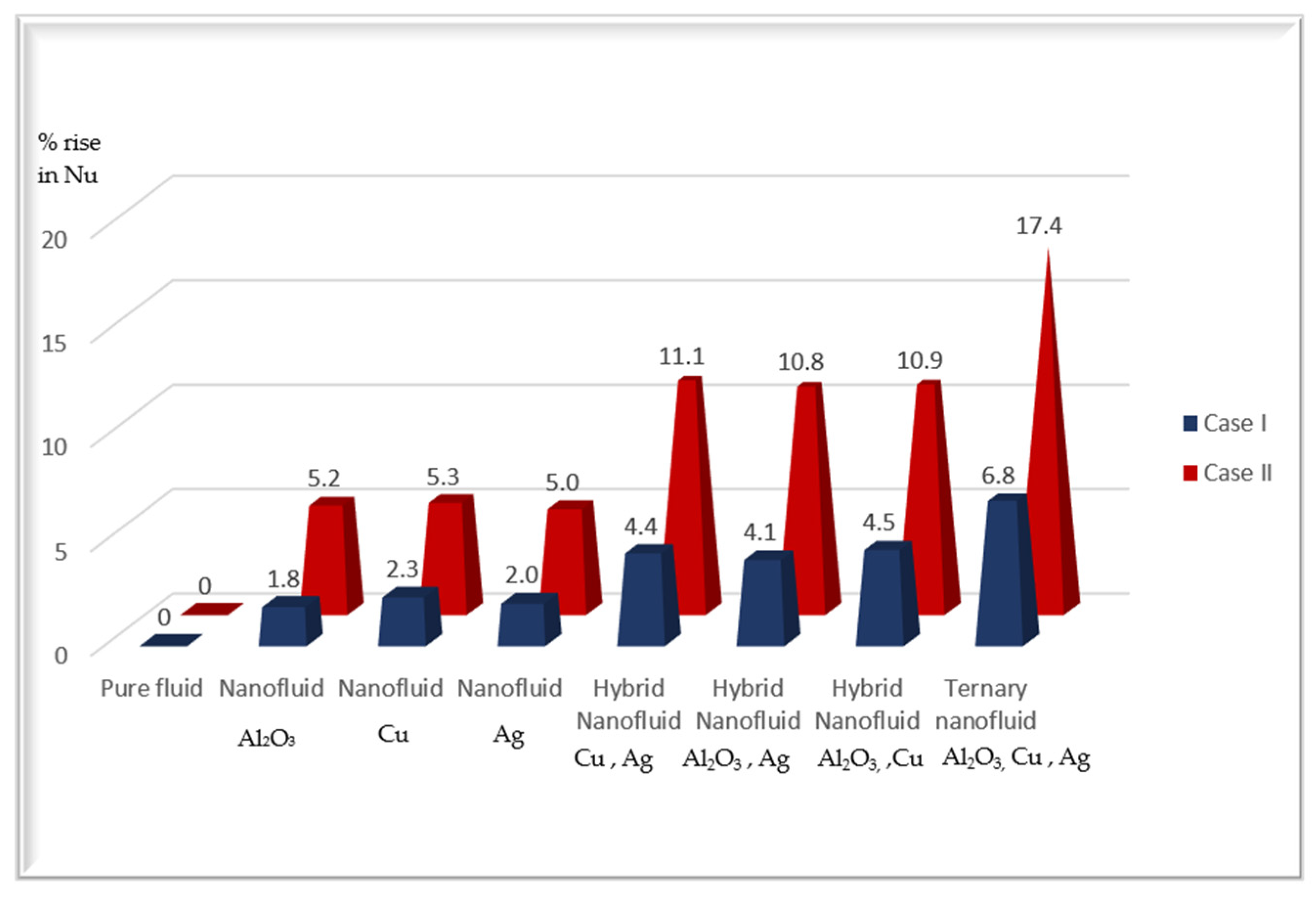
- The increase in heat transfer rates reveals that tri-hybrid nanofluids offer the most significant improvement in thermal conductivity, while hybrid nanofluids show notable enhancements, and mono nanofluids provide the least improvement among the three types.
- The Sherwood number for various material parameters is validated through a comparison of numerical data under specific conditions with previously reported results and results obtained using the FDM. This comparison confirms the accuracy of the numerical method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Nomenclature
| dimensionless exponential parameter | |
| external magnetic field {A/m} | |
| dimensionless skin friction | |
| specific heat at constant pressure {J kg−1 K−1} | |
| concentration of dimensions {kg m−3} | |
| fluid content at the plate {kg m−3} | |
| fluid concentration at a distance from the plate {kg m−3} | |
| non-dimensional concentration | |
| chemical molecular diffusivity | |
| thermal diffusivity {m2 s −1} | |
| error function | |
| complementary error function | |
| gravity {m s−2} | |
| Grashof number related to temperature | |
| Grashof number related to mass | |
| chemical reaction term | |
| porosity parameter | |
| magnetic field strength | |
| rate of heat transfer | |
| Prandtl number | |
| coefficient of heat absorption | |
| radiative heat flux | |
| heat flux | |
| thermal radiation parameter | |
| Schmidt number | |
| Soret effect | |
| Sherwood number | |
| dimensional temperature {K} | |
| temperature of the fluid at the plate {K} | |
| ambient temperature {K} | |
| fluid velocity in direction {ms−1} | |
| plate velocity {ms−1} | |
| non-dimensional velocity | |
| coordinate axis positioned along vertical surface | |
| coordinate axis perpendicular to plate | |
| non-dimensional coordinate axis perpendicular to plate | |
| Greek Symbols | |
| dimensionless temperature | |
| coefficient of viscosity {kgm−1 s−1} | |
| thermal conductivity of the fluid {Wm−1s−1} | |
| density of the fluid {kgm−3} | |
| volume fraction of nanoparticle | |
| volume fraction of nanoparticle | |
| volume fraction of nanoparticle | |
| kinematic viscosity {m2s−1} | |
| electrical conductivity {sm−1} | |
| volumetric coefficient of thermal expansion | |
| volumetric coefficient of expansion with concentration | |
| time {s} | |
| dimensionless time | |
| Subscript | |
| plate conditions | |
| conditions of free stream | |
| base fluid | |
| nanofluid | |
| hybrid nanofluid | |
| ternary hybrid nanofluid | |
| nanoparticle | |
| nanoparticle | |
| nanoparticle | |
Appendix A
References
- Carnahan, B.; Luther, H.A.; Wilkes, J.O. Applied Numerical Methods; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Rajesh, V.; Varma, S.V.K. Chemical reaction effects on free convection flow past an exponentially accelerated vertical plate. Ann. J. Eng. 2010, 13, 181–188. [Google Scholar]
- Kumar, A.V.; Kumaresan, E.; Varma, S.V.K. An exact analysis of unsteady MHD free convective chemically reacting elasto-viscous fluid flow past an impulsively started infinite vertical plate through porous medium in the presence of radiation absorption. Int. J. Appl. Comput. Math. 2017, 3, 2257–2274. [Google Scholar] [CrossRef]
- Islam, S.H.; Ahmed, N. Effect of thermal diffusion and chemical reaction on MHD free convective flow past an infinite isothermal vertical plate with heat source. Ital. J. Pure Appl. Math. 2019, 42, 559–574. [Google Scholar]
- Goud, B.S.; Babu, B.S.; Shekar, M.R.; Srinivas, G. Mass transfer effects on MHD flow through porous medium past an exponentially accelerated inclined plate with variable temperature and thermal radiation. Int. J. Thermofluid Sci. Technol. 2019, 6, 19060402. [Google Scholar] [CrossRef]
- Goud, B.S.; Reddy, Y.D. Chemical reaction and Soret effect on an unsteady MHD heat and mass transfer fluid flow along an infinite vertical plate with radiation and heat absorption. J. Indian Chem. Soc. 2022, 99, 100762. [Google Scholar] [CrossRef]
- Bafakeeh, O.T.; Raghunath, K.; Ali, F.; Khalid, M.; Tag-ElDin, E.S.M.; Oreijah, M.; Guedri, K.; Ben Khedher, N.; Khan, M.I. Hall current and Soret effects on unsteady MHD rotating flow of second-grade fluid through porous media under the influences of thermal radiation and chemical reactions. Catalysts 2022, 12, 1233. [Google Scholar] [CrossRef]
- Narmatha, M.; Kavitha, R. Analysis of unsteady heat and mass transfer in rotating MHD convection flow over a porous vertical plate. Arch. Thermodyn. 2024, 45, 179–187. [Google Scholar] [CrossRef]
- Abbas, S.; Nazar, M. Fractional analysis of unsteady magnetohydrodynamics Jeffrey flow over an infinite vertical plate in the presence of Hall current. Math. Methods Appl. Sci. 2025, 48, 253–272. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Laboratory (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Sedki, A.M. Effect of thermal radiation and chemical reaction on MHD mixed convective heat and mass transfer in nanofluid flow due to nonlinear stretching surface through porous medium. Results Mater. 2022, 16, 100334. [Google Scholar] [CrossRef]
- Reddy, Y.D.; Mebarek-Oudina, F.; Goud, B.S.; Ismail, A.I. Radiation, velocity and thermal slips effect toward MHD boundary layer flow through heat and mass transport of Williamson nanofluid with porous medium. Arab. J. Sci. Eng. 2022, 47, 16355–16369. [Google Scholar] [CrossRef]
- Sudarsana Reddy, P.; Sreedevi, P. Impact of chemical reaction and double stratification on heat and mass transfer characteristics of nanofluid flow over porous stretching sheet with thermal radiation. Int. J. Ambient Energy 2022, 43, 1626–1636. [Google Scholar] [CrossRef]
- Dharmaiah, G.; Mebarek-Oudina, F.; Prasad, J.R.; Rani, C.B. Exploration of bio-convection for slippery two-phase Maxwell nanofluid past a vertical induced magnetic stretching regime associated for biotechnology and engineering. J. Mol. Liq. 2023, 391, 123408. [Google Scholar] [CrossRef]
- Kodi, R.; Ali, F.; Khalid, M.; Abdullaeva, B.S.; Altuijri, R.; Khan, M.I. Heat and mass transfer on MHD flow of Jeffrey nanofluid based on Cu and TiO2 over an inclined plate and diffusion-thermo and radiation absorption effects. Pramana 2023, 97, 202. [Google Scholar] [CrossRef]
- Raghunath, K. Study of heat and mass transfer of an unsteady magnetohydrodynamic (MHD) nanofluid flow past a vertical porous plate in the presence of chemical reaction, radiation and Soret effects. J. Nanofluids 2023, 12, 767–776. [Google Scholar] [CrossRef]
- Ramesh, K.; Mebarek-Oudina, F.; Ismail, A.I.; Jaiswal, B.R.; Warke, A.S.; Lodhi, R.; Sharma, T. Computational analysis on radiative non-Newtonian Carreau nanofluid flow in a microchannel under the magnetic properties. Sci. Iran. 2023, 30, 376–390. [Google Scholar] [CrossRef]
- Venkateswarlu, B.; Kim, S.C.; Joo, S.W.; Chavan, S. Numerical investigation of nanofluid as a coolant in a prismatic battery for thermal management systems. J. Therm. Sci. Eng. Appl. 2024, 16, 031003. [Google Scholar] [CrossRef]
- Galal, A.M.; Alharbi, F.M.; Arshad, M.; Alam, M.M.; Abdeljawad, T.; Al-Mdallal, Q.M. Numerical investigation of heat and mass transfer in three-dimensional MHD nanoliquid flow with inclined magnetization. Sci. Rep. 2024, 14, 1207. [Google Scholar] [CrossRef]
- Dharmaiah, G.; Mebarek-Oudina, F.; Balamurugan, K.S.; Vedavathi, N. Numerical analysis of the magnetic dipole effect on a radiative ferromagnetic liquid flowing over a porous stretched sheet. Fluid Dyn. Mater. Process. 2024, 20, 293–310. [Google Scholar] [CrossRef]
- Rahman, A.; Hasnain, S.M.M.; Pandey, S.; Tapalova, A.; Akylbekov, N.; Zairov, R. Review on nanofluids: Preparation, properties, stability, and thermal performance augmentation in heat transfer applications. ACS Omega 2024, 9, 32328–32349. [Google Scholar] [CrossRef]
- Basit, M.A.; Imran, M.; Mohammed, W.W.; Ali, M.R.; Hendy, A.S. Thermal analysis of mathematical model of heat and mass transfer through bioconvective Carreau nanofluid flow over an inclined stretchable cylinder. Case Stud. Therm. Eng. 2024, 63, 105303. [Google Scholar] [CrossRef]
- Saleem, M.; Al-Zubaidi, A.; Tufail, M.N.; Fiaz, Z.; Saleem, S. Exploration of numerical simulation for unsteady Casson nanofluid thin film flow over stretching surface with mixed convection effects using Buongiorno’s nanofluid model. Zamm 2024, 104, e202400165. [Google Scholar] [CrossRef]
- Waseem, M.; Jawad, M.; Aldalbahi, M.M.; Naeem, S.; Gull, H.; Majeed, A. Statistical and mathematical modeling of viscoelastic 3D Casson nanofluid flow with activation energy and motile microbes induced by exponential sheet bounding with Darcy-Forchheimer porous medium. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 14. [Google Scholar] [CrossRef]
- Mishra, A.; Upreti, H. A comparative study of Ag–MgO/water and Fe3O4–CoFe2O4/EG–water hybrid nanofluid flow over a curved surface with chemical reaction using Buongiorno model. Partial Differ. Equ. Appl. Math. 2022, 5, 100322. [Google Scholar]
- Lone, S.A.; Alyami, M.A.; Saeed, A.; Dawar, A.; Kumam, P.; Kumam, W. MHD micropolar hybrid nanofluid flow over a flat surface subject to mixed convection and thermal radiation. Sci. Rep. 2022, 12, 17283. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Chabani, I.; Vaidya, H.; Ismail, A.A.I. Hybrid-nanofluid magneto-convective flow and porous media contribution to entropy generation. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 809–836. [Google Scholar] [CrossRef]
- Shamshuddin, M.D.; Saeed, A.; Mishra, S.; Katta, R.; Eid, M.R. Homotopic simulation of MHD bioconvective flow of water-based hybrid nanofluid over a thermal convective exponential stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 31–53. [Google Scholar] [CrossRef]
- Khan, M.N.; Aldosari, F.M.; Wang, Z.; Yasir, M.; Afikuzzaman, M.; Elseesy, I.E. Overview of solar thermal applications of heat exchangers with thermophysical features of hybrid nanomaterials. Nanoscale Adv. 2024, 6, 136–145. [Google Scholar] [CrossRef]
- Agbaje, T.M.; Panda, S.; Mishra, S.R.; Baithalu, R. Free convection of Cattaneo-Christov heat flux model for the micropolar hybrid nanofluid through permeable stretching surface with inertial drag and irregular heat sink/source. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 184. [Google Scholar] [CrossRef]
- Ishaq, M.; Khan, S.U.; AL Garalleh, H.; Sowayan, A.S.; Tlili, I. Thermal performance of casson hybrid nanofluid with radiative effects and convective conditions: Applications to energy systems and industrial heat transfer. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 141. [Google Scholar] [CrossRef]
- Al Oweidi, K.F.; Shahzad, F.; Jamshed, W.; Usman; Ibrahim, R.W.; El Din, E.S.M.T.; AlDerea, A.M. Partial differential equations of entropy analysis on ternary hybridity nanofluid flow model via rotating disk with hall current and electromagnetic radiative influences. Sci. Rep. 2022, 12, 20692, [Label Retracted]. [Google Scholar] [CrossRef]
- Alshahrani, S.; Ahammad, N.A.; Bilal, M.; Ghoneim, M.E.; Ali, A.; Yassen, M.F.; Tag-Eldin, E. Numerical simulation of ternary nanofluid flow with multiple slip and thermal jump conditions. Front. Energy Res. 2022, 10, 967307. [Google Scholar] [CrossRef]
- Vinutha, K.; Nagaraja, K.V.; Sajjan, K.; Khan, U.; Madhukesh, J.K.; Kolli, U.C.; Muhammad, T. Thermal performance of Fe3O4, SWCNT, MWCNT and H2O based on magnetohydrodynamic nanofluid flow across a wedge with significant impacts of Soret and Dufour. Nanoscale Adv. 2023, 5, 5952–5964. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Sarris, I.E.; Prasannakumara, B.C.; Abdulrahman, A. Investigation of thermal performance of ternary hybrid nanofluid flow in a permeable inclined cylinder/plate. Energies 2023, 16, 2630. [Google Scholar] [CrossRef]
- Mahmood, Z.; Khan, U.; Saleem, S.; Rafique, K.; Eldin, S.M. Numerical analysis of ternary hybrid nanofluid flow over a stagnation region of stretching/shrinking curved surface with suction and lorentz force. J. Magn. Magn. Mater. 2023, 573, 170654. [Google Scholar] [CrossRef]
- Souayeh, B.; Ramesh, K. Numerical scrutinization of ternary nanofluid flow over an exponentially stretching sheet with gyrotactic microorganisms. Mathematics 2023, 11, 981. [Google Scholar] [CrossRef]
- Ramzan, M.; Kumam, P.; Lone, S.A.; Seangwattana, T.; Saeed, A.; Galal, A.M. A theoretical analysis of the ternary hybrid nanofluid flows over a non-isothermal and non-isosolutal multiple geometries. Heliyon 2023, 9, e14875. [Google Scholar] [CrossRef]
- Vishalakshi, A.B.; Mahabaleshwar, U.S.; Laroze, D.; Zeidan, D. A study of mixed convective ternary hybrid nanofluid flow over a stretching sheet with radiation and transpiration. Spec. Top. Rev. Porous Media Int. J. 2023, 14, 33–51. [Google Scholar] [CrossRef]
- Mandal, G. Stability analysis and multiple solutions of MHD mixed convective Cu–Ag-Al2O3/H2O ternary hybrid nanofluid over an exponential permeable shrinking surface with radiation and slip impacts: An estimation of entropy production. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Khan, M.N.; Ahmad, S.; Alrihieli, H.F.; Wang, Z.; Hussien, M.A.; Afikuzzaman, M. Theoretical study on thermal efficiencies of Sutterby ternary-hybrid nanofluids with surface catalyzed reactions over a bidirectional expanding surface. J. Mol. Liq. 2023, 391, 123412. [Google Scholar] [CrossRef]
- Jamrus, F.N.; Waini, I.; Khan, U.; Ishak, A. Effects of magnetohydrodynamics and velocity slip on mixed convective flow of thermally stratified ternary hybrid nanofluid over a stretching/shrinking sheet. Case Stud. Therm. Eng. 2024, 55, 104161. [Google Scholar] [CrossRef]
- Chandel, S.; Sharma, D. Ternary nanofluid dynamics in stagnated flow with exponential heat and inclined magnetic field: Applications in advanced cooling and aerospace system. Int. J. Heat Fluid Flow 2024, 109, 109508. [Google Scholar] [CrossRef]
- Saleem, M.; Al-Zubaidi, A.; Radwan, N.; Saleem, S.; Adawi, H. Thermal effects of ternary Casson nanofluid flow over a stretching sheet: An investigation of Thomson and Troian velocity slip. Case Stud. Therm. Eng. 2025, 65, 105561. [Google Scholar] [CrossRef]




| Physical Properties | H2O | Al2O3 | Cu | Ag |
|---|---|---|---|---|
| [Kg/m3] | 997.1 | 3970 | 8933 | 10,500 |
| [W/mK] | 0.613 | 40 | 400 | 429 |
| [s/m] | 5.5 × 10−5 | 35 × 106 | 59.6 × 106 | 63 × 106 |
| [K−1] | 21 × 10−5 | 0.85 × 10−5 | 1.67 × 10−5 | 1.89 × 10−5 |
| [J/kgK] | 4179 | 765 | 385 | 235 |
| Properties | Ternary Nanofluid |
|---|---|
| Density | |
| Dynamic viscosity | |
| Heat capacity | |
| Thermal expansion | |
| Thermal conductivity | |
| Electrical conductivity |
| Sherwood Number | ||||||
|---|---|---|---|---|---|---|
| Case I | Case II | |||||
| Present Work | Rajesh and Varma [2] | Present Work | FDM | |||
| 0.6 | 0.5 | 0.2 | 0.40378 | 0.40378 | 1.07333 | 1.07410 |
| 1.2 | 0.5 | 0.2 | 0.57104 | 0.57104 | 1.51792 | 1.51610 |
| 0.6 | 1 | 0.2 | 0.41643 | 0.41643 | 1.16638 | 1.16680 |
| 0.6 | 1.5 | 0.2 | 0.42885 | 0.42885 | 1.25654 | 1.25620 |
| 0.6 | 0.5 | 0.4 | 0.58893 | 0.58893 | 0.82476 | 0.82500 |
| 0.6 | 0.5 | 0.6 | 0.74278 | 0.74278 | 0.72547 | 0.72580 |
| (Case I) | (Case II) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.57717 | 2.56086 |
| 2 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 4.89578 | 3.87947 |
| 3 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 6.58052 | 5.56421 |
| 1 | 10 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.45592 | 2.44736 |
| 1 | 15 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.33467 | 2.33385 |
| 1 | 5 | 10 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.43225 | 1.39189 |
| 1 | 5 | 15 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.28733 | 0.22291 |
| 1 | 5 | 5 | 2 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.88697 | 2.89935 |
| 1 | 5 | 5 | 3 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 4.18391 | 3.22317 |
| 1 | 5 | 5 | 1 | 2 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.58953 | 2.52583 |
| 1 | 5 | 5 | 1 | 3 | 0.5 | 1 | 0.5 | 0.5 | 0.2 | 3.60188 | 2.49080 |
| 1 | 5 | 5 | 1 | 1 | 1 | 1 | 0.5 | 0.5 | 0.2 | 3.26861 | 2.22310 |
| 1 | 5 | 5 | 1 | 1 | 1.5 | 1 | 0.5 | 0.5 | 0.2 | 3.16273 | 2.10706 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 2 | 0.5 | 0.5 | 0.2 | 3.53503 | 2.55352 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 3 | 0.5 | 0.5 | 0.2 | 3.49710 | 2.54805 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 1 | 0.5 | 0.2 | 3.58963 | 2.56159 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 1.5 | 0.5 | 0.2 | 3.60062 | 2.56230 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 1 | 0.2 | 3.57819 | 2.57568 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 1.5 | 0.2 | 3.57919 | 2.58998 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.4 | 3.74613 | 2.48693 |
| 1 | 5 | 5 | 1 | 1 | 0.5 | 1 | 0.5 | 0.5 | 0.6 | 4.25229 | 2.86999 |
| (Case I) | (Case II) | |||
|---|---|---|---|---|
| 1 | 0.5 | 0.2 | 2.47811 | 2.21831 |
| 2 | 0.5 | 0.2 | 3.68045 | 2.70341 |
| 3 | 0.5 | 0.2 | 4.88279 | 3.11383 |
| 1 | 1 | 0.2 | 2.23465 | 2.29004 |
| 1 | 1.5 | 0.2 | 2.01510 | 2.36036 |
| 1 | 0.5 | 0.4 | 2.23465 | 3.23860 |
| 1 | 0.5 | 0.6 | 2.01510 | 4.08827 |
| (Case I) | (Case II) | |||||
|---|---|---|---|---|---|---|
| 1 | 0.5 | 1 | 0.5 | 0.2 | 0.514745 | 0.750490 |
| 2 | 0.5 | 1 | 0.5 | 0.2 | 0.507204 | 0.826423 |
| 3 | 0.5 | 1 | 0.5 | 0.2 | 0.501581 | 0.870622 |
| 1 | 1 | 1 | 0.5 | 0.2 | 0.501660 | 0.736548 |
| 1 | 1.5 | 1 | 0.5 | 0.2 | 0.490165 | 0.722835 |
| 1 | 0.5 | 2 | 0.5 | 0.2 | 0.625706 | 0.427651 |
| 1 | 0.5 | 3 | 0.5 | 0.2 | 0.736668 | 0.104812 |
| 1 | 0.5 | 1 | 1 | 0.2 | 0.526214 | 0.846894 |
| 1 | 0.5 | 1 | 1.5 | 0.2 | 0.537482 | 0.940298 |
| 1 | 0.5 | 1 | 0.5 | 0.4 | 0.685766 | 0.353279 |
| 1 | 0.5 | 1 | 0.5 | 0.6 | 0.827372 | 0.130117 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satish, R.; B. T, R.; Raju, S.S.K.; Al Mukahal, F.H.H.; Souayeh, B.; Varma, S.V.K. Radiated Free Convection of Dissipative and Chemically Reacting Flow Suspension of Ternary Nanoparticles. Processes 2025, 13, 1030. https://doi.org/10.3390/pr13041030
Satish R, B. T R, Raju SSK, Al Mukahal FHH, Souayeh B, Varma SVK. Radiated Free Convection of Dissipative and Chemically Reacting Flow Suspension of Ternary Nanoparticles. Processes. 2025; 13(4):1030. https://doi.org/10.3390/pr13041030
Chicago/Turabian StyleSatish, Rekha, Raju B. T, S. Suresh Kumar Raju, Fatemah H. H. Al Mukahal, Basma Souayeh, and S. Vijaya Kumar Varma. 2025. "Radiated Free Convection of Dissipative and Chemically Reacting Flow Suspension of Ternary Nanoparticles" Processes 13, no. 4: 1030. https://doi.org/10.3390/pr13041030
APA StyleSatish, R., B. T, R., Raju, S. S. K., Al Mukahal, F. H. H., Souayeh, B., & Varma, S. V. K. (2025). Radiated Free Convection of Dissipative and Chemically Reacting Flow Suspension of Ternary Nanoparticles. Processes, 13(4), 1030. https://doi.org/10.3390/pr13041030








