Digital Simulation of Hydraulic Fracturing in Laminated Shale Formation Containing Varying Bedding Planes
Abstract
1. Introduction
2. DEM-Based Hydromechanical Coupling Model
2.1. Pore Network Model
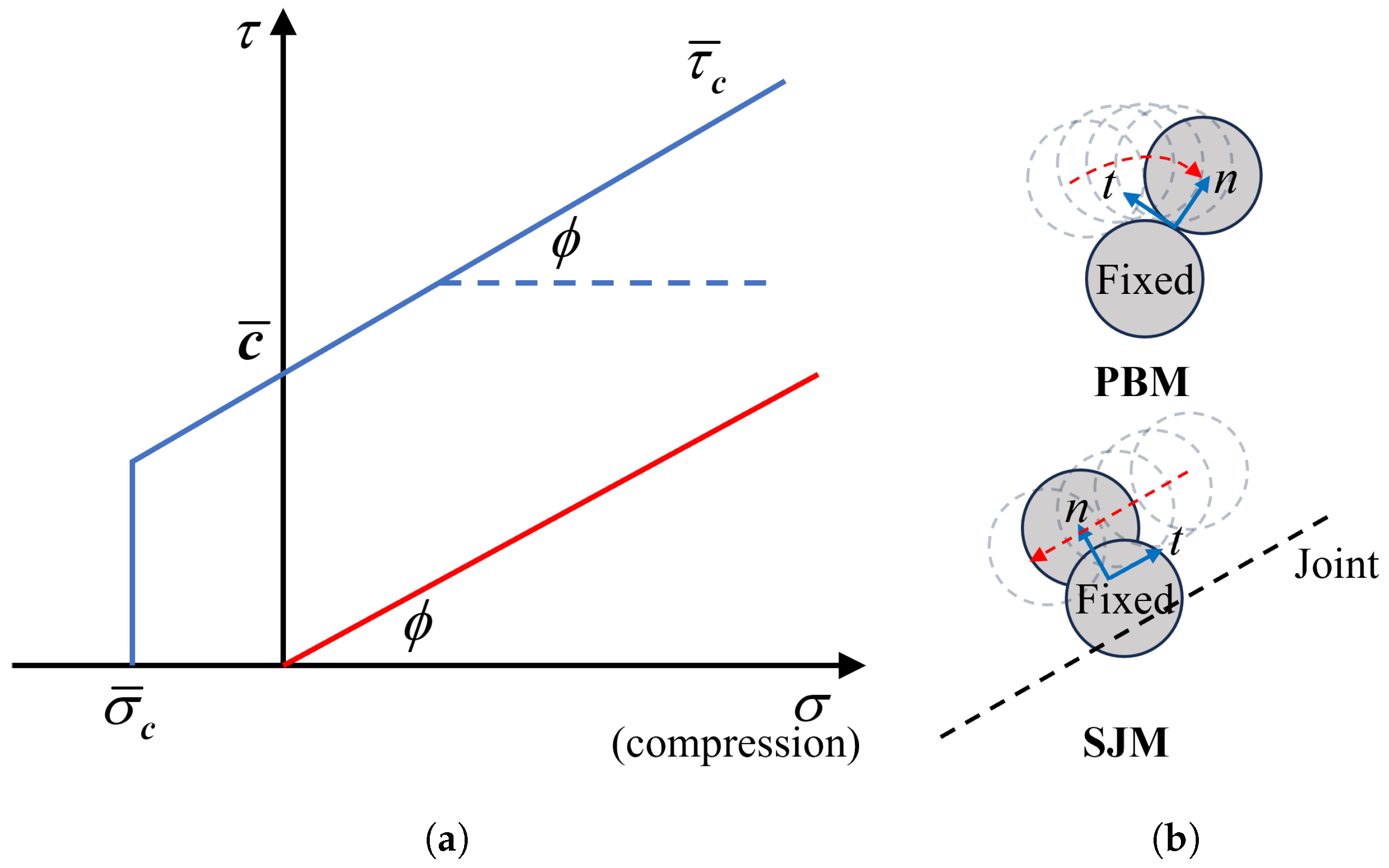
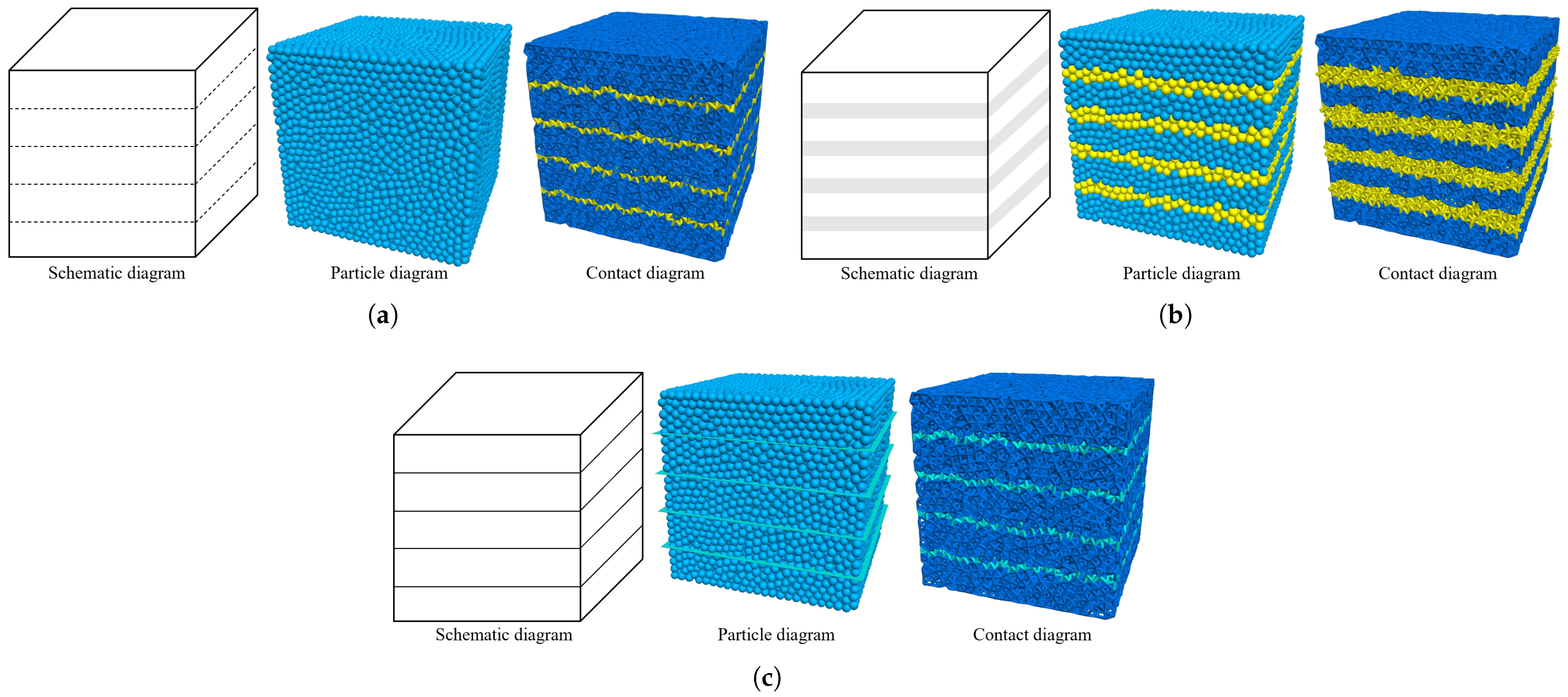
2.2. Model Adaptation for Bedding Planes
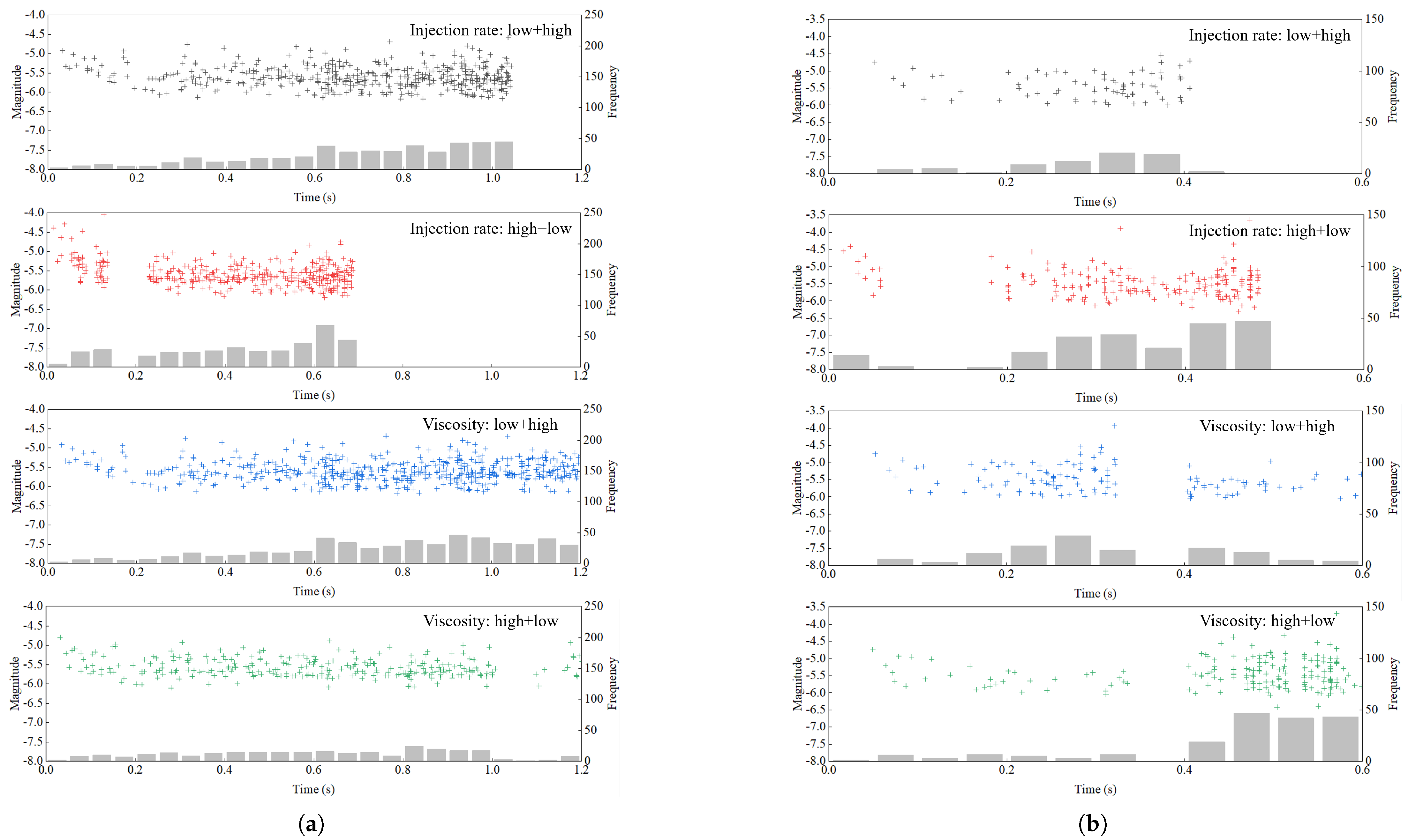
2.3. Seismicity Computation
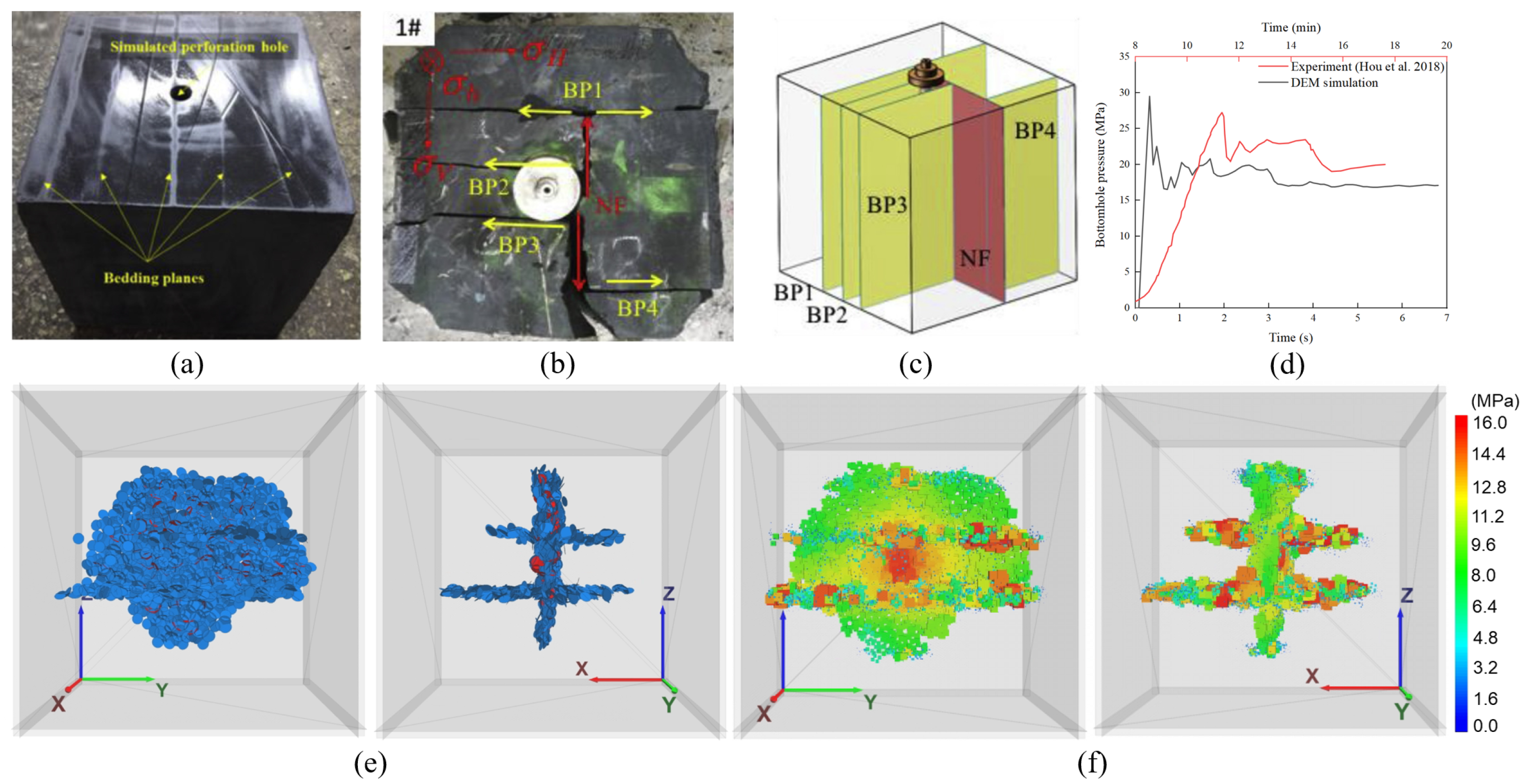
3. Model Setup, Calibration, and Validation
3.1. Model Setup
3.2. Calibration of Mechanical Parameters
3.3. Calibration of Hydraulic Parameters
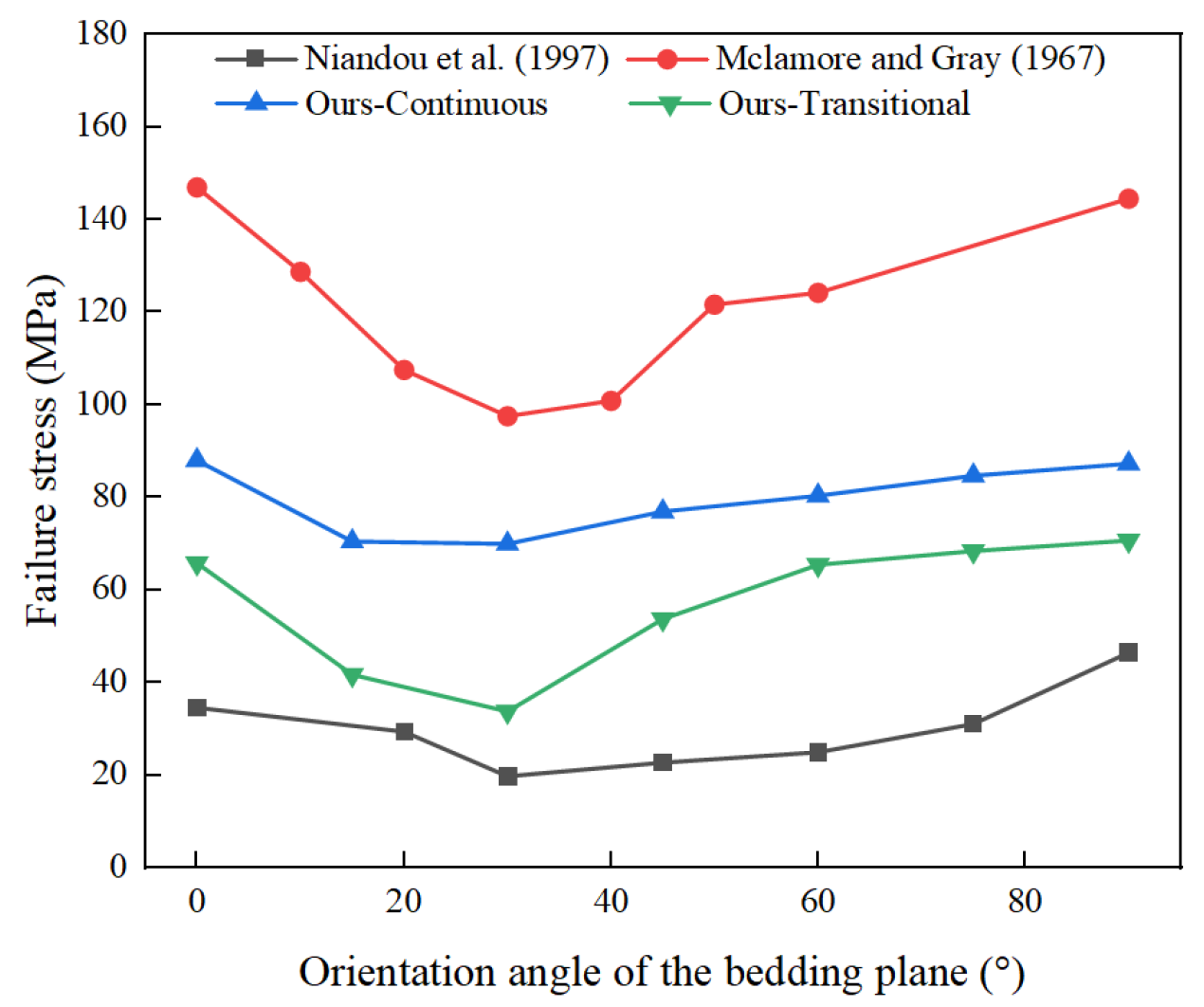
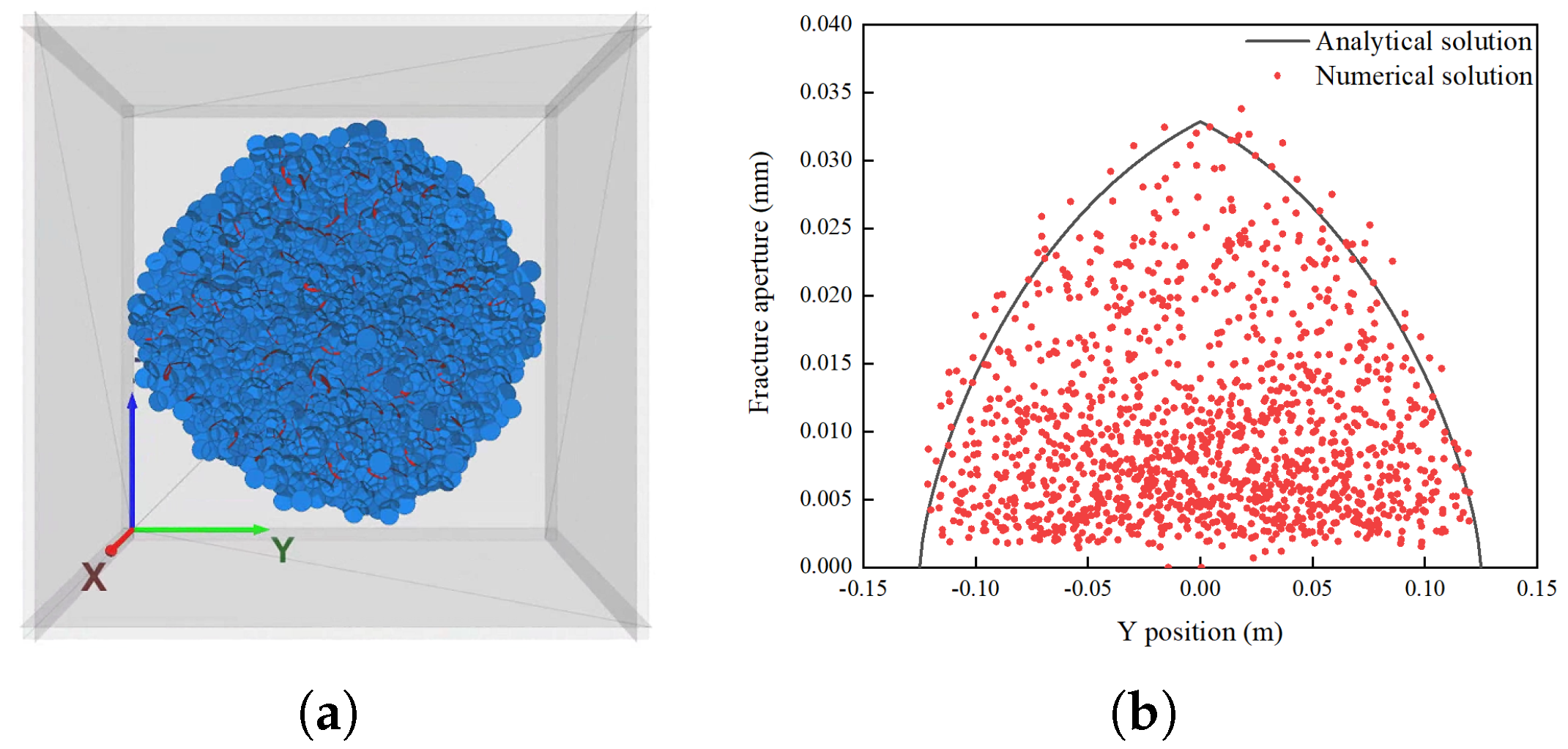
3.4. Model Validation
4. Results and Discussion
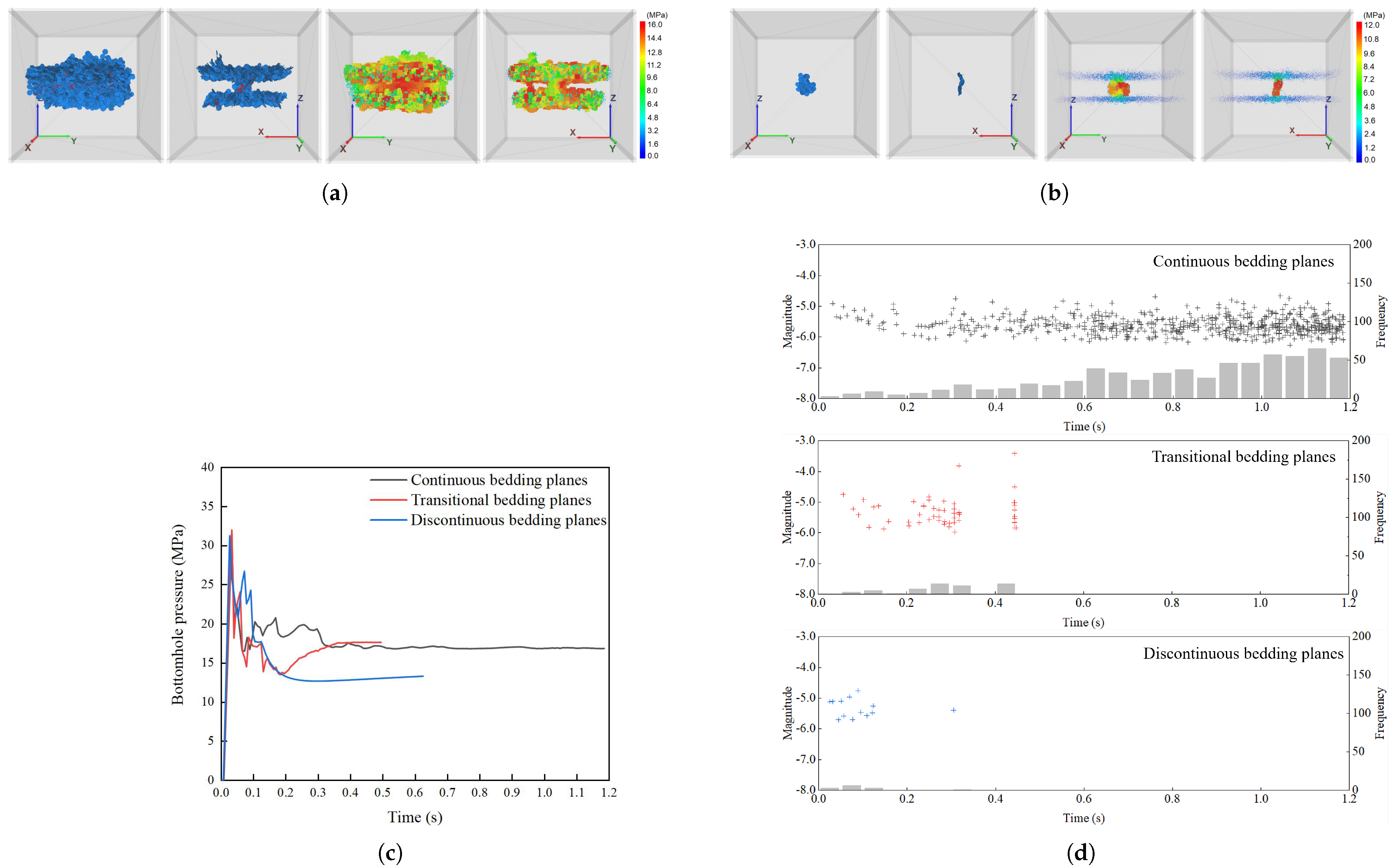
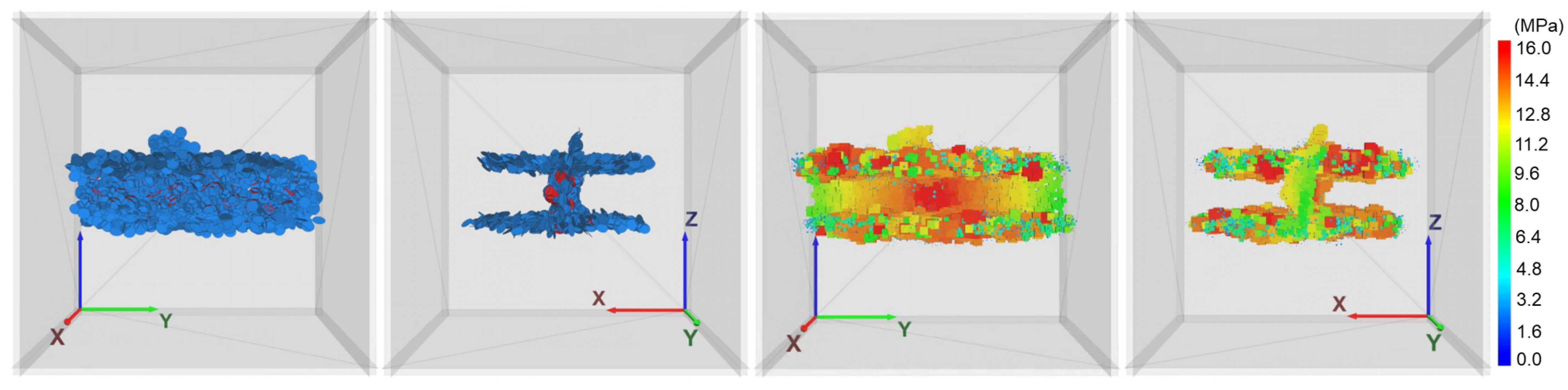
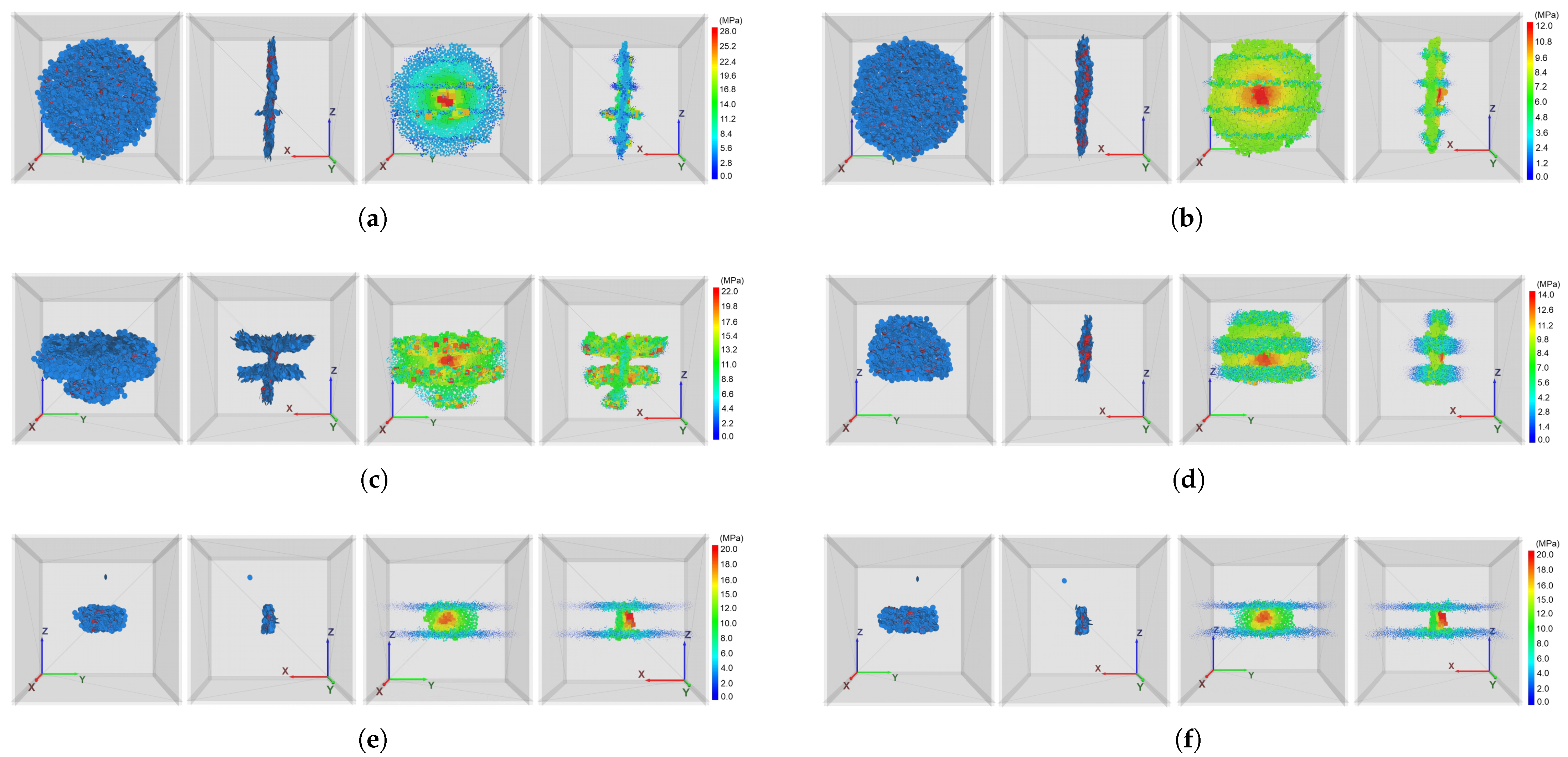
4.1. Impact Comparison of Different Bedding Planes
4.2. Influences of the Plane Thickness and Permeability
4.3. Influences of the Orientation Angle
4.4. Influences of the Fluid Properties
4.5. Injection Scheme Optimization
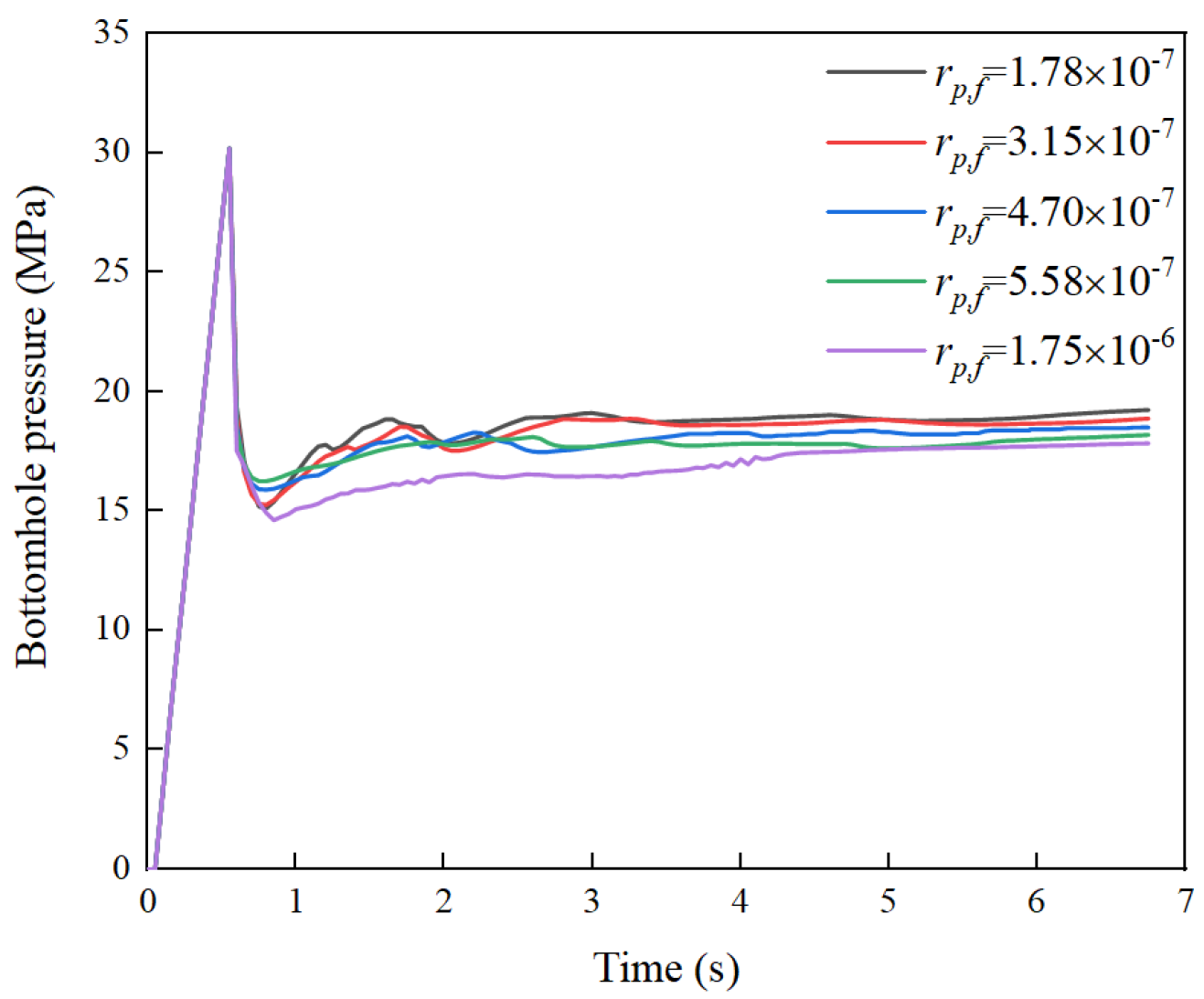
4.6. Impacts of Small-Scale Bedding Planes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, C. Breakthrough and significance of unconventional oil and gas to classical petroleum geology theory. Pet. Explor. Dev. 2017, 44, 1–10. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, G.; Yang, Z.; Tao, S.; Hou, L.; Zhu, R.; Yuan, X.; Ran, Q.; Li, D.; Wang, Z. Geological concepts, characteristics, resource potential and key techniques of unconventional hydrocarbon: On unconventional petroleum geology. Pet. Explor. Dev. 2013, 40, 385–399. [Google Scholar] [CrossRef]
- Li, G.; Luo, K.; Shi, D. Key technologies, engineering management and important suggestions of shale oil/gas development: Case study of a Duvernay shale project in western Canada sedimentary basin. Pet. Explor. Dev. 2020, 47, 791–802. [Google Scholar] [CrossRef]
- Cheng, W.; Jin, Y.; Chen, M. Reactivation mechanism of natural fractures by hydraulic fracturing in naturally fractured shale reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 431–439. [Google Scholar] [CrossRef]
- Cooke, M.L.; Underwood, C.A. Fracture termination and step-over at bedding interfaces due to frictional slip and interface opening. J. Struct. Geol. 2001, 23, 223–238. [Google Scholar] [CrossRef]
- Delale, F.; Erdogan, F. On the mechanical modeling of the interfacial region in bonded half-planes. J. Appl. Mech. 1988, 55, 317–324. [Google Scholar] [CrossRef]
- Teufel, L.W. An Experimental Study of Hydraulic Fracture Propagation in Layered Rock; Texas A&M University: College Station, TX, USA, 1979. [Google Scholar]
- Thiercelin, M.; Roegiers, J.; Boone, T.; Ingraffea, A. An investigation of the material parameters that govern the behavior of fractures approaching rock interfaces. In Proceedings of the 6th ISRM Congress, OnePetro, Montreal, QC, Canada, 30 August–3 September 1987. [Google Scholar]
- Lazar, O.R.; Bohacs, K.M.; Macquaker, J.H.; Schieber, J.; Demko, T.M. Capturing key attributes of fine-grained sedimentary rocks in outcrops, cores, and thin sections: Nomenclature and description guidelines. J. Sediment. Res. 2015, 85, 230–246. [Google Scholar] [CrossRef]
- Shi, Z.; Qiu, Z.; Dong, D.; Lu, B.; Liang, P.; Zhang, M. Lamina characteristics of gas-bearing shale fine-grained sediment of the Silurian Longmaxi Formation of Well Wuxi 2 in Sichuan Basin, SW China. Pet. Explor. Dev. 2018, 45, 358–368. [Google Scholar] [CrossRef]
- Yawar, Z.; Schieber, J. On the origin of silt laminae in laminated shales. Sediment. Geol. 2017, 360, 22–34. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Q.; Zhu, R.; Dong, L.; Fu, J.; Liu, H.; Lu, Y.; Liu, G.; Li, M.; Zhao, X.; et al. Classification of lacustrine shale oil reservoirs in China and its significance. Oil Gas Geol. 2023, 44, 801–810. [Google Scholar]
- Shi, Z.; Dong, D.; Wang, H.; Sun, S.; Wu, J. Reservoir characteristics and genetic mechanisms of gas-bearing shales with different laminae and laminae combinations: A case study of Member 1 of the Lower Silurian Longmaxi shale in Sichuan Basin, SW China. Pet. Explor. Dev. 2020, 47, 888–900. [Google Scholar]
- Gale, J.F.; Laubach, S.E.; Olson, J.E.; Eichhubl, P.; Fall, A. Natural fractures in shale: A review and new observations. AAPG Bull. 2014, 98, 2165–2216. [Google Scholar]
- Zeng, L.; Lü, W.; Xu, X.; Tian, H.; Lu, S.; Zhang, M. Development characteristics, formation mechanism and hydrocarbon significance of bedding fractures in typical tight sandstone and shale. Acta Pet. Sin. 2022, 43, 180. [Google Scholar]
- Ingram, R.L. Terminology for the thickness of stratification and parting units in sedimentary rocks. Geol. Soc. Am. Bull. 1954, 65, 937–938. [Google Scholar]
- Gale, J.F.; Reed, R.M.; Holder, J. Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments. AAPG Bull. 2007, 91, 603–622. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Han, K.; Hou, B.; Chen, M.; Guo, X.; Gao, J. Analysis of hydraulic fracture initiation and vertical propagation behavior in laminated shale formation. Fuel 2017, 206, 482–493. [Google Scholar]
- Zhang, F.; Wu, J.; Huang, H.; Wang, X.; Luo, H.; Yue, W.; Hou, B. Technological parameter optimization for improving the complexity of hydraulic fractures in deep shale reservoirs. Nat. Gas Ind. 2021, 41, 125–135. [Google Scholar]
- Suarez-Rivera, R.; Burghardt, J.; Stanchits, S.; Edelman, E.; Surdi, A. Understanding the effect of rock fabric on fracture complexity for improving completion design and well performance. In Proceedings of the IPTC 2013: International Petroleum Technology Conference. European Association of Geoscientists & Engineers, Beijing, China, 26–28 March 2013; p. cp–350. [Google Scholar]
- Guo, T.; Zhang, S.; Qu, Z.; Zhou, T.; Xiao, Y.; Gao, J. Experimental study of hydraulic fracturing for shale by stimulated reservoir volume. Fuel 2014, 128, 373–380. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J. Experimental investigation of the effect of bedding planes on hydraulic fracturing under true triaxial stress. Rock Mech. Rock Eng. 2017, 50, 2627–2643. [Google Scholar]
- Hou, B.; Zhang, R.; Zeng, Y.; Fu, W.; Muhadasi, Y.; Chen, M. Analysis of hydraulic fracture initiation and propagation in deep shale formation with high horizontal stress difference. J. Pet. Sci. Eng. 2018, 170, 231–243. [Google Scholar] [CrossRef]
- Zhang, R.; Hou, B.; Han, H.; Fan, M.; Chen, M. Experimental investigation on fracture morphology in laminated shale formation by hydraulic fracturing. J. Pet. Sci. Eng. 2019, 177, 442–451. [Google Scholar]
- Zhang, Y.; Long, A.; Zhao, Y.; Zang, A.; Wang, C. Mutual impact of true triaxial stress, borehole orientation and bedding inclination on laboratory hydraulic fracturing of Lushan shale. J. Rock Mech. Geotech. Eng. 2023, 15, 3131–3147. [Google Scholar]
- Sun, K.; Zhang, S.; Xin, L. Impacts of bedding directions of shale gas reservoirs on hydraulically induced crack propagation. Nat. Gas Ind. B 2016, 3, 139–145. [Google Scholar]
- He, Z.; Duan, B. Dynamic modeling of bedding-plane slip during hydraulic fracturing. Geophysics 2019, 84, KS95–KS104. [Google Scholar]
- Sun, C.; Zheng, H.; Liu, W.D.; Lu, W. Numerical simulation analysis of vertical propagation of hydraulic fracture in bedding plane. Eng. Fract. Mech. 2020, 232, 107056. [Google Scholar]
- Figueiredo, B.; Tsang, C.F.; Rutqvist, J.; Niemi, A. Study of hydraulic fracturing processes in shale formations with complex geological settings. J. Pet. Sci. Eng. 2017, 152, 361–374. [Google Scholar] [CrossRef]
- Liu, J.; Liang, X.; Xue, Y.; Fu, Y.; Yao, K.; Dou, F. Investigation on crack initiation and propagation in hydraulic fracturing of bedded shale by hybrid phase-field modeling. Theor. Appl. Fract. Mech. 2020, 108, 102651. [Google Scholar]
- Nagel, N.; Sanchez-Nagel, M.; Zhang, F.; Garcia, X.; Lee, B. Coupled numerical evaluations of the geomechanical interactions between a hydraulic fracture stimulation and a natural fracture system in shale formations. Rock Mech. Rock Eng. 2013, 46, 581–609. [Google Scholar]
- Zhang, Y.; Liu, Z.; Han, B.; Zhu, S.; Zhang, X. Numerical study of hydraulic fracture propagation in inherently laminated rocks accounting for bedding plane properties. J. Pet. Sci. Eng. 2022, 210, 109798. [Google Scholar] [CrossRef]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar]
- Zhou, T.; Wang, H.; Li, F.; Li, Y.; Zou, Y.; Zhang, C. Numerical simulation of hydraulic fracture propagation in laminated shale reservoirs. Pet. Explor. Dev. 2020, 47, 1117–1130. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, H.; Zhao, Z.; Chen, Z. DEM modeling of interaction between the propagating fracture and multiple pre-existing cemented discontinuities in shale. Rock Mech. Rock Eng. 2019, 52, 1993–2001. [Google Scholar] [CrossRef]
- Lei, B.; Zuo, J.; Liu, H.; Wang, J.; Xu, F.; Li, H. Experimental and numerical investigation on shale fracture behavior with different bedding properties. Eng. Fract. Mech. 2021, 247, 107639. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.; Stephansson, O. Numerical investigation on optimized stimulation of intact and naturally fractured deep geothermal reservoirs using hydro-mechanical coupled discrete particles joints model. Geothermics 2014, 52, 165–184. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Discrete element modeling of cyclic rate fluid injection at multiple locations in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2015, 74, 15–23. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.; Stephansson, O.; Hofmann, H.; Zimmermann, G. Discrete element modelling of hydraulic fracture propagation and dynamic interaction with natural fractures in hard rock. Procedia Eng. 2017, 191, 1023–1031. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E.; Mack, M. Fully coupled simulation of a hydraulic fracture interacting with natural fractures with a hybrid discrete-continuum method. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1430–1452. [Google Scholar] [CrossRef]
- Zhang, F.; Damjanac, B.; Maxwell, S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling. Rock Mech. Rock Eng. 2019, 52, 5137–5160. [Google Scholar] [CrossRef]
- Kwok, C.Y.; Duan, K.; Pierce, M. Modeling hydraulic fracturing in jointed shale formation with the use of fully coupled discrete element method. Acta Geotech. 2020, 15, 245–264. [Google Scholar] [CrossRef]
- Liu, M.; Luo, X.; Bi, R.; Zhou, J.; Du, K. Impacts of bedding angle and cementation type of bedding planes on mechanical behavior of thin-layer structured bedded rocks under uniaxial compression. Geomech. Energy Environ. 2023, 35, 100473. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Yang, L.; Chang, T.; Jiang, Q. Effects of bedding geometry and cementation strength on shale tensile strength based on discrete element method. Shock Vib. 2021, 2021, 7805617. [Google Scholar] [CrossRef]
- Itasca, C. PFC (particle flow code in 2 and 3 dimensions), version 5.0 [User’s manual]. Numer. Anal. Methods Geomech. 2014, 32, 189–213. [Google Scholar]
- Potyondy, D.O.; Cundall, P. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Mas Ivars, D.; Potyondy, D.; Pierce, M.; Cundall, P. The smooth-joint contact model. In Proceedings of the WCCM8-ECCOMAS, Lido Island, Italy, 30 June–5 July 2008; Volume 2008. 8th. [Google Scholar]
- Deisman, N.; Mas Ivars, D.; Pierce, M. PFC2D Smooth joint contact model numerical experiments. In Proceedings of the GeoEdmonton, Edmonton, AB, Canada, 21–24 September 2008; Volume 8. [Google Scholar]
- Lambert, C.; Coll, C. Discrete modeling of rock joints with a smooth-joint contact model. J. Rock Mech. Geotech. Eng. 2014, 6, 1–12. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Young, R.P. Moment tensors and micromechanical models. Tectonophysics 2002, 356, 181–197. [Google Scholar] [CrossRef]
- Hazzard, J.; Young, R.P. Dynamic modelling of induced seismicity. Int. J. Rock Mech. Min. Sci. 2004, 41, 1365–1376. [Google Scholar] [CrossRef]
- Heng, S.; Li, X.; Liu, X.; Chen, Y. Experimental study on the mechanical properties of bedding planes in shale. J. Nat. Gas Sci. Eng. 2020, 76, 103161. [Google Scholar] [CrossRef]
- Liu, L.; Li, H.; Chen, S.; Shao, Z.; Zhou, C.; Fu, S. Effects of bedding planes on mechanical characteristics and crack evolution of rocks containing a single pre-existing flaw. Eng. Geol. 2021, 293, 106325. [Google Scholar] [CrossRef]
- Niandou, H.; Shao, J.; Henry, J.; Fourmaintraux, D. Laboratory investigation of the mechanical behaviour of Tournemire shale. Int. J. Rock Mech. Min. Sci. 1997, 34, 3–16. [Google Scholar] [CrossRef]
- Mclamore, W. The mechanical behavior of anisotropic sedimentary rocks. Trans. Am. Soc. Mech. Engrs. 1967, 89, 62–76. [Google Scholar]
- Yoon, J.S.; Zimmermann, G.; Zang, A.; Stephansson, O. Discrete element modeling of fluid injection–induced seismicity and activation of nearby fault. Can. Geotech. J. 2015, 52, 1457–1465. [Google Scholar]
- Ghanizadeh, A.; Gasparik, M.; Amann-Hildenbrand, A.; Gensterblum, Y.; Krooss, B.M. Experimental study of fluid transport processes in the matrix system of the European organic-rich shales: I. Scandinavian Alum Shale. Mar. Pet. Geol. 2014, 51, 79–99. [Google Scholar]
- Savitski, A.; Detournay, E. Propagation of a penny-shaped fluid-driven fracture in an impermeable rock: Asymptotic solutions. Int. J. Solids Struct. 2002, 39, 6311–6337. [Google Scholar] [CrossRef]
- Zou, Y.; Ma, X.; Zhang, S.; Zhou, T.; Li, H. Numerical investigation into the influence of bedding plane on hydraulic fracture network propagation in shale formations. Rock Mech. Rock Eng. 2016, 49, 3597–3614. [Google Scholar]
- Zhang, Q.; Zhang, X.P.; Ji, P.Q. Numerical study of interaction between a hydraulic fracture and a weak plane using the bonded-particle model based on moment tensors. Comput. Geotech. 2019, 105, 79–93. [Google Scholar]
- Campbell, C.V. Lamina, laminaset, bed and bedset. Sedimentology 1967, 8, 7–26. [Google Scholar]









| Parameters and Properties | Value | ||||
|---|---|---|---|---|---|
| Model parameter | |||||
| Model size (m) | |||||
| Particle diameter (m) | 1.20–1.44 | ||||
| Porosity (%) | 5.0 | ||||
| Particle count | 21,103 | ||||
| Number of the bedding planes | 4 | ||||
| Mechanical properties | Rock matrix | CBP | TBP | DBP | |
| Elastic modulus (GPa) | 32.10 | 8.97 | 8.97 | - | |
| Poisson’s ratio | 0.16 | 0.23 | 0.23 | - | |
| UCS (MPa) | 100.4 | 30.8 | 30.8 | - | |
| Tensile strength (MPa) | 17.5 | 5.1 | 5.1 | - | |
| Friction stress (MPa) | - | - | - | 0.1 |
| Characteristics and Strategies | CBP | TBP | DBP |
|---|---|---|---|
| Structural characteristics in nature samples | |||
| Thickness (mm) | <1.0 | 1.0–10.0 | <1.0 |
| Spatially continuous | ✔ | ✔ | × |
| Fill-in minerals | quartz, calcite, etc. | quartz, calcite, etc. | - |
| Modeling strategy in DEM model | |||
| Thickness (mm) | - | 2.0 | - |
| Distinct particle property | × | ✔ | × |
| Inter-particle bonding | ✔ | ✔ | × |
| Inter-particle contact model | PBM | PBM | SJM |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Rock matrix | Transitional bedding planes | ||
| Particle elastic modulus (GPa) | 12.0 | Particle elastic modulus (GPa) | 3.4 |
| Particle stiffness ratio | 3.0 | Particle stiffness ratio | 2.5 |
| Particle friction coefficient | 0.9 | Particle friction coefficient | 0.9 |
| PBM elastic modulus (GPa) | 12.0 | PBM elastic modulus (GPa) | 3.4 |
| PBM stiffness ratio | 3.0 | PBM stiffness ratio | 2.5 |
| PBM tensile strength (MPa) | 12.0 | PBM tensile strength (MPa) | 3.7 |
| PBM cohesion (MPa) | 12.0 | PBM cohesion (MPa) | 3.7 |
| PBM friction angle ) | 40.0 | PBM friction angle ) | 30.0 |
| Continuous bedding planes | Discontinuous bedding planes | ||
| PBM elastic modulus (GPa) | 3.4 | SJM friction coefficient | 0.76 |
| PBM stiffness ratio | 2.5 | SJM friction angle ) | 37.5 |
| PBM tensile strength (MPa) | 3.7 | ||
| PBM cohesion (MPa) | 3.7 | ||
| PBM friction angle ) | 30.0 |
| Parameters | Value |
|---|---|
| Sensitive coefficient | −1.5 |
| Zero external load pipe radius (m) | 1.78 |
| Infinite external load pipe radius (m) | 1.78 |
| Breakage pipe radius (m) | 4.70 |
| Permeability scaling coefficient | 5.0 |
| Parameter | Value |
|---|---|
| Vertical stress (MPa) | 25 |
| Maximum horizontal stress (MPa) | 20 |
| Minimum horizontal stress (MPa) | 13 |
| Flow rate (/s) | 5.0 |
| Fluid viscosity (mPa·s) | 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.; Shentu, J.; Lin, B.; Wei, S.; Jin, Y.; Yoon, J.S. Digital Simulation of Hydraulic Fracturing in Laminated Shale Formation Containing Varying Bedding Planes. Processes 2025, 13, 1017. https://doi.org/10.3390/pr13041017
Shi C, Shentu J, Lin B, Wei S, Jin Y, Yoon JS. Digital Simulation of Hydraulic Fracturing in Laminated Shale Formation Containing Varying Bedding Planes. Processes. 2025; 13(4):1017. https://doi.org/10.3390/pr13041017
Chicago/Turabian StyleShi, Can, Junjie Shentu, Botao Lin, Shiming Wei, Yan Jin, and Jeoung Seok Yoon. 2025. "Digital Simulation of Hydraulic Fracturing in Laminated Shale Formation Containing Varying Bedding Planes" Processes 13, no. 4: 1017. https://doi.org/10.3390/pr13041017
APA StyleShi, C., Shentu, J., Lin, B., Wei, S., Jin, Y., & Yoon, J. S. (2025). Digital Simulation of Hydraulic Fracturing in Laminated Shale Formation Containing Varying Bedding Planes. Processes, 13(4), 1017. https://doi.org/10.3390/pr13041017






