Multi-Objective Evaluation Strategy Based on Data Envelopment Analysis for Working Fluid Selection in the Organic Rankine Cycle

Abstract

Currently, in Chinese industry substantial amounts of low-grade waste heat are underutilized. Effectively harnessing these low-temperature waste heat sources is instrumental in promoting energy conservation and emission reduction objectives. The organic Rankine cycle (ORC) serves as an effective method for utilizing low-grade waste heat. The selection of a suitable working fluid is a pivotal aspect of the design of an ORC system. There are many kinds of working fluid and they have complex molecular structures, which increases the difficulty of screening working fluids. A novel approach is proposed based on data envelopment analysis (DEA) for multi-objective evaluation of working fluids. This method takes into account the thermodynamic performance of the working fluid in the ORC (thermal efficiency, net power output, exergy efficiency), economic aspects (investment cost, exergy loss cost), and environmental considerations (exergy environmental factors, CO₂ emission reduction). DEA offers a distinct advantage by objectively balancing these conflicting objectives through data-driven optimization, eliminating the need for subjective weight assignment and enabling simultaneous evaluation of thermodynamic, economic, and environmental metrics in working fluid selection. A total of 62 different working fluids were evaluated in the integrated technology. Heptane working fluid screened out by DEA was compared with working fluid R245fa, a fluid commonly used in existing literatures. The exergy loss of the Heptane working fluid is reduced by 5.02%, the thermal efficiency is increased by 0.24%, and the net output work is increased by 2.04%. The proposed evaluation method introduces a novel perspective for the efficient screening of working fluids in the ORC system for low-temperature waste heat power generation.

1. Introduction

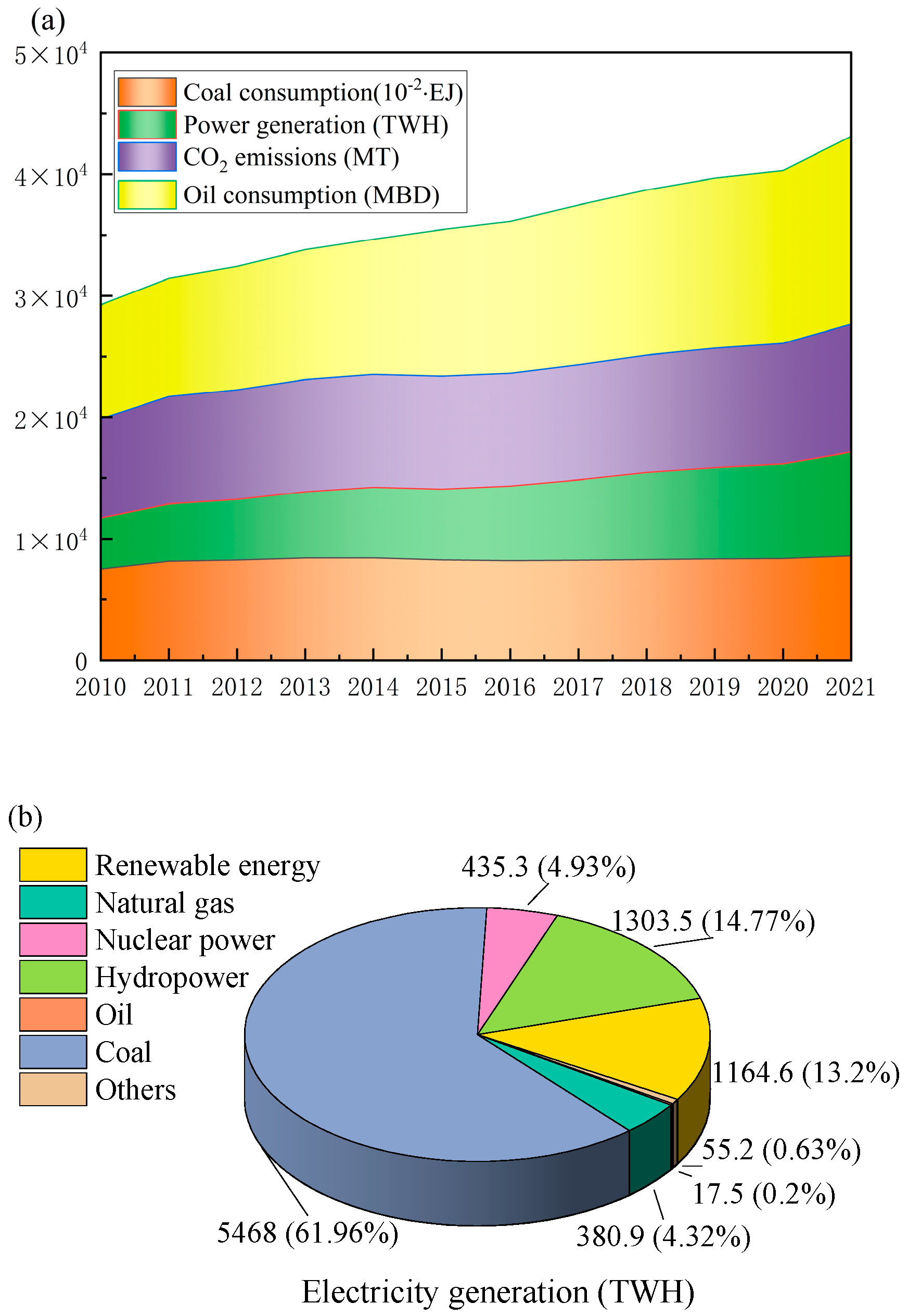
Energy is the cornerstone of contemporary civilization, a pivotal driver for economic development, and an essential material foundation indispensable for the survival and advancement of all entities. With societal development and progress, almost all sectors require increased energy, and the relentless exploitation and utilization of finite energy sources, such as coal and oil, have been ongoing. This unbridled exploitation has led to the depletion of reserves. The global energy issue has emerged as a prominent challenge faced collectively by nations across the globe. According to data from the BP 2022 Statistical Yearbook of World Energy, global primary energy consumption experienced a notable resurgence in 2021, escalating by almost 6%. China’s primary energy consumption showed an annual growth of 7.1%, accounting for approximately 70% of the nation’s total energy consumption. Energy scarcity and environmental pollution become critical bottlenecks constraining the development of ecological civilization and the low-carbon progression of the national economy. As a developing nation, China has proactively implemented measures to meet its energy conservation and carbon reduction targets. Analyzing energy consumption trends from 2010 to 2021 reveals a relatively modest increase in coal consumption (refer to Figure 1) [1]. Nevertheless, China’s energy consumption rate remains elevated, with electricity consumption increasing annually. The advancement of high-efficiency, energy-saving, and emission-reducing technologies holds profound strategic significance in propelling national economic development, mitigating environmental pollution, and expediting the transformation of the energy landscape.

Within industrial production, there is inefficient use of low-temperature waste heat, which contributes to energy scarcity. To address this, the proficient recovery and utilization of low-temperature waste heat is a strategic approach for its recovery. In recent years, low-temperature waste heat power generation technology has received considerable attention [1,2]. Notably, the ORC is a Rankine cycle employing low-boiling-point organic matter as the working fluid, offering advantages such as a broad range of applicable heat source temperatures, simple equipment, and safety and environmental benefits [1,3]. The properties of the organic working fluid have a significant impact on system performance [4], which highlights the crucial importance of choosing the right organic working fluid for the effective application of ORC technology [5,6]. Xie Pan et al. [7] conducted an assessment of working fluid compatibility at different waste heat temperatures, utilizing thermal efficiency as an evaluation criterion. Guo Hao et al. [8], employing an exergic analysis methodology, evaluated diverse working fluids based on exergic efficiency and the exergic loss of individual components under specific heat source temperatures. Notably, common research practices indicate a tendency among scholars to employ one or several thermodynamic characteristics, consolidating them into a singular objective function through linear weighting for the optimization of working fluid performance, which can be subject to inherent subjectivity.

DEA is a quantitative method used to assess the relative efficacy of comparable homogeneous units. The establishment of a linear programming model, based solely on input and output indices, enables the derivation of quantitative evaluation results through solution procedures [9]. The DEA methodology presents distinct advantages, particularly in avoiding subjective biases, simplifying the evaluation process, and enabling quantitative assessments. The methodology offers distinct advantages over traditional evaluation approaches [10]:

Eliminates Subjectivity: Unlike weighted aggregation methods, DEA does not require predefined weights for evaluation criteria, thus avoiding the subjectivity inherent in subjective weight assignment [11].

Handles Multi-Dimensionality: DEA effectively manages complex scenarios with multiple inputs and outputs, making it particularly suitable for evaluating systems with interdependent performance indicators.

Data-Driven Objectivity: By directly analyzing raw data without assuming functional relationships, DEA provides a transparent and empirical basis for efficiency assessment [12].

Benchmarking Capability: DEA identifies efficient DMUs as reference points, enabling underperforming units to benchmark and improve their operations.

These characteristics make DEA an ideal tool for comprehensive performance evaluation in systems where multiple conflicting objectives need to be balanced, such as the organic Rankine cycle (ORC) working fluid selection problem addressed in this study.

This paper proposes a new multi-objective evaluation method for the selection of organic Rankine cycle (ORC) working fluids, and applies this method in the ethylene glycol plant [13,14]. First, we conduct ORC process simulations and optimize all candidate working fluids to determine the operating conditions that yield optimal thermal efficiency for each fluid. Under these conditions, we calculate thermodynamic, economic, and environmental indices for each candidate working fluid.

Finally, we perform a multi-objective evaluation to select a working fluid with optimal overall performance. This analytical method establishes a new criterion for screening organic working fluids in ORC applications. The main innovations and contributions include the following:

(1)

A new methodology based on data envelopment analysis (DEA) for multi-objective assessment of workflows.

(2)

The evaluation of 62 different working fluids and quantitative assessment of the advantages and disadvantages of these fluids in ORC systems.

(3)

The evaluation methodology presented in this paper can be extended to the design of hybrid working fluids, thereby saving significant costs related to simulation and experimental studies. It provides a new perspective for the effective screening of working fluids in ORC systems for low-temperature waste heat power generation.

2. Optimization of the Orc System

Low-temperature waste heat power generation technology has the capability to transform the thermal energy within waste gases and liquids generated during industrial production into electrical energy. The ORC system includes an expander, a working fluid pump, and a heat exchanger, as delineated in Figure 2. The operational principle involves pressurizing a low-temperature and low-pressure working fluid through the pump and sending the medium into the heat exchanger. Within the heat exchanger, the working fluid absorbs heat from the heat source, transitioning into a high-temperature and high-pressure gas. Subsequently, the working fluid enters the expander, whereby a portion of the working fluid’s internal energy is converted into mechanical energy.

In the context of the ORC system for low-temperature waste heat power generation, the cyclic thermal efficiency serves as a pivotal indicator, elucidating the efficacy of converting low-temperature waste heat into electrical energy. Consequently, leveraging the specified low-temperature heat source, the cyclic thermal efficiency is designated as the objective function, with the pump and expander pressures serving as control variables. The Aspen Plus process simulation software is employed for the simulation and optimization of the ORC process. This approach facilitates the derivation of optimal operating conditions for the working fluid, ensuring maximal thermal efficiency.

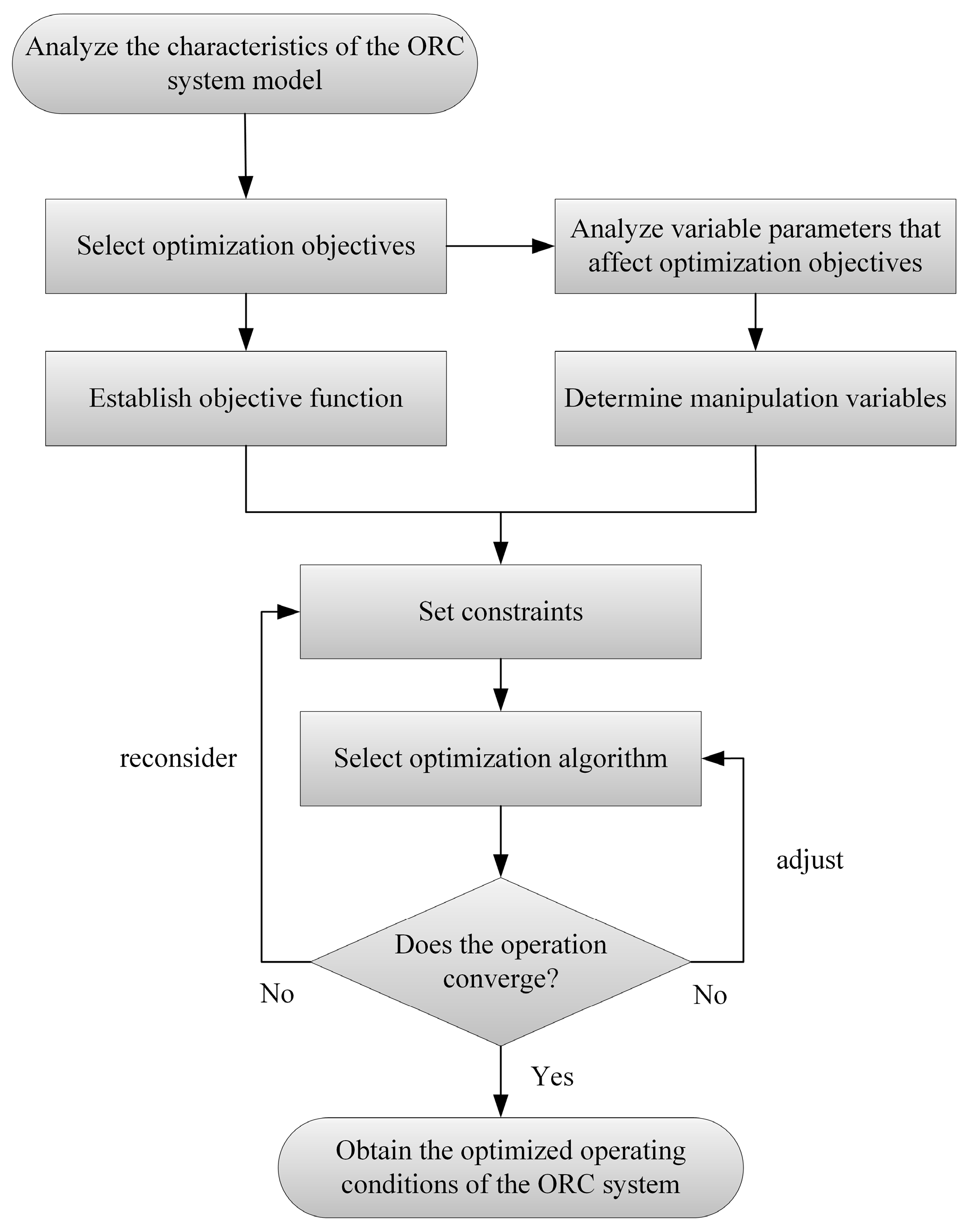
This ORC system operating status optimization diagram starts by analyzing the characteristics of the ORC system model. Then, it progresses through two parallel processes: one is selecting optimization objectives and establishing the objective function, the other is analyzing variable parameters that influence optimization objectives and determining manipulation variables. After setting constraints, an optimization algorithm is chosen. Subsequently, a convergence check is conducted. If the operation does not converge, the algorithm is adjusted or constraints are reconsidered. Once convergence is achieved, the optimized operating conditions of the ORC system are obtained. The optimization procedure is illustrated in Figure 3.

Optimization is predicated on the following assumptions and conditions:

(1)

The ORC system maintains a steady-state flow.

(2)

Friction and pressure losses associated with the flow of organic working fluids in the system are disregarded.

(3)

Isentropic efficiencies of the expander and pump are set at 0.8.

(4)

No pressure drops are considered for the evaporator and condenser, with the evaporating temperature fixed at 120 °C.

The specific optimization model is outlined as follows:

Objective function:

$$max\eta =\left(W_{Exp}-W_{Pum}\right)/Q_{Eva}$$

(1)

Constraint condition:

(1) To ensure that the working fluid steam can be condensed by cooling water, the outlet temperature of the expander is set higher than the cooling water temperature:

$$T_{Exp,out}\ge 40 °\mathrm{C}$$

(2)

(2) According to the cyclic process of the ORC system, the evaporation pressure is higher than the condensation pressure, meaning the outlet pressure of the expander is lower than the inlet pressure of the expander:

$$P_{Exp,out}<P_{Exp,in}$$

(3)

(3) The maximum pressure in the system is set below the corresponding subcritical pressure of the working fluid:

$$P_{Pum}\le 0.9P_c$$

(4)

(4) To safeguard the expander from damage and extend its lifespan, the outlet flow rate is set to be devoid of liquid phase, and the inlet pressure is lower than the saturated vapor pressure of the working fluid at the evaporation temperature:

$${\alpha }_{Exp,out}=1, P_{Eva,in}\le P_{T_{Eva}}^s$$

(5)

(5) To ensure that the expander’s outlet steam is neither superheated nor fails to condense successfully, the outlet pressure is set higher than the saturated vapor pressure of the working fluid at 40 °C:

$$P_{Exp,out}\ge P_{T=40°\mathrm{C}}^s$$

(6)

Following optimization, the operational conditions corresponding to the optimum thermal efficiency of the ORC system are determined for the working fluid, subsequently enabling the calculation of various performance parameters.

3. Calculation of Evaluation Indicators

3.1. Thermodynamic Model

The system’s thermal efficiency, exergic efficiency, and net output work are outcomes derived from the principles of the first and second laws of thermodynamics. These metrics serve to elucidate the efficacy of waste heat recovery within the system. Specifically, the system’s thermal efficiency is articulated as follows:

$${\eta }_{sys}={\displaystyle \frac{W_{net}}{Q_{Eva}}}$$

(7)

Q_Eva (kW) signifies the heat absorbed by the working fluid at intermediate pressure within the evaporator, while W_net (kW) denotes the system’s net output work, computed as follows:

$$Q_{Eva}=m_{wf}\left(h_1-h_5\right)$$

(8)

$$W_{net}=W_{Exp}-W_{Pum}$$

(9)

where m_wf represents the mass flow rate of the organic working fluid (kg·s⁻¹) and hi signifies the enthalpy value at each point measured (J·kg⁻¹). W_Exp (kW) quantifies the work accomplished through the entropy expansion of the working fluid within the expander, while W_Pum (kW) denotes the work expended due to the entropy compression of the working fluid within the pump.

The exergic efficiency of the system is as follows:

$${\eta }_{exg}={\displaystyle \frac{W_{net}}{E_{sys}}}={\displaystyle \frac{W_{net}}{W_{net}+I_{sys}}}$$

(10)

$$I_{sys}=I_{Eva}+I_{Exp}+I_{Con}+I_{Pum}$$

(11)

$E_{sys}$ is the exergic loss of the system and $I_{sys}$ is the total exergic loss of all components in the system. The exergic loss of all components can be calculated as follows:

Exergic loss of evaporator I_Eva (kW):

$$I_{Eva}=E_{hot,in}+E_{cold,in}-E_{hot,out}-E_{cold,out}$$

(12)

Exergic loss of expander I_Exp (kW):

$$I_{Exp}=E_{Exp,in}-E_{Exp,out}-W_{Exp}$$

(13)

Exergic loss of condenser I_Con (kW):

$$I_{Con}=E_{Con,out}+E_{XQ}-E_{Con,in}$$

(14)

$$E_{XQ}=Q_{Con}\left(1-{\displaystyle \frac{T_0}{T_m}}\right)$$

(15)

$$T_m={\displaystyle \frac{\left(T_{Con,out}-T_{Con,in}\right)}{\ln \frac{T_{Con,out}}{T_{Con,in}}}}$$

(16)

Exergic loss of pump I_Pum (kW):

$$I_{Pum}=E_{Pum,in}-E_{Pum,out}+W_{Pum}$$

(17)

where the subscripts delineate distinct parameters: “hot” denotes the heat flow from the heat exchanger, “cold” designates the cold flow, “out” signifies the output of the unit component, and “in” corresponds to the input. “E_XQ” symbolizes the heat from a constant-temperature heat source Q, kW. “E_i” represents the exergy of component i, kW. “T₀” denotes the ambient temperature, K, while “Tm” signifies the temperature of the heat source, K.

3.2. Economic Model

Investment costs predominantly encompass both equipment costs and annual operating costs. The equipment cost, specifically pertaining to the expander, evaporator, condenser, and pump, can be determined through the application of the subsequent formula [15]:

$$Y={\left({\displaystyle \frac{Q}{Q_B}}\right)}^M{Z}_B{f}_P{f}_T{f}_m$$

(18)

Y signifies the cost of each component (USD). For pumps and expanders, Q represents the work (kW), while for evaporators and condensers Q denotes the heat transfer area (m²). Q_B represents the basic size of the unit component, M corresponds to the cost index of the unit component, and Z_B represents the benchmark cost of the unit component. The associated cost calculation coefficient for each unit component [16,17] is outlined in

Table 1. Cost calculation for each unit component in the system.

Unit Component	Basic Size	Cost Index	Benchmark Costs	fP	fT	fm	Material
expander	250	0.46	98,400	1	1.6	1	carbon steel
pump	4	0.55	9840	1.5	1	1	carbon steel
evaporator	80	0.68	32,800	1.5	1.6	1	carbon steel
condenser	80	0.68	32,800	1	1.6	1	carbon steel

.

Annual operating expenditures comprise both annual electricity consumption and annual water consumption. The annual cost attributed to electricity consumption is denoted as V (USD) and determined by the subsequent formula:

$$V=C_{ele}{W}_{Pum}t$$

(19)

C_ele represents the unit price of electricity, set at 0.11 USD/kWh, and t denotes the annual operating time of the system device, calculated as 8000 h [18].

Annual water charges are recorded as U (USD) and are calculated as follows:

$$U=C_{cw}{Q}_{Con}t$$

(20)

C_cw is the unit price of water charge, set at 0.35 USD/GJ, Q_Con is the condenser heat load (GJ/h), and t is the system operating time in a year, calculated as 8000 h.

The ORC system will have exergic loss during operation, and the economic waste caused by exergic loss is called the exergic loss cost, which is calculated as follows:

$$C_{D_{sys}}=C_{D_{Exp}}+C_{D_{Eva}}+C_{D_{Con}}+C_{D_{Pum}}$$

(21)

$C_{D_{\mathit{sys}}}$ represents the overall exergic loss cost of the system, while $C_{D_{\mathit{Exp}}}$, $C_{D_{\mathit{Eva}}}$, $C_{D_{\mathit{Con}}}$, and $C_{D_{\mathit{Pum}}}$ represent the exergic loss cost of the expander, evaporator, condenser, and pump, respectively. The formula is as follows:

$$C_{D_k}=3600{\displaystyle \frac{I_k{C}_{F_k}}{{10}^6}}$$

(22)

$C_{D_k}$ indicates the exergic cost of a unit part k, I_k indicates the exergic cost of a unit part K, and $C_{F_k}$ indicates the average cost of fuel used per exergic unit.

For the convenience of explanation, based on the fact that the investment cost dominates compared with the operation and maintenance cost [18], this study has employed a simplified model that ignores the operation and maintenance cost. If it is necessary to further establish a more accurate and rigorous model, the operation and maintenance cost should be taken into account.

3.3. Environmental Model

The organic Rankine cycle (ORC) system stands as a means to repurpose industrial waste heat, geothermal energy, and other energy sources, concurrently diminishing CO₂ emissions in accordance with energy conservation and emission reduction imperatives. Consequently, the reduction in CO₂ emissions assumes significance as a pivotal metric for gauging the operational efficacy of the system. Exergic environmental factors, including CO₂ emission reduction, are chosen to appraise the merits and drawbacks of the organic working medium within the ORC system. The calculation model for these indices is articulated as follows:

System CO₂ emission reduction [19]:

$$m_{C{O}_2}=W_{net}{\beta }_{C{O}_2}$$

(23)

where ${\beta }_{{CO}_2}$ is the CO₂ emission coefficient: that is, the amount of CO₂ emitted during the production of unit electric energy, usually 0.872 kg/(kWh) [20].

The exergic environmental factors of the system are as follows:

$$f_{ei}={\displaystyle \frac{I_{sys}}{E_{sys,in}}}={\displaystyle \frac{I_{sys}}{E_{Eva,in}+E_{Exp,in}+E_{Con,in}+E_{Pum,in}}}$$

(24)

The exergy environmental factor serves as an indicator of the potential impact on the environment. A smaller exergy value implies a reduced environmental impact.

4. Multi-Objective Evaluation Strategy

The DEA method is an outcome of interdisciplinary research involving operations research, management science, and mathematical economics. Primarily applied for assessing the relative efficiency of homogeneous decision-making units (DMUs) with multiple inputs and outputs, DEA stands out as a non-parametric method.

As a non-parametric methodology that does not require predefined weights [21], DEA automatically optimizes the combined weight of the input and output through linear programming. It is completely data-driven and avoids subjective assignment biases. Its advantages lie in not requiring preset weights. It is suitable for multi-input and multi-output scenarios and objectively reflects the relative efficiency of decision-making units.

Its principal advantage over other methods lies in its exemption from assuming the production function and estimating pertinent parameters in advance. Instead, it yields relatively objective and practical quantitative evaluation results based directly on the original input and output data. The fundamental models of DEA are categorized into the Charnes–Cooper–Rhodes (CCR) model, based on constant returns to scale [22], and the Bankers–Charnes–Cooper (BCC) model, based on variable returns to scale [23]. The efficiency calculated by the CCR model typically represents overall efficiency, while that derived from the BCC model signifies pure technical efficiency. In this study, we mainly focused on overall efficiency and chose the CCR model to comprehensively evaluate the working fluid of the ORC system.

Consider a scenario where there exists n decision units (DMUs), each possessing m inputs and s outputs. Denoted as input X_j and output Y_j, respectively, we express these as X_j = (x_1j, x_2j, …, x_mj)^T, Y_j = (y_1j, y_2j, …, y_sj)^T, and j = 1, 2, …, n. For a designated DMU_k, with k = 1, 2, … n, the dual programming of the CCR model, essential for assessing its validity, is formulated as follows [13]:

$$\left\{\begin{array}{l}Min\left[\theta -\epsilon \left({\displaystyle \sum _{i=1}^m{S}_i^{+}}+{\displaystyle \sum _{r=1}^s{S}_r^{-}}\right)\right]\\ s.t.{\displaystyle \sum _{j=1}^n{\lambda }_j{x}_{ij}}+S^{-}=\theta x_{ik},S^{-}\ge 0,\\ {\displaystyle \sum _{j=1}^n{\lambda }_j{y}_{rj}}-S^{+}=y_{rk},S^{+}\ge 0,{\lambda }_j\ge 0.\end{array}\right.$$

(25)

where ε denotes a non-Archimedean infinitesimally small quantity (typically an arbitrarily small positive number, often set at 10⁻⁶); θ represents the effective value of DMUk, signifying the efficient utilization degree of output relative to input; λ is the combination ratio of the jth decision unit within an effectively reconstructed DMU combination relative to DMUk; and S⁺ denotes the slack variable, while S⁻ represents the residual variable, indicating potential input redundancy and output deficiency of the DMU. A DMU is deemed optimal when θ equals 1, and both S⁺ and S⁻ are zero. In cases where θ equals 1 but S⁺ or S⁻ is non-zero, the DMU is considered a weak DEA efficient. In such instances, within a system comprising DMUs, the input index can reduce S⁻ while maintaining the original output or increase the output S⁺ without altering the original input. When θ is less than 1, the DMU is categorized as non-DEA efficient, with smaller values indicating a greater distance from the optimal frontier.

Utilizing the DEA method, a multi-objective evaluation of the organic working fluid within the ORC system is conducted, considering performance, economy, and environmental aspects. The evaluation framework is delineated in Figure 4. The objective of this assessment is to identify the optimal working fluid from a myriad of options for the system. As depicted in the figure, the evaluation strategy encompasses three assessment systems: thermodynamic and economic performance, thermodynamic and environmental performance, and thermodynamic, economic, and environmental performance. Through a cross-combination approach, working fluid evaluation outcomes catering to diverse user requirements are ascertained.

The working fluid is a crucial working fluid for realizing waste heat power conversion. It can transfer heat from a lower temperature to a higher temperature. The existing literature reports that there are more than 140 kinds of working fluids suitable for ORC systems. Based on the concept of low-carbon environmental protection, in order to better achieve the goal of low-carbon and near-zero emissions, according to the content of the Kigali Amendment to the Montreal Protocol, the application of hydrofluorocarbon CFCs, HCFCs, PFCs, and other working fluids has been gradually canceled, which can meet the ORC system. The working fluid is gradually reduced to more than 60 kinds. The 62 working fluids selected in this paper take into account environmental factors (global warming potential ozone depletion potential (ODP), global warming potential (GWP)), basic physical properties of working fluids, and other factors, and study the comprehensive performance of these working fluids in ORC systems, as detailed in

Table 2. Working fluid to be evaluated.

CAS	Alias or English Name	CAS	Alias or English Name	CAS	Alias or English Name
75-69-4	R11	71-43-2	Benzene	460-73-1	R245fa
75-71-8	R12	108-88-3	Toluene	677-56-5	R236cb
76-13-1	R113	67-64-1	Acetone	690-39-1	R236fa
76-14-2	R114	756-13-8	Novec649	431-63-0	R236ea
76-15-3	R115	115-10-6	E170	406-58-6	R365mfc
74-98-6	R290	75-45-6	R22	156-59-2	R1132(Z)
75-19-4	R270	75-10-5	R32	156-60-5	R1132(E)
106-97-8	R600	75-43-4	R21	102687-65-0	R1233zd(E)
75-28-5	R600a	306-83-2	R123	29118-24-9	R1234ze(e)
78-78-4	R601a	63938-10-3	R124	754-12-1	R1234yf
109-66-0	R601	75-68-3	R142b	29118-25-0	R1234ze(Z)
107-83-5	NSC66496	76-19-7	R218	690-27-7	R1225zc
463-82-1	2,2-Dime	355-25-9	R3110	5528-43-8	R1225ye(Z)
110-82-7	CHX	115-25-3	RC318	116-15-4	R1216
110-54-3	Hexane	678-26-2	DDFP	677-21-4	R1243zf
142-82-5	Heptane	353-36-6	R161	359-11-5	R1123
111-65-9	1-Octane	811-97-2	R134a	355-42-0	FC-72
115-07-1	R1270	420-46-2	R143a	56-23-5	R10
106-98-9	Butene	75-37-6	R152a	616-38-6	DMC
115-11-7	Isobutene	431-89-0	R227ea	1885-48-9	RE245fa2
74-99-7	Propyne	679-86-7	R245ca

.

This DEA-based multi-objective evaluation strategy for ORC working fluids starts by selecting a working fluid set, obtaining its basic physical properties, and building both the ORC system and its optimization model, iterating the optimization process until convergence to acquire optimal operating parameters. It then incorporates economic performance indicators (investment cost, effective energy loss cost), thermodynamic performance indicators (thermal efficiency, exergy efficiency, net output power), and environmental performance indicators (effective energy environmental factors, CO₂ reduction emissions). Finally, through three DEA evaluations (DEA evaluation 1, DEA evaluation 2, DEA evaluation 3), the strategy integrates these multi-objective indicators and outputs comprehensive evaluation results. The procedure is illustrated in Figure 4.

5. Results

5.1. Single-Objective Evaluation Results

Leveraging the optimization and computational outcomes (normalization) of the ORC system, a univariate evaluation of the working fluid is undertaken, employing thermodynamic performance metrics such as thermal efficiency, net output work, and exergic efficiency. Furthermore, economic performance is gauged using investment cost and exergic loss cost, while environmental considerations encompass CO₂ emission reduction and exergic environmental factors. These parameters collectively serve as the evaluation indices for this comprehensive assessment of the working fluid.

5.1.1. Thermodynamic Index Evaluation Results

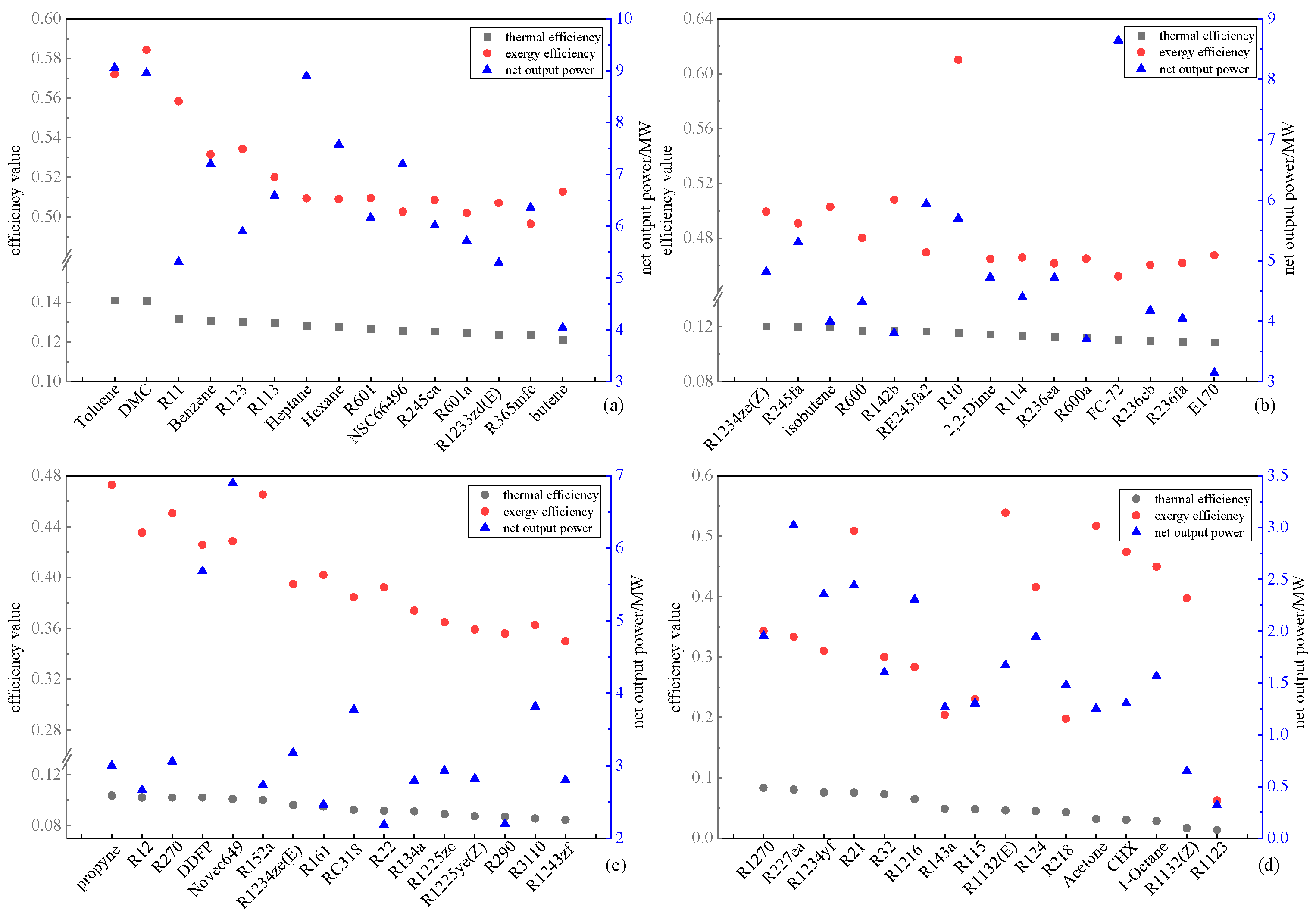
The results of the single-objective evaluation, utilizing thermodynamic performance as the primary index, are presented in Figure 5. Thermodynamic performance serves as a metric reflecting the extent of the ORC system’s recovery and utilization of waste heat. Taking thermal efficiency as an illustrative example, a higher thermal efficiency signifies an improved waste heat recovery effect, consequently elevating the priority of the corresponding working fluid. The working fluids are categorized into four grades—A, B, C, and D—based on the thermal efficiency value, ranging from high to low, as depicted in Figure 5 (a), (b), (c), and (d), respectively. Grade A denotes the superior working fluid, followed by grades B and C, with Grade D representing the least favorable. It is evident that substantial disparities exist in the single-objective evaluation outcomes across the three indices. For instance, working fluid R1132(E) holds the 55th and 53rd positions in the thermal efficiency and net work output evaluations, designating it as a Grade D working fluid. However, it secures the fifth position in the exergic efficiency evaluation, classifying it as a Grade A working fluid. Notably, the figure illustrates a counteractive trend between net output work and thermal efficiency for certain working fluids like Heptane, R10, DDFP, Novec649, etc. This phenomenon is linked to the working fluid’s capacity to absorb heat in the evaporator, where the rate of heat absorption surpasses the increase in net output work, resulting in a scenario where thermal efficiency decreases with the rise in net power generation.

5.1.2. Evaluation Results of Economic Indicators

As depicted in Figure 6, both exergic cost and exergic loss cost represent expenses incurred during enterprise operations. A lower cost is advantageous for enterprise functionality, signifying a higher priority for the corresponding working fluid. Hence, the working fluids are categorized into four grades—A, B, C, and D—based on the order of investment cost, ranging from low to high. Reflecting Figure 6 (a), (b), (c), and (d), respectively, Grade A designates the superior working fluid, followed by Grades B and C, with Grade D representing the least favorable. Notably, substantial differences emerge in the ranking of working chemicals concerning investment cost and exergic loss cost, including instances of inverse rankings. For instance, R1123 is classified as Grade A and optimal in the assessment of investment cost, while earning a Grade C in the evaluation of exergic loss cost.

5.1.3. Environmental Index Evaluation Results

Exergic environmental factors and CO₂ reduction serve as measures to assess whether an enterprise’s operations align with the principles of green and low-carbon development, as illustrated in Figure 7. A lower exergic environmental factor implies reduced environmental impact, elevating the priority of the corresponding working fluid. Exergic environmental factors associated with working fluids are categorized into four grades—A, B, C, and D—aligning with Figure 7 (a), (b), (c), and (d), respectively. Grade A denotes the superior working fluid, followed by Grades B and C, with Grade D representing the least favorable. Notably, working fluids such as R1132(Z), Acetone, 1-Octane, CHX, and R1132(E) exhibit minimal exergic factors, indicating optimal performance. Conversely, when CO₂ emission reduction is utilized as an evaluation index, Toluene, DMC, Heptane, and FC-72 emerge with the highest CO₂ emission reduction and superior performance. The two evaluation outcomes display inconsistencies, with some working fluids even securing opposing rankings. For instance, working fluid R1132(Z) claims the top position in the former evaluation, marking it as the best, while it ranks second to last in the latter assessment.

In conclusion, it becomes evident that the single-objective evaluation method, when applied to assess working fluids, tends to be one-sided and lacks objectivity. The adoption of multiple single-objective evaluation combinations may result in disparities or even contradictions in the categorization of working quality across different evaluation indexes, preventing the effective screening of working fluids. Consequently, we propose the subsequent multi-objective evaluation method based on the DEA method.

5.2. Results of Multi-Objective Evaluation

Exergic loss cost, investment cost, and exergic environmental factors are designated as input indices, whereas exergic efficiency, net output work, exergic efficiency, and CO₂ emission reduction are designated as output indices. This consideration is based on the thermodynamic, economic, and environmental performance of the ORC system during operation, stemming from the optimization and computation results of various indices. The evaluation and screening of the working fluid for the ORC system are undertaken using the DEA multi-objective evaluation method.

5.2.1. Evaluation of Thermodynamic and Economic Performance

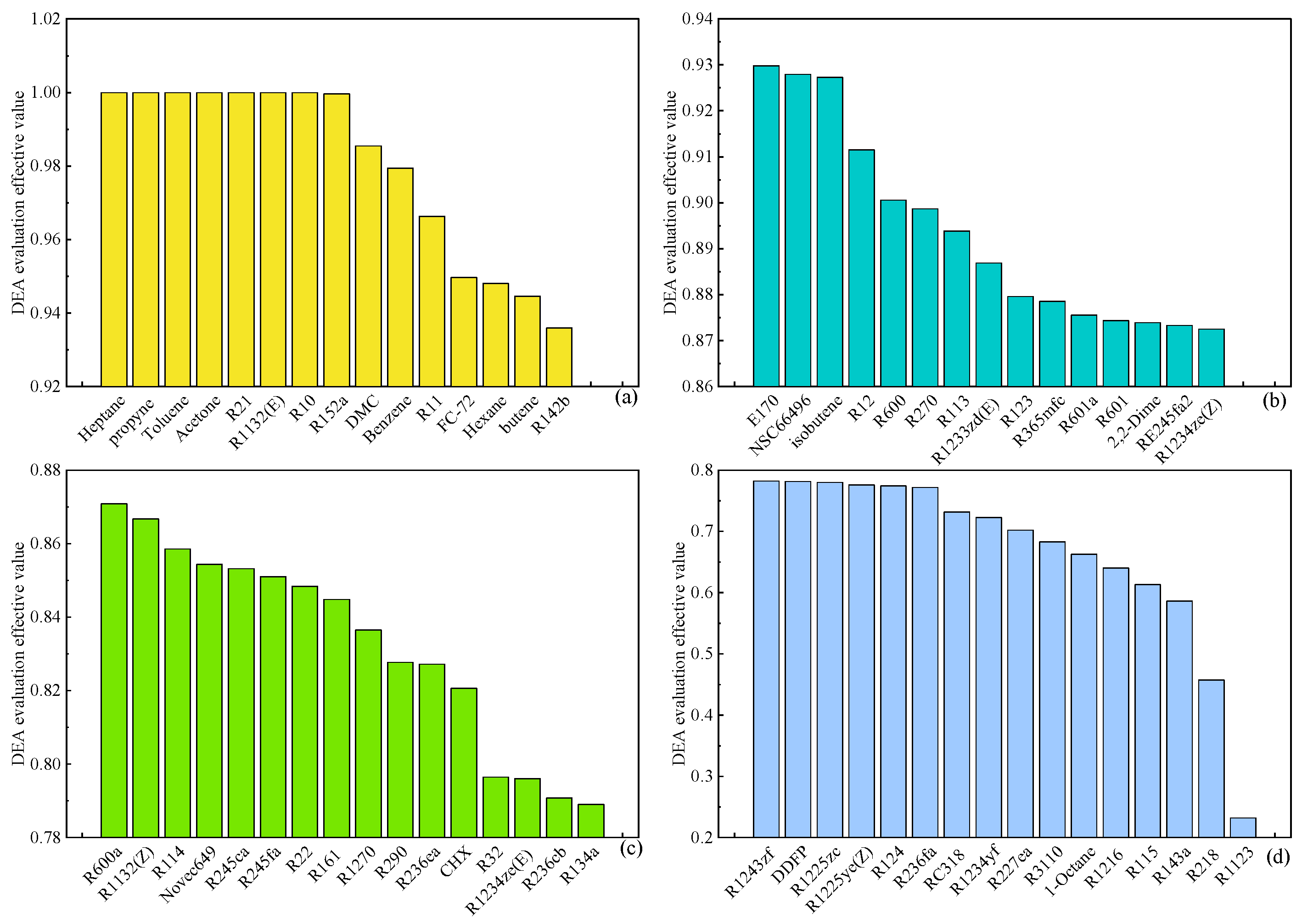
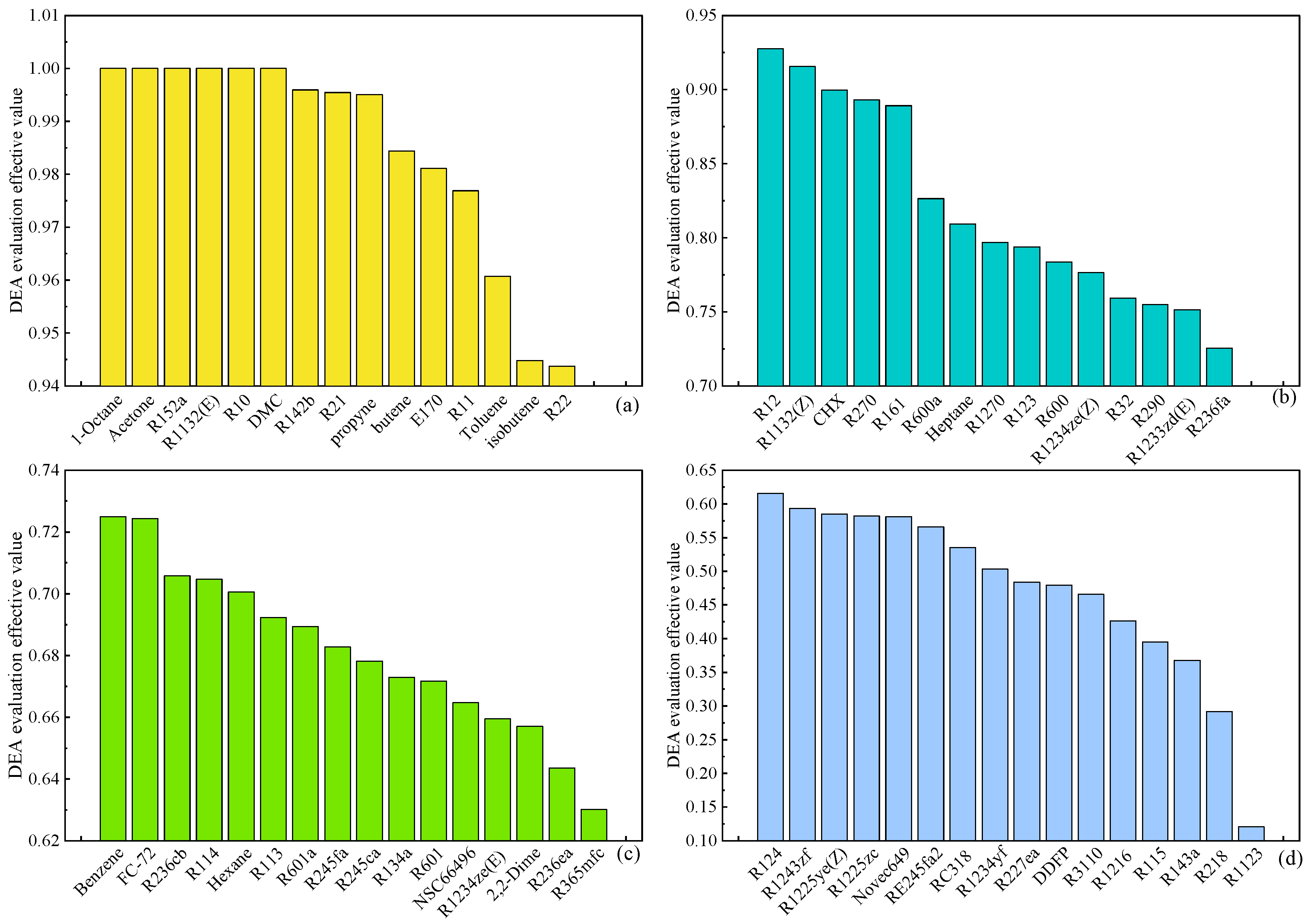
Figure 8 illustrates the outcomes of the DEA multi-objective evaluation of organic working fluids in the ORC system, utilizing thermodynamic and economic performance parameters as indices at an evaporation temperature of 120 °C. The working fluids are categorized into four grades—A, B, C, and D—based on the effective values of the DEA evaluation, corresponding to Figure 8 (a), (b), (c), and (d), respectively, with Grade D representing the least favorable category. Working substances such as Heptane, Propyne, Toluene, Acetone, R21, R1132(E), and R10 achieved Grade A status, each with an evaluation effective value of 1. This denotes that these working substances exhibit the most comprehensive performance among all evaluated options and should be prioritized when selecting working substances for the ORC system. Conversely, working fluids like R1123, R218, R143a, and others falling under Grade D demonstrate a poor overall performance, making them unsuitable for the ORC system.

5.2.2. Evaluation Based on Thermodynamic and Environmental Performance

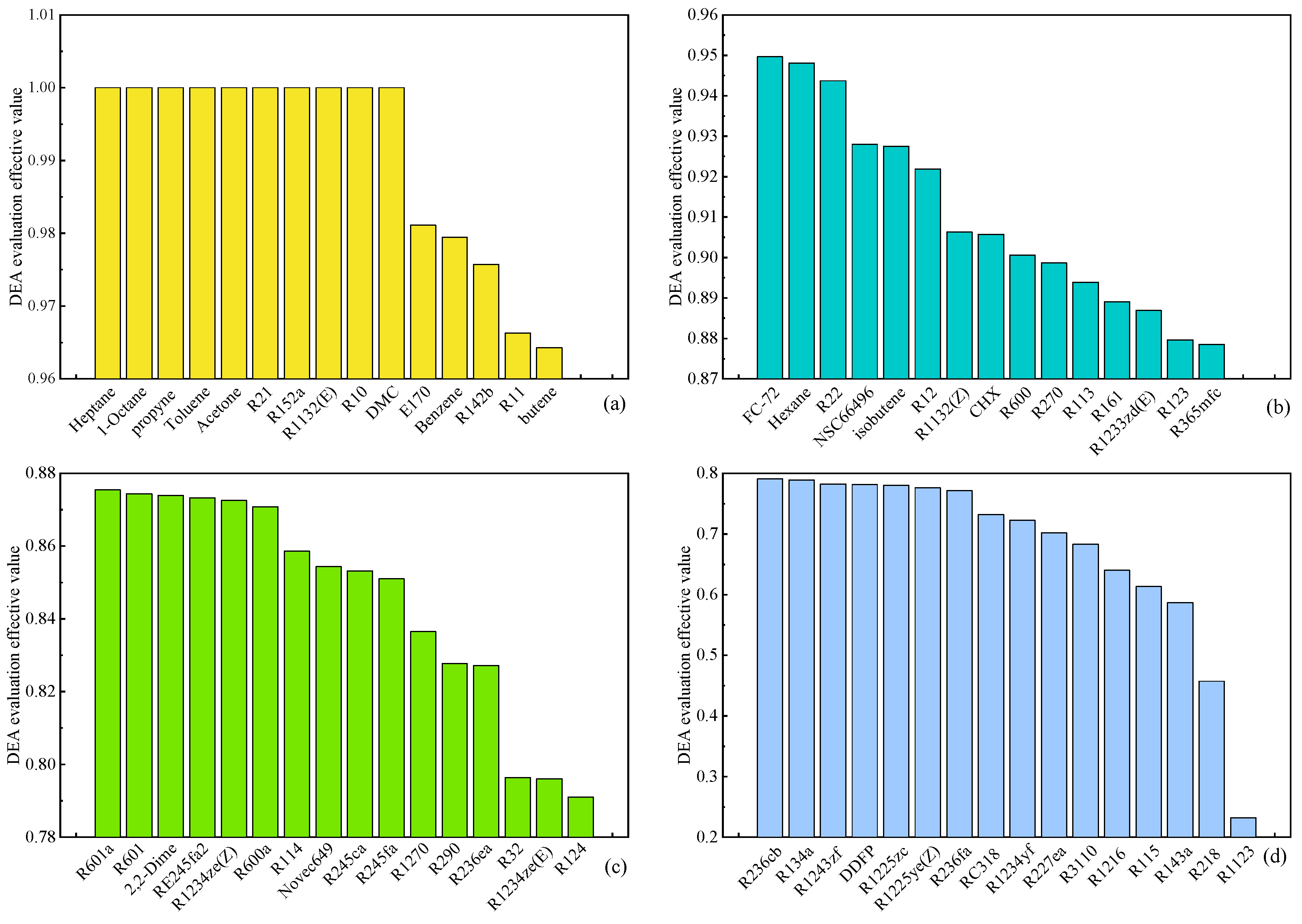
Figure 9 depicts the outcomes of the multi-objective DEA evaluation for organic working fluids in the ORC system, utilizing thermodynamic and environmental performance parameters as indices at an evaporation temperature of 120 °C. The working fluids are classified into four grades—A, B, C, and D—based on the effective values of the DEA evaluation, corresponding to Figure 9 (a), (b), (c), and (d), respectively, with Grade D being the least favorable. Notably, working fluids such as 1-Octane, Acetone, R152a, R1132(E), R10, and DMC achieved an effective value of 1, showcasing the most optimal comprehensive performance when applied in the ORC system. On the contrary, working fluids like R1123, R218, R143a, and others falling under Grade D exhibited lower effective values and an inferior comprehensive performance compared to other options, rendering them unsuitable for use as circulating working fluids in the ORC system.

5.2.3. Evaluation Based on Thermodynamic, Economic, and Environmental Performance

The evaluation outcomes of ORC system working fluids utilizing the DEA multi-objective evaluation method are illustrated in Figure 10. The effective value derived from the DEA evaluation serves as an indicator of the comprehensive performance of a given working fluid under the current evaluation criteria. A higher effective value correlates with a more superior comprehensive performance of the working fluid. As denoted in Figure 10 (a), (b), (c), and (d), respectively, Grade A represents the optimal working fluid, Grade B follows, then Grade C, and finally Grade D is deemed the least favorable. Notably, Heptane, 1-Octane, Propyne, Toluene, Acetone, R21, R152a, R1132(E), R10, and DMC are classified as Grade A working substances, each achieving an effective value of 1 in the DEA evaluation. This signifies that the comprehensive performance of these working substances surpasses that of others, recommending them as the preferred circulating working fluids for the ORC system. Conversely, Class D working fluids exhibit an inferior performance compared to others, warranting their exclusion from the recommended circulating working fluids for the ORC system.

The findings reveal that the count of optimal working fluid rises as the evaporation temperature declines, aligning with the characteristic of system performance fluctuations in response to evaporation temperature variations. Discrepancies in the optimal working fluid across the three scenarios signify that the DEA method comprehensively assesses and ranks the performance of organic working fluids, taking into account variations in evaluation indices. The overall trend observed in the majority of working fluids remains consistent, indicating that the assessment ranking of working fluids adheres to the performance patterns of these fluids under each evaluation index.

In conclusion, upon contrasting the outcomes of multi-objective evaluation with those of single-objective evaluation, it becomes apparent that the evaluation and ranking outcomes of working fluid quality by the DEA method generally exhibit greater conformity with the single-objective evaluation criteria for working fluid. This alignment indicates consistency with the corresponding system performance characteristics of the working fluid. Nevertheless, within a limited scope, the ranking of working fluid deviates from the single-objective result, suggesting a comprehensive evaluation outcome achieved through the reconciliation of multiple evaluation indicators.

5.3. Application Cases of Multi-Objective Evaluation

To validate the precision of the multi-objective evaluation outcomes, we conducted applied research on the working fluid Heptane, chosen due to its commendable performance in the multi-objective evaluation results. A comparative analysis of the application effects between Heptane and the working fluid R245fa commonly used in the existing literature was undertaken [24,25]. The results, depicted in Figure 11, reveal notable advantages for Heptane. Specifically, in contrast to R245fa, Heptane demonstrates a 5.02% reduction in exergy damage, a 0.24% increase in thermal efficiency, and a substantial 2.04% augmentation in net work output. These findings underscore the superior performance of Heptane, affirming the efficacy of the multi-objective evaluation approach in selecting the optimal working fluid.

6. Conclusions

In this study, single-objective and multi-objective evaluations were conducted to study the screening of working fluids in the ORC system. The limitations inherent in the single-objective evaluation approach were duly addressed. A multi-objective evaluation method, employing data envelopment analysis (DEA), was introduced to comprehensively assess and rank organic working fluids within the ORC system, facilitating the selection of the optimal working fluid.

Although some traditional refrigerants have acceptable performance in terms of CO₂ emission reduction, some may have high global warming potential (GWP) values that could offset the benefits brought about by the emission reduction. Some are also accompanied by potential hazards due to their toxicity. Therefore, they need to be selected with caution. We suggest giving priority to working fluids with a low GWP and complying with safety standards to meet international environmental protection regulations and safety requirements, and to enhance the practical guiding value of the research.

The key conclusions derived from this study are as follows:

(1) Single-objective evaluations were performed for 62 working fluids, resulting in disparate screening outcomes due to the singular nature of the evaluations and subjective influences. The results indicated that Toluene and DMC have a better advantage in thermodynamic performance. The investment cost of R1123 is the lowest, while the exergy loss of R1132(Z) is the lowest.

(2) The DEA multi-objective evaluation method emerged as a robust approach capable of harmonizing diverse evaluation indicators. It swiftly and accurately gauged the comprehensive performance of various working fluids within the ORC system, delineating their prioritized applications. This method effectively overcame the limitations associated with single-objective evaluations.

(3) The working fluid Heptane obtained by DEA multi-objective evaluation showed better advantages than R245fa, the working fluid commonly used in the literature. The application results of multi-objective evaluation indicated that Heptane demonstrates a 5.02% reduction in exergy damage, a 0.24% increase in thermal efficiency, and a substantial 2.04% augmentation in net work output.

The proposed multi-objective evaluation method, grounded in DEA, offers an innovative approach for assessing and ranking ORC working fluids under distinct evaporation temperatures and varied combination indexes. This method circumvents issues related to a limited working fluid dataset and reliance on singular evaluation indices. The strategy provides precise, concise data, offering practical guidance for the intricate process of selecting working fluids, especially when confronted with variations in low-temperature heat source temperatures and diverse operational requisites in industrial production. Hence, this screening strategy holds substantial practical application value.