Optimization of Gas–Water Two-Phase Holdup Calculation Methods for Upward and Horizontal Large-Diameter Wells
Abstract
1. Introduction
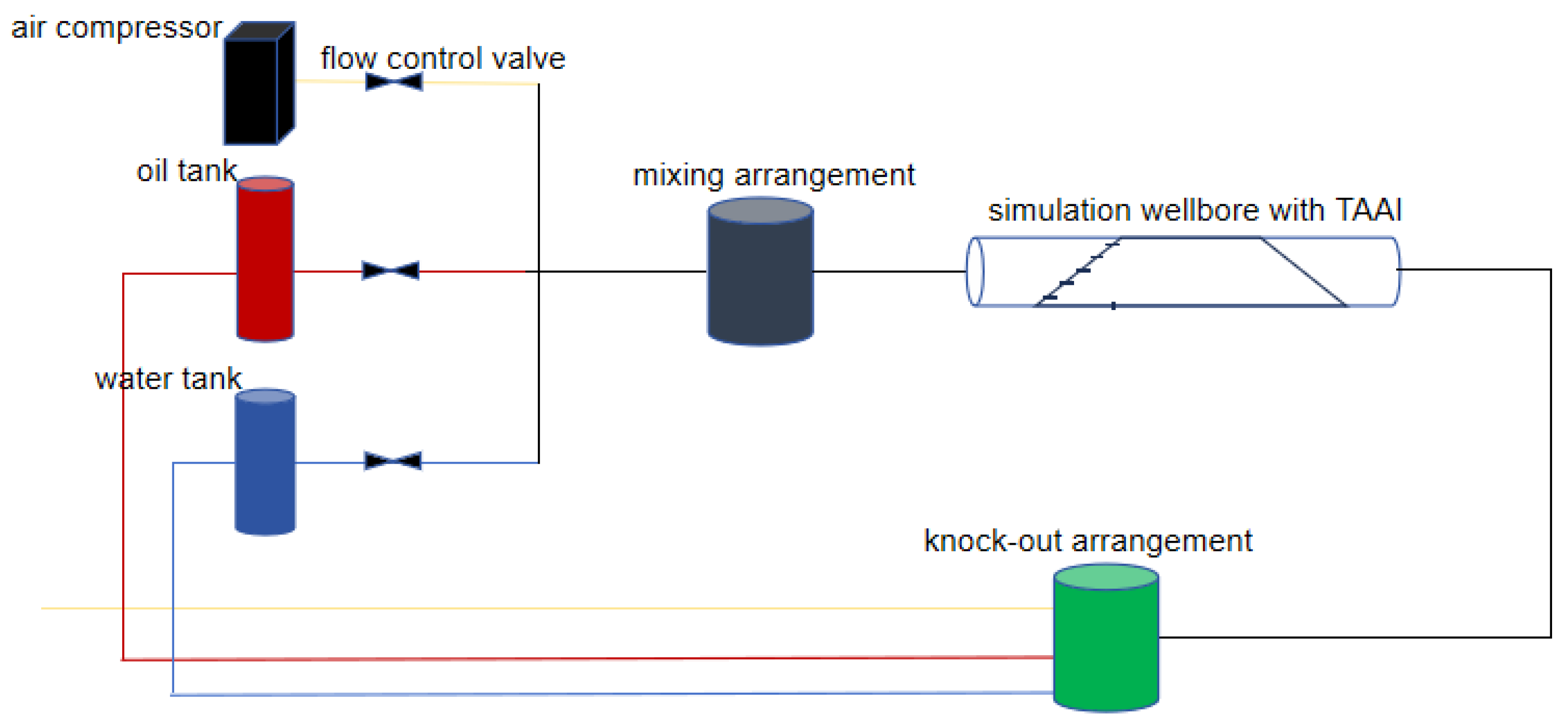
2. Gas-Water Two-Phase Simulation Experiments
2.1. Simulation Experiments
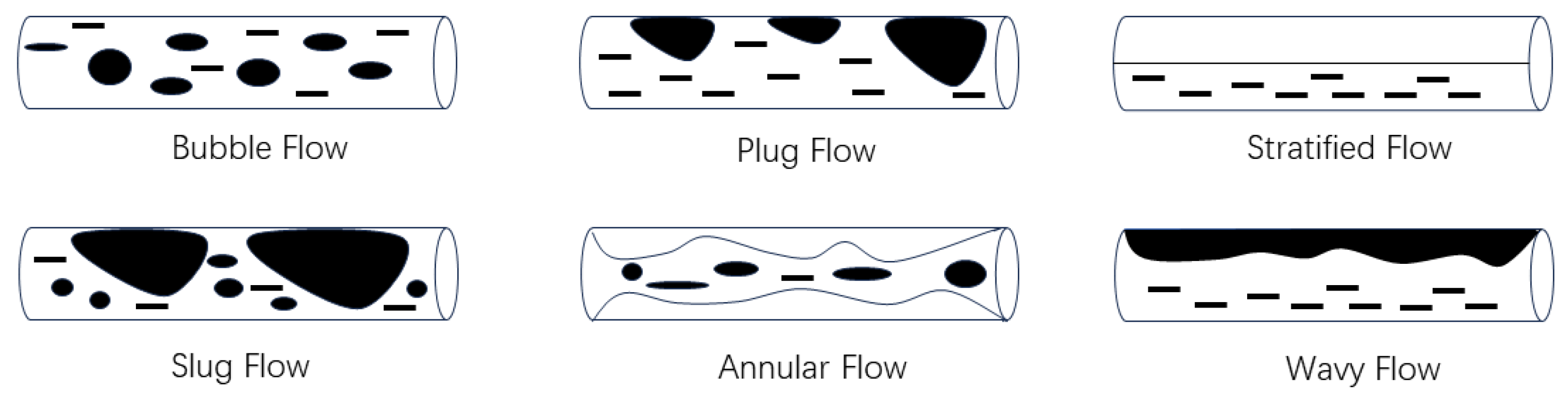
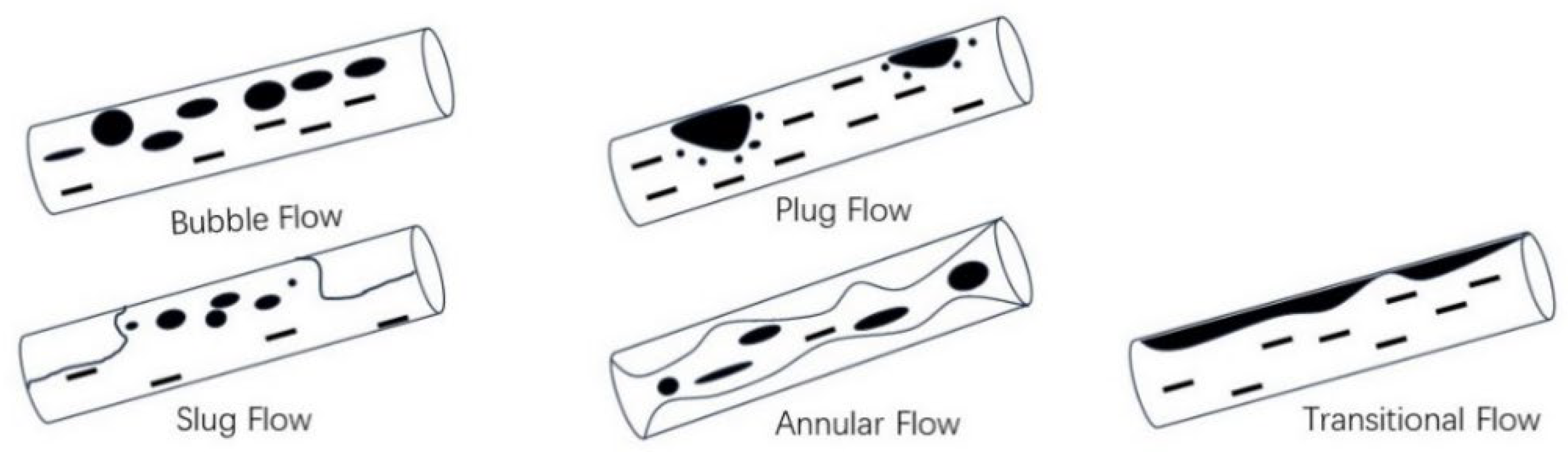
2.2. Flow Pattern Analysis
3. Water Holdup Calculation
3.1. Calculation of Actual Water Holdup
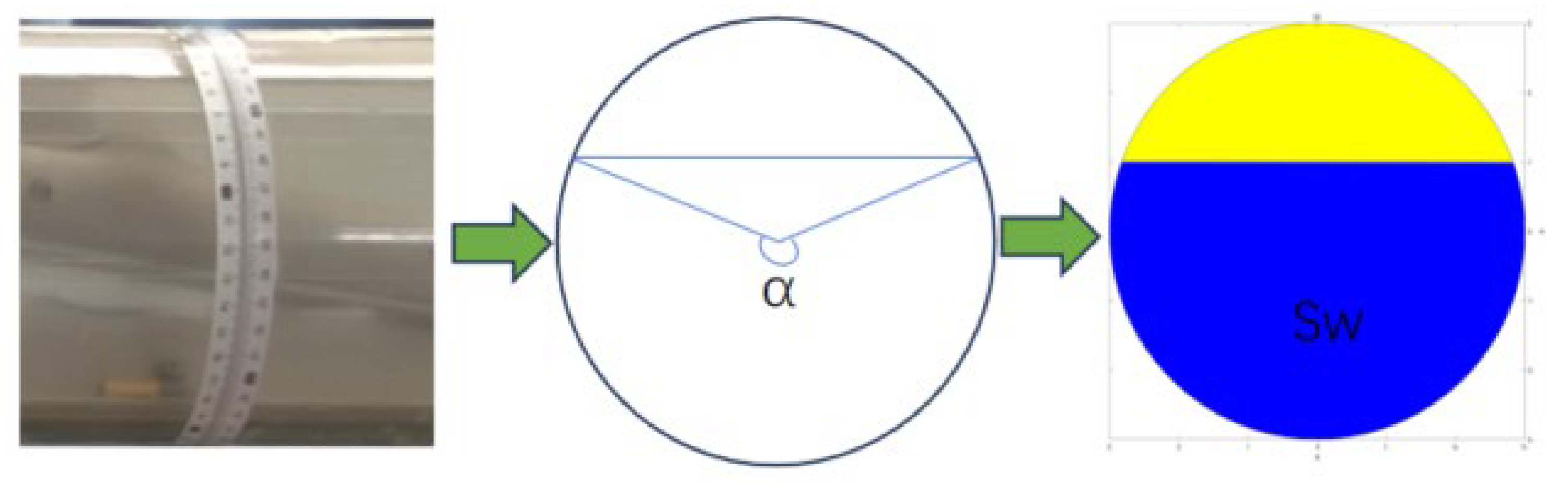
3.2. Calculation of Local Water Holdup Using Probes
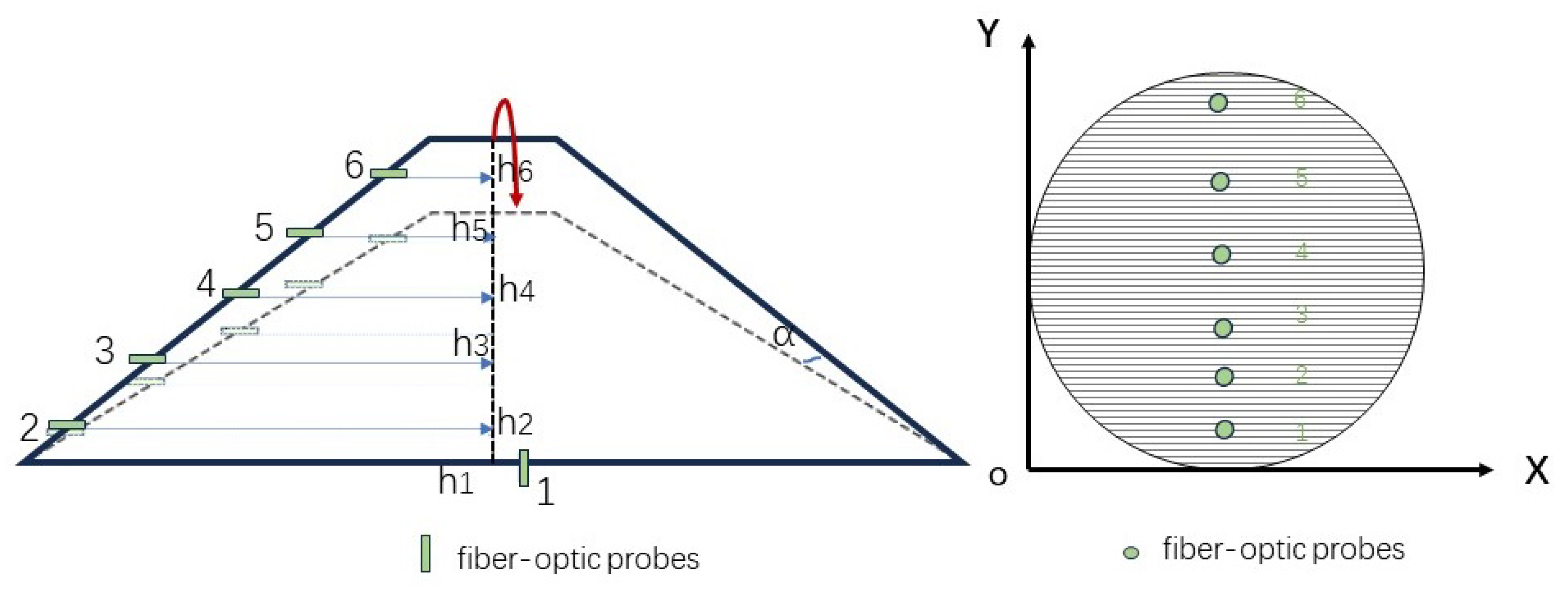
3.3. Calculation of Probe Positions
3.4. Segmentation of Wellbore Cross-Section
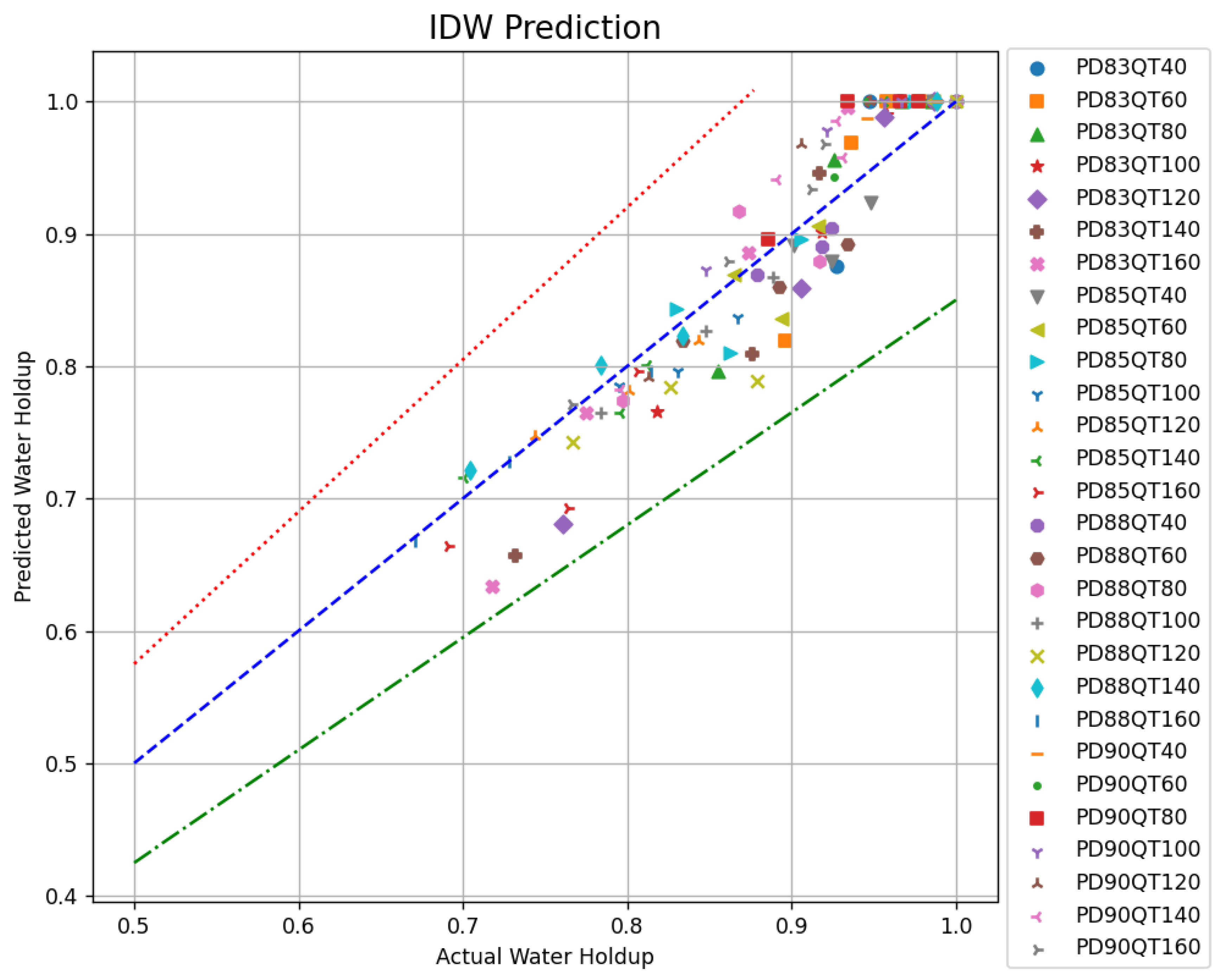
3.5. Comparison of GRBF and IDW Interpolation Algorithms
3.6. Principle of the L-M Algorithm
4. Analysis of Optimization Results with the L-M Algorithm
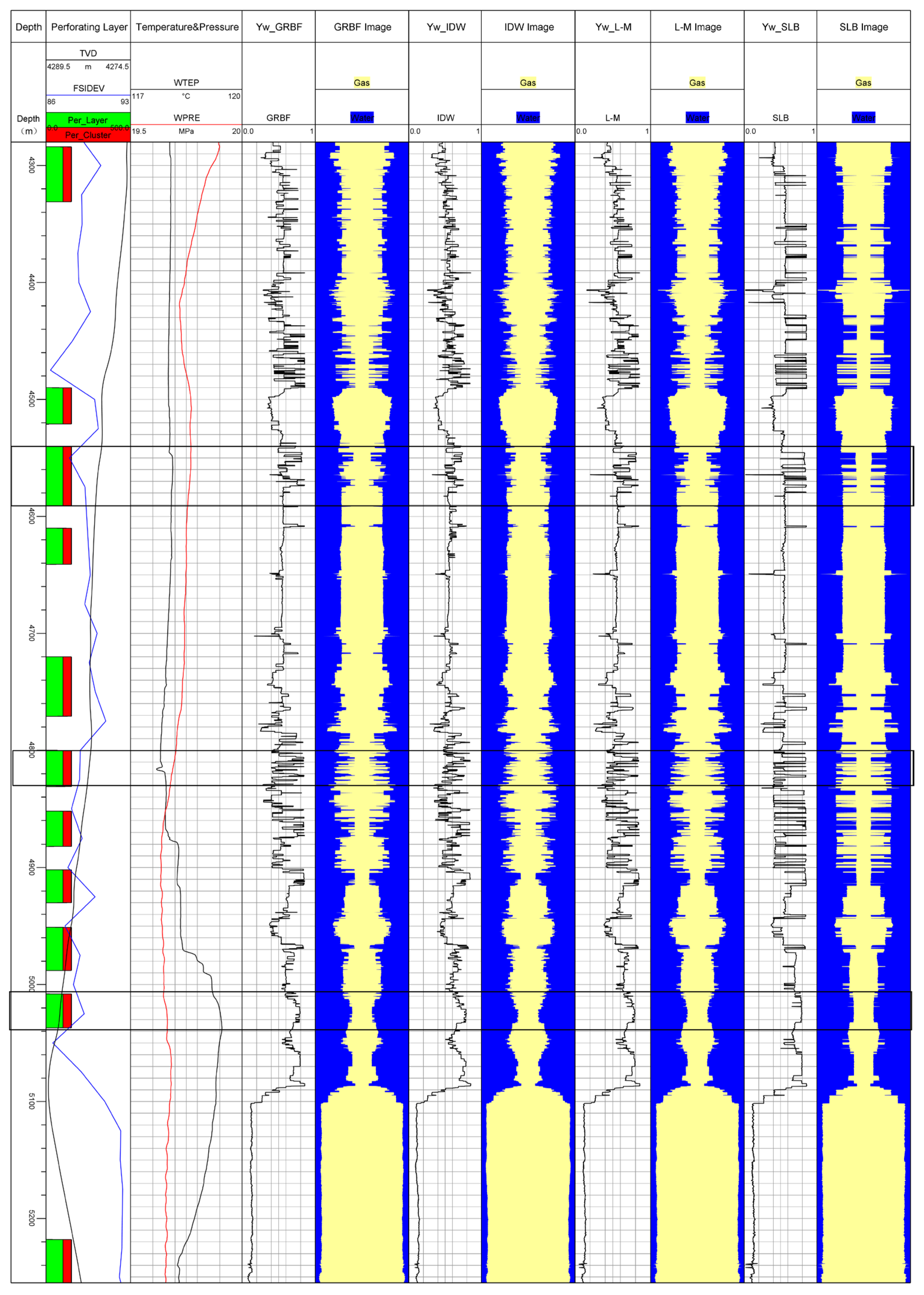
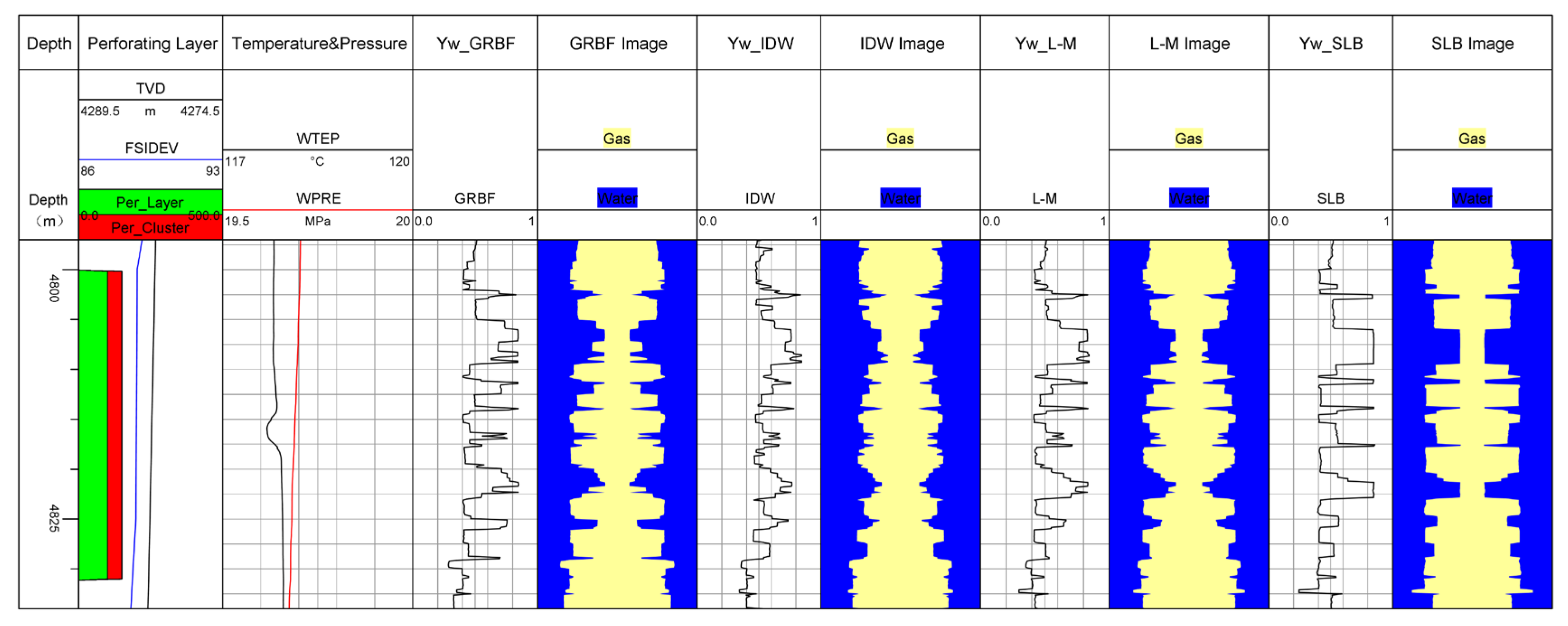
5. Case Study and Analysis
6. Conclusion and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, S.F. Research on Simulation Experiment and Interpretation Method of Horizontal Well Array Flow Imager. Master’s Thesis, Yangtze University, Jingzhou, China, 2022. [Google Scholar]
- Chen, H.; Sun, W.; Zou, S. Applied Study of Three-Phase Flow Production Profile Testing Technology with FAST Array Tools. J. Jianghan Pet. Univ. Staff. Work. 2024, 37, 23–25, 32. [Google Scholar]
- Wang, T.; Liu, J.; Li, B.; Deng, H.; Cui, S. Analysis of gas-water two-phase holdup of horizontal well based on array fiber probe. Yunnan Chem. Technol. 2020, 47, 60–61. [Google Scholar]
- Mu, H.; Liu, W.; Kong, L.; Li, Y.; Liu, C.; Liu, X. Experimental study on the response characteristics to the optical fiber gas holdup in the gas/water two-phase flow. Opt. Instrum. 2012, 34, 66–69. [Google Scholar]
- Yang, R.; Liu, J.; Li, M.; Cui, S.; Hu, H.; Li, Y. Simulation Experiment and Interpretation Research of Gas-Water Two-Phase Horizontal Well Array Imager. Available online: http://kns.cnki.net/kcms/detail/11.2982.p.20241205.1223.073.html (accessed on 16 January 2025).
- Li, A.; Guo, H.; Niu, Y.; Lu, X.; Zhang, Y.; Liang, H.; Sun, Y.; Guo, Y.; Wang, D. Application of Imaging Algorithms for Gas–Water Two-Phase Array Fiber Holdup Meters in Horizontal Wells. Sensors 2024, 24, 7285. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.L. Application of gas array tool in monitoring gas production profile of highly-deviated wells. Oil Gas Well Detect. 2024, 33, 56–60. [Google Scholar]
- Xing, W.; Chen, Q.; Liu, G. Gas-holding rate imaging method for gas-liquid two-phase flow based on single-mode fiber probe. Opt. Commun. Technol. 2025, 49, 78–82. [Google Scholar]
- Song, W.R.; Li, W.H.; Lin, S.Y.; Ye, H.R.; Li, G. Experimental and numerical investigation of flow pattern evolution and flow-induced vibrations in an M-shaped subsea jumper under gas-liquid two-phase flow conditions. Ocean. Eng. 2025, 327, 120964. [Google Scholar] [CrossRef]
- Muhammad Waqas, Y.; Ramasamy, M.; Risza, R.; Reddy Prasad, D.M.; Rajashekhar, P. Review on gas–liquid–liquid three–phase flow patterns, pressure drop, and liquid holdup in pipelines. Chem. Eng. Res. Des. 2020, 159, 505–528. [Google Scholar]
- Yan, P. Research on Measurement Method of Gas Holdup of Horizontal Gas-Liquid Two-Phase Flow Based on Array Optical Fiber Sensing. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2023. [Google Scholar]
- Wu, Y. Measurement Method of Acoustic-Electric Sensors for Phase Holdup in Horizontal Gas-Liquid Two-Phase Flow. Ph.D. Thesis, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Kong, W.; Li, S.; Hao, H.; Yan, P.; Zhuo, C.; Li, H. Measurement method of gas holdup in horizontal gas-liquid two-phase flow based on fiber-optic probe array. Flow Meas. Instrum. 2024, 97, 102588. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, L.; Chen, Y.; Liu, Z.; Yuan, H.; Wen, Y. Study on prediction model of liquid hold up based on random forest algorithm. Chem. Eng. Sci. 2023, 268, 118383. [Google Scholar] [CrossRef]
- Ma, T.; Wang, T.; Wang, L. A hybrid deep learning model towards flow pattern identification of gas-liquid two-phase flows in horizontal pipe. Energy 2025, 320, 135–141. [Google Scholar]
- Shi, Y.; Sun, Y.; Wang, M.; Zhang, S.; Yang, Z. Flow pattern recognition for horizontal gas-liquid two-phase flow with a hybrid deep-learning model. Flow Meas. Instrum. 2025, 102, 102829. [Google Scholar]
- Saisorn, S.; Benjawun, P.; Suriyawong, A.; Wongwises, S. Experimental investigation on flow pattern and void fraction for two-phase gas-liquid upflow in a vertical helically coiled micro-channel. Int. J. Thermofluids 2025, 26, 101124. [Google Scholar]
- Liu, D.W.; Yang, B.J.; Zhang, W.B.; Xue, X.B. Analysis of gas-liquid two-phase flow characteristics of wellbore in horizontal wells. China Pet. Chem. Stand. Qual. 2023, 43, 81–84. [Google Scholar]
- Chen, S.; Liu, S.; Liu, L.; Li, Y.; Zhang, J.; Cong, T.; Gu, H. Experimental study on flow patterns and pressure gradient of decaying swirling gas-liquid flow in a horizontal pipe. Prog. Nucl. Energy 2024, 177, 105445. [Google Scholar]
- Ma, H.; Xu, Y.; Huang, H.; Yuan, C.; Wang, J.; Yang, Y.; Wang, D. Intelligent predictions for flow pattern and phase fraction of a horizontal gas-liquid flow. Energy 2024, 303, 131944. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, L.; Zhu, Z.; Liu, J.; Sun, X.; Hu, Z. Flow pattern identification of gas-liquid two-phase flow based on integrating mechanism analysis and data mining. Geoenergy Sci. Eng. 2023, 228, 212013. [Google Scholar]
- Liu, Y.; Luo, C.; Liu, T.; Ren, G.; Wang, Z. Prediction of Gas-liquid Two-phase Flow Patterns in Horizontal Gas Wells. J. Southwest Pet. Univ. 2019, 41, 107–112. [Google Scholar]
- Yang, Q.; Jin, N.; Wang, F.; Ren, W. Measurement of Gas Phase Distribution Using Multifiber Optical Probes in a Two-Phase Flow. IEEE Sens. J. 2020, 20, 6642–6651. [Google Scholar] [CrossRef]
- Karimi, N.; Kazem, S.; Ahmadian, D.; Adibi, H.; Ballestra, L.V. On a generalized Gaussian radial basis function: Analysis and applications. Eng. Anal. Bound. Elem. 2020, 112, 46–57. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Zhu, R.; Zhang, Z.; Weng, Z. Integrating data-to-data correlation into inverse distance weighting. Comput. Geosci. 2020, 24, 203–216. [Google Scholar] [CrossRef]
- Jin, G.D.; Liu, Y.C.; Niu, W.J. Comparison between Inverse Distance Weighting Method and Kriging. J. Chang. Univ. Sci. Technol. 2003, 24, 53–57. [Google Scholar]
- de Jesús Rubio, J. Stability Analysis of the Modified Levenberg–Marquardt Algorithm for the Artificial Neural Network Training. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3510–3524. [Google Scholar] [CrossRef] [PubMed]
- Shaik, N.B.; Sayani, J.K.S.; Benjapolakul, W.; Asdornwised, W.; Chaitusaney, S. Experimental investigation and ANN modelling on CO2 hydrate kinetics in multiphase pipeline systems. Sci. Rep. 2022, 12, 13642. [Google Scholar] [CrossRef] [PubMed]





| Feature | GRBF | IDW |
|---|---|---|
| Interpolation principle | It uses a Gaussian function to weight sample points and obtain the interpolated result through a weighted summation. | It weights by the inverse of distance, adding more weight to nearer points. |
| Data requirement | It requires a sufficient number of sample points to fit the Gaussian function. | It can achieve interpolation results with relatively fewer sample points. |
| Smoothness | It provides smoothness and effectively suppresses noise. | It is sensitive to noise and may be affected by local extreme values. |
| Data distribution | It has no special assumptions about data distribution. | It works well with densely distributed data but may be less suitable for unevenly distributed data. |
| Parameter adjustment | It requires adjusting parameters of the Gaussian function, needing some experience. | It has only one parameter (power exponent), making it relatively easy to adjust. |
| Computational complexity | It involves calculations with Gaussian functions, leading to higher computational complexity. | It is simple to compute and suitable for large-scale data interpolation. |
| Global and local characteristics of interpolation results | Its results are local to some extent, focusing more on the influence of nearby sample points. | Its results are global, with all sample points influencing the interpolation result equally. |
| Total Flow (m3/d) | Water Holdup (%) | Real Water Holdup | IDW Water Holdup | GRBF Water Holdup | L-M Water Holdup | IDW Relative Error (%) | GRBF Relative Error (%) | L-M Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 20 | 0.927 | 0.876 | 0.896 | 0.936 | 5.50 | 3.34 | 0.97 |
| 40 | 0.947 | 1 | 1 | 1 | 5.60 | 5.60 | 5.60 | |
| 60 | 0.986 | 1 | 1 | 1 | 1.42 | 1.42 | 1.42 | |
| 80 | 0.993 | 1 | 1 | 1 | 0.70 | 0.70 | 0.70 | |
| 140 | 20 | 0.732 | 0.657 | 0.687 | 0.697 | 10.2 | 6.15 | 4.78 |
| 40 | 0.876 | 0.809 | 0.904 | 0.904 | 7.65 | 3.20 | 3.20 | |
| 60 | 0.917 | 0.946 | 0.956 | 0.936 | 3.16 | 4.25 | 2.07 | |
| 80 | 0.966 | 1 | 1 | 1 | 3.52 | 3.52 | 3.52 | |
| 160 | 20 | 0.718 | 0.634 | 0.734 | 0.734 | 11.7 | 2.23 | 2.23 |
| 40 | 0.775 | 0.765 | 0.785 | 0.785 | 1.29 | 1.29 | 1.29 | |
| 60 | 0.874 | 0.744 | 0.786 | 0.787 | 14.87 | 10.07 | 9.95 | |
| 80 | 0.934 | 0.996 | 0.996 | 0.996 | 6.64 | 6.64 | 6.64 |
| Total Flow (m3/d) | Water Holdup (%) | Real Water Holdup | IDW Water Holdup | GRBF Water Holdup | L-M Water Holdup | IDW Relative Error (%) | GRBF Relative Error (%) | L-M Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 20 | 0.901 | 0.831 | 0.859 | 0.921 | 7.77 | 4.66 | 2.22 |
| 40 | 0.924 | 0.821 | 0.839 | 0.869 | 11.15 | 9.20 | 5.95 | |
| 60 | 0.948 | 1 | 1 | 1 | 5.49 | 5.49 | 5.49 | |
| 80 | 0.986 | 1 | 1 | 1 | 1.42 | 1.42 | 1.42 | |
| 140 | 20 | 0.701 | 0.716 | 0.679 | 0.689 | 2.14 | 3.14 | 1.71 |
| 40 | 0.796 | 0.765 | 0.815 | 0.815 | 3.89 | 2.39 | 2.39 | |
| 60 | 0.812 | 0.801 | 0.791 | 0.791 | 1.35 | 2.59 | 2.59 | |
| 80 | 0.956 | 1 | 1 | 1 | 4.60 | 4.60 | 4.60 | |
| 160 | 20 | 0.691 | 0.664 | 0.644 | 0.674 | 3.91 | 6.80 | 2.46 |
| 40 | 0.764 | 0.733 | 0.783 | 0.783 | 4.06 | 2.49 | 2.49 | |
| 60 | 0.806 | 0.776 | 0.786 | 0.786 | 3.72 | 2.48 | 2.48 | |
| 80 | 0.947 | 1 | 1 | 1 | 5.60 | 5.60 | 5.60 |
| Total Flow (m3/d) | Water Holdup (%) | Real Water Holdup | IDW Water Holdup | GRBF Water Holdup | L-M Water Holdup | IDW Relative Error (%) | GRBF Relative Error (%) | L-M Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 20 | 0.879 | 0.869 | 0.889 | 0.886 | 1.14 | 1.14 | 0.80 |
| 40 | 0.918 | 0.88 | 0.87 | 0.89 | 4.14 | 5.23 | 3.05 | |
| 60 | 0.924 | 0.904 | 0.974 | 0.934 | 2.16 | 5.41 | 1.08 | |
| 80 | 0.939 | 1 | 1 | 1 | 6.50 | 6.50 | 6.50 | |
| 140 | 20 | 0.704 | 0.679 | 0.741 | 0.721 | 3.55 | 5.26 | 2.41 |
| 40 | 0.784 | 0.801 | 0.801 | 0.801 | 2.17 | 2.17 | 2.17 | |
| 60 | 0.834 | 0.823 | 0.863 | 0.863 | 1.32 | 3.48 | 3.48 | |
| 80 | 0.988 | 1 | 1 | 1 | 1.21 | 1.21 | 1.21 | |
| 160 | 20 | 0.671 | 0.678 | 0.678 | 0.668 | 1.04 | 1.04 | 0.45 |
| 40 | 0.728 | 0.688 | 0.758 | 0.748 | 5.49 | 4.12 | 2.75 | |
| 60 | 0.814 | 0.796 | 0.796 | 0.796 | 2.21 | 2.21 | 2.21 | |
| 80 | 0.967 | 1 | 1 | 1 | 3.41 | 3.41 | 3.41 |
| Total Flow (m3/d) | Water Holdup (%) | Real Water Holdup | IDW Water Holdup | GRBF Water Holdup | L-M Water Holdup | IDW Relative Error (%) | GRBF Relative Error (%) | L-M Relative Error (%) |
|---|---|---|---|---|---|---|---|---|
| 40 | 20 | 0.846 | 0.866 | 0.837 | 0.856 | 2.36 | 1.06 | 1.18 |
| 40 | 0.898 | 0.875 | 0.921 | 0.882 | 2.56 | 2.56 | 1.78 | |
| 60 | 0.928 | 0.908 | 0.978 | 0.918 | 2.16 | 5.39 | 1.08 | |
| 80 | 0.988 | 1 | 1 | 1 | 1.21 | 1.21 | 1.21 | |
| 80 | 0.957 | 1 | 1 | 1 | 4.49 | 4.49 | 4.49 | |
| 140 | 20 | 0.736 | 0.716 | 0.757 | 0.748 | 2.72 | 2.85 | 1.63 |
| 40 | 0.851 | 0.876 | 0.834 | 0.867 | 2.94 | 2.00 | 1.88 | |
| 60 | 0.891 | 0.914 | 0.862 | 0.908 | 2.58 | 3.25 | 1.91 | |
| 80 | 0.950 | 1 | 1 | 1 | 5.26 | 5.26 | 5.26 | |
| 160 | 20 | 0.667 | 0.688 | 0.657 | 0.675 | 3.15 | 1.50 | 1.20 |
| 40 | 0.721 | 0.704 | 0.744 | 0.709 | 2.36 | 3.19 | 1.66 | |
| 60 | 0.812 | 0.786 | 0.854 | 0.799 | 3.20 | 5.17 | 1.60 | |
| 80 | 0.920 | 0.896 | 0.965 | 0.94 | 2.61 | 4.89 | 2.17 |
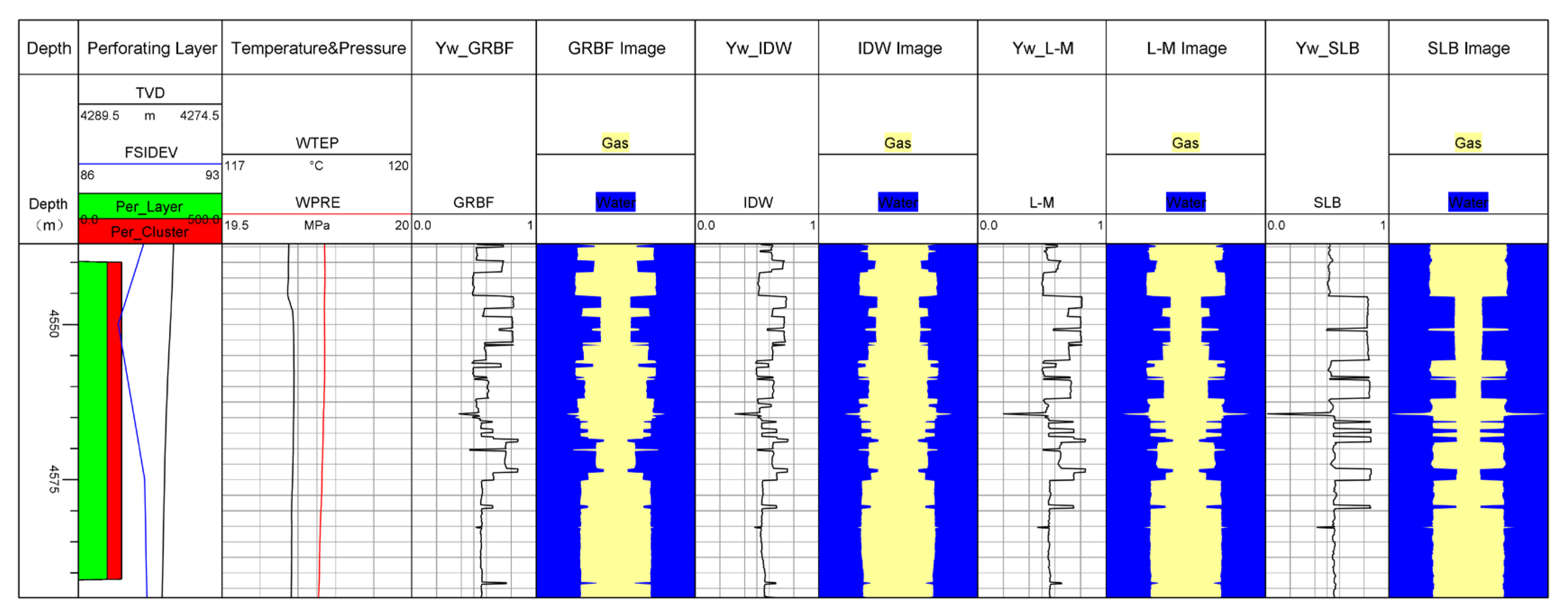
| Layer | Yw_SLB | Yw_GRBF | Yw_IDW | Yw_L-M | GRBF Relative Error (%) | IDW Relative Error (%) | L-M Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 2 | 0.794 | 0.694 | 0.707 | 0.724 | 12.6% | 11.0 | 8.8% |
| 6 | 0.579 | 0.521 | 0.518 | 0.533 | 10.0% | 10.5 | 7.9% |
| 9 | 0.725 | 0.648 | 0.632 | 0.789 | 10.6% | 12.8 | 8.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Liu, J.; Gao, F.; Yuan, X.; Zhang, B. Optimization of Gas–Water Two-Phase Holdup Calculation Methods for Upward and Horizontal Large-Diameter Wells. Processes 2025, 13, 1004. https://doi.org/10.3390/pr13041004
Chen Y, Liu J, Gao F, Yuan X, Zhang B. Optimization of Gas–Water Two-Phase Holdup Calculation Methods for Upward and Horizontal Large-Diameter Wells. Processes. 2025; 13(4):1004. https://doi.org/10.3390/pr13041004
Chicago/Turabian StyleChen, Yu, Junfeng Liu, Feng Gao, Xiaotao Yuan, and Boxin Zhang. 2025. "Optimization of Gas–Water Two-Phase Holdup Calculation Methods for Upward and Horizontal Large-Diameter Wells" Processes 13, no. 4: 1004. https://doi.org/10.3390/pr13041004
APA StyleChen, Y., Liu, J., Gao, F., Yuan, X., & Zhang, B. (2025). Optimization of Gas–Water Two-Phase Holdup Calculation Methods for Upward and Horizontal Large-Diameter Wells. Processes, 13(4), 1004. https://doi.org/10.3390/pr13041004







