Dual-Branch Discriminative Transmission Line Bolt Image Classification Based on Contrastive Learning
Abstract
1. Introduction
- Section 1 introduces the background and research approach.
- Section 2 describes the network architecture, the functionality of each module, and the design of the loss function.
- Section 3 details the selection of hyperparameters and the design and results of comparative and ablation experiments.
- Section 4 summarizes the contributions and conclusions of this study.
- Section 5 discusses the limitations of the proposed model, its potential applications in other domains, and future research directions.
2. Materials and Methods
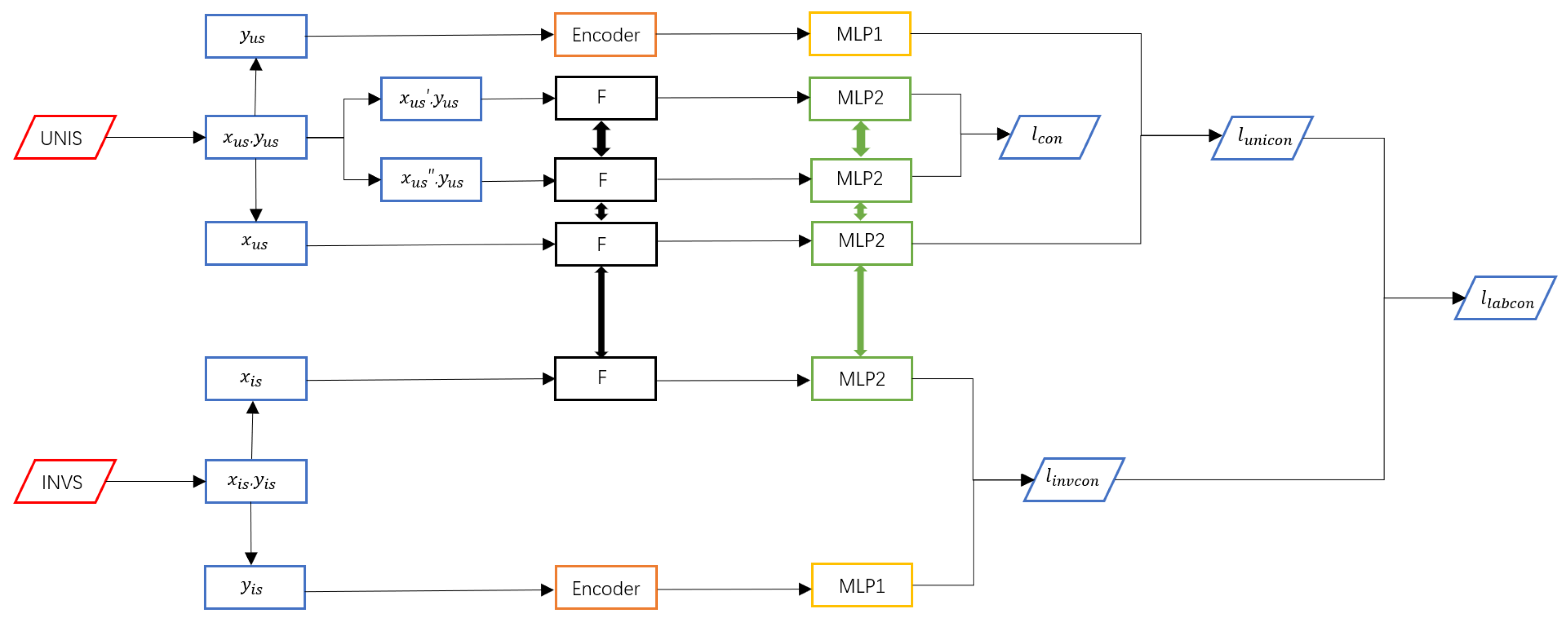
2.1. An Overview of the Training Phase
- (1)
- Input: The samples collected by UNIS contain two modalities: label information and image information. The images undergo random augmentation before being used for contrastive learning training. The labels and original images are fed into the image channel and label channel, respectively. INVS follows the same processing pipeline as UNIS, except that it does not perform random augmentation or contrastive learning.
- (2)
- Feature extraction: All F modules adopt the ResNet18 architecture with shared weights.
- (3)
- Contrastive learning: The samples collected by UNIS are augmented and then used for contrastive learning, where the similarity between positive sample pairs is maximized, and the differences between negative sample pairs are minimized.
- (4)
- Feature normalization: Both image and label feature vectors are processed through an MLP (multilayer perceptron) layer to ensure that they are mapped into the same feature space, facilitating effective contrastive learning.
- (5)
- Output: The output consists of the contrastive loss of randomly augmented images, , and the contrastive loss of labels, .
2.2. Sampler Module
2.3. Feature Extraction Module
2.4. Contrastive Learning Module
2.5. Category Label Module
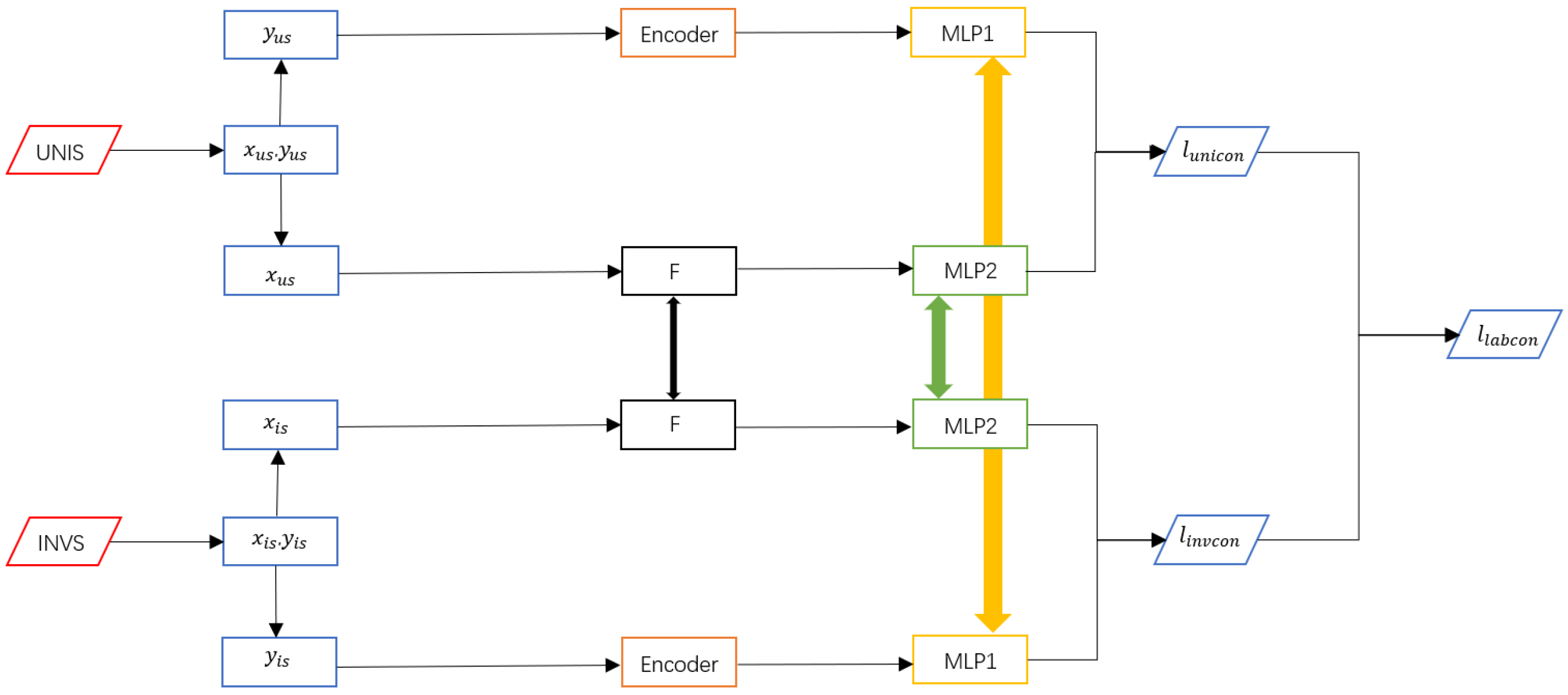
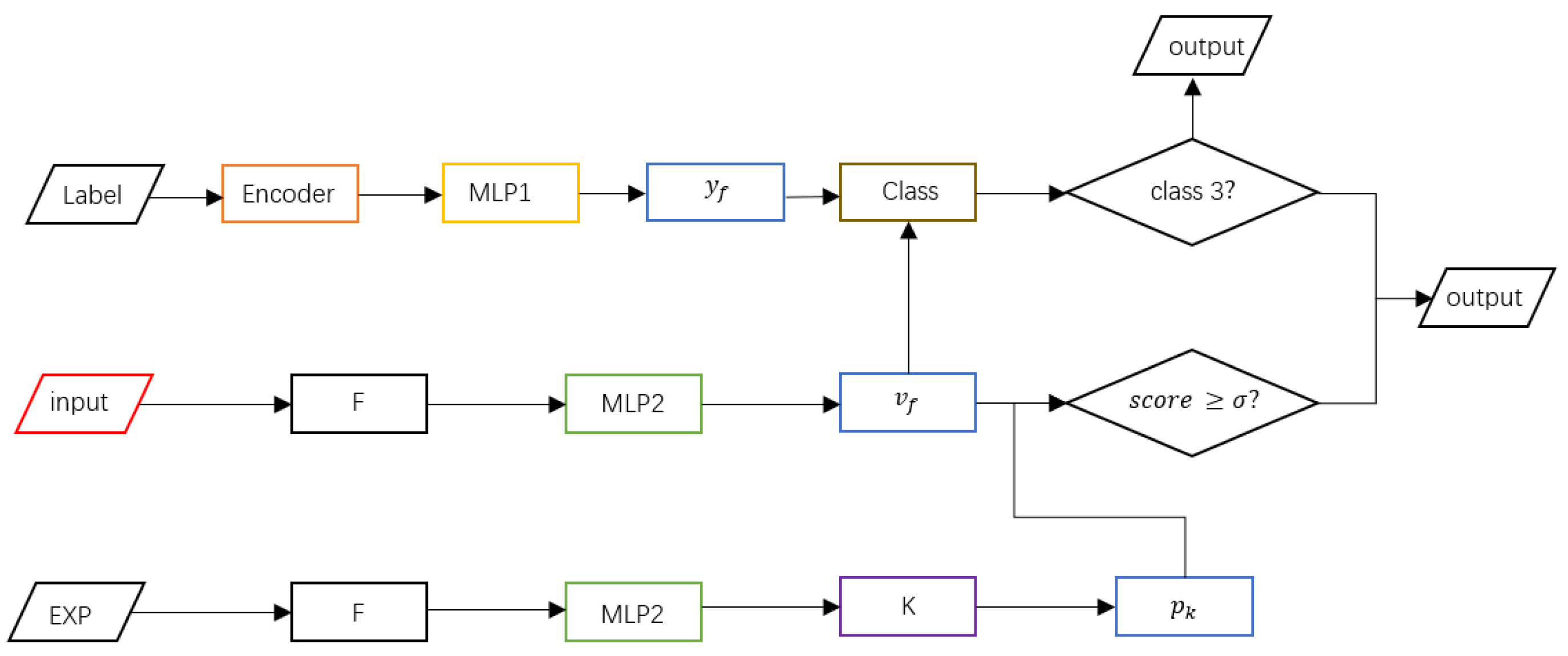
2.6. An Overview of the Detection Phase
2.7. Loss Function Calculation
2.7.1. Contrastive Learning Loss
2.7.2. The Label Contrastive Loss of the Uniform Sampler
2.7.3. The Label Contrastive Loss of the Inverted Sampler
2.7.4. Overall Loss
3. Results
3.1. Introduction to the Dataset
3.2. Experimental Setup
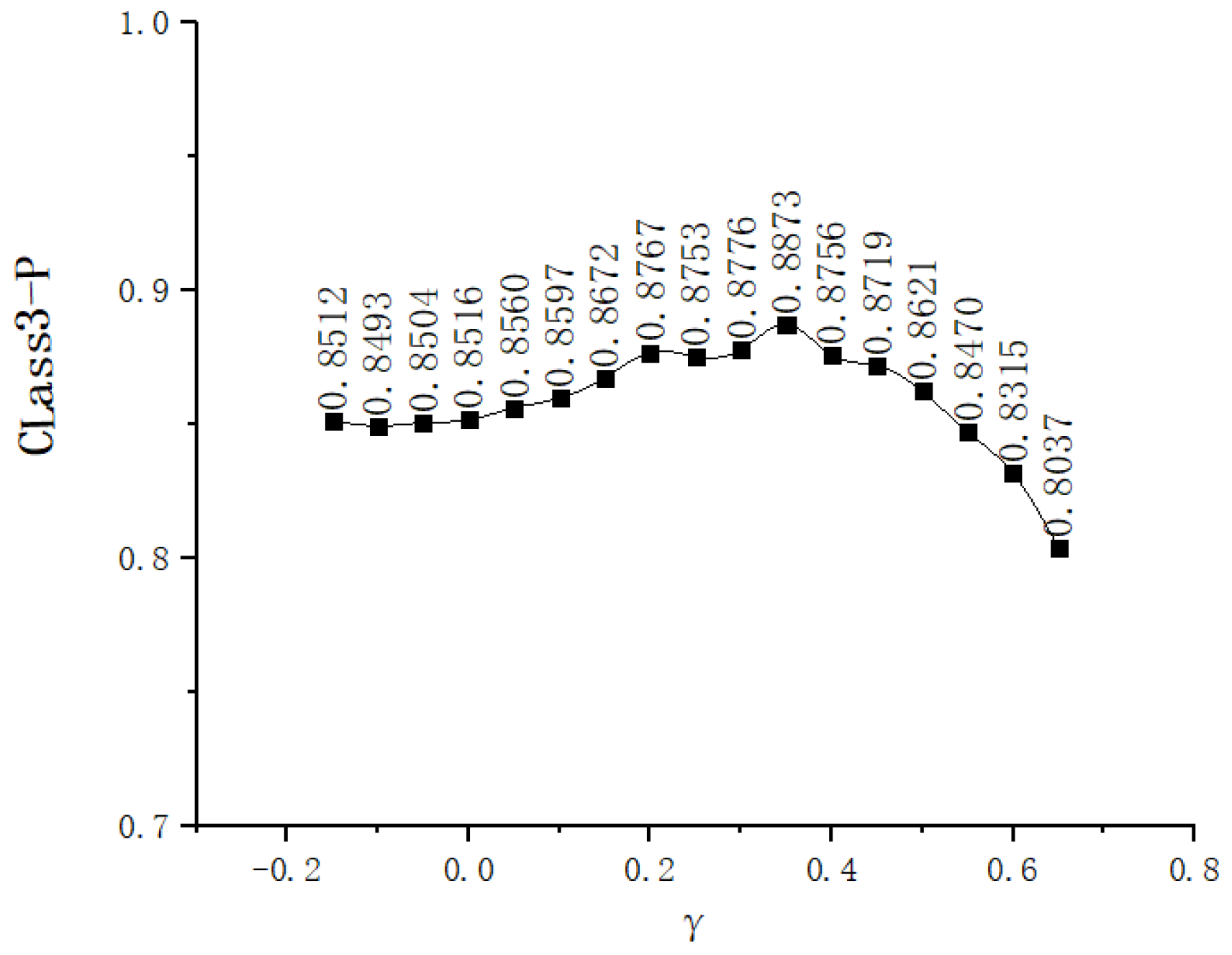
3.3. Hyperparameter Analysis
3.4. The Results of the Control Group Experiments
3.5. Ablation Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Zhang, Y.; Zhai, D.; Xu, D. Pin Defect Detection of Transmission Line Based on Improved SSD. High Volt. Eng. 2021, 47, 3795–3802. [Google Scholar]
- Yi, H.; Liu, B.; Zhao, B.; Liu, E. Small Object Detection Algorithm Based on Improved YOLOv8 for Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1734–1747. [Google Scholar] [CrossRef]
- Ren, K.; He, R.; Girshick, R. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.W.; Vasconcelos, N. Cascade R-CNN: High Quality Object Detection and Instance Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1483–1498. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9726–9735. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical Networks for Few-Shot Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.M.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; Liu, J.; Fang, X.; Wang, J.; Zhou, L. A Double-Branch Surface Detection System for Armatures in Vibration Motors with Miniature Volume Based on ResNet-101 and FPN. Sensors 2020, 20, 2360. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the 37th International Conference on Machine Learning (ICML), Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means Clustering Algorithms: A Comprehensive Review, Variants Analysis, and Advances in the Era of Big Data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X. SimpleMKKM: Simple Multiple Kernel K-Means. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5174–5186. [Google Scholar] [CrossRef] [PubMed]
- Cao, K.D.; Wei, C.L.; Gaidon, A.; Arechiga, N.; Ma, T.Y. Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss. In Proceedings of the Advances in Neural Information Processing Systems 32 (NIPS), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Gozalo-Brizuela, R.; Garrido-Merchan, E.C. A Survey of Generative AI Applications. arXiv 2023, arXiv:2306.02781. [Google Scholar] [CrossRef]



| Hyperparameter | ||||
|---|---|---|---|---|
| 0.9086 | 0.9128 | 0.9171 | 0.8936 | |
| 0.9093 | 0.9166 | 0.9186 | 0.8967 | |
| 0.9104 | 0.9172 | 0.9196 | 0.9005 | |
| 0.9102 | 0.9185 | 0.9194 | 0.9015 |
| Overall Accuracy | Class 3—Precision | Class 3—Recall | |
|---|---|---|---|
| 0.5 | 0.7274 | 0.5365 | 0.6742 |
| 0.8914 | 0.8641 | 0.7891 | |
| 0.9196 | 0.8873 | 0.7707 | |
| 0.6236 | 0.8915 | 0.8038 | |
| 0.8541 | 0.8747 | 0.7656 |
| Name | Overall Accuracy | Class 3—Precision | Predict FPS | Train FPS |
|---|---|---|---|---|
| Baseline | 0.8574 | 0.4751 | / | / |
| Resnet18-softmax | 0.7532 | 0.3283 | 466.3 | 195.4 |
| Resnet18-Focal Loss | 0.8142 | 0.6919 | 465.7 | 193.6 |
| ResNet18-LDAM Loss | 0.7983 | 0.7159 | 466.1 | 194.7 |
| Swin Transformer | 0.8750 | 0.7341 | 285.7 | 41.3 |
| OURS without Dual Branch | 0.9227 | 0.8495 | 406.2 | 23.7 |
| OURS with Dual Branch | 0.9196 | 0.8873 | 291.5 | 23.7 |
| Name | Overall Accuracy | Class 3—Precision | Class 3—Recall |
|---|---|---|---|
| SimCLR-Resnet18 | 0.8174 | 0.4165 | 0.5595 |
| SimCLR + Lable-contrast | 0.8572 | 0.4205 | 0.6131 |
| SimCLR + Double Sampling | 0.9013 | 0.7826 | 0.6816 |
| SimCLR + Lable-contrast + Dual-Sampling | 0.9227 | 0.8495 | 0.7905 |
| SimCLR + Lable-contrast + Dual-Sampling + Dual-Branch | 0.9196 | 0.8873 | 0.7707 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.-P.; Zhao, J.-L.; Liu, L.-S.; Feng, H.-Y.; Du, J.-Q.; Fang, X. Dual-Branch Discriminative Transmission Line Bolt Image Classification Based on Contrastive Learning. Processes 2025, 13, 898. https://doi.org/10.3390/pr13030898
Ji Y-P, Zhao J-L, Liu L-S, Feng H-Y, Du J-Q, Fang X. Dual-Branch Discriminative Transmission Line Bolt Image Classification Based on Contrastive Learning. Processes. 2025; 13(3):898. https://doi.org/10.3390/pr13030898
Chicago/Turabian StyleJi, Yan-Peng, Jian-Li Zhao, Liang-Shuai Liu, Hai-Yan Feng, Jia-Qi Du, and Xia Fang. 2025. "Dual-Branch Discriminative Transmission Line Bolt Image Classification Based on Contrastive Learning" Processes 13, no. 3: 898. https://doi.org/10.3390/pr13030898
APA StyleJi, Y.-P., Zhao, J.-L., Liu, L.-S., Feng, H.-Y., Du, J.-Q., & Fang, X. (2025). Dual-Branch Discriminative Transmission Line Bolt Image Classification Based on Contrastive Learning. Processes, 13(3), 898. https://doi.org/10.3390/pr13030898






