Interpretable Analysis of the Viscosity of Digital Oil Using a Combination of Molecular Dynamics Simulation and Machine Learning
Abstract
1. Introduction
2. Methods
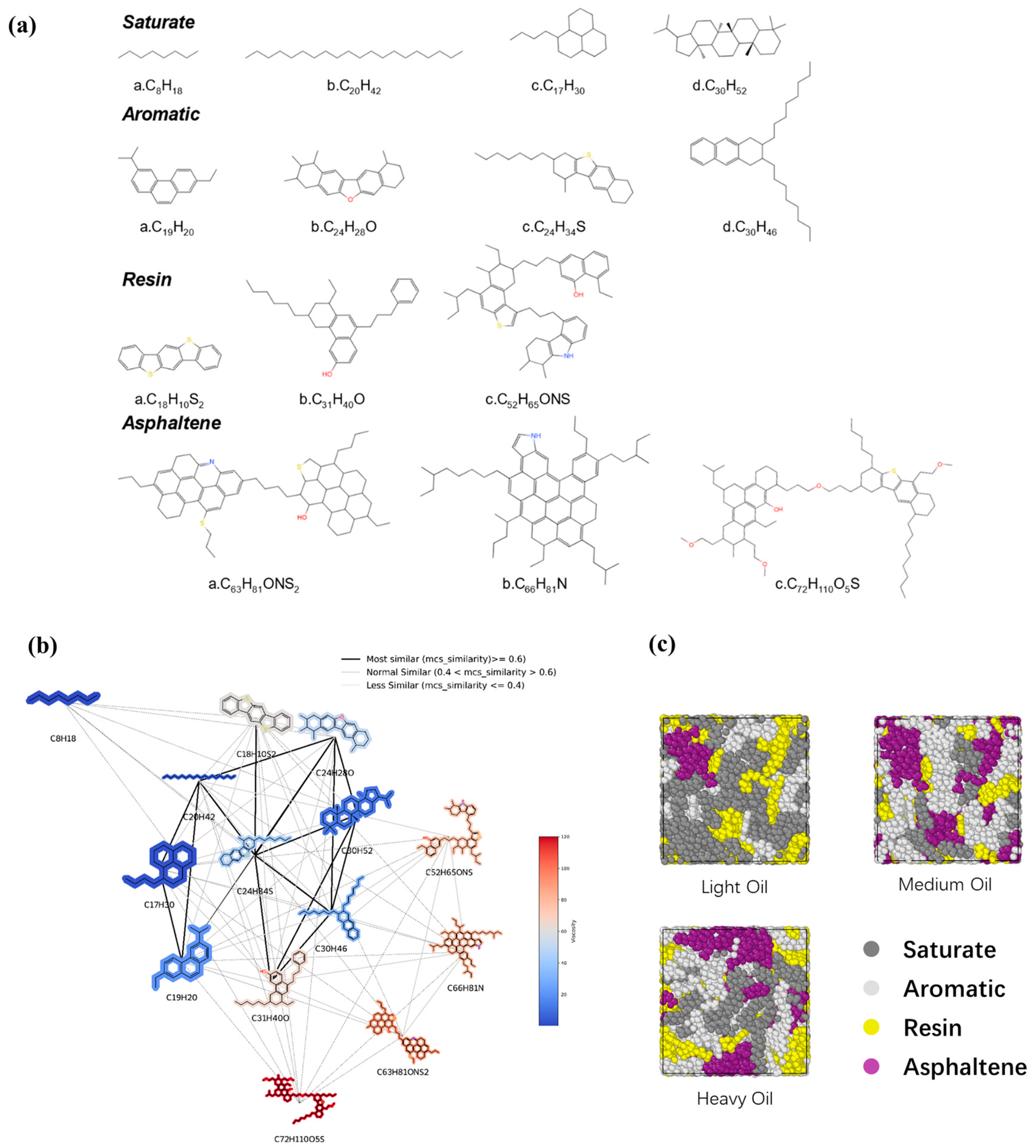
2.1. Molecular Models
2.2. Simulation Parameters
3. Results and Discussion
3.1. Density
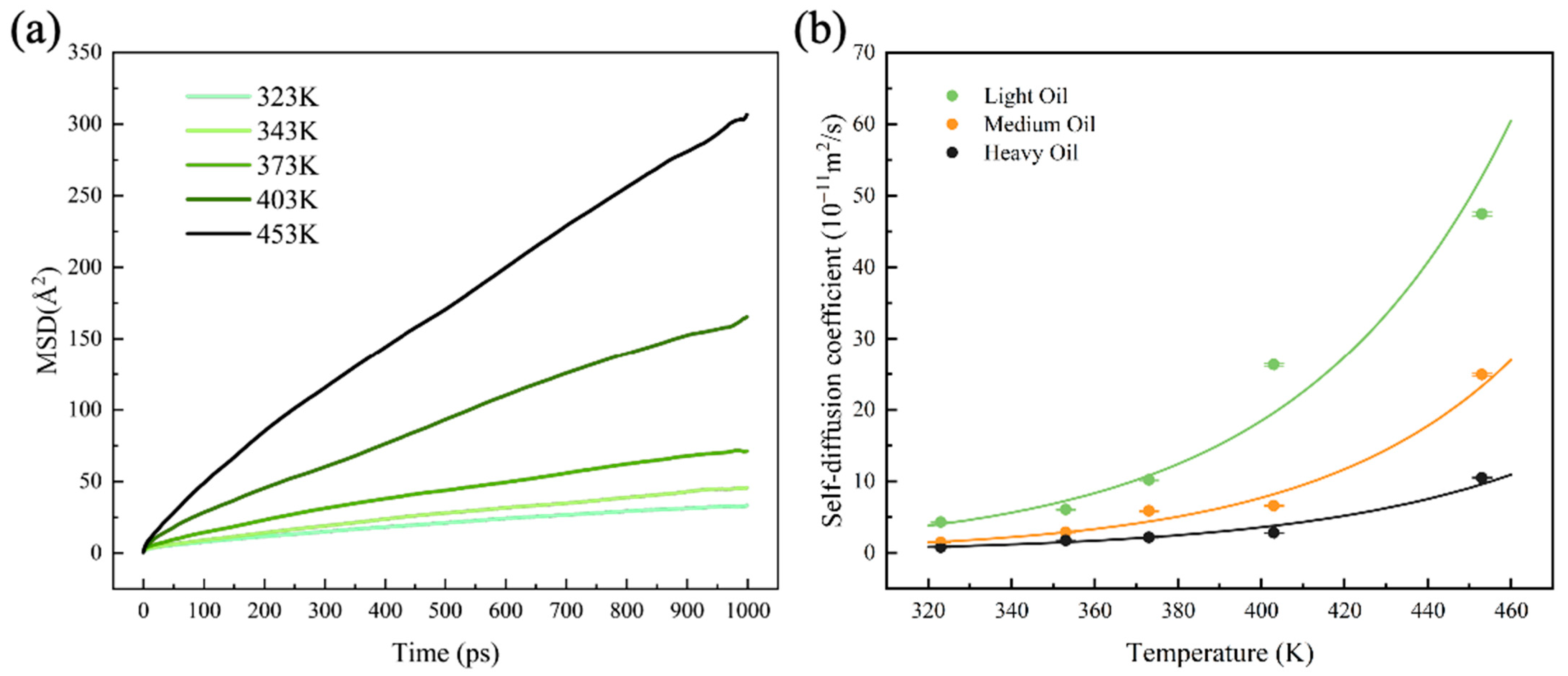
3.2. Self-Diffusion Coefficient
3.3. Viscosity
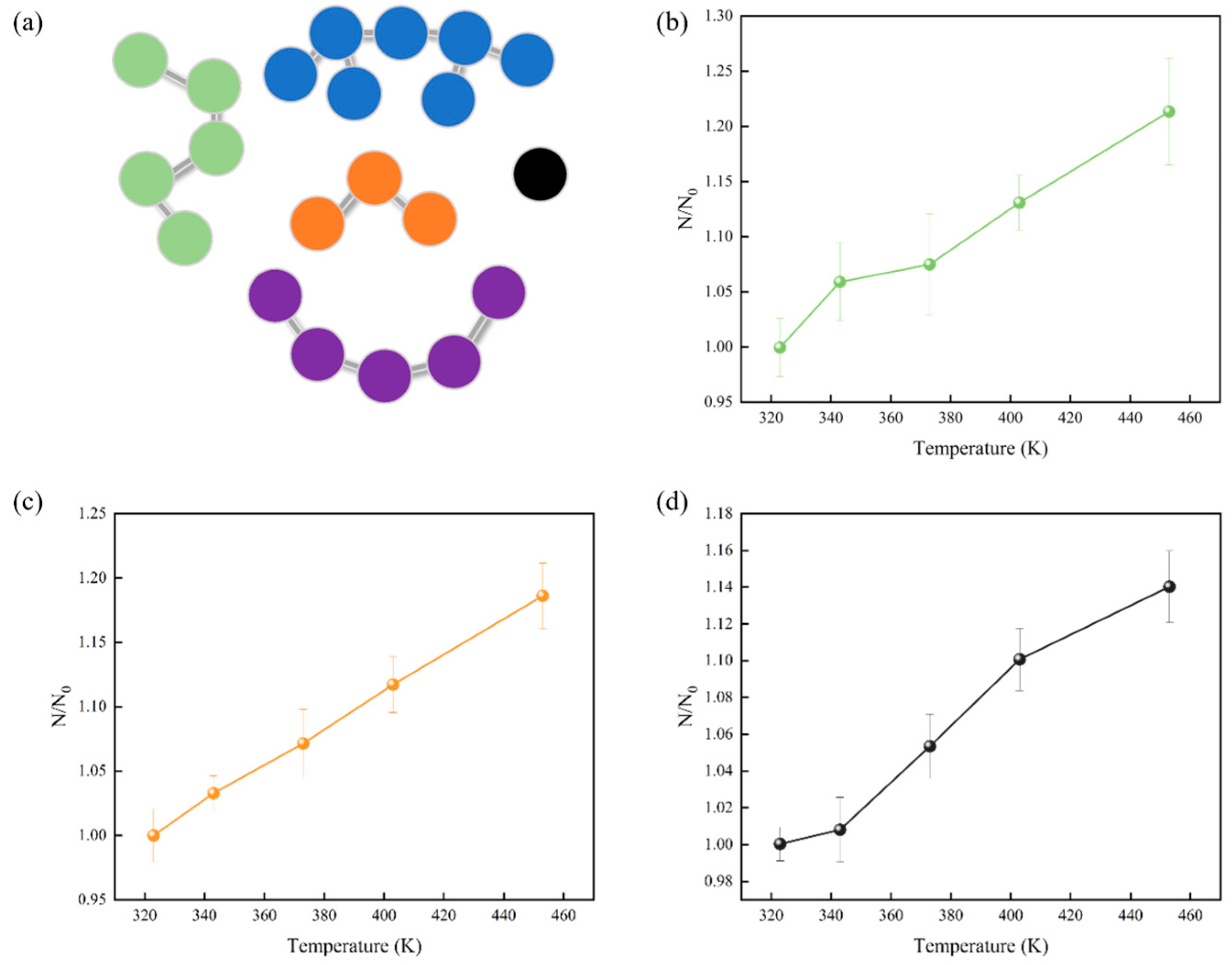
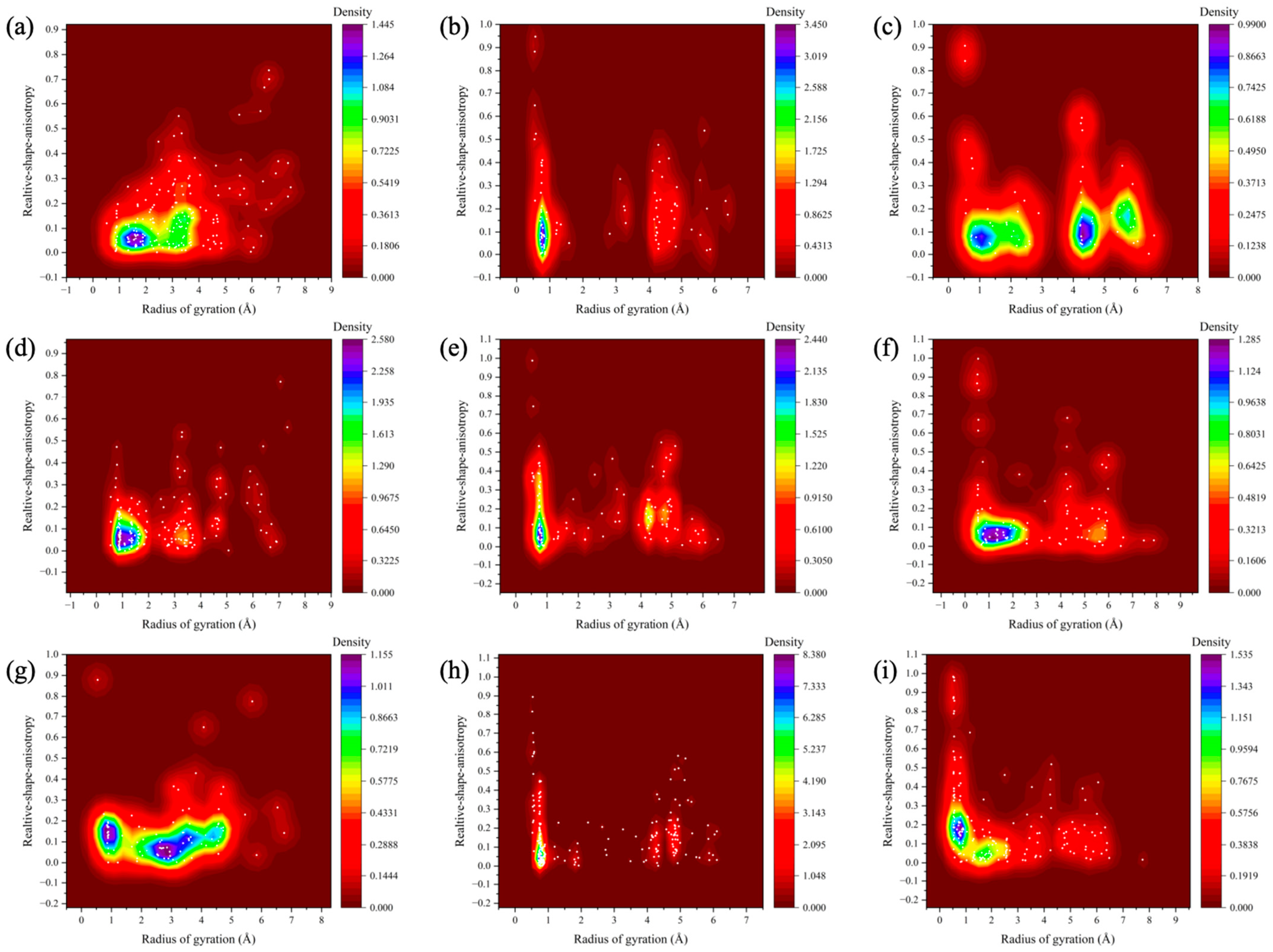
3.4. Cluster Analysis
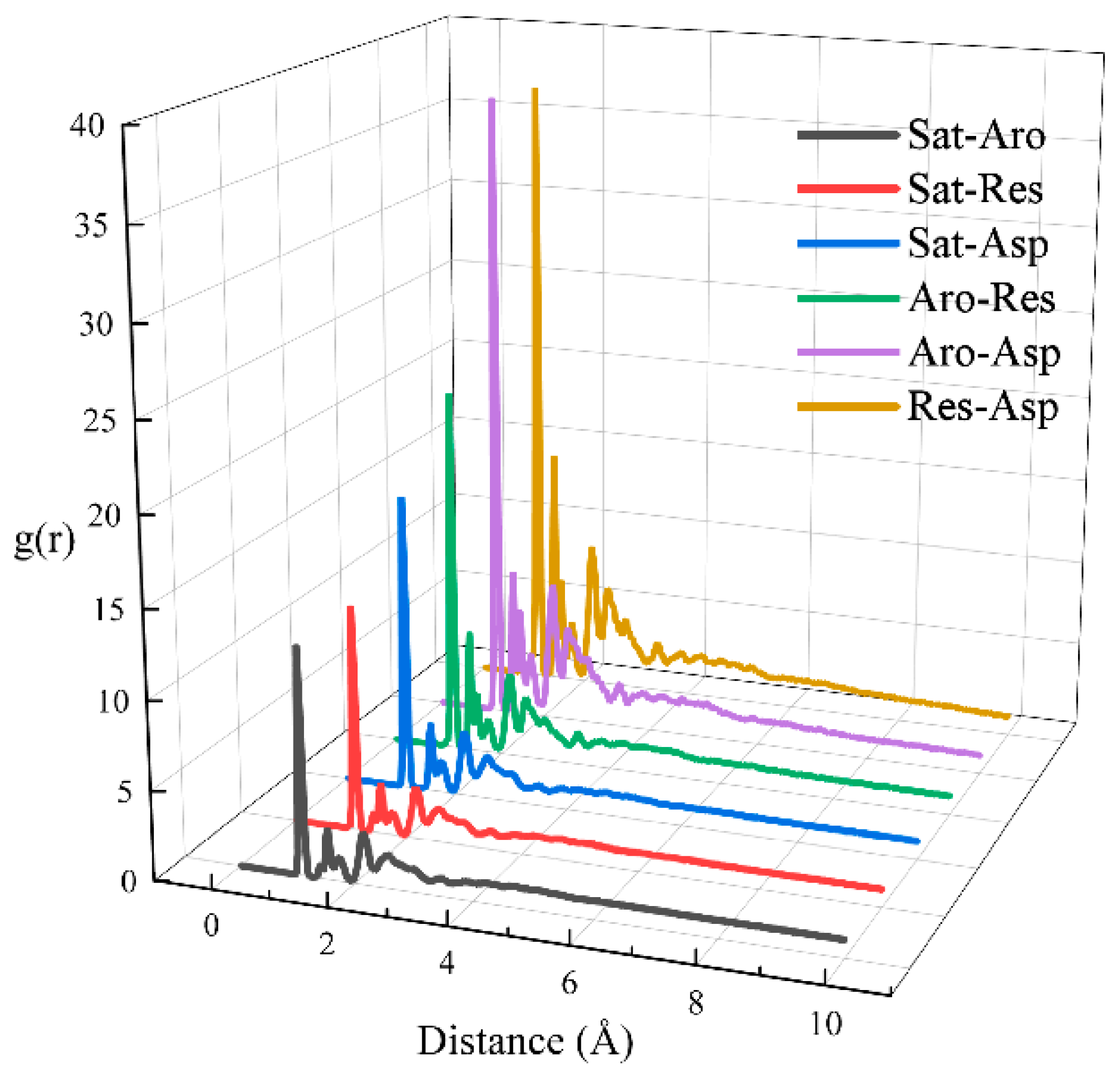
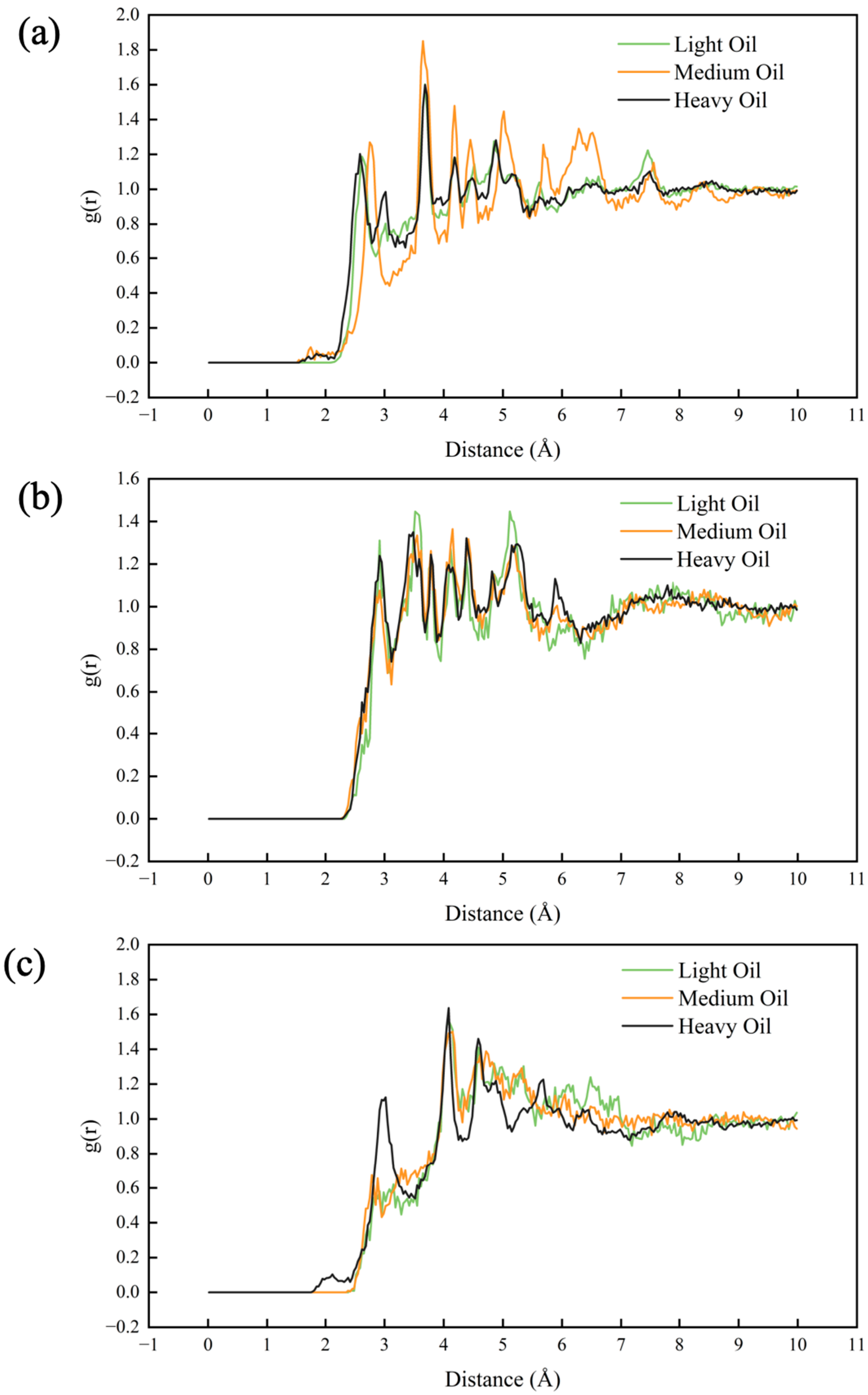
3.5. Radial Distribution Function (RDF) Analysis
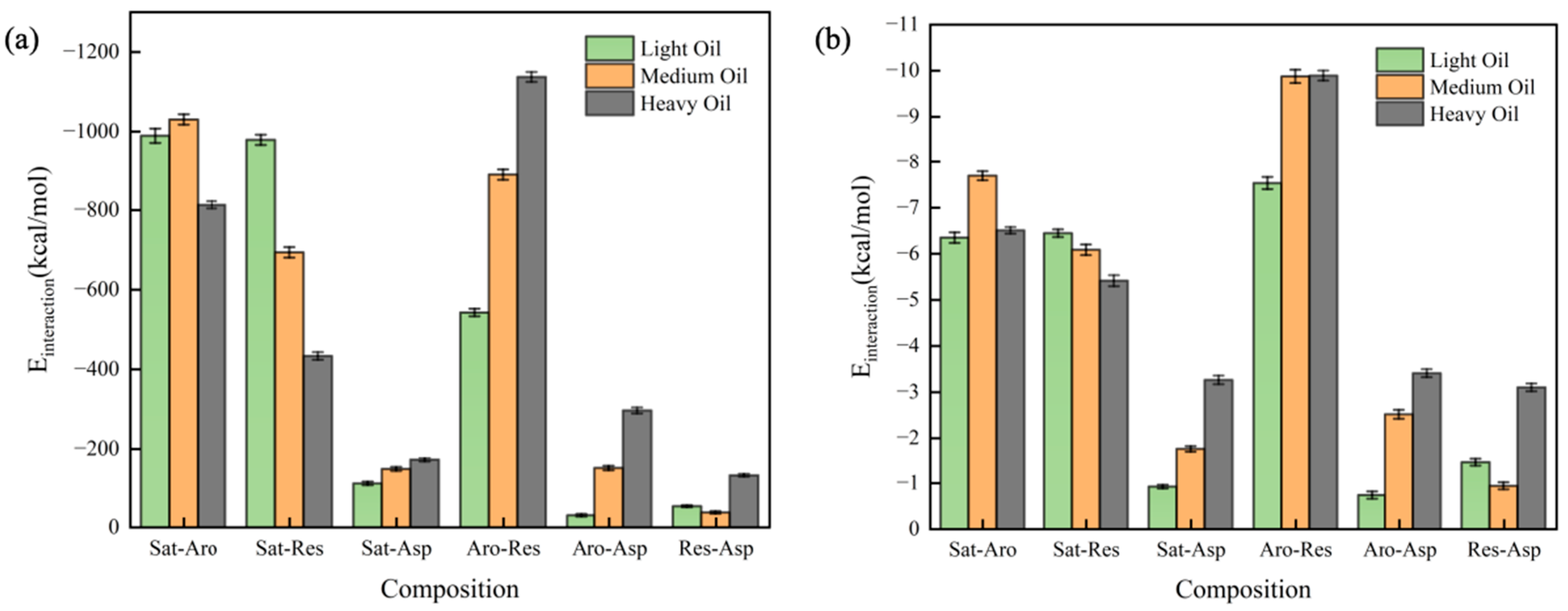
3.6. Effects of Heteroatoms
3.7. Effects of Metal Ions
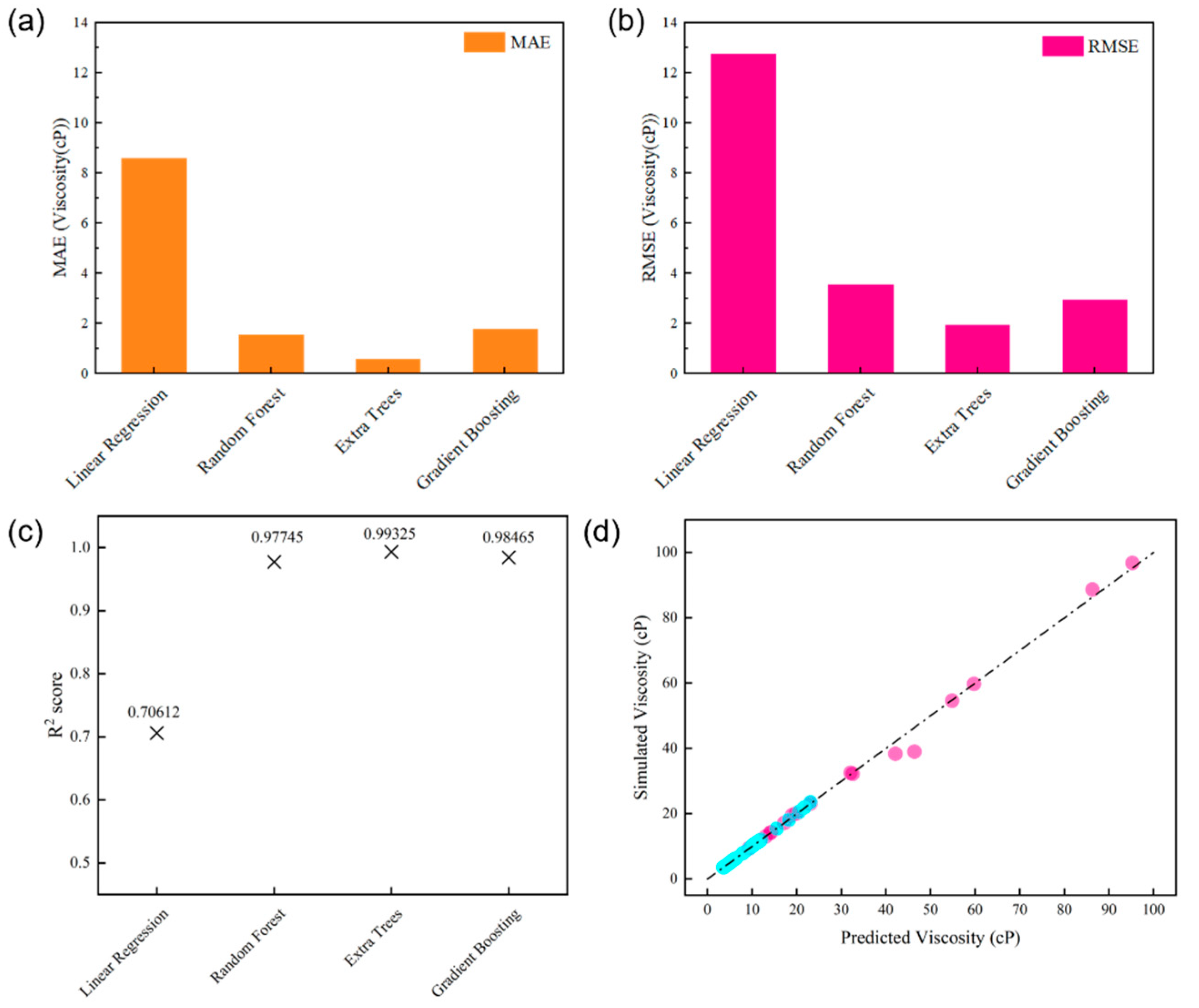
3.8. Prediction and Interpretable Analysis of Digital Oil Viscosity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| MSD | Mean square displacement |
| DS | Self-diffusion coefficient |
| ri(t) | Position vector of the atoms at time t |
| η | Viscosity |
| kB | Boltzmann constant |
| Pαβ | Non-diagonal element of the stress tensor |
| Rg | Radius of gyration |
| κ2 | Relative shape anisotropy |
| RDF | Radial distribution function |
References
- Wang, Z. Global Oil and Gas Development in 2022: Situation, Trends and Enlightenment. Pet. Explor. Dev. 2023, 50, 1167–1186. [Google Scholar] [CrossRef]
- Hasan, S.W.; Ghannam, M.T.; Esmail, N. Heavy Crude Oil Viscosity Reduction and Rheology for Pipeline Transportation. Fuel 2010, 89, 1095–1100. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Zou, R.; Zou, R.; Huang, L.; Liu, Y.; Lei, H. Molecular Dynamics Investigation of DME Assisted CO2 Injection to Enhance Shale Oil Recovery in Inorganic Nanopores. J. Mol. Liq. 2023, 385, 122389. [Google Scholar] [CrossRef]
- Huang, T.; Cheng, L.; Cao, R.; Wang, X.; Jia, P.; Cao, C. Molecular Simulation of the Dynamic Distribution of Complex Oil Components in Shale Nanopores during CO2-EOR. Chem. Eng. J. 2024, 479, 147743. [Google Scholar] [CrossRef]
- Fang, T.; Li, S.; Zhang, Y.; Su, Y.; Yan, Y.; Zhang, J. How the Oil Recovery in Deep Oil Reservoirs Is Affected by Injected Gas Types: A Molecular Dynamics Simulation Study. Chem. Eng. Sci. 2021, 231, 116286. [Google Scholar] [CrossRef]
- Zhu, B.; Yang, M.; Yan, Y.; Zhong, J.; Li, J.; Li, Z.; Zhang, J. Insights into the Effect of Water Content on Asphaltene Aggregation Behavior and Crude Oil Rheology: A Molecular Dynamics Simulation Study. J. Mol. Liq. 2024, 396, 124042. [Google Scholar] [CrossRef]
- Cao, H.; Cao, X.; Zhao, X.; Guo, D.; Liu, Y.; Bian, J. Molecular Dynamics Simulation of Wax Molecules Aggregational Crystallization Behavior during Cooling of Crude Oil Mixture. Case Stud. Therm. Eng. 2022, 37, 102298. [Google Scholar] [CrossRef]
- Su, G.; Zhang, H.; Geng, T.; Yuan, S. Effect of SDS on Reducing the Viscosity of Heavy Oil: A Molecular Dynamics Study. Energy Fuels 2019, 33, 4921–4930. [Google Scholar] [CrossRef]
- Park, J.W.; Lee, K.B. Molecular Dynamics Simulations of Asphaltene Aggregation in Heavy Oil System for the Application to Solvent Deasphalting. Fuel 2022, 323, 124171. [Google Scholar] [CrossRef]
- Xu, J.; Li, X.; Hou, C.; Wang, L.; Zhou, G.; Ge, W.; Li, J. Engineering Molecular Dynamics Simulation in Chemical Engineering. Chem. Eng. Sci. 2015, 121, 200–216. [Google Scholar] [CrossRef]
- Xiong, H.; Devegowda, D.; Huang, L. EOR Solvent-Oil Interaction in Clay-Hosted Pores: Insights from Molecular Dynamics Simulations. Fuel 2019, 249, 233–251. [Google Scholar] [CrossRef]
- Zhang, W.; Yi, X.; Yi, Q.; Sun, L. Performance Evaluation and Molecular Dynamics Simulation in the Liquid–Liquid Extraction Process of Low Transition Temperature Mixture + n-Hexane + 1,2-Dichloroethane. J. Mol. Liq. 2022, 364, 119913. [Google Scholar] [CrossRef]
- Iwase, M.; Sugiyama, S.; Liang, Y.; Masuda, Y.; Morimoto, M.; Matsuoka, T.; Boek, E.S.; Ueda, R.; Nakagawa, K. Development of Digital Oil for Heavy Crude Oil: Molecular Model and Molecular Dynamics Simulations. Energy Fuels 2018, 32, 2781–2792. [Google Scholar] [CrossRef]
- Cui, W.; Huo, K.; Sugiyama, S.; Liang, Y.; Masuda, Y.; Morimoto, M.; Matsuoka, T.; Boek, E.S.; Kaito, Y.; Nakagawa, K.; et al. Microstructural Evolution of Bitumen during the Glass Transition: An Application of Digital Oil. Fuel 2023, 335, 127048. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Q.; Ma, Y.; Xie, J.; Cao, B. Molecular Dynamics Study on the Kinematic Viscosity, Density and Structure of Fuel Blends Containing n-Decane and Biofuel Compound of Ethyl Decanoate or Ethyl Dodecanoate. J. Mol. Liq. 2023, 379, 121680. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, S.; Li, X.; Ma, D.; Sun, X.; Wang, H.-Z.; Yan, Y.; Xu, J.; Yang, C. Molecular Dynamics Simulation Reveals Unique Rheological and Viscosity–Temperature Properties of Karamay Heavy Crude Oil. Energy Fuels 2021, 35, 7956–7966. [Google Scholar] [CrossRef]
- Li, J.; Chen, D.; Sun, K.; Pan, R.; Tang, Y. Molecular Dynamics Simulation and Experimental Study of the Rheological Performance of Graphene Lubricant Oil. Diam. Relat. Mater. 2024, 141, 110721. [Google Scholar] [CrossRef]
- Guo, J.; Xiao, H.; Wu, F. Prediction of Viscosity of Kerosene-Based Nanographene Fluids by Molecular Dynamics Simulation Analysis. J. Mol. Liq. 2023, 391, 123417. [Google Scholar] [CrossRef]
- Li, G.; Tan, Y.; Fu, Y.; Liu, P.; Fu, C.; Oeser, M. Density, Zero Shear Viscosity and Microstructure Analysis of Asphalt Binder Using Molecular Dynamics Simulation. Constr. Build. Mater. 2022, 345, 128332. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Q.; Zhang, X.; Ji, C.; Cao, B. A Molecular Dynamics Simulation Study of the Densities and Viscosities of 1,2,4-Trimethylbenzene and Its Binary Mixture with n-Decane. Fluid Phase Equilibria 2022, 562, 113566. [Google Scholar] [CrossRef]
- Cartes, M.; Chaparro, G.; Alonso, G.; Mejía, A. Density and Viscosity of Liquid Mixtures Formed by N-Hexane, Ethanol, and Cyclopentyl Methyl Ether. J. Mol. Liq. 2022, 359, 119353. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, S.; Li, L.; Liu, G. Sub-to-Supercritical Properties and Inhomogeneity of JP-10 Using Molecular Dynamics Simulation. Fuel 2021, 288, 119696. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, Z.; Lu, Y.; Zhou, T.; Zhang, H.; Zhao, X.; Liu, L.; Zhang, L.; Gao, Y. Molecular Dynamics Simulation on the Heat Transfer in the Cross-Linked Poly(Dimethylsiloxane). J. Phys. Chem. B 2023, 127, 10243–10251. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Q.; Xie, Q.; Zhu, H.; Xu, W.; Liu, Z. Mechanism Analysis of Heavy Oil Viscosity Reduction by Ultrasound and Viscosity Reducers Based on Molecular Dynamics Simulation. ACS Omega 2022, 7, 36137–36149. [Google Scholar] [CrossRef]
- Su, Z.; Liu, X.; Xing, J.; Jiao, Y.; Zhu, Z.; Qi, J.; Wang, Y. Separation of Butyl Acetate and Propyl Acetate from Wastewater by Liquid-Liquid Extraction and Molecular Dynamics Simulation. J. Mol. Liq. 2023, 379, 121699. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, T.; Lan, X.; Xu, C. The Practice and Prospect of Artificial Intelligence Driving Chemical Innovation Design. Chem. Prog. 2023, 42, 3910–3916. [Google Scholar] [CrossRef]
- Bhimineni, S.H.; Zhou, T.; Mahmoodpour, S.; Singh, M.; Li, W.; Bag, S.; Sass, I.; Müller-Plathe, F. Machine-Learning-Assisted Investigation of the Diffusion of Hydrogen in Brine by Performing Molecular Dynamics Simulation. Ind. Eng. Chem. Res. 2023, 62, 21385–21396. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Chen, H.; Yu, X.; Li, Y.; Yang, K. Influence of Ether Group on Viscosity and Film Lubrication of Diester Lubricants: Integrated Quantitative Structure–Property Relationship and Molecular Dynamics Simulation Methods. J. Mol. Liq. 2024, 398, 124254. [Google Scholar] [CrossRef]
- Kirch, A.; Celaschi, Y.M.; de Almeida, J.M.; Miranda, C.R. Brine–Oil Interfacial Tension Modeling: Assessment of Machine Learning Techniques Combined with Molecular Dynamics. ACS Appl. Mater. Interfaces 2020, 12, 15837–15843. [Google Scholar] [CrossRef] [PubMed]
- Freitas, R.S.M.; Lima, Á.P.F.; Chen, C.; Rochinha, F.A.; Mira, D.; Jiang, X. Towards Predicting Liquid Fuel Physicochemical Properties Using Molecular Dynamics Guided Machine Learning Models. Fuel 2022, 329, 125415. [Google Scholar] [CrossRef]
- Omrani, S.; Ghasemi, M.; Singh, M.; Mahmoodpour, S.; Zhou, T.; Babaei, M.; Niasar, V. Interfacial Tension–Temperature–Pressure–Salinity Relationship for the Hydrogen–Brine System under Reservoir Conditions: Integration of Molecular Dynamics and Machine Learning. Langmuir 2023, 39, 12680–12691. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, S.; Wen, G.; Liu, Q.; Tang, P. Thermal Conductivity Prediction and Structure-Property Relationship of CaO-SiO2-Al2O3 Ternary System: A Combination of Molecular Dynamics Simulations and Machine Learning. J. Mol. Liq. 2021, 324, 114697. [Google Scholar] [CrossRef]
- Li, X.; Cao, X.; Yuan, Y.; Deng, M.; Yang, X. Construction and Validation of the Average Molecular Structure Model of the Bio-Oil from Solvent-Thermal Liquefaction of Sawdust Using Molecular Characterization and Molecular Simulation. J. Mol. Liq. 2023, 379, 121689. [Google Scholar] [CrossRef]
- Xiong, Q.-A.; Zhang, Y.-M.; Qiao, P.; Li, G.-T.; Li, J.-Z.; Zhang, W. Comparative Pyrolysis Kinetics of Heavy Oil and Its SARA Fractions Using Distributed Activation Energy Model. Pet. Sci. 2023, 20, 3231–3239. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, L.; Liu, S.; Zhang, J.; Yang, M.; Song, Y. Molecular Dynamics Simulation of Bubble Nucleation and Growth during CO2 Huff-n-Puff Process in a CO2-Heavy Oil System. Geoenergy Sci. Eng. 2023, 227, 211852. [Google Scholar] [CrossRef]
- Li, B.; Guo, Z.; Li, N.; Wang, D.; Li, G.; Zheng, L.; Qi, B.; Jiao, T. Molecular Dynamics Simulation of Wax Deposition in Crude Oil Systems. Colloids Surf. A Physicochem. Eng. Asp. 2023, 674, 131965. [Google Scholar] [CrossRef]
- Scalfani, V.F.; Patel, V.D.; Fernandez, A.M. Visualizing Chemical Space Networks with RDKit and NetworkX. J. Cheminform. 2022, 14, 87. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. P ACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Jewett, A.I.; Stelter, D.; Lambert, J.; Saladi, S.M.; Roscioni, O.M.; Ricci, M.; Autin, L.; Maritan, M.; Bashusqeh, S.M.; Keyes, T.; et al. Moltemplate: A Tool for Coarse-Grained Modeling of Complex Biological Matter and Soft Condensed Matter Physics. J. Mol. Biol. 2021, 433, 166841. [Google Scholar] [CrossRef] [PubMed]
- Maskey, S.; Morrow, B.H.; Gustafson, M.Z.; Luning Prak, D.J.; Mikulski, P.T.; Harrison, J.A. Systematic Examination of the Links between Composition and Physical Properties in Surrogate Fuel Mixtures Using Molecular Dynamics. Fuel 2020, 261, 116247. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Yamada, H.; Fujiwara, T.; Hori, K. Simulations of Dielectric Constants and Viscosities of Organic Electrolytes by Quantum Mechanics and Molecular Dynamics. J. Mol. Liq. 2020, 312, 113288. [Google Scholar] [CrossRef]
- Bashiri, M.; Shojaeefard, M.H.; Qasemian, A. Molecular Dynamics Simulations and Experimental Investigation of Viscosity of CuO-Oil Nanolubricant at Different Temperatures and Volume Fractions of Nanoparticles. J. Mol. Graph. Model. 2024, 129, 108750. [Google Scholar] [CrossRef]
- Yao, N.; Yu, L.; Fu, Z.-H.; Shen, X.; Hou, T.-Z.; Liu, X.; Gao, Y.-C.; Zhang, R.; Zhao, C.-Z.; Chen, X.; et al. Probing the Origin of Viscosity of Liquid Electrolytes for Lithium Batteries. Angew. Chem. 2023, 135, e202305331. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Shen, K.; Cui, L.; Yang, L.; Wei, X.; Liu, X.; Ren, M.; Cao, F.; Xu, J. Molecular Dynamics Simulations of the Nickel Removal from Crude Oil by Neutral and Charged Spherical Polymer Brushes. Fuel 2023, 345, 128179. [Google Scholar] [CrossRef]




| Fitted Equation | |
|---|---|
| Light oil | |
| Medium oil | |
| Heavy oil |
| Model | Hyperparameter | Value |
|---|---|---|
| RF | nest | 800 |
| maxdep | 13 | |
| maxfeat | 5 | |
| ET | nest | 100 |
| maxdep | 10 | |
| maxfeat | 5 | |
| GB | nest | 600 |
| learning rate | 0.1 | |
| maxdep | 2 | |
| maxfeat | 5 |
| Overall Dataset Containing Samples with Different Temperatures | 323 K ≤ T ≤ 453 K | 323 K ≤ T ≤ 403 K | 403 K ≤ T ≤ 453 K |
|---|---|---|---|
| Feature | Importance value | ||
| T | 0.7183 | 0.4907 | 0.301 |
| Saturate/SARA | 0.064 | 0.0496 | 0.0644 |
| Aromatic/SARA | 0.0734 | 0.1409 | 0.1018 |
| Resin/SARA | 0.016 | 0.0654 | 0.0819 |
| Asphaltene/SARA | 0.0148 | 0.0012 | 0.005 |
| C, m% | 0.0003 | 0.0015 | 0.0156 |
| H, m% | 0.0065 | 0.0857 | 0.1372 |
| O, m% | 0.0508 | 0.1245 | 0.1583 |
| N, m% | 0.0552 | 0.0397 | 0.1323 |
| S, m% | 0.0006 | 0.0008 | 0.0026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, H.; Mao, Y.; Zhang, Z.; Guan, W.; Wu, Z.; Lan, X.; Xu, C.; Zhou, T. Interpretable Analysis of the Viscosity of Digital Oil Using a Combination of Molecular Dynamics Simulation and Machine Learning. Processes 2025, 13, 881. https://doi.org/10.3390/pr13030881
Zhang Y, Li H, Mao Y, Zhang Z, Guan W, Wu Z, Lan X, Xu C, Zhou T. Interpretable Analysis of the Viscosity of Digital Oil Using a Combination of Molecular Dynamics Simulation and Machine Learning. Processes. 2025; 13(3):881. https://doi.org/10.3390/pr13030881
Chicago/Turabian StyleZhang, Yunjun, Haoming Li, Yunfeng Mao, Zhongyi Zhang, Wenlong Guan, Zhenghao Wu, Xingying Lan, Chunming Xu, and Tianhang Zhou. 2025. "Interpretable Analysis of the Viscosity of Digital Oil Using a Combination of Molecular Dynamics Simulation and Machine Learning" Processes 13, no. 3: 881. https://doi.org/10.3390/pr13030881
APA StyleZhang, Y., Li, H., Mao, Y., Zhang, Z., Guan, W., Wu, Z., Lan, X., Xu, C., & Zhou, T. (2025). Interpretable Analysis of the Viscosity of Digital Oil Using a Combination of Molecular Dynamics Simulation and Machine Learning. Processes, 13(3), 881. https://doi.org/10.3390/pr13030881








