Machine Learning for the Optimization and Performance Prediction of Solid Oxide Electrolysis Cells: A Review

Abstract

Solid oxide electrolysis cells (SOECs) represent a promising technology because they have the potential to achieve greater efficiency than existing electrolysis methods, making them a strong candidate for sustainable hydrogen production. SOECs utilize a solid oxide electrolyte, which facilitates the migration of oxygen ions while maintaining gas impermeability at temperatures between 600 °C and 900 °C. This review provides an overview of the recent advancements in research and development at the intersection of machine learning and SOECs technology. It emphasizes how data-driven methods can improve performance prediction, facilitate material discovery, and enhance operational efficiency, with a particular focus on materials for cathode-supported cells. This paper also addresses the challenges associated with implementing machine learning for SOECs, such as data scarcity and the need for robust validation techniques. This paper aims to address challenges related to material degradation and the intricate electrochemical behaviors observed in SOECs. It provides a description of the reactions that may be involved in the degradation mechanisms, taking into account thermodynamic and kinetic factors. This information is utilized to construct a fault tree, which helps categorize various faults and enhances understanding of the relationship between their causes and symptoms.

1. Introduction

The world’s population is growing gradually and is anticipated to reach 9.7 billion by 2050 [1]. In addition to the increase in population, industrialization and urbanization of developing countries (increasing energy demand in the industrial sector), long journeys, maritime transport, and cargo are growing rapidly [2]. As a result, the worldwide demand for energy services—encompassing transportation, power generation, and industrial applications—is expected to rise significantly throughout this century [3]. In the situation of the energy transition on the road to green sources and achieving greenhouse gas reduction targets by 2050, hydrogen is premeditated as a crucial energy carrier because it has the ability to store, transport, and produce green energy [4]. In addition, the ongoing reliance on fossil fuels is linked to an increase in benchmark pollutants and greenhouse gas emissions. Emissions from the combustion of fossil fuels reduce air quality, create health risks for humans, and exacerbate global climate change. Global energy-related CO₂ emissions reached a record high of 37.4 billion tons (Gt) in 2023, reflecting an increase of 1.1%, or 410 million tons, from the previous year. This rise in emissions was largely driven by coal, which accounted for over 65% of the increase. Notably, emissions in China saw the largest growth globally, contributing approximately 565 million tons to the overall increase, continuing its emissions-intensive economic trajectory post-pandemic [5]. Global industrial demand for hydrogen has grown sharply since 1980. Hydrogen is used as a raw material in a range of industries, including refining, iron and steel, semiconductors, propellant fuels, glass production, and so on [6].

One method of producing hydrogen is the use of solid oxide electrolysis cells (SOECs). Solid oxide electrolysis cells have advanced extensively in recent years. Enhancing efficiency can substantially lower hydrogen production costs since electricity consumption is the primary driver of expenses in the electrolysis process [7,8]. Ni [9] created a two-dimensional heat transfer model, along with chemical and electrochemical reactions in an SOEC. He posited that the reversible reactions of methanation and reforming adversely affect the electrolysis of SOECs. To overcome the limitations of steady-state models, Ali et al. [10] suggested that a review can yield valuable insights for enhancing SOECs performance and endorse the future progress of SOECs, including the development of electrolysis efficiency. Yin et al. [11] introduced a non-static SOECs model aimed at analyzing transient behaviors produced by different time coefficients of the components involved. The electrolyzer has been identified as the component that consumes the most energy and causes the greatest exergy loss. A dynamic simulation of the stack temperature is conducted to assess its response to different control inputs and disturbances. Zhang et al. [12] developed and confirmed a real-time multi-physics model for pressurized SOECs, recommending operation at the maximum endothermic point to optimize thermal energy utilization. The results indicated that the maximum endothermic point could offer significant chances for heat transfer addition in SOECs hybrids. Additionally, the developed SOECs model showcased its capability for real-time execution.

To tackle various challenges with electrolytic cells, machine learning (ML) offers a powerful approach for uncovering potential rules and relationships among different features, such as material properties, structural aspects, operational parameters, and output characteristics. This is achieved through effective data collection methods [13,14,15]. Advancements in the application of artificial neural networks for hydrogen production were studied by Abdelkareem et al. [16]. The results indicated that the coefficient of determination (R²) and cruel squared error were utilized as recital metrics for assessing the effectiveness of the artificial neural networks (ANNs) applied across various production methods. Additionally, the study presents recommendations for future research and highlights emerging topics of interest in the field. Olabi et al. [17] investigated the use of artificial intelligence for predicting, optimizing, and controlling thermal energy storage systems in their study. This study examined the advancements achieved in the application of artificial intelligence and its various subfields to enhance, forecast, and manage the performance of energy systems. Mohamed et al. [18] highlighted that polynomial and logistic modeling are the most suitable algorithms for developing ML models specifically for proton exchange membrane (PEM) fuel cells. Raeesi et al. [19] found that deep neural networks provided superior predictive performance when analyzing the efficiency of PEM fuel cell stacks. This suggests that advanced ML techniques can significantly enhance our understanding of fuel cell operations. A review of the application of ML in optimizing PEM full cells was presented by Ding et al. [20]. Machine learning models can significantly lower the expenses associated with experimental trials by forecasting the desired output. Acting as surrogate models, the ML approach can also substantially decrease the computational costs associated with numerical simulations, including first-principle or multi-physics simulations.

Salehi et al. [21] studied the performance prediction of a range of diverse solid oxide fuel cells (SOFCs) using deep learning and principal component analysis. They employed a deep neural network (DNN) to predict the output voltage of the cells, effectively capturing the non-linear voltage drop due to concentration polarization in the current density–voltage (J-V) curves. This approach allows for enhanced predictive accuracy and a better understanding of the factors influencing cell performance across different operating conditions. The findings underscore the potential of integrating advanced machine learning techniques in optimizing SOFC performance and operational efficiency. Topology-informed machine learning for efficient prediction of solid oxide fuel cell (SOFC) electrode polarization was analyzed by Szemer et al. [22]. They developed an artificial neural network (ANN) model capable of replicating the current–voltage characteristics of unseen microstructures based on their persistent image representation.

By employing this approach, the research seeks to uncover valuable insights that can lead to improved efficiency and performance of SOECs technology. The exploration of parameter interactions is crucial, as it allows for a comprehensive understanding of how various factors influence the overall operation of the SOECs system. Ultimately, this work aims to contribute significantly to the field by providing a framework for optimizing SOECs performance through advanced ML techniques, thereby addressing existing challenges and paving the way for future advancements in electrolysis technology.

This article starts with an examination of different methods for producing hydrogen, then shifts focus to SOECs and the equipment used in this technology. It provides a detailed analysis of SOECs, discussing their operational principles and components. Furthermore, a dedicated section explores the mathematical aspects of SOECs, particularly the mass and energy balance equations that are essential for understanding the system’s efficiency and performance. This comprehensive approach aims to (1) provide insights into both the practical and theoretical foundations of hydrogen production through SOECs technology. In this paper, we (2) provide a comprehensive overview of solid oxide electrolysis cells and their operating principles. In the final sections, (3) extensive research is conducted on optimization and the main goal of this project, using machine learning to increase system efficiency. This study seeks to identify key SOECs parameters and examine their interactions to achieve multi-objective optimization.

2. Hydrogen Production

Approximately 95% of hydrogen production comes from natural gas [23]. Various methods are commonly employed for hydrogen generation, including photovoltaic–electrolysis systems, electrolysis, coal gasification, photoelectrochemical hydrogen production, and thermolysis. At present, water electrolysis stands as the fundamental industrial method for producing nearly pure hydrogen, and its importance is anticipated. The primary electrochemical technologies for hydrogen production include alkaline electrolysis (AK), PEM, and SOECs [24,25,26,27]. A classification of the types of hydrogen production methods is shown in Figure 1 [28].

Dincer and Acar conducted a review and assessment of hydrogen production methods to enhance sustainability [29]. They provided a comprehensive analysis of various hydrogen production techniques, assessing their sustainability and environmental impacts. The review highlighted that while hydrogen is a multipurpose energy transporter with the potential to reduce greenhouse gas emissions, the predominant methods of production, such as steam methane reforming and water electrolysis, come with significant ecological footprints. Comparative life cycle analysis of electrolyzer technologies (AWE, PEM, and SOC) for hydrogen production was investigated by Wei et al. [30]. The results reveal that AWE has the lowest environmental footprint and capital costs (CAPEX, 700–1100 USD/kW) due to its mature technology and use of abundant materials like nickel and steel, making it ideal for large-scale, steady-state hydrogen production. PEM electrolyzers, while more expensive (CAPEX, 1300–1800 USD/kW) due to precious metal catalysts (e.g., platinum, iridium), offer flexibility for renewable energy integration and lower operational energy demands, though with higher operational costs (OPEX, 0.7–1.3 USD/kg H₂). SOE stands out with the highest efficiency potential (3.6–4.0 kWh/Nm³) and reduced greenhouse gas emissions when integrated with waste heat, but its pre-commercial status results in elevated CAPEX (1800–2800 USD/kW) and durability challenges, positioning it as a promising yet costly option for future decarbonized industrial applications. Comparisons of hydrogen production methods using AK, PEM, and SOECs are presented in

Table 1. Comparison of hydrogen production methods using alkaline electrolyzers, PEM, and SOE [27,28,29,30,31,32,33].

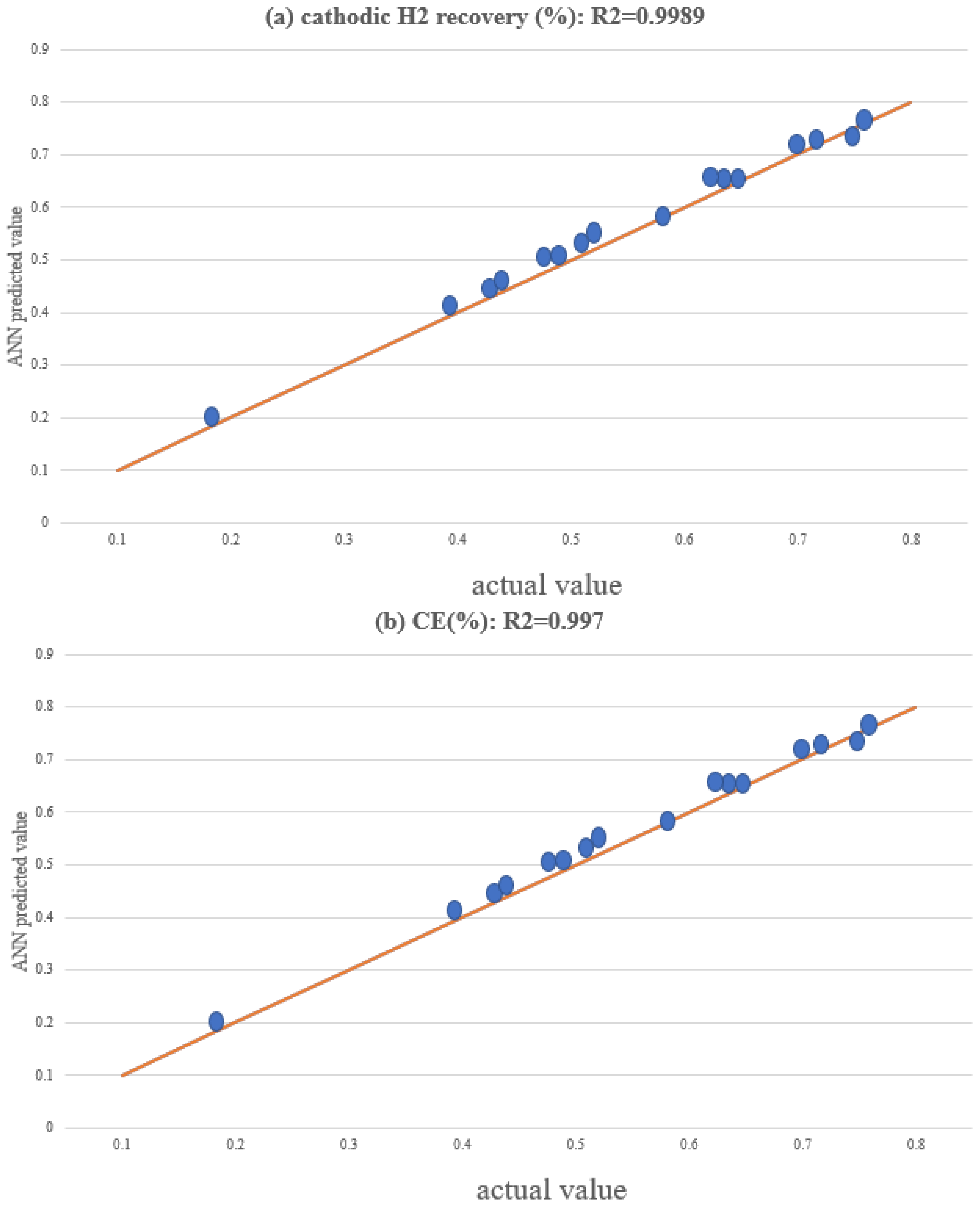
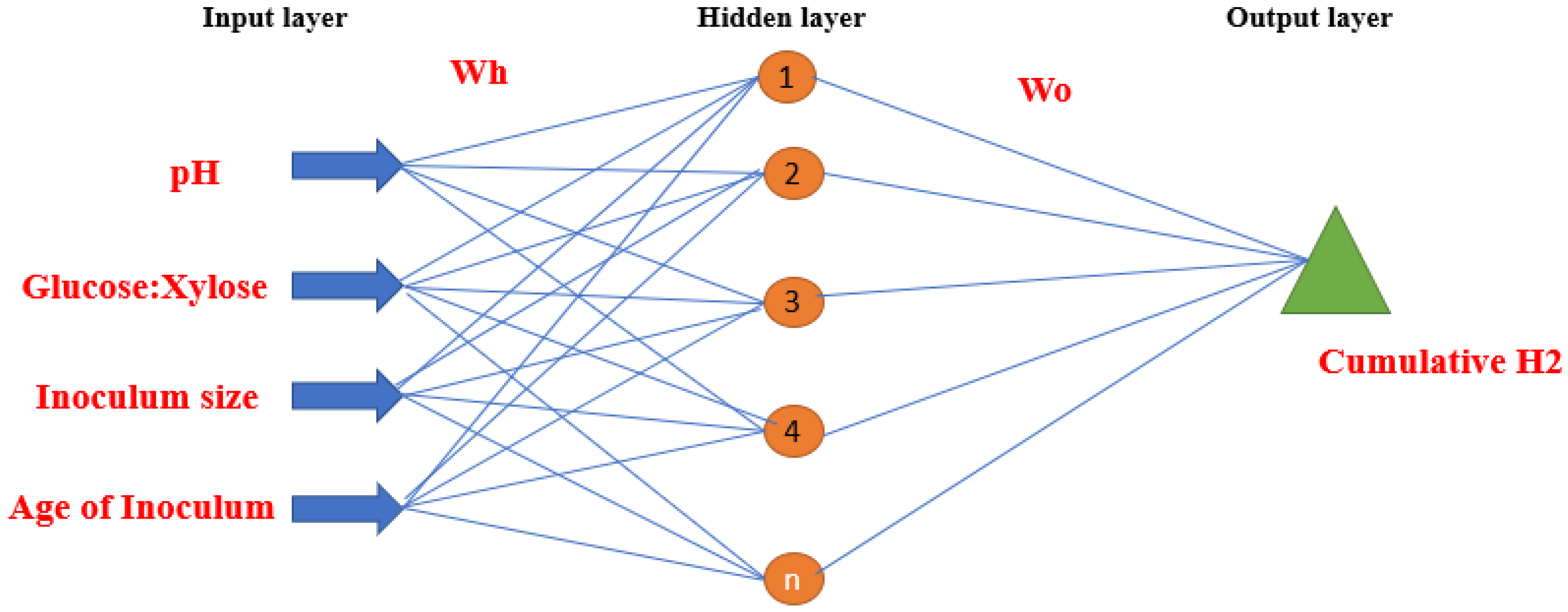
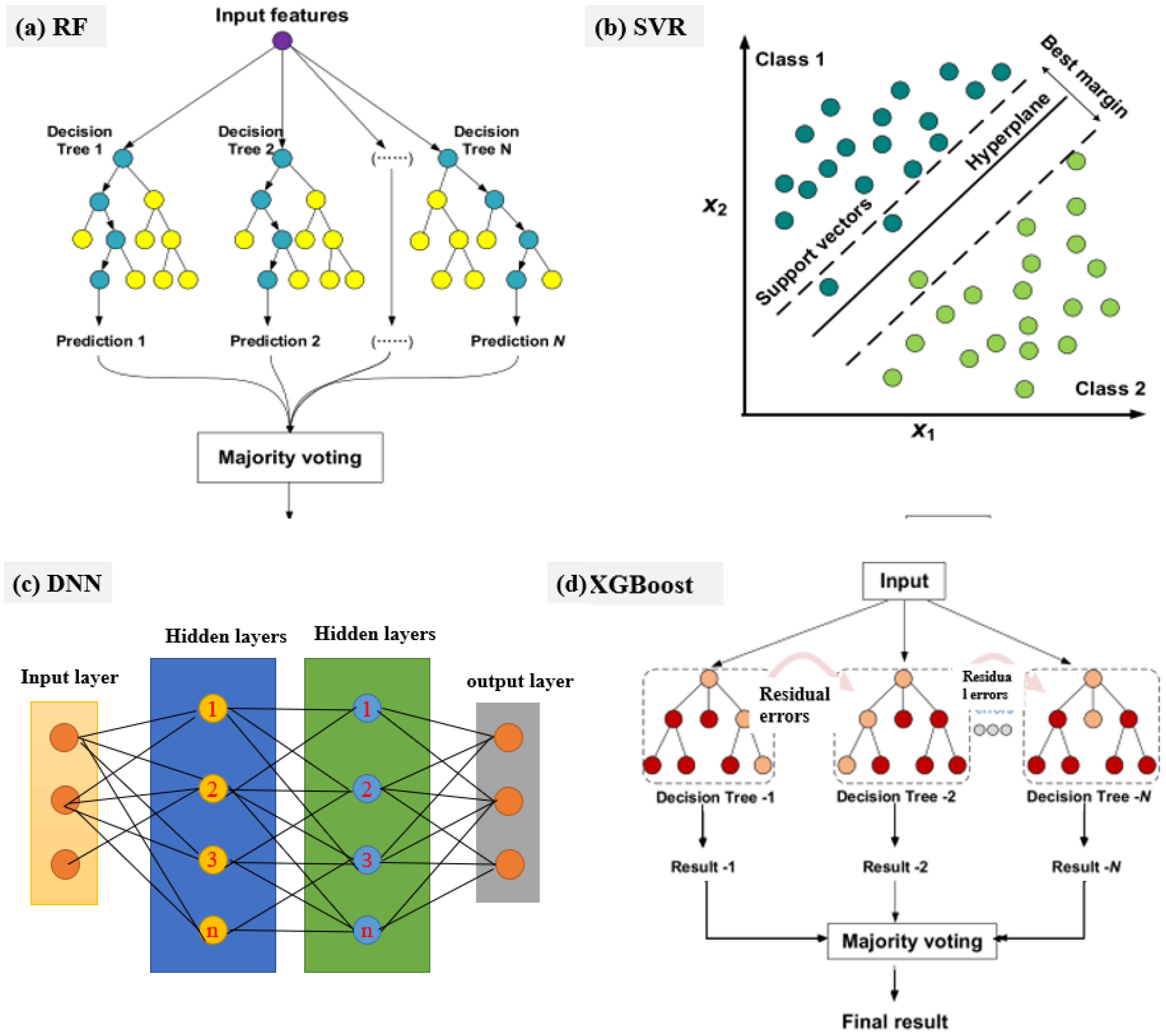
Parameter	Alkaline Electrolyzers (AWE)	PEM Electrolyzers	Solid Oxide Electrolyzers (SOE)
Cell Temperature (°C)	60–100	50–90	500–850
Cell Pressure (bar)	1–30	20–50	1–15
Current Density (A/cm2)	0.2–0.5	1.0–2.0	0.3–1.0
Cell Voltage (V)	1.8–2.4	1.6–2.0	1.0–1.5
Power Density (W/cm2)	0.4–1.2	1.6–4.0	0.3–1.5
Voltage Efficiency (%)	60–70	65–80	85–95
Specific System Energy Consumption (kWh/Nm3)	4.5–5.5	4.2–5.0	3.5–4.0
Hydrogen Production (Nm3/hr)	10–1000 (system-dependent)	10–500 (system-dependent)	5–200 (system-dependent)
Hydrogen Purity (%)	99.5–99.9	99.99–99.999	99.9–99.99
CAPEX Cost (USD/kW)	800–1200	1400–2000	2000–3000 (pre-commercial)
OPEX Cost (USD/kg H2)	0.5–1.0	0.8–1.5	0.7–1.2 (estimated)
Type of Membrane	Diaphragm (e.g., asbestos-free polysulfone)	Solid polymer (e.g., Nafion)	Solid ceramic (e.g., yttria-stabilized zirconia, YSZ)
Type of Anode	Nickel (Ni) or Ni-based alloys	Platinum (Pt) or Iridium oxide (IrO2)	Perovskite (e.g., LSM: La0.8Sr0.2MnO3)
Type of Cathode	Nickel (Ni) or Ni-Mo alloys	Platinum (Pt) or Pt/C	Ni-YSZ cermet

[27,28,29,30,31,32,33].

Figure 2 displays data on energy and exergy efficiency, as well as the production costs (in dollars per kilogram of hydrogen) for various hydrogen production methods [34]. The findings suggest that fossil fuel reforming, plasma arc decomposition, and gasification of coal and biomass offer advantages compared to other methods. Conversely, hydrogen production methods based on photonic energy demonstrate the lowest performance among the options evaluated. As shown in Figure 2, the cost of hydrogen production using SOE is approximately 4.5 USD/kg of hydrogen produced, and the energy and exergy efficiencies of this method are 29 and 26 percent, respectively.

The energy efficiency for all methods ($\eta$) can be calculated as follows:

$$\eta ={\displaystyle \frac{energycontentofHydrogenproduced}{totalenergyinput}}={\displaystyle \frac{m_{H2}\ast {LHV}_{H2}}{E_{input}}}\ast 100$$

(1)

where $m_{H2}$, ${LHV}_{H2}$, and $E_{input}$ are the mass of hydrogen produced (kg), lower heating value of hydrogen (approximately 33.33 kWh/kg), and total energy input to hydrogen systems, respectively.

3. SOECs Operation

During the SOECs process, water molecules are originally reduced at the cathode into hydrogen (H₂) and oxide ions (O²⁻) through the addition of two electrons. The hydrogen produced at the cathodic surface and the remaining oxide ions (O²⁻) migrate through the ion exchange membrane to the anode side [35,36].

At the anode, the oxide ions (O²⁻) undergo further reduction to produce oxygen and electrons. The generated oxygen is released from the anodic surface, while the electrons travel through the external circuit back to the cathode due to the positive attraction of the cathode. The cathode is typically made of a porous nickel–yttria-stabilized zirconia (Ni-YSZ) cermet, while the anode is usually a perovskite material such as lanthanum strontium manganite (LSM) [37,38,39]. The solid oxide electrolyte, which is the heart of the SOECs, is a dense ceramic material, most commonly yttria-stabilized zirconia (YSZ), that conducts oxygen ions at high temperatures. During operation, steam is introduced to the cathode side of the SOECs, where it is converted into hydrogen gas and oxygen ions. The oxygen ions then move through the solid oxide electrolyte to the anode side, where they combine to produce oxygen gas [40,41,42,43]. A general schematic of the equipment and operation of SOECs is shown in Figure 3.

The performance of SOECs is contingent on various operating conditions and parameters, such as temperature, pressure, current density, and voltage. Several factors can influence the performance of SOECs, such as material properties, cell design, and mass transport limitations [44].

At the cathode, water vapor is reduced to form hydrogen gas and oxygen ions [44], as shown in Equation (2)

$$2{\mathrm{H}}_2\mathrm{O}+4{\mathrm{e}}^{-}\to 2{\mathrm{H}}_2+2{\mathrm{O}}^{2-}$$

(2)

At the anode, oxygen ions are oxidized to produce oxygen gas, as shown in Equation (3)

$$2{\mathrm{O}}^{2-}\to {\mathrm{O}}_2+4{\mathrm{e}}^{-}$$

(3)

4. Mathematical Modeling of SOECs

Mathematical modeling of SOECs is vital for understanding the complex electrochemical processes and optimizing their performance, which is an important target for hydrogen production. Several studies have been conducted in this field, demonstrating the importance of simulation techniques in investigating the Multiphysics interactions that occur in SOECs [45,46,47,48]. These models help to clarify the relationships between various operating parameters and the overall system efficiency and cost production of hydrogen in SOECs. Udagawa et al. [49] created a comprehensive model that incorporates an electrochemical framework, mass balance, and four energy balances to analyze the steady-state behavior of an SOECs stack under varying current densities and temperatures. Similarly, Xie et al. [50] advanced an SOECs model aimed at syngas production, utilizing a button cell test system as a foundational platform. Their model effectively integrated multiple transport processes, including charge, mass, momentum, and energy, along with detailed surface chemistry, and was validated against experimental polarization curves.

Luo et al. [51] introduced a one-dimensional kinetic model for SOE-assisted steam electrolysis cells that combines heterogeneous elementary reactions with electrochemical reaction kinetics for heat transfer. Their model was standardized and legalized using experimental data from button cell tests. Kazempour et al. [52] designed a dynamic cell model that integrates reversible electrochemistry, reactant chemistry, and thermo-fluidic phenomena within the cell channel. This model was adjusted and validated with existing experimental and numerical data for button cells, single cells, and multi-cell stacks operating on either steam or syngas.

Menon et al. [53] explored the performance of an SOECs during co-electrolysis by examining the interactions between transport processes and electrochemical parameters. This comprehensive body of work highlights the ongoing advancements in modeling SOECs to enhance their efficiency and performance in hydrogen production and syngas generation. By employing CFD techniques, the study investigated how factors like reactant flow rates and temperature gradients influence hydrogen production efficiency and overall cell performance. The findings indicate that a well-optimized flow distribution can significantly enhance the electrochemical reactions occurring within the SOECs, leading to improved hydrogen output. Overall, this research contributes valuable insights into the design and operational strategies for SOECs, highlighting the importance of computational modeling in understanding and optimizing hydrogen production processes. The results can inform future developments of SOECs technology, aiming for more efficient and sustainable hydrogen generation methods.

4.1. Electrochemical Model

Charge transfer happens at the interface where the electrolyte, electrode, and gas phase meet. The operating voltage of the cell includes both the Nernst voltage and additional losses due to overpotential [54]:

$$V_{cell}=E_N+{\mathsf{\eta }}_{act}+{\mathsf{\eta }}_{ohm}+{\mathsf{\eta }}_{con}$$

(4)

The Nernst potential represents the minimum electrical potential necessary to dissociate steam, taking into consideration factors such as species concentration, operating temperature, and pressure [54]:

$$E_N=E^0+{\displaystyle \frac{RT}{nF}}+\ast Ln({\displaystyle \frac{P_{H_2}{{\times (P}_{O_2})}^{0.5}}{P_{H_{2O}}}})$$

(5)

The standard reversible voltage ($E^0$) is determined by calculating the Gibbs energy change of the reaction at the temperature and standard pressure, as described in Equation (6) [54]:

$$E^0={\displaystyle \frac{∆G{(H}_{2}O\to H_2+\frac{1}{2}{O}_2)}{nF}}$$

(6)

The Butler–Volmer equation is fundamental in electrochemistry, describing how the current moving through an electrode is affected by the voltage difference between the electrode and the electrolyte. It effectively models charge transfer reactions by considering both anodic (oxidation) and cathodic (reduction) processes, thus capturing the kinetics involved. By examining the activation overpotential—representing the energy required for charge transfer at the electrode surface—researchers can evaluate the efficiency of electrochemical reactions. This analysis helps identify various factors that influence performance, making the Butler–Volmer equation an essential tool for understanding and optimizing electrochemical systems. Its application spans various fields, including batteries, fuel cells, and electrolysis, where insights from this equation can lead to improved designs and enhanced performance of energy conversion and storage technologies [55].

$$\begin{array}{c}{J}_{ca}={\mathrm{J}}_{0,H_2}\ast \left\{\exp ({\displaystyle \frac{n_e{\alpha }_{ca}F{\eta }_{act,ca}}{RT}})-\exp (-{\displaystyle \frac{(1-{\alpha }_{ca})n_{e}F{\eta }_{act,ca}}{RT}})\right\}\\ J_{an}={\mathrm{J}}_{0,O_2}\ast \left\{\exp ({\displaystyle \frac{n_e{\alpha }_{an}F{\eta }_{act,an}}{RT}})-\exp (-{\displaystyle \frac{(1-{\alpha }_{an})n_{e}F{\eta }_{act,an}}{RT}})\right\}\end{array}$$

(7)

4.2. Mass Balance

The mass balance equations for various species are outlined below [55]:

$${\displaystyle \frac{d{X}_{H_{2}O}}{dt}}={\displaystyle \frac{{\dot{n}}_{H_{2}O,in}-{\dot{n}}_{H_{2}O}+\frac{\mathrm{I}}{n_e\ast F}-r_{SF}\ast V_{ca}-r_{WGS}\ast V_{ca}}{\frac{P_{ca}\ast V_{ca}}{R\ast T_{ca}}}}$$

(8)

$${\displaystyle \frac{d{X}_{H_2}}{dt}}={\displaystyle \frac{{\dot{n}}_{H_2,in}-{\dot{n}}_{H_2,out}+\frac{\mathrm{I}}{n_e\ast F}+3\ast r_{SR}\ast V_{ca}+r_{WSG}\ast V_{ca}}{\frac{P_{ca}\ast V_{ca}}{R\ast T_{ca}}}}$$

(9)

4.3. Energy Balance

The energy balance equations for the cathode and anode streams, as well as the PEN and bipolar plate, are outlined below:

$$\left({\displaystyle \frac{P_{ca}\ast V_{ca}}{R\ast T}}\right)\ast {\overline{C}}_{P,ca})\ast {\displaystyle \frac{dT}{dt}}=\sum _{species}{\dot{H}}_{in}-\sum _{species}{\dot{H}}_{out}+\sum {\dot{Q}}_{conv,ca}+\sum {\dot{Q}}_{conv,ca}-{\displaystyle \frac{\mathrm{I}}{n_e\ast F}}(h_{H_2}-h_{H_{2O}})$$

(10)

$$\left({\displaystyle \frac{P_{an}\ast V_{an}}{R\ast T}}\right)\ast {\overline{C}}_{P,an})\ast {\displaystyle \frac{dT}{dt}}=\sum _{species}{\dot{H}}_{in}-\sum _{species}{\dot{H}}_{out}+\sum {\dot{Q}}_{conv,an}+\sum {\dot{Q}}_{conv,an}-{\displaystyle \frac{\mathrm{I}}{{2\ast n}_e\ast F}}(h_{O_2})$$

(11)

In the case of steam and air flows within channels, the Reynolds numbers are significantly lower than the critical value. This is primarily due to the small cross-sectional areas of the channels and the relatively low mean velocities of both steam and air. Under these conditions, a fully advanced laminar flow with a uniform surface temperature is typically observed throughout most control volumes. For this analysis, a constant Nusselt number of four was utilized based on engineering tables to calculate the local convection heat transfer coefficient. This approach allows for accurate assessment of heat transfer characteristics in laminar flow scenarios, which is crucial for optimizing thermal performance in various engineering applications involving steam and air flows [56]:

$$h={\displaystyle \frac{N_{ud}\ast k}{D_h}}$$

(12)

5. Optimization of SOEC

Mansilla et al. [57] created a techno-economic optimization model for a high-temperature electrolysis system that incorporates the SOECs stack along with a high-temperature heat exchanger network. Their study focused on integrating geothermal energy with SOECs technology to decrease electrical energy consumption by leveraging the available heat from geothermal sources. Mogensen et al. [58] highlighted the significant potential of SOECs technology for producing hydrogen from sustainable energy sources like renewable energy. However, they pointed out that realizing this potential requires additional research and development efforts. Their ongoing work aims to improve the stability of SOECs systems to ensure they can operate effectively over a long lifespan. In another study, Gopalan et al. [59] utilized modeling and simulation techniques to demonstrate that the efficiency of hydrogen production could be enhanced by optimizing the operating conditions of the SOECs. Specifically, their analysis of a recuperative SOECs, which utilizes thermal energy from exhaust gases, revealed that operating the electrolysis cell at voltages above the thermoneutral point could lead to increased hydrogen production efficiency. This finding underscores the importance of optimizing operational parameters to maximize performance in electrolysis processes. Collectively, these studies emphasize the need for continued innovation and research in SOECs technology, focusing on integrating renewable energy sources and improving system stability and efficiency to advance hydrogen production capabilities in sustainable energy applications.

The main objective of the SOECs is to enhance hydrogen gas production while simultaneously reducing power consumption [60]. This research focuses on two main objectives: lowering current density and increasing the hydrogen production rate, as outlined in Equation (13). These limits act as constraints for the multi-objective optimization process defined in Equations (14)–(16). This methodology aims to effectively determine the best trade-off between the two objectives, ensuring that improvements in hydrogen production do not come at an excessive cost in terms of energy consumption. By utilizing advanced optimization techniques, this research seeks to contribute valuable visions to the design and operation of SOECs, ultimately promoting more efficient and sustainable hydrogen production. The integration of these approaches is expected to lead to significant advancements in the performance and viability of SOECs technology in practical applications [61].

$$\mathrm{objective}\mathrm{functions}:MaxF={\omega }_1{f}_{H_2}\left(\mathrm{EC},\mathrm{OP},\mathrm{FC}\right)-{\omega }_1{f}_{H_2}\left(\mathrm{EC},\mathrm{OP},\mathrm{FC}\right)$$

(13)

Constraint 1: LB of EC < OE, Area, Electrolyte CT, ET < UB of EC

(14)

Constraint 2: LB of OP < Humidity, Voltage, Flow, T, GC, P < UB of OP

(15)

Constraint 3: LB of FC < H₂, CO₂, H₂O < UB of FC

(16)

Wolf et al. [62] discussed how SOECs are a highly efficient technology for producing valuable chemicals and fuels from renewably generated electricity at temperatures between 600 °C and 900 °C, thus providing a carbon-neutral method for energy storage. Successful industrial implementation requires long-term stability of all system components, with a concurrent overall degradation rate of a maximum of 0.75% per 1000 h or even better, 0.5% per 1000 h, corresponding to a performance loss of 20% over approximately five years under constant operating parameters. This review presents the state-of-the-art materials in current industrial use for planar SOECs as well as future challenges regarding materials design and degradation.

Feasibility study and techno-economic assessment of power to gas (P₂G) technology based on SOE was studied by Martsinchyk et al. [63]. Power-to-Gas (P₂G) technology, particularly when employing SOE, is gaining recognition as a promising long-term energy storage solution, driven by the increasing integration of intermittent renewable energy sources. A recent feasibility study analyzed a P₂G system comprising an SOE, a CO₂ separation unit, and a methanation reactor, assessing its performance across various operating conditions and capacities. The techno-economic assessment (TEA) included CAPEX/OPEX estimations and a defined cost structure, enabling system-level optimization based on technical and economic factors. The study considered nominal scales of 10 kW and 40 GW for SOE capacity, projecting a 15–21% reduction in synthetic natural gas (SNG) production costs by 2030 and a 29–37% reduction by 2050 for systems exceeding 10 MW SOE power. These cost reductions are anticipated due to material advancements and large-scale production efficiencies affecting the system’s CAPEX. The research suggests that the technology will become cost-effective by 2050, with a large-scale 40 GW system achieving a product price of 2.4 EUR2023/kgSNG at a conversion efficiency of 68%.

6. Machine Learning for SOECs

Machine learning (ML) can uncover potential rules between the various features of materials, structures, and outputs of electrolytic cells through data collection. In recent years, several studies have demonstrated the use of machine learning and deep learning techniques to enhance the efficiency of SOECs. Kabir et al. [64] conducted a comparative study of five machine learning (ML) models aimed at improving green hydrogen production through dark fermentation and proton exchange membrane (PEM) technology. Their research focused on identifying the most effective approaches for enhancing hydrogen production efficiency. Additionally, a comprehensive bibliometric analysis was performed to explore notable research gaps and applications of machine learning in predicting hydrogen production technologies from wastewater treatment resources (WRIs) for a circular renewable energy (CRE) framework. Additionally, Bilgiç et al. [65] utilized an artificial ANN to forecast hydrogen production in magnetic field-assisted water electrolysis, finding that their predictions closely matched experimental results, thereby supporting optimal electrolyzer design. In their study, statistics of hybrid studies with ANNs are given, and future research proposals and hot research topics are briefly discussed. Recent advancements in microbial electrolysis cells (MECs) have highlighted their potential as a cutting-edge bio electrochemical technology for producing pure hydrogen from various organic materials. A significant study conducted by Hosseinzadeh et al. [66] focused on improving the modeling of hydrogen production and energy recovery in MECs through the use of ANNs and an adaptive network-based fuzzy inference system (ANFIS). The model inputs included key parameters such as voltage, electrical conductivity, and anode potential. The outputs of interest were cathodic hydrogen recovery (rcat) and coulombic efficiency, which were then utilized to assess hydrogen production (HP) and overall energy recovery. It is crucial to consider the limitations of machine learning models used in SOECs optimization for a balanced application of these approaches. Data dependency, complexity of electrochemical processes, interpretability, overfitting risks, integration with existing systems, and dynamic operating conditions are some key limitations.

As shown in Figure 4, the findings indicate that the sum of squared error values for the ANN models was slightly higher than those for the ANFIS models. Cathodic hydrogen recovery (rcat) refers to the efficiency of hydrogen production in electrochemical systems, specifically measuring the ratio of electrons recovered as hydrogen gas to the total electrons supplied by the current. Specifically, the error for rcat was measured at 0.0017 for the ANN approach, while the ANFIS model achieved a lower error of 0.0005. In terms of coulombic efficiency, the ANN recorded an error of 0.0163 compared to ANFIS’s 0.0091. For hydrogen production rate, the ANN model yielded a value of 0.1062, whereas the ANFIS model performed better, with a value of 0.1247. Lastly, for total energy recovery, the errors were 0.0136 for ANN and 0.0148 for ANFIS. These results suggest that ANFIS may offer a more precise modeling framework for analyzing hydrogen production and energy recovery in MECs compared to traditional ANN approaches. This research underscores the importance of utilizing advanced modeling techniques to enhance the efficiency and effectiveness of bio electrochemical systems in renewable energy applications.

Gu et al. [67] proposed a three-layer neural network (NN) model aimed at predicting the yield distribution of products from solid waste pyrolysis. This model uses 13 input parameters to generate outputs for char, tar, and gas yields. Additionally, Aydinli et al. [68] employed ANN modeling to predict the primary pyrolysis products: coal, tar, and gas. Ozbay and Kökten [69] developed an ANN model for predicting pyrolysis liquid products, attaining a mean squared error (MSE) of 0.00058 and a correlation coefficient (R) of 0.9849. Their relative effect analysis identified catalyst type as the most significant factor influencing bio-oil yield, followed by biomass properties, catalyst ratio, particle size, temperature, and time. For modeling biomass hydrogen production (BHP), Nasr et al. [70] created a backpropagation neural network (BPNN) configuration with layers structured as 5-6-4-1. The consequences indicated that the skilled ANN effectively forecast the hydrogen production outline over time for new datasets, with an R value of 0.976. Hannah O. Kargbo et al. [71] advanced this field by developing a robust model utilizing a bootstrap aggregated neural network to optimize hydrogen production from biomass gasification processes. Their model demonstrated exceptional accuracy in predicting gas composition and determining optimal conditions for maximizing hydrogen output while minimizing CO₂ emissions, achieving an R² value of 0.999. These studies collectively illustrate the effectiveness of ANN and related methodologies in enhancing the prediction and optimization of pyrolysis processes and hydrogen production from various biomass sources, highlighting their potential in advancing renewable energy technologies. Iqbal et al. [72] proposed that ML could provide significant visions for modeling, overcoming limitations related to specific biomass gasification inputs. Furthermore, ML approaches have been employed to examine the generalized structure–performance relationships in Metal–Organic Frameworks (MOFs), photovoltaic systems, and electrochemical green hydrogen production. These methodologies demonstrate the versatility of ML in optimizing various aspects of energy production and conversion technologies.

Yang et al. [73] introduced a machine learning approach to predict the performance degradation of solid oxide fuel cell (SOFCs) cathodes caused by chromium (Cr) poisoning. Chromium poisoning is a significant factor in the long-term performance decline of SOFCs. The mechanism of Cr poisoning-induced degradation is complex, making accurate prediction of degradation rate difficult. This study uses machine learning algorithms to address this challenge. They chose cathode materials based on SrFeO₃ with different dopants as model systems to study the effect of dopant elements on resistance to Cr poisoning. Electrochemical impedance spectroscopy (EIS) data were collected for up to 96 h for each composition and used to train and validate a neural network. The predicted data at 156 h matched the experimental results well, demonstrating the prediction power of the machine-learning-assisted (MLA) method. The study showed that the MLA approach could significantly reduce the time needed to extract the degradation rate of SOFC cathode materials.

Prakasham et al. [74] (as can see in Figure 5) developed a model aimed at optimizing fermentative hydrogen production using mixed anaerobic microbial consortiums. Their approach involved an artificial neural network integrated with a genetic algorithm, structured in a 4-10-1 configuration. The model utilized several input variables, including original pH, mixed substrate composition, inoculum age, and concentration, to predict the output, which was biohydrogen yield. By employing the genetic algorithm, the researchers identified optimal conditions and parameters for maximizing hydrogen production. The effectiveness of their model was demonstrated by achieving an impressive R² value of 0.9999, indicating a high level of accuracy in their predictions. This study highlights the potential of combining ANN with GA to enhance biohydrogen production processes through effective modeling and optimization strategies.

According to Figure 6, Yang et al. [75] established a data-driven machine learning (ML) model for the SOECs to identify its important limitations and examine interactions, aiming for multi-objective optimization. They developed and compared several algorithms, including random forest (RF) regression, support vector regression (SVR), DNN, and extreme gradient boosting (XGBoost), to determine the most effective ML approach for SOECs. Additionally, they utilized the Shapley additive explanations (SHAP) method to identify and rank the primary factors influencing electricity consumption and hydrogen production rates in SOECs.

In order to determine the most appropriate machine learning (ML) model for SOECs process, this study assessed and compared several potential models, including Random Forest (RF) regression, Support Vector Regression (SVR), DNN, and XGBoost. The basic principles of these models are summarized as follows: RF is an ensemble learning model based on decision trees that utilizes a bagging approach. This method generates multiple training sets from the original dataset using dropout sampling, which allows for the independent training of various base learners. Once trained, the predictions from these learners are combined to produce a final output through a voting mechanism. In this study, the RF class from the Scikit Learn library was employed to implement RF regression. Support Vector Regression (SVR) is another widely used method in regression analysis. It transforms input data into a high-dimensional space to identify a hyperplane that minimizes errors within a specified range. This approach is particularly useful for capturing complex relationships in data and ensuring robust predictions. Deep Neural Networks (DNNs) represent a computational model inspired by the biological nervous system. DNNs consist of multiple interconnected neurons, each equipped with an activation function, allowing them to process inputs from other neurons. This architecture enables DNNs to learn intricate patterns in data, making them suitable for various predictive tasks. XGBoost is a machine learning algorithm that builds on the principles of gradient boosting trees. It enhances the performance of weak base learners through a stacking approach. Notably, XGBoost incorporates advanced regularization techniques that help prevent overfitting and improve the model’s ability to generalize to new data compared to other gradient boosting methods.

Through their evaluation of RF regression, SVR, DNN, and XGBoost, the study aimed to identify the most effective ML model for optimizing the SOECs process, ultimately contributing to advancements in hydrogen production technologies (Figure 7). The study highlighted the importance of selecting appropriate ML algorithms to optimize SOECs performance effectively. By comparing different models, Yang et al. [75] aimed to pinpoint the algorithm that provided the best predictive capabilities regarding key operational metrics. This comparative analysis is crucial for understanding how various factors interact within the SOECs and their impact on overall efficiency. Additionally, the application of the SHAP approach allowed for a detailed examination of feature importance, providing insights into how different parameters affect the performance of SOECs. This methodology not only enhances the interpretability of ML models but also aids in making informed decisions for optimizing hydrogen production processes in electrolytic cells.

In one study, Zhang et al. [76] focused on developing a data-driven model to assess the steady-state performance of SOECs under varying gas compositions. Utilizing the Levenberg–Marquardt (LM) algorithm, the study aimed to enhance modeling accuracy and efficiency compared to traditional methods. The research demonstrated how LM can effectively capture the complex relationships between operational parameters and SOECs performance metrics such as hydrogen production rates. By leveraging the rapid learning capabilities and robust generalization performance of ML, the model provides valuable insights into optimizing SOECs operations. Overall, this work contributes to the understanding of SOECs by presenting a novel approach that integrates machine learning techniques, specifically focusing on ML, for enhanced performance modeling and optimization in hydrogen production technologies.

In the future, the optimization of solid oxide electrolysis cell (SOECs) models using the integration of MATLAB R2024b and COMSOL 6.3 Multiphysics software can be considered as an effective and innovative approach in this field. This combination allows researchers to exploit the advanced simulation capabilities of COMSOL 6.3, which includes various modules for Multiphysics analysis, while at the same time using the computational capabilities and optimization algorithms in MATLAB R2024b.

Using these two software tools helps researchers analyze complex SOECs models more accurately and perform the necessary optimizations. In particular, the COMSOL 6.3 optimization module can be used to define the objective functions and design variables, while MATLAB R2024b can be used to process data and execute machine learning algorithms. This approach can lead to increased efficiency and reduced costs in green hydrogen production.

In addition, the integration of MATLAB R2024b and COMSOL 6.3 can help develop dynamic models and predict the performance of SOECs under different operating conditions. Given the increasing importance of renewable energy and the need for clean technologies, this type of optimization will not only be effective in improving the performance of SOECs but will also play an important role in achieving global goals such as decarbonization and advancing green hydrogen initiatives.

Machine learning models have limitations concerning data quality and quantity, time, accuracy, biases, and comprehension. These limitations can affect their effectiveness when applied to technologies like the SOECs system. ML algorithms require large amounts of high-quality data for training. Overfitting, where a model is too complex and fits the training data too closely, and underfitting, where a model is too simple to capture underlying patterns, are common issues. ML models can also reflect biases present in the training data, leading to discriminatory outcomes. They also lack common-sense understanding, requiring human involvement. Additionally, ML systems may fail when encountering invalid or noisy inputs, or inputs from a distribution different from the training data. Processing sensitive data also raises concerns about privacy and security breaches. Chen et al. [77] discussed the advantages and limitations of different machine learning methods, specifically ANN and Support Vector Machines (SVMs), in predicting hydrogen production from SOECs. The study found that different machine learning methods may exhibit different advantages and limitations when dealing with SOECs specific problems. The ANN model generally performed better, especially for the global dataset, while the SVM model was superior in error distribution equalization. Using 50 h of SOECs system data, the study evaluated the effectiveness of the ANN and SVM methods, incorporating hydrogen production time as an input variable. The results indicated that the ANN model generally performed better in hydrogen production prediction, especially with a communication delay time ε = 0.01–0.02 h, while the SVM model was superior in error distribution equalization.

Golbabaei et al. [78] presented a machine learning approach using a multi-layer perceptron (MLP) regressor to predict the performance of anode-supported solid oxide fuel cells (SOFCs). The results showed that the built neural network could predict the effect of cell parameters on current–voltage dependency more accurately than previous mathematical and artificial neural network models. The model achieved a prediction accuracy of 0.997 R₂ score, a mean squared error of 9.6 × 10⁻⁵, and a mean absolute error of 6 × 10⁻³ (V). Conventional models such as the Gaussian process, as one of the most powerful models, exhibits a prediction accuracy of 0.996 R₂ score, 10⁻⁴ mean squared error, and 6 × 10⁻³ (V) absolute error.

Future studies should focus on incorporating more comprehensive information about microstructures in NNA. Improving datasets, standardizing data, methodological reporting, and incorporating complete microstructural information are improvements for future research. Given the increasing reliance on ML for optimizing and predicting the performance of solid oxide electrolysis cells (SOECs), future research must prioritize data privacy and security. Researchers should adopt privacy-enhancing technologies like differential privacy and federated learning to protect the confidentiality of SOECs data. Moreover, robust security measures are needed to prevent unauthorized access and manipulation of datasets and trained models. Failing to address these concerns could hinder the adoption of ML in SOECs research and development, undermining the potential benefits of this technology for advancing clean energy solutions.

7. Conclusions

In recent years, there has been a notable increase in hydrogen production aimed at the transportation and industrial sectors. Various methods exist for hydrogen generation, including alkaline electrolysis and solid oxide electrolysis cells (SOECs), each presenting unique advantages and drawbacks. SOECs are particularly efficient, operating at elevated temperatures ranging from 700 to 1000 °C, which enhances their performance compared to other methods. The rise in optimization techniques, particularly machine learning (ML), has opened new avenues for improving the efficiency of SOECs while simultaneously reducing capital expenditure (capex) costs.

This study introduced refined mass and energy balance equations tailored to high-temperature SOECs operations, providing a more accurate representation of energy efficiency and hydrogen recovery. The integration of ML with these equations enabled dynamic optimization, resulting in improved hydrogen production strategies and reduced operational costs.

The application of machine learning in the context of SOECs is emerging as a dominant trend, as it allows for more precise modeling and optimization of the electrolysis process. This paper provides a comprehensive review of how machine learning can be integrated into SOECs technology to enhance its efficiency and economic viability. By leveraging advanced algorithms, researchers can analyze vast datasets to identify patterns and optimize operational parameters, ultimately leading to more effective hydrogen production strategies. The integration of ML not only intends to optimize the overall performance of SOECs but also contributes to making hydrogen a more viable alternative energy source for a sustainable future.

The synergy between machine learning and solid oxide electrolysis not only fosters advancements in hydrogen production but also contributes significantly to the broader goals of sustainable energy solutions. As we continue to explore these technologies, it is imperative to focus on both their technical improvements and their integration into existing energy systems to ensure a sustainable and economically viable future for hydrogen as a clean energy source. Additionally, the introduction of refined mass and energy balance equations tailored to high-temperature SOECs operations provides a more accurate representation of energy efficiency and hydrogen recovery. These advancements not only optimize SOECs technology but also contribute meaningfully to global energy goals, such as achieving carbon neutrality and promoting green hydrogen initiatives, thereby supporting the transition to sustainable energy solutions for a cleaner future.