Transient Collapse Failure Prediction of Production Casing After Packer Unsetting in High-Pressure and High-Temperature Deep Oil Wells
Abstract
1. Introduction
2. Model Development
2.1. Basic Assumptions
- (1)
- The production casing, tubing, and packer rubber are concentric cylinders.
- (2)
- The width of the annular clearance between the packer rubber and production casing are only changed by the radial deformation of the packer rubber, which means that the wall thickness reduction from corrosion or mechanical damage is ignored for the production casing and packer rubber.
- (3)
- The completion fluid and oil are both regarded as incompressible and inviscid ideal fluids.
- (4)
- After the packer unsetting, the deformation of the packer rubber recovers in a very short time and a micro-annulus forms between the rubber and production casing.
- (5)
- The A-annulus and tubing are connected to form a U-type tube, and the location of the production packer can be regarded as a constant-pressure surface.
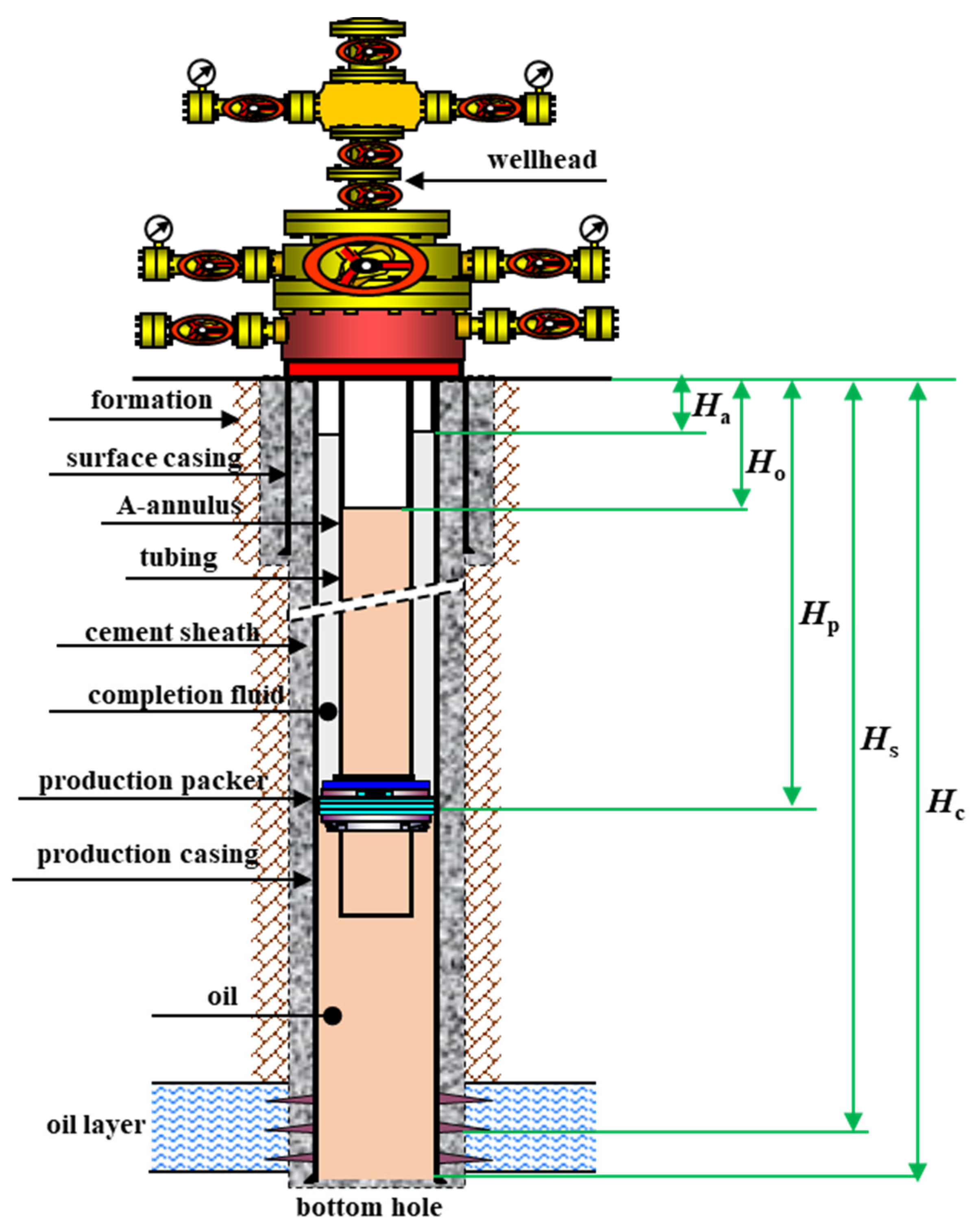
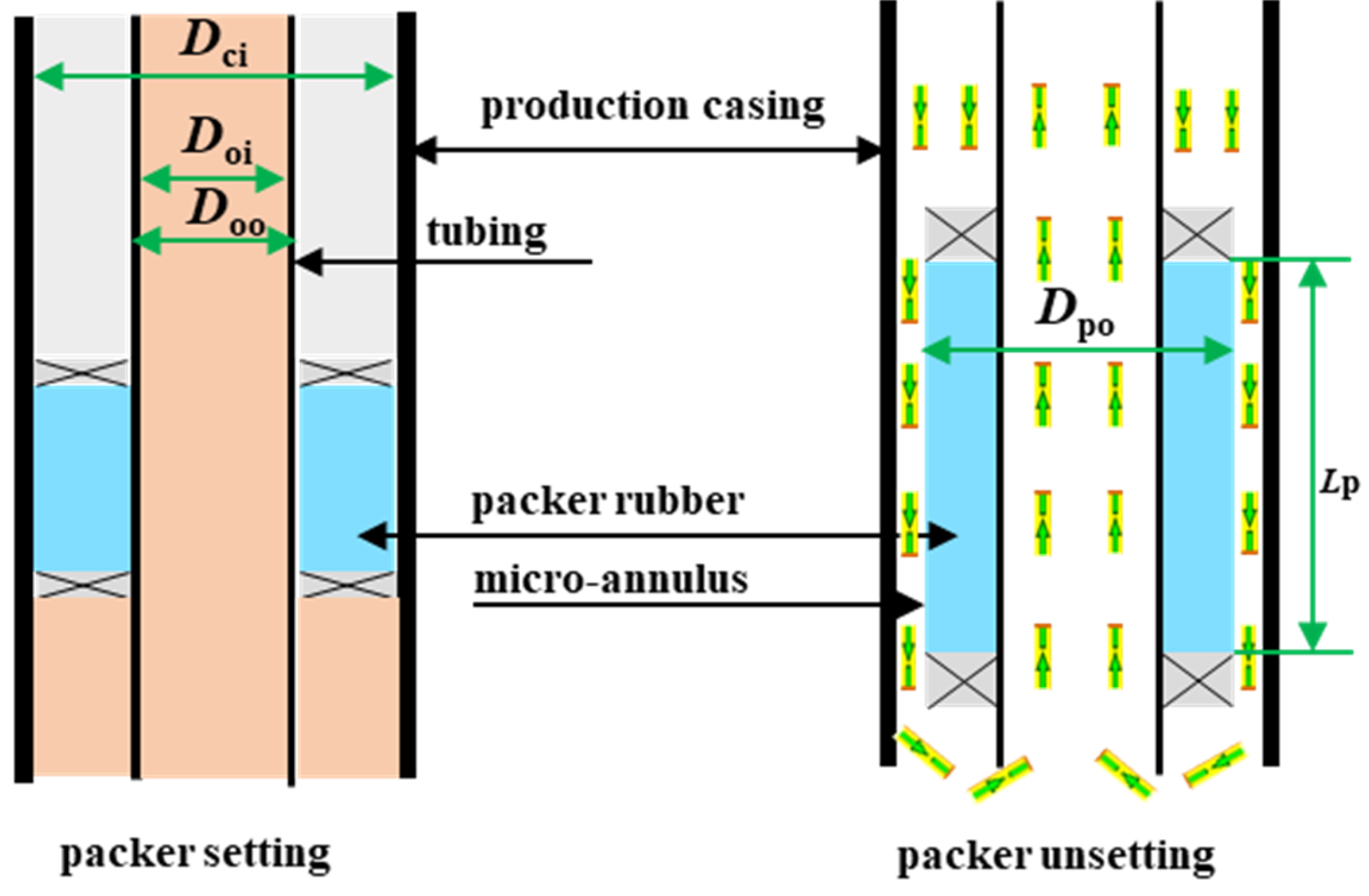
2.2. Transient Swab Pressure After Packer Unsetting
2.3. Collapse Failure Prediction of Production Casing
3. Example Study
3.1. Basic Parameters
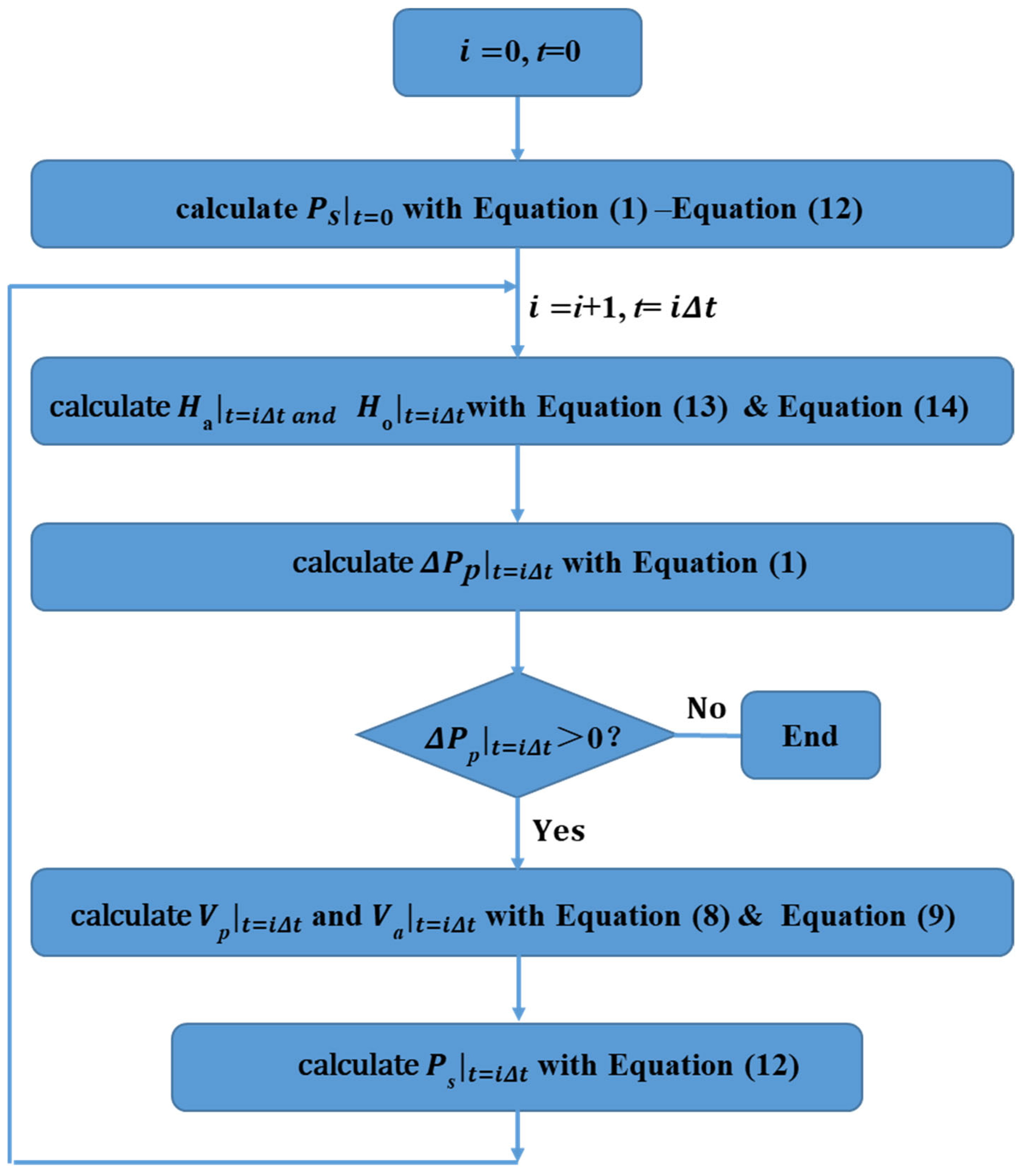
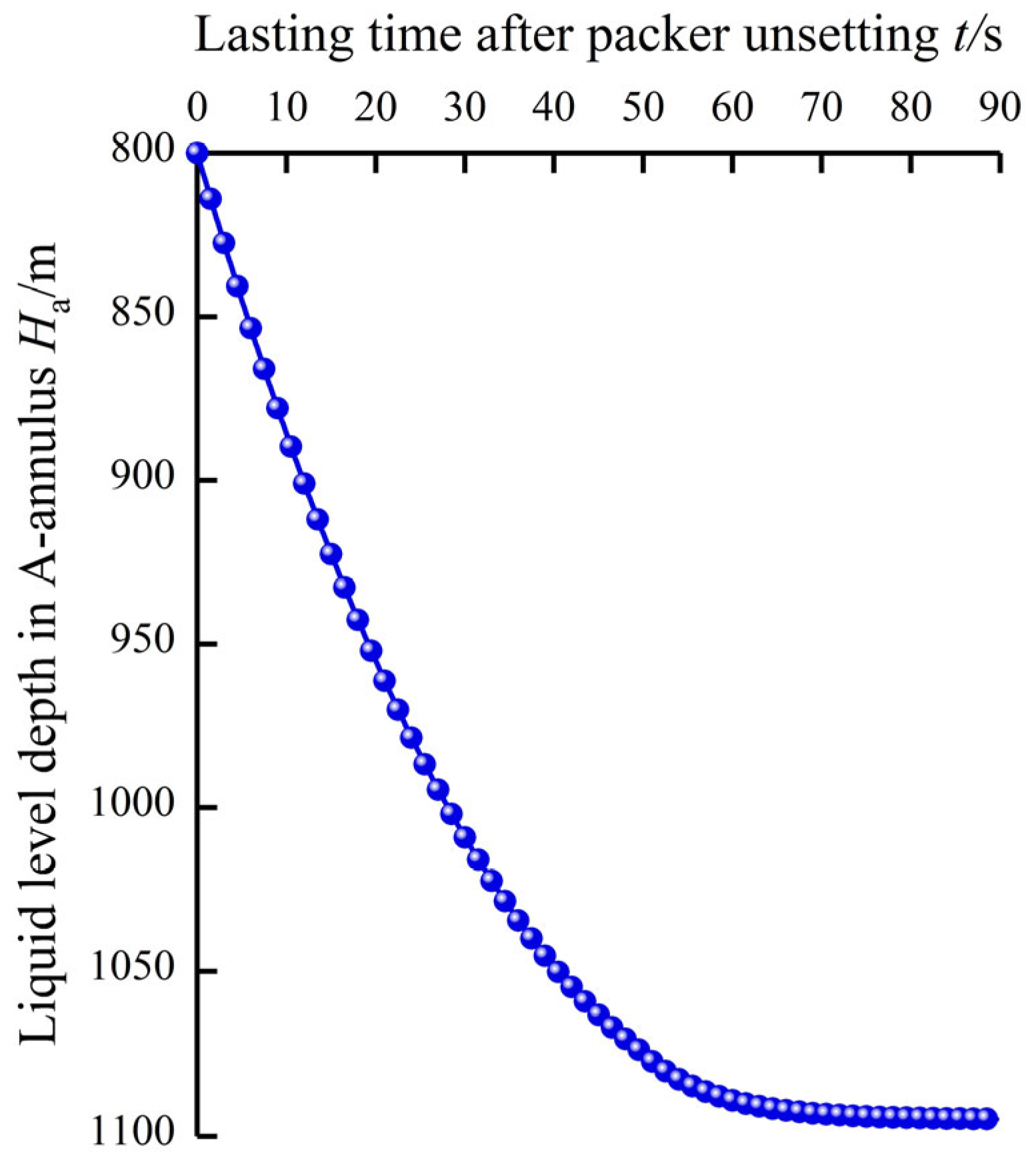
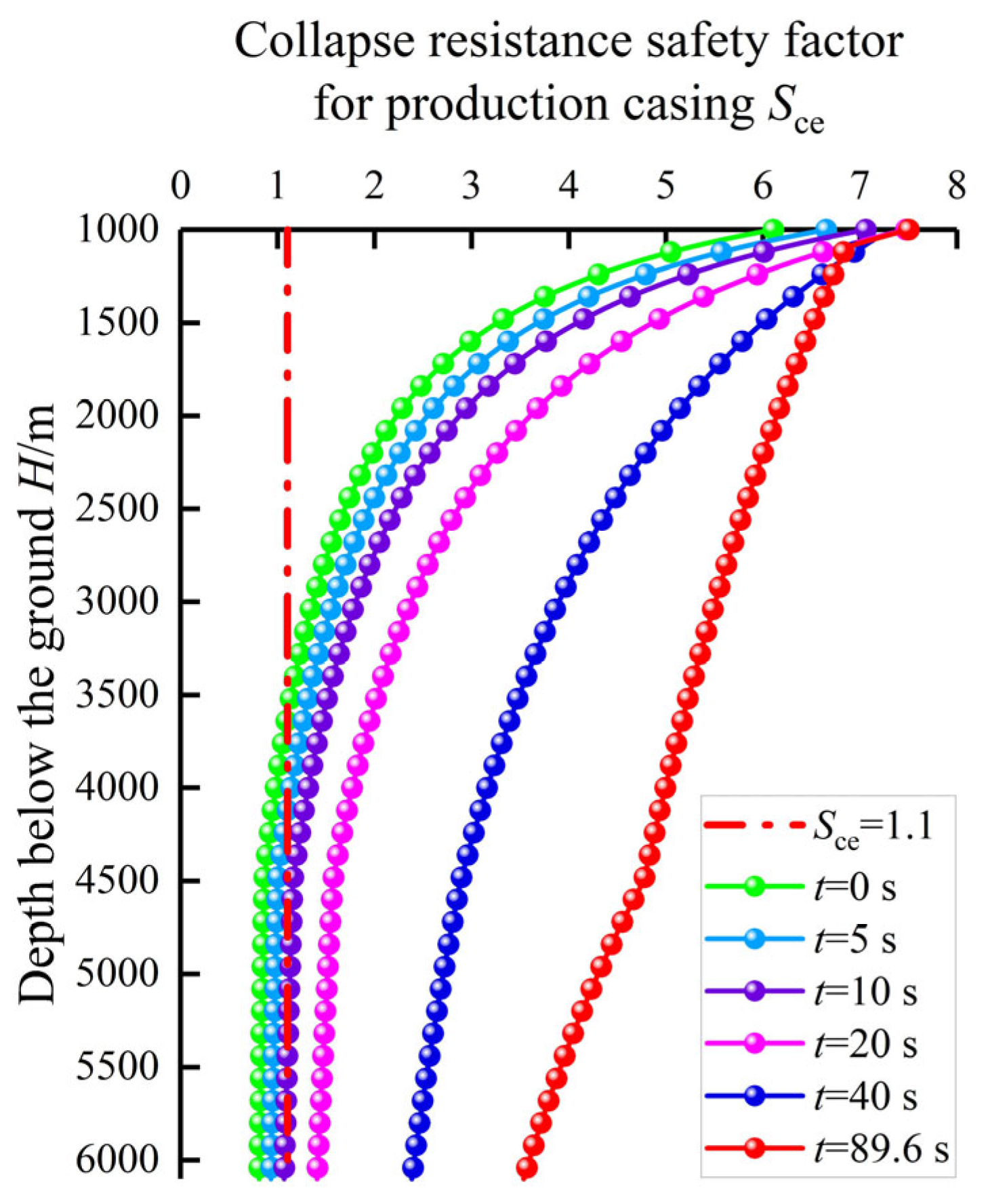
3.2. Prediction Results and Model Validation
3.3. Sensitivity Analysis
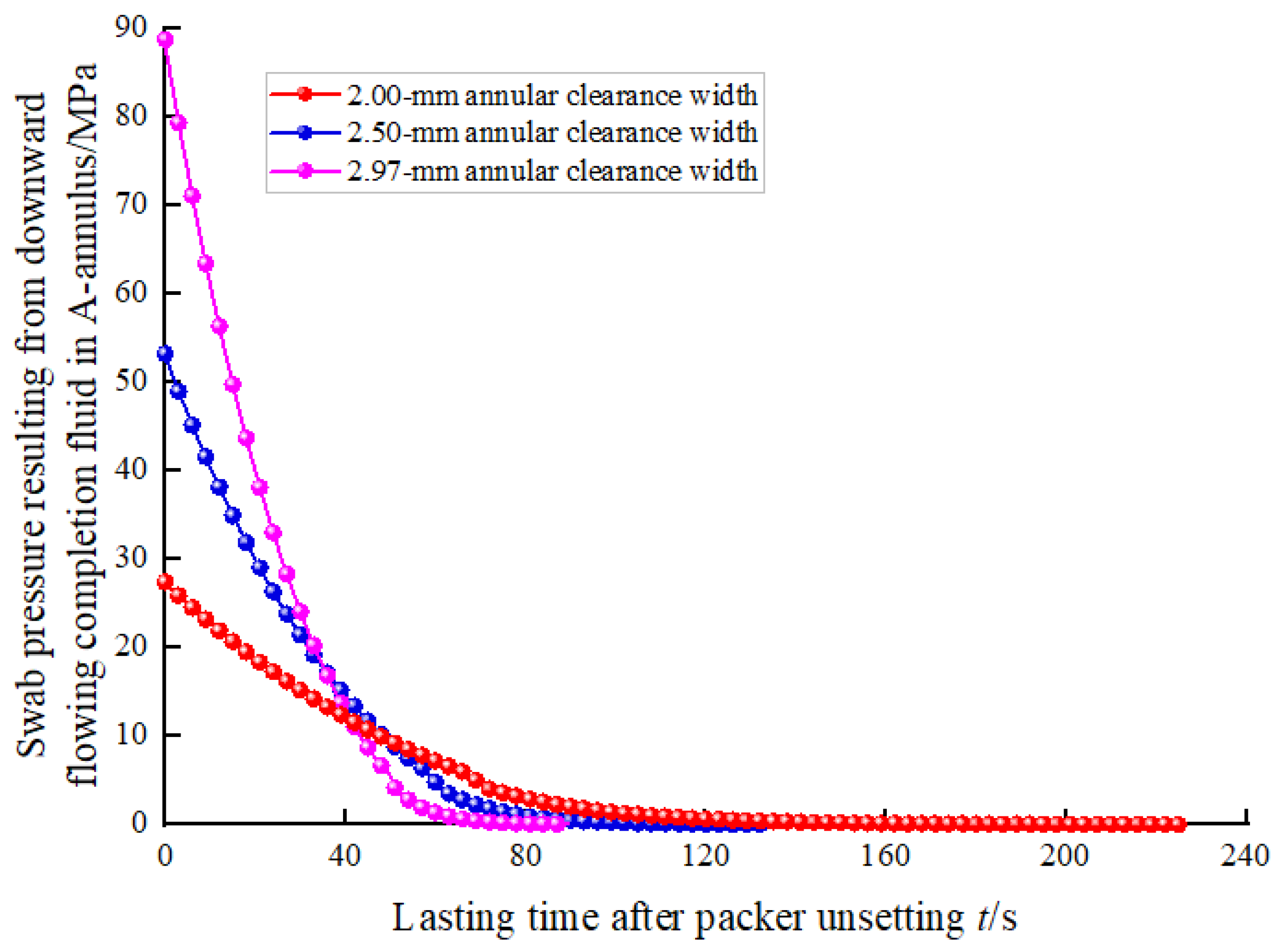
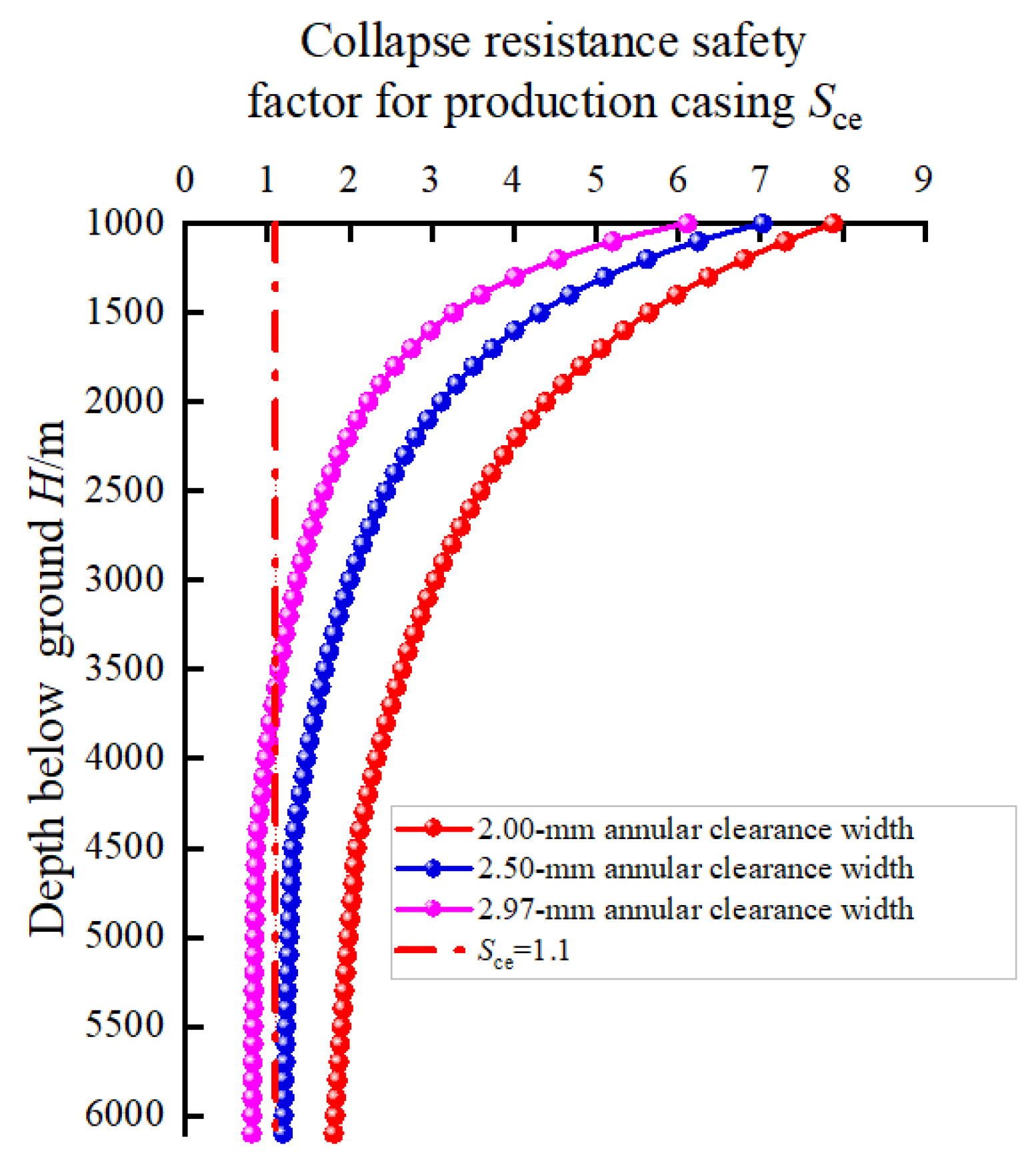
3.3.1. Width of Annular Clearance Between Packer Rubber and Production Casing
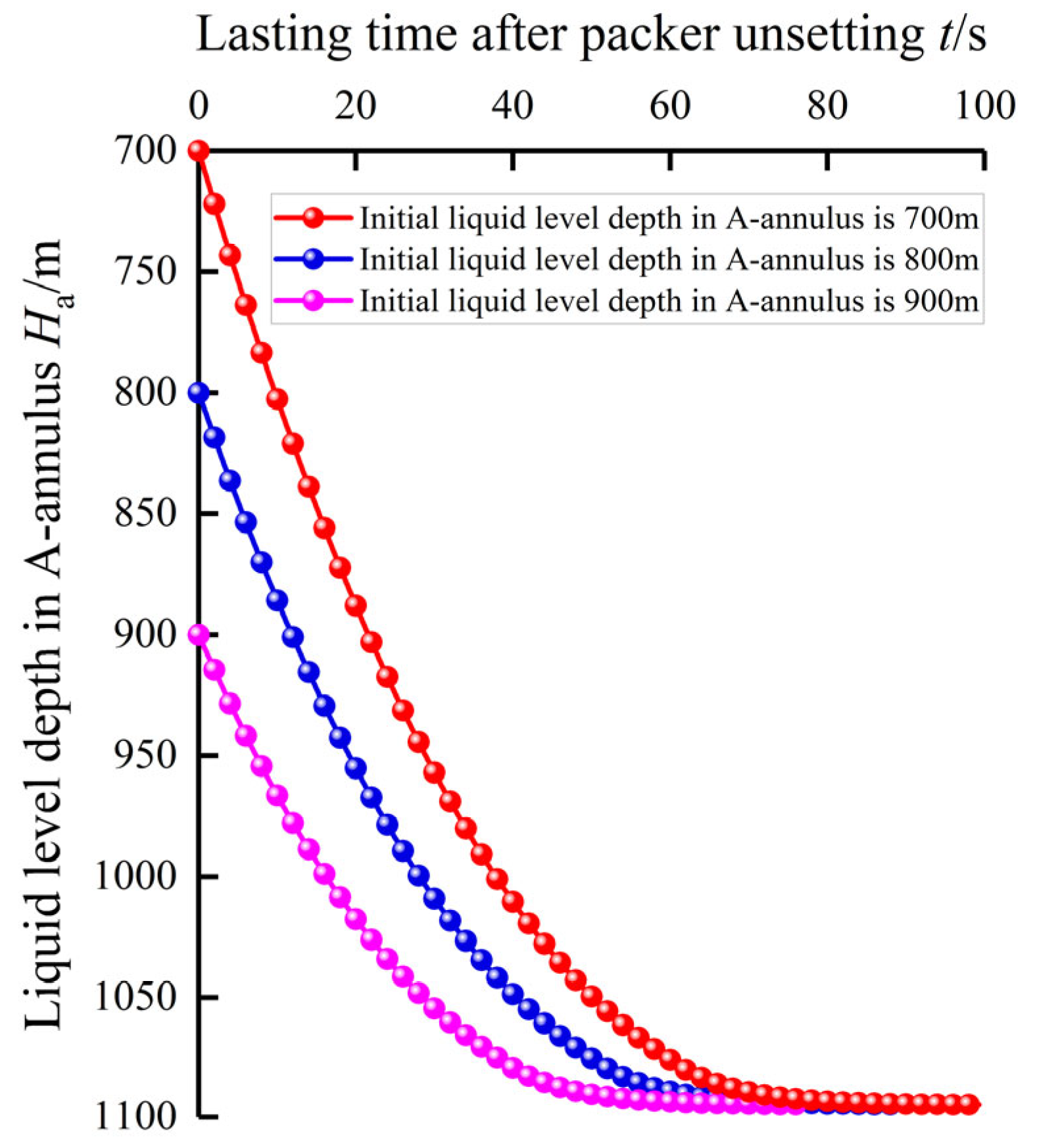
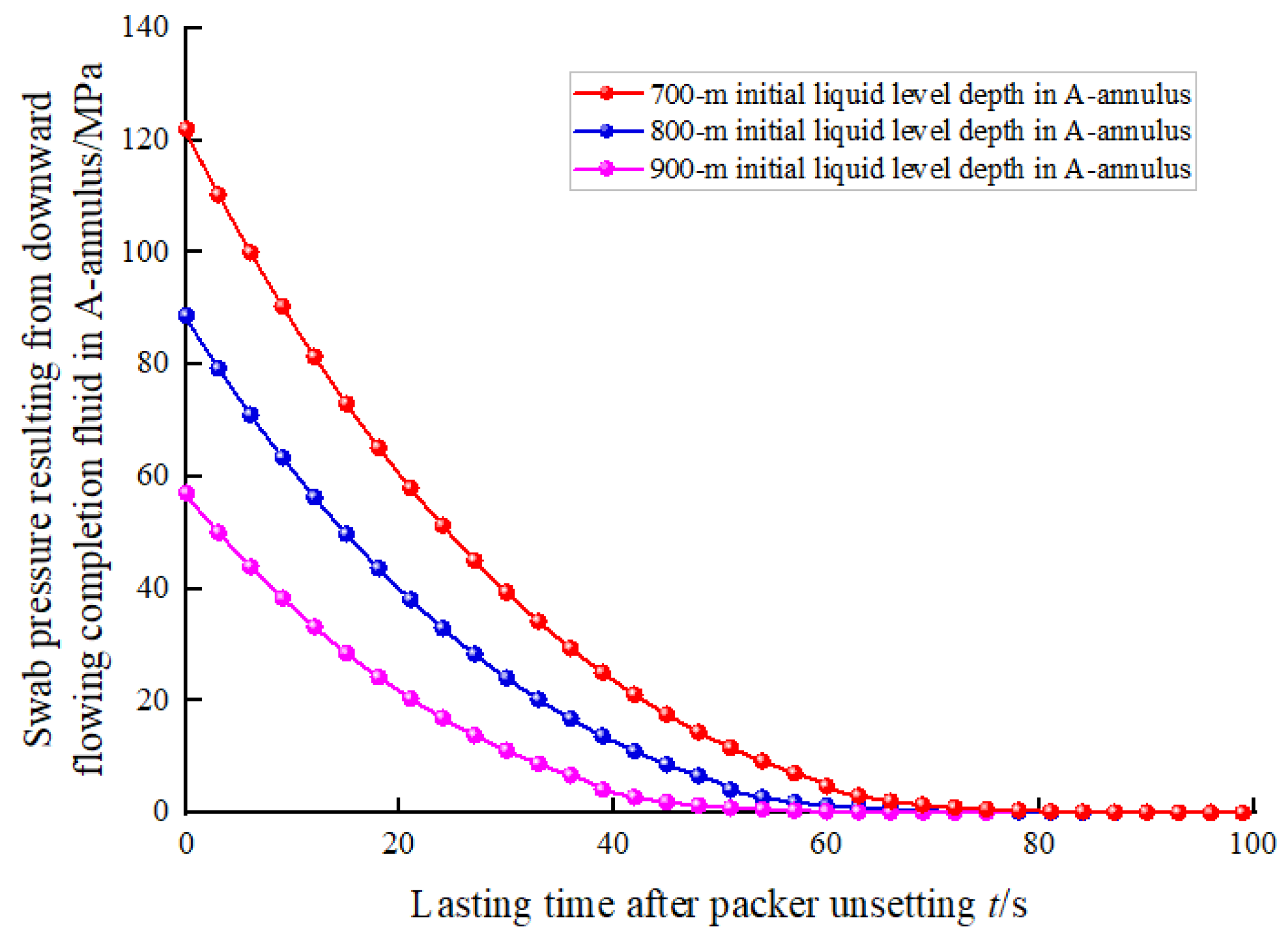
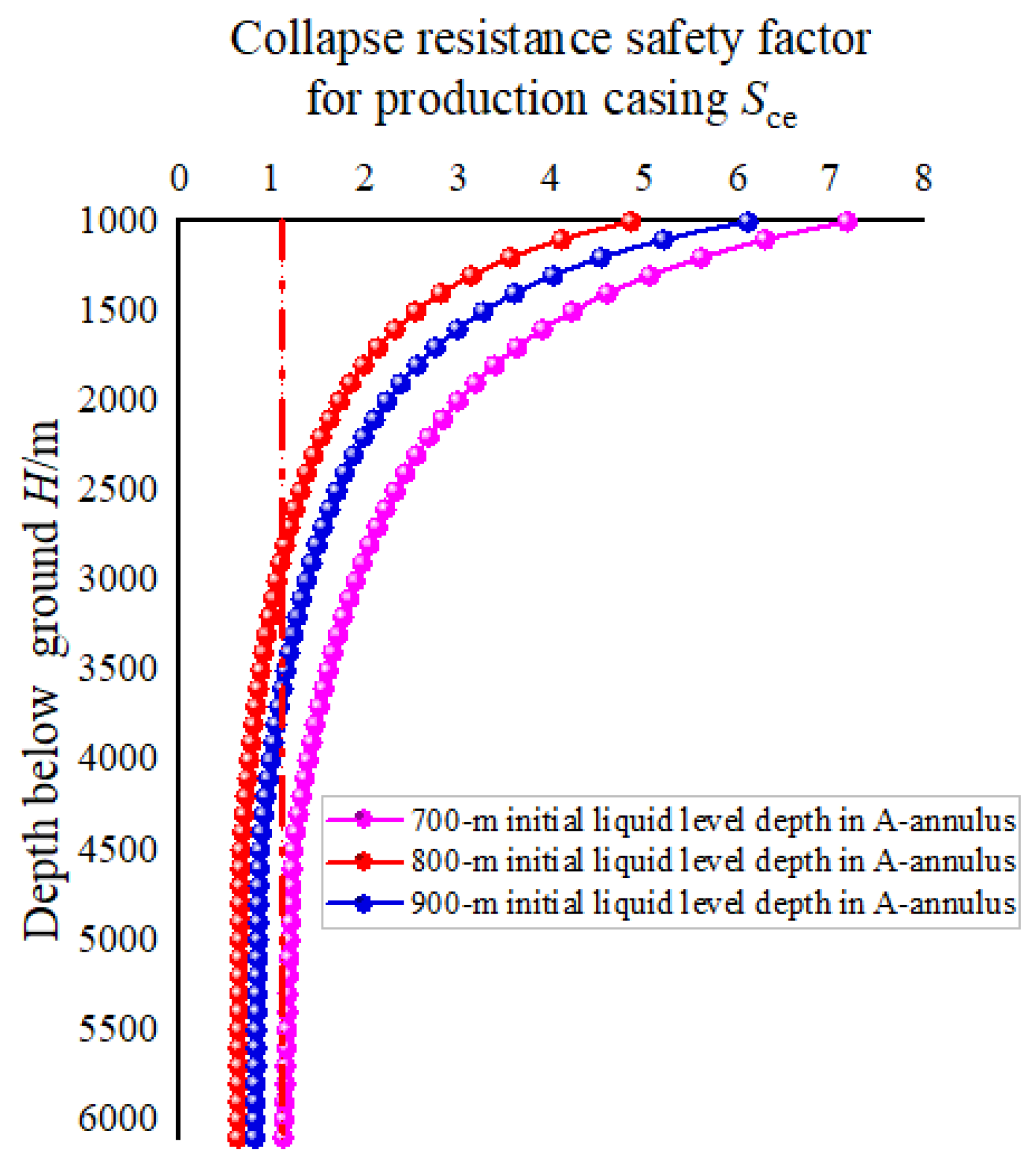
3.3.2. Initial Liquid Level Depth in A-Annulus
4. Discussion
5. Conclusions
- (1)
- This paper first proposes an analytical model to predict the transient swab pressure after packer unsetting and evaluates the collapse failure risk of the production casing in deep HPHT oil wells.
- (2)
- The largest swab pressure occurs at the initial time of packer unsetting, which would lead to collapse failure of the deeper production casing.
- (3)
- After packer unsetting, a smaller width of the annular clearance between the packer rubber and production casing and a larger initial liquid level depth in the A-annulus can both reduce the swab pressure in the A-annulus.
- (4)
- To lower the collapse failure risk of the production casing because of packer unsetting, packer rubber with a reasonable larger outer diameter and good deformation recovery ability is recommended, and the initial liquid level depth in the A-annulus should be reasonably controlled.
- (5)
- The present model can be further improved by considering more complex well completion geometries and the effects of non-Newtonian fluids and the randomness of the parameters on the transient swab pressure after packer unsetting.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| H | depth below ground, m; |
| Hs | middle depth of oil layer, m; |
| Hc | depth of production casing shoe, m; |
| Hp | packer setting depth, m; |
| Ha | liquid level depth in A-annulus, m; |
| Ho | liquid level depth in tubing, m; |
| ρc | density of completion fluid in A-annulus, kg/m3; |
| μc | dynamic viscosity of completion fluid in A-annulus Pa·s; |
| ρo | density of oil in tubing, kg/m3; |
| ρw | density of drilling fluid during well cementation, kg/m3; |
| g | gravitational acceleration, m/s2; |
| t | lasting time after packer unsetting, s; |
| i | number of time step, integer; |
| Pf | present static pressure for oil layer, Pa; |
| Doi | inner diameter of tubing, m; |
| Doo | outer diameter of tubing, m; |
| Dci | inner diameter of production casing, m; |
| Dpo | outer diameter of packer rubber after unsetting, m; |
| Lp | length of packer rubber, m; |
| ΔPp | pressure difference between the upper and lower packer, Pa; |
| λ | hydraulic friction coefficient, dimensionless; |
| Re1 | Reynolds number for flowing completion fluid in micro-annulus, dimensionless; |
| Re2 | Reynolds number for flowing completion fluid in A-annulus, dimensionless; |
| Vp | flow velocity of completion fluid in micro-annulus between the packer rubber and production casing, m/s; |
| Vp1 | assuming laminar flow velocity of completion fluid in micro-annulus, m/s; |
| Vp2 | assuming turbulent flow velocity of completion fluid in micro-annulus, m/s; |
| Va | flow velocity of completion fluid in A-annulus between the tubing and the production casing, m/s; |
| Ps | swab pressure resulting from downward flowing completion fluid in A-annulus, Pa; |
| Pci | inner pressure supporting production casing, Pa; |
| Pce | effective collapse pressure acting on the outer wall of production casing, Pa; |
| Sce | collapse resistance safety factor for production casing, dimensionless; |
| [Pc] | collapse strength for production casing, Pa. |
References
- Taheri, S.R.; Pak, A.; Shad, S.; Mehrgini, B.; Razifar, M. Investigation of rock salt layer creep and its effects on casing collapse. Int. J. Min. Sci. Technol. 2020, 30, 357–365. [Google Scholar] [CrossRef]
- Ai, C.; Zhao, W.; Guo, B. Casing-collapse strength reduction under lateral loads from yielding shales in the Daqing oilfield. SPE Drill. Complet. 2008, 23, 348–352. [Google Scholar] [CrossRef]
- Mitchell, R.F. Thick-Wall Elastic Collapse for Casing Design. SPE Drill. Complet. 2021, 36, 738–744. [Google Scholar] [CrossRef]
- Deng, K.; Lin, Y.; Qiang, H.; Zeng, D.; Sun, Y.; Xinxin, L. New high collapse model to calculate collapse strength for casing. Eng. Fail. Anal. 2015, 58, 295–306. [Google Scholar] [CrossRef]
- Zhou, X.; He, S.; Tang, M.; Fang, L.; Zhou, X.; Liu, Z. Mechanism of collapse failure and analysis of yield collapse resistance of casing under combined load. Eng. Struct. 2019, 191, 12–22. [Google Scholar] [CrossRef]
- Dashtaki, B.B.; Lashkaripour, G.R.; Ghafoori, M.; Moghaddas, N.H. Numerical modeling of casing collapse in Gachsaran formation in Sirri-E oilfield in Persian Gulf. J. Pet. Sci. Eng. 2021, 196, 108009. [Google Scholar] [CrossRef]
- Hou, B.; Chen, M.; Jin, Y. The study of casing collapse deformation for slump fault. In Rock Mechanics: Achievements and Ambitions, Proceedings of the 2nd ISRM International Young Scholars’ Symposium on Rock Mechanics, Beijing, China, 14–16 October 2011; Cai, M., Ed.; CRC Press: Boca Raton, FL, USA, 2011; pp. 896–899. [Google Scholar]
- Liu, S.; Zheng, H.; Zhu, X.; Tong, H. Equations to calculate collapse strength of defective casing for steam injection wells. Eng. Fail. Anal. 2014, 42, 240–251. [Google Scholar] [CrossRef]
- Cao, Y.; Dou, Y.; Li, M.; Suo, H. Theoretical and Simulation Study on the Collapse Strength of a Curved Casing in Horizontal Wells. Procedia Struct. Integr. 2019, 22, 84–92. [Google Scholar] [CrossRef]
- Shaygan, K.; Lari, S.H.; Mahani, H.; Jamshidi, S. Geomechanical investigation of casing collapse using finite element modeling: The role of cement sheath integrity. Geoenergy Sci. Eng. 2024, 233, 212579. [Google Scholar] [CrossRef]
- Mohamadian, N.; Ghorbani, H.; Wood, D.A.; Mehrad, M.; Davoodi, S.; Rashidi, S.; Soleimanian, A.; Shahvand, A.K. A geomechanical approach to casing collapse prediction in oil and gas wells aided by machine learning. J. Pet. Sci. Eng. 2021, 196, 107811. [Google Scholar] [CrossRef]
- Rashidi, S.; Mohamadian, N.; Ghorbani, H.; Wood, D.A.; Shahbazi, K.; Alvar, M.A. Shear modulus prediction of embedded pressurized salt layers and pinpointing zones at risk of casing collapse in oil and gas wells. J. Appl. Geophys. 2020, 183, 104205. [Google Scholar] [CrossRef]
- Buchmiller, D.; Bjørset, A.; Hørte, T.; Pettersen, S. Casing collapse design using structural reliability analysis for a subsea well on the norwegian continental shelf. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Zhu, X.; Liu, B. The reliability-based evaluation of casing collapsing strength and its application in marine gas reservoirs. Eng. Fail. Anal. 2018, 85, 1–13. [Google Scholar] [CrossRef]
- China National Development and Reform Commission. Design for Casing String Structure and Strength; SYT 5724-2008; China National Development and Reform Commission: Beijing, China, 2008. [Google Scholar]
- American Petroleum Institute. Calculating Performance Properties of Pipe Used as Casing or Tubing, 7th ed.; API TR 5C3; American Petroleum Institute: Washington, DC, USA, 2018. [Google Scholar]
- Zheng, X.; Li, B. Study on sealing performance of packer rubber based on stress relaxation experiment. Eng. Fail. Anal. 2021, 129, 105692. [Google Scholar] [CrossRef]
- Dong, L.; Li, K.; Zhu, X.; Li, Z.; Zhang, D.; Pan, Y.; Chen, X. Study on high temperature sealing behavior of packer rubber tube based on thermal aging experiments. Eng. Fail. Anal. 2020, 108, 104321. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S.; Zhang, L.; Wang, F.; Wang, P.; Han, L.; Ma, Y.; Zhang, H. Analysis of sealing mechanical properties of fracturing packer under complex conditions. J. Fail. Anal. Prev. 2019, 19, 1569–1582. [Google Scholar] [CrossRef]
- Deng, Q.; Zhang, H.; Chen, A.; Li, J.; Hou, X.; Wang, H. Effects of perforation fluid movement on downhole packer with shock loads. J. Pet. Sci. Eng. 2020, 195, 107566. [Google Scholar] [CrossRef]
- Krishna, S.; Ridha, S.; Vasant, P.; Ilyas, S.U.; Irawan, S.; Gholami, R. Explicit flow velocity modelling of yield power-law fluid in concentric annulus to predict surge and swab pressure gradient for petroleum drilling applications. J. Pet. Sci. Eng. 2020, 195, 107743. [Google Scholar] [CrossRef]
- Andrea, M. Extension of the Galilean-Invariant Formulation of Bernoulli’s Equation. J. Hydraul. Eng. 2024, 150, 13827. [Google Scholar]
- White, F. Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, USA, 2011; pp. 357–366. [Google Scholar]



| Symbol | Value | Unit | Symbol | Value | Unit |
|---|---|---|---|---|---|
| Hs | 6000 | m | Lp | 150 | mm |
| Hc | 6100 | m | ρc | 1050 | kg/cm3 |
| Hp | 4500 | m | ρo | 800 | kg/cm3 |
| Ha | 800 | m | ρw | 1220 | kg/cm3 |
| Doo | 88.9 | mm | μc | 0.07 | Pa·s |
| Doi | 76 | mm | g | 9.81 | m/s2 |
| Dci | 152.5 | mm | Pf | 46.8 | MPa |
| Dpo | 146.56 | mm | [Pc] | 89.8 | MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.-L.; Xiang, S.-L.; Pei, D.-D.; Wu, X.-D.; Zhang, Z. Transient Collapse Failure Prediction of Production Casing After Packer Unsetting in High-Pressure and High-Temperature Deep Oil Wells. Processes 2025, 13, 839. https://doi.org/10.3390/pr13030839
Xu H-L, Xiang S-L, Pei D-D, Wu X-D, Zhang Z. Transient Collapse Failure Prediction of Production Casing After Packer Unsetting in High-Pressure and High-Temperature Deep Oil Wells. Processes. 2025; 13(3):839. https://doi.org/10.3390/pr13030839
Chicago/Turabian StyleXu, Hong-Lin, Shi-Lin Xiang, Dong-Dong Pei, Xing-Dong Wu, and Zhi Zhang. 2025. "Transient Collapse Failure Prediction of Production Casing After Packer Unsetting in High-Pressure and High-Temperature Deep Oil Wells" Processes 13, no. 3: 839. https://doi.org/10.3390/pr13030839
APA StyleXu, H.-L., Xiang, S.-L., Pei, D.-D., Wu, X.-D., & Zhang, Z. (2025). Transient Collapse Failure Prediction of Production Casing After Packer Unsetting in High-Pressure and High-Temperature Deep Oil Wells. Processes, 13(3), 839. https://doi.org/10.3390/pr13030839





