Power System Loss Reduction Strategy Considering Security Constraints Based on Improved Particle Swarm Algorithm and Coordinated Dispatch of Source–Grid–Load–Storage
Abstract
1. Introduction
- (1)
- A bi-level optimization model is proposed for addressing distribution network loss reduction. The upper-level objective minimizes the total annual planning cost, while the lower-level objectives focus on minimizing both the load curve variance and the node voltage deviation. By considering economic efficiency and operational characteristics at both global and local levels, this model provides a theoretical foundation for the collaborative optimization of loss reduction strategies.
- (2)
- In response to the constructed bi-level optimization model, this paper proposes and applies an improved particle swarm optimization algorithm. The results demonstrate the algorithm’s superior performance in terms of search speed and convergence accuracy, thereby confirming the effectiveness and feasibility of the proposed method for distribution network loss reduction optimization.
2. Model of the Distribution Network
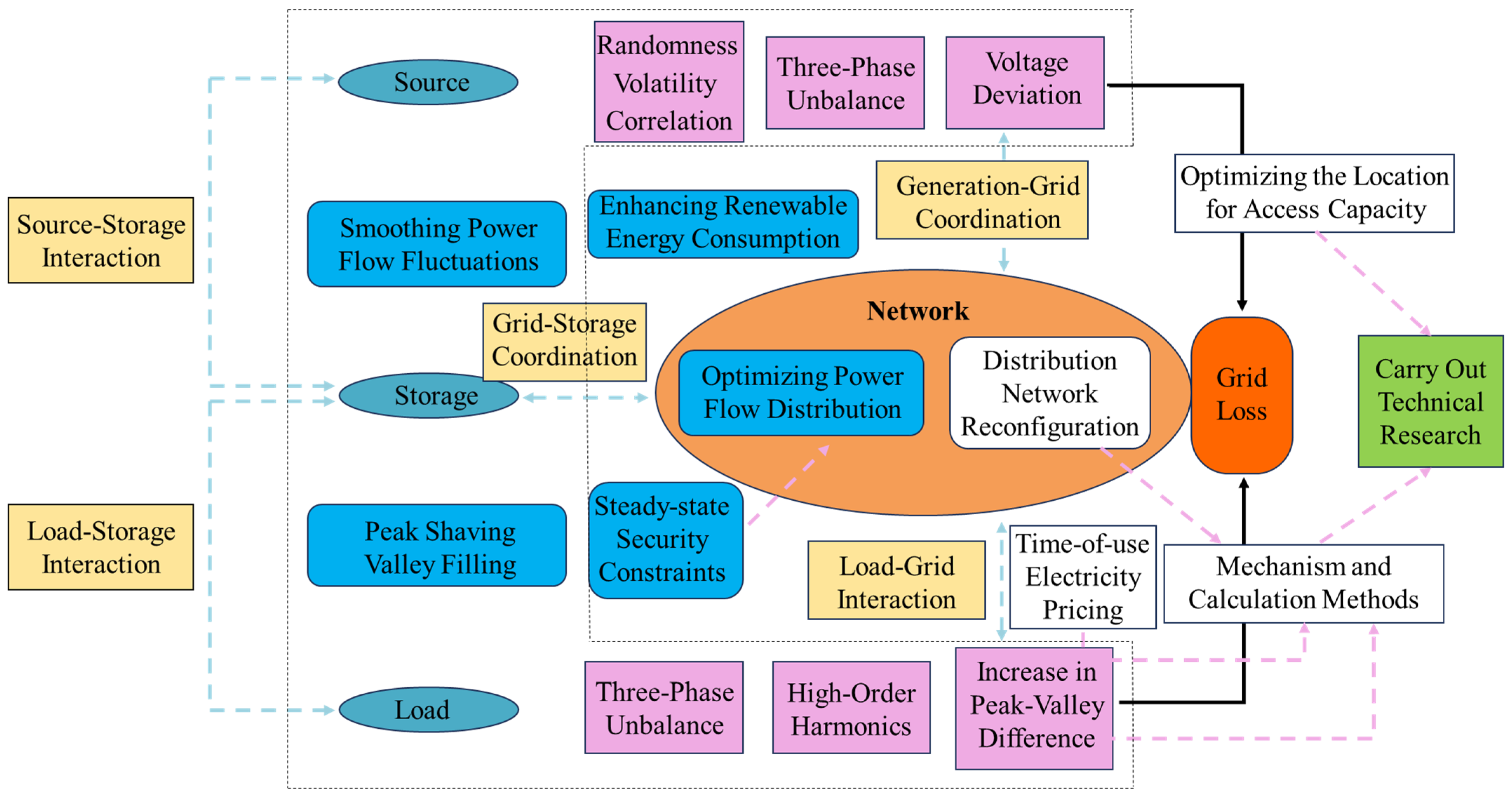
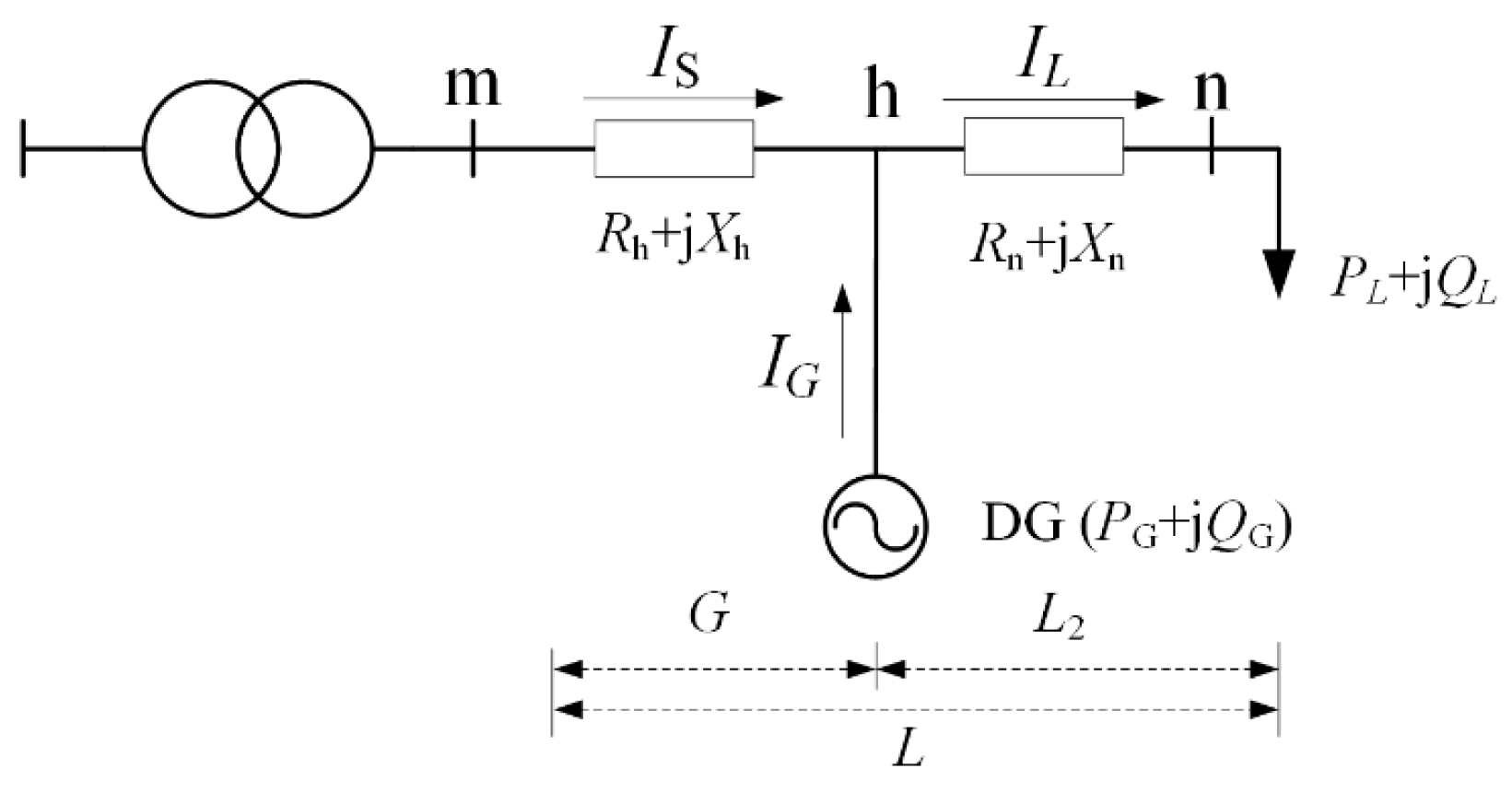
2.1. The Interaction Mechanism of “Source-Grid-Load-Storage” in the Distribution Network
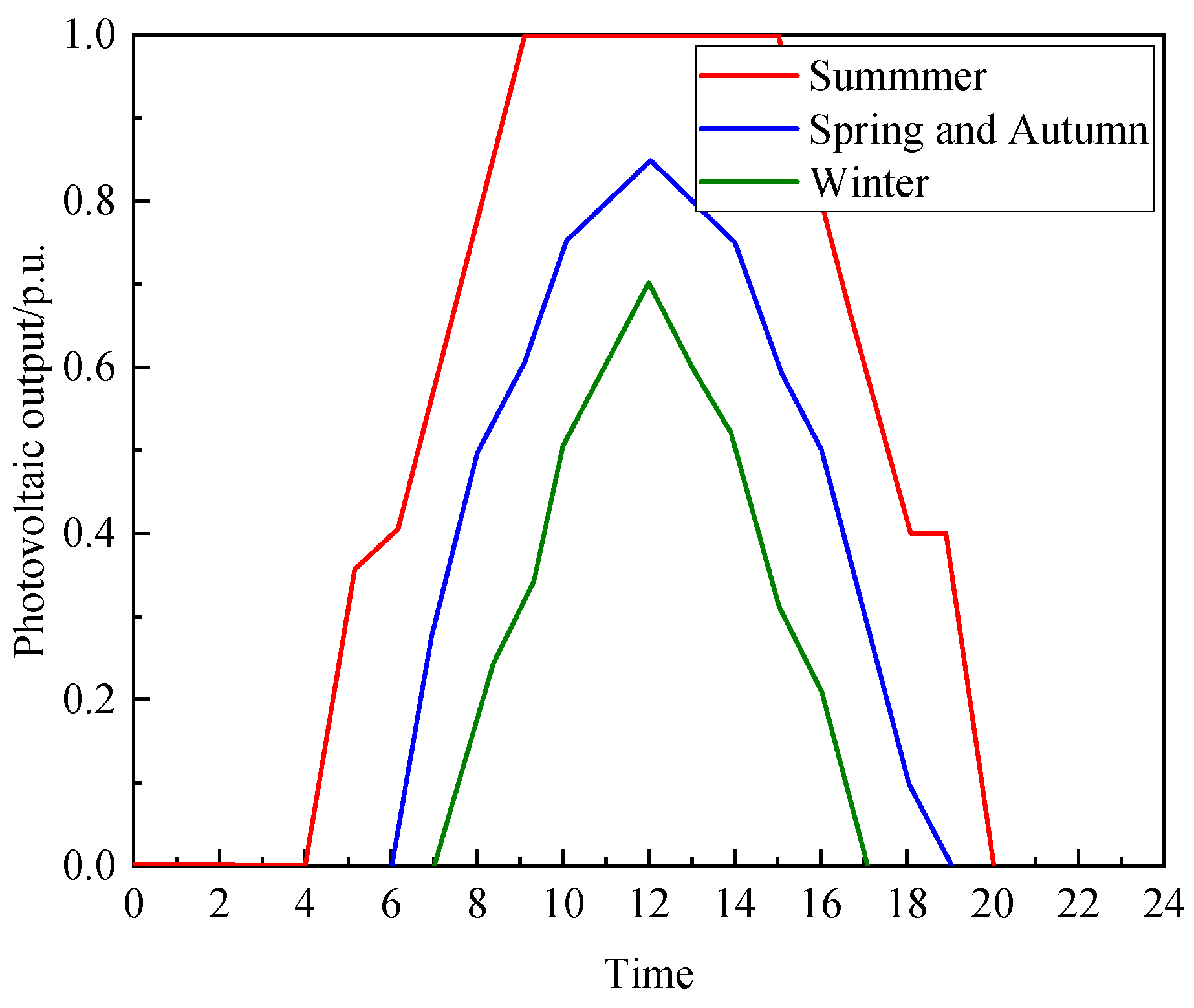
2.2. Model of Distributed Photovoltaic Power Source
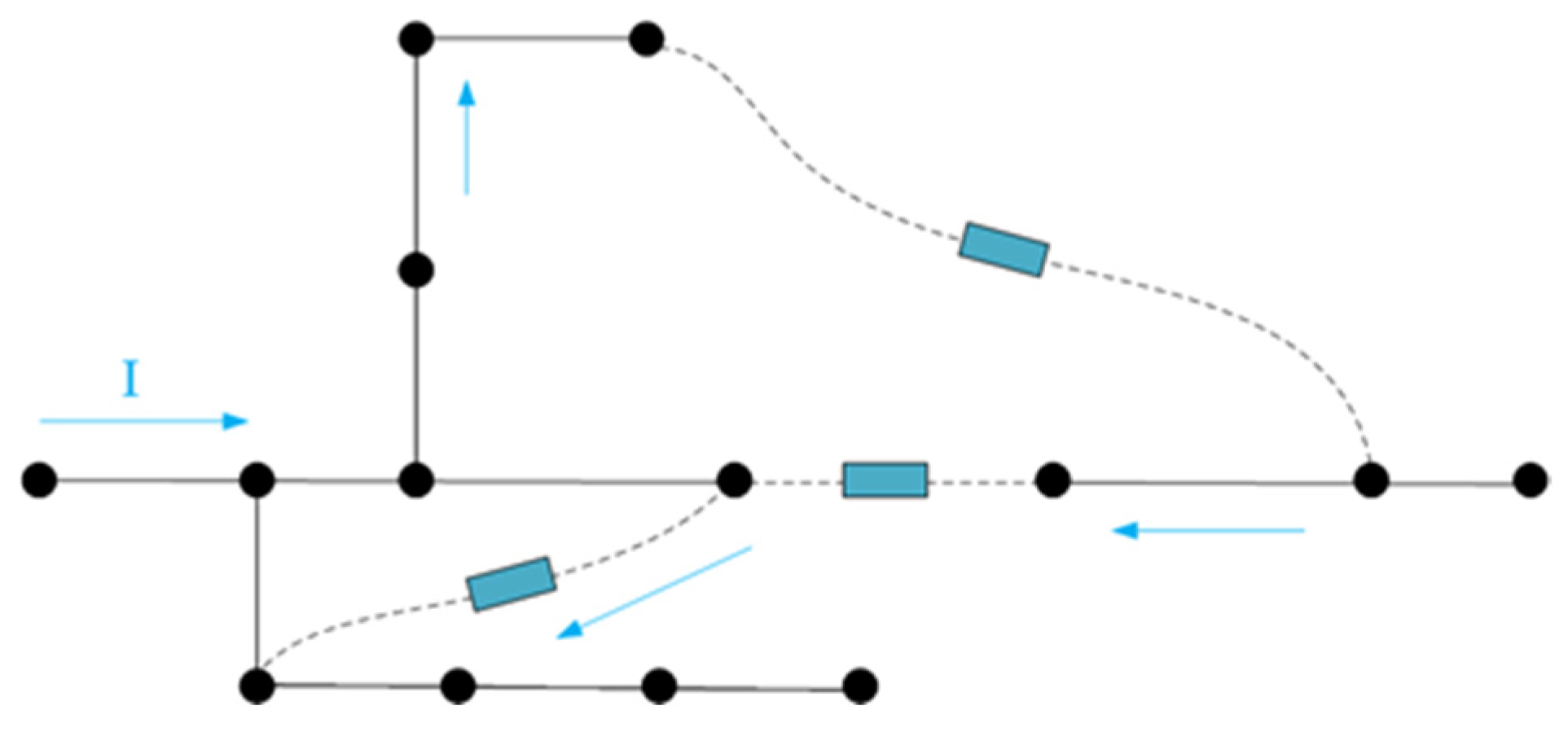
2.3. Model of Distribution Network Reconfiguration
2.4. Model of Energy Storage
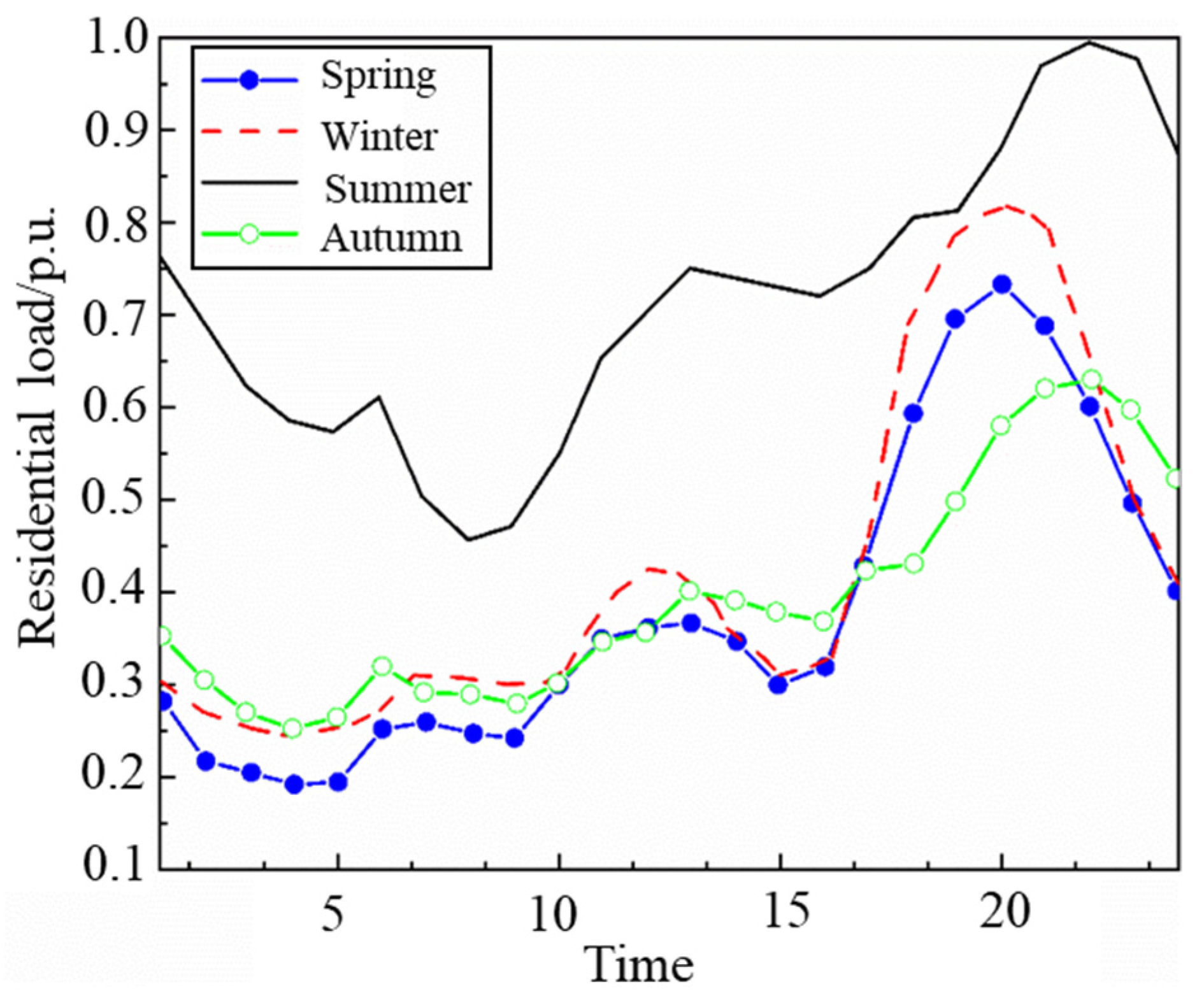
2.5. Model of Loads
2.5.1. Model of Electric Car
2.5.2. Model of Load Power
3. Analysis of Factors Affecting Network Losses in Distribution Networks
4. Improved Particle Swarm Optimization Algorithm
4.1. Conventional Particle Swarm Optimization Algorithm
4.2. Improved PSO
4.2.1. Population Initialization
4.2.2. Adaptive Inertia Weight
4.2.3. Update the Velocity and Position of the Particles
4.2.4. Treatment of Border Crossings
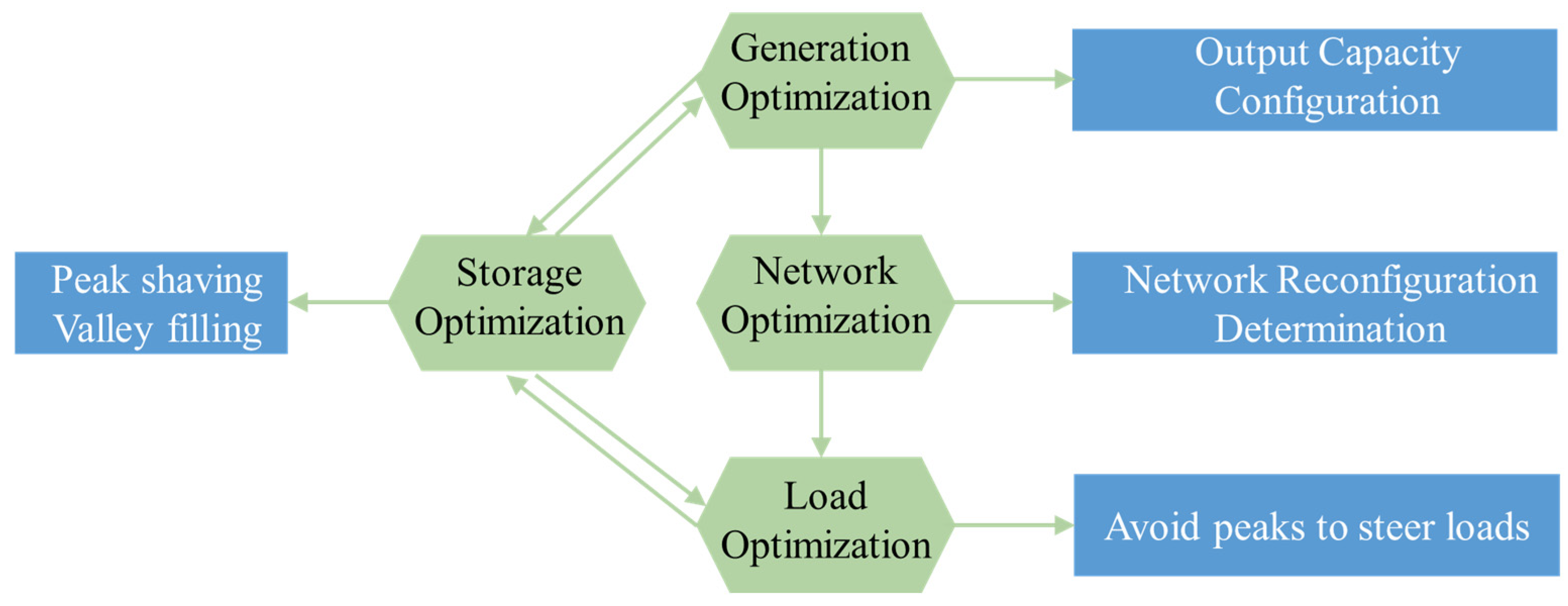
5. Loss Reduction in Distribution Networks with “Source-Network-Hoist-Storage” Coordination
5.1. Analysis of Loss Reduction Strategies for Distribution Network Losses
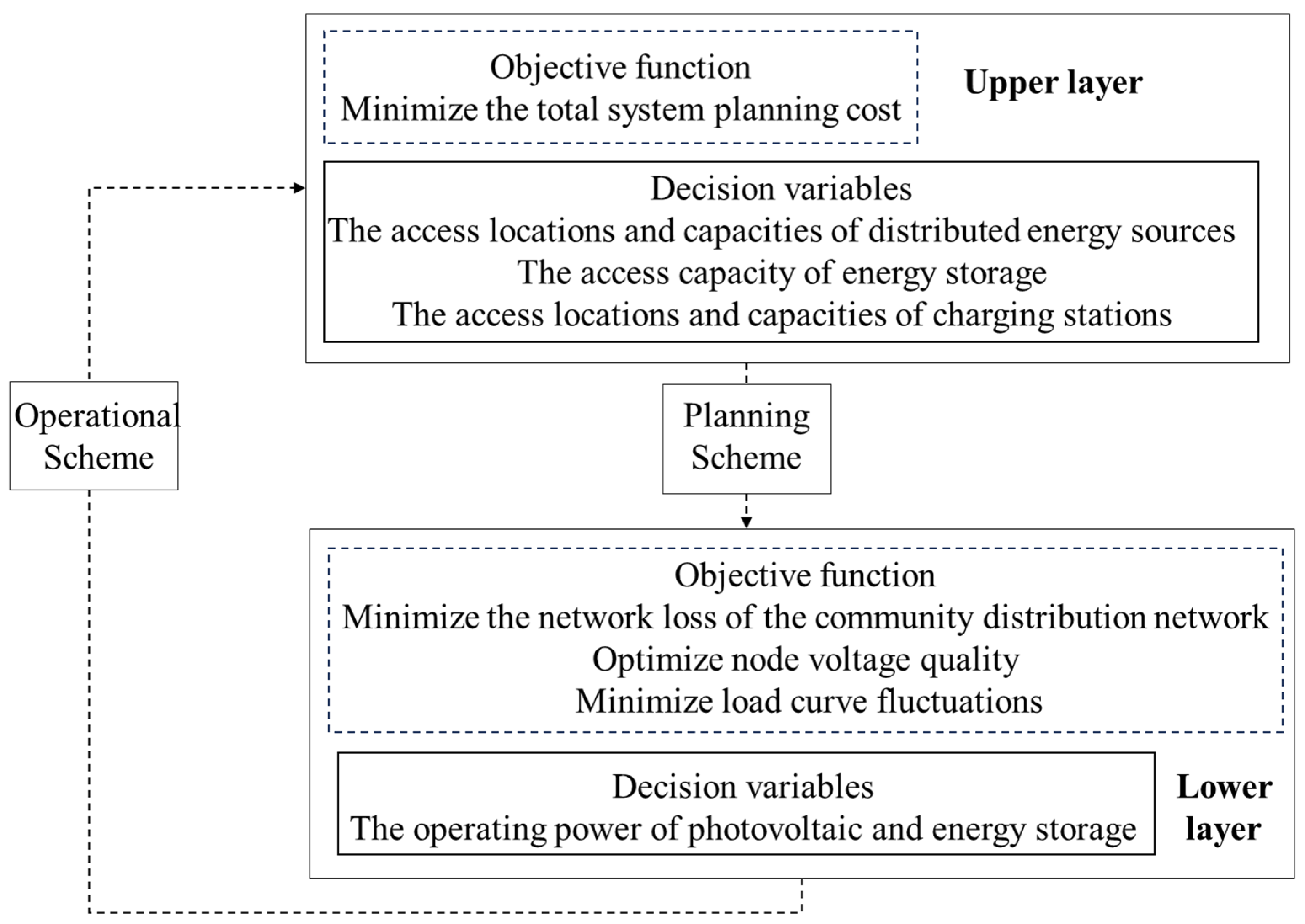
5.2. The Coordinated Bi-Level Optimization Model of Source–Grid–Load–Storage
5.2.1. Upper-Level Planning Mathematical Model
- (1)
- Capacity constraints for distributed PV power.
- (2)
- The constraints on the installed capacity, charging and discharging efficiency, and state of charge of the energy storage system are given in (5) to (9).
- (3)
- Power balance constraints in the distribution system.
- (4)
- Contact line power constraint.
5.2.2. Lower-Level Planning Mathematical Model
- (1)
- Electric power flow constraints.
- (2)
- Distributed PV power supply, energy storage system output constraints, node voltage constraints, and line power constraints.
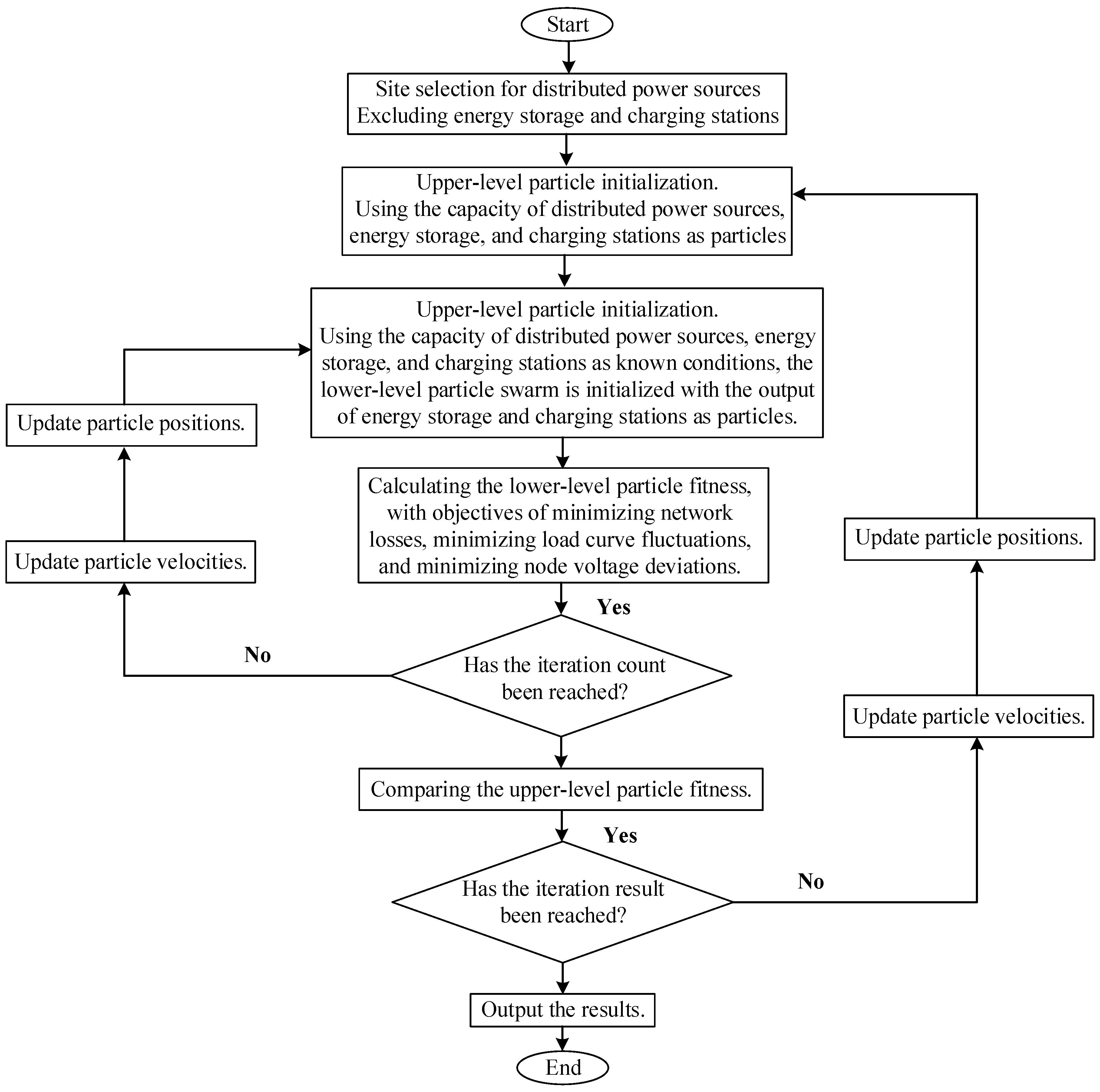
5.3. Model Solving Method
6. Case Study
6.1. Parameters of Case
6.2. The Role of “Source-Grid-Load-Storage” Coordination on Distribution Network Loss Reduction
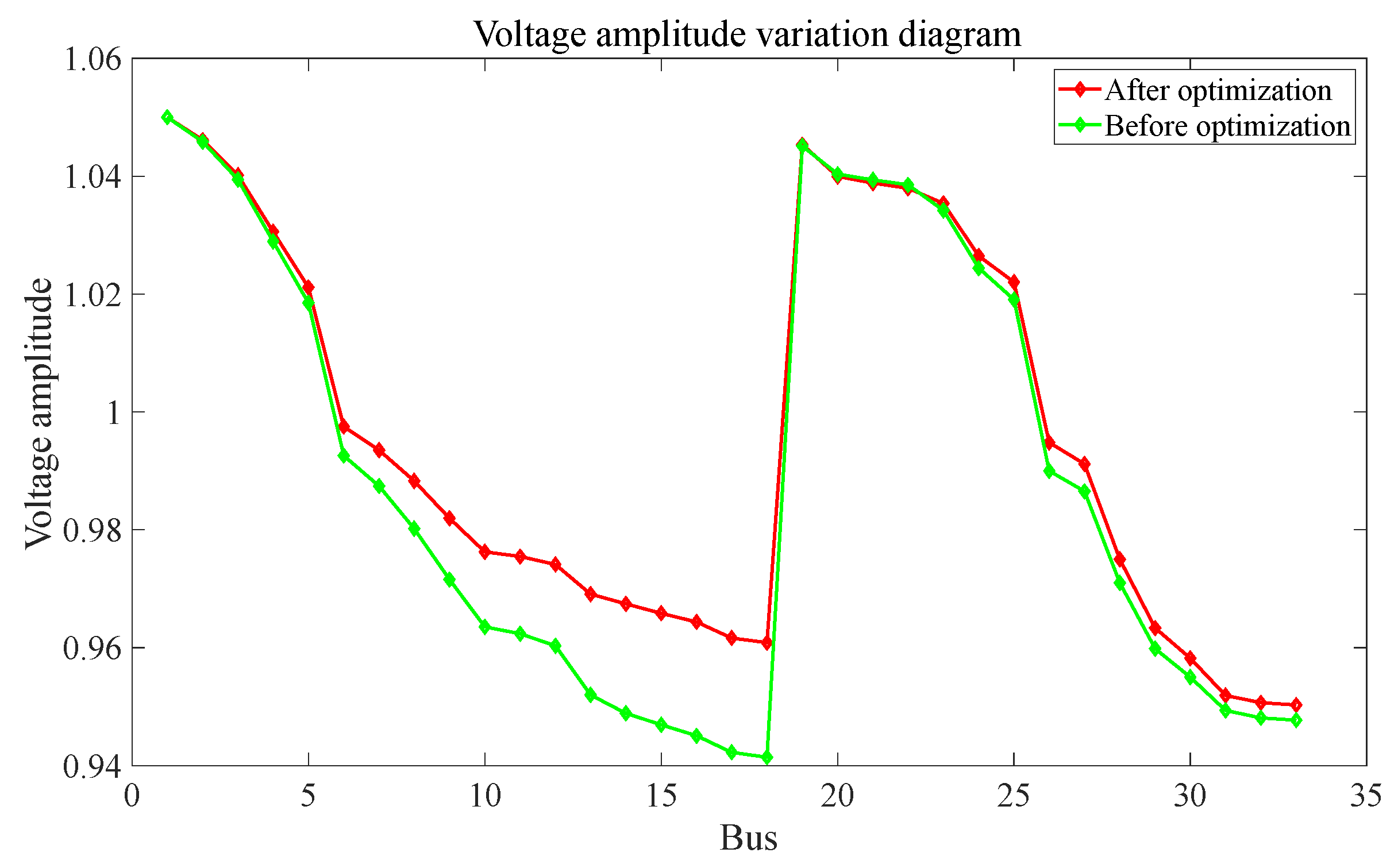
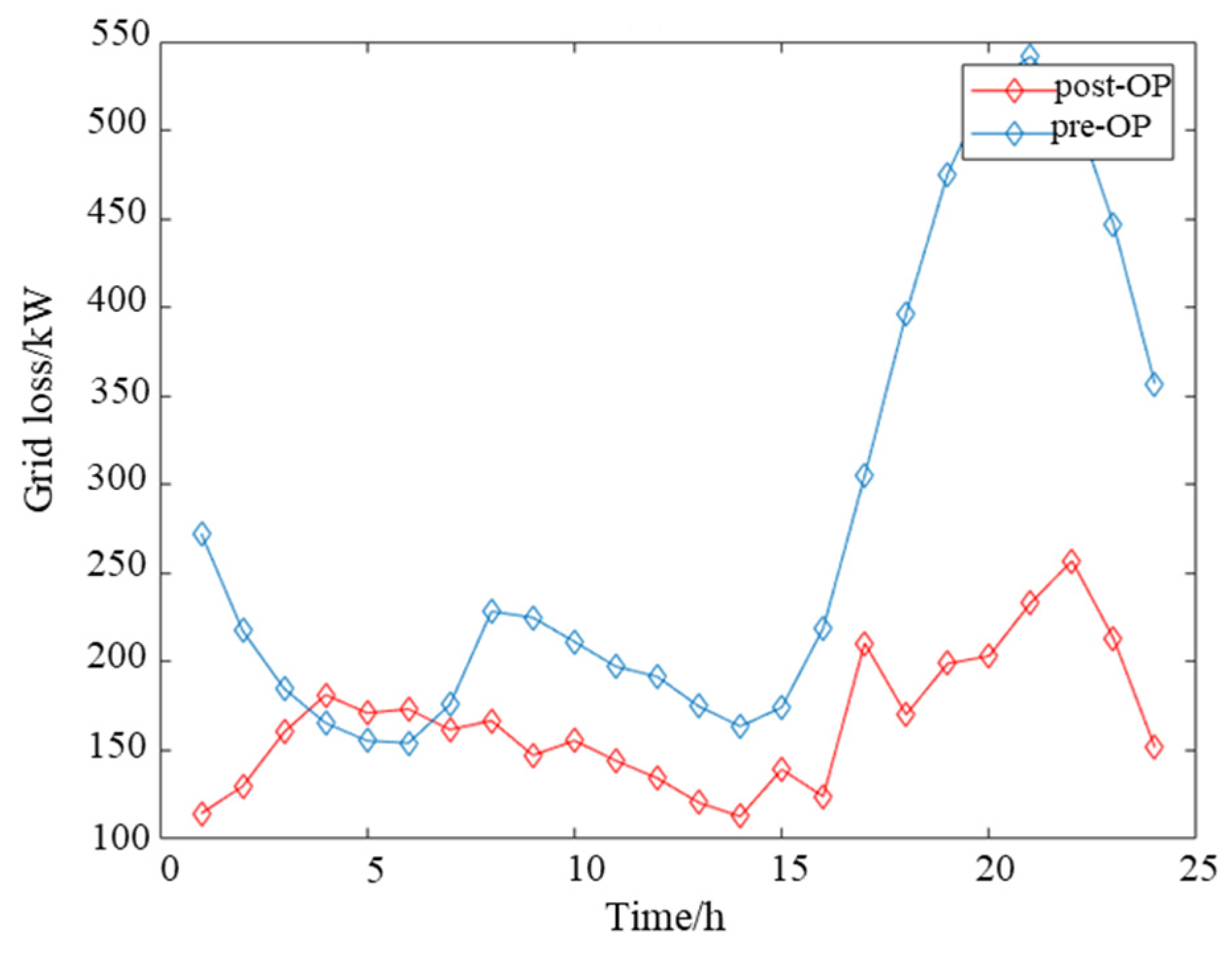
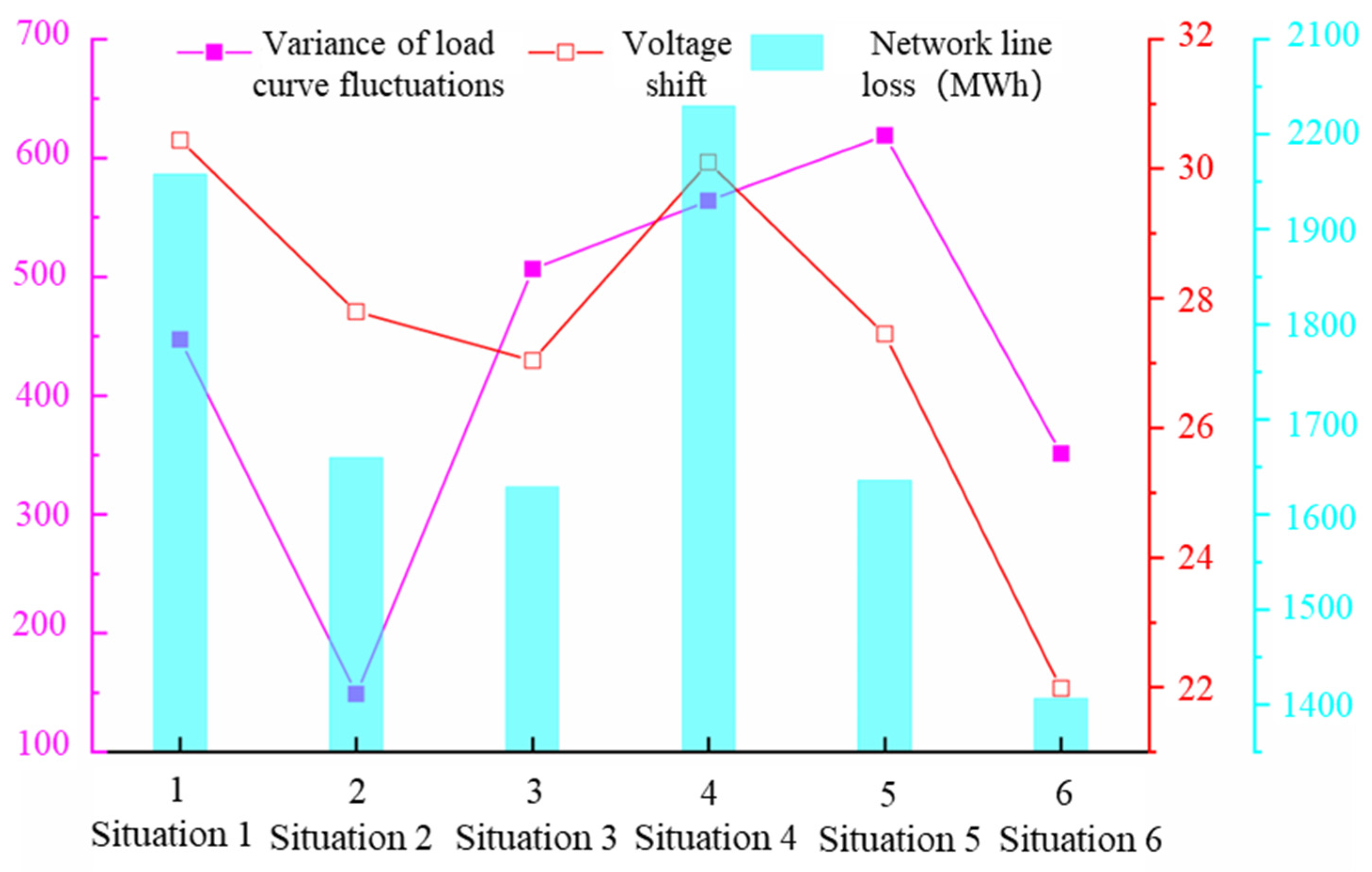
6.3. Rationality and Effectiveness Analysis
7. Conclusions
- (1)
- Integrating distributed PV power generation systems into the distribution network reduces network losses and annual power purchase costs; integrating energy storage systems into the distribution network decouples simultaneous load demands, reduces peak-to-valley differences in the load curve, and thus reduces network losses; coordinated optimization of source–storage–load maximizes the consumption of PV power generation, reduces network losses, improves the system security levels, and reduces the fluctuation of the load curve.
- (2)
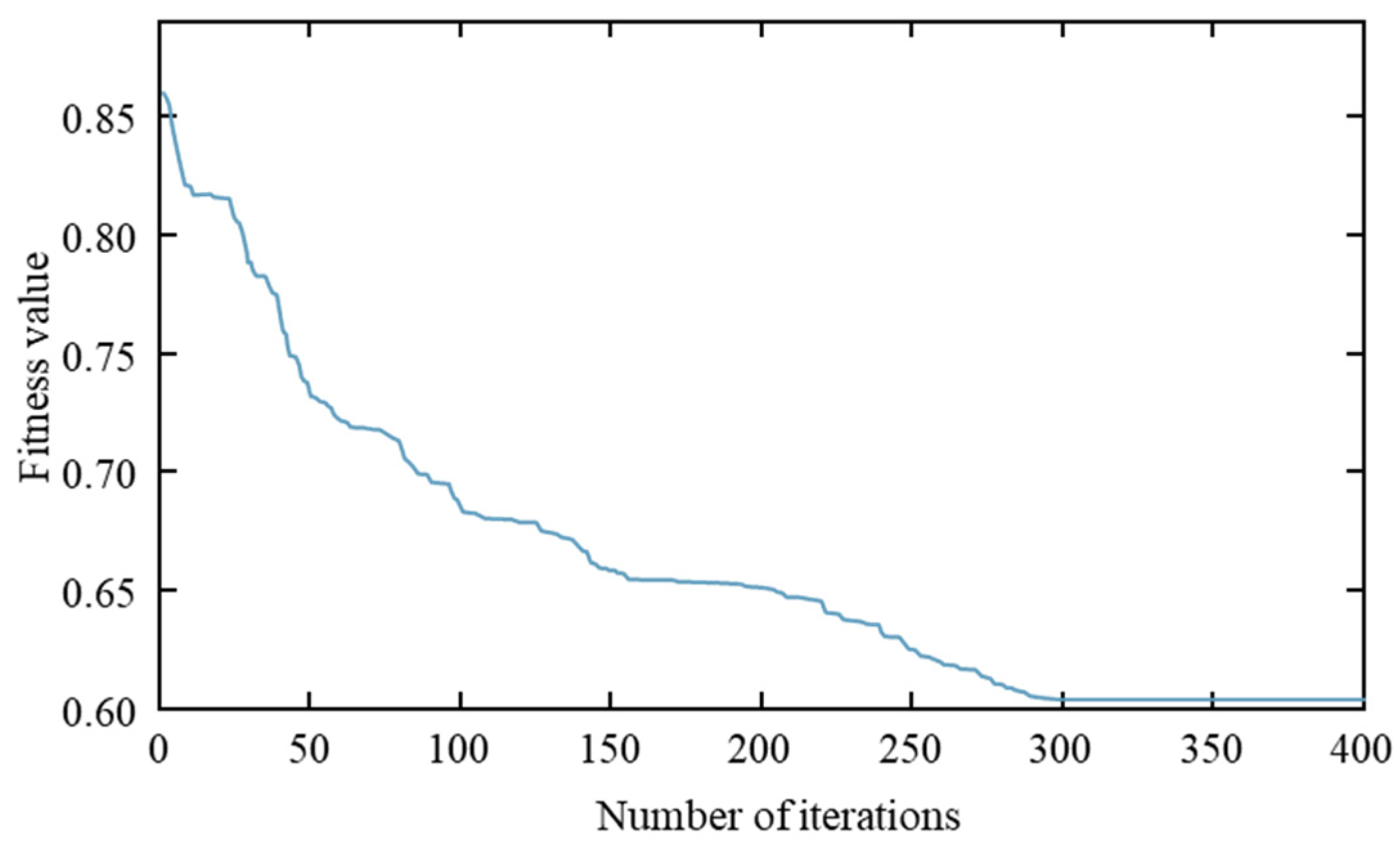
- The improved particle swarm algorithm proposed in this paper outperforms the traditional algorithm in terms of minimum fitness value, number of iterations, and computation time, and it provides higher solution accuracy and computational efficiency for the distribution network coordination optimization problem.
- (3)
- Through the IEEE 33-node distribution network and the IEEE 118-node and DTU 7K 47-node systems, the proposed method shows good applicability in different sizes and types of distribution networks, which can significantly reduce network losses and improve economic efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameters and variables | Meaning |
| Tcell(t) | the temperature of the PV cell |
| Ten(t) | the ambient temperature |
| S(t) | the solar irradiance |
| Tno | the rated battery operating temperature |
| UMPP | the voltage and current corresponding to the maximum power emitted by a single PV module |
| IMPP | the current and current corresponding to the maximum power emitted by a single PV module |
| Uoc | the open-circuit voltage |
| Isc | the short-circuit current |
| Ωb | all branches of the distribution network |
| SOCt | the charge storage states of the energy storage device battery at moment t |
| d | charging and discharging rate |
| ηc | the charging efficiency of energy storage |
| ηd | the discharging efficiency of energy storage |
| Ebess | the rated capacity of the energy storage |
| μs | the expected value of the final arrival moment of the electric vehicle |
| μD | the expected daily driving range of an electric vehicle |
| ftch | the probability density function of electric vehicle charging duration |
| IL | the load current |
| IS | the supply current |
| IG | the injection current of the DG |
| Ploss1 | the first half of the line network loss between the substation to the DG |
| Ploss2 | the second half of the line network loss between the DG to the end of the line |
| LSFPt | the sensitivity of DG active power to affect network losses |
| LSFQt | the sensitivity of DG reactive power to affect network losses |
| F(∙) | the objective function of the upper level |
| w(∙) | the objective function of the lower level |
| G(∙) | the constraints associated with the upper-level objective function |
| g(∙) | the constraints of the lower-level objective function |
| Cinv | the total investment cost |
| Cope | the system’s operation and maintenance costs |
| Cen | the cost of purchasing electricity for the system |
| PL,t | the net load power of the load distribution network |
| PPV(t) | the actual output of PVs at moment t |
| the maximum power limit for energy storage charging and discharging | |
| SLi | the apparent power of line i. |
References
- Tong, H.; Zeng, X.; Yu, K.; Zhou, Z. A Fault Identification Method for Animal Electric Shocks Considering Unstable Contact Situations in Low-Voltage Distribution Grids. IEEE Trans. Ind. Inform. 2025, 1–12. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, J.; Jin, Z. Optimal extreme random forest ensemble for active distribution network forecasting-aided state estima-tion based on maximum average energy concentration VMD state decomposition. Energies 2023, 16, 5659. [Google Scholar] [CrossRef]
- Yu, Y.; Jin, Z.; Ćetenović, D.; Ding, L.; Levi, V.; Terzija, V. A robust distribution network state estimation method based on enhanced clustering Algo-rithm: Accounting for multiple DG output modes and data loss. Int. J. Electr. Power Energy Syst. 2024, 157, 109797. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, B.; Chung, C.Y.; Wu, T.; Zheng, L.; Shuai, Z. A coordinated emergency response scheme for electricity and watershed networks con-sidering spatio-temporal heterogeneity and volatility of rainstorm disasters. IEEE Trans. Smart Grid 2024, 15, 3528–3541. [Google Scholar] [CrossRef]
- Xia, Y.; Li, Z.; Xi, Y.; Wu, G.; Peng, W.; Mu, L. Accurate Fault Location Method for Multiple Faults in Transmission Networks Using Travelling Waves. IEEE Trans. Ind. Inform. 2024, 20, 8717–8728. [Google Scholar] [CrossRef]
- Xu, Y.; Han, J.; Yin, Z.; Liu, Q.; Dai, C.; Ji, Z. Voltage and reactive power-optimization model for active distribution networks based on sec-ond-order cone algorithm. Computers 2024, 13, 95. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W. Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses. Sustainability 2024, 16, 2019. [Google Scholar] [CrossRef]
- Wang, K.; Wang, C.; Yao, W.; Zhang, Z.; Liu, C.; Dong, X.; Yang, M.; Wang, Y. Embedding P2P transaction into demand response exchange: A cooperative demand response management framework for IES. Appl. Energy 2024, 367. [Google Scholar] [CrossRef]
- Gallegos, J.; Arévalo, P.; Montaleza, C.; Jurado, F. Sustainable electrification—Advances and challenges in electrical-distribution networks: A review. Sustainability 2024, 16, 698. [Google Scholar] [CrossRef]
- Garibello-Narváez, D.R.; Gómez-Luna, E.; Vasquez, J.C. Performance Evaluation of Distance Relay Operation in Distribution Systems with Integrated Distributed Energy Resources. Energies 2024, 17, 4735. [Google Scholar] [CrossRef]
- Wang, H. A novel feature selection method based on quantum support vector machine. Phys. Scr. 2024, 99, 056006. [Google Scholar] [CrossRef]
- Xu, D.; Song, X.; Wu, Z.; Xu, J.; Hu, Q. A Levenberg–Marquardt algorithm-based line parameters identification method for distribution network considering multisource measurement. IET Renew. Power Gener. 2024, 18, 3743–3752. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, X. A biogeography-based optimization algorithm with local search for large-scale heterogeneous distributed scheduling with multiple process plans. Neurocomputing 2024, 595, 127897. [Google Scholar] [CrossRef]
- Pan, K.; Liang, C.-D.; Lu, M. Optimal scheduling of electric vehicle ordered charging and discharging based on improved gravitational search and particle swarm optimization algorithm. Int. J. Electr. Power Energy Syst. 2024, 157. [Google Scholar] [CrossRef]
- Jia, J.; Yan, X.; Wang, Y.; Aslam, W.; Liu, W. Parameter identification and modelling of photovoltaic power generation systems based on LVRT tests. IET Gener. Transm. Distrib. 2020, 14, 3089–3098. [Google Scholar] [CrossRef]
- Cui, D.; Wang, Z.; Liu, P.; Zhang, Z.; Wang, S.; Zhao, Y.; Dorrell, D.G. Coordinated charging scheme for electric vehicle fast-charging station with demand-based priority. IEEE Trans. Transp. Electrif. 2023, 10, 6449–6459. [Google Scholar] [CrossRef]
- Pomilio, J.A.; Deckmann, S.M. Characterization and compensation of harmonics and reactive power of residential and commercial loads. IEEE Trans. Power Deliv. 2007, 22, 1049–1055. [Google Scholar] [CrossRef]
- Sotkiewicz, P.; Vignolo, J. Nodal pricing for distribution networks: Efficient pricing for efficiency enhancing DG. IEEE Trans. Power Syst. 2006, 21, 1013–1014. [Google Scholar] [CrossRef]
- Dey, B.; Krishnamurthy, S.; Fose, N.; Ratshitanga, M.; Moodley, P. A metaheuristic approach to analyze the techno-economical impact of energy storage systems on grid-connected microgrid systems adapting load-shifting policies. Processes 2024, 13, 65. [Google Scholar] [CrossRef]
- Bai, J.; Yan, J.; Ablameyko, S.V.; Wang, J. Adaptive Pyramid Particle Swarm Algorithm with Competitive and Cooperative Strategies. In Proceedings of the 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 20–22 September 2024; pp. 716–720. [Google Scholar]
- Li, G.; Xu, Z.; Zhou, Y. Wind power prediction based on PSO-BP neural network. In Proceedings of the 2024 6th International Conference on Energy Systems and Electrical Power (ICESEP), Wuhan, China, 21–23 June 2024; pp. 34–37. [Google Scholar]
- Zhang, P.; Wu, X. Research on multi-objective microgrid operation optimization based on improved particle swarm optimiza-tion. In Proceedings of the 2024 4th International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Hangzhou, China, 5–7 July 2024; pp. 161–165. [Google Scholar]
- Gao, S.; Wang, H.; Wang, C.; Gu, S.; Xu, H.; Ma, H. Reactive power optimization of low voltage distribution network based on improved particle swarm optimization. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar]
- Yan, J.; Gou, Z.; Wang, W.; Yan, Z.; Ren, M.; Huang, Y.; Meng, J.; Wang, X. A PID Control Algorithm Optimized by PSO-BP Neural Network and Kalman Filter. In Proceedings of the 2024 International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 16–18 August 2024; pp. 95–99. [Google Scholar]
- Xiao, S.; Lei, X.; Huang, T.; Wang, X. Coordinated planning for fast charging stations and distribution networks based on an im-proved flow capture location model. CSEE J. Power Energy Syst. 2023, 9, 1505–1516. [Google Scholar]
- Feng, M.; Qu, H.; Yi, Z.; Kurths, J. Subnormal distribution derived from evolving networks with variable elements. IEEE Trans. Cybern. 2017, 48, 2556–2568. [Google Scholar] [CrossRef]


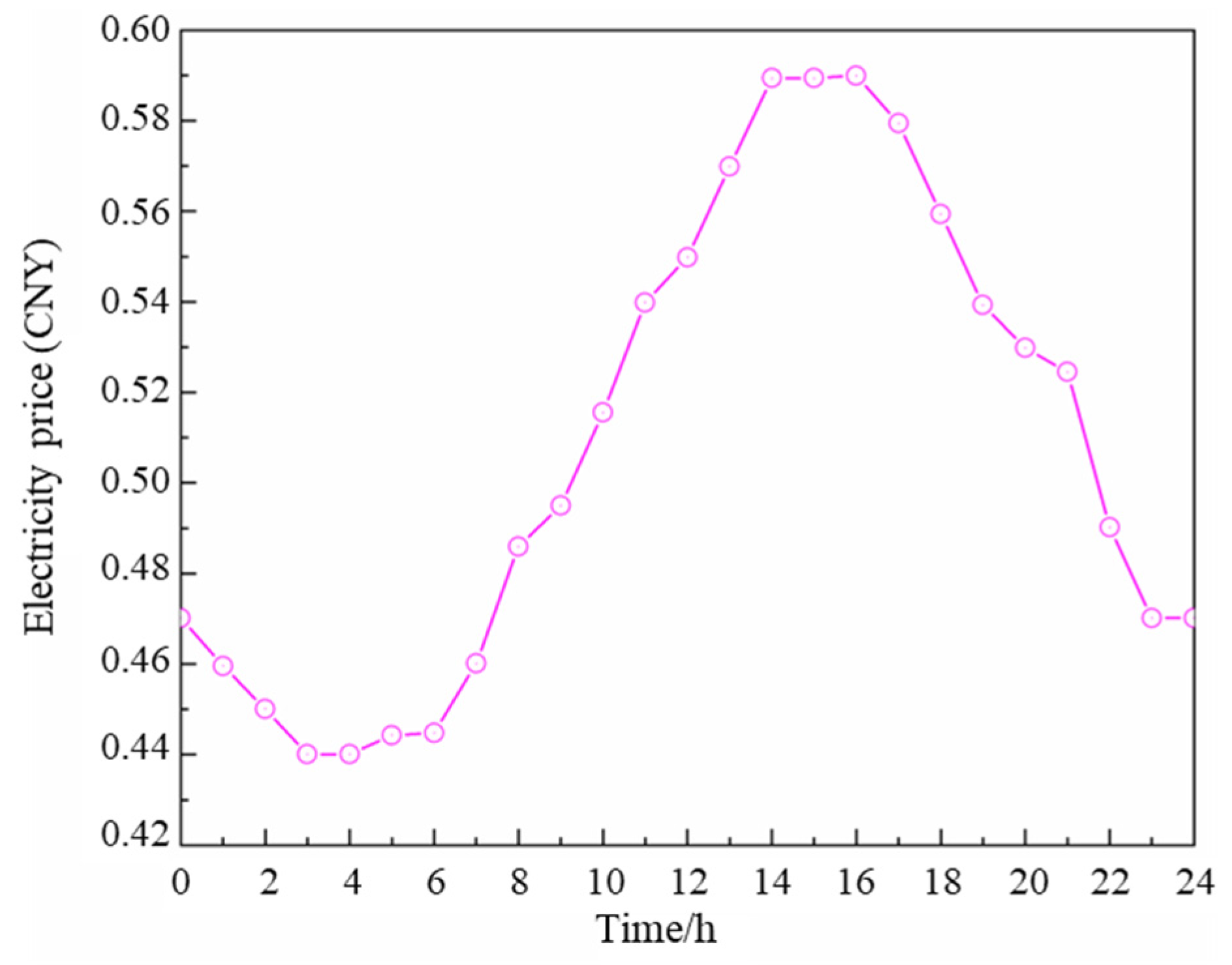
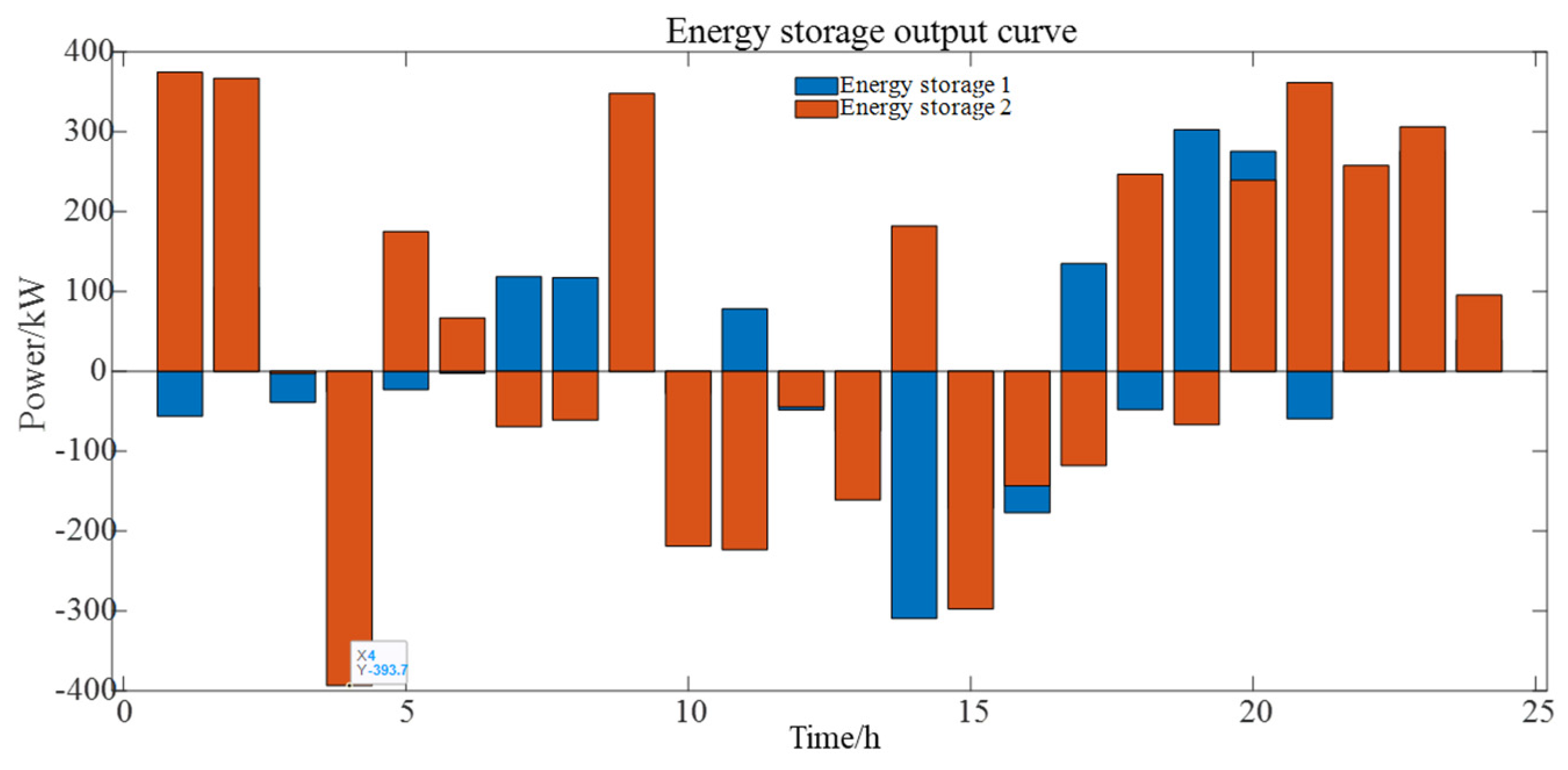

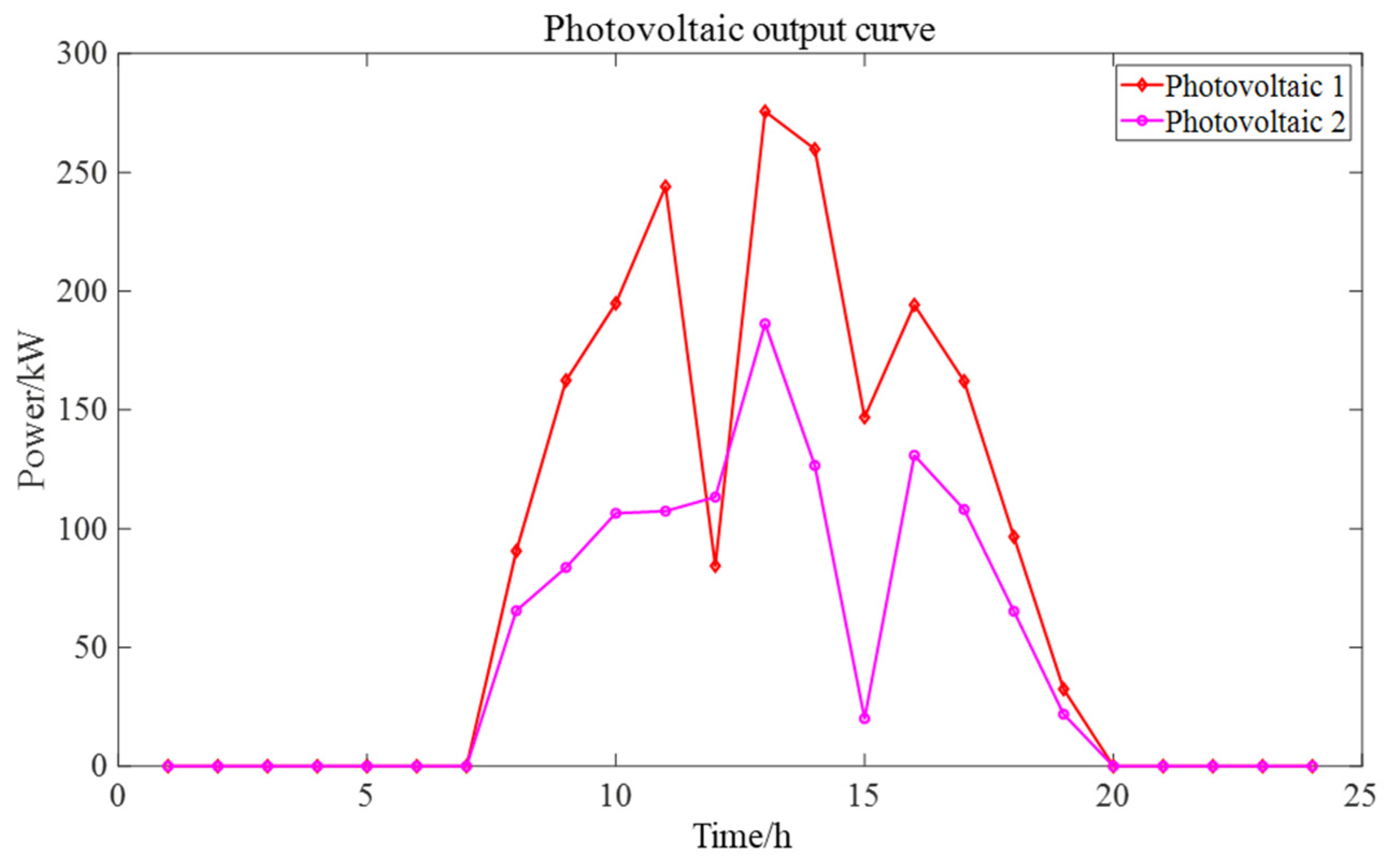

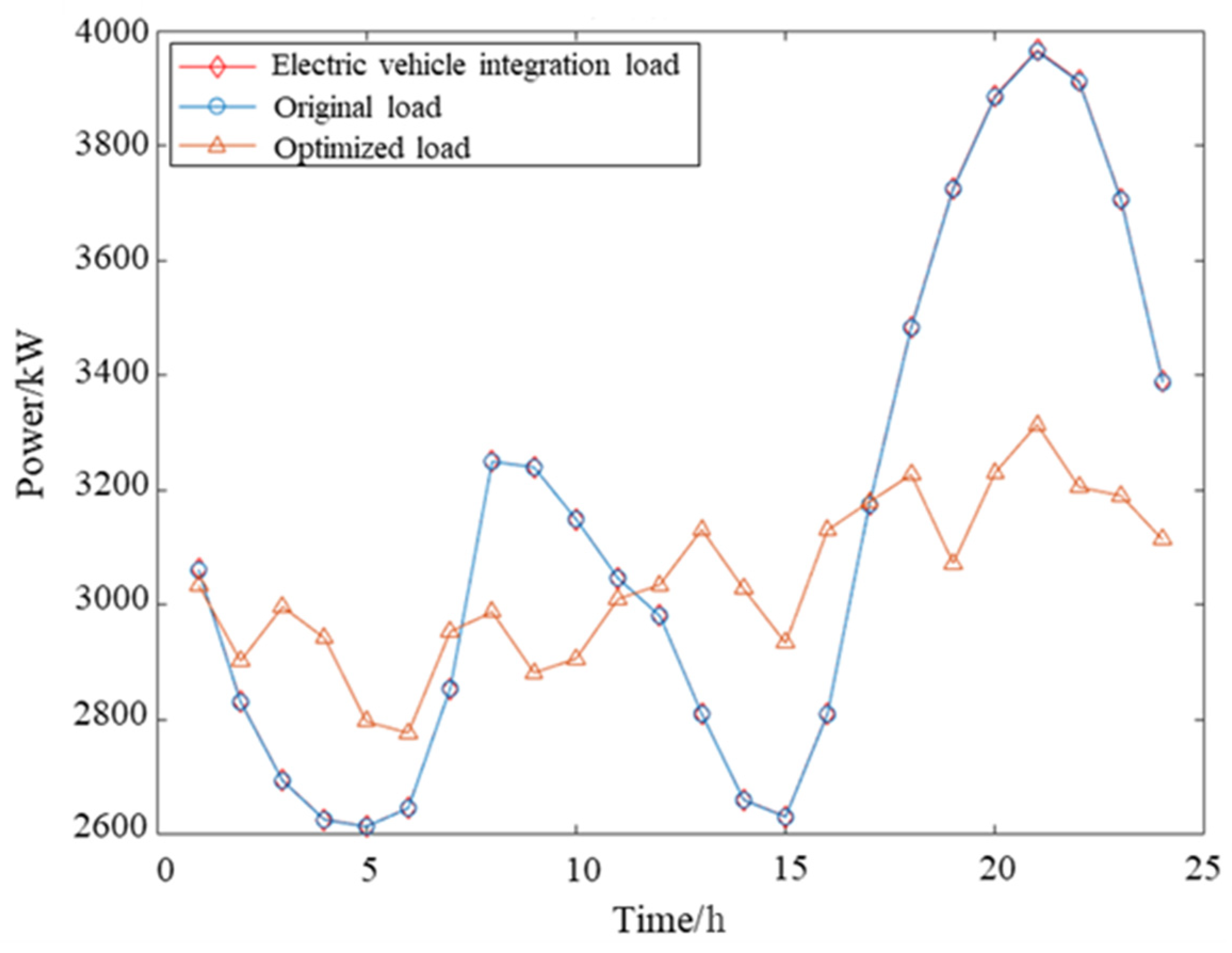
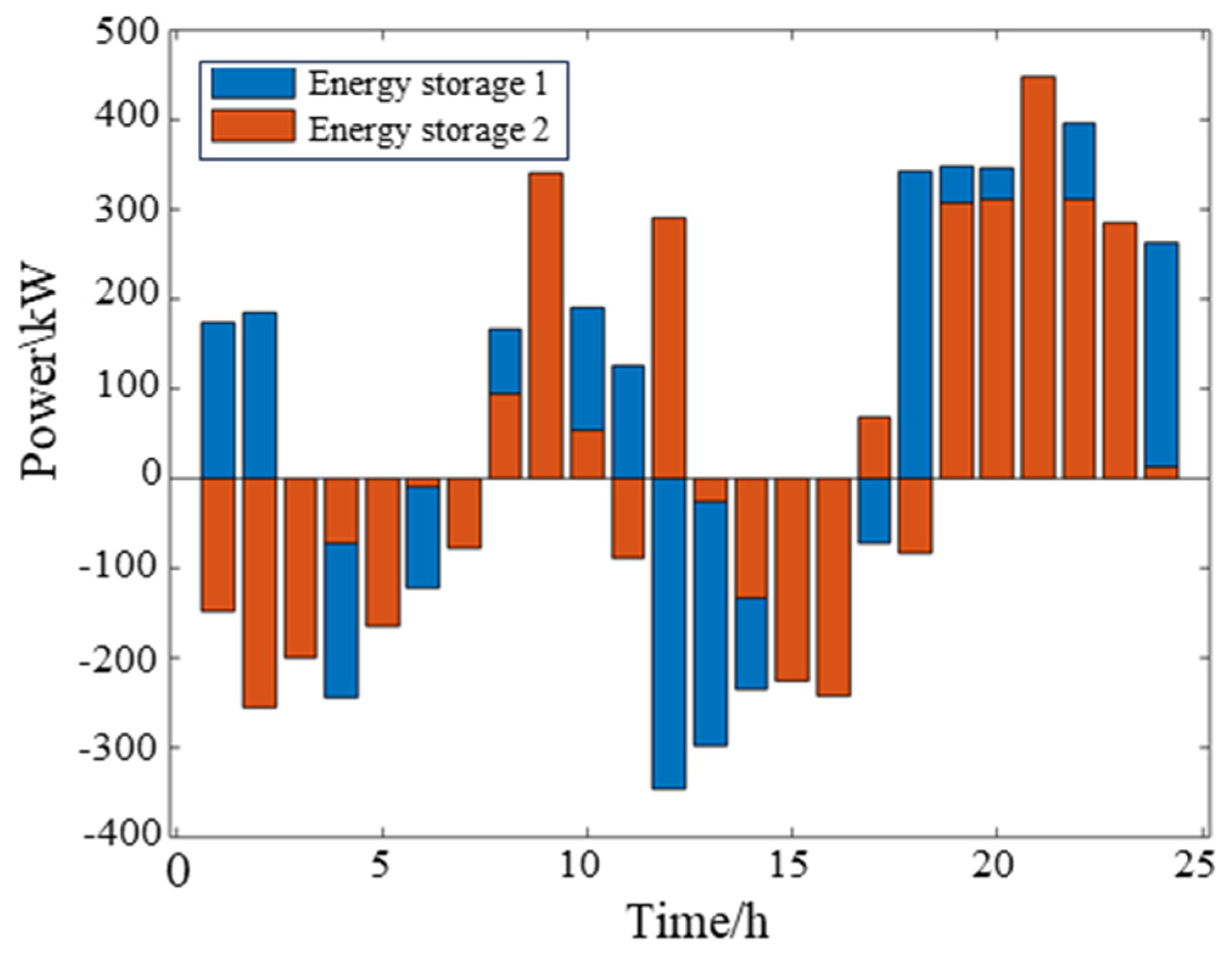


| Photovoltaic (kW) | Energy Storage (kWh) | Electric Vehicle (kW) |
|---|---|---|
| Node 18: 381.1 (400) | Node 6: 517.5 (500) | Node 1: 259.1 (250) |
| Node 24: 200.1 (200) | Node 13: 537.9 (500) | Node 20: 247.5 (250) |
| Algorithm | Minimum Fitness Value | Number of Iterations | Computation Time(s) |
|---|---|---|---|
| Improved PSO | 0.603 | 289 | 19.65 |
| PSO | 0.712 | 472 | 29.08 |
| GA | 0.725 | 392 | 28.66 |
| SOA | 0.734 | 413 | 34.75 |
| Distribution Network | Optimized Total Line Losses (MWh) | Savings in Network Loss Costs (CNY) |
|---|---|---|
| IEEE-33 | 1406.7 | 311,000 |
| IEEE-118 | 4185.2 | 902,000 |
| DTU | 1828.7 | 429,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Yan, J.; Xie, P.; Zhai, P.; Tao, Y. Power System Loss Reduction Strategy Considering Security Constraints Based on Improved Particle Swarm Algorithm and Coordinated Dispatch of Source–Grid–Load–Storage. Processes 2025, 13, 831. https://doi.org/10.3390/pr13030831
Zhang S, Yan J, Xie P, Zhai P, Tao Y. Power System Loss Reduction Strategy Considering Security Constraints Based on Improved Particle Swarm Algorithm and Coordinated Dispatch of Source–Grid–Load–Storage. Processes. 2025; 13(3):831. https://doi.org/10.3390/pr13030831
Chicago/Turabian StyleZhang, Shuolin, Jiongcheng Yan, Pengteng Xie, Pengming Zhai, and Ye Tao. 2025. "Power System Loss Reduction Strategy Considering Security Constraints Based on Improved Particle Swarm Algorithm and Coordinated Dispatch of Source–Grid–Load–Storage" Processes 13, no. 3: 831. https://doi.org/10.3390/pr13030831
APA StyleZhang, S., Yan, J., Xie, P., Zhai, P., & Tao, Y. (2025). Power System Loss Reduction Strategy Considering Security Constraints Based on Improved Particle Swarm Algorithm and Coordinated Dispatch of Source–Grid–Load–Storage. Processes, 13(3), 831. https://doi.org/10.3390/pr13030831






