Abstract
A new molecular theory of slag suggests that complex oxides in the phase diagram are also present in liquid slag. In contrast to the ion‒molecule coexistence theory, basic oxides (CaO, MgO, MnO, FeO, etc.) in slag are considered to agglomerate in the liquid state due to their strong mutual attraction, although they are ionized (M2+ and O2−). The predicted slag structure agrees with the experimental results, and when the model is applied to the CaO-SiO2, CaO-Al2O3, and CaO-SiO2-Al2O3 slag systems, the calculated molar fractions of CaO, SiO2, and Al2O3 () are close to the measured activities () reported by different researchers. In the CaO-Al2O3 slag system, the results based on the new molecular theory are closer to the experimental values than the results of other theoretical calculations. In the practical application of the new molecular theory, the maximum concentration of each complex molecule is consistent with the position of the melting point of the same solid‒liquid components in the phase diagram, indicating that complex molecules have a strong influence on the melting point of slag. In addition, it is believed that the formation and decomposition of different complex molecules are responsible for changes in component activity in the CaO-SiO2 and CaO-Al2O3 slag systems, and it is further deduced that 3CaO-SiO2 is formed in two steps.
1. Introduction
Slag is irreplaceable in the metallurgical smelting process and substantially impacts the occurrence of smooth smelting, the chemical composition of the metal, aspects related to production technology, and economic indicators [1,2,3,4]. The above functions can be modified by controlling the slag temperature, viscosity, chemical composition, electrical conductivity, surface tension, and other physicochemical properties during production [5,6]; notably, the structure of slag is closely related to its physical and chemical properties [7].
Slag systems of simple oxides such as CaO-SiO2, CaO-Al2O3, and CaO-SiO2-Al2O3 are particularly important as the basic slag systems in ferrous metallurgy. Many domestic and international scholars have studied the structures of such slag systems and determined the activity of each component in the system. For example, Chipman [8] et al. studied the equilibrium between C-saturated Fe liquid and the above slag systems by using the “slag-metal” equilibrium method to obtain the activity of SiO2, and the activity of other components was calculated via the Gibbs‒Duhem integral method. Zhang et al. [9] used the slag‒gold equilibrium method to determine the CaO activity of CaO-SiO2-Al2O3 in equilibrium with metallic Sn and plotted the iso-CaO activity curve. The activities of CaO, SiO2, and Al2O3 in the CaO-SiO2-Al2O3 slag system were directly determined by Koji Mihonki and Yasuo Omor [10] using the electromotive force method with a concentration cell. Uchida et al. [11] measured the MnO activity in a CaO-MnO-SiO2 ternary slag system at 1400 °C via a steel-slag equilibrium test. Ding [12] analyzed the relationship between slag systems and the alloy equilibrium reaction in the smelting process of a ferromanganese alloy via slag-gold and gas-slag-gold equilibrium experiments. However, the structure of slag melt is very complicated at high temperatures, and the experimental conditions required to measure the activity of slag components differ, resulting in differences in the activity values obtained by different researchers. The basic slag system in blast furnace iron making and molten steel refining is CaO-SiO2-Al2O3; thus, the activity of these slag system components was measured by former Soviet scholars and Japanese scholars [13], but the measured values substantially differ. Later, Kay and Zou et al. carried out further research on this slag system; the results differed to a certain degree from the experimental data obtained by other researchers, but the range of deviation was small [14,15]. Therefore, it is very important to determine the activity of each component in slag according to its existence form in the slag.
At present, methods for directly observing slag structure through experimental techniques are not mature, but slag solutions can be assumed to have a certain microstructure according to thermodynamic theory, and the activity of each component in slag can be studied by establishing a structure theory of slag. At present, the widely used slag theories are shown in Table 1 as follows: (1) Ion theory [16]. This theory was proposed by Herasymenko and suggests that liquid slag consists of simple ions and complex ions, which have a strong covalent bonding structure and change with the composition of the slag. This theory describes the interslag reaction well, but it ignores the electrostatic potential between different charges, which can lead to an uneven distribution of anions and cations. However, the more widely used Masson model is difficult to calculate in the case of ternary or multivariate slag systems [17]. (2) Molecular theory [18], proposed by H. Schenck and further developed by J. Chipman. The structure of the liquid slag is believed to be the same as that of slag in the solid state, and the slag can be viewed as an ideal solution consisting of various molecule-like plasmas, i.e., it is an ideal solution consisting of each electrically neutral simple oxide molecule and complex compounds, and the two types of molecules reach equilibrium at different temperatures. The molecular theory suggests that the combination of acidic and basic oxides is complete in the liquid slag system, so the activity of the acidic oxide molecules SiO2 and P2O5 and other components’ activity is considered to be zero in basic slag systems. In the early stage of development of this molecular theory, computer programs were not sufficiently advanced to solve multiple higher-order equations. Therefore, for ternary and higher-order liquid slag systems with high alkalinity, it is assumed that the activity of acidic oxides is zero and that alkaline oxides and acid oxides completely react to form complex oxides; under this assumption, an ideal solution is formed. The molar fraction of alkaline oxides calculated on this basis is equal to the activity, but crucially, the activity of acidic oxides cannot be approximated to zero. Nevertheless, at the time, the occurrence and trend of chemical reactions between slag and steel were well explained by the activity of the desired alkaline oxides. (3) The coexistence theory [19]. This theory was first proposed by the Soviet scholar Chuyikau and later improved by the Chinese scholars Zhang et al. Molecules and ions are assumed to coexist in slag on the basis of differences in crystallization chemistry and slag conductivity. Coexistence theory suggests that slag consists of simple ions (Mi+ and O2−) formed by the ionization of alkaline oxides in the liquid state, acidic oxide molecules, such as SiO2, P2O5, etc., and complex compound molecules, such as silicates, phosphates, etc.; that there exists a dynamic equilibrium between simple ions and molecules; and that chemical reactions between ions ionized from alkaline oxides in the slag, acidic oxide molecules, and complex compound molecules obey the mass action law. This theory allows the calculation of the concentration of the role of structural units in all multivariate slag systems under the assumption of the simultaneous presence of molecules and ions in the slag. According to the coexistence theory, the alkaline oxides CaO, MgO, MnO, FeO, and CaF2 in slag are assumed to be in the form of (Ca2+ + O2−), (Mg2+ + O2−), (Mn2+ + O2−), (Fe2+ + O2−), and (Ca2+ + 2F−), respectively.

Table 1.
Advantages and limitations of various slag theories.
In the above theories, the coexistence theory and the molecular theory assume that the formation of complex compounds of acidic and basic oxides yields an ideal solution, under which conditions the molar fractions of basic oxides, acid oxides, and complex compound molecules are equal to the so-called activity. There are two differences between the coexistence theory and the molecular theory, one of which is that the molecular theory regards all alkaline oxides, such as CaF2, CaS, etc., as one molecule, whereas the coexistence theory regards alkaline oxides such as (Ca2+ + O2−), (Mg2+ + O2−), (Mn2+ + O2−), and (Fe2+ + O2−) after ionization as two units, while the (Ca2+ + 2F−) and (Ca2+ + S2−) formed after the ionization of CaF2 and CaS are regarded as three units and two units, respectively. The total number of moles in the system is calculated on the above basis, e.g., the mole fraction of alkaline oxides is calculated by dividing the number of moles of alkaline oxides by two times the total number of moles. The second difference is that the theory of coexistence arose along with the development of computers and has been gradually perfected. More than three systems can be used to solve the multivariate higher-order equations through modern computer programs, and the principle of chemical equilibrium can be used to accurately calculate the number of complex compounds. Then, the activity of the acidic oxides can be obtained by later using the principle of ideal solutions to find the mole fraction of each group element. Because the molecular theory cannot explain the conductivity of slag [20], few scholars have studied this theory since the 1970s; however, because the charges of positive and negative ions in slag are always equal, and it is assumed that the content of each component in the liquid state is the same as that in the solid state, with the only difference being the state itself. Given the high degree of precision of current calculation methods, the original molecular theory can be used to accurately calculate the mole fraction of each acidic oxide and basic oxide component at different temperatures in equilibrium with the corresponding complex compound, that is, the so-called activity of these components. This theory is defined as the “new molecular theory”.
Notably, regardless of whether the ion‒molecule coexistence theory or the new molecular theory is used, if the activity of a simple molecule can be calculated on the basis of chemical equilibrium, the concept of component activity in the slag will no longer be valid, which is a very bold hypothesis and needs to be verified by many calculations. In addition, thus far, it has not been possible to experimentally determine or observe various compounds in liquid slag and their states of existence according to the new molecular theory or coexistence theory. At present, the thermodynamic theory still assumes that compounds exist in the form of molecules in the liquid state and that acidic and alkaline compounds form complex compounds to calculate the activity of components. The accuracy of the calculation is largely determined by the choice of complex compounds or the source of thermodynamic data, which may affect the universality and accuracy of the theory.
Based on the molecular theory and coexistence theory, the new molecular theory assumes that all complex oxides in the solid state in the phase diagram are present in the liquid slag. Because the positive and negative charges in the slag are equal, even if basic oxides (CaO, MgO, etc.) are ionized, positive and negative ions are still attracted to each other, and they are still a whole in the liquid state. The slag formed by acidic and basic oxides is an ideal solution, which is not affected by the problem of molecular ions. However, is the activity calculated using the new theory more accurate than that calculated using the coexistence theory? Here, first, the K values of the standard Gibbs free energies used by different researchers are used in the model based on the new molecular theory, and the most suitable K value is determined. The experimental results of Zhang, Zou, and Chipman in different slag systems are used to verify the feasibility of the new molecular theory. A comparison of the new molecular theory with the molecular theory and other theories demonstrates the applicability and accuracy of the new molecular theory. Finally, the theory is applied to the CaO-SiO2 and CaO-Al2O3 slag systems. The main objective of this study is to synthesize the advantages of the molecular theory and coexistence theory and propose a new molecular theory that is more in line with the actual situation to better complement the coexistence theory.
2. Calculation Model of Basic Slag Activity
2.1. Theoretical Assumptions
In the new molecular theory proposed in this paper, the activity of slag components is calculated on the basis of multivariate multiphase equilibrium among metallurgical processes. Here, the CaO-SiO2 slag system is taken as an example to demonstrate the following assumptions regarding structural units of the liquid slag:
- (1)
- The slag structure is composed of simple molecules of CaO and SiO2 and complex molecules of CaO·SiO2, 2CaO·SiO2, and 3CaO·SiO2, which are collectively referred to as different structural units, and these structural units form an ideal solution.Note: The simple molecules CaO and SiO2 and the complex compound molecules CaO·SiO2, 2CaO·SiO2, and 3CaO·SiO2 considered in the new molecular theory are called structural units rather than molecules per se. There is a debate that CaO may ionize to (Ca2+ + O2−). This complex compound is also called a structural unit here because its existence cannot currently be observed experimentally but is only a hypothesis.
- (2)
- At a given temperature, the formation and decomposition of various oxides and their structural units are balanced, resulting in the formation of complex compounds, and these chemical reactions follow the mass action law.
- (3)
- The various structural units in the slag change continuously within the selected concentration range, exhibiting continuity; that is, no phase change occurs.
- (4)
- Under the above three assumptions, each structural unit in the slag follows the ideal solution model, and the mole fraction of a structural unit representing a simple molecule is equal to the activity of the molecule.
2.2. The Calculation Model of the Mass Action Concentration of Structural Units in the Fundamental Slag System
Since the CaO-SiO2, CaO-Al2O3, and CaO-Al2O3-SiO2 slag systems are the fundamental slag systems in iron and steel metallurgy and experimental data on these systems are the most abundant, they were selected to verify the accuracy of the new molecular theory. The theoretical results of the new molecular theory for these three systems were then compared with previously reported experimental results.
- 1.
- CaO-SiO2 slag system
According to the new molecular theory, the initial numbers of moles of each oxide in the CaO-SiO2 slag system are defined as b1 = and b2 = , and these values are considered to represent the initial chemical composition of the slag. In the binary phase diagram shown in Figure 1, three complex molecules, CaO-SiO2, 2CaO-SiO2, and 3CaO-SiO2, exist in the solid state, and these three molecules are also considered to exist as structural units in the liquid slag at 1873 K.
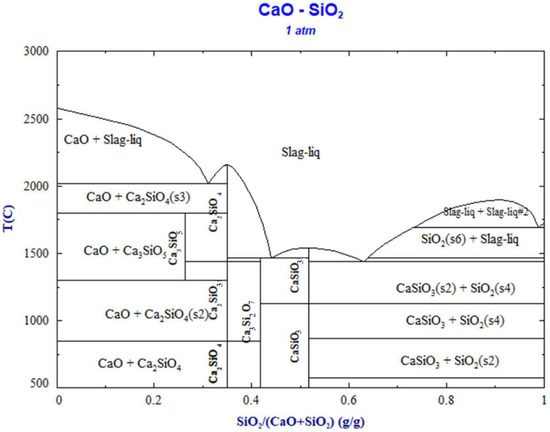
Figure 1.
Phase diagram of CaO-SiO2.
All simple and complex molecules in the slag and their chemical reactions are shown in Table 2 and Table 3. The total equilibrium molarity of all structural units in 100 g of slag can be expressed as

Table 2.
Structural unit definitions and mass action concentrations in CaO-SiO2 slag according to the new molecular theory.

Table 3.
Chemical reactions that may produce complex molecules in CaO-SiO2 slag.
The mass action concentration Ni for a structural unit in a closed system, i.e., the ratio of the number of moles of structural units i to the total number of moles of all structural units at reaction equilibrium, is calculated via Equation (2). The equations defining Ni for all simple and complex molecules in the CaO-SiO2 slag system are included in Table 2.
Equations (3)–(5) can be obtained from the new molecular theory and include three unknown parameters (, , and ) and three independent equations. The unique solution can be obtained by using the fsolve function of Matlab R2022b.
- 2.
- CaO-Al2O3 slag system
To study the activity of each structural unit in the CaO-Al2O3-SiO2 ternary slag system, it is necessary to systematically study CaO-Al2O3 slag systems containing a larger number of complex compounds. According to the new molecular theory, the initial numbers of moles of each oxide in the CaO-Al2O3 slag system are defined as b1 = and b2 = , which correspond to the initial chemical composition of the slag. The binary phase diagram of CaO-Al2O3 shown in Figure 2 reveals five complex molecules, CaO·Al2O3, CaO·2Al2O3, CaO·6Al2O3, 3CaO·Al2O3, and 12CaO·7Al2O3 [22].
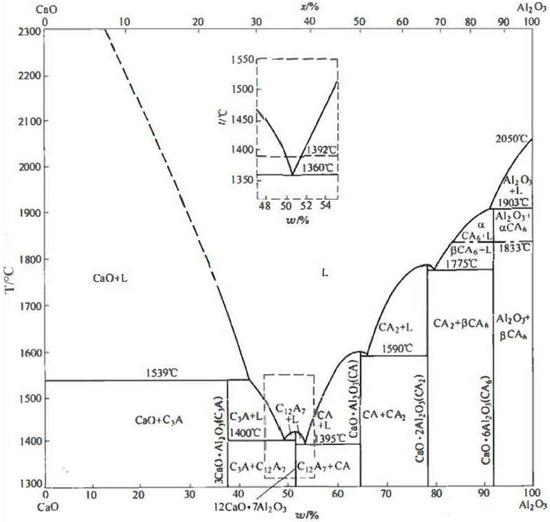
Figure 2.
CaO-Al2O3 phase diagram [22].
The mass action concentration (or molar fraction) of Ni for each structural unit can be calculated from Equation (2). The obtained expressions for all structural units of Ni in the CaO-Al2O3 slag system are presented in Table 4, and the reaction equations are presented in Table 5.

Table 4.
Structural unit definitions and mass action concentrations in CaO-Al2O3 slag based on the new molecular theory.

Table 5.
Chemical reactions that may form complex molecules in CaO-Al2O3 slag.
Under the assumptions of the new molecular theory, two material balance conditions, Equations (6) and (7), and the normalized total mole fraction shown in Equation (8) can be established.
- 3.
- CaO-Al2O3-SiO2 slag system
According to the new molecular theory, the initial molarity of each oxide in the CaO-SiO2-Al2O3 slag system can be defined as b1 = , b2 = , and b3 = , which correspond to the initial chemical composition of the slag. The CaO-SiO2-Al2O3 ternary phase diagram shown in Figure 3 reveals that 11 complex compound molecules exist in the slag in the solid state: CaO·SiO2, 2CaO·SiO2, 3CaO·SiO2, CaO·Al2O3, CaO·2Al2O3, CaO·6Al2O3, 3CaO·Al2O3, 12CaO·7Al2O3, 2CaO·Al2O3·SiO2, CaO·Al2O3·2SiO2, and 3Al2O3·2SiO2 [22].

Figure 3.
Phase diagram of CaO-SiO2-Al2O3 [22].
The Ni of structural units in slag can be calculated via Equation (2). The definitions of Ni for simple and complex molecules in the CaO-SiO2-Al2O3 slag system are given in Table 6, and the reaction equations are presented in Table 7.

Table 6.
Structural unit definitions and mass action concentrations in CaO-SiO2-Al2O3 slag based on the new molecular theory.

Table 7.
Chemical reactions that may form complex molecules in CaO-SiO2-Al2O3 slag.
Three material balance equations (Equations (9)–(11)) and the normalized equation of the total molar fraction (Equation (12)) can be obtained using the new molecular theory.
2.3. Principle of Standard Free Energy Selection for Complex Molecular Reactions
Due to the controversy over whether the components in liquid slag are molecules or ions, the new molecular theory defines any component, i, as a structural unit, which is represented by Ni. The physicochemical significance of Ni is consistent with the activity of a traditional slag element, i, and there is a corresponding standard state in liquid at a high temperature. Its activity is characterized by the pure solid or pure liquid state corresponding to the and values that result in complex reactions, as shown in Table 2, Table 4 and Table 6.
For group element i, different standard states are chosen, corresponding to different values and equilibrium constants, K. Theoretically, the choice of standard state is determined by the available thermodynamic data (). Reported standard Gibbs free energy values vary, corresponding to one of four scenarios: (1) The standard Gibbs free energy used by Zhang [25,26] and Chipman [8] is directly used in most studies [27,28] to determine the K value. (2) Yang [29,30] considered the existence state of slag components at a high temperature and calculated the Gibbs free energy of the pure solid and pure liquid as the standard states. The value for the reaction of complex CaO·SiO2 molecules generated in the CaO-SiO2 slag system is taken as an example as follows:
- (1)
- The standard state of component i is a pure liquid. Since the melting point of CaO is 2845 K and the temperature of the general slag is approximately 1873 K, which is far lower than the melting point of CaO, CaO is dissolved in the slag in a liquid state. Either pure liquid CaO or pure solid CaO must be chosen as the standard state. If liquid CaO is selected as the standard state for subsequent conversion, CaO, SiO2, and CaO·SiO2 melt from the solid state to a virtual liquid state, and their free energy changes are shown in Equations (13), (15) and (17), respectively.
While
According to Equations (13)–(19), the standard Gibbs free energy of CaO and SiO2 and the reaction when the slag is a pure liquid are as follows:
- (2)
- If the pure solid state is taken as the standard state, reaction (23) becomes Equation (21), where CaO, SiO2, and CaO·SiO2 change only in terms of expression, from a solid pure substance not in the slag to a solid pure substance in the slag, and there is no substantial change.
Equations (20) and (21) indicate that when different standard states are selected, the calculated K values are 189.154 and 187.623, which are very similar. Therefore, the K values of the components in the slag are almost unchanged regardless of whether a pure liquid or pure solid is selected as the standard state. In the CaO-SiO2 slag system, when the temperature is 1873 K and the pure solid state is taken as the standard state, the equilibrium constants of the CaO·SiO2, 2CaO·SiO2, and 3CaO·SiO2 reactions are K1 = 338.797, K2 = 13019.749, and K3 = 4607.123, respectively. This is basically consistent with the calculated values of Duan [30] and Li [31] et al.
- (3)
- Zhang divided the CaO-SiO2 slag system into four intervals: below 1523 K, in the range of 1523‒1737 K, in the range of 1737‒2073 K, and above 2073 K. Different standard Gibbs free energies were used to calculate the equilibrium constant K values of the reactions, and the results were slightly different [21].
Eight different components of the CaO-SiO2 slag system at an experimental temperature of 1873 K were selected to calculate their activities using a model established based on the new molecular theory, and the Gibbs free energy values used in model calculations in different studies were compared with the experimentally obtained activity [8,21,29,32], as shown in Figure 4. In the CaO-SiO2 slag system, the activity calculated by using the standard Gibbs free energy used by Zhang and Chipman in the model has the best agreement with the experimental results, which indicates that the activity calculation model based on the new molecular theory can accurately calculate the activity of slag components when appropriate Gibbs free energy data are selected. For the CaO-Al2O3 and CaO-SiO2-Al2O3 slag systems, the standard Gibbs free energy used in this study is used.
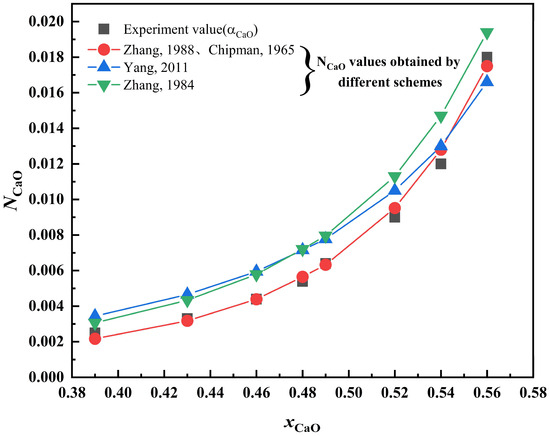
Figure 4.
Comparison between NCaO values obtained by different schemes and measured in experiments [8,21,29,32].
3. Results and Discussion
3.1. Comparison of Component Activity with Actual Activity Based on New Molecular Theory
Equation (2) indicates that the physical meaning of Ni is the equilibrium molar fraction of structural unit i in the closed system, that is, the activity of component i in the slag. The CaO-SiO2 and CaO-Al2O3 slag system models derived by using the new molecular theory described in Equation (2) are shown in Figure 5 for the correct standard free energy of the complex compound formation. For both the CaO-SiO2 slag system and the CaO-Al2O3 slag system, the mole fraction of the CaO structural unit calculated using the new molecular theory is the same as the measured value, but for the CaO-Al2O3 slag system, when the activity of CaO is greater than 0.5, there is a large deviation from the research results of Zou. The results show that the theory has good accuracy.
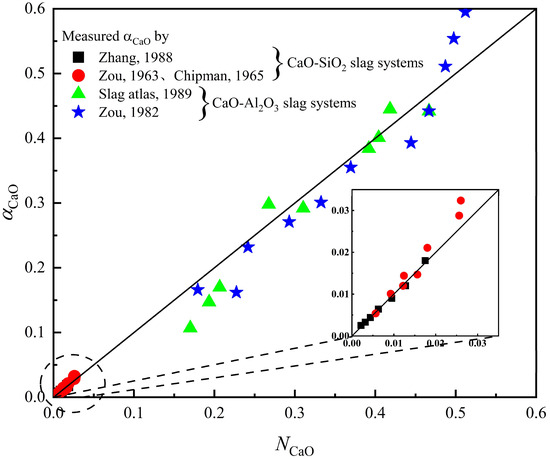
Figure 5.
The measured activity values in the CaO-SiO2 and CaO-Al2O3 slag systems and values calculated via the current model [8,15,21,33,34].
3.2. Limitations of Molecular Theory
The early molecular theory suggested that the combination of acidic and basic oxides is complete. Due to the complex state of existence of slag compounds and the difficulty of determining this state using existing analytical methods, the complex molecules in the slag are all assumed to be in the solid state. In the case of binary systems where more than one complex molecule can be formed in the solid state, only one molecule can be selected for calculations.
For example, when using molecular theory to calculate the FeO activity in slag composed of , , , , , and , due to the limitations of the calculation tools available when the theory was developed, three basic oxides, CaO, MgO, and MnO, are combined into CaO, which is collectively denoted as RO. It is assumed that only one compound, 2RO·SiO2, is generated in the RO-SiO2 binary system, and only one compound, 4RO·P2O5, is generated in the RO-P2O5 binary system. The structural units in the system are thus RO, FeO, 2RO·SiO2, and 4RO·P2O5. The amount of each oxide substance in 100 g of slag is as follows:
Since the complex compound formation reaction is complete,
The amount of RO remaining in the slag is
The total number of moles of each structural unit in the system is
The activity of RO is calculated as
The activity of FeO is
Thus, the early molecular theory can only combine the three basic oxides of CaO, MgO, and MnO into RO when calculating the activity of multicomponent systems and can only choose one of the multiple complex compounds that may be formed through combination with acidic oxides. Taking the binary CaO-SiO2 system as an example, we determined the difference between the calculated activity and the experimental activity [8,15] when only one of the three complex combinations of CaO·SiO2, CaO·2SiO2, and CaO·3SiO2 is selected, and the results are shown in Table 8.

Table 8.
The activity of the CaO-SiO2 slag system under the molecular theory and the activity of various complex molecules, wherein (1) includes only CaO·SiO2, (2) includes only CaO·2SiO2, and (3) includes only CaO·3SiO2.
As shown in Table 8, the values calculated using the molecular theory differ greatly from the actual measurements [8,15]. However, when the complex molecular activity of the system is calculated via the new molecular theory, the values of and are much greater than the activities of other slag components, and the mass action concentration cannot be ignored. In other words, if complex molecules with a larger action concentration are brought into the model, the error is reduced, as shown in Figure 6.
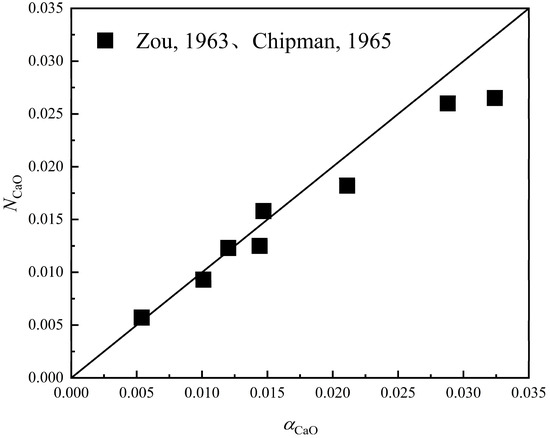
Figure 6.
A comparison of the values of CaO·SiO2 and 2CaO·SiO2 in the new molecular theory with actual measurements [8,15].
3.3. Verification of the New Molecular Theory by Comparison with Different Theories
From the above, it can be seen that the accuracy of the molecular theory depends largely on the selection of complex molecules, which is difficult to apply in practice; although the ionic theory describes the slag–steel reaction better, the Masson model, which is widely used, is difficult to compute in the case of multivariate slag systems. Therefore, in this section, the accuracy of the new molecular theory is investigated by using the coexistence theory and the new molecular theory for comparative validation in the CaO-SiO2 [8,15,21], CaO-Al2O3 [33,34], and CaO-SiO2-Al2O3 [9,28,34] slag systems. The results for the basic slag system are shown in Figure 7.
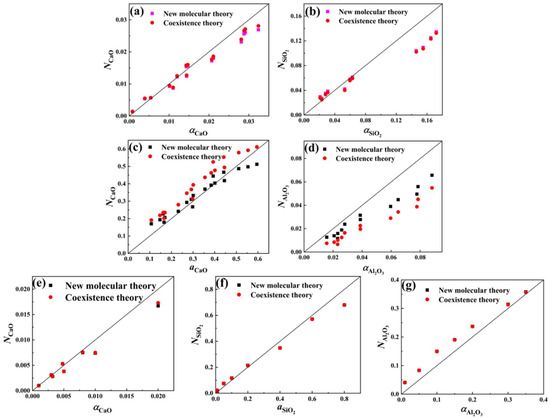
Figure 7.
(a,b) The measured and calculated activities of basic components in the CaO-SiO2 slag system; (c,d) the measured and calculated activities of basic components in the CaO-Al2O3 slag system; (e–g) the measured and calculated activities of basic components in the CaO-SiO2-Al2O3 slag system.
The above figure shows that in the CaO-SiO2 slag system, most of the calculated and experimental values of the new molecular theory and the coexistence theory correspond well, and the error rates of the two theories are close to each other, so it is impossible to know which theory has better accuracy. For the CaO-Al2O3 slag system, the results obtained using the new molecular theory are closer to the experimental results than the results obtained based on the coexistence theory, and the error rate is smaller than that of the experimental data in the literature. For the CaO-SiO2-Al2O3 ternary slag system, the values calculated via the new molecular theory and coexistence theory are close to the experimental values, with similarly small error rates for the two theories.
3.4. Practical Application of New Molecular Theory
- (1)
- The relationship between complex molecules and the melting point of slag
To verify the change in the combined concentration of complex molecules in the CaO-SiO2 and CaO-Al2O3 slag systems with slag components, different initial slag components were set at 1873 K, and the activity of different slag components after the slag systems were balanced is shown in Figure 8. As shown in the figure, the combined concentration of complex molecules in different slag systems first increases and then decreases with increasing %SiO2 or %Al2O3, and the change trend is the same across different systems. The initial slag composition corresponding to the highest combined concentration of different complex molecules is consistent with the melting point of the complex molecules in the solid and liquid phases of the slag system diagram (Figure 1 and Figure 2), which also indicates that the complex molecules have a very important influence on the melting point of the slag [21].
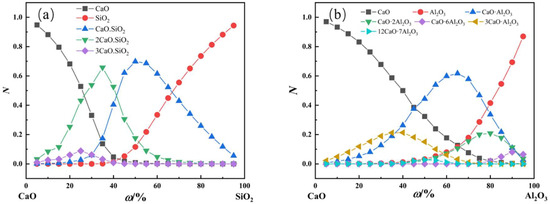
Figure 8.
(a) Changes in the action concentration of the CaO-SiO2 slag system with respect to %SiO2 at 1600 °C; (b) changes in the action concentration of the CaO-Al2O3 slag system with respect to %Al2O3.
- (2)
- Changes in the CaO-SiO2 slag system components with different alkalinity
The temperature of the CaO‒SiO2 slag system is set to 1873 K, and the alkalinity is defined as the binary alkalinity, . The activity of different components of the slag system varies with alkalinity, as shown in Figure 9. The ratio is the largest when the alkalinity is low, indicating that the slag consists mainly of CaO·SiO2 when the system reaches equilibrium. When the alkalinity is less than 1.4, increases with increasing alkalinity, but shows the opposite trend. However, the magnitude of these changes is small. When the alkalinity is greater than 1.4, the trend becomes more obvious, and reaches a maximum. When the alkalinity reaches 1.4, CaO reacts with some CaO·2SiO2 to produce CaO·3SiO2, but the scale of the reaction is small, resulting in an increasing trend and decreasing trend, while CaO·2SiO2, as an “intermediate product”, reaches a maximum value. This indicates that with increasing basicity, CaO·3SiO2 is formed in two steps, as shown in Equations (22) and (23). First, CaO reacts with CaO·SiO2 to form CaO·2SiO2, and then CaO reacts with CaO·2SiO2 to form CaO·3SiO2.
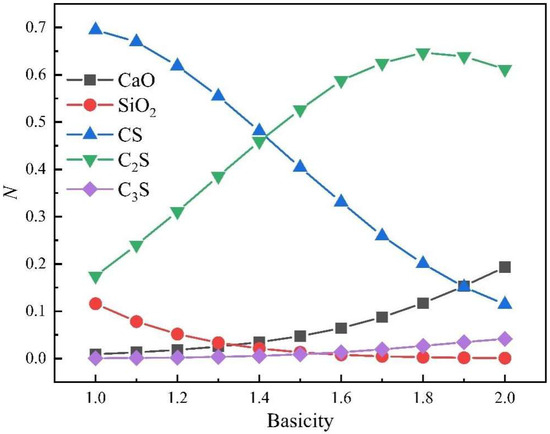
Figure 9.
The activities of different components in the CaO-SiO2 slag system at different alkalinities. CS, C2S, and C3S represent CaO·SiO2, 2CaO·SiO2, and 3CaO·SiO2, respectively.
- (3)
- Variations in CaO-Al2O3 slag system components with different calcium‒aluminum ratios
The temperature was set to 1873 K, and the calcium‒aluminum ratio was defined as . The activity of different components of this slag system with varying calcium‒aluminum ratios is shown in Figure 10. As the calcium‒aluminum ratio rises, increases while decreases, but the activity values are negligible, indicating that the degree of reaction of Equations (2) and (5) in Table 5 is small. When the calcium‒aluminum ratio is less than 1.5, and increase, whereas decreases by the same amount. The main reason for this is evident from Equation (24): CaO molecules react with each other to form 3CaO·Al2O3.
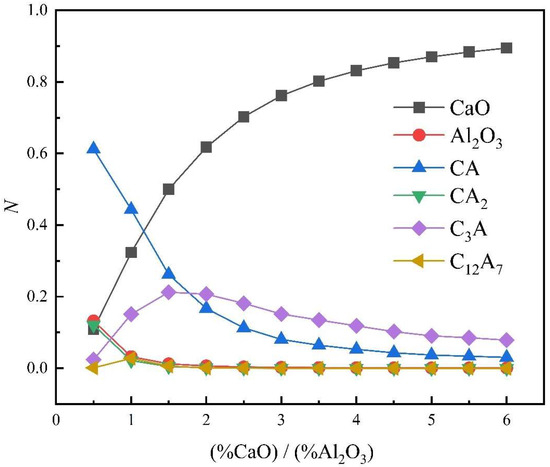
Figure 10.
Activities of different groups of elements in CaO-Al2O3 slag systems with different calcium‒aluminum ratios. CA, CA2, C3A, and C12A7 represent CaO·Al2O3, CaO·2Al2O3, 3CaO·Al2O3, and 12CaO·7Al2O3, respectively.
4. Conclusions
The calculated results of this new molecular theory are compared with the experimental values reported in the literature and the calculated values of other theories, and the theory is tested in the CaO-SiO2, CaO-Al2O3, and CaO-SiO2-Al2O3 slag systems for practical application. The main conclusions can be summarized as follows:
- (1)
- The calculated value based on the new molecular theory is very close to the measured value in different slag systems (CaO-SiO2 and CaO-Al2O3 slag systems). Through the application of the new molecular theory, the limitations of the earlier molecular theory are identified.
- (2)
- In the comparative validation of different theories, the calculated values for the new theory and the coexistence theory are close to the experimental values in the CaO-SiO2 and CaO-SiO2-Al2O3 slag systems, and the results obtained from the new molecular theory are closer to the experimental values in the CaO-Al2O3 slag system than those of other theories.
- (3)
- In the practical application of the new molecular theory, the maximum concentration of each complex molecule is consistent with the position of the melting point of the same solid‒liquid components in the phase diagram. The formation and decomposition of different complex molecules lead to changes in histone activity in the CaO-SiO2 and CaO-Al2O3 slag systems.
Author Contributions
Writing—original draft, Q.W.; validation, S.D.; investigation, J.H.; validation, X.P.; software, W.Y.; resources, X.Z.; writing—review and editing, H.G. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the financial support from the National Science Foundation for Young Scientists of China [grant number 52204366, 52404335].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
All authors extend their sincere thanks to the editors and reviewers for their helpful comments, suggestions, and encouragement.
Conflicts of Interest
Author Wensheng Yang was employed by the company GRINM Group Co., Ltd., GRIMAT Engineering Institute Co., Ltd. Author Xiaodan Zheng was employed by the company Beijing Shougang Gitane New MATERIALS Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The companies had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Li, X. Chemical Metallurgical Behaviour of Quasi-Steady State Welded Steel-Slag Interface Based on Non-Equilibrium Thermodynamics. Ph.D. Thesis, Tianjin University, Tianjin, China, 2007. [Google Scholar]
- Zhou, X.; Ersson, M.; Zhong, L.; Jönsson, P. Optimization of Combined Blown Converter Process. ISIJ Int. 2014, 54, 2255. [Google Scholar] [CrossRef]
- Tsukasaki, A.; Suzumura, M.; Nishijima, W. Fractionation of Phosphorus in Steelmaking Slags and Aquatic Particulate Materials Using a Sequential Extraction Technique. ISIJ Int. 2015, 55, 183–189. [Google Scholar] [CrossRef][Green Version]
- Dippenaar, R. Industrial uses of slag (the use and re-use of iron and steelmaking slags). Ironmak. Steelmak. 2013, 32, 35–46. [Google Scholar] [CrossRef]
- Stovpchenko, G.; Togobitskaya, D.; Lisova, L.; Stepanenko, D.; Medovar, L. Predictive models for molten slags viscosity and electrical conductivity based on directed chemical bonds concept. Ironmak. Steelmak. 2022, 49, 572–580. [Google Scholar] [CrossRef]
- Min, D.J.; Tsukihashi, F. Recent advances in understanding physical properties of metallurgical slags. Met. Mater. Int. 2017, 23, 1–19. [Google Scholar] [CrossRef]
- Zhao, L. Study on Thermodynamic Properties of CaO-SiO2-Al2O3-MgO-FetO slag System. Ph.D. Thesis, Northeastern University, Shenyang, China, 2013. [Google Scholar]
- Rein, R.H.; Chipman, J. Activities in the liquid solution SiO2-CaO-MgO-Al2O3 at 1600 °C. Trans. Metall. Soc. AIME 1965, 233, 415–425. [Google Scholar]
- Zhang, Z.Q.; Zhou, J.-C.; Zou, Y.-X. Activity of CaO in SiO2-CaO-MgO-Al2O3 slag. J. Met. 1986, 22, 76–84. [Google Scholar]
- Mikimoto, G.; Omori, Y. Activity of CaO in CaO-SiO2-Al2O3 slag system. J. Jpn. Soc. Met. 1961, 25, 139–143. [Google Scholar]
- Uchida, S.; Tsukihashi, F.; Sano, N. The Phase Relations of the CaO-MnO-SiO2 System in Connection with the Smelting Reduction of Manganese Ore. Tetsu-to-Hagane 2009, 77, 490–495. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ding, W.; Olsen, S.E. Reaction equilibria in the production of manganese ferroalloys. Metall. Mater. Trans. B 1996, 27, 5–17. [Google Scholar] [CrossRef]
- Deo, J.B.; Gaye, H. Investigation on the properties of components in liquid slags by EMF method. Ber. Bunsen-Ges. Phys. Chem. 1952, 32, 54–60. [Google Scholar]
- Kay, D.A.R.; Taylor, J. Activities of silica in the lime-alumina-silica system. Trans. Faraday Soc. 1960, 56, 1372–1386. [Google Scholar] [CrossRef]
- Zou, Y.; Zhao, P.; Cao, Z. Activity of CaO in liquid CaO-SiO2 and CaO-SiO2-Al2O3 slags. J. Met. 1963, 6, 121–130. [Google Scholar]
- Huang, X. Principles of Iron and Steel Metallurgy; Metallurgical Industry Press: Beijing, China, 1990. [Google Scholar]
- Guo, Y. Influence of Desulfurization Capacity and a(Al2O3) of CaO-SiO2-MgO-Al2O3 Quaternary Slag System. Master’s Thesis, Northeastern University, Shenyang, China, 2019. [Google Scholar]
- Wei, Q.C. Metallurgical Thermodynamics; Chongqing University Press: Chongqing, China, 1996. [Google Scholar]
- Zhang, J. Computational Thermodynamics of Metallurgical Melts; Metallurgical Industry Press: Beijing, China, 1998. [Google Scholar]
- Tan, J. Theoretical Activity Calculation and Viscosity Determination of Ionic Molecular Coexistence in Converter Slag. Ph.D. Thesis, Liaoning University of Science and Technology, Anshan, China, 2019. [Google Scholar]
- Zhang, J. Calculation model for the concentration of CaO-SiO2 slag system. J. Beijing Iron Steel Inst. 1988, 10, 412–421. [Google Scholar]
- Chen, J. Handbook of Commonly Used Steelmaking Charts and Data; Metallurgical Industry Press: Beijing, China, 2010. [Google Scholar]
- Turkdogan, E.T. Physical Chemistry of High Temperature Technology; Academic Press: New York, NY, USA, 1980; pp. 5–24. [Google Scholar]
- Liang, Y.; Che, Y. Inorganic Thermodynamics Data Book; Northeastern University Press: Shenyang, China, 1993; p. 86. [Google Scholar]
- Zhang, J. Thermodynamic Calculations of Metallurgical Melts and Solutions; Metallurgical Industry Press: Beijing, China, 2007. [Google Scholar]
- Zhang, J.; Yuan, W.X. Calculation model for the action concentration of CaO-Al2O3-SiO2 slag. J. Beijing Iron Steel Inst. 1995, 17, 7. [Google Scholar] [CrossRef]
- Yu, J. Modeling and Application of CaO-SiO2-MgO-Al2O3 Activity in Quaternary Slag System. Ph.D. Thesis, Northeastern University, Shenyang, China, 2016. [Google Scholar]
- Li, Z.; Ma, G.; Liu, M.; Zou, J. Calculation Model for Activity of FeO in Quaternary Slag System SiO2-CaO-Al2O3-FeO. Metals 2018, 8, 714. [Google Scholar] [CrossRef]
- Yang, X.M.; Duan, J.P.; Shi, C.B.; Zhang, M.; Zhang, Y.L.; Wang, J.C. A Thermodynamic Model of Phosphorus Distribution Ratio between CaO-SiO2-MgO-FeO-Fe2O3-MnO-Al2O3-P2O5 Slags and Molten Steel during a Top–Bottom Combined Blown Converter Steelmaking Process Based on the Ion and Molecule Coexistence Theory. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2011, 42, 738–770. [Google Scholar] [CrossRef]
- Duan, S.C.; Li, C.; Guo, X.L.; Guo, H.J.; Guo, J.; Yang, W.S. A thermodynamic model for calculating manganese distribution ratio between CaO-SiO2-MgO-FeO-MnO-Al2O3-TiO2-CaF2 ironmaking slags and carbon saturated hot metal based on the IMCT. Ironmak. Steelmak. 2018, 45, 655–664. [Google Scholar] [CrossRef]
- Li, P. Characterization of Slag Desulfurization and Dephosphorization Capacity Based on Slag Ion and Molecular Coexistence Theory. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2016. [Google Scholar]
- Zhang, J. On the coexistence theory of slag structure. J. Beijing Iron Steel Inst. 1984, 18, 21–29. [Google Scholar]
- Zou, Y.X.; Zhou, J.C.; Xu, Y.S. Some studies on the thermodynamics of metallurgical melts. J. Met. 1982, 18, 127–139. [Google Scholar]
- Meta Techx Engineers. Association of Iron and Steel Engineers of the Federal Republic of Germany. In Slag Atlas; Metallurgical Industry Press: Beijing, China, 1989; pp. 147–148. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).