Adaptive Sliding Mode Control of an Interleaved Buck Converter–Proton Exchange Membrane Electrolyzer for a Green Hydrogen Production System
Abstract
1. Introduction
2. IBC–PEM Electrolyzer System Details, Analysis, and Modeling
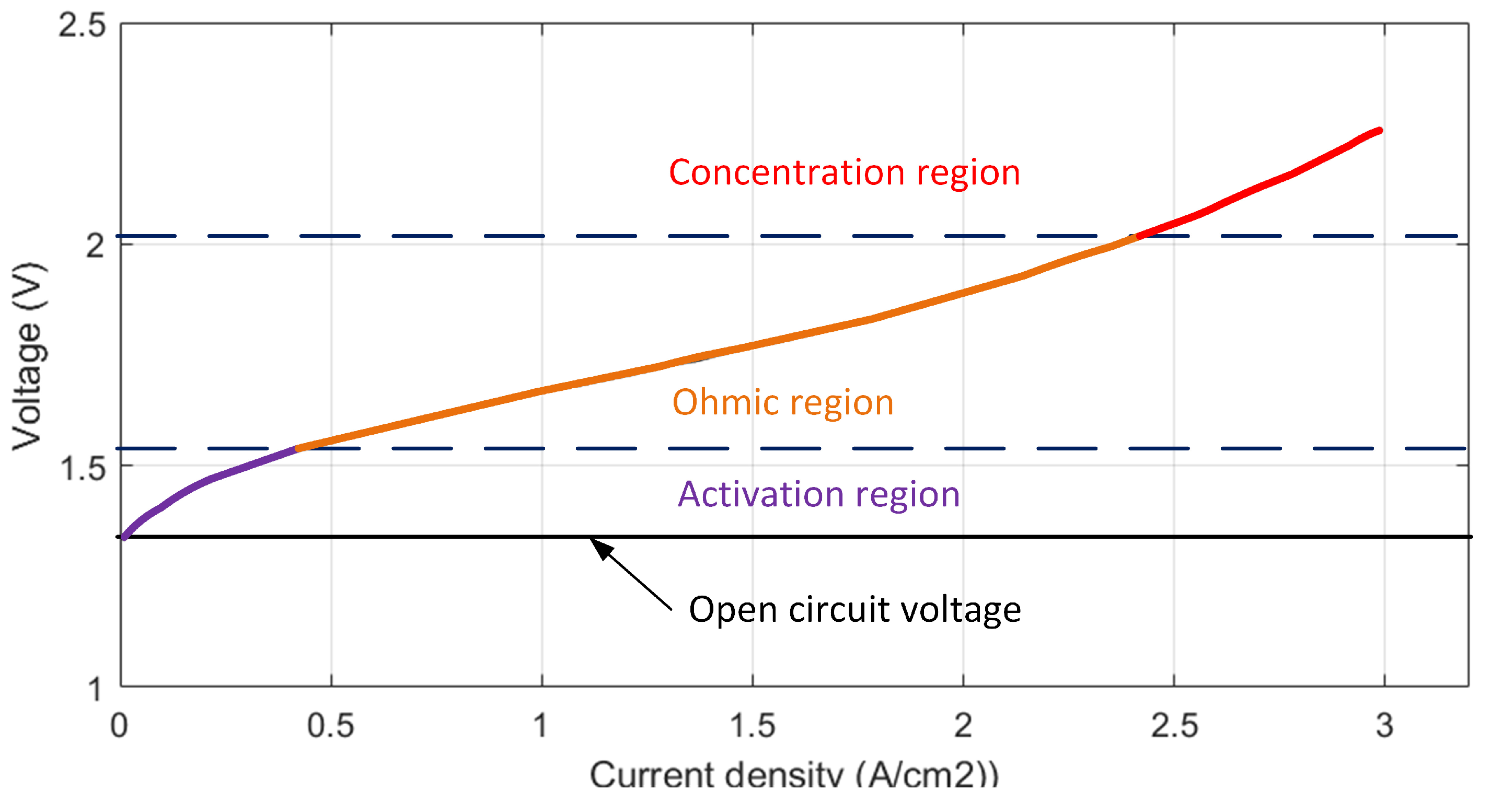
3. PEM Electrolyzer Modeling Analysis and Approximation
4. Nonlinear Modeling of an IBC–PEM Electrolyzer
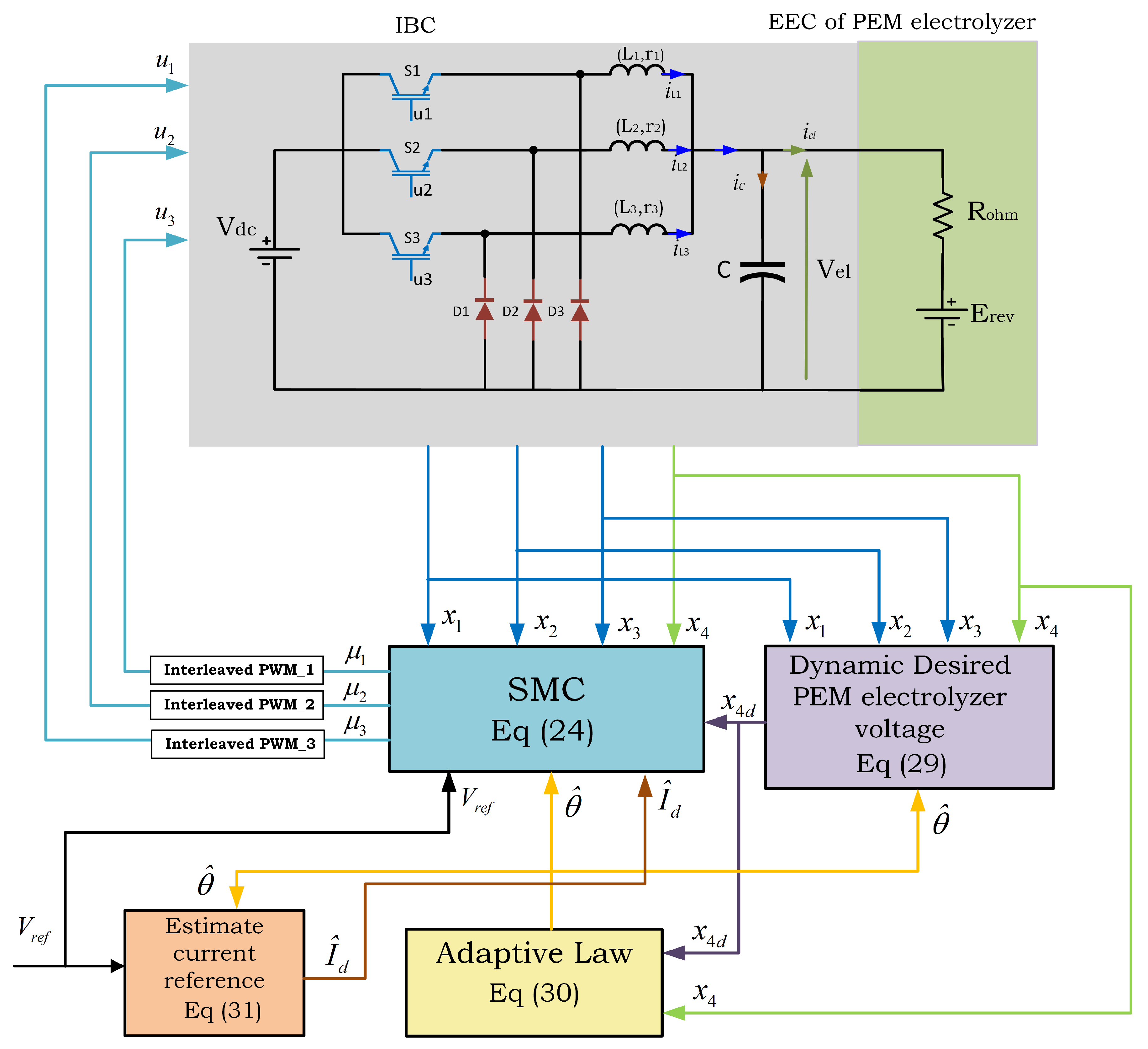
5. Adaptive Sliding Mode Controller Design
5.1. Control Objectives
- Ensure global stability of the control system across a wide range of operating conditions.
- Maintain precise regulation of the PEM electrolyzer voltage despite significant model uncertainties.
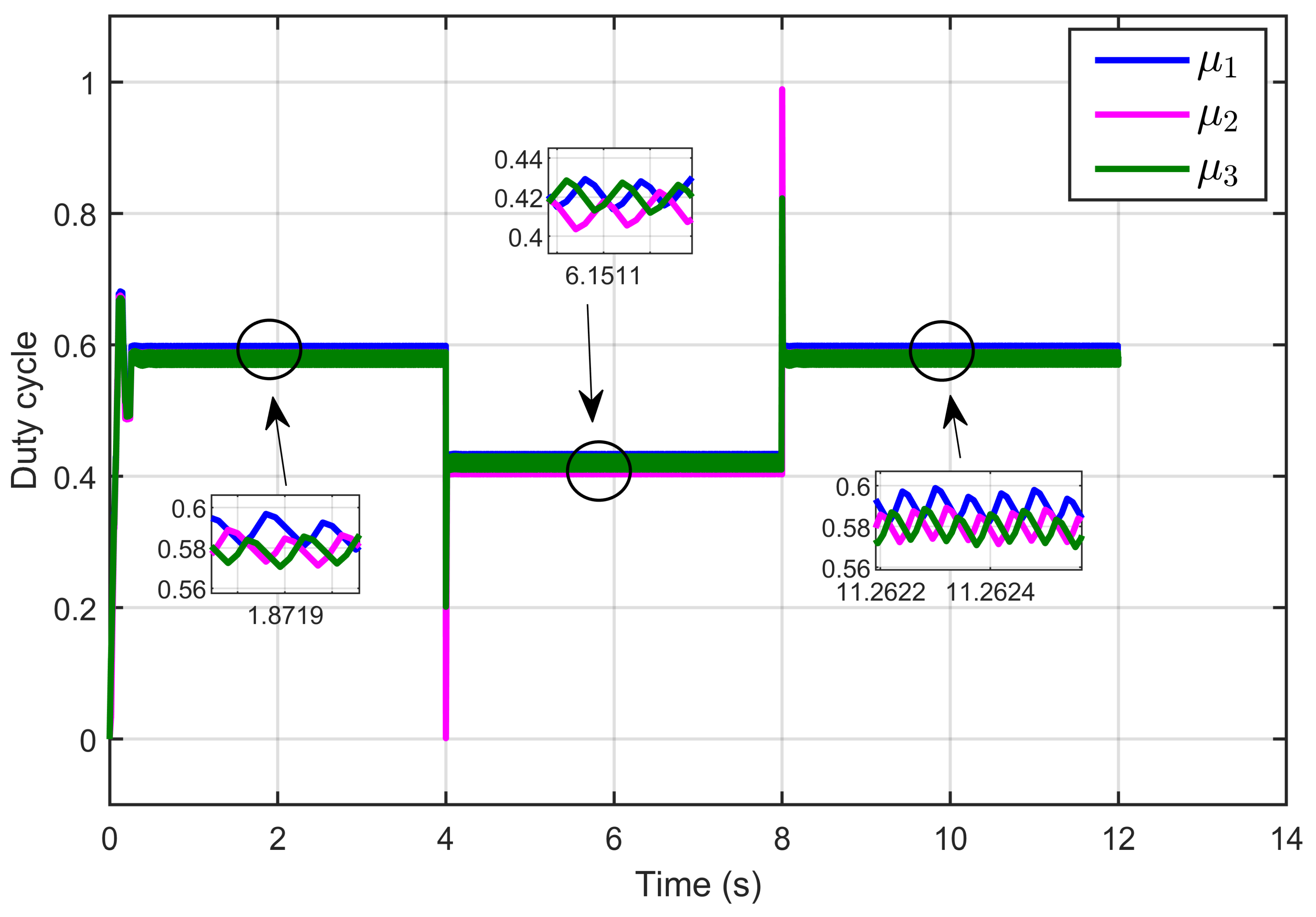
- Guarantee equal current sharing between the three inductors, regardless of variations in their inductance values.
5.2. Sliding Mode Controller Design
5.3. Design of Adaptive Controller and Stability Analysis
- I.
- The errors (e1, e2, and e3) converge asymptotically to zero, implying equal current sharing between the three inductors.
- II.
- The PEM electrolyzer voltage x4 perfectly tracks its reference value xref.
6. Simulation Results
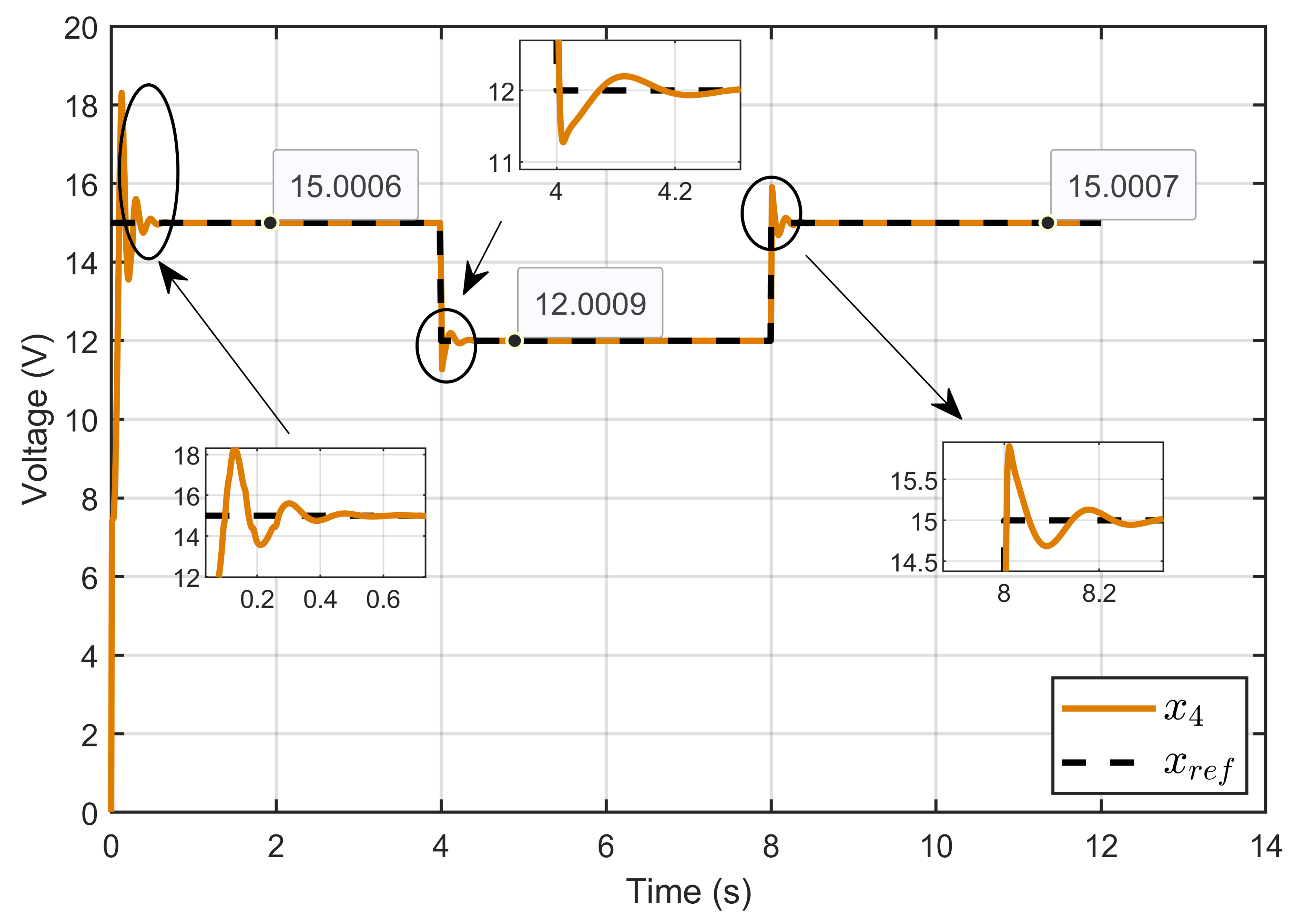
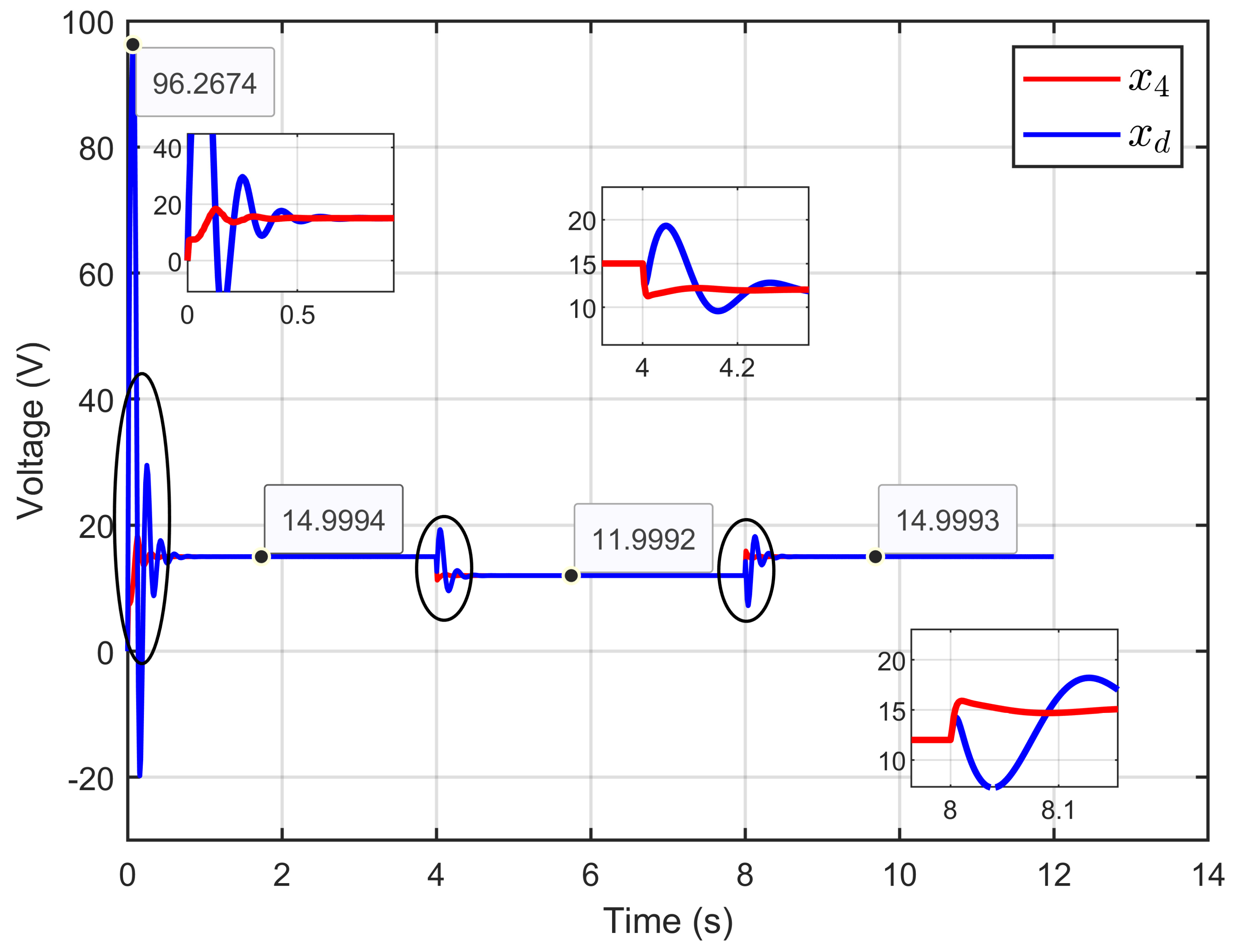
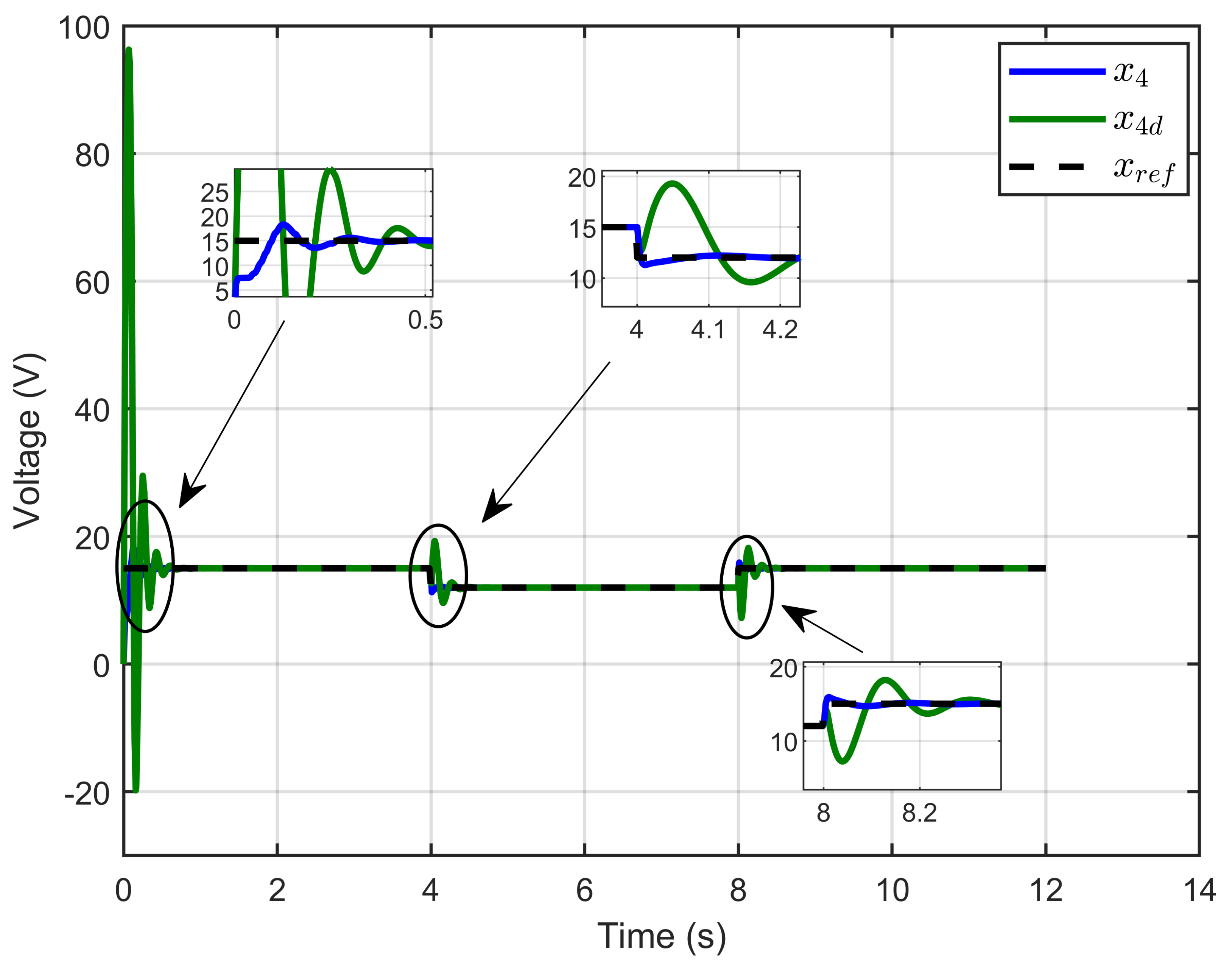
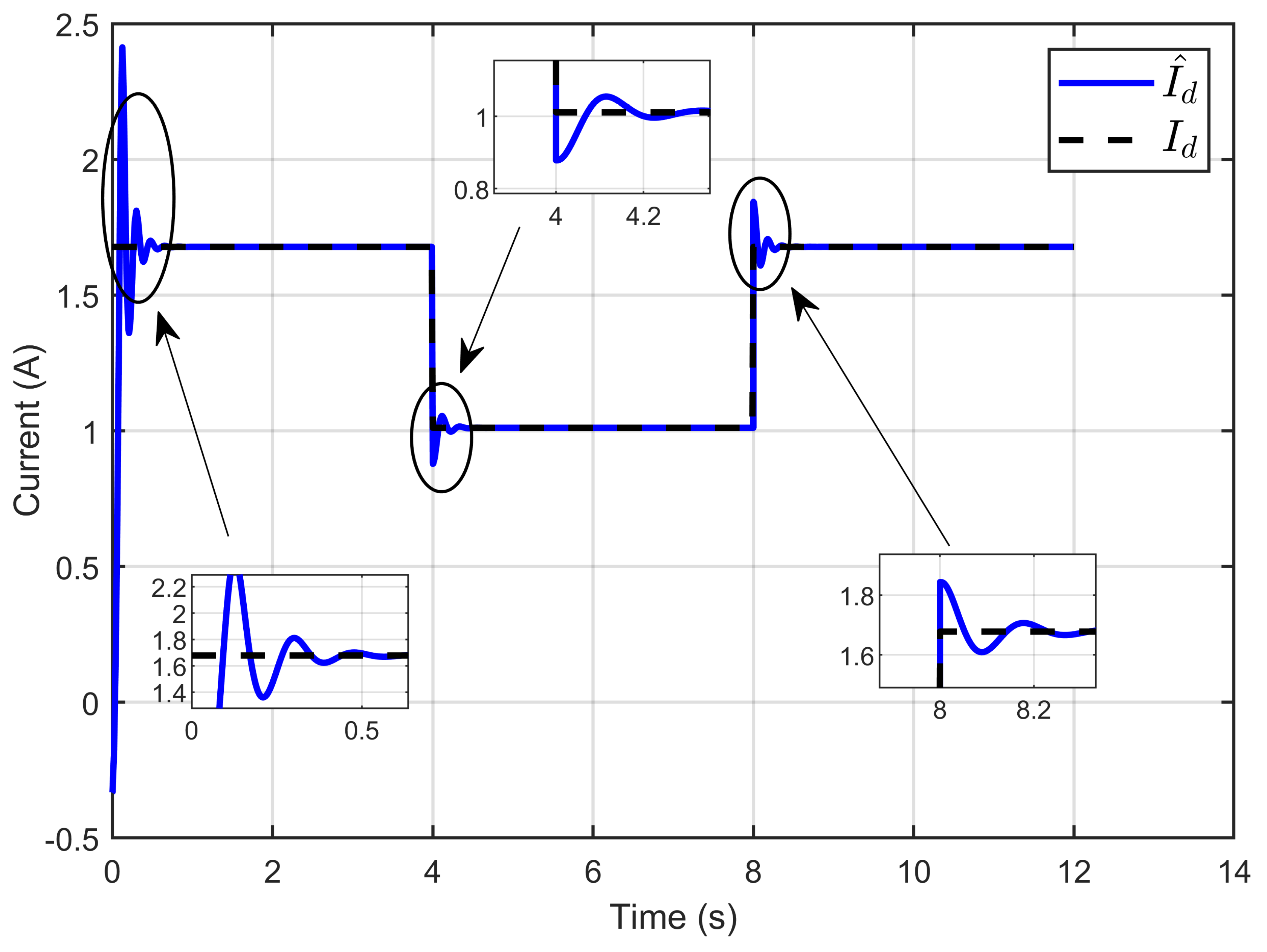
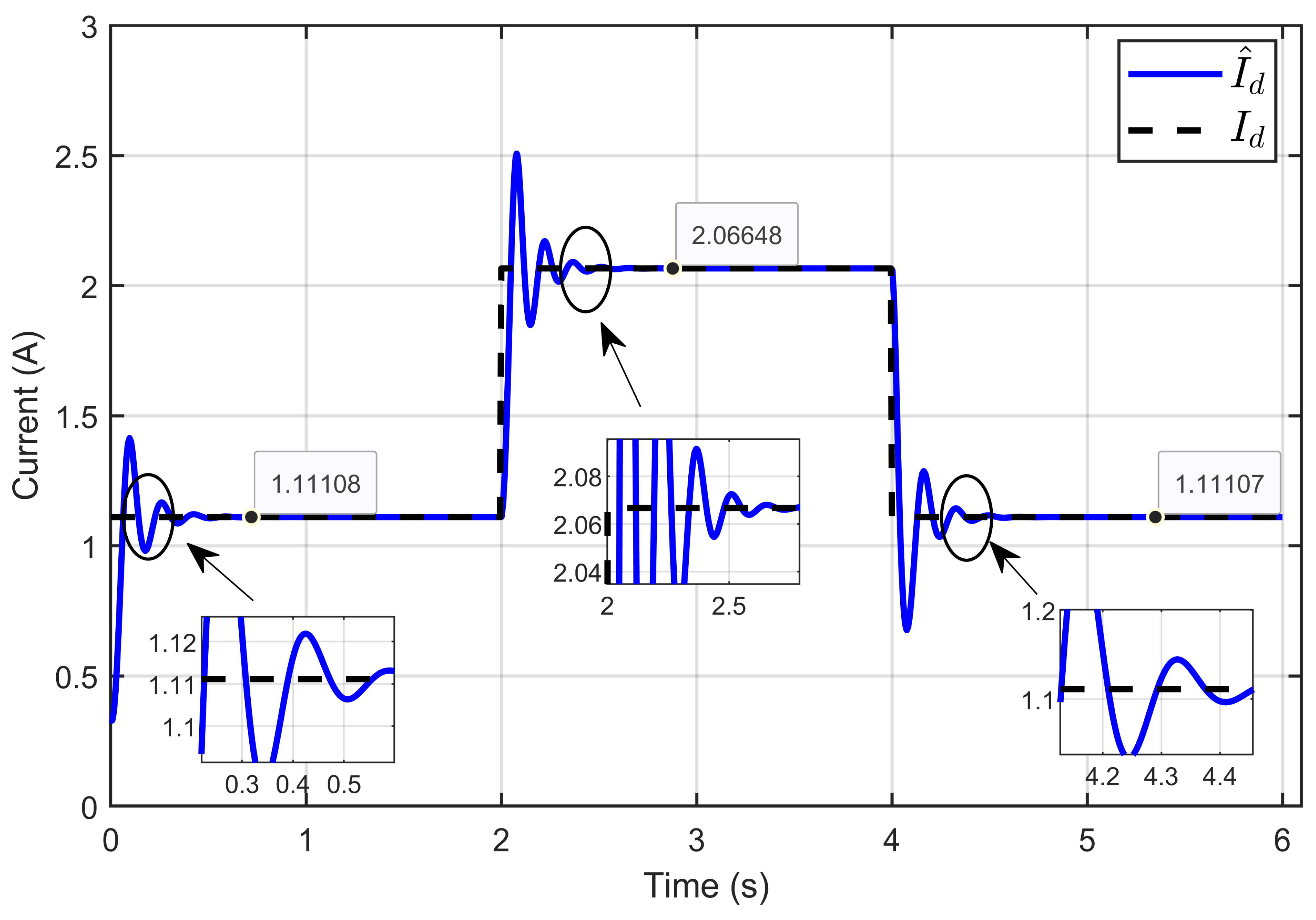
6.1. Performance Validation of Adaptive Sliding Mode Control for a Reference Step in PEM Electrolyzer Voltage
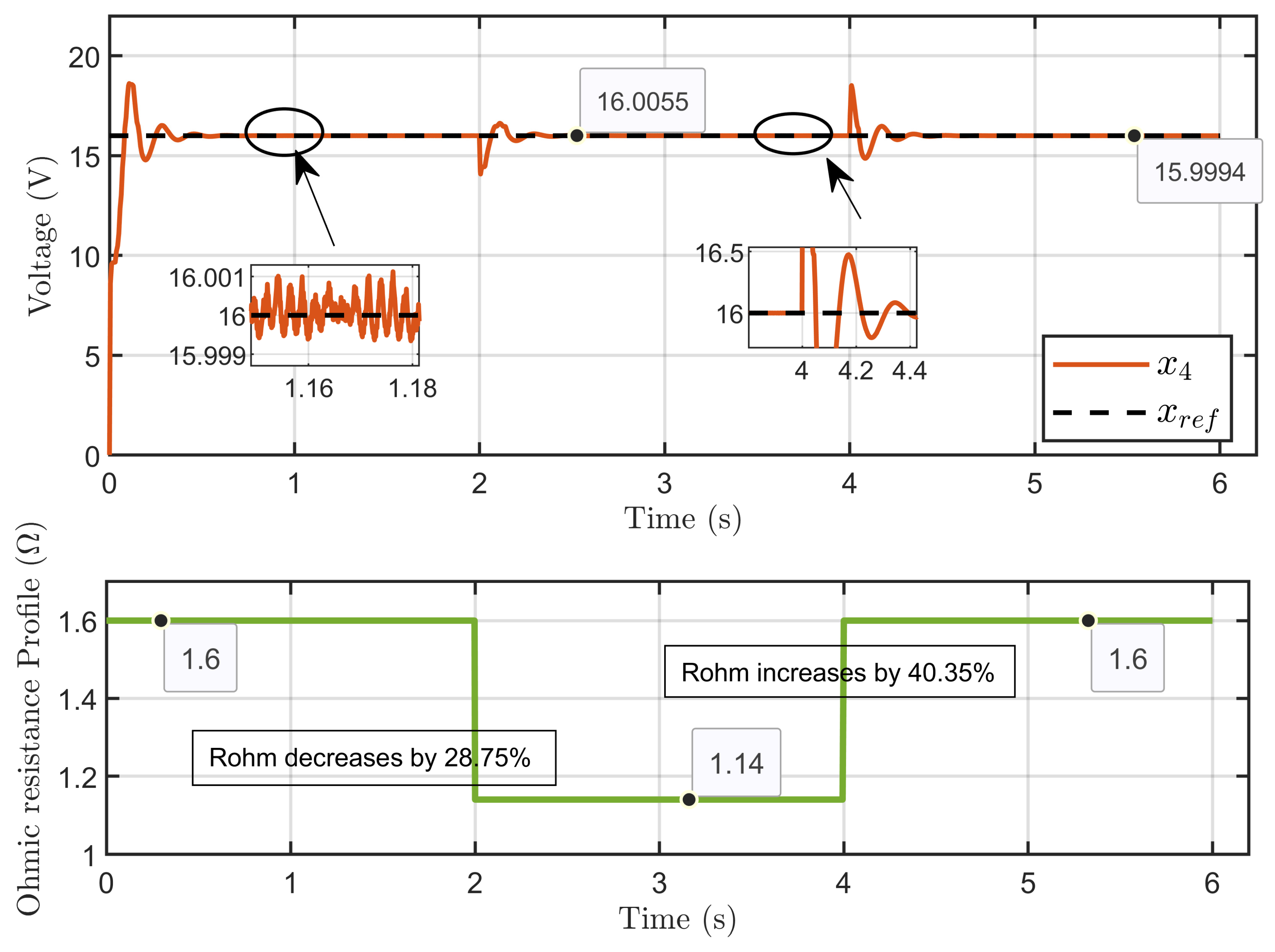
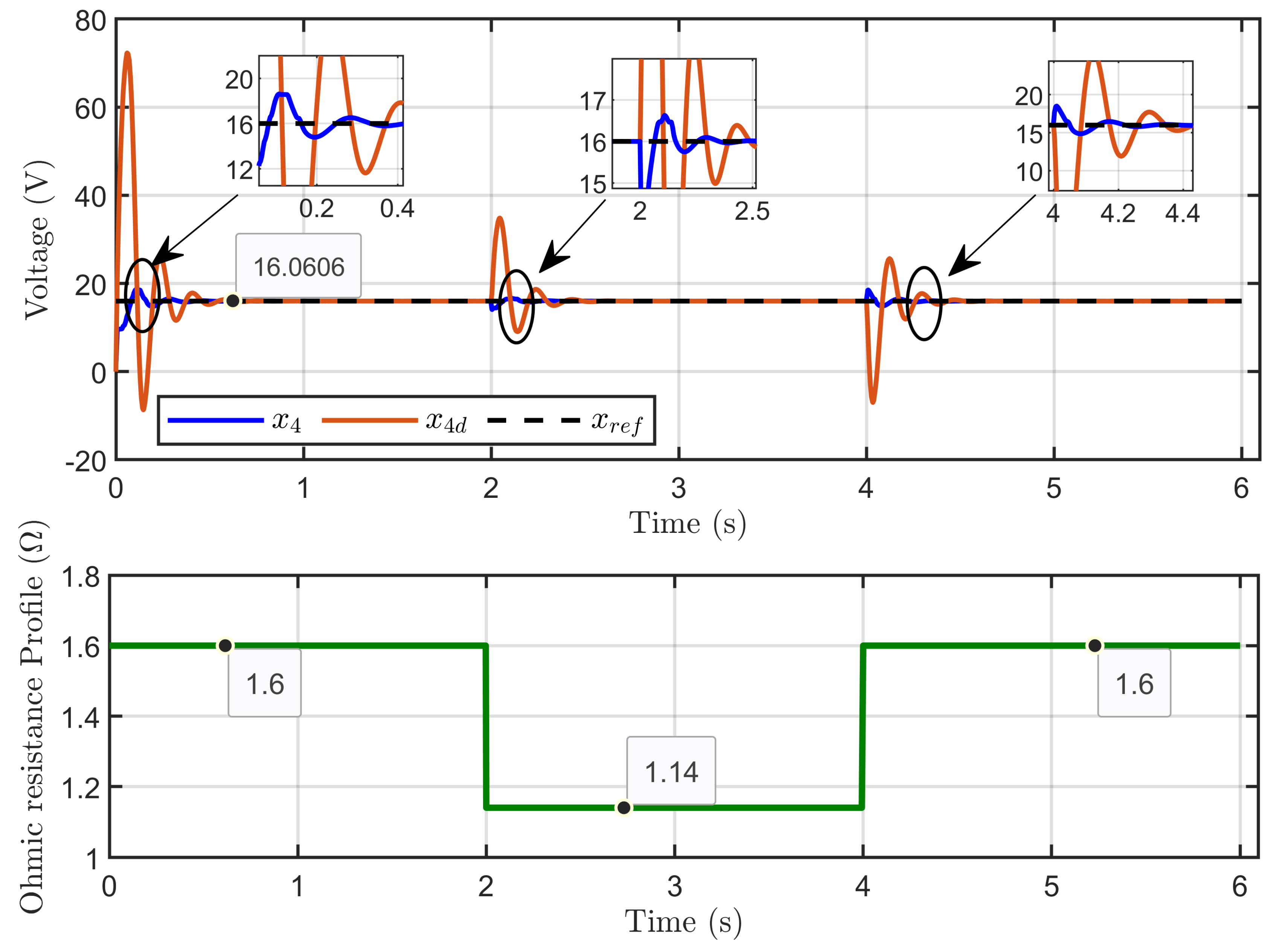
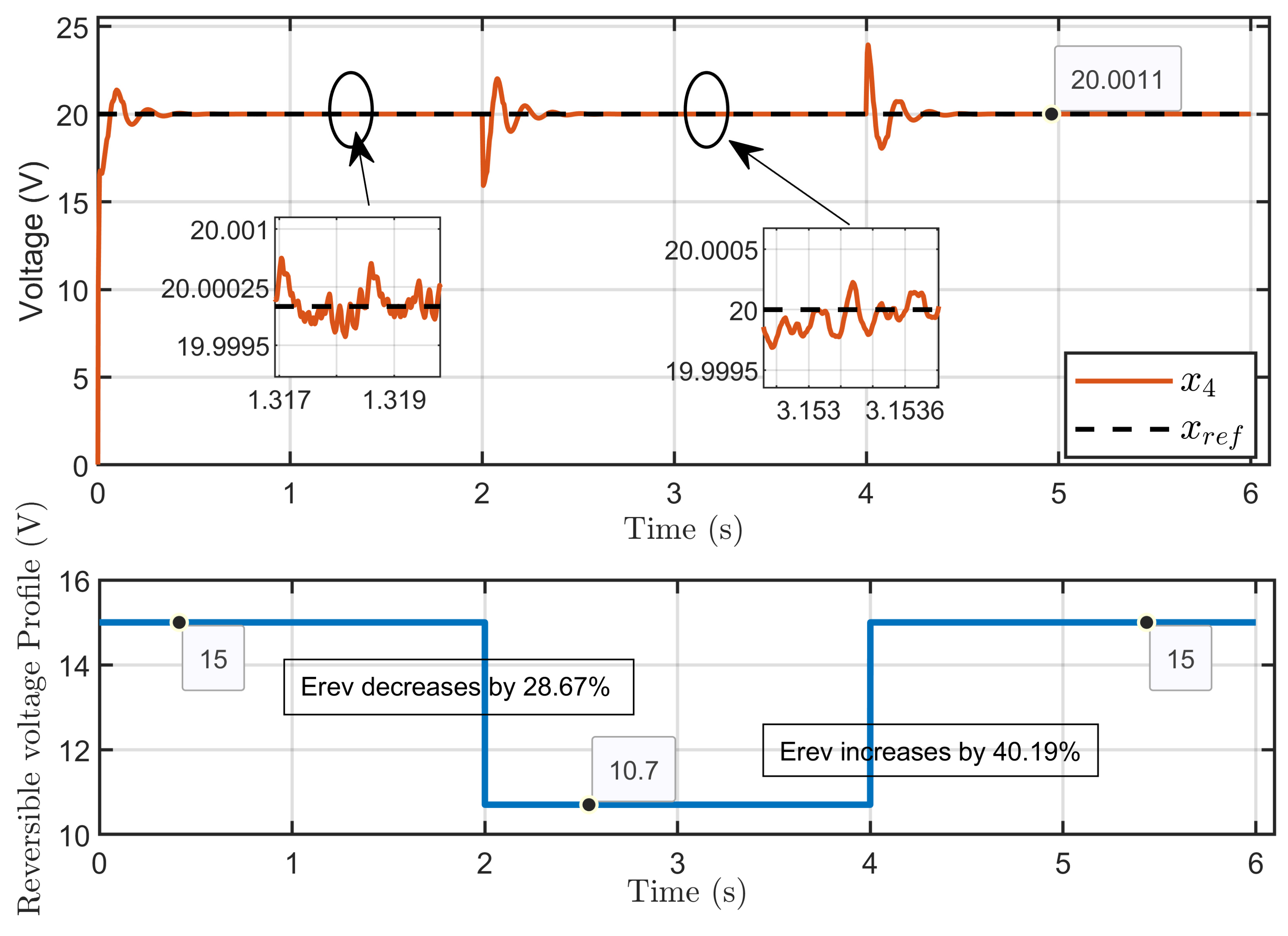
6.2. Performance Validation of the Controller Sensitivity to Perturbations Caused by Sudden Variations in PEM Electrolyzer Operation Conditions
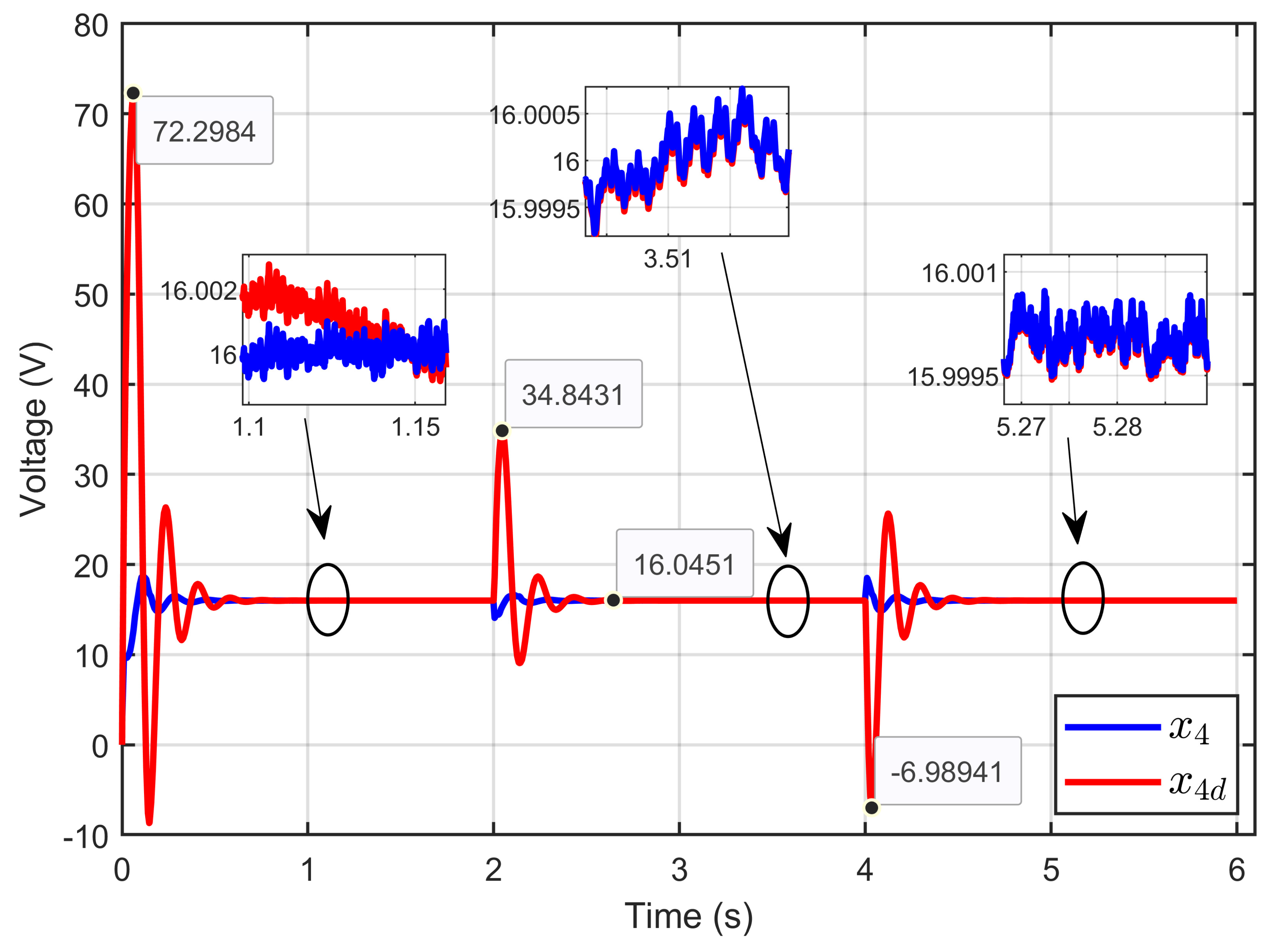
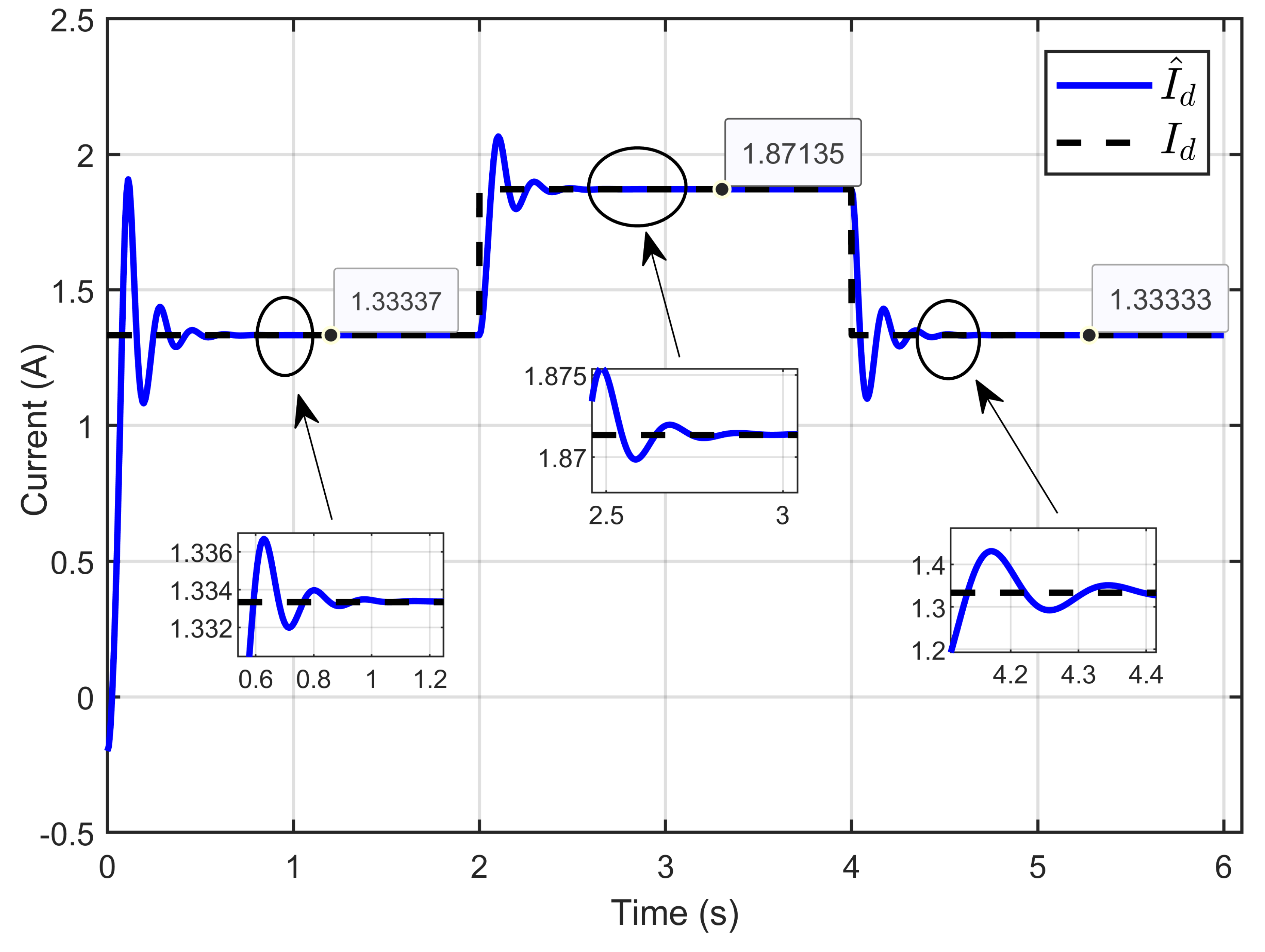
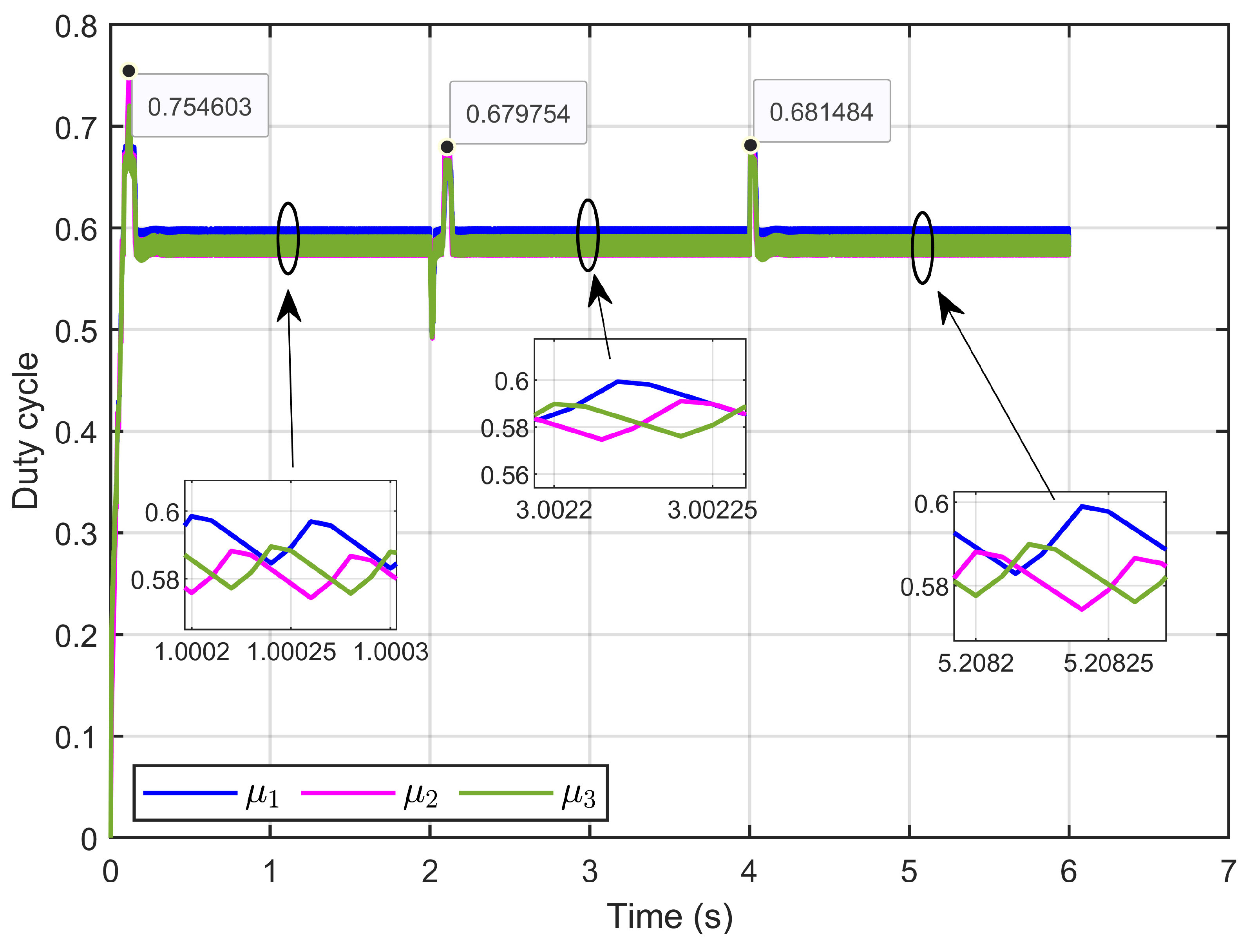
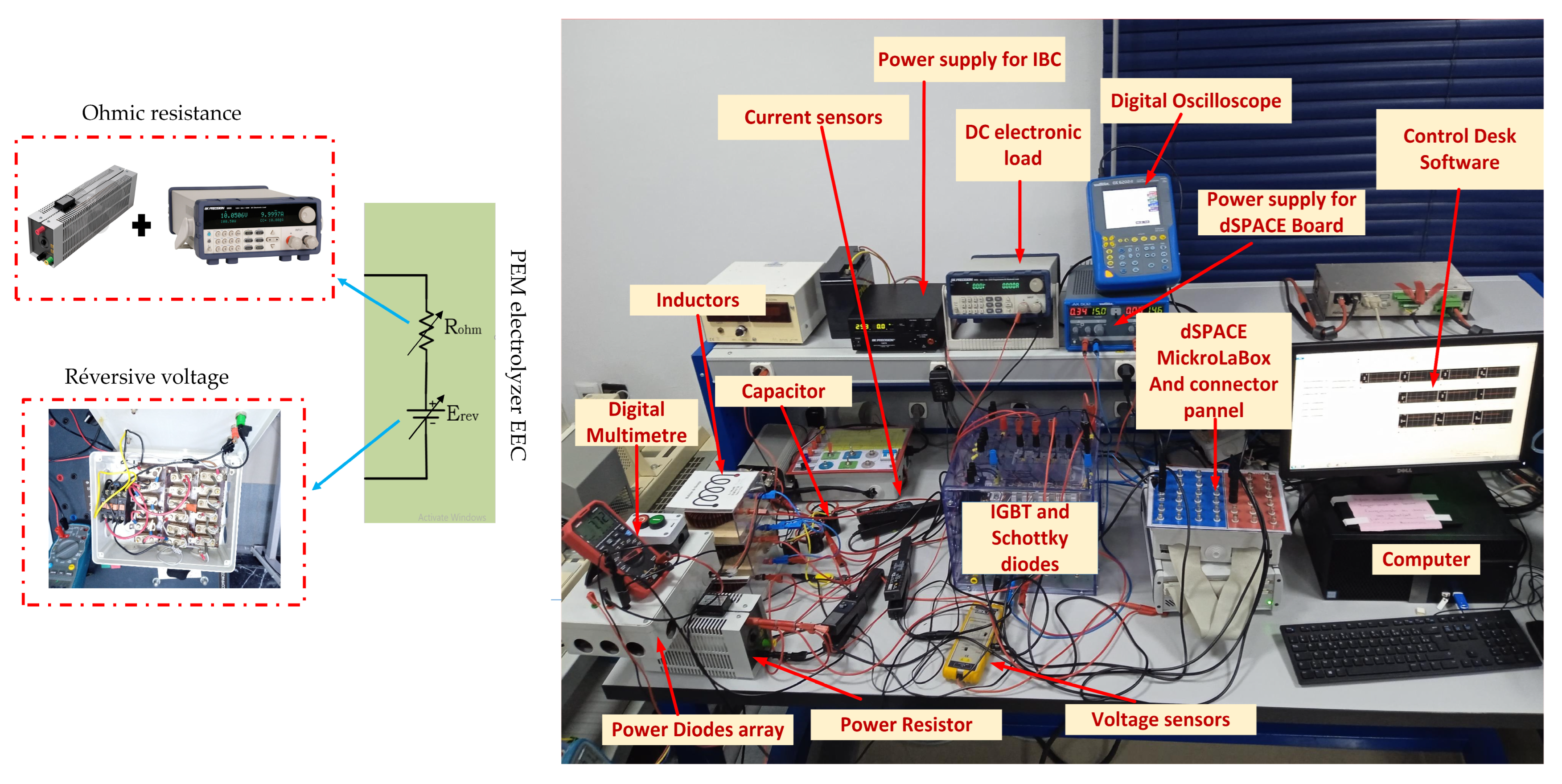
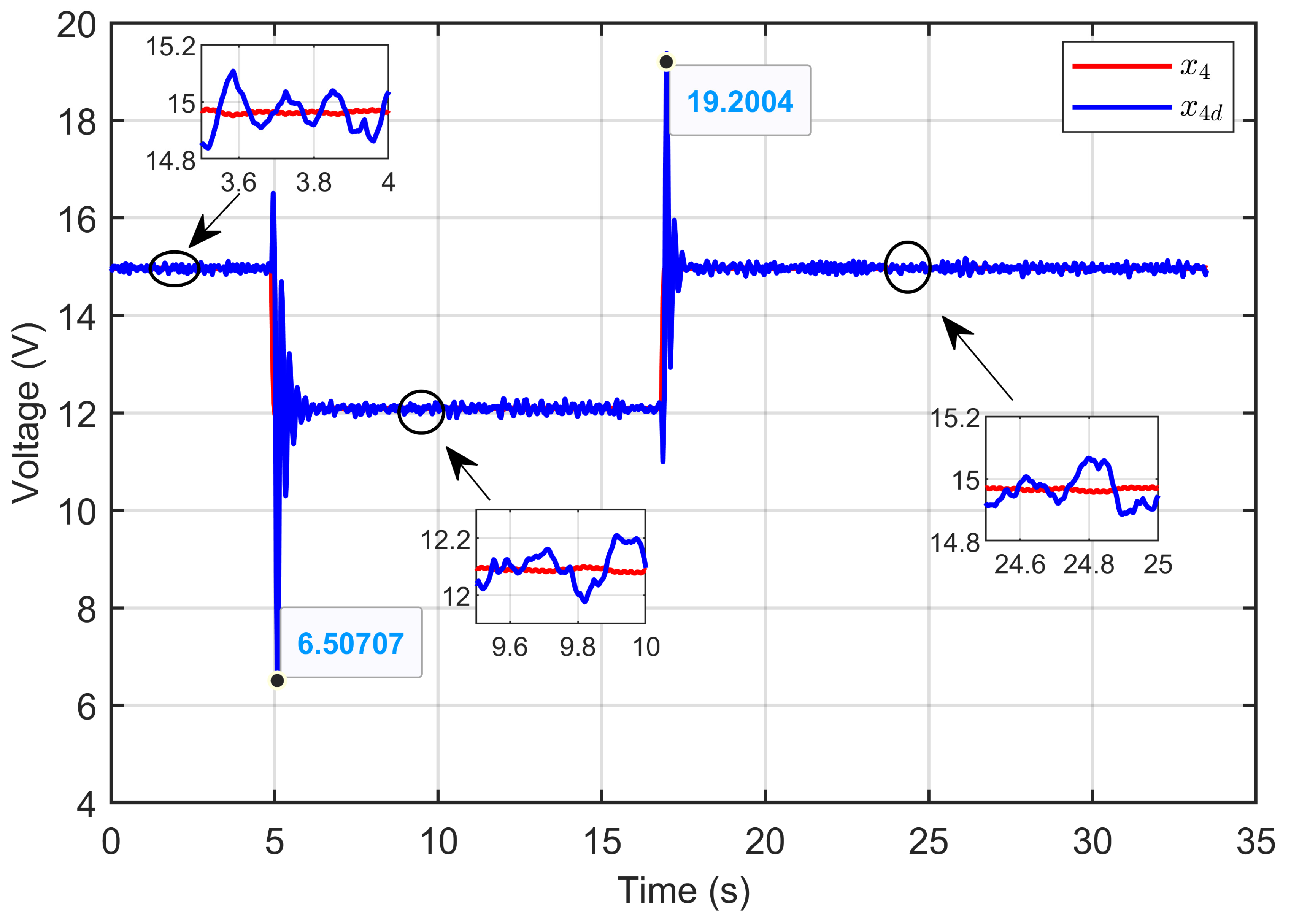
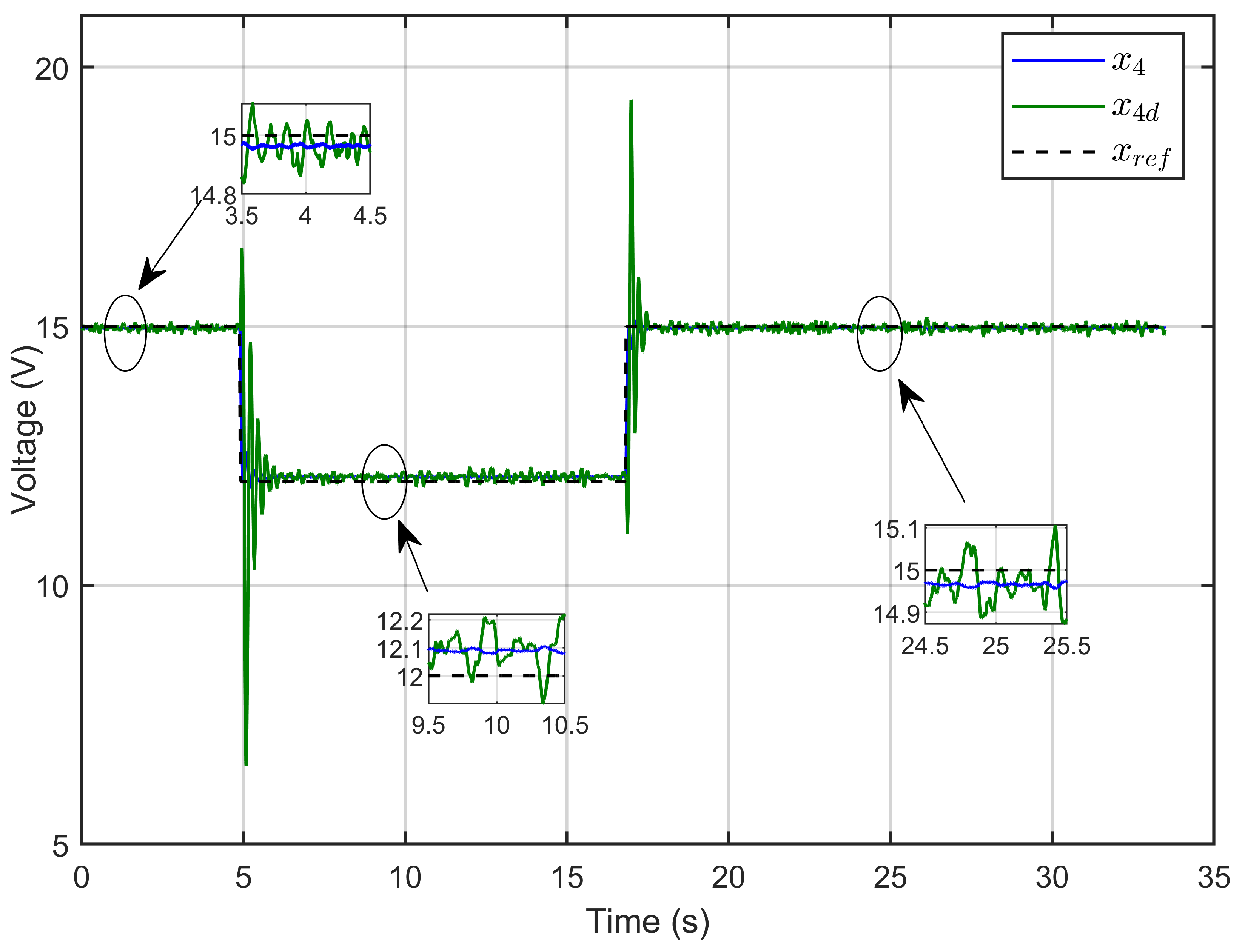
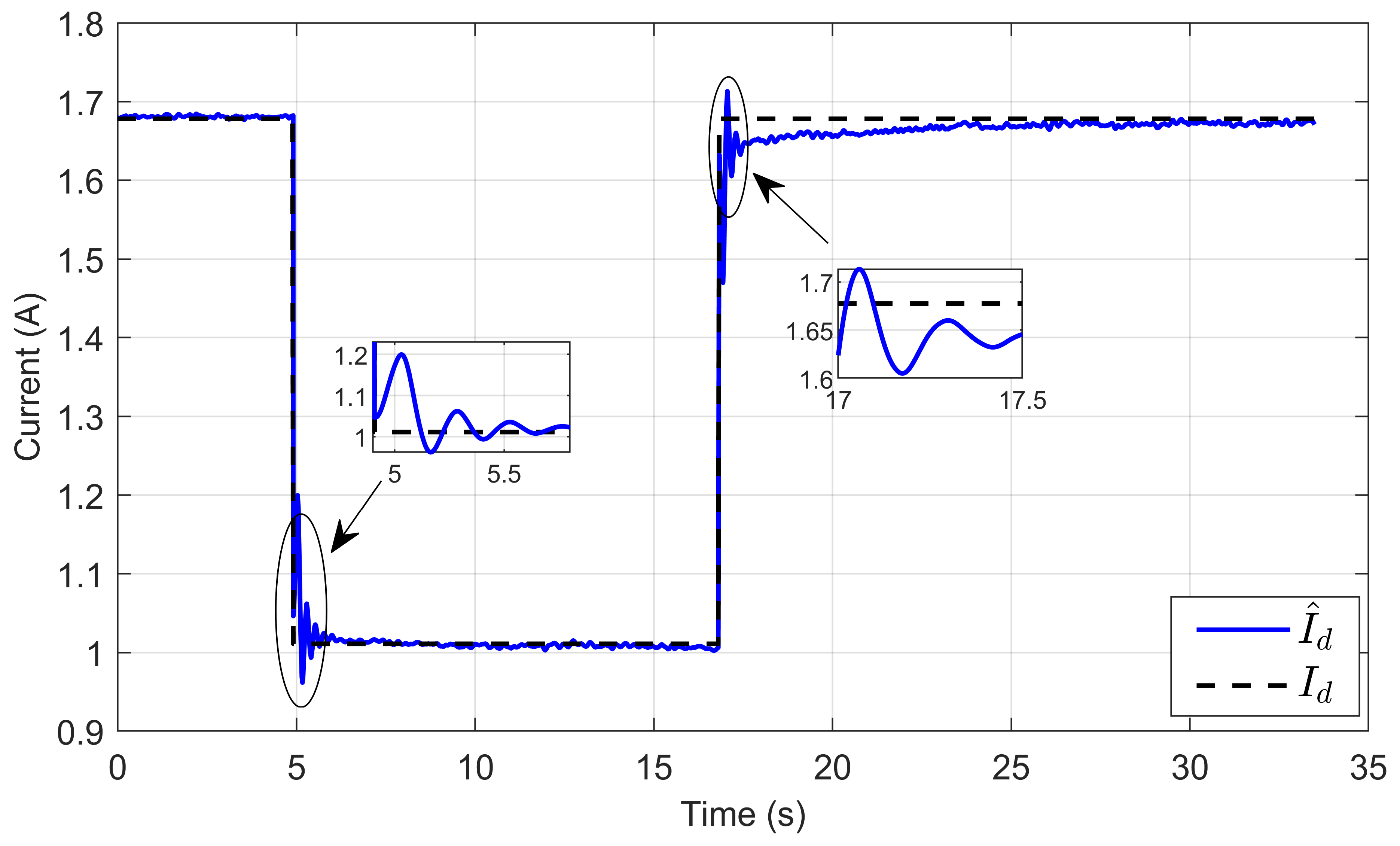
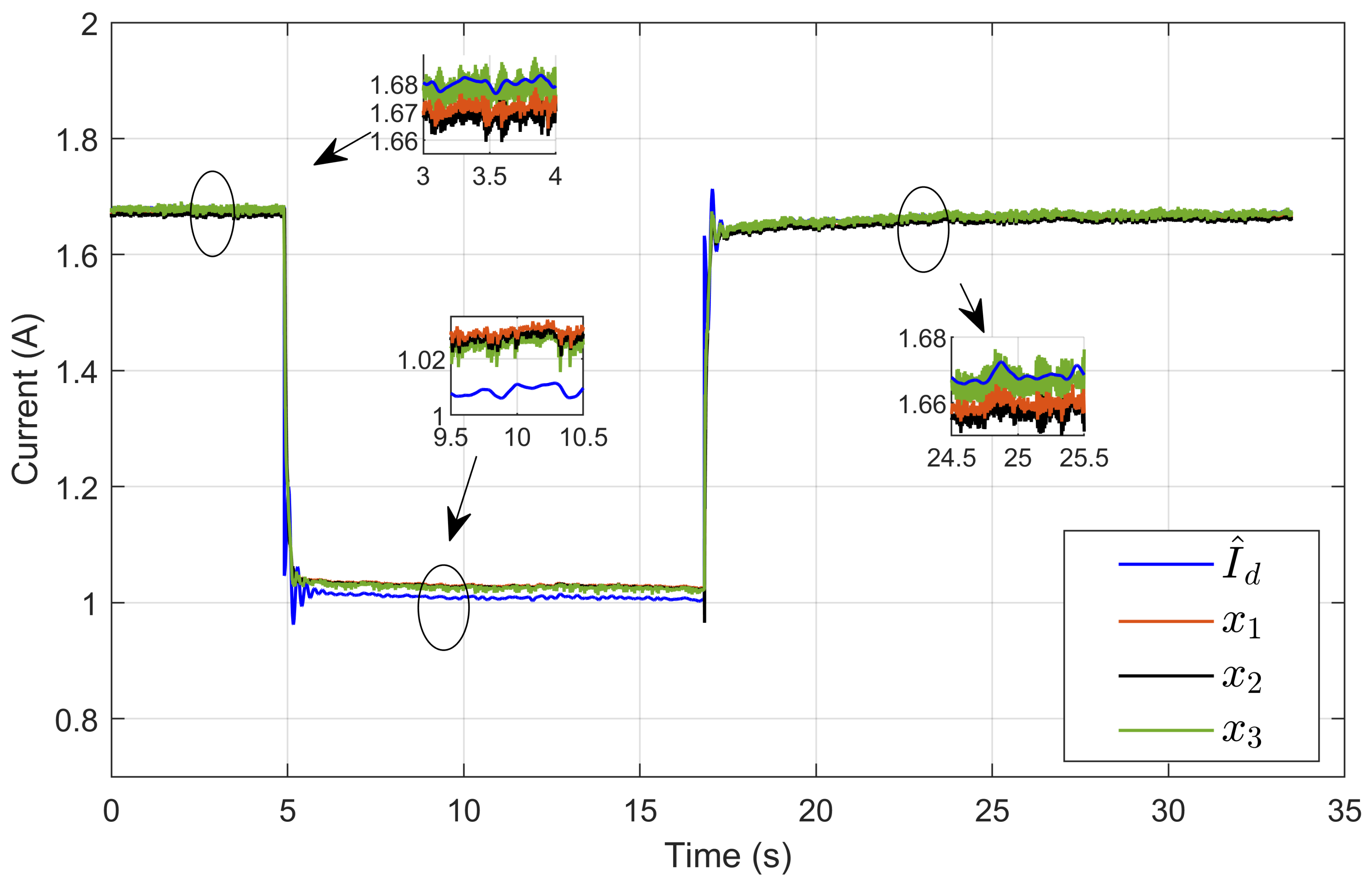
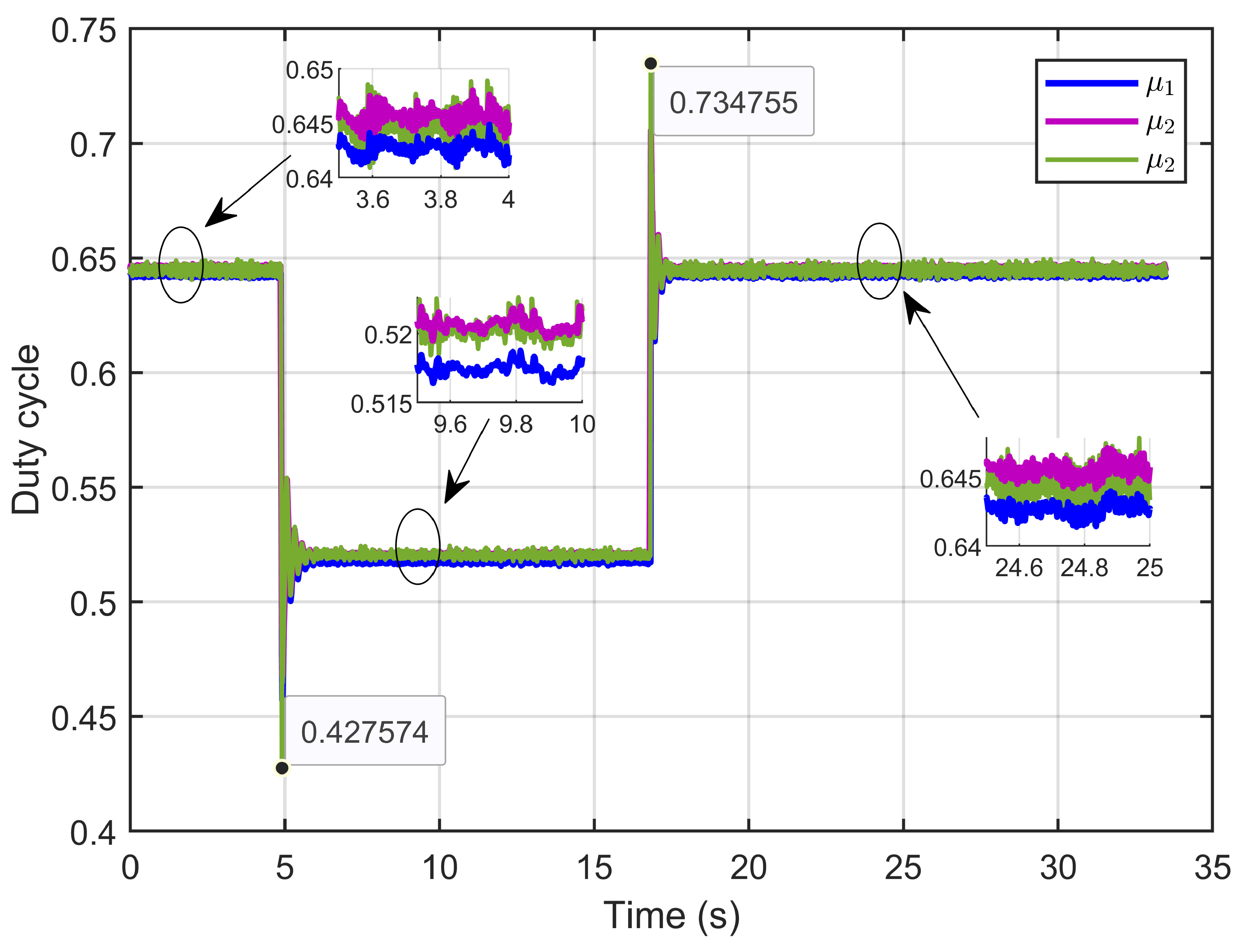
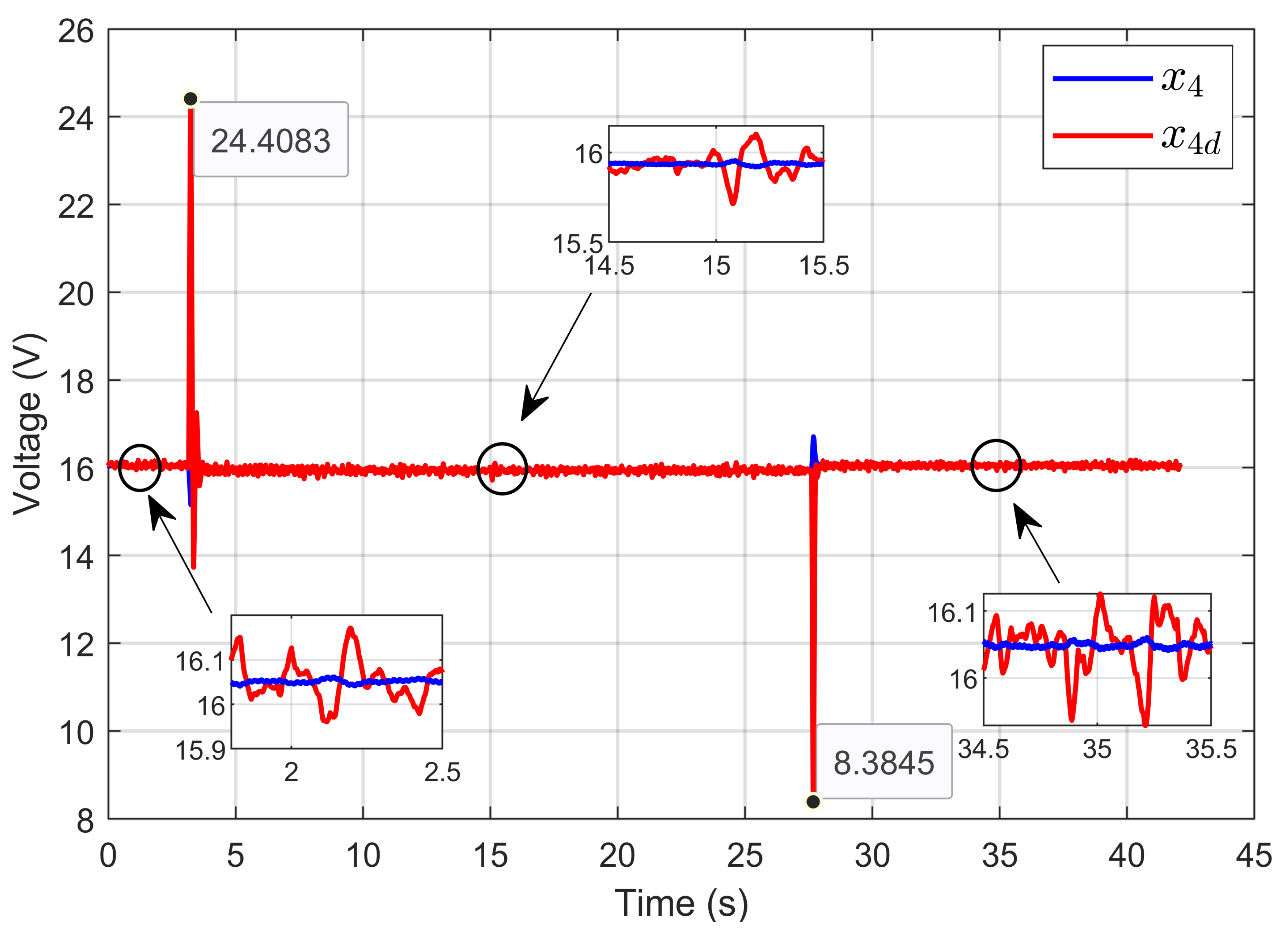
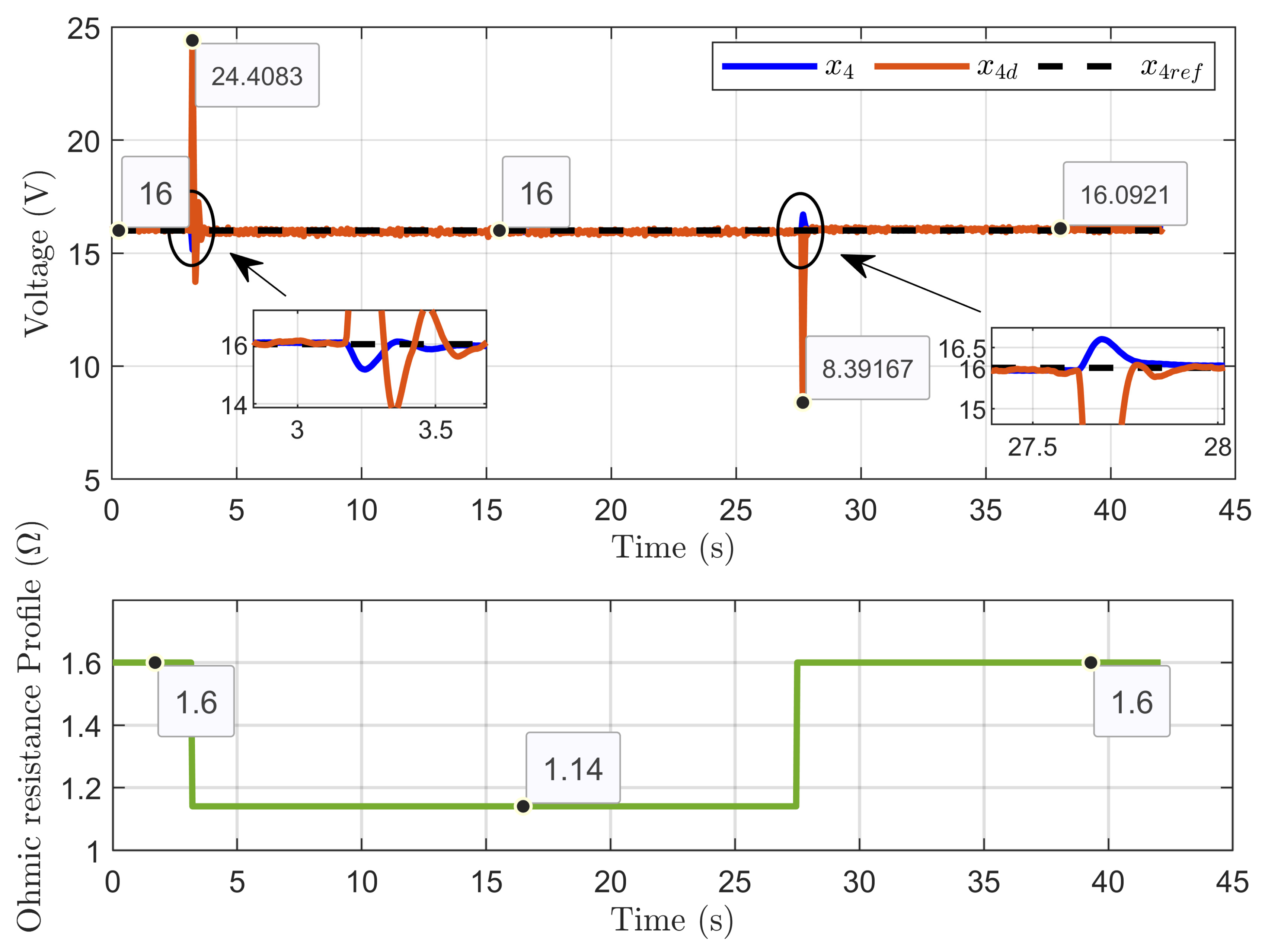
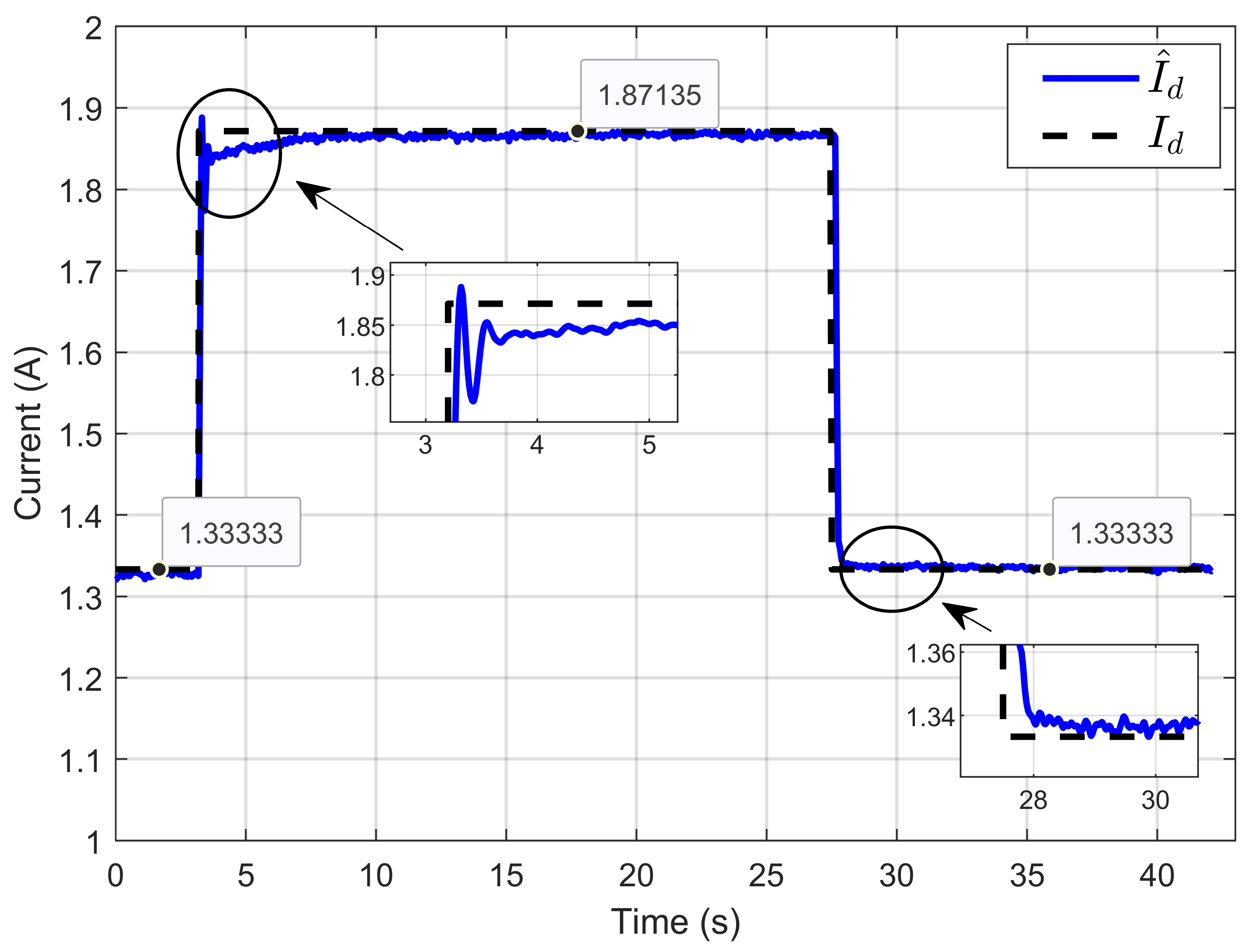
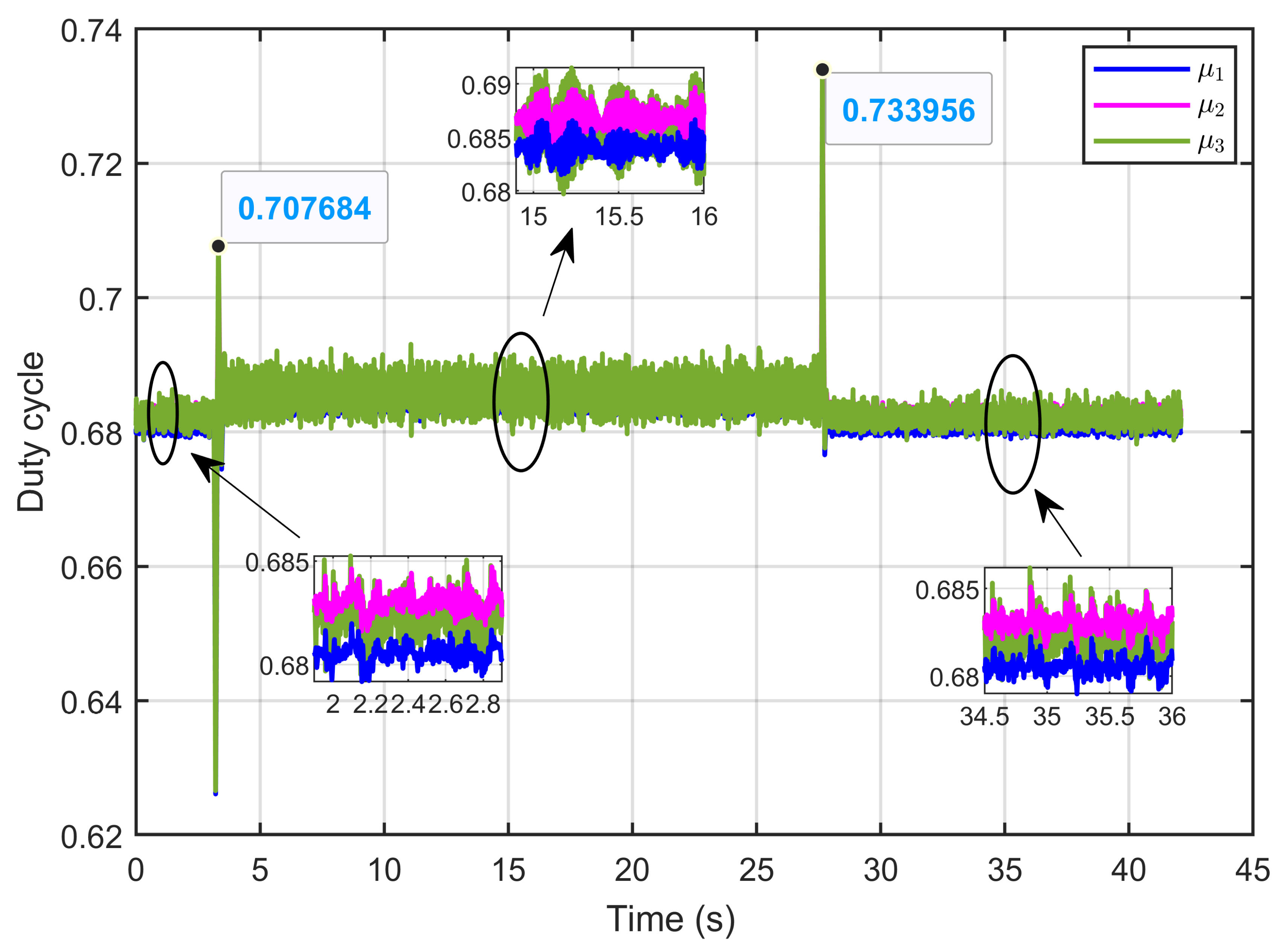
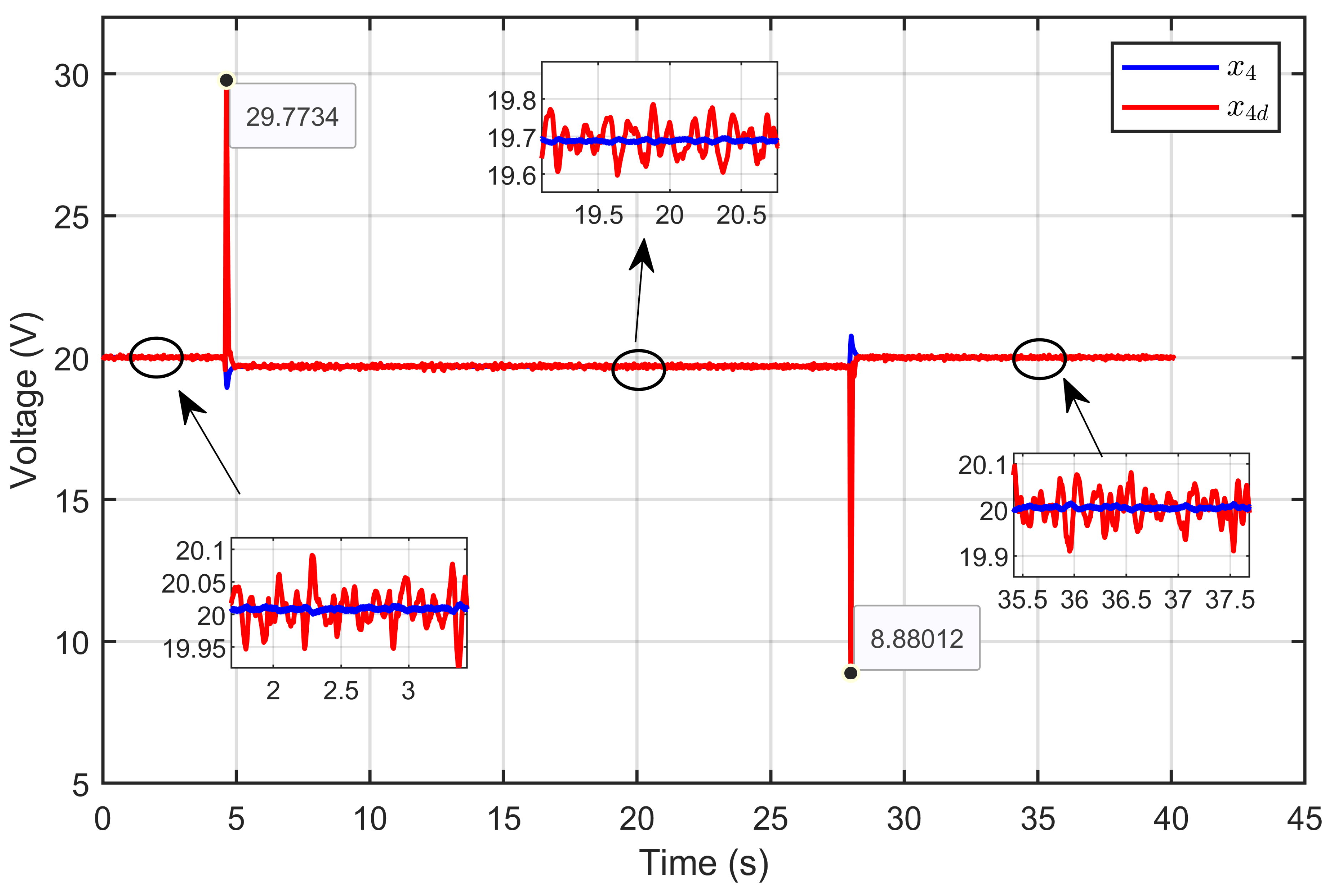
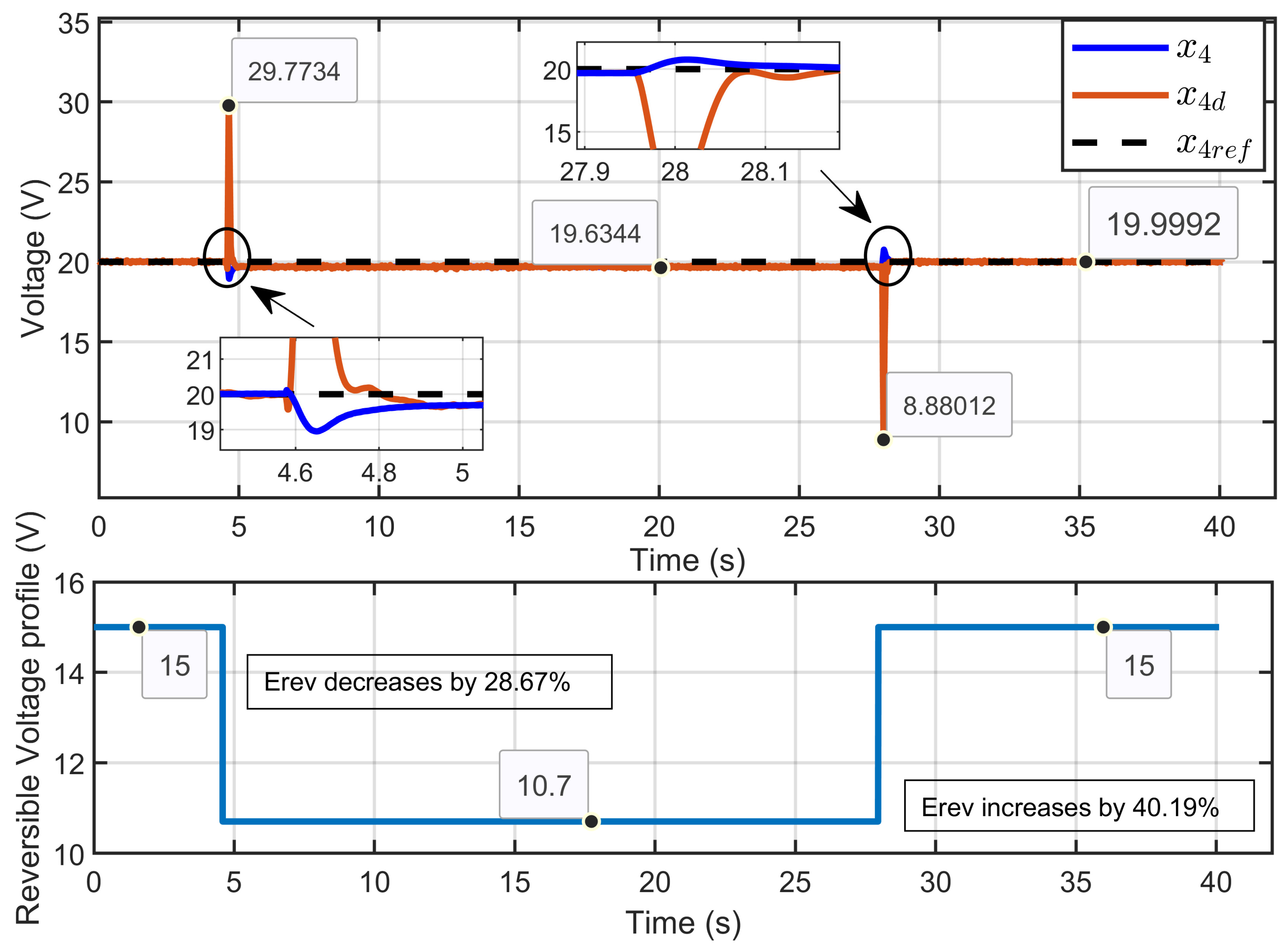
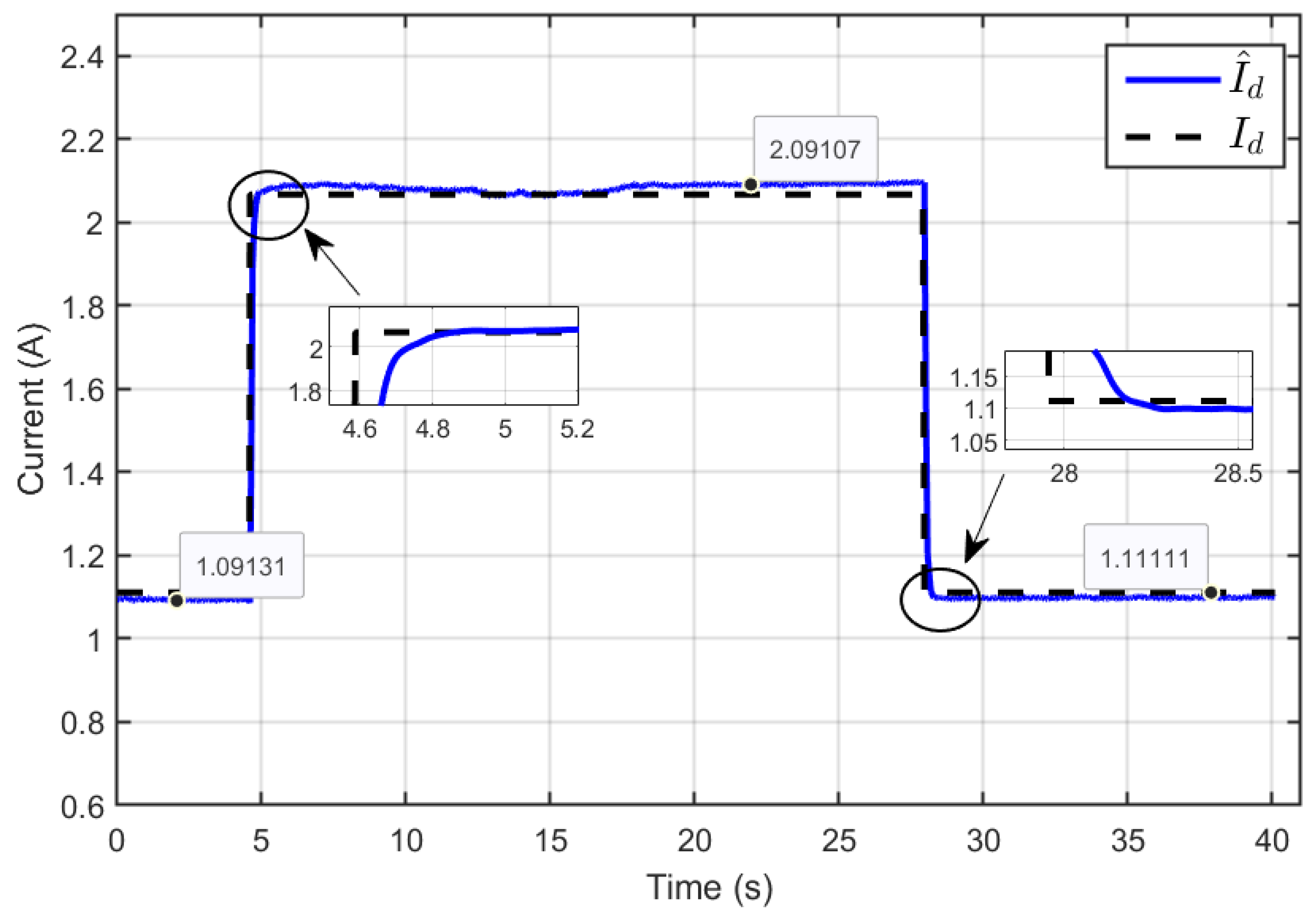
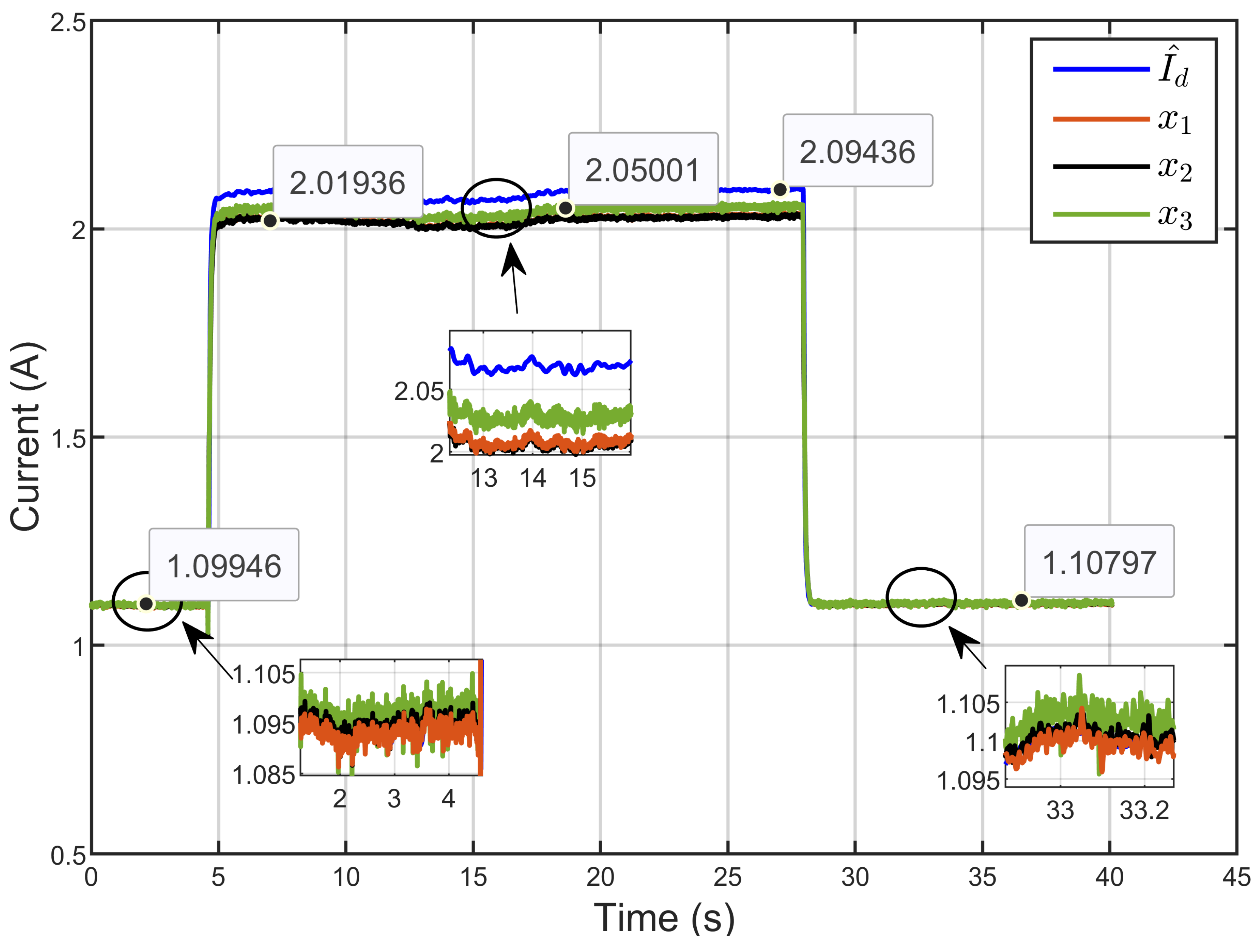
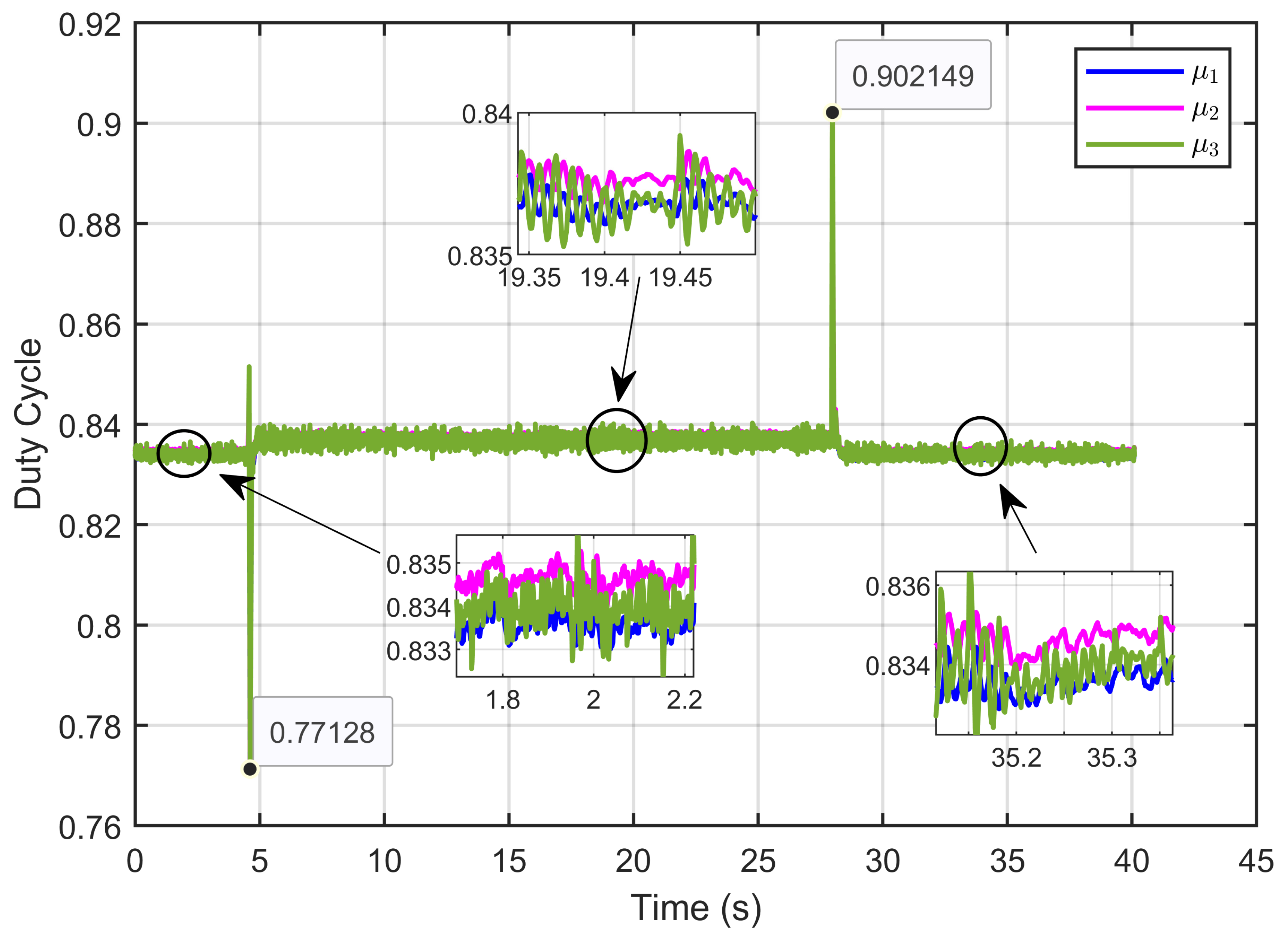
7. Experimental Results
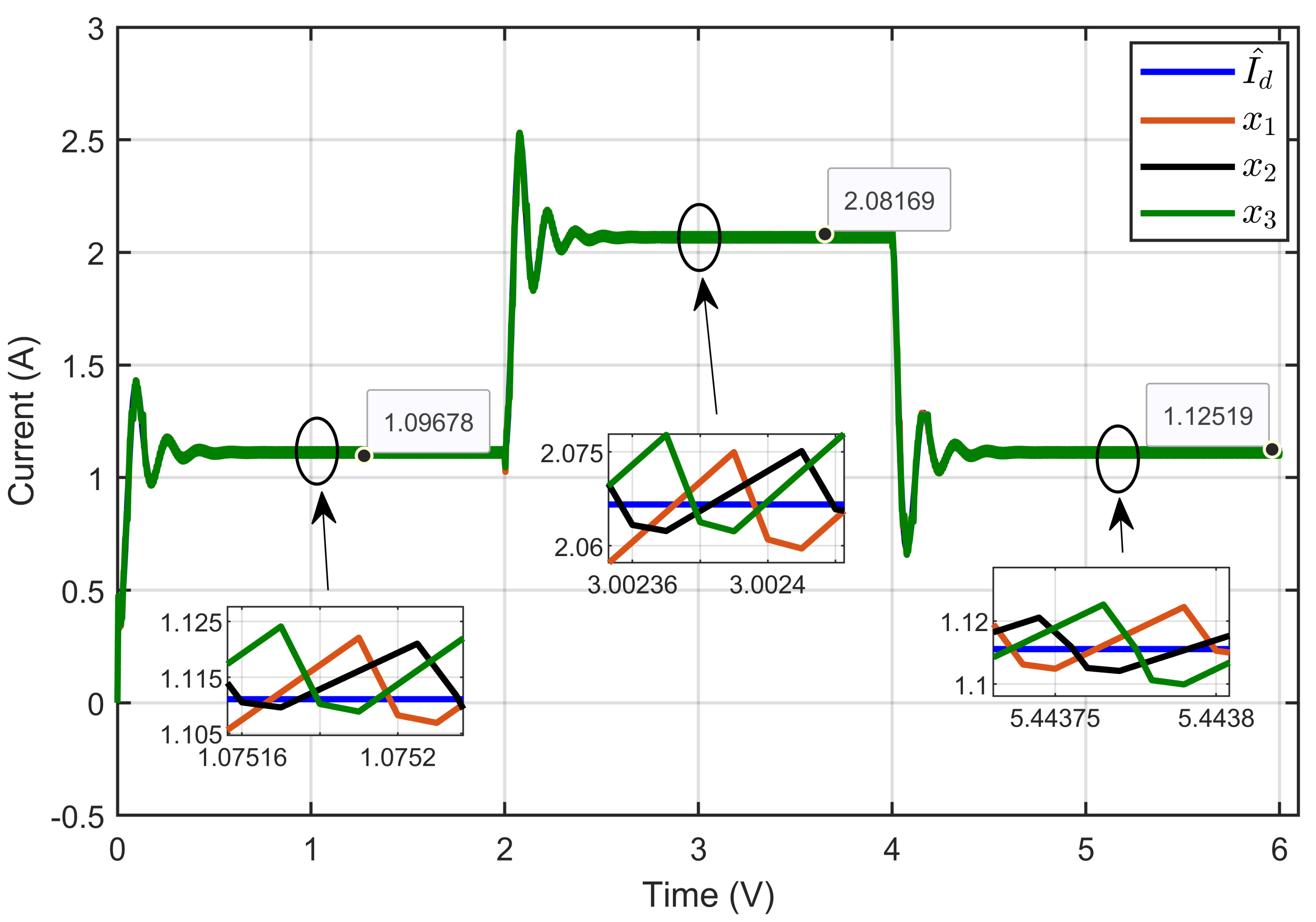
7.1. Performance Validation of Adaptive Sliding Mode Control for a Reference Step in PEM Electrolyzer Voltage
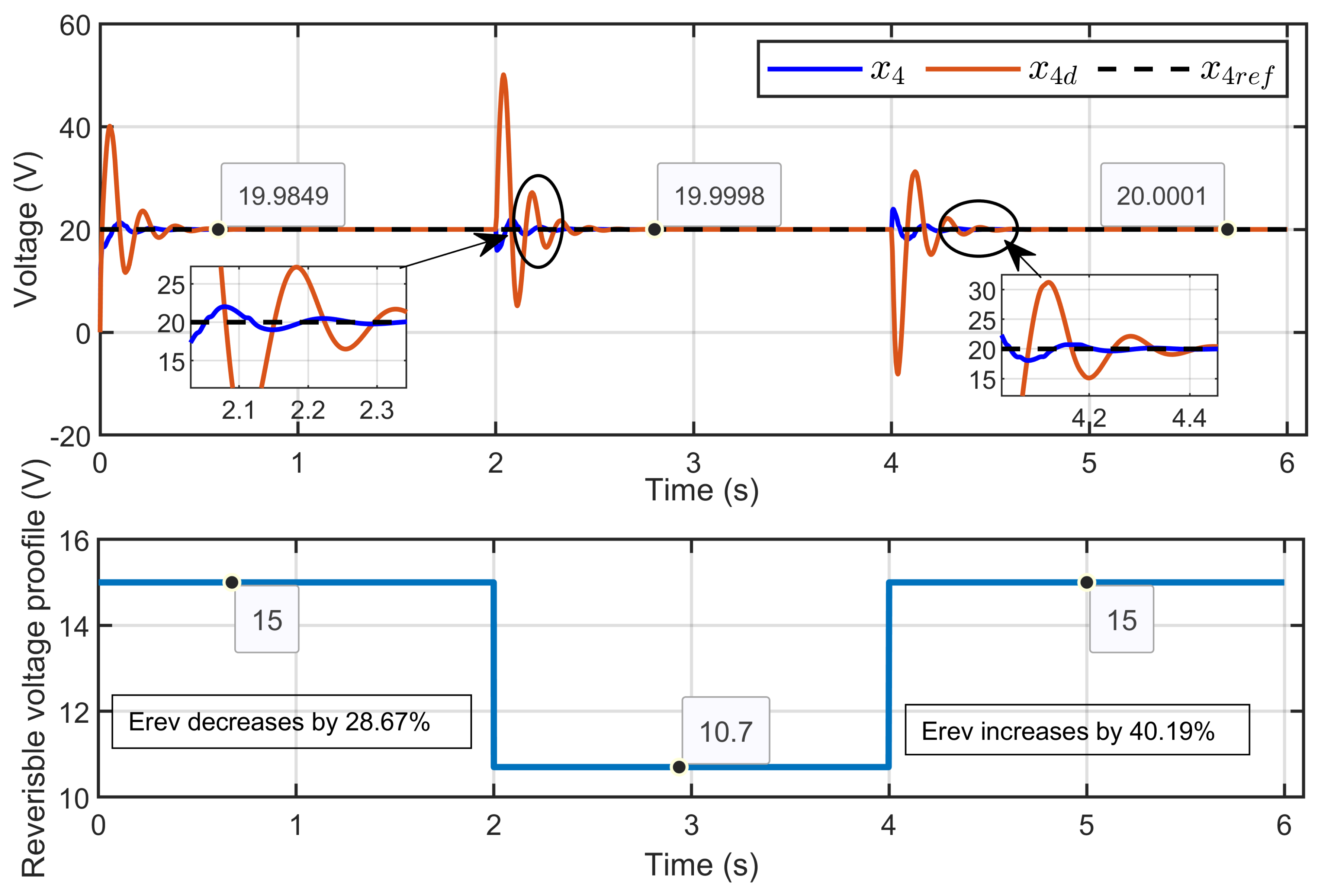
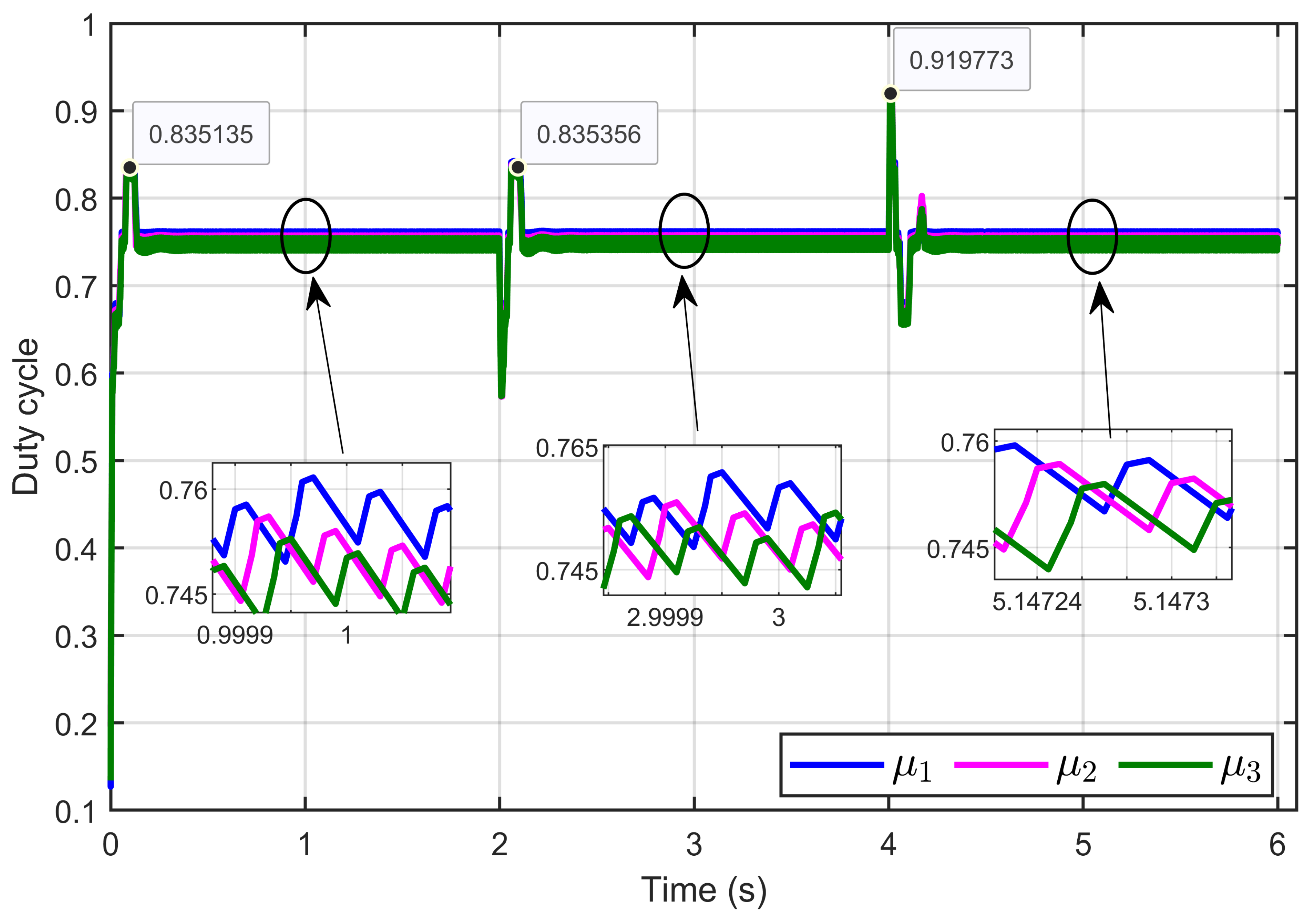
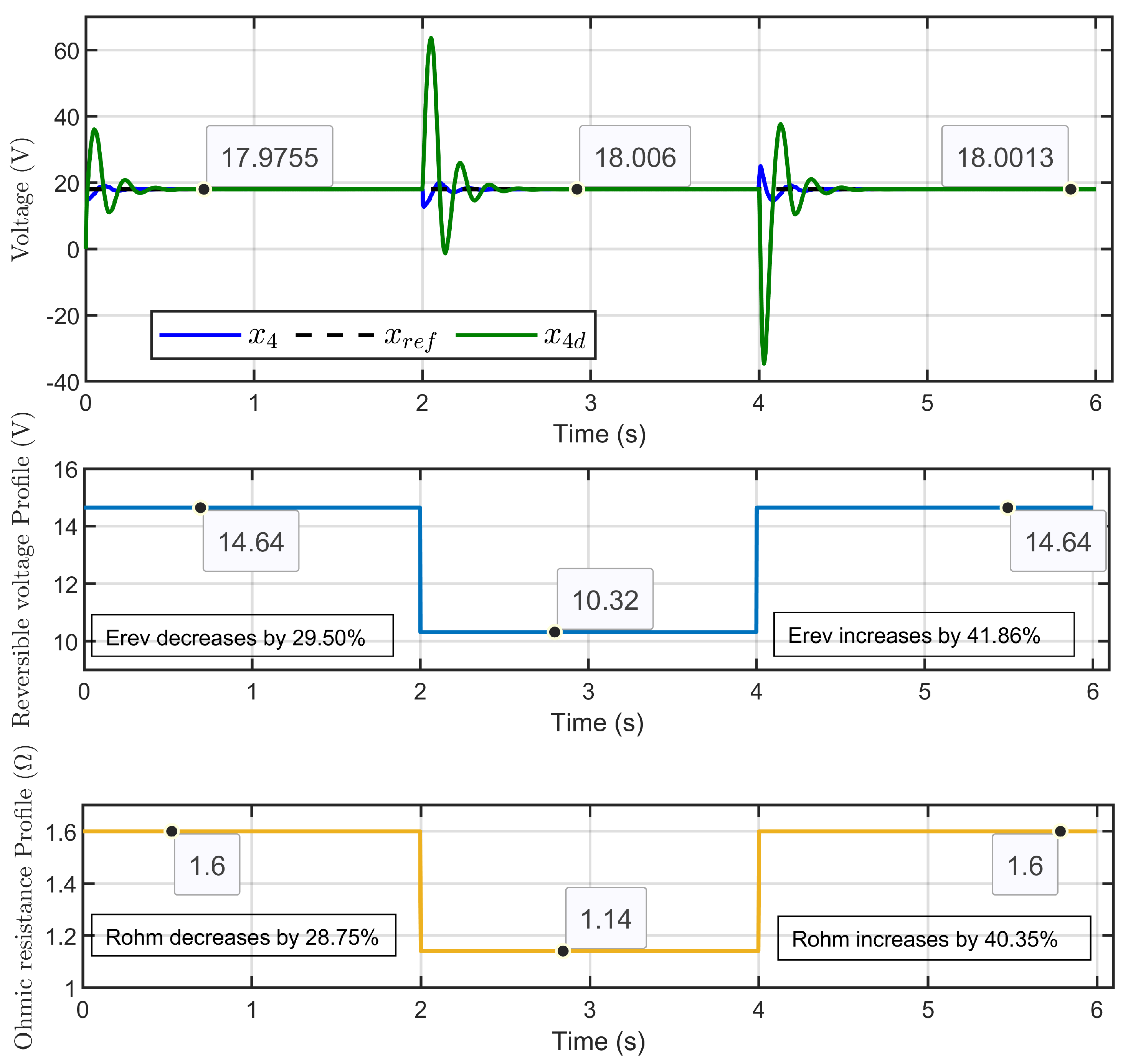
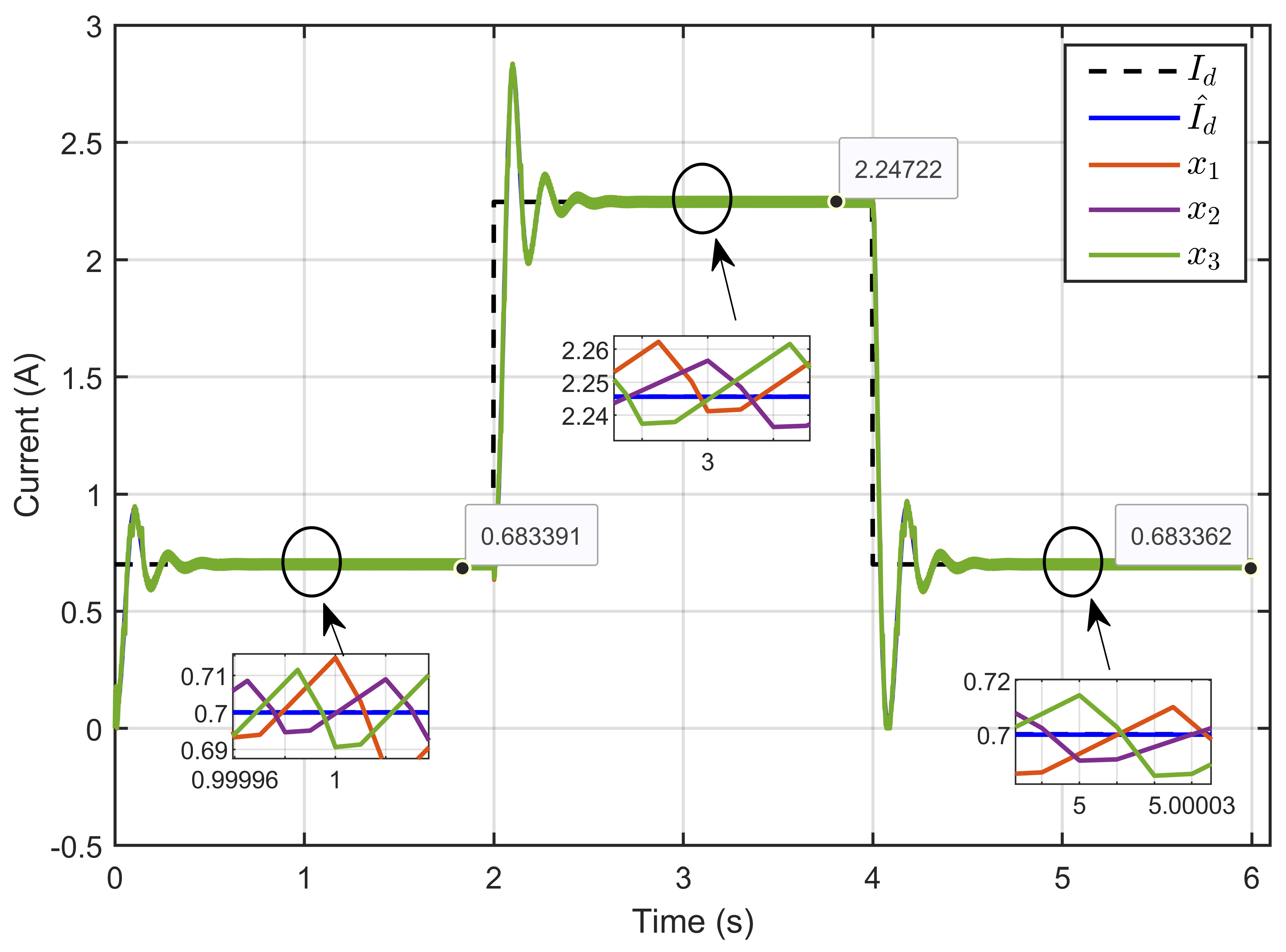
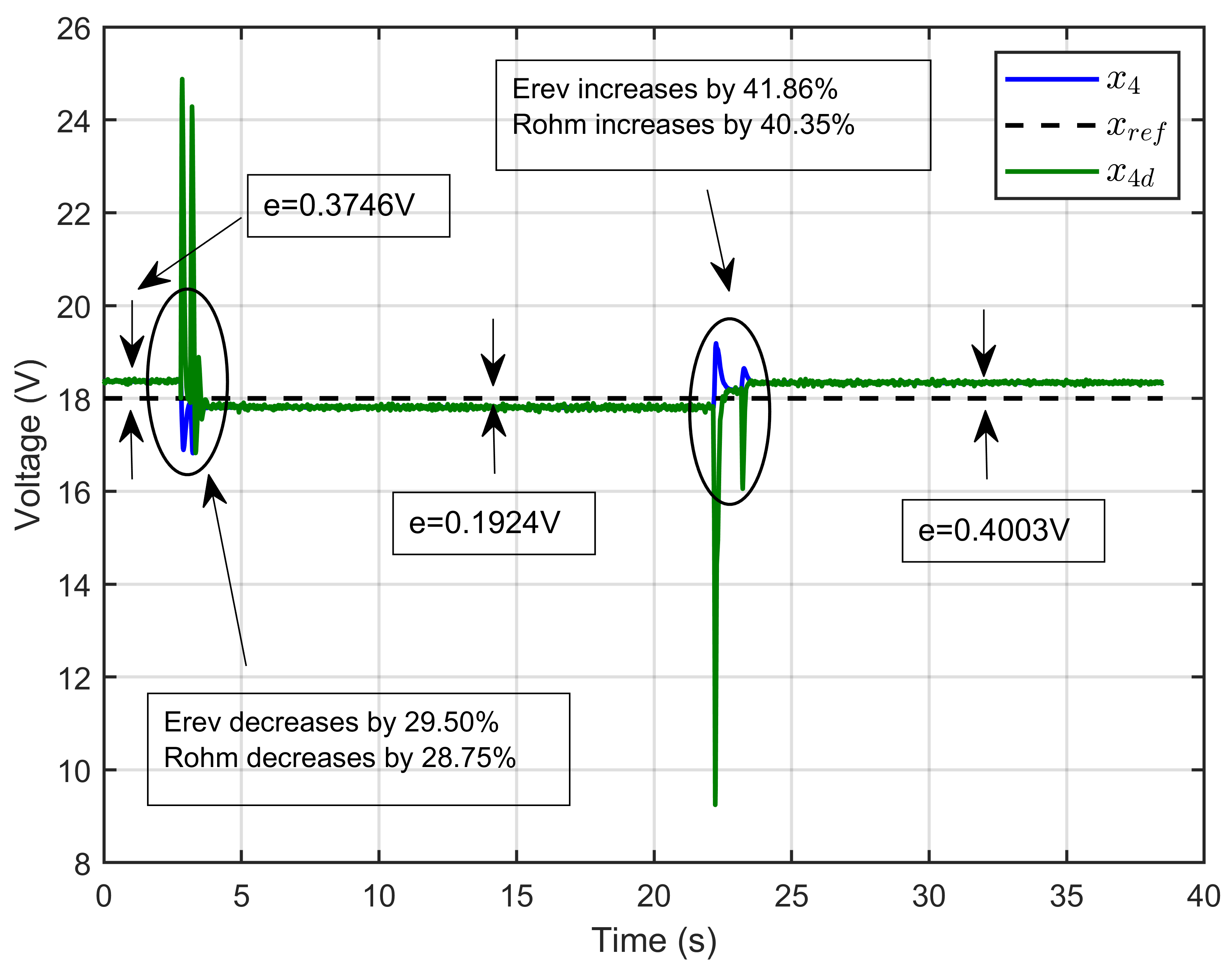
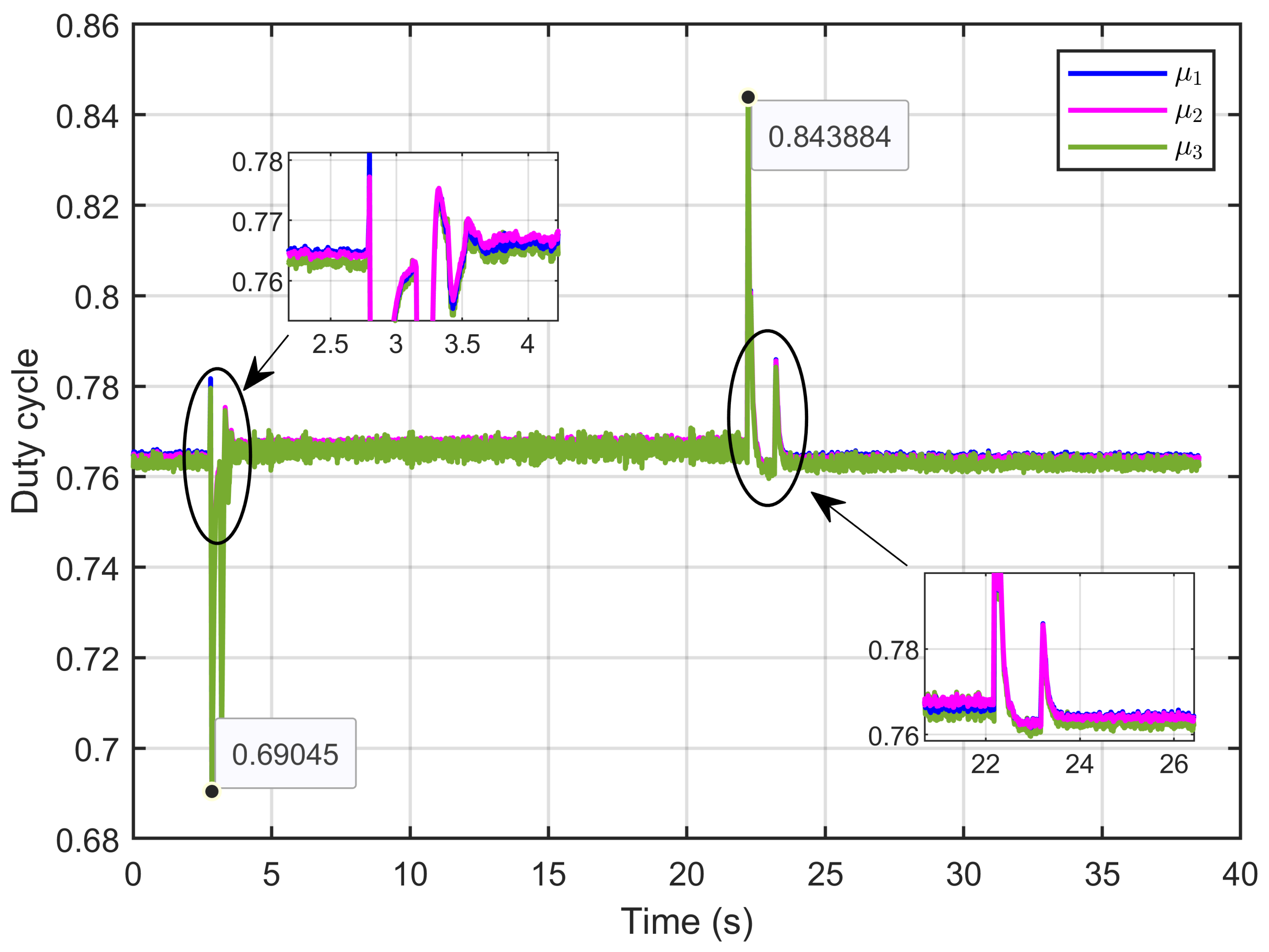
7.2. Experimental Validation of Performance and Sensitivity to Perturbations Caused by Sudden Variations in PEM Electrolyzer Operation Conditions
8. Discussion
9. Conclusions
- ▪
- Accurate regulation of the PEM electrolyzer voltage under varying operating conditions.
- ▪
- Equal current sharing between the parallel legs of the IBC despite different inductance values.
- ▪
- Ensure overall stability system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Selection of Filtering Capacitance
Appendix A.1.1. Capacitance Value
Appendix A.1.2. Voltage Rating
Appendix A.2. Selection of Filtering Inductance
Appendix A.2.1. Inductance Value
Appendix A.2.2. Current Rating (IL)
Appendix A.2.3. Core Material
Appendix A.3. Selection of the Schottky Diode
Appendix A.3.1. Reverse Voltage Rating (VRRM)
Appendix A.3.2. Forward Current Rating (IF)
Appendix A.4. Selection of the IGBT Transistor
Appendix A.4.1. Collector-Emitter Voltage Rating (VCE)
Appendix A.4.2. Current Rating (IC)
Appendix A.4.3. Switching Frequency and Switching Losses
Appendix A.4.4. Gate Drive Requirements
Appendix A.5. Thermal Considerations
References
- Yodwong, B.; Guilbert, D.; Phattanasak, M.; Kaewmanee, W.; Hinaje, M.; Vitale, G. Proton Exchange Membrane Electrolyzer Modeling for Power Electronics Control: A Short Review. C—J. Carbon Res. 2020, 6, 29. [Google Scholar] [CrossRef]
- Yodwong, B.; Guilbert, D.; Phattanasak, M.; Kaewmanee, W.; Hinaje, M.; Vitale, G. AC-DC converters for electrolyzer applications: State of the art and future challenges. Electronics 2020, 9, 912. [Google Scholar] [CrossRef]
- Koundi, M.; El Fadil, H.; EL Idrissi, Z.; Lassioui, A.; Intidam, A.; Bouanou, T.; Nady, S.; Rachid, A. Investigation of hydrogen production system-based PEM EL: PEM EL modeling, DC/DC power converter, and controller design approaches. Clean Technol. 2023, 5, 531–568. [Google Scholar] [CrossRef]
- Ganeshan, I.S.; Manikandan, V.V.S.; Ram Sundhar, V.; Sajiv, R.; Shanthi, C.; Kottayil, S.K.; Ramachandran, T. Regulated hydrogen production using solar powered electrolyser. Int. J. Hydrogen Energy 2016, 41, 10322–10326. [Google Scholar] [CrossRef]
- Ingole, D.; Drgoňa, J.; Kalúz, M.; Klaučo, M.; Bakošová, M.; Kvasnica, M. Model predictive control of a combined electrolyzer-fuel cell educational pilot plant. In Proceedings of the 2017 21st International Conference on Process Control (PC), Strbske Pleso, Slovakia, 6–9 June 2017; pp. 149–154. [Google Scholar]
- Koundi, M.; El Fadil, H.; Rachid, A.; El Idrissi, Z.; Giri, F.; Guerrero, J. Output Feedback Sliding Mode Control of PEM EL-IBC System for Hydrogen Production. IFAC-PapersOnLine 2019, 52, 85–90. [Google Scholar] [CrossRef]
- Şahin, M.E.; Okumuş, H.İ.; Aydemir, M.T. Implementation of an electrolysis system with DC/DC synchronous buck converter. Int. J. Hydrogen Energy 2014, 39, 6802–6812. [Google Scholar] [CrossRef]
- Yodwong, B.; Guilbert, D.; Kaewmanee, W.; Phattanasak, M. Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer. Electronics 2019, 8, 933. [Google Scholar] [CrossRef]
- Guilbert, D.; Sorbera, D.; Vitale, G. A stacked interleaved DC-DC buck converter for proton exchange membrane electrolyzer applications: Design and experimental validation. Int. J. Hydrogen Energy 2020, 45, 64–79. [Google Scholar] [CrossRef]
- Albarghot, M.; Rolland, L. MATLAB/Simulink modelling and experimental results of a PEM electrolyzer powered by a solar panel. In Proceedings of the 2016 IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016. [Google Scholar]
- Nafeh, A.E.-S.A. Hydrogen production from a PV/PEM electrolyzer system using a neural-network-based MPPT algorithm. Int. J. Numer. Model. Electron. Netw. Devices Fields 2011, 24, 282–297. [Google Scholar] [CrossRef]
- Koundi, M.; El Idrissi, Z.; El Fadil, H.; Belhaj, F.Z.; Lassioui, A.; Gaouzi, K.; Rachid, A.; Giri, F. State-Feedback Control of Interleaved Buck–Boost DC–DC Power Converter with Continuous Input Current for Fuel Cell Energy Sources: Theoretical Design and Experimental Validation. World Electr. Veh. J. 2022, 13, 124. [Google Scholar] [CrossRef]
- Hernández-Gómez, Á.; Ramirez, V.; Guilbert, D. Investigation of PEM electrolyzer modeling: Electrical domain, efficiency, and specific energy consumption. Int. J. Hydrogen Energy 2020, 45, 14625–14639. [Google Scholar] [CrossRef]
- Maamouri, R.; Guilbert, D.; Zasadzinski, M.; Rafaralahy, H. Proton exchange membrane water electrolysis: Modeling for hydrogen flow rate control. Int. J. Hydrogen Energy 2021, 46, 7676–7700. [Google Scholar] [CrossRef]
- Makineni, R.R.; Agalgaonkar, A.P.; Muttaqi, K.M.; Islam, M.R.; Sutanto, D. Integral sliding mode control of a stacked interleaved buck converter for electrolyzers supplied with renewable energy sources. IEEE Trans. Ind. Appl. 2024, 61, 450–462. [Google Scholar] [CrossRef]
- Guilbert, D.; Yodwong, B.; Kaewmanee, W.; Phattanasak, M.; Hinaje, M. Hydrogen Flow Rate Control of a Proton Exchange Membrane Electrolyzer. In Proceedings of the 2019 Research, Invention, and Innovation Congress (RI2C), Bangkok, Thailand, 11–13 December 2019. [Google Scholar]
- Torok, L.; Mathe, L.; Nielsen, C.K.; Munk-Nielsen, S. Modeling and Control of Three-Phase Grid-Connected Power Supply With a Small DC-Link Capacitor for Electrolyzers. IEEE Trans. Ind. Appl. 2017, 53, 4634–4643. [Google Scholar] [CrossRef]
- Török, L.; Nielsen, C.K.; Munk-Nielsen, S.; Rømer, C.; Flindt, P. High efficiency electrolyser power supply for household hydrogen production and storage systems. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–9. [Google Scholar]
- Collura, S.M.; Guilbert, D.; Vitale, G.; Luna, M.; Alonge, F.; D’Ippolito, F.; Scipioni, A. Design and experimental validation of a high voltage ratio DC/DC converter for proton exchange membrane electrolyzer applications. Int. J. Hydrogen Energy 2019, 44, 7059–7072. [Google Scholar] [CrossRef]
- Azer, P.; Emadi, A. Generalized state space average model for multi-phase interleaved buck, boost and buck-boost DC-DC converters: Transient, steady-state and switching dynamics. IEEE Access 2020, 8, 77735–77745. [Google Scholar] [CrossRef]
- Slotine, J.J.E. Sliding Controller Design for Nonlinear Systems. Int. J. Control 1984, 40, 421. [Google Scholar] [CrossRef]











| Parameter | Value | |
|---|---|---|
| PEM electrolyzer | PEM electrolyzer voltage | Vel = 8–22 V |
| PEM electrolyzer current | Iel = 0–13 A | |
| Reversible voltage | Erev = 7.45–15 V | |
| Ohmic resistance | Rmem = 1.14–1.6 Ω | |
| DC/DC IBC | Filtering inductors | L1 = L3 = 10 mH L2 = 15 mH |
| ERS of the inductances | r1 = r2 = r3 = 0.1 Ω | |
| Filtering capacitor | C = 1410 µF | |
| Switching frequency | Fs = 20 kHz | |
| Adaptive SMC controller | Adaptive law | |
| k4 = 20 | ||
| SMC controller | k1 = k2 = k3 = 200 | |
| λ21 = λ22 = λ23 = 103 | ||
| Sample time | th = 10−5 s |
| Metric | Relative Error (Step 1) | Relative Error (Step 2) |
|---|---|---|
| PEM electrolyzer voltage regulation (x4 − xref) | 0.004% | 0.0075% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.0040% | 0.0067% |
| Reference current estimation error (Id − ) | 0.0054% | 9.8902 × 10−4% |
| Current sharing error | 0.0715% | 0.1216% |
| Scenario | Metric | Relative Error |
|---|---|---|
| Scenario 1: Erev = 9.6 V; Rohm changes: −28.75%, +40.35% | PEM electrolyzer voltage regulation (x4 − ref) | 0.0042% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.3% | |
| Reference current estimation error (Id − ) | 0.4515% | |
| Current sharing error | 0.7037% | |
| Scenario 2: Rohm = 1.5 Ω; changes: −28.75%, +40.19% | PEM electrolyzer voltage regulation (x4 − xref) | 0.0035% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.0070% | |
| Reference current estimation error (Id − ) | 0.0019% | |
| Current sharing error | 0.1166% | |
| Scenario 3: Erev changes: −29.50%, +41.86%; Rohm changes: −28.75%, +40.35% | PEM electrolyzer voltage regulation (x4 − xref) | 0.0028% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.004% | |
| Reference current estimation error (Id − and current sharing error | 0.1069% |
| Parameter | Value | |
|---|---|---|
| Adaptive SMC | Adaptive Law | |
| k4 = 12 | ||
| SMC Controller | k1 = k2 = k3 = 50 | |
| λ21 = λ22 = λ23 = 6 × 102 | ||
| Sampling Time | th = 10−4 s |
| Metric | Relative Error (Step 1) | Relative Error (Step 2) |
|---|---|---|
| PEM electrolyzer voltage regulation (x4 − xref) | 0.2313% | 0.6642% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.2812% | 0.9267% |
| Reference current estimation error (Id − | 0.2482% | 0.4351% |
| Current sharing error | 1.7607% | 0.4320% |
| Scenario | Metric | Relative Error |
|---|---|---|
| Scenario 1: Erev = 9.6 V; Rohm changes: −28.75%, +40.35% | PEM electrolyzer voltage regulation (x4 − xref) | 0.0044% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.0012% | |
| Reference current estimation error (Id − ) | 0.0016% | |
| Current sharing error | 0.2811% | |
| Scenario 2: Rohm = 1.5 Ω; changes: −28.75%, +40.19% | PEM electrolyzer voltage regulation (x4 − xref) | 0.0035% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.0070% | |
| Reference current estimation error (Id − ) | 0.0019% | |
| Current sharing error | 0.1166% | |
| Scenario 3: Erev changes: −29.50%, +41.86%; Rohm changes: −28.75%, +40.35% | PEM electrolyzer voltage regulation (x4 − xref) | 0.0028% |
| PEM electrolyzer voltage tracking error (x4 − xd) | 0.004% | |
| Reference current estimation error (Id − and current sharing error | 0.1069% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koundi, M.; El Fadil, H.; Lassioui, A.; El Asri, Y. Adaptive Sliding Mode Control of an Interleaved Buck Converter–Proton Exchange Membrane Electrolyzer for a Green Hydrogen Production System. Processes 2025, 13, 795. https://doi.org/10.3390/pr13030795
Koundi M, El Fadil H, Lassioui A, El Asri Y. Adaptive Sliding Mode Control of an Interleaved Buck Converter–Proton Exchange Membrane Electrolyzer for a Green Hydrogen Production System. Processes. 2025; 13(3):795. https://doi.org/10.3390/pr13030795
Chicago/Turabian StyleKoundi, Mohamed, Hassan El Fadil, Abdellah Lassioui, and Yassine El Asri. 2025. "Adaptive Sliding Mode Control of an Interleaved Buck Converter–Proton Exchange Membrane Electrolyzer for a Green Hydrogen Production System" Processes 13, no. 3: 795. https://doi.org/10.3390/pr13030795
APA StyleKoundi, M., El Fadil, H., Lassioui, A., & El Asri, Y. (2025). Adaptive Sliding Mode Control of an Interleaved Buck Converter–Proton Exchange Membrane Electrolyzer for a Green Hydrogen Production System. Processes, 13(3), 795. https://doi.org/10.3390/pr13030795









