Analytical Solutions and Stability Analysis of a Fractional-Order Open-Loop CSTR Model for PMMA Polymerization
Abstract
1. Introduction
2. Mathematical Preliminaries and Definitions
- Riemann–Liouville Integral
- Caputo Fractional Derivative
- Auxiliary Functions
- Stability of Linearised Fractional Dynamical Systems
- Stable if and only if for all , there exist , such that given , then for all ;
- Asymptotically stable if and only if it is stable and .
3. Laplace Transformation of Caputo Fractional Derivatives
4. Problem Statement
4.1. Dynamic Model That Incorporates Integer Orders
4.2. Integer Order Dimensionless Dynamic Model
| Symbol | Parameter | Numerical Value | Units |
|---|---|---|---|
| T | Reactor temperature | 333 | K |
| V | Reactor volume | 1 | dm3 |
| Q | Volumetric flow rate | 0.1 | min−1 |
| Residence time | 10 | min | |
| Inlet initiator concentration | 0.0258 | mol·dm−3 | |
| Inlet monomer concentration | 9.98 | mol·dm−3 | |
| Kinetic coefficient for initiator | 1.28 × | min−1 | |
| Kinetic coefficient for propagation step | 3.54 × | dm3min−1 mol−1 | |
| Kinetic coefficient for termination step | 5.73 × | dm3min−1 mol−1 | |
| f | Initiator efficiency | 0.58 | dimensionless |
4.3. Fractional-Order Linearised Mathematical Model
5. Results and Discussion
5.1. Mathematical Model and Numerical Values
| Dimensionless Parameter | Numerical Value |
|---|---|
| 1.06565232 | |
| 0.17366676 | |
| 6732.4740 | |
| 6316.7022 | |
| 1.00000000 | |
| 1.17366676 | |
| 0.14796940 | |
| 1.14796940 | |
| 12,634.4044 | |
| 6316.7022 | |
| 2.00000000 | |
| 1.00000000 | |
| 0.85203060 | |
| 1.00000000 |
| Variable in the Steady State | Steady State | Steady State |
|---|---|---|
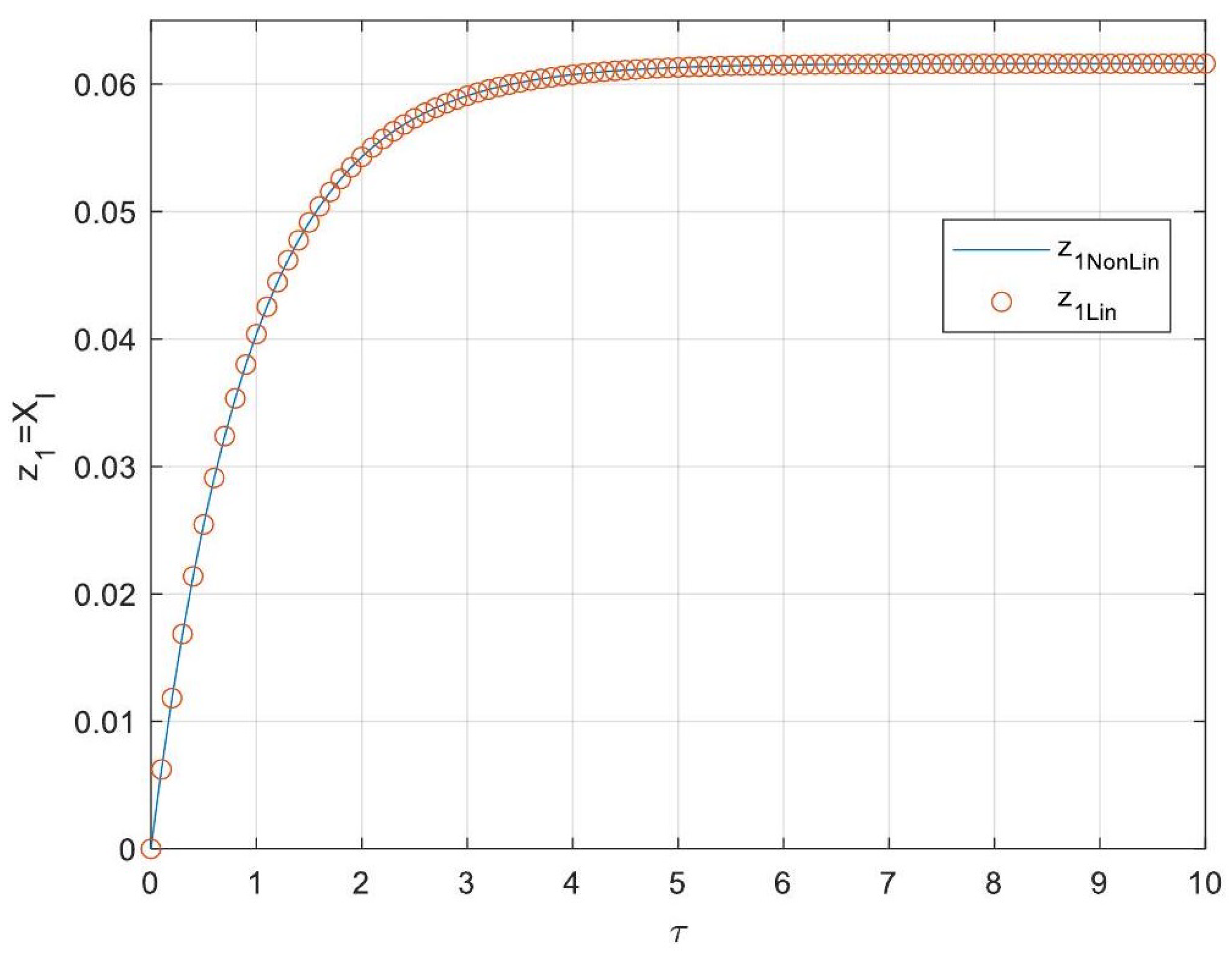
| 0.0242 | 0.0242 | |
| 8.5033 | 12.0779 | |
| Variable in the Steady State | Steady State 1 | Steady State 2 |
|---|---|---|
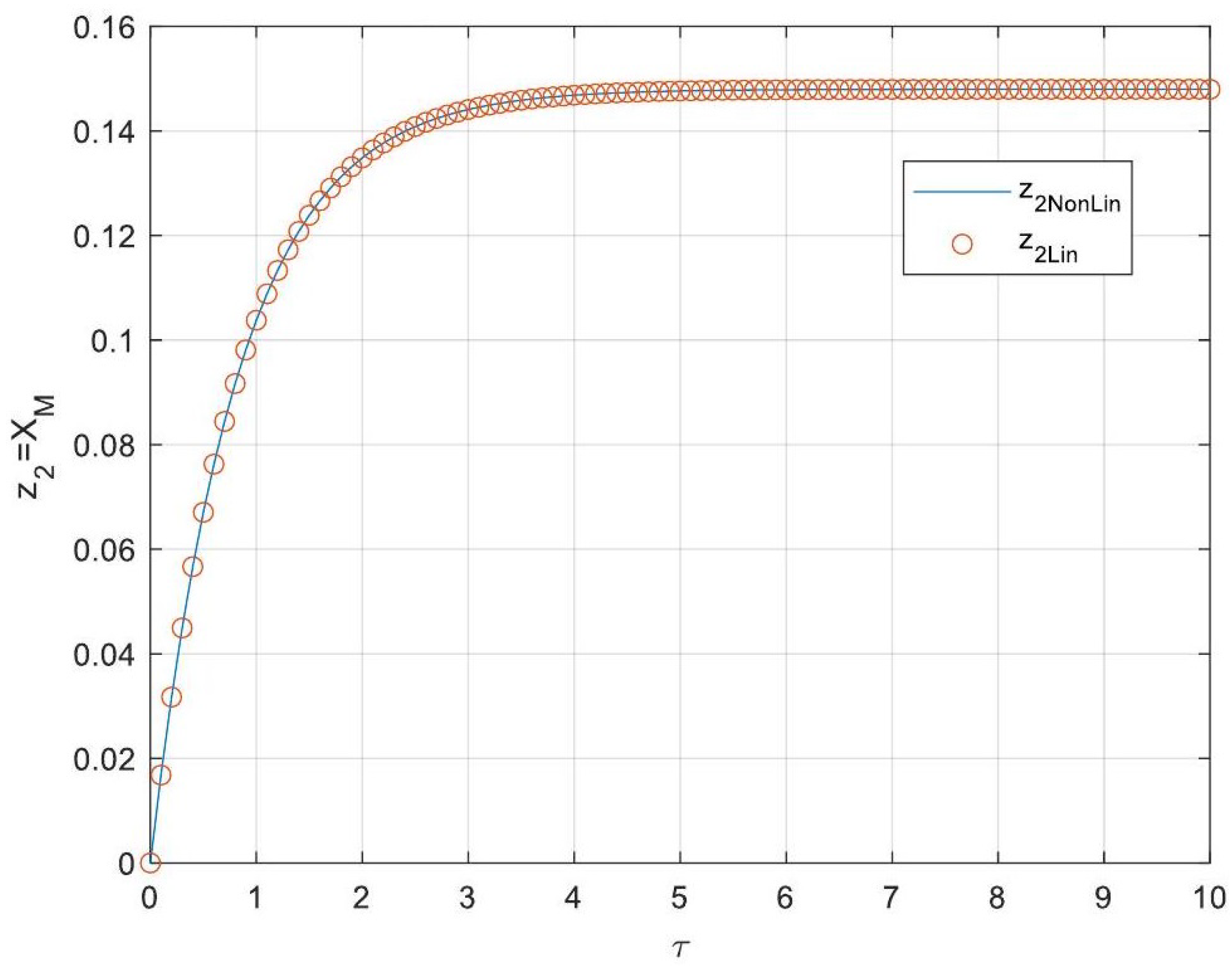
| 0.9384 | 0.9384 | |
| 0.8520 | 1.2102 | |
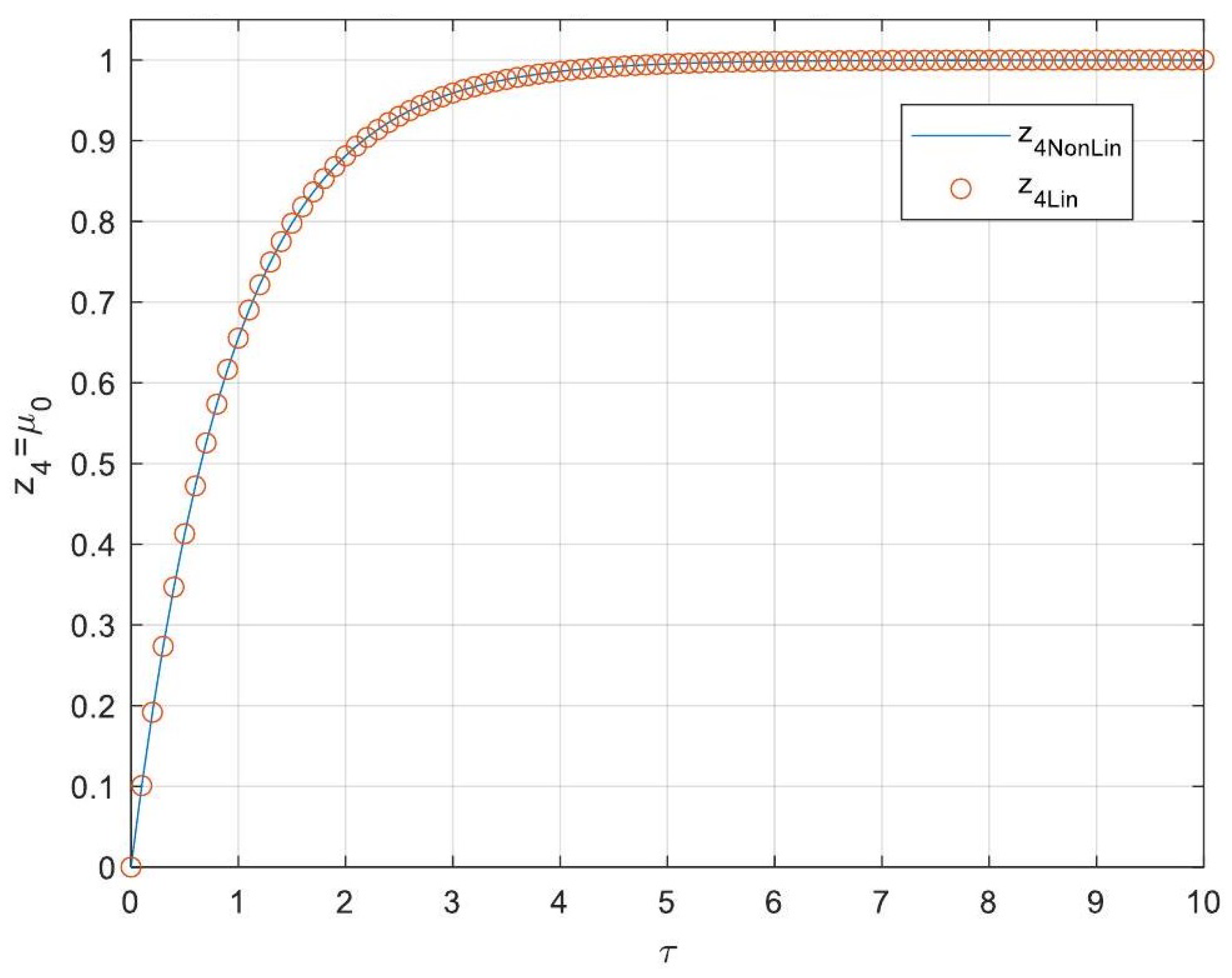
| 1 | −1.0001 | |
| 1 | 1.0003 |
5.2. Stability Analysis
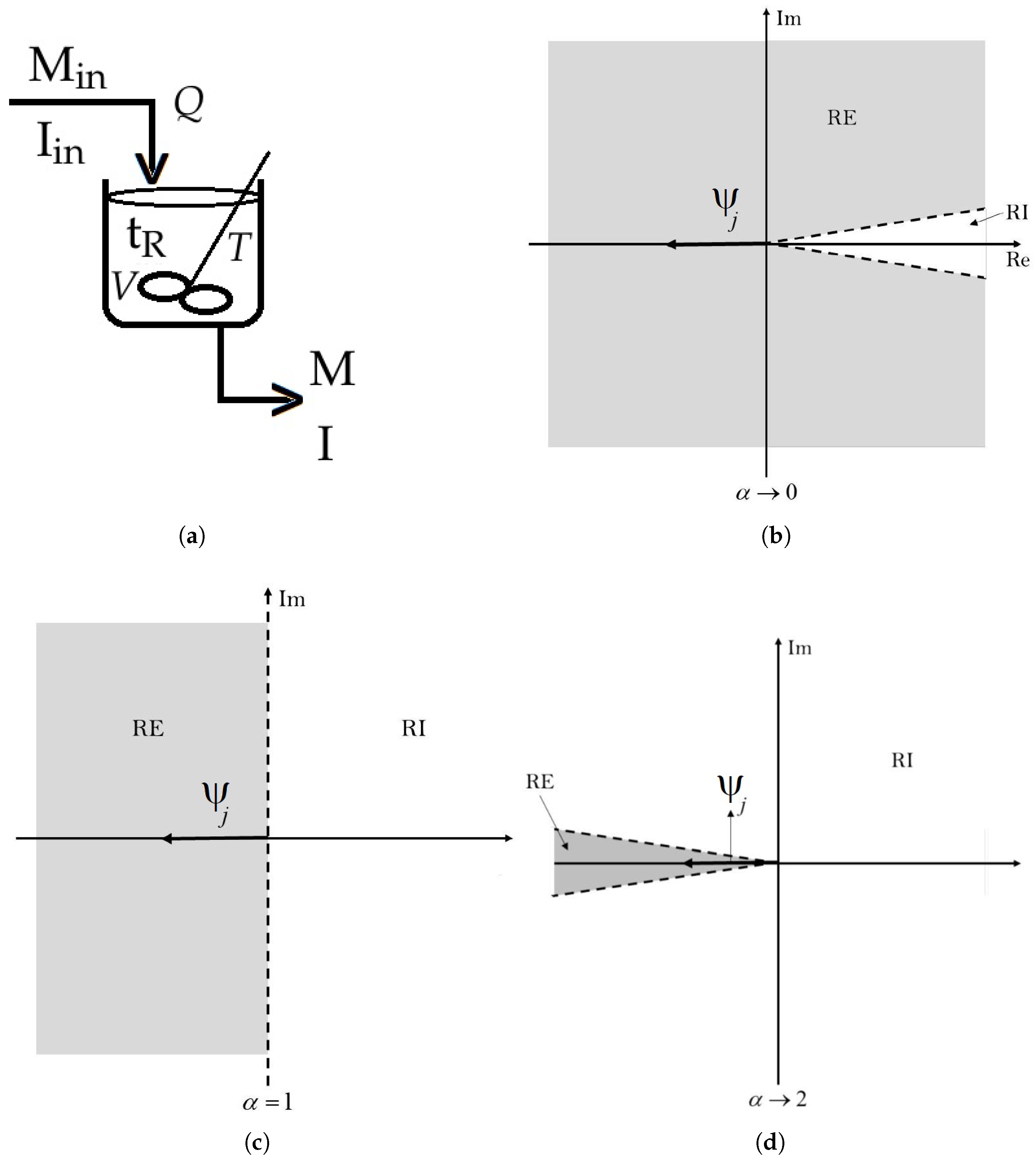
- When lies within the open interval , the mathematical analysis depicted in Figure 1b shows that as approaches zero, the limit of as tends to 0 is 0. Consequently, the stable region expands until it almost covers the entire complex plane, while the unstable region shrinks. As approaches one, the limit of as approaches 1 is . In this case, the stable and unstable regions almost become equal in size, resembling the stability regions of a first-order system. Therefore, for this specific scenario, falls within the open interval , where for any value of in , is greater than . . Hence, we can conclude that Equation (8) is met in this case.
- When equals 1, the fractional order system is transformed into an integer order system. In this case, , and the condition C is satisfied, which implies that . This situation is depicted in Figure 1c.
- For ranging between 1 and 2, the subsequent mathematical examination holds, as shown in Figure 1d: as approaches 1, , and the stability regions have been previously elucidated in case 1; as approaches 2, , leading to an expansion of the unstable region almost throughout the complex plane, while the stable region tends to shrink. Therefore, in this third scenario, is within the range , where for every value of , exceeds it, indicating thatTherefore, we can infer that in this particular scenario, Equation (8) is also met. Given that the condition given by Equation (8) is satisfied in all three cases examined above, we can deduce that the fractional order dynamical system of the CSTR polymerisation reactor for poly(methyl methacrylate) is asymptotically stable in its physically feasible steady state. This observation does not imply that fractional calculus is neither essential nor intriguing to mathematically model the reactor under investigation in this study. These mathematical techniques enable the expansion or contraction of unstable regions based on operational requirements while also helping to define the boundaries of desirable and safe operation.
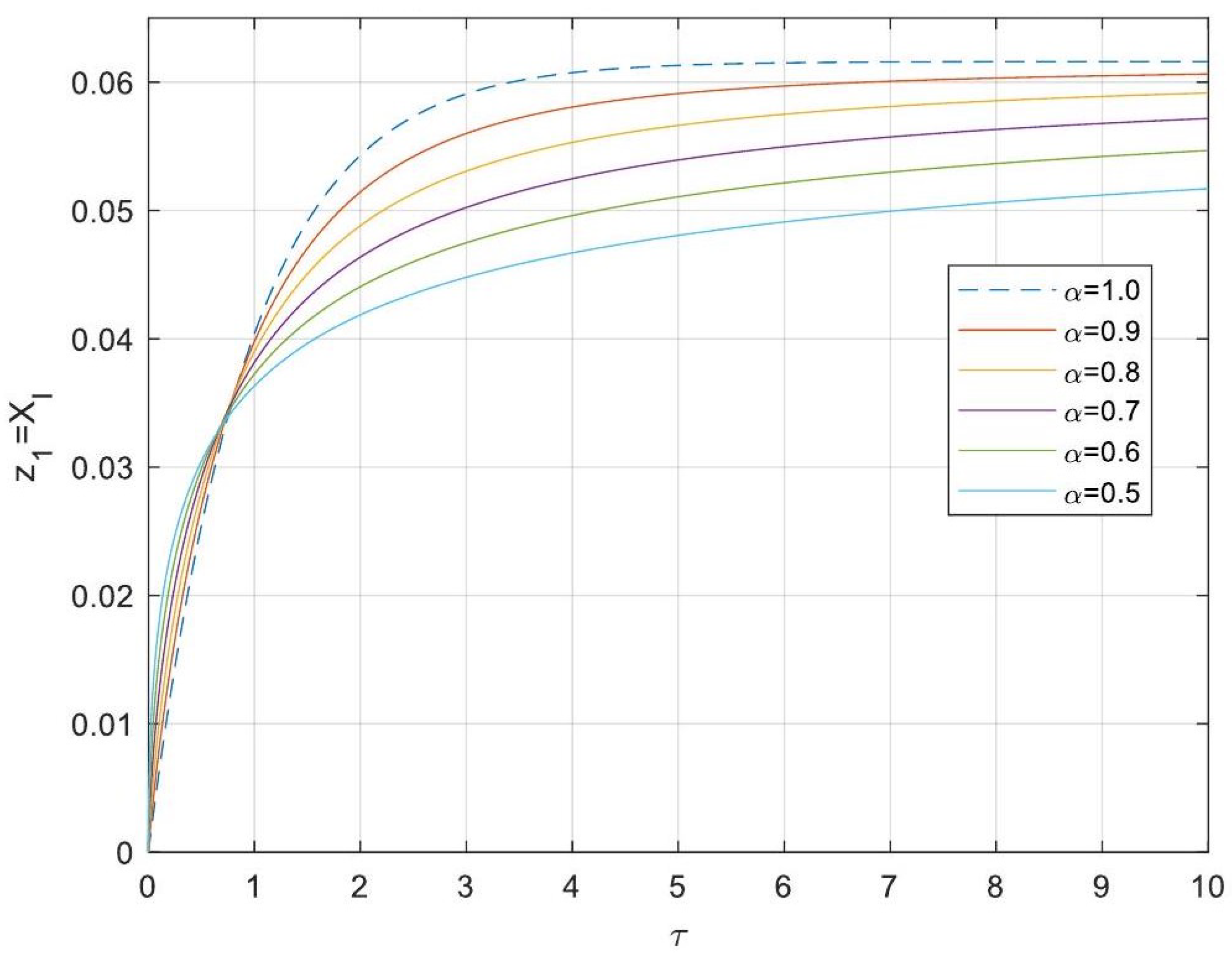
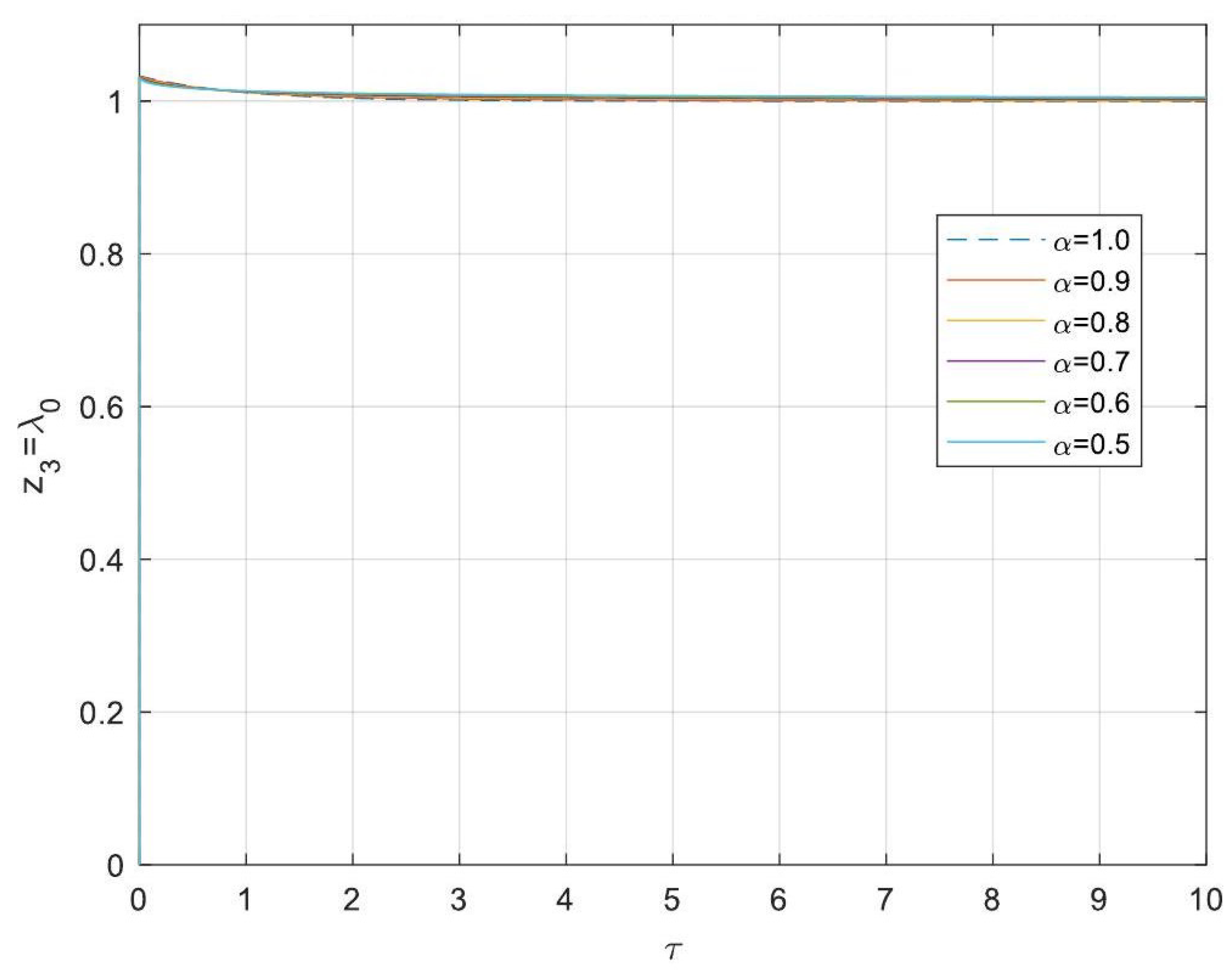
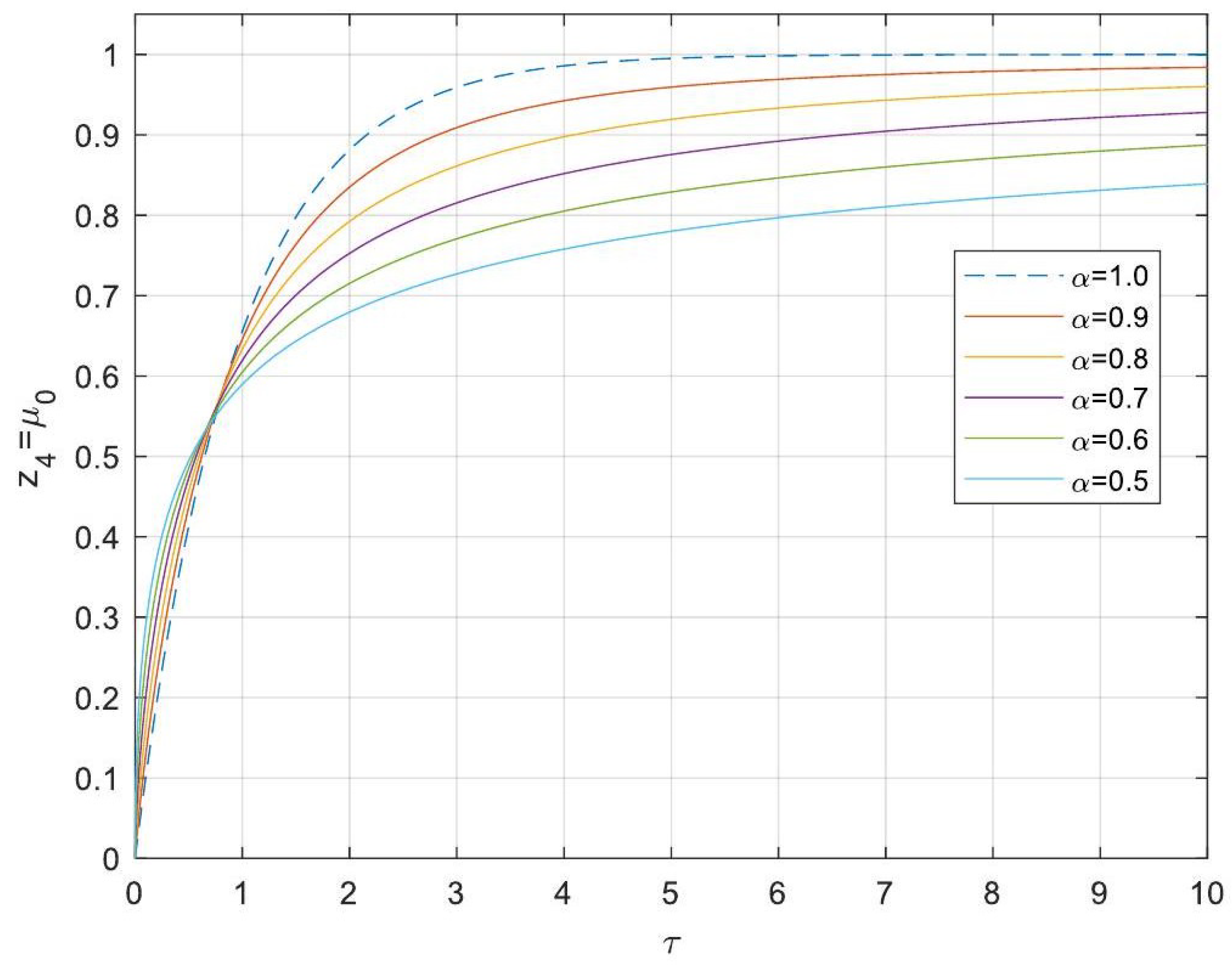
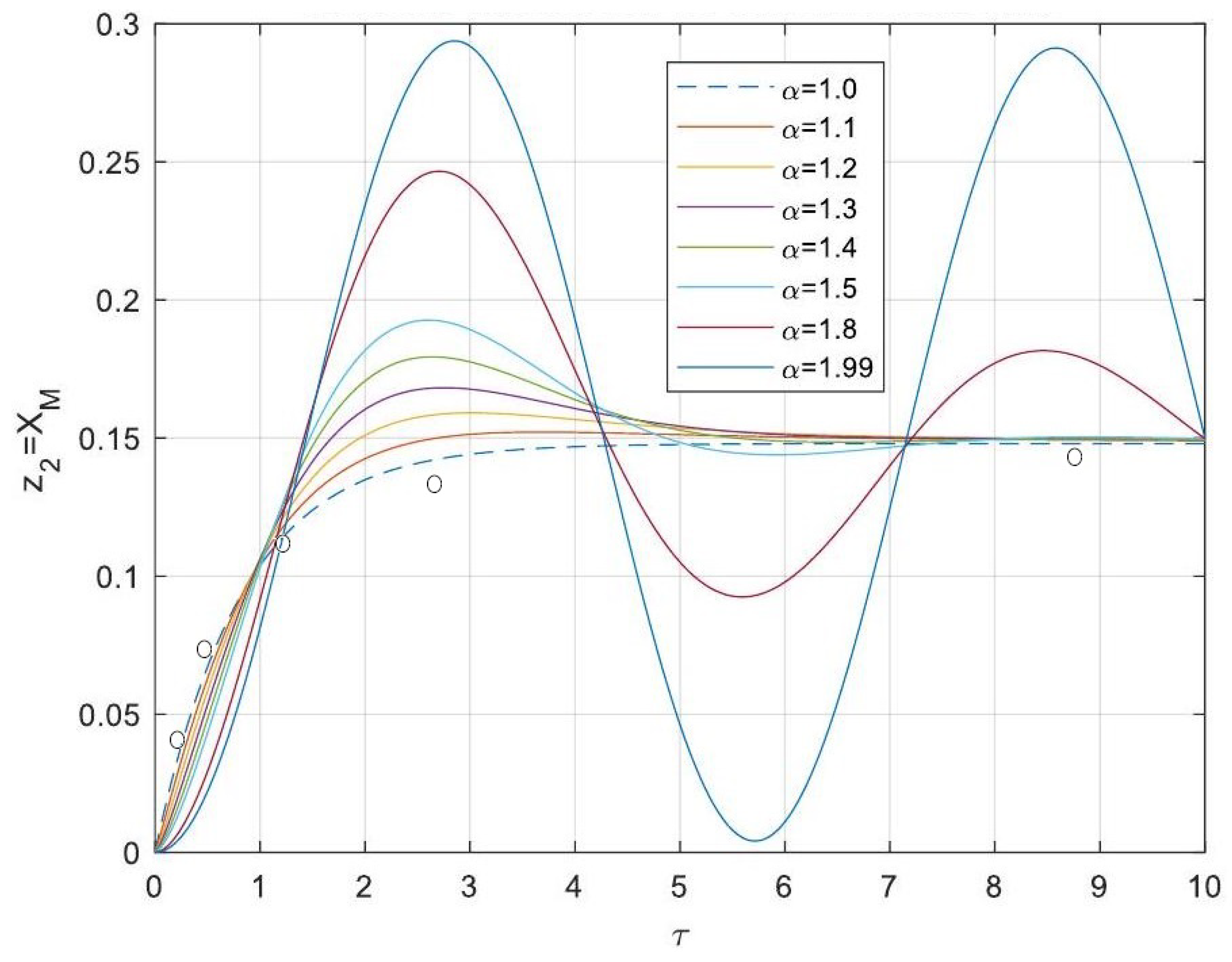
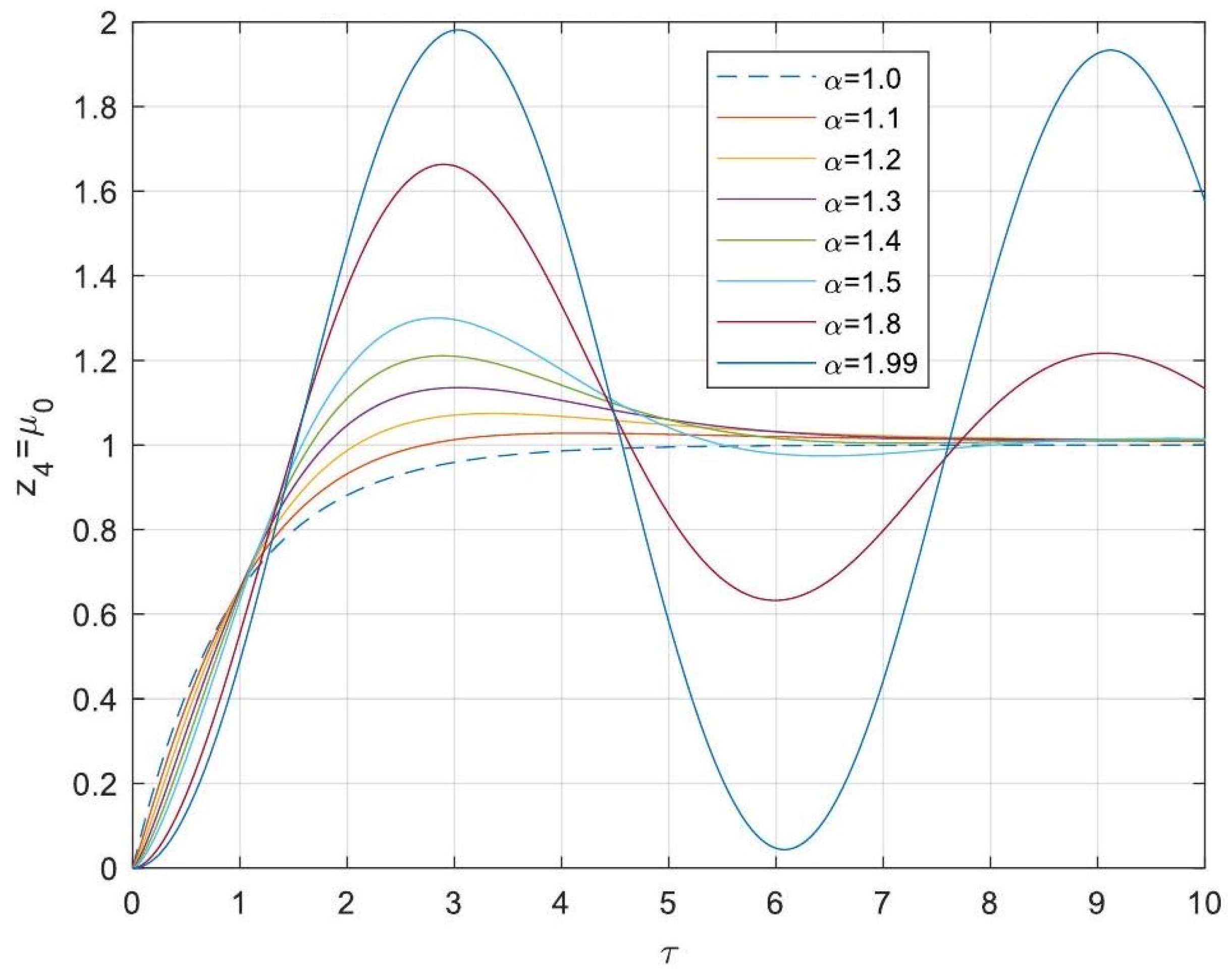
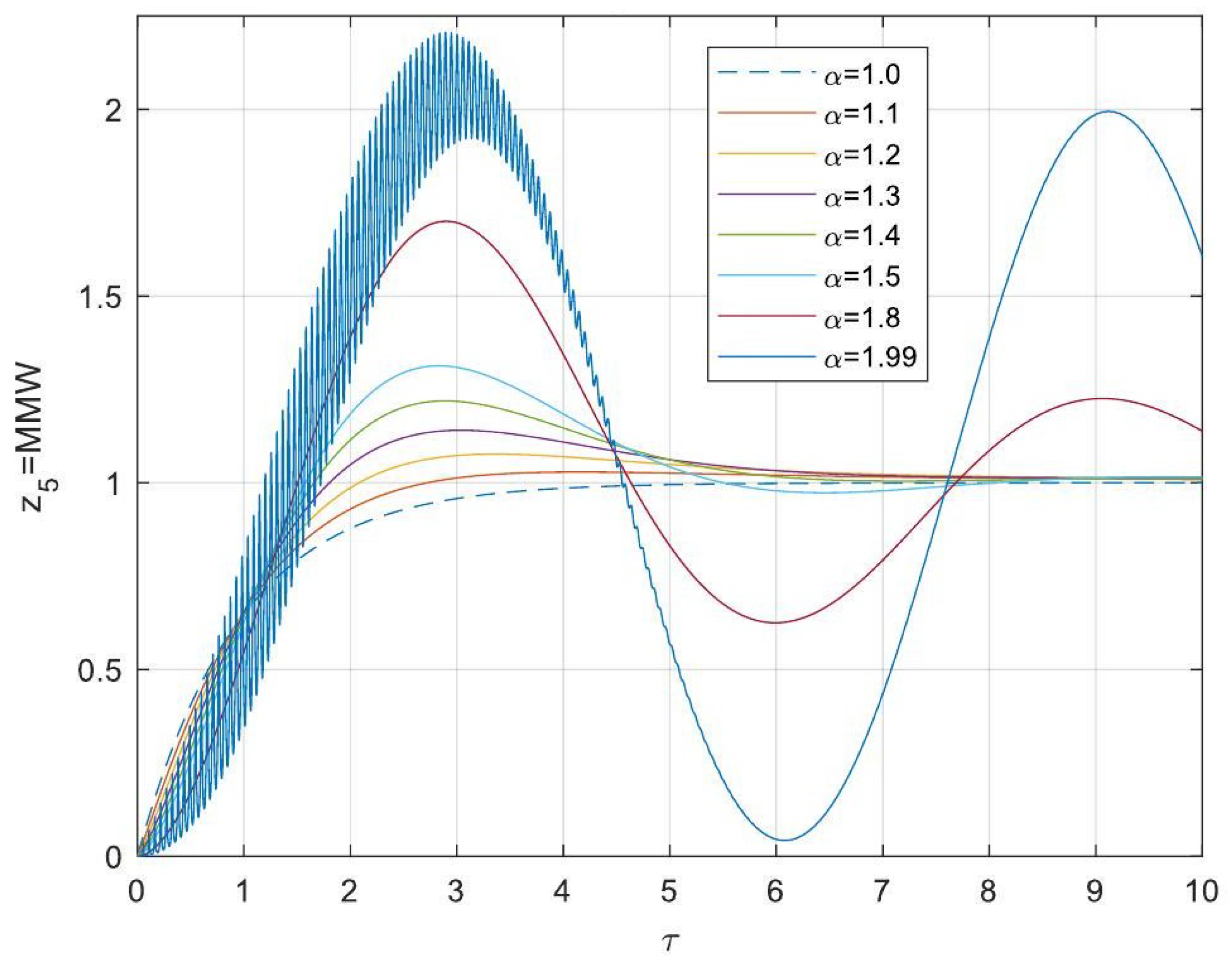
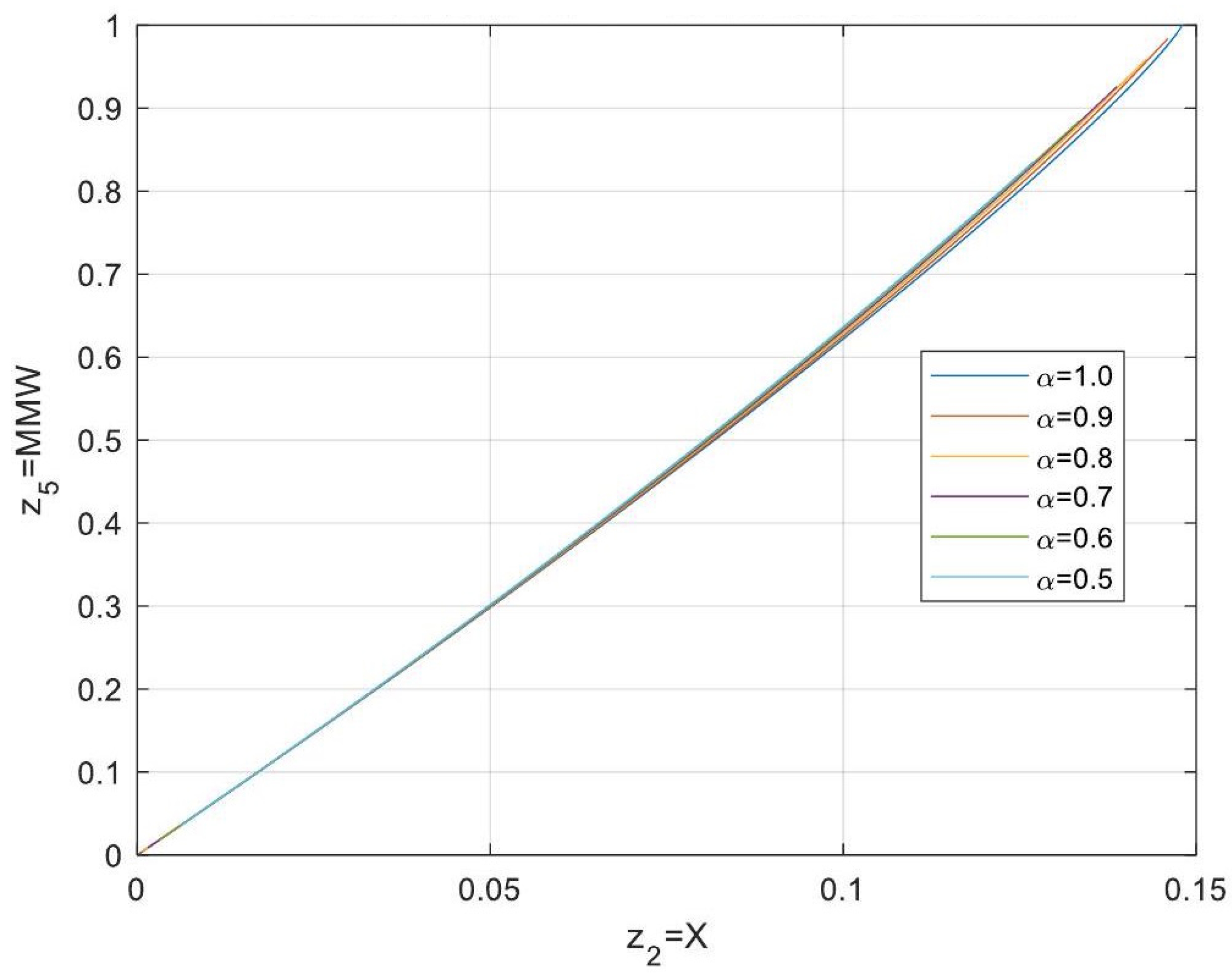
5.3. Analytical Solutions of the Linearised Model
6. Conclusions
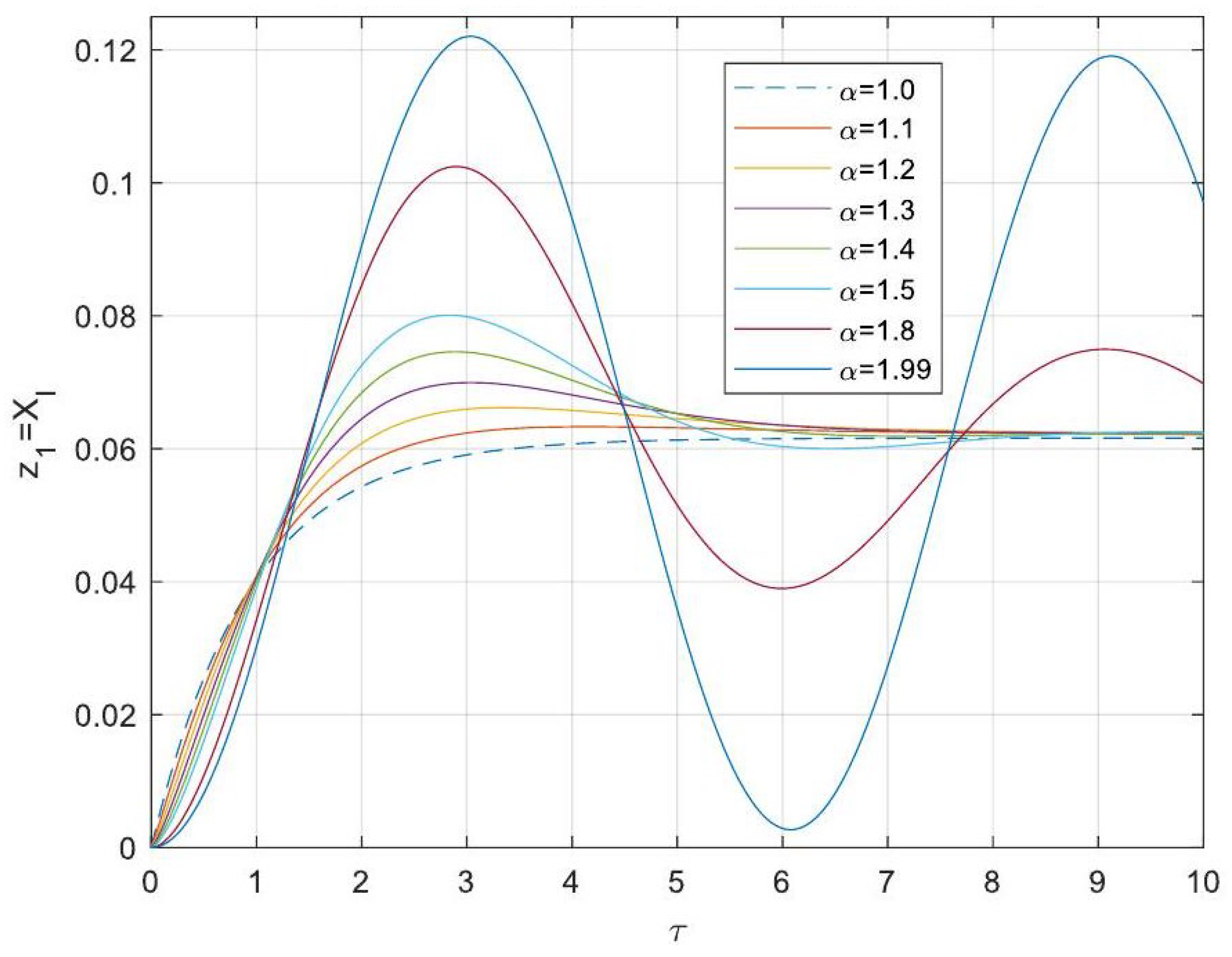
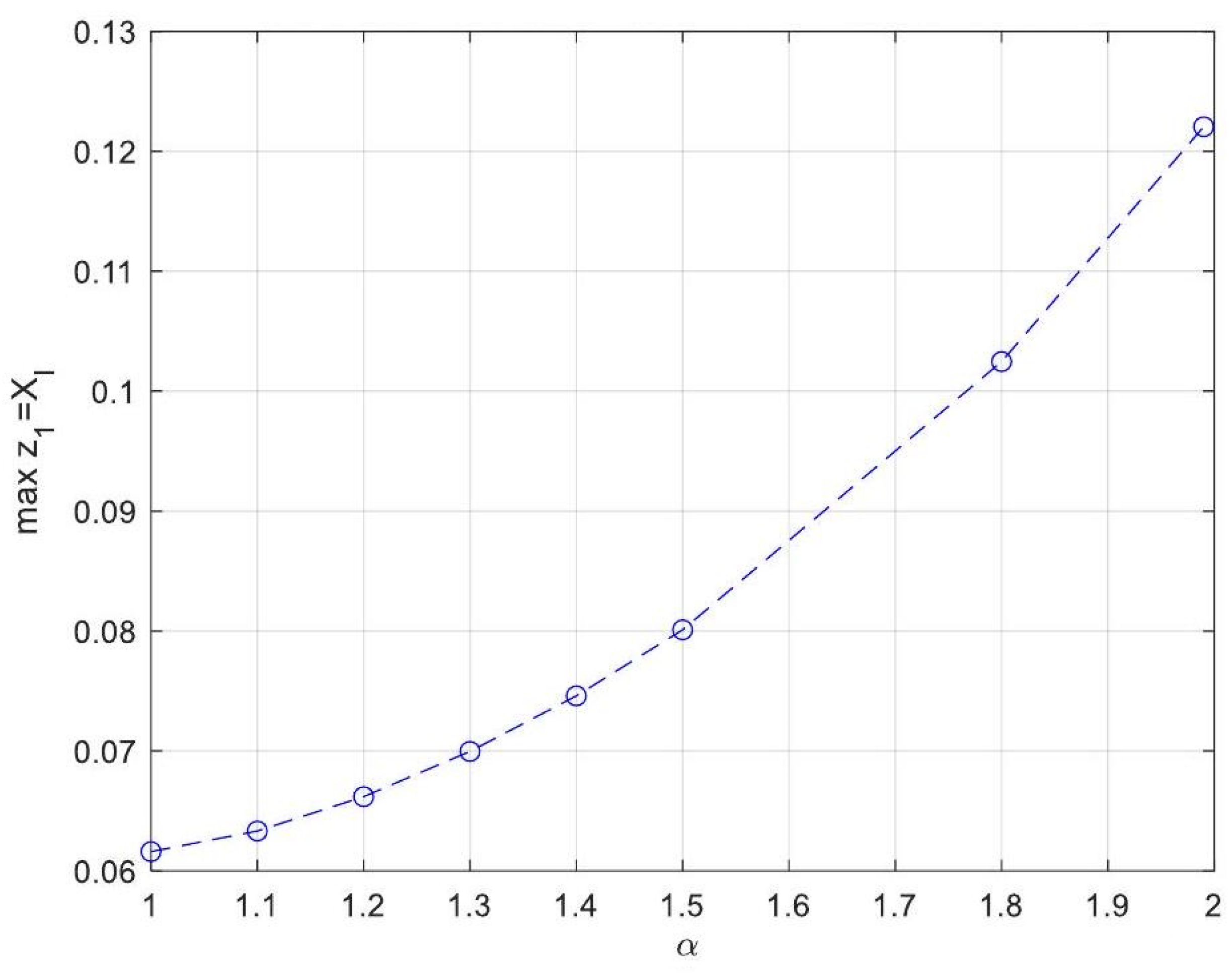
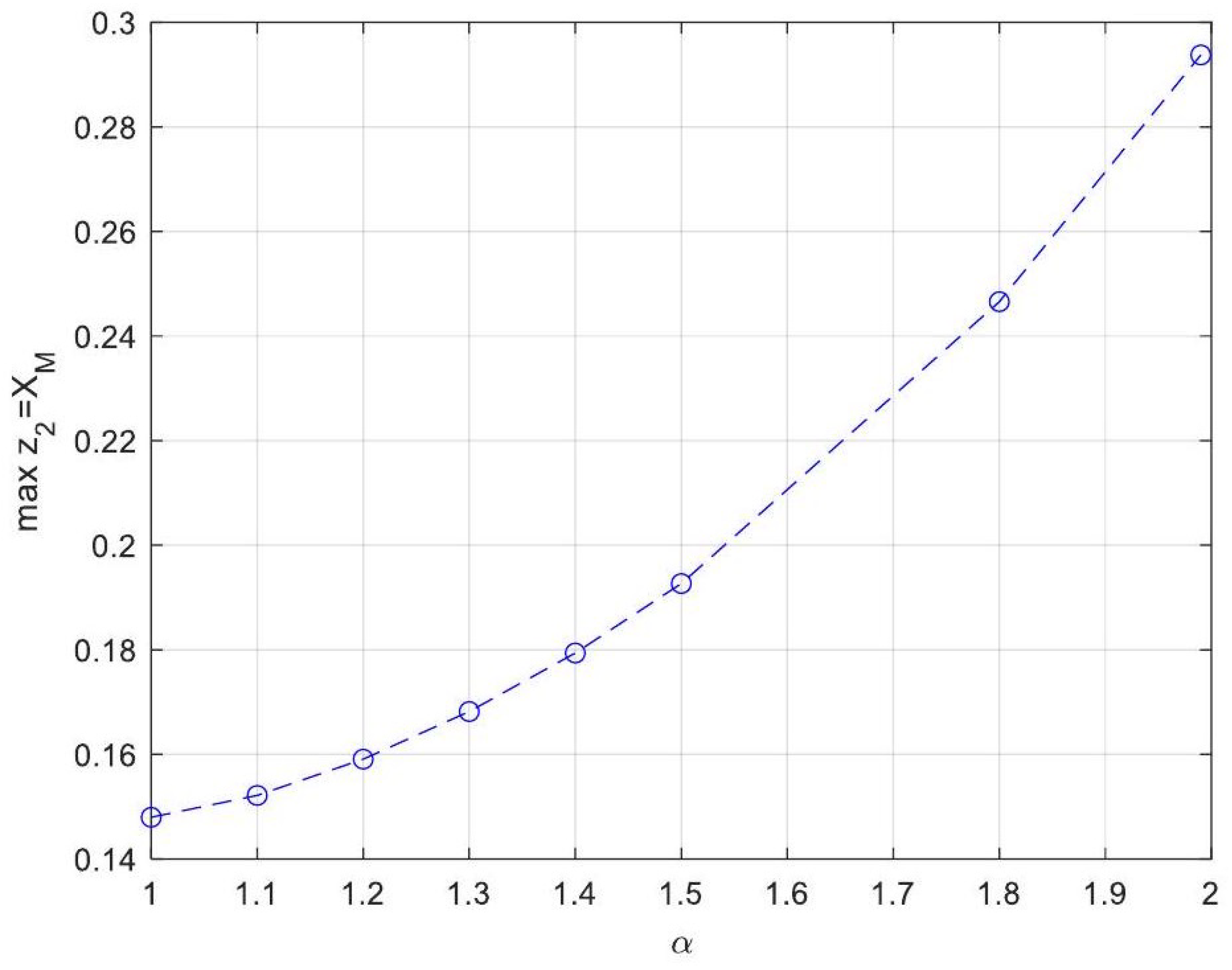
- Enhanced Process Performance with Fractional Operators: Fractional-order derivatives enable improved monomer conversion, polymer concentration, and weight average molecular weight, particularly for derivative orders in the range (1, 1.3]. This provides a notable advantage over integer-order systems, which are limited in stability region adaptability.
- Operational Windows for Optimal Performance: This study identified different operating windows for safe and effective reactor operation. Specifically: For initiator and monomer conversions, free radical concentration and weight-average molecular weight, the optimal derivative order lies in the range (1, 1.3]. And for polymer concentration, the optimal range narrows to (1, 1.2]. Beyond these ranges, increased derivative orders lead to instability and a potential degradation of product quality.
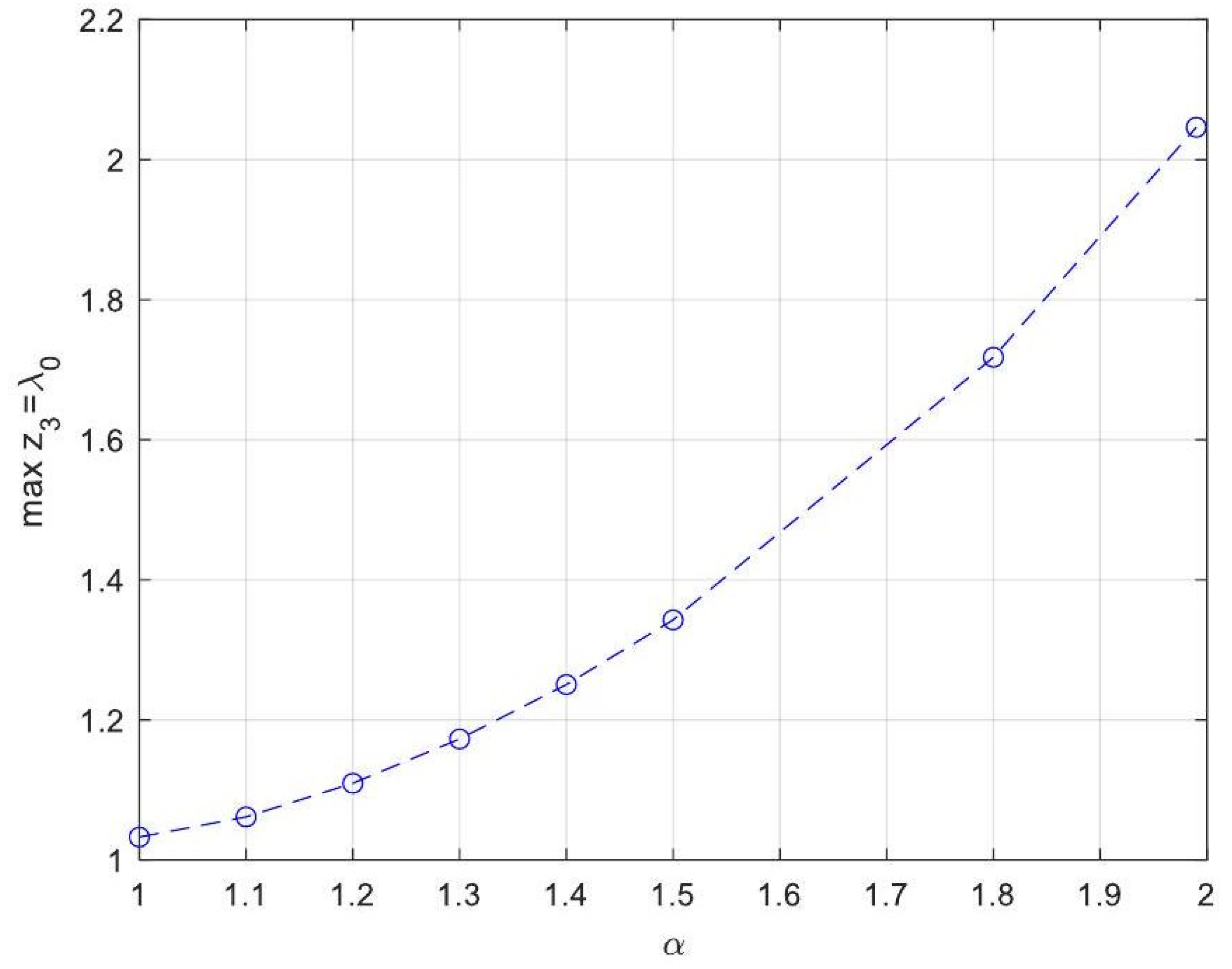
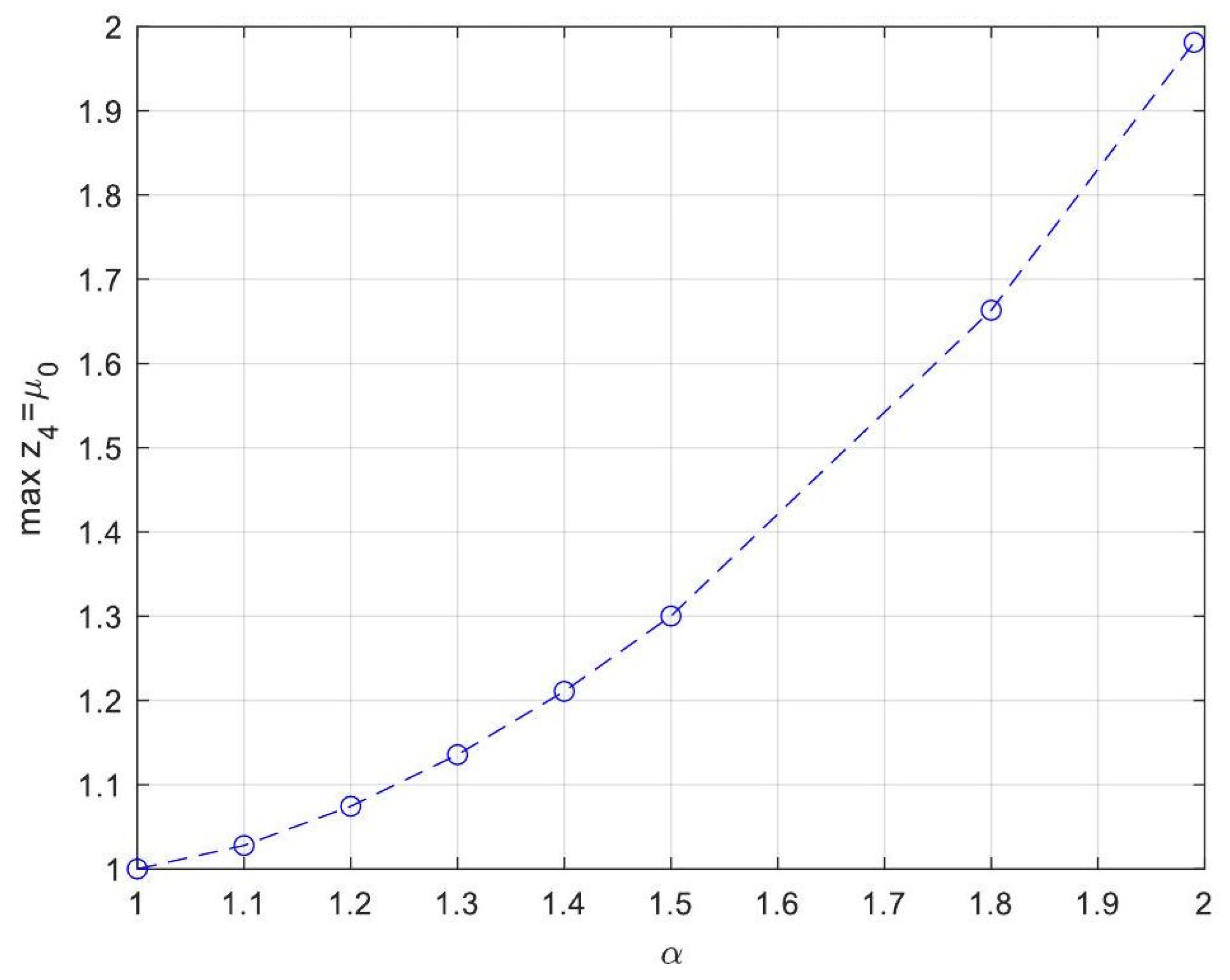
- Asymptotic Stability Across Derivative Ranges: Fractional-order systems exhibit a broader stability region for derivative orders in (0, 1), while narrowing as the derivative order approaches 2. This flexibility allows the system to be tuned for specific performance objectives without compromising stability.
- Comparison Between Fractional- and Integer-Order Models: Fractional-order models outperformed their integer-order counterparts in terms of stability, precision, and operational adaptability. The analytical solutions derived for fractional systems generalised those of the models of integer order, offering a deeper insight into reactor dynamics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Dimensionless Variables and Groups
References
- Chiu, W.; Carrat, G.; Soong, S. A Computer Method for the Gel Effect in Free Radical Polymerization. Macromolecules 1983, 16, 348–357. [Google Scholar] [CrossRef]
- Maschio, G.; Moutier, C. Polymerization reactor: The influence of “gel effect” in batch and continuous solution polymerization of methyl methacrylate. J. Appl. Polym. Sci. 1989, 37, 825–840. [Google Scholar] [CrossRef]
- Zavala, V.; Flores, A.; Vivaldo-Lima, E. Dynamic optimization of a semi-batch reactor for polyurethane production. Chem. Eng. Sci. 2005, 60, 3061–3079. [Google Scholar] [CrossRef]
- Flores-Tlacuahuac, A.; Zavala-Tejeda, V.; Saldívar-Guerra, E. Complex Nonlinear Behavior in the Full-Scale High-Impact Polystyrene Process. Ind. Eng. Chem. Res. 2005, 44, 2802–2814. [Google Scholar] [CrossRef]
- Zavala-Tejeda, V.; Flores, A.; Vivaldo-Lima, E. The bifurcation behavior of a polyurethane continuous stirred tank reactor. Chem. Eng. Sci. 2006, 61, 7368–7385. [Google Scholar] [CrossRef]
- Heymans, N. Fractional Calculus Description of Non-Linear Viscoelastic Behaviour of Polymers. Nonlinear Dyn. 2004, 38, 221–231. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus: Theory and Applications. Mathematics 2018, 6, 145. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications Of Fractinal Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar] [CrossRef]
- Shen, X. Applications of Fractional Calculus in Chemical Engineering. Master’s Thesis, University of Ottawa, Ottawa, ON, Canada, 2018. [Google Scholar]
- Toledo-Hernandez, R.; Rico-Ramirez, V.; Iglesias-Silva, G.; Diwekar, U. A fractional calculus approach to the dynamic optimization of biological reactive systems. Part I: Fractional models for biological reactions. Chem. Eng. Sci. 2014, 117, 217–228. [Google Scholar] [CrossRef]
- Toledo-Hernandez, R.; Rico-Ramirez, V.; Rico-Martínez, R.; Hernandez-Castro, S.; Diwekar, U. A fractional calculus approach to the dynamic optimization of biological reactive systems. Part II: Numerical solution of fractional optimal control problems. Chem. Eng. Sci. 2014, 117, 239–247. [Google Scholar] [CrossRef]
- Qi, H.T.; Xu, H.Y.; Guo, X.W. The Cattaneo-type time fractional heat conduction equation for laser heating. Comput. Math. Appl. 2013, 66, 824–831. [Google Scholar] [CrossRef]
- Banizaman, H.; Amirsalari, S.M.Z. Designing a Fractional Order PID Controller for Bioreactor Control. Unique J. Eng. Adv. Sci. 2014, 2. [Google Scholar]
- Thirumavalavan, V. Design of Fractional Order Controller for Biochemical Reactor. IFAC Proc. Vol. 2013, 46, 205–208. [Google Scholar] [CrossRef]
- Palomares-Ruiz, J.; Rodríguez-Madrigal, M.; Castro-Lugo, J.; Rodríguez-Soto, A. Fractional viscoelastic models applied to biomechanical constitutive equations. Rev. Mex. De Física 2015, 61, 261–267. [Google Scholar]
- Nagarajan, M.; Asokan, A.; Manikandan, M.; Sivakumar, D. Concentration Control of Isothermal CSTR using Particle Swarm Optimization based FOPID Controller. Middle-East J. Sci. Res. 2016, 24, 967–971. [Google Scholar]
- Ravari, M.; Yaghoobi, M. Optimum Design of Fractional Order Pid Controller Using Chaotic Firefly Algorithms for a Control CSTR System. Asian J. Control 2018, 21, 2245–2255. [Google Scholar] [CrossRef]
- Lisci, S.; Grosso, M.; Tronci, S. A Robust Nonlinear Estimator for a Yeast Fermentation Biochemical Reactor. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2020; Volume 48, pp. 1303–1308. [Google Scholar] [CrossRef]
- Bhusari, B.P.; Patil, M.D.; Jadhav, S.P.; Vyawahare, V.A. Modeling nonlinear fractional-order subdiffusive dynamics in nuclear reactor with artificial neural networks. Int. J. Dyn. Control 2020, 11, 1995–2020. [Google Scholar] [CrossRef]
- Schmidt, A.D.; Ray, W. The dynamic behavior of continuous polymerization reactors—I: Isothermal solution polymerization in a CSTR. Chem. Eng. Sci. 1981, 36, 1401–1410. [Google Scholar] [CrossRef]
- Khan, N.; Jamil, M.; Ara, A.; Das, S. Explicit Solution for Time-Fractional Batch Reactor System. Int. J. Chem. React. Eng. 2011, 9, A115. [Google Scholar] [CrossRef]
- Khan, N.; Ara, A.; Mahmood, A. Approximate Solution of Time-Fractional Chemical Engineering Equations: A Comparative Study. Int. J. Chem. React. Eng. 2010, 8. [Google Scholar] [CrossRef]
- Al-Basir, F.; Elaiw, A.M.; Kesh, D.; Roy, P.K. Optimal control of a fractional-order enzyme kinetic model. Control Cybern. 2015, 44, 443–461. [Google Scholar]
- Magin, R.L.; Lenzi, E.K. Fractional Calculus Extension of the Kinetic Theory of Fluids: Molecular Models of Transport within and between Phases. Mathematics 2022, 10, 4785. [Google Scholar] [CrossRef]
- Ahmadian, A.; Salahshour, S.; Baleanu, D.; Amirkhani, H.; Yunus, R. Tau method for the numerical solution of a fuzzy fractional kinetic model and its application to the oil palm frond as a promising source of xylose. J. Comput. Phys. 2015, 294, 562–584. [Google Scholar] [CrossRef]
- Haubold, H.; Mathai, A.; Saxena, R. Mittag-Leffler Functions and Their Applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef]
- Hristov, J. Non-Local Kinetics: Revisiting and Updates Emphasizing Fractional Calculus Applications. Symmetry 2023, 15, 632. [Google Scholar] [CrossRef]
- Oldham, K. Fractional differential equations in electrochemistry. Adv. Eng. Softw. 2010, 41, 9–12. [Google Scholar] [CrossRef]
- Chung, W.; Hassanabadi, H.; Maghsoodi, E. A new fractional mechanics based on fractional addition. Rev. Mex. De Física 2021, 67, 68. [Google Scholar] [CrossRef]
- Povstenko, Y. Time-fractional heat conduction in a two-layer composite slab. Fract. Calc. Appl. Anal. 2016, 19, 940–953. [Google Scholar] [CrossRef]
- Hristov, J. Magnetic field diffusion in ferromagnetic materials: Fractional calculus approaches. Int. J. Optim. Control. Theor. Appl. (IJOCTA) 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Wang, C. Fractional Kinetics of Photocatalytic Degradation. J. Adv. Dielectr. 2018, 8, 1850034. [Google Scholar] [CrossRef]
- Rauf, A.; Rubbab, Q.; Shah, N.A.; Malik, K.R. Simultaneous Flow of n-Immiscible Fractional Maxwell Fluids with Generalized Thermal Flux and Robin Boundary Conditions. Adv. Math. Phys. 2021, 2021, 5572823. [Google Scholar] [CrossRef]
- Lazopoulos, K.; Lazopoulos, A. Fractional vector calculus and fluid mechanics. J. Mech. Behav. Mater. 2017, 26, 43–54. [Google Scholar] [CrossRef]
- Vargas, R.D. Fractional Calculus in Chemical Engineering: From Mathematics, to Underlying Physics, to Aplications. Master’s Thesis, Universidad de los Andes, Bogotá, Colombia, 2012. [Google Scholar]
- Ali, G.E.H.; Asaad, A.A.; Elagan, S.K.; Mawaheb, E.A.; AlDien, M.S. Using Laplace transform method for obtaining the exact analytic solutions of some ordinary fractional differential equations. Glob. J. Pure Appl. Math. 2017, 13, 5021–5035. [Google Scholar]
- Cresson, J. Fractional Calculus in Analysis, Dynamics and Optimal Control; Nova Science Publishers, Inc.: New York, NY, USA, 2014. [Google Scholar]
- Shitikova, M. Fractional Operator Viscoelastic Models in Dynamic Problems of Mechanics of Solids: A Review. Mech. Solids 2021, 57, 1–33. [Google Scholar] [CrossRef]
- Magin, R. Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 2010, 59, 1586–1593. [Google Scholar] [CrossRef]
- Meilanov, R.; Magomedov, R. Thermodynamics in Fractional Calculus. J. Eng. Phys. Thermophys. 2014, 87, 1521–1531. [Google Scholar] [CrossRef]
- Flores, A.; Biegler, L. Optimization of Fractional Order Dynamic Chemical Processing Systems. Ind. Eng. Chem. Res. 2014, 53, 5110–5127. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus; Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Garrappa, R. Numerical Evaluation of Two and Three Parameter Mittag-Leffler Functions. SIAM J. Numer. Anal. 2015, 53, 1350–1369. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational Engineering in Systems Applications, Lille, France, 9–12 July 1996; Volume 2, pp. 963–968. [Google Scholar]
- Petráš, I. Fractional-Order Systems. In Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011; pp. 43–54. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering; Academic Press: London, UK, 1999. [Google Scholar]
- Anne, B.; Kuolu, Q.; Arkun, G. Modeling of an Industrial Delayed Coker Unit. In 33rd European Symposium on Computer Aided Process Engineering; Computer Aided Chemical, Engineering; Kokossis, A.C., Georgiadis, M.C., Pistikopoulos, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 52, pp. 525–531. [Google Scholar] [CrossRef]
- Zhou, Y.N.; Li, J.J.; Wang, T.T.; Wu, Y.Y.; Luo, Z.H. Precision polymer synthesis by controlled radical polymerization: Fusing the progress from polymer chemistry and reaction engineering. Prog. Polym. Sci. 2022, 130, 101555. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; The book can be consulted by contacting: PH-AID:Wallet, Lionel. [Google Scholar]
- Stephanopoulos, G. Chemical Process Control: An Introduction to Theory and Practice; Prentice Hall PTR: Hoboken, NJ, USA, 1984. [Google Scholar]
- Rivera-Toledo, M.; García-Crispín, L.; Flores, A.; Vílchis-Ramírez, L. Dynamic Modeling and Experimental Validation of the MMA Cell-Cast Process for Plastic Sheet Production. Ind. Eng. Chem. Res. 2006, 45, 8539–8553. [Google Scholar] [CrossRef]
- Kazem, S. Exact Solution of Some Linear Fractional Differential Equations by Laplace Transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Lozano, R.; Brogliato, B.; Egeland, O.; Maschke, B. Dissipative Systems Analysis and Control. Theory and Applications. Meas. Sci. Technol. 2001, 12, 2211. [Google Scholar] [CrossRef]






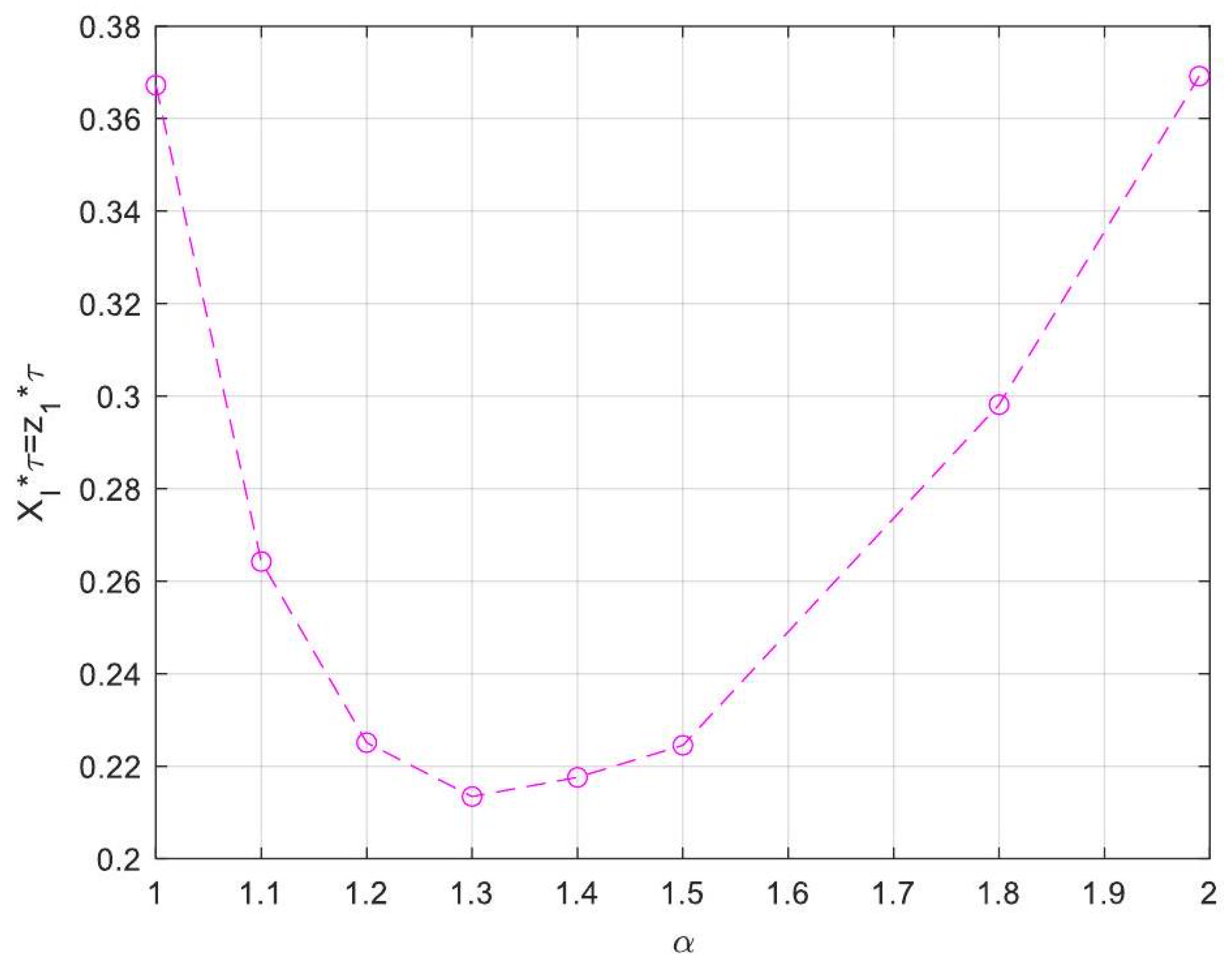

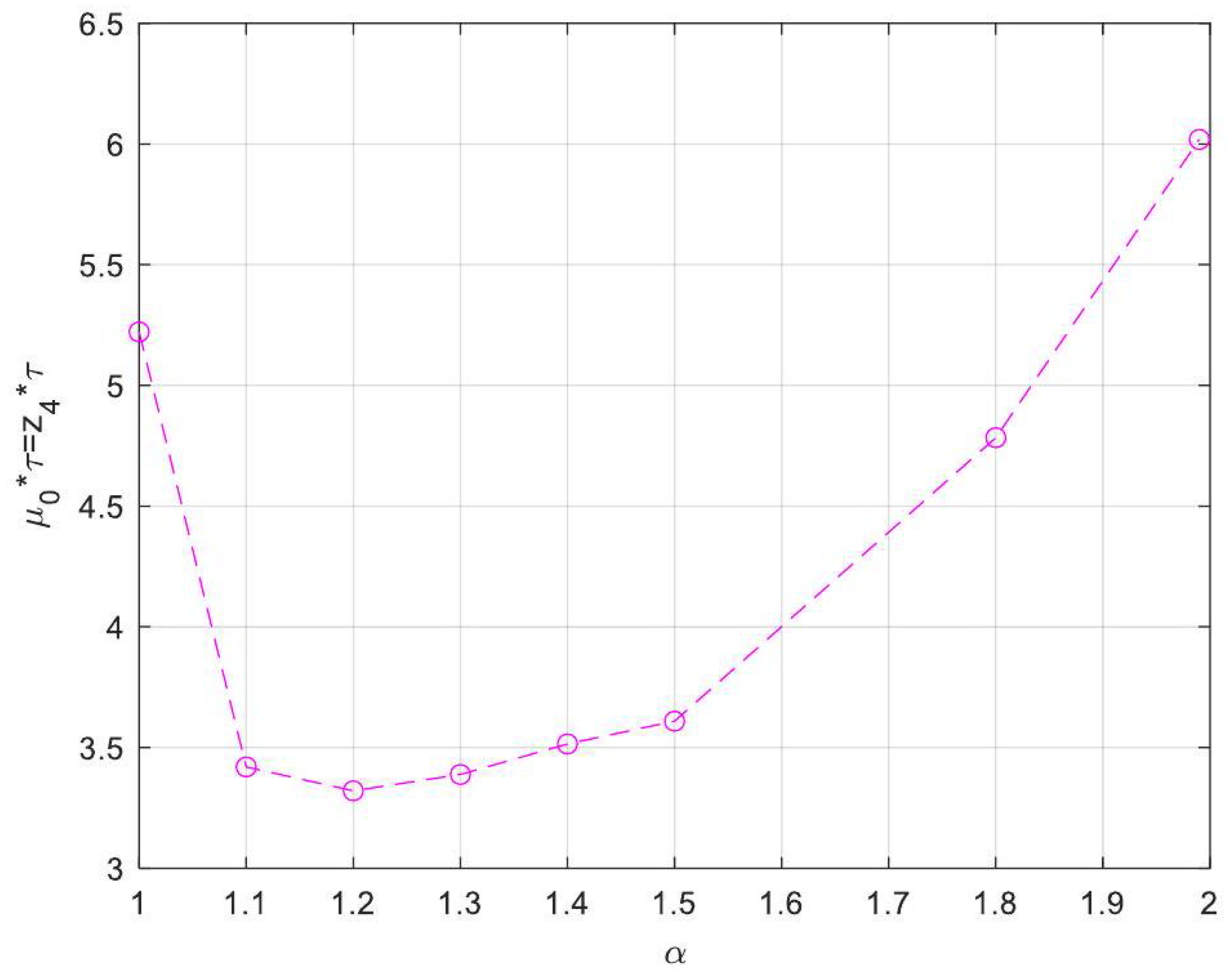
| Symbol for Mean Deviation Value | Description | Deviation Value |
|---|---|---|
| Initiator conversion | ||
| Monomer conversion | ||
| Dimensionless free | ||
| concentration of radicals | ||
| Dimensionless | ||
| polymer concentration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velázquez-León, L.-F.; Rivera-Toledo, M.; Fernández-Anaya, G. Analytical Solutions and Stability Analysis of a Fractional-Order Open-Loop CSTR Model for PMMA Polymerization. Processes 2025, 13, 793. https://doi.org/10.3390/pr13030793
Velázquez-León L-F, Rivera-Toledo M, Fernández-Anaya G. Analytical Solutions and Stability Analysis of a Fractional-Order Open-Loop CSTR Model for PMMA Polymerization. Processes. 2025; 13(3):793. https://doi.org/10.3390/pr13030793
Chicago/Turabian StyleVelázquez-León, Luis-Felipe, Martín Rivera-Toledo, and Guillermo Fernández-Anaya. 2025. "Analytical Solutions and Stability Analysis of a Fractional-Order Open-Loop CSTR Model for PMMA Polymerization" Processes 13, no. 3: 793. https://doi.org/10.3390/pr13030793
APA StyleVelázquez-León, L.-F., Rivera-Toledo, M., & Fernández-Anaya, G. (2025). Analytical Solutions and Stability Analysis of a Fractional-Order Open-Loop CSTR Model for PMMA Polymerization. Processes, 13(3), 793. https://doi.org/10.3390/pr13030793








