An Improved Nishihara Model Considering the Influence of Moisture Content on the Whole Shear Creep Process of Shale
Abstract
1. Introduction
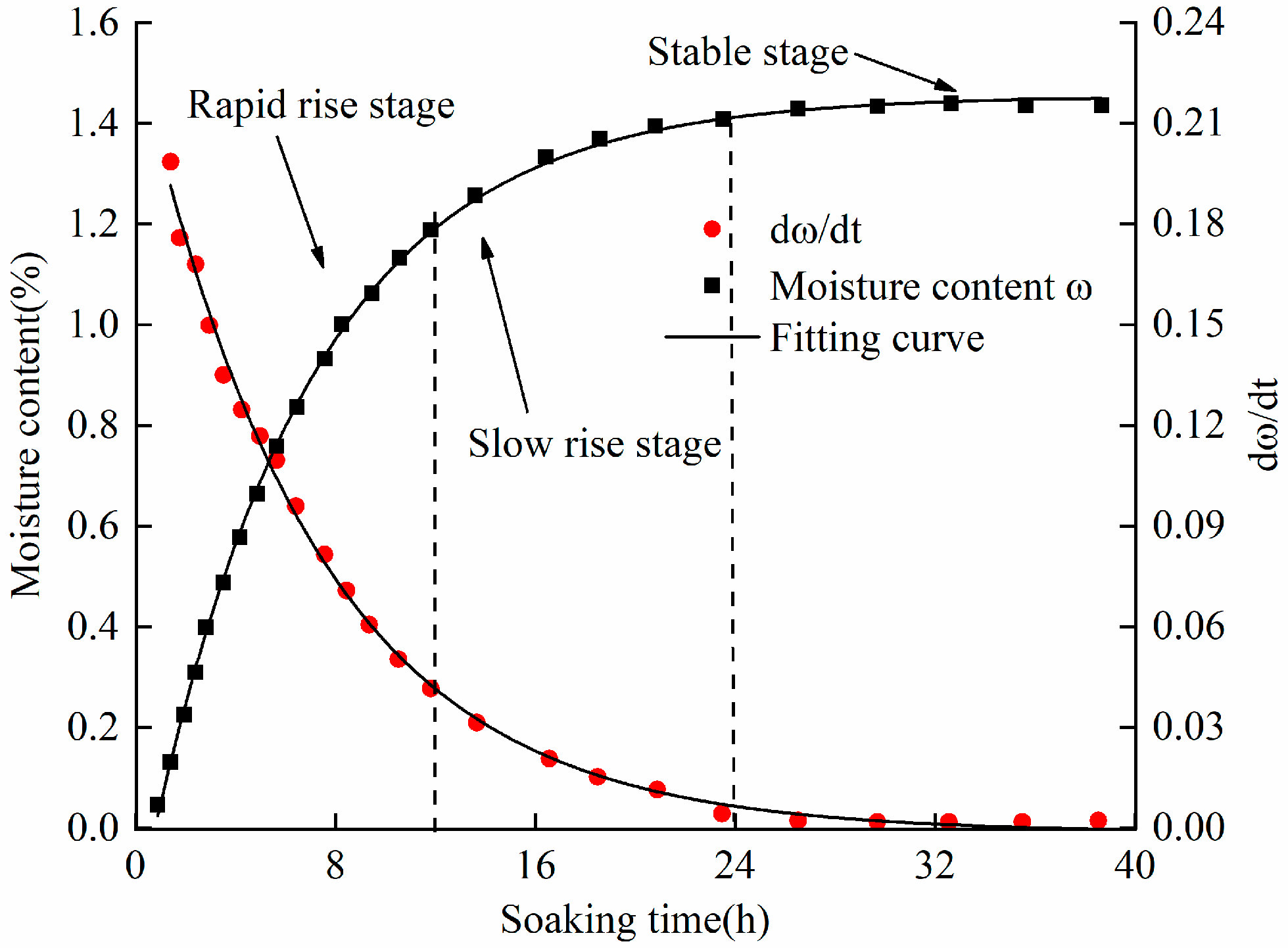
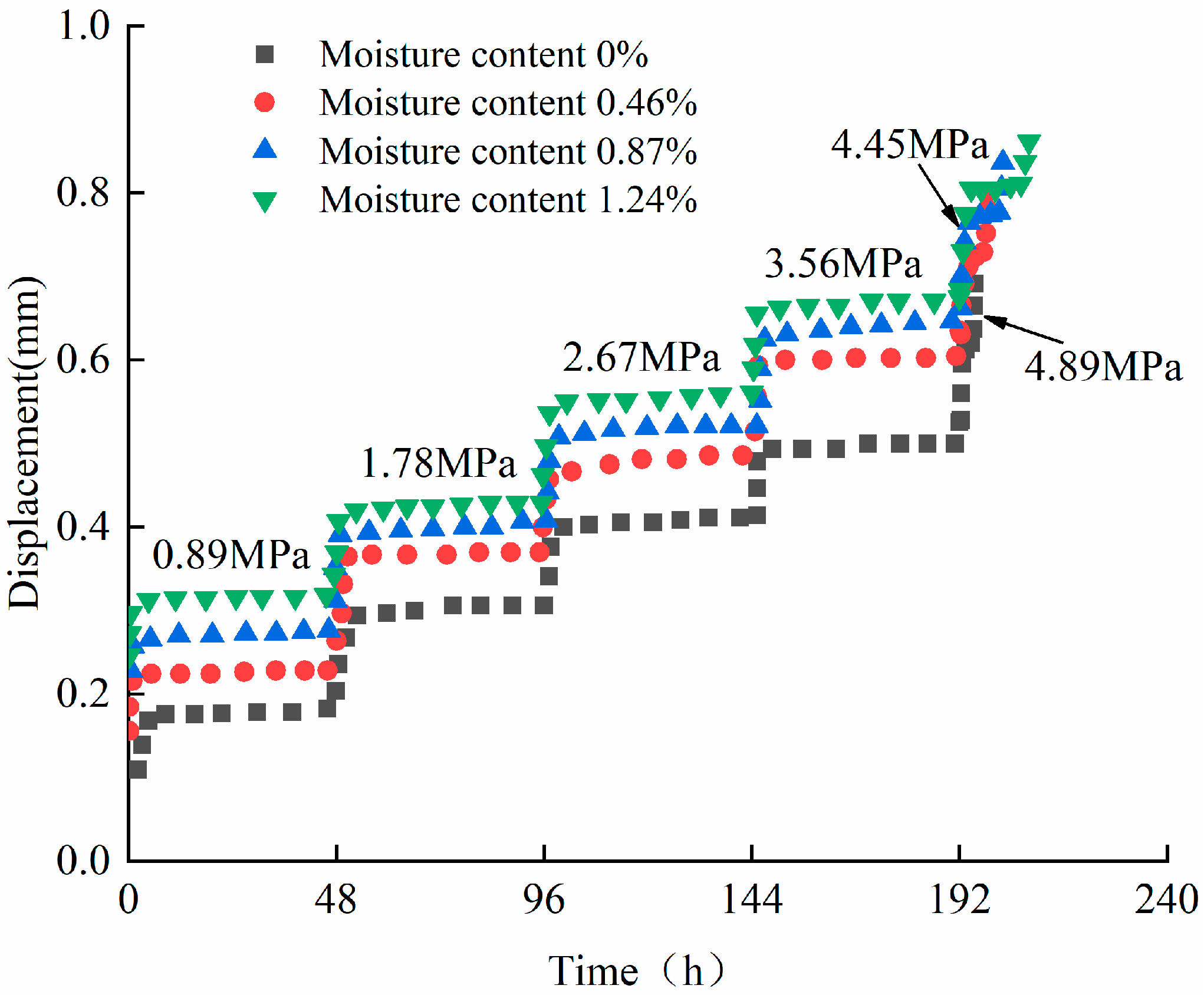
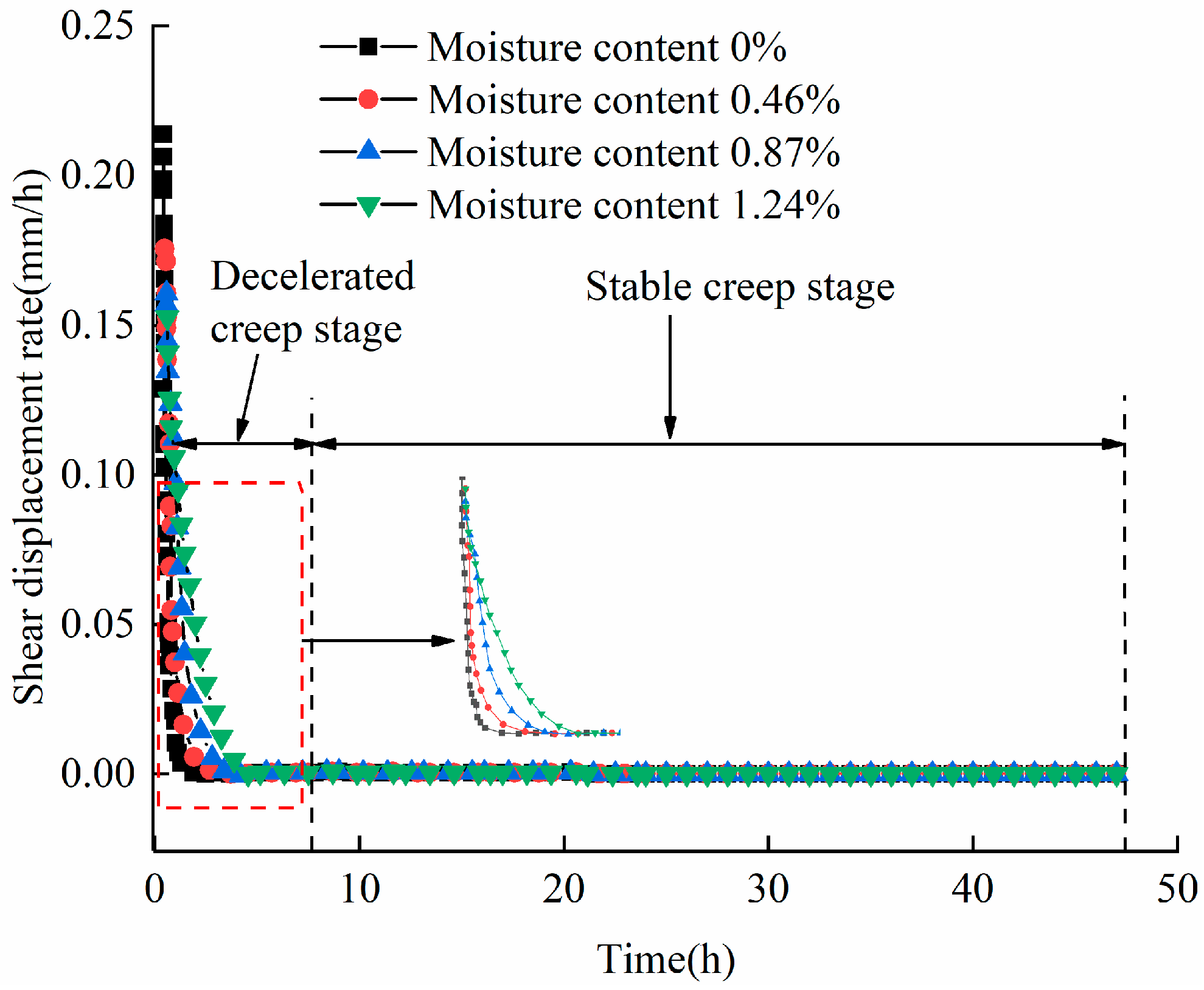
2. Rock Shear Creep Experiment
3. Improved Nishihara Creep Model
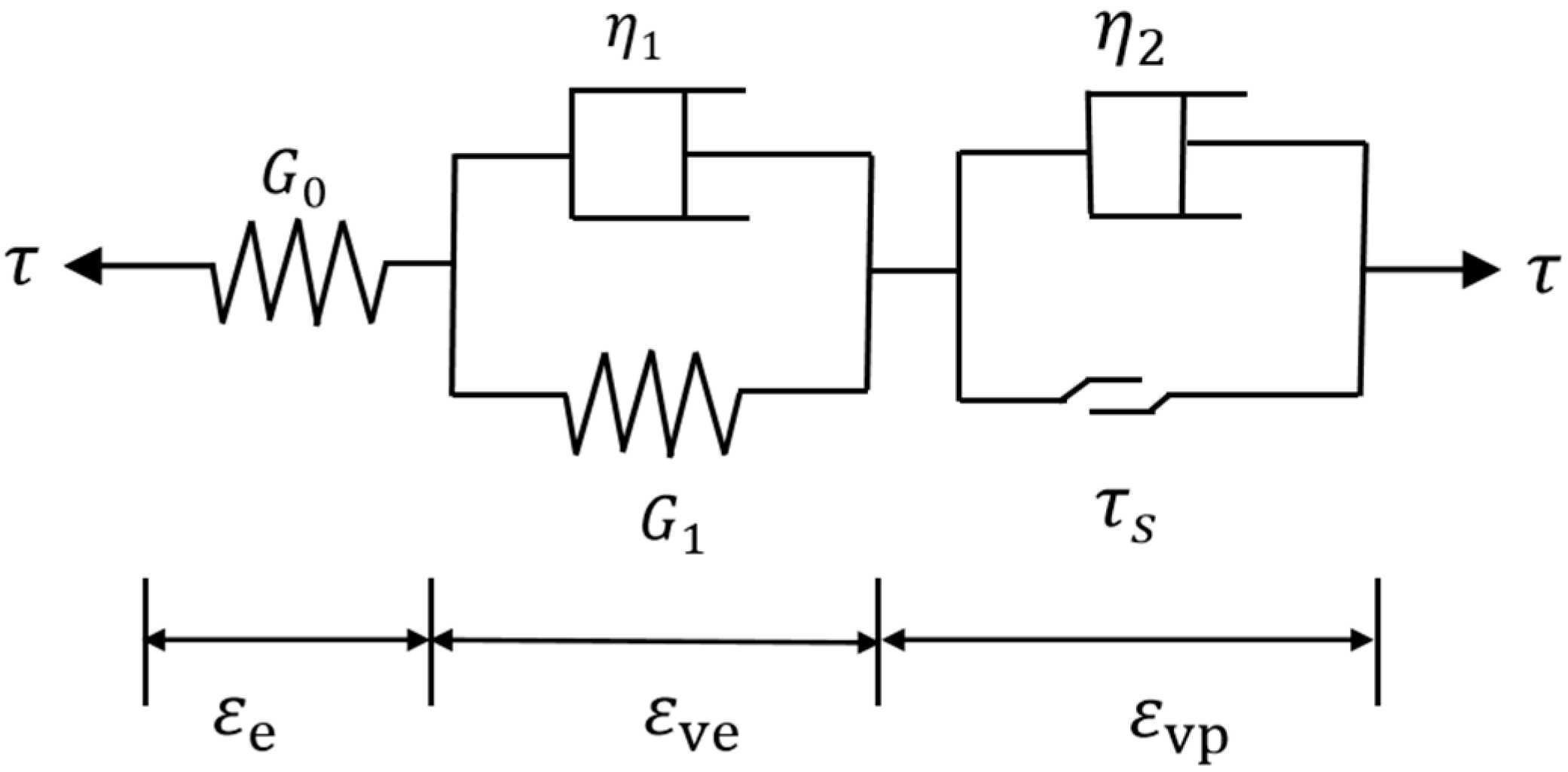
3.1. Classical Nishihara Creep Model
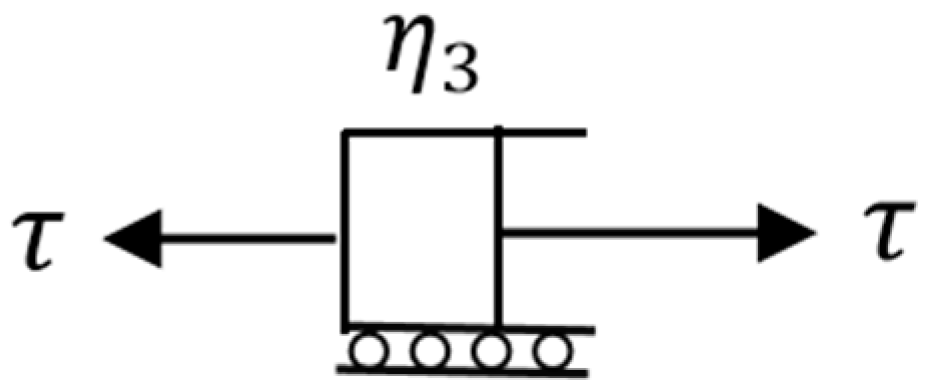
3.2. A Nonlinear Dashpot Triggered by Strain
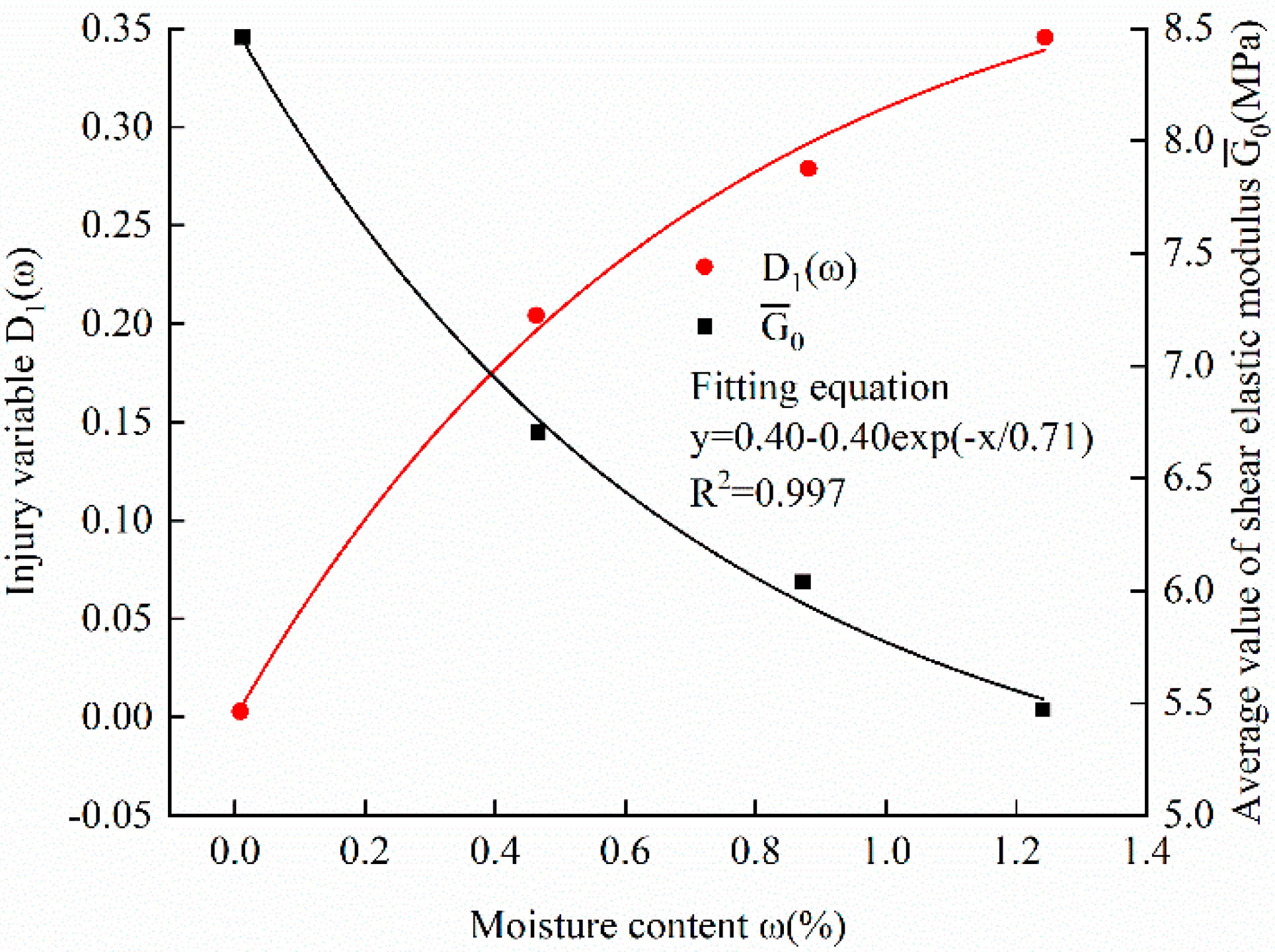
3.3. Moisture-Related Damage Factor
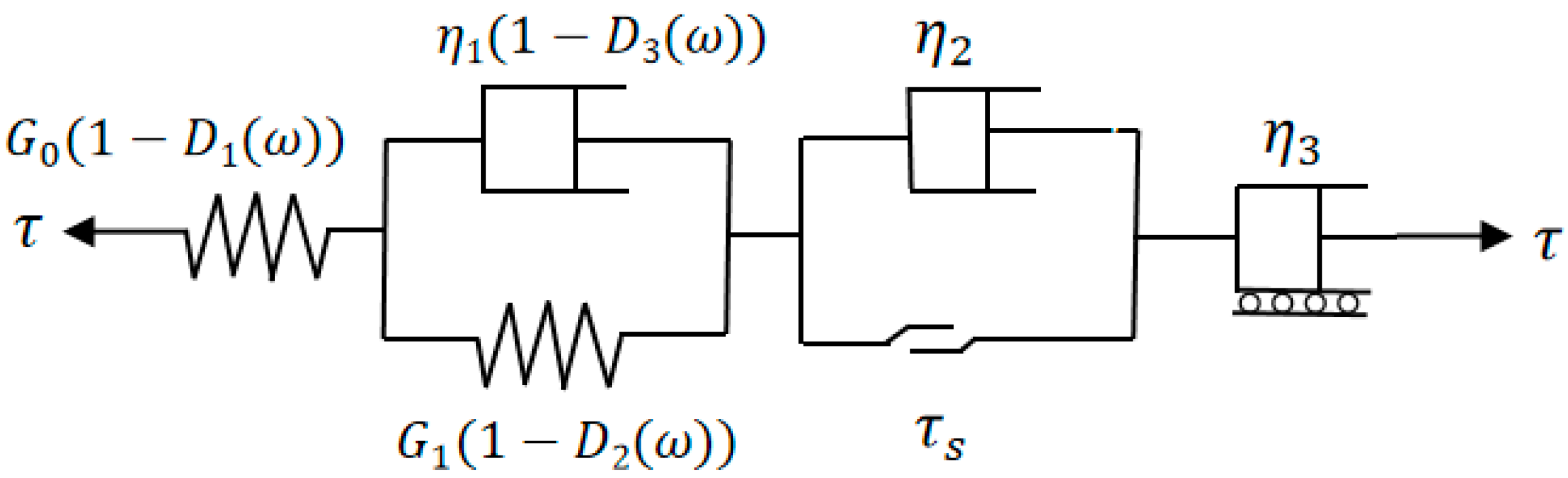
3.4. Establishment of Improved Nishihara Model
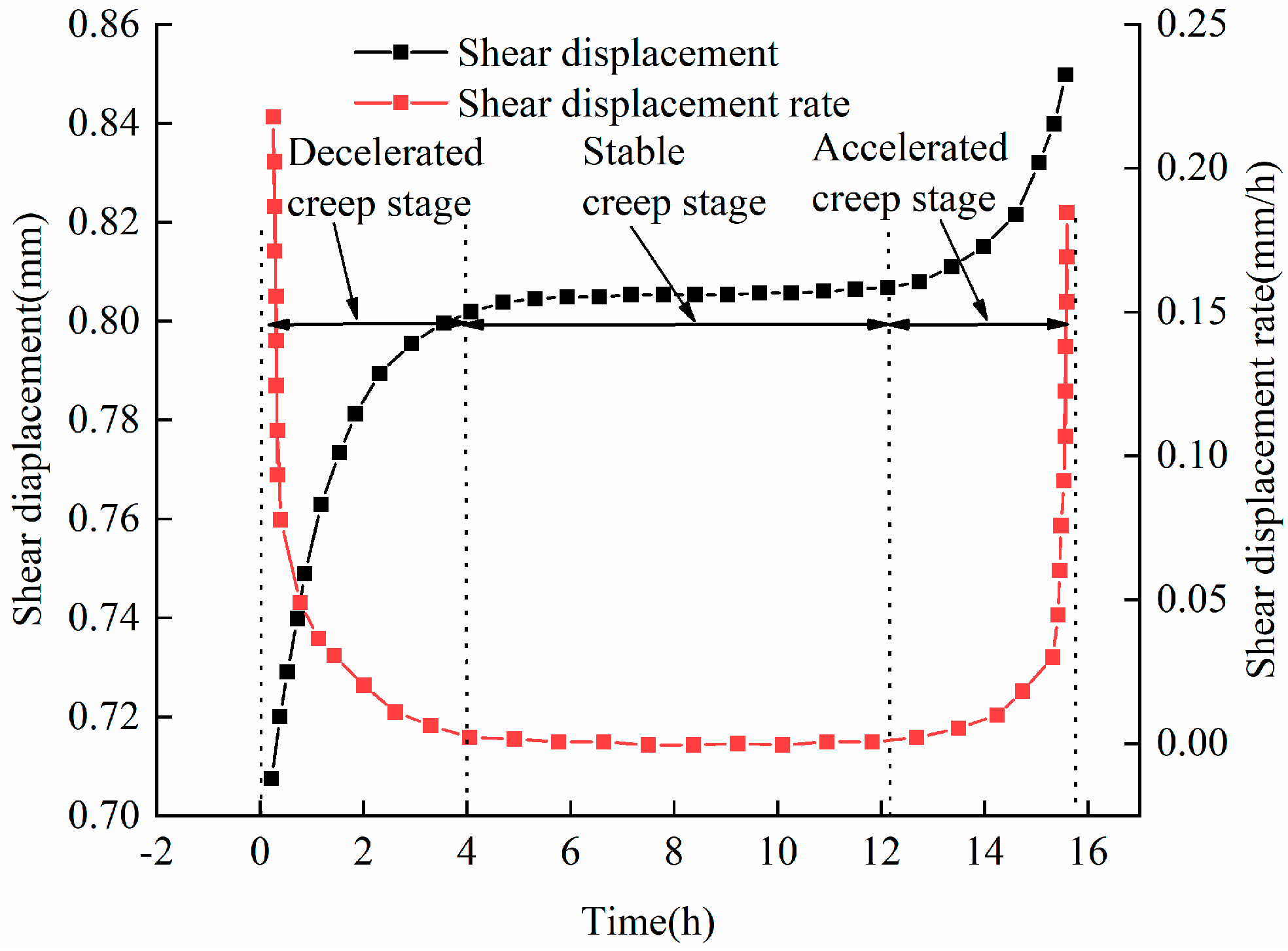
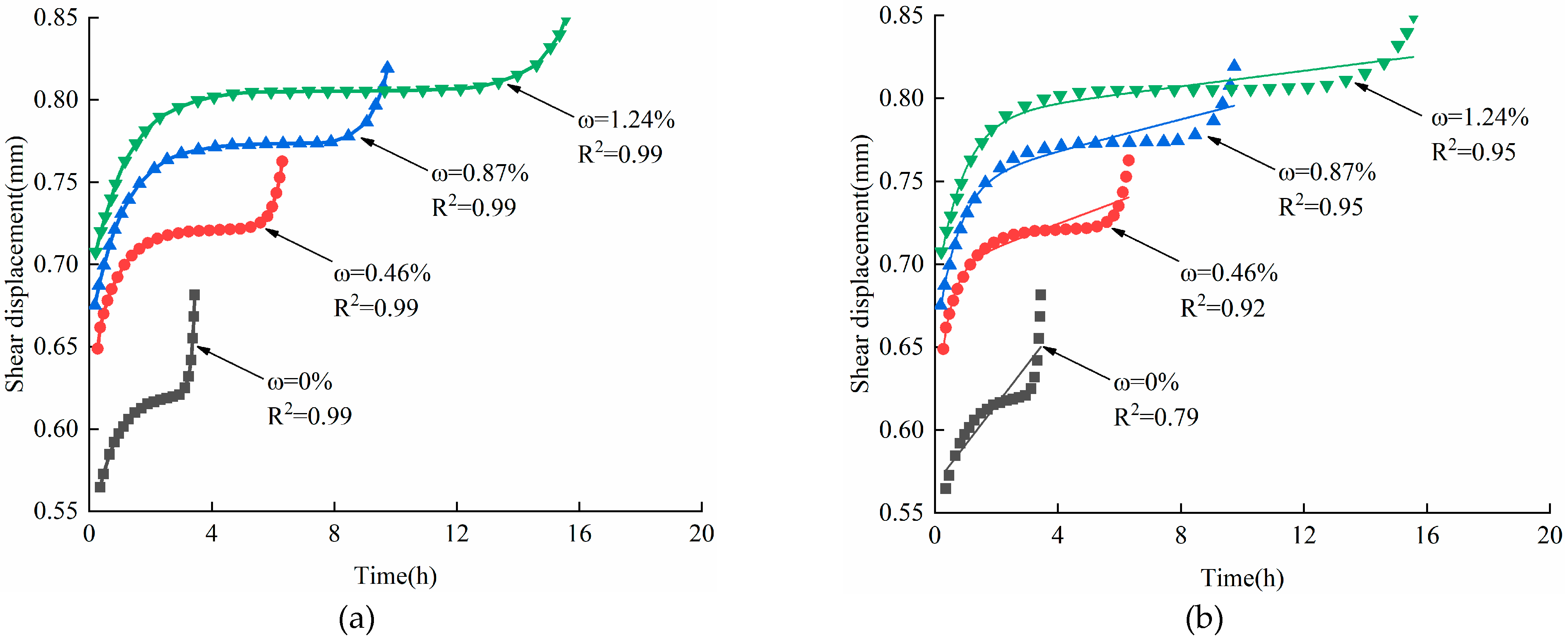
4. Validation of Improved Nishihara Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Zhang, D.; Huang, S. Creep Characteristics and Creep Model of Coal Based on Pore Water Pressure. Processes 2023, 11, 638. [Google Scholar] [CrossRef]
- Chen, C.; Xie, H.; Xu, J.; Peng, S.; Li, C.; Li, M. Creep behavior of sandstone under the coupling action of stress and pore water pressure using three-dimensional digital image correlation. Int. J. Damage Mech. 2024, 33, 147–173. [Google Scholar] [CrossRef]
- Miao, C.; Jiang, M.; Wang, L.; Yang, J.; Sun, X. Experimental Study on Long-Term Strength and Creep Characteristics of Sandstone Under Different Water Content and Confining Pressure. Rock. Mech. Rock. Eng. 2024, 57, 9035–9054. [Google Scholar] [CrossRef]
- Gu, Q.; Tan, Y.; Zhao, G.; Meng, X.; Cheng, X. Creep behavior of dry and saturated medium-grain sandstone and its relationship with conventional mechanical properties. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 52. [Google Scholar] [CrossRef]
- Feng, W.; Qiao, C.; Niu, S.; Yang, Z.; Wang, T. An improved nonlinear damage model of rocks considering initial damage and damage evolution. Int. J. Damage Mech. 2020, 29, 1117–1137. [Google Scholar] [CrossRef]
- Hu, D.; Liang, X.; Li, Y.; Wu, Y.; Jiang, L. Deformation Prediction of Tunnel-Surrounding Rock Considering the Time Effect of the Viscosity Coefficient: A Case of an NATM-Excavated Tunnel. Front. Earth Sci. 2022, 10, 843545. [Google Scholar] [CrossRef]
- Xiu, X.; Wang, Y.; Zhou, Y.; Niu, G.; Zhao, S.; Chang, D. Creep Model and Experimental Verification of Sandstone under the Coupled Effect of Chemical Corrosion and Temperature. Appl. Sci. 2024, 14, 7847. [Google Scholar] [CrossRef]
- Gu, H.; Lai, X.; Tao, M.; Cao, W.; Yang, Z. The role of porosity in the dynamic disturbance resistance of water-saturated coal. Int. J. Rock. Mech. Min. 2023, 166, 105388. [Google Scholar] [CrossRef]
- Deng, X.; Shi, J.; Li, X.; Wang, R.; Zhang, J.; Yang, X. The Secondary Development and Application of the Improved Nishihara Creep Model in Soft Rock Tunnels. Buildings 2023, 13, 2082. [Google Scholar] [CrossRef]
- Wu, L.Z.; Luo, X.H.; Li, S.H. A new model of shear creep and its experimental verification. Mech. Time-Depend. Mat. 2021, 25, 429–446. [Google Scholar] [CrossRef]
- Du, S.; Zhang, C.; Mao, D.; Ruan, B.; Lu, X. A case study of the failure mechanism analysis and support design of a tailrace tunnel in a weak fracture zone containing expansive minerals. B. Eng. Geol. Environ. 2022, 81, 495. [Google Scholar] [CrossRef]
- Li, D.; Du, S.; Zhang, C.; Mao, D.; Ruan, B. Time-dependent deformation behavior of completely weathered granite subjected to wetting immersion. Rock. Mech. Rock. Eng. 2021, 54, 6373–6391. [Google Scholar] [CrossRef]
- Gao, X.; Hu, T.; Su, Z. Nonlinear Nishihara model of soft rock based on damage mechanics and its parameter identification. Mater. Today Commun. 2024, 39, 108715. [Google Scholar] [CrossRef]
- Du, S.; Li, D.; Zhang, C.; Mao, D.; Ruan, B. Deformation and strength properties of completely decomposed granite in a fault zone. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 1–21. [Google Scholar] [CrossRef]
- Du, S.; Li, D.; Ruan, B.; Wu, G.; Pan, B.; Ma, J. Deformation and fracture of circular tunnels under non-tectonic stresses and its support control. Eur. J. Environ. Civ. Eng. 2022, 26, 1654–1677. [Google Scholar] [CrossRef]
- Yan, B.; Guo, Q.; Ren, F.; Cai, M. Modified Nishihara model and experimental verification of deep rock mass under the water-rock interaction. Int. J. Rock. Mech. Min. 2020, 128, 104250. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, D.; Wang, J.; Wang, X.; Cong, Y.; Wang, Z. A nonlinear creep model of rocks based on memory-dependent derivative. Constr. Build. Mater. 2023, 391, 131618. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Q.; Lian, B.; Liu, N.; Zhang, J. Modified Nishihara Rheological Model considering the Effect of Thermal-Mechanical Coupling and Its Experimental Verification. Adv. Mater. Sci. Eng. 2018, 2018, 4947561. [Google Scholar] [CrossRef]
- Li, X.; Liu, E.; Song, B.; Liu, X. An Improved Nishihara Model for Frozen Loess considering the Influence of Temperature. Adv. Mater. Sci. Eng. 2018, 2018, 9073435. [Google Scholar] [CrossRef]
- Cui, K.; Hu, B.; Cui, A.; Li, J.; Wei, E.; Zhang, Z. An extended super/subloading surface model for soft rock considering structure degradation. PLoS ONE 2021, 16, e0258813. [Google Scholar] [CrossRef]
- Yi, X.; Feng, W.; Bai, H.; Shen, H.; Li, H. Catastrophic landslide triggered by persistent rainfall in Sichuan, China: August 21, 2020, Zhonghaicun landslide. Landslides 2021, 18, 2907–2921. [Google Scholar] [CrossRef]
- Zhuang, Y.; Hu, X.; He, W.; Shen, D.; Zhu, Y. Stability Analysis of a Rocky Slope with a Weak Interbedded Layer under Rainfall Infiltration Conditions. Water 2024, 16, 604. [Google Scholar] [CrossRef]
- Basu, S.; Jones, A.; Mahzari, P. Best Practices for Shale Core Handling: Transportation, Sampling and Storage for Conduction of Analyses. J. Mar. Sci. Eng. 2020, 8, 136. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sheng, J.; Zhang, Z. Failure mechanism and treatment of mine landslide with gently-inclined weak interlayer: A case study of Laoyingzui landslide in Emei, Sichuan, China. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 61. [Google Scholar] [CrossRef]
- Liang, X.; Tang, S.; Tang, C.; Wang, J. The influence of water on the shear behaviors of intact sandstone. B. Eng. Geol. Environ. 2021, 80, 6077–6091. [Google Scholar] [CrossRef]
- Wang, X.; Hu, B.; Tang, H.; Hu, X.; Wang, J.; Huang, L. A constitutive model of granite shear creep under moisture. J. Earth. Sci-China 2016, 27, 677–685. [Google Scholar] [CrossRef]
- Ma, C.; Zhang, T.; Yao, W. An Assessment of the Osmotic Pressure Effect on the Creep Properties of Silty Mudstone. Soil. Mech. Found. Eng. 2019, 56, 314–320. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, Q.; Zhang, L.; Duan, K.; Xue, T.; Fan, Q. The Influence of Water Content on the Time-Dependent Mechanical Behavior of Argillaceous Siltstone. Rock. Mech. Rock. Eng. 2022, 55, 3939–3957. [Google Scholar] [CrossRef]
- Zhao, Z.; Dai, W.; Yang, J.; Zhou, M.; Liu, Z. Creep mechanical tests and shear rheological model of the anchorage rock mass under water-rock coupling. PLoS ONE 2023, 18, e0284569. [Google Scholar] [CrossRef]
- Hu, B.; Zhang, Z.; Li, J.; Xiao, H.; Cui, K. Statistical Damage Model of Rock Based on Compaction Stage and Post-Peak Shape under Chemical-Freezing-Thawing-Loading. J. Mar. Sci. Eng. 2022, 10, 696. [Google Scholar] [CrossRef]
- Wei, E.; Hu, B.; Tian, K.; Cen, P.; Zhang, Z.; Wang, Z.; Chang, S. Study on the Nonlinear Damage Creep Model of the Weak Interlayer. Adv. Civ. Eng. 2022, 2022, 3566521. [Google Scholar] [CrossRef]


| Element Name | Elastic Element | Plastic Element | Viscous Element |
|---|---|---|---|
| Element model |  | 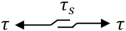 | 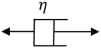 |
| Constitutive equation |
| (MPa/mm) | (MPa/mm) | (MPa h/mm) | |
| 0% | 8.47 | 34.91 | 31.75 |
| 0.46% | 6.74 | 29.74 | 29.92 |
| 0.87% | 6.10 | 27.91 | 27.92 |
| 1.24% | 5.53 | 26.75 | 24.36 |
(MPa) | (MPa/mm) | (MPa/mm) | (MPa·h /mm) | (h/mm) | (MPa h/mm) | R2 | ||
| 0% | 4.89 | 9.23 | 52.98 | 63.40 | 2.95 × 10−19 | 6.93 × 1013 | 0.12 | 0.99 |
| 0.46% | 4.45 | 6.84 | 50.00 | 56.52 | 4.50 × 10−18 | 7.02 × 1011 | 0.27 | 0.99 |
| 0.87% | 4.45 | 6.59 | 43.80 | 52.33 | 2.69 × 10−17 | 8.27 × 1010 | 0.40 | 0.99 |
| 1.24% | 4.45 | 6.29 | 40.01 | 45.12 | 3.17 × 10−16 | 6.70 × 109 | 0.84 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Lei, M.; Wang, L.; Hu, B.; Zhao, Y.; Zhang, J. An Improved Nishihara Model Considering the Influence of Moisture Content on the Whole Shear Creep Process of Shale. Processes 2025, 13, 783. https://doi.org/10.3390/pr13030783
Ma L, Lei M, Wang L, Hu B, Zhao Y, Zhang J. An Improved Nishihara Model Considering the Influence of Moisture Content on the Whole Shear Creep Process of Shale. Processes. 2025; 13(3):783. https://doi.org/10.3390/pr13030783
Chicago/Turabian StyleMa, Liyao, Mingfeng Lei, Lichuan Wang, Bin Hu, Yaqian Zhao, and Jingjing Zhang. 2025. "An Improved Nishihara Model Considering the Influence of Moisture Content on the Whole Shear Creep Process of Shale" Processes 13, no. 3: 783. https://doi.org/10.3390/pr13030783
APA StyleMa, L., Lei, M., Wang, L., Hu, B., Zhao, Y., & Zhang, J. (2025). An Improved Nishihara Model Considering the Influence of Moisture Content on the Whole Shear Creep Process of Shale. Processes, 13(3), 783. https://doi.org/10.3390/pr13030783





