Research on Optimization of Diesel Engine Speed Control Based on UKF-Filtered Data and PSO Fuzzy PID Control

Abstract

With the continuous development of industrial automation, diesel engines play an increasingly important role in various types of construction machinery and power generation equipment. Improving the dynamic and static performance of the speed control system of single-cylinder diesel engines can not only significantly improve the efficiency of the equipment, but also effectively reduce energy consumption and emissions. Particle swarm optimization (PSO) fuzzy PID control algorithms have been widely used in many complex engineering problems due to their powerful global optimization capability and excellent adaptability. Currently, PSO-based fuzzy PID control research mainly integrates hybrid algorithmic strategies to avoid the local optimum problem, and lacks optimization of the dynamic noise suppression of the input error and the rate of change of the error. This makes the algorithm susceptible to the coupling of the system uncertainty and measurement disturbances during the parameter optimization process, leading to performance degradation. For this reason, this study proposes a new framework based on the synergistic optimization of the untraceable Kalman filter (UKF) and PSO fuzzy PID control for the speed control system of a single-cylinder diesel engine. A PSO-optimized fuzzy PID controller is designed by obtaining accurate speed estimation data using the UKF. The PSO is capable of quickly adjusting the fuzzy PID parameters so as to effectively alleviate the nonlinearity and uncertainty problems during the operation of diesel engines. By establishing a Matlab/Simulink simulation model, the diesel engine speed step response experiments (i.e., startup experiments) and load mutation experiments were carried out, and the measurement noise and process noise were imposed. The simulation results show that the optimized diesel engine speed control system is able to reduce the overshoot by 76%, shorten the regulation time by 58%, and improve the noise reduction by 25% compared with the conventional PID control. Compared with the PSO fuzzy PID control algorithm without UKF noise reduction, the optimized scheme reduces the overshoot by 20%, shortens the regulation time by 48%, and improves the noise reduction effect by 23%. The results show that the PSO fuzzy PID control method with integrated UKF has superior control performance in terms of system stability and accuracy. The algorithm significantly improves the responsiveness and stability of diesel engine speed, achieves better control effect in the optimization of diesel engine speed control, and provides a useful reference for the optimization of other diesel engine control systems. In addition, this study establishes the GT-POWER model of a 168 F single-cylinder diesel engine, and compares the cylinder pressure and fuel consumption under four operating conditions through bench tests to ensure the physical reasonableness of the kinetic input parameters and avoid algorithmic optimization on the distorted front-end model.

1. Introduction

With the strengthening of global environmental awareness and the increasingly serious energy crisis, countries around the world have introduced strict emission regulations and energy efficiency standards to reduce the environmental pollution and energy consumption of internal combustion engines. In China, with the introduction of the National VI emission standard, the emission requirements of diesel engines are higher, and the manufacturers of internal combustion engines are constantly adjusting the performance of internal combustion engine products to meet the requirements of emission regulations [1]. In recent years, the country has vigorously developed agricultural mechanization and small power generation equipment intelligence, and the state has invested much manpower and material resources, as well as policies to implement various plans. The National Agricultural Mechanization Development “14th Five-Year Plan” [2] clearly put forward the improvement of the level of agricultural machinery intelligence, and promoted efficient, safe, and environmentally friendly agricultural production. The above policy opens up a broad market and policy conditions for the research on, and application of, single-cylinder diesel engine speed control systems.

The single-cylinder diesel engine is widely used in agricultural machinery, small power generation equipment [3], and ship propulsion and other fields. The stability of the speed control of this engine has a vital impact on its operational efficiency and reliability in the whole system; therefore, improving the dynamic and static performance of the speed control system of the single-cylinder diesel engine is one of the key points in the research on the control of its power mechanical system. 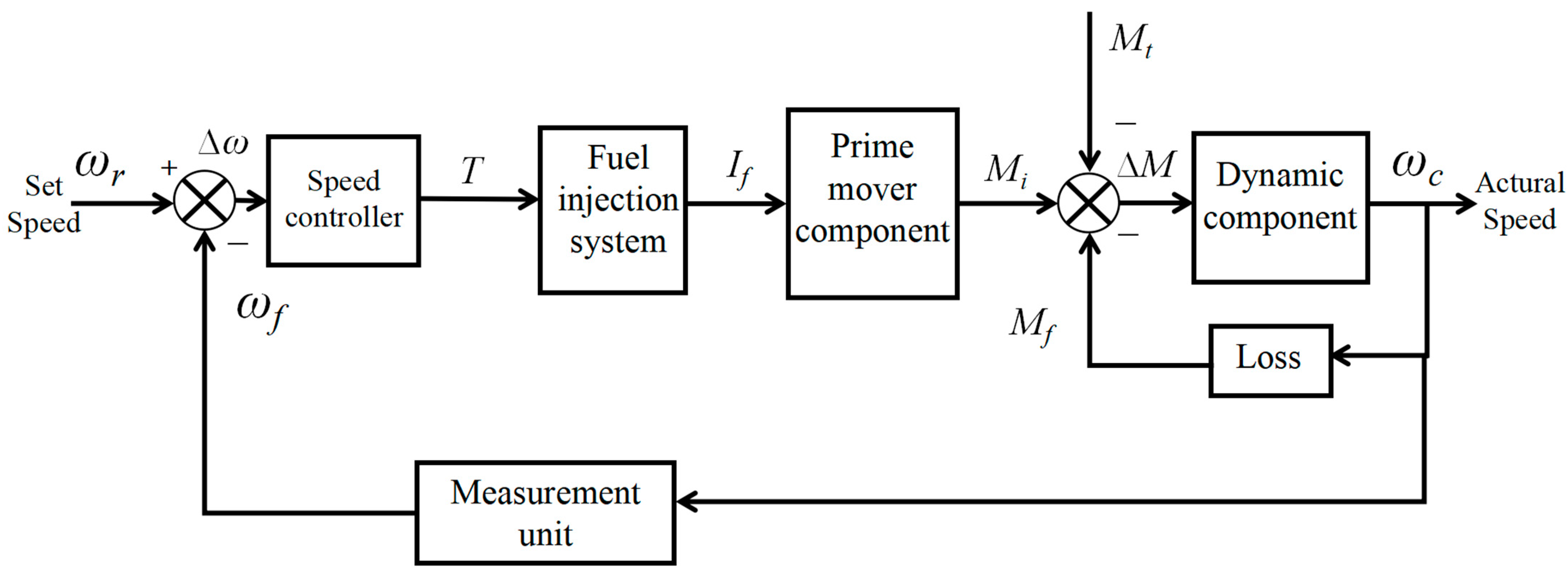Figure 1 shows the complexity of the control system of the diesel engine, from the generation of the speed signal to the adjustment of the control system, the injection of fuel, the combustion of the cylinder to do work, and then to synchronization of the output to produce the crankshaft torque and thus the output of power. This is a very complex mechanical body involving a variety of disciplines such as fluid dynamics, combinatorics, mechanical principles, and control theory. This diesel engine has very strong nonlinearities, response hysteresis, and coupling phenomena [4].

Because the diesel engine system has relatively complex time-varying nonlinear and multi-input and multi-output characteristics, in the whole process of diesel engine operation, the sudden changes in load, mechanical wear, and other problems often make the control performance problematic [5]; at the same time, in the diesel engine, after a long period of time, the mechanical wear and tear makes the system dynamic characteristics change, which will also increase the difficulty of control. These factors will trigger the system’s dynamic and static performance deterioration, affecting the overall stability of the system as well as the operating efficiency [6], so the use of simple PID control of the diesel engine speed may not be ideal for performance improvement. Especially regarding diesel engine load changes and other complex operating conditions, some parameters in the PID controller cannot be adapted to the changes in the control requirements, and system performance is easily and obviously reduced. Therefore, how to find a suitable diesel engine speed control system is of particular significance.

In response to the above problems of control performance optimization, many scholars have proposed and used a fuzzy PID controller combining fuzzy logic and PID in the literature, and achieved certain practical results in some engineering fields: reference [7] proposed a fuzzy PID-based control method to solve the problem of a rice-planting robotic arm being affected by external disturbances, which affected the displacement tracking of the hydraulic rice-planting system, leading to the problem of reduced output accuracy. The method improves the step response time of the system by 56%. By using fuzzy PID control, the system is able to solve the problems related to nonlinearity and low control accuracy, thus improving its stability and dynamic performance. Reference [8] describes an enhanced fuzzy PID control system based on a grey model that adjusts the residuals using an improved gated recursive unit (GM-IPSO-GRU) based on particle swarm optimization. In addition, the system optimizes the control parameters by using the Improved Gray Wolf Optimization (IGWO) algorithm. Although the system overcomes the problems of nonlinearity, time variation, and time delay, the response speed and stability of the system still need to be improved. Compared with the traditional PID controller, the fuzzy PID controller can better deal with nonlinearity, uncertainty, and ambiguity in complex systems, and it can automatically adjust the parameters without manual adjustment, thus saving the adjustment time and adjustment cost [9].

However, the fuzzy PID control methodology still faces limitations such as reliance on manual parameter configuration, absence of self-adaptive adjustment mechanisms, and suboptimal performance when applied to complex systems with nonlinear and time-varying characteristics. Specifically, these constraints may lead to convergence to local optima and exhibit sluggish response dynamics in practical implementations. In order to facilitate the automatic optimization of control parameters to improve the performance, in recent years, global optimization algorithms such as Particle Swarm Optimization (PSO) have become an effective method to optimize the fuzzy PID parameters. PSO simulates the search of particles in the solution space, and is able to search for optimal scaling factors and quantization factors in the multidimensional space, thus significantly improving the control performance of fuzzy PID control. In terms of agricultural machinery, reference [10] used an IPSO-optimized fuzzy PID controller to implement adaptive head trimming for a cabbage harvester and verified the control accuracy of ±3 mm of gripping gap in a field test. However, this work failed to account for the real-time effects of dynamic changes in crop size on the control parameters. Similarly, reference [11] developed a dual closed-loop seeding system with radar speed measurement that achieved a field pass rate of 93.99% for corn seeding, but terrain-induced speed measurement errors still constrained the uniformity of seeding spacing. In vehicle engineering, reference [12] proposed a PSO fuzzy PID controller for in-wheel brushless DC motors, which can reduce the tire slip rate by 12%. Reference [13] pioneered a PSO-Fuzzy-PID controller for a greenhouse glass cleaner, which achieved an inter-wheel speed difference of 0.086 deg/s through Adams–Matlab co-simulation. For wind energy applications, reference [14] combined fuzzy inverse stepping sliding mode control with MOPSO to improve the power extraction efficiency by 18.7%, but the mechanical load fluctuation under sudden change of wind speed was still not optimal. For grid frequency regulation, reference [15] innovatively integrated supercapacitors and redox flow batteries to suppress system oscillations by 64%.

In the field of robotics and motor control, in reference [16], three different PSO algorithms based on cost function were used to optimize the fuzzy logic controller parameters of a two-degree-of-freedom planar robot, and the improved controller was derived by changing the model parameters and the reference trajectory, varying the model parameters, adding white noise for testing, and testing the robustness of the adjusted controller to provide valuable test method improvement results. Reference [17] proposed a two-dimensional fuzzy fractional PID controller to cope with a large number of parameters in a fractional order controller and designed a multi-objective PSO algorithm capable of determining the system parameters to optimize the parameter determination process. Reference [18] proposed a Genetic Particle Swarm Optimization (GAPSO) strategy for optimizing fuzzy PID control parameters for motor control. The method combines a genetic algorithm and particle swarm optimization through a genetic screening method to optimize the initial values of quantization factor, scale factor, and eigenfunction, which provides a new method for the adjustment of fuzzy PID control parameters.

Like fuzzy PID control, PSO-optimized fuzzy control is also widely used in many temperature control systems. The heat transfer process in temperature control is a typical nonlinear process, which is affected by factors such as the heat source, heat capacity, environmental conditions, etc. For the research object involved in this study, the system diesel engine speed control is affected by nonlinear factors such as engine load, fuel supply, and mechanical friction, and both systems are nonlinear systems. The application of the literature [19] can optimize the proportional weight coefficients of the fuzzy PID controller in the temperature control system of the resistance furnace, and this method better improves the key control indexes such as overshoot and steady-state error of this control system, and improves the quality and stability of temperature control. Reference [20] reduced the temperature response time of a PEM fuel cell under step disturbance to 2.3 s; reference [21] reduced the failure rate of an air handling unit by 64% through NARMAX modeling. While these studies validate the robustness of the PSO fuzzy PID architecture, few studies have fully utilized the state of the thermodynamic system for temperature estimation.

Currently, there are two common limitations in engineering research for PSO fuzzy PID algorithms: firstly, the problems of sensor error and noise; and secondly, the lack of real-time prediction of changes in environmental dynamics (e.g., gusts of wind, road friction, and crop morphology, etc.). The use of filters can effectively improve the above problems and enhance the control accuracy, while the speed control of diesel engines has certain nonlinearities, load perturbations, fuel supply issues, etc., that will affect the dynamic response of the speed, and the traditional Kalman filter (KF) is only applicable to linear systems, and is not able to solve the nonlinear problems. The Untraceable Kalman Filter (UKF), as an advanced filtering method, can provide high-precision state estimation in complex nonlinear systems and effectively suppress noise disturbances. Reference [22] describes a novel algorithm to simultaneously estimate the state of charge (SOC) and state of health (SOH) using a strongly tracking dual adaptive extended Kalman filter (ST-DAEKF). To enhance the tracking capability, an attenuation factor is incorporated in the method and an adaptive filter is used to dynamically adjust the noise parameters of the system. This approach is designed to mitigate the problems arising from large estimation errors in the SOC and SOH. Reference [23] designed an irrigation system based on Kalman filter PID controller using IAE, ISE, and cumulative ITAE for simulation. By modeling the dynamics using historical real-time data, the KF reduces the sensor output noise and improves the estimation accuracy. Reference [24] presents a hybrid optimization model that integrates an adaptive neuro-fuzzy inference system (ANFIS), a recursive Kalman filter, and neural wavelets for wind power prediction driven by a doubly-fed induction generator, which exhibits excellent performance. Reference [25] designed an algorithm for vehicle traveling state estimation by applying an adaptive Kalman filter combined with a fuzzy PID controller, demonstrating the accuracy of the Kalman filter in state estimation. Reference [26] optimized the PID gain of a hydraulic servo system using a genetic algorithm and combined it with Kalman filtering to reduce the external disturbances and amplitude fluctuations, and verified the effectiveness of the method in hydraulic servo systems. Reference [27] developed an observer for diagnosis and fault tolerant control of aging SCR (Selective Catalytic Reduction) systems using UKF, further highlighting the effectiveness of the filtering approach in fault detection and system management. Reference [28] proposed a temperature control system based on Kalman filtering fuzzy PID design. From the experimental results, the algorithm has short tuning time and almost zero overshoot, but its adaptability under complex operating conditions has not yet been clearly addressed. The current research results show that traceless Kalman filtering is an advanced filtering method that can provide high-precision state estimation in complex nonlinear systems and effectively suppress noise interference. If UKF is combined with PSO fuzzy PID control, it is expected to further improve the estimation accuracy and control performance of the system, and overcome the limitations of PID control and fuzzy PID control under noise and disturbances.

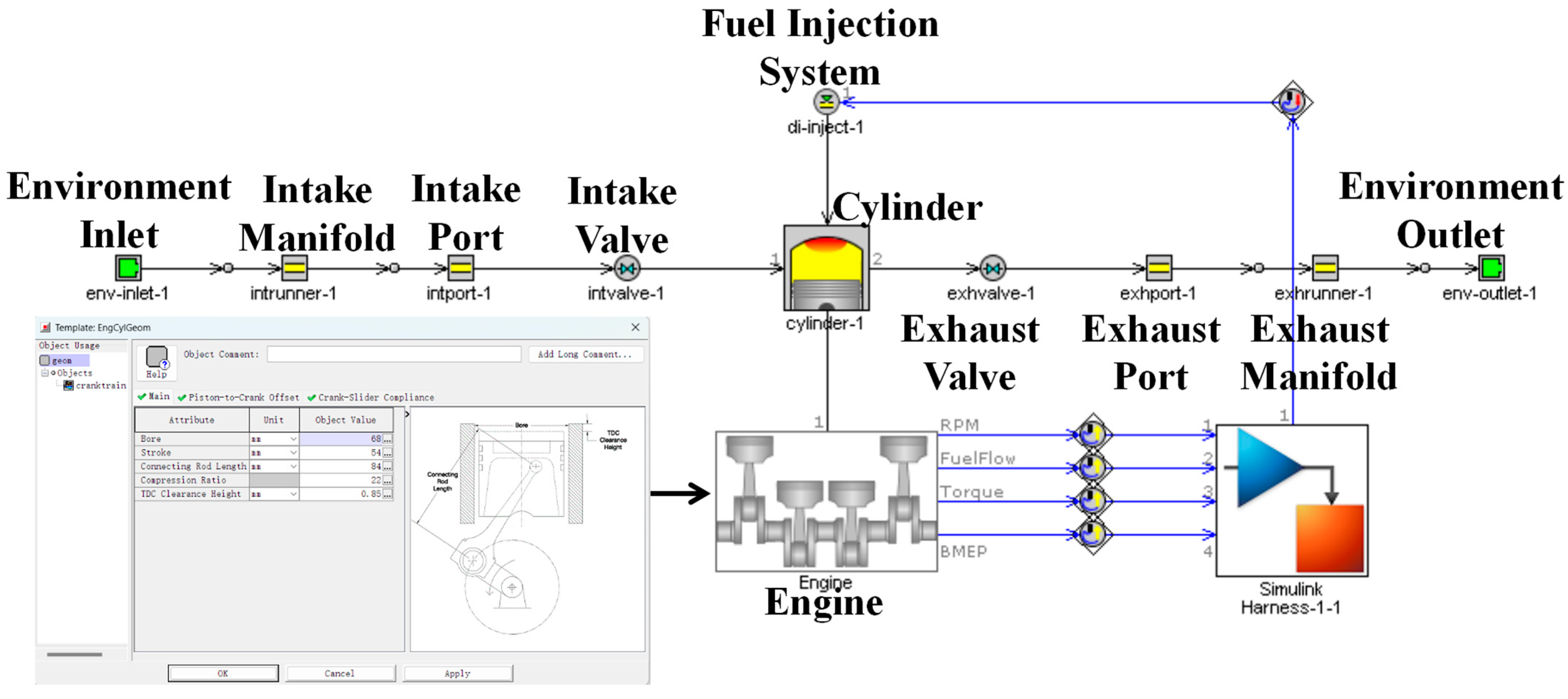
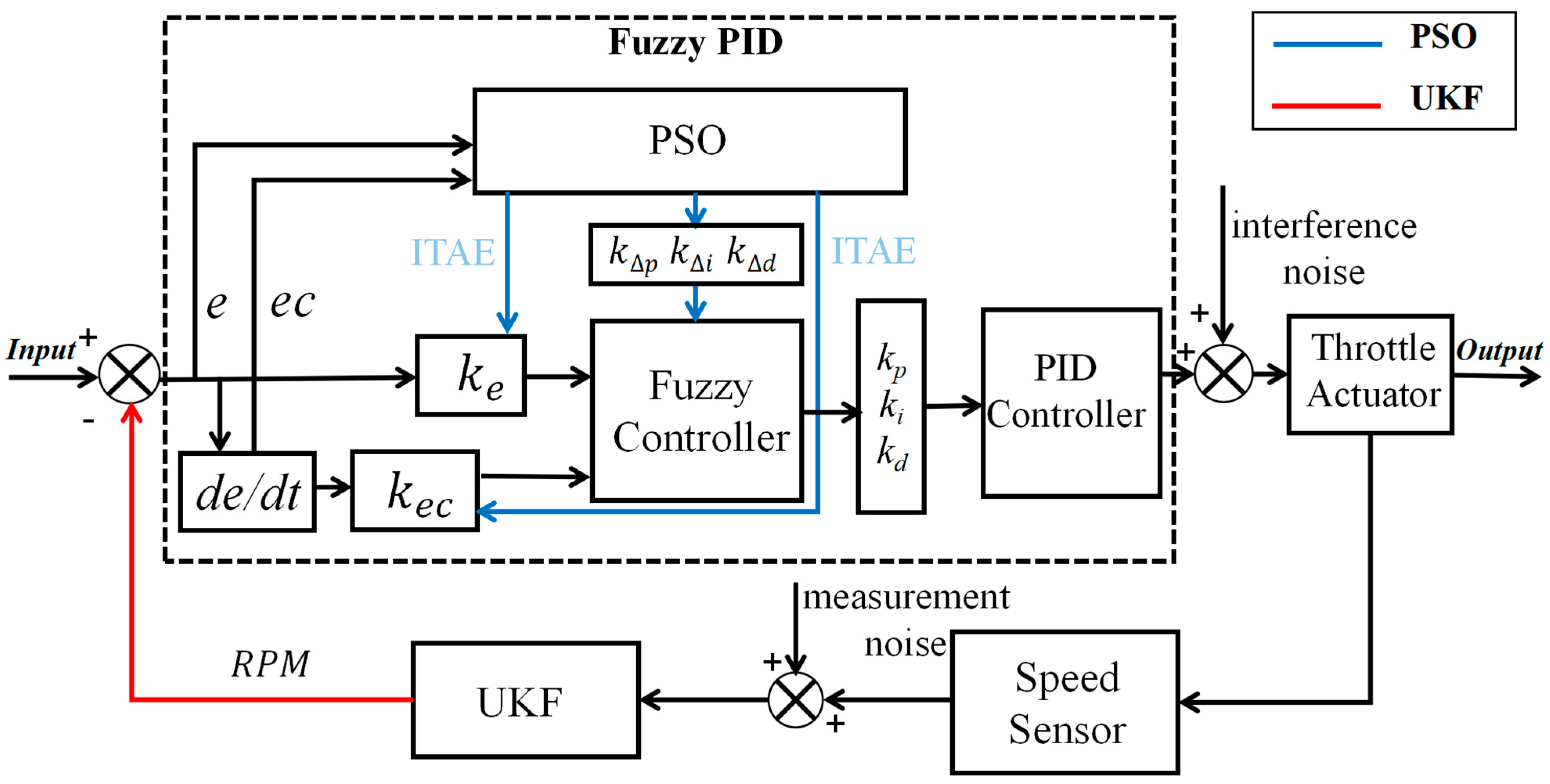
In response to the above research analysis, a PSO fuzzy PID control strategy for diesel engine speed optimization based on UKF filtered data is proposed. The strategy provides accurate estimation of diesel engine speed through UKF, effectively eliminating the influence of measurement noise and process noise on speed accuracy. Based on the accurate rotational speed data, the parameters of the fuzzy PID controller are optimized in combination with the PSO algorithm to achieve more accurate and robust control performance. We established a dynamic model of a single-cylinder diesel engine and built a simulation model of the algorithm in Matlab/Simulink (R2022b). By comparing it with four algorithms such as traditional PID control, we analyzed the optimization improvement of the proposed algorithm in terms of response time, overshooting amount, and steady-state error. Meanwhile, in the extension work of this study, the GT-POWER model of a 168 F single-cylinder diesel engine is built, and the cylinder pressure and fuel consumption parameters are verified through bench experiments, which lays the foundation for future joint simulation studies.

2. Single-Cylinder Diesel Engine Model

2.1. Diesel Engine Dynamics Model

The speed control system of a single-cylinder diesel engine is mainly composed of a governor, a fuel injection system, engine working parts, dynamic parts, and a measuring unit. The schematic diagram of the diesel engine system is shown in Figure 2, and the descriptions of the variables are shown in

Table 1. Diesel engine dynamics modeling symbol.

Symbol	Description	Unit
${\omega }_r$	Set crankshaft angular speed	$\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$
${\omega }_f$	Measure crankshaft angular speed	$\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$
$∆\omega$	Speed difference	$\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$
$T$	Fuel injection time	$\mathrm{s}$
$I_f$	Fuel injection quantity	$\mathrm{m}\mathrm{g}$
$M_i$	Output torque	$\mathrm{N}·\mathrm{m}$
$M_f$	Friction torque	$\mathrm{N}·\mathrm{m}$
$M_t$	Load torque	$\mathrm{N}·\mathrm{m}$
$∆M$	Torque difference	$\mathrm{s}$

.

Under balance conditions, the output torque $M$ of the diesel engine equals the sum of the friction and torque $M_f$ and the crankshaft load torque $M_t$. By linearizing the system using the small deviation method, the motion equation of the diesel engine shaft system is obtained as follows:

$$\begin{array}{c}J{\displaystyle \frac{d(∆M)}{dt}}=∆M-M_f-M_t\end{array}$$

(1)

where

• J is the rotational inertia of the diesel engine unit.
• ω is the crankshaft angular velocity.

Under balanced conditions, with the diesel load remaining constant, and only considering the effect of the rack position, Equation (1) is simplified to give the diesel engine’s motion equation as

$$T_{\alpha }{\displaystyle \frac{dy\left(t\right)}{dt}}+T_{g}y\left(t\right)=K_{\eta }\eta \left(t\right)$$

(2)

where

• y(t) is the diesel engine speed.
• η(t) is the rack displacement.
• T_α is the acceleration time constant of the diesel engine, representing the time required for the engine to reach the rated speed from zero in an idle state.
• T_g is the self-stability coefficient, representing the diesel engine’s ability to automatically stabilize its speed.
• K_η is the dynamic characteristic parameter of the diesel engine, representing the effect of the oil pump rack position change on the output torque of the crankshaft.

By applying the Laplace transform, the transfer function is derived as

$$\begin{array}{c}{G}_d(s)={\displaystyle \frac{Y\left(s\right)}{\eta \left(s\right)}}={\displaystyle \frac{K_{\eta }}{T_{\alpha }s+1}}\end{array}$$

(3)

During the operation of the diesel engine, factors such as the thermal inertia of the combustion chamber in the fuel injection system cause delay in the engine’s response. The transfer function for this delay is

$$\begin{array}{c}{G}_{\tau }\left(s\right)=e^{-\tau s}\end{array}$$

(4)

The diesel engine speed control system has many state variables and exhibits time-varying characteristics. Through practical application, it has been proven that after dimensionless and linear processing, the diesel engine speed control system can be modeled using a first-order inertia system. The simplified model is as follows:

$$\begin{array}{c}{G}_1\left(s\right)=G_d\left(s\right)G_{\tau }\left(S\right)={\displaystyle \frac{1}{T_{\tau }s+1}}·e^{-\tau s}\\ K_{\eta }=1,T_g=1\end{array}$$

(5)

The technical parameters of the 168 F single-cylinder diesel engine are shown in

Table 2. Main parameters of single cylinder diesel engine.

Parameter	Value
Engine	168 F Single Cylinder Diesel Engine
Main Type	Inline, Four-Stroke
Bore	68 mm
Stroke	54 mm
Connecting Rod Length	84 mm
Piston Displacement	0.196 L
Maximum Power	2.2 kw/3000 rpm
Compression Ratio	8.5:1
Piston Top Dead Center Clearance	0.85 mm

.

Based on the above diesel engine technical parameters, the following diesel engine parameters can be calculated:

Rated angular velocity:

$${\omega }_e={\displaystyle \frac{\pi }{30}}{n}_e=345.4\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$$

(6)

Rated torque:

$$\begin{array}{c}{M}_e={\displaystyle \frac{30P_e}{\pi n_e}}=0.0092\mathrm{N}·\mathrm{M}\end{array}$$

(7)

Referring to the diesel engine speed characteristic experimental literature [29], the rotational inertia of the diesel engine unit is calculated as

$$\begin{array}{c}J=0.0006\mathrm{k}\mathrm{g}·{\mathrm{m}}^2\end{array}$$

(8)

The diesel engine acceleration time constant $T_{\alpha }$ is given by

$$\begin{array}{c}{T}_{\alpha }=J{\displaystyle \frac{{\omega }_e}{M_e}}=0.22\mathrm{s}\end{array}$$

(9)

The delay time $\tau$ of the diesel engine is related to the number of cylinders $z$, stroke number, and speed $n$. For a four-stroke diesel engine, the delay time can be estimated as

$$\begin{array}{c}{\displaystyle \frac{15}{n}}\le \tau \le {\displaystyle \frac{15}{n}}+{\displaystyle \frac{120}{nz}}\end{array}$$

(10)

Thus, $0.0045\le \tau \le 0.036(\mathrm{t}\mathrm{a}\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{g}\tau =0.02\mathrm{s})$.

The diesel engine speed control actuator is an electromagnetic actuator. Electromagnetic actuators have advantages such as good dynamic characteristics, fast response, and strong anti-interference performance. The transfer function for the electromagnetic actuator is

$$\begin{array}{c}{G}_2(s)={\displaystyle \frac{F\left(s\right)}{P\left(s\right)}}={\displaystyle \frac{k}{1+T_{k}s}}\end{array}$$

(11)

where

• k is the maximum displacement of the actuator, which is selected as 20 mm in this study.
• T_k is the first-order inertia parameter, taken as 1.

Therefore, the whole speed control model of the diesel engine is

$$\begin{array}{c}G(s)=G_1(s)G_2(s)={\displaystyle \frac{20}{0.22s^2+1.22s+1}}{e}^{-0.02s}\end{array}$$

(12)

2.2. GT-POWER Model

The focus of this study is the optimization of the diesel engine speed control algorithm, and the control objective is to improve the speed tracking accuracy and anti-interference ability. The cylinder pressure of a diesel engine directly affects the output torque, which is closely related to the speed. Although the existing transfer function model takes into account the delay of the fuel injection system, engine inertia, and the dynamic characteristics of the actuator, there are still certain simplifications and limitations, such as not fully considering the complex effects of cylinder pressure and temperature fluctuations, changes in fuel characteristics, and other factors. In order to compensate for this deficiency, cylinder pressure was used as an internal state variable for model validation in the previous study to verify the accuracy of the transfer function. In the future, Matlab/Simulink and GT-POWER can be co-simulated to significantly improve the dynamic accuracy of the diesel engine model, especially in the cylinder pressure–fuel consumption multi-condition coupled analysis, to provide a more accurate dynamic response and a more realistic prediction of the operating state.

In Figure 3, the basic working principle of the diesel engine speed control system is as follows: First, the system sets a target speed. The microcontroller then receives this input signal and begins executing the fuzzy PID control algorithm. This algorithm primarily calculates the output duty cycle of the adjustable pulse width modulation (PWM) square wave signal based on the deviation between the target speed and the actual speed [30]. This PWM signal is then used by the driving circuit to control the opening of the electronic throttle, thereby accurately adjusting the speed of the diesel engine to ensure it reaches or maintains the set target speed.

The speed sensor is responsible for real-time monitoring of the diesel engine’s speed and converting it into an analog signal. This analog signal is converted into a digital signal by the TLV2548 analog-to-digital conversion chip, which is then transmitted to the microcontroller. Within the microcontroller, a dedicated speed data conversion program processes the received digital signal to obtain specific speed values and their trends, displaying this data and graphics on the upper computer’s monitoring interface through a serial port. Figure 4 illustrates the diesel engine test bench.

In this study, a simulation model of a 168 F single-cylinder diesel engine was built using GT-POWER, as shown in Figure 5. This diesel engine model includes several modules such as the external environment model, intake and exhaust duct system, intake and exhaust valves, fuel injector, cylinder, crankcase, and an external receiving device for the fuel injector signal [31]. The detailed key parameters in the GT-POWER simulation model are shown in

Table 3. Key parameters in the GT-POWER simulation model.

Module	Attribute	Unit	Value
Environment Inlet/Outlet	Pressure (Absolute)	$\mathrm{b}\mathrm{a}\mathrm{r}$	$2.4$
	Temperature	$\mathrm{K}$	$350$
	Composition	/	$Air$
Intake/Exhaust Manifold	Diameter at Inlet End	$\mathrm{m}\mathrm{m}$	$40/30$
	Length	$\mathrm{m}\mathrm{m}$	$120/150$
	Discretization Length	$\mathrm{m}\mathrm{m}$	$40/55$
Intake/Exhaust Port	Diameter at Inlet End	$\mathrm{m}\mathrm{m}$	$40/30$
	Length	$\mathrm{m}\mathrm{m}$	$80/60$
	Discretization Length	$\mathrm{m}\mathrm{m}$	$40/55$
Intake/Exhaust Value	Cam Timing Angle	$\mathrm{C}\mathrm{a}\mathrm{m}$$\mathrm{A}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}$	$239/126$
	Cam Timing Anchor Reference	/	TDCFiring
Fuel Injection System	Injected Mass	$\mathrm{m}\mathrm{g}$	$50$
	Fluid Object	/	diesel
	Injected Fluid Temperature	$\mathrm{K}$	$300$
	Injection Timing	$\mathrm{d}\mathrm{e}\mathrm{g}$	$-10$
	Injection Duration	$\mathrm{d}\mathrm{e}\mathrm{g}$	$18$
Engine (The remaining parameters are shown in Table 2)	Engine Type	/	4-stroke
	Speed or Load Specification	/	speed
	Engine Friction Object or FMEP	/	friction
	Start of Cycle (CA at IVC)	/	$-95$

.

In the calculation of the in-cylinder heat transfer model, the main use of the “Woschni” model, the “Woschni” formula is more recognized at home and abroad in the internal combustion engine heat transfer model; the calculation formula is as follows:

$$\begin{array}{c}{\partial }_g=2.06\times {10}^{-7}{p}^{0.8}{T}^{-0.53}{D}^{-0.2}{\left[S_1{S}_m+S_2{\displaystyle \frac{T_a·V_s}{p_a·V_a}}(p-p_1)\right]}^{0.8}(2-1)\end{array}$$

(13)

where $D\left(\mathrm{m}\mathrm{m}\right)$ is the cylinder diameter; $S_m(\mathrm{m}/\mathrm{s})$ is the average piston speed; $p_a(Pa),T_a(Pa),V_a(pa)$ are the pressure, temperature $\left(\mathrm{K}\right)$, and volume $\left(\mathrm{L}\right)$ of the work material in the cylinder at the end of compression, respectively; $p_1(Pa)$ is the cylinder pressure when the engine is backed up and dragged; $S_1$ is the coefficient of the airflow velocity; and $S_2$ is the shape coefficient of the combustion chamber, and the direct-injection combustion chamber is taken to be $2$.

The dual Weber combustion model is selected for calculating cylinder combustion, which simulates combustion in two main parts: premixed combustion and diffusion combustion. The formula for premixed combustion is as follows:

$$\begin{array}{c}{\displaystyle \frac{d{x}_1}{d\phi }}=\left[6.908\left(m_q+1\right){\left({\displaystyle \frac{1}{2\gamma }}\right)}^{m_q+1}{\left(\phi -{\phi }_B\right)}^{m_q}{e}^{-6.908{\left({\displaystyle \frac{1}{2\gamma }}\right)}^{m_q+1}{\left(\phi -{\phi }_B\right)}^{m_q+1}}\right](1-Q_d)\end{array}$$

(14)

where $x_1$ is the percentage of combustion in premixed combustion; $\phi$ is the crankshaft rotation angle, ${\phi }_B$ is the combustion start angle, $\gamma$ is the premixed combustion leading angle; and $m_q$ is the combustion quality index of premixed combustion. The formula for diffusion combustion is shown below:

$$\begin{array}{c}{\displaystyle \frac{d{x}_2}{d\phi }}=\left[6.908\left(m_p+1\right){\left({\displaystyle \frac{1}{{\phi }_{zd}}}\right)}^{m_p+1}{\left(\phi -{\phi }_B-\gamma \right)}^{m_p}{e}^{-6.908{\left({\displaystyle \frac{1}{2\gamma }}\right)}^{m_p+1}{\left(\phi -{\phi }_B-\gamma \right)}^{m_p+1}}\right]Q_d\end{array}$$

(15)

where $x_2$ is the percentage of combustion in premixed combustion, ${\phi }_{zd}$ is the diffusion combustion duration angle, and $m_p$ is the combustion quality index of diffusion combustion.

Injections can be set in the “Profile” column according to the actual situation of the corresponding injection flow map curve, which also supports the signal receiver module or external actuator to receive the injection signal from the outside world. The single-cylinder cycle injection volume is calculated from the simulation analysis of power, fuel consumption rate, operating speed, and other parameters:

$$\begin{array}{c}{m}_{fuel}={\displaystyle \frac{P_e·g_e}{60·n·N_c·\rho }}(\mathrm{g}/\mathrm{c}\mathrm{y}\mathrm{l})\end{array}$$

(16)

where $P_e$ is the average effective power, eg is the fuel consumption rate, $N_c$ is the number of cylinders, $n$ is the rotational speed, and $\rho$ is the stroke coefficient, taking 1 for two-stroke and 0.5 for four-stroke.

To verify the accuracy of the model and its reliability, the single-cylinder diesel engine model was simulated under different loads of 100%, 75%, 50%, and 25%. The cylinder pressure curves obtained from the simulation calculations at different loads were compared with the actual cylinder pressure curves, as well as the fuel consumption data. The comparison results are as follows.

As can be seen in Figure 6 and Figure 7, the simulated cylinder pressure curves as well as the trajectories of the simulated and experimental fuel consumption values are very similar under the four different operating conditions. Comparison with the experimental values shows that the error of cylinder pressure calculation is about 3%; specifically, the maximum value of the error rate is 5.7% and the average value is 3.3%, while the error of the fuel consumption data is about 7.6%. Therefore, it can be concluded that the combustion sub-model simulation calculations of this diesel engine model under different loads have high accuracy and can be used for further analytical calculations in the future [32].

3. Methods

In order to further improve the static and dynamic performance of the diesel engine speed control system, this paper proposes an improved method that combines the untraceable Kalman filter with the particle swarm optimized fuzzy PID control technique. The speed sensor data received by the untraceable Kalman filter (UKF) accurately estimates the diesel engine speed through information such as torque and fuel injection, while filtering for the interference of Hall sensor measurement noise and process noise in the control system, and provides accurate speed data for the control system. Fuzzy PID control utilizes fuzzy logic to change the $k_p$, $k_i$, $k_d$ of the PID controller, effectively overcoming the shortcomings of the traditional PID method of poor control performance under nonlinear, time-varying, and complex operating conditions. At the same time, a PSO optimization algorithm is introduced to globally optimize the proportional factor and quantization factor in the fuzzy controller. By simulating the process of particle swarm searching for the optimal solution, the PSO algorithm realizes the indirect dynamic adjustment of the PID parameters, which further enhances the adaptability and robustness of the controller. By combining the accurate state estimation of the UKF with PSO-optimized fuzzy PID control, not only can the control parameters be precisely adjusted, but also can effectively deal with disturbances and uncertainties to ensure that the diesel engine maintains accurate speed control under different operating conditions. The technical flow chart of this paper is shown in Figure 8, and the principle of the collection of the UKF and PSO Fuzzy PID controllers is shown in Figure 9. The design and implementation methods of this control strategy are described in detail in the following section.

3.1. Unscented Kalman Filter

The Kalman filter is optimal for linear systems with Gaussian noise, but the noise in diesel engines is high and nonlinear, with time-varying dynamics and coupled disturbances. In the environment of a diesel generator system, diesel engines experience significant interference and noise. To improve the system’s control performance, this study uses UKF filtering to control the impact of disturbances and measurement noise on the system. The UKF filtering method approximates the nonlinear distribution using a sampling strategy, where the probability distribution of the nonlinear function is approximated. Based on the Unscented Transform, the Unscented Kalman Filtering framework is employed, with deterministic sampling as the form of sampling, unlike the random sampling in Particle Filtering, thus avoiding the particle degradation issue. It outperforms the Extended Kalman Filter and does not require the calculation of the Jacobian matrix [33].

The nonlinear system model in this study is converted into a discrete model, and its state and observation equations are

$$\begin{array}{c}\left\{\begin{array}{ll}{x}_{k+1}& =f\left(x_k,u_k\right)+w_k\\ y_{k+1}& =h\left(x_k,u_k\right)+v_k\end{array}\right.\end{array}$$

(17)

where $x_k=[{{\omega }_k{L}_k]}^T$ is the system state vector, where ${\omega }_k$ represents the diesel engine speed and $L_k$ is the system load.

$f\left(x\right)$ is the state transition function, describing the dynamic evolution of the diesel engine from time step $k$ to time step $k+1$.

The rotational inertia $J$ governs the speed response to net torque:

$$\begin{array}{c}{\omega }_{k+1}={\omega }_k+{\displaystyle \frac{\mathsf{\Delta }t}{J}}\left(T_e({\omega }_k,u_k)-T_l\left(L_k\right)-T_f\left({\omega }_k\right)\right)+w_{\omega ,k}\end{array}$$

(18)

where $T_{\mathrm{e}}$ depends nonlinearly on fuel injection quantity and combustion efficiency, and $u_k$ is the control input, which includes factors such as fuel injection quantity, throttle position, etc. $T_f$ represents speed-dependent friction losses, and $w_{\omega ,k}$ is the process noise for speed, assumed to be Gaussian noise with covariance $Q_k.$

$y_k$ is the observation vector, which here represents the actual measured engine speed. $h\left(x_k\right)$ is the observation function, describing the system’s measurement process. $v_k$ is the observation noise, assumed to be Gaussian noise with covariance $R_k$.

Load torque $L_k$ evolves as

$$\begin{array}{c}{L}_{k+1}=L_k+\mathsf{\Delta }{L}_k+w_{L,k}\end{array}$$

(19)

where $\mathsf{\Delta }{L}_k$ models external load variations, and $w_{L,k}$ captures unmodeled disturbances.

The observation equation $h\left(x_k\right)={\omega }_k+v_k$ directly measures the engine speed, with $v_k$ representing Hall sensor quantization noise ($R_k=diag({\sigma }_{\omega }^2)$). Sensor noise is calibrated using the root mean square error (RMSE):

$$\begin{array}{c}{\sigma }_{\omega }=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}(r_i-r{)}^2}(N=1000)\end{array}$$

(20)

where $r_i$ is the $i\mathrm{t}\mathrm{h}$ rotational speed sampling point.

The calibration method is to calculate the standard deviation by recording 1000 rpm sampling points under the steady-state error condition, and the typical value is taken as ±50 rpm, which corresponds to $5\%$ FS.

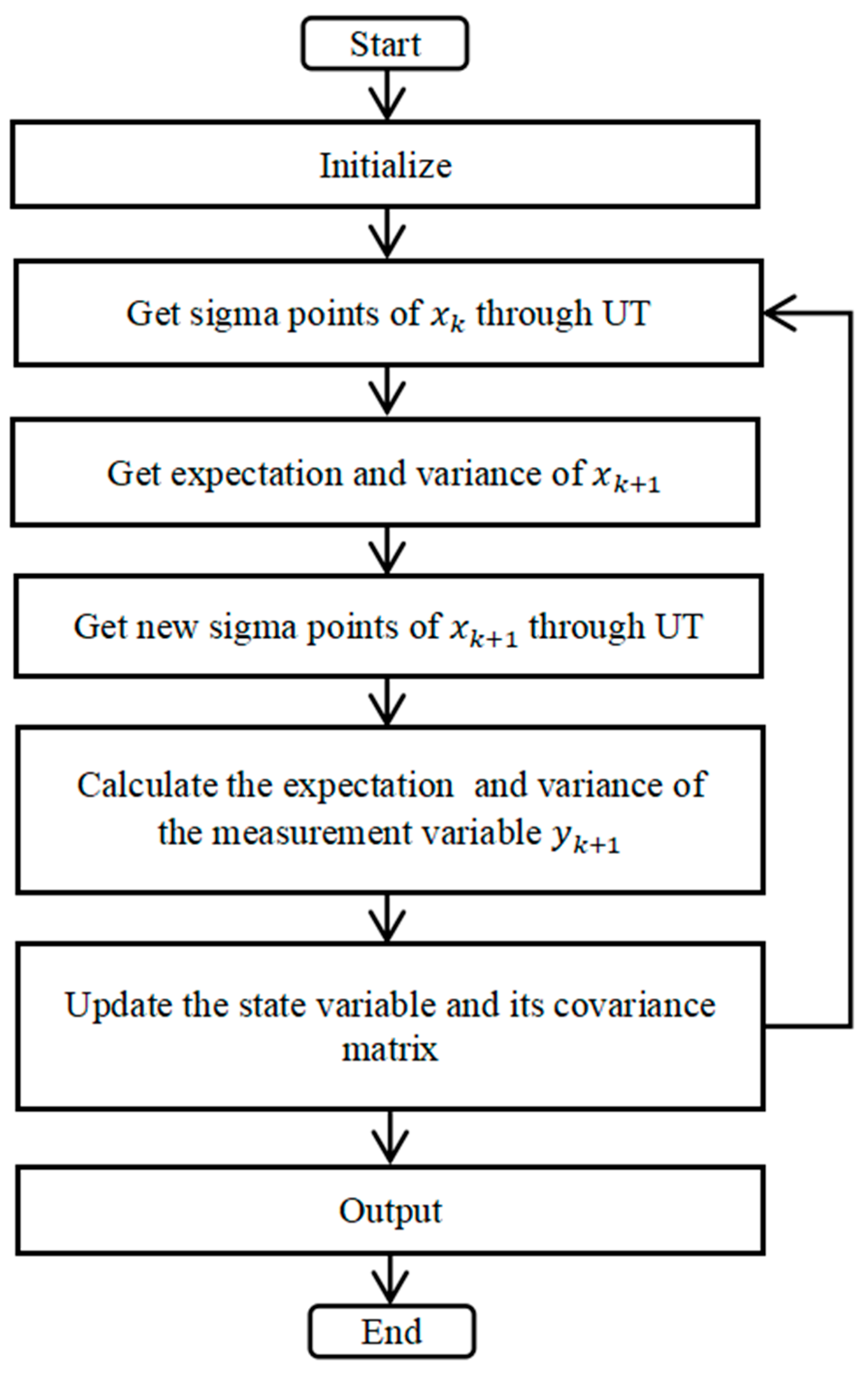
The flowchart of the UKF is shown in Figure 10.

Step 1: Initialization.

$$\begin{array}{c}k=0,E\left[x_0\right]={\widehat{x}}_0,E\left[x_0-{\widehat{x}}_0\right]{\left[x_0-{\widehat{x}}_0\right]}^T=P_0\end{array}$$

(21)

Calculate the Sigma sample points of the input variable within each sampling period $\left(k=\mathrm{1,2},3,\cdots n\right)$:

$$\begin{array}{c}\begin{array}{c}{\chi }_{k-1}\hspace{0.25em}=\hspace{0.25em}\left[\hspace{0.25em}{\widehat{x}}_{k-1},\hspace{0.25em}{\widehat{x}}_{k-1}\hspace{0.25em}+\hspace{0.25em}\gamma \hspace{0.25em}{\left(\hspace{0.25em}\sqrt{P_{k-1}}\right)}_i,\hspace{0.25em}{\widehat{x}}_{k-1}\hspace{0.25em}-\hspace{0.25em}\gamma \hspace{0.25em}{\left(\hspace{0.25em}\sqrt{P_{k-1}}\right)}_i\right]\end{array}\end{array}$$

(22)

where $\gamma =\sqrt{n+\lambda },\lambda ={\alpha }^2\left(n+\kappa \right)-n$, where the parameter $\alpha \in [0.0001,1]$; $\kappa$ is a secondary sampling factor; ${\left(\sqrt{P_{k-1}}\right)}_i$ represents the $i$-th row or column of the matrix square root.

Step 2: For each sigma point, perform the nonlinear transformation and then take the average to update the state.

$$\begin{array}{c}\begin{array}{c}{\chi }_{i,k|k-1}\hspace{0.25em}=\hspace{0.25em}f\left({\chi }_{i,k-1},u_{k-1}\right)\end{array}\end{array}$$

(23)

Then compute predicted mean ${\widehat{x}}_{k|k-1}$ and covariance $P_{k|k-1}$:

$$\begin{array}{c}\begin{array}{c}{\widehat{x}}_{k|k-1}\hspace{0.25em}=\hspace{0.25em}{\displaystyle \sum _{i=0}^{2L}}{W}_i^{\left(m\right)}{\widehat{\chi }}_{i,k|k-1}\end{array}\end{array}$$

(24)

$$\begin{array}{c}\begin{array}{c}{P}_{k|k-1}\hspace{0.25em}=\hspace{0.25em}{\displaystyle \sum _{i\hspace{0.25em}=\hspace{0.25em}0}^{2L}}{W}_i^{\left(c\right)}\hspace{0.25em}\{{\widehat{\chi }}_{i\hspace{0.25em},k|k-1}\hspace{0.25em}-{\widehat{x}}_{k|k-1}\}\{{\widehat{\chi }}_{i\hspace{0.25em},k|k-1}\hspace{0.25em}-{\widehat{x}}_{k|k-1}{\}}^T\hspace{0.25em}+\hspace{0.25em}{Q}_k\end{array}\end{array}$$

(25)

where $W_0^{\left(c\right)}={\displaystyle \frac{\lambda }{n+\lambda }}+1-{\alpha }^2+\beta$, $W_0^{\left(m\right)}={\displaystyle \frac{\lambda }{n+\lambda }}$, $W_i^{\left(c\right)}=W_i^{\left(m\right)}={\displaystyle \frac{0.5}{n+\lambda }}\beta$, $i=\mathrm{1,2},3,\cdots ,2n$; where $\beta$ is a higher-order error sampling factor. The optimal value of β when the error is Gaussian distributed is 2.

Step 3: Measurement update.

$$\begin{array}{c}\begin{array}{c}{\widehat{y}}_{i,}=h\left({\widehat{\chi }}_{i,k|k-1}\right)\end{array}\end{array}$$

(26)

$$\begin{array}{c}\begin{array}{c}{y}_k^{-}={\displaystyle \sum _{i=0}^{2n}}{W}_i^{\left(m\right)}{y}_{i,k|k-1}\end{array}\end{array}$$

(27)

$$\begin{array}{c}\begin{array}{c}{P}_{\widehat{y}k\widehat{y}k}={\displaystyle \sum _{i=0}^{2n}}{W}_i^{\left(c\right)}\{{\widehat{y}}_{i,k|k-1}-{\widehat{y}}_k^{-}\}\{{\widehat{y}}_{i,k|k-1}-{\widehat{y}}_k^{-}{\}}^T+R_k\end{array}\end{array}$$

(28)

$$\begin{array}{c}\begin{array}{c}{P}_{xkyk}={\displaystyle \sum _{i=0}^{2n}}{W}_i^{\left(c\right)}\{{\widehat{\chi }}_{i,k|k-1}-{\widehat{x}}_{k|k-1}\}\{{\widehat{y}}_{i,k|k-1}-{\widehat{y}}_k^{-}{\}}^T\end{array}\end{array}$$

(29)

Step 4: Update the state estimate using Kalman gain $K_k$.

$$K_k=P_{xkyk}{P}_{\widehat{y}k\widehat{y}k}^{-1}$$

(30)

$${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k(y_k-y_k^{-})$$

(31)

$$\begin{array}{c}\begin{array}{c}{P}_{k|k}=P_{k|k-1}-K_k{P}_{\widehat{y}k\widehat{y}k}{K}_k^T\end{array}\end{array}$$

(32)

Process noise $Q_k=diag({\sigma }_{\omega }^2,{\sigma }_L^2)$ accounts for mechanical nonlinearities (gear backlash, friction hysteresis) and electromagnetic interference, approximated as Gaussian white noise. Measurement noise $R_k={\sigma }_{\omega }^2$ is calibrated via RMSE.

Above is the processing of the UKF algorithm for filtering and estimation of diesel engine speed. The algorithm uses the state augmentation method [34]. After determining the process noise covariance matrix $Q_k$, the measurement noise covariance matrix $R_k$, and the initial filter values ${\widehat{\mathit{x}}}_{0/0}$ and $P_{0/0}$, the state estimate ${\widehat{\mathit{x}}}_{k/k}$ at time $k$ can be obtained from the computed measurement value $y_k$ using the above calculation formulas.

In order to verify the noise reduction effect of the unscaled Kalman filter on the speed measurement data, we use Matlab (R2022b) to simulate the diesel engine speed step from 1500 rpm to 1000 rpm, and the results are shown in Figure 11.

It can be shown in

Table 4. Data from the UKF filtered diesel engine speed simulation experiment.

Norm	Sensor Data	UKF	Improvement
Standard deviation (rpm)	51.8	13.5	73.9%
Peak Noise (rpm)	98.7	20.8	78.9%

that the UKF can effectively suppress the measurement noise and provide a more accurate estimation of the diesel engine speed.

Under environmental disturbances, when using fuzzy PID control alone, the system often fails to avoid fluctuations and struggles to effectively handle control disturbances and eliminate measurement noise, resulting in suboptimal control performance. Given the significant advantage of the Unscented Kalman Filter in suppressing and eliminating noise, this paper proposes combining the Unscented Kalman Filter with a Particle Swarm Optimization fuzzy PID controller for joint system control.

3.2. Fuzzy PID Controller

In the single-cylinder diesel engine speed control system, the fuzzy PID control algorithm is used to adjust the fuel supply of the diesel engine in real time to ensure speed stability and response speed. When the working environment of the diesel engine is more complex and the load change is too large, due to the fluctuation of fuel quality, the change in ambient temperature and other factors will cause engine speed fluctuation, and the PID control algorithm is hard to adapt to the complex diesel engine operating conditions, which are prone to overshooting, oscillating, or excessive adjustment time [35]. Consequently, we selected the fuzzy PID control algorithm in this study, and the PID parameters were adjusted according to the changes in the operating conditions in which the diesel engine was located.

When the diesel engine load increases abruptly, the system generates a large deviation; at this time, the fuzzy controller recognizes this condition and immediately increases its proportionality coefficient $K_p$ and integral coefficient $K_i$, increasing the response speed of the system and reducing the steady-state error. Conversely, when the system tends towards stability, the fuzzy controller will gradually decrease the proportional coefficient and increase the integral coefficient to eliminate residual deviations, thus ensuring stable engine speed under various operating conditions.

Accurate real-time data acquisition and processing are fundamental to ensuring control precision. The current actual speed of the diesel engine is obtained through sensors, and these data are filtered to remove noise interference. Subsequently, the filtered actual speed is compared with the preset target speed to obtain the speed deviation $e$ and the rate of change of the deviation $ec$, which serve as the inputs to the fuzzy PID controller. After fuzzification, fuzzy reasoning is performed based on the established fuzzy rules, and finally, the defuzzified output provides the adjustment values for the PID parameters $∆k_p$, $∆k_i$, and $∆k_d$.

A traditional PID controller performs proportional, derivative, and integral operations on the input–output error $e\left(t\right)$. It then weights and sums the results of these three operations to output control commands to the actuator, ensuring that the controlled object reaches the desired value. The proportional coefficient $K_p$, integral coefficient $K_i$, and derivative coefficient $K_d$ are critical factors that influence the system’s response speed, overshoot, stability, and steady-state error.

The PID control law is as follows:

$$\begin{array}{c}\begin{array}{c}u\left(n\right)=K_p\left\{e\left(n\right)+{\displaystyle \frac{T}{T_i}}{\displaystyle \sum _{i=0}^{n-1}}+{\displaystyle \frac{T_d}{T}}\left[e\left(n\right)-e\left(n-1\right)\right]\right\}\end{array}\end{array}$$

(33)

The output of the controller at the nth sampling instant is $u\left(n\right)$, and the input value at this instant is $e\left(n\right)$. $K_p$ is the proportional gain, $T$ is the sampling period, and $T_i$ and $T_d$ are the integral and derivative time constants, respectively. From this, the gain of the control action between the $(n-1)$-th and $n$-th sampling instants can be derived as follows:

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}∆u\left(n\right)=u\left(n\right)-u\left(n-1\right)\end{array}\end{array}\end{array}$$

(34)

$$\begin{array}{c}\begin{array}{c}=K_p\left\{\begin{array}{c}e\left(n\right)-e\left(n-1\right)+{\displaystyle \frac{T}{T_i}}e\left(n-1\right)\\ +{\displaystyle \frac{T_d}{T}}\left[e\left(n\right)-2e\left(n-1\right)+e\left(n-2\right)\right]\end{array}\right\}\end{array}\end{array}$$

(35)

$$\begin{array}{c}\begin{array}{c}=K_p\left[e\left(n\right)-e\left(n-1\right)\right]K_{i}e\left(n\right)+K_d\left[e\left(n\right)-2e\left(n-1\right)+e\left(n-2\right)\right]\end{array}\end{array}$$

(36)

where $K_p$, $K_i$, and $K_d$ are the proportional, integral, and derivative coefficients, respectively. The fuzzy sets for speed deviation $e$, rate of change of speed deviation $ec$, and outputs $K_p$, $K_i$, and $K_d$ are all {NB, NM, NS, ZE, PS, PM, PB}. The membership functions for the fuzzy subsets NB and PB are Gaussian functions, while the others are uniformly distributed, equidistant, and highly sensitive triangular functions [36]. The universes of discourse for $e$ and $ec$ are set to $[-6,6]$, and $K_p$, $K_i$, and $K_d$ are set to $[-3,3]$, with quantization levels {−3, −2, −1, 0, 1, 2, 3}. A fuzzy control rule table is formulated based on actual conditions. Summarized in

Table 5. Fuzzy control rules.

u		ec
		NB	NM	NS	ZE	PS	PM	PB
e	NB	PB	PB	PB	PB	PM	PS	Z
	NM	PB	PB	PM	PM	PS	Z	Z
	NS	PB	PM	PM	PS	Z	Z	NS
	Z0	PB	PM	PS	Z	NS	NM	NB
	PS	PS	Z	Z	NS	NM	NM	NB
	PM	Z	Z	NS	NM	NM	NB	NB
	PB	Z	NS	NM	NB	NB	NB	NB

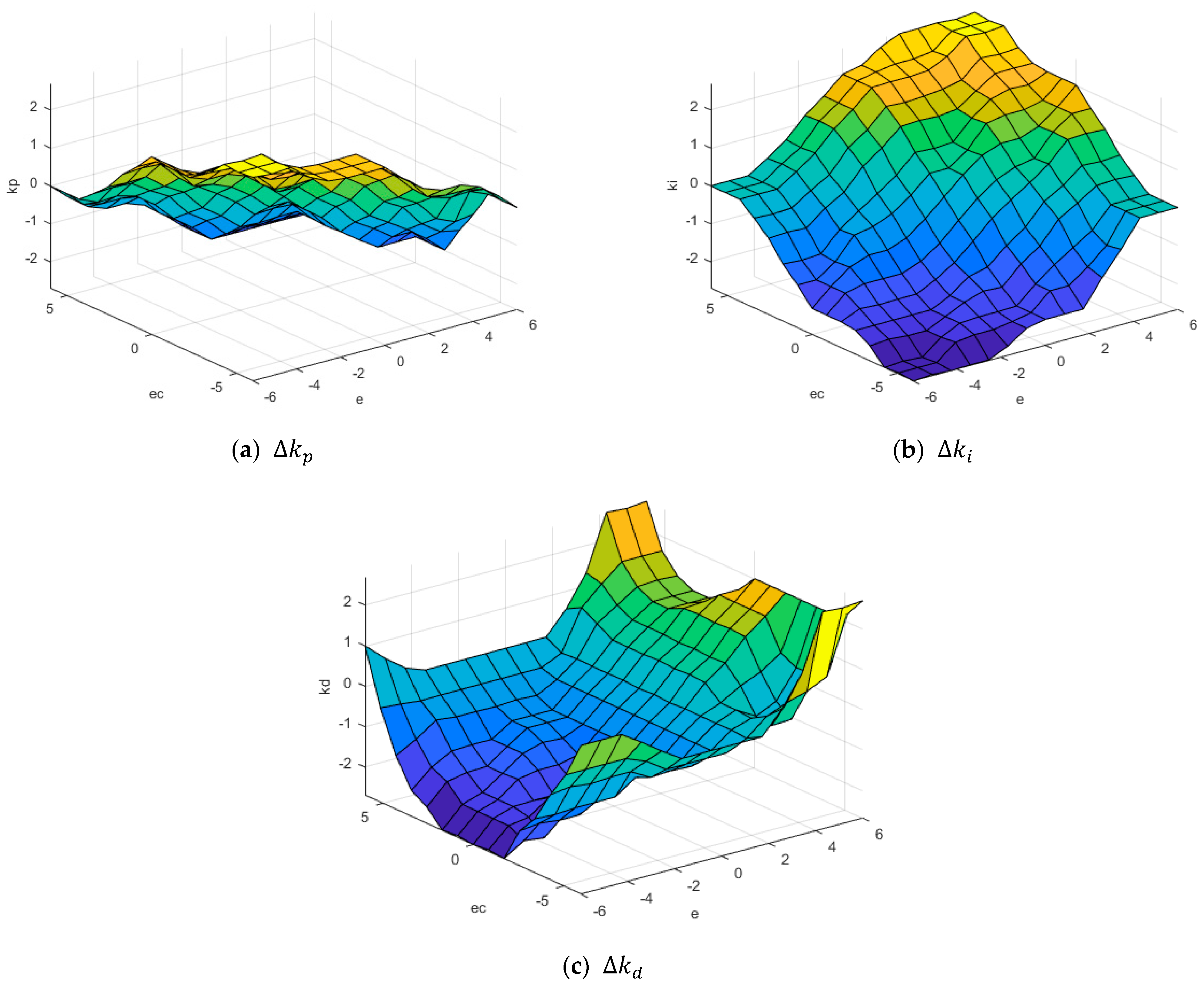
are 49 fuzzy control rules [36]. Figure 12 is the characteristic face of the fuzzy inference system.

Through fuzzy logic inference, the output is a fuzzy set, and defuzzification is performed using the centroid method:

$$u\left(n\right)={\displaystyle \frac{\sum _{i=1}^n{u}_{i}A\left(u_i\right)}{\sum _{i=1}^{n}A\left(u_i\right)}}$$

(37)

where $A\left(ui\right)$ is the membership function of the fuzzy set $A$ at the element $ui$ in the universe of discourse $u$, and $ui$ is the $i$-th element in the universe of discourse $u$.

By combining the PID controller and the fuzzy controller, the system continuously monitors the error $e$ and the rate of change of the error $ec$. Through a specified fuzzy algorithm, appropriate $Kp$, $Ki$, and $Kd$ values are determined and then output to the PID controller, thereby controlling the system’s operation.

3.3. PSO-Fuzzy-PID Controller

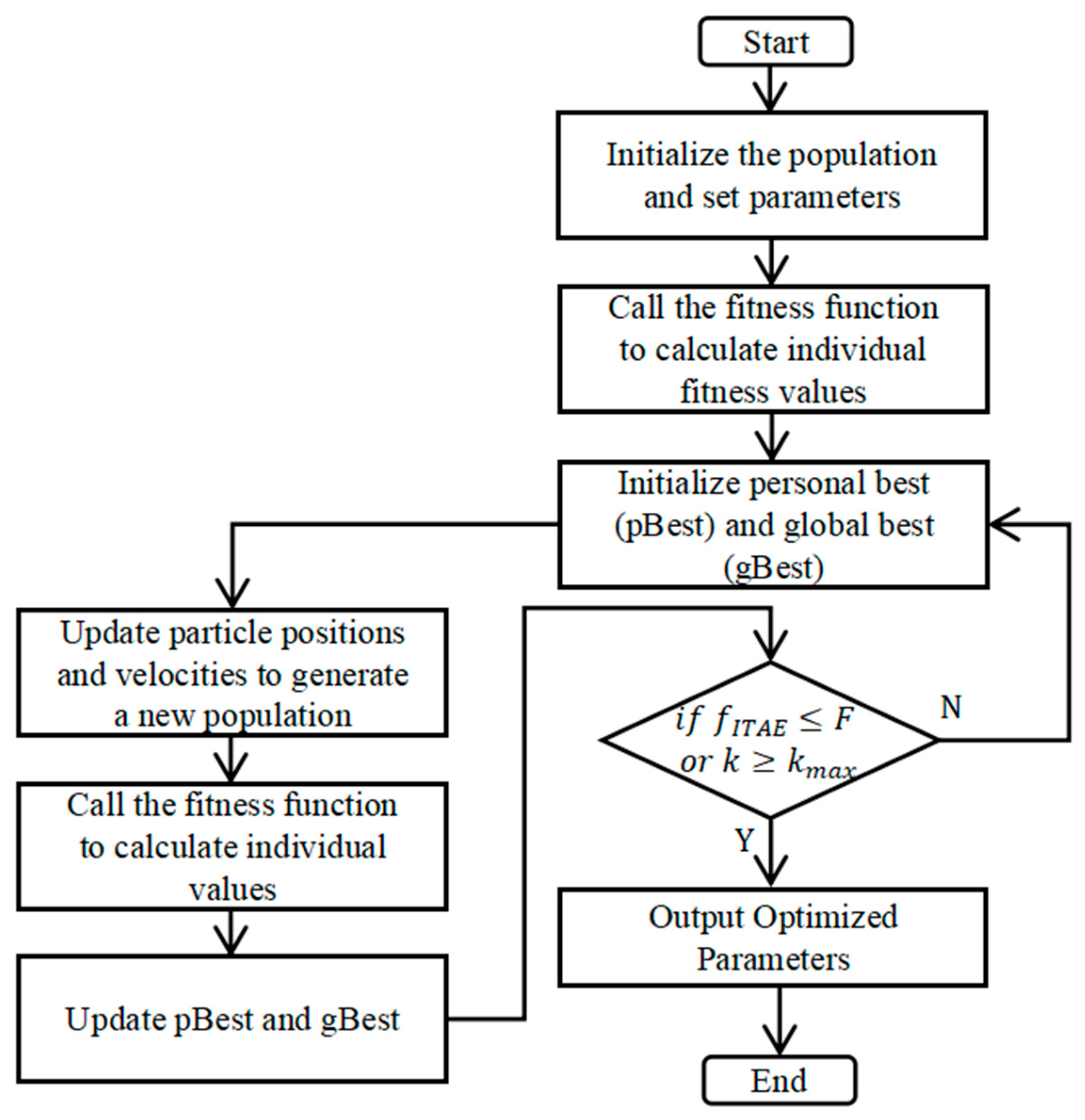
While fuzzy control can dynamically adjust PID parameters to effectively respond to environmental changes, the initial PID parameters and the quantization and scaling factors of the fuzzy control remain fixed and cannot be modified in real time, suggesting room for further optimization. The Particle Swarm Optimization (PSO) algorithm [37] is a heuristic optimization technique that mimics the collective behavior of bird flocks or fish schools. It searches for the optimal solution by adjusting the position and velocity of particles, updating based on both individual and group best historical solutions, with the goal of identifying the global optimum. In this study, the PSO optimization is run offline, mainly considering the computational time-consuming and safety issues. Since each simulation takes several minutes to hours, it cannot meet the real-time control requirements, and the offline optimization can avoid the interference of online debugging on the operating state of the diesel engine. The optimized parameters are solidified into the controller after experimental verification, and can be combined with edge computing to realize quasi-online optimization in the future. The steps of the PSO optimization algorithm are shown in Figure 13.

In a 1-$D$ search space, there are $N$ particles forming a population, with the $i\mathrm{th}$ particle represented as a $D$-dimensional vector:

$$\begin{array}{c}{X}_i=(x_{i1},x_{i2},\cdots ,x_{iD}),i=\mathrm{1,2},\cdots ,N\end{array}$$

(38)

The velocity of the $i$-th particle is

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}{V}_i=\left(v_{i1},v_{i2},\cdots ,v_{iD}\right),i=\mathrm{1,2},\cdots ,N\end{array}\end{array}\end{array}$$

(39)

Each particle also needs to store the best solution it has found so far, denoted as $Pbest$, as well as the global best solution found by the entire population, denoted as $Pgbest$. The velocity and position of the $i$-th particle are revised using the following equation:

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}{v}_{id}=w{v}_{id}+c_1{r}_1(p_{id}-x_{id})+c_2{r}_2(p_{gd}-x_{id})\end{array}\end{array}\end{array}$$

(40)

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}{x}_{id}=x_{id}+v_{id}\end{array}\end{array}\end{array}$$

(41)

where

• p_id is the personal best solution for the i-th particle.
• p_gd is the global best solution for the entire population.
• w is the inertia weight.
• c₁ and c₂ are learning factors.
• r₁ and r₂ are random numbers in the range [0, 1].

Steps for PSO fuzzy PID Control in this study:

Step 1: Initialize the particle swarm:

• Swarm size N = 10, reducing computation time while ensuring convergence.
• Dimension D = 5.
• Inertia weight w = 0.8.
• Acceleration constants and c₁ = c₂ = 0.2, lower learning rate to avoid particle oscillations.
• Maximum particle velocity V_max = 0.01, minimum velocity V_min = −0.01.
• Maximum number of iterations k_max = 50.
• Minimum fitness value F = 0.2.

Step 2: Evaluate all particles in the population and calculate their fitness values. Compare each particle’s current fitness with its personal best, $Pbest$, and assess the fitness of all particles against the global best, $Pgbest$. In this study, the fitness is measured using the ITAE, which represents the integral of the absolute time error. A lower ITAE value indicates better performance [38]. ITAE serves as a comprehensive metric to assess both the dynamic and static performance of the system. The calculation method is as follows:

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}{f}_{ITAE}={\int }_0^{T}t\left|e\left(t\right)\right|dt\end{array}\end{array}\end{array}$$

(42)

where T is the finite simulation time, which corresponds to the total duration of the simulation. In the initial stage, each particle calculates its fitness value based on its current position and takes it as the initial personal best solution. Meanwhile, the fitness values of all particles in the population are compared with the historical global best solution. If a better fitness value is found, the current global best solution is updated.

Step 3: Update the particle state. Compute the new velocity and new position for the particle to be updated [39]. Then, calculate the fitness of the new position. If the fitness of the new position is higher, the particle’s position is updated; otherwise, the position is not updated.

Step 4: Check if the termination conditions are met. Determine if the iteration count or other conditions meet the stopping criteria. If satisfied, exit the loop and output the optimal result; otherwise, return to Step 2 and continue iterating.

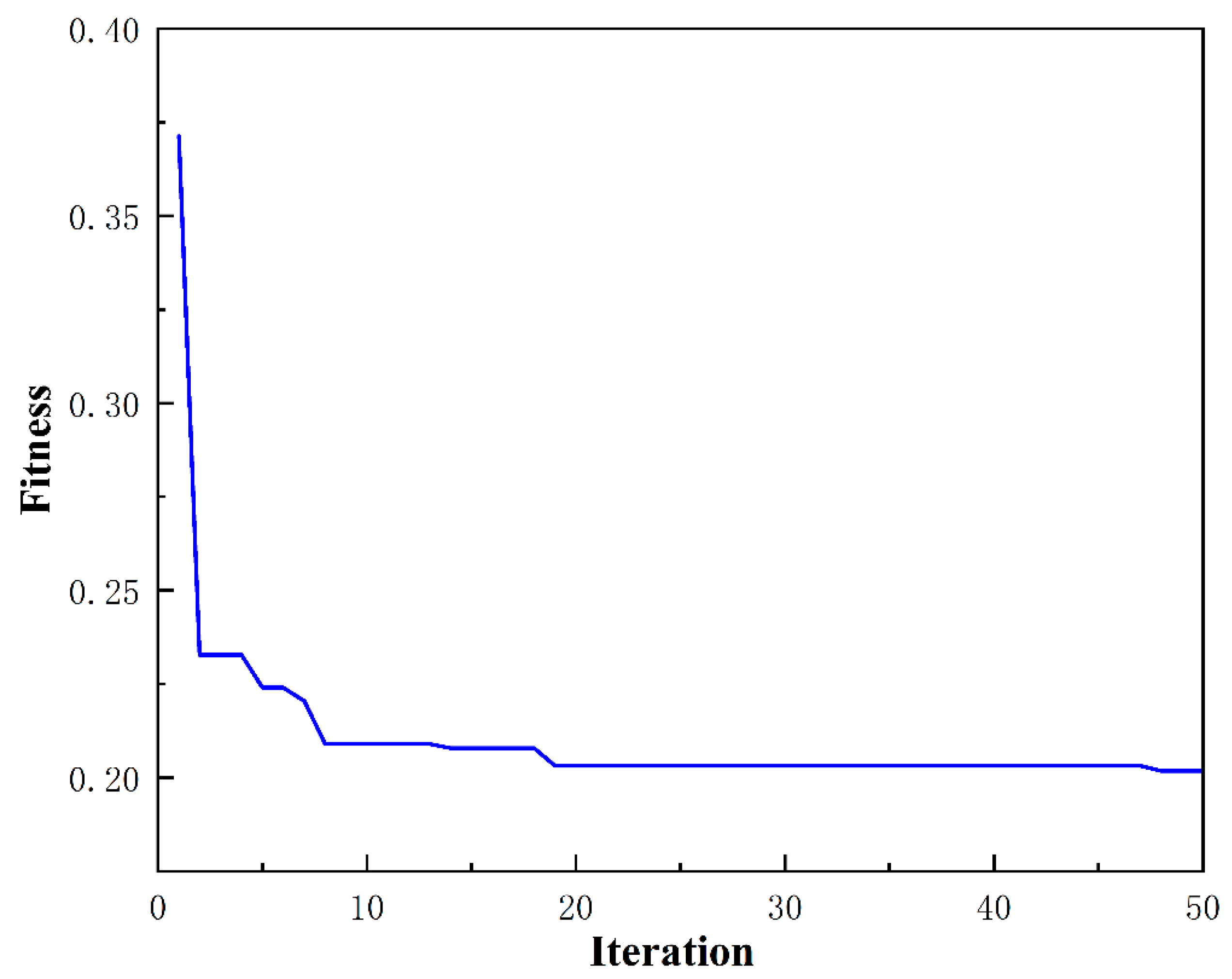
The PSO-optimized quantization factors and scale factors are shown in

Table 6. PSO-optimized quantization factors and scale factors.

Parameters	Description	Before Optimization	After Optimization
$k_{∆p}$	Proportional gain	13.5	42.2
$k_{∆i}$	Integral gain	1.9	0.5
$k_{∆d}$	Derivative gain	9.32	6.31
$k_e$	Scaling factor for $e$	6.32	7.86
$k_{ec}$	Scaling factor for $ec$	0.240	0.226

, and the optimization results of the fitness values are shown in Figure 14.

4. Results

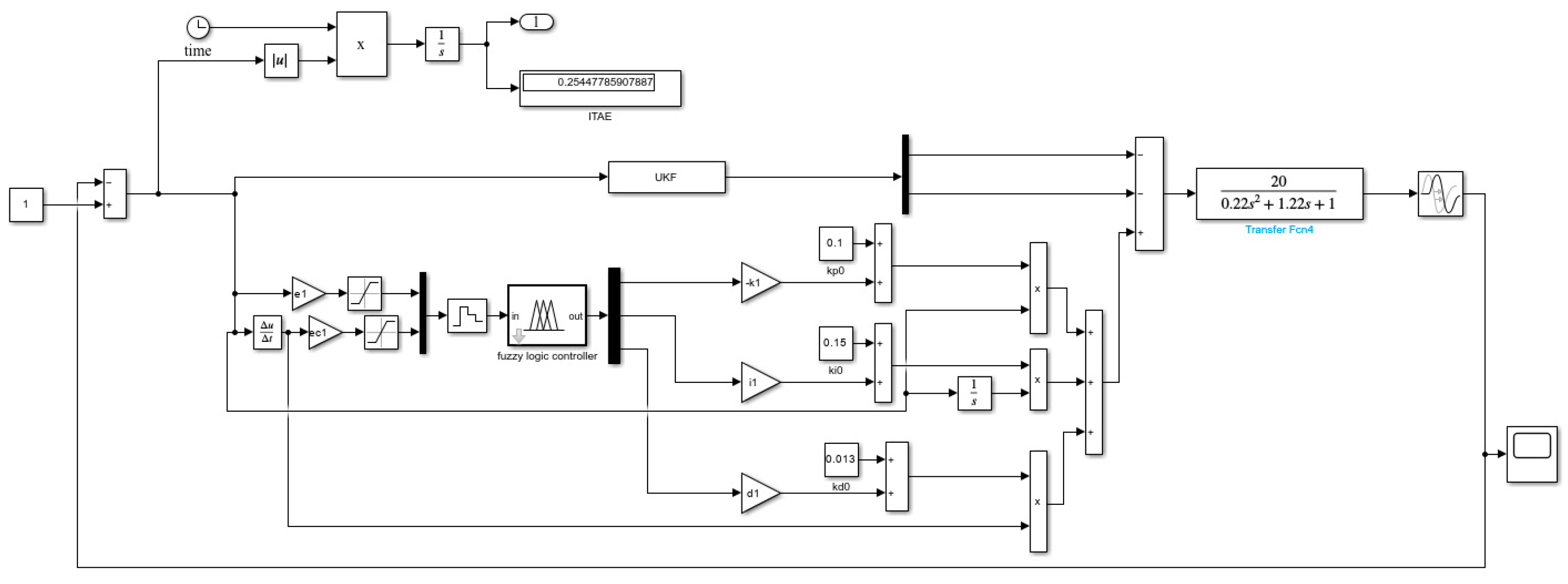
The model of the algorithm discussed in this study is shown in Figure 15. Four algorithms are modeled using Matlab/Simulink (R2022b): traditional PID control algorithm, fuzzy PID control algorithm, combination of UKF and fuzzy PID control, and fuzzy PID control algorithm based on particle swarm optimization of UKF, as shown in Figure 16.

The 168 F single cylinder diesel engine used for simulation and experimentation has a maximum power of $3.3\mathrm{k}\mathrm{w}$ and a maximum speed of $3000\mathrm{r}\mathrm{p}\mathrm{m}$. The step response experimental condition is that the diesel engine is under a constant load $0\mathrm{N}·\mathrm{m}$; the speed was increased to $1000\mathrm{r}\mathrm{p}\mathrm{m}$, and the load decreased from $6\mathrm{N}·\mathrm{m}$ to $2\mathrm{N}·\mathrm{m}$ at $1000\mathrm{r}\mathrm{p}\mathrm{m}$ for sudden load change experiments. The entire simulation process lasted for 100 s, with a sampling interval of $0.5$ s.

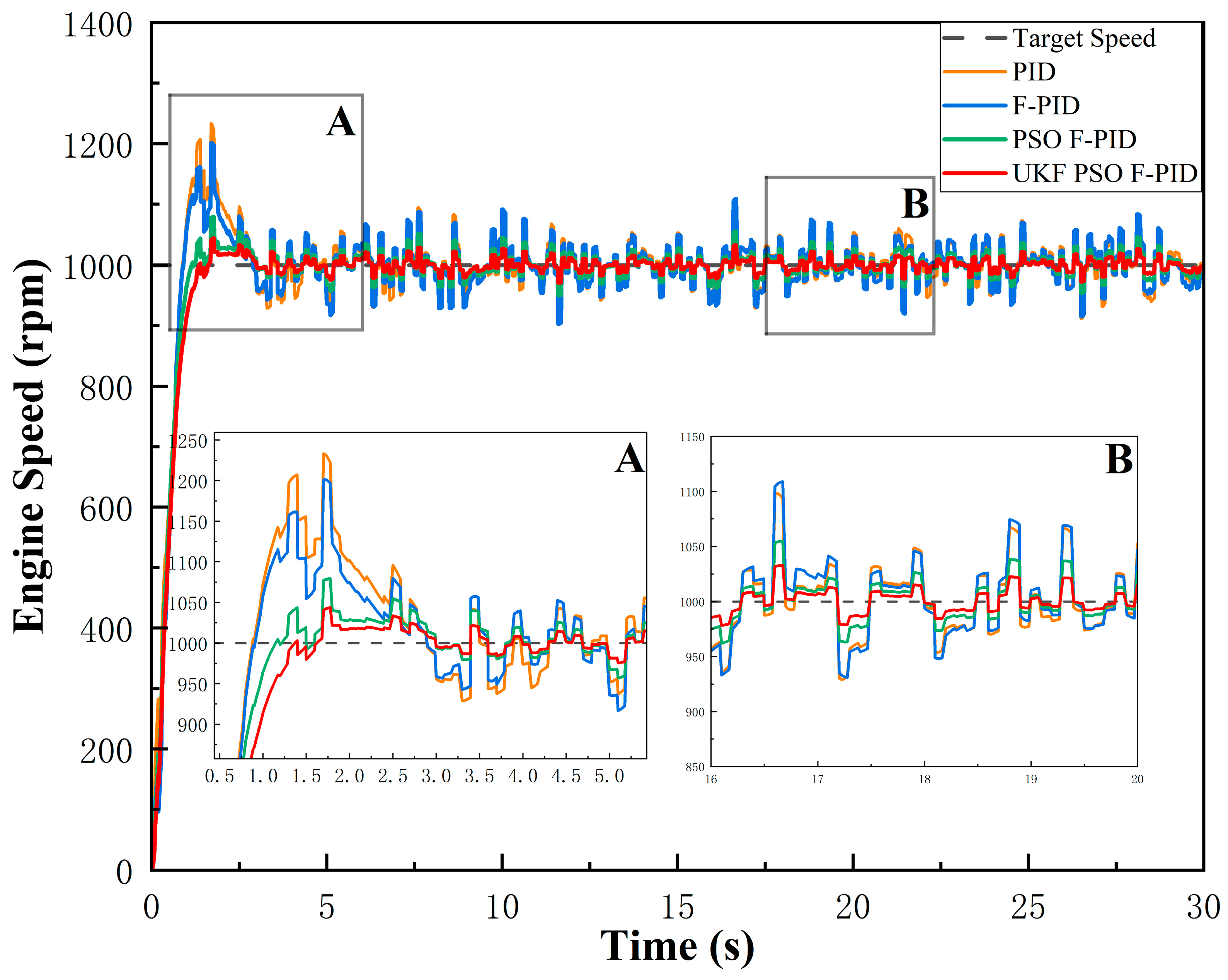
To better simulate the interference and measurement noise present in the actual working environment of the diesel engine, the same noise was attached to each of the control algorithms. During the simulation process, the system response characteristics and control effects of each control algorithm were recorded. Figure 17 and Figure 18 present the response curves of the different control algorithms, while

Table 7. Comparison of parameters for different control methods in step response experiment.

Control Algorithm	Rise Time/s	Overshoot/%	Response Time/s	Steady-State Error/n
PID	2.44	30	3.21	0.98
F-PID	2.65	21	2.73	0.62
PSO-F-PID	1.87	7.6	2.19	0.37
UKF PSO F-PID	1.32	7.1	1.32	0.12

and

Table 8. Comparison of parameters for different control methods in Load disturbance experiment.

Control Algorithm	Overshoot/%	Response Time/s	Steady-State Error/n
PID	27.5	0.74	1.26
F-PID	26.3	0.69	1.38
PSO-F-PID	22.3	0.62	1.24
UKF PSO F-PID	20.7	0.63	0.56

list a comparison of their parameters.

By analyzing the response curves in Figure 17 and Figure 18, it is obvious that the UKF PSO-Fuzzy-PID algorithm has significant advantages under the same disturbing noise conditions. The specific advantages are as follows:

Reduced Overshoot: Compared with the traditional PID algorithm, the speed overshoot of the diesel engine using the UKF PSO-Fuzzy-PID algorithm is reduced by 76% under the starting condition, and the overshoot is reduced by 27% under the load disturbance condition. This shows that the system is more stable when reaching the target speed.

Shorter Adjustment Time: The UKF PSO-Fuzzy-PID algorithm reduces the tuning time for the speed step by 1.89 s, and the tuning time for the load disturbance condition by 0.1 s. The diesel engine speed reaches the target speed faster under the step condition, but the responsiveness performance is less improved for the load disturbance condition.

Smaller steady-state error: Under steady-state conditions, the steady-state error of UKF PSO-Fuzzy-PID algorithm is smaller; compared with PID, the steady-state error is reduced by 87% and 55%, respectively, which indicates that the diesel engine can accurately maintain the target speed under the influence of noise, and the algorithm performs well in filtering the noise.

Stronger noise reduction capability: The use of UKF improves the noise reduction ability of the system and reduces the influence of interference noise on the control accuracy; the experimental results verify that the UKF PSO-Fuzzy-PID algorithm improves the noise reduction effect under the high-noise environment by 25% and 31%, respectively.

5. Conclusions

Aiming at the single-cylinder diesel engine speed control, an improved fuzzy PID controller is designed based on the mathematical model of the diesel engine, analyzing the fuzzy control theory and using empirical data to design the type, number, and membership functions of the input and output fuzzy subsets.

The Unscented Kalman Filter is used to improve the robustness of the system against noise and disturbances. The UKF has the predictive ability to filter noise and disturbances, which improves the estimation accuracy of the system state, and thus can improve the accuracy of the feedback data of the speed control system of the diesel engine. The estimation of the system state by the UKF can tell the actual speed of the diesel engine more accurately, so that the fuzzy controller can obtain more accurate input data.

Finally, the PSO fuzzy PID diesel engine speed controller is designed according to the data screened by the UKF. The globally optimized PI parameters of the PSO-optimized fuzzy PID algorithm improve the adaptability of the system to nonlinear and dynamic changes, and the PSO fuzzy PID algorithm possessed the capability to adapt itself to the complex conditions of the diesel engine speed control by online adjusting of the PID control parameters, so that the system control accuracy and accuracy can be improved. Through the online adjustment of PID control parameters, the PSO fuzzy PID algorithm has the ability to adapt itself to the complex working conditions of diesel engine speed control, so that the control accuracy and robustness of the system are improved.

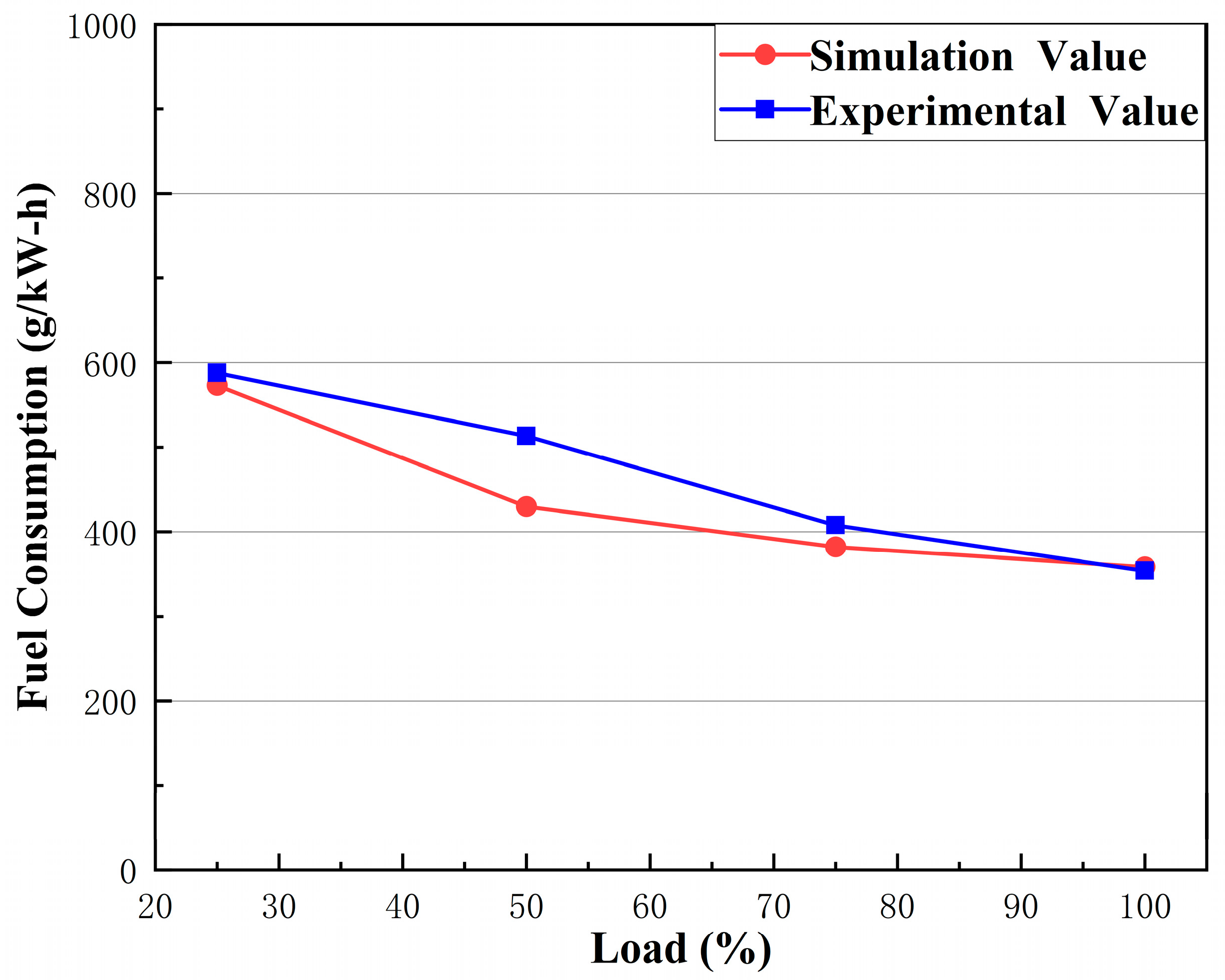
The cylinder pressure and fuel consumption parameters in the mathematical model of the modeled diesel engine are compared through simulation of, and experiment on, various diesel engine conditions. Finally, a joint simulation was conducted to compare the improved controller with the conventional PID controller, and the results show that the control accuracy and stability of the PSO fuzzy PID control over the UKF data are significantly better than those of the conventional PID controller.

The computational model of this study has several potential limitations and uncertainties, as follows:

The error due to model simplification is mainly reflected in the limitation of the first-order inertia assumption, Equation (5), which simplifies the complex diesel engine system to $G_1\left(s\right)=G_d\left(s\right)G_{\tau }\left(S\right)={\displaystyle \frac{1}{T_{\tau }s+1}}·e^{-\tau s}$, but this assumption may fail under transient operating conditions (e.g., sudden unloading), especially when high-frequency characteristics such as turbocharger dynamics, intake and exhaust fluctuations, and so forth are not taken into account.

The shortcomings of the linear actuator model are also of concern. The electromagnetic actuator transfer function in Equation (11) ignores nonlinear factors such as magnetic saturation and hysteresis loops, which may lead to phase lag under high-frequency control signals. Regarding parameter uncertainty, the time-varying nature of the friction torque $T_f$ is caused by mechanical wear during long-term operation, resulting in a change in the friction coefficient, while the model assumes that $T_f$ is a constant value, whose potential impact on the stability of the control needs to be further discussed.

The idealized assumptions of the sensor noise model is assumed to be Gaussian white noise, and do not take into account the periodic disturbances of the actual Hall sensors (e.g., harmonic noise due to the eccentricity of the gear disk mounting).

The current work only verifies the static matching between GT-POWER and Matlab/Simulink (R2022b), but does not realize the dynamic co-simulation with the GT-POWER model, which may underestimate the coupling effect under transient conditions.

The goal of future research is to implement the controller in the hardware of a real diesel engine system to further verify its effectiveness and reliability in industrial applications.