A Deep Reinforcement Learning-Based Evolutionary Algorithm for Distributed Heterogeneous Green Hybrid Flowshop Scheduling
Abstract
1. Introduction
2. Literature Review
3. Problem Description and Mathematical Model
3.1. Problem Description
3.2. MILP Model for DHGHFSP
3.3. A Small Example of DHGHFSP
4. Description of DRLBEA
4.1. Motivation
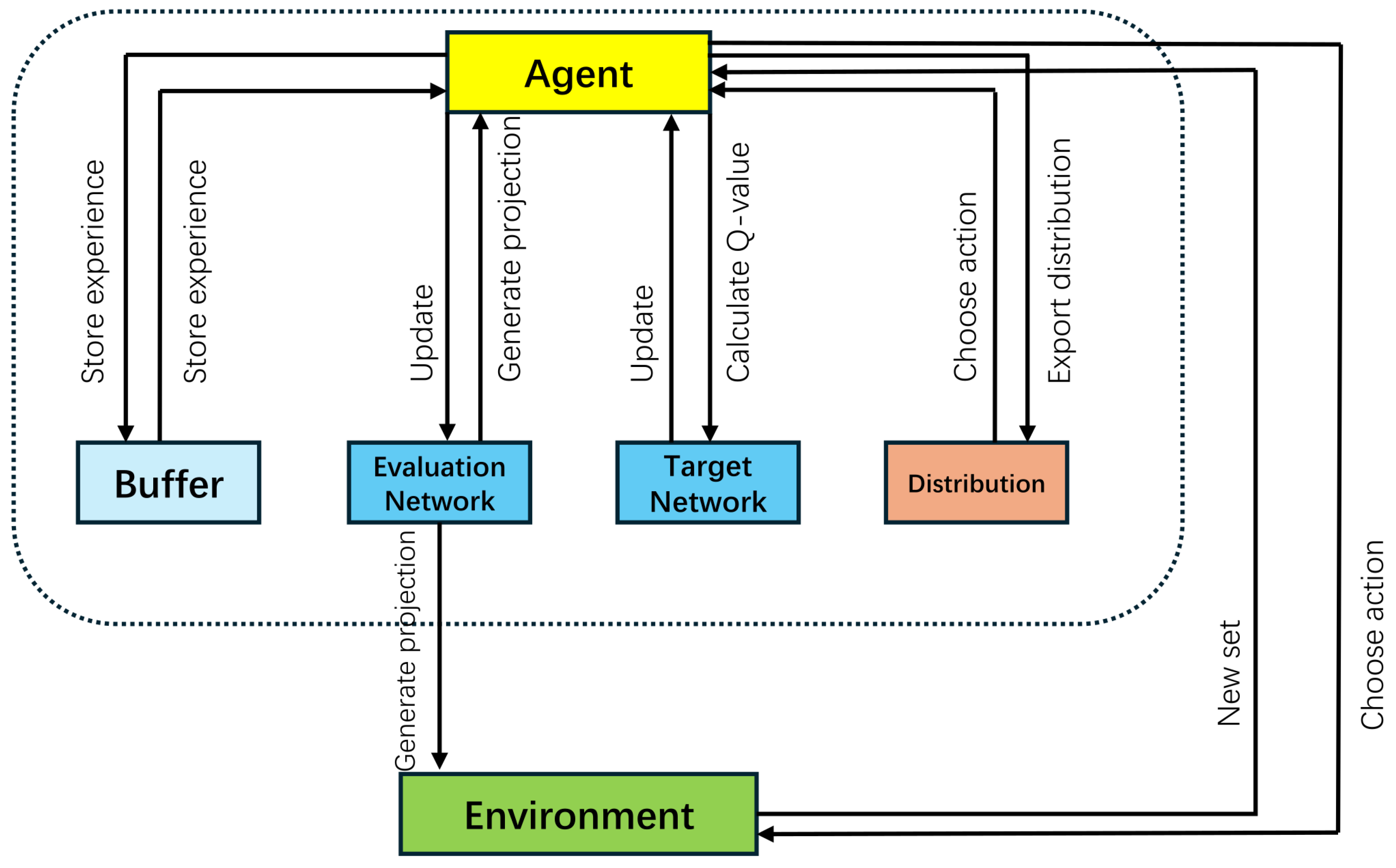
4.2. Framework of DRLBEA
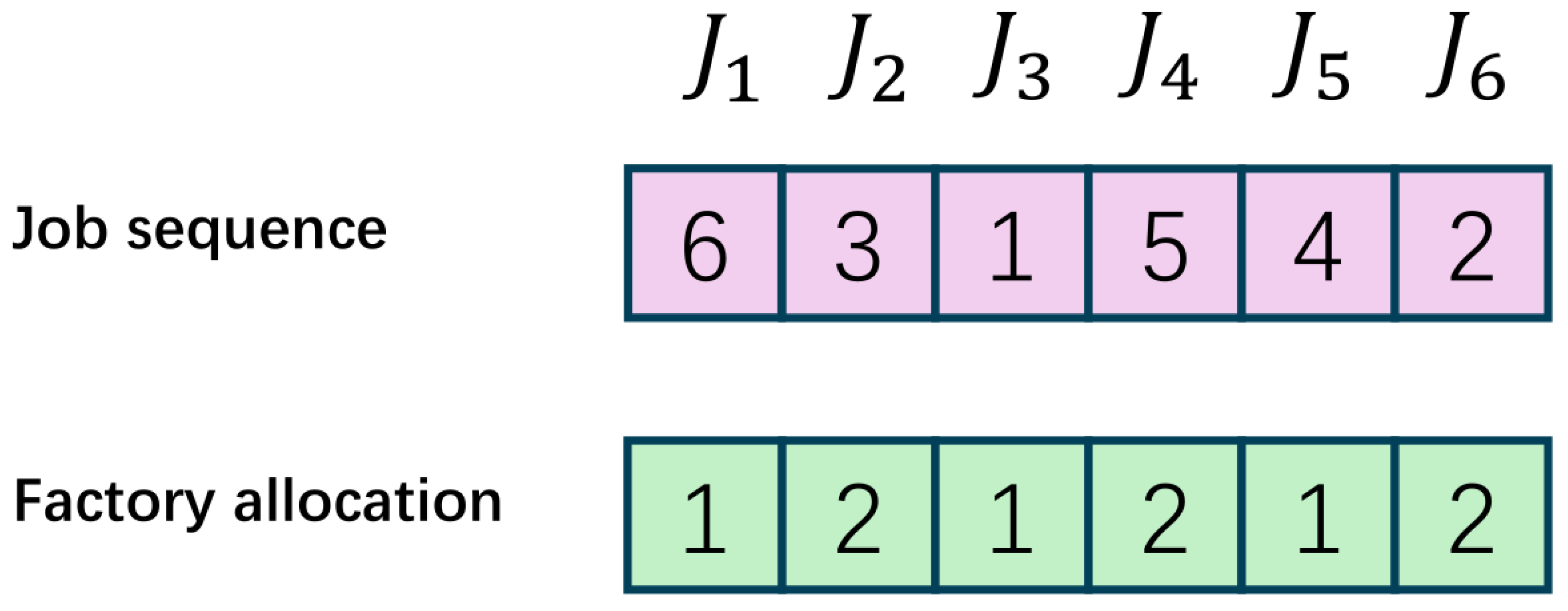
4.3. Encoding and Decoding
| Algorithm 1 The framework of the DRLBEA |
|
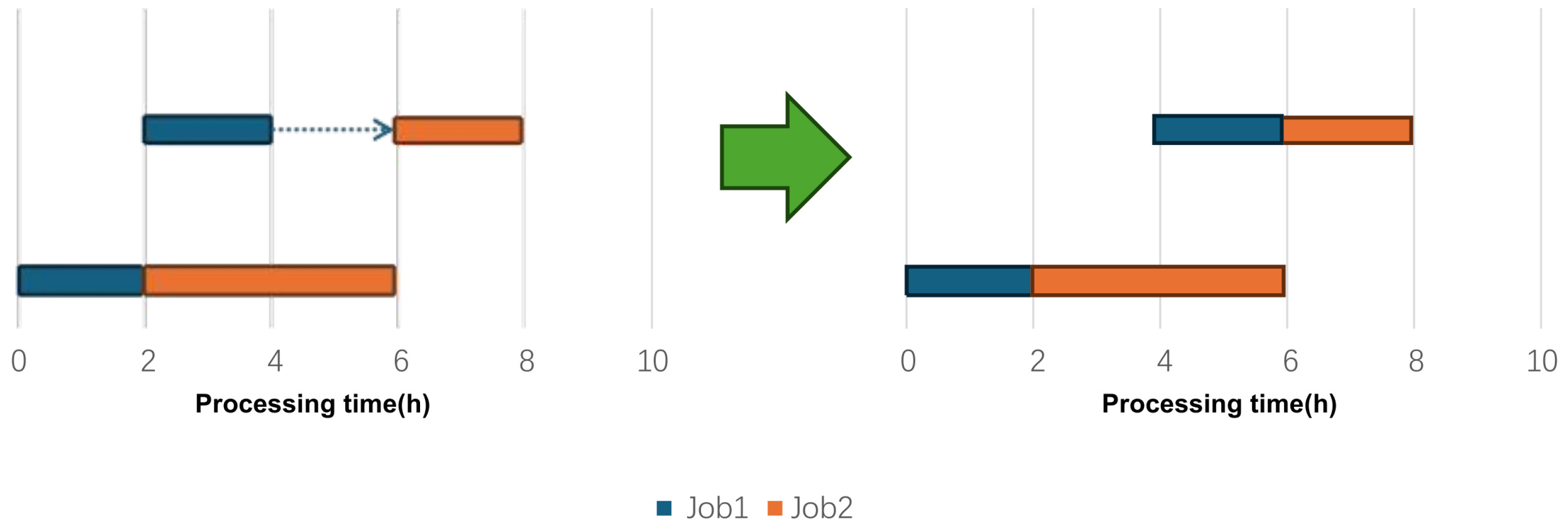
4.4. Energy-Saving Strategy
4.5. Initialization of DRLBEA
| Algorithm 2 Rank based on the priority and the due date |
|
4.6. Global Search and Local Search
| Algorithm 3 Global search |
|
4.7. Distributional DQN for Operator Selection
| Algorithm 4 Training process of Distributional DQN |
|
5. Experimental Results and Discussion
5.1. Evaluation Metrics
- (1)
- HV metric:
- (2)
- IGD metric:
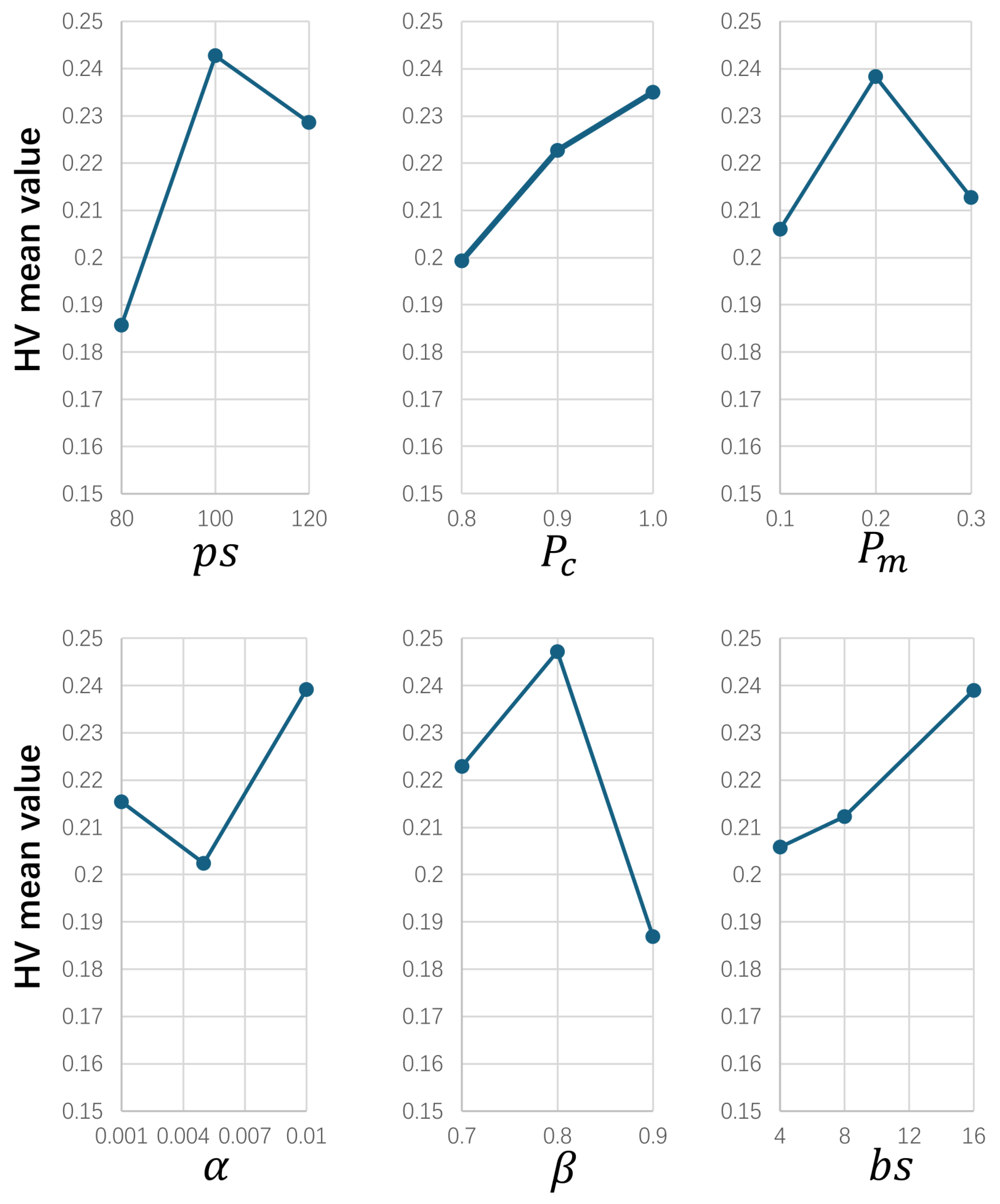
5.2. Parameter Setting
5.3. Evaluation of Each Strategy of DRLBEA
5.4. Comparison with Other Algorithms
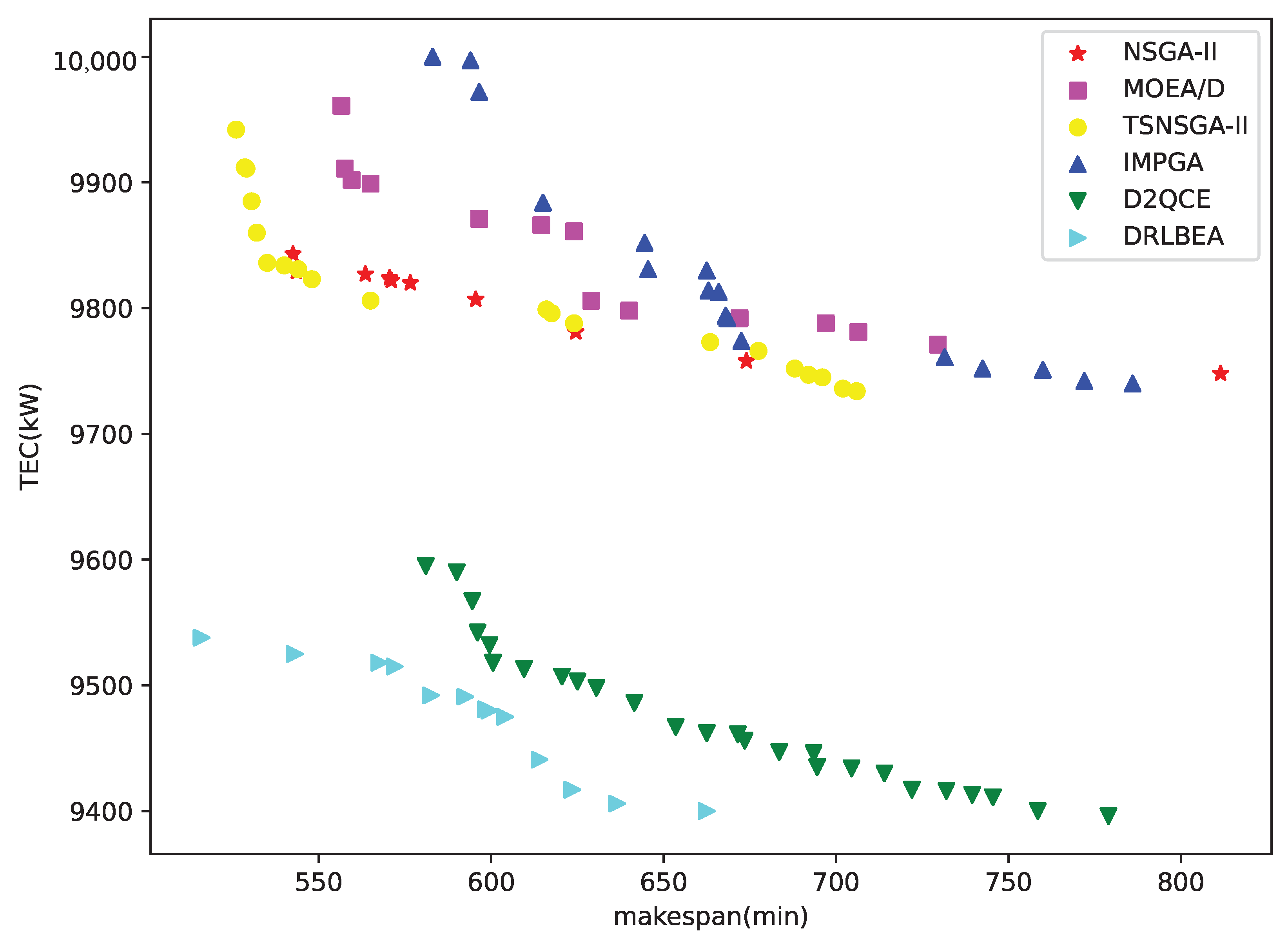
5.5. Experiment on Real-World Case
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adel, A. Future of industry 5.0 in society: Human-centric solutions, challenges and prospective research areas. J. Cloud Comput.-Adv. Syst. Appl. 2022, 11, 40. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; He, X.; Wang, L. A Two-Stage Cooperative Evolutionary Algorithm with Problem-Specific Knowledge for Energy-Efficient Scheduling of No-Wait Flow-Shop Problem. IEEE Trans. Cybern. 2021, 51, 5291–5303. [Google Scholar] [CrossRef] [PubMed]
- Li, J.Q.; Sang, H.Y.; Han, Y.Y.; Wang, C.G.; Gao, K.Z. Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J. Clean. Prod. 2018, 181, 584–598. [Google Scholar] [CrossRef]
- Neufeld, J.S.; Schulz, S.; Buscher, U. A systematic review of multi-objective hybrid flow shop scheduling. Eur. J. Oper. Res. 2023, 309, 1–23. [Google Scholar] [CrossRef]
- Li, Y.Z.; Pan, Q.K.; Gao, K.Z.; Tasgetiren, M.F.; Zhang, B.; Li, J.Q. A green scheduling algorithm for the distributed flowshop problem. Appl. Soft Comput. 2021, 109. [Google Scholar] [CrossRef]
- Ying, K.C.; Lin, S.W. Minimizing makespan for the distributed hybrid flowshop scheduling problem with multiprocessor tasks. Expert Syst. Appl. 2018, 92, 132–141. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Wang, Y.; Gu, X. A knowledge-driven many-objective algorithm for energy-efficient distributed heterogeneous hybrid flowshop scheduling with lot-streaming. Swarm Evol. Comput. 2024, 91, 107526. [Google Scholar] [CrossRef]
- Fernandes, J.M.R.C.; Homayouni, S.M.; Fontes, D.B.M.M. Energy-Efficient Scheduling in Job Shop Manufacturing Systems: A Literature Review. Sustainability 2022, 14, 6264. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Yi, J.; Li, X. Energy-Efficient Scheduling of Distributed Flow Shop With Heterogeneous Factories: A Real-World Case From Automobile Industry in China. IEEE Trans. Ind. Inform. 2021, 17, 6687–6696. [Google Scholar] [CrossRef]
- He, L.; Sun, S.; Luo, R. A hybrid two-stage flowshop scheduling problem. Asia-Pacific J. Oper. Res. 2007, 24, 45–56. [Google Scholar] [CrossRef]
- Fan, J.; Li, Y.; Xie, J.; Zhang, C.; Shen, W.; Gao, L. A Hybrid Evolutionary Algorithm Using Two Solution Representations for Hybrid Flow-Shop Scheduling Problem. IEEE Trans. Cybern. 2023, 53, 1752–1764. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.J.; Wang, G.G.; Tian, F.M.; Gong, D.W.; Pedrycz, W. Solving energy-efficient fuzzy hybrid flow-shop scheduling problem at a variable machine speed using an extended NSGA-II. Eng. Appl. Artif. Intell. 2023, 121, 105977. [Google Scholar] [CrossRef]
- Chen, R.; Yang, B.; Li, S.; Wang, S. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Comput. Ind. Eng. 2020, 149, 106778. [Google Scholar] [CrossRef]
- Qiao, J.; He, M.; Sun, N.; Sun, P.; Fan, Y. Factors affecting the final solution of the bike-sharing rebalancing problem under heuristic algorithms. Comput. Oper. Res. 2023, 159, 106368. [Google Scholar] [CrossRef]
- Ge, Z.; Wang, H. Integrated Optimization of Blocking Flowshop Scheduling and Preventive Maintenance Using a Q-Learning-Based Aquila Optimizer. Symmetry 2023, 15, 1600. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, L. A Bi-Population Cooperative Memetic Algorithm for Distributed Hybrid Flow-Shop Scheduling. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 947–961. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, L.; Wang, J. A cooperative coevolution algorithm for multi-objective fuzzy distributed hybrid flow shop. Knowl.-Based Syst. 2020, 194, 105536. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, B.; Wang, L.; Yu, D.; Xing, K. Distributed Co-Evolutionary Memetic Algorithm for Distributed Hybrid Differentiation Flowshop Scheduling Problem. IEEE Trans. Evol. Comput. 2022, 26, 1043–1057. [Google Scholar] [CrossRef]
- Zhang, G.; Ma, X.; Wang, L.; Xing, K. Elite Archive-Assisted Adaptive Memetic Algorithm for a Realistic Hybrid Differentiation Flowshop Scheduling Problem. IEEE Trans. Evol. Comput. 2022, 26, 100–114. [Google Scholar] [CrossRef]
- Wang, J.J.; Wang, L. A Cooperative Memetic Algorithm with Learning-Based Agent for Energy-Aware Distributed Hybrid Flow-Shop Scheduling. IEEE Trans. Evol. Comput. 2022, 26, 461–475. [Google Scholar] [CrossRef]
- Qin, H.X.; Han, Y.Y. A collaborative iterative greedy algorithm for the scheduling of distributed heterogeneous hybrid flow shop with blocking constraints. Expert Syst. Appl. 2022, 201, 117256. [Google Scholar] [CrossRef]
- Shao, W.; Shao, Z.; Pi, D. An Ant Colony Optimization Behavior-Based MOEA/D for Distributed Heterogeneous Hybrid Flow Shop Scheduling Problem Under Nonidentical Time-of-Use Electricity Tariffs. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3379–3394. [Google Scholar] [CrossRef]
- Lin, C.C.; Peng, Y.C.; Chang, Y.S.; Chang, C.H. Reentrant hybrid flow shop scheduling with stockers in automated material handling systems using deep reinforcement learning. Comput. Ind. Eng. 2024, 189, 109995. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.; Wang, L.; Lu, C.; Dong, C. Co-Evolution With Deep Reinforcement Learning for Energy-Aware Distributed Heterogeneous Flexible Job Shop Scheduling. IEEE Trans. Syst. Man Cybern.-Syst. 2024, 54, 201–211. [Google Scholar] [CrossRef]
- Vasquez, O.C. On the complexity of the single machine scheduling problem minimizing total weighted delay penalty. Oper. Res. Lett. 2014, 42, 343–347. [Google Scholar] [CrossRef]
- Lim, B.; Vu, M. Distributed Multi-Agent Deep Q-Learning for Load Balancing User Association in Dense Networks. IEEE Wirel. Commun. Lett. 2023, 12, 1120–1124. [Google Scholar] [CrossRef]
- Cui, H.; Li, X.; Gao, L. An improved multi-population genetic algorithm with a greedy job insertion inter-factory neighborhood structure for distributed heterogeneous hybrid flow shop scheduling problem. Expert Syst. Appl. 2023, 222, 119805. [Google Scholar] [CrossRef]
- Yang, J.; Xu, H.; Cheng, J.; Li, R.; Gu, Y. A decomposition-based memetic algorithm to solve the biobjective green flexible job shop scheduling problem with interval type-2 fuzzy processing time. Comput. Ind. Eng. 2023, 183, 109513. [Google Scholar] [CrossRef]
- Liu, S.C.; Chen, Z.G.; Zhan, Z.H.; Jeon, S.W.; Kwong, S.; Zhang, J. Many-Objective Job-Shop Scheduling: A Multiple Populations for Multiple Objectives-Based Genetic Algorithm Approach. IEEE Trans. Cybern. 2023, 53, 1460–1474. [Google Scholar] [CrossRef]
- Yang, J.; Soh, C. Structural optimization by genetic algorithms with tournament selection. J. Comput. Civ. Eng. 1997, 11, 195–200. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Rao, Y.; Li, S. A new hybrid GA/SA algorithm for the job shop scheduling problem. In Lecture Notes in Computer Science, Proceedings of the 5th European Conference on Evolutionary Computation in Combinatorial Optimization (EvoCOP 2005), Lausanne, Switzerland, 30 March–1 April 2005; Raidl, G., Gottlieb, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3448, pp. 246–259. [Google Scholar]
- Yang, W.; Wang, B.; Quan, H.; Hu, C. Strategy uniform crossover adaptation evolution in a minority game. Chin. Phys. Lett. 2003, 20, 1659–1661. [Google Scholar]
- Huang, L.; Fu, M.; Rao, A.; Irissappane, A.A.; Zhang, J.; Xu, C. A Distributional Perspective on Multiagent Cooperation with Deep Reinforcement Learning. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 4246–4259. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Yang, T.; Tang, H.; Bai, C.; Liu, J.; Meng, Z.; Liu, P.; Wang, Z. Exploration in Deep Reinforcement Learning: From Single-Agent to Multiagent Domain. IEEE Trans. Neural Networks Learn. Syst. 2024, 35, 8762–8782. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.; Wang, L.; Lu, C.; Pan, Z.; Zhuang, X. Double DQN-Based Coevolution for Green Distributed Heterogeneous Hybrid Flowshop Scheduling With Multiple Priorities of Jobs. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6550–6562. [Google Scholar] [CrossRef]
- Reynolds, P.S. Between two stools: Preclinical research, reproducibility, and statistical design of experiments. BMC Res. Notes 2022, 15, 73. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Wang, L. A Two-Stage Evolutionary Algorithm with Balanced Convergence and Diversity for Many-Objective Optimization. IEEE Trans. Syst. Man Cybern.-Syst. 2022, 52, 6222–6234. [Google Scholar] [CrossRef]

| Problem | Method | Advantage | Disadvantage |
|---|---|---|---|
| HFSP | EA-MOA | Good robustness and effectiveness | Local search capabilities |
| HEA | Balances the optimality and efficiency | Time-consuming when solving large-scale instances | |
| ENSGA-II | Powerful parameter adjustment | Interruption and pre-emption | |
| DHFSP | BCMA | Balances global search and local search | Solving other distributed scheduling problems |
| CCA | Balances exploration and exploitation | Hard to solve scheduling problems with uncertainties | |
| DCMA | Architecture and modules | Multiobjective and heterogeneous scenarios | |
| EAMA | Excellent architecture and components | More realistic DHFSP | |
| CMA | Enhances search operators | Other energy-aware DHFSP | |
| DHHFSP | KDMaOEA | Exploitation ability | Costs and uncertainties |
| CIG | Local intensification strategy | Adjustment of jobs | |
| ACO_MOEA/D | Energy saving | Global search |
| Type | Symbol | Definition |
|---|---|---|
| Index | i | Index of the job; |
| f | Index of the factory; | |
| S | Index of the stage; | |
| k | Index of the machine; | |
| t | Index of the position; | |
| Parameter | n | Number of jobs |
| F | Number of factories | |
| S | Number of stages for each factory | |
| m | Number of machines in each factory | |
| T | Number of positions for each machine | |
| L | A large positive number | |
| Energy consumption of idle time | ||
| Energy consumption of processing time | ||
| Deadline of job i | ||
| Priority of job i; | ||
| The duration required for job i during stage s at factory f | ||
| Punishment factor; for each , | ||
| Variable | The initiation timestamp of job i during stage s at factory f | |
| The completion timestamp of job i during s at factory f | ||
| The start time of machine during stage s at position t in factory f | ||
| The idle energy consumption on machine during stage s at position t in factory f | ||
| The deadline violation of job i; | ||
| 1 if job i is allocated to factory f and 0 otherwise | ||
| 1 if job i is processed at position t of machine during stage s in factory f, and 0 otherwise. |
| Job | ||||||
|---|---|---|---|---|---|---|
| 5 | 4 | 6 | 5 | 15 | 2 | |
| 8 | 7 | 7 | 6 | 12 | 1 | |
| 7 | 6 | 5 | 4 | 18 | 3 | |
| 6 | 5 | 8 | 7 | 14 | 2 | |
| 9 | 8 | 7 | 6 | 10 | 1 | |
| 10 | 9 | 6 | 5 | 16 | 3 | |
| Trial | Level | HV | |||||
|---|---|---|---|---|---|---|---|
| ps | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.1835 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 0.2603 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 0.1661 |
| 4 | 2 | 1 | 2 | 2 | 3 | 1 | 0.1873 |
| 5 | 2 | 2 | 3 | 3 | 1 | 2 | 0.2463 |
| 6 | 2 | 3 | 1 | 1 | 2 | 3 | 0.2855 |
| 7 | 3 | 1 | 3 | 1 | 2 | 1 | 0.2121 |
| 8 | 3 | 2 | 1 | 2 | 3 | 2 | 0.1566 |
| 9 | 3 | 3 | 2 | 3 | 1 | 3 | 0.2974 |
| 10 | 1 | 1 | 3 | 3 | 2 | 1 | 0.1826 |
| 11 | 1 | 2 | 1 | 1 | 3 | 2 | 0.1508 |
| 12 | 1 | 3 | 2 | 2 | 1 | 3 | 0.1711 |
| 13 | 2 | 1 | 1 | 2 | 1 | 2 | 0.2081 |
| 14 | 2 | 2 | 2 | 3 | 2 | 3 | 0.2913 |
| 15 | 2 | 3 | 3 | 1 | 3 | 1 | 0.2381 |
| 16 | 3 | 1 | 2 | 1 | 3 | 3 | 0.2223 |
| 17 | 3 | 2 | 3 | 2 | 1 | 1 | 0.2311 |
| 18 | 3 | 3 | 1 | 3 | 2 | 2 | 0.2516 |
| Instances | HV | ||||
|---|---|---|---|---|---|
| DRLBEA | |||||
| 20J3S2F | 0.7862 | 0.7970 | 0.8171 | 0.7865 | 0.8231 |
| 20J3S3F | 0.6689 | 0.6637 | 0.6741 | 0.6159 | 0.6893 |
| 20J5S2F | 0.7514 | 0.6690 | 0.7474 | 0.7656 | 0.7430 |
| 20J5S3F | 0.7459 | 0.7208 | 0.7608 | 0.7808 | 0.8104 |
| 40J3S2F | 0.7649 | 0.7509 | 0.7741 | 0.7747 | 0.8201 |
| 40J3S3F | 0.7208 | 0.7171 | 0.7248 | 0.6949 | 0.8004 |
| 40J5S2F | 0.6574 | 0.6603 | 0.6810 | 0.7036 | 0.7923 |
| 40J5S3F | 0.7270 | 0.7200 | 0.7100 | 0.7095 | 0.8348 |
| 60J3S2F | 0.6848 | 0.7324 | 0.6877 | 0.6210 | 0.7409 |
| 60J3S3F | 0.6938 | 0.6458 | 0.7083 | 0.6402 | 0.7315 |
| 60J5S2F | 0.7146 | 0.6936 | 0.6992 | 0.6382 | 0.7630 |
| 60J5S3F | 0.6836 | 0.6852 | 0.6940 | 0.7398 | 0.6929 |
| 80J3S2F | 0.6373 | 0.6604 | 0.6742 | 0.5783 | 0.7354 |
| 80J3S3F | 0.8105 | 0.7776 | 0.8166 | 0.8455 | 0.8968 |
| 80J5S2F | 0.7362 | 0.7529 | 0.7522 | 0.7813 | 0.7852 |
| 80J5S3F | 0.6686 | 0.6760 | 0.6755 | 0.7515 | 0.6630 |
| 100J3S2F | 0.4982 | 0.6278 | 0.5097 | 0.6725 | 0.7109 |
| 100J3S3F | 0.7674 | 0.7885 | 0.7791 | 0.7632 | 0.8424 |
| 100J5S2F | 0.6644 | 0.6989 | 0.6823 | 0.5229 | 0.7899 |
| 100J5S3F | 0.6597 | 0.6278 | 0.6641 | 0.6075 | 0.6329 |
| Instances | IGD | ||||
|---|---|---|---|---|---|
| DRLBEA | |||||
| 20J3S2F | 0.0328 | 0.0289 | 0.0244 | 0.0434 | 0.0225 |
| 20J3S3F | 0.0136 | 0.0094 | 0.0121 | 0.0103 | 0.0120 |
| 20J5S2F | 0.0406 | 0.0581 | 0.0304 | 0.0334 | 0.0294 |
| 20J5S3F | 0.0191 | 0.0200 | 0.0247 | 0.0099 | 0.0168 |
| 40J3S2F | 0.0510 | 0.0554 | 0.0495 | 0.0508 | 0.0418 |
| 40J3S3F | 0.0385 | 0.0507 | 0.0562 | 0.0585 | 0.0335 |
| 40J5S2F | 0.0839 | 0.0734 | 0.0956 | 0.0828 | 0.0689 |
| 40J5S3F | 0.0568 | 0.0805 | 0.0839 | 0.0908 | 0.0701 |
| 60J3S2F | 0.0366 | 0.0363 | 0.0411 | 0.0424 | 0.0280 |
| 60J3S3F | 0.0414 | 0.0440 | 0.0516 | 0.0634 | 0.0348 |
| 60J5S2F | 0.0667 | 0.0613 | 0.0773 | 0.0817 | 0.0536 |
| 60J5S3F | 0.0585 | 0.0679 | 0.0533 | 0.0519 | 0.0459 |
| 80J3S2F | 0.0691 | 0.0685 | 0.0624 | 0.0841 | 0.0527 |
| 80J3S3F | 0.0838 | 0.1405 | 0.1015 | 0.0779 | 0.0549 |
| 80J5S2F | 0.0991 | 0.1060 | 0.1411 | 0.1058 | 0.0657 |
| 80J5S3F | 0.0984 | 0.0996 | 0.0887 | 0.0816 | 0.0863 |
| 100J3S2F | 0.0832 | 0.0793 | 0.1052 | 0.0522 | 0.0338 |
| 100J3S3F | 0.0567 | 0.1108 | 0.0702 | 0.0824 | 0.0879 |
| 100J5S2F | 0.0821 | 0.0981 | 0.0973 | 0.1022 | 0.0631 |
| 100J5S3F | 0.0787 | 0.0884 | 0.0912 | 0.1085 | 0.0634 |
| Algorithms | HV | IGD | ||||
|---|---|---|---|---|---|---|
| Mean | Rank | p-Value | Mean | Rank | p-Value | |
| 0.7021 | 3.70 | 4.4191 × 10−5 | 0.0595 | 3.05 | 2.0633 × 10−5 | |
| 0.7033 | 3.55 | 0.0689 | 3.50 | |||
| 0.7116 | 2.75 | 0.0679 | 3.55 | |||
| 0.6997 | 3.45 | 0.0657 | 3.50 | |||
| DRLBEA | 0.7649 | 1.55 | 0.0483 | 1.40 | ||
| Instances | HV | |||||
|---|---|---|---|---|---|---|
| NSGA-II | MOEA/D | TSNSGA-II | IMPGA | D2QCE | DRLBEA | |
| 20J3S2F | 0.6866 | 0.6783 | 0.6684 | 0.1617 | 0.8261 | 0.9078 |
| 20J3S3F | 0.7135 | 0.6463 | 0.7405 | 0.4143 | 0.6738 | 0.7056 |
| 20J5S2F | 0.6969 | 0.7010 | 0.7454 | 0.3059 | 0.7678 | 0.8750 |
| 20J5S3F | 0.7350 | 0.6771 | 0.7321 | 0.4468 | 0.7558 | 0.8328 |
| 40J3S2F | 0.6740 | 0.5982 | 0.6624 | 0.4251 | 0.7425 | 0.8378 |
| 40J3S3F | 0.6853 | 0.6619 | 0.7090 | 0.3005 | 0.7013 | 0.7914 |
| 40J5S2F | 0.7008 | 0.7316 | 0.7431 | 0.5164 | 0.7231 | 0.8379 |
| 40J5S3F | 0.6714 | 0.6871 | 0.6821 | 0.5812 | 0.7443 | 0.8572 |
| 60J3S2F | 0.7214 | 0.7049 | 0.7458 | 0.5234 | 0.7030 | 0.7581 |
| 60J3S3F | 0.6976 | 0.7037 | 0.7540 | 0.6577 | 0.7019 | 0.7925 |
| 60J5S2F | 0.7609 | 0.7602 | 0.7282 | 0.5477 | 0.7135 | 0.8088 |
| 60J5S3F | 0.6898 | 0.7180 | 0.7309 | 0.5109 | 0.6957 | 0.7508 |
| 80J3S2F | 0.7754 | 0.6963 | 0.7894 | 0.5585 | 0.8073 | 0.7354 |
| 80J3S3F | 0.7323 | 0.6285 | 0.7275 | 0.4277 | 0.7911 | 0.8987 |
| 80J5S2F | 0.7438 | 0.6648 | 0.7658 | 0.4925 | 0.7500 | 0.8908 |
| 80J5S3F | 0.6965 | 0.7060 | 0.6960 | 0.6745 | 0.7615 | 0.7623 |
| 100J3S2F | 0.7730 | 0.7346 | 0.7378 | 0.4686 | 0.7249 | 0.7981 |
| 100J3S3F | 0.7154 | 0.6775 | 0.7567 | 0.5471 | 0.7594 | 0.8693 |
| 100J5S2F | 0.7752 | 0.6995 | 0.7848 | 0.2812 | 0.7853 | 0.8214 |
| 100J5S3F | 0.7131 | 0.7131 | 0.6811 | 0.3651 | 0.7331 | 0.7849 |
| Instances | IGD | |||||
|---|---|---|---|---|---|---|
| NSGA-II | MOEA/D | TSNSGA-II | IMPGA | D2QCE | DRLBEA | |
| 20J3S2F | 0.0939 | 0.0922 | 0.0540 | 0.4536 | 0.0346 | 0.0132 |
| 20J3S3F | 0.1014 | 0.0693 | 0.0341 | 0.4324 | 0.0139 | 0.0077 |
| 20J5S2F | 0.0945 | 0.0896 | 0.0197 | 0.2354 | 0.0458 | 0.0056 |
| 20J5S3F | 0.0814 | 0.1034 | 0.0462 | 0.2131 | 0.0180 | 0.0068 |
| 40J3S2F | 0.1128 | 0.1575 | 0.0840 | 0.2800 | 0.0715 | 0.0599 |
| 40J3S3F | 0.1216 | 0.1780 | 0.1005 | 0.2875 | 0.0532 | 0.0464 |
| 40J5S2F | 0.0938 | 0.1545 | 0.0914 | 0.1702 | 0.0704 | 0.0438 |
| 40J5S3F | 0.1235 | 0.2123 | 0.0979 | 0.1349 | 0.0656 | 0.0404 |
| 60J3S2F | 0.1045 | 0.1107 | 0.1018 | 0.2690 | 0.0360 | 0.0442 |
| 60J3S3F | 0.1329 | 0.1018 | 0.1670 | 0.1995 | 0.0494 | 0.0274 |
| 60J5S2F | 0.1101 | 0.1237 | 0.0823 | 0.1389 | 0.0626 | 0.0476 |
| 60J5S3F | 0.1129 | 0.1593 | 0.1022 | 0.1593 | 0.0704 | 0.0582 |
| 80J3S2F | 0.0811 | 0.1840 | 0.1144 | 0.1962 | 0.1236 | 0.0679 |
| 80J3S3F | 0.1532 | 0.1580 | 0.1470 | 0.1783 | 0.0626 | 0.0622 |
| 80J5S2F | 0.1145 | 0.2501 | 0.1304 | 0.1263 | 0.1217 | 0.0793 |
| 80J5S3F | 0.1489 | 0.2219 | 0.1361 | 0.1275 | 0.0728 | 0.0539 |
| 100J3S2F | 0.1339 | 0.1120 | 0.0955 | 0.1750 | 0.0744 | 0.0329 |
| 100J3S3F | 0.1642 | 0.1638 | 0.1821 | 0.0939 | 0.0870 | 0.0429 |
| 100J5S2F | 0.1381 | 0.2201 | 0.1450 | 0.3440 | 0.0864 | 0.0462 |
| 100J5S3F | 0.1736 | 0.2145 | 0.2160 | 0.2539 | 0.0892 | 0.0557 |
| Algorithms | HV | IGD | ||||
|---|---|---|---|---|---|---|
| Mean | Rank | p-Value | Mean | Rank | p-Value | |
| NSGA-II | 0.7179 | 3.60 | 1.0074 × 10−13 | 0.1195 | 4.00 | 1.3734 × 10−15 |
| MOEA/D | 0.6894 | 4.15 | 0.1538 | 4.75 | ||
| TSNSGA-II | 0.7291 | 3.10 | 0.1074 | 3.50 | ||
| IMPGA | 0.4603 | 6.00 | 0.2234 | 5.55 | ||
| D2QCE | 0.7431 | 2.90 | 0.0655 | 2.15 | ||
| DRLBEA | 0.8158 | 1.25 | 0.0422 | 1.05 | ||
| Algorithms | HV | IGD | ||
|---|---|---|---|---|
| Mean | p-Value | Mean | p-Value | |
| NSGA-II | 0.7254 | 2.3241 × 10−9 | 0.0914 | 1.2150 × 10−9 |
| MOEA/D | 0.6896 | 0.1854 | ||
| TSNSGA-II | 0.6135 | 0.1635 | ||
| IMPGA | 0.4512 | 0.2154 | ||
| D2QCE | 0.7345 | 0.0854 | ||
| DRLBEA | 0.8606 | 0.0729 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Huang, L.; Tao, J.; Zhang, C.; Zheng, J. A Deep Reinforcement Learning-Based Evolutionary Algorithm for Distributed Heterogeneous Green Hybrid Flowshop Scheduling. Processes 2025, 13, 728. https://doi.org/10.3390/pr13030728
Xu H, Huang L, Tao J, Zhang C, Zheng J. A Deep Reinforcement Learning-Based Evolutionary Algorithm for Distributed Heterogeneous Green Hybrid Flowshop Scheduling. Processes. 2025; 13(3):728. https://doi.org/10.3390/pr13030728
Chicago/Turabian StyleXu, Hua, Lingxiang Huang, Juntai Tao, Chenjie Zhang, and Jianlu Zheng. 2025. "A Deep Reinforcement Learning-Based Evolutionary Algorithm for Distributed Heterogeneous Green Hybrid Flowshop Scheduling" Processes 13, no. 3: 728. https://doi.org/10.3390/pr13030728
APA StyleXu, H., Huang, L., Tao, J., Zhang, C., & Zheng, J. (2025). A Deep Reinforcement Learning-Based Evolutionary Algorithm for Distributed Heterogeneous Green Hybrid Flowshop Scheduling. Processes, 13(3), 728. https://doi.org/10.3390/pr13030728





