Study of Particle Discharge from a Fluidized Bed: Experimental Investigation and Comparative Modeling Analysis
Abstract
1. Introduction
2. Methods and Materials
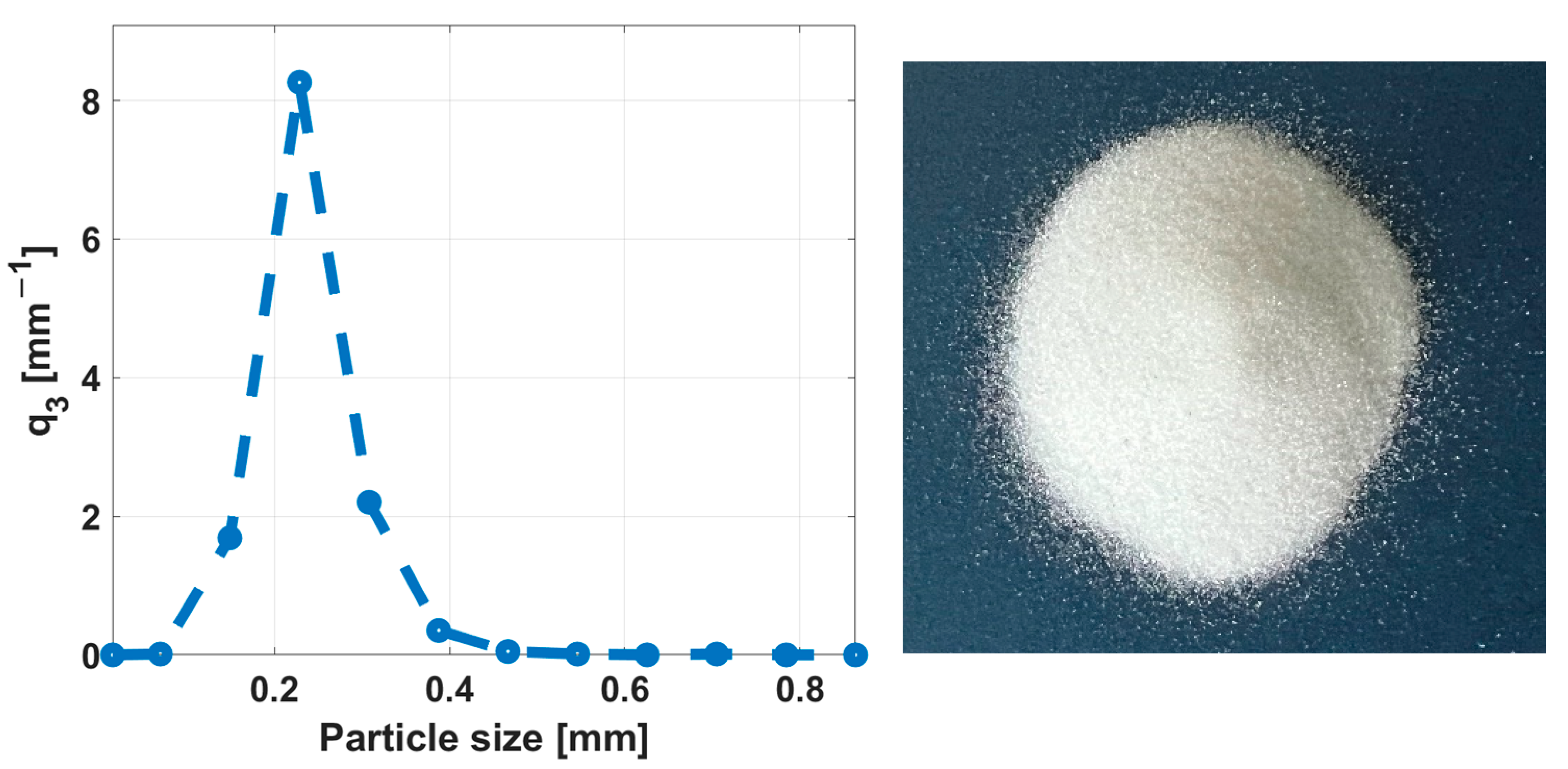
2.1. Material
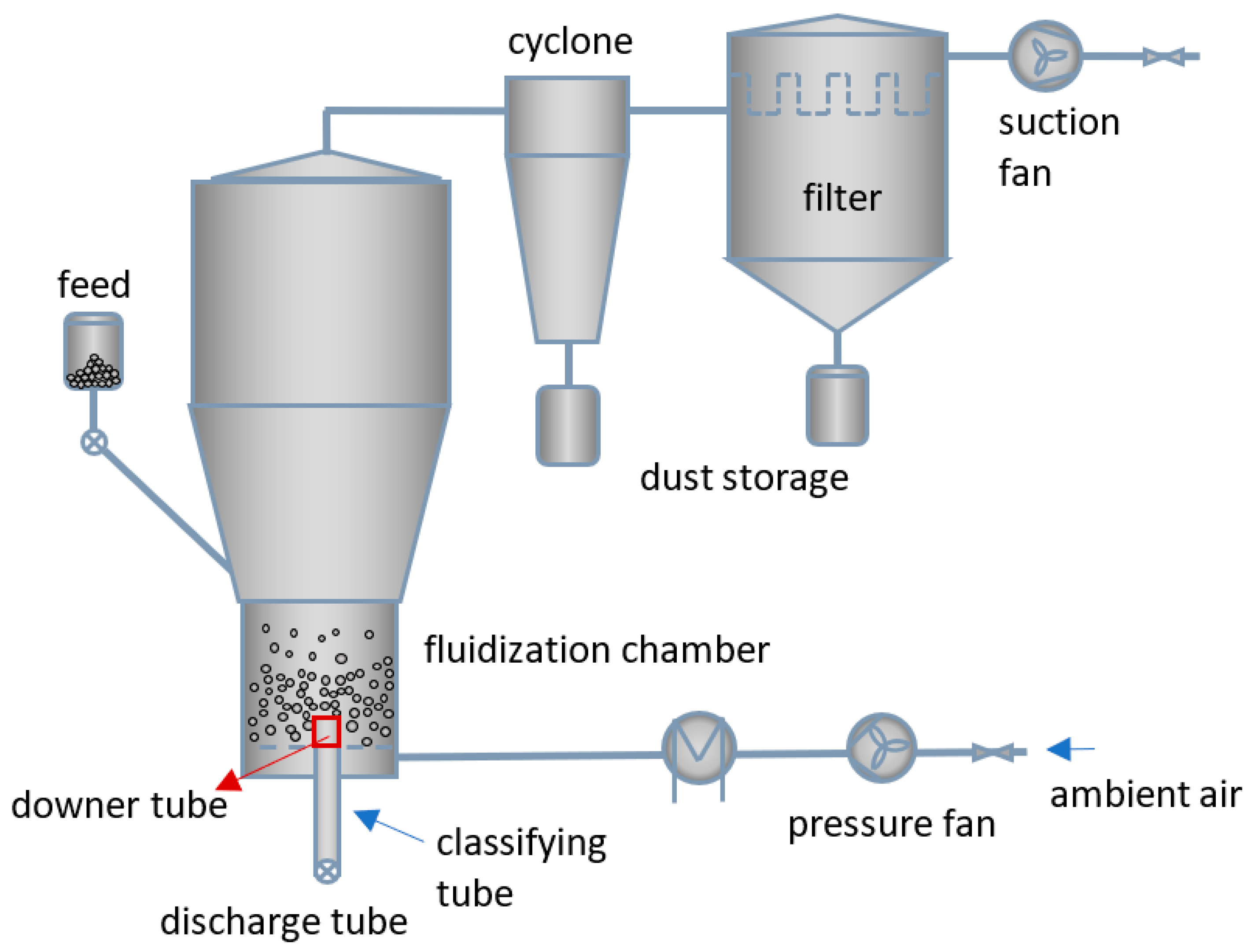
2.2. Experimental Setup
2.3. Experimental Plan
3. Mathematical Modeling
3.1. Mass Balance Equation
3.2. Mass Outflow Rate Equations
- is the discharge coefficient with a value of 0.5, as given by the authors [22];
- is the cross-sectional area of the downer tube;
- is the bed density;
- is the gravitational acceleration;
- is the expanded fluidized bed height;
- is the downer tube height.
- is the Reynolds number at superficial gas velocity ;
- is the Reynolds number at minimum fluidization;
- is an empirically derived pulsation factor exponent, based on experimental measurements.
3.3. Determination of Bed Height and Fluidization Parameters
- is the cross-sectional area of the fluidized bed;
- is particle density;
- is bed porosity.
- is the Reynolds number at the elutriation point;
- is an exponent.
- Reynolds number at superficial gas velocity, , characterizes the general flow conditions in the bed:where is the kinematic viscosity of the gas, while the superficial gas velocity is obtained as:where is the gas density.
- Reynolds number at minimum fluidization,, indicates the point at which fluidization begins, according to Martin [33]:where the Archimedes number, , is defined as:
- The Reynolds number at the elutriation point, corresponds to the gas velocity needed to carry particles out of the bed. This is obtained for heterogeneous fluidization after Reh [34]:
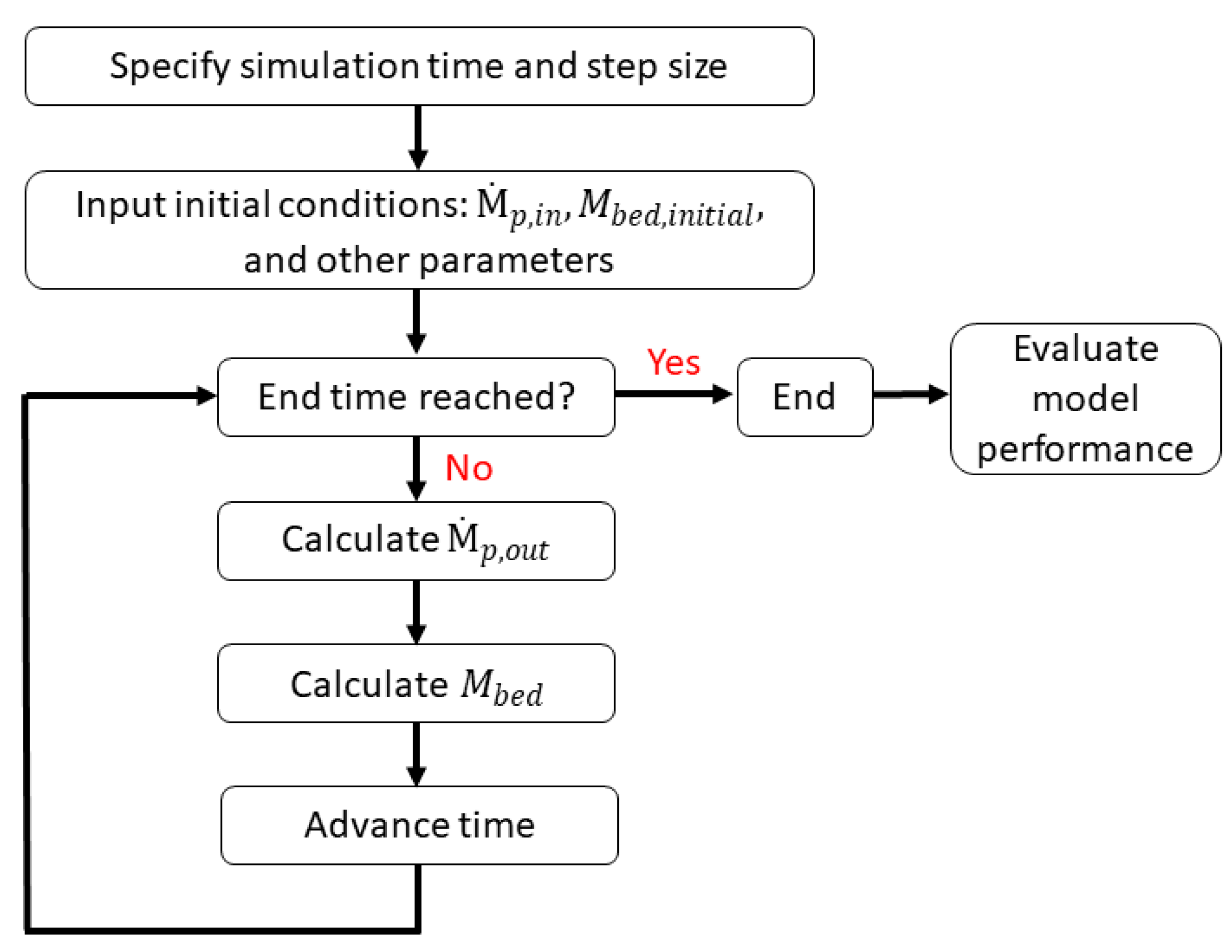
3.4. Fluidized Bed Parameters and Model Implementation
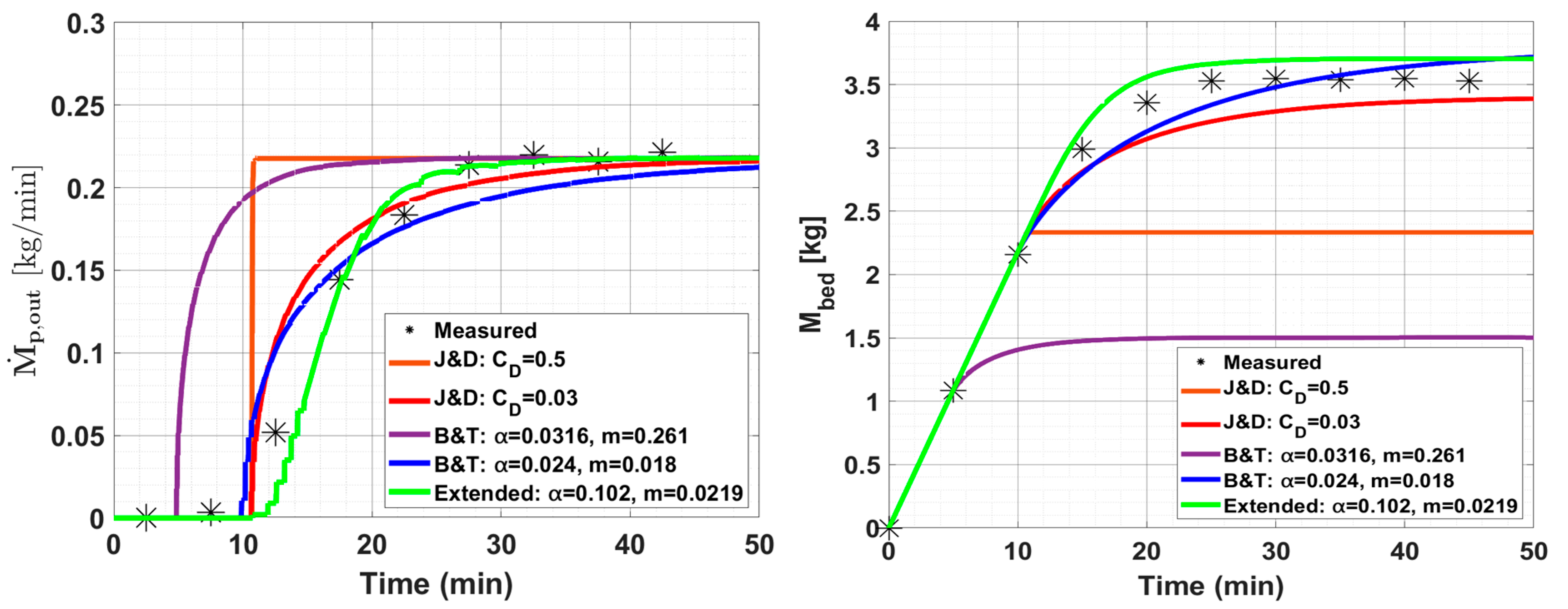
4. Results and Discussion
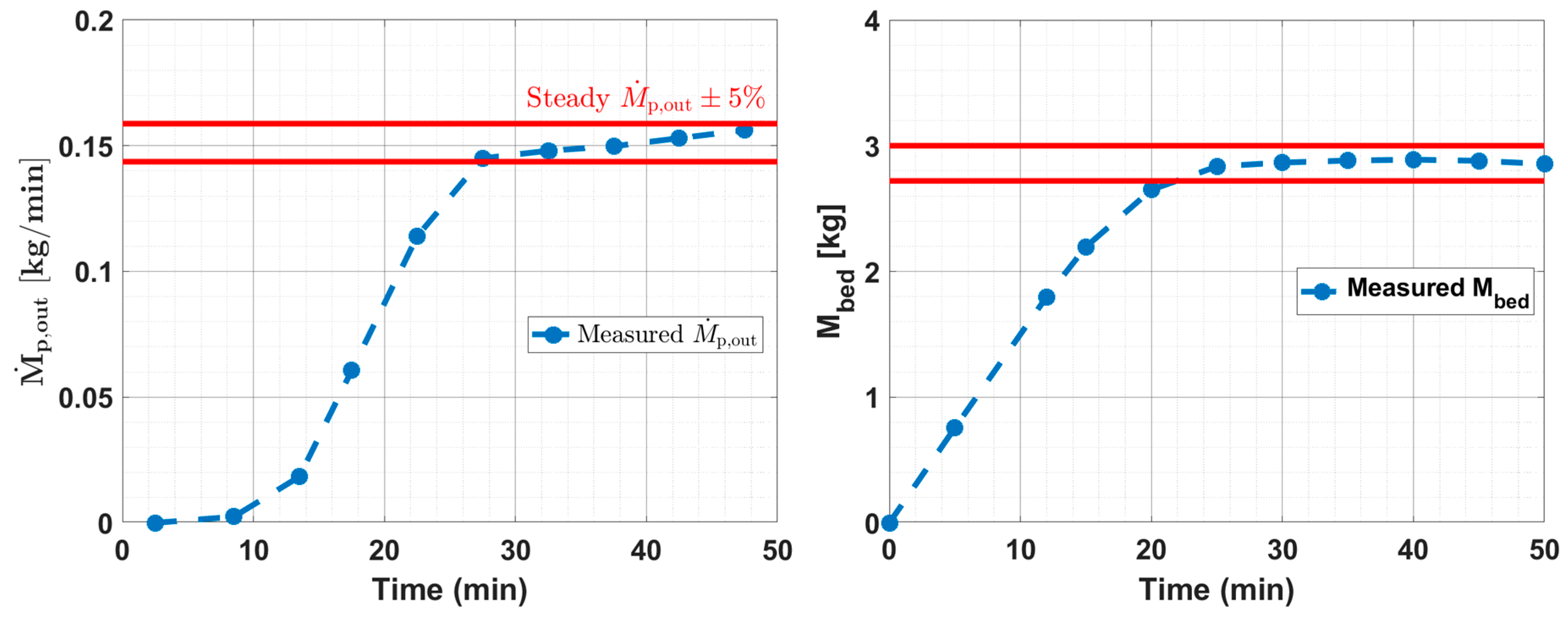
4.1. Experimental Results
4.2. Mathematical Modeling Results
- Initial period (0–10 min): In the initial phase, both the J&D equation with its condition and the B&T and extended equations with their conditions captured the zero-outflow behavior effectively. The R2 values for both and are 0.999, confirming that the models accurately represent this period.
- Transition period (10–30 min): In the transition period, where starts to increase and changes more dynamically, the equations showed differences in accuracy. The J&D and B&T equations saw drops in R2, with values of 0.840 and 0.927 for and 0.756 and 0.792 for , respectively, indicating some limitations in capturing these dynamics. In contrast, the extended equation achieved higher R2 values of 0.940 for and 0.863 for , suggesting that its exponential term provides better responsiveness to the changing conditions of this period.
- Steady-state period (30–45 min): In the final steady-state period, in which the conditions stabilize, all equations led to improved accuracy. The B&T achieved the highest R2 value for at 0.982, while the extended equation performed best for with an R2 of 0.998. The J&D also performed well, with R2 values of 0.951 for and 0.990 for , showing satisfactory alignment with the experimental data. This suggests that while all models are suitable for steady-state conditions, the extended model has a slight edge in predicting .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-sectional area, m2 |
| Ar | Archimedes number, - |
| discharge coefficient, - | |
| d | diameter, m |
| acceleration of gravity, m/s2 | |
| height, m | |
| M | mass, kg |
| m | exponent, - |
| Ṁ | mass flow rate, kg/s |
| Re | Reynolds number, - |
| time, s | |
| velocity, m/s | |
| Greek letters | |
| ⍺ | inflow parameter |
| ε | porosity |
| κ | pulsation factor |
| ν | kinematic viscosity, m2/s |
| ρ | density, kg/m3 |
| Subscripts | |
| 0 | superficial |
| bed | fluidized bed |
| elu | elutriation |
| gas | |
| in | inlet |
| mf | minimal fluidization |
| out | outlet |
| p | particle |
| st | steady |
| tube | downer tube |
References
- Rhodes, M.J.; Seville, J.P.K. Introduction to Particle Technology; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Horio, M. Overview of fluidization science and fluidized bed technologies in Fluidized-Bed Technologies for Near-Zero Emission Combustion and Gasification; Woodhead Publishing: Cambridge, UK, 2013; pp. 3–41. [Google Scholar]
- Teunou, E.; Poncelet, D. Batch and continuous fluid bed coating: Review and state of the art. J. Food Eng. 2002, 53, 325–340. [Google Scholar] [CrossRef]
- Lim, D.; Letona, A.; Lee, M.; Lim, D.; Han, N.; Chung, D. Fluidized-bed granulation of probiotics-encapsulated spray-dried milk powder:Effects of a fluidizing aid, moisture-activation and dehydration. Foods 2021, 10, 1600. [Google Scholar] [CrossRef]
- Gu, C.; Zhao, H.; Xu, B.; Yang, J.; Zhang, J.; Du, M.; Liu, Y.; Tikhankin, D.; Yuan, Z. CFD-DEM simulation of distribution and agglomeration characteristics of bendable chain-like biomass particles in a fluidized bed reactor. Fuel 2023, 340, 127570. [Google Scholar] [CrossRef]
- Mujumdar, A.S. Handbook of Industrial Drying, 3rd ed.; CRC, Taylor & Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Razzak, S.A. Characteristics and diverse applications of (gas)-liquid-solid circulating fluidized beds: A comprehensive review. Powder Technol. 2024, 435, 119359. [Google Scholar] [CrossRef]
- Won, Y.S.; Youn, P.S.; Kim, D.; Joo, J.B.; Choi, J.-H.; Ryu, H.-J. Bed pressure drop of a bubbling fluidized-bed with overflow solid discharge. Adv. Powder Technol. 2019, 30, 1165–1173. [Google Scholar] [CrossRef]
- Radichkov, R.; Müller, T.; Kienle, A.; Heinrich, S.; Peglow, M.; Mörl, L. A numerical bifurcation analysis of continuous fluidized bed spray granulation with external product classification. Chem. Eng. Process.—Process Intensif. 2006, 45, 826–837. [Google Scholar] [CrossRef]
- Khanali, M.; Rafiee, S.; Jafari, A.; Banisharif, A. Study of residence time distribution of rough rice in a plug flow fluid bed dryer. Int. J. Adv. Sci. 2012, 48, 103–114. [Google Scholar]
- Bachmann, P.; Chen, K.; Bück, A.; Tsotsas, E. Prediction of particle size and layer-thickness distributions in a continuous horizontal fluidized-bed coating process. Particuology 2020, 50, 1–12. [Google Scholar] [CrossRef]
- Chen, K.; Bachmann, P.; Bück, A.; Jacob, M.; Tsotsas, E. CFD simulation of particle residence time distribution in industrial scale horizontal fluidized bed. Powder Technol. 2019, 345, 129–139. [Google Scholar] [CrossRef]
- Diez, E.; Kieckhefen, P.; Meyer, K.; Bück, A.; Tsotsas, E. Heinrich, Particle dynamics in a multistaged fluidized bed: Particle transport behavior on micro-scale by disrete particle modelling. Adv. Powder Technol. 2019, 30, 2014–2031. [Google Scholar] [CrossRef]
- Zhu, X.; Dong, P.; Tu, Q.; Zhu, Z.; Yang, W.; Wang, H. Investigation of gas-solids flow characteristics in a pressurised circulating fluidised bed by experiment and simulation. Powder Technol. 2020, 366, 420–433. [Google Scholar] [CrossRef]
- Tu, Q.; Wang, H.; Ocone, R. Application of three-dimensional full-loop CFD simulation in circulating fluidized bed combustion reactors—A review. Powder Technol. 2022, 399, 117181. [Google Scholar] [CrossRef]
- Bachmann, P.; Bück, A.; Tsotsas, E. Experimental investigation and correlation of the Bodenstein number in horizontal fluidized beds with internal baffles. Powder Technol. 2017, 308, 378–387. [Google Scholar] [CrossRef]
- Mielke, L.; Bück, A.; Tsotsas, E. Multi-stage and multi-compartment model for dynamic simulation of horizontal fluidized bed granulator. Dry. Technol. 2021, 39, 203–218. [Google Scholar] [CrossRef]
- Du, J.; Strenzke, G.; Bück, A.; Tsotsas, E. Monte Carlo modeling of spray agglomeration in a cylindrical fluidized bed: From batch-wise to continuous processes. Powder Technol. 2022, 396, 113–126. [Google Scholar] [CrossRef]
- Meyer, K.; Bück, A.; Tsotsas, E. Determination of particle exchange rates at over-flow weirs in horizontal fluidised beds by particle tracking velocimetry. Particuology 2017, 32, 1–9. [Google Scholar] [CrossRef]
- Vollmari, K.; Kruggel-Emden, H. Numerical and experimental analysis of particle residence times in a continuously operated dual-chamber fluidized bed. Powder Technol. 2018, 338, 625–637. [Google Scholar] [CrossRef]
- Lau, P.; Arlt, C.-R.; Potthoff, M.; Kind, M. Particle exchange in horizontal two-compartment fluidized beds: CFD simulation and experimental validation. Adv. Powder Technol. 2017, 28, 543–552. [Google Scholar] [CrossRef]
- Jones, D.R.M.; Davidson, J.F. The flow of particles from a fluidised bed through an orifice. Rheol. Acta 1965, 4, 180–192. [Google Scholar] [CrossRef]
- Bertin, D.E.; Cotabarren, I.M.; Bucala, V.; Pin, J. Analysis of the product granulometry, temperature and mass flow of an industrial multichamber fluidized bed urea granulator. Powder Technol. 2011, 206, 122–131. [Google Scholar] [CrossRef]
- Bertin, D.E.; Cotabarren, I.; Pin, J.; Bucala, V. Granule size distribution for a multi-chamber fluidized-bed melt granulator: Modeling and validation using process measurement data. Chem. Eng. Sci. 2013, 104, 319–329. [Google Scholar] [CrossRef]
- Burgschweiger, J.; Tsotsas, E. Experimental investigation and modelling of continuous fluidized bed drying under steady-state and dynamic conditions. Chem. Eng. Sci. 2002, 57, 5021–5038. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, S.; Xu, X.; Zhao, Y.; Dong, L.; Chen, Z. Particle flow characteristics in a gas-solid separation fluidized bed based on machine learning. Fuel 2022, 314, 123039. [Google Scholar] [CrossRef]
- Sigmund Linder GmbH. Product Data Sheet. Available online: https://www.sili.eu/wp-content/uploads/2023/04/SiLibeads_Solid_2025.pdf (accessed on 9 February 2025).
- Liu, B.; Zhang, X.; Wang, L.; Hong, H. Fluidization of non-spherical particles: Sphericity, Zingg factor, and other fluidization parameters. Particuology 2008, 6, 125–129. [Google Scholar] [CrossRef]
- Grace, J.R. Essentials of Fluidization Technology; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Coperion. Twin Screw Feeders—Process Equipment. Available online: https://www.coperion.com/en/products-services/process-equipment/feeders/twin-screw-feeders (accessed on 9 February 2025).
- Sartorius. Laboratory Balances. Available online: https://www.sartorius.com/en/products/weighing/laboratory-balances#id-934518 (accessed on 9 February 2025).
- Richardson, J.F.; Zaki, W.N. The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Eng. Sci. 1954, 3, 65–73. [Google Scholar] [CrossRef]
- Martin, H. Wärme- und Stoffübertragung in der Wirbelschicht. Chem. Ing. Tech. 1980, 52, 199–209. [Google Scholar] [CrossRef]
- Reh, L. Verbrennung in der Wirbelschicht. Chem. Ing. Tech. 1968, 40, 509–515. [Google Scholar] [CrossRef]



| Experiment | Continuous | Semi-Batch | |||
|---|---|---|---|---|---|
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
| [mm] | 70 | 70 | 70 | 110 | 70 |
| [kg] | 0 | 0 | 0 | 0 | 6.21 |
| [kg/min] | 0.151 | 0.218 | 0.272 | 0.258 | 0 |
| Parameter | Value |
|---|---|
| [kg/m3] | 1.18 |
| [m2/s] | 0.0000155 |
| [kg/s] | 0.08 |
| [m/s2] | 9.81 |
| [m] | 0.000226 |
| [m2] | 0.0687 |
| Parameter | Equation Number | Value |
|---|---|---|
| [−] | 9 | 0.804 |
| [−] | 10 | 4.29 |
| [−] | 11 | 14.6 |
| [m/s] | 11 | 0.0487 |
| [m/s] | 12 | 0.975 |
| [−] | 13 | 0.729 |
| [−] | 14 | 1038.3 |
| [−] | 15 | 37.2 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |
|---|---|---|---|---|---|
| [kg/min] | 0.151 | 0.221 | 0.270 | 0.256 | 0.0150 |
| [kg] | 2.93 | 3.49 | 3.89 | 5.96 | 2.52 |
| [kg] | 2.84 | 3.53 | 3.82 | 5.80 | 2.55 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Process time [min] | 50 | 45 | 40 | 60 |
| [min] | 25 | 20 | 20 | 30 |
| [min] | 30 | 30 | 25 | 40 |
| Model | Initial Period (0–10 min) | Transition Period (10–30 min) | Steady-State Period (30–45 min) |
|---|---|---|---|
| J&D | : 0.999 : 0.999 | : 0.840 : 0.756 | : 0.951 : 0.990 |
| B&T | : 0.999 : 0.999 | : 0.927 : 0.792 | : 0.982 : 0.962 |
| Extended | : 0.999 : 0.999 | : 0.940 : 0.863 | : 0.958 : 0.998 |
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Predicted | R2 | Predicted | R2 | Predicted | R2 | Predicted | R2 | Predicted | R2 | ||
[kg] | J&D | 2.85 | 0.998 | 3.40 | 0.973 | 3.99 | 0.981 | 4.77 | 0.905 | 2.34 | 0.696 |
| B&T | 2.97 | 0.997 | 3.77 | 0.988 | 4.61 | 0.955 | 4.87 | 0.956 | 2.22 | 0.657 | |
| Extended | 3.46 | 0.802 | 3.70 | 0.987 | 3.90 | 0.998 | 5.74 | 0.999 | 2.58 | 0.900 | |
[kg/min] | J&D | 0.151 | 0.966 | 0.218 | 0.946 | 0.271 | 0.942 | 0.258 | 0.917 | 0 | 0.750 |
| B&T | 0.151 | 0.966 | 0.215 | 0.946 | 0.267 | 0.919 | 0.257 | 0.930 | 0 | 0.690 | |
| Extended | 0.151 | 0.896 | 0.217 | 0.971 | 0.272 | 0.995 | 0.258 | 0.991 | 0.00162 | 0.900 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajalova, A.; Chen, K.; Hoffmann, T.; Tsotsas, E. Study of Particle Discharge from a Fluidized Bed: Experimental Investigation and Comparative Modeling Analysis. Processes 2025, 13, 562. https://doi.org/10.3390/pr13020562
Ajalova A, Chen K, Hoffmann T, Tsotsas E. Study of Particle Discharge from a Fluidized Bed: Experimental Investigation and Comparative Modeling Analysis. Processes. 2025; 13(2):562. https://doi.org/10.3390/pr13020562
Chicago/Turabian StyleAjalova, Aisel, Kaicheng Chen, Torsten Hoffmann, and Evangelos Tsotsas. 2025. "Study of Particle Discharge from a Fluidized Bed: Experimental Investigation and Comparative Modeling Analysis" Processes 13, no. 2: 562. https://doi.org/10.3390/pr13020562
APA StyleAjalova, A., Chen, K., Hoffmann, T., & Tsotsas, E. (2025). Study of Particle Discharge from a Fluidized Bed: Experimental Investigation and Comparative Modeling Analysis. Processes, 13(2), 562. https://doi.org/10.3390/pr13020562







