A Comprehensive Optimization for Path Planning: Combining Improved ACO and Smoothing Techniques

Abstract

The ant colony algorithm is an approach for path planning that is used in multiple industries. This paper proposes an improved robot path planning method, referred to as Improved-ACO. First, the heuristic information calculation is optimized to increase algorithm efficiency and shorten convergence time. Secondly, an enhanced Tanh function is included into the heuristic information, allowing dynamic modifications during the search period and preventing the algorithm’s convergence to local optima. Then, a novel pheromone update strategy is employed to accelerate convergence. Next, a novel pheromone diffusion mechanism is proposed to strengthen the ants’ search capability. Additionally, a collision avoidance system and improved B-spline curves are included for path smoothing, guaranteeing that the optimized pathways conform to the robot’s kinematic limitations. Simulation results indicate that the improved ant colony algorithm decreases the average number of turns by $37.5\%$ and accelerates convergence time by $39.45\%$ relative to existing methods across diverse map dimensions. The experiments confirm that Improved-ACO achieves rapid convergence and constructs smooth curves that adhere to the robot’s kinematic constraints. Consequently, Improved-ACO is confirmed as an efficient and adaptable route planning method for robotic navigation under complicated situations.

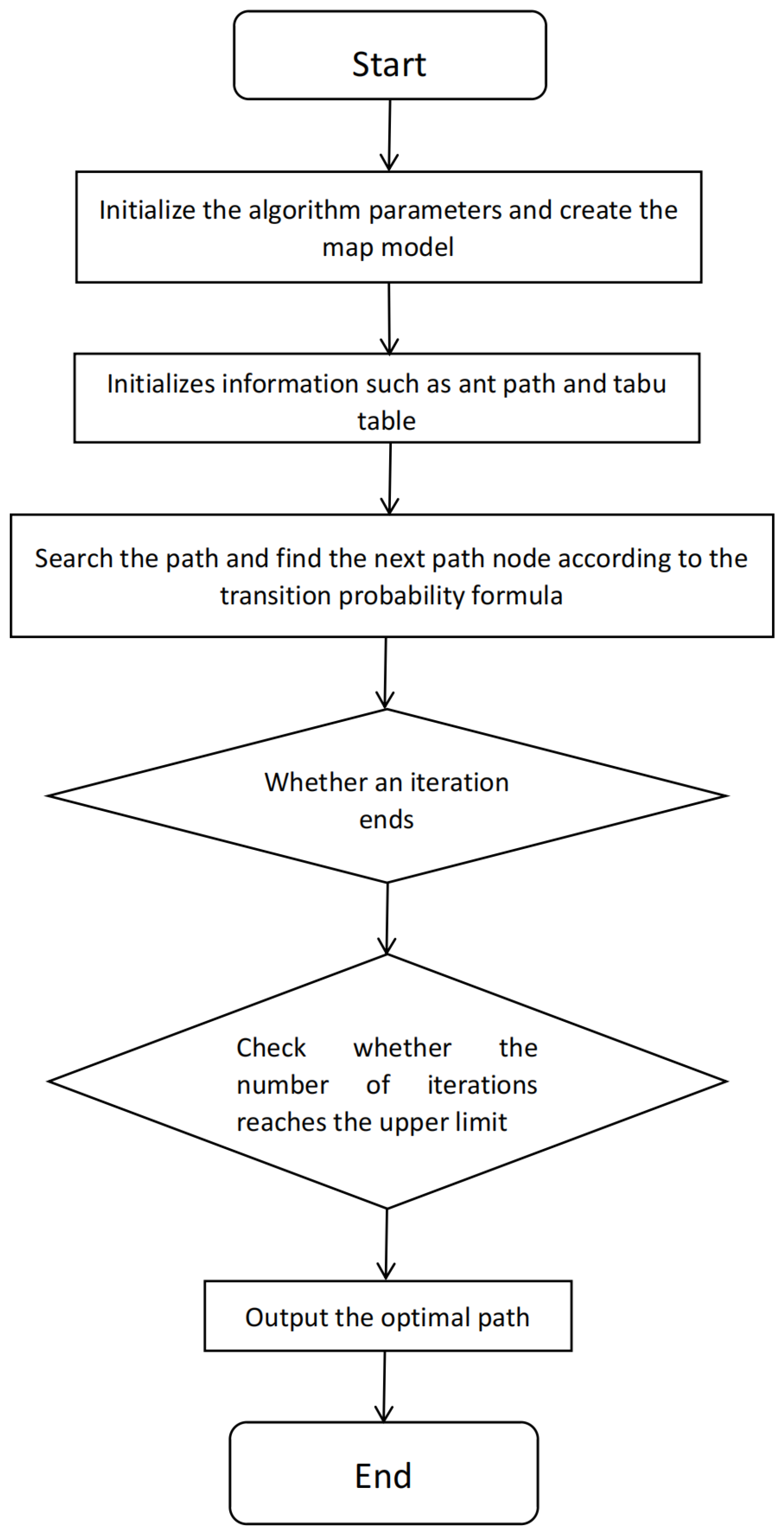
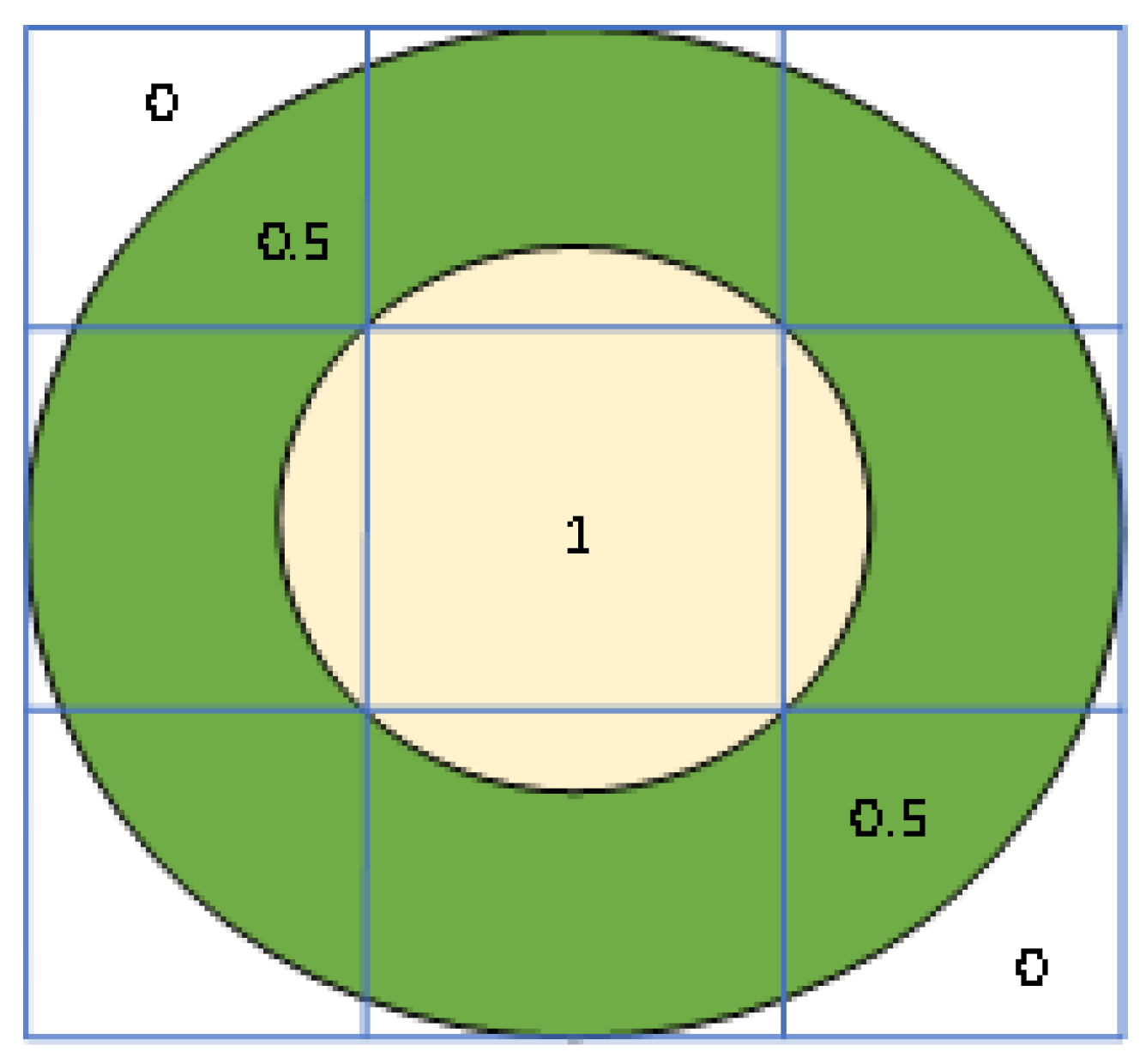
1. Introduction

Path planning for mobile robots is a significant subject in robotics research, having widespread applications in contemporary technology [1]. It makes autonomous navigation and task execution possible, including the handling of commodities in warehouses and the transportation of materials in factories and manufacturing processes. This capability greatly improves production efficiency and workplace productivity [2]. Path planning enables mobile robots to dynamically adjust their paths using real-time environmental data, such as sensor feedback, to avoid obstacles and hazards. This feature is crucial in complex environments, including disaster rescue, medical care, and exploration missions [3]. Effective path planning minimizes energy consumption and operating time, reducing costs and prolonging equipment lifespan. Research on mobile robot path planning advances automation and artificial intelligence while fostering interdisciplinary applications in fields like machine vision, sensor technology, and deep learning [4].

Dijkstra’s algorithm [5], the artificial potential field technique, the RRT algorithm [6], simulated annealing, the A* algorithm, and the genetic particle algorithm [7] are examples of traditional path planning methods. Dijkstra’s algorithm effectively solves the single-source shortest path problem and is both simple to implement and understand [8]. However, it consumes substantial memory and computational resources for large-scale graphs (with numerous nodes and edges), leading to inefficiency. It is common practice to use the artificial potential field approach in situations that call for high real-time performance and settings that are reasonably stable or that change slowly [9]. However, its susceptibility to being trapped in local minima or suboptimal solutions often results in failure. The A* algorithm is a well-known and efficient heuristic search method for graph traversal [10]. It uses a priority queue to select paths and is extensively applied in path planning, artificial intelligence, and robotic navigation. By combining breadth-first search and greedy algorithm features, it ensures efficiency while guaranteeing optimal solutions. The simulated annealing algorithm, a probabilistic optimization method, is computationally simple, highly versatile [11], and robust. It supports parallel processing and effectively addresses complex nonlinear optimization problems. However, its slow convergence speed, lengthy execution time, and sensitivity to initial parameters introduce uncertainty into the solving process. With increasing grid size complexity and computational demands, traditional path planning algorithms struggle to meet requirements. The ant colony algorithm, artificial fish crowd algorithm, and bird flocking method are examples of biomimetic path planning algorithms [12] that often rely on variables like pheromone concentration and inter-individual communication frequency. Selecting these parameters typically demands experience and experimentation; domain-specific adjustments are often required, complicating algorithm design and optimization.

Dorigo et al. created the ant colony algorithm [13], an established heuristic technique for robot route planning that imitates ant foraging behavior. The method has drawbacks, including sluggish early convergence, search stagnation, and vulnerability to local optima, despite its benefits, which include distributed computing, parallelism, and great flexibility. In the past few decades, academics have suggested a number of changes to address these issues. To tackle difficult problems such as the Traveling Salesman Problem (TSP) and airport gate allocation, Wu et al. [14] introduced an expanded cooperative co-evolutionary ant colony optimization method (MSICEAO). To improve convergence speed and solution quality, the method uses techniques such adaptive pheromone evaporation updates, weighted pheromone initialization, elite retention, and multi-population co-evolution. Experimental results indicate that MSICEAO surpasses five advanced algorithms in optimization capability. An increased adapted ant colony algorithm (IAACO) for route planning optimization was created by Miao et al. [15]. The method reformulates route planning as an optimization issue with multiple goals for comprehensive solutions, improving convergence velocity and search capacity by integrating angle-guiding and obstacle-exclusion components. Experimental results confirm that IAACO achieves global path optimization across various environments, exhibiting high real-time performance and stability. Wu et al. [16] introduced the MAACO algorithm, an improved adaptive ant colony optimization method for path planning, to address the issues of optimum locality and delayed convergence in traditional methods. By using a directed heuristic mechanism, a new heuristic function, dynamic pseudo-random guidelines, and a non-uniform pheromone distribution, the program increases search efficiency and global optimality. Experimental results demonstrate that MAACO surpasses existing algorithms by achieving shorter paths, fewer turns, and faster convergence. Zhang et al. [17] developed a vessel navigation method that leverages AIS (Automatic Identification System) data to construct a high-precision environmental model for shortest-path computation by combining the ant colony algorithm (ACA) with the A* search. The method determines the initial path area with ACA, applies A* to find the shortest path, and optimizes it using Bézier curves. Experimental results confirm that this method efficiently plans shorter routes, validating its applicability. DYACO, an improved ant colony optimization method for underwater extraction equipment navigation, was presented by Liang et al. [18]. It was developed in order to circumvent the issues of local optimum and slow convergence that are associated with current algorithms. DYACO outperforms traditional algorithms by achieving a $70.0\%$ decrease in turns and a $15.3\%$ reduction in path length. By combining non-uniform pheromone initiation and pseudo-random state transition criteria, Luo et al. [19] improved the ant colony algorithm for mobile robot route planning. Gao et al. [20] introduced the EH-ACO method, enhancing ant colony optimization through four principal tactics and attaining remarkable outcomes in intricate route planning situations. In prior studies, such as Karakostas and Sifaleras (2022) et al. [21], advanced metaheuristics like the GA for TSP were exploreed but faced challenges in real-world multi-constraint routing. Building on Malik and Kim’s (2019) [22] trip optimization framework, this study introduces a hybrid GA combining Position-Based and One-Point Crossover (PBX + OX1), validated on Konya’s bus transit data. Results demonstrate PBX + OX1 (Bolotbekova et al., 2025) [23] outperforms ABC (Karaboga, 2005) [24], ACO (Dorigo et al., 2006) [25], and PSO (Kennedy & Eberhart, 1995) [26], achieving the shortest feasible route (70.59 km) with enhanced convergence.

To fully leverage the performance metrics of robots in real-world scenarios, a global path planning algorithm that accommodates robotic kinematic constraints is essential [27]. Li et al. [28] presented the IACO-IABC technique, which effectively integrates the advantages of ACO and ABC to handle efficiency and optimization challenges in mobile robot route planning. It excels in minimizing turns and enhancing convergence speed. Wu et al. [29] proposed a temperature parameter and an automated annealing procedure that improved the traditional artificial potential field method, culminating in the DA-APF algorithm. Simulation investigations in U-shaped obstacle situations and intricate settings confirmed the superiority of the DA-APF algorithm. It demonstrated considerable benefits in path length, route length of time, and success rate, successfully addressing the local minima problem in mobile robot path planning. Using Q-learning to continuously change the coefficients of weight within the DWA algorithm, Kobayashi et al. [30] presented a novel path planning method for mobile robots functioning in complex scenarios. Simulation and experimental comparisons indicate that DQDWA outperforms alternatives under various environmental conditions, particularly in crowded settings, effectively avoiding collisions and identifying shorter paths. By adding a combination of the global search method and adaptive dynamic zone searches to the NSGA-II approach, Duan et al. [31] improved the performance of mobile robots in multi-objective route planning. Extensive simulations show that the INSGA-II algorithm surpasses existing multi-objective evolutionary algorithms across various metrics, proving its efficacy in complex path planning. By fusing the artificial potential field approach with Q-learning, Orozco-Rosas et al. [32] created the QAPF algorithm, which greatly enhanced the performance of mobile robot path planning. Li et al. [33] introduced the MAGAT model, integrating Graph Attention Networks (GATs) into multi-robot path planning to enhance efficiency and success rates in complex environments. Wang et al. [34] presented G2RL, a novel hierarchical route planning method that combines local reinforcement learning with global guidance, to address path planning issues in uncertain circumstances.

Previous research indicated a substantial improvement in the average convergence rate of the ant colony method and a substantial reduction in route length relative to traditional versions. However, the ant colony algorithm still struggles to meet the kinematic constraints of mobile robots in certain cases. In this study, improvements are provided that aim to reduce the number of path twists and maintain compliance with the kinematic constraints that mobile robots are subject to. The following is a summary of the most important contributions that this study makes:

(a)

It is recommended that a better ant colony algorithm be developed in order to overcome the constraints of previous implementations. These disadvantages include inadequate global search efficiency, slow convergence, and sensitivity to local minima in complicated situations. For resolving these constraints, a new heuristic formula is devised that includes the squared distance between the current and destination goals. Additionally, an enhanced Tanh function is employed to optimize the pheromone evaporation process. The pheromone update strategy is refined using an optimal–worst ant system, improving pheromone distribution. Finally, a pheromone diffusion model is introduced to enhance ant search capabilities and avoid stagnation in suboptimal solutions.

(b)

To account for the kinematic constraints of mobile robots, collision avoidance mechanisms and B-spline curves are integrated to maintain safe distances from obstacles. The B-spline formula is improved, enabling control points to adjust away from obstacles while maintaining path smoothness and adhering to the robot’s angular constraints.

By integrating these mechanisms, a new ant colony algorithm (Improved-ACO) is developed. The paths generated by Improved-ACO are compared with those from traditional and enhanced algorithms on various maps, validating its effectiveness and superiority.

The order in which the sections of this paper are presented is found below.

Section 2 presents the principles of the conventional ant colony algorithm, establishing a foundation for future enhancements. Section 3 details the specific content of the four improvement mechanisms. Section 4 presents the specific measures for path smoothing. Section 5 outlines the overall process of Improved-ACO. Section 6 performs simulated studies that evaluate the algorithm’s superiority. Finally, Section 7 presents the conclusions of the conducted research.

2. Basis of Algorithm

2.1. Origin and Development of Ant Colony Optimization (ACO)

Ant Colony Optimization (ACO) is a meta-heuristic algorithm inspired by the foraging behavior of ants in nature, mainly used to solve combinatorial optimization problems. Ants mark paths by releasing pheromones, which other ants sense and select, ultimately forming a self-reinforcing mechanism of the shortest path. Inspired by the foraging behavior of real ants, Marco Dorigo and his colleagues first proposed ant colony optimization (ACO) algorithms in the early 1990s. Their pioneering work shows how artificial ants can collaboratively solve combinatorial optimization problems through pheromone deposition and route selection. The ACO path planning flow chart is shown in Figure 1. The main basic algorithms are as follows:

2.1.1. Ant System (AS)

In 1996, Dorigo et al. [13] introduced the first ACO algorithm, the Ant System (AS), to solve the Traveling Salesman Problem (TSP). AS simulated artificial ants depositing pheromones on edges of a graph, with path selection governed by a probabilistic rule combining pheromone intensity and heuristic information (e.g., inverse distance). The positive feedback mechanism of pheromone accumulation enabled ants to converge toward shorter paths, mimicking biological swarm intelligence.

2.1.2. MAX-MIN Ant System (MMAS)

The Max-Min Ant System (MMAS), as an efficient variant of the Ant Colony Optimization (ACO) algorithm, has shown significant advantages in solving complex optimization problems. By introducing an upper and lower limit mechanism for pheromone concentration and an improved pheromone update rule, MMAS effectively solves the problems of premature convergence and slow convergence speed in basic ACO.

2.1.3. Ant Colony System (ACS)

The Ant Colony System (ACS), as an efficient variant of the Ant Colony Optimization algorithm, has shown significant advantages in solving complex optimization problems. By introducing the candidate list and local search strategy, ACS effectively solves the problems of slow convergence and easily falling into local optimal solutions which afflict the basic ACO.

2.2. The Establishment of Grid Environment

The grid approach is the main methodology for environmental map simulation in path planning. The application of the ant colony method to problems involving route planning optimization requires the establishment of a grid environment as a necessary step [35]. The grid technique provides distinct geographical segmentation, straightforward implementation, and significant flexibility, hence reducing the complexity of environmental simulation. As a result, the environmental model in this study is established using the grid approach, where a value of 0 represents free space in the environment map, corresponding to white-filled grids, and a value of 1 represents obstacle areas, corresponding to black-filled grids. Figure 2 illustrates that the robot’s simulated environment space has been substituted with a grid model, whereby each grid has a distinct coordinate value.

An environmental model for route planning has been developed using the grid approach, with all grids numbered in accordance with the relationship between coordinate values and grid indices. The relationship between coordinate values and grid sequence numbers is illustrated in Equation (1).

$$\left\{\begin{array}{c}\mathrm{x}=mod\left(i,N\right)-0.5\\ y=M+0.5-ceil\left(i/N\right)\end{array}\right.$$

(1)

2.3. Traditional ACO Mathematical Model

Based on ant feeding behavior, Ant Colony Optimization (ACO) is primarily used to solve complicated optimization problems, including the Traveling Salesman Problem (TSP), vehicle routing conundrums, and route planning issues [36,37]. ACO makes use of ants’ pheromone deposition mechanism in order to determine the path that is the shortest distance between a food supply and nests containing ants. The algorithm can identify the most effective solution by using the collaboration of individual ants as well as the constant iteration and updating of pheromones.

2.3.1. State Transition Probability in ACO

In the use of the ant colony algorithm for route planning, it is assumed that there are initially M ants, each representing an individual path. In this process, the ants have to figure out which node comes after the starting point using a state transition probability calculation. This is symbolized by P, which stands for the chance that the ant will go to the next node. The next node is chosen by ant m (m = 1, 2, 3, …, M) using the transition probability as follows:

$$P_{ij}^m=\left\{\begin{array}{cc}{\displaystyle \frac{{\left[{\tau }_{ij}\left(k\right)\right]}^{\alpha }{\left[{\eta }_{ij}\left(k\right)\right]}^{\beta }}{{\sum }_{s\in alowe{d}_m}\left[{\tau }_{is}\left(k\right)\right]{\left[{\eta }_{is}\left(k\right)\right]}^{\beta }}}\hfill & j\in allowe{d}_m\\ 0\hfill & other\end{array}\right.$$

(2)

In Equation (2), the pheromone concentration between nodes i and j in iteration k is denoted by ${\tau }_{ij}\left(k\right)$. The ant’s current path node is denoted by s. This indicates the nodes to which ant m may transition as their next visited node. $\alpha$ denotes the significance of the pheromone. $\beta$ signifies the significance of the heuristic element. ${\eta }_{ij}\left(k\right)$ represents the heuristic information. $d_{ij}$ is the distance from node i to node j.

$${\eta }_{ij}={\displaystyle \frac{1}{d_{ij}}}$$

(3)

In Equation (3), $d_{ij}$ represents the Euclidean distance between nodes i and j.

2.3.2. Pheromone Update Strategy

To prevent the ant colony algorithm from being stuck in the local optimal state and to reduce excessive pheromone concentration on certain paths, a pheromone evaporation technique is used. During each round, the pheromone is perpetually changed, allowing successive ants to demonstrate enhanced search efficacy. Equations (4)–(6) describe the pheromone updating method as follows:

$${\tau }_{ij}\left(k+1\right)=\left(1-\rho \right){\tau }_{ij}\left(k\right)+\sum _{m=1}^M\Delta {\tau }_{ij}^m\left(k\right)$$

(4)

$$\Delta {\tau }_{ij}^m\left(k\right)={\displaystyle \frac{Q}{L_m}},\mathrm{if}\mathrm{ant}\mathrm{m}\mathrm{passes}\mathrm{through}\mathrm{path}ij$$

(5)

$$\Delta {\tau }_{ij}^m\left(k\right)=0,\mathrm{if}\mathrm{ant}\mathrm{m}\mathrm{does}\mathrm{not}\mathrm{pass}\mathrm{through}\mathrm{path}ij$$

(6)

where the pheromone evaporation factor is denoted by $\rho$. Iteration k’s pheromone level from node i to node j is denoted as ${\tau }_{ij}\left(k\right)$. The total number of ants is denoted by the letter M in iteration k. ${\tau }_{ij}^m\left(k\right)$ is the increment of pheromone deposited by ant m from node i to node j in iteration k. Q denotes the intensity of the pheromone. The value of $L_m$ is a representation of the complete length of the route that ant m has traveled during this iteration.

3. Improved Ant Colony Algorithm

3.1. Improved Heuristic Information

Heuristic information is usually computed as the inverse of the Euclidean distance between two nodes in traditional ant colony methods. This paper, according to Equation (7), suggests an alteration to the traditional heuristic information computation by using the current grid as a reference and integrating the squared distance between the original grid and the goal grid. By decreasing the search area, this change successfully guides ants toward the target spot. The weights of the heuristic information are dynamically adjusted through Equation (8). By giving greater weight to the heuristic information through larger values of $\phi$ in the early iterations of the algorithm, the algorithm’s ability to determine the shortest path can be improved and the search efficiency can be significantly increased. In order to improve the efficiency of the algorithm to perform global search, the value of $\phi$ is gradually reduced, and thus the heuristic information decreases in the final stage. This dynamic adjustment mechanism allows the algorithm to balance the ability to perform global and local searches at different stages, thus improving overall performance. For the purpose of computing heuristic information, the improved versions of Equations (7) and (8) are as follows:

$${\eta }_{\mathrm{ij}}=\phi {\displaystyle \frac{1}{{\left(d_{ij}+d_{jg}\right)}^2}}$$

(7)

$$\phi =w\left[{\displaystyle \frac{e^{-\left(\frac{k}{K}\right)}}{{\left(1+e^{-\left(\frac{k}{K}\right)}\right)}^2}}\right]$$

(8)

The distance between the ith and jth grids is denoted by $d_{ij}$. The distance between the target grid g and the jth grid is denoted by $d_{jg}$. The derivative of the sigmoid function after transformation is denoted by $\phi$. The total number of iterations is denoted by K. w is a parameter.

3.2. The Pheromone Evaporation Factor

In traditional ant colony algorithms, the pheromone serves as a key factor in path selection and is often treated as a fixed value. But it cannot adapt to changes in the ants’ iteration cycles. The accumulation of pheromones on suboptimal paths may result in local optima, hindering the discovery of the global optimal path. In this paper, we propose an improved dynamic pheromone volatilisation formula based on reference [18], which uses the $Tanh$ function to extend the evaporation coefficients. Consequently, it can be ensured that the pheromone’s guiding effect is optimized across the initial, intermediate, and final stages of the algorithm. This approach prevents excessive pheromone accumulation on various paths during iterations, reducing the risk of converging to local optima. As a consequence, it improves the effectiveness of the algorithm’s global search. In order to determine the increased pheromone fluctuation factor, Equation $\left(9\right)$ is as follows:

$${\rho }_{dy}={\displaystyle \frac{1}{1+e^{-t\left(\frac{k}{K}\right)}}}$$

(9)

The dynamic pheromone fluctuation factor is represented by ${\rho }_{dy}$. And the enhanced Tanh function’s parameter is indicated by t. The total number of iterations is denoted by K. The current iteration number is k.

3.3. Pheromone Update Strategy

Because the pheromone on the paths traversed in a cycle changes at the end of each cycle in the classic ACO algorithm, ants can make unnecessary turns in the beginning. Nonetheless, the pheromone update mechanism in ACO systems alters pheromone levels on both the primary and secondary pathways. This may disrupt the following ant colony path selection process and perhaps lead the ACO algorithm to settle on a local optimum. The pheromone supplied by previous ants influences the ants’ selection of the next node in the current iteration. If the acquired path is suboptimal, it may cause successive ants to diverge more from the ideal path. This research utilizes the paths established by elite ants and integrates pheromone intensity into the global update mechanism, hence enhancing the algorithm’s convergence rate. At the same time, the introduction of the historical optimal path length can improve the ability of the algorithm to dynamically adapt to the environment. When the current path length $L^{*}\left(i\right)$ is close to $L_{global-best}$, the pheromone strength increases to encourage the ants to choose shorter paths; when $L^{*}\left(i\right)$ is significantly larger than $L_{global-best}$, the pheromone strength decreases to avoid converging to the sub-optimal path prematurely. The updated global pheromone update Equations (10) and (11) with improvements are as follows:

$${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\sum _{k=1}^m\Delta {\tau }_{ij}^k\left(t\right)+q\left(t\right)$$

(10)

$$q\left(t\right)=\left\{\begin{array}{cc}Q{\displaystyle \frac{K{L}_{global-best}}{k{L}^{*}\left(i\right)}}\hfill & L^{*}\left(i\right)=min\left(L\right)\\ 0\hfill & other\end{array}\right.$$

(11)

where m is the total quantity of ants. Q represents the pheromone concentration of the ants. K and k represent the maximum iteration count and the current iteration count, respectively. The optimal route length for the current iteration is denoted by $min\left(L\right)$. The path length of the ith elite ant is indicated by $L^{*}\left(i\right)$. $L_{global-best}$ is the historically optimal path length.

The ant colony algorithm utilizes pheromone updates to modify the appeal of pathways, directing ants towards the ideal solution. In this paper, ants are categorized based on the shortest and longest paths after each iteration. Local pheromone updates are then applied using Equations (12)–(14) to enhance the guiding effect of the shortest path.

$$\Delta {\tau }_{ij}^k\left(t\right)=\left\{\begin{array}{cc}\Delta {\tau }^{best}-\Delta {\tau }^{worst}\hfill & j\in allowe{d}_i\\ 0\hfill & otherwise\end{array}\right.$$

(12)

$$\Delta {\tau }^{best}=\begin{array}{cc}{\displaystyle \frac{Q_1}{L_{best}}},& Q_1=\theta Q\end{array}$$

(13)

$$\Delta {\tau }^{worst}=\begin{array}{cc}{\displaystyle \frac{Q_2}{L_{worst}}},& Q_2={\displaystyle \frac{Q}{\varsigma }}\end{array}$$

(14)

where $\Delta {\tau }^{best}$ and $\Delta {\tau }^{best}$ are the pheromone increments of the optimal and worst paths in the current iteration, respectively. $L_{best}$ and $L_{worst}$ indicate the lengths of the two paths, whereas $\theta$ denotes the parameters, respectively. $Q_1$ and $Q_2$ represent the pheromone intensities of the two types of ants.

3.4. Pheromone Diffusion Mechanism

In the majority of current ACO algorithms, pheromone is only deposited on the paths used by ants. Consequently, ants can perceive this information only when they are sufficiently close to existing paths, increasing the likelihood of falling into local optima. To address this issue, some studies propose that pheromones deposited by ants can diffuse to adjacent grids. This paper introduces a novel pheromone diffusion model. As illustrated in Figure 3, the proposed model is a unit-based pheromone diffusion model. In this model, the pheromone intensity is defined as follows: At the ant’s current position, it is denoted as a; at the adjacent grid, as b; and at the outer layer, as c. Thus, the new pheromone diffusion gradient Equation (15) is designed as follows:

$$\mathrm{\Phi }\left(r,r_0\right)=\left\{\begin{array}{cc}a\hfill & R\left(r,r_0\right)=0\\ b\hfill & {\displaystyle \frac{\sqrt{2}}{2}}\le R\le {\displaystyle \frac{3}{2}}\\ c\hfill & R\left(r,r_0\right)>{\displaystyle \frac{3}{2}}\end{array}\right.$$

(15)

where $r_0$ is the grid where the ant is located. a, b, and c represent the current pheromone intensities.

Figure 4 illustrates the process diagram of the improved ACO.

4. Path Smoothing

This paper presents a solution that combines a collision avoidance mechanism with B-spline curves to satisfy the kinematic restrictions of mobile robots and address the problem of discontinuous route curvature. The collision avoidance mechanism addresses the dead-end problem in the ant colony algorithm, preventing mobile robots from colliding with obstacles in practical scenarios. Additionally, when using the ant colony algorithm to generate paths for mobile robots, the curvature at path waypoints is often discontinuous, negatively impacting the robot’s movement. This paper utilizes B-spline curves to smooth the path and incorporates a control point adjustment formula based on the distance between control points and obstacle centers. This adjustment ensures that the generated path satisfies the robot’s kinematic constraints in practical scenarios.

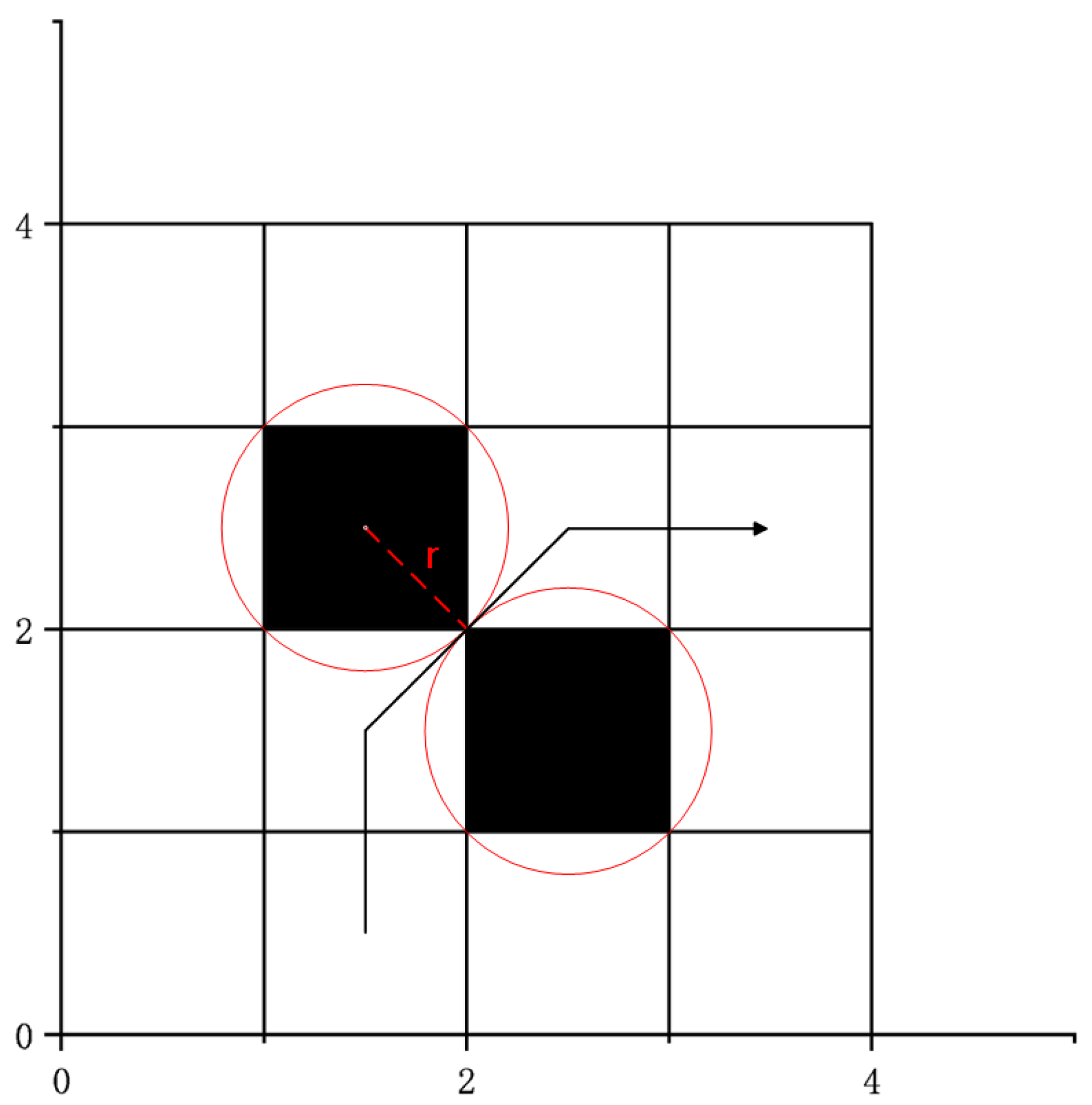
4.1. Anti-Collision

Figure 5 indicates that two obstacle vertices are often connected when the ant colony method is used for path planning on a grid map. If the planned path crosses the connection between these obstacle vertices, it may cause a collision between the robot’s moving frame and the obstacles, rendering it unsuitable for real-world applications. Therefore, considering the actual distance $d_i$ between grid nodes and obstacles and its relationship with the safety distance D, this paper introduces a collision avoidance mechanism for the robot. In order to ascertain whether or not the way is safe, the distance between the obstacle center and the path is taken into consideration. For example, connecting nodes A and B form segment $AB$, and the distance $OD$ ($d_i$) between segment $AB$ and obstacle point O is evaluated. If $d_i\le D$, the alternative option is eliminated. Figure 6 illustrates a schematic representation of the collision avoidance method. Here, the obstruction’s radius is indicated by r. L is the distance between $OE$, and $d_i$ is the distance between the path $AB$ and the obstacle’s center O. The distance $d_i$ from obstacle point O to path $AB$ is calculated using Equations (16)–(18) as follows:

$$L=\left|y_c-\left[\left({\displaystyle \frac{y_a-y_b}{x_a-x_b}}\right)\left(x_c-x_b\right)+y_a\right]\right|$$

(16)

$$\theta =\left|arctan{\displaystyle \frac{y_a-y_b}{x_a-x_b}}\right|$$

(17)

$$d_i=Lcos\alpha$$

(18)

In Equations (16)–(18), $\theta$ is the angle between segment $AB$ and the line mapped to the horizontal axis by segment $AB$. One can determine the safety distance D ($D>r$) for anti-collision, and the evaluative connection between distance $d_i$ and safety distance d as follows:

(1)

If $d_i\le D$, the path is ignored;

(2)

If $d_i\ge D$, the path is selected.

4.2. B-Spline Smoothing Path

This study utilizes a grid map as the habitat for the ant colony method. The path planning lines produced by the enhanced ant colony algorithm often display spikes at inflection points. In such cases, the path curvature becomes discontinuous, violating the robot’s kinematic constraints. B-spline curves [38] are employed for path optimization. Such curves offer advantages such as simple parameterization, local modification, and convexity. The cubic quasi-uniform B-spline curve is often used to make sure that the best path goes through both the starting point and the end point while staying smooth and continuous. The B-spline curve is defined in Equation (19). When $k=3$, it becomes a cubic quasi-uniform B-spline curve, as defined in Equation (20).

$$C\left(t\right)=\sum _{i=0}^n{N}_{i,k}\left(t\right)P_i$$

(19)

$$C\left(t\right)=\sum _{i=0}^n{N}_{i,3}\left(t\right)P_i$$

(20)

where $C\left(t\right)$ is the generated curve, $P_i$ is the control point, the B-spline’s basis function is $N_{i,k}\left(t\right)$, and k is the degree. The basis function $N_{i,3}$ is calculated by using a recursive formula. For the cubic basis function, the recursive Equations (21)–(22) are as follows:

$$N_{i,0}\left(t\right)=\left\{\begin{array}{cc}1\hfill & u_i\le t\le u_{i+1}\\ 0\hfill & otherwise\end{array}\right.$$

(21)

$$N_{i,k}\left(t\right)={\displaystyle \frac{t-u_i}{u_{i+k}-u_i}}{N}_{i,k-1}\left(t\right)+{\displaystyle \frac{u_{i+k+1}-t}{u_{i+k+1}-u_{i+1}}}{N}_{i+1,k-1}\left(t\right)$$

(22)

where $u=[u_0,u_1,u_2,\cdots u_m]$ is the node vector. Therefore, when $k=3$, the Equation (23) of cubic B-spline curve is as follows:

$$\left\{\begin{array}{c}{C}_{0,3}\left(t\right)={\displaystyle \frac{1}{6}}\left(-t^3+3t^2-3t+1\right)\\ C_{1,3}\left(t\right)={\displaystyle \frac{1}{6}}\left(3t^3-6t^2+4\right)\\ C_{2,3}\left(t\right)={\displaystyle \frac{1}{6}}\left(-3t^3+3t^2+3t+1\right)\\ C_{3,3}\left(t\right)={\displaystyle \frac{1}{6}}{t}^3\end{array}\right.$$

(23)

When a collision of the produced spline with an obstacle ($d_i\le D$) occurs, the control point must be modified to shift in the direction opposite to the impediment, thus guaranteeing the spline maintains a safe distance ($d_i>D$). The vector normalization Equations (24) and (25) from the control point $P_i$ ($x_i,y_i$) to the obstacle center point $O_j$ ($x_j,y_j$) are as follows:

$$\overrightarrow{v}=\left(x_i-x_j,y_i-y_j\right)$$

(24)

$$\widehat{v}={\displaystyle \frac{\overrightarrow{v}}{∥\overrightarrow{v}∥}}$$

(25)

Equation (26) of the control point movement is as follows:

$$P_i^{\prime }=P_i+\left(D-d_i+\epsilon \right)\widehat{v}$$

(26)

where $\epsilon$ is a small control quantity, which is used to ensure that the control point is far away from obstacles.

4.3. Steps for Path Smoothing

The following are the path smoothing steps using the anti-collision mechanism and B-spline curve:

Step 1: output preliminarily generated path points (discrete path point sequence);

Step 2: traverse each segment $AB$ of path nodes $\{P_0,P_1,\dots \dots ,P_n\}$;

Step 3: extract path key points (such as initial point, target point, inflection point) from the generated path as the control point set $\{P_0,P_1,\dots ,P_m\}$;

Step 4: set spline degree k to generate node vectors $[u_0,u_1,\dots ,u_m]$;

Step 5: traverse the parameter value t, recursively calculate the basis function $N_{i,k}\left(t\right)$, and calculate the smooth curve point $C\left(t\right)$;

Step 6: calculate the actual distance $d_i$ from the obstacle center O to the line segment $AB$. If $d_i\le d$, ignore the path, regenerate the path, and return to the first step. If $d_i>d$, the path is selected;

Step 7: output the smooth path points $\{C\left(t_0\right),C\left(t_1\right),\dots ,C\left(t_m\right)\}$.

In addition, the pseudocode on smoothing paths is on page 14:

Pseudocode of the path smoothing

1. Establish the initialization environment, and define the map size, starting point and ending point, obstacle position and safe distance;

2. Run the improved ant colony algorithm to generate the initial path;

3. For $i\in \left(0,n\right)$ do

4.  If Safe Path [i] is turning point

5.    Add Safe Path [i] to the control point set Control Points;

6.  End If

7. End For

8. For $t\in \left(u_0,u_m\right)$

9.  If $k=0$ then

10.    $N_{i,0}\left(t\right)=\left\{\begin{array}{cc}1\hfill & u_i\le t<u_{i+1}\hfill \\ 0\hfill & else\hfill \end{array}\right.$

11.  else

12.    $N_{i,k}\left(t\right)={\displaystyle \frac{t-u_i}{u_{i+k}-u_i}}{N}_{i,k-1}\left(t\right)+{\displaystyle \frac{u_{i+k+1}-t}{u_{i+k+1}-u_{i+1}}}{N}_{i+1,k-1}\left(t\right)$

13.  End If

14. End for

15. For each obstacle center point O, calculate the distance to the path do

16.  If $d_i\le D$ then

17.    Calculate the movement direction vector;                          $\widehat{v}={\displaystyle \frac{\overrightarrow{v}}{∥\overrightarrow{v}∥}}$

18.    Calculate the adjustment distance;                      $P_i^{\prime }=P_i+\left(D-d_i+\epsilon \right)\widehat{v}$

19.     Adjusted control points;                     $p_i^{\prime }=\left({x_i}^{\prime },{y_i}^{\prime }\right)$

20.  Else         Adjusted Control Points.Append $P_i=\left(x_i,y_i\right)$

21.  End If

22. End For

23. For $t\in \left(u_0,u_m\right)$

24.  Calculate smooth curve points;                      $C\left(t\right)={\displaystyle \sum _{i=0}^n}{N}_{i,k}\left(t\right)P_i$

25. End For

26. output smooth path

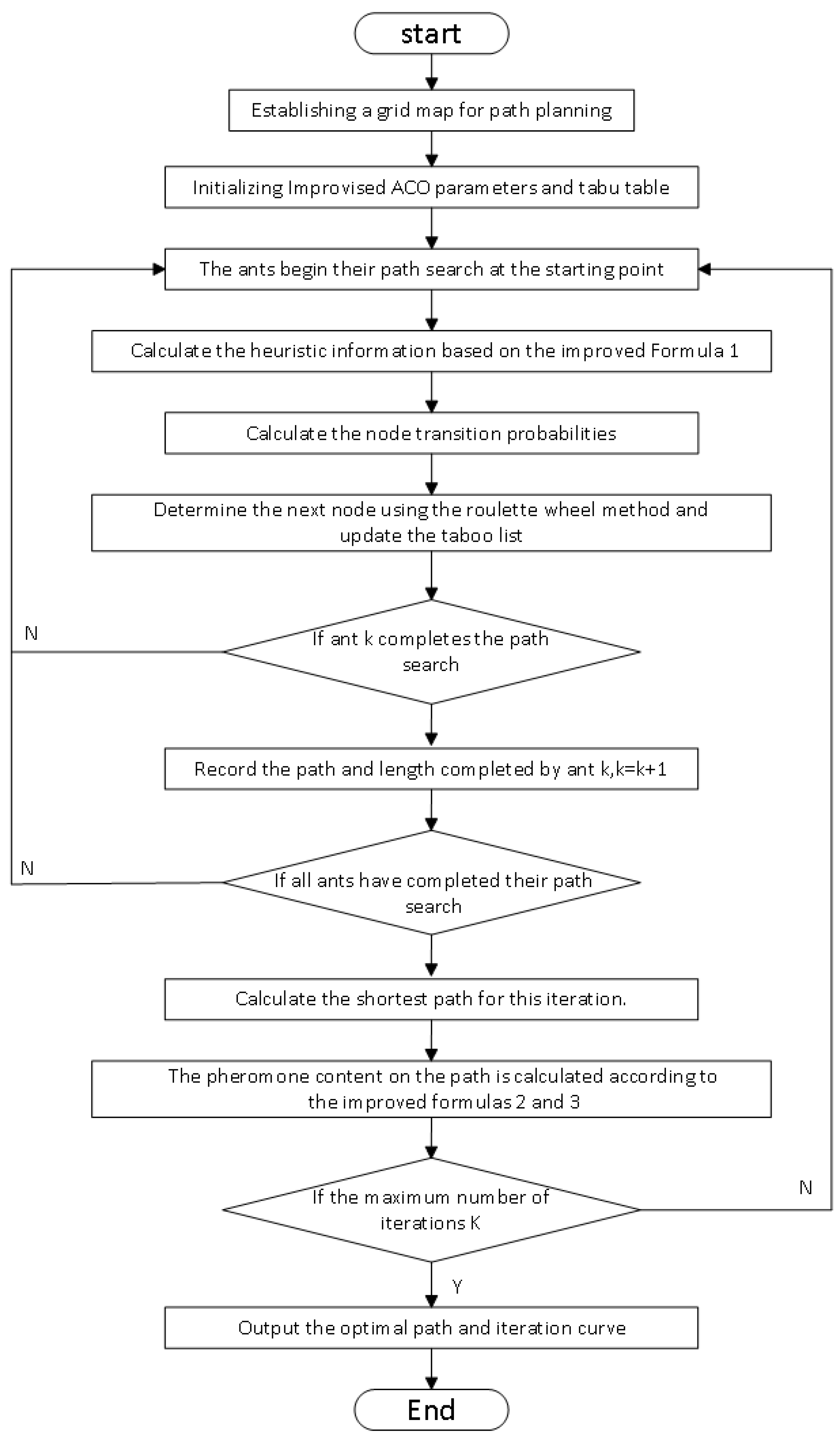
5. Overall Process of Improved-ACO

The Improved-ACO consists of three phases: environmental modeling, first route generation with an enhanced ant colony algorithm, and optimization of the initial path through a smoothing methodology. The overall process of the algorithm is as follows:

Step 1: The grid approach is used to generate the route planning map by partitioning the environment into grids, each represented by a coordinate. A value of 0 signifies an unoccupied region (white-filled), while 1 indicates an obstructed area (black-filled). For grid numbering, a correspondence is established between the grid serial numbers and their corresponding actual coordinates.

Step 2: For parameter initialization, set the optimum number of iterations $\left(K\right)$ and the number of ants $\left(M\right)$ so they are both defined. Initialize the pheromone matrix, and define the pheromone volatilization factor and the important heuristic factors $\alpha$ and $\beta$.

Step 3: Utilize the enhanced heuristic information formula by integrating the square of the distance between the current node and the destination node, while dynamically modifying the weight of the heuristic information.

Step 4: The ant starts at the origin, updates the path selection matrix, records the path length, and the state transition probability formula is used to determine which node will be the next one to be selected.

Step 5: Local update involves adjusting the pheromone level according to the path length to minimize redundant searches. The global update implements a sophisticated ant method to augment pheromone levels along the ideal path, and a dynamic pheromone volatilization factor is employed to prevent local optimization.

Step 6: Use a cubic B-spline curve for route optimization after extracting important points from the path produced by the ant colony method, such as the start point, inflection point, and terminus.

Step 7: If the generated spline conflicts with an obstacle (where $d_i\le D$), adjust the control point by moving it away from the obstacle until $d_i>D$.

Step 8: Output the generated path and end the algorithm.

6. Simulation Experiment and Comparative Analysis

In this section, a simulation environment is developed using $MATLABR2022b$. The efficacy of path planning with the enhanced ant colony algorithm is validated, and its performance contrasted with other methods.

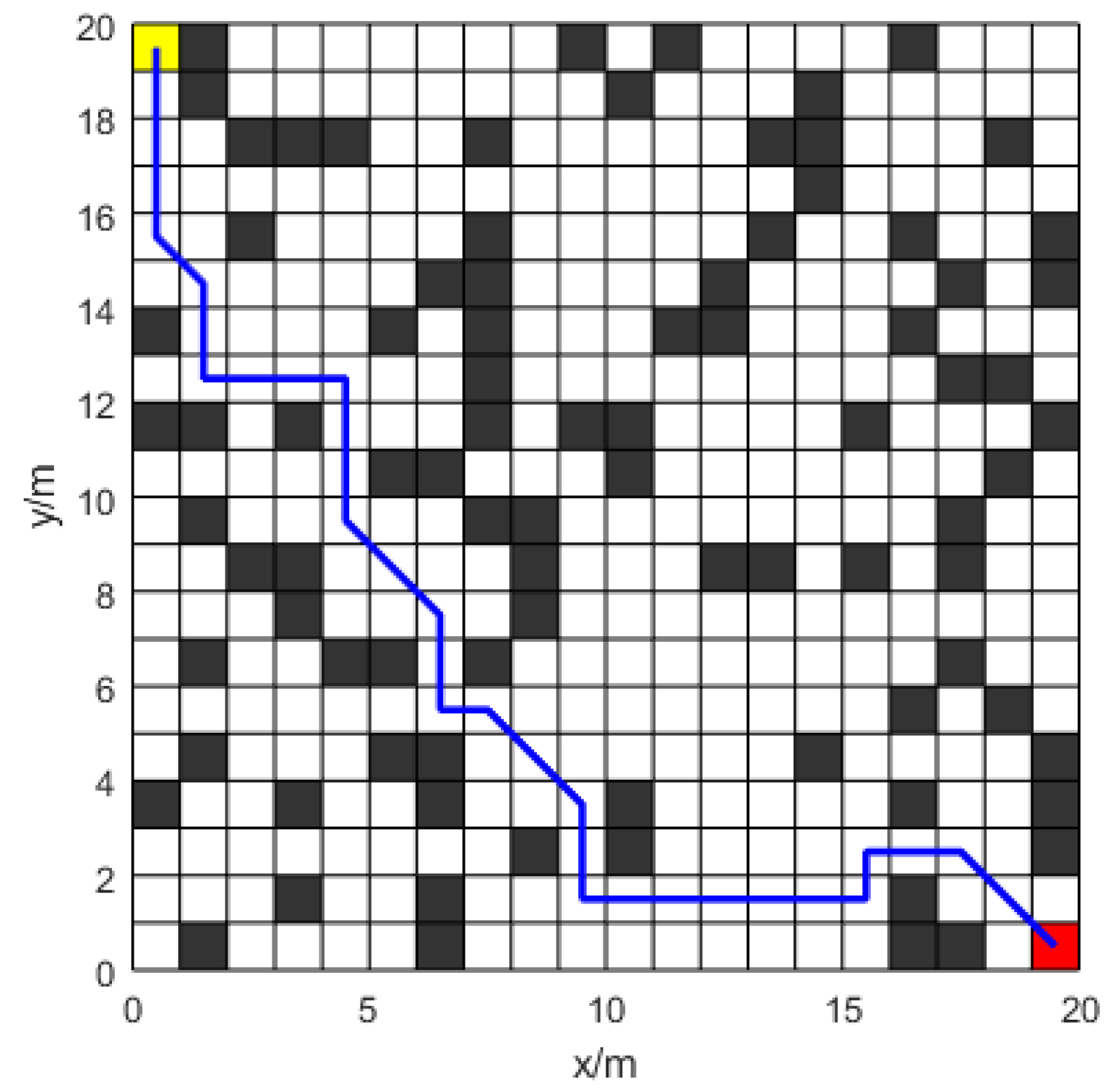
The grid map is defined with sizes of $20\times 20$, $30\times 30$, and $31\times 31$, with each grid cell measuring $1m$. The traversable area is represented by white grids and obstacles by black grids. A red grid indicates the terminal site, while a yellow grid indicates the starting node.

Parameter initialization in the ant colony algorithm lacks theoretical foundations and is typically determined through empirical values, experimental comparisons, and literature references. To identify appropriate initialization parameters, key parameters of the improved ACO algorithm are evaluated through statistical tests and comparative experiments. In each experiment, only one parameter is varied while others are held constant to isolate its impact. The simulations were conducted for each parameter combination. The examination of the primary parameters in the enhanced ACO algorithm determines the ideal configuration: $M=50$, $K=100$, $\alpha =1$, $\beta =1$, $Q=5$, $w=2$, $t=1.5$, $\theta =2$, $\varsigma =2$, $a=1$, $b=0.5$, $c=0$.

6.1. Simulation Experiment 1

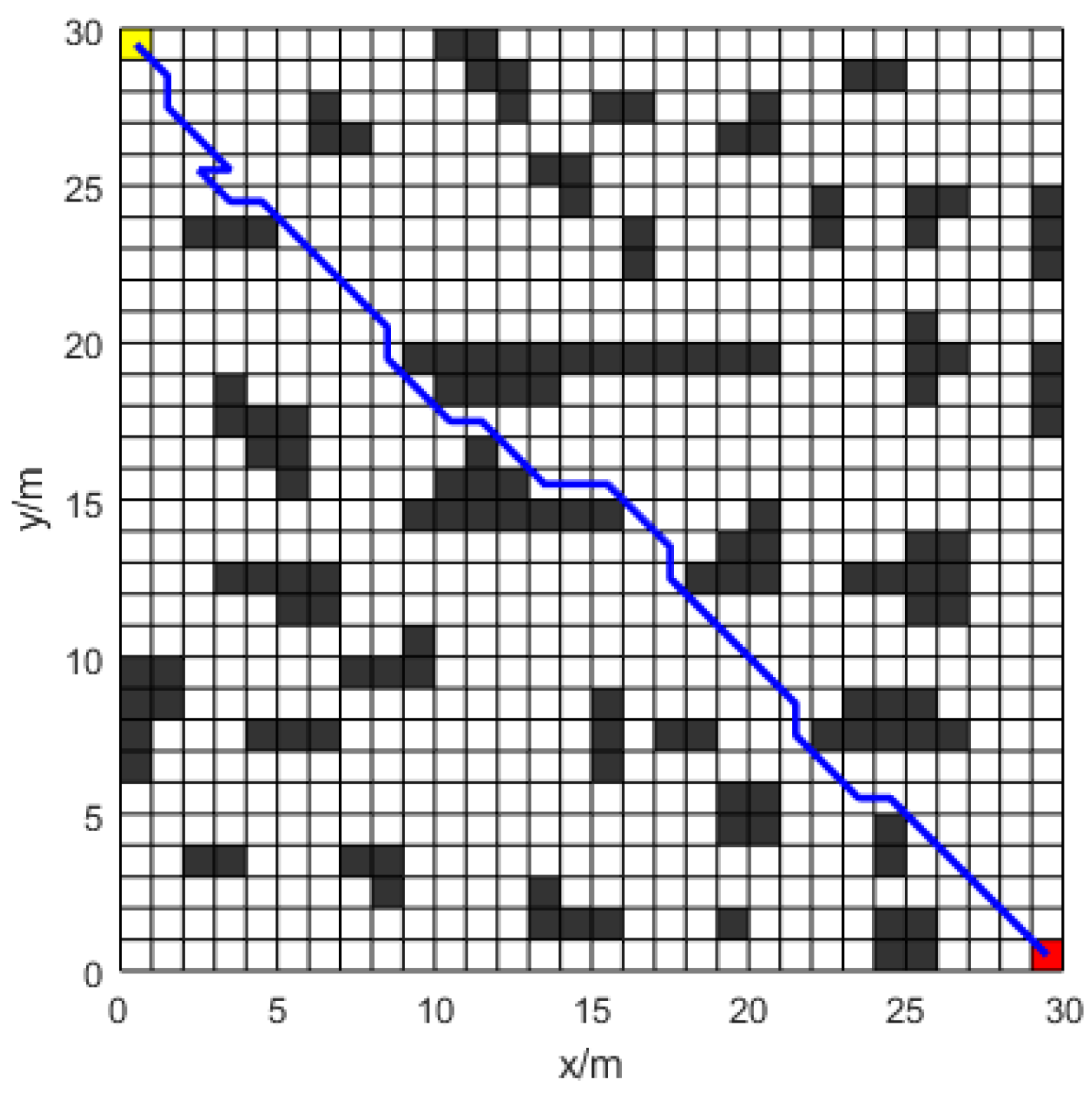
In simulation experiment 1, the Improved-ACO is evaluated against the standard ACO method, the A* algorithm, and Dijkstra’s algorithm. Each algorithm and its performance criteria are assessed on a $30\times 30$ grid map.

Table 1. Performance index of simulation experiment 1.

Algorithm	Iterations/Search Space	Length	Number of Turns	Smoothness (Average Curvature)
ACO	42 iterations	45.36	18	0.85
Dijkstra	762 nodes	43.08	8	0.92
A*	265 nodes	44.09	12	0.89
Improved-ACO	18 iterations	45.01	6	0.45

provides a summary of the performance metrics with regard to each algorithm:

As shown in Figure 7, Figure 8, Figure 9 and Figure 10, the paths generated by the unimproved ant colony algorithm exhibit cross-generation due to insufficient heuristic information, causing ants to wander in certain areas. The Dijkstra and A* algorithms prioritize shorter paths toward the target but often neglect obstacles, leading to more path turns. The Improved-ACO has a path length $4\%$ longer than Dijkstra’s algorithm and $2\%$ longer than the A* algorithm but achieves $25\%$ fewer turns than Dijkstra’s and $50\%$ fewer than the A* algorithm. Additionally, the anti-collision device maintains a safe distance between the mobile robot and obstructions, therefore averting collisions. Table 1 shows that the Dijkstra and A* algorithms require larger search spaces, whereas the Improved-ACO algorithm identifies near-optimal paths within smaller search spaces, demonstrating higher resource efficiency. The Improved-ACO algorithm demonstrates a reduction of $57.1\%$ in iterations and exhibits accelerated convergence relative to the traditional ACO method.

6.2. Simulation Experiment2

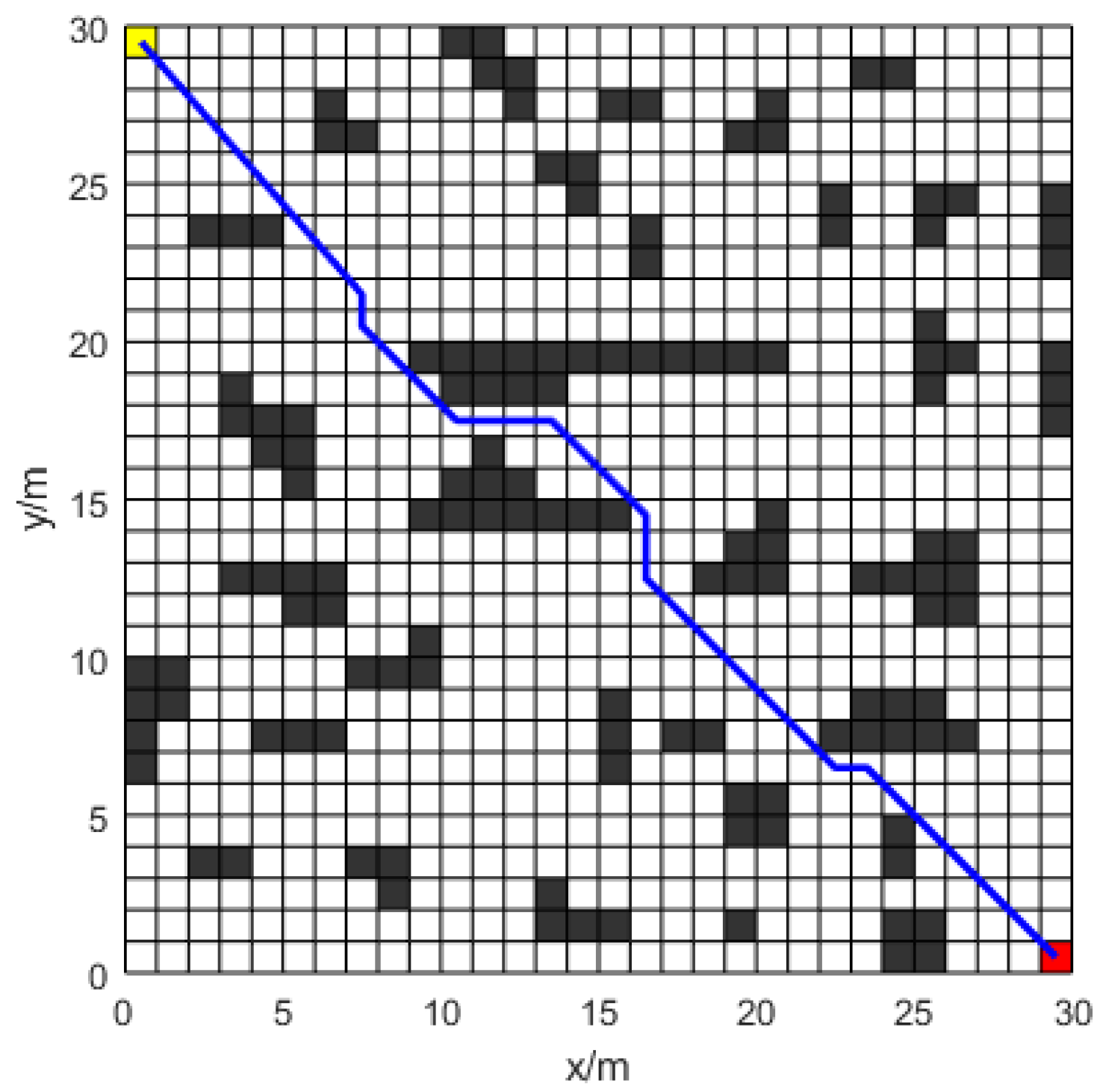
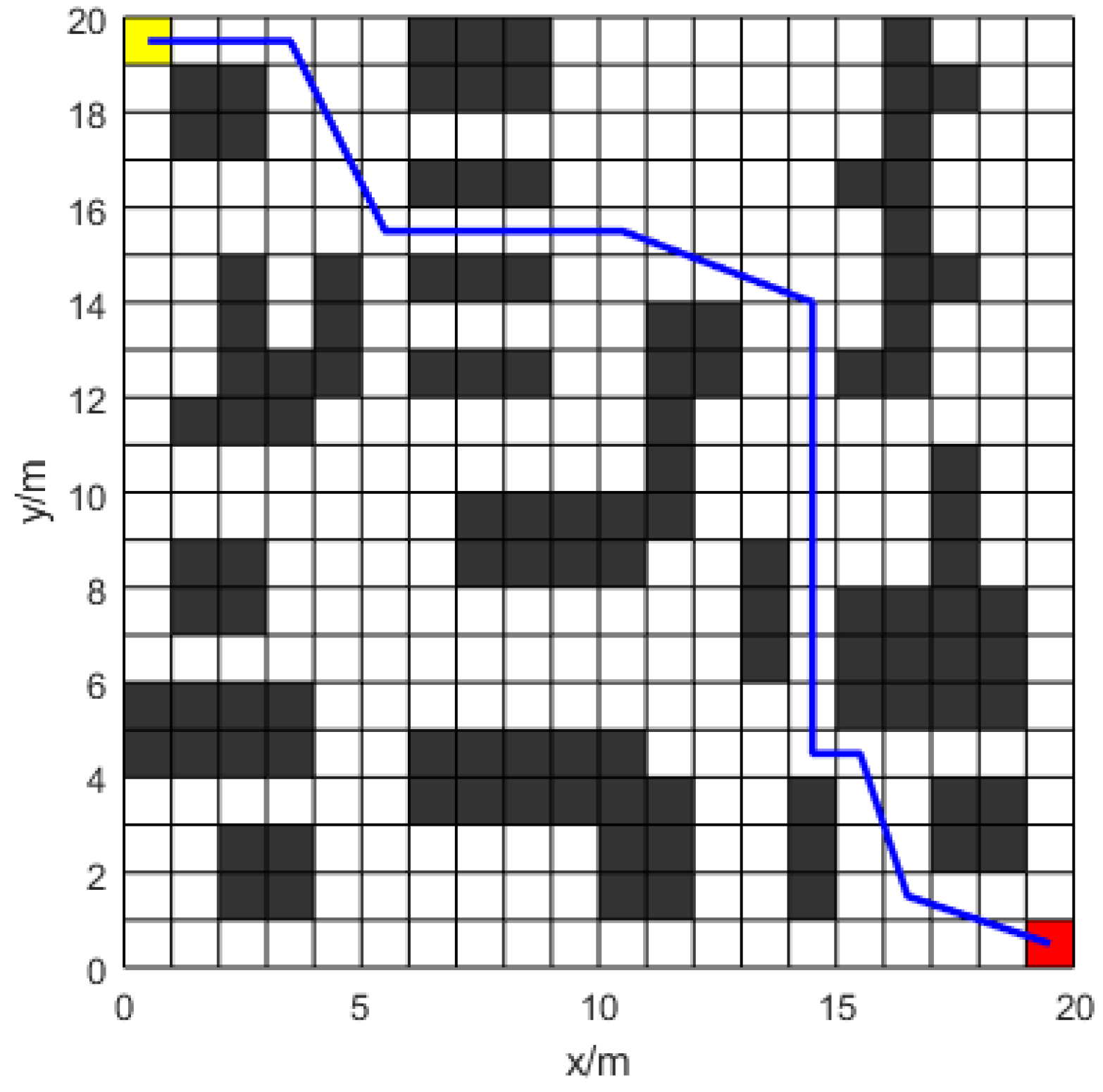
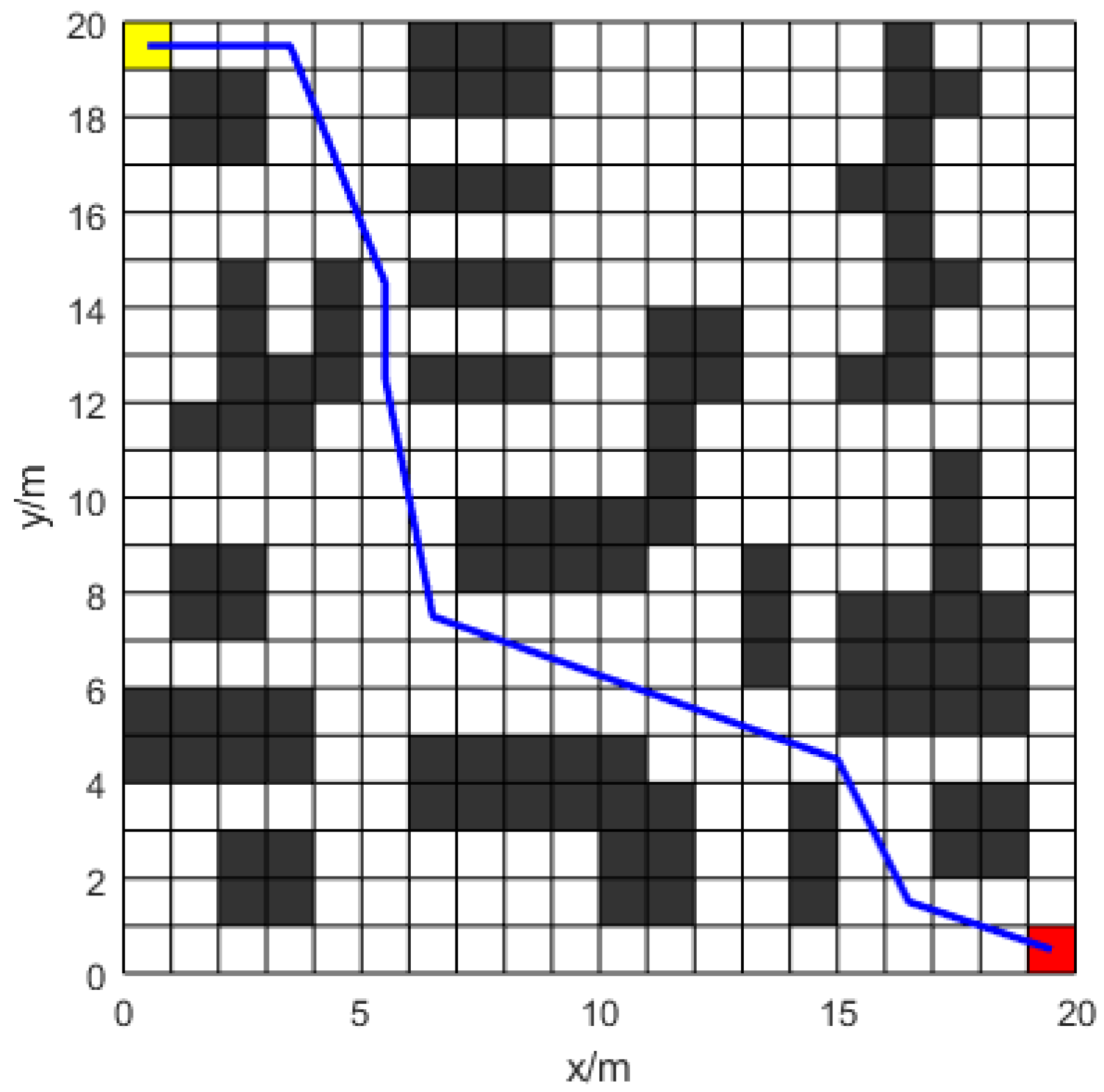
A $20\times 20$ grid map was used for a gradient comparison experiment. The gradient experiment seeks to evaluate the efficacy of the suggested enhancements, which are progressively integrated into the traditional ant colony algorithm. In experiment 1, improved heuristic information and an enhanced pheromone volatilization factor are incorporated to test for faster convergence and a broader search scope. In experiment 2, pheromone expansion rules and a diffusion mechanism are added to evaluate the pheromone’s ability to guide and identify the optimal path. Finally, the collision prevention mechanism and B-spline curve optimization are applied to identify an optimal path that satisfies the robot’s kinematic constraints. Each algorithm was executed 20 times.

Simulation experiments of the traditional ACO algorithm (Figure 11) show that the paths appear to be collapsed. Figure 12, Figure 13 and Figure 14 and

Table 2. Performance indicators of each optimization algorithm on different maps.

Maps	Features	Algorithm	Path Length	Turntimes	Iterations	Smoothness (Average Curvature)
		ACO	34.48	12	49	0.88
		Experiment 1	33.57	7	28	0.72
Map1	20*20	Experiment 2	31.73	6	18	0.68
		Experiment 2 after smoothing path	31.03	6	18	0.41
		ACO	28.62	10	40	0.85
Map2	20*20	ACO-PDG	35.89	13	22	0.78
		Improved-ACO	30.52	8	17	0.43
		ACO	45.36	15	53	0.91
Map3	31*31	ACO-PDG	54.14	25	18	0.82
		Improved-ACO	48.01	9	15	0.47

show that the generated paths neither cross nor fold. Experiment 1 demonstrates that introducing Equations (6)–(8) effectively guides ants to the target and avoids local optima. Experiment 2 indicates that the elite ant strategy in Equations (12) and (13) guides ants in finding better paths. Additionally, the pheromone diffusion mechanism enhances the elite ants’ guidance. The new pheromone update strategy minimizes redundant searches and enhances the algorithm’s global search capability in complex environments. Figure 14 shows that the smoothed path in experiment 2 improves smoothness while retaining short path advantages, meeting robot kinematic requirements. By incorporating path smoothing and safety distances, Improved-ACO effectively avoids obstacles and ensures robot path feasibility and safety. 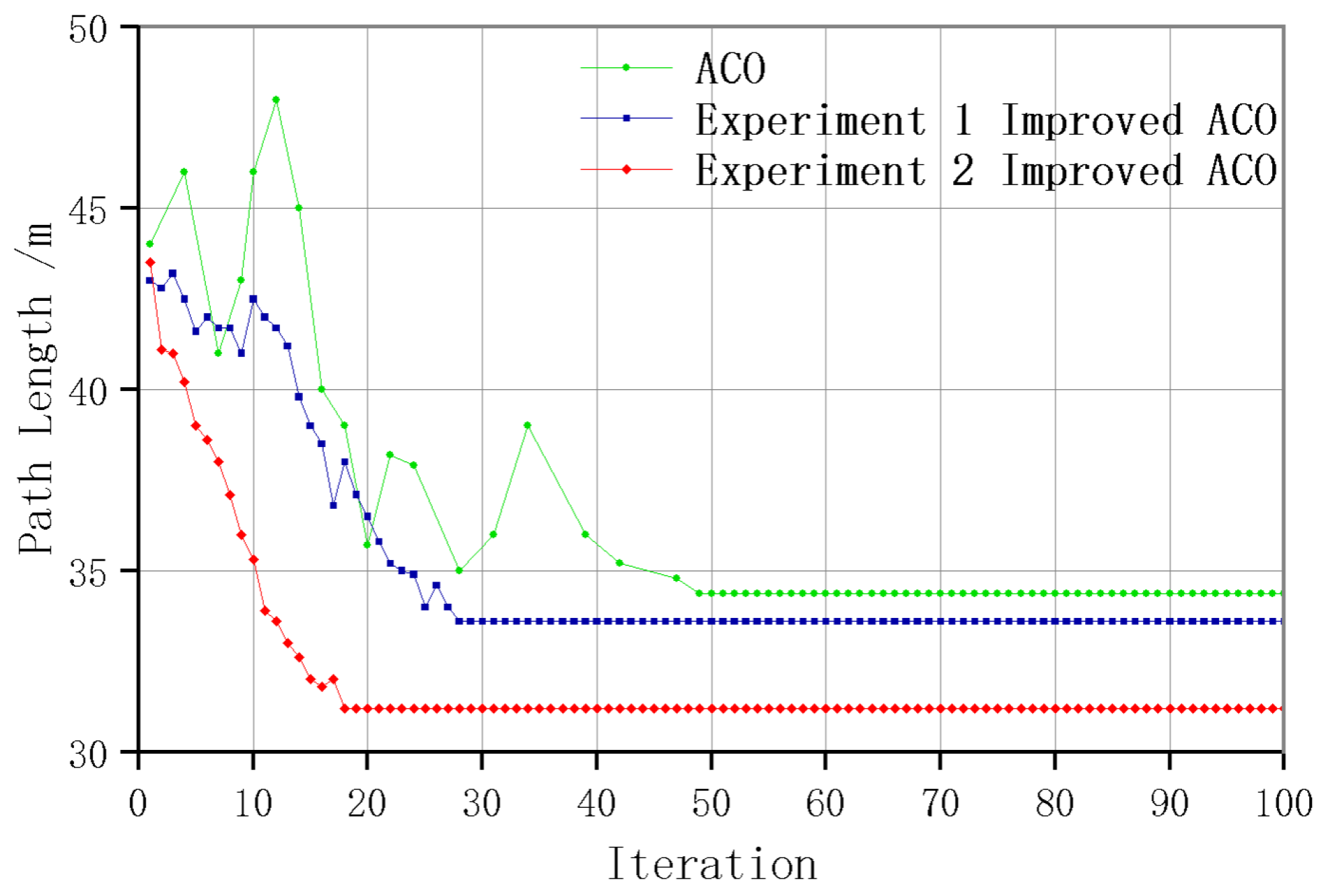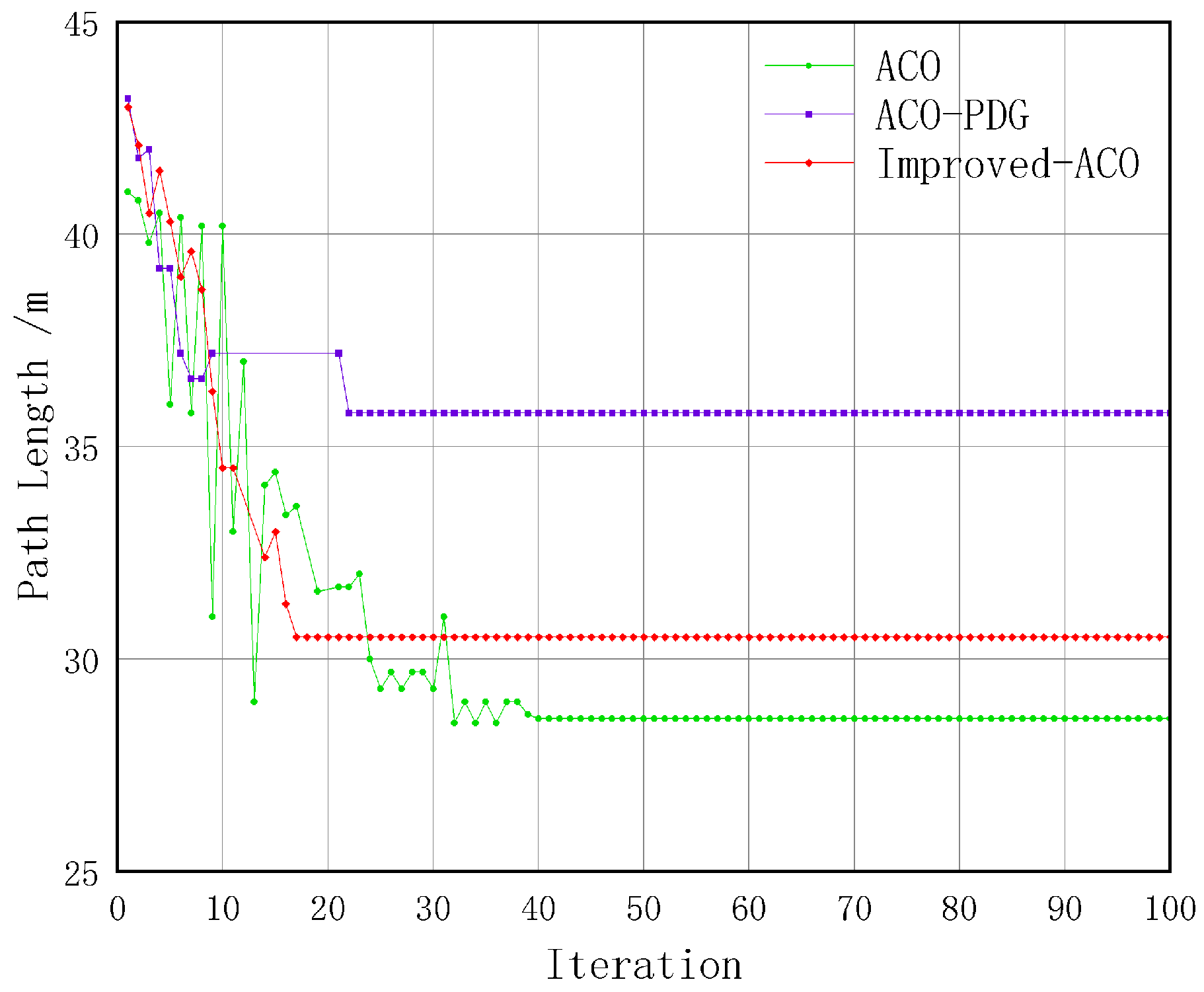Figure 15 illustrates the convergence outcomes of the methods. Table 2 indicates that experiment 1 achieves a path $2.6\%$ shorter than the traditional ACO algorithm. Experiment 2 reduces path length by $7.6\%$ compared to experiment 1, while smoothing increases the path length by $2.1\%$ but significantly enhances overall smoothness. Experiment 1 reduces iterations by approximately $42.9\%$ compared to the traditional ACO algorithm, while experiment 2 reduces iterations by $36\%$ compared to experiment 1. Experiment 1 reduces turns by $41.7\%$ compared to the traditional ACO algorithm, while experiment 2 achieves a $14\%$ reduction compared to experiment 1. Improved-ACO significantly improves path length, convergence rate, and smoothness in path planning.

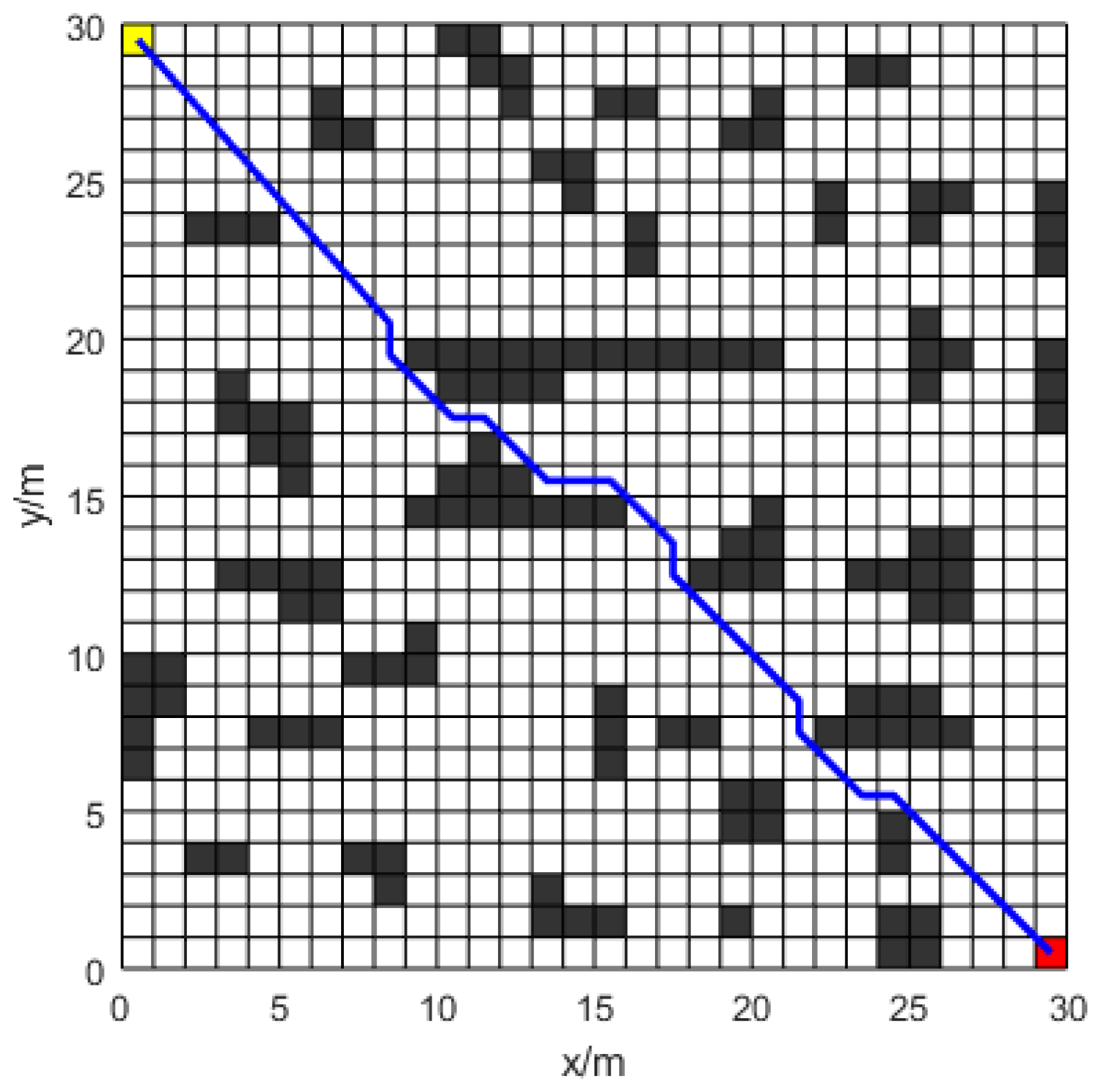
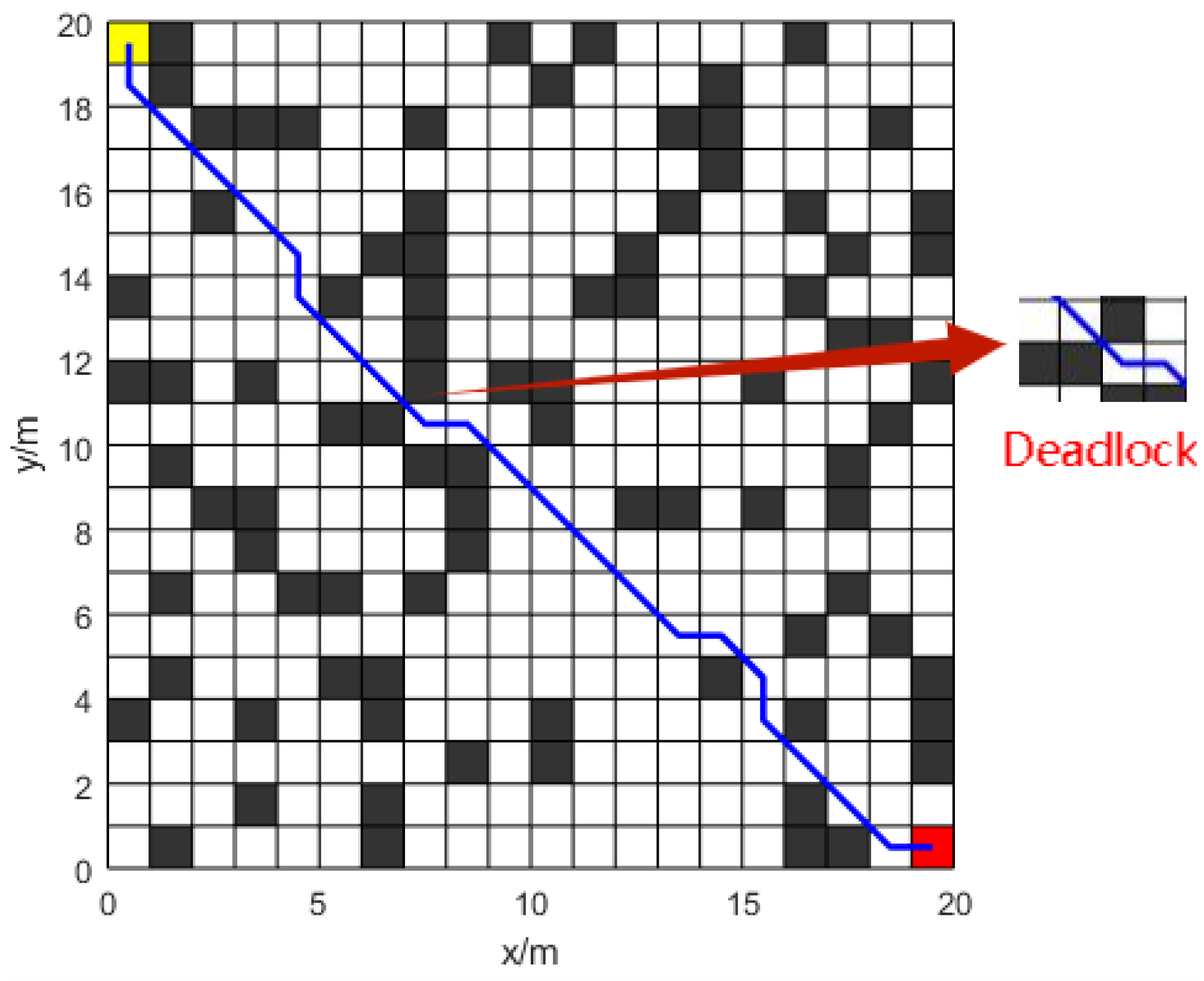
6.3. Simulation Experiment 3

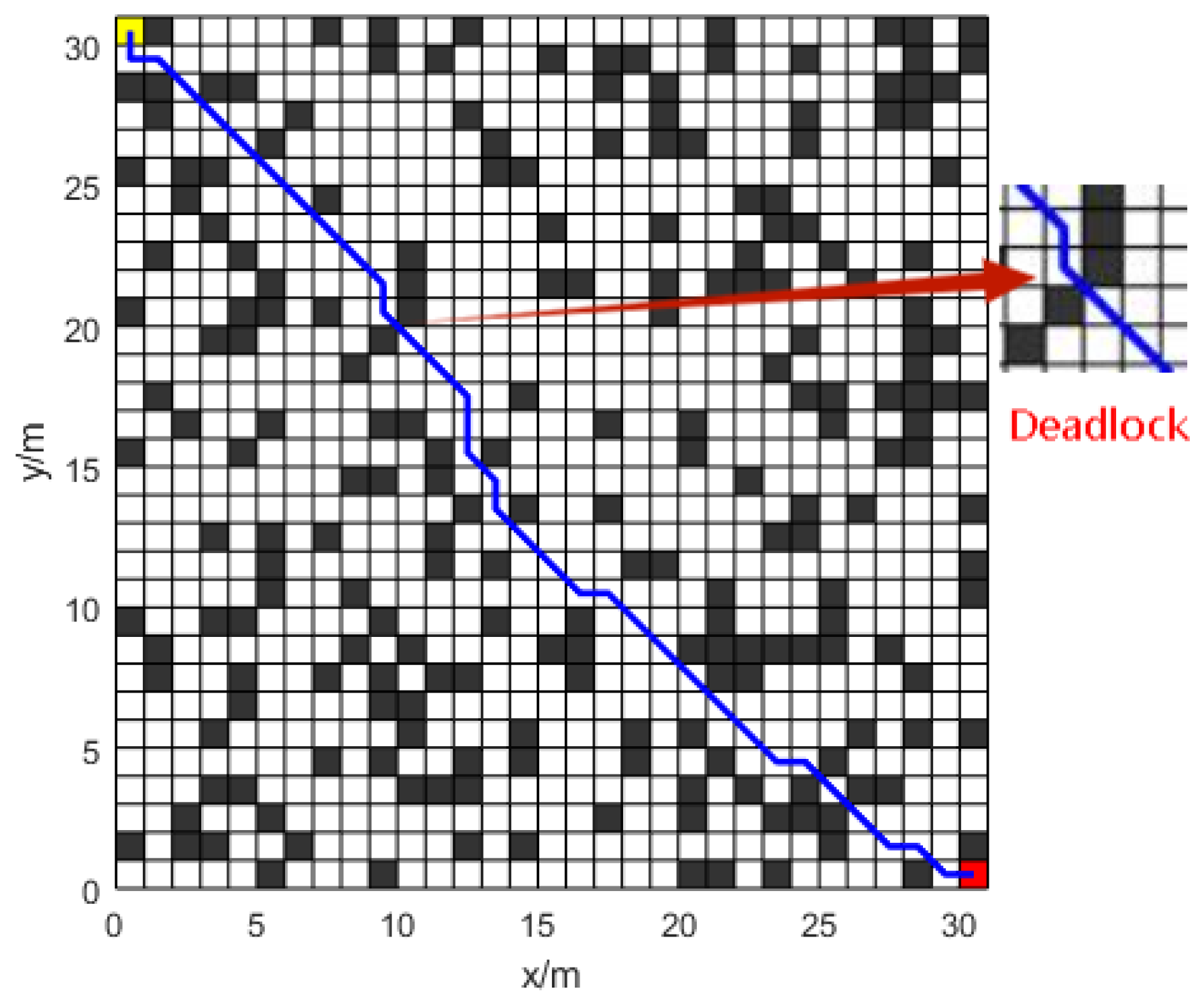
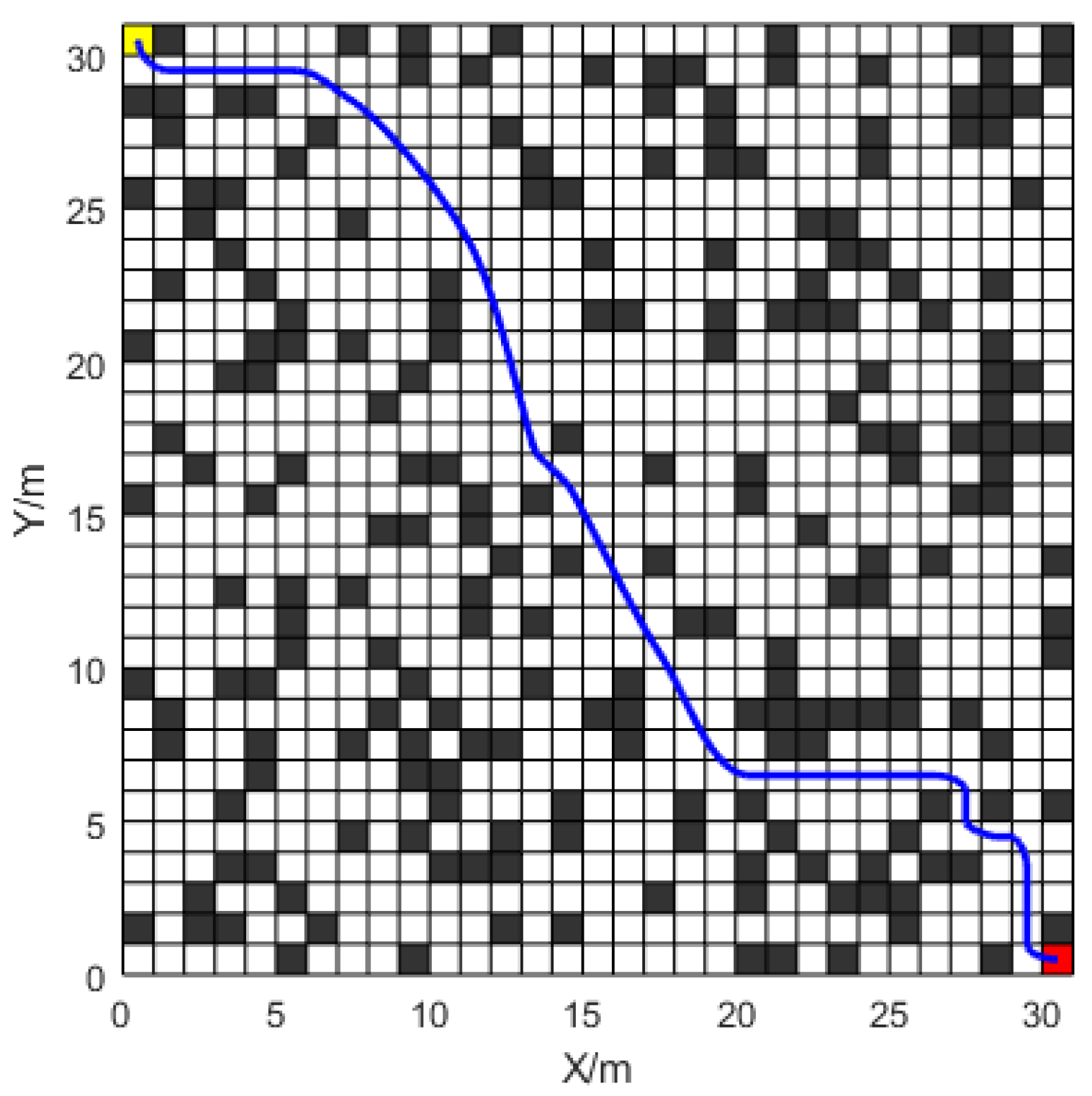
In simulation experiment 3, a $20\times 20$ grid map (map 2) is used. For ACO, ACO-PDG [39], and Improved-ACO, the initialization parameters are adjusted based on those proposed in this paper.

As shown in Figure 16, Figure 17 and Figure 18 and Table 2, the traditional ACO algorithm exhibits a deadlock phenomenon in simulation experiment 3. The ACO-PDG algorithm employs a non-uniform initial pheromone strategy to prevent ants from entering deadlock paths. This paper presents an enhanced ACO algorithm that integrates an anti-collision technique to prevent ants from traversing stalemate pathways. Regarding path length, the traditional ACO algorithm produces a path length of $28.62$ due to deadlock encounters. The Improved-ACO algorithm achieves a path length of $30.52$, approximately $15\%$ shorter than that of the ACO-PDG algorithm. 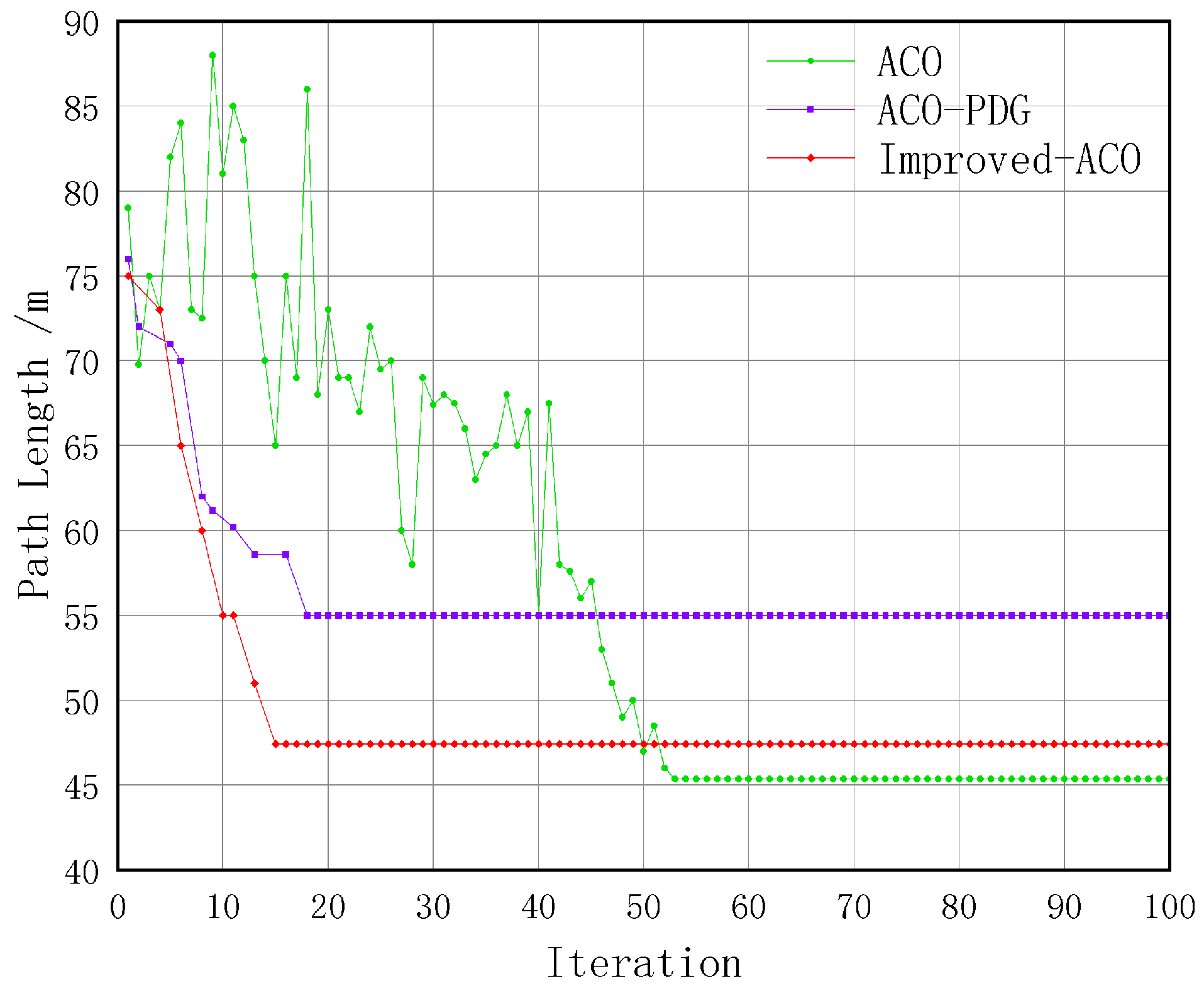The Improved-ACO algorithm, as shown in Figure 19, is able to lower the number of iterations by about $22.7\%$ when compared to the ACO-PDG framework. Regarding turning frequency, the Improved-ACO algorithm reduces turning instances by approximately $38.5\%$ compared to the ACO-PDG algorithm.

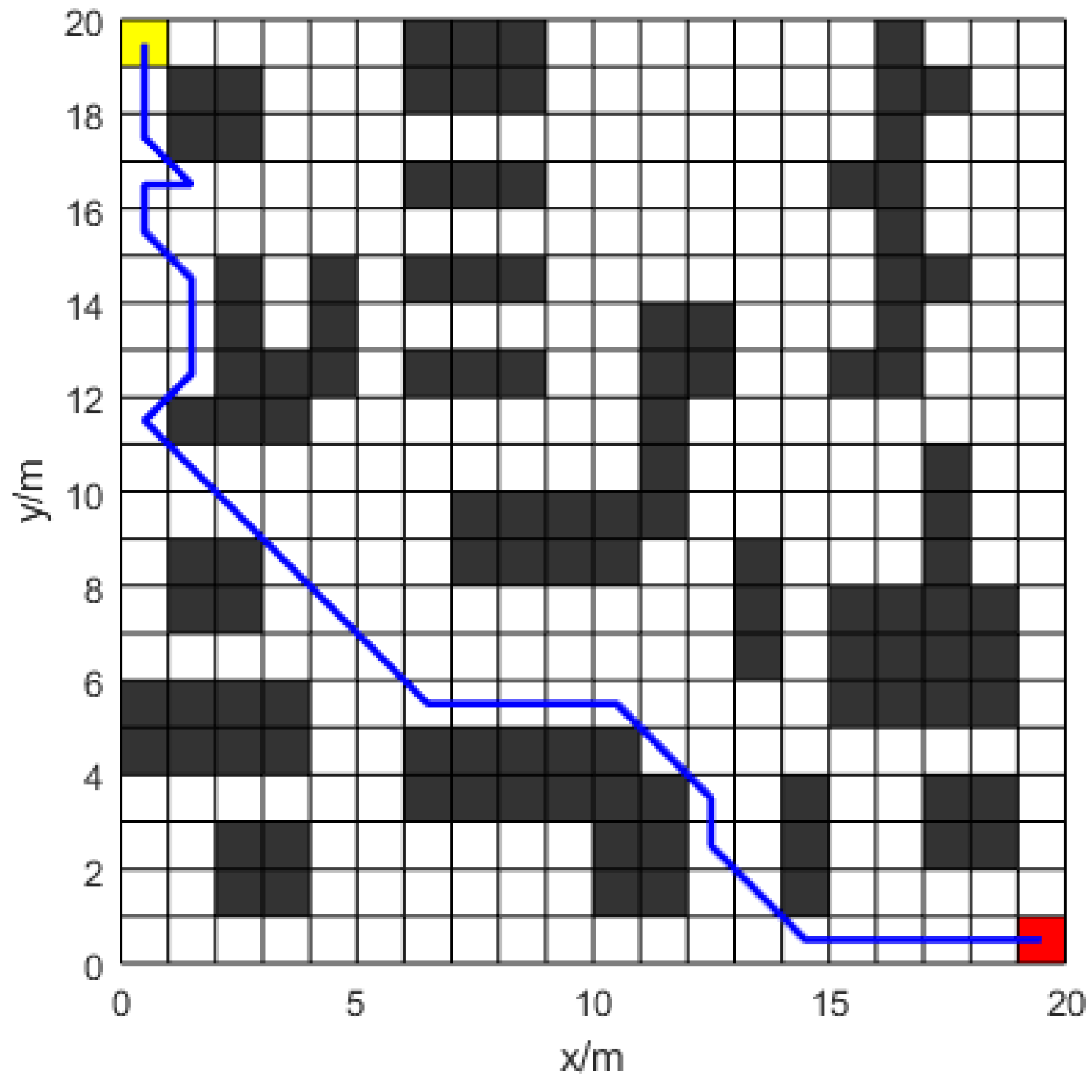
6.4. Simulation Experiment 4

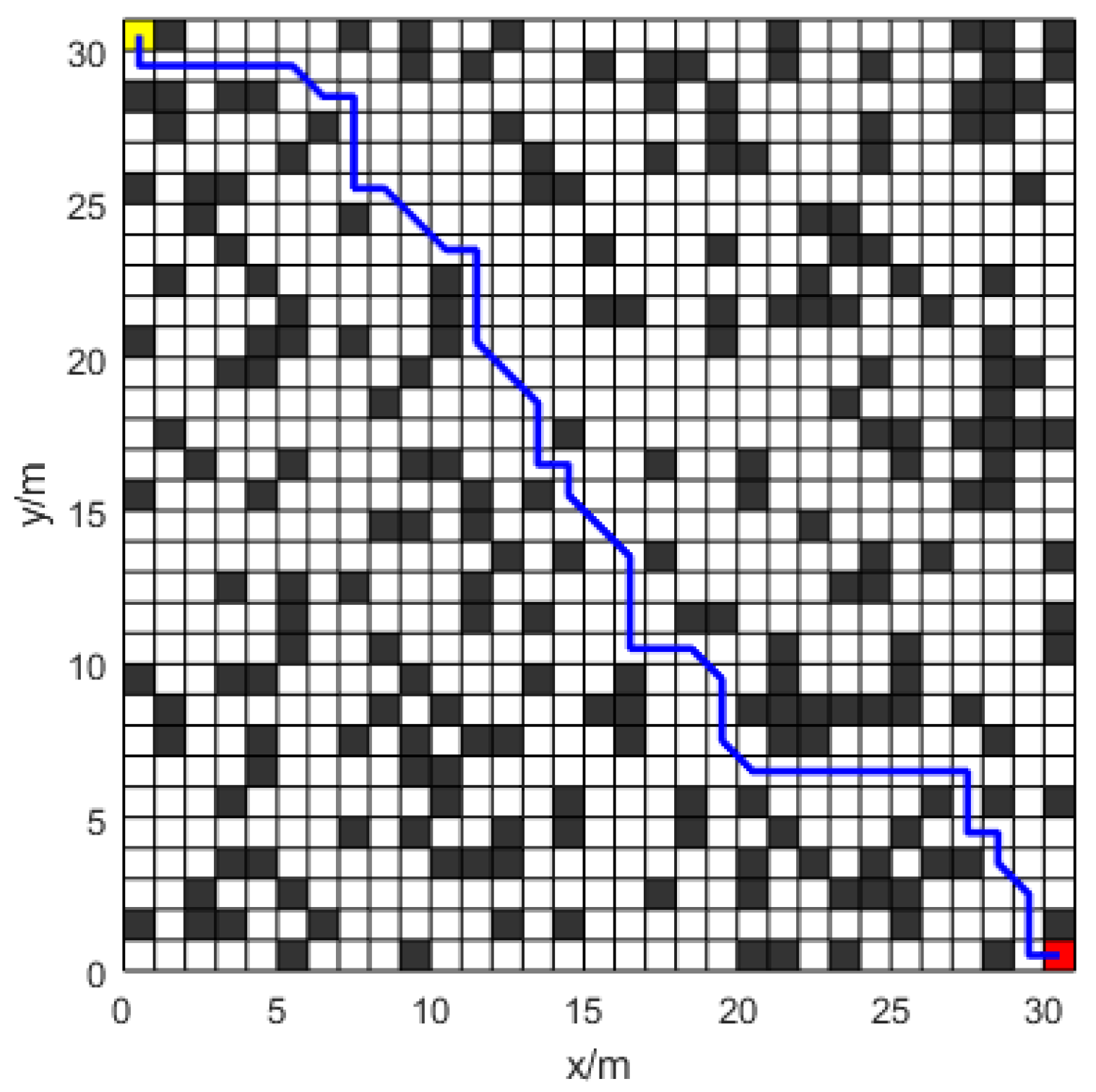
To achieve greater differentiation from the grid map in simulation experiment 1 and to account for the map’s complexity, a $31\times 31$ grid map, labeled map 3, was configured. A comparison is established between the performance of ACO, ACO-PDG, and the Improved-ACO algorithm.

When compared to the ACO-PDG technique, the significantly Improved-ACO algorithm reduces the path length by roughly $11.3\%$, as shown in Figure 20, Figure 21 and Figure 22 and Table 2. The Improved-ACO algorithm decreases the number of turns by $64\%$ relative to ACO-PDG in terms of turning frequency. Comparing the Improved-ACO algorithm to ACO-PDG, Figure 23 indicates that the former decreases the number of iterations by almost $17\%$.

The results indicate that Improved-ACO significantly enhances both the efficiency and performance of the path planning process. Compared to traditional algorithms, Improved-ACO reduces the average number of turns by $37.5\%$ and enhances convergence speed by $39.45\%$. Additionally, the path smoothing mechanism, which incorporates B-spline curves, ensures that the generated paths are both smooth and feasible for practical robot navigation. The experiments confirm that the Improved-ACO algorithm performs effectively across various map sizes and in complex environments, establishing it as a robust and adaptable solution for robotic navigation tasks.

7. Conclusions

This study first outlines the path planning ideas derived from the traditional ant colony optimization (ACO) technique. Next, the paper elucidates the Improved-ACO algorithm, which mitigates challenges such as sluggish convergence, early stagnation, and the tendency to get stuck in local optima, which are characteristic of the traditional ACO algorithm. The improved heuristic information and pheromone volatilization factor help ants converge more effectively towards the target point. Dynamic pheromone volatilization improves the utilization ratio of pheromones before and after the ant search. The pheromone updating strategy and diffusion mechanism enhance the attraction of the optimal path to ants, reduce redundant searches, and improve the algorithm’s global search capability in complex environments. Path smoothing, the anti-collision mechanism, and B-spline curves are then applied to prevent ants from walking into dead-end paths, ensure curvature continuity, and satisfy the robot’s kinematic limitations, improving the path’s smoothness. Finally, a simulation experiment is conducted using MATLAB. The simulation results show a $37.5\%$ reduction in the average number of turns compared to other traditional algorithms. Additionally, it confirms that this method offers higher resource utilization, reduces redundant computations, and significantly improves path planning efficiency. In the gradient comparison experiment, continuous improvements to the traditional ACO algorithm demonstrate significant enhancements in path length, convergence speed, and smoothness, with a $39.45\%$ reduction in the average number of iterations. Compared to other algorithms, this method demonstrates higher adaptability in path planning, especially in complex situations, effectively balancing path length, smoothness, and convergence speed. By reducing the number of turns and iterations, this method enhances the practicality of path planning, offering a superior path selection solution for mobile robots in real-world applications. However, this method also has some limitations. Improved-ACO performs better than certain other algorithms in terms of path length; still, in some situations, it is somewhat longer than traditional ACO. If the path length requirement is stringent, further optimization of the algorithm’s heuristic information calculation may be needed in specific environments. Although Improved-ACO offers advantages in turning frequency and convergence speed, it is slightly inferior to the Dijkstra and A* algorithms in path length. In this study, some parameters (such as heuristic information weight and pheromone volatilization factor) can still be further optimized through experimentation to achieve the method’s optimal state. Future work could explore dynamic environments, such as obstacle movement or target position changes, though real-time performance and algorithm adaptability still require further investigation. Future research may consider integrating automated parameter optimization techniques, such as genetic algorithms or deep reinforcement learning, to further enhance algorithm performance.