Three-Dimensional Computational Fluid Dynamics-Based Improvements in Radial Turbine Design for Enhanced Thermal Energy Utilization: A Case Study in Ha’il Cement Company
Abstract
1. Introduction
| Ref. | Research Approach | Rotor Approach | Stator Approach |
|---|---|---|---|
| [26] | 1D | Glassman | Simpson |
| [27] | 1D, 3D | Glassman | Simpson |
| [28] | 1D | Glassman | Simpson |
| [29] | 1D, 3D | Glassman | Simpson |
| [30] | 1D | Glassman | Simpson |
| [31] | 1D, 3D | Glassman | Simpson |
| [32] | 1D, 3D | Glassman | - |
| [33] | 1D, 3D | Glassman | - |
| [34] | 1D, 3D | Jamieson | Simpson |
| [35] | 1D | Glassman, Whitfield and Baines | - |
| [36] | 1D, 3D | Glassman | 12 vanes (input) |
| [37] | 1D, 3D | Whitfield and Baines | - |
| [38] | 1D, 3D | Glassman | 17 vanes (input) |
| [39] | 3D | varies (9, 15, 19, 27) | 12 vanes (input) |
| [40] | 1D | Glassman | - |
| [41] | 1D | 9 blades (input) | 5 vanes (input) |
| [42] | 1D | Rohlik | Simpson |
| [43] | 1D, 3D | Glassman | 19 vanes (input) |
| [44] | 1D, 3D | 16 blades (input) | 22 vanes (input) |
| [45] | 1D | 11 blades (input) | + 3 |
| [46] | 1D | Rohlik | Simpson |
2. System Description and Modelling
2.1. Description of Engine ORC
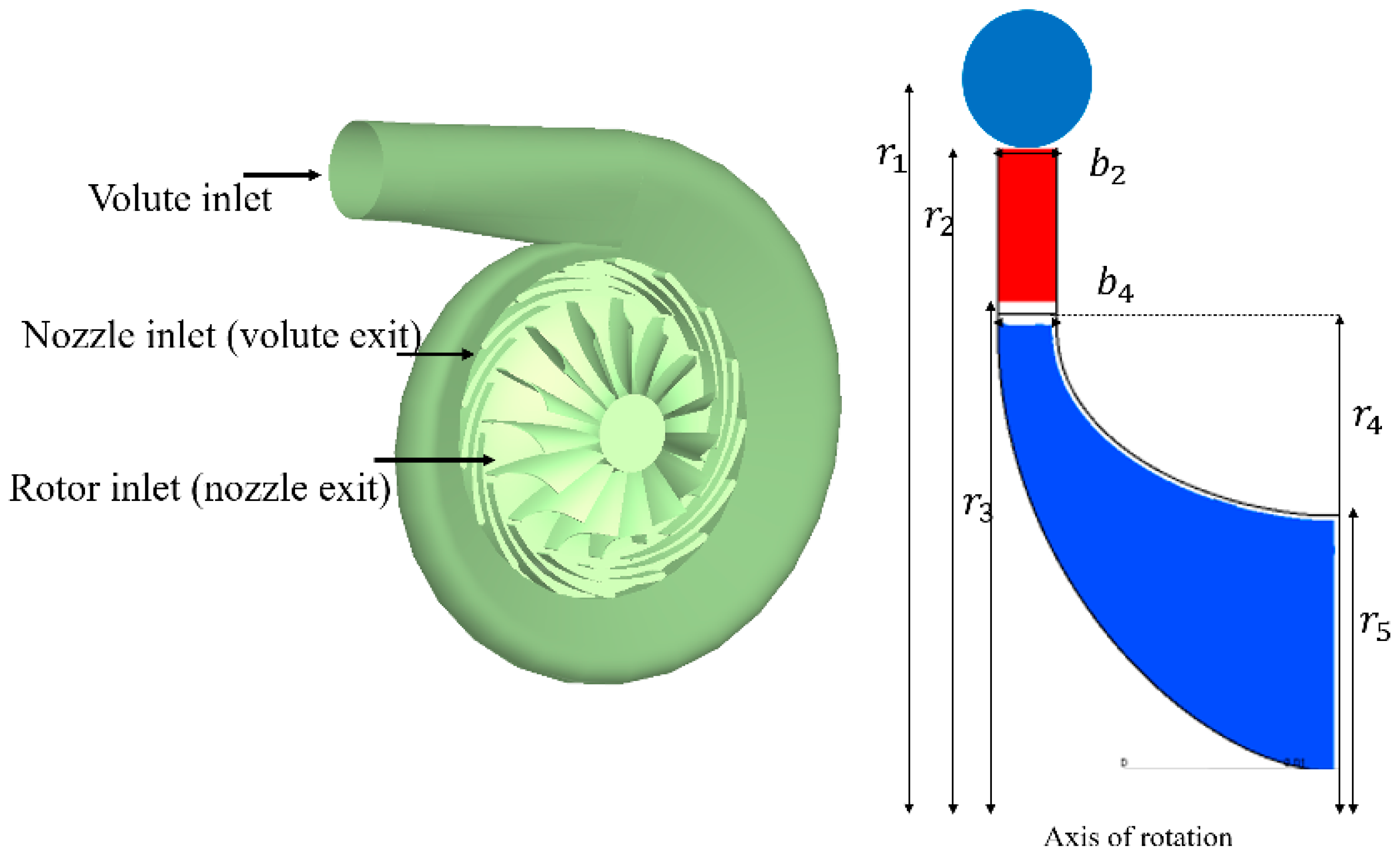
2.2. Description of Radial Turbine Stage
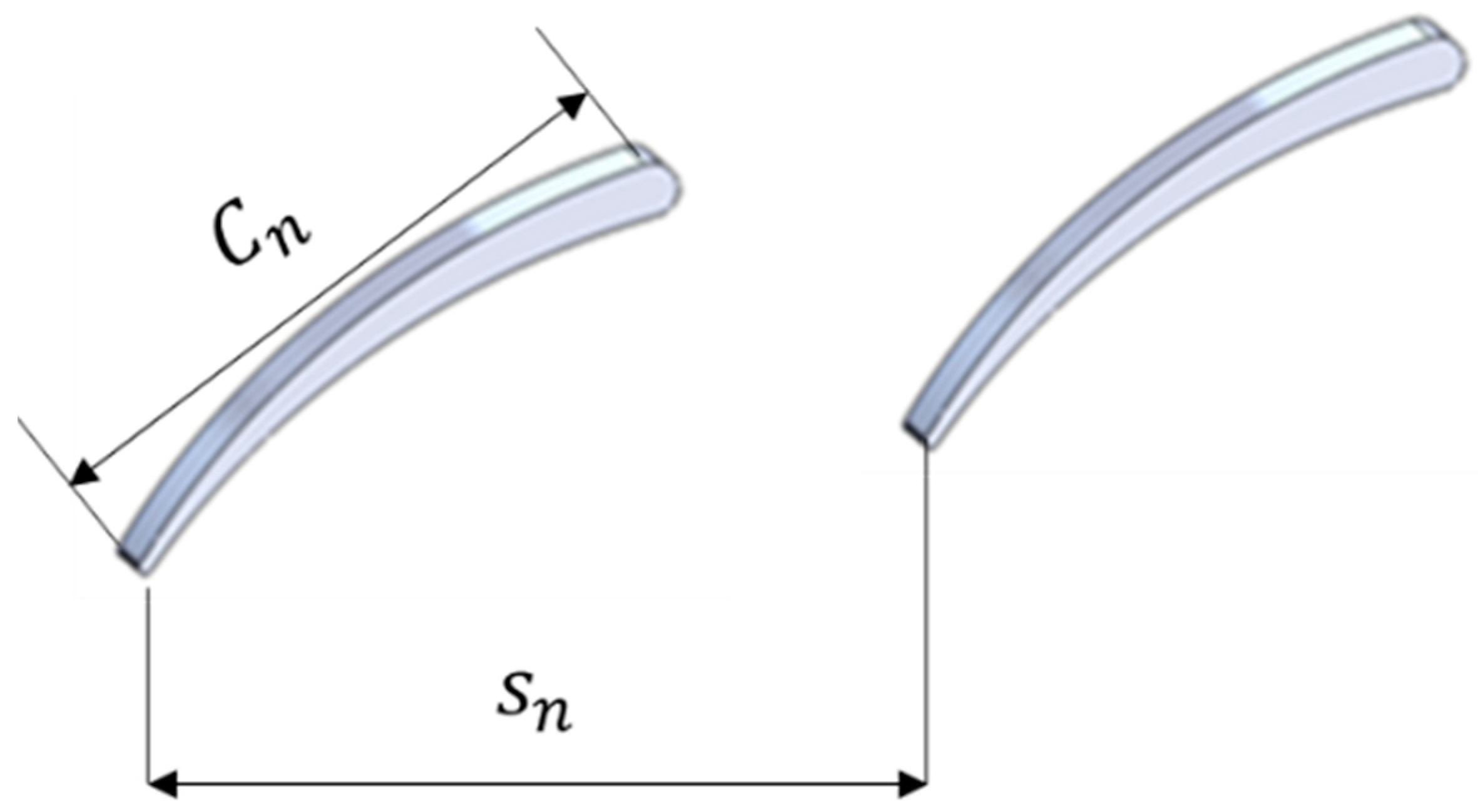
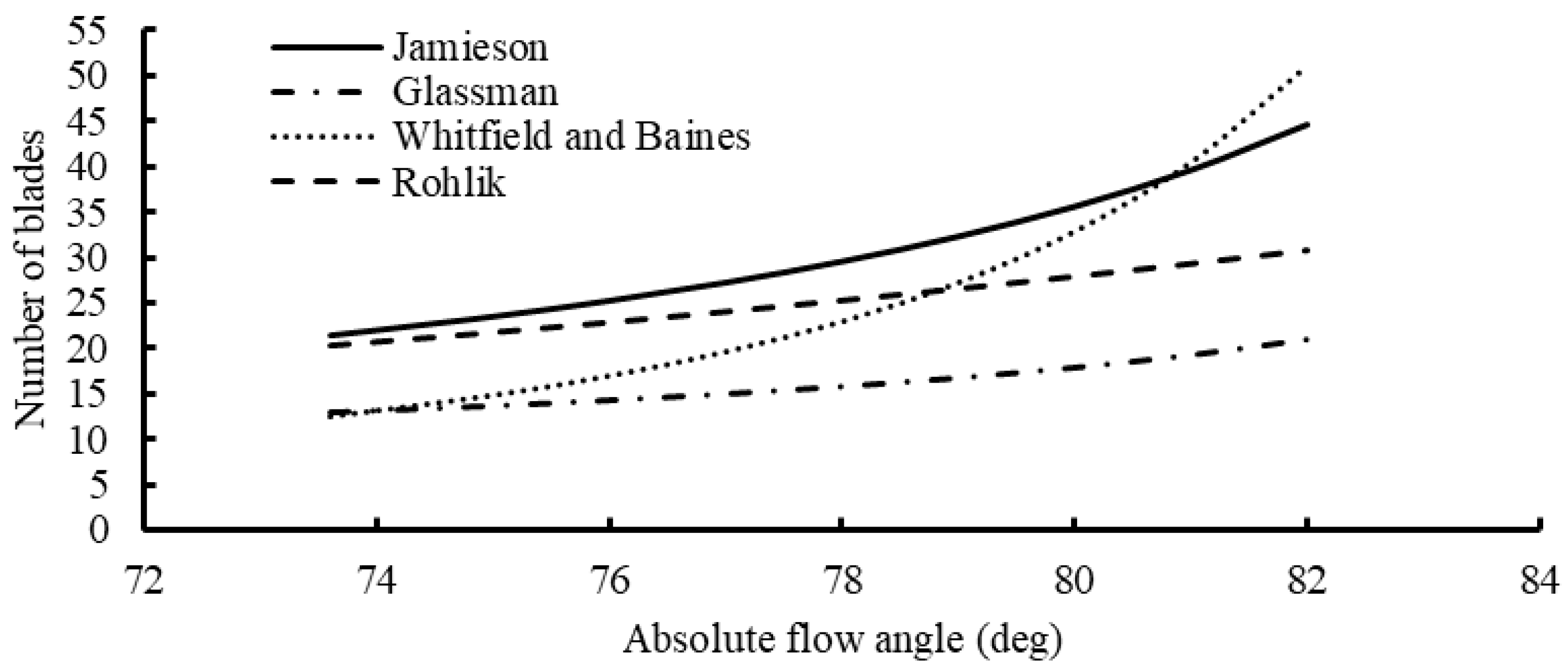
2.2.1. Description of Correlation Models of Rotor Blades
2.2.2. Description of Correlation Model of Stator Vanes
2.2.3. Flow Losses in Radial Turbine
3. Numerical Simulation
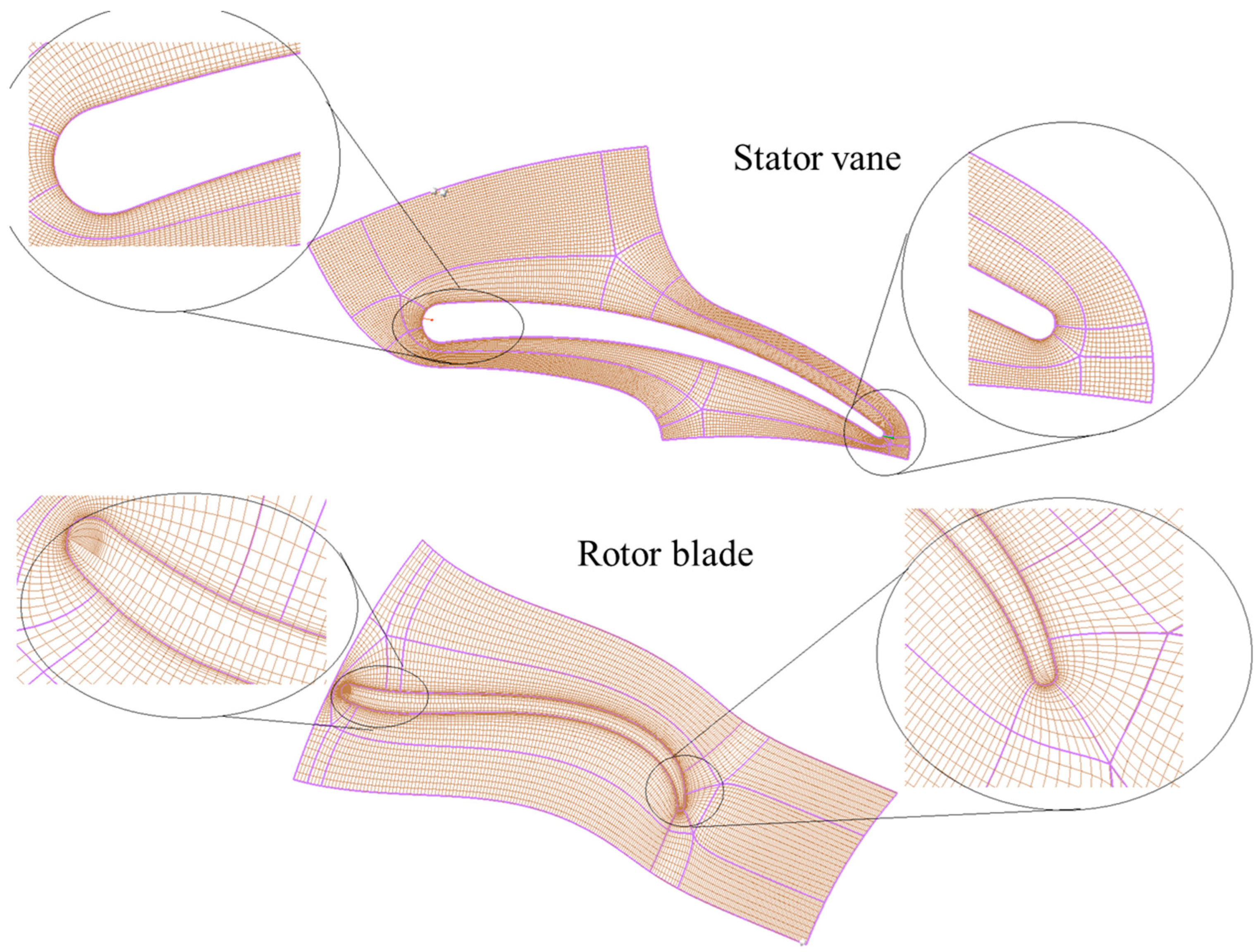
3.1. Establishment of 3D Shape
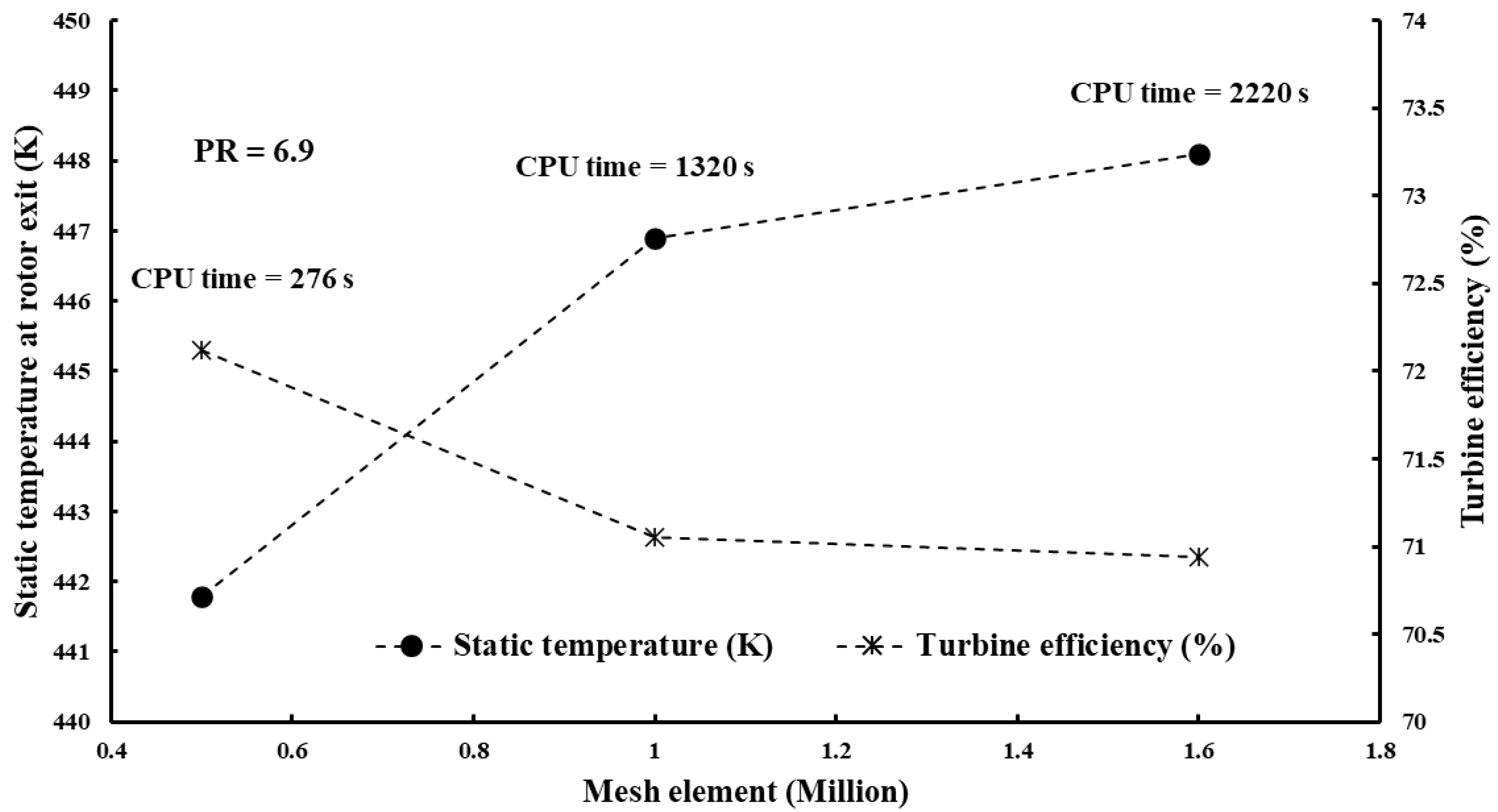
3.2. Governing Equations, Turbulence Model and Grid Generation, and Boundary Conditions
3.3. Validation of Numerical Model
4. Results and Discussion
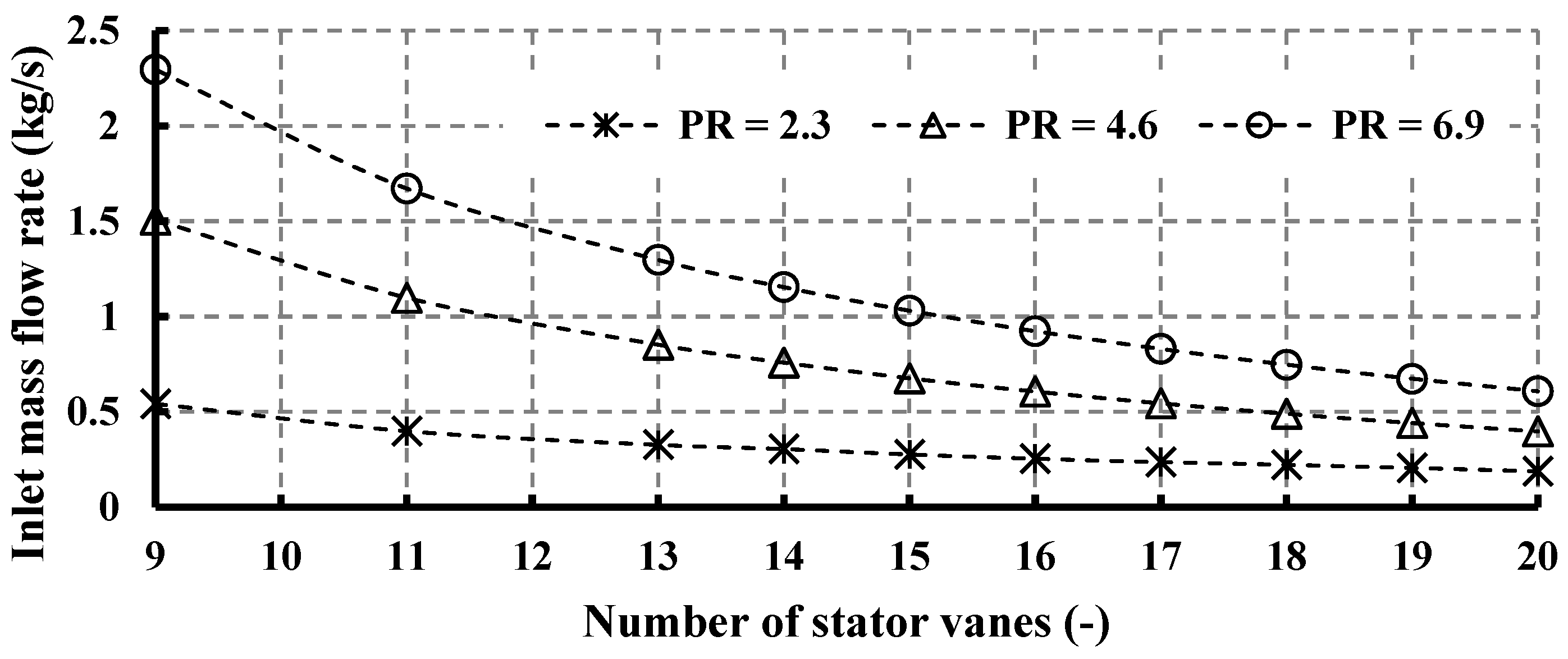
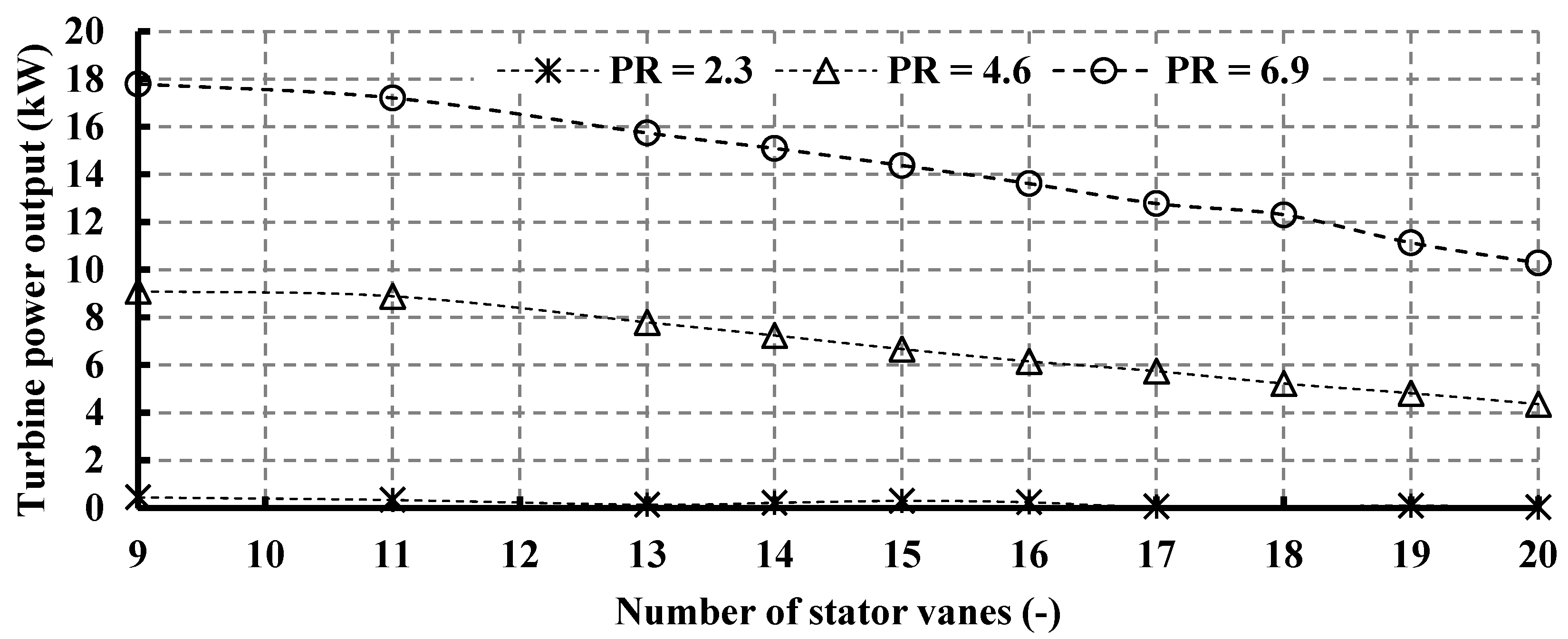
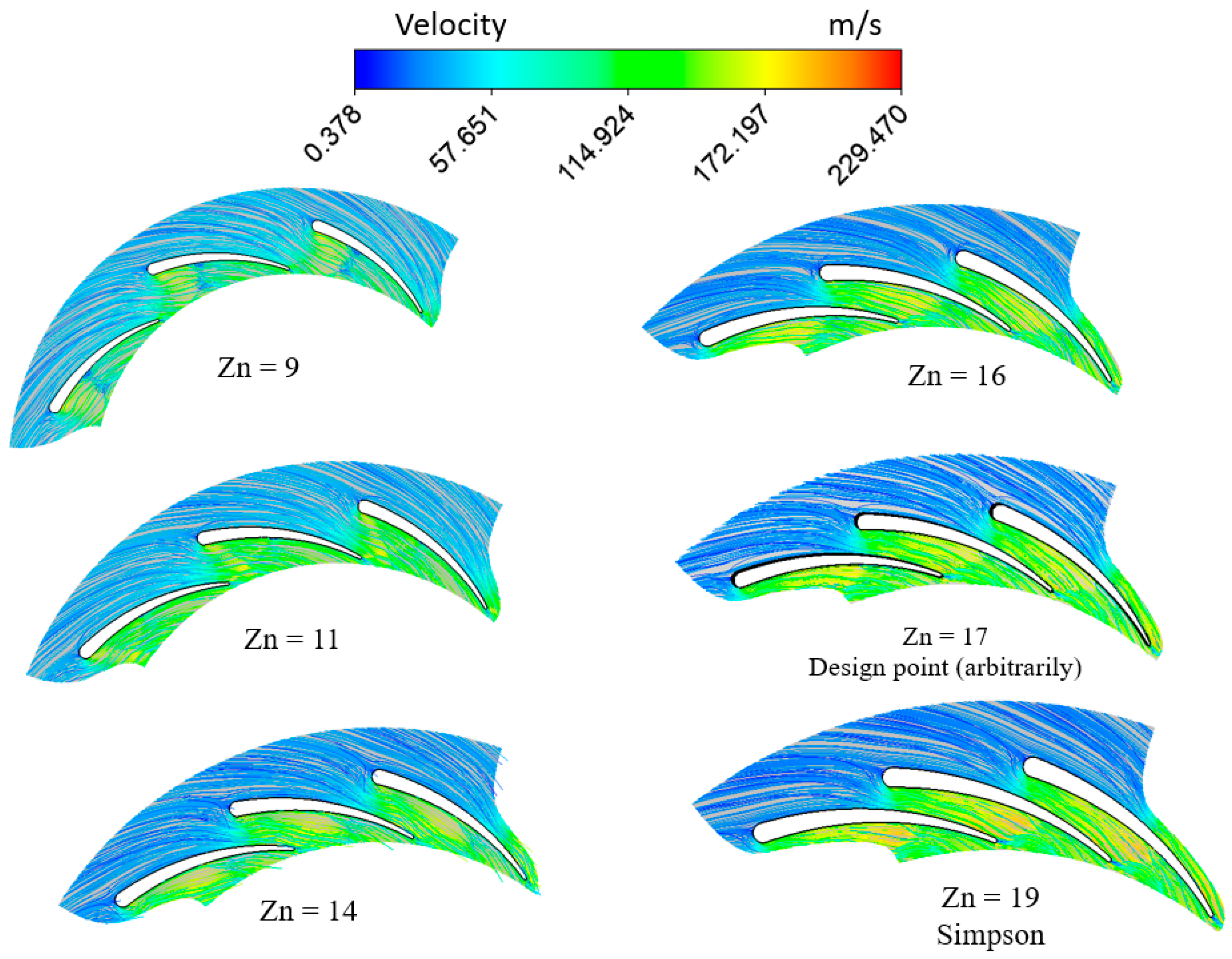
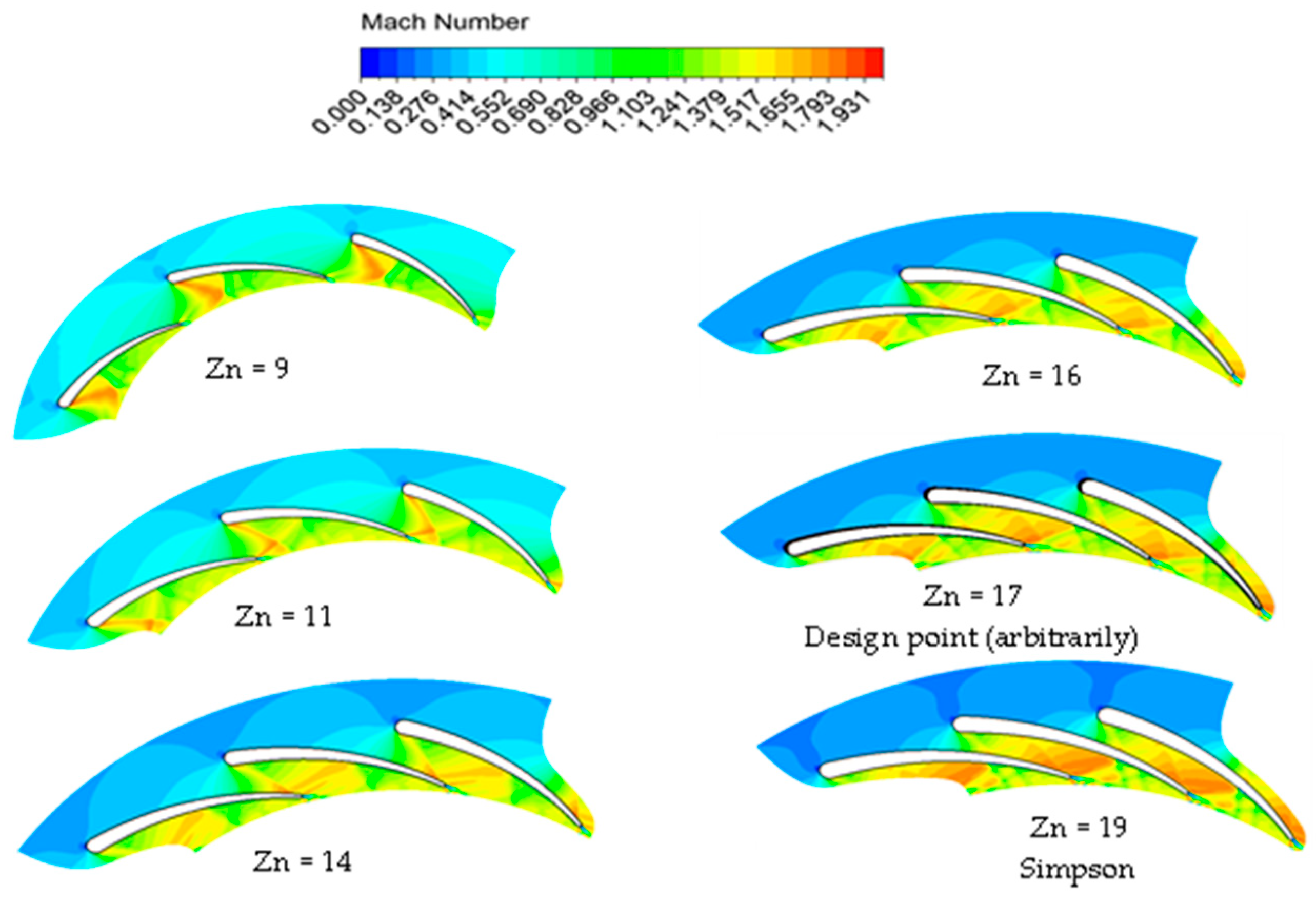
4.1. Impact of Stator Vane Number
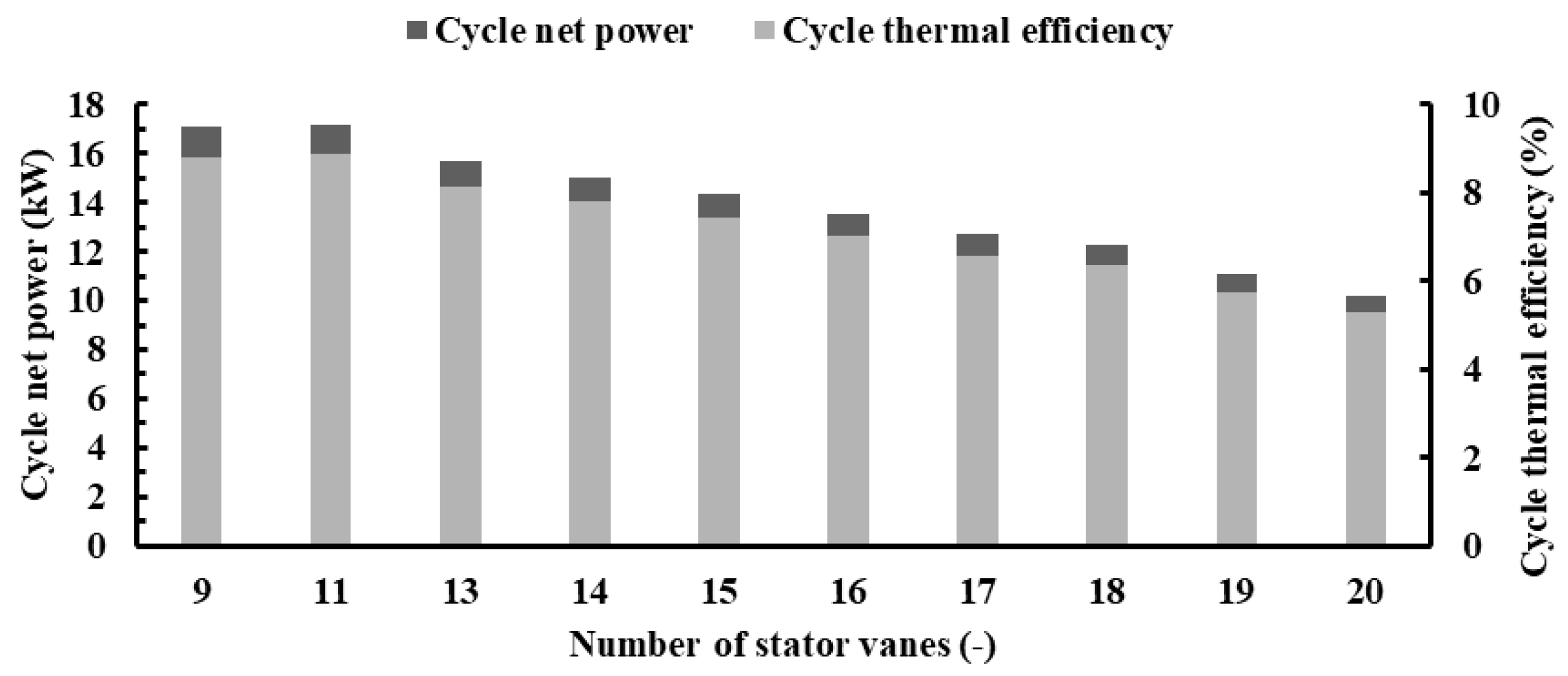
4.1.1. Impact of Vane Number on Global Parameters
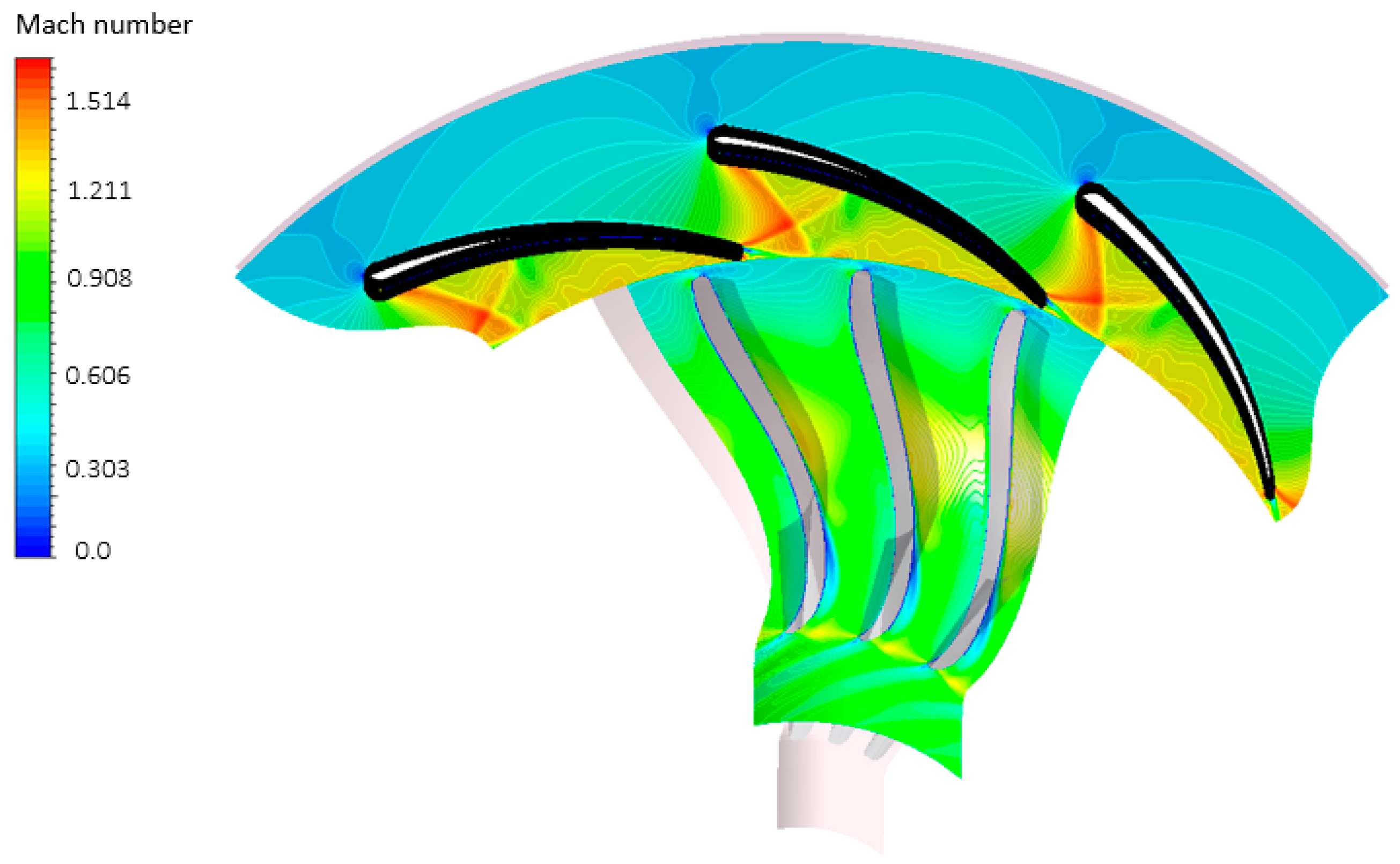
4.1.2. Impact of Vane Number on Flow Regime
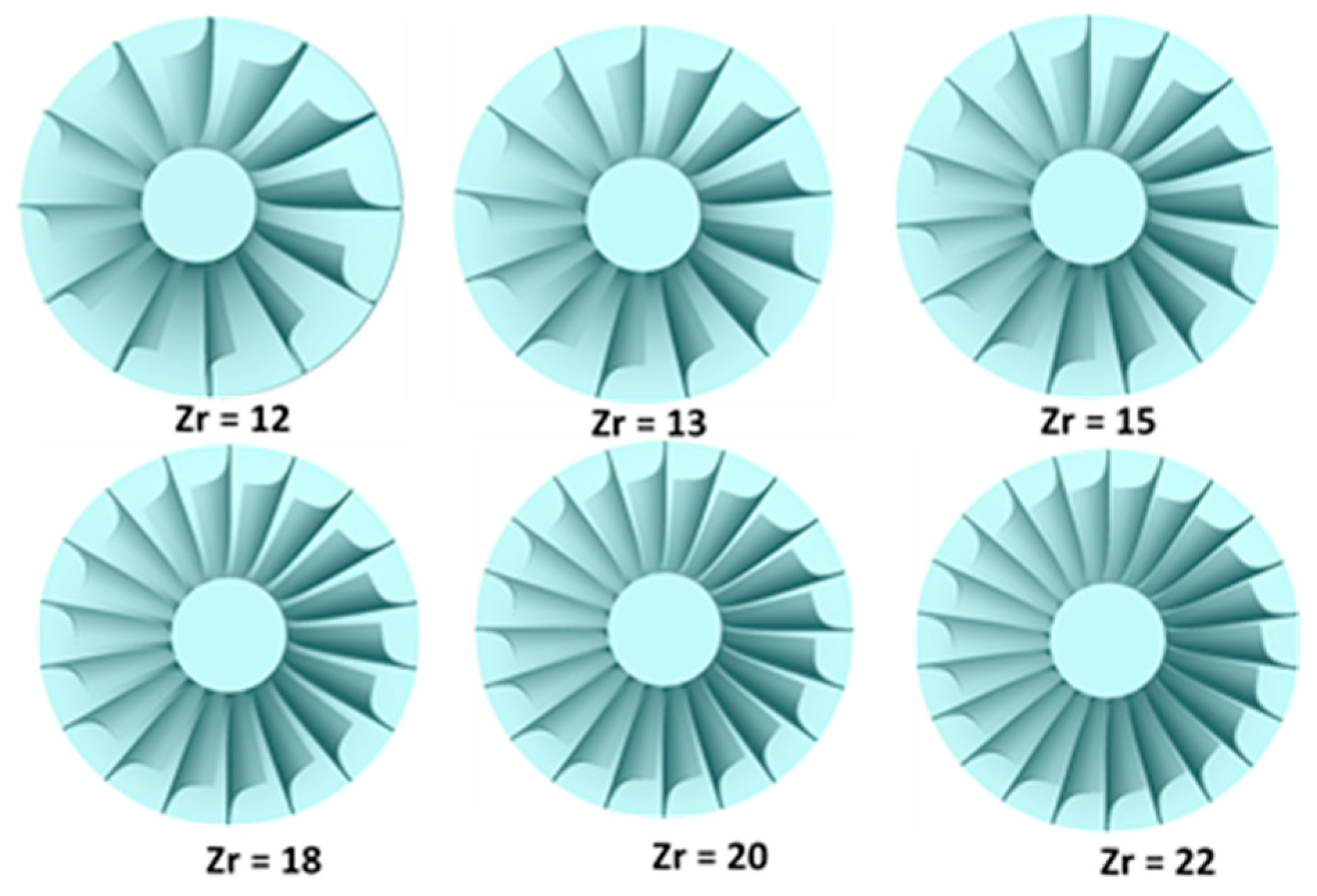
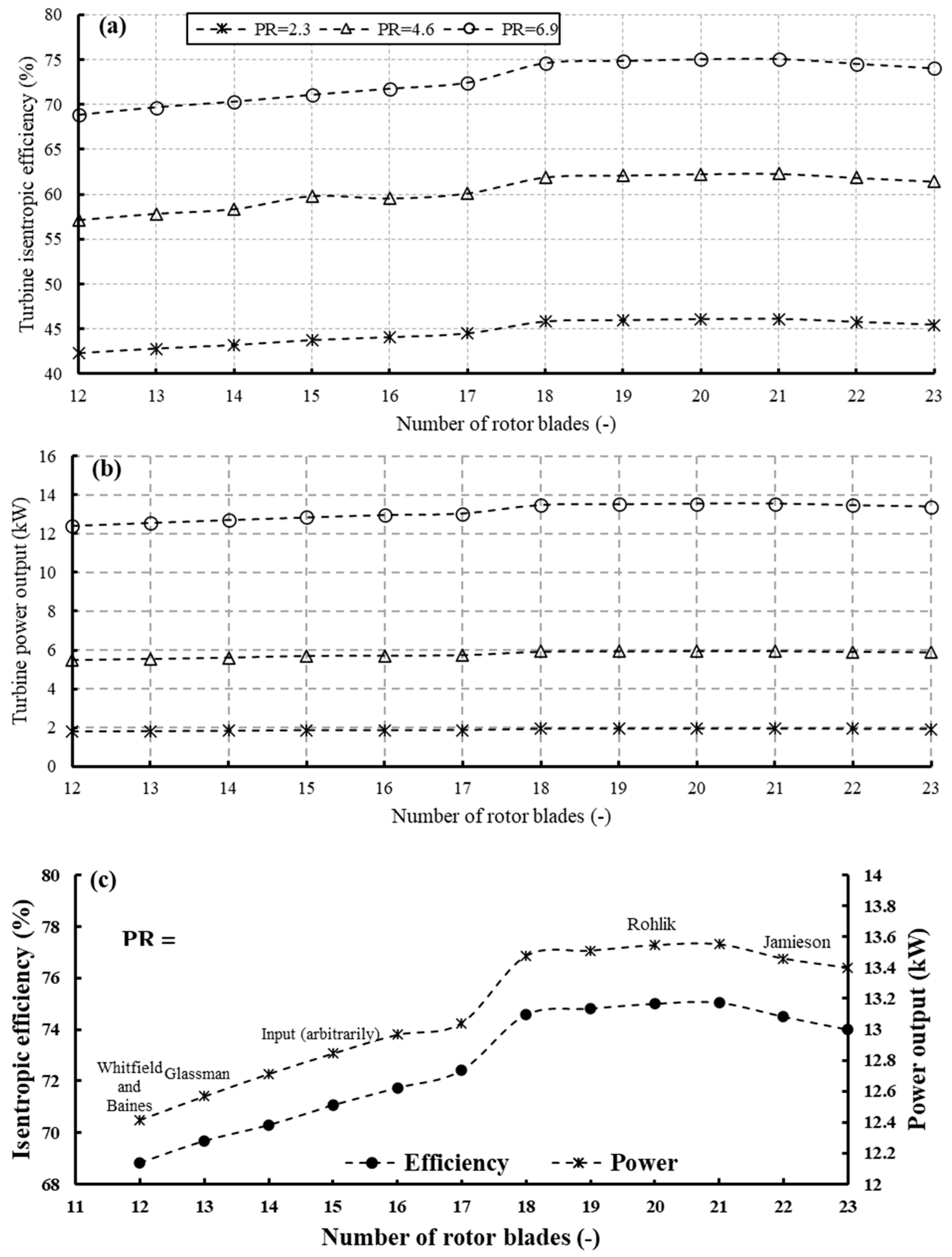
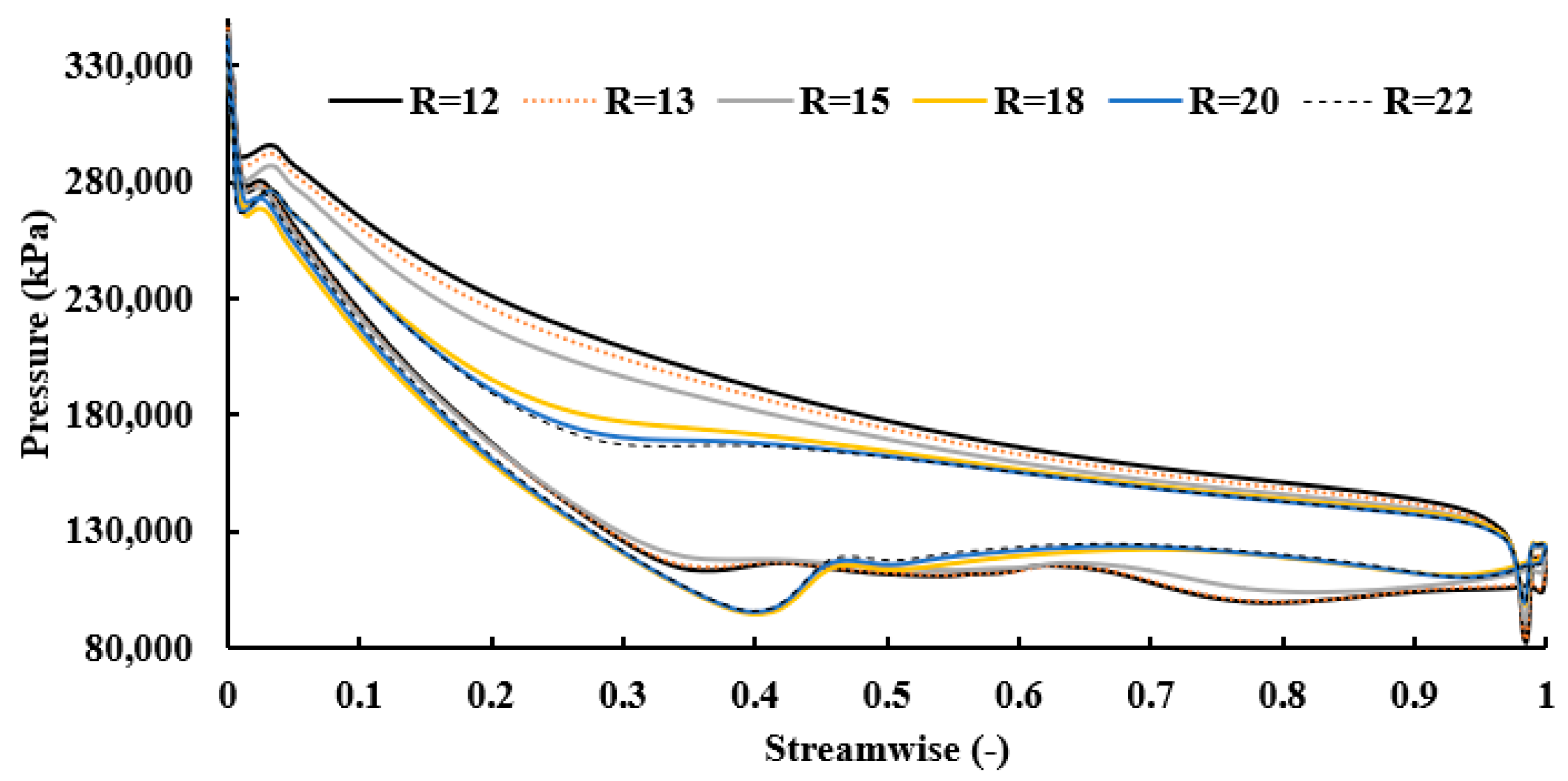
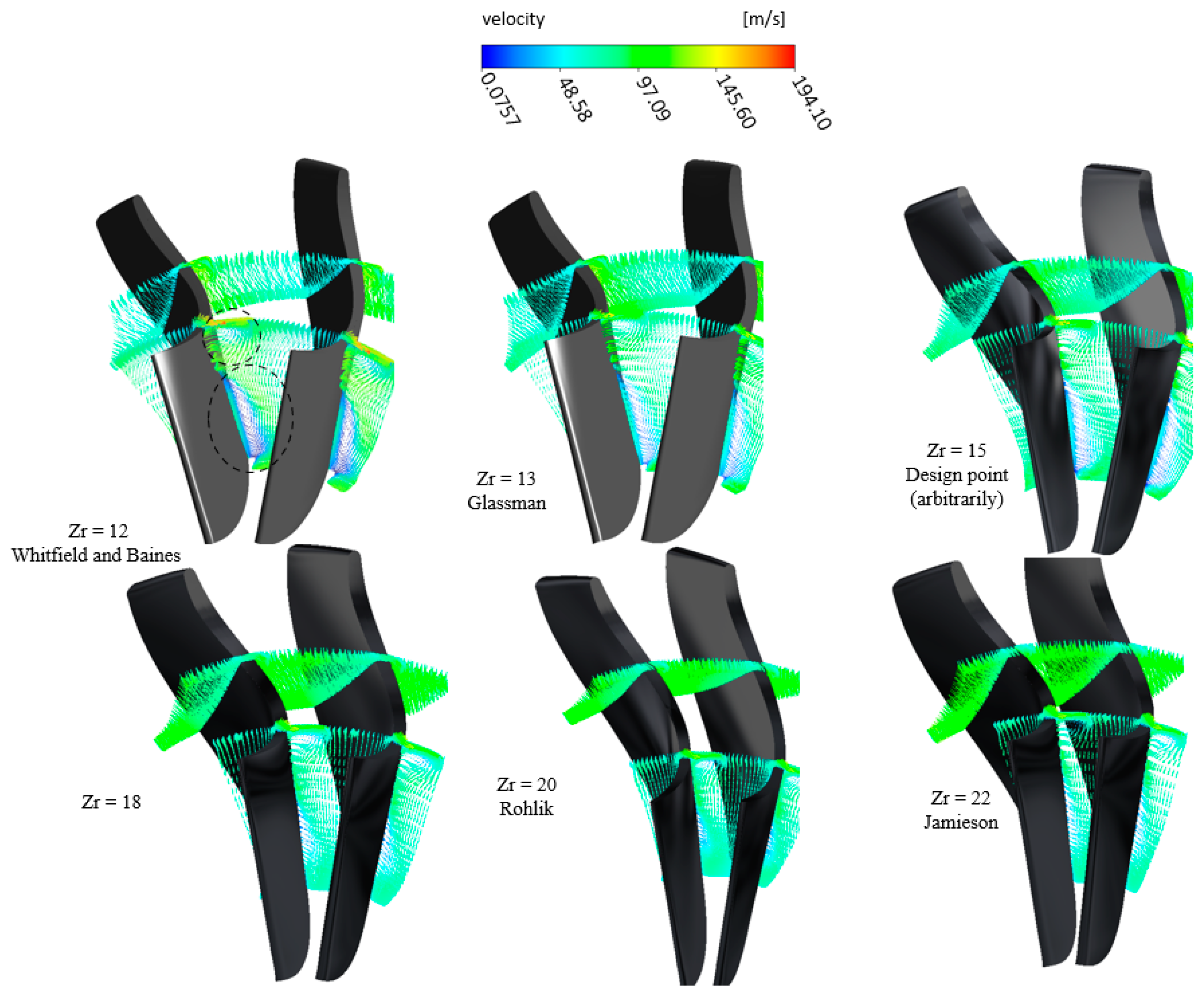
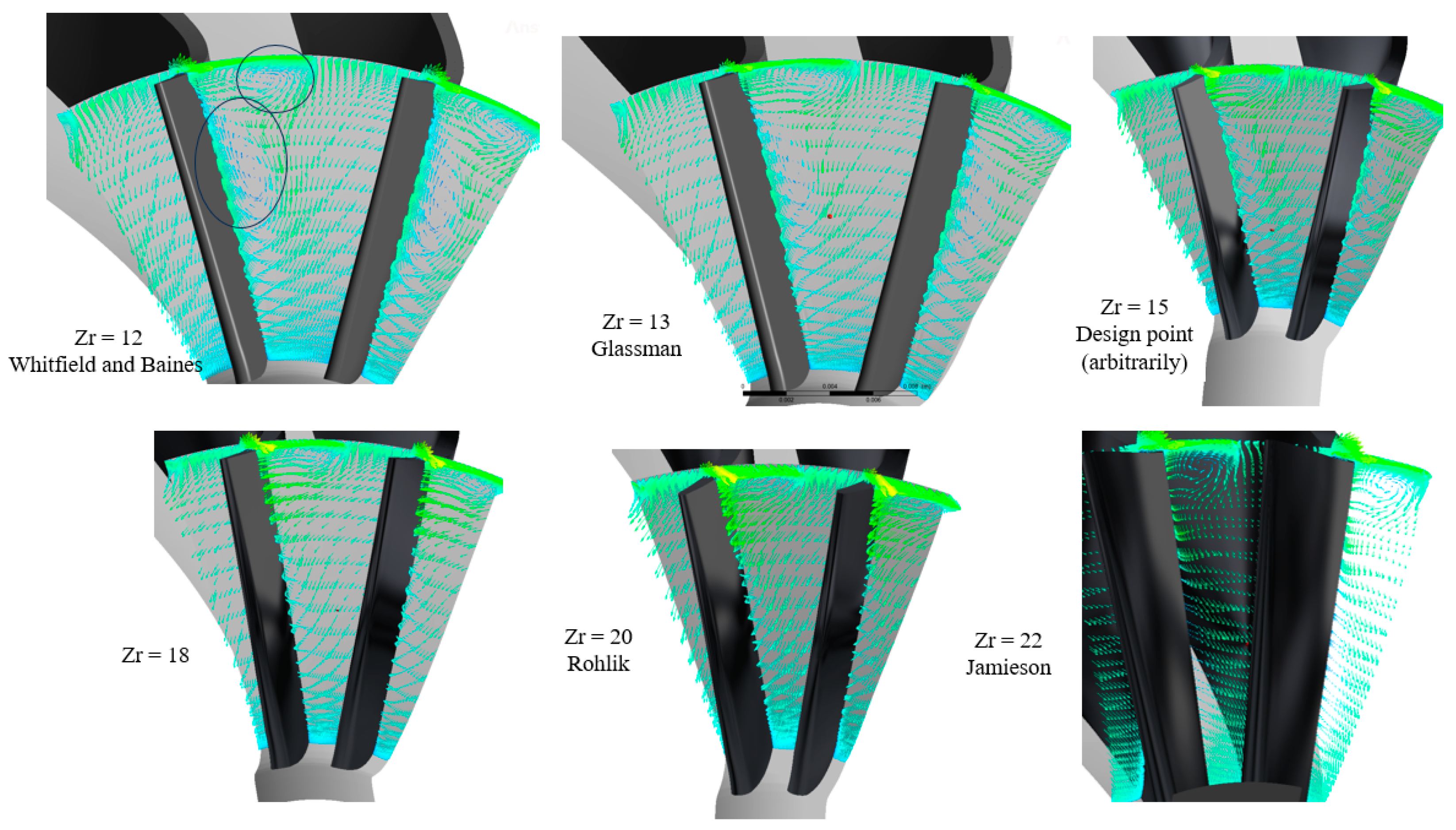
4.2. Impact of Rotor Blade Number
4.2.1. Impact of Blade Number on Global Parameters
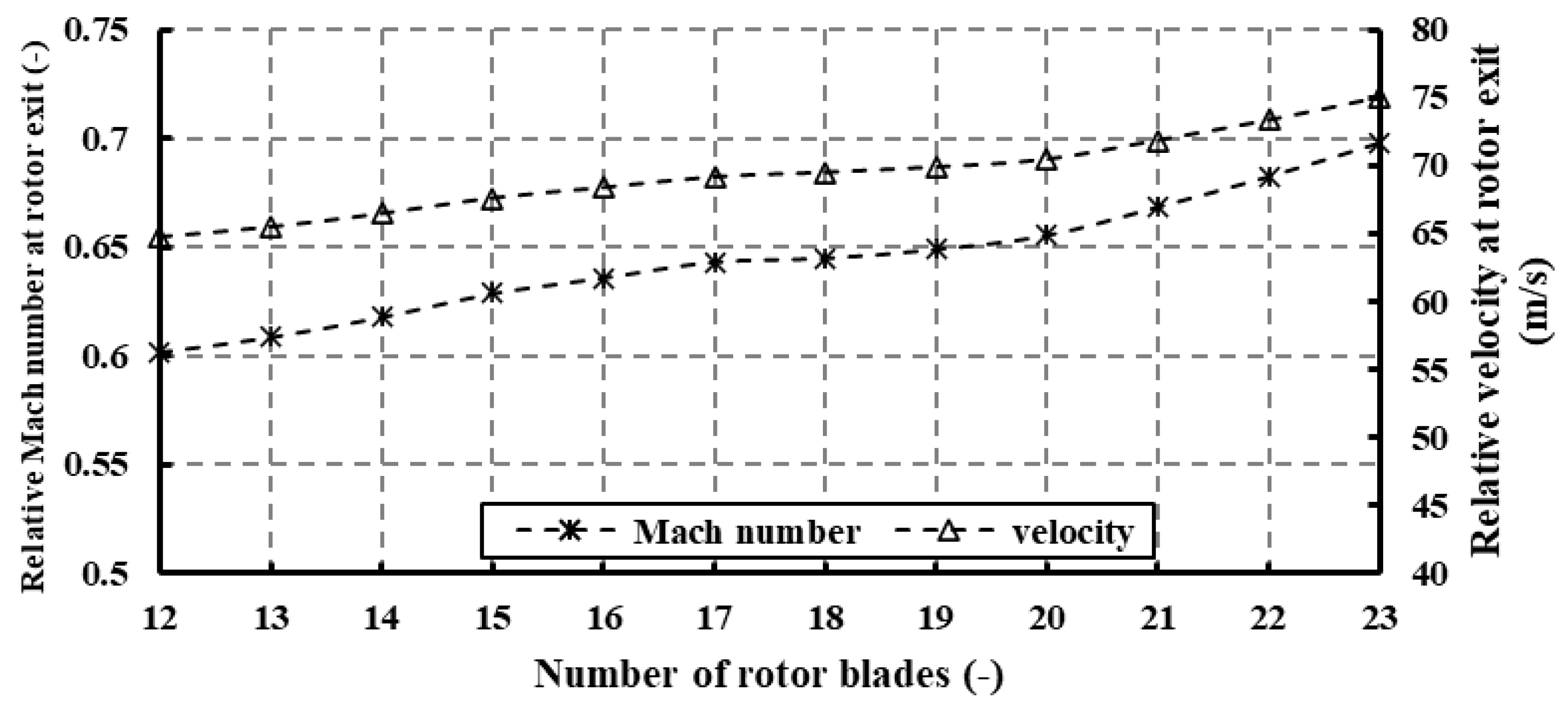
4.2.2. Impact of Blade Number on Flow Regime
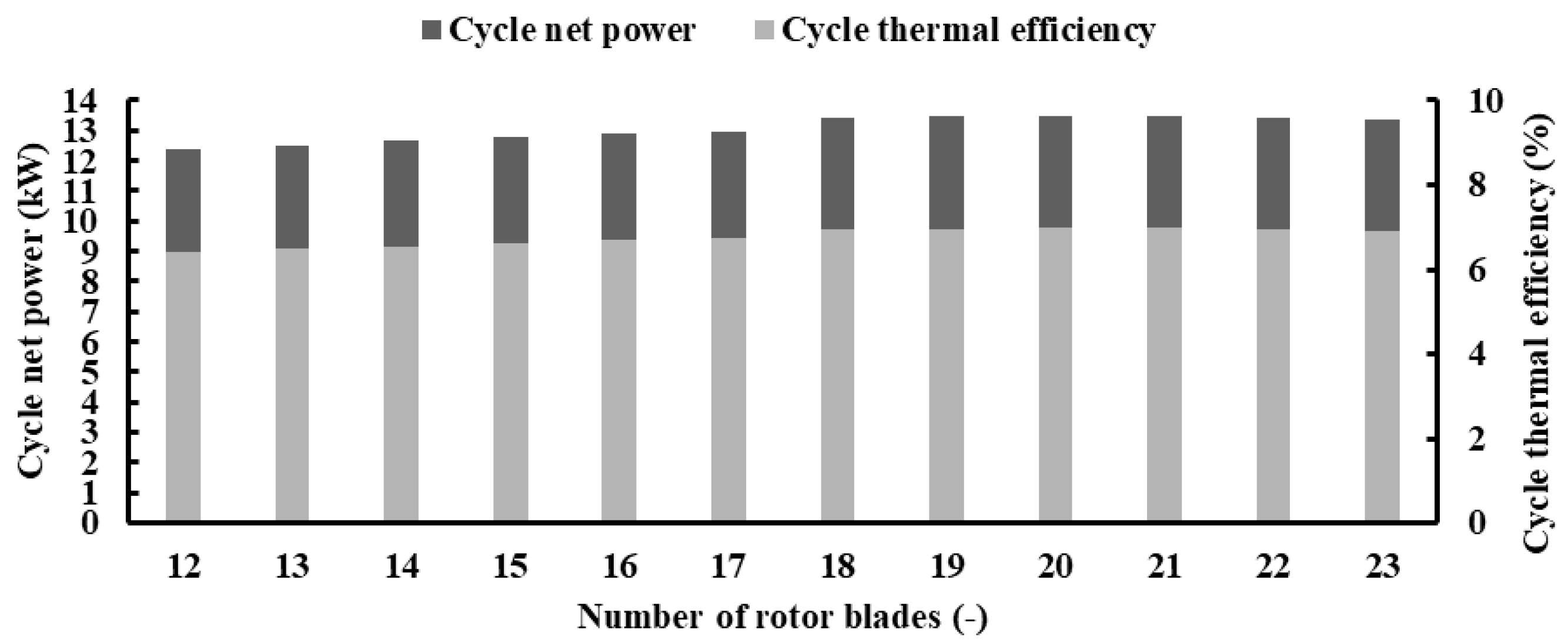
4.3. Impact of Blade and Vane Numbers on Cycle Performance
4.4. Flow Regime, Turbine Performance, and Cycle Performance
5. Conclusions
- At high pressure ratios, augmenting the number of stator vanes adversely affects the overall system performance, owing to the heightened stator losses. Nonetheless, when stator vane numbers are exceedingly low, the system experiences suboptimal operation, due to elevated Mach numbers and flow reversal. The turbine with 11 vanes demonstrates enhancements in turbine power, efficiency, and thermal efficiency by 34.8%, 4.17%, and 35.16%, respectively, compared to that with 17 vanes.
- On the contrary, augmenting the number of rotor blades initially improves system performance up to a specific threshold, after which it diminishes at excessively high blade numbers, attributed to heightened rotor losses. Compared to the other traditional correlations, the Rohlik correlation with 20 blades yields optimal outputs of 13.54 kW turbine power, 75% turbine efficiency, and 6.98% thermal efficiency. The Whitefield and Baines correlation with 12 blades demonstrates the minimum outputs of 12.42 kW turbine power, 68.81% turbine efficiency, and 6.40% thermal efficiency.
- Rotor losses vary as the number of rotor blades increases, with incidence loss being predominant, followed by passage loss, while trailing edge loss remains relatively minor.
- In small-to-medium organic Rankine cycle applications operating under high pressure ratios, the integration of 11 vanes and 20 blades is advantageous for achieving enhanced performance and flow characteristics. The configuration of 11 vanes and 20 blades yields a turbine power of 16 kW, a turbine efficiency of 77%, and a thermal efficiency of 9% for the current application.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variable | Subscript | ||
| a | speed of sound | 0 | stagnation/total |
| b | blade height | 1–7 | states through the cycle |
| C | speed | 1–5 | states through the turbine |
| Cn | chord length | act | actual |
| h | enthalpy | C | condenser |
| mass flow rate | E | evaporator | |
| M | Mach number | is | isentropic |
| o | throat opening | m | meridional |
| P | pressure | n | nozzle |
| PR | pressure ratio | P | pump |
| heat transfer | T | turbine | |
| r | radius | th | thermal |
| sn | vane pitch | Greek symbol | |
| U | tip speed | α | absolute angle |
| power | Ƞ | efficiency | |
| W | relative velocity | ρ | density |
| nozzle vane number | σ | solidity | |
| rotor blade number | ω | rotational speed | |
| Abbreviations | |||
| CO | carbon monoxide | ||
| NOx | nitrogen oxides | ||
| ORC | organic Rankine cycle | ||
| PM | particulate matter | ||
References
- Sanabria, E.; Maldonado, M.; Matiz, C.; Ribeiro, A.C.F.; Esteso, M.A. Methods of Capture and Transformation of Carbon Dioxide (CO2) with Macrocycles. Processes 2025, 13, 117. [Google Scholar] [CrossRef]
- Mikky, Y.A.; Bhran, A.A.; El-Araby, R.Y.; Mohamed, A.M.A.; Gadallah, A.G.; Shoaib, A.M. Optimization of Biodiesel–Nanoparticle Blends for Enhanced Diesel Engine Performance and Emission Reduction. Processes 2024, 12, 2471. [Google Scholar] [CrossRef]
- Özyalcin, C.; Sterlepper, S.; Roiser, S.; Eichlseder, H.; Pischinger, S. Exhaust gas aftertreatment to minimize NOX emissions from hydrogen-fueled internal combustion engines. Appl. Energy 2024, 353, 122045. [Google Scholar] [CrossRef]
- Dang, H.; Han, Y. Research on the Performance Characteristics of a Waste Heat Recovery Compound System for Series Hybrid Electric Vehicles. Processes 2024, 12, 605. [Google Scholar] [CrossRef]
- Corigliano, O.; Algieri, A.; Fragiacomo, P. Turning Data Center Waste Heat into Energy: A Guide to Organic Rankine Cycle System Design and Performance Evaluation. Appl. Sci. 2024, 14, 6046. [Google Scholar] [CrossRef]
- Yang, S.; Liang, A.; Jin, Z.; Xie, N. Investigation of a Cogeneration System Combining a Solid Oxide Fuel Cell and the Organic Rankine Cycle: Parametric Analysis and Multi-Objective Optimization. Processes 2024, 12, 2873. [Google Scholar] [CrossRef]
- Feng, J.; Cheng, X.; Yan, Y.; Zhao, L.; Dong, H. Thermodynamic and thermo-economic analysis, performance comparison and parameter optimization of basic and regenerative organic Rankine cycles for waste heat recovery. Case Stud. Therm. Eng. 2023, 52, 103816. [Google Scholar] [CrossRef]
- Rybiński, W.; Maurin, A.; Krzemianowski, Z.; Bykuć, S. Similarity Model of a Rotary Lobe Expander Working with Various Fluids. Appl. Sci. 2025, 15, 120. [Google Scholar] [CrossRef]
- Feng, J.; Cheng, X.; Wang, H.; Zhao, L.; Wang, H.; Dong, H. Performance analysis and multi-objective optimization of organic Rankine cycle for low-grade sinter waste heat recovery. Case Stud. Therm. Eng. 2024, 53, 103915. [Google Scholar] [CrossRef]
- Wang, H.-X.; Lei, B.; Wu, Y.-T.; Yang, P.-H.; Zhang, X.-M. Regulation strategies and optimizations of the expander and pump in organic Rankine cycle under off-design conditions. Appl. Therm. Eng. 2025, 259, 124807. [Google Scholar] [CrossRef]
- Witanowski, Ł. Numerical Investigation of Multi-Stage Radial Turbine Performance Under Variable Waste Heat Conditions for ORC Systems. Appl. Sci. 2024, 14, 11600. [Google Scholar] [CrossRef]
- Senyuk, M.; Beryozkina, S.; Safaraliev, M.; Nadeem, M.; Odinaev, I.; Kamalov, F. Methodology for Transient Stability Enhancement of Power Systems Based on Machine Learning Algorithms and Fast Valving in a Steam Turbine. Mathematics 2024, 12, 1644. [Google Scholar] [CrossRef]
- Guendaoui, S.; El Ouadefli, L.; El Akkad, A.; Elkhalfi, A.; Vlase, S.; Scutaru, M.L. Comparative Analysis of NURBS and Finite Element Method in Computational Fluid Dynamics Applications: Case Study on NACA 2412 Airfoil Aerodynamics. Mathematics 2024, 12, 3211. [Google Scholar] [CrossRef]
- Ariga, I.; Watanabe, I.; Fujie, K. Investigations Concerning Flow Patterns Within the Impeller Channels of Radial-Inflow Turbines, With Some Reference to the Influence of the Splitter Vanes. J. Eng. Power 1967, 89, 463–476. [Google Scholar] [CrossRef]
- Denton, J.D. The turboexpander a design, make and test student project. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, GT 1996, Birmingham, UK, 10–13 June 1996; Volume 5. [Google Scholar] [CrossRef]
- Watanabe, I.; Ando, T. Experimental study on radial turbine, with special reference to the influence of the number of impeller blades on performance characteristics. Bull. JSME 1959, 2, 457–462. [Google Scholar] [CrossRef]
- Chen, H.; Abidat, M.; Baines, N.C.; Firth, M.R. The Effects of Blade Loading in Radial and Mixed Flow Turbines. In Proceedings of the ASME 1992 International Gas Turbine and Aeroengine Congress and Exposition, Cologne, Germany, 1–4 June 1992. [Google Scholar]
- 3M Science Applied to Life. Organic Fluids. Available online: https://www.3m.com/ (accessed on 5 February 2018).
- Karvountzis-Kontakiotis, A.; Pesiridis, A.; Zhao, H.; Alshammari, F.; Franchetti, B.; Pesmazoglou, I.; Tocci, L. Effect of an ORC Waste Heat Recovery System on Diesel Engine Fuel Economy for Off-Highway Vehicles. SAE Tech. Pap. 2017-01-0136 2017. [Google Scholar] [CrossRef]
- Alshammari, F.; Elashmawy, M.; Ben Hamida, M.B. Effects of working fluid type on powertrain performance and turbine design using experimental data of a 7.25ℓ heavy-duty diesel engine. Energy Convers. Manag. 2021, 231, 113828. [Google Scholar] [CrossRef]
- Jamieson, A.W.H. ‘The Radial Turbine’, Gas Turbine Principles and Practice; Roxbee-Cox: Birmingham, UK, 1955. [Google Scholar]
- Glassman, A. Computer Program for Design Analysis of Radial-Inflow Turbines; NASA: Washington, DC, USA, 1976.
- Whitfield, A.; Baines, N.C. Design of Radial Turbomachines; Longman Scientific and Technical: Harlow, UK, 1990. [Google Scholar]
- Rohlik, H.E. Analytical Determination of Radial Inflow Turbine Design Geometry for Maximum Efficiency; TN D-4384; NASA: Washington, DC, USA, 1968.
- Simpson, J.; Spence, A.; Watterson, S. Numerical and Experimental Study of the Performance Effects of Varying Vaneless Space and Vane Solidity in Radial Inflow Turbine Stators. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea and Air GT2008, Berlin, Germany, 9–13 June 2008. [Google Scholar]
- Alshammari, F.; Karvountzis-Kontakiotis, A.; Pesyridis, A.; Alatawi, I. Design and study of back-swept high pressure ratio radial turbo-expander in automotive organic Rankine cycles. Appl. Therm. Eng. 2020, 164, 114549. [Google Scholar] [CrossRef]
- Zheng, Y.; Hu, D.; Cao, Y.; Dai, Y. Preliminary design and off-design performance analysis of an Organic Rankine Cycle radial-inflow turbine based on mathematic method and CFD method. Appl. Therm. Eng. 2017, 112, 25–37. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N. Modelling and optimization of organic Rankine cycle based on a small-scale radial inflow turbine. Energy Convers. Manag. 2015, 91, 186–198. [Google Scholar] [CrossRef]
- Al Jubori, A.M.; Al-Mousawi, F.N.; Rahbar, K.; Al-Dadah, R.; Mahmoud, S. Design and manufacturing a small-scale radial-inflow turbine for clean organic Rankine power system. J. Clean. Prod. 2020, 257, 120488. [Google Scholar] [CrossRef]
- Ventura, C.A.; Jacobs, P.A.; Rowlands, A.S.; Petrie-Repar, P.; Sauret, E. Preliminary design and performance estimation of radial inflow turbines: An automated approach. J. Fluids Eng. 2012, 134, 031102. [Google Scholar] [CrossRef]
- Wu, T.; Shao, L.; Wei, X.; Ma, X.; Zhang, G. Design and structure optimization of small-scale radial inflow turbine for organic Rankine cycle system. Energy Convers. Manag. 2019, 199, 111940. [Google Scholar] [CrossRef]
- Barsi, D.; Perrone, A.; Ratto, L.; Simoni, D.; Zunino, P. Radial inflow turbine design through multi-disciplinary optimisation technique. In Proceedings of the ASME Turbo Expo, Montreal, QC, Canada, 15–19 June 2015; Volume 8, pp. 1–12. [Google Scholar] [CrossRef]
- Kim, D.-Y.; Kim, Y.-T. Preliminary design and performance analysis of a radial inflow turbine for organic Rankine cycles. Appl. Therm. Eng. 2017, 120, 549–559. [Google Scholar] [CrossRef]
- Noughabi, A.K.; Sammak, S. Detailed design and aerodynamic performance analysis of a radial-inflow turbine. Appl. Sci. 2018, 8, 2207. [Google Scholar] [CrossRef]
- Han, Z.; Jia, X.; Li, P. Preliminary design of radial inflow turbine and working fluid selection based on particle swarm optimization. Energy Convers. Manag. 2019, 199, 111933. [Google Scholar] [CrossRef]
- Nithesh, K.; Chatterjee, D. Numerical prediction of the performance of radial inflow turbine designed for ocean thermal energy conversion system. Appl. Energy 2016, 167, 1–16. [Google Scholar] [CrossRef]
- Sarmiento, A.L.E.; Camacho, R.G.R.; de Oliveira, W. Performance analysis of radial-inflow turbine of ORC: New combined approach of preliminary design and 3D CFD study. J. Mech. Sci. Technol. 2020, 34, 2403–2422. [Google Scholar] [CrossRef]
- Li, X.; Lv, C.; Yang, S.; Li, J.; Deng, B.; Li, Q. Preliminary design and performance analysis of a radial inflow turbine for a large-scale helium cryogenic system. Energy 2019, 167, 106–116. [Google Scholar] [CrossRef]
- De Servi, C.M.; Burigana, M.; Pini, M.; Colonna, P. Design method and performance prediction for radial-inflow turbines of high-temperature mini-organic rankine cycle power systems. J. Eng. Gas Turbines Power 2019, 141, 091021. [Google Scholar] [CrossRef]
- Hu, D.; Li, S.; Zheng, Y.; Wang, J.; Dai, Y. Preliminary design and off-design performance analysis of an Organic Rankine Cycle for geothermal sources. Energy Convers. Manag. 2015, 96, 175–187. [Google Scholar] [CrossRef]
- Demierre, J.; Rubino, A.; Schiffmann, J. Modeling and experimental investigation of an oil-free microcompressor-turbine unit for an organic rankine cycle driven heat pump. J. Eng. Gas Turbines Power 2015, 137, 032602. [Google Scholar] [CrossRef]
- Da Lio, L.; Manente, G.; Lazzaretto, A. A mean-line model to predict the design efficiency of radial inflow turbines in organic Rankine cycle (ORC) systems. Appl. Energy 2017, 205, 187–209. [Google Scholar] [CrossRef]
- Zhou, A.; Song, J.; Li, X.; Ren, X.; Gu, C. Aerodynamic design and numerical analysis of a radial inflow turbine for the supercritical carbon dioxide Brayton cycle. Appl. Therm. Eng. 2018, 132, 245–255. [Google Scholar] [CrossRef]
- Lee, S.; Yaganegi, G.; Mee, D.J.; Guan, Z.; Gurgenci, H. Part-load performance prediction model for supercritical CO2 radial inflow turbines. Energy Convers. Manag. 2021, 235, 113964. [Google Scholar] [CrossRef]
- Schuster, S.; Markides, C.N.; White, A.J. Design and off-design optimisation of an organic Rankine cycle (ORC) system with an integrated radial turbine model. Appl. Therm. Eng. 2020, 174, 115192. [Google Scholar] [CrossRef]
- Alshammari, F.; Alghafis, A.; Alatawi, I.; Alshammari, A.S.; Alzamil, A.; Alrashidi, A. Potential of Variable Geometry Radial Inflow Turbines as Expansion Machines in Organic Rankine Cycles Integrated with Heavy-Duty Diesel Engines. Appl. Sci. 2023, 13, 12139. [Google Scholar] [CrossRef]
- Alshammari, F.; Pesyridis, A. Experimental study of organic Rankine cycle system and expander performance for heavy-duty diesel engine. Energy Convers. Manag. 2019, 199, 111998. [Google Scholar] [CrossRef]
- Hagen, B.A.; Agromayor, R.; Nekså, P. Equation-oriented methods for design optimization and performance analysis of radial inflow turbines. Energy 2021, 237, 121596. [Google Scholar] [CrossRef]
- Alshammari, F.; Pesyridis, A.; Elashmawy, M. Turbine optimization potential to improve automotive Rankine cycle performance. Appl. Therm. Eng. 2021, 186, 116559. [Google Scholar] [CrossRef]
- Uusitalo, A.; Grönman, A. Analysis of radial inflow turbine losses operating with supercritical carbon dioxide. Energies 2021, 14, 3561. [Google Scholar] [CrossRef]
- Lemmon, E.; Huber, M.; McLinden, M. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.0; National Institute of Standards and Technology, Standard Reference Data Program: Gaithersburg, MD, USA, 2010.
- ANSYS Inc. ANSYS CFX-Solver Theory Guide, Release 18.0; ANSYS Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Simpson, A.T.; Spence, S.W.T.; Watterson, J.K. A Comparison of the Flow Structures and Losses Within Vaned and Vaneless Stators for Radial Turbines. J. Turbomach. 2009, 131, 31010–31015. [Google Scholar] [CrossRef]
- Savcı, İ.H.; Şener, R.; Duman, I. A study of signal noise reduction of the mass air flow sensor using the flow conditioner on the air induction system of heavy-duty truck. Flow Meas. Instrum. 2022, 83, 102121. [Google Scholar] [CrossRef]












| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Displaced Volume | 7230 cc | Number of Cylinders | 6 |
| Stroke | 135 mm | Number of Valves | 4 |
| Bore | 110 mm | Maximum Torque | 1200 Nm @ 1600–1700 RPM |
| Compression Ratio | 18.5:1 | Maximum Power | 205 kW @ 2400 RPM |
| Component | Equation | Equation # | Comments |
|---|---|---|---|
| Evaporator | (1) | is the heat transfer in the evaporator, in kW. | |
| Turbine | (2) | is the turbine power output, in kW. | |
| Condenser | (3) | is the heat transfer in the condenser, in kW. | |
| Pump | (4) | is the pump power output, in kW. | |
| - | (5) | is the cycle’s thermal efficiency. |
| Equation | Equation # | Comments |
|---|---|---|
| (6) | Calculate the tip speed, | |
| (7) | Calculate the rotor radius, | |
| (8) | Calculate the meridional speed, , and complete the velocity triangles | |
| (9) | Calculate the rotor blade height, | |
| (10) | Calculate the stator vane radius, | |
| (11) | Calculate the stator vane height, | |
| (12) | Calculate the stator vane throat, |
| Parameter | Unit | Value |
|---|---|---|
| Turbine inlet temperature | K | 471.55 |
| Turbine inlet pressure | kPa | 900 |
| Working fluid mass flow rate | kg/s | 0.92 |
| Turbine exit pressure | kPa | 130 |
| Turbine speed | rpm | 40,000 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| Nozzle inlet radius | cm | 4.28 | |
| Nozzle throat opening | cm | 0.158 | |
| Nozzle exit radius | cm | 3.43 | |
| Nozzle inlet flow angle | Degree | 68.8 | |
| Nozzle exit flow angle | Degree | 73.6 | |
| Nozzle exit Mach number | - | 1.9 | |
| Nozzle exit total pressure | KPa | 1622 | |
| Nozzle exit total temperature | K | 470 | |
| Nozzle exit total enthalpy | KJ/Kg | 471 | |
| Rotor inlet radius | cm | 3.29 | |
| Rotor inlet blade height | cm | 0.34 | |
| Rotor axial length | cm | 1.97 | |
| Rotor inlet tip speed | m/s | 137 | |
| Rotor inlet relative speed | m/s | 96 | |
| Rotor exit radius | cm | 2.42 | |
| Rotor exit absolute speed | m/s | 82 | |
| Rotor exit Mach number | - | 0.78 | |
| Rotor exit total pressure | KPa | 178 | |
| Rotor exit total temperature | K | 439 | |
| Rotor exit total enthalpy | KJ/Kg | 452 |
| Parameter | Test [47] | CFD | Deviation (%) |
|---|---|---|---|
| (°C) | 176.49 | 183.5 | 3.97 |
| (kg/s) | 0.43 | 0.45 | 5.12 |
| 35% | 36.40 | 4 | |
| 9.50 | 9.88 | 4 |
| Blade Number Correlation | Value | Vane Number Correlation | Value |
|---|---|---|---|
| Jamieson [21] | 22 | Simpson et al. [25] | 19 |
| Glassman [22] | 13 | + 2 | * |
| Whitfield and Baines [23] | 12 | + 3 | * |
| Rohlik [24] | 20 | Input (design point) | 17 |
| Input (design point) | 15 |
| Parameter | Unit | Value |
|---|---|---|
| Turbine power | kW | 16 |
| Turbine efficiency | % | 77 |
| Cycle thermal efficiency | % | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, F.; Alshammari, A.S.; Alzamil, A. Three-Dimensional Computational Fluid Dynamics-Based Improvements in Radial Turbine Design for Enhanced Thermal Energy Utilization: A Case Study in Ha’il Cement Company. Processes 2025, 13, 500. https://doi.org/10.3390/pr13020500
Alshammari F, Alshammari AS, Alzamil A. Three-Dimensional Computational Fluid Dynamics-Based Improvements in Radial Turbine Design for Enhanced Thermal Energy Utilization: A Case Study in Ha’il Cement Company. Processes. 2025; 13(2):500. https://doi.org/10.3390/pr13020500
Chicago/Turabian StyleAlshammari, Fuhaid, Ahmed S. Alshammari, and Ahmed Alzamil. 2025. "Three-Dimensional Computational Fluid Dynamics-Based Improvements in Radial Turbine Design for Enhanced Thermal Energy Utilization: A Case Study in Ha’il Cement Company" Processes 13, no. 2: 500. https://doi.org/10.3390/pr13020500
APA StyleAlshammari, F., Alshammari, A. S., & Alzamil, A. (2025). Three-Dimensional Computational Fluid Dynamics-Based Improvements in Radial Turbine Design for Enhanced Thermal Energy Utilization: A Case Study in Ha’il Cement Company. Processes, 13(2), 500. https://doi.org/10.3390/pr13020500






