Research on the Optimization of Continuous Gas Lift Production from Multiple Wells on the Platform
Abstract
1. Introduction
2. Platform Continuous Gas Lift Optimization Model
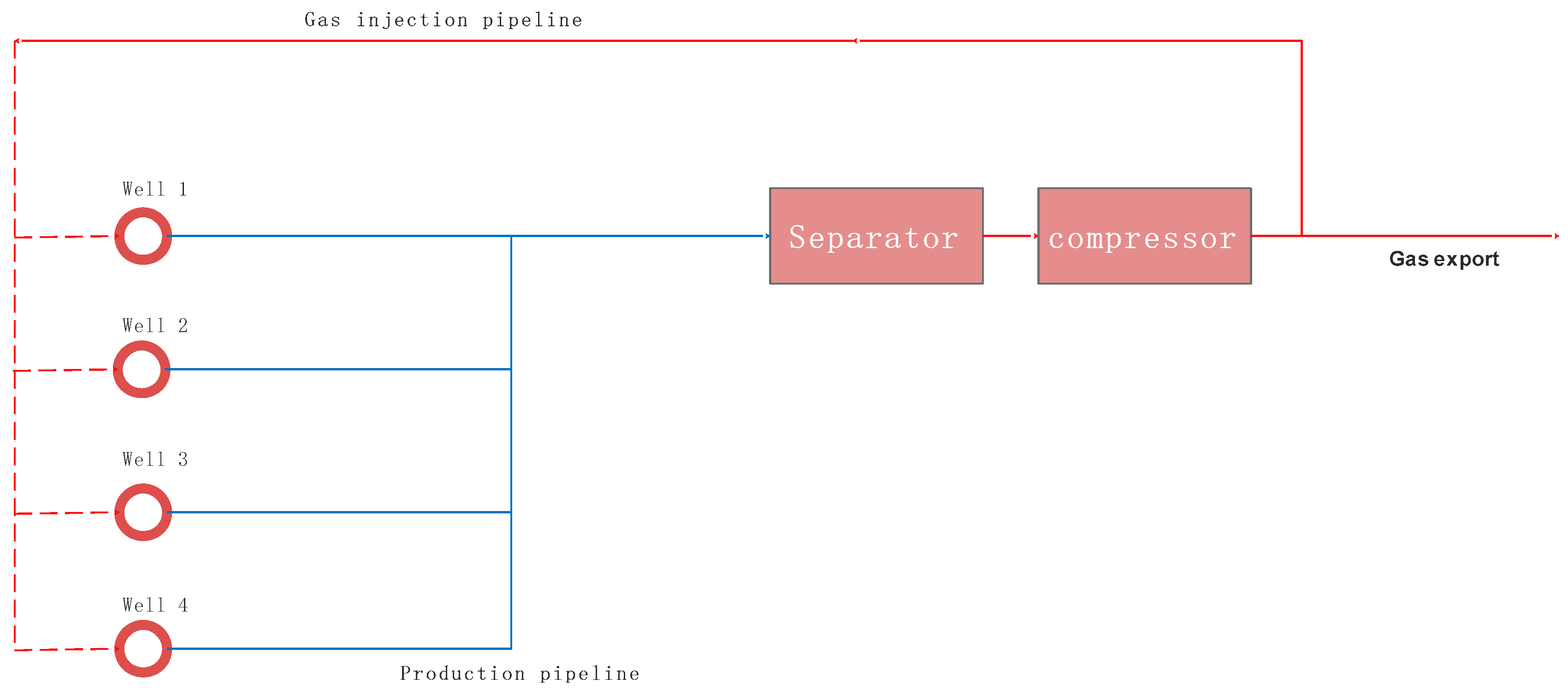
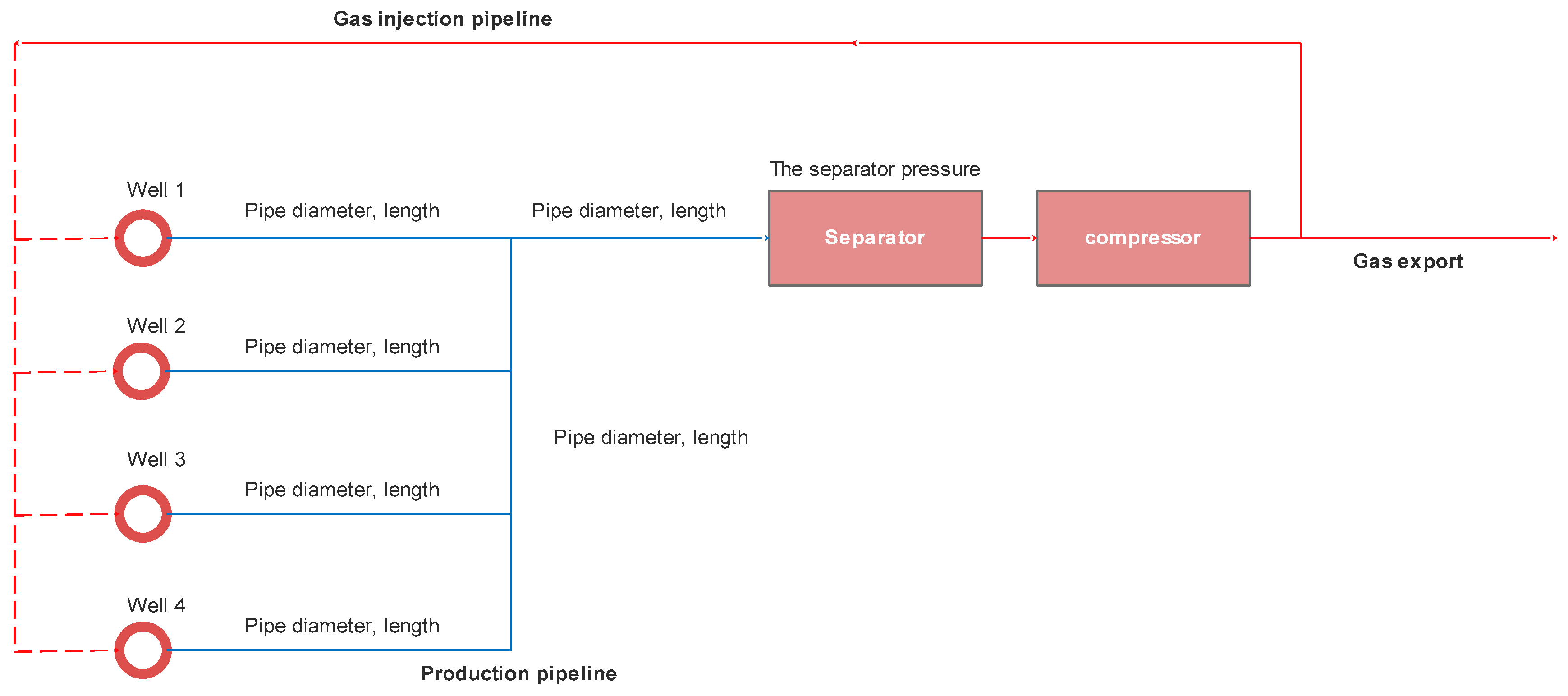
2.1. Problem Description
2.2. Mathematical Modeling
2.2.1. Establish Optimization Model
2.2.2. Basic Calculations
- (1)
- Critical liquid-carrying flow calculation model
- (2)
- Performance calculation of gas well inflow
- (3)
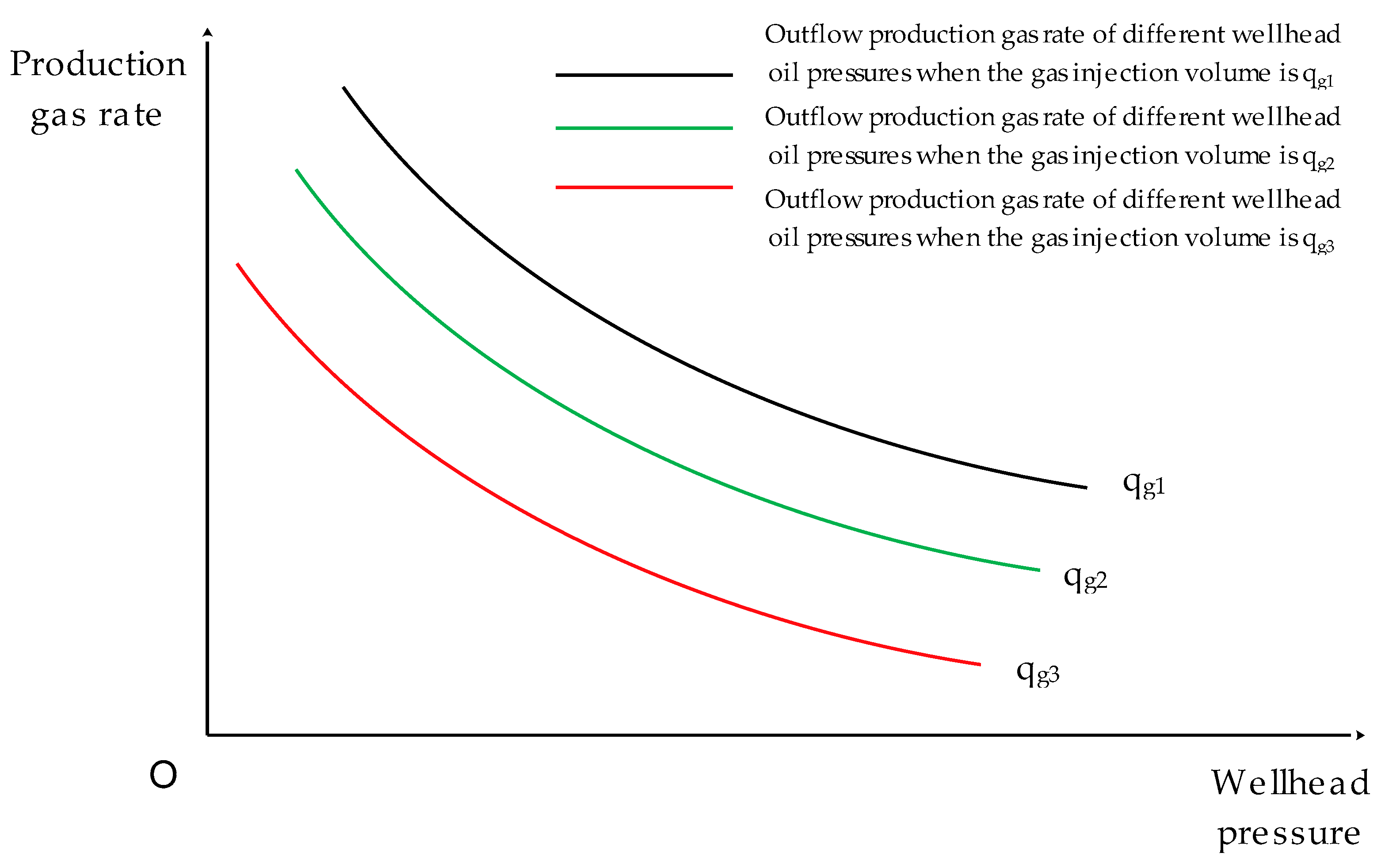
- Gas well gas lift performance curve
2.3. Optimization Algorithm
- (1)
- Draw the inflow curve of each well with the wellhead as the node under different gas injection rates.
- (2)
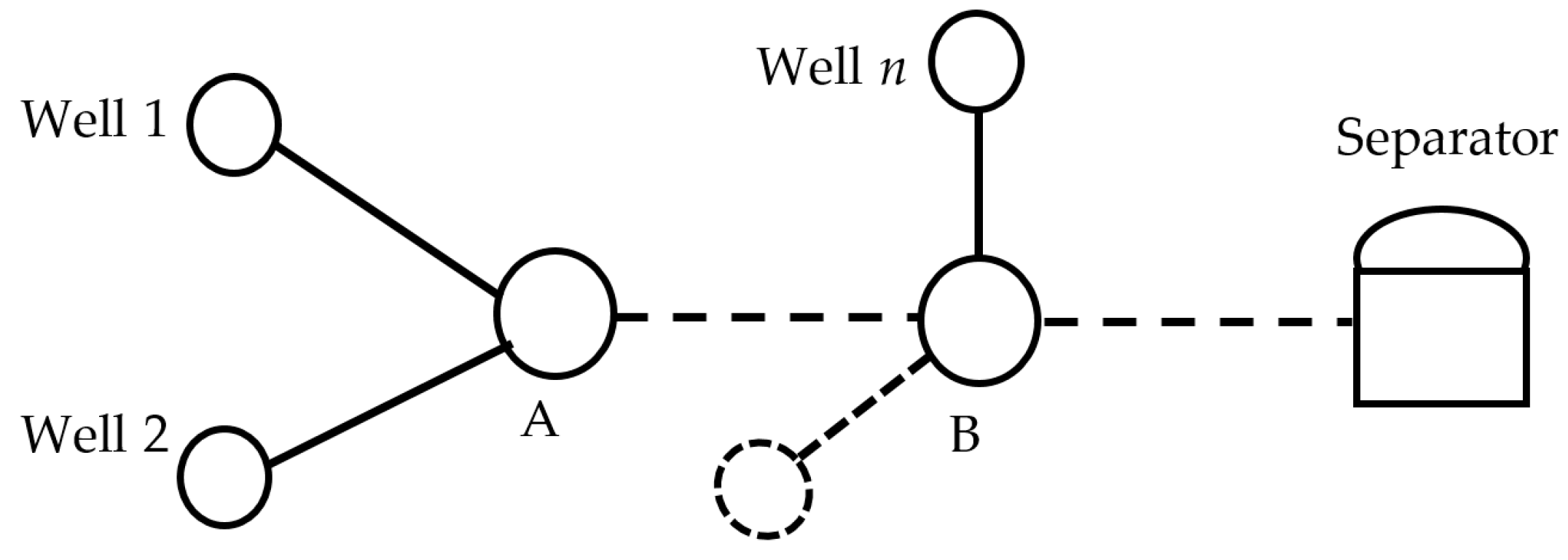
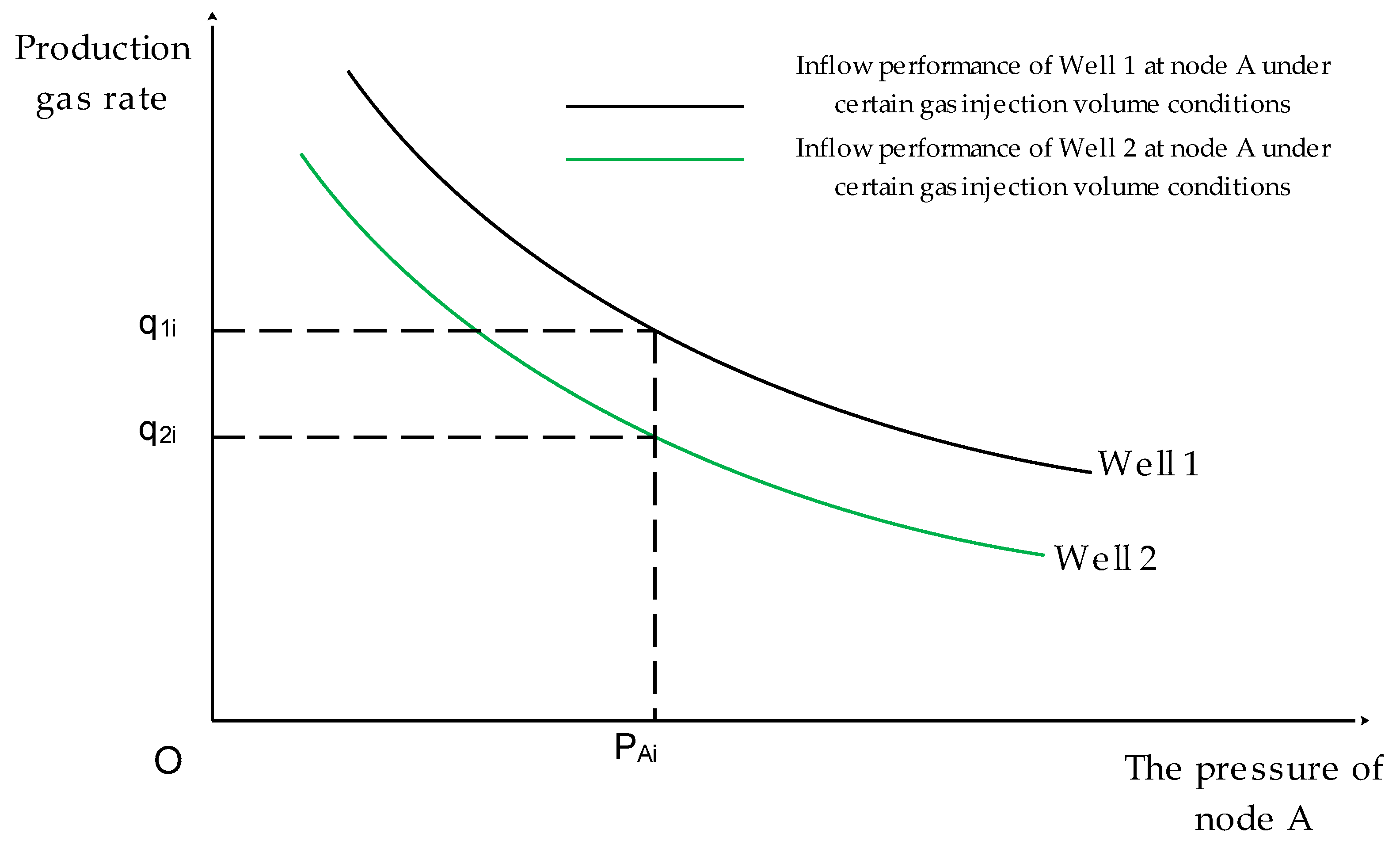
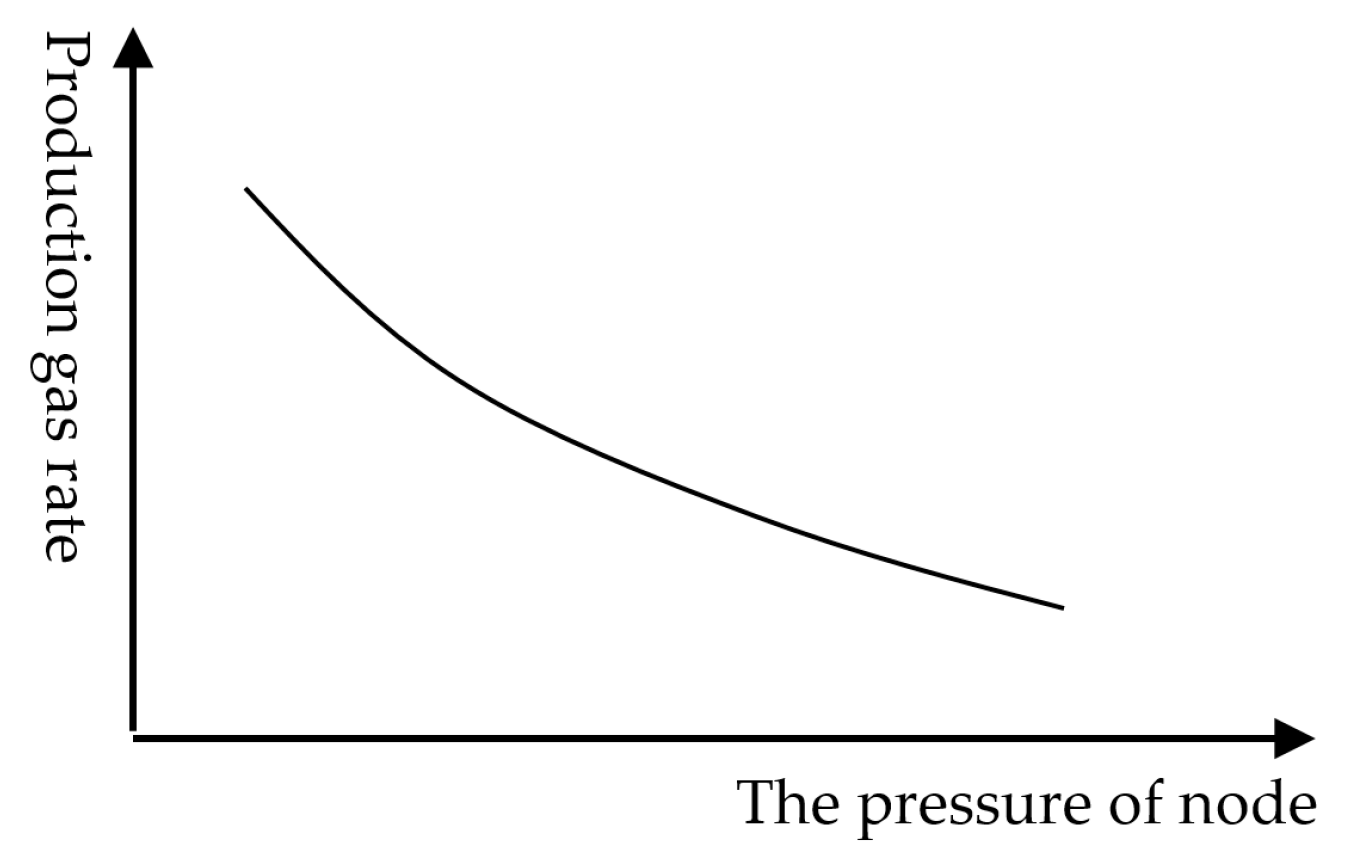
- For any solution (, ,..., ), use the interpolation method to find the wellhead inflow curve of each gas lift well. The fluid at node A comes from wells 1 and 2. For well 1, take a series of points on the inflow curve, calculate to node A according to the multiphase pipe flow theory and obtain the inflow curve of well 1 for node A. In the same way, the inflow curve of well 2 to node A can be obtained, as shown in Figure 6.
- (3)
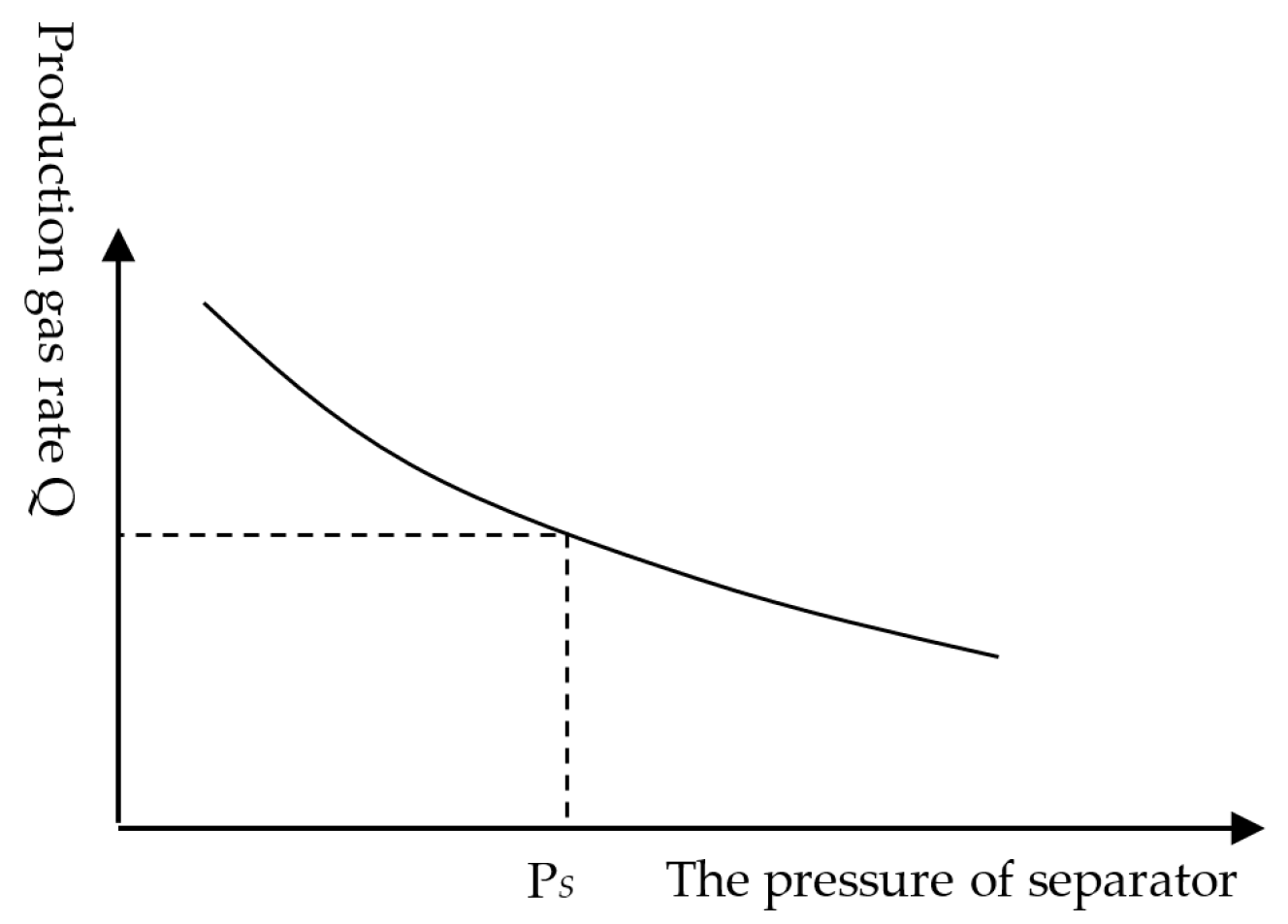
- When the pressure of node A is PAi, the gas flow rates q1i and q2i of well 1 and well 2 flowing into node A can be obtained from Figure 6. The gas rate of node A is qAi = q1i + q2i. In this way, a series of (PA1, qA1), (PA2, qA2)... (PAm, qAm) can be obtained. That is, the inflow curve of node A is obtained. See Figure 7.
- (4)
- According to the above method, the inflow curve of each node and the inflow curve with the separator as the node can be further obtained, as shown in Figure 8. According to the set separator pressure, the total gas production and liquid production can be obtained from the inflow curve of the separator. That is, the solution of the optimized gas distribution plan of the platform is divided by the maximum gas production of the system to obtain the fitness of the particle.
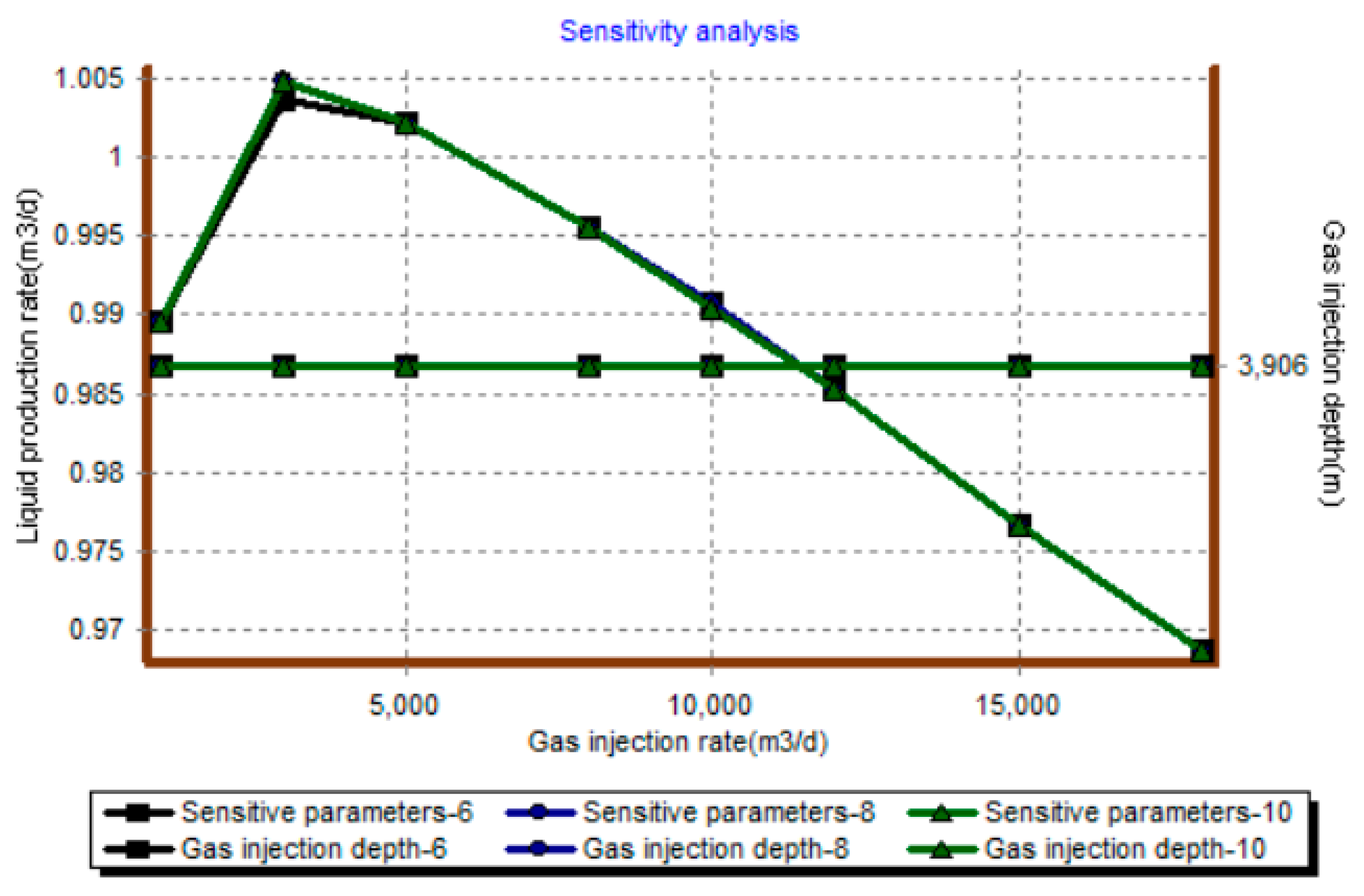
3. Example Calculation Analysis
3.1. Basic Parameters of the Platform
- (1)
- Ground pipe network parameters of the platform
- (2)
- Basic parameters of each well
3.2. Basic Calculations
- (1)
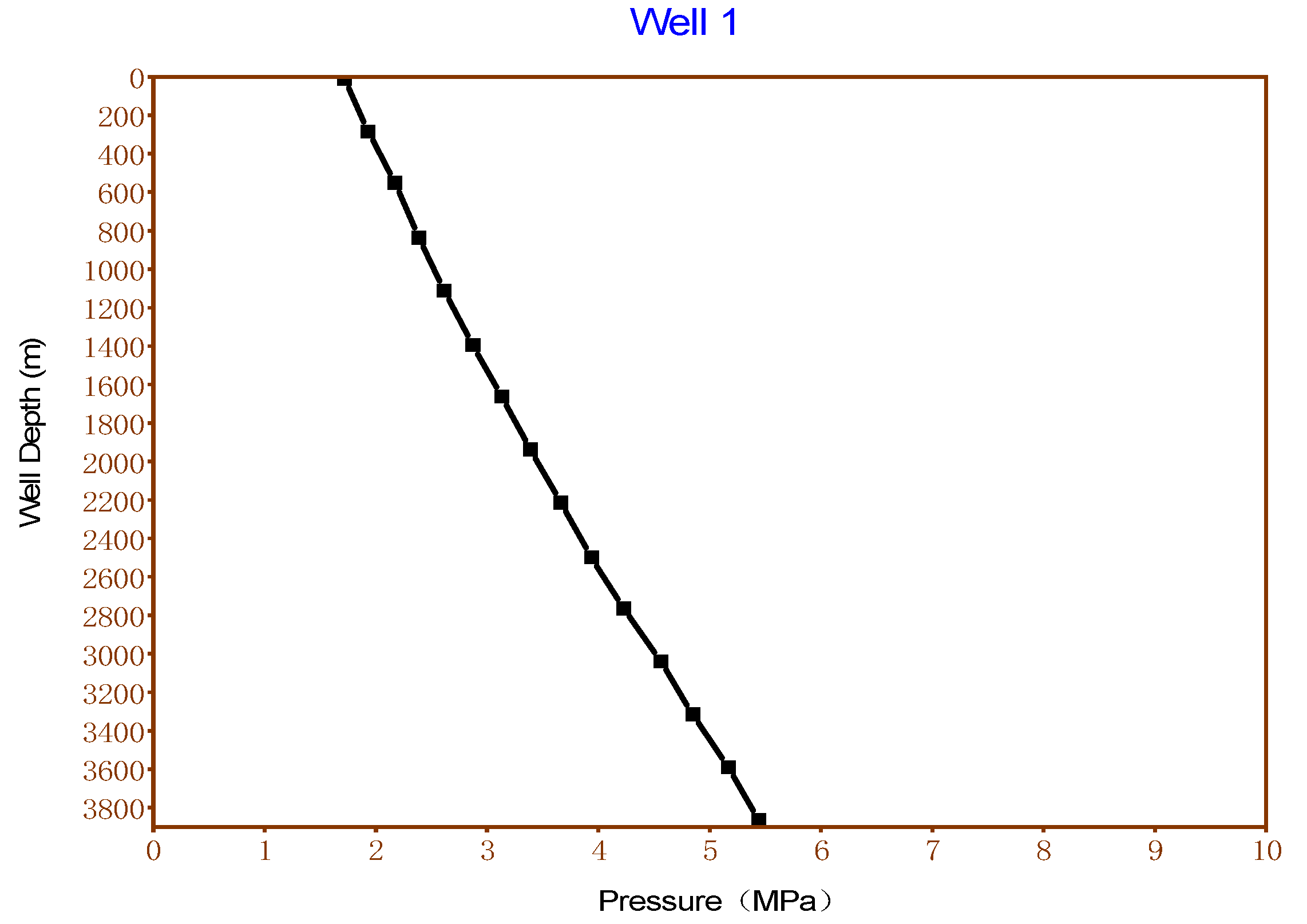
- Calculation of bottom hole flow pressure of each well
- (2)
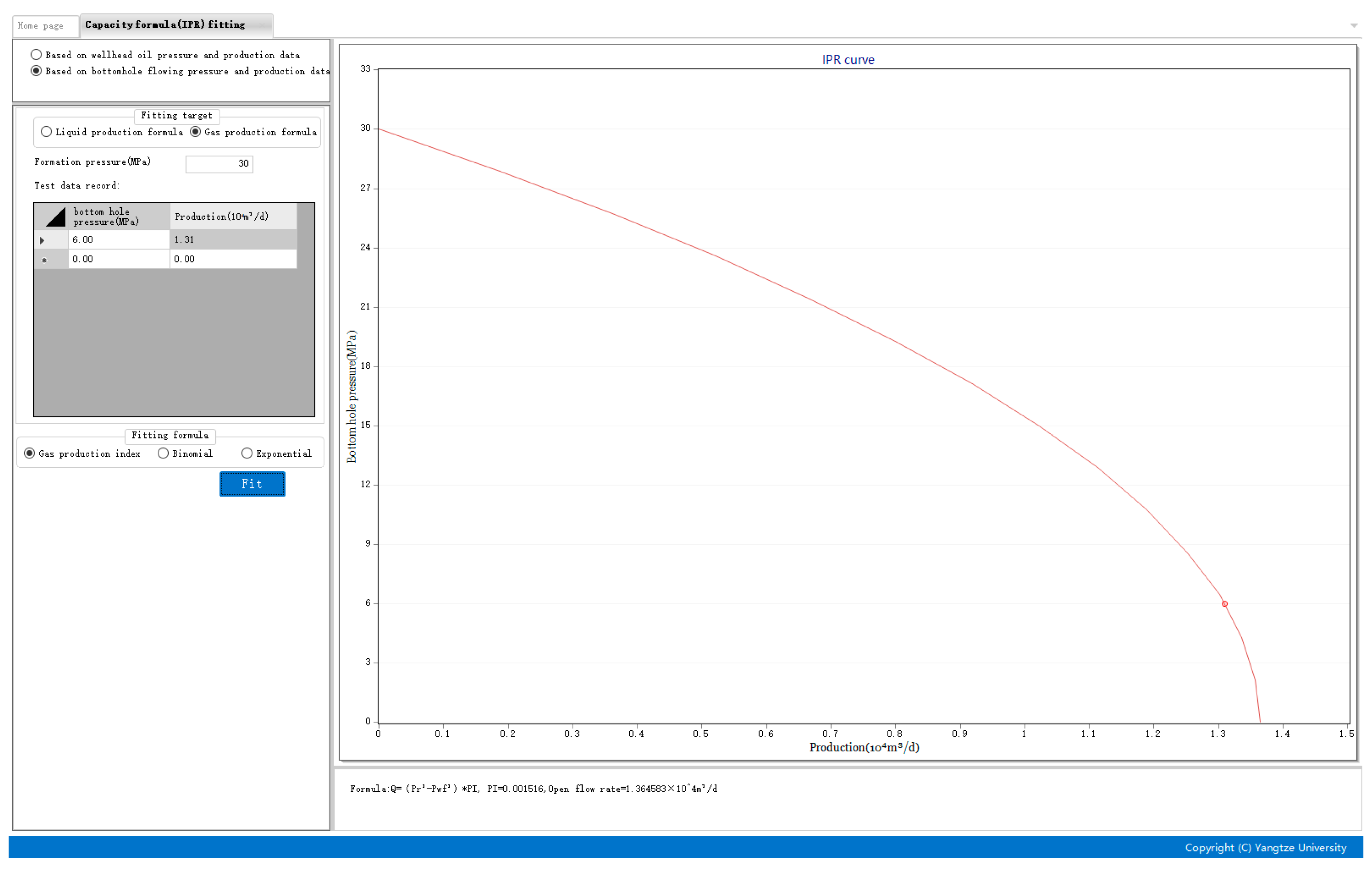
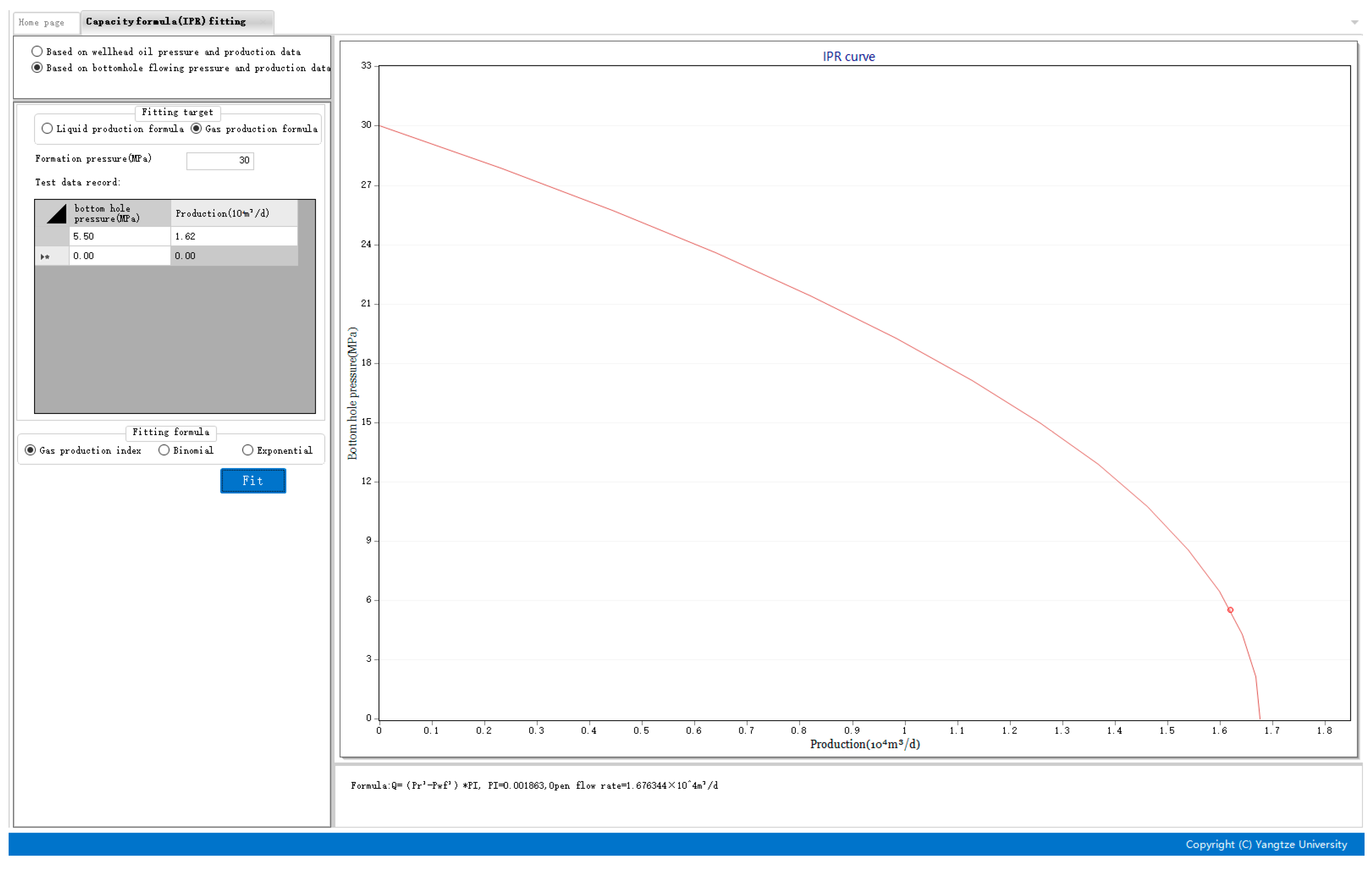
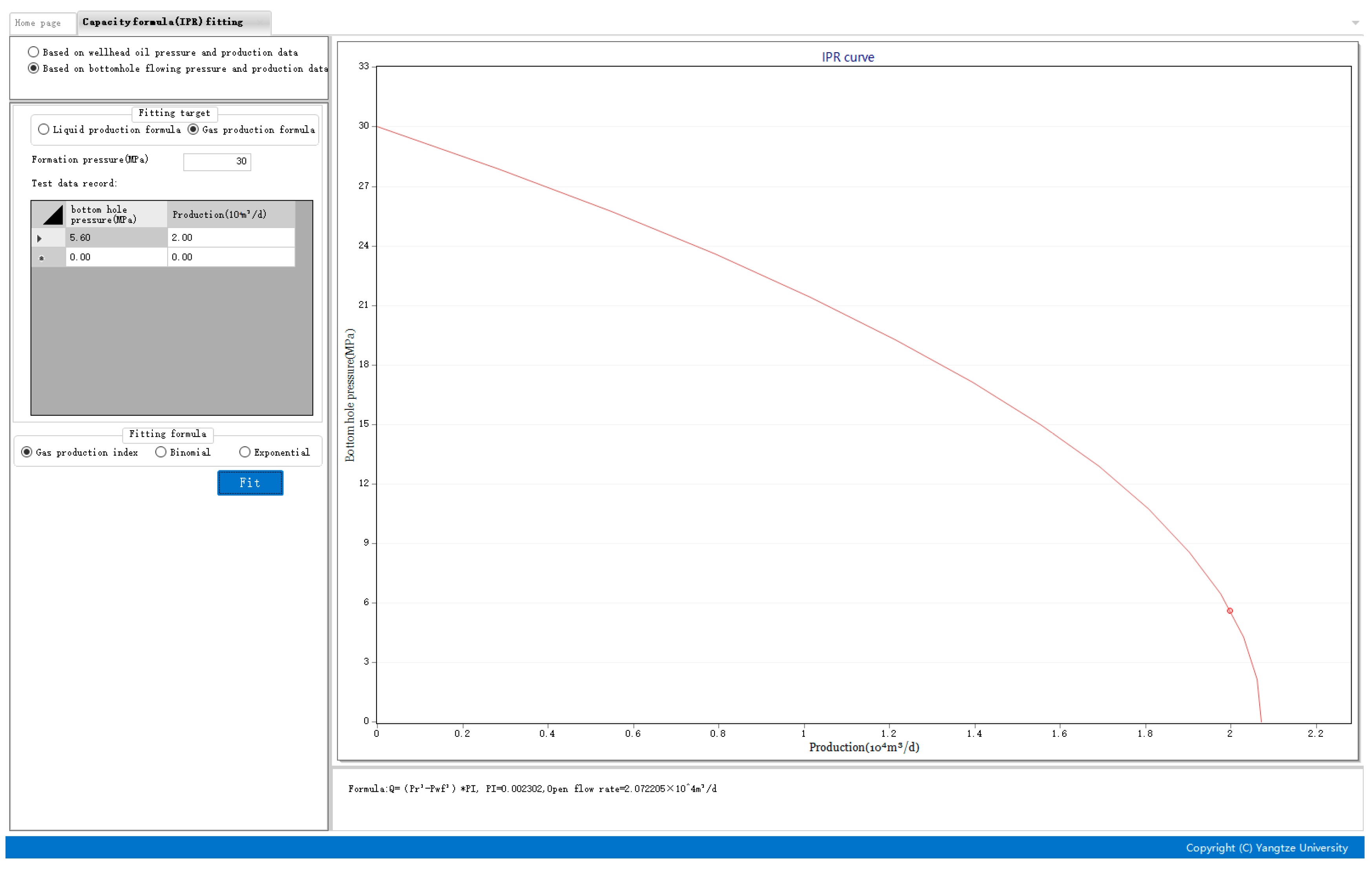
- Calculation of gas production index of each well
- (3)
- Gas lift performance curve drawing
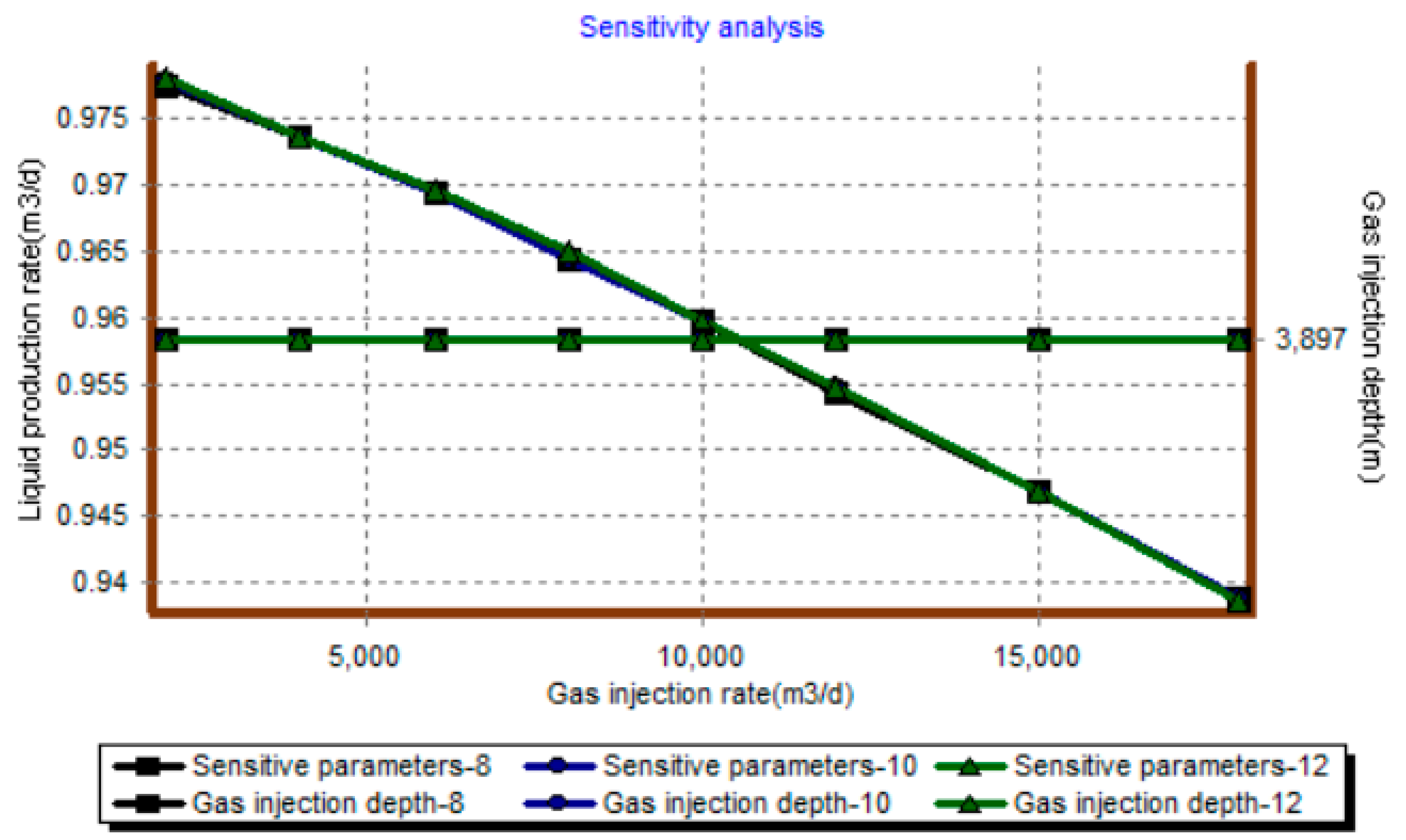
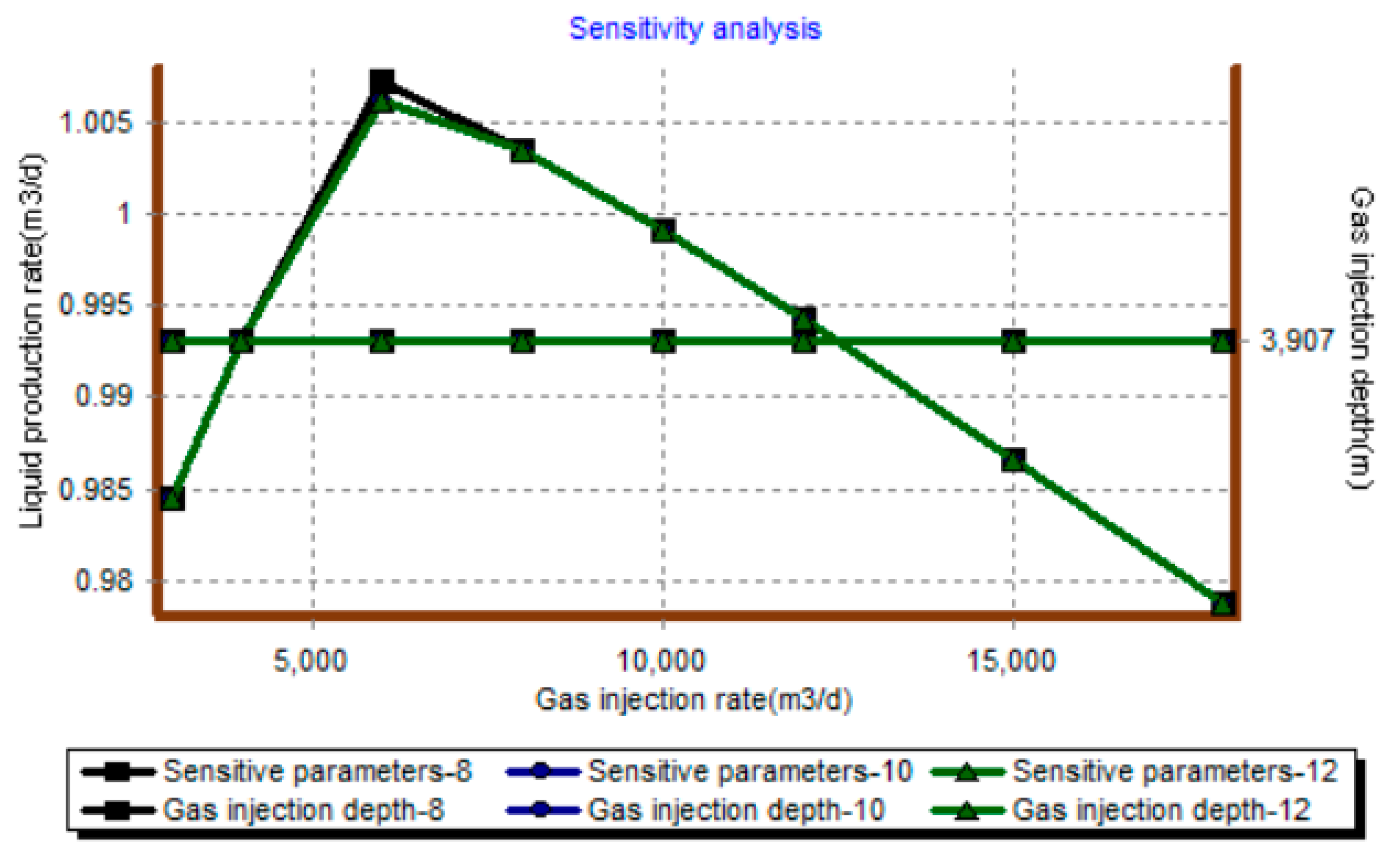
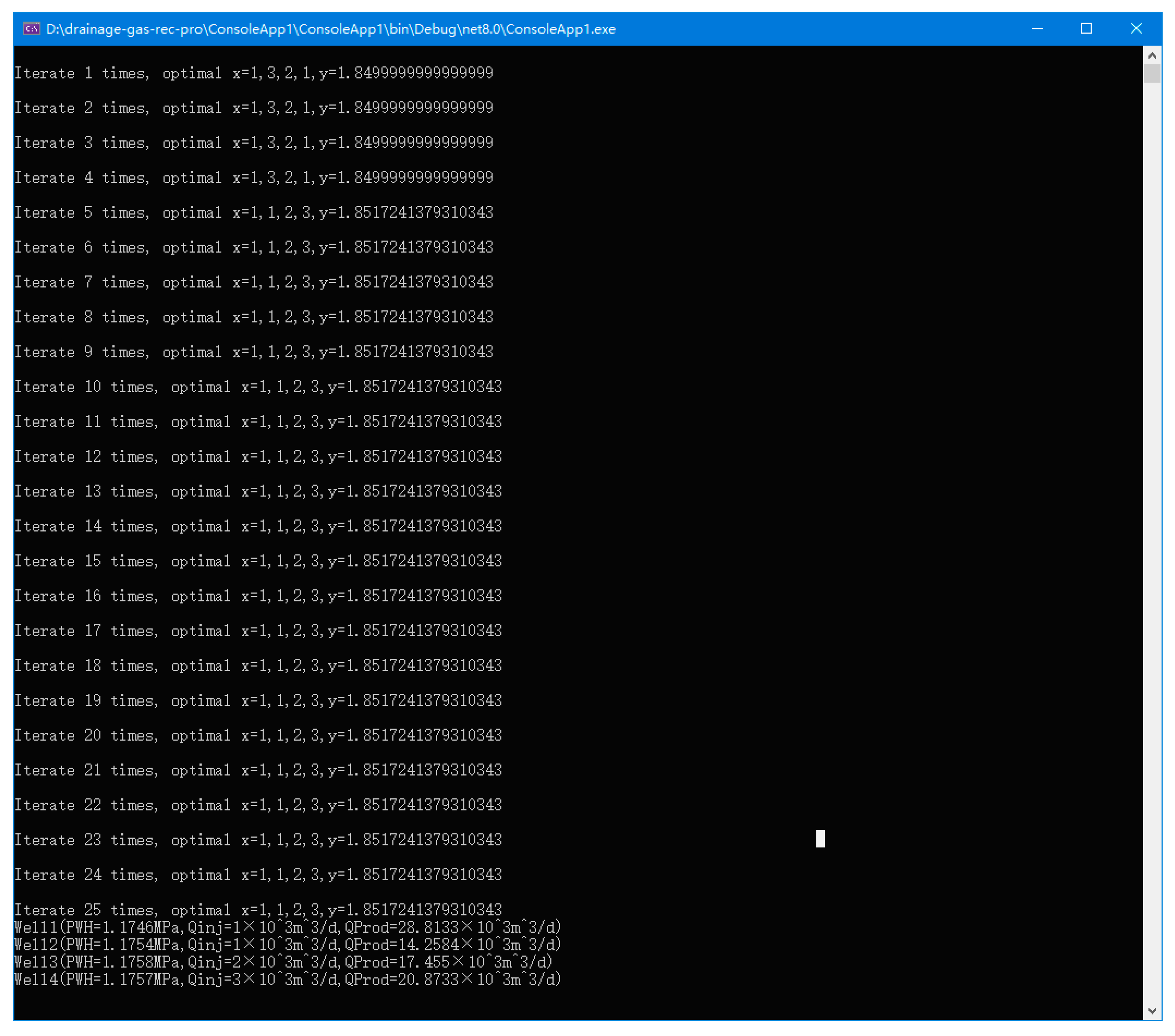
3.3. Optimize Calculation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martinez, E.R.; Moreno, W.J.; Moreno, J.A.; Maggiolo, R. Application of genetic algorithm on the distribution of gas-lift injection. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 27–29 April 1994. SPE-26993-MS. [Google Scholar]
- Wang, Q.; Zhang, B.; Liu, X.; Liao, R. Optimization for a Continuous Gas lift system with quadratic programming. J. Jianghan Pet. Inst. 1994, 16, 78–81. [Google Scholar]
- Liu, X.; Zhang, B.; Wang, Q.; Liao, R.; Guan, D. A multiobjective optimum approach to the allocation of gas quantity for a continuous gas-lift unit. Pet. Explor. Dev. 1995, 22, 59–62+99. [Google Scholar]
- Liu, X.; Wang, Q.; Liao, R.; Zhang, B. An application of optimum theory to gas allocation in a continuous gas lift well system. J. Jianghan Pet. Inst. 1997, 19, 52–56. [Google Scholar]
- Yang, Y. Continuous Gas Lift Optimized Gas Distribution and Optimal Design Technology. Master's Thesis, Southwest Petroleum University, Chengdu, China, 2002. [Google Scholar]
- Alarco, G.A.; Torres, C.F.; Gomez, L. Global optimization of gas allocation to a group of wells in artificial lift using nonlinear constrained programming. J. Energy Resour. Technol. 2002, 124, 262–268. [Google Scholar] [CrossRef]
- Wang, L.; Geng, L.; Yang, Y.; Wang, J. Establishment and application of mathematic model of gas distribution optimization for continuous gas lift to Wendong oilfield. Pet. Geol. Recovery Effic. 2003, 10, 76–78. [Google Scholar]
- Yu, L.; Wu, X.; Guan, J.; Zhang, Q. Optimal gas allocation Technique in Gas lift and its economic evaluation. J. Jianghan Pet. Inst. 2003, 25, 87–88+10. [Google Scholar]
- Zhong, H.; Li, Y.; Liu, Y.; Ling, R. Approach for optimization of gas allocation to a group of well and oilfield in artificial lift. Drill. Prod. Technol. 2005, 28, 27–30+4. [Google Scholar]
- Zhong, H.; Li, Y.; Liu, Y. Solution of optimum gas allocation model for gas lift block with sequential unconstrained minimization technique. Acta Pet. Sin. 2007, 28, 146–150. [Google Scholar]
- Nakashima, P.; Camponogara, E. Optimization of lift-gas allocation using dynamic programming. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2006, 36, 407–414. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, B.; Wang, N.; Xie, J.; Yi, G. Improved non-dominated genetic algorithm for solving gas lifting allocation optimization problem. J. Southwest Pet. Univ. Sci. Technol. Ed. 2009, 31, 64–66+182. [Google Scholar]
- Garcia, A.P.; Rosa, V.R. A Genetic Algorithm for Gas Lift Optimization With Compression Capacity Limitation. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Mexico City, Mexico, 16–18 April 2012; pp. 1–9. [Google Scholar]
- Ghaedi, M.; Ghotbi, C.; Aminshahidy, B. Optimization of gas allocation to a group of wells in gas lift in one of the Iranian oil fields using an efficient hybrid genetic algorithm (HGA). Pet. Sci. Technol. 2013, 31, 949–959. [Google Scholar] [CrossRef]
- Wei, R.; Yuan, X.; Zhang, G.; Zhang, Y.; Yang, F. Optimizing gas distribution method for multi-objective gas lift system. China Pet. Chem. Ind. Stand. Qual. 2013, 34, 111. [Google Scholar]
- Ghaedi, M.; Ghotbi, C.; Aminshahidy, B. The optimization of gas allocation to a group of wells in a gas lift using an efficient Ant Colony Algorithm (ACO). Energy Sources Part A Recovery Util. Environ. Eff. 2014, 36, 1234–1248. [Google Scholar] [CrossRef]
- Aoun, A.E.; Maougal, F.; Kabour, L.; Liao, T.; Abdallah Elhadj, B.; Behaz, S. Hydrate Mitigation and Flare Reduction Using Intermittent Gas Lift in Hassi Messaoud, Algeria. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018; pp. 1–23. [Google Scholar]
- Miresmaeili, S.O.H.; Zoveidavianpoor, M.; Jalilavi, M.; Jalilavi, M.; Gerami, S.; Rajabi, A. An improved optimization method in gas allocation for continuous flow gas-lift system. J. Pet. Sci. Eng. 2019, 172, 819–830. [Google Scholar] [CrossRef]
- Namdar, H. Developing an improved approach to solving a new gas lift optimization problem. J. Pet. Explor. Prod. Technol. 2019, 9, 2965–2978. [Google Scholar] [CrossRef]
- Khoshkbarchi, M.; Rahmanian, M.; Cordazzo, J.; Nghiem, L. Application of Mesh Adaptive Derivative-Free Optimization Technique for Gas-Lift Optimization in an Integrated Reservoirs, Wells, and Facilities Modeling Environment. In Proceedings of the SPE Canada Heavy Oil Conference, Virtual, 28 September–2 October 2020; pp. 1–18. [Google Scholar]
- Bondarenko, A.V.; Islamov, S.R.; Ignatyev, K.V.; Mardashov, D.V. Laboratory studies of polymer compositions for well-kill under increased fracturing. Perm J. Pet. Min. Eng. 2020, 20, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Merzoug, A.; Chemmakh, A.; Ouadi, H.; Laalam, A.; Djezzar, S.; Boualam, A.; Mouedden, N.; Rasouli, V.; Ibrahim, E. A New Model for Optimized Gas Allocation in Gas Lift Operation Using Metaheuristic Algorithms. In Proceedings of the SPE Middle East Artificial Lift Conference and Exhibition, Manama, Bahrain, 25–26 October 2022; pp. 1–12. [Google Scholar]
- Carpenter, C. Numerical simulation of gas lift optimization uses genetic algorithm. J. Pet. Technol. 2022, 74, 65–67. [Google Scholar] [CrossRef]
- Janatian, N.; Sharma, R. A robust model predictive control with constraint modification for gas lift allocation optimization. J. Process Control 2023, 128, 102996. [Google Scholar] [CrossRef]
- Han, L.; Li, J.; Li, W.; Zhang, Y. Robust Optimization of gas distribution Scheme. Comput. Simul. 2023, 40, 71–76+88. [Google Scholar]
- Van Thang, N.; Thang Vinh, P.; Rogachev, M.; Korobov, G.; Zhurkevich, A.; Islamov, S. A comprehensive method for determining the dewaxing interval period in gas lift wells. J. Pet. Explor. Prod. Technol. 2023, 13, 1163–1179. [Google Scholar] [CrossRef]
- Belousov, A.; Lushpeev, V.; Sokolov, A.; Sultanbekov, R.; Tyan, Y.; Ovchinnikov, E.; Shvets, A.; Bushuev, V.; Islamov, S. Hartmann–Sprenger Energy Separation Effect for the Quasi-Isothermal Pressure Reduction of Natural Gas: Feasibility Analysis and Numerical Simulation. Energies 2024, 17, 2010. [Google Scholar] [CrossRef]


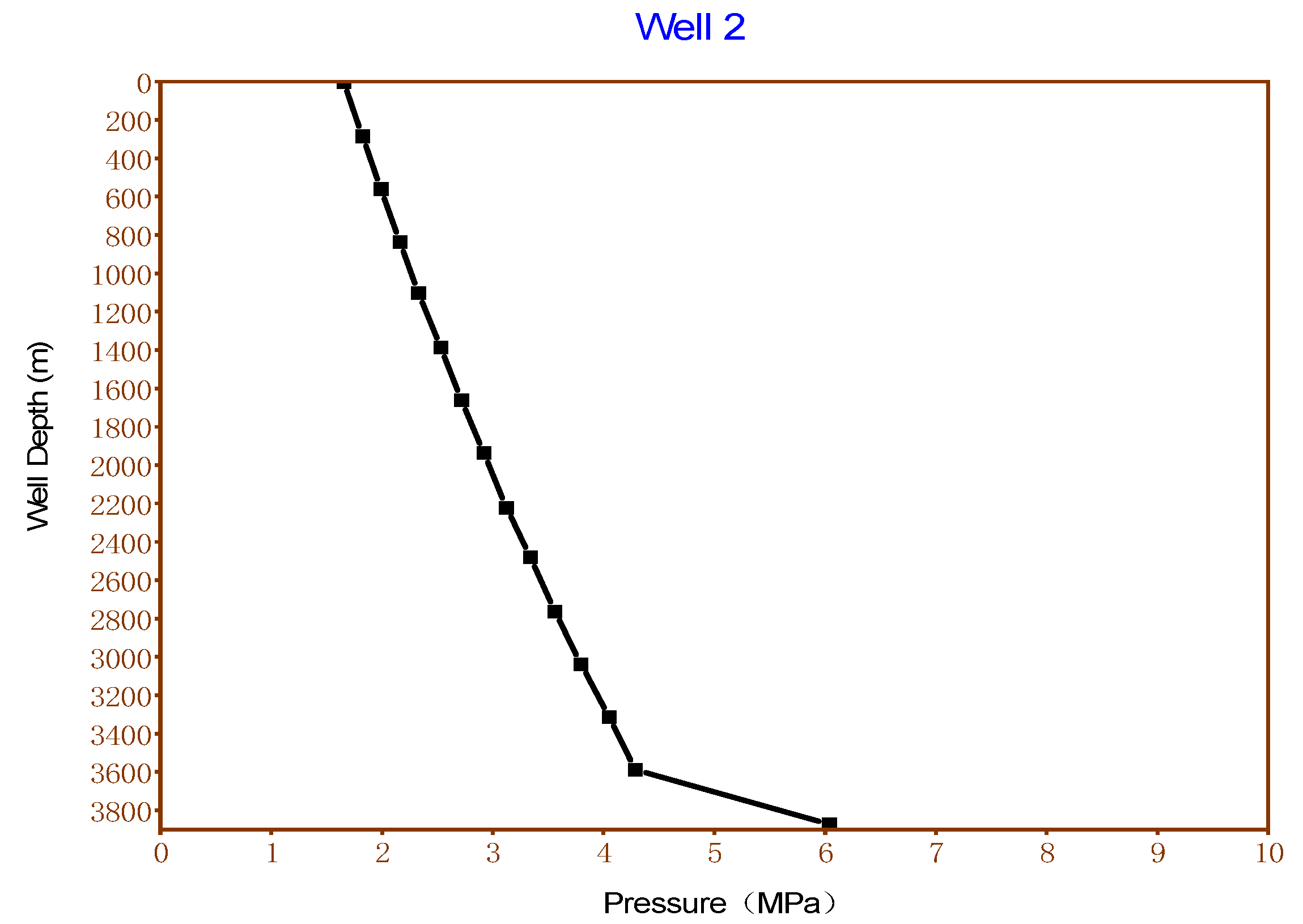
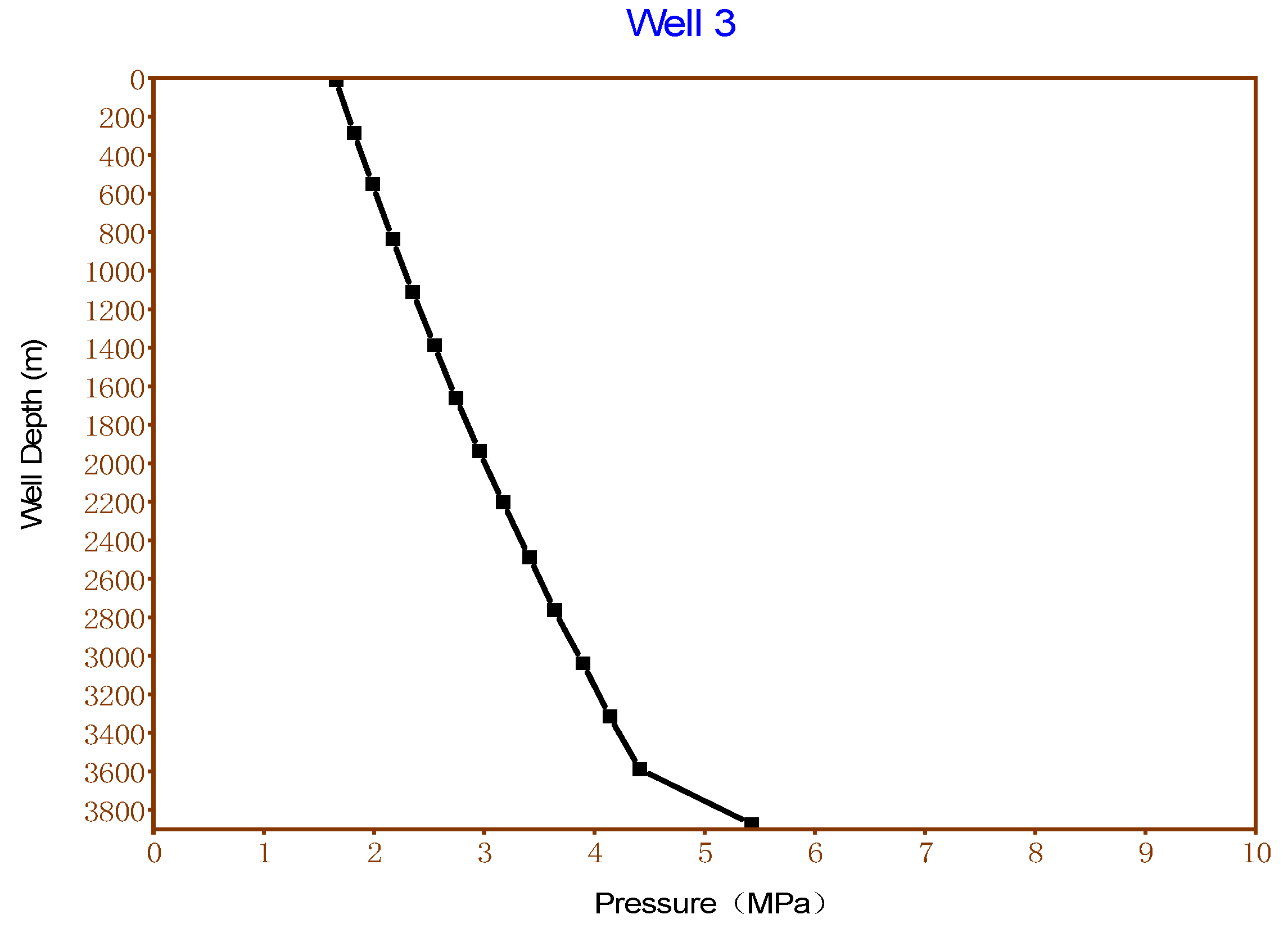
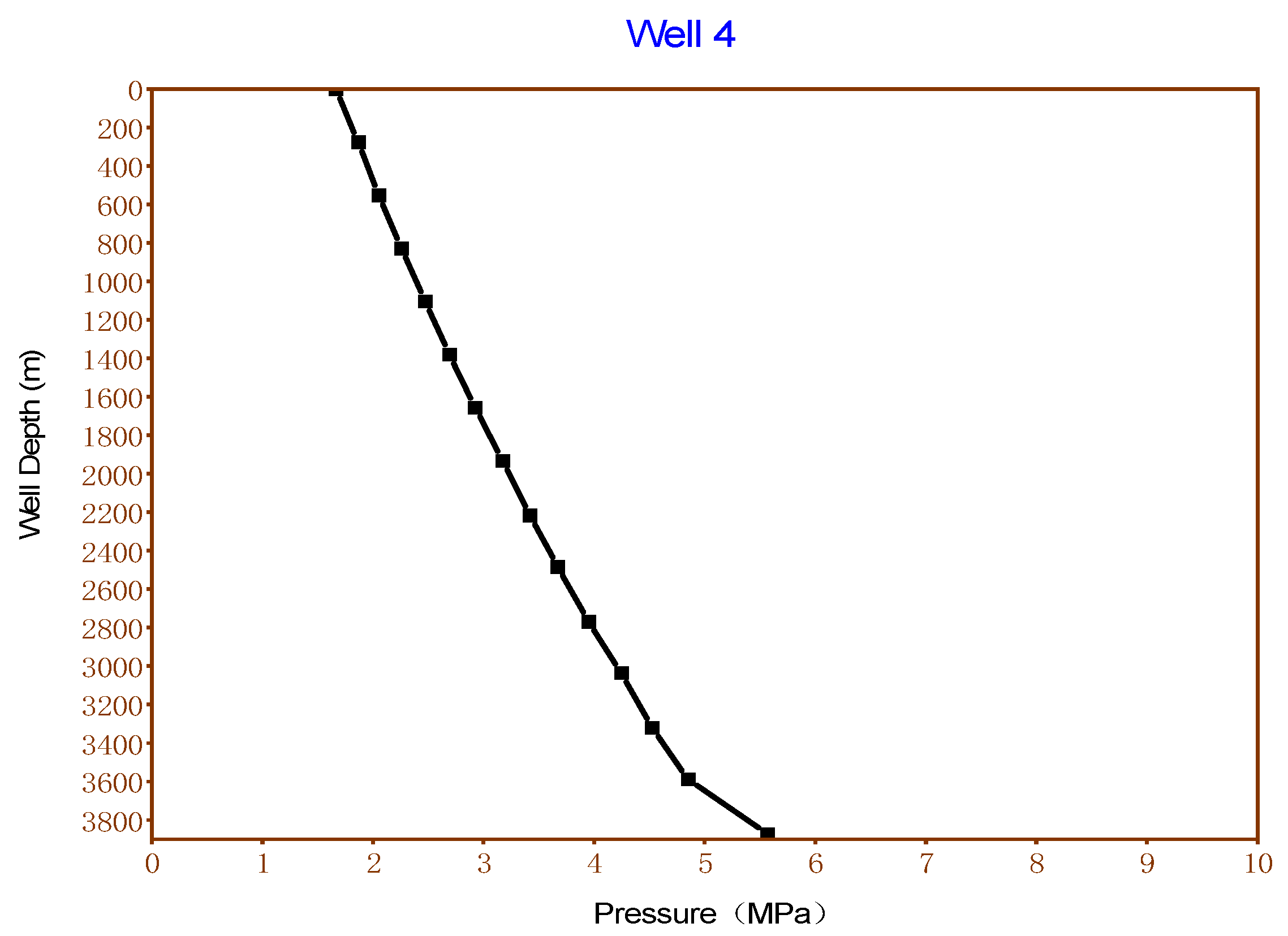


| Well Name | Well 1 | Well 2 | Well 3 | Well 4 | |
|---|---|---|---|---|---|
| Static pressure | MPa | 20–34 | |||
| Production gas index | |||||
| Production liquid index or LGR | |||||
| Oil pipe inner diameter | mm | 62 | 62 | 62 | 62 |
| Deep oil pipe | m | 3967.78 | 3967.78 | 3976.36 | 4038.54 |
| Casing inner diameter | mm | 114.3 | 114.3 | 114.3 | 114.3 |
| Formation temperature | °C | 142 | 141 | 140 | 40 |
| Surface temperature | °C | 15 | 15 | 15 | 15 |
| Relative density of formation water | - | 1.02 | 1.02 | 0 | 0 |
| Natural gas relative density | - | 0.7 | 0.7 | 0 | 0 |
| Wellhead oil pressure | MPa | 1.7 | 1.65 | 1.64 | 1.66 |
| Wellhead casing pressure | MPa | 2.49 | 2.44 | 2.41 | 2.86 |
| Gas production rate | m3/d | 27,710 | 13,085 | 16,164 | 20,013 |
| Liquid production rate | m3/d | 1 | 1 | 1 | 2 |
| Well Name | Pressure of Wellhead/MPa | Injection Gas Rate/103 m3/d | Production Gas Rate (Excluding Injection Gas Rate)/103 m3/d |
|---|---|---|---|
| Well1 | 1.1746 | 1 | 28.813 |
| Well2 | 1.1754 | 1 | 14.258 |
| Well3 | 1.1758 | 2 | 17.455 |
| Well4 | 1.1757 | 3 | 20.873 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Yang, Z.; Zeng, L.; Du, A.; Chen, Y.; Luo, W. Research on the Optimization of Continuous Gas Lift Production from Multiple Wells on the Platform. Processes 2025, 13, 478. https://doi.org/10.3390/pr13020478
Wang Q, Yang Z, Zeng L, Du A, Chen Y, Luo W. Research on the Optimization of Continuous Gas Lift Production from Multiple Wells on the Platform. Processes. 2025; 13(2):478. https://doi.org/10.3390/pr13020478
Chicago/Turabian StyleWang, Qingrong, Zhi Yang, Linjuan Zeng, Anqi Du, Yi Chen, and Wei Luo. 2025. "Research on the Optimization of Continuous Gas Lift Production from Multiple Wells on the Platform" Processes 13, no. 2: 478. https://doi.org/10.3390/pr13020478
APA StyleWang, Q., Yang, Z., Zeng, L., Du, A., Chen, Y., & Luo, W. (2025). Research on the Optimization of Continuous Gas Lift Production from Multiple Wells on the Platform. Processes, 13(2), 478. https://doi.org/10.3390/pr13020478






