Improved Fruit Fly Algorithm to Solve No-Idle Permutation Flow Shop Scheduling Problem
Abstract
1. Introduction
- (1)
- Using the characteristics of specific problems, multiple perturbation operators are designed to enhance the global search ability of the algorithm.
- (2)
- A probabilistic model based on elite subsets is constructed, and the concept of common sequence is introduced. The evolution of fruit flies is achieved through location sequences and common sequences.
- (3)
- The iterative greedy algorithm is used to conduct local searches for the best individuals and guide the fruit fly population to move to a more promising area.
- (4)
- Finally, the experiment verifies that DFFO is an effective method to solve NIPFSP.
2. Problem Description
3. DFFO Algorithm
3.1. Population Initialization
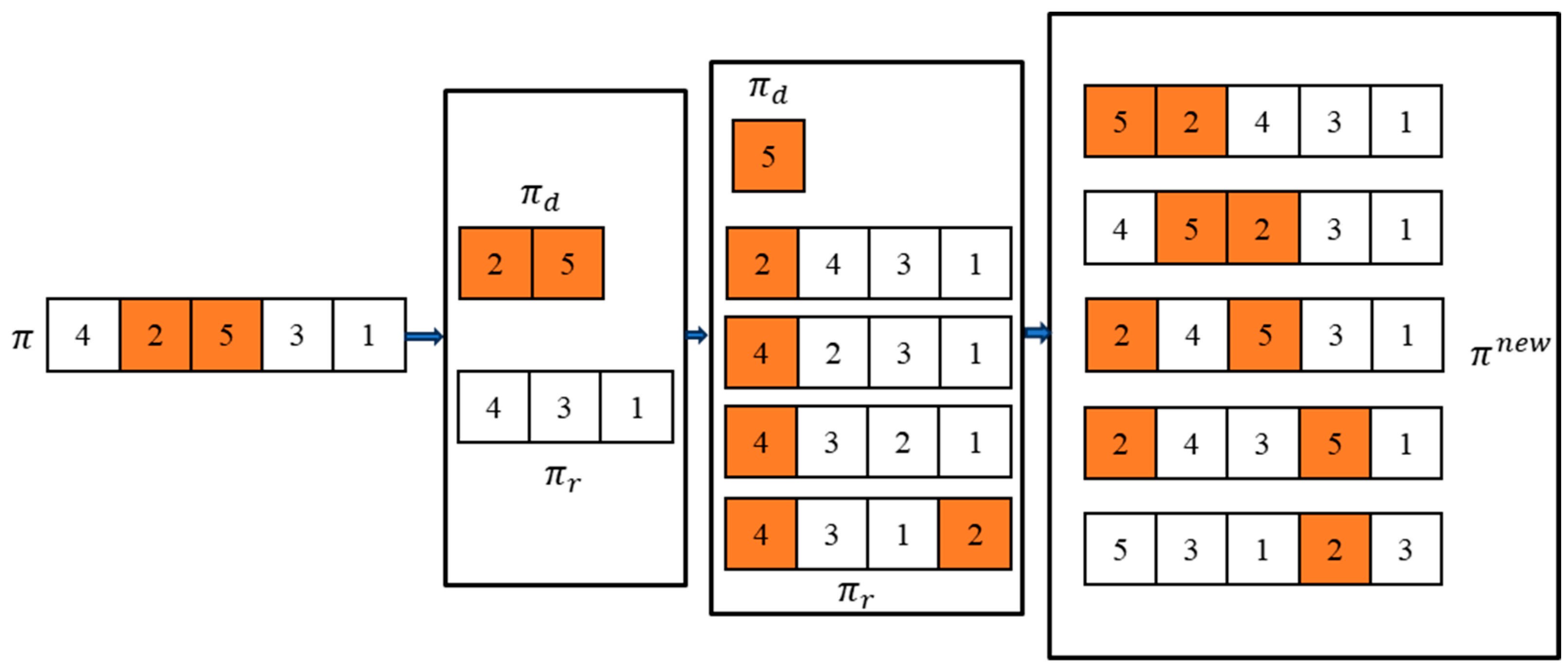
3.2. Smell Search Phase Based on Variable Neighborhoods
3.3. Visual Search Phase Based on a Probability Model
3.4. Local Search
3.5. Complexity Analysis
4. Numerical Results and Comparison
4.1. Experimental Setup
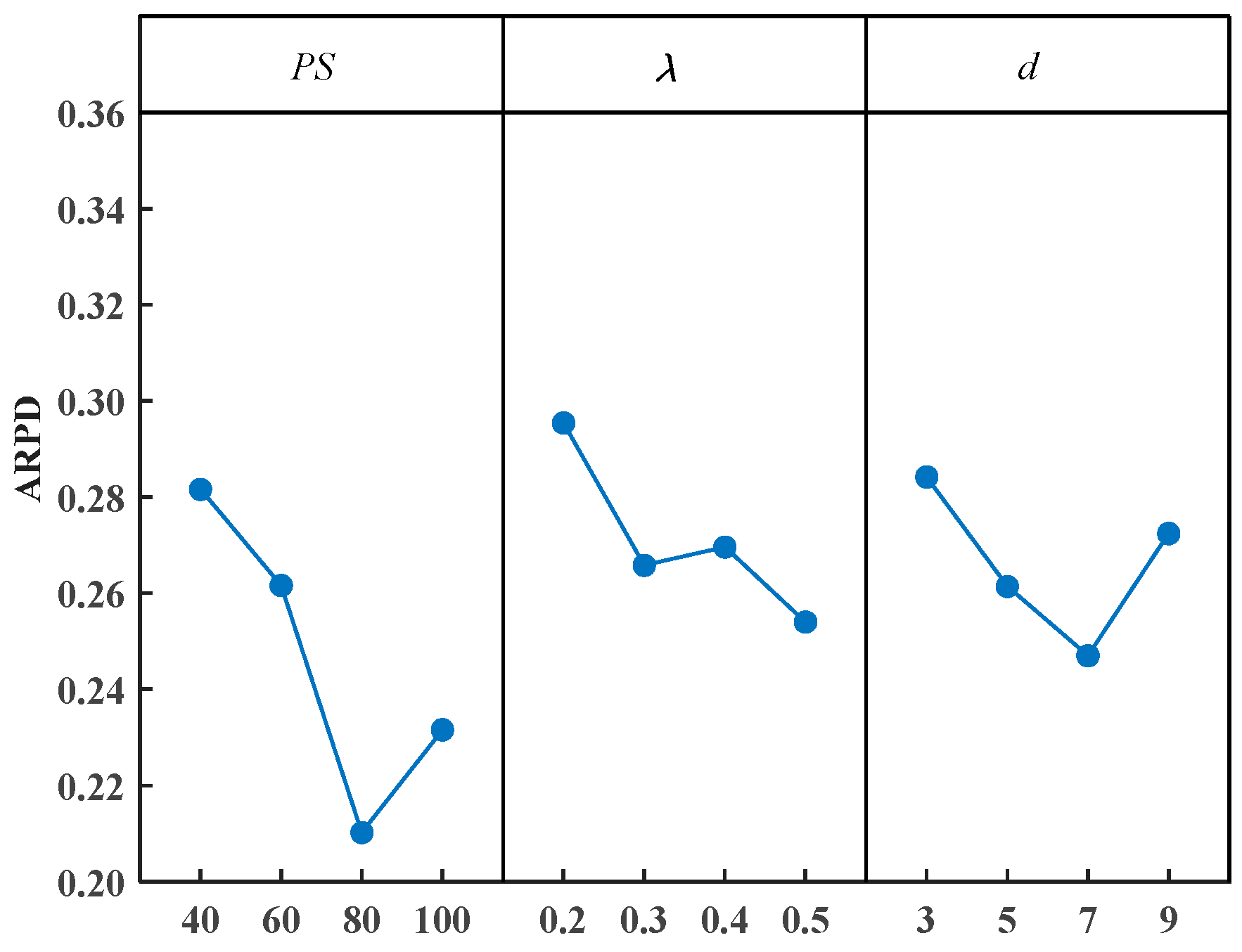
4.2. Parameter Configuration
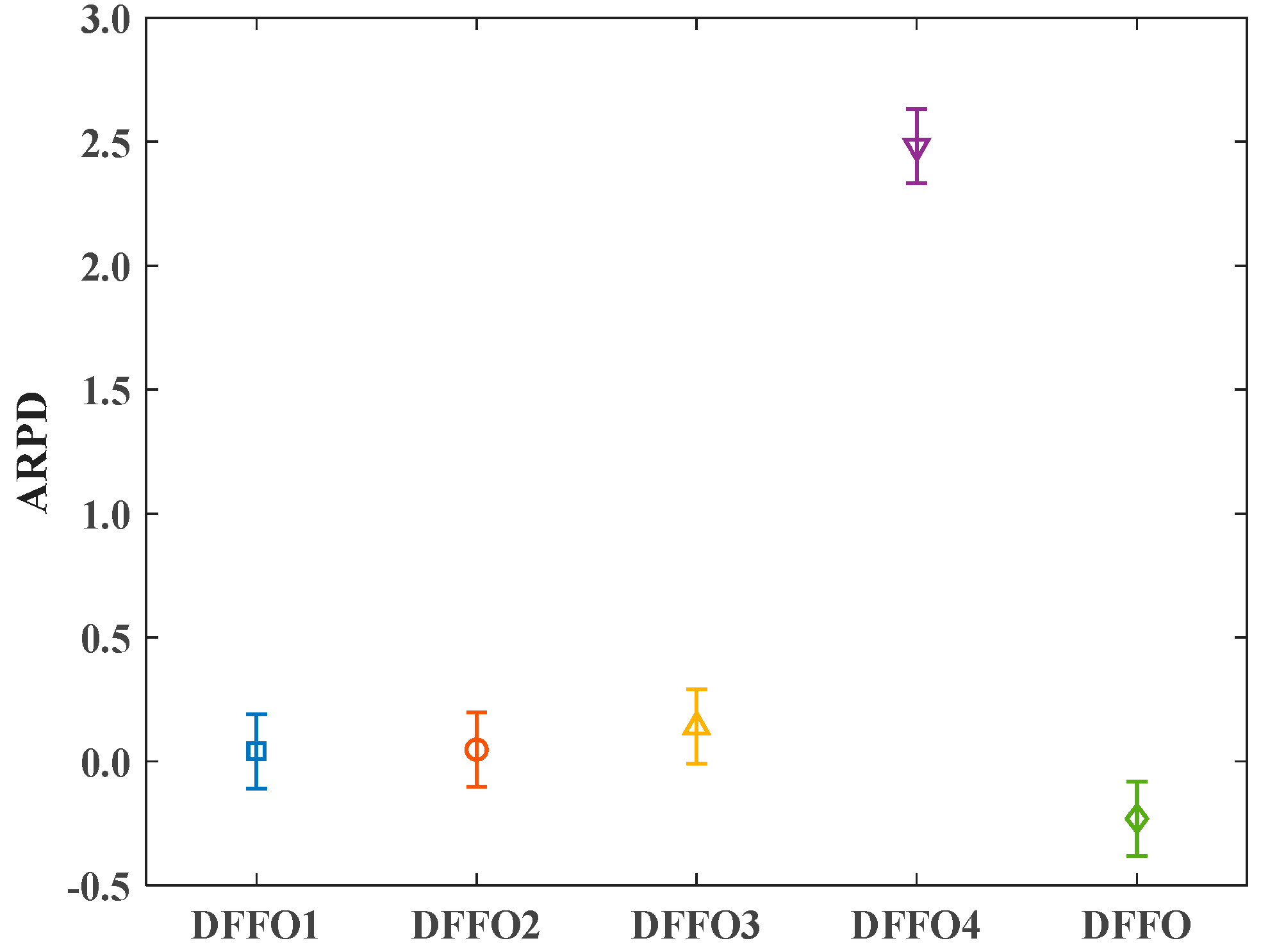
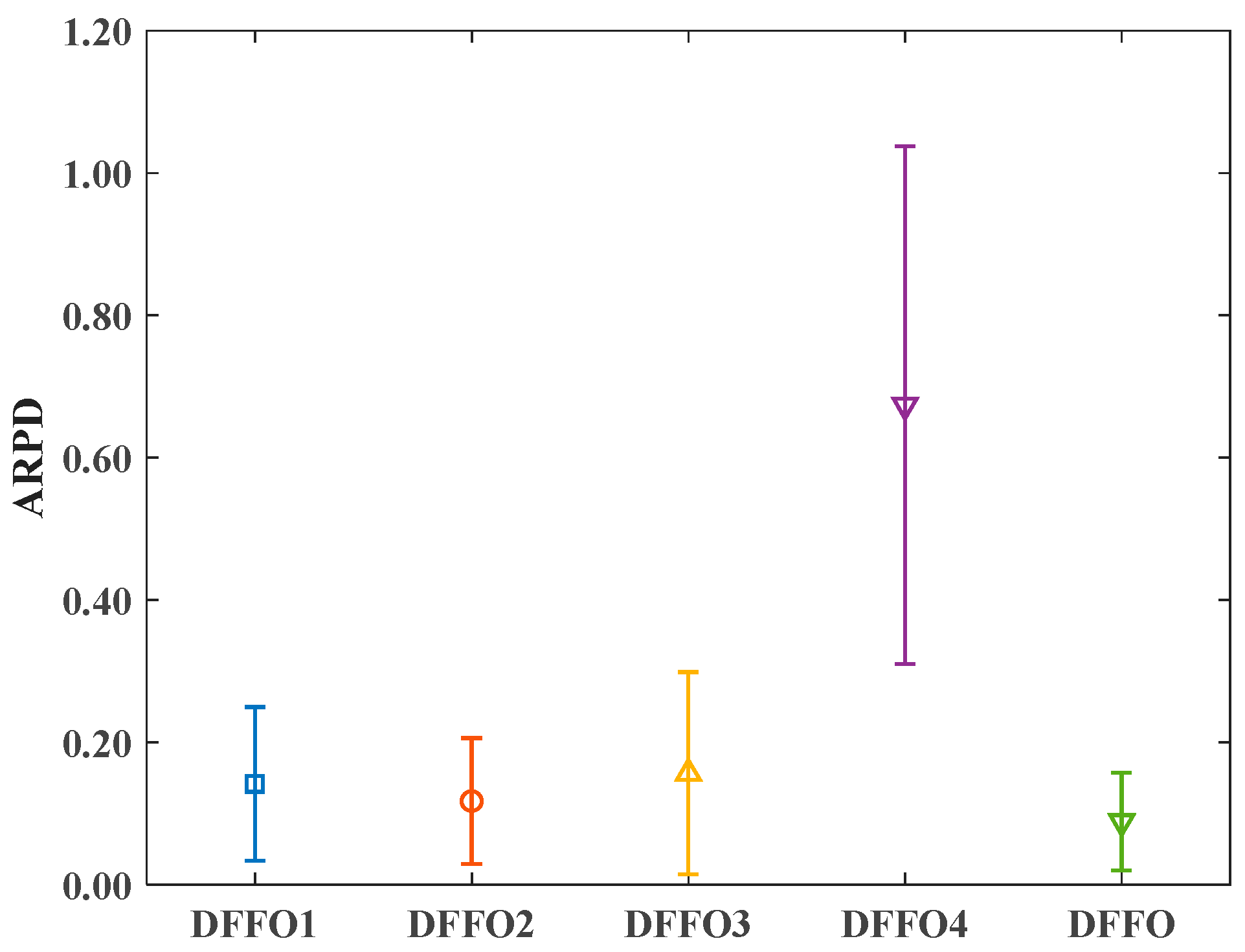
4.3. Performance Analysis of DFFO Components
- (1)
- DFFO1: random initialization of the fruit fly population’s central positions.
- (2)
- DFFO2: replacing variable neighborhood search with single neighborhood search.
- (3)
- DFFO3: removing the visual search phase based on the probability model and using the original update mechanism of the algorithm.
- (4)
- DFFO4: removing the local search strategy.
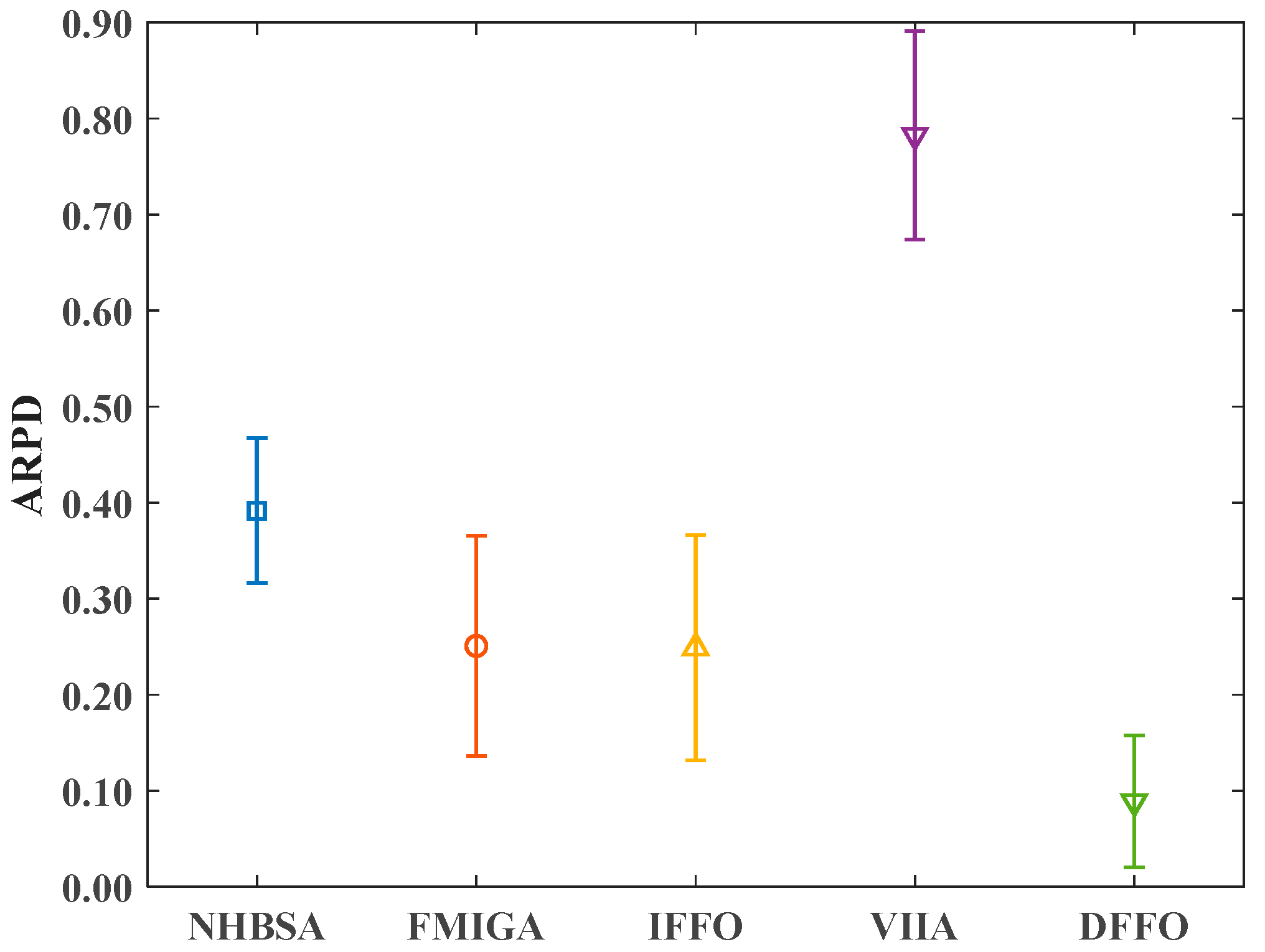
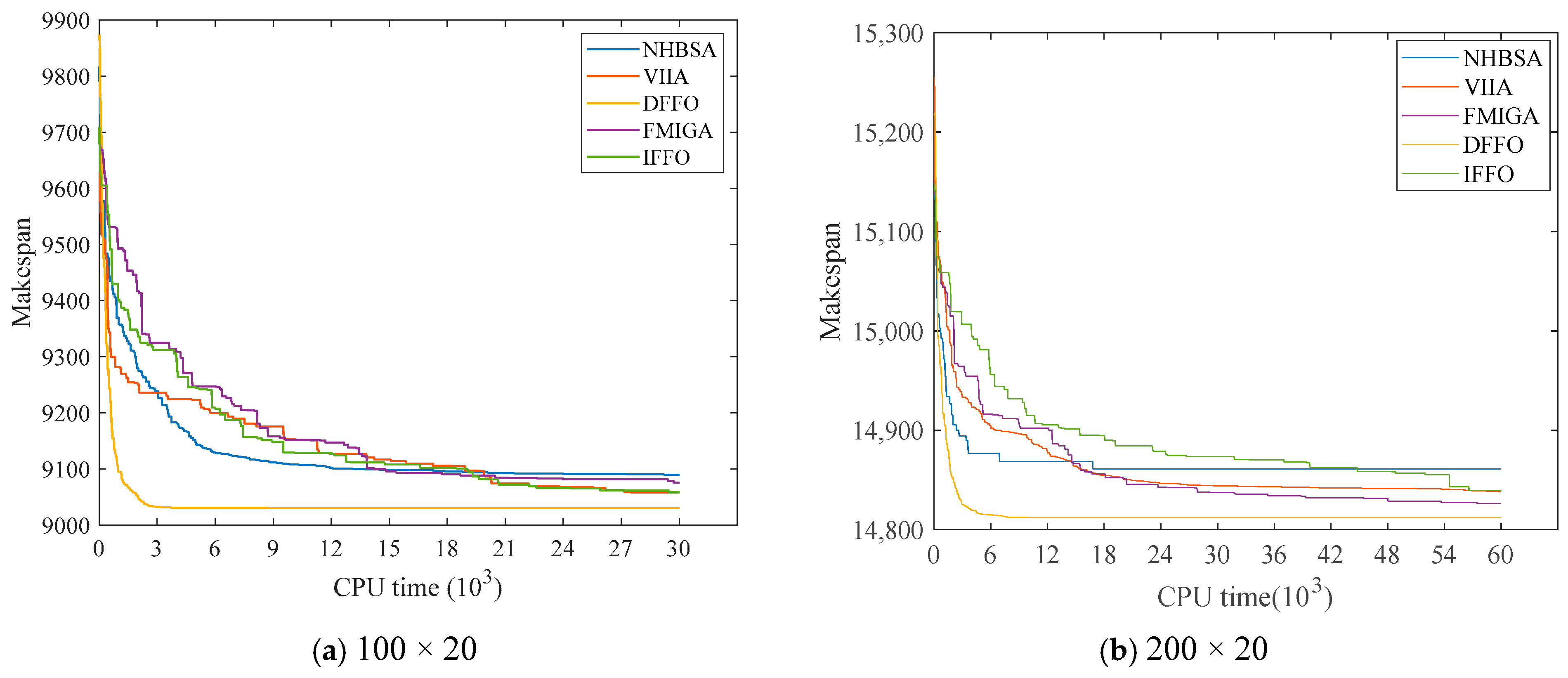
4.4. Comparative Analysis with Related Algorithms
4.5. Experimental Summary
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandez-Viagas, V.; Molina-Pariente, J.M.; Framinan, J.M. Generalised accelerations for insertion-based heuristics in permutation flowshop scheduling. Eur. J. Oper. Res. 2020, 282, 858–872. [Google Scholar] [CrossRef]
- Bagheri Rad, N.; Behnamian, J. Recent trends in distributed production network scheduling problem. Artif. Intell. Rev. 2022, 55, 2945–2995. [Google Scholar] [CrossRef]
- Huang, J.P.; Pan, Q.K.; Gao, L. An effective iterated greedy method for the distributed permutation flowshop scheduling problem with sequence-dependent setup times. Swarm Evol. Comput. 2020, 59, 100742. [Google Scholar] [CrossRef]
- Yin, R.X.; Feng, X.Q.; Wu, T. Improved fruit fly algorithm for no idle flow shop scheduling problem. Modul. Mach. Tool Autom. Manuf. Technol. 2022, 32, 142–150. [Google Scholar]
- Yan, H.C.; Tang, W.; Yao, B. New hybrid bird swarm Algorithm for no idle flow shop scheduling Problem. Microelectron. Comput. 2022, 39, 98–106. [Google Scholar]
- Zhao, Z.M.; Wang, J.H.; Zhu, K. Minimum iterative greedy algorithm for total delay in no-idle permutation flow shop. Modul. Mach. Tool Autom. Process. Technol. 2023, 3, 177–182. [Google Scholar]
- Zhao, R.; Lang, J.; Gu, X.S. Hybrid no-idle permutation flow shop scheduling based on multi-objective discrete sine optimization algorithm. J. East China Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 48, 76–86. [Google Scholar]
- Pei, X.B.; Li, Y.Z. Application of improved hybrid evolutionary Algorithm to no-idle permutation flow shop scheduling problem. Oper. Res. Manag. 2019, 29, 204–212. [Google Scholar]
- Pan, W.T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Y.N.; Li, S.; Zeng, Y.R. New fruit fly optimization algorithm with joint search strategies for function optimization problems. Knowl.-Based Syst. 2021, 176, 77–96. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.J.; Duck, B.C. A hybrid wind driven-based fruit fly optimization algorithm for identifying the parameters of a double-diode photovoltaic cell model considering degradation effects. Sustain. Energy Technol. Assess. 2022, 50, 101685. [Google Scholar] [CrossRef]
- Saminathan, K.; Thangavel, R. Energy efficient and delay aware clustering in mobile adhoc network: A hybrid fruit fly optimization algorithm and whale optimization algorithm approach. Concurr. Comput. Pract. Exp. 2022, 34, 6867. [Google Scholar] [CrossRef]
- Hu, G.; Xu, Z.; Wang, G.; Zeng, B.; Liu, Y.; Lei, Y. Forecasting energy consumption of long-distance oil products pipeline based on improved fruit fly optimization algorithm and support vector regression. Energy 2021, 224, 120153. [Google Scholar] [CrossRef]
- Zhu, N.; Zhao, F.; Wang, L.; Ding, R.; Xu, T. A discrete learning fruit fly algorithm based on knowledge for the distributed no-wait flow shop scheduling with due windows. Expert Syst. Appl. 2022, 198, 116921. [Google Scholar] [CrossRef]
- Guo, H.W.; Sang, H.Y.; Zhang, B.; Meng, L.L.; Liu, L.L. An effective metaheuristic with a differential flight strategy for the distributed permutation flowshop scheduling problem with sequence-dependent setup times. Knowl.-Based Syst. 2022, 242, 108328. [Google Scholar] [CrossRef]
- Guo, H.W.; Sang, H.Y.; Zhang, X.J.; Duan, P.; Li, J.Q.; Han, Y.Y. An effective fruit fly optimization algorithm for the distributed permutation flowshop scheduling problem with total flowtime. Eng. Appl. Artif. Intell. 2023, 123, 106347. [Google Scholar] [CrossRef]
- Namaz, M.; Enscore, E.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar]
- Ceberio, J.; Irurozki, E.; Mendiburu, A.; Lozano, J.A. A distance-based ranking model estimation of distribution algorithm for the flowshop scheduling problem. IEEE Trans. Evol. Comput. 2014, 18, 286–300. [Google Scholar] [CrossRef]
- Wang, S.Y.; Wang, L.; Liu, M.; Xu, Y. An order-based estimation of distribution algorithm for stochastic hybrid flow-shop scheduling problem. Int. J. Comput. Integr. Manuf. 2014, 28, 307–320. [Google Scholar] [CrossRef]
- Ruiz, R.; Thoama, S. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Ruiz, R.; Vallada, E.; Fernandez-Martinez, C. Scheduling in flowshops with no-idle machines. In Computational Intelligence in Flow Shop and Job Shop Scheduling; Springer: Berlin/Heidelberg, Germany, 2009; pp. 21–51. [Google Scholar]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.W. Variable block internal iteration algorithm for no idle flow shop problem. Appl. Res. Comput. 2022, 39, 3667–3672. [Google Scholar]



| Symbol | Implication |
|---|---|
| i | |
| j | |
| Represents a complete job ordering | |
| Represents a partial sequence of | |
| Represents the difference in completion times between machines k and k + 1 after completing sequence | |
| Denotes the processing time of job on machine k | |
| The makespan |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Ratio | p-Value |
|---|---|---|---|---|---|
| 0.39 | 3 | 0.1894 | 1.32 | 0.0000 | |
| 181.26 | 3 | 35.2652 | 266.32 | 0.0000 | |
| 5.32 | 3 | 0.8365 | 6.01 | 0.0000 | |
| 2.03 | 9 | 0.2156 | 0.48 | 0.5489 | |
| 2.89 | 9 | 0.4856 | 0.52 | 0.6629 | |
| 4.16 | 9 | 0.2769 | 0.09 | 0.8413 |
| n | m | DFFO1 | DFFO2 | DFFO3 | DFFO4 | DFFO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ARPD | SD | ARPD | SD | ARPD | SD | ARPD | SD | ARPD | SD | ||
| 10 | 0.184 | 0.091 | 0.214 | 0.221 | 0.417 | 0.218 | 3.446 | 0.965 | 0.123 | 0.095 | |
| 50 | 20 | 0.080 | 0.130 | 0.008 | 0.107 | 0.452 | 0.273 | 4.241 | 1.235 | 0.036 | 0.128 |
| 30 | 0.021 | 0.372 | 0.025 | 0.205 | 0.521 | 0.518 | 1.354 | 0.025 | −0.070 | 0.190 | |
| 10 | 0.102 | 0.060 | 0.123 | 0.072 | 0.150 | 0.045 | 2.154 | 0.681 | 0.062 | 0.070 | |
| 100 | 20 | 0.060 | 0.168 | −0.018 | 0.231 | 0.156 | 0.184 | 3.050 | 1.201 | −0.085 | 0.130 |
| 30 | −0.154 | 0.331 | −0.133 | 0.296 | 0.276 | 0.405 | 4.903 | 1.201 | −0.310 | 0.210 | |
| 10 | 0.004 | 0.002 | 0.008 | 0.003 | 0.008 | 0.002 | 0.717 | 0.356 | 0.003 | 0.002 | |
| 150 | 20 | 0.093 | 0.150 | 0.185 | 0.093 | 0.232 | 0.167 | 3.265 | 0.686 | 0.001 | 0.088 |
| 30 | 0.006 | 0.258 | 0.132 | 0.221 | 0.049 | 0.232 | 3.425 | 0.814 | −0.178 | 0.165 | |
| 10 | 0.004 | 0.014 | −0.001 | 0.010 | 0.022 | 0.055 | 0.472 | 0.252 | −0.005 | 0.002 | |
| 200 | 20 | 0.143 | 0.146 | 0.060 | 0.138 | 0.080 | 0.103 | 2.204 | 0.594 | −0.001 | 0.108 |
| 30 | −0.096 | 0.235 | −0.025 | 0.145 | −0.011 | 0.239 | 3.394 | 0.701 | −3.478 | 0.156 | |
| 10 | 0.004 | 0.014 | −0.003 | 0.007 | −0.005 | 0.004 | 0.478 | 0.256 | −0.005 | 0.004 | |
| 250 | 20 | 0.088 | 0.124 | 0.079 | 0.079 | 0.088 | 0.085 | 2.023 | 0.591 | −0.010 | 0.005 |
| 30 | −0.020 | 0.165 | −0.021 | 0.121 | −0.059 | 0.126 | 3.381 | 1.083 | −0.158 | 0.129 | |
| 10 | 0.001 | 0.001 | 0.003 | 0.004 | 0.006 | 0.012 | 0.628 | 0.254 | 0.000 | 0.002 | |
| 300 | 20 | 0.098 | 0.095 | 0.112 | 0.056 | 0.046 | 0.012 | 2.364 | 0.487 | −0.016 | 0.040 |
| 30 | 0.132 | 0.195 | 0.116 | 0.108 | 0.099 | 0.140 | 3.175 | 0.745 | −0.046 | 0.072 | |
| Mean | 0.044 | 0.142 | 0.048 | 0.118 | 0.140 | 0.157 | 2.481 | 0.699 | −0.230 | 0.088 | |
| Algorithm | Parameter Value |
|---|---|
| NHBSA | PS = 80, learning factor c1 = 0.5, and learning factor c2 = 0.5 |
| FGMIGA | PS = 80 and = 7 |
| IFFO | PS = 80 and local search times LS = 10 |
| VIIA | PS = 80 and = 7 |
| DFFO | PS = 80, = 0.3, and = 7 |
| n | m | NHBSA | FMIGA | IFFO | VIIA | DFFO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ARPD | SD | ARPD | SD | ARPD | SD | ARPD | SD | ARPD | SD | ||
| 10 | 0.479 | 0.415 | 0.442 | 0.299 | 0.353 | 0.289 | 0.542 | 0.709 | 0.123 | 0.095 | |
| 50 | 20 | 1.586 | 0.284 | 0.387 | 0.186 | 0.321 | 0.183 | 1.158 | 0.673 | 0.036 | 0.128 |
| 30 | 0.583 | 0.344 | 0.574 | 0.180 | 0.792 | 0.188 | 0.216 | 0.801 | −0.070 | 0.190 | |
| 10 | 0.154 | 0.435 | 0.243 | 0.195 | 0.187 | 0.169 | 0.090 | 0.855 | 0.062 | 0.070 | |
| 100 | 20 | 0.319 | 0.302 | 0.299 | 0.192 | 0.177 | 0.157 | 0.158 | 0.563 | −0.085 | 0.130 |
| 30 | 0.508 | 0.343 | 0.631 | 0.202 | 0.210 | 0.210 | 0.243 | 0.805 | −0.310 | 0.210 | |
| 10 | 0.005 | 0.346 | 0.034 | 0.229 | 0.009 | 0.559 | 0.020 | 0.753 | 0.003 | 0.002 | |
| 150 | 20 | 0.394 | 0.479 | 0.385 | 0.247 | −0.044 | 0.283 | −0.127 | 0.919 | 0.001 | 0.088 |
| 30 | 0.257 | 0.349 | 0.287 | 0.577 | 0.184 | 0.195 | 0.194 | 0.819 | −0.178 | 0.165 | |
| 10 | 0.006 | 0.463 | 0.058 | 0.283 | 0.010 | 0.337 | 0.000 | 0.907 | −0.005 | 0.002 | |
| 200 | 20 | 0.103 | 0.455 | 0.274 | 0.178 | 0.192 | 0.221 | 0.124 | 0.931 | −0.001 | 0.108 |
| 30 | 0.119 | 0.319 | 0.250 | 0.194 | 0.091 | 0.164 | 0.001 | 0.699 | −3.478 | 0.156 | |
| 10 | 0.006 | 0.406 | 0.051 | 0.195 | 0.040 | 0.188 | 0.035 | 0.941 | −0.005 | 0.004 | |
| 250 | 20 | 0.135 | 0.316 | 0.181 | 0.190 | 0.089 | 0.233 | 0.067 | 0.597 | −0.010 | 0.005 |
| 30 | 0.124 | 0.434 | 0.350 | 0.330 | 0.070 | 0.300 | −0.012 | 0.816 | −0.158 | 0.129 | |
| 10 | 0.001 | 0.486 | 0.044 | 0.226 | 0.414 | 0.199 | 0.103 | 0.803 | 0.000 | 0.002 | |
| 300 | 20 | 0.162 | 0.326 | 0.223 | 0.154 | 0.129 | 0.162 | 0.087 | 0.754 | −0.016 | 0.040 |
| 30 | 0.239 | 0.348 | 0.420 | 0.156 | 0.155 | 0.147 | 0.181 | 0.741 | −0.046 | 0.072 | |
| Mean | 0.288 | 0.142 | 0.285 | 0.118 | 0.188 | 0.157 | 0.171 | 0.699 | −0.230 | 0.088 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, F.; Cui, J. Improved Fruit Fly Algorithm to Solve No-Idle Permutation Flow Shop Scheduling Problem. Processes 2025, 13, 476. https://doi.org/10.3390/pr13020476
Zeng F, Cui J. Improved Fruit Fly Algorithm to Solve No-Idle Permutation Flow Shop Scheduling Problem. Processes. 2025; 13(2):476. https://doi.org/10.3390/pr13020476
Chicago/Turabian StyleZeng, Fangchi, and Junjia Cui. 2025. "Improved Fruit Fly Algorithm to Solve No-Idle Permutation Flow Shop Scheduling Problem" Processes 13, no. 2: 476. https://doi.org/10.3390/pr13020476
APA StyleZeng, F., & Cui, J. (2025). Improved Fruit Fly Algorithm to Solve No-Idle Permutation Flow Shop Scheduling Problem. Processes, 13(2), 476. https://doi.org/10.3390/pr13020476





