A Vertical Federated Learning Method for Electric Vehicle Charging Station Load Prediction in Coupled Transportation and Power Distribution Systems

Abstract

The continuous growth of electric vehicle (EV) ownership has increased the proportion of EV charging station load (EVCSL) in the distribution network (DN). The prediction of EVCSL is important for the safe and stable operation of the DN. However, simply predicting the EVCSL based on the characteristics of the DN, ignoring the impact of coupled transportation network (TN) characteristics, will reduce prediction performance. Few studies focus on combining DN and TN data for EVCSL prediction. On the premise of protecting the privacy of TN data, this paper proposes a vertical adaptive attention-based federated prediction method of EVCSL based on an edge aggregation graph attention network combined with a long- and short-term memory network (V2AFedEGAT combined with LSTM) to fully utilize the characteristics of DN and TN. This method introduces a spatio-temporal hybrid attention module to alleviate the characteristic distribution skew of DN and TN. Furthermore, to balance the privacy protection and training efficiency after multiple modules are integrated into the secure federated linear regression framework, the training strategy of the federated framework and the update strategy of the model are optimized. The simulation results show that the proposed federated method improves the prediction performance by about 4% and has a sub-second response speed.

1. Introduction

Countries around the world are gradually increasing their attention to environmental protection. For the TN, the Chinese government has promulgated many EV-related policies to encourage low-carbon travel, which has led to a continuous increase in the ownership of EVs. Furthermore, the EV charging station number and EVCSL continue to increase, which poses a huge challenge to the safe and stable operation of the DN. The EVCSL prediction, which has the ability to provide guidance for subsequent dispatching and planning tasks of the DN, has become particularly important.

The EVCSL prediction methods can be generally divided into two types: the model-driven method and the data-driven method [1]. According to the techniques involved in this paper, the data-driven method can be divided into the local data-driven method and the federated data-driven method.

1.1. Model-Driven Prediction Method

The model-driven method requires data characteristics to tailor an existing model to obtain prediction results. The most typical model-driven method is the auto-regressive integrated moving average (ARIMA). The EV charging station’s selection of EVs is influenced by multiple factors, such as travel peak hours and road congestion situations, which endows the EVCSL with a spatio-temporal correlation [2]. Therefore, the ARIMA method was developed into spatial and temporal ARIMA in [3] to improve fitting performance by extracting and learning the spatio-temporal correlation of EVCSL. However, the EVCSL data with spatio-temporal correlation are nonlinearity data, which are difficult to learn by model-driven methods [4].

1.2. Local Data-Driven Prediction Method

The data-driven method requires model self-correction to match data characteristics, which has the ability to analyze and learn the randomness and nonlinearity in data to obtain accurate prediction results. Machine learning, a typical data-driven method, mainly includes K-nearest neighbor [5,6], support vector machines, artificial neural networks [7], and deep learning. However, traditional machine learning methods usually lack network depth. The spatio-temporal correlation of EVCSL is difficult to analyze by traditional machine learning methods [8].

Deep learning, utilizing multi-nonlinear layers to deeply explore the spatio-temporal correlation of predicted object [9], has achieved good prediction and detection results [10] in multiple fields. Deep neural networks (DNNs) mainly include recurrent neural networks, convolutional neural networks, and graph neural networks. The traditional recurrent neural network can capture temporal correlations that exist in time series data. The LSTM as an upgraded network for recurrent neural networks is adopted in [11,12] to analyze and predict uncertain EVCSL affected by load demand and charging station electricity price. Faced with the strong volatility of EV travel demand, the neural hierarchical interpolation for time series method [13] effectively captures multi-scale features through a layered strategy, which endows it with strong robustness. However, only considering the temporal correlations of EVCSL will lose spatial information. The excellent processing ability of graph neural networks in non-Euclidean data is utilized in [14] to extract the shape and motion direction characteristic of changing and irregular clouds, improving the accuracy of solar energy prediction. Graph convolutional networks and multi-solution-based convolutional neural networks are, respectively, adopted in [15] to extract spatio-temporal correlations of wind power, improving the accuracy of wind power prediction. However, the increase in the EV number is accompanied by a rapid growth of training data, which causes the model’s difficulty in finding key parts of the training data.

The attention mechanism was proposed in [16] to extract and analyze key parts of large-scale training data, improving the prediction accuracy and training efficiency. Transformers, as a widely adopted method in attention mechanisms, have been compared with other deep learning methods in [17] to demonstrate the advantage for temporal series EVCSL prediction problems. The attention mechanism was combined with a graph neural network in [18] to propose the graph attention network (GAT), which improves the efficiency of topology learning. The DN topology node characteristics such as node voltage and power can effectively reflect the EVCSL. However, the edge characteristic in the topology also contains the information of EVCSL, which cannot be analyzed by the GAT method. The EGAT, a development method of GAT, has the ability to learn the edge characteristic information in the topology [19]. Meanwhile, the development of society has led to strengthened coupling relationships between different departments. In many cases, local data cannot effectively describe the regression relationship between characteristics and labels [20], reducing the prediction accuracy.

With the increase in the number of EVs, the impact of TN characteristics such as traffic congestion and charging prices on EVCSL become more significant. Meanwhile, the increase in the number of charging stations makes the interactive relationship between charging stations more complex. This means that DN characteristics alone insufficiently describe the EVCSL changes with the strengthening of the coupling relationship between the DN and the TN. And there are also data privacy protection issues between the DN and TN. Few studies pay attention to combining multiple data sources for EVCSL prediction. Thus, how to train prediction models by combining DN and TN characteristic data while protecting data privacy is the research focus of this paper.

1.3. Federated Data-Driven Prediction Method

Federated learning, a distributed learning method for protecting participant data privacy, was first proposed by Google in 2016. In 2019, Yang Q et al. further refined the classification and application prospect of federated learning, dividing it into horizontal, vertical, and transfer federated learning [21].

Horizontal federated learning is suitable for the situation where the characteristic types mostly coincide and the identity documents (IDs) are different for federated learning participants. The most typical horizontal federated learning method is the federated average algorithm. A hypernetwork is embedded in federated learning [22] to improve learning effectiveness. The recurrent neural network and federated average algorithm are combined in [20,23] to integrate multi-participant information and achieve accurate prediction without leaking the privacy of local data. This is one of the explorations that integrates deep neural networks into horizontal federated learning. However, the federated average algorithm shows insufficient performance in the situation of participant devices and data heterogeneity [24]. The federated optimization in heterogeneous networks, optimizing the objective function of the local model and increasing the penalty of the proximal term [25], ensures the local model update does not deviate from the global model. The federated community graph convolutional network is proposed in [26] to achieve safe and accurate traffic state predictions, in which the graph information is introduced to capture spatial correlations.

Vertical federated learning is suitable for the situation where the IDs mostly coincide and the characteristic types are different for federated learning participants. Considering privacy protection between different organizations in the TN, federated deep learning based on the spatio-temporal long- and short-term network algorithm is proposed in [27] to predict traffic flow.

In the context of EV charging stations as coupling points, the DN and TN in the coupled transportation and power distribution systems (CTPS) have the same training data ID and different characteristic types. In this system, ID is a series of time points that meet the range of vertical federated learning. The typical vertical federated learning framework is the secure federated linear regression framework [16]. However, there may be a non-IID problem with the characteristic data of the DN and TN. Moreover, there is also an imbalance of privacy leakage and training efficiency in the backpropagation process when integrating multiple DNN modules into the above framework.

This paper proposes the V2AFedEGAT combined with LSTM prediction method. A spatio-temporal hybrid attention method is introduced in a secure federated linear regression framework to more effectively integrate DN and TN data for training federated models. Meanwhile, this paper adjusts the training strategy of the federated framework and the update strategy of model parameters to alleviate the imbalance between privacy security and training efficiency caused by the introduction of multiple modules in the above framework.

The paper is organized as follows. Firstly, the current problems existing in the prediction task of charging station load are clarified. Secondly, this paper introduces the proposed method and its composition structure. Subsequently, the offline training and online application process of the proposed method are carefully introduced. Finally, the predictive performance of the proposed method is validated through two simulation cases of different scales, and the results of data privacy protection and application efficiency are discussed. The contributions of this paper are summarized as follows.

(1) The V2AFedEGAT combined with LSTM EVCSL prediction method combines characteristic data from the DN and TN to train the EGAT–LSTM prediction model. On the premise of protecting the TN data privacy, the input characteristic diversity of the prediction model is enriched.

(2) The vertical federated framework combines a spatio-temporal hybrid attention method, including that the EGAT module and time-aware attention module are, respectively, adopted at the local data extraction and global data aggregation levels, which equivalently alleviate the characteristic distribution skew from the spatial and temporal dimensions.

(3) This method adjusts the training strategy of the federated framework, including information transmission and encryption/decryption processes. Meanwhile, this method also adjusts the update strategy of the model, updating the model parameters through intermediate results. These alleviate the imbalance between privacy protection and training efficiency.

(4) The simulation results show that the V2AFedEGAT combined with LSTM method is well adapted to EVCSL prediction tasks under the CTPS data background, which improves prediction performance.

2. Problem Statement and Method Introduction

The characteristic data and adjacency relationship in both the DN and TN can be accurately and efficiently described by topology, which is convenient for spatio-temporal correlation subsequent extraction by the DNN models. The fusing topological information with the graph model can be found in reference [12]. The characteristic selection of the DN and TN during the model training process in this paper are shown in

Table 1. The CTPS node and edge characteristic information.

Type	DN Characteristic	TN Characteristic
Node	Voltage	Traffic flow
	Active power
	Reactive power
Edge	Line active power	Congestion rate
	Line reactive power	Electricity price

. Among them, the DN bus is considered as topology nodes, and the DN lines and TN roads are considered as topology edges.

As shown in Figure 1, for the DN, under the optimal power flow control strategy, characteristic data such as the voltage and power on the bus and the power on the line all have the ability to reflect EVCSL information. For the TN, the EVCSL is influenced by characteristic data such as road congestion rate and electricity price. The prediction model only adopts the characteristic data of the DN for training, which will lose the important information of the TN characteristic data. However, there is a data privacy protection mechanism between the DN and TN, as shown in Figure 1, which means that local data cannot interact between the DN and TN. The secure federated linear regression framework can achieve global training by interacting the intermediate results on the premise of protecting local data privacy.

Meanwhile, ID is a series of time points, not confidential data. This indicates there is rarely a distribution skew in sample quantity and labels in the federated dataset. Starting from the properties of DN and TN data, both are spatio-temporal correlated data. As shown in Figure 1, the characteristic distribution skew exists in both the temporal and spatial dimensions. This paper introduces a spatio-temporal hybrid attention method. In the spatial dimension, the distribution skew of adjacency relationships, nodes, and edge types is relatively static. In the local data extraction stage, the EGAT module is introduced to reduce the quantity of data on characteristics unrelated to key characteristics. This means that the characteristic aggregation of DN and TN data is easier. In the temporal dimension, the skew degree of the characteristic distribution is dynamic, as shown in Figure 1. In the global data aggregation stage, a time-aware attention module is introduced to adaptively adjust the weights of data information from participants according to time points. In the federated learning framework, by introducing this hybrid attention mechanism, the characteristic data skew of DN and TN data in the spatial and temporal dimensions is alleviated.

Moreover, the attention modules will increase the model training burden in encryption environments of federated learning. This paper balances privacy protection and training efficiency by adjusting the training strategy of the federated framework and the update strategy of the model. The following text will provide a detailed introduction to it.

3. The V2AFedEGAT Combined with LSTM EVCSL Prediction Method

In Figure 2, the V2AFedEGAT combined with LSTM EVCSL prediction method for the background of CTPS consists of the EGAT–LSTM spatio-temporal prediction model and the time-aware attention-based secure federated training framework. The DN, TN and cloud collaborate to achieve model training and prediction under data privacy protection.

3.1. EGAT–LSTM Prediction Model

The proposed prediction model is composed of the EGAT characteristic extraction module and the LSTM load prediction module, which achieve spatio-temporal correlation prediction. Among them, the advantage of the EGAT module is the ability to extract traffic flow on TN roads and power flow on DN lines. Meanwhile, the attention mechanism in the EGAT module can assign attention scores to characteristics from the perspective of the local data extraction, which reduces data redundancy and alleviates the characteristic distribution skew. The principles of attention score calculation and characteristic aggregation in the EGAT module can be found in reference [18].

3.2. The Attention-Based Secure Federated Training Framework

The framework includes three parts: encrypted entity alignment, encrypted model training, and encrypted prediction. Among them, the time-aware attention module [28] is introduced to the collaborative cloud. The unique time-aware mechanism achieves adaptive parameter control by evaluating input data and time. From the perspective of global data aggregation, the attention scores of different participant data are adaptively changed with time, which conforms to the properties of DN and TN spatio-temporal data. The characteristic distribution skew is further alleviated.

3.2.1. Encrypted Entity Alignment

The parts of the data with the same ID need to be determined on the premise of protecting data privacy in federated learning, which is called encrypted entity alignment. The most common method is an encryption-based private set intersection technique. In this paper, the time point is adopted as the ID. The federated training can be conducted by coordinating the time period for model training between the DN and TN in the actual training process. This time alignment method does not involve the leakage of private data. The encrypted entity alignment technology is not the focus of this paper.

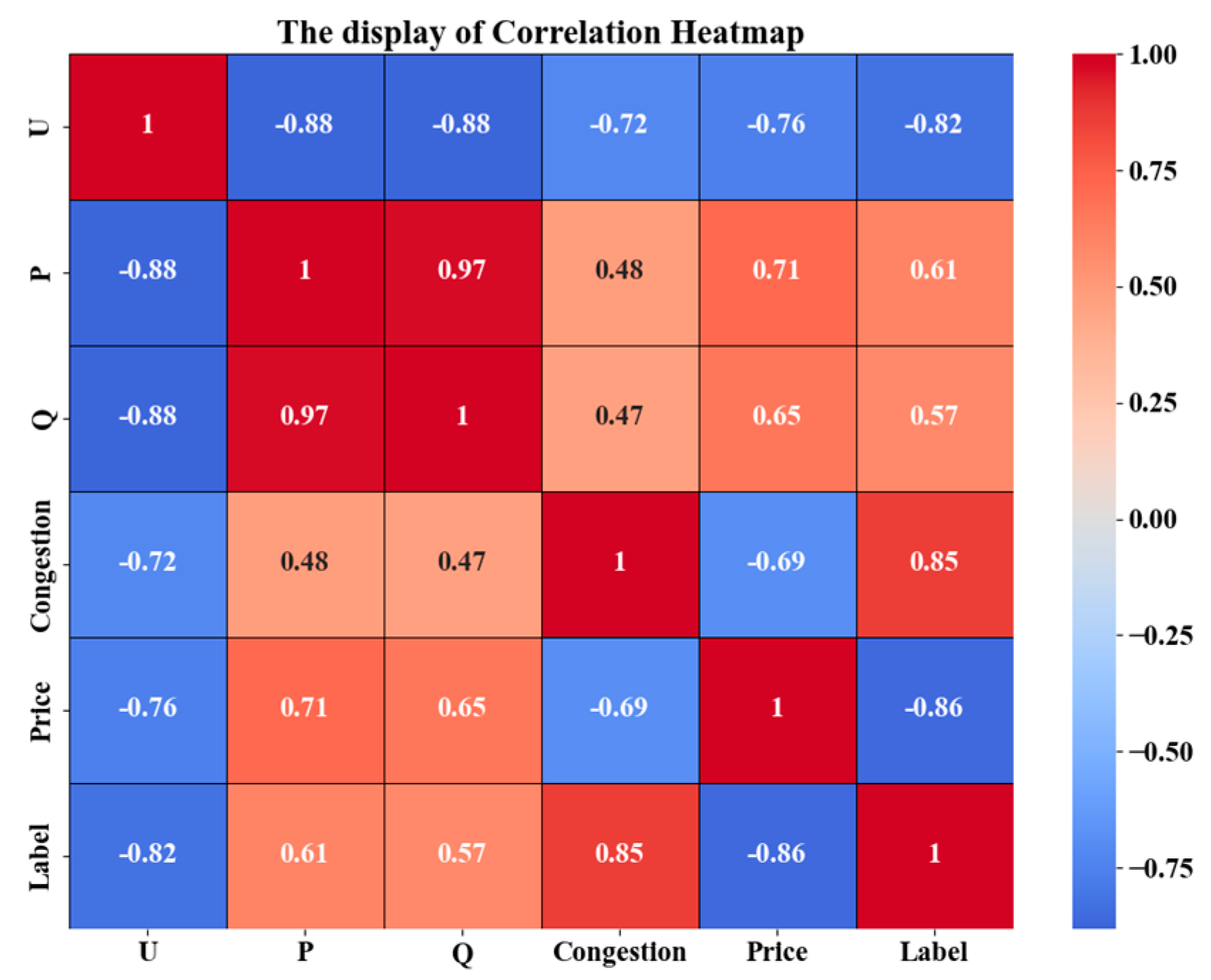
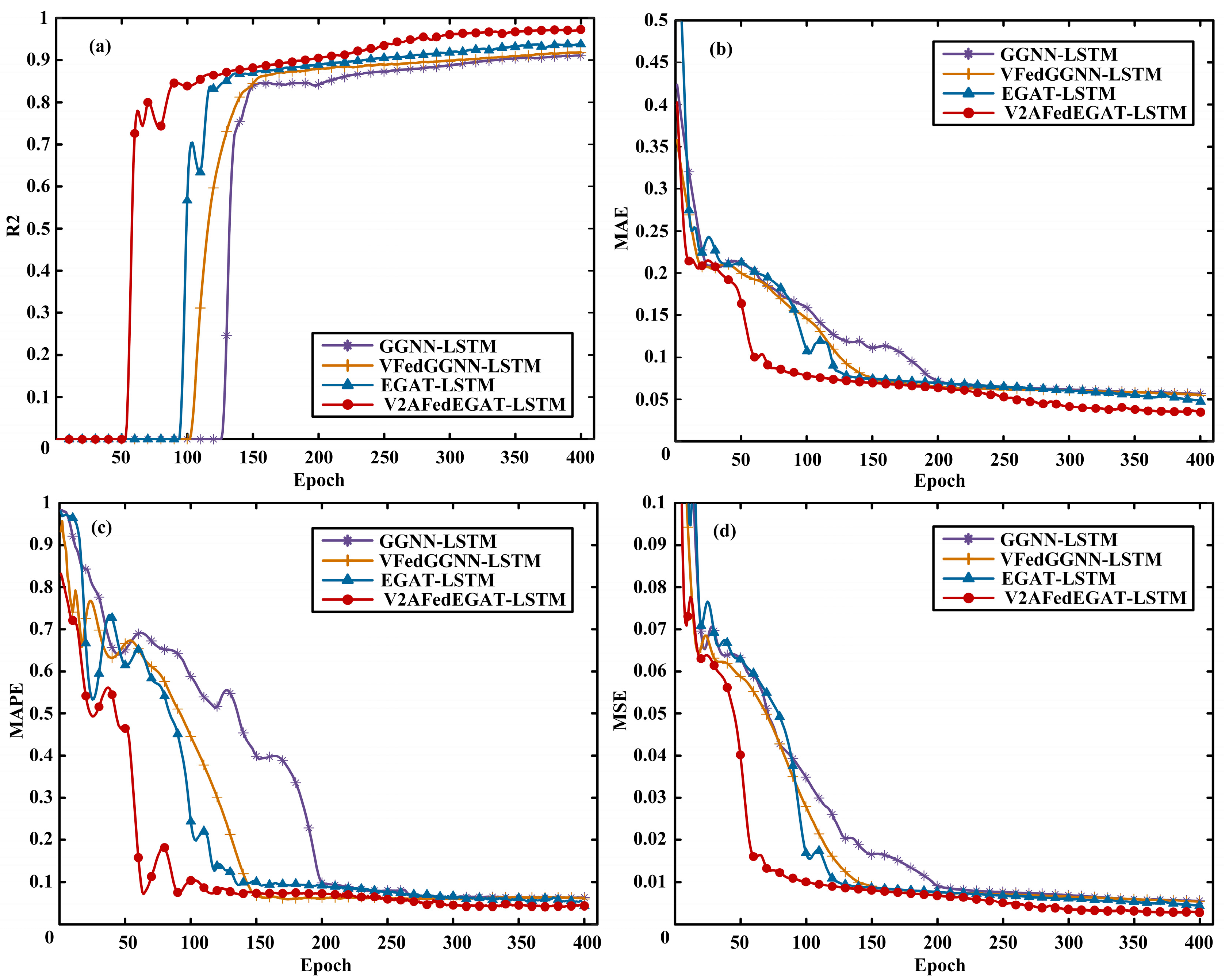
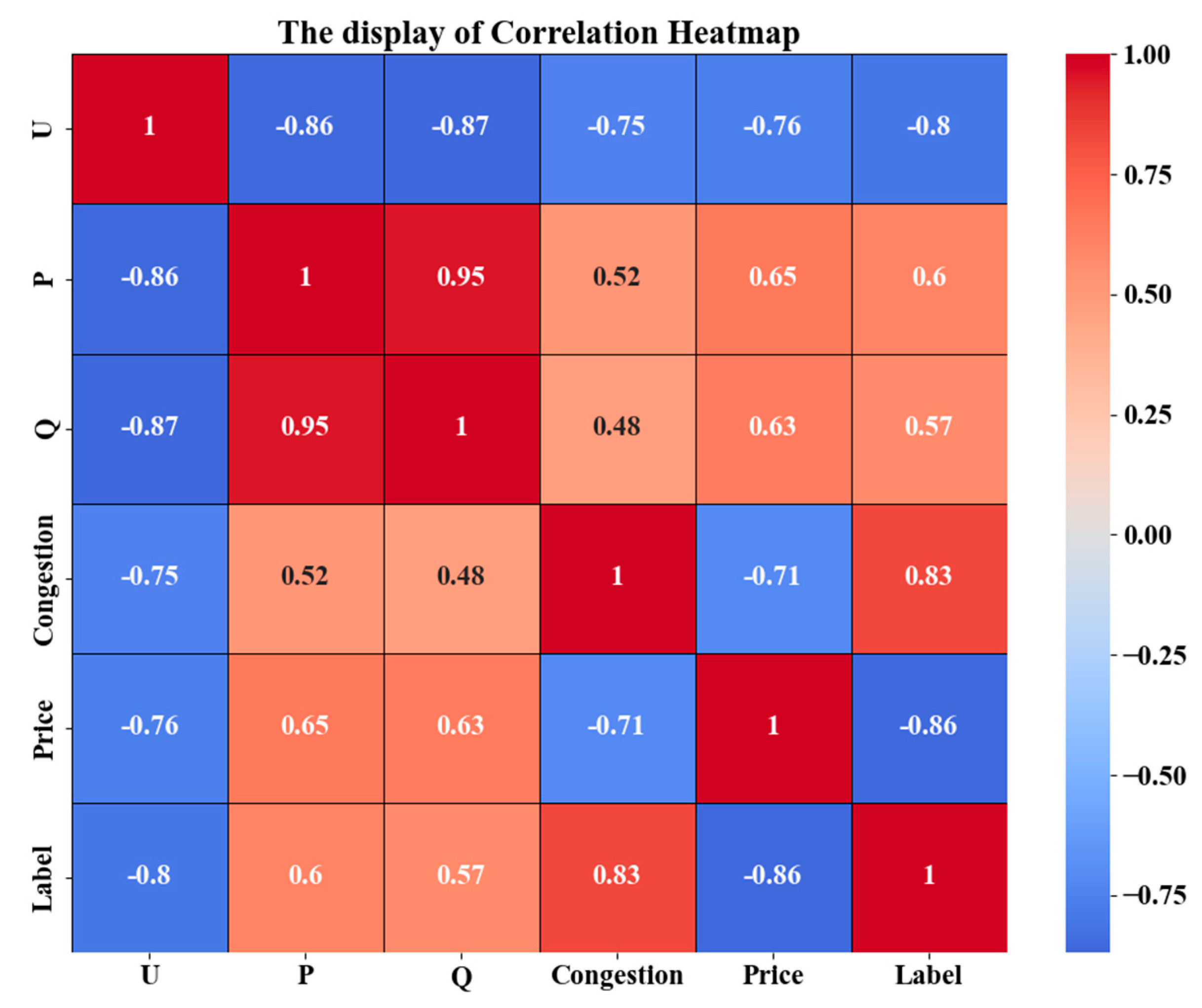
3.2.2. Encrypted Model Training

Multiple deep network modules are integrated into the traditional secure federated linear regression framework, where each training EPOCH requires loss backpropagation in a homomorphic encryption environment to obtain encrypted gradient information. The derivative computation in the homomorphic encryption environment will greatly increase the computational burden [29]. Meanwhile, the update process of the last layer parameters needs to be directly guided by the loss value. This also poses a risk of leakage of privacy data.

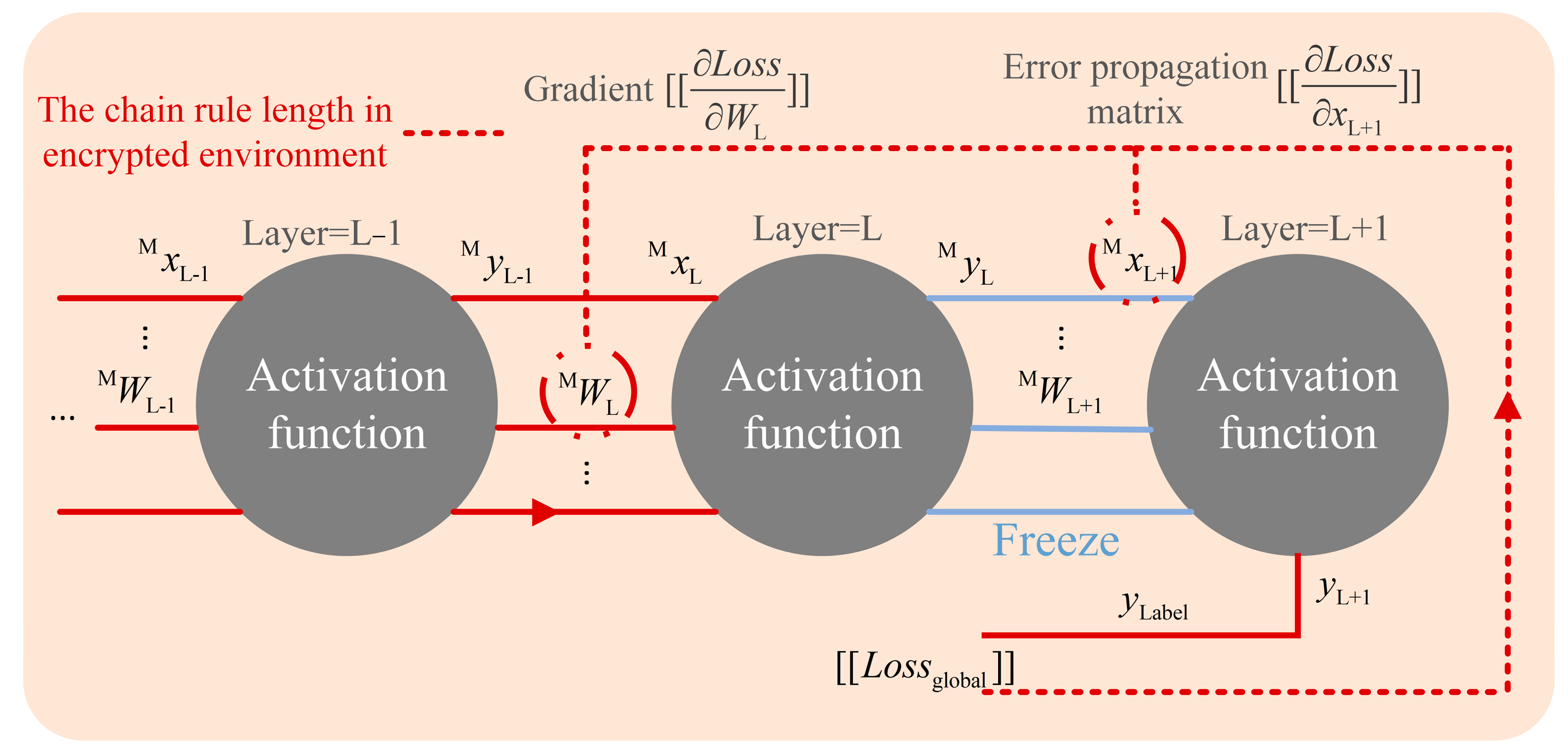
By exploring the backpropagation process, the intermediate result containing the error propagation matrix is considered a key point for updating deep models. This is because the majority of parameter matrices are not square matrices, and they do not have inverse matrices. It is difficult to infer the true value of loss through the intermediate result. Meanwhile, this also reduces the transmission length and derivative superposition of the chain rule in homomorphic encryption environments. The visualization is shown in Figure 3.

The proposed framework adjusts the update strategy of the prediction model, including freezing the last layer parameters of the local model, and the model is updated through intermediate results, which further decreases the privacy leakage risk and computation complexity. The analysis process for adjusting the update strategy of the prediction model is as follows.

In the prediction tasks based on DNNs, the fully connected layer should be added after the model to obtain the desired output result type. For the last fully connected layer L + 1, the parameter gradient calculation [30] is as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}+1}}}& ={\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}+1}}}\hfill \\ & ={\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial y_{\mathrm{L}+1}}}\cdot {\displaystyle \frac{\partial y_{\mathrm{L}+1}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}+1}}}\hfill \\ & ={\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial y_{\mathrm{L}+1}}}\cdot {\mathrm{A}}_{\mathrm{L}+1}^{\prime }\left({}^{\mathrm{M}}x_{\mathrm{L}+1}\right)\cdot {}^{\mathrm{M}}y_{\mathrm{L}}\hfill \end{array}$$

(1)

The mean square error (MSE) is adopted as the loss function, ${Loss}_{\mathrm{global}}={\displaystyle \frac{1}{2}}{\left(y_{\mathrm{L}+1}-y_{\mathrm{Label}}\right)}^2$.

When updating the parameter of the L + 1 fully connected layer in the cloud, the cloud must calculate the value of ${\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial y_{\mathrm{L}+1}}}=y_{\mathrm{L}+1}-y_{\mathrm{Label}}$, but it includes the label information $y_{\mathrm{Label}}$ of the DN submodel, which will leak information of the DN to the cloud. Therefore, the last fully connected layer of the model is frozen, which stops the last fully connected layer from being updated.

The parameter gradient for layer L is calculated as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}}}}& ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}}}}\hfill \\ & ={\displaystyle \frac{{\partial Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}^{\mathrm{DN}}}}\cdot {}^{\mathrm{M}}y_{\mathrm{L}-1}^{\mathrm{DN}}\hfill \end{array}$$

(2)

where the L layer error propagation matrix ${\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}}$ is as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}}& ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}{\partial {}^{\mathrm{M}}y_{\mathrm{L}}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}y_{\mathrm{L}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}}\hfill \\ & ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}\cdot {\left({}^{\mathrm{M}}W_{\mathrm{L}+1}\right)}^{\mathrm{T}}\cdot {\mathrm{A}}_{\mathrm{L}}^{\prime }\left({}^{\mathrm{M}}x_{\mathrm{L}}\right)\hfill \end{array}$$

(3)

where ${\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}$ is the error propagation matrix of the L + 1 layer. Obviously, as long as the error propagation matrix value of the next layer is known, the model parameters of this layer can be updated. The particularity of the ${\left({}^{\mathrm{M}}W\right)}^{\mathrm{T}}$ matrix is that it is not a square matrix in most cases, which indicates the actual inverse matrix does not exist. Therefore, the intermediate result $u={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}\cdot {\left({}^{\mathrm{M}}W_{\mathrm{L}+1}\right)}^{\mathrm{T}}$ is adopted directly to update the parameters of layer L, which does not leak the loss value and label value to the cloud.

Similarly, the parameter gradient for layer L − 1 is calculated as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}-1}}}& ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}-1}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}x_{\mathrm{L}-1}}{\partial {}^{\mathrm{M}}W_{\mathrm{L}-1}}}\hfill \\ & ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}-1}^{\mathrm{DN}}}}\cdot {}^{\mathrm{M}}y_{\mathrm{L}-2}^{\mathrm{DN}}\hfill \end{array}$$

(4)

where the L − 1 layer error propagation matrix ${\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}-1}}}$ is as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}-1}}}& ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}{\partial {}^{\mathrm{M}}y_{\mathrm{L}-1}}}\cdot {\displaystyle \frac{\partial {}^{\mathrm{M}}y_{\mathrm{L}-1}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}-1}}}\hfill \\ & ={\displaystyle \frac{\partial {Loss}_{\mathrm{global}}}{\partial {}^{\mathrm{M}}x_{\mathrm{L}}}}\cdot {\left({}^{\mathrm{M}}W_{\mathrm{L}}\right)}^{\mathrm{T}}\cdot {\mathrm{A}}_{\mathrm{L}-1}^{\prime }\left({}^{\mathrm{M}}x_{\mathrm{L}-1}\right)\hfill \end{array}$$

(5)

Among them, the error propagation matrix of the L layer has been obtained in the parameter update process of the L layer. The error propagation matrix of the L layer is directly adopted to calculate the propagation error matrix of the L − 1 layer, and the parameters of the L − 1 layer are updated. In summary, the backpropagation process can proceed to the first layer of the model to update all model parameters.

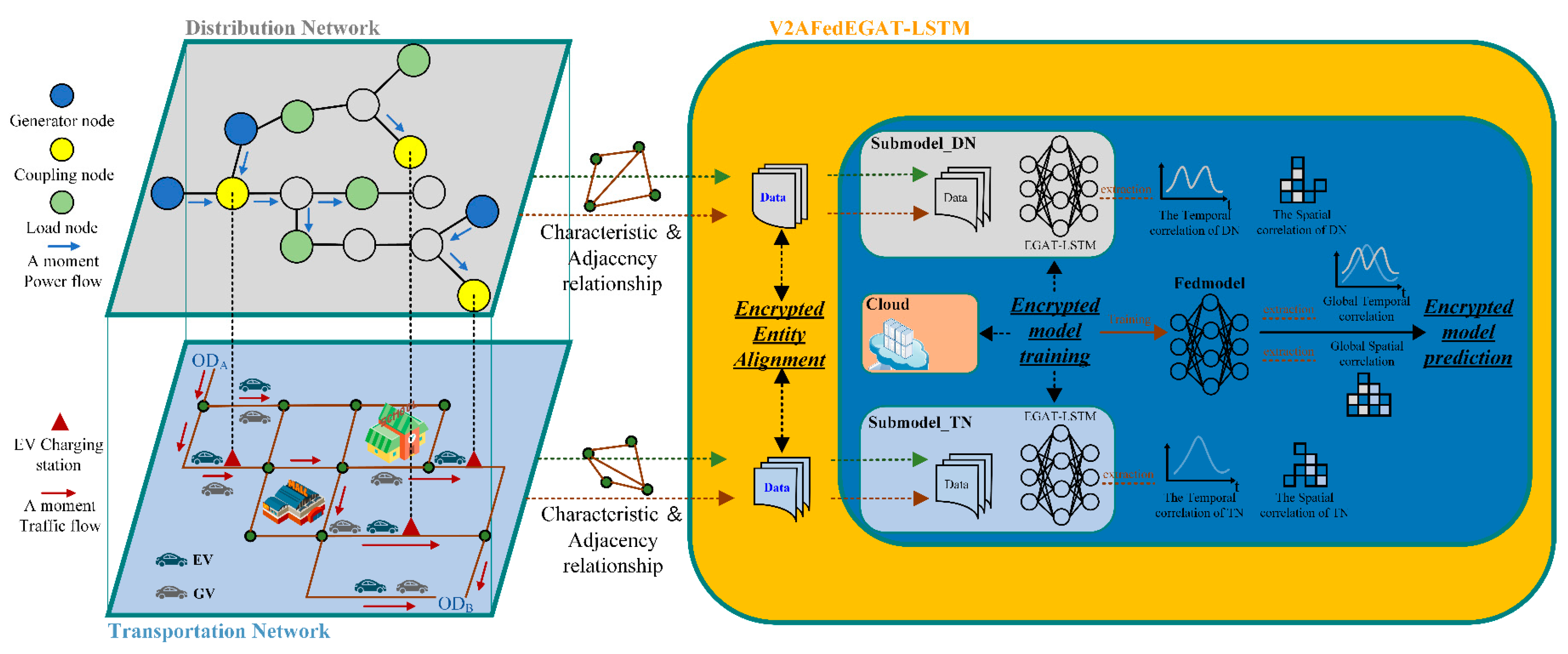
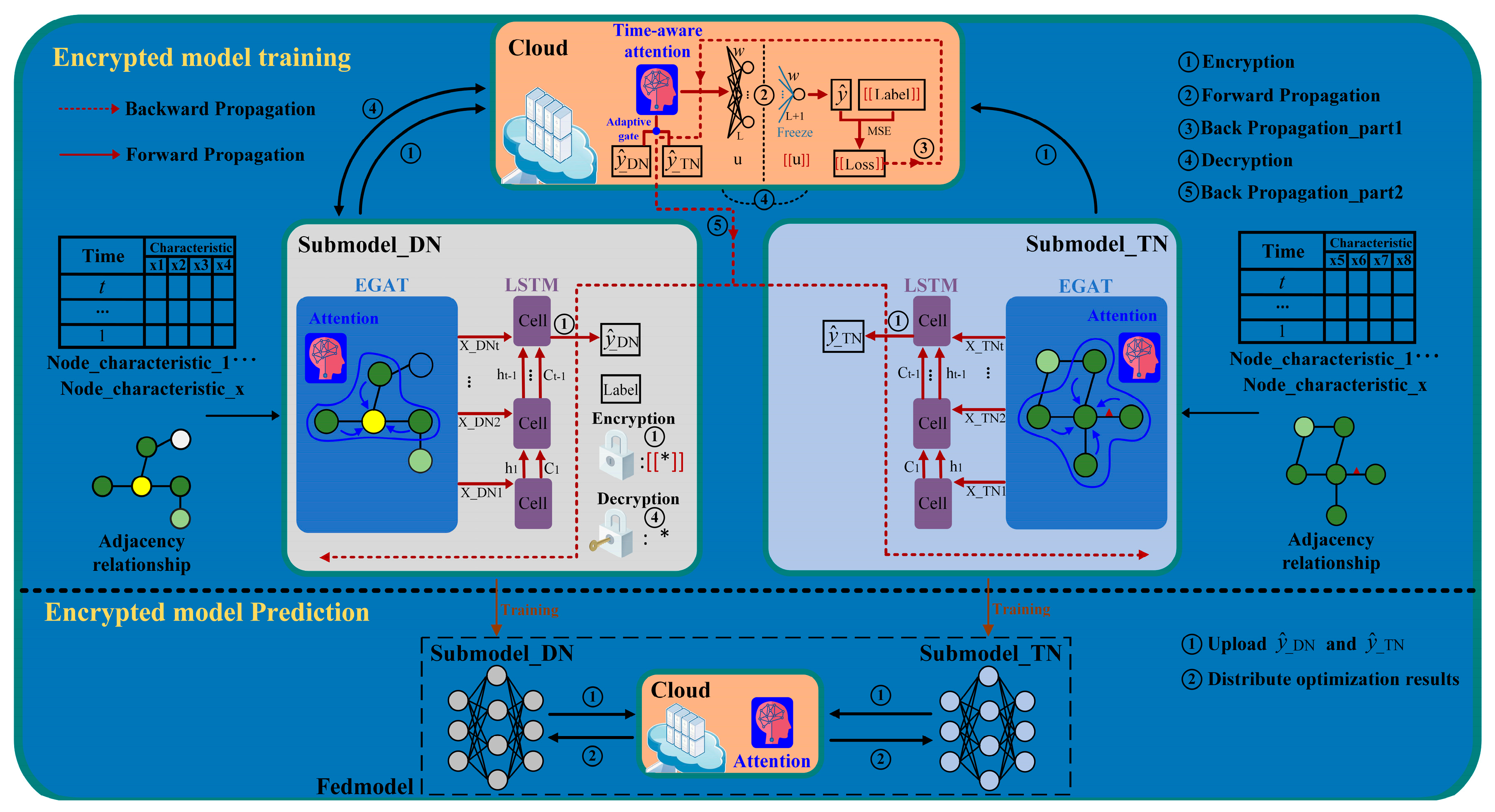
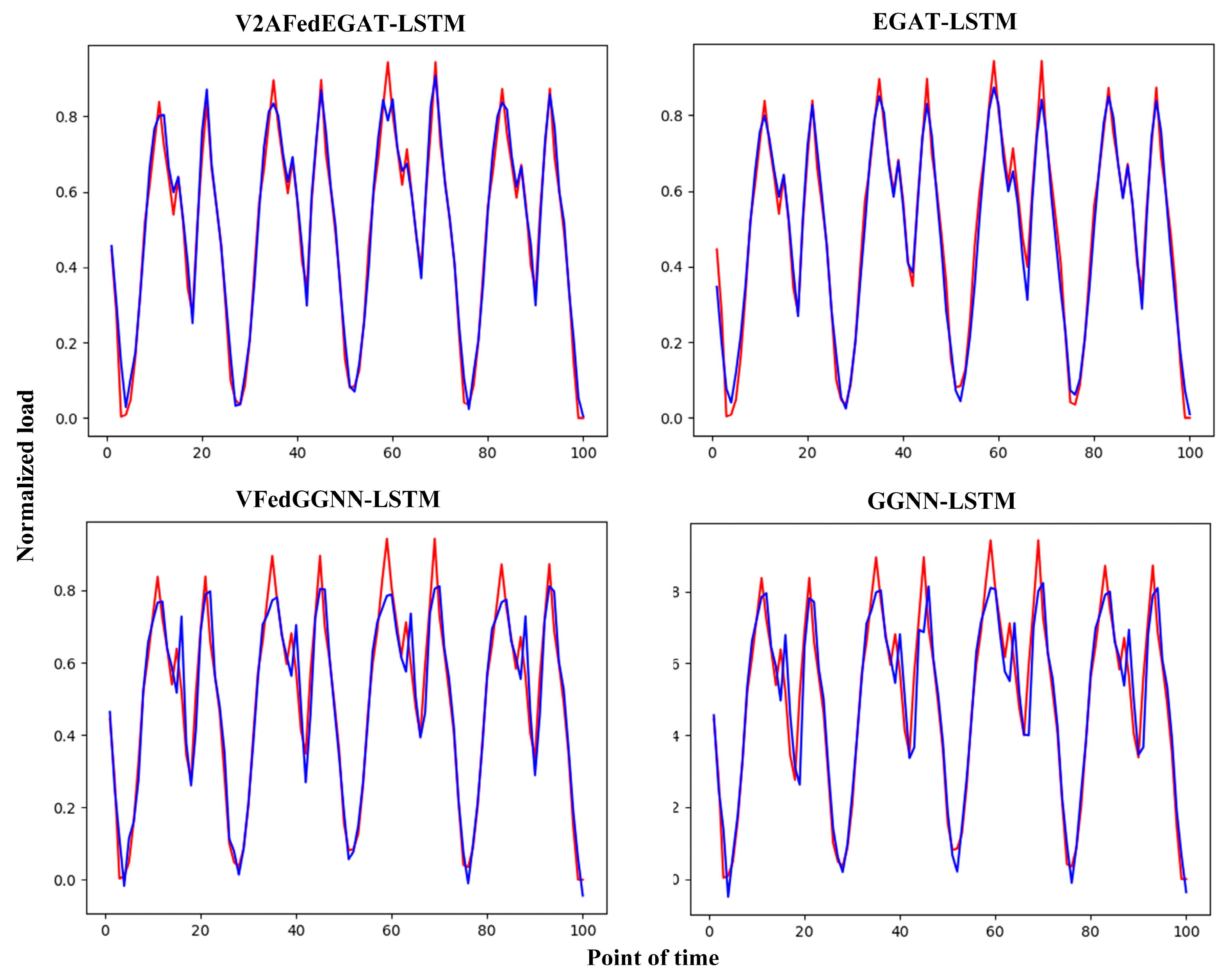
The training strategy of the V2AFedEGAT combined with LSTM EVCSL prediction method is shown in Figure 4. The detailed training and prediction process is as follows.

Preparation: The label side creates a key pair, and the DN and TN initialize local submodel parameters $W^{\mathrm{DN}}$ and $W^{\mathrm{TN}}$. The encrypted method applied in the federated framework is partial homomorphic encryption (PHE), which consists of key pair generation, encryption, and decryption.

Step ①: The DN and TN submodel outputs $y^{\mathrm{DN}}$ and $y^{\mathrm{TN}}$ are obtained by their own forward propagation process and the DN encrypting the label. The TN and DN upload the $y^{\mathrm{TN}}$, $y^{\mathrm{DN}}$, and $[[\mathrm{Label}]]$ to the collaborator cloud.

Step ②: The TN and DN submodel results $y^{\mathrm{DN}}$ and $y^{\mathrm{TN}}$ are input into the time-aware attention module for attention score calculation. This assigns different attention scores to data information from different participants, equivalently alleviating the problem of characteristic distribution skew of DN and TN from the perspective of local data aggregation. The cloud calculates the global encryption loss $[[Loss]]$ through MSE.

Step ③: According to the updated strategy of freezing the last layer parameters proposed in this paper, the backpropagation process is divided into two parts. In the backpropagation process of the first part, the encryption intermediate result $[[u]]=[[{\displaystyle \frac{\partial Loss}{\partial {}^{\mathrm{M}}x_{\mathrm{L}+1}}}\cdot {\left({}^{\mathrm{M}}W_{\mathrm{L}+1}\right)}^{\mathrm{T}}]]$ is calculated through the obtained $[[Loss]]$.

Step ④: The collaborator cloud sends the $[[u]]$ to the DN for decryption by the private key. The decryption result $u$ is returned to the collaborator cloud. The intermediate result will not be leaked to the third-party collaborator cloud because it is difficult to reverse-calculate the loss value.

Step ⑤: The parameters of the attention module are updated by the $u$. During the local model backpropagation, the gradient information output by the attention module is transmitted to the DN and TN to update their respective local models. Similarly, privacy information is effectively protected due to the difficulty of inferring the loss value. In this way, the second part of the backpropagation process can be completed.

3.2.3. Encrypted Prediction

The prediction process of the V2AFedEGAT combined with LSTM method is shown in Figure 4.

Step ①: The DN and TN upload their respective submodel prediction results to the collaborator cloud, and the federated prediction result is obtained after passing through the attention module.

Step ②: The collaborator cloud adopts the federated learning prediction results for subsequent coupling optimization tasks, and the optimization results are distributed to the DN and TN through the collaborator cloud.

4. Simulation Analysis

4.1. Data Preparation

The systems applied to simulation analysis in this paper include the CTPS composed of an IEEE 33 bus DN and a seven-node TN and the CTPS composed of an IEEE 69 bus DN and a 12-node TN [31]. In the simulation of this paper, the charging load of charging station 1 (labeled as (1)) is taken as the predicted object. The CTPS structure adopted in the simulation is shown in Appendix A, Figure A1 and Figure A2.

In this paper, the mainstream GGNN and EGAT characteristic extraction models are combined with LSTM modules, and the formed prediction methods are compared with the V2AFedEGAT combined with LSTM method. The performance of the V2AFedEGAT combined with LSTM method is analyzed by different evaluation indicators. The evaluation indicators adopted include determination coefficient R2, mean absolute error (MAE), mean absolute percentage error (MAPE), and mean squared error (MSE). Moreover, the super-parameters and structure of the EGAT and LSTM module in the V2AFedEGAT combined with LSTM prediction method are consistent with the EGAT–LSTM prediction method. The output new node characteristic dimension of the EGAT model is set to six. The Seq_len of the LSTM module is five. The head number of the multi-head attention mechanism in EGAT is set to four. The number of LSTM layers is set to two, the number of hidden layers is set to 16, and dropout is set to 0.05. The input dimension of the time-aware attention module is 32, the Batch_size is set to 16, and the learning rate is set to 0.005. The prediction methods related to this paper are built on the Pycharm platform and trained on a server with an Intel(R) Xeon(R) Platinum 8255C CPU @ 2.50GHz.

The characteristic dataset of the DN and TN (as shown in Table 1) required for federated model training is generated through a CTPS optimal dispatching model, referring to [32]. Among them, the optimization task of coupled transportation and power distribution systems is a two-layer optimization problem. The distribution network adopts the Distflow model. The decision variables are the active and reactive power output of the generator and the load of each charging station. The transportation network adopts a mixed-integer programming model. The decision variables are the charging and non-charging traffic flow on the path, as well as the load of charging stations. The charging station load of the two optimal models is adopted as the criterion for an iterative solution. The electricity price of charging stations is determined through an iterative calibration step pricing model. Then, the IPOPT solver is adopted to solve the two-layer optimization problems. The dispatching and predicted time scale is one hour. Of the generated 8760 h dataset, 80% is the training set and 20% is the testing set through the IPOPT solver. The other parameters and data required for the CTPS optimal dispatching model are detailed in Section 4.1.1 and Section 4.1.2 below.

4.1.1. DN Training Data Generation

In this simulation, a typical daily load curve from the NYISO database is selected as the baseline, and the load data are scaled accordingly and added with ±15% fluctuation, which generates 8760 h of load datasets through Matlab simulation. They are then allocated to load nodes in the IEEE-33 node system and IEEE-69 node system. The load situation is shown in Appendix A, Figure A3. The active power output limit of the generator set in the DN is 8 MW, and the reactive power limit is −5–8 MW. The cost coefficients of the generator units are $a_g=0.3(\mathrm{USD}/{\mathrm{MW}}^2\mathrm{h})$ and $b_g=150(\mathrm{USD}/\mathrm{MWh})$. The cost of purchasing electricity from the higher-level main network is $\varphi =140(\mathrm{USD}/\mathrm{MWh})$. The capacity and impedance values of distribution lines are all executed according to the standard IEEE 33 and IEEE 69 bus DN system in MATPOWER.

4.1.2. TN Training Data Generation

This simulation takes the multiple origin–destination (OD) pairs in the TN as an example, as shown in Appendix A,

Table A1. The travel OD pairs of the 7-node transportation network.

OD	Origin Point	Destination Point
1	O1	D5
2	O1	D7

and

Table A2. The travel OD pairs of the 12-node transportation network.

OD	Origin Point	Destination Point
1	O1	D10
2	O1	D12
3	O3	D6
4	O3	D10
5	O4	D12

. Considering the randomness of travel demand, the simulation adopts a set of typical 24 h EV and GV travel demand data that conform to spatio-temporal characteristics as a benchmark and combines fluctuation to generate an 8760 h EV and GV travel demand dataset. The fluctuation range is ±15%. Take the travel demand for the first OD in a seven-node TN as an example, as shown in Appendix A, Figure A4. The road parameters in the seven-node and twelve-node TN system are shown in Appendix A,

Table A3. The road parameters of the 7-node TN system.

Road	Type_1	Type_2	Type_3	Type_4	Type_5	Charging
$C_R(\mathrm{p}.\mathrm{u}.)$	300	70	50	40	60	60
$t_R^0(\min )$	8	18	3.5	10	12	20

and

Table A4. The road parameters of the 12-node TN system.

Road	Type_1	Type_2	Type_3	Type_4	Charging
$C_R(\mathrm{p}.\mathrm{u}.)$	100	100	80	60	60
$t_R^0(\min )$	8	13	8	10	20

. The coefficient of the queuing theory model is J = 5, and the time value is W = 10 (USD/h). Moreover, the charging time of the EV is calculated by the reference model.

4.2. Simulation Result

In this section, the correlation between characteristics and between characteristics and labels is analyzed first. Secondly, we mainly analyze the prediction performance of the proposed federated method and other prediction methods on evaluation indicators and exhibit the visualization fitting result of different prediction methods. Finally, the balance between training efficiency and privacy security is analyzed.

4.2.1. Simulation Analysis of the IEEE33 Bus DN Seven-Node TN System

The Pearson correlation coefficient is calculated through the 8760 h of data, which ensures the correlation results satisfy generality. The typical characteristics of the DN and TN are selected for characteristic analysis in this section. These are node voltage (U) and power flow (P, Q) in the DN, and the road congestion (Congestion) and charging electricity prices (Price) in the TN. The above characteristics are all taken from the coupling point of the predicted charging station in the DN and TN at a fixed time. The congestion situation on the road is equivalently reflected by the volume-to-capacity ratio. The correlation heatmap between characteristics and between characteristics and labels is shown in Figure 5.

As shown in Figure 5, the characteristic correlation between the DN and the TN is not strong. Therefore, there is a slight characteristic distribution skew problem between the DN and the TN. Meanwhile, the correlation between the characteristics and labels of both parties is strong. This also indicates that combining the characteristics of DN and TN can significantly improve characteristic diversity, which further enhances prediction performance.

As shown in Figure 6, the convergence speed of the prediction model is approximately equivalent to the learning ability of the prediction model. In addition, the EPOCH of the federated method reaching R2 convergence is around 70, the EPOCH of the EGAT–LSTM method reaching R2 convergence is around 100, and the EPOCH of the GGNN–LSTM and VFedGGNN–LSTM methods reaching R2 convergence is around 150, which indicates the learning ability of the three prediction models has a gap.

The convergence epoch of the prediction model is approximately equivalent to the learning ability of the prediction model. As shown in Figure 7, the EPOCH of the federated method reaching R2 convergence is around 70, the EPOCH of the EGAT–LSTM method reaching R2 convergence is around 100, and the EPOCH of the GGNN–LSTM and VFedGGNN–LSTM methods reaching R2 convergence is around 150, which indicates the learning ability of the three prediction models has a gap. The reason that the learning ability of the EGAT–LSTM method is better than that of the GGNN–LSTM method is that the EGAT module can extract node and edge characteristics from the DN, equivalently improving the number of characteristics. Similarly, the V2AFedEGAT combined with LSTM prediction method with the whole characteristic data of the CTPS has the highest learning ability. This is because the number of equivalent characteristics available for training is greater than the DN local prediction methods.

The convergence R2 value in the evaluation indicator can evaluate the prediction performance of the prediction method. As shown in Figure 6a, the result of the convergence R2 value indicates the prediction performance of the four prediction methods has a gap, and the V2AFdEGAT–LSTM method has the best convergence R2 value. As shown in Figure 6b–d, the V2AFedEGAT combined with LSTM method is also superior to other prediction methods in the MAE, MAPE, and MSE evaluation indicators. The results of different evaluation indicators are shown in

Table 2. The evaluation indicator results.

	Indicator	R2	MAE	MAPE	MSE
Method
GGNN–LSTM		0.911	0.0593	0.0625	0.0063
VFedGGNN–LSTM		0.919	0.0573	0.0602	0.0058
EGAT–LSTM		0.936	0.0523	0.0542	0.0050
V2AFedEGAT combined with LSTM		0.973	0.0382	0.0421	0.0023

. The reason that the EGAT–LSTM method is better than the GGNN–LSTM method in prediction performance is that the EGAT module can assign attention scores to different characteristics, which indicates the model can better learn the regression relationship between characteristics and labels. Meanwhile, the prediction performance of VFedGGNN–LSTM and GGNN–LSTM is not significantly different, and the prediction performance of the V2AFdEGAT–LSTM method significantly differs from the EGAT–LSTM method. This indicates that the proposed federated framework is effective for the characteristic distribution skew between DN and TN data, ensuring the performance of federated learning. The V2AFedEGAT combined with LSTM method can learn better regression relationships with characteristics and labels compared to the other prediction methods.

Figure 7 shows the visualization fitting performance of different prediction methods in EVCSL prediction. The visualization fitting performance is generated by selecting 0–100 time points in the test dataset and utilizing the image generation syntax in Pytorch. The horizontal axis represents time, and the vertical axis represents the normalized load value. The blue line represents the predicted value, and the red line represents the true value of the EVCSL.

4.2.2. Simulation Analysis of IEEE69 Bus DN 12-Node TN System

As shown in Figure 8, the characteristic correlation of larger-scale systems exhibits similar properties to smaller-scale systems. Only some correlation coefficients have changed. The characteristic correlation between some DNs and TNs increases, while the characteristic correlation between other DNs and TNs decreases. This indicates that the characteristics exhibit more complex coupling and nonlinear relationships as the scale of the coupled system increases, which means that the TN characteristics become increasingly important in describing the charging station load changes; thus, relying solely on the characteristics of the DN is insufficient to describe the complex changes in charging station load.

Figure 9 shows the evaluation indicator results of the different prediction methods in an IEEE 69 bus DN and 12-node TN system, and the results of different evaluation indicators are shown in

Table 3. The evaluation indicator results.

	Indicator	R2	MAE	MAPE	MSE
Method
GGNN–LSTM		0.902	0.0615	0.0645	0.0065
VFedGGNN–LSTM		0.911	0.0591	0.0613	0.0062
EGAT–LSTM		0.938	0.0520	0.0538	0.0049
V2AFedEGAT combined with LSTM		0.976	0.0385	0.0425	0.0023

. Figure 10 shows the visualization fitting performance of different prediction methods in EVCSL prediction. Compared with the small-scale system, there is no significant change in the fitting performance of the V2AFedEGAT combined with LSTM method in the large-scale system. However, the fitting performance of other methods slightly decreased. This is because of the insufficient representation and distribution skew of DN and TN data characteristics.

Similar to small-scale systems, the V2AFedEGAT combined with LSTM method has the smallest convergence EPOCH and the best convergence R2 values. This indicates that the V2AFedEGAT combined with LSTM method has certain scalability and stability. This is because the V2AFedEGAT combined with LSTM method combines DN and TN side characteristic data while protecting privacy data, allowing the model to quickly learn the regression relationship between characteristics and labels, which means the model converges faster. Meanwhile, the spatio-temporal hybrid attention method can adaptively allocate attention scores to the data during the local data extraction in the spatial dimension and the global data aggregation in the temporal dimension. This alleviates the characteristic distribution skew of DN and TN data, improving the prediction performance.

4.2.3. Simulation Analysis of Privacy Protection and Computing Time

The privacy protection analysis of the proposed federated framework is shown in

Table 4. Privacy protection display of the federated framework.

Method	Participant	Data
The traditional training strategy	DN	$y^{\mathrm{TN}}$, $Loss$
	TN	$Loss$
	Cloud
The proposed training strategy	DN
	TN
	Cloud	$y^{\mathrm{DN}}$, $y^{\mathrm{TN}}$

. The table contains the data that participants may obtain in the training process. As shown in Table 4, the proposed federated training framework will not leak information to participants. However, the collaborator cloud will obtain the results of the local model. And the local model results in this paper are simple low-dimensional vectors, and the collaborator cloud cannot obtain gradient information and the structure and parameters of the local complex model, which means the leakage risk of local privacy data to the cloud is very small. Assuming we adopt a broadcast mechanism for the key pairs held by the DN between local models, encrypted local results and labels are uploaded to the cloud. The complex attention model achieves the whole updates in encrypted environments, which significantly increases the computational burden.

The computing time of the local and federated prediction methods is shown in

Table 5. Computing time display.

Scale	Method	Offline Training Time (s/EPOCH)	Online Application Time (s)
Small	EGAT–LSTM	50.705	0.088
	V2AFedEGAT combined with LSTM *	523.256	0.313
	V2AFedEGAT combined with LSTM	590.360	0.312
Large	EGAT–LSTM	76.962	0.103
	V2AFedEGAT combined with LSTM *	653.326	0.330
	V2AFedEGAT combined with LSTM	732.985	0.332

. The method with * annotation adopts the proposed updating strategy in this paper. The computing time in Table 5 is the average value. During the offline training stage, each federated prediction method significantly increases the computation time due to the process of homomorphic encryption. The training efficiency of the federated learning model using the proposed updated strategy is improved by about 11%. This is because the mathematical computation of the proposed update strategy is less in homomorphic encryption environments. During the online application stage, the prediction process of the federated model does not require a homomorphic encryption environment, which greatly reduces the computation time and meets the real-time requirements of subsequent dispatching tasks.

5. Discussion

This paper aims to propose a new prediction method for charging station load that is suitable for the properties of DN and TN data. When integrating attention modules in traditional secure federated linear regression frameworks. The extensive adoption of homomorphic encryption and differential privacy methods significantly increases model training time. The research path of this method is to balance privacy security and training efficiency in the federated framework. This paper considers that the collaborative cloud is not purely malicious in the training strategy of the proposed federated framework. In future research, we will carefully consider data decomposition and multi-cloud collaborative training methods. Among them, as a malicious collaborator, the cloud will deeply infer data of other parties.

6. Conclusions

At present, as the coupling relationship between DN and TN deepens, the prediction model relying solely on DN characteristic data is insufficient to describe the complex situation of EVCSL. This paper proposes a federated learning method for charging station load prediction, which combines the characteristic data of DN and TN, to enrich the characteristic diversity of the model input while protecting the data privacy of both parties. Meanwhile, compared with the traditional federated framework, this paper optimizes the traditional framework from the CTPS data non-IID problem and the subsequent challenges of privacy protection and training efficiency. Firstly, for the problem of characteristic distribution skew in the DN and TN, from the perspective of local data extraction in the spatial dimension and global data aggregation in the temporal dimension, a spatio-temporal hybrid attention method is introduced to adaptively reduce redundant data and equivalently alleviate the characteristic distribution skew. To balance data privacy and training efficiency, this paper adjusted the training strategy of the federated framework and the update strategy of the model. In this way, the model has relatively high privacy security during the training process while maintaining relatively high training efficiency of the model by reducing the training quantity in encrypted environments. The simulation results show that compared with traditional prediction methods, the proposed federated prediction method improves the prediction accuracy by about 4% in simulation cases of different scales. Meanwhile, compared to traditional federated frameworks, the training efficiency increases by about 11%.