Abrasive Flow Material Removal Mechanism Under Multifield Coupling and the Polishing Method for Complex Titanium Alloy Surfaces
Abstract
1. Introduction
2. Theoretical Models
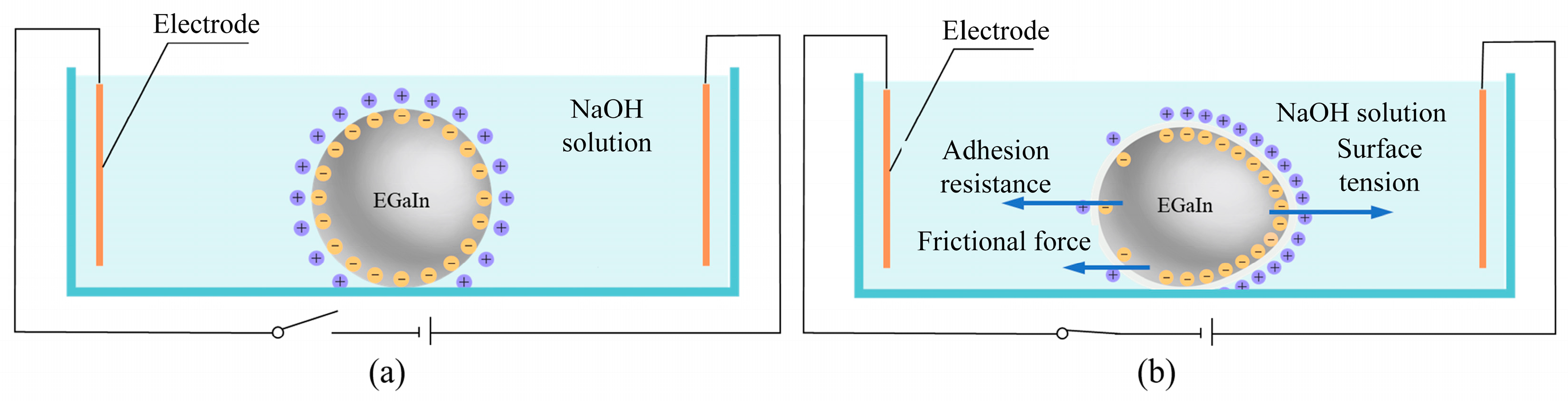
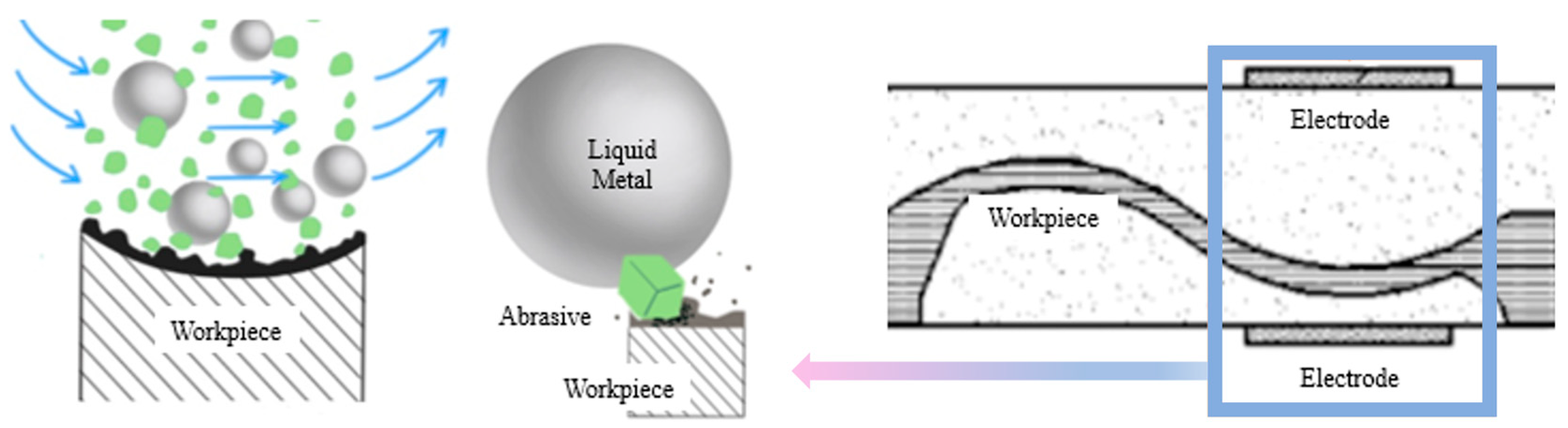
2.1. The Principle of the Liquid Metal Mixed Abrasive Flow Polishing
2.2. The Mixture Turbulence Model
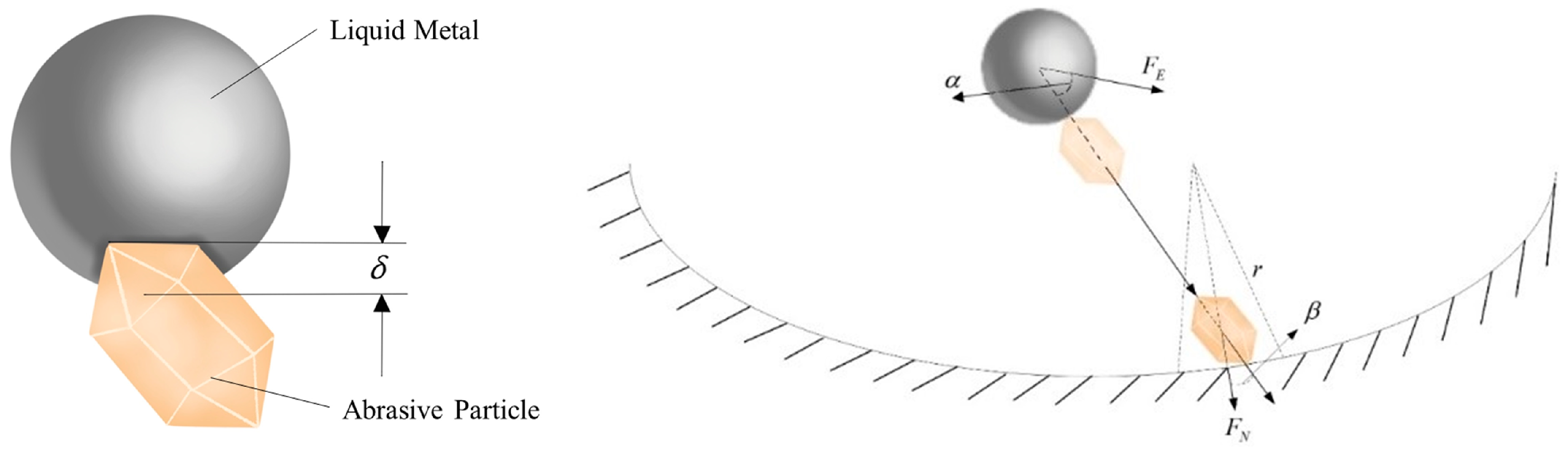
2.3. The Contact Model Between Liquid Metal and Abrasive Particles Under Electric Field
2.4. The Material Removal Mechanism Under Multifield Coupling
3. Numerical Model
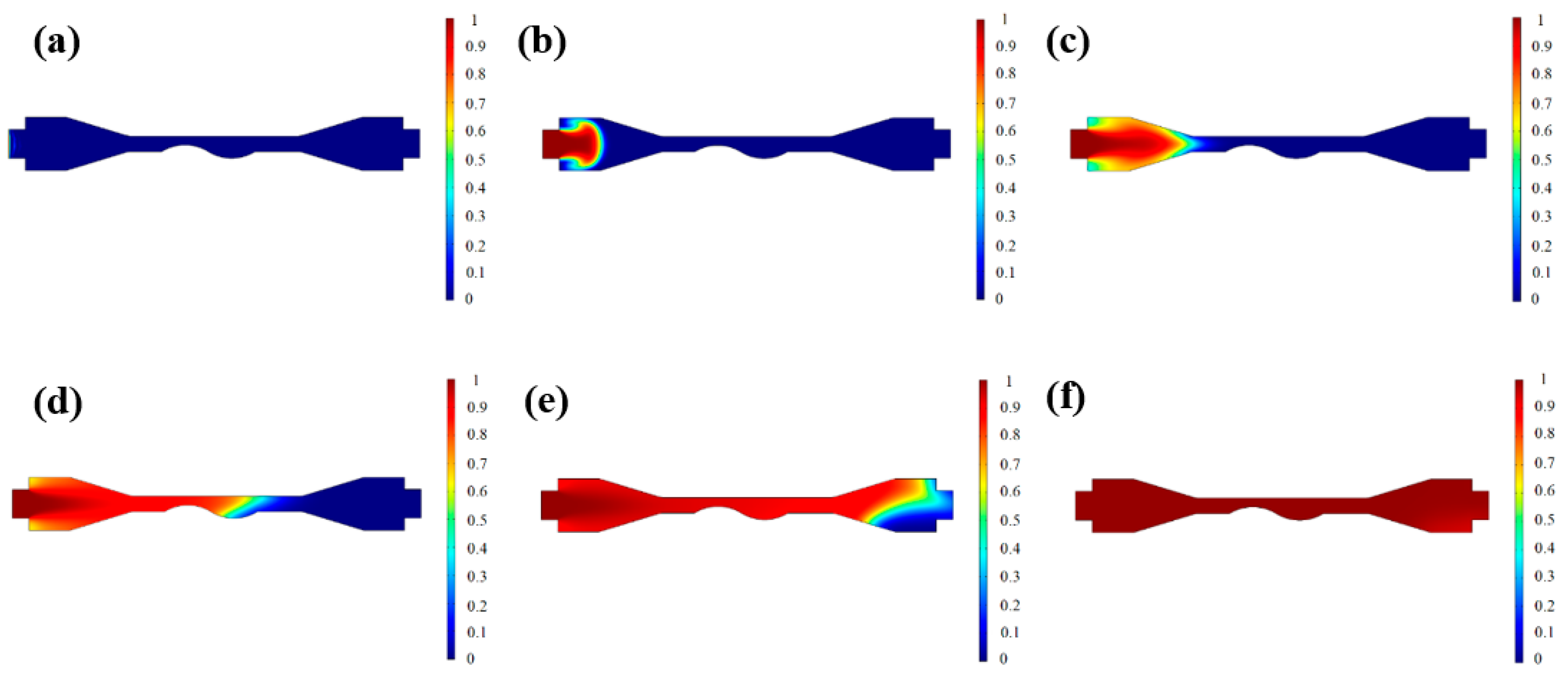
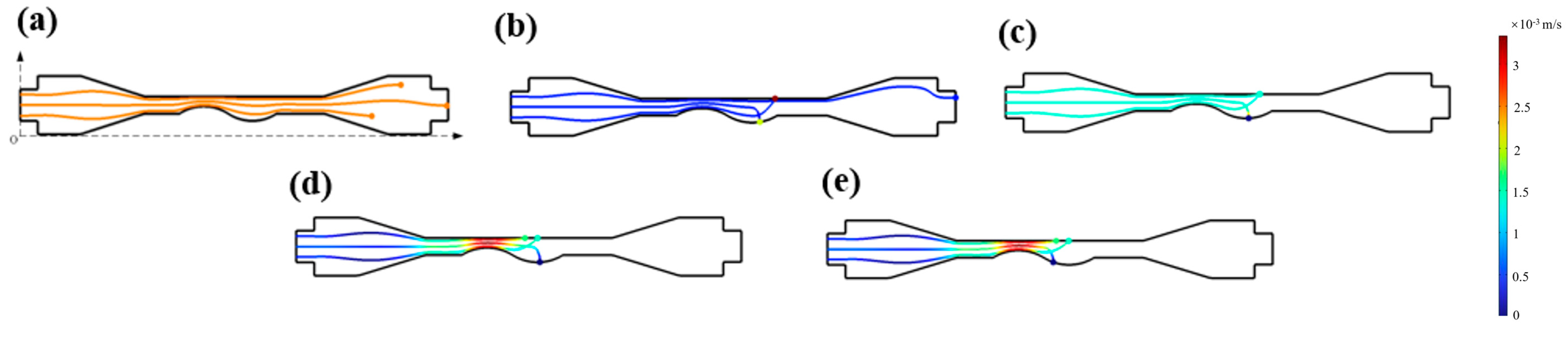
4. The Abrasive Particle Motion and Material Removal Mechanism
5. Experiment and Discussion
6. Conclusions
- (1)
- The physical models involved in the liquid metal-abrasive flow process were analyzed. An alternating electric field model, the SST turbulence model, and the Mixture model were selected as the physical field models. Simulations of the motion trajectories of liquid metal particles under the influence of alternating electric fields demonstrate the feasibility of using liquid metal particles as a driving medium for abrasives in polishing.
- (2)
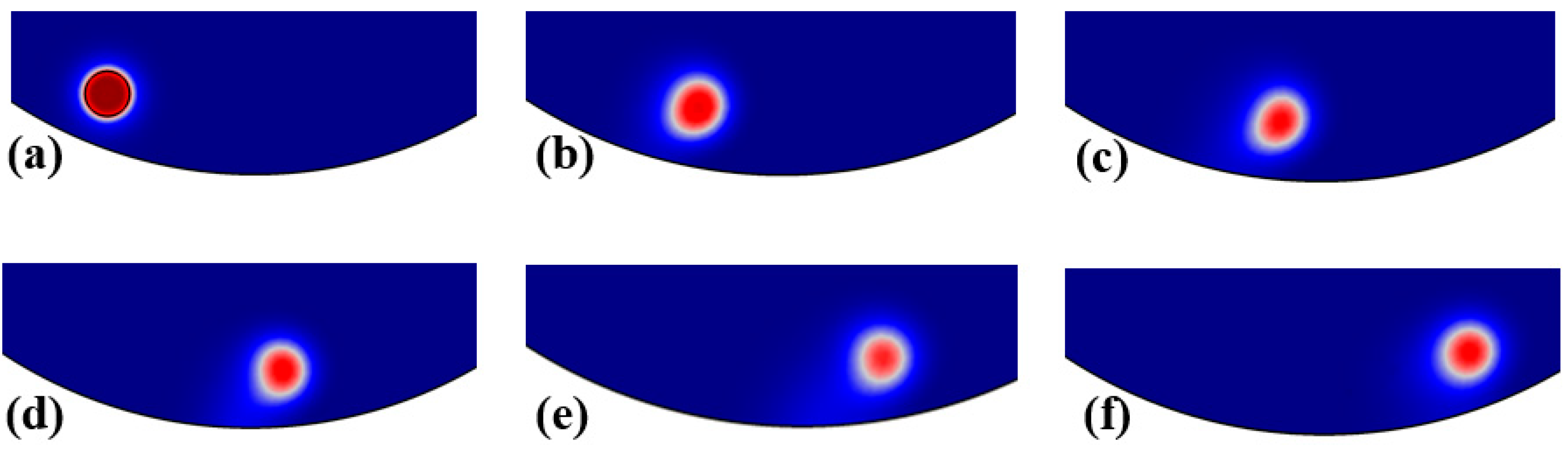
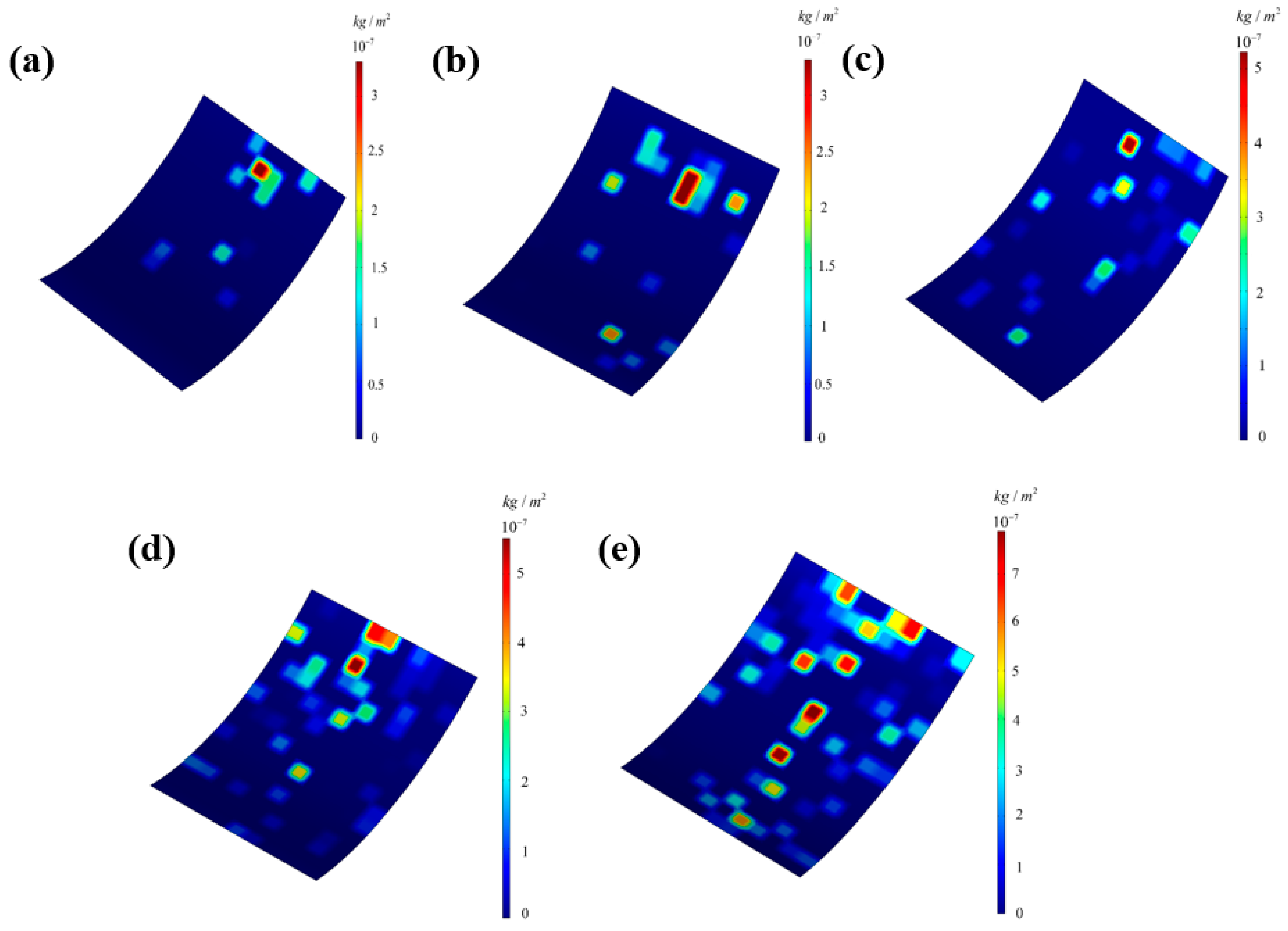
- Through simulations of the liquid phase of liquid metal particles, the change in the Pv value of the workpiece surface as the particles move across the weak flow field areas of the curved workpiece under the electric field was examined. The results indicate that the Pv value of the workpiece surface continuously increases during the particle motion process, showing significant improvement compared to the original surface Pv value.
- (3)
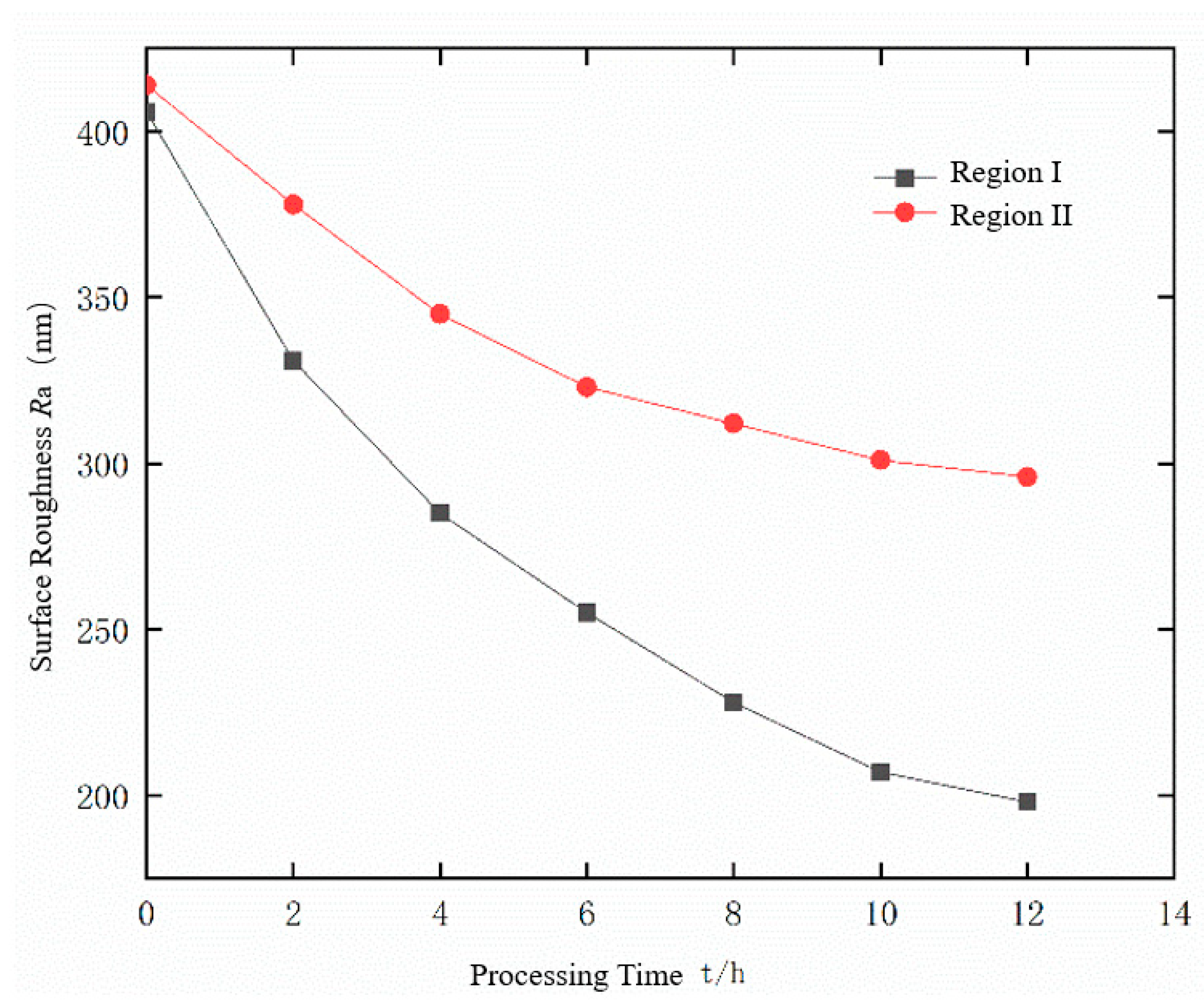
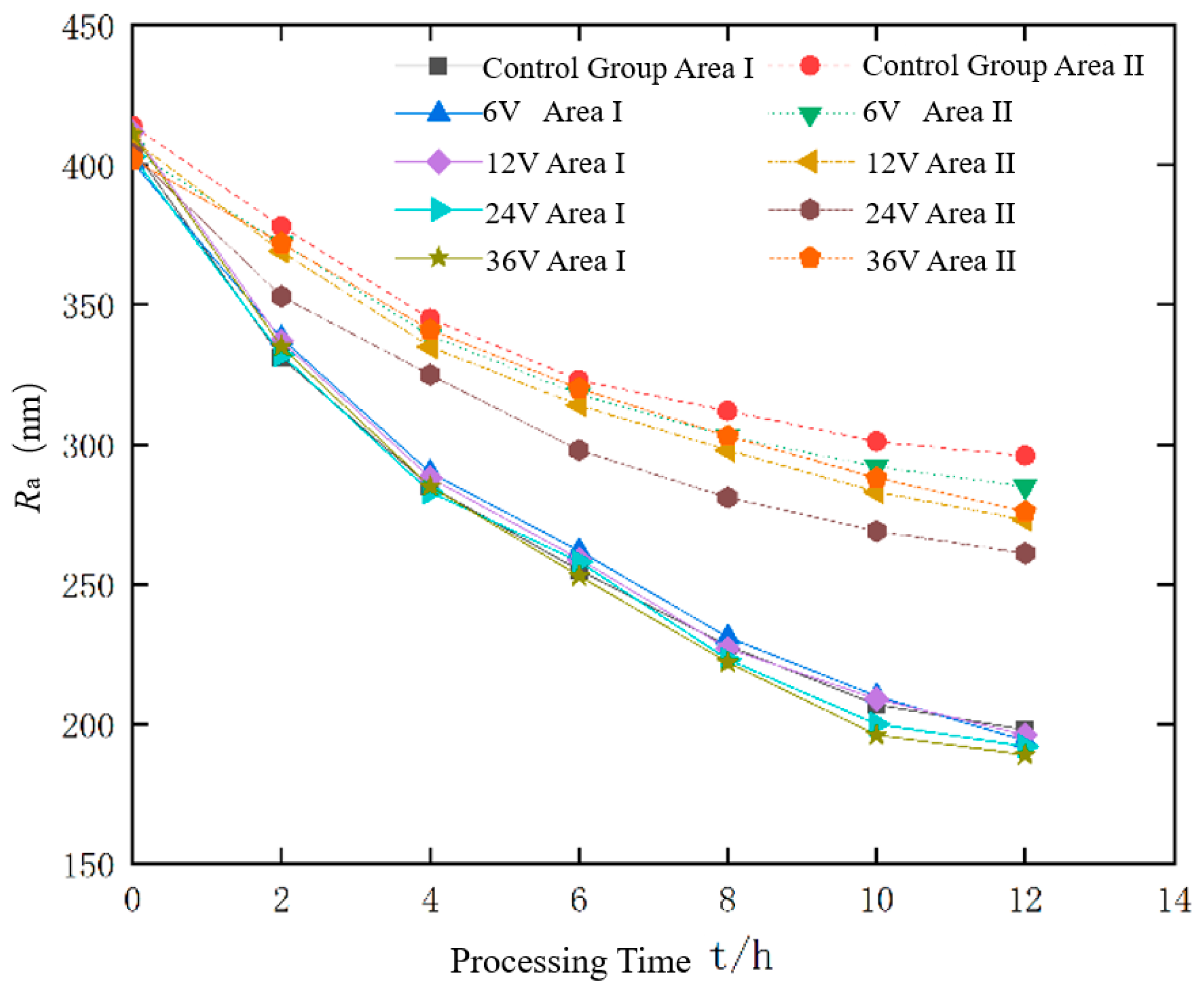
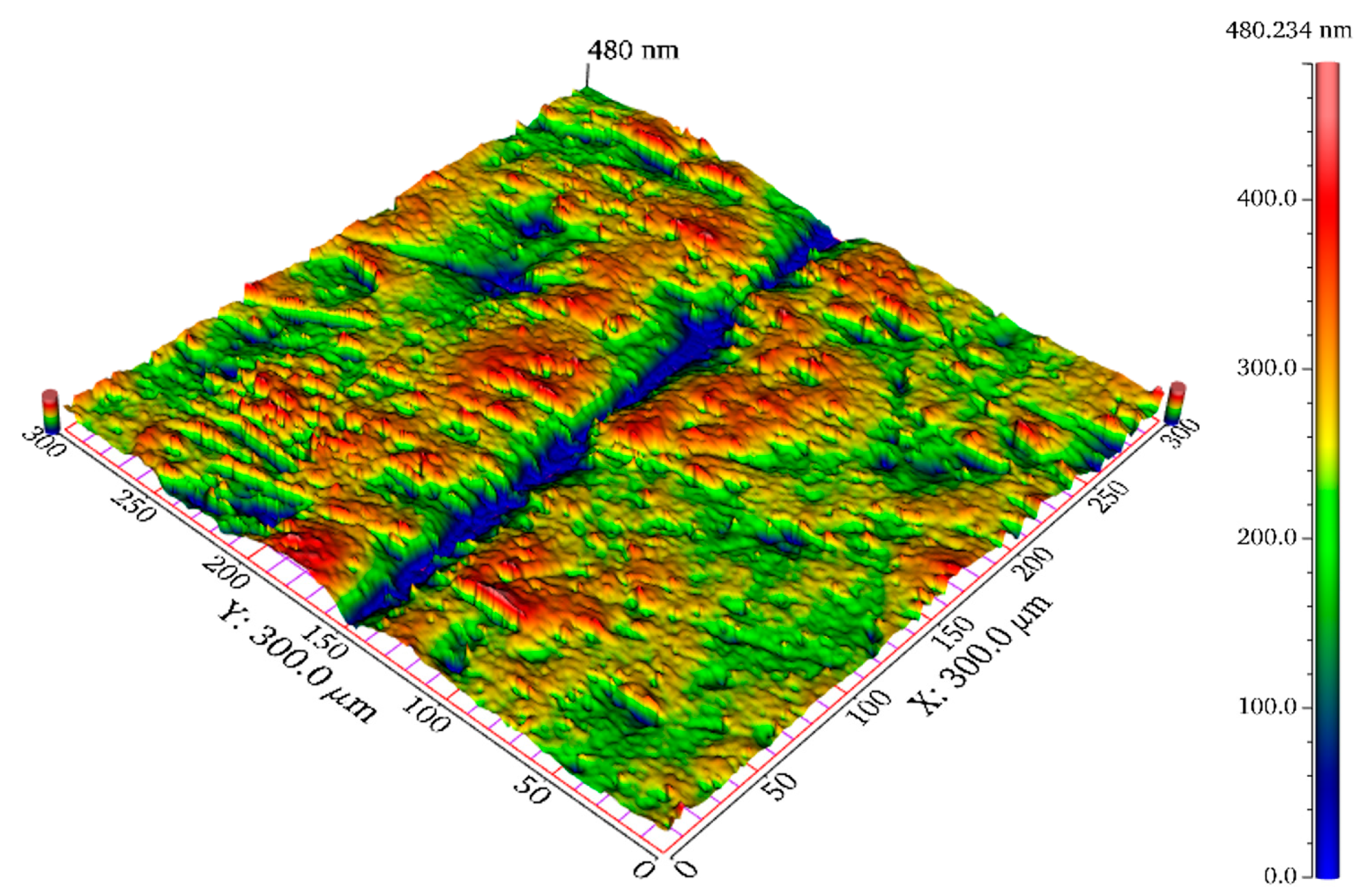
- A comparative experiment was conducted between abrasive flow polishing (control group) and liquid metal-abrasive flow polishing under different alternating voltage conditions (experimental group), focusing on surface roughness and morphology. The results show that in the control group, surface roughness in the strong flow field is 100 nm lower than in the weak flow field, while in the experimental group, the roughness difference is reduced, with the 24 V alternating electric field achieving the smallest difference of 58 nm and a 44% improvement in polishing uniformity. This demonstrates that electrostatic field-controlled liquid metal-abrasive flow polishing enhances surface polishing uniformity on curved components.
- (4)
- The interaction of parameters such as flow rate, voltage, and abrasive concentration may lead to mismatches in the polishing process, complicating optimal parameter selection. To address these challenges, a synergistic optimization of the fluid and electric field, along with numerical simulations, is essential for improving experimental accuracy and reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Genc, O.; Unal, R. Development of gamma titanium aluminide (γ-TiAl) alloys: A review. J. Alloys Compd. 2022, 929, 167262. [Google Scholar] [CrossRef]
- NIInomi, M.; Narushima, T.; Nakano, T. Recent Research and Development in the Processing, Microstructure, and Properties of Titanium and Its Alloy. Mater. Trans. 2024, 65, 1600–1611. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, B.; Qu, W.; Sun, L. Advancements and Applications of Laser Surface Treatment on Titanium Alloys. Rare Met. Mater. Eng. 2024.
- Tetsui, T. Identifying low-cost, machinable, impact-resistant TiAl alloys suitable for last-stage turbine blades of jet engines. Intermetallics 2024, 168, 108263. [Google Scholar] [CrossRef]
- Tetsui, T.; Mizuta, K. Detrimental Effects of βo-Phase on Practical Properties of TiAl Alloys. Metals 2024, 14, 908. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, L.; Wang, Y.; Qin, Y.; Xie, Z.; Lila, A.; Xu, N.; Huang, K.; Wang, J.; Huang, J. Improving fatigue life of a titanium alloy through coupled electromagnetic treatments. Int. J. Fatigue 2025, 191, 108676. [Google Scholar] [CrossRef]
- Zheng, G.A.; Xu, P.; Wang, T.; Yan, Q. Study on the bubble collapse characteristics and heat transfer mechanism of the microchannel reactor. Processes 2025, 13, 281. [Google Scholar] [CrossRef]
- Liu, J.; Zeng, X.; Zhang, P.; Peng, X.; Yu, D. Counterion-Driven Mechanochemical Reactions at TC4 Alloy/SiO2 Interfaces: Electrical Double Layer and Dynamic Ionic Radius. Tribol. Lett. 2025, 73, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, Z.; Du, Y.; Yua, Z.; Guo, L.; Guo, D. A novel approach of chemical mechanical polishing for a titanium alloy using an environment-friendly slurry. Appl. Surf. Sci. 2018, 427, 409–415. [Google Scholar] [CrossRef]
- Deng, C.; Jiang, L.; Qian, L. Synergistic Effect of F−and Persulfate in Efficient Titanium Alloy Chemical Mechanical Polishing. ECS J. Solid State Sci. Technol. 2021, 10, 114003. [Google Scholar] [CrossRef]
- Jaritngam, P.; Tangwarodomnukun, V.; Qi, H.; Dumkum, C. Surface and subsurface characteristics of laser polished Ti6Al4V titanium alloy. Opt. Laser Technol. 2020, 126, 106102. [Google Scholar] [CrossRef]
- Li, P.; Liu, B.; Li, L.; Gong, Y.; Zhou, J.; Lu, J. Study on surface quality of ultrasonic assisted underwater laser polishing. J. Mater. Res. Technol. 2023, 27, 5761–5771. [Google Scholar] [CrossRef]
- Obeidi, M.A.; Mussatto, A.; Dogu, M.N.; Sreenilayam, S.P.; McCarthy, E.; Ahad, I.U.; Keaveney, S.; Brabazon, D. Laser surface polishing of Ti-6Al-4V parts manufactured by laser powder bed fusion. Surf. Coat. Technol. 2022, 434, 128179. [Google Scholar] [CrossRef]
- Fu, D.N.; Sheng, J.; Wang, L.J.; Zhang, X.J.; Yang, R.D.; Li, X.K.; Wang, Y. In situ silver-loaded cellulose for high-strength antibacterial composite air filtration paper. Cellulose 2025, in press. [Google Scholar]
- Wang, S.-F.; Wang, Y.; Wen, J.-C.; Suo, H.-L.; Liu, Z.-Z.; Suo, W.-h.; Zhao, C.-C. Study on electrochemical polishing of TC4 alloy. Mater. Res. Express 2021, 8, 106520. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Yin, X.; Zhou, Y.; Feng, M.; Li, S. Study on electrochemical polishing mechanism of TC4 titanium alloy. Phys. Scr. 2024, 99, 085983. [Google Scholar] [CrossRef]
- Xu, W.X.; Xu, P.; Yang, Y.; Tan, D.P.; Li, L. The utilization and advancement of laser ultrasound testing in the assessment of aerospace composite characteristics: A review. Chin. J. Aeronaut. 2025, in press. [Google Scholar]
- Shen, M.; Wu, L.; Wei, M.; Chen, H.; Yuan, J.; Lyu, B.; Deng, H.; To, S.; Beri, T.H.; Hang, W. High-efficiency free-damage electrochemical shear-thickening polishing of single-crystal silicon carbide. J. Manuf. Process. 2024, 132, 532–543. [Google Scholar] [CrossRef]
- Dong, J.; Shi, J.; Ma, Z.; Yu, T. Research of the FLC + PID switching control strategy based on real-time error for the pneumatic polishing force regulating system. Eng. Sci. Technol. Int. J. 2024, 51, 101659. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Li, Z.; Li, L.; Wang, C.Y.; Wu, J.F.; Xie, Y.S.; Yin, Z.C.; Tan, D.P. Deposition mechanism of microscopic impacting droplets on flexible porous substrates. Int. J. Mech. Sci. 2025, in press. [Google Scholar]
- Zhu, G.; Zeng, X.; Gao, Z.; Gong, Z.; Duangmu, W.; Zeng, Y.; Lu, C. Study on vibration stability of aircraft engine blades polished by robot controlled pneumatic grinding wheel. J. Manuf. Process. 2023, 99, 636–651. [Google Scholar] [CrossRef]
- Du, H.; Sun, Y.; Feng, D.; Xu, J. Automatic robotic polishing on titanium alloy parts with compliant force/position control. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 1180–1192. [Google Scholar] [CrossRef]
- Hung, J.-C.; Yang, P.-J.; Lin, X.-H.; Jian, S.-Y.; Kao, C.-H.; Ferng, Y.-C.; Huang, Y.-S.; Jen, K.-K. Surface passivation and brightening of titanium-based AM materials using a robotic electrochemical mechanical polishing system. Int. J. Adv. Manuf. Technol. 2024, 134, 4339–4352. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, S.; Wang, H.; Qin, Y.; Song, Z. Surface Performance of Titanium Alloy Brake Shell Polished by Industrial Robot Based on Digital Twin. Int. J. Aerosp. Eng. 2024, 2024, 6130930. [Google Scholar] [CrossRef]
- Zeng, X.; Zhu, G.; Gao, Z.; Ji, R.; Ansari, J.; Lu, C. Surface polishing by industrial robots: A review. Int. J. Adv. Manuf. Technol. 2023, 125, 3981–4012. [Google Scholar] [CrossRef]
- Jaritngam, P.; Saetang, V.; Qi, H.; Dumkum, C. Surface polishing of additively manufactured Ti6Al4V titanium alloy by using a nanosecond pulse laser. Int. J. Adv. Manuf. Technol. 2023, 127, 3463–3480. [Google Scholar] [CrossRef]
- Tahir, A.F.M.; Aqida, S.N. An investigation of laser cutting quality of 22MnB5 ultra high strength steel using response surface methodology. Opt. Laser Technol. 2017, 92, 142–149. [Google Scholar] [CrossRef]
- Telegin, S.V.; Lyasnikova, A.V.; Dudareva, O.A.; Grishina, I.P.; Markelova, O.A.; Lyasnikov, V.N. Laser Modification of the Surface of Titanium: Technology, Properties and Prospects of Application. J. Surf. Investig. X-Ray Synchrotron Neutron Tech. 2019, 13, 228–231. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Shao, X.; Zhou, K.; Deng, Q.; Yuan, Z.; Lyu, B. Electrochemical Polishing Method for Titanium Alloys with a Microgroove Structure. Processes 2024, 12, 1114. [Google Scholar] [CrossRef]
- Dai, Y.; Li, S.; Feng, M.; Chen, B.; Qiao, J. Fundamental Study of Phased Array Ultrasonic Cavitation Abrasive Flow Polishing Titanium Alloy Tubes. Materials 2024, 17, 5185. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X.; Zhu, L.; Zhou, Z. Theoretical and Experimental Investigation on a Novel Cavitation-Assisted Abrasive Flow Polishing Method. Micromachines 2024, 15, 1142. [Google Scholar] [CrossRef] [PubMed]
- Ji, R.; Qi, Z.; Chen, J.; Zhang, L.; Lin, K.; Lu, S.; Li, Y. Numerical and Experimental Investigation on the Abrasive Flow Machining of Artificial Knee Joint Surface. Crystals 2023, 13, 430. [Google Scholar] [CrossRef]
- Choopani, Y.; Khajehzadeh, M.; Razfar, M.R. An experimental study on the abrasive flow machining of aluminum alloy (AA 2024). SN Appl. Sci. 2023, 5, 151. [Google Scholar] [CrossRef]
- Peta, K. Multiscale Wettability of Microtextured Irregular Surfaces. Materials 2024, 17, 5716. [Google Scholar] [CrossRef]
- Lin, Z.; Li, T.; Yang, S.; Ji, B.; Wang, Z. Revolutionizing flexible electronics with liquid metal innovations. Device 2024, 2, 100331. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, B.; Li, K.; Zhang, L. Application of liquid metal driven-abrasive flow to material removal for the inner surface of channel. Powder Technol. 2025, 452, 120487. [Google Scholar] [CrossRef]
- Zhang, X.-D.; Liu, J. Perspective on liquid metal enabled space science and technology. Sci. China-Technol. Sci. 2020, 63, 1127–1140. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.Y.; Li, L.; Wu, J.F.; Yin, Z.C.; Tan, D.P. Numerical investigation of mesoscale multiphase mass transport mechanism in fibrous porous media. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2363246. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Q.; Zhang, L. Titanium Alloy Thin-walled Curved Surface Liquid Metal-abrasive Flow Machining Simulation and Experimental Research. J. Mech. Eng. 2021, 57, 220–231. [Google Scholar]
- Zheng, G.A.; Weng, X.X.; Wang, T.; Xu, P.; Xu, W.X.; Li, L.; Xu, X.F.; Tan, D.P. Piezoelectric ultrasonic coupling-based polishing of micro-tapered holes with abrasive flow. J. Zhejiang Univ. Sci. A 2025. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, B.; Xie, Y.; Ji, R.; Li, Y.; Mao, W. Control Mechanism of Particle Flow in the Weak Liquid Metal Flow Field on Non-Uniform Curvature Surface Based on Lippmann Model. Front. Mater. 2022, 9, 895263. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, H.; Yan, Q.; Wang, X.; Wang, X. Rheological characterisation of abrasive media and finishing behaviours in abrasive flow machining. Int. J. Adv. Manuf. Technol. 2020, 107, 3569–3580. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Wu, J.; Li, L.; Tan, D. Machinability evolution of gas–liquid-solid three-phase rotary abrasive flow finishing. Int. J. Adv. Manuf. Technol. 2023, 131, 2145–2164. [Google Scholar] [CrossRef]
- Liu, M.; Wang, J.; He, H.; Yuan, J.; Lyu, B.; Chen, H.; Peng, G. Performance of flexible CeO2 composite abrasive in force rheological polishing of fused silica glass. J. Manuf. Process. 2024, 126, 175–184. [Google Scholar] [CrossRef]
- Liu, M.; Wang, J.; Liu, W.; Wu, H.; Yuan, J.; Lyu, B.; Peng, G.; Zhang, J. Force rheological polishing of polycrystalline magnesium aluminate spinel using agglomerated diamond abrasive. Ceram. Int. 2024, 50, 55275–55285. [Google Scholar] [CrossRef]
- Li, L.; Xu, P.; Li, Q.H.; Zheng, R.Y.; Xu, X.M.; Wu, J.F.; He, B.Y.; Bao, J.J.; Tan, D.P. A coupled LBM-LES-DEM particle flow modeling for microfluidic chip and ultrasonic-based particle aggregation control method. Appl. Math. Model. 2025, in press. [Google Scholar]
- Tan, Y.F.; Ni, Y.S.; Xu, W.X.; Xie, Y.S.; Li, L.; Tan, D.P. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ. Sci. A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]
- Li, L.; Xu, P.; Li, Q.H.; Yin, Z.C.; Zheng, R.Y.; Wu, J.F.; Bao, J.J.; Qi, H.; Tan, D.P. Multi-field coupling particle flow dynamic behaviors of the microreactor and ultrasonic control method. Powder Technol. 2025, in press. [Google Scholar] [CrossRef]
- Wang, C.Y.; Li, Z.; Xu, P.; Hou, Y.Q.; Tan, D.P.; Li, L. Collision modelling approach and transient response mechanism of ring-ribbed cylindric shells for underwater vehicles. Appl. Math. Model. 2025, 141, 115923. [Google Scholar] [CrossRef]
- Wu, J.F.; Xu, P.; Li, L.; Li, Z.; Qi, H.; Wang, C.Y.; Zhang, Y.K.; Xie, Y.S.; Tan, D.P. Multiphase dynamic interfaces and abrasive transport dynamics for abrasive flow machining in shear thickening transition states. Powder Technol. 2024, 446, 120150. [Google Scholar] [CrossRef]
- Xu, P.; Li, Q.H.; Wang, C.Y.; Li, L.; Tan, D.P.; Wu, H.P. Interlayer healing mechanism of multipath deposition 3D printing models and interlayer strength regulation method. J. Manuf. Process. 2025, in press. [Google Scholar]
- Guo, X.M.; Yang, M.Y.; Li, F.Q.; Zhu, Z.C.; Cui, B.L. Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects. Energies 2024, 17, 3627. [Google Scholar] [CrossRef]
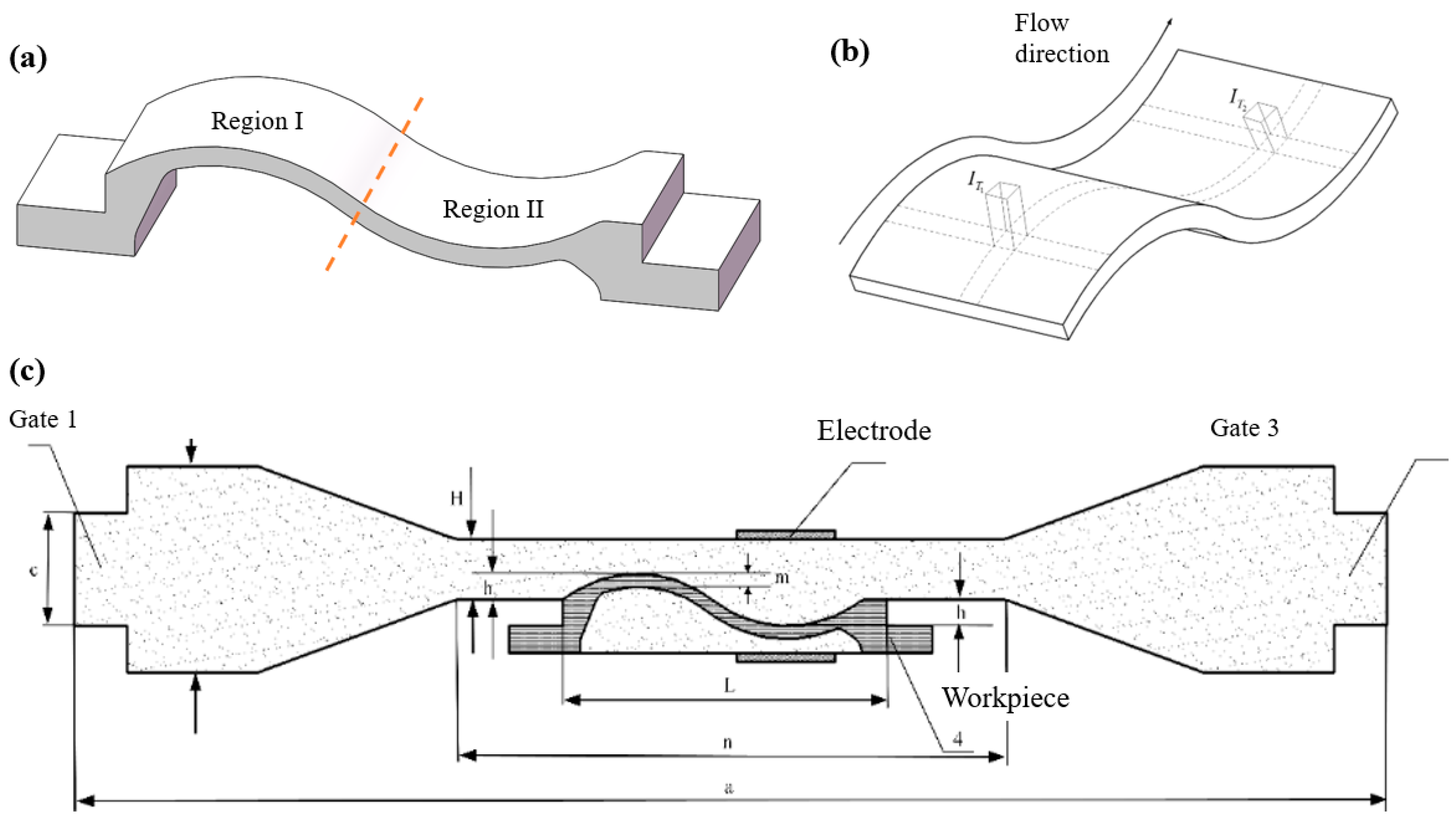

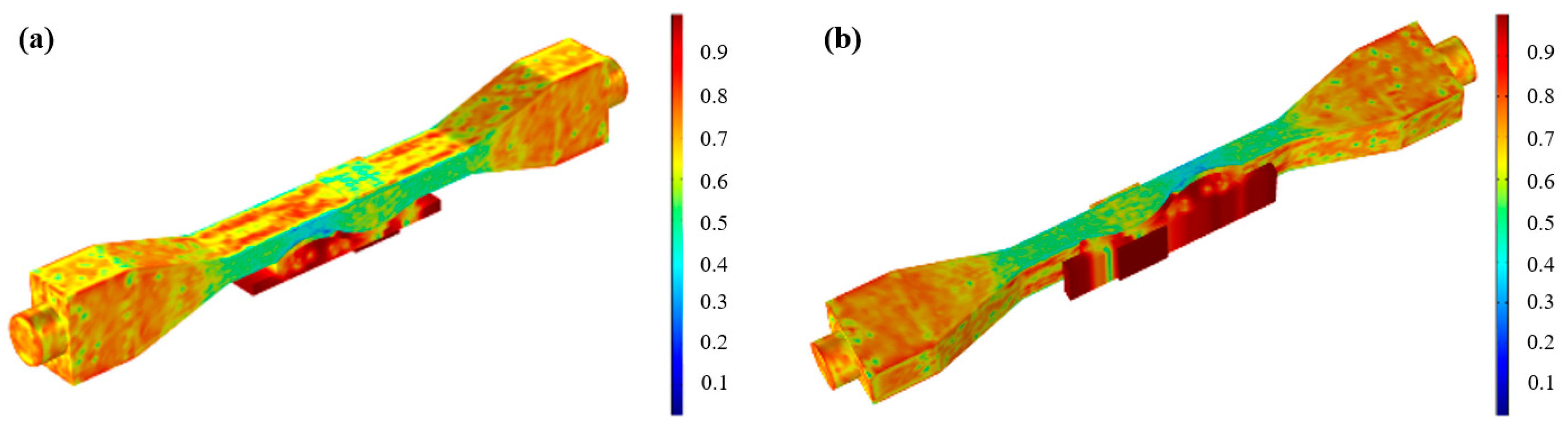

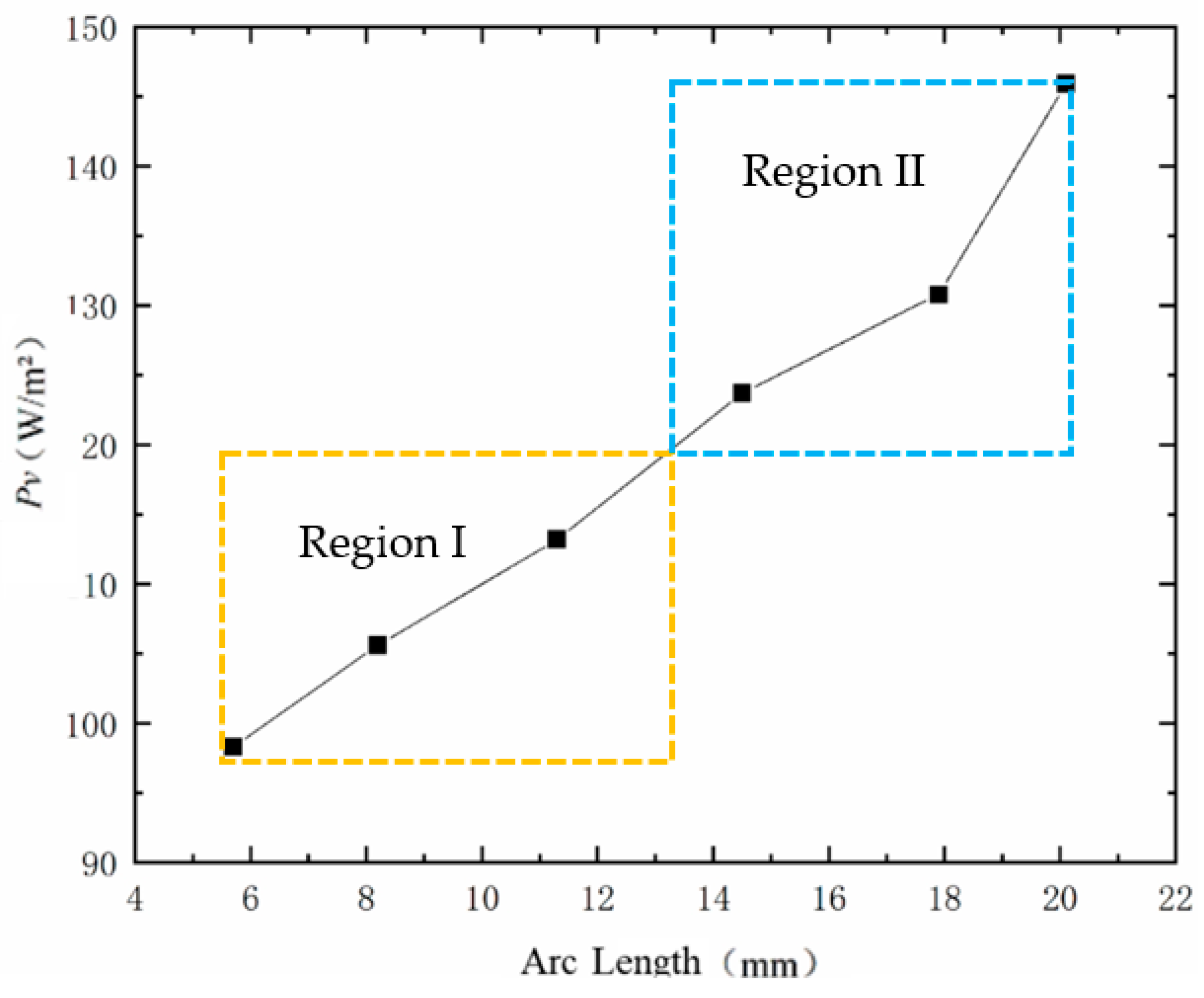
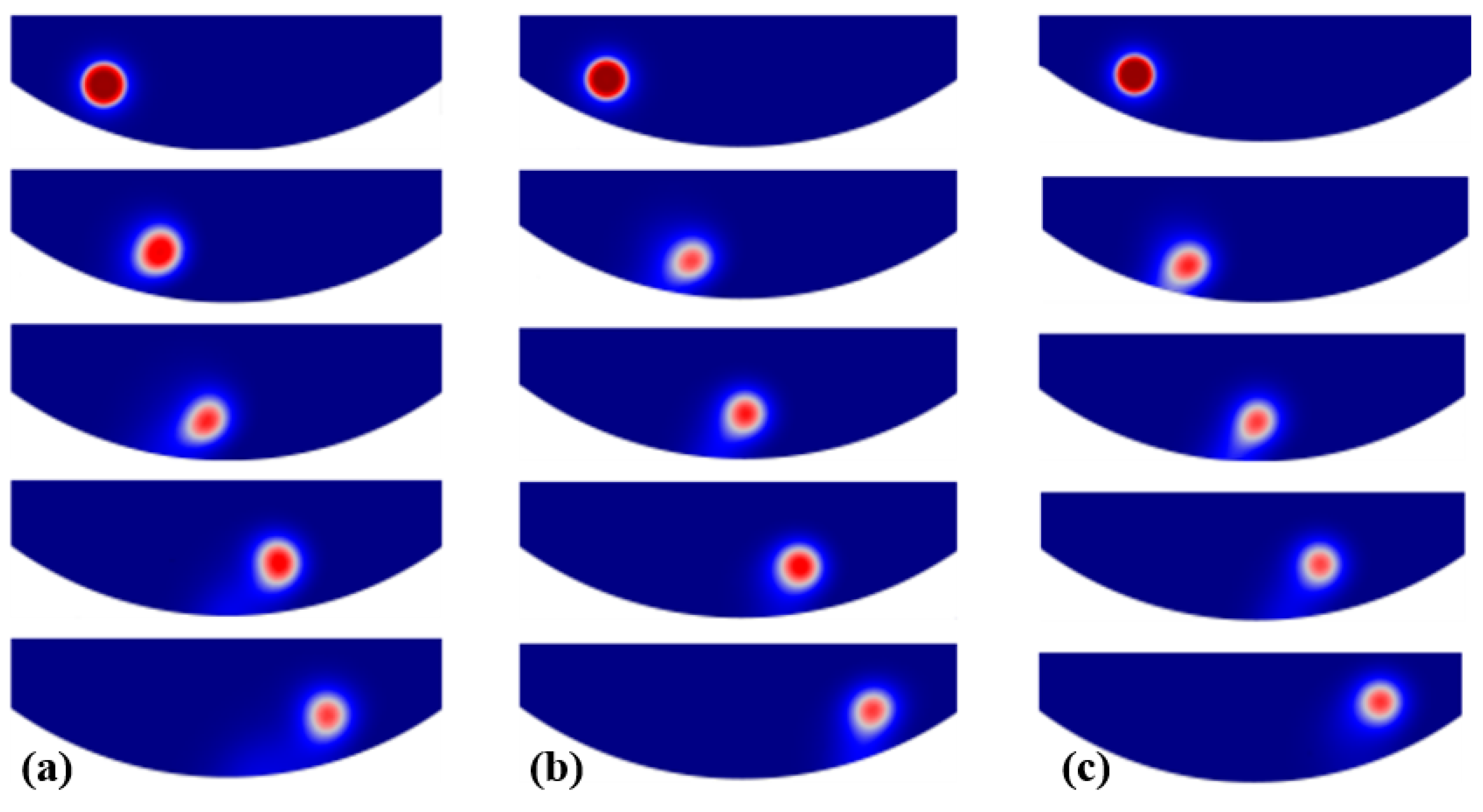
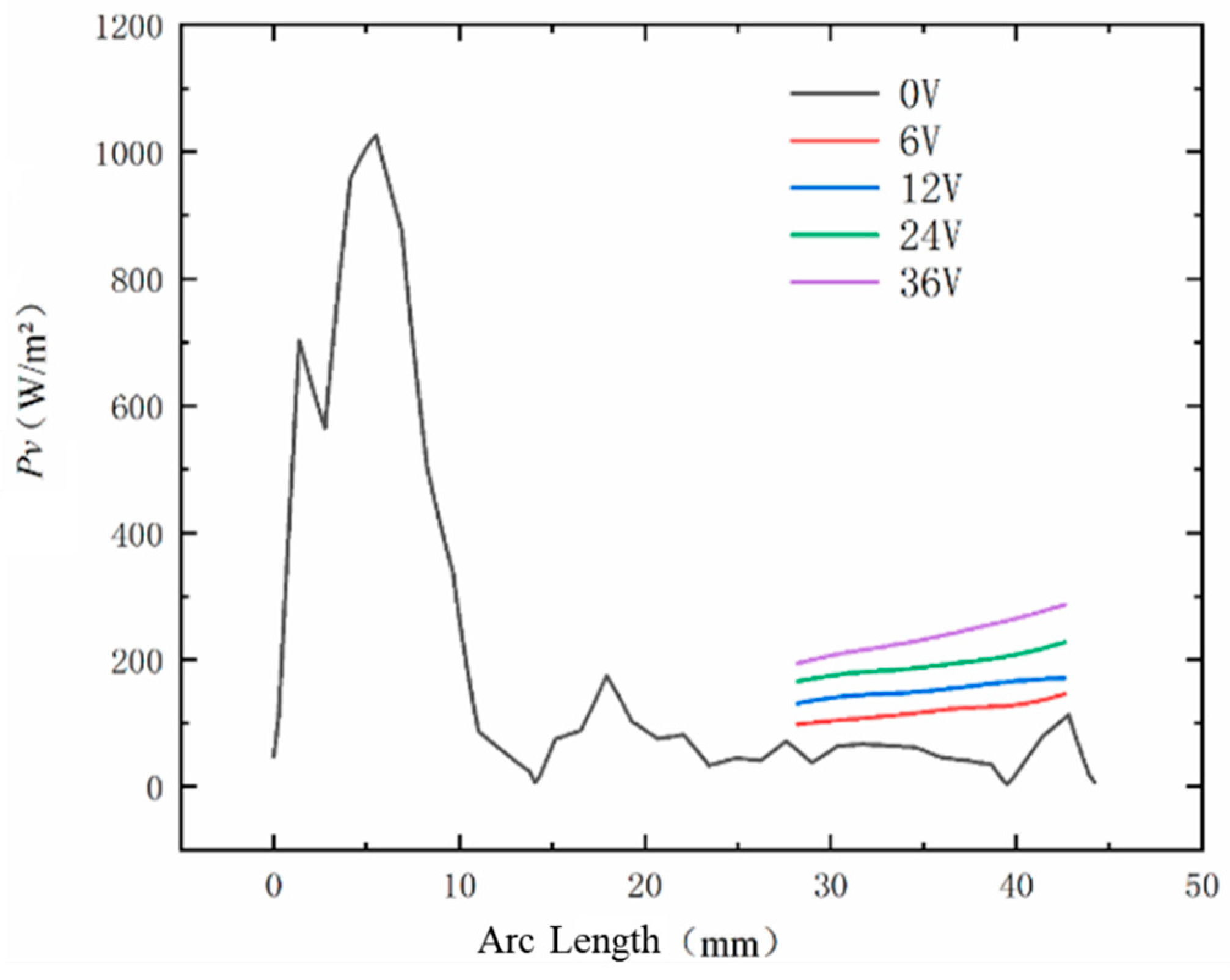
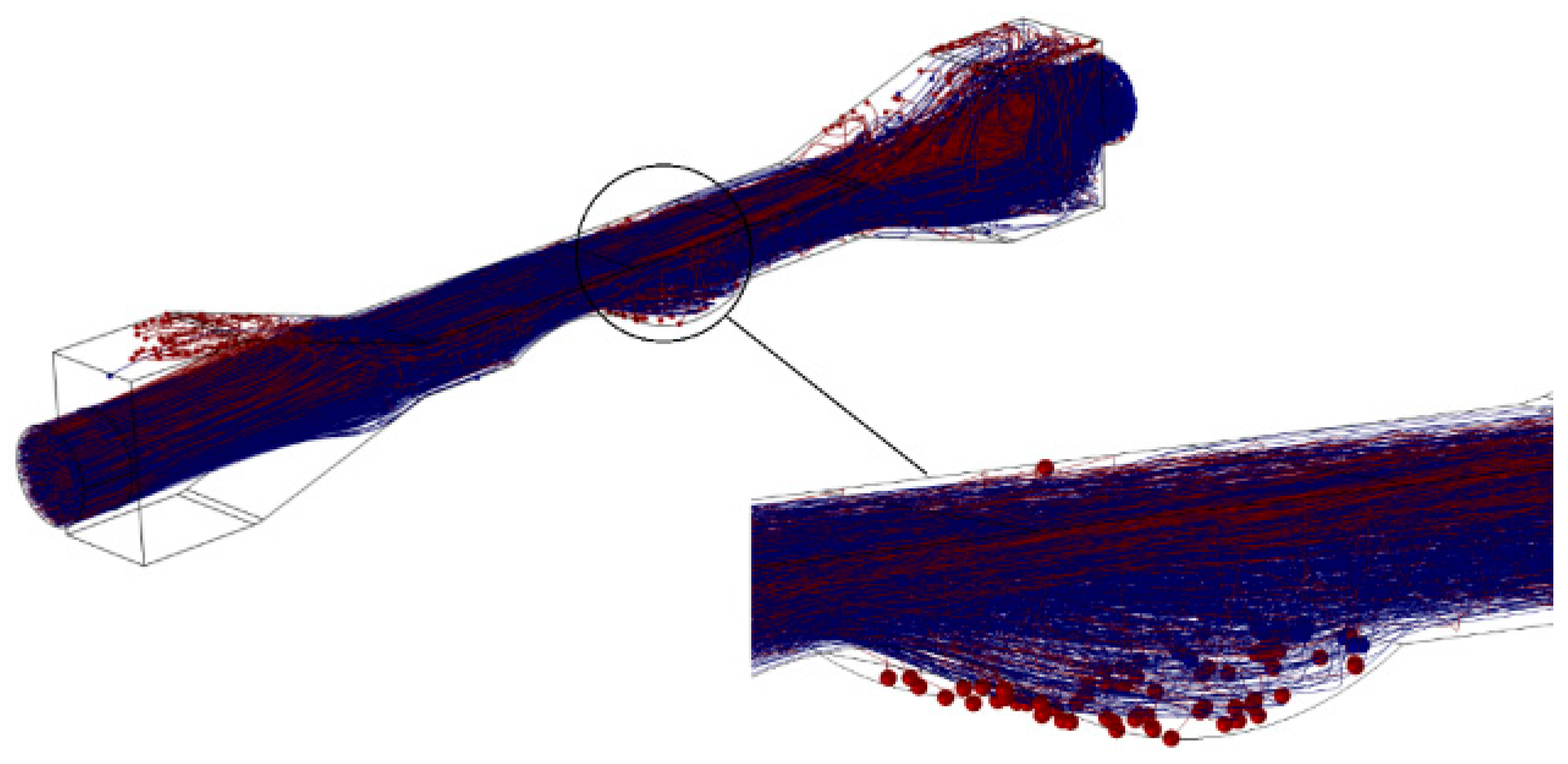





| Geometrical Parameter | a | b | c | n | L | H | h | m |
|---|---|---|---|---|---|---|---|---|
| size (mm) | 185 | 24 | 16 | 76 | 46 | 5 | 2.5 | 1.2 |
| Simulation Parameters | Parameter Value |
|---|---|
| Curved workpiece material | Ti-2Al-1.5Mn titanium alloy |
| Fluid density, / | 1000 |
| Fluid conductivity, | 9.7 |
| Abrasive density, / | 3200 |
| Average diameter of abrasive particles, | 50 |
| Abrasive particle volume fraction, /% | 10 |
| Liquid metal particle volume fraction, /% | 5 |
| Liquid metal particle density, | 6400 |
| Liquid metal particle density, /V | 6, 12, 24, 36 V AC, 50 Hz |
| Average diameter of liquid metal particles, D/mm | 1 |
| Fluid inflow conditions | Normal inflow 4 m/s |
| Fluid outlet conditions | p = 0, inhibit backflow |
| Process Parameter | Liquid Metal-Abrasive Flow Parameter | Abrasive Flow Parameter |
|---|---|---|
| Abrasive type | Silicon carbide | Silicon carbide.0 |
| Liquid phase | 1 mol/L NaOH aqueous solution | 1 mol/L NaOH aqueous solution |
| Abrasive mesh size | 800 mesh | 800 mesh |
| Abrasive volume fraction (%) | 10 | 10 |
| Liquid metal volume fraction (%) | 5 | 5 |
| AC voltage (V) | 6 V, 12 V, 24 V, 36 V | 0 V |
| Processing time (h) | 10 h | 10 h |
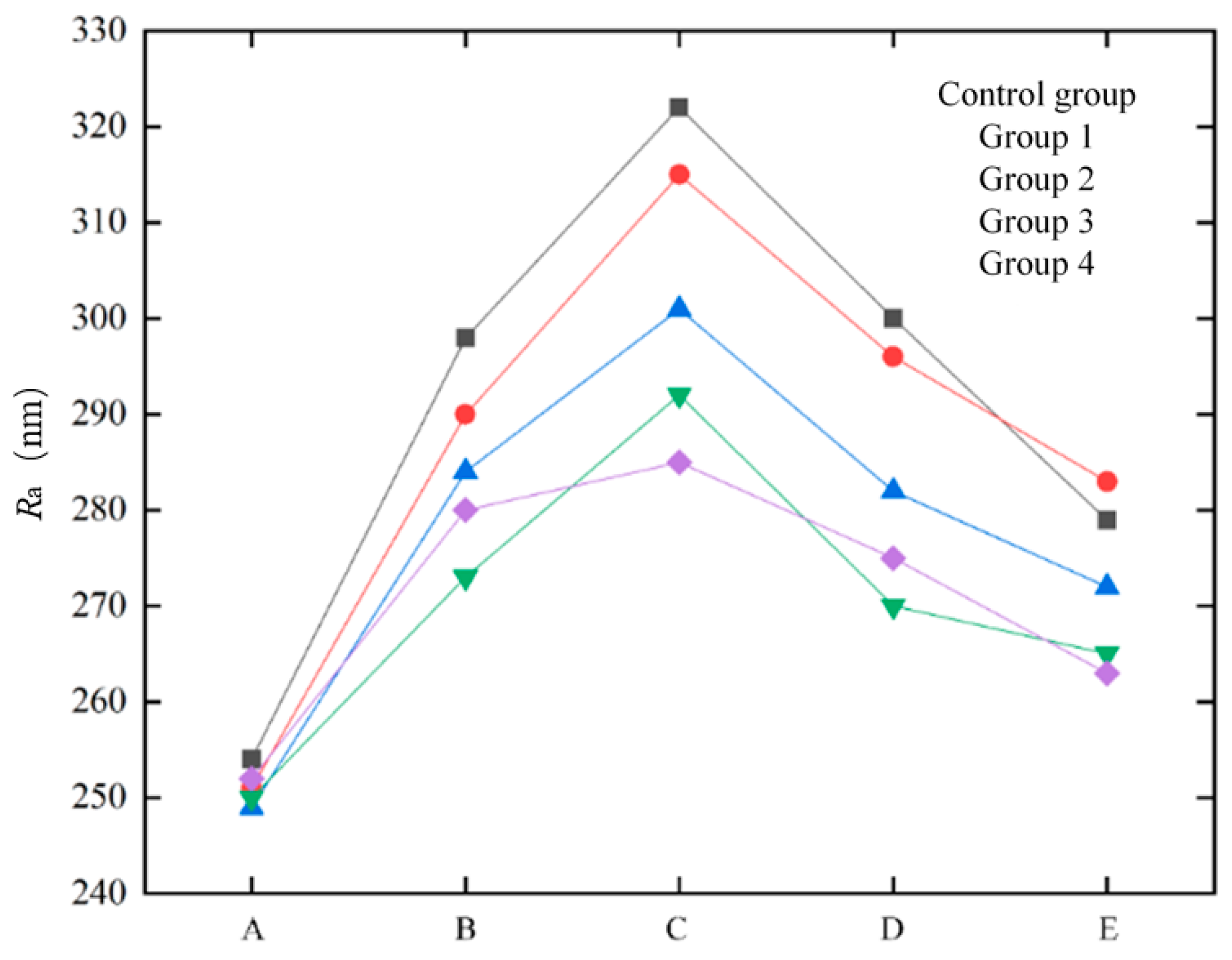
| Group | Sa (nm) | |
|---|---|---|
| Region I | Region II | |
| Group 1 | 401 | 405 |
| Group 2 | 412 | 409 |
| Group 3 | 403 | 404 |
| Group 4 | 411 | 402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Wang, R.; Wang, Z.; Zheng, B.; Zhang, L. Abrasive Flow Material Removal Mechanism Under Multifield Coupling and the Polishing Method for Complex Titanium Alloy Surfaces. Processes 2025, 13, 416. https://doi.org/10.3390/pr13020416
Fu Y, Wang R, Wang Z, Zheng B, Zhang L. Abrasive Flow Material Removal Mechanism Under Multifield Coupling and the Polishing Method for Complex Titanium Alloy Surfaces. Processes. 2025; 13(2):416. https://doi.org/10.3390/pr13020416
Chicago/Turabian StyleFu, Yufei, Rui Wang, Zhongfei Wang, Bingjun Zheng, and Li Zhang. 2025. "Abrasive Flow Material Removal Mechanism Under Multifield Coupling and the Polishing Method for Complex Titanium Alloy Surfaces" Processes 13, no. 2: 416. https://doi.org/10.3390/pr13020416
APA StyleFu, Y., Wang, R., Wang, Z., Zheng, B., & Zhang, L. (2025). Abrasive Flow Material Removal Mechanism Under Multifield Coupling and the Polishing Method for Complex Titanium Alloy Surfaces. Processes, 13(2), 416. https://doi.org/10.3390/pr13020416




