Abstract
Coal seam gas drainage is a primary measure for mitigating coal and gas outburst hazards. Grouting sealing can form coal-slurry consolidated bodies, significantly improving the sealing quality of gas drainage boreholes and alleviating coal and gas outburst risks. Therefore, this study conducts triaxial loading and seepage experiments to analyze the mechanical failure characteristics and permeability variation of coal-slurry consolidated bodies under loading conditions following grouting sealing of gas drainage boreholes. Based on the “cube” model, a permeability model for the damaged coal-slurry consolidated body under loading conditions is established. The findings provide guidance for evaluating the leakage prevention performance of sealing materials in field engineering and optimizing the sealing efficiency of grouting materials. Future research may explore the damage and seepage evolution of coal-slurry consolidated bodies under various loading conditions and sealing material types.
1. Introduction
Coal remains China’s primary energy source, but the depletion of shallow coal resources has led to increased mining depths. Deep coal seams exhibit complex geological conditions, characterized by low permeability, high in-situ stress, and high gas content [1,2,3]. These factors worsen mining conditions and increase the frequency of coal and gas outburst disasters [4,5,6]. Gas drainage in coal seams is the primary measure to mitigate such disasters, with the sealing quality of drainage boreholes directly affecting gas extraction efficiency. After grouting and sealing, the slurry fills fractures and bonds with the fractured coal and rock to form a high-strength, low-permeability, and stable consolidation body. However, under the combined effects of deep in-situ stress, mining-induced stress, and negative drainage pressure, fractures easily develop around the borehole, leading to gas leakage and seal failure. This results in a rapid decline in gas concentration and reduces drainage efficiency. Therefore, investigating the mechanical failure characteristics and permeability evolution of coal-slurry consolidation bodies under loading is crucial for optimizing sealing materials, enhancing borehole sealing quality, improving gas extraction efficiency, and ensuring safe coal mine operations.
Recent studies on grouting sealing have progressed significantly. Celik et al. [7] conducted experiments on permeability grouting for soil reinforcement, developed a flow model, and designed key slurry parameters. They analyzed the factors affecting differences between cylindrical and spherical flow models. Ren et al. [8] developed a fractal permeability model considering multiple influences of micro—pore fractures on the coal body. Zhu et al. [9] created a green grouting material and evaluated its anti-permeability properties using permeability tests. In coal-rock loading studies, many researchers simulated the seepage behavior of damaged coal under triaxial conditions. Du et al. [10] developed a true triaxial gas-solid coupling system to study deformation, failure, and permeability evolution of briquettes and raw coal. Liu et al. [11] used a true triaxial test system to analyze fracture failure modes and permeability variations in coal. Wang et al. [12,13,14] explored crack propagation and permeability evolution in gas-bearing coal under axial and confining stresses. In permeability modeling, Wu et al. [15] used CT scanning and a triaxial loading seepage system to test gas-containing coals and constructed a damage ontology model reflecting the deformation behavior of the coal body. Shi et al. [16] proposed a permeability model for elastic coal under uniaxial strain, incorporating pore pressure and gas adsorption. Xue Yi [17] refined Seidle’s study by including damage effects in post-peak coal permeability models. Connell et al. [18] developed permeability models for coal under various rigid constraints. Bai et al. [19] established a cubic structural model for coal permeability under triaxial loading and unloading, validating it through experimental analysis.
Wang et al. [20] investigated the deformation and gas flow characteristics of coal under true triaxial stress conditions. They observed that during the entire stress-strain process of coal, the stress-strain curve initially increases and then decreases, while the permeability-strain curve initially decreases and then increases. A “stress-sensitive zone” exists regarding the influence of intermediate principal stress on the minimum permeability of coal. Lu et al. [21] measured the permeability of layered composite coal-rock under true triaxial stress conditions using a true triaxial apparatus and proposed a permeability model for layered composite coal-rock under such conditions. They found that the variation in the thickness of coal seams and sandstone layers significantly influences the evolution of composite coal-rock permeability, with permeability increasing as the ratio of sandstone to coal thickness increases. Liu [22] conducted a series of triaxial compression and unloading tests on cemented fractured specimens with varying coal particle contents. The results showed that as the coal particle content increases, both the peak strength and cohesion of the specimens decrease, while the internal friction angle in both tests increases. In the triaxial compression test, dissipated energy increased with coal particle content, while in the triaxial unloading test, dissipated energy initially increased and then decreased. Shen [23] investigated the mechanical properties, energy evolution, and brittleness of coal under various true triaxial stress states. They developed an energy dissipation evolution equation based on the logistic function, defining dissipated energy as a damage factor (D), and established a three-dimensional damage constitutive model for coal, considering residual strength. Cao [24] developed a method capable of reproducing in-situ stress and loading/unloading paths of coal under field conditions. They studied the damage and failure characteristics of coal samples under true triaxial loading and dynamic unloading conditions. As the level of the maximum principal stress (σ1) increased, the peak number of acoustic emission (AE) events in coal samples initially increased and then decreased. With increasing triaxial load, the energy release zone shifted and expanded. Under higher triaxial load levels, the coal sample failed and was severely damaged, with dynamic unloading of the minimum principal stress (σ3) leading to the ejection of coal fragments. Liang [25] studied the failure evolution process of coal under true triaxial cyclic loading. They analyzed the evolution of deformation, elastic modulus, Poisson’s ratio, and peak strength, and characterized the volume strain of fractures, dissipated energy, and failure modes. The results indicated that, under true triaxial cyclic loading, internal damage and failure in coal were more severe, with shear failure being the predominant mode, complemented by tensile failure. Duan et al. [26] used a true triaxial system to investigate the impact of cyclic loading of each principal stress on the deformation, energy evolution, and damage characteristics of coal, revealing the mechanical evolution of coal under excavation disturbance in true triaxial conditions. They found that the total dissipated energy of coal increased exponentially with increasing amplitude of true triaxial layered cyclic loading. As the amplitude of the cyclic loading increased, the damage variable exhibited a pronounced S-shaped change, showing a trend of deceleration, acceleration, and then deceleration.
In conclusion, extensive research has been conducted on the mechanical properties and permeability models of coal-rock grout bodies, as well as the damage evolution of coal under triaxial loading conditions, yielding valuable results. However, most studies have focused on improving the mechanical properties of grout materials and developing theoretical permeability models for coal-rock structures. Research on the permeability characteristics of coal slurry grout bodies after grouting or their permeability evolution under loading conditions is limited. Unlike previous studies, this research integrates volumetric deformation and structural deformation, establishing a damage-permeability evolution model for coal slurry grout bodies. Triaxial creep-permeability experiments were conducted to investigate the mechanical and permeability changes under dynamic loading conditions. The results show that under stress loading, the permeability of coal slurry grout bodies exhibits a “V”-shaped trend before instability. After instability, the degree of permeability increase is higher with increasing initial axial and confining pressures. The average relative error between the experimental and theoretical permeability values is 8.7%, and the experimental results validate the theoretical model, providing guidance for optimizing grouting techniques and addressing the challenges of gas extraction in deep coal seams.
2. Model Building
2.1. Model Assumption
Gas flow in coal is influenced by the coupled effects of stress, seepage, and temperature fields. To analyze the seepage evolution of coal-slurry consolidated bodies under load, the study simplifies the physical model using a cubic structure. A theoretical permeability model is developed with the following assumptions:
(1) The consolidated body exhibits a dual-porosity structure, consisting of pores and fractures, and remains in an isothermal state during the seepage process.
(2) The gas within the consolidated body is considered an ideal gas, with its migration governed by Fick’s law in the coal matrix and Darcy’s law in the fractures.
(3) The deformation of the matrix elements within the consolidated body is isotropic, encompassing expansion and compression.
(4) The consolidated body undergoes two types of deformation mechanisms: bulk deformation and structural deformation.
2.2. Deformation of Coal-Slurry Cementation Under Effective Stresses
Before damage, the coal-slurry consolidated body remains in the elastic deformation phase, during which fracture aperture changes are reversible and no damage occurs. The study adopts a cubic model for analysis, as shown in Figure 1 [27].
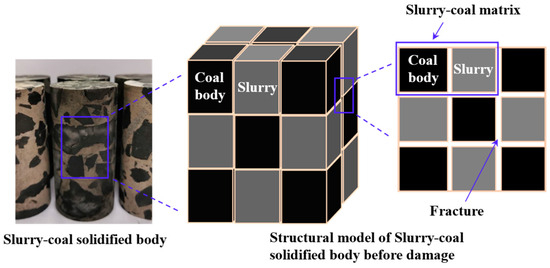
Figure 1.
Physical model of coal-slurry consolidation body.
The coal-slurry consolidated body, formed around grouted boreholes, undergoes strain under the combined effects of external stress and coal seam gas pressure. Based on the classical Terzaghi effective stress principle, the study establishes effective stress for the coal-slurry consolidated body using the dual effective stress principle for porous media [28]. The model considers two deformation mechanisms: bulk deformation and structural deformation, corresponding to bulk effective stress and structural effective stress, respectively.
(1) Bulk Effective Stress [27]. Bulk deformation refers to the overall deformation of the coal-slurry matrix framework caused by bulk effective stress. In the coal-slurry porous medium, consider a cross-section OO1 (Figure 2) with an area S (including pores and the matrix). The total stress applied on this section satisfies the equilibrium relationship expressed by the following equation:
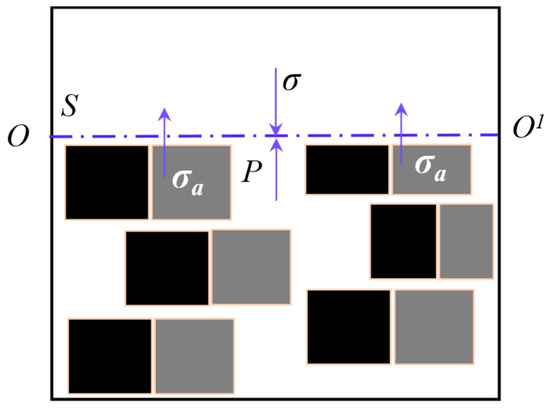
Figure 2.
Relation established for the effective stress of the body.
The stress relation equation for coal-slurry porous media can be obtained from Equation (1):
Equating over the entire matrix cross-sectional area yields the effective stresses in the coal-slurry consolidation body proper:
Equations (2) and (3) are obtained:
From the relationship between effective stress and strain, it is obtained that:
where, : Effective stress of the body; : Total stress; : Pore pressure (pore pressure between matrices); : Matrix average skeleton pressure; : Porosity of coal-slurry cementation body; : Intrinsic Stress; : Average modulus of elasticity of the sum of the modulus of elasticity of the coal body and the modulus of elasticity of the slurry body.
(2) Structural Effective Stress [27]. Structural deformation refers to changes in the spatial structure at the contact interface between the coal matrix and the slurry, including the contact interface between the slurry and the coal. Structural effective stress causes this deformation. In the coal-slurry porous medium, as shown in Figure 3, consider a curved surface AA1 formed by connecting contact points. Contact points refer to the interface points between the matrix and the slurry or within the coal. The curved surface does not pass through the interior of the matrix. Let represent the vertical component of the stress at the i-th contact point, and represent the vertical area corresponding to (horizontal area). Based on the equilibrium of forces, the following equation is derived:
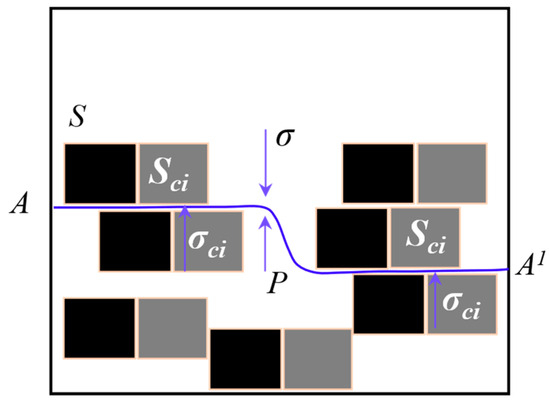
Figure 3.
Structural effective stress establishment relationship.
Based on the balance of forces the following equation holds:
Equating over the entire surface yields the following relation:
Associative Equations (6)–(8) give the structural effective stresses of the coal-slurry cementation:
From the relationship between effective stress and strain, it can be obtained that:
The total effective stress of the coal-slurry consolidation under load can be obtained by coupling Equations (4) and (9):
Associating (5) and (10) yields the total strain of the coal-slurry consolidation under load:
where, : Structural effective stress; φc: Contact porosity; : Structural strain, where is between and 1, the value is determined according to the slurry-coal cementation body cementation and reinforcement condition, which is divided into two kinds: For loose and porous media with low degree of cementation, ; For dense porous media with a high degree of cementation, .
After the formation of the coal-slurry consolidated body around the gas borehole, it undergoes deformation not only due to the applied stress but also from the deformation caused by the expansion of gas adsorbed by the consolidated body matrix. Since the strain induced by matrix adsorption is relatively small, it is assumed that the deformation of the coal-slurry consolidated body is primarily caused by the effective stress. Based on the coal permeability model considering effective matrix deformation [29], the permeability model for the coal-slurry consolidated body in the elastic phase can be derived.
where represents the average effective stress increment when loaded and represents the strain increment. Combining the principles of effective stress in the solid body and effective stress in the structure, i.e., Equations (11) and (12), it can be obtained:
Associative Equations (13)–(15) yield an elastic coal-slurry cementation permeability model based on the principles of principal effective stress and structural effective stress:
where, , : represents the initial permeability and permeability of the cemented body, mD, respectively; : effective stress coefficient of the cemented body, , , : overall bulk modulus of the cemented body, MPa; : bulk modulus of the matrix of the cemented body, MPa; : modulus of elasticity, MPa; : Poisson’s ratio; : initial porosity, %; : initial pore pressure, MPa; : deformation influence coefficient of cemented body, 0~1; : average elastic modulus of coal body and slurry, MPa; : initial strain, %.
2.3. Modeling the Permeability of Damaged Coal-Slurry Consolidates
After damage, coal-slurry consolidation enters an elastic deformation stage. During this stage, the consolidation body experiences damage and cracking, leading to an increase in crack quantity, with irreversible changes in crack apertures. Based on the effective stress-permeability model principle [19], the cubic structural model shown in Figure 4 establishes a permeability model for damaged coal-slurry consolidation. This model also accounts for the combined effects of matrix effective stress and structural effective stress.
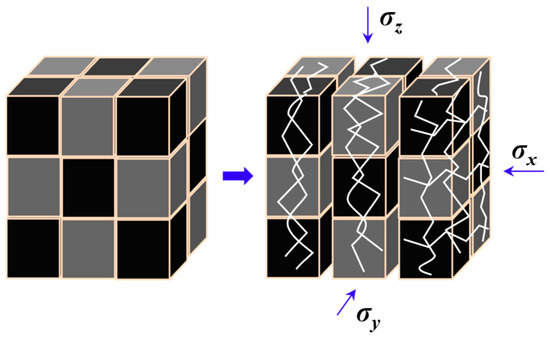
Figure 4.
Structural model of damaged coal-slurry cementation body.
According to the classical Poiseuille’s law, the flow of fluid through a single crack [30] is:
Since cracks develop in large numbers after damage to the solidified body and many cross-cracks appear, the flow rate of fluid through multiple cross-cracks is:
where, : crack opening; : crack length; : sum of cross-crack lengths; : fluid flow distance; : hydrodynamic viscosity; : pressure difference between the two ends of the crack.
Assuming that the fluid flow satisfies Darcy’s law:
Associative Equations (18) and (19) give the permeability of the solidus containing multiple cracks:
Assuming that the crack area per unit volume of the solidified body is , combining Equation (20) yields:
The effective stress determines the change in permeability of the solidus, which can be obtained by biasing the effective force:
Associative Formulas (21) and (22) are obtained:
In Equation (23) let denote the amount of variation of the solidus crack with effective stress, then Equation (23) can be expressed as:
After the damage, the cracks in the solid body will be developed in large quantities, and this crack development brings about the damage destruction of the solid body in the macroscopic level. Therefore, in order to simplify the computational amount of , the degree of damage is introduced here to describe the crack development in the solidus according to the damage variables [31] defined based on the elastic modulus degradation:
The damage variable indicates the degree of development or damage of the cracks in the solidus; is the initial modulus of elasticity. It is also easy to see in Equation (25) that as the solid body is loaded, the cracks continue to develop, continues to decrease, and the damage value of the solid body continues to increase. can be obtained by simplifying with :
In the formula, denotes the influence coefficient of effective stress change on crack development, , is the volume modulus of the crack, and is the matrix volume modulus of the cemented body, and the integral of the coupling Formulas (24) and (26) can get the model of the permeability of the damaged coal-slurry cemented body:
3. Coal-Slurry Cementation Seepage Test
3.1. Sample Preparation
The coal samples for the experiment were collected from the Jiulishan Mine, which belongs to the Jiaozuo Mining Company under the Henan Coal and Chemical Industry Group, located in Jiaozuo, Henan Province, China. The coal type is anthracite, and its industrial analysis results are shown in Table 1. To better simulate the fractured coal around actual boreholes, the coal samples were dried in the laboratory, then crushed into irregular pieces with dimensions smaller than 3 cm using a crusher. These crushed coal pieces served as the injected medium to replicate the grouting effect around fractured coal near gas drainage boreholes, as illustrated in Figure 5.

Table 1.
Basic industrial parameters of coal samples.

Figure 5.
Coal-slurry consolidation system preparation process.
The grouting material used in the experiment is a composite cement-based sealing material, primarily composed of P.O42.5 Portland cement, combined with accelerants, alkali activators, suspending agents, expanding agents, and reinforcing agents in specific proportions. The basic properties of the grouting material are listed in Table 2.

Table 2.
Basic properties of grouting materials.
The grouting sealing simulation device, independently designed and constructed, injects grout into crushed coal blocks. The grout fully diffuses and fills the fractured coal, bonding and reinforcing it into a coal-slurry consolidation body. Cores are then extracted from the consolidated body and processed into standard cylindrical specimens with a diameter of 50 mm and a height of 100 mm. The preparation process for the coal-slurry consolidation body is shown in Figure 5.
3.2. Test Program and Procedures
This study uses the RLW-500G coal-rock triaxial creep-permeability test apparatus, independently developed by Henan Polytechnic University, located in Jiaozuo, Henan Province, China, to investigate the mechanical failure characteristics and permeability evolution of coal-slurry consolidation bodies under loading. The test apparatus consists of a system console, servo controller, triaxial pressure chamber, seepage control system, temperature control system, and pressure transmission device. It enables simultaneous monitoring of mechanical and seepage properties under temperature and stress loading conditions. The test apparatus is shown in Figure 6.

Figure 6.
Schematic diagram of the test setup.
The coal-slurry grout bodies with dimensions of φ50 mm × 100 mm were prepared for the experiments. The flatness error of the sample’s end faces was controlled to be no greater than 0.05 mm, and the end faces were parallel and perpendicular to the sample’s axial line, with an error not exceeding 0.25°. During the experiments, the sample was first loaded to the preset axial and confining pressures using a servo control system. Axial pressure was then applied at a rate of 10 N/s to simulate the permeability variation under different loading conditions. The experimental plan is shown in Table 3, with no fewer than three samples used for each experimental condition to ensure the reliability of the results.

Table 3.
Experimental program.
(1) Specimen Installation: Place the polished specimen on the installation base of the triaxial pressure chamber. Evenly apply silicone around the specimen, cover it with a heat-shrink tube, and shrink it with a hot air blower. Secure both ends with clamps and seal the specimen. After curing the silicone for 8 h, install strain sensors and connect the air pipes and circuits.
(2) Prestress Loading: Inject hydraulic oil into the triaxial chamber until filled. Use axial/confining pressure controllers to load the specimen to the test conditions. Stabilize the pressures via the servo controller.
(3) Nitrogen Injection: Connect the gas pipeline, open the seepage system’s inlet and outlet valves, and adjust the pressure-reducing valve. Introduce nitrogen and monitor the flowmeter. Begin testing once the flow stabilizes.
(4) Loading Test: The system console controls the servo system to apply axial loading at 10 N/s until the specimen fails.
4. Analysis of Test Results
The experiment follows the test plan in Table 3 to obtain mechanical and seepage parameters of coal-slurry consolidation bodies under various conditions. The permeability of specimens is calculated using the following formula:
where, is the permeability, mD; is the gas seepage flow rate, cm3/s; is the gas dynamic viscosity coefficient, Pa-s; is the length of the specimen, mm; is the cross-sectional area of the specimen, cm2; is the pressure of the inlet end, MPa; is the pressure of the outlet end, MPa.
Changes in permeability reveal grouting sealing and fracture growth in coal-slurry bodies. Stress-strain and permeability curves under varying loads are shown in Figure 7.
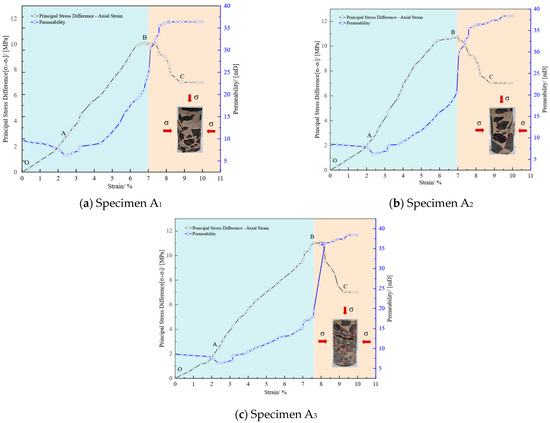
Figure 7.
Variation of triaxial seepage test of coal-slurry cementation under different loadings.
Figure 7a illustrates the stress-strain and permeability variation curves of the coal-slurry consolidated specimen A1 under initial axial stress of 0.5 MPa and confining pressure of 1 MPa. As shown in the figure, with the continuous loading of axial stress, the pore-fracture structure of the specimen is compressed under the applied load (OA stage), and the permeability decreases gradually from 9.66 mD to 6.35 mD. Under further compression of the axial stress (AB stage), the specimen does not exhibit a significant reduction in bearing capacity; instead, it gradually yields as the principal stress difference increases, reaching a peak strength of 10.1 MPa. During this stage, the cracks in the specimen develop and expand, and the permeability steadily increases to 25.8 mD, forming a ’V’-shaped variation trend with the permeability in the OA stage, which first decreases and then increases. At point B, the specimen reaches the maximum bearing capacity and undergoes an instantaneous instability failure, causing the permeability to rapidly increase from 25.8 mD to 35.45 mD, a 37.4% increase. After instability, internal damage in the specimen continues to develop, and during this stage, the permeability steadily increases to 36.35 mD, fluctuating until the specimen is completely destroyed.
Figure 7b illustrates the stress-strain and permeability variation curves of the coal-slurry consolidated specimen A2 under initial axial stress of 0.5 MPa and confining pressure of 2 MPa. As shown in the figure, with the increase in principal stress difference, the permeability of the specimen decreases gradually from 8.56 mD to 6.34 mD (OA stage). When the principal stress difference gradually increases to 10.78 MPa (AB stage), the bearing capacity of the specimen increases, the slope of the stress-strain curve gradually decreases, and the volumetric strain of the specimen shifts from compression to expansion, with permeability steadily increasing to 20.55 mD. This forms a ‘V’-shaped variation trend with the permeability in the OA stage. At the instability failure point B, the specimen undergoes an instantaneous failure, and the permeability rapidly increases from 20.55 mD to 32.78 mD, a 59.51% increase. Subsequently, internal damage continues to develop, and the permeability further increases to 35.85 mD.
Figure 7c illustrates the stress-strain and permeability variation curves of the coal-slurry consolidated specimen A3 under initial axial stress of 1 MPa and confining pressure of 2 MPa. As shown in the figure, during the OA stage, the permeability of the specimen decreases gradually from 8.53 mD to 6.35 mD, maintaining a low level. During the AB stage, with the continued loading of axial stress, the specimen begins to yield, and the permeability steadily increases to 19.45 mD. Similar to specimens A1 and A2, the permeability during the OB stage exhibits a ‘V’-shaped variation trend. When the axial stress increases to 11.01 MPa (point B), the specimen undergoes instability failure, and the permeability rapidly increases from 19.45 mD to 36.38 mD, a 87.04% increase. Subsequently, the permeability continues to increase to 38.39 mD.
The experimental study on the damage and seepage of coal-slurry consolidated specimens under different initial confining pressure and axial stress conditions indicates that the specimen is compressed under the applied load (OA stage), resulting in a decrease in permeability. With continued stress loading (AB stage), the specimen undergoes a transition from volumetric compression to expansion, internal damage begins to develop, cracks start to form and expand, and permeability gradually increases. The permeability exhibits a ‘V’-shaped variation trend before instability failure (point B). When the specimen reaches its maximum bearing capacity, instability failure occurs instantaneously, and the bearing capacity sharply decreases. Micro-pores and cracks with poor internal connectivity begin to develop and connect over a wide area, causing permeability to increase rapidly and resulting in a seepage breakthrough phenomenon, as shown in Figure 8. The above analysis indicates that the permeability of the three specimens increased by 37.4%, 59.51%, and 87.04%, respectively, at the moment of instability failure, suggesting that the extent of permeability increase is greater with higher axial and confining pressures under different loading conditions. The analysis suggests that the cause of this phenomenon is that the specimen remains in a compressed state under the applied load, with continued axial stress loading leading to damage of the coal matrix and mineral particles in the slurry. However, due to the constant compression, the expansion of pores and cracks, as well as the development of new pore-crack structures, which could facilitate gas migration, are not fully expressed. When the coal body is suddenly decompressed, the specimen undergoes an instantaneous failure, and the bearing capacities of the three specimens decrease by 30.49%, 34.87%, and 36.23%, respectively. The internal damaged cracks open and become interconnected, allowing gas to rapidly desorb and seep, migrating from the connected pores and cracks, resulting in a continuous increase in permeability.
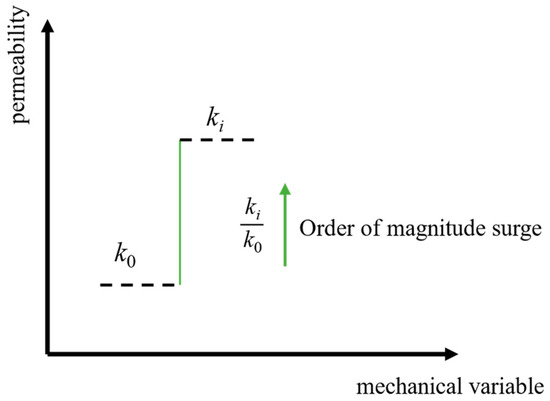
Figure 8.
Generalized model for sudden changes in seepage.
5. Model Validation
5.1. Model Basic Parameters
To verify the rationality of the permeability model established in Section 2, theoretical analysis of the permeability is conducted using Equation (27), based on the triaxial seepage test results of coal-slurry consolidated specimens under different loading conditions in Section 4 and the quasi-Newton method. Table 4 lists the relevant basic parameter values of the coal-slurry consolidated specimen. The pore pressure is taken as the triaxial seepage gas pressure of 1 MPa, and the initial pore pressure is set as atmospheric pressure. The contact porosity is assigned a fixed value of: .

Table 4.
Values of basic parameters of coal-slurry consolidation body.
5.2. Validation of Experimental Versus Theoretical Values of Permeability of Coal-Slurry Consolidates
Figure 9 presents a comparison between the experimental and theoretical permeability values for the three specimens under different loading conditions, with some data shown in Table 5. Statistical methods are applied to analyze the mean, variance, and standard deviation of the theoretical and experimental permeability values. This results in the mean permeability variation curve, variance fluctuation curve, and error bar distribution. The formula for calculating the variance is as follows:
where, is the th sample data value; is the sample mean, ; is the number of data points in the sample.
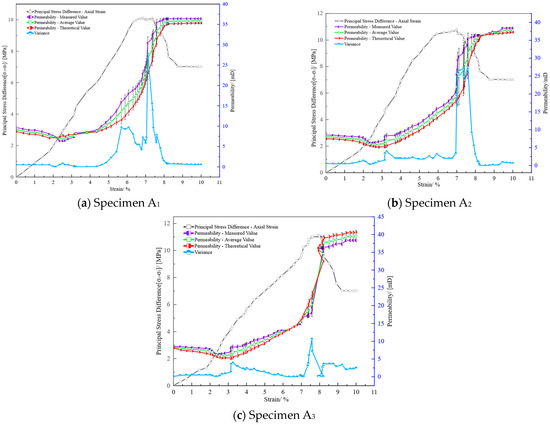
Figure 9.
Comparison of experimental and theoretical values of permeability of coal-slurry consolidation under different loadings.

Table 5.
Selected data related to permeability of coal-slurry cementation under different loadings.
As can be seen from the figure, the error bar distribution between the theoretical permeability values derived from the model established in this study and the experimentally measured permeability values of coal-slurry consolidated specimens under different loading conditions is relatively narrow, with no large gaps in the error bar distribution, indicating a high degree of agreement. The relative errors between the theoretical and experimental curves for specimens A1, A2, and A3 are 9.5%, 8.6%, and 8.1%, respectively, with an average relative error of 8.7%, indicating that the theoretical permeability values calculated from the model are close to the experimental values and exhibit a strong agreement in terms of trend. From the variance fluctuation curves of the specimens in the figure, it can be observed that the theoretical and experimental permeability variations fluctuate significantly near the yield stage (around point B), while fluctuations are more stable in other stages. This indicates that the errors between the theoretical and experimental values primarily occur when the specimen reaches its maximum bearing capacity and undergoes instability failure. There are two main reasons for this: first, experimental errors. During the damage deformation stage of the coal-consolidated specimen, it is initially compressed under sustained stress, followed by volumetric expansion, resulting in an increase in experimental permeability; second, the permeability model established in this study is based on a cubic structure, assuming that fracture damage occurs as uniform, continuous plastic deformation without sudden changes. However, the actual slurry has a high degree of brittleness, causing the specimen to experience an instantaneous failure after reaching its maximum bearing capacity, leading to experimental values that exceed theoretical values.
The above analysis indicates that the permeability model established in this study can accurately describe the dynamic evolution of permeability in coal-slurry consolidated specimens under loading conditions, and that analyzing the damage, rupture, and key gas leakage stages during loading reveals that optimizing and improving the plasticity of the slurry can enhance the impermeability of sealing materials under loading conditions, which is beneficial for gas extraction operations.
6. Conclusions
Grouting sealing can form coal-slurry consolidated bodies, significantly improving the sealing quality of gas drainage boreholes and mitigating coal and gas outburst hazards. Therefore, building on previous research, this study focuses on the coal-slurry consolidated bodies formed after grouting and sealing gas drainage boreholes. True triaxial loading and seepage experiments were conducted, and a permeability model of coal-slurry consolidated bodies under loading conditions was established. The findings provide guidance for analyzing the leakage prevention effectiveness of sealing materials in field engineering and optimizing the sealing performance of grouting materials. Future research can further explore the damage and seepage evolution of coal-slurry consolidated bodies under various loading conditions and sealing material types. The main conclusions are as follows:
(1) Based on the ‘cubic’ model, a permeability model for coal-slurry consolidated specimens under loading conditions was established, considering the intrinsic and structural deformations induced by consolidation body damage under triaxial stress.
(2) Triaxial stress loading permeability tests under different initial confining pressures and axial pressures show that the coal-slurry consolidated specimens remain in a compressed state under stress loading. In the compaction stage (OA phase), the micropores and fractures within the consolidated body are gradually compressed and closed, leading to a reduction in permeability. In the elastic-plastic stage (AB phase), damage and failure begin to develop within the specimen, and fractures gradually expand, causing an increase in permeability. The permeability exhibits a ‘V’ shaped trend prior to instability failure (point B). After continued stress loading, instability failure occurs at the maximum bearing capacity, and in the BC phase, the poorly connected micropores and fractures within the specimen begin to develop large-scale connections, causing a rapid increase in permeability and the occurrence of seepage mutation. A large number of damaged fractures rupture and interconnect, leading to a stabilization of permeability after reaching its maximum value. Under different loading conditions, the extent of permeability increase after instability failure of the coal-slurry consolidated specimens increases with higher initial axial and confining pressures.
(3) The comparison between experimental and theoretical permeability values under different loading conditions shows that the theoretical permeability values from the model are close to the experimental values, with an average relative error of 8.7%, indicating that the coal-slurry consolidated body damage permeability evolution model established in this study can accurately describe the dynamic changes in permeability under loading conditions. The research findings provide valuable guidance for analyzing the sealing effectiveness of sealing materials and optimizing their performance.
Author Contributions
Conceptualization, Y.T.; Methodology, P.L.; Software, J.Z.; Validation, J.Z.; Investigation, W.J.; Data curation, W.J.; Writing—original draft, Y.T.; Writing—review & editing, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52204264); Sponsored by Program for Science & Technology Innovation Talents in Universities of Henan Province (25HASTIT015); Training Plan for Young Backbone Teachers of undergraduate universities in Henan Province (2024GGJS092); Training Plan for Young Backbone Teachers of Zhongyuan University of Technology (2023XQG05); Subject Backbone Teacher Support Program of Zhongyuan University of Technology (GG202420); Key Scientific Research Project of Colleges and Universities in Henan Province (25A620001).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We would like to thank the Yima Coal Industry Group Co., Ltd., Henan Polytechnic University, and Zhongyuan University of Technology for their valuable suggestions and all the support provided for this research.
Conflicts of Interest
The author Tang Yao-Cai was employed by Yima Coal Industry Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Total stress | MPa | |
| Effective stress of the body | MPa | |
| Matrix average skeleton pressure | MPa | |
| Structural effective stress | MPa | |
| Pore pressure | MPa | |
| Porosity of coal-slurry cementation body | % | |
| Initial porosity | % | |
| Contact porosity | % | |
| Intrinsic Stress | % | |
| Initial strain | % | |
| Modulus of elasticity | MPa | |
| Initial permeability | mD | |
| Overall bulk modulus of the cemented body | MPa | |
| Bulk modulus of the matrix of the cemented body | MPa | |
| Gas seepage flow rate | cm3/s | |
| Gas dynamic viscosity coefficient | Pa·s | |
| Length of the specimen | mm | |
| Cross-sectional area of the specimen | cm2 |
References
- Li, S.; Gao, M.; Wu, B.; Xu, Y.; Li, Y.; Zeng, G. Dynamic compressive failure of coal at different burial depths. Geomech. Geophys. Geo 2023, 9, 53. [Google Scholar] [CrossRef]
- Shi, Z.; Li, B.; Li, L.; Wang, N.; Zhang, J. Study on the directional extension law of hydraulic fractures induced by pre-cast slot under true-triaxial. Theor. Appl. Fract. Mech. 2024, 133, 104546. [Google Scholar] [CrossRef]
- Li, B.; He, Y.; Shi, Z.; Jian, W.; Wang, N.; Zhang, Y. Mutual feedback and fracturing effect of hydraulic fractures in composite coal-rock reservoirs under different fracturing layer sequence conditions. Int. J. Rock. Mech. Min. Sci. 2024, 184, 105968. [Google Scholar] [CrossRef]
- Fan, C.; Li, S.; Luo, M.; Du, W.; Yang, Z. Coal and gas outburst dynamic system. Int. J. Min. Sci. Technol. 2017, 27, 49–55. [Google Scholar] [CrossRef]
- Chen, L.; Wang, E.; Ou, J.; Fu, J. Coal and gas outburst hazards and factors of the No. B-1 Coalbed, Henan, China. Geosci. J. 2018, 22, 171–182. [Google Scholar] [CrossRef]
- Li, A.; Ding, X.; Yu, Z.; Wang, M.; Mu, Q.; Dai, Z.; Li, H.; Zhang, B.; Han, T. Prediction model of fracture depth and water inrush risk zoning in deep mining coal seam floor. Environ. Earth Sci. 2022, 81, 315. [Google Scholar] [CrossRef]
- Celik, F. The observation of permeation grouting method as soil improvement technique with different grout flow models. Geomech. Eng. 2019, 17, 367–374. [Google Scholar] [CrossRef]
- Ren, Y.; Wei, J.; Zhang, L.; Zhang, J.; Zhang, L. A Fractal Permeability Model for Gas Transport in the Dual-Porosity Media of the Coalbed Methane Reservoir. Transp. Porous Med. 2021, 140, 511–534. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Zhang, W.; Shao, J.; Wang, Z.; Wu, X. Experimental Study on the Basic Properties of a Green New Coal Mine Grouting Reinforcement Material. ACS Omega 2020, 5, 16722–16732. [Google Scholar] [CrossRef]
- Du, W.; Zhang, Y.; Meng, X.; Zhang, X.; Li, W. Deformation and seepage characteristics of gas-containing coal under true triaxial stress. Arab. J. Geosci. 2018, 11, 190. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, E.; Jiang, C.; Zhang, D.; Li, M.; Yu, B.; Zhao, D. True triaxial experimental study of anisotropic mechanical behavior and permeability evolution of initially fractured coal. Nat. Resour. Res. 2023, 32, 567–585. [Google Scholar] [CrossRef]
- Wang, K.; Du, F.; Zhang, X.; Wang, L.; Xin, C. Mechanical properties and permeability evolution in gas-bearing coal-rock combination body under triaxial conditions. Environ. Earth Sci. 2017, 76, 815. [Google Scholar] [CrossRef]
- Wang, K.; Du, F. Experimental investigation on mechanical behavior and permeability evolution in coal-rock combined body under unloading conditions. Arab. J. Geosci. 2019, 12, 422. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, P.; Wei, J.; Yu, C. The seepage properties and permeability enhancement mechanism in coal under temperature shocks during unloading confining pressures. J. Nat. Gas Sci. Eng. 2020, 77, 103242. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, D.; Wei, J.; Yao, B.; Zhang, H.; Fu, J.; Zeng, F. Damage constitutive model of gas-bearing coal using industrial CT scanning technology. J. Nat. Gas Sci. Eng. 2022, 101, 104543. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown induced changes in permeability of coalbeds: A new interpretation of the reservoir response to primary recovery. Transp. Porous Med. 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Xue, Y.; Dang, F.; Cao, Z.; Du, F.; Ren, J.; Chang, X.; Gao, F. Deformation, permeability and acoustic emission characteristics of coal masses under mining-induced stress paths. Energies 2018, 11, 2233. [Google Scholar] [CrossRef]
- Connell, L.D.; Lu, M.; Pan, Z. An analytical coal permeability model for tri-axial strain and stress conditions. Int. J. Coal Geol. 2010, 84, 103–114. [Google Scholar] [CrossRef]
- Bai, X.; Wang, Y.; He, G.; Zhou, Z.; Wang, D.; Zhang, D. Research on a permeability model of coal damaged under triaxial loading and unloading. Fuel 2023, 354, 129375. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Z.; Wang, P.; Guo, Y.; Wang, W.; Huang, T.; Li, W. The effect of gas migration on the deformation and permeability of coal under the condition of true triaxial stress. Arab. J. Geosci. 2019, 12, 486. [Google Scholar] [CrossRef]
- Lu, J.; Yin, G.; Deng, B.; Zhang, W.; Li, M.; Chai, X.; Liu, C.; Liu, Y. Permeability characteristics of layered composite coal-rock under true triaxial stress conditions. J. Nat. Gas Sci. Eng. 2019, 66, 60–76. [Google Scholar] [CrossRef]
- Liu, B.; Zhu, L.; Liu, X.; Liu, Q.; Fan, Y.; Yao, W.; Deng, W. Energy evolution and damage deformation behavior of cemented broken coal specimen under triaxial compression condition. Energy 2024, 310, 133203. [Google Scholar] [CrossRef]
- Shen, R.; Wang, X.; Li, H.; Gu, Z.; Liu, W. Brittleness characteristics and damage evolution of coal under true triaxial loading based on the energy principle. Nat. Resour. Res. 2024, 33, 421–434. [Google Scholar] [CrossRef]
- Cao, A.; Wang, C.; Zhang, N.; Li, H.; Liu, Z.; Zhi, S. Experimental study on damage characteristics of coal samples under true triaxial loading and dynamic unloading. Lithosphere 2022, 2022, 5447973. [Google Scholar] [CrossRef]
- Liang, Y.; Ran, Q.; Zou, Q.; Zhang, B.; Hong, Y. Experimental study of mechanical behaviors and failure characteristics of coal under true triaxial cyclic loading and unloading and stress rotation. Nat. Resour. Res. 2022, 31, 971–991. [Google Scholar] [CrossRef]
- Duan, M.; Jiang, C.; Yin, W.; Yang, K.; Li, J.; Liu, Q. Experimental study on mechanical and damage characteristics of coal under true triaxial cyclic disturbance. Eng. Geol. 2021, 295, 106445. [Google Scholar] [CrossRef]
- Lu, S.; Li, M.; Ma, Y.; Wang, S.; Zhao, W. Permeability changes in mining-damaged coal: A review of mathematical models. J. Nat. Gas Sci. Eng. 2022, 106, 104739. [Google Scholar] [CrossRef]
- Liu, C.; Yu, B.; Zhao, H.; Hong, Z.; Tian, Z.; Zhang, D.; Liu, Y. Effective stress effect and slippage effect of gas migration in deep coal reservoirs. Int. J. Rock. Mech. Min. Sci. 2022, 155, 105142. [Google Scholar] [CrossRef]
- Guo, P.; Cheng, Y.; Jin, K.; Li, W.; Tu, Q.; Liu, H. Impact of effective stress and matrix deformation on the coal fracture permeability. Transp. Porous Med. 2014, 103, 99–115. [Google Scholar] [CrossRef]
- Kai, W.; Ang, L.; Zhou, A. Theoretical analysis of influencing factors on resistance in the process of gas migration in coal seams. Int. J. Min. Sci. Technol. 2017, 27, 315–319. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, L.; Ding, K.; Wang, S.; Ren, B.; Guo, J. Experimental study on mechanical and damage evolution characteristics of coal during true triaxial cyclic loading and unloading. Materials 2023, 16, 2384. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).