Insights from the Last Decade in Computational Fluid Dynamics (CFD) Design and Performance Enhancement of Darrieus Wind Turbines
Abstract
1. Introduction
2. Summary of Darrieus Wind Turbine Parameters and CFD Studies
| References | Blade Profile | Rotor Diameter (mm) | Rotor Height (mm) | Blade Chord (mm) | Number of Rotor Blades | Rotor Solidity | Investigations |
|---|---|---|---|---|---|---|---|
| Tian et al. [10] | NACA0021 | 1030 | - | 85.8 | 2-10 | 0.33–1.66 | Yield Of Darrieus Enhanced Using A Gear Device |
| Chegini et al. [18] | NACA0021 | 1030 | - | 85.8 | 3 | 0.25 | CFD-Based Study On Darrieus–Savonius Hybrid Wind Turbine, Focusing On Self-Starting And Performance With Deflectors |
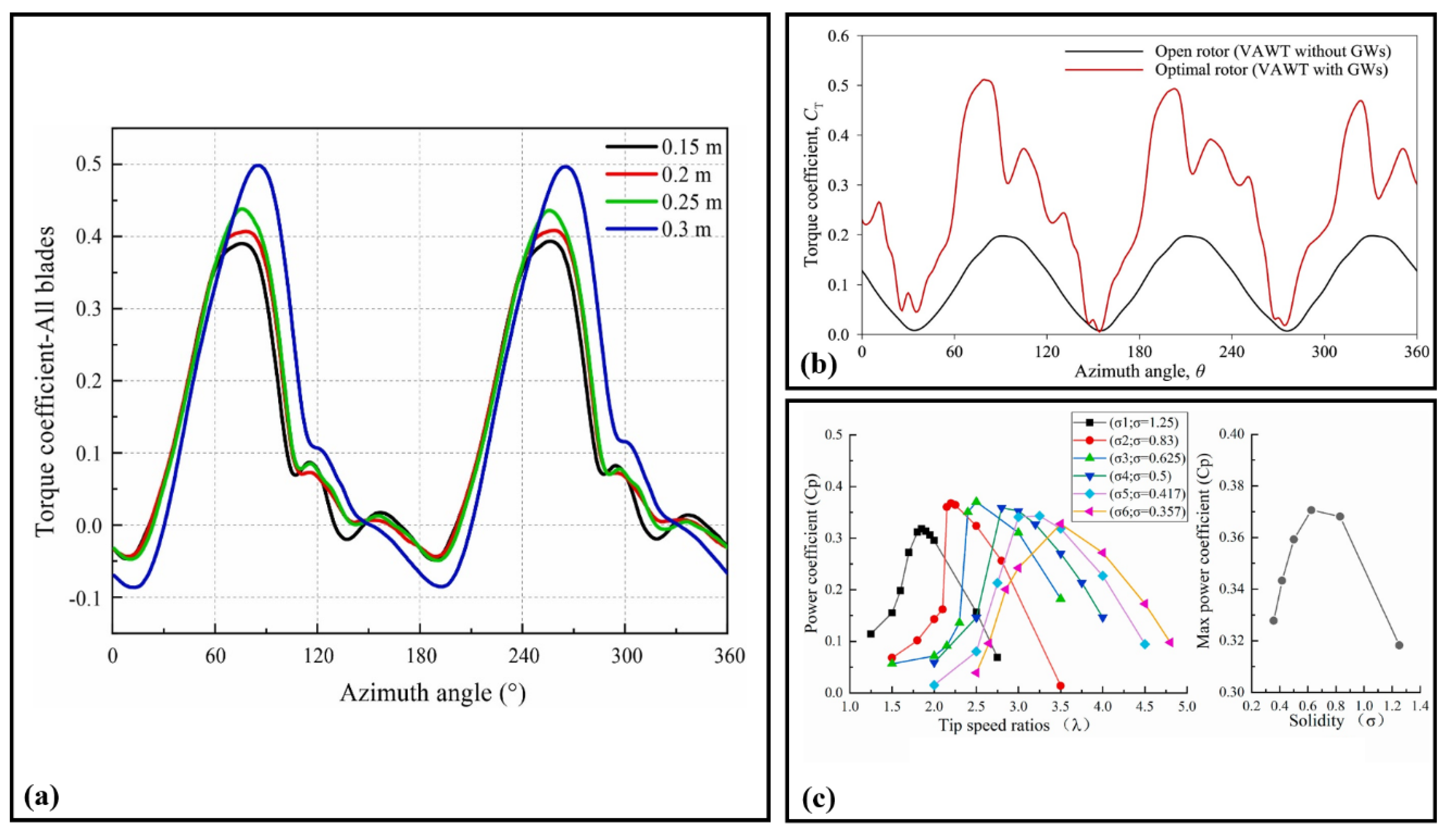
| Zidane et al. [47] | NACA0021 | 1030 | 1000 | 85.80 | 3 | 0.5 | Optimization Study On H-Darrieus Turbine Performance Using Upstream Deflectors |
| Singh et al. [48] | NACA0021 | 1030 | 1456 | 85.8 | 3 | 0.25 | Numerical Analysis Of Darrieus With Varying Aspect Ratios For Energy Harvesting |
| Ibrahim et al. [11] | NACA0021 | 1030 | - | 85.8 | 3 | 0.25 | Power Of Darrieus Turbine Blades Enhanced Using Trapped Vortex Cavity |
| Roshan et al. [49] | NACA0021 | 1030 | - | 85.8 | 3 | - | Performance Of Darrieus Turbines Improved With Different Cavity Layouts |
| Rasekh et al. [50] | NACA0021 | 1030 | - | 85.8 | 3 | 0.5 | Multi-Objective Optimization Of Variable Pitch VAWT Using NSGA-II With CFD |
| Rasekh et al. [51] | NACA0021 | 1030 | - | 85.8 | 3 | - | Sensitivity Analysis Of Variable Pitch VAWT Using Taguchi–CFD Approach |
| Ansaf et al. [6] | NACA0021 | 1030 | 1000 | 85 | 3 | - | Efficiency Optimization Of Darrieus Using Fixed Guiding Walls |
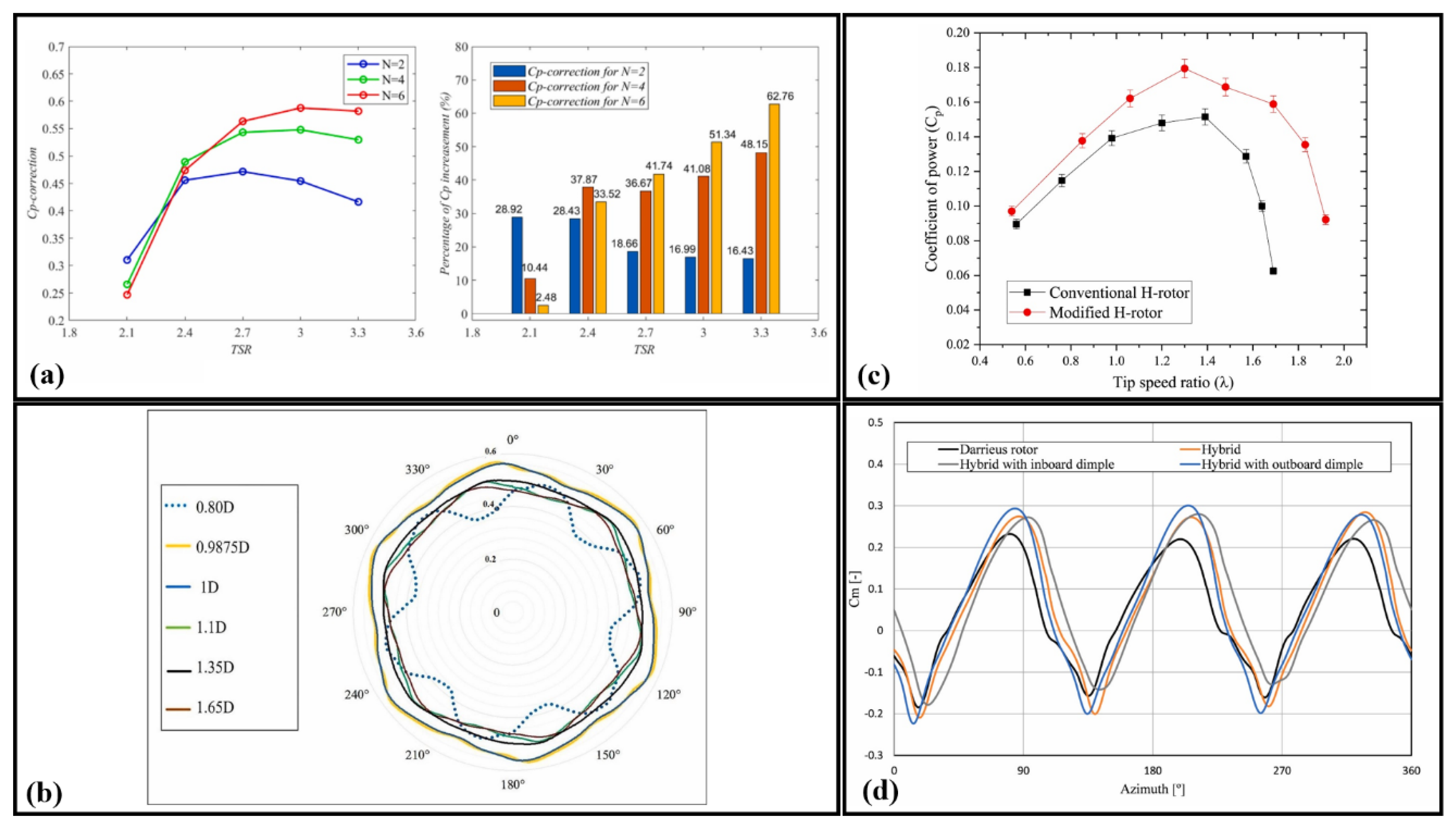
| Shen et al. [4] | NACA0021 | 800/2000 | 1200 | 300 | 4 | - | Study On The Impact Of Structural Indicators On Double Darrieus Turbine Aerodynamic Efficiency |
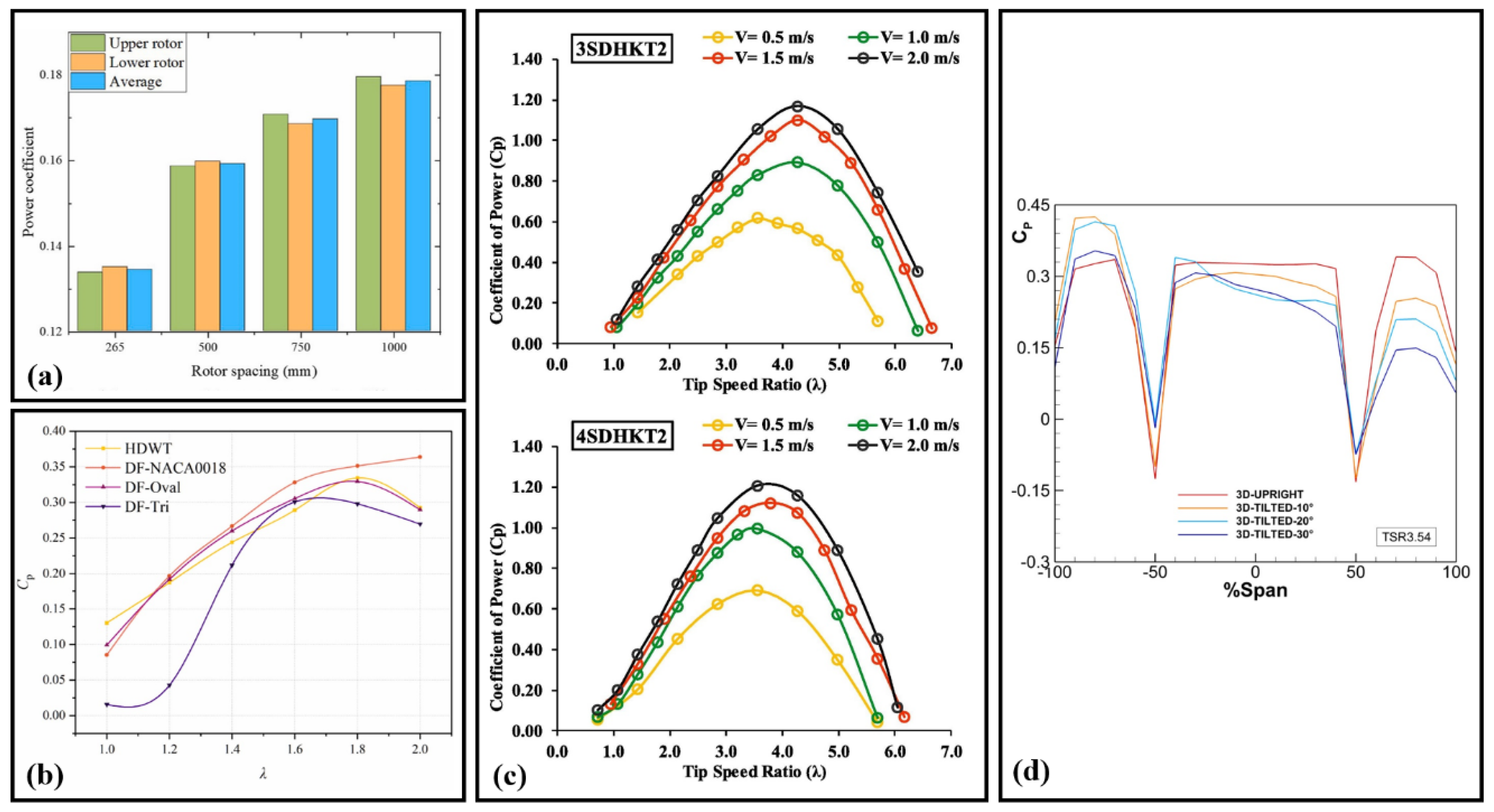
| Hijazi et al. [13] | NACA0021 | 2000 | 1200 | 265 | 2 | 0.265 | CFD Investigation Of The Use Of Flexible Blades For Darrieus |
| Zheng et al. [2] | NACA0021 | 2000 | 1200 | 265 | 2 | - | Indicator Optimization CFD Method Of Contra-Rotating VAWT |
| Ghareghani et al. [52] | NACA0021 | 1980 | 1150 | 300 | 3 | - | CFD Investigation On The Helix Angle To Smoothen The Torque Output Of The 3-PB Darrieus |
| Franchina et al. [53] | NACA0021 | 1030 | 2914 | 86 | 3 | 0.25 | 3D URANS Calculations Of A H-Shaped Darrieus |
| Eltayesh et al. [23] | NACA0021 | 1028 | 1460 | 85 | 3 | - | Aerodynamic Enhancement Of A Small Scale Darrieus |
| Franchina et al. [45] | NACA0021 | 1510 | 151 | 85 | 3 | - | 3D CFD Modeling Of A Troposkein Turbine At Different Operating Regimes |
| Baghdadi et al. [15] | NACA0021 | 2000 | - | 265 | 3 | 0.127 | Designs Enhancement Of A VAWT Using Blade Morphing Method |
| Kouaissah et al. [54] | NACA0021 | 1000 | 1000 | 101 | 3 | - | CFD Study On The Performance Of A Tilted H-Darrieus Turbine |
| Jiang et al. [19] | NACA0018 | 800 | - | 125 | 3 | - | CFD Evaluation Of A H-Darrieus Equipped With A DD Flow Layout |
| Yadav et al. [5] | NACA0018 | 1030 | - | 85.8 | 3 | 0.25 | Effect Of Several Indicators On The Performance Of A Coupled Twin Darrieus Rotor Using CFD |
| Marzec et al. [17] | NACA0018 | 2000 | 1900 | 287 | 3 | - | Structural Optimization Of H-Darrieus Using One-Way FSI |
| Reddy et al. [55] | NACA0018 | 300 | 300 | 100 | 3 | - | Wind Tunnel Testing And CFD Analysis Of Wooden-Bladed Darrieus At Low TSR |
| Kong et al. [56] | NACA0018 | 800 | - | 200 | 3 | 0.75 | Enhancement Of Self-Starting And Power Extraction In H-Type Hydrokinetic Rotor Using Blade Deflection |
| Bundi et al. [57] | NACA0018 | 1700 | (Aspect ratio 12) | 246 | 3 | - | Pitch Control Of Darrieus Using Gain Scheduling Methods |
| Tirandaz et al. [58] | NACA0018 | 1000 | - | 60 | 1 | 0.06 | Effect Of Symmetric Airfoil On Power Coefficient Of Vawts In Dynamic Stall Regime |
| Yan et al. [14] | NACA0018 | 1700 | 780 | 246 | 3 | - | Aerodynamic Enhancement Of Darrieus Improved By Leading-Edge Layout |
| Ahmad et al. [1] | NACA0018 | 3854 | 3120 | 546 | 3 | - | Shape Enhancement Of DD Hybrid Rotor |
| Celik et al. [9] | NACA0018 | 750 | - | 83 | 3 | - | CFD Analysis Of Self-Starting Darrieus With J-Shaped Blades |
| Bakhumbsh et al. [16] | NACA0018 | 2800 | 1000 | 140 | 3 | - | Impact Of Micro-Cylinder R On Darrieus Efficiency |
| Huang et al. [8] | NACA0018 | 600–2100 | - | 75 | 5 | 0.357–1.25 | Optimal Design Of Darrieus With Variable Solidity |
| Geng et al. [59] | NACA0018 | 1000 | 1000 | 60 | 2 | 0.12 | CFD Investigations And Fatigue Modeling For Lifetime Prediction Of Vawts |
| Reddy et al. [20] | NACA0020 | 200 | 150–350 | 62.80 | 3 | 0.30 | Effect Of Aspect Ratio On The Efficiency And Wake Recovery Of Helical Hydrokinetic Turbines |
| Abdolahifar et al. [12] | NACA0020 | 240 | 460 | 56 | 3 | - | Performance Evaluation And Flow Analysis Of Darrieus Turbines With V-Shaped Swept Blades |
| Tunio et al. [60] | NACA0020 | 1500 | 1500 | 200 | 3 | - | Analysis Of Duct Augmentation Impacts On The Performance Of Straight-Blade Darrieus Hydrokinetic Turbines |
| Wilberforce et al. [61] | NACA0012 | 1000 | 1000 | 100 | 3 | - | Innovative Concepts For Domestic Wind Energy In Areas With Suboptimal Wind Conditions |
| Gupta et al. [43] | NACA0015 | 2500 | - | 400 | 3 | - | Analysis Of Flow Patterns And Performance Sensitivity In Variable Pitching Vawts |
| Anggara et al. [44] | NACA0015 | 1650 | 1000 | 375 | 3 | - | Evaluation Of Vortex Addition Influence On Darrieus H-Rotor Turbine Performance Through Numerical Simulation |
| Ahmad et al. [7] | NACA0015 | 2500 | 3000 | 400 | 3 | - | Multifaceted Examination Of Leading-Edge Tubercle Effects On VAWT Efficiency Improvement |
| Mohamed et al. [62] | DU06W200 | 2000 | - | 250 | 2 | 0.25 | Study On The Mechanisms Behind Power Augmentation In Counter-Rotating Darrieus Turbine Pairs |
| Reddy et al. [22] | NREL S823 | 300 | - | 100/50 | 6 | - | Study On The Influence Of Auxiliary Blades In Traditional H-Darrieus Rotors |
| Kamal et al. [63] | S-1046 | 200 | 150 | 60 | 3 | - | Impact Of Changing System And Operational Conditions On The Performance Of Hybrid Hydrokinetic Turbines |
| Satrio et al. [3] | NACA63(4)021 | 500 | 666 | 70 | 3 | - | Study Of The Impact Of Circular Flow Disturbance Distance On The Performance Of Vawts: Experimental And Numerical Approaches |
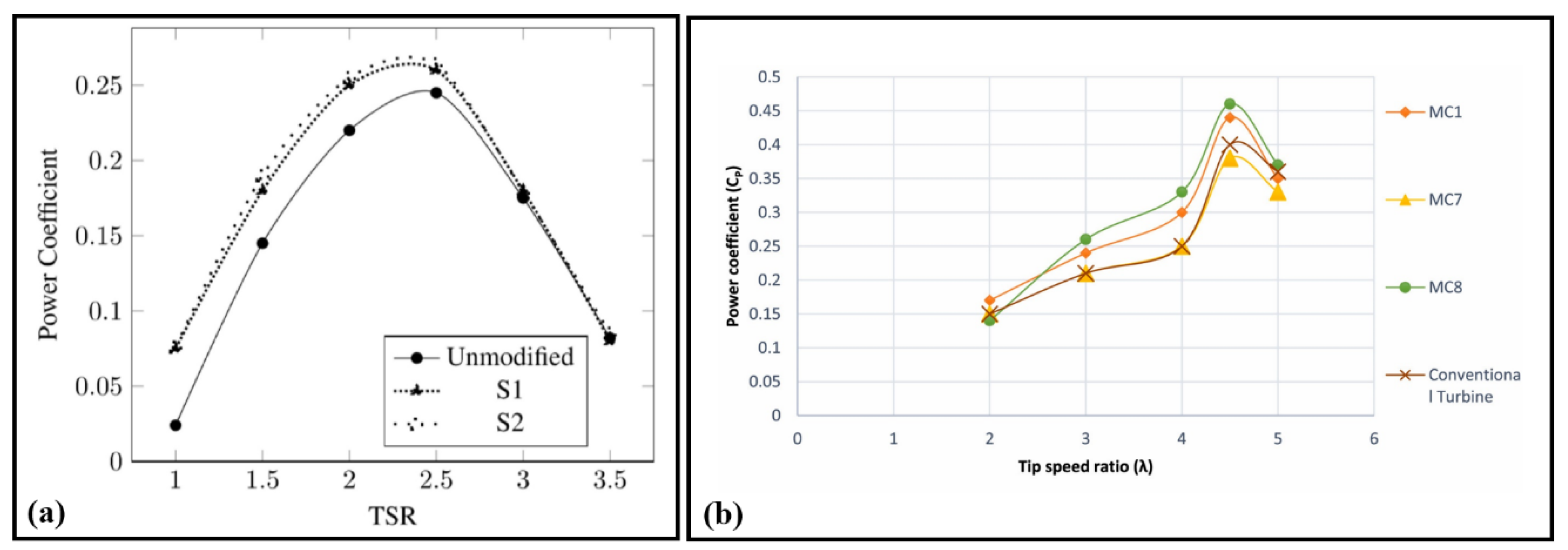
| Kumar et al. [21] | NACA4421 | 64, 68, 72 | - | 14 | 3, 4 | 0.288–0.324/ 0.385–0.433 | Investigation Of Spherical Darrieus Hydrokinetic Turbine Performance For In-Pipe Hydropower Systems |
| Durkacz et al. [64] | NACA7715 | 4000 | 1000 | 1000 | 3 | - | Numerical Simulation And Prototype Testing Of Vawts In Planetary Cluster Systems |
| References | Mesh Resolution and Boundary Layer Thickness | Turbulence Model and | Boundary Conditions | Solver Settings |
|---|---|---|---|---|
| Jiang et al. [19] |
| Transition k-(SST) | Velocity inlet, pressure outlet, rotation field, stationary field |
|
| Gupta et al. [43] |
| k-(SST) | Velocity inlet, pressure outlet, free-slip wall, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Satrio et al. [3] |
| k-ε | Velocity inlet, pressure outlet, symmetry, no-slip wall boundary on the blade surfaces, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Anggara et al. [44] |
| -Realizable k-ε -(-) | Velocity inlet, pressure outlet, symmetry, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Tian et al. [10] |
| k-(SST) | Velocity inlet, pressure outlet, zero shear-wall, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Yadav et al. [5] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, moving walls for the blades, overset interface, interface, rotating zone, sliding mesh technique |
|
| Chegini et al. [18] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Zidane et al. [47] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Reddy et al. [55] |
| k- | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Jain et al. [65] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry |
|
| Reddy et al. [22] |
| Standard k- | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Wilberforce et al. [61] |
| k-(SST) | Velocity inlet, pressure outlet, walls, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Rasekh et al. [50] |
| k-(SST) | Velocity inlet, pressure outlet, no friction wall, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Geng et al. [59] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Rasekh et al. [51] |
| k-(SST) | Velocity inlet, pressure outlet, no friction wall, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Huang et al. [8] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Ibrahim et al. [11] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| Bakhumbsh et al. [16] |
| k-(SST) | Velocity inlet, pressure outlet, symmetry, rotating zone, fixed zone, interface, rotating zone, sliding mesh technique |
|
| References | Mesh Resolution and Boundary Layer Thickness | Turbulence Model and | Boundary Conditions | Solver Settings |
|---|---|---|---|---|
| Shen et al. [4] |
| k- SST | Velocity inlet, pressure outlet, slip walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Hijazi et al. [13] |
| k- SST | Velocity inlet, pressure outlet, slip walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Zheng et al. [2] |
| Improved Delayed Detached Eddy Simulation (IDDES) | Velocity inlet, pressure outlet, slip walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) | (-) |
| Ahmad et al. [7] |
| k- SST | Velocity inlet, pressure outlet, slip walls, symmetry, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Marzec et al. [17] |
| k- SST | Velocity inlet, pressure outlet, symmetry, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Kumar et al. [21] |
| k- SST | Velocity inlet, pressure outlet, no-slip walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Singh et al. [48] |
| k- SST | Velocity inlet, pressure outlet, symmetry, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Abdolahifar et al. [12] |
| Realizable k- | Velocity inlet, pressure outlet, slip walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Ghareghani et al. [52] |
| k- SST (-) | Velocity inlet, pressure outlet, symmetry, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Kamal et al. [63] |
| RNG k- | Velocity inlet, pressure outlet, free slip condition, no-slip walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Ahmad et al. [1] |
| k- | Velocity inlet, pressure outlet, symmetry, wall conditions were applied to the turbine blades, (use of the sliding mesh technique) |
|
| Franchina et al. [45] |
| Spalart–Allmaras | Velocity inlet, pressure outlet, no-slip walls, symmetry, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Yan et al. [14] |
| LES | Velocity inlet, pressure outlet. The blade surface was set as non-slip walls. A periodic condition was enforced at the spanwise direction, (use of the sliding mesh technique) |
|
| Chen et al. [46] |
| k- SST | Velocity inlet, pressure outlet, symmetry, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Tunio et al. [60] |
| k- SST | Velocity inlet, pressure outlet, stationary wall with the no-slip condition, (use of the Moving Frame of Reference (MRF) technique) |
|
| Ortiz-Rodríguez et al. [66] |
| k- SST | Velocity inlet, pressure outlet, symmetry, walls, rotating zone, stationary zone, interface, (use of the sliding mesh technique) |
|
| Reddy et al. [20] |
| RNG k- | Velocity inlet, pressure outlet, free-slip walls, no-slip walls (blades) |
|
| Kouaissah et al. [54] |
| k- SST | Velocity inlet, pressure outlet, no-slip condition was imposed at solid surfaces |
|
3. Aerodynamic Parameters Used in Darrieus Turbines Performance Evaluation
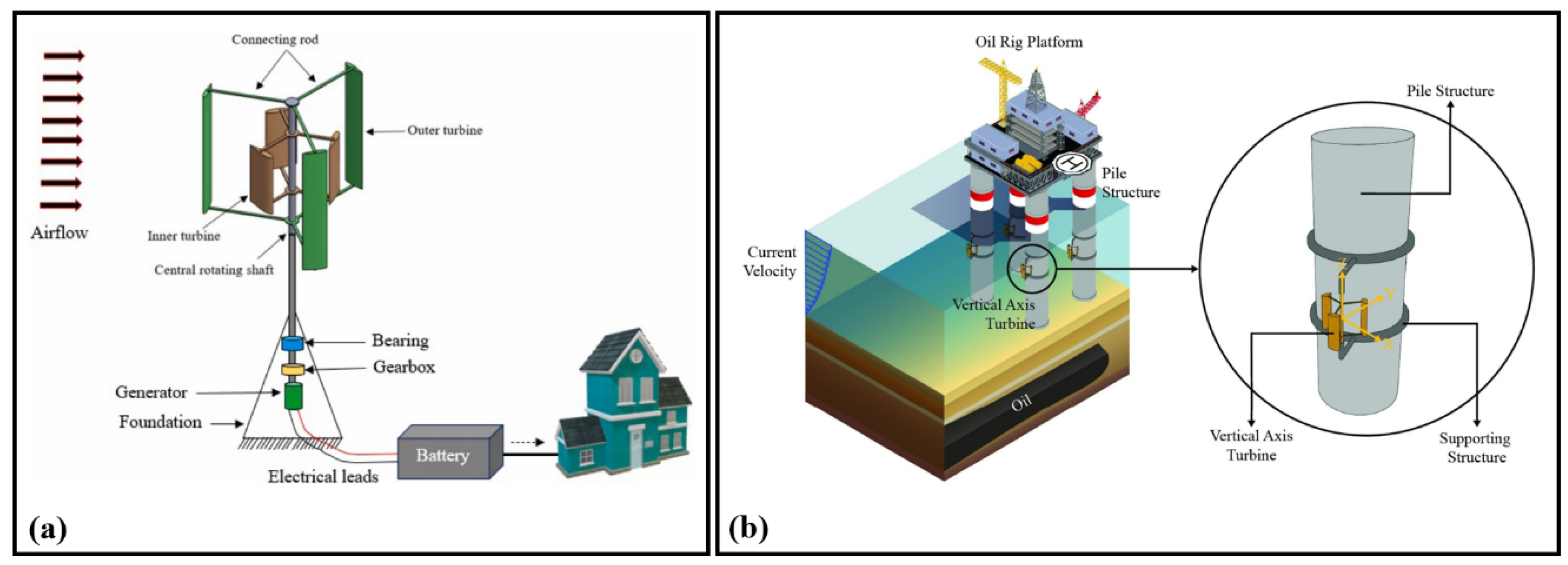
4. Design and Deployment Concepts of Darrieus Turbines for Renewable Energy Harvesting in Terrestrial and Offshore Environments
5. Parametric Optimization of Darrieus Rotor Design for Enhanced Aerodynamic Efficiency
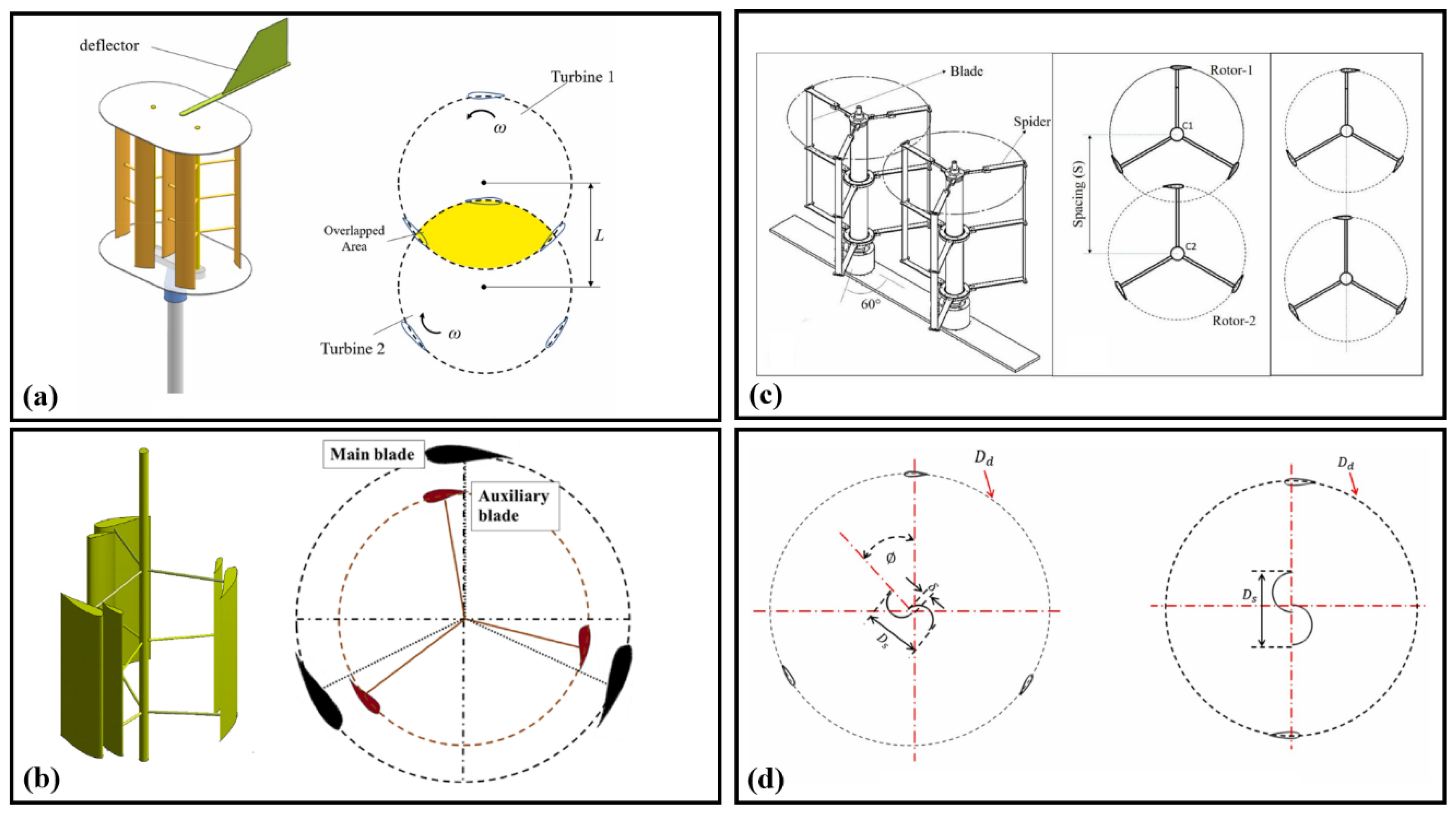
5.1. Analysis of Structural Design, Performance Enhancement, and Experimental Evaluation of Hybrid Darrieus Rotors
- Tubercles applied exclusively to the blades of the inner turbine.
- Tubercles applied solely to the blades of the outer turbine.
- Tubercles incorporated on the blades of both the inner and outer turbines.
5.2. Parametric Design and Performance Analysis of Darrieus with Advanced Configurations and Enhanced Stability
5.3. Performance Impact of Strut Configurations and Blade Geometry on Vertical and Hydrokinetic Turbines
5.4. Aerodynamic Performance Enhancement of Darrieus Turbines Using Gear-like Layouts and Auxiliary Blades
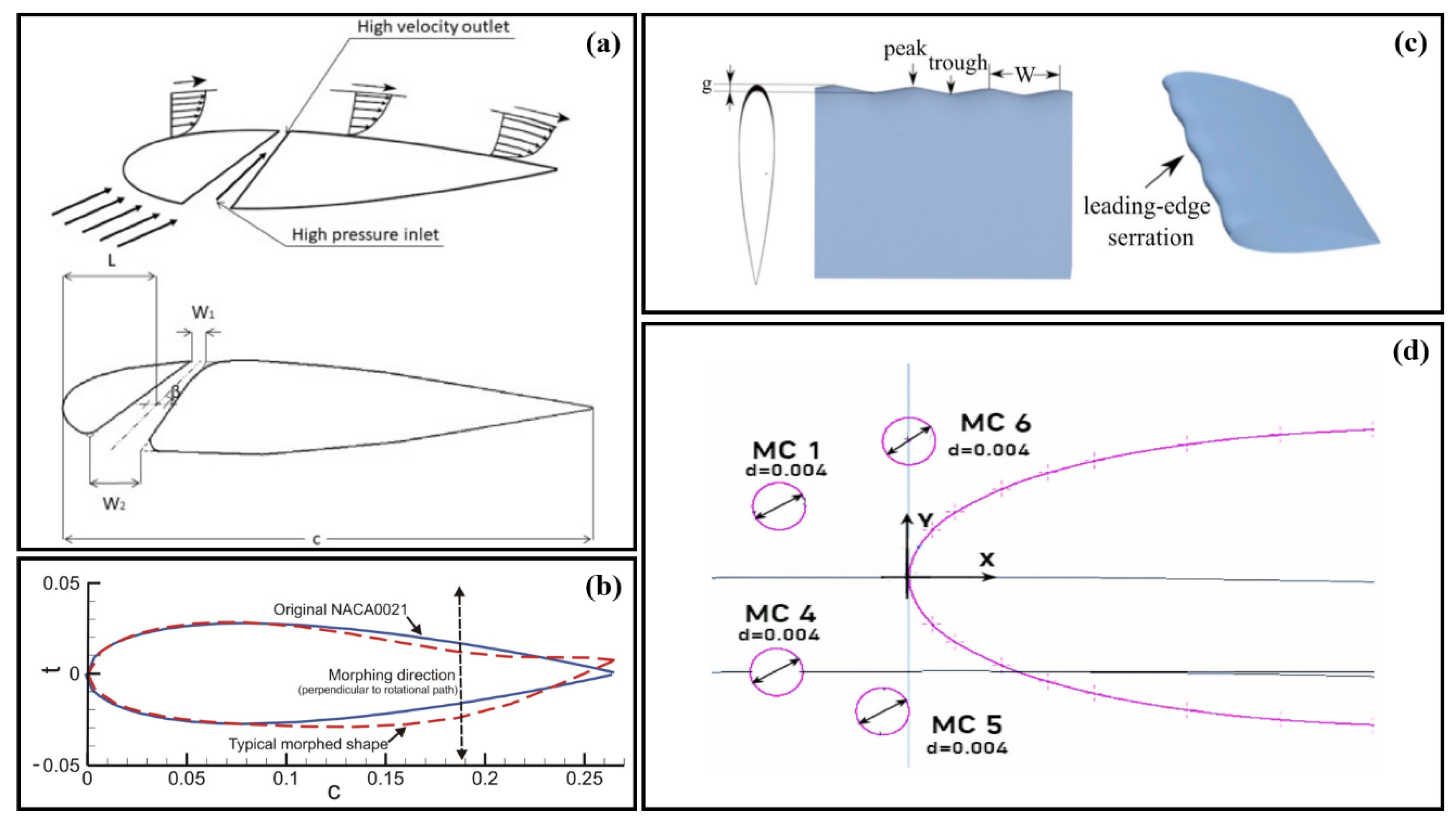
5.5. Analysis of Advanced Aerodynamic Modifications for Enhancing Darrieus Turbine Performance
5.6. Aerodynamic Optimization Techniques for Enhanced Darrieus Turbine Performance
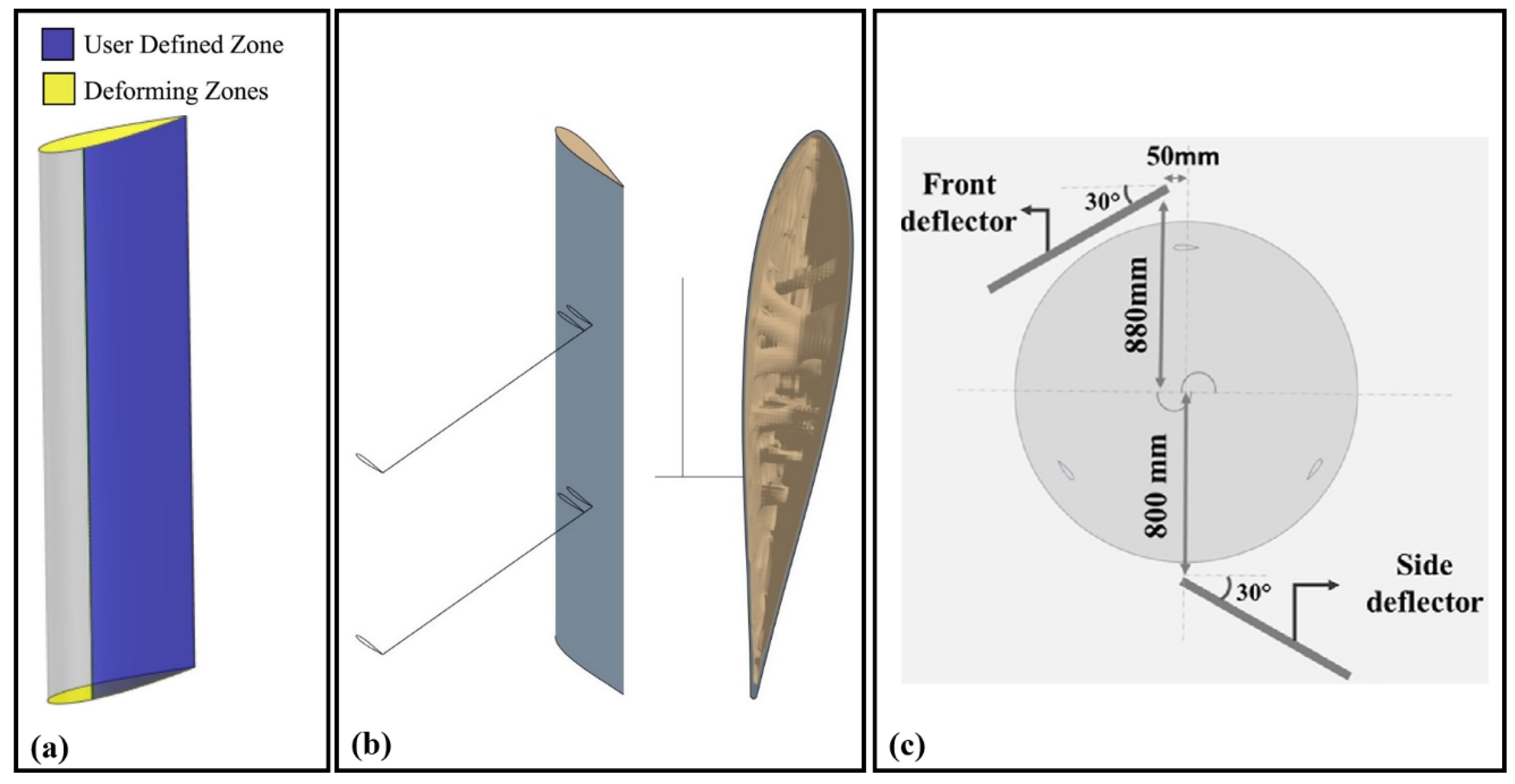
5.7. Mesh Techniques and Structural Optimization for Enhanced Darrieus Turbine Performance
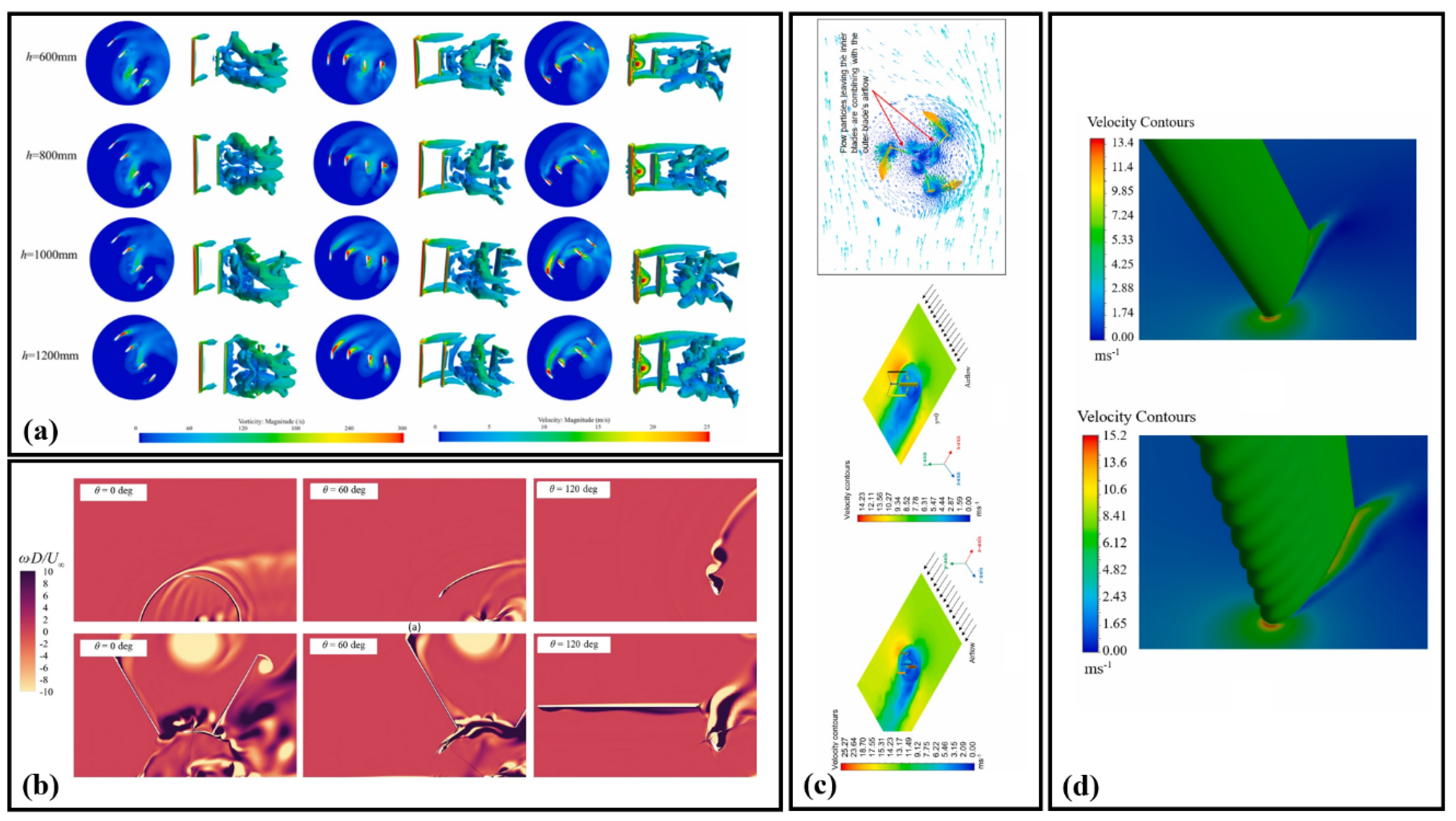
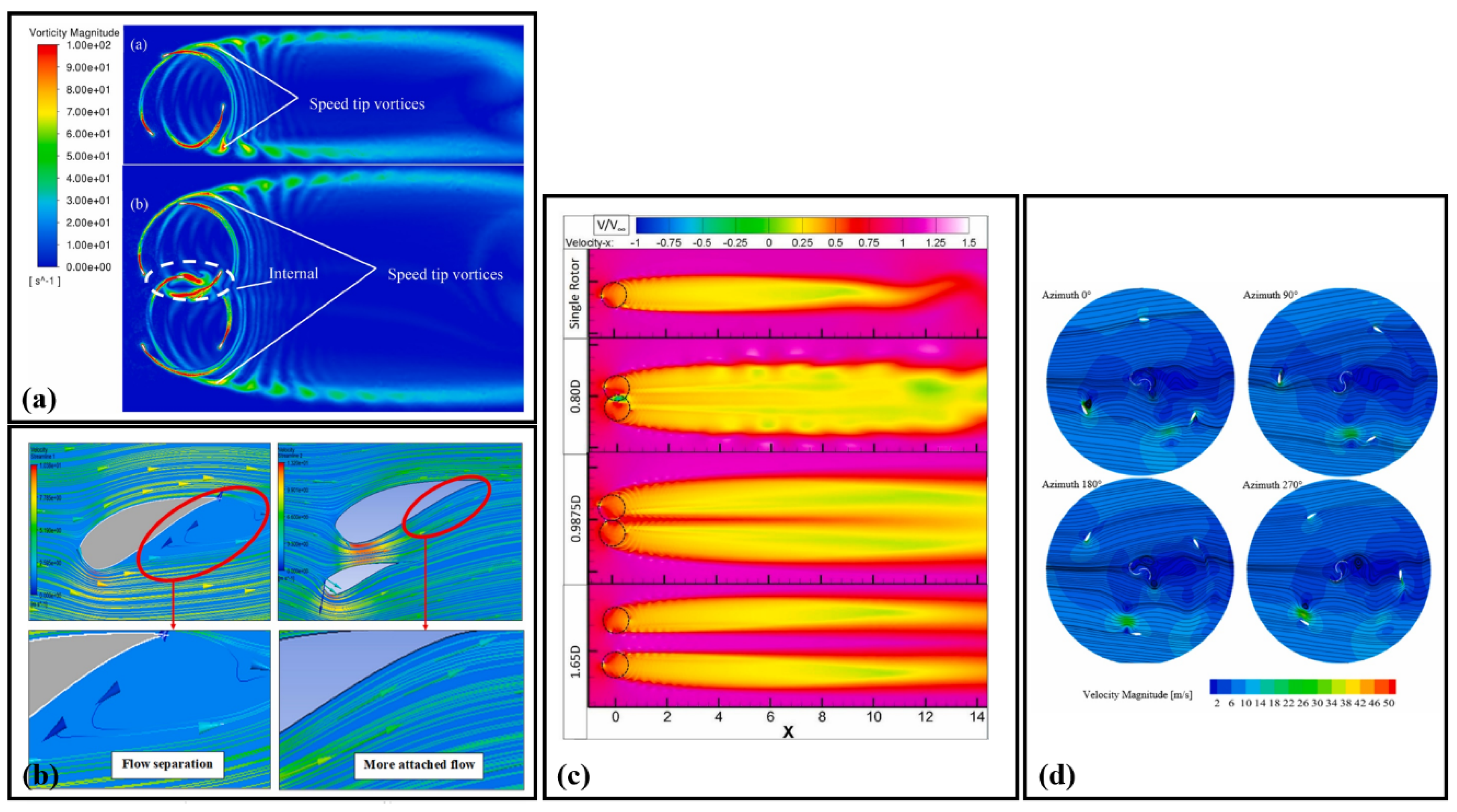
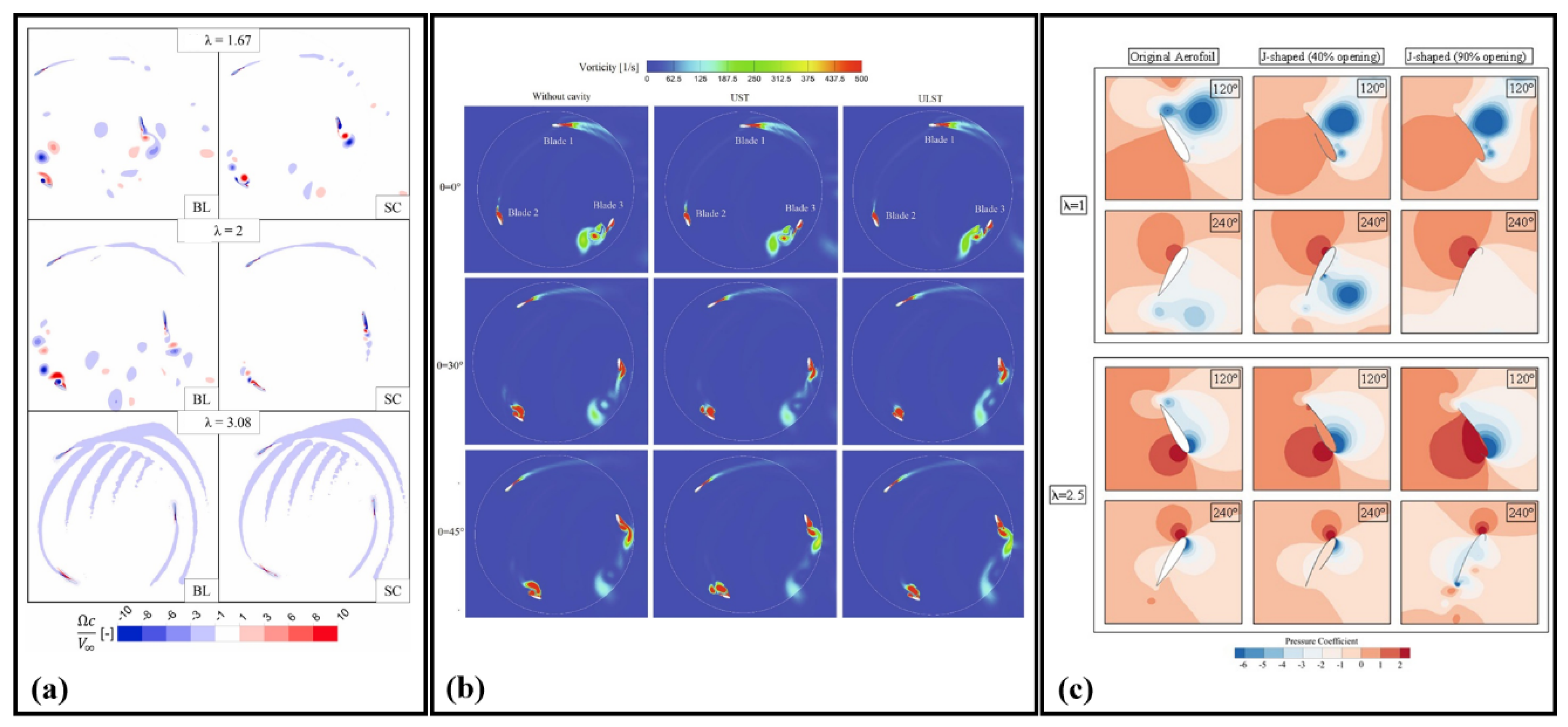
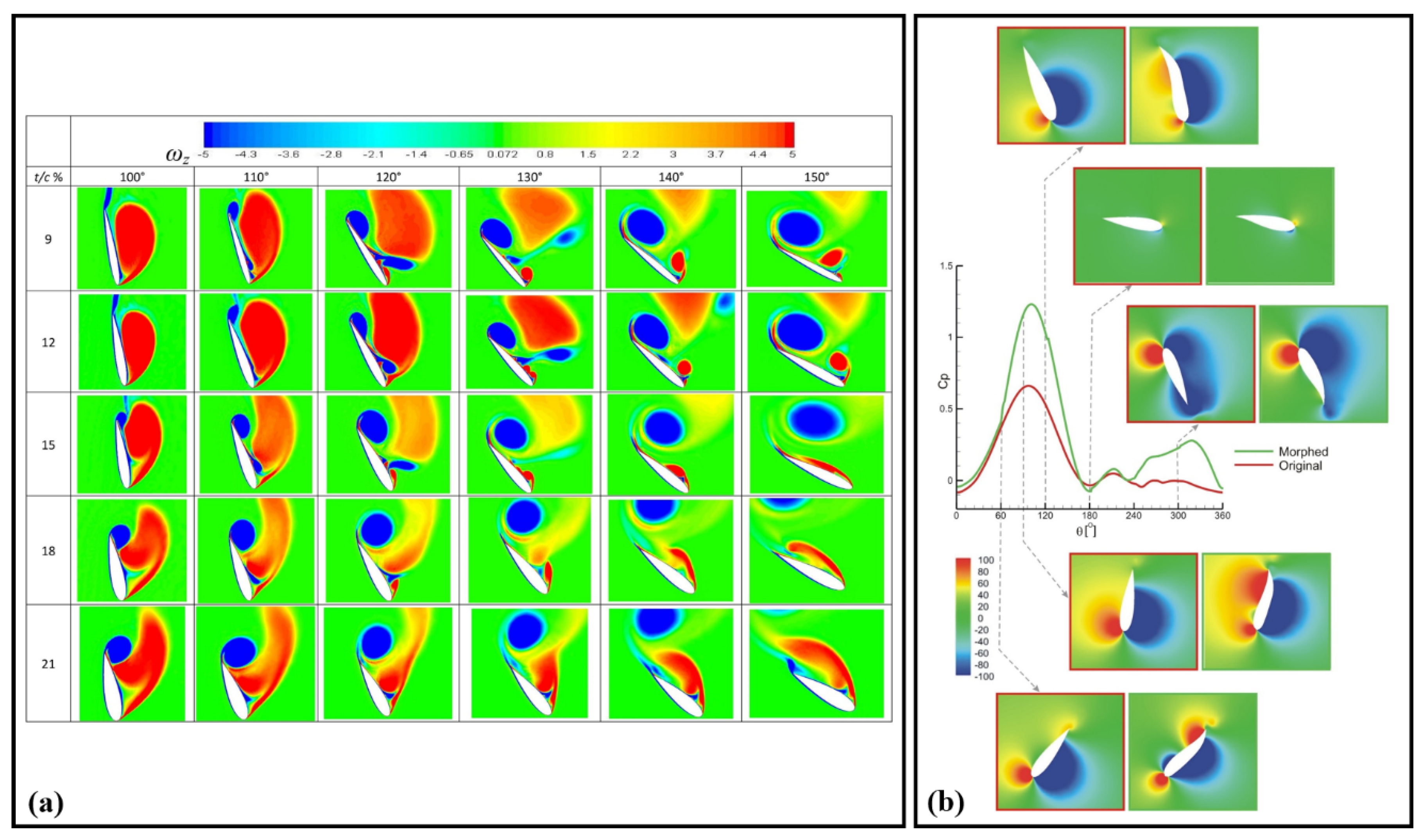
6. CFD Contours for Visualizing Design Effects on Complex Flow Structures: Parametric Studies on Darrieus Rotors
6.1. Vortex Dynamics and Velocity Contours in Advanced Double-Darrieus Turbine Configurations
6.2. Influence of Rotor Spacing and Flow Dynamics on Darrieus Performance
6.3. Vorticity and Flow Dynamics of Darrieus Turbines with Varying Blade Designs
6.4. Flow Dynamics and Vortex Behavior in Various Darrieus Turbines Configurations
6.5. Vortex Shedding and Performance Analysis of Modified Darrieus Turbines Blades
6.6. Impact of Vortex Dynamics and Blade Morphing on Darrieus Turbines Performance
6.7. Vortex Dynamics and Velocity Distribution in Darrieus Blades: Effects of AoA and Micro-Cylinder Integration
6.8. Aerodynamic and Structural Analysis of Darrieus Turbines: Effects of Blade Flexibility, Topology Optimization, and Flow Separation
7. Investigations on Performance Indicators Enhancement for Improved Energy Efficiency of Darrieus Turbines
7.1. Effects of Chord Length, Solidity, and Azimuth Angle on Aerodynamic Performance and Torque Coefficients in Darrieus Rotors
7.2. Impact of Rotor Spacing, Flow Disturbance, Blockage Ratios, and Tilt Angles on Wind and Hydro Darrieus Performance
7.3. Influence of Blade Geometry, Strut Curvature, Aspect Ratio, and TSR on Darrieus Turbines Power Performance and Flow Dynamics
7.4. Performance Enhancement and Flow Dynamics in Multi-Turbine Arrays, H-Rotors, and Hybrid Darrieus Turbines
7.5. Impact of Blade Modifications on Aerodynamic Performance and Torque Generation of Darrieus Turbines
7.6. Impact of Leading-Edge Modifications on Power Coefficient of Darrieus Turbines
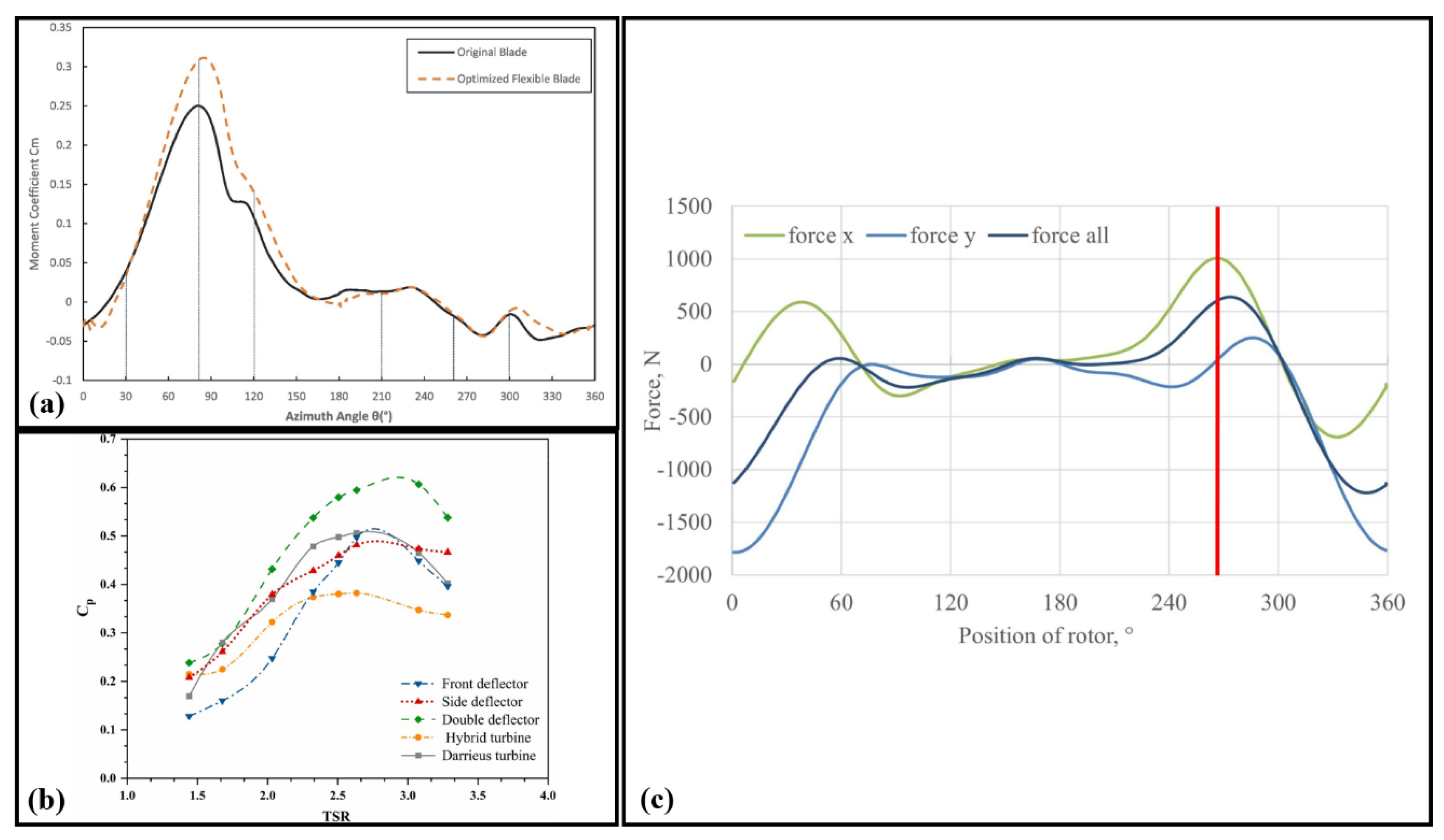
7.7. Enhanced Darrieus Turbines Performance Through Flexible Blade Design and Deflector Integration
8. Gaps in Current Research and Directions for Future Studies
9. Conclusions
10. Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Chord length of the main blade (mm) | Tip speed Ratio (-) | ||
| Chord length ratio between the main blade and the auxiliary blade (-) | Azimuthal angle (degrees) | ||
| Chord length of the auxiliary blade (mm) | Blade–strut angle (degrees) | ||
| Drag coefficient (-) | Solidity (-) | ||
| Lift coefficient (-) | Angular position of turbine blade (degrees) | ||
| Moment coefficient (-) | |||
| Power coefficient (-) | 3SDHKT | Three-stage ducted hydrokinetic turbine | |
| Average power coefficient across multiple operating conditions (-) | 4SDHKT | Four- stage ducted hydrokinetic turbine | |
| Maximum power coefficient (-) | AR | Aspect ratio | |
| Maximum static torque coefficient (-) | AoA | Angle of attack | |
| Torque coefficient (-) | BL | Baseline airfoil | |
| Suction momentum ratio (-) | BR | Blockage ratio | |
| Corrected power coefficient (-) | CAD | Computer-aided design | |
| Diameter of the turbine rotor (mm) | CFD | Computational fluid dynamics | |
| Spacing between rotors (mm) | CRVAWT | Contra-rotating vertical axis wind turbine | |
| Diameter-to-chord ratio of the micro-cylinder placed around the airfoil (-) | CW | Clockwise | |
| Cavity diameter (mm) | DD-VAWT | Double-Darrieus hybrid vertical axis wind turbine | |
| Rotor height (mm) | D-DF | Drag-disturbed flow | |
| Gap between adjacent turbines (mm) | DF-Tri | Specific type of D-DF device | |
| Number of turbines in a Darrieus configuration (-) | DSV | Dynamic stall vortex | |
| Q-criterion (vorticity-based criterion for identifying vortices) (-) | FSI | Fluid–structure interaction | |
| Rotor radius (mm) | HDWT | Horizontal-Darrieus wind turbine | |
| $ | Curvature radius to chord length ratio (-) | HKT | Hydrokinetic turbine |
| Cylindrical coordinates of the blade stacking line at mid-chord (mm) | IGES | Initial graphics exchange specification | |
| Reynolds number (-) | LE | Leading edge | |
| Rotor separation distance (mm) | LEV | Leading edge vortex | |
| Ratio of relative spacing to rotor diameter (-) | LHHT | Lift-type helical hydrokinetic turbine | |
| Thickness-to-chord ratio (-) | LR | Low-Reynolds turbulence model | |
| Freestream wind speed | LSB | Laminar separation bubble | |
| Longitudinal distance between the aerodynamic centers of the main and auxiliary blades (mm) | MC | Micro-cylinder | |
| Vertical distance between the main and auxiliary blades (mm) | SA | Shear-algebraic turbulence model | |
| Axial displacement (in terms of chord length) (-) | SC | Suction cavity airfoil | |
| Non-dimensional spanwise distance (-) | SDHKT | Spherical Darrieus hydrokinetic turbine | |
| Radial displacement (in terms of rotor radius) (-) | SLS | Selective laser sintering (3D printing technology) | |
| Rotor radius (mm) | TE | Trailing edge | |
| Non-dimensional height above the turbine base (-) | TEV | Trailing edge vortex | |
| Greek symbols | TSR | Tip speed ratio | |
| Angle of attack (degrees) | TSST | Transitional shear stress transport model | |
| Pitch angle (degrees) | URANS | Unsteady Reynolds-averaged Navier–Stokes | |
| Increment of the angle of attack due to leading-edge deflection (degrees) | VAWT | Vertical axis wind turbine | |
| Suction blower efficiency (-) | VIS | Vortex-induced separation |
References
- Ahmad, M.; Shahzad, A.; Akram, F.; Ahmad, F.; Shah, S.I.A. Design optimization of Double-Darrieus hybrid vertical axis wind turbine. Ocean Eng. 2022, 254, 111171. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, H.; Zhang, Z.; Salman, W.; Abdelrahman, M. Parameter optimization method of contra-rotating vertical axis wind turbine: Based on numerical simulation and response surface. J. Clean. Prod. 2024, 435, 140475. [Google Scholar] [CrossRef]
- Satrio, D.; Widyawan, H.B.; Ramadhani, M.A.; Muharja, M. Effects of the distance ratio of circular flow disturbance on vertical-axis turbine performance: An experimental and numerical study. Sustain. Energy Technol. Assess. 2024, 63, 103635. [Google Scholar] [CrossRef]
- Shen, Z.; Gong, S.; Xie, G.; Lu, H.; Guo, W. Investigation of the effect of critical structural parameters on the aerodynamic performance of the double darrieus vertical axis wind turbine. Energy 2024, 290, 130156. [Google Scholar] [CrossRef]
- Yadav, S.; Veeravalli, S.V.; Singh, S.N. Effect of rotor spacing, overlapping and non-overlapping, on the performance of a coupled counter-rotating twin-rotor VAWT using CFD. Renew. Energy 2024, 221, 119811. [Google Scholar] [CrossRef]
- Ansaf, R.; Abdelhameed, H.S.; Hashem, I.; Harun, Z. Efficiency-based design optimization of the H-type Darrieus wind turbine with fixed guiding-walls. Energy Rep. 2023, 9, 3576–3592. [Google Scholar] [CrossRef]
- Ahmad, M.; Zafar, M.H. Enhancing vertical axis wind turbine efficiency through leading edge tubercles: A multifaceted analysis. Ocean Eng. 2023, 288, 116026. [Google Scholar] [CrossRef]
- Huang, H.; Luo, J.; Li, G. Study on the optimal design of vertical axis wind turbine with novel variable solidity type for self-starting capability and aerodynamic performance. Energy 2023, 271, 127031. [Google Scholar] [CrossRef]
- Celik, Y.; Ingham, D.; Ma, L.; Pourkashanian, M. Design and aerodynamic performance analyses of the self-starting H-type VAWT having J-shaped aerofoils considering various design parameters using CFD. Energy 2022, 251, 123881. [Google Scholar] [CrossRef]
- Tian, W.; Ni, X.; Li, B.; Yang, G.; Mao, Z. Improving the efficiency of Darrieus turbines through a gear-like turbine layout. Energy 2023, 267, 126580. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Elbaz, A.M.; Melani, P.F.; Mohamed, O.S.; Bianchini, A. Power augmentation of Darrieus wind turbine blades using trapped vortex cavity. J. Wind Eng. Ind. Aerodyn. 2022, 223, 104949. [Google Scholar] [CrossRef]
- Abdolahifar, A.; Azizi, M.; Zanj, A. Flow structure and performance analysis of Darrieus vertical axis turbines with swept blades: A critical case study on V-shaped blades. Ocean Eng. 2023, 280, 114857. [Google Scholar] [CrossRef]
- Hijazi, A.; ElCheikh, A.; Elkhoury, M. Numerical investigation of the use of flexible blades for vertical axis wind turbines. Energy Convers. Manag. 2024, 299, 117867. [Google Scholar] [CrossRef]
- Yan, Y.; Avital, E.; Williams, J.; Cui, J. Aerodynamic performance improvements of a vertical axis wind turbine by leading-edge protuberance. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104535. [Google Scholar] [CrossRef]
- Baghdadi, M.; Elkoush, S.; Akle, B.; Elkhoury, M. Dynamic shape optimization of a vertical-axis wind turbine via blade morphing technique. Renew. Energy 2020, 154, 239–251. [Google Scholar] [CrossRef]
- Bakhumbsh, S.A.; Mohamed, M.H. Effect of micro-cylinder as a passive controller on the Darrieus wind turbine performance. Ocean Eng. 2022, 266, 113118. [Google Scholar] [CrossRef]
- Marzec, Ł.; Buliński, Z.; Krysiński, T.; Tumidajski, J. Structural optimisation of H-Rotor wind turbine blade based on one-way Fluid Structure Interaction approach. Renew. Energy 2023, 216, 118957. [Google Scholar] [CrossRef]
- Chegini, S.; Asadbeigi, M.; Ghafoorian, F.; Mehrpooya, M. An investigation into the self-starting of Darrieus-Savonius hybrid wind turbine and performance enhancement through innovative deflectors: A CFD approach. Ocean Eng. 2023, 287, 115910. [Google Scholar] [CrossRef]
- Jiang, T.; Zhao, Y.; Wang, S.; Zhang, L.; Li, G. Aerodynamic characterization of a H-Darrieus wind turbine with a Drag-Disturbed Flow device installation. Energy 2024, 292, 130522. [Google Scholar] [CrossRef]
- Reddy, K.B.; Bhosale, A.C. Influence of aspect ratio on the performance and wake recovery of lift-type helical hydrokinetic turbine. Energy 2024, 289, 129996. [Google Scholar] [CrossRef]
- Kumar, R.; Sarkar, S. Performance analysis of spherical-shaped Darrieus hydrokinetic turbine for an in-pipe hydropower system. Energy Convers. Manag. 2023, 294, 117600. [Google Scholar] [CrossRef]
- Reddy, K.U.; Deb, B.; Roy, B. A numerical and experimental study on the performance of a conventional H-Darrieus wind rotor with auxiliary blades. Ocean Eng. 2023, 280, 114697. [Google Scholar] [CrossRef]
- Eltayesh, A.; Castellani, F.; Natili, F.; Burlando, M.; Khedr, A. Aerodynamic upgrades of a Darrieus vertical axis small wind turbine. Energy Sustain. Dev. 2023, 73, 126–143. [Google Scholar] [CrossRef]
- Iddou, H.; Bouda, N.N.; Zereg, K. Computational fluid dynamics study on the efficiency of straight-bladed vertical axis wind turbine. Int. J. Thermofluids 2024, 22, 100672. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Melani, P.F.; Soraperra, G.; Brighenti, A.; Ferrara, G.; Betti, V.; Schippa, L.; Guerrero, M.; Balduzzi, F.; Bianchini, A. Three-dimensional CFD-ALM-VOF modeling of hydrokinetic turbines in realistic open-channel conditions. Ocean Eng. 2024, 313, 119411. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Melani, P.F.; Papi, F.; Balduzzi, F.; Bianchini, A. Is the Actuator line method able to reproduce the interaction between closely-spaced Darrieus rotors? a critical assessment on wind and hydrokinetic turbines. Energy Convers. Manag. 2023, 293, 117473. [Google Scholar] [CrossRef]
- Khedr, A.; Castellani, F. Critical issues in the moving reference frame CFD simulation of small horizontal axis wind turbines. Energy Convers. Manag. X 2024, 22, 100551. [Google Scholar] [CrossRef]
- Eltayeb, W.A.; Somlal, J. Performance Enhancement of Darrieus Wind Turbines Using Plain Flap and Gurney Flap Configurations: A CFD Analysis. Results Eng. 2024, 24, 103400. [Google Scholar] [CrossRef]
- Sanaye, S.; Farvizi, A. Optimizing a vertical axis wind turbine with helical blades: Application of 3D CFD and Taguchi method. Energy Rep. 2024, 12, 2527–2547. [Google Scholar] [CrossRef]
- Chen, W.H.; Wang, Y.S.; Chang, M.H.; Show, P.L.; Hoang, A.T. Operation parameter interaction and optimization of vertical axis wind turbine analyzed by Taguchi method with modified additive model and ANOVA. Energy Rep. 2024, 11, 5189–5200. [Google Scholar] [CrossRef]
- Fatahian, E.; Mishra, R.; Jackson, F.F.; Fatahian, H. Optimization and analysis of self-starting capabilities of vertical axis wind turbine pairs: A CFD-Taguchi approach. Ocean Eng. 2024, 302, 117614. [Google Scholar] [CrossRef]
- Batista, N.C.; Melício, R.; Mendes, V.M.F.; Calderón, M.; Ramiro, A. On a self-start Darrieus wind turbine: Blade design and field tests. Renew. Sustain. Energy Rev. 2015, 52, 508–522. [Google Scholar] [CrossRef]
- Marwa, F.; Wael, B.A.; Malek, A.; Aref, M. Exploring the influence of flexibility on rotor performance in turbulent flow environments. Eur. J. Mech. -B/Fluids 2025, 109, 199–212. [Google Scholar]
- Tian, W.; Zhang, C.; Mao, Z.; Li, B.; Zhang, T.; Song, B. Numerical investigation on the suppression of vortex-induced vibration system by assembling different rotors based on quasi-active control method. Ocean Eng. 2024, 311, 119015. [Google Scholar] [CrossRef]
- Shen, Z.; Gong, S.; Zuo, Z.; Chen, Y.; Guo, W. Darrieus vertical-axis wind turbine performance enhancement approach and optimized design: A review. Ocean Eng. 2024, 311, 118965. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Yang, M.; Xu, H.; Hu, Z. A comprehensive review of the theoretical approaches for the airfoil design of lift-type vertical axis wind turbine. Renew. Sustain. Energy Rev. 2015, 51, 1709–1720. [Google Scholar] [CrossRef]
- Tayebi, A.; Torabi, F. Flow control techniques to improve the aerodynamic performance of Darrieus vertical axis wind turbines: A critical review. J. Wind Eng. Ind. Aerodyn. 2024, 252, 105820. [Google Scholar] [CrossRef]
- Ghasemian, M.; Ashrafi, Z.N.; Sedaghat, A. A review on computational fluid dynamic simulation techniques for Darrieus vertical axis wind turbines. Energy Convers. Manag. 2017, 149, 87–100. [Google Scholar] [CrossRef]
- Li, Y.; Yang, S.; Feng, F.; Tagawa, K. A review on numerical simulation based on CFD technology of aerodynamic characteristics of straight-bladed vertical axis wind turbines. Energy Rep. 2023, 9, 4360–4379. [Google Scholar] [CrossRef]
- Reddy, K.B.; Bhosale, A.C.; Saini, R.P. Performance parameters of lift-based vertical axis hydrokinetic turbines-A review. Ocean Eng. 2022, 266, 113089. [Google Scholar] [CrossRef]
- Díaz, A.V.; Moya, I.H. Urban wind energy with resilience approach for sustainable cities in tropical regions: A review. Renew. Sustain. Energy Rev. 2024, 199, 114525. [Google Scholar] [CrossRef]
- Peng, H.Y.; Liu, H.J.; Yang, J.H. A review on the wake aerodynamics of H-rotor vertical axis wind turbines. Energy 2021, 232, 121003. [Google Scholar] [CrossRef]
- Gupta, A.; Abderrahmane, H.A.; Janajreh, I. Flow analysis and sensitivity study of vertical-axis wind turbine under variable pitching. Appl. Energy 2024, 358, 122648. [Google Scholar] [CrossRef]
- Anggara, B.; Tjahjana, D.D.D.P.; Budiana, E.P. Numerical Study of Effect of High Efficiency Vortex Addition on Darrieus H Rotor Wind Turbine Performance. Procedia Struct. Integr. 2023, 47, 675–684. [Google Scholar] [CrossRef]
- Franchina, N.; Kouaissah, O.; Persico, G.; Savini, M. Three-dimensional modeling and investigation of the flow around a troposkein vertical axis wind turbine at different operating conditions. Renew. Energy 2022, 199, 368–381. [Google Scholar] [CrossRef]
- Chen, W.C.; Hsu, Y.Y.; Hsieh, L.F.; Tai, P.H. A systematic optimization approach for assembly sequence planning using Taguchi method, DOE, and BPNN. Expert Syst. Appl. 2010, 37, 716–726. [Google Scholar] [CrossRef]
- Zidane, I.F.; Ali, H.M.; Swadener, G.; Eldrainy, Y.A.; Shehata, A.I. Effect of upstream deflector utilization on H-Darrieus wind turbine performance: An optimization study. Alex. Eng. J. 2023, 63, 175–189. [Google Scholar] [CrossRef]
- Singh, E.; Roy, S.; San Yam, K.; Law, M.C. Numerical analysis of H-Darrieus vertical axis wind turbines with varying aspect ratios for exhaust energy extractions. Energy 2023, 277, 127739. [Google Scholar] [CrossRef]
- Roshan, M.Y.; Khaleghinia, J.; Nimvari, M.E.; Salarian, H. Performance improvement of Darrieus wind turbine using different cavity layouts. Energy Convers. Manag. 2021, 246, 114693. [Google Scholar] [CrossRef]
- Rasekh, S.; Aliabadi, S.K. Toward improving the performance of a variable pitch vertical axis wind turbine (VP-VAWT), Part 2: Multi-objective optimization using NSGA-II with CFD in the loop. Ocean Eng. 2023, 278, 114308. [Google Scholar] [CrossRef]
- Rasekh, S.; Aliabadi, S.K.; Hansen, M.O. Toward improving the performance of a variable pitch vertical axis wind turbine (VP-VAWT), Part 1: Sensitivity analysis using Taguchi-CFD approach. Ocean Eng. 2023, 279, 114478. [Google Scholar] [CrossRef]
- Ghareghani, M.S.M.; Abdolahifar, A.; Karimian, S.M.H. Numerical investigation on the helix angle to smoothen aerodynamic torque output of the 3-PB Darrieus vertical axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2023, 234, 105323. [Google Scholar] [CrossRef]
- Franchina, N.; Persico, G.; Savini, M. Three-dimensional unsteady aerodynamics of a H-shaped vertical axis wind turbine over the full operating range. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104273. [Google Scholar] [CrossRef]
- Kouaissah, O.; Franchina, N.; Siddiqui, M.S.; Persico, G. A computational study on the performance and wake development of a tilted H-Shaped VAWT rotor. Renew. Energy 2024, 222, 119932. [Google Scholar] [CrossRef]
- Reddy, K.U.; Deb, B.; Roy, B. Wind tunnel test and numerical analysis of wooden-bladed Darrieus wind rotor at low wind speed conditions. Mater. Today Proc. 2024, 103, 289–296. [Google Scholar] [CrossRef]
- Kong, Z.; Zhou, D.; Sun, X. Improvement of self-starting and power extraction performance of an H-type vertical-axis hydrokinetic turbine by partial deflection of its blades. Ocean Eng. 2024, 296, 116855. [Google Scholar] [CrossRef]
- Bundi, J.M.; Ban, X.; Wekesa, D.W.; Ding, S. Pitch control of small H-type Darrieus vertical axis wind turbines using advanced gain scheduling techniques. Renew. Energy 2020, 161, 756–765. [Google Scholar] [CrossRef]
- Tirandaz, M.R.; Rezaeiha, A. Effect of airfoil shape on power performance of vertical axis wind turbines in dynamic stall: Symmetric Airfoils. Renew. Energy 2021, 173, 422–441. [Google Scholar] [CrossRef]
- Geng, F.; Suiker, A.S.; Rezaeiha, A.; Montazeri, H.; Blocken, B. A computational framework for the lifetime prediction of vertical-axis wind turbines: CFD simulations and high-cycle fatigue modeling. Int. J. Solids Struct. 2023, 284, 112504. [Google Scholar] [CrossRef]
- Tunio, I.A.; Shah, M.A.; Hussain, T.; Harijan, K.; Mirjat, N.H.; Memon, A.H. Investigation of duct augmented system effect on the overall performance of straight blade Darrieus hydrokinetic turbine. Renew. Energy 2020, 153, 143–154. [Google Scholar] [CrossRef]
- Wilberforce, T.; Olabi, A.G.; Sayed, E.T.; Alalmi, A.H.; Abdelkareem, M.A. Wind turbine concepts for domestic wind power generation at low wind quality sites. J. Clean. Prod. 2023, 394, 136137. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Melani, P.F.; Balduzzi, F.; Ferrara, G.; Bianchini, A. An insight on the physical mechanisms responsible of power augmentation in a pair of counter-rotating Darrieus turbines. Energy Convers. Manag. 2023, 284, 116991. [Google Scholar] [CrossRef]
- Kamal, M.M.; Saini, R.P. Performance investigations of hybrid hydrokinetic turbine rotor with different system and operating parameters. Energy 2023, 267, 126541. [Google Scholar] [CrossRef]
- Durkacz, J.; Islam, S.; Chan, R.; Fong, E.; Gillies, H.; Karnik, A.; Mullan, T. CFD modelling and prototype testing of a Vertical Axis Wind Turbines in planetary cluster formation. Energy Rep. 2021, 7, 119–126. [Google Scholar] [CrossRef]
- Jain, S.; Saha, U.K. On the influence of blade thickness-to-chord ratio on dynamic stall phenomenon in H-type Darrieus wind rotors. Energy Convers. Manag. 2020, 218, 113024. [Google Scholar] [CrossRef]
- Ortiz-Rodríguez, J.M.; Martínez-Blanco, M.R.; Vega-Carrillo, H.R. Robust design of artificial neural networks applying the Taguchi methodology and DoE. In Proceedings of the Electronics, Robotics and Automotive Mechanics Conference (CERMA’06), Cuernavaca, Mexico, 26–29 September 2006; Volume 2, pp. 131–136. [Google Scholar]
- Li, L.; Lu, B.; Xu, W.; Wang, C.; Wu, J.; Tan, D. Dynamic behaviors of multiphase vortex-induced vibration for hydropower energy conversion. Energy 2024, 308, 132897. [Google Scholar] [CrossRef]
- Rehman, S.; Rafique, M.M.; Alam, M.M.; Alhems, L.M. Vertical axis wind turbine types, efficiencies, and structural stability-A review. Wind. Struct. 2019, 29, 15–32. [Google Scholar]
- Parente, V.; Ferreira, D.; dos Santos, E.M.; Luczynski, E. Offshore decommissioning issues: Deductibility and transferability. Energy Policy 2006, 34, 1992–2001. [Google Scholar] [CrossRef]
- Sommer, B.; Fowler, A.M.; Macreadie, P.I.; Palandro, D.A.; Aziz, A.C.; Booth, D.J. Decommissioning of offshore oil and gas structures–Environmental opportunities and challenges. Sci. Total Environ. 2019, 658, 973–981. [Google Scholar] [CrossRef] [PubMed]
- Zawawi, N.W.A.; Liew, M.S.; Na, K.L. Decommissioning of offshore platform: A sustainable framework. In Proceedings of the 2012 IEEE Colloquium on Humanities, Science and Engineering (CHUSER), Sabah, Malaysia, 3–4 December 2012; pp. 26–31. [Google Scholar]
- Mia, M.J.; Islam, M.A.; Islam, M. Powering Offshore Structure Using Renewable Energy: A Review Study. Bangladesh Marit. J. (BMJ) 2021, 5, 1840–2520. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, D.; Wang, T.; Shen, W.; Liu, H.; Chen, M. A review: Approaches for aerodynamic performance improvement of lift-type vertical axis wind turbine. Sustain. Energy Technol. Assess. 2022, 49, 101789. [Google Scholar]
- Maeda, T.; Kamada, Y.; Murata, J.; Yamamoto, M.; Ogasawara, T.; Shimizu, K.; Kogaki, T. Study on power performance for straight-bladed vertical axis wind turbine by field and wind tunnel test. Renew. Energy 2016, 90, 291–300. [Google Scholar]
- Kumar, R.; Sarkar, S. Effect of design parameters on the performance of helical Darrieus hydrokinetic turbines. Renew. Sustain. Energy Rev. 2022, 162, 112431. [Google Scholar] [CrossRef]
- De Marco, A.; Coiro, D.P.; Cucco, D.; Nicolosi, F. A numerical study on a vertical-axis wind turbine with inclined arms. Int. J. Aerosp. Eng. 2014, 2014, 180498. [Google Scholar] [CrossRef]
- Villeneuve, T.; Winckelmans, G.; Dumas, G. Increasing the efficiency of vertical-axis turbines through improved blade support structures. Renew. Energy 2021, 169, 1386–1401. [Google Scholar] [CrossRef]
- Talukdar, P.K.; Kulkarni, V.; Saha, U.K. Field-testing of model helical-bladed hydrokinetic turbines for small-scale power generation. Renew. Energy 2018, 127, 158–167. [Google Scholar] [CrossRef]
- Battisti, L.; Persico, G.; Dossena, V.; Paradiso, B.; Castelli, M.R.; Brighenti, A.; Benini, E. Experimental benchmark data for H-shaped and troposkien VAWT architectures. Renew. Energy 2018, 125, 425–444. [Google Scholar] [CrossRef]
- Castelli, M.R.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Asadi, M.; Hassanzadeh, R. Effects of internal rotor parameters on the performance of a two bladed Darrieus-two bladed Savonius hybrid wind turbine. Energy Convers. Manag. 2021, 238, 114109. [Google Scholar] [CrossRef]
- Sobhani, E.; Ghaffari, M.; Maghrebi, M.J. Numerical investigation of dimple effects on darrieus vertical axis wind turbine. Energy 2017, 133, 231–241. [Google Scholar] [CrossRef]
- Song, C.; Wu, G.; Zhu, W.; Zhang, X. Study on aerodynamic characteristics of Darrieus vertical axis wind turbines with different airfoil maximum thicknesses through computational fluid dynamics. Arab. J. Sci. Eng. 2020, 45, 689–698. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Ibrahim, A.A.; Etman, A.K.; Abdelfatah, A.A.; Elbaz, A.M. Numerical investigation of Darrieus wind turbine with slotted airfoil blades. Energy Convers. Manag. X 2020, 5, 100026. [Google Scholar] [CrossRef]
- Syawitri, T.P.; Yao, Y.; Yao, J.; Chandra, B. Optimisation of straight plate upstream deflector for the performance enhancement of vertical axis wind turbine at low, medium and high regimes of tip speed ratios. Wind. Eng. 2022, 46, 1487–1510. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Y.; Ju, W.; He, J.; Xie, S. Investigation into parameter influence of upstream deflector on vertical axis wind turbines output power via three-dimensional CFD simulation. Renew. Energy 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Chen, W.H.; Wang, J.S.; Chang, M.H.; Mutuku, J.K.; Hoang, A.T. Efficiency improvement of a vertical-axis wind turbine using a deflector optimized by Taguchi approach with modified additive method. Energy Convers. Manag. 2021, 245, 114609. [Google Scholar] [CrossRef]
- Beri, H.; Yao, Y.Y. Effect of camber airfoil on self starting of Vertical Axis Wind Turbine. J. Environ. Sci. Technol. 2011, 4, 302–312. [Google Scholar] [CrossRef]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renewable energy 2010, 35, 412–422. [Google Scholar] [CrossRef]
- Mobini, K.; Niazi, M. Large eddy simulation of the flow across a rotating circular cylinder. Int. J. Fluid Mech. Res. 2014, 41, 1–15. [Google Scholar] [CrossRef]
- Wei, N.J.; Brownstein, I.D.; Cardona, J.L.; Howland, M.F.; Dabiri, J.O. Near-wake structure of full-scale vertical-axis wind turbines. J. Fluid Mech. 2021, 914, A17. [Google Scholar] [CrossRef]
- Tescione, G.; Ragni, D.; He, C.; Ferreira, C.S.; Van Bussel, G.J.W. Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. Renew. Energy 2014, 70, 47–61. [Google Scholar] [CrossRef]
- Posa, A. Dependence of the wake recovery downstream of a Vertical Axis Wind Turbine on its dynamic solidity. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104212. [Google Scholar] [CrossRef]
- Simpson, R.L. Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 1989, 21, 205–232. [Google Scholar] [CrossRef]
- Simpson, R.L. Aspects of turbulent boundary-layer separation. Prog. Aerosp. Sci. 1996, 32, 457–521. [Google Scholar] [CrossRef]
- Pallotta, A.; Pietrogiacomi, D.; Romano, G.P. HYBRI–A combined Savonius-Darrieus wind turbine: Performances and flow fields. Energy 2020, 191, 116433. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fertahi, S.e.-D.; Rehman, S.; Benini, E.; Lahrech, K.; Samaouali, A.; Arbaoui, A.; Kadiri, I.; Agounoun, R. Insights from the Last Decade in Computational Fluid Dynamics (CFD) Design and Performance Enhancement of Darrieus Wind Turbines. Processes 2025, 13, 370. https://doi.org/10.3390/pr13020370
Fertahi Se-D, Rehman S, Benini E, Lahrech K, Samaouali A, Arbaoui A, Kadiri I, Agounoun R. Insights from the Last Decade in Computational Fluid Dynamics (CFD) Design and Performance Enhancement of Darrieus Wind Turbines. Processes. 2025; 13(2):370. https://doi.org/10.3390/pr13020370
Chicago/Turabian StyleFertahi, Saïf ed-Dîn, Shafiqur Rehman, Ernesto Benini, Khadija Lahrech, Abderrahim Samaouali, Asmae Arbaoui, Imad Kadiri, and Rachid Agounoun. 2025. "Insights from the Last Decade in Computational Fluid Dynamics (CFD) Design and Performance Enhancement of Darrieus Wind Turbines" Processes 13, no. 2: 370. https://doi.org/10.3390/pr13020370
APA StyleFertahi, S. e.-D., Rehman, S., Benini, E., Lahrech, K., Samaouali, A., Arbaoui, A., Kadiri, I., & Agounoun, R. (2025). Insights from the Last Decade in Computational Fluid Dynamics (CFD) Design and Performance Enhancement of Darrieus Wind Turbines. Processes, 13(2), 370. https://doi.org/10.3390/pr13020370










