Optimizing Reactive Compensation for Enhanced Voltage Stability in Renewable-Integrated Stochastic Distribution Networks
Abstract
1. Introduction
- (1)
- Considering the possible new renewable energy scale in the distribution network in the future and the load growth rate, the optimization scenario of reactive compensation equipment under different ratios of the two is established, and the corresponding SVG siting and operation strategies are obtained.
- (2)
- A multi-objective siting strategy for SVG has been developed, focusing on voltage–loss sensitivity. The entropy weight method is employed to mitigate the influence of subjective factors in multi-objective planning. This approach aims to minimize both voltage fluctuations and line loss, effectively addressing the limitations associated with single-objective siting methodologies.
- (3)
- To address the challenge of output uncertainty in multiple renewable energy sources, we propose the robust IGDT. This approach effectively quantifies the uncertainties associated with renewable energy generation and aligns more closely with the actual assessment of system configuration.
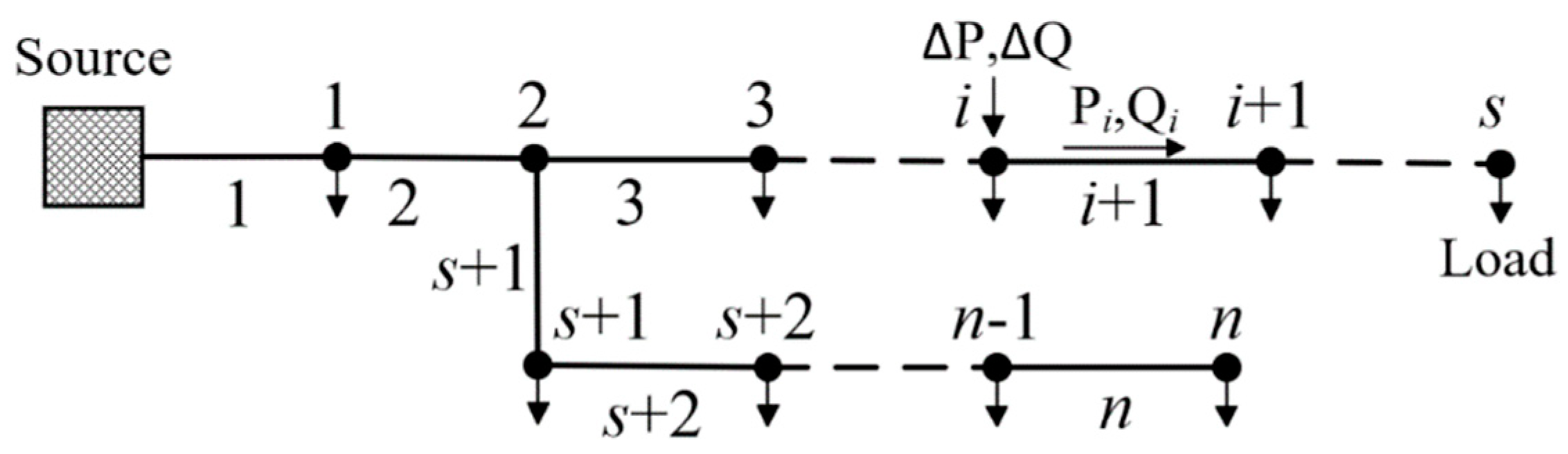
2. SVG Siting Strategy Considering Multi-Objective Voltage and Loss Sensitivity
2.1. Voltage–Loss Sensitivity Calculation
2.2. Constraint Conditions
3. Uncertainty Quantification Model of Renewable Energy Based on Robust IGDT
| Algorithm 1. The pseudocode of proposed robust IGDT | |
| 1: | Input new energy output and load data; |
| 2: | for do |
| 3: | Establishing an SVG siting and operation planning model in a deterministic environment; |
| 4: | end for |
| 5: | ; |
| 6: | Initialize and define variables ; |
| 7: | for do |
| 8: | Establish a robust IGDT based SVG siting and operation planning using Equation (23); |
| 9: | end for |
| 10: | Solving a robust IGDT model to obtain SVG siting and operation planning under uncertain new energy output scenarios; |
4. Simulation and Discussion
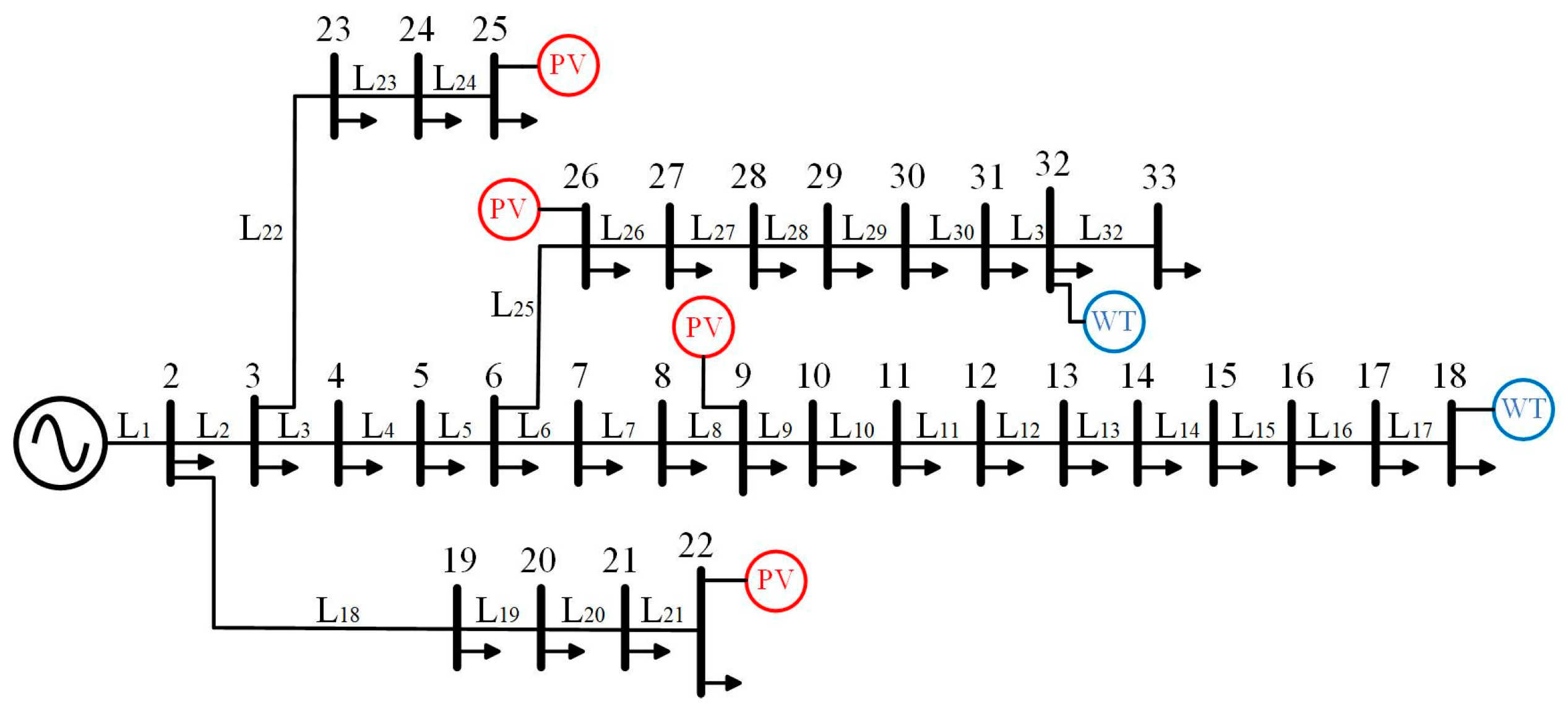
4.1. Parameter Settings
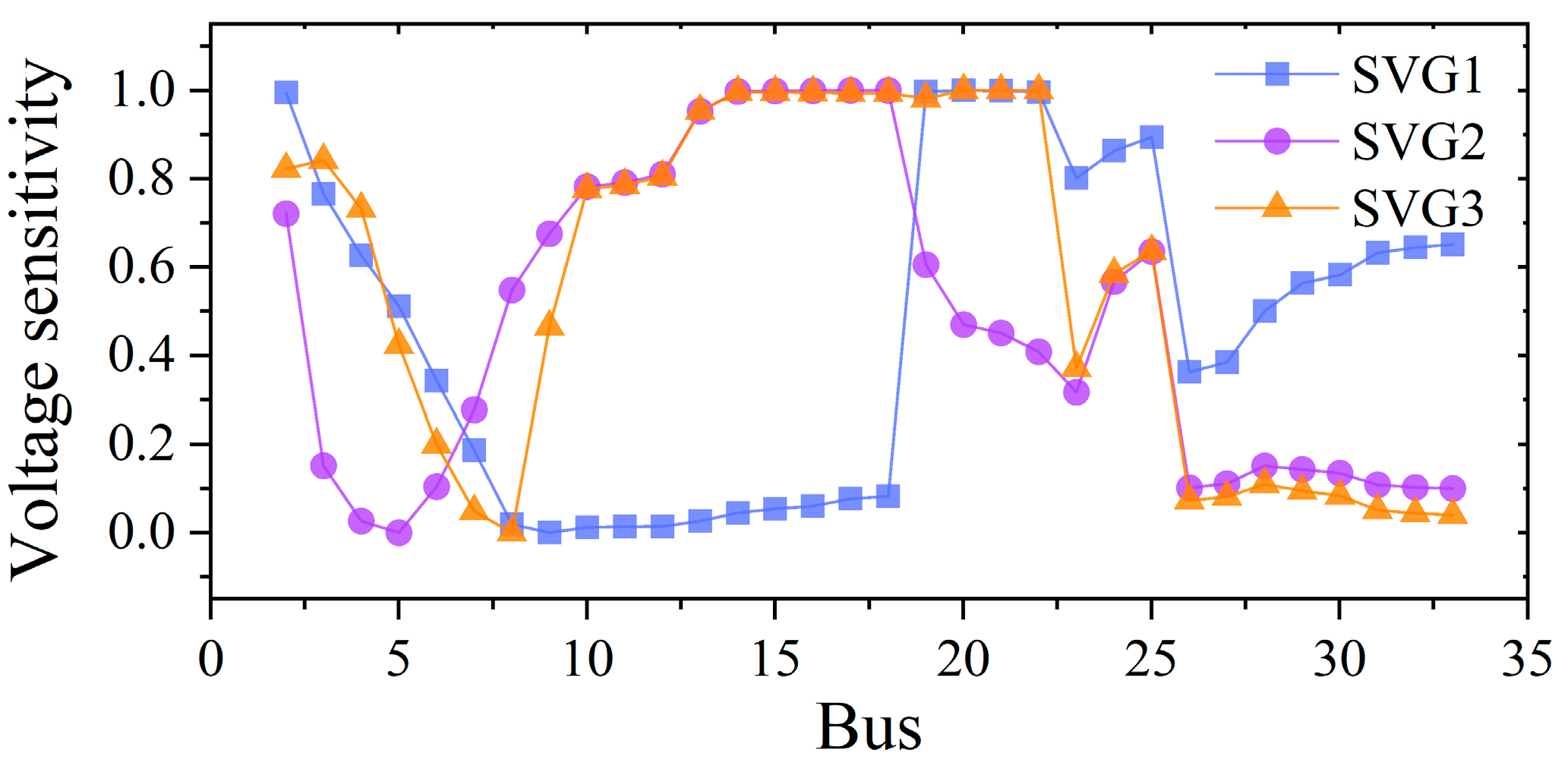
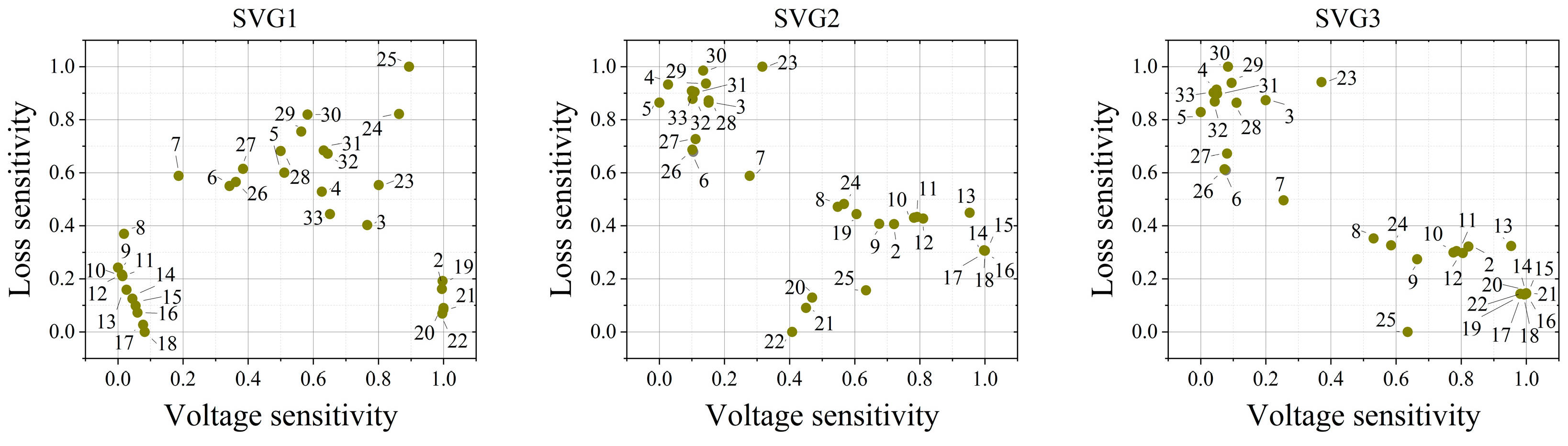
4.2. The Influence of Voltage–Loss Sensitivity Siting Strategy on SVG Siting and Operation Planning
4.3. Optimization for SVG Siting and Operation Under Different Renewable and Load Scales in the Future
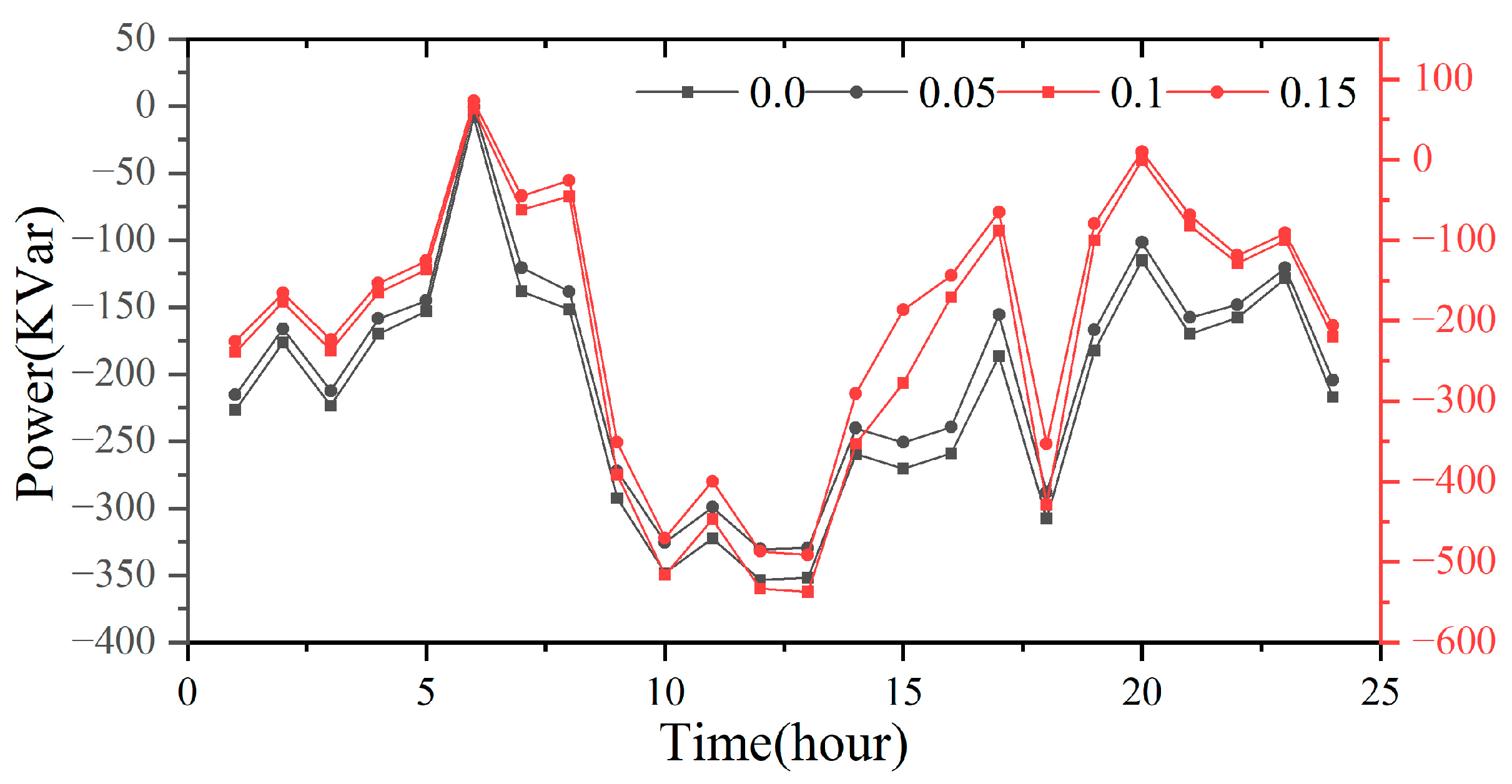
4.4. Optimization for SVG Siting and Operation Under Different Risk Preferences
5. Conclusions
- (1)
- In this paper, considering the possible renewable energy scale in the distribution network in the future and the load growth rate, the scenarios of reactive compensation equipment under different ratios of the two are established, and the siting and operation strategy of SVG under the corresponding scenarios is given.
- (2)
- A multi-objective SVG siting planning based on voltage–loss sensitivity is established. Compared with the non-interference power network, the proposed method can reduce the voltage fluctuation and loss of the distribution network by 29.53% and 7.75%, respectively.
- (3)
- The robust IGDT is used to effectively quantify the uncertainty of multiple renewable energy power plants, which solves the problem that the model is difficult to solve due to the uncertainty of multiple renewable energy outputs. The operation schemes of decision-makers in various scenarios are given, which is convenient for decision makers to choose.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | |
| Acronyms | |
| PV | Photovoltaic |
| WT | Wind turbine |
| SVG | Static var generator |
| PDN | Power distribution network |
| IGDT | Information gap decision theory |
| Variables | |
| The voltage change at bus m caused by the power change of the load at bus i at the time of t | |
| Voltage sensitivity weight | |
| Voss sensitivity weight | |
| Time-of-use price | |
| The total load of the distribution network at the moment t | |
| The total active power of WT and PV in the distribution network at the moment t | |
| Predicted value of new energy output | |
| Actual value of new energy output | |
| Uncertainty coefficient of IGDT | |
| The expected deviation coefficient of cost | |
| The reference value of income under deterministic conditions | |
| The number of renewable energy stations | |
References
- Zhang, Y.Q.; Chen, J.J.; Wang, Y.X.; Feng, L. Enhancing resilience of agricultural microgrid through electricity–heat–water based multi-energy hub considering irradiation intensity uncertainty. Renew. Energy 2024, 220, 119739. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Yan, G.; Chen, W.; Xu, B. Clustering and dynamic recognition based auto-reservoir neural network: A wait-and-see approach for short-term park power load forecasting. iScience 2023, 26, 107456. [Google Scholar] [CrossRef] [PubMed]
- Ruan, H.; Gao, H.; Liu, Y.; Wang, L.; Liu, J. Distributed voltage control in active distribution network considering renewable energy: A novel network partitioning method. IEEE Trans. Power Syst. 2020, 35, 4220–4231. [Google Scholar] [CrossRef]
- Brinkel, N.B.G.; Gerritsma, M.K.; AlSkaif, T.A.; Lampropoulos, I.; Van Voorden, A.M.; Fidder, H.A.; Van Srark, W.G.J.H.M. Impact of rapid PV fluctuations on power quality in the low-voltage grid and mitigation strategies using electric vehicles. Int. J. Electr. Power Energy Syst. 2020, 118, 105741. [Google Scholar] [CrossRef]
- Drosos, D.; Kyriakopoulos, G.L.; Arabatzis, G.; Tsotsolas, N. Evaluating customer satisfaction in energy markets using a multicriteria method: The case of electricity market in Greece. Sustainability 2020, 12, 3862. [Google Scholar] [CrossRef]
- Zhou, Z.; Mastoi, M.S.; Wang, D.; Haris, M. Control strategy of DFIG and SVG cooperating to regulate grid voltage of wind power integration point. Electr. Power Syst. Res. 2023, 214, 108862. [Google Scholar] [CrossRef]
- Li, Y.; Gesang, J.; Long, D.; Xu, Z.; Tan, Z.; Huang, Z.; Song, Y.; Chen, Y. Siting and sizing of synchronous compensator based on electromagnetic transient simulation. Energy Rep. 2022, 8, 1350–1357. [Google Scholar] [CrossRef]
- Tian, S.; Jia, Q.; Xue, S.; Shi, L.; Lv, C.; Bu, L.; Zhou, W. Two-layer model of siting and sizing for active power filters and static var generators considering reactive power capability and active power curtailment of DGs. IET Gener. Transm. Distrib. 2022, 16, 2913–2927. [Google Scholar] [CrossRef]
- Xue, S.; Zeng, S.; Jia, Q.; Hu, X.; Luo, P.; Liang, J. Collaborative Optimization Allocation of Grid-Forming and Grid-Following Reactive Power Resources Considering Auxiliary Equipment Services. IEEE Access 2023, 11, 95840–95857. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Pitakaso, R. Multi-objective optimization design of sustainable biofuel network with integrated fuzzy analytic hierarchy process. Expert Syst. Appl. 2024, 240, 122586. [Google Scholar] [CrossRef]
- Zhou, X.; Tan, W.; Sun, Y.; Huang, T.; Yang, C. Multi-objective optimization and decision making for integrated energy system using STA and fuzzy TOPSIS. Expert Syst. Appl. 2024, 240, 122539. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Q.; Zhang, B. What kinds of building energy-saving retrofit projects should be preferred? Efficiency evaluation with three-stage data envelopment analysis (DEA). Renew. Sustain. Energy Rev. 2022, 161, 112392. [Google Scholar] [CrossRef]
- Banadkouki, M.R.Z. Selection of strategies to improve energy efficiency in industry: A hybrid approach using entropy weight method and fuzzy TOPSIS. Energy 2023, 279, 128070. [Google Scholar] [CrossRef]
- Wang, C.; Shuai, J.; Ding, L.; Lu, Y.; Chen, J. Comprehensive benefit evaluation of solar PV projects based on multi-criteria decision grey relation projection method: Evidence from 5 counties in China. Energy 2022, 238, 121654. [Google Scholar] [CrossRef]
- Mohseni, S.; Brent, A.C. Quantifying the effects of forecast uncertainty on the role of different battery technologies in grid-connected solar photovoltaic/wind/micro-hydro micro-grids: An optimal planning study. J. Energy Storage 2022, 51, 104412. [Google Scholar] [CrossRef]
- Fan, W.; Changyuan, W.; Jiekang, W.; Huiling, T.; Chen, L. Collaborative management of multi-type energy for optimal control of voltage and loss of distribution systems with DGs and SVCs. Electr. Power Compon. Syst. 2022, 50, 194–205. [Google Scholar] [CrossRef]
- Wang, M.; Liao, K.; Yang, J.; Zheng, S.; Lu, D. Three-stage robust voltage/var optimal control of wind farms at multiple time scales. IET Renew. Power Gener. 2022, 16, 594–606. [Google Scholar] [CrossRef]
- Li, J.Y.; Chen, J.J.; Wang, Y.X.; Chen, W.G. Combining multi-step reconfiguration with many-objective reduction as iterative bi-level scheduling for stochastic distribution network. Energy 2024, 290, 130198. [Google Scholar] [CrossRef]
- Ding, T.; Liu, S.; Yuan, W.; Bie, Z.; Zeng, B. A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks. IEEE Trans. Sustain. Energy 2015, 7, 301–311. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, Q.; Jiao, L. Optimum exploitation of multiple energy system using IGDT approach and risk aversion strategy and considering compressed air storage with solar energy. Energy 2024, 291, 130369. [Google Scholar] [CrossRef]
- Wang, Y.X.; Chen, J.J.; Zhao, Y.L.; Xu, B.Y. Incorporate robust optimization and demand defense for optimal planning of shared rental energy storage in multi-user industrial park. Energy 2024, 301, 131721. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, J.; Wu, P.; Zhang, L.; Wu, Q. Dynamic particle swarm optimizer with escaping prey for solving constrained non-convex and piecewise optimization problems. Expert Syst. Appl. 2017, 86, 208–223. [Google Scholar] [CrossRef]
- Téllez, A.Á.; López, G.; Isaac, I.; González, J.W. Optimal reactive power compensation in electrical distribution systems with distributed resources. Review. Heliyon 2018, 4, e00746. [Google Scholar] [CrossRef] [PubMed]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Seljom, P.; Madsen, H.; Fischer, D.; Korpås, M. Long-term electricity load forecasting: Current and future trends. Util. Policy 2019, 58, 102–119. [Google Scholar] [CrossRef]
- Wang, J.; Gao, J.; Wei, D. Electric load prediction based on a novel combined interval forecasting system. Appl. Energy 2022, 322, 119420. [Google Scholar] [CrossRef]

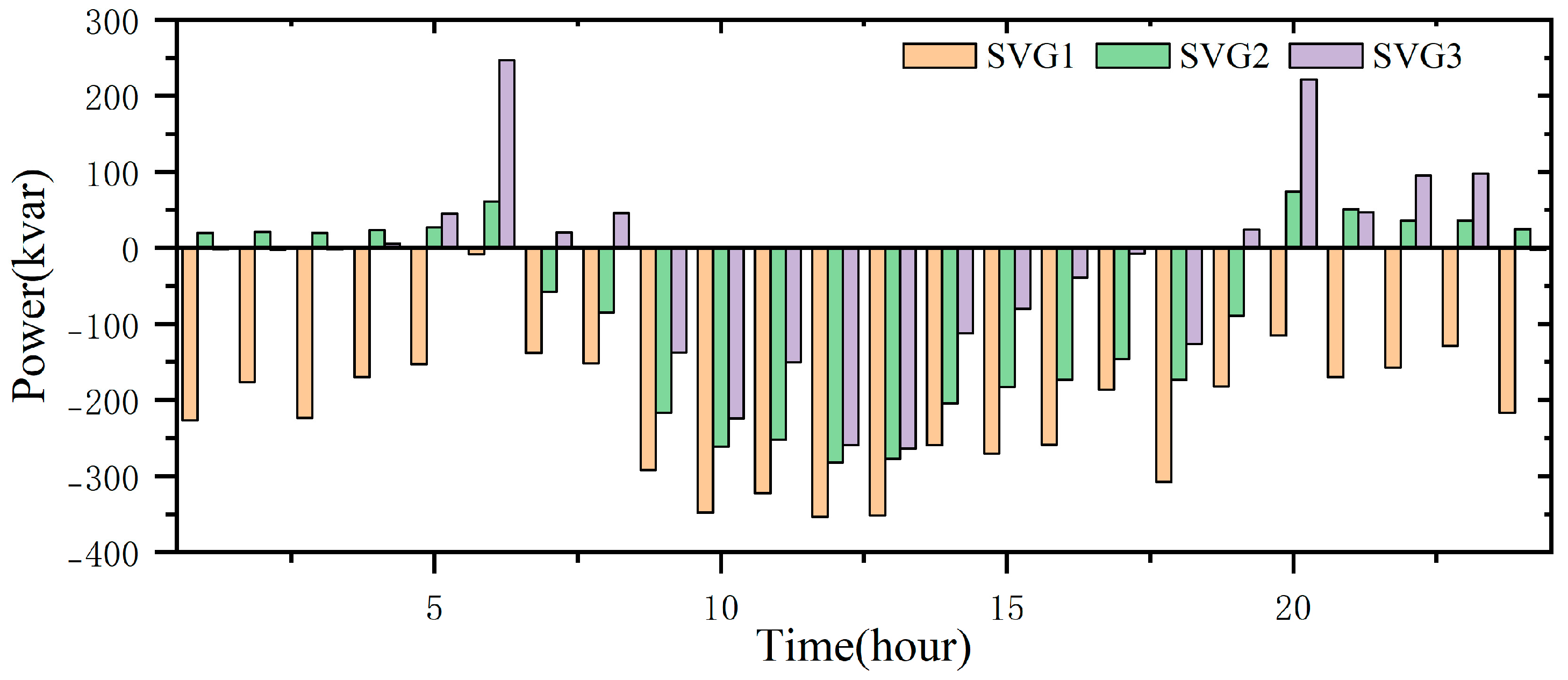
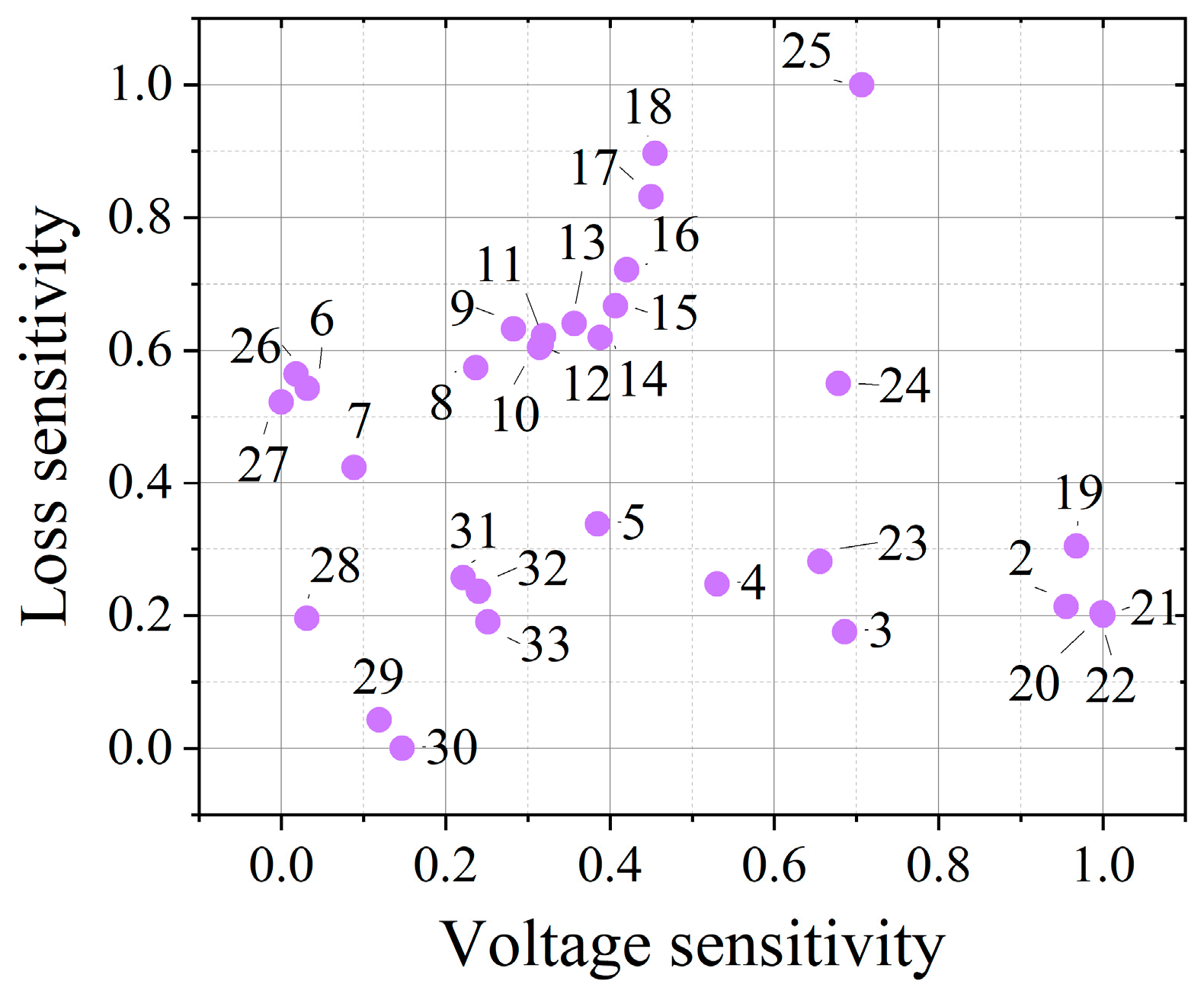
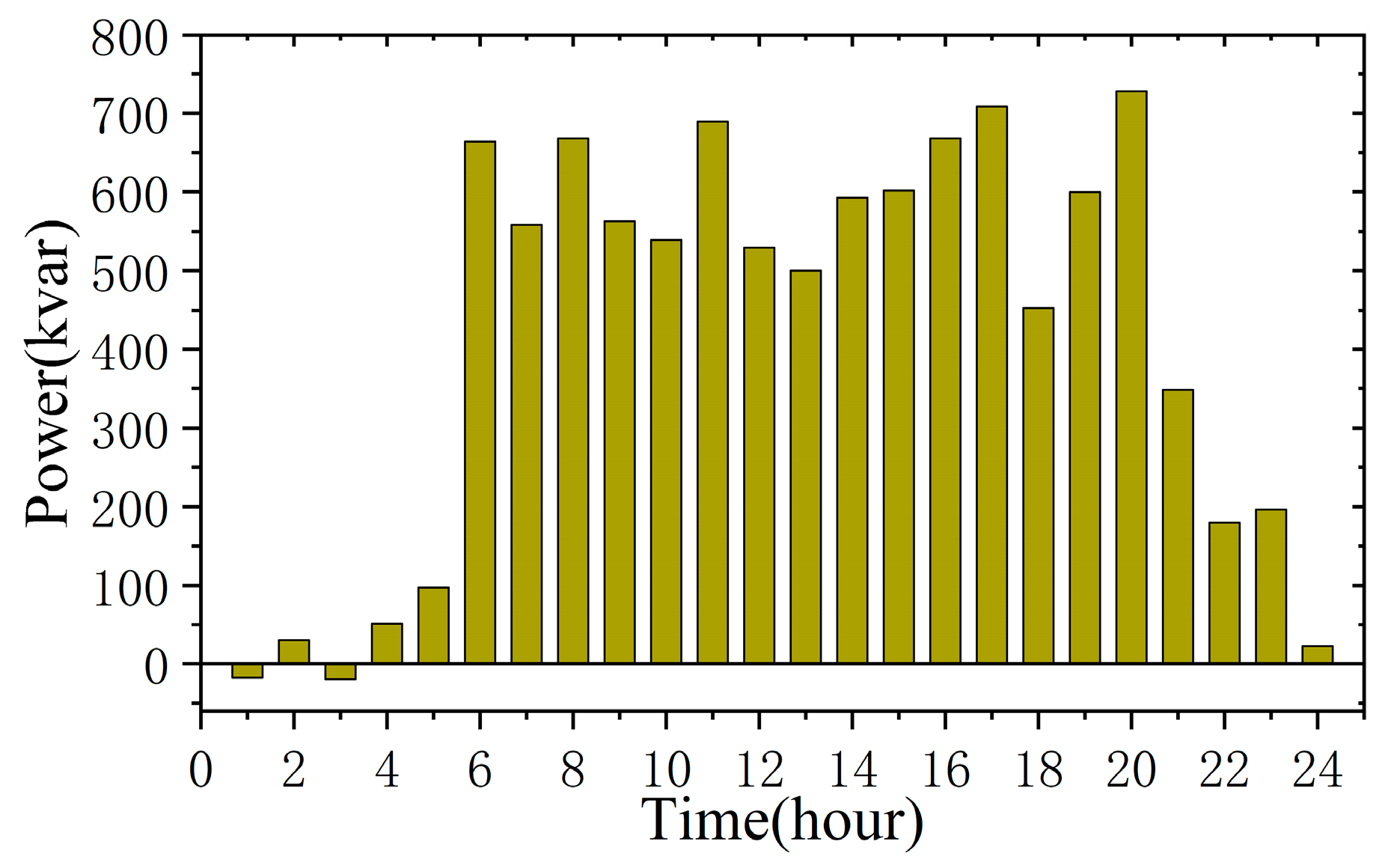
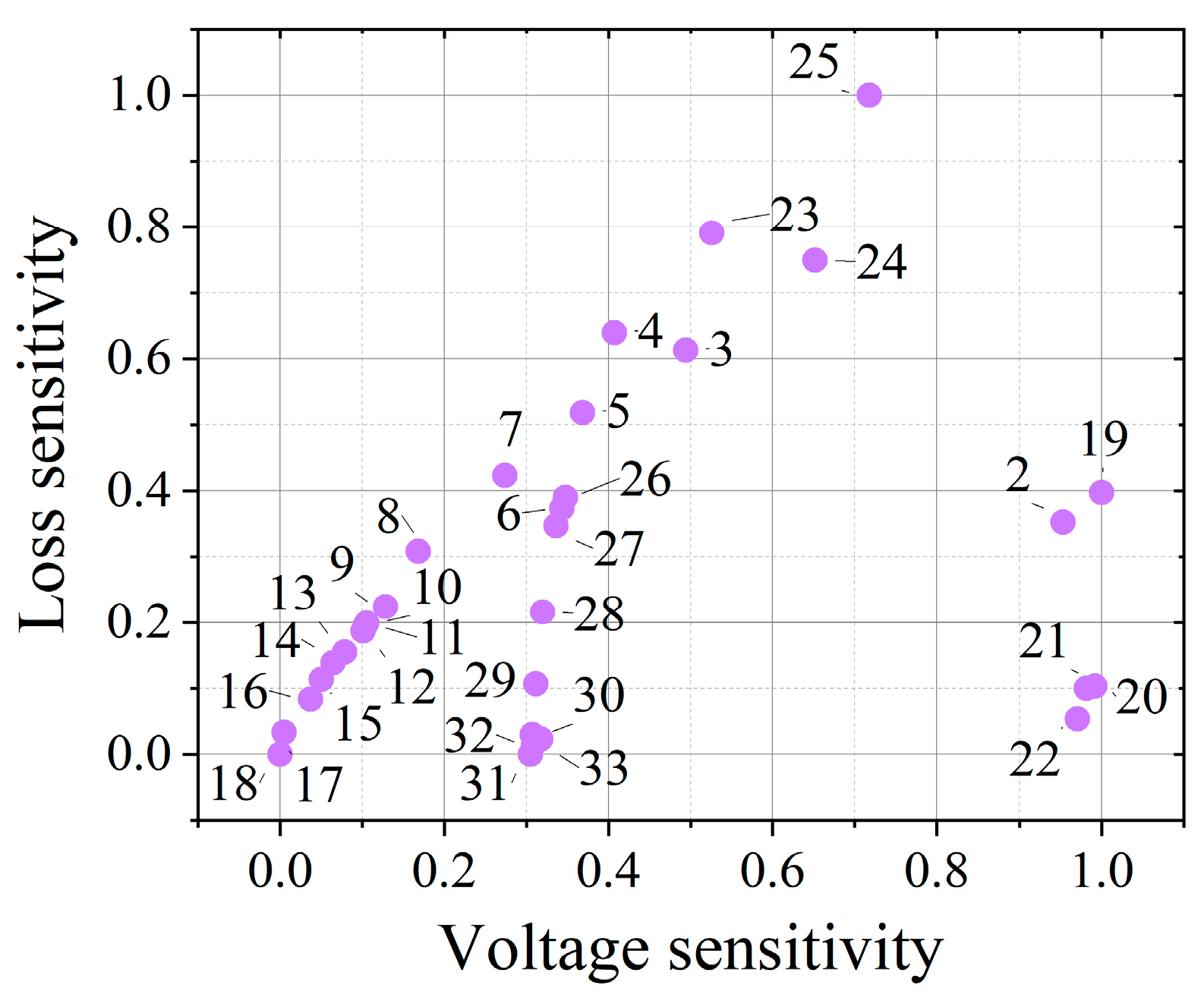

| SVG1 | SVG2 | SVG3 | ||
|---|---|---|---|---|
| Siting bus | 18 | 22 | 26 | |
| Sensitivity coefficient | Voltage | 0.5745 | 0.5281 | 0.5057 |
| Loss | 0.4255 | 0.4719 | 0.4943 | |
| No SVG | Voltage Sensitivity | Loss Sensitivity | Voltage–loss Sensitivity | ||
|---|---|---|---|---|---|
| Access position | SVG 1 | × | 9 | 18 | 18 |
| SVG 1 | × | 5 | 32 | 22 | |
| SVG 1 | × | 8 | 25 | 26 | |
| Voltage p.u. (10−2) | Maximum | 1.243 | 1.142 | 3.535 | 1.322 |
| Minimum | 0.045 | 0.046 | 0.041 | 0.043 | |
| Mean | 0.982 | 0.440 | 1.463 | 0.692 | |
| Loss p.u. (10−2) | Mean | 0.723 | 0.763 | 0.553 | 0.667 |
| Bus | Load (kW/kvar) | Bus | Load (kW/kvar) | Bus | Load (kW/kvar) |
|---|---|---|---|---|---|
| 1 | 0/0 | 12 | 60/35 | 23 | 90/50 |
| 2 | 100/60 | 13 | 60/35 | 24 | 420/200 |
| 3 | 90/40 | 14 | 120/80 | 25 | 420/200 |
| 4 | 120/80 | 15 | 60/10 | 26 | 60/25 |
| 5 | 60/30 | 16 | 60/20 | 27 | 60/25 |
| 6 | 60/20 | 17 | 60/20 | 28 | 60/20 |
| 7 | 200/100 | 18 | 90/40 | 29 | 120/70 |
| 8 | 200/100 | 19 | 90/40 | 30 | 200/600 |
| 9 | 60/20 | 20 | 90/40 | 31 | 150/70 |
| 10 | 60/20 | 21 | 90/40 | 32 | 210/100 |
| 11 | 45/30 | 22 | 90/40 | 33 | 60/40 |
| 0.0 | 0.05 | 0.1 | 0.15 | |
| Risk factor | 0.0 | 0.013 | 0.026 | 0.039 |
| Siting bus | 18 | 18 | 32 | 32 |
| Average voltage deviation | 0.863 | 0.882 | 0.872 | 0.879 |
| Power loss | 0.787 | 0.732 | 0.745 | 0.794 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Fu, Y.; Li, J.; Chen, J. Optimizing Reactive Compensation for Enhanced Voltage Stability in Renewable-Integrated Stochastic Distribution Networks. Processes 2025, 13, 303. https://doi.org/10.3390/pr13020303
Guo Y, Fu Y, Li J, Chen J. Optimizing Reactive Compensation for Enhanced Voltage Stability in Renewable-Integrated Stochastic Distribution Networks. Processes. 2025; 13(2):303. https://doi.org/10.3390/pr13020303
Chicago/Turabian StyleGuo, Yiguo, Yimu Fu, Jingxuan Li, and Jiajia Chen. 2025. "Optimizing Reactive Compensation for Enhanced Voltage Stability in Renewable-Integrated Stochastic Distribution Networks" Processes 13, no. 2: 303. https://doi.org/10.3390/pr13020303
APA StyleGuo, Y., Fu, Y., Li, J., & Chen, J. (2025). Optimizing Reactive Compensation for Enhanced Voltage Stability in Renewable-Integrated Stochastic Distribution Networks. Processes, 13(2), 303. https://doi.org/10.3390/pr13020303






