A Comprehensive Review of Research on Pulsating Beds

Abstract

Despite the recognized potential of pulsating fluidized beds (PFBs), a systematic review that links pulsation parameters to macroscopic enhancements and the underlying microscopic mechanisms is currently lacking. This review addresses this gap by first synthesizing how pulsating airflow can surpass traditional fluidization in reducing the minimum fluidization velocity (Umf), improving bed stability, and precisely regulating bubble dynamics. Furthermore, we demonstrate that the frequency of pulsation influences particle mixing and separation efficiency, while the amplitude of pulsation has a direct effect on heat and mass transfer. Importantly, we identify a critical knowledge gap: there is insufficient understanding of the microscopic interactions—such as inter-particle collision dynamics and local force networks—that underpin these macroscopic phenomena. This work establishes a foundational framework that connects operational parameters to multiscale outcomes, thereby guiding future research toward targeted optimization of PFB systems.

1. Introduction

Traditional fluidized beds are widely used in industrial processes, but their operation is often plagued by issues such as bubble formation and particle agglomeration, which lead to uneven gas-solid contact and consequently affect fluidization quality and heat transfer efficiency. To address this problem, pulsating fluidized beds have been proposed as an improved solution. By introducing controlled periodic disturbances into the fluidizing gas or bed structure, they promote orderly particle movement, effectively suppress flow instability, and thereby enhance system performance. For instance, the study by Hamed et al. [1] demonstrated that under high-frequency pulsating gas flow conditions, the minimum fluidization velocity of silica/alumina particles was significantly reduced compared to traditional fluidized beds. Despite these advances, the interaction between pulsation parameters and particle characteristics remains difficult to quantify precisely, which poses a challenge for the design and optimization of pulsating fluidized beds in complex particle systems. Additionally, Emma et al. [2] conducted an early systematic review of research on pulsating fluidized beds, focusing on the effects of pulsating flow on the fluidization behavior (e.g., minimum fluidization velocity, bed expansion) of different Geldart classification particles. They highlighted the core challenge of the unclear relationship between pulsation frequency and particle characteristics. Subsequently, the review by Maysam et al. [3] systematically compared and evaluated the progress and limitations of both experimental and computational fluid dynamics (CFD) simulation research methods for the first time. They noted that the research trend in this field is shifting from being predominantly experimental to a balanced approach combining experiments and numerical simulations, providing important references for subsequent methodological choices. Against this backdrop, this paper presents a critical summary and comprehensive analysis of the latest advancements in the field of pulsating fluidized beds.

2. Introducing Pulsation into a Fluidized Bed

There are several approaches for introducing pulsation into a fluidized bed. The most common method involves the periodic interruption of fluid or mechanical motion through coordinated control of valves or mechanical structures, thereby generating a pulsating airflow output. Key parameters—such as pulsation frequency, pressure peak, intermittent cycle accuracy, and energy conversion efficiency—must be meticulously controlled within specific ranges. For example, Li et al. [4] employed an electric butterfly valve to produce periodic variations in flow rate, resulting in a pulsating airflow. In this configuration, the electric butterfly valve served as both the opening and closing mechanism. Similarly, A frequency converter was utilized by Zhu to regulate the rotational speed of the motor, this controlled the opening and closing of the butterfly valve to generate pulsating airflow [5]. Moreover, adjustments were made to the airflow meter’s flow valve to ensure effective entry of the pulsating airflow into the fluidized bed. Chen et al. [6] also adopted a motor-driven butterfly valve system wherein each rotation of the device generated two cycles of pulsating airflow. Alternatively, another approach involves designing specialized pulsating airflow distributors such as engineered nozzles or rotating distribution discs that directly create pulsations upon gas entry into the fluidized bed. This method offers significant advantages by enabling integration within the structure of the fluidized bed without necessitating additional driving mechanisms.

3. Pulsation Parameters

In pulsating fluidized beds, the core distinction from traditional fluidized beds lies in the introduction of dynamic gas inlet conditions that are time-dependent. These conditions are defined by a set of pulsation parameters, primarily including pulsation frequency, pulsation amplitude/air distribution ratio, waveform, and base flow gas velocity. These parameters collectively determine the temporal distribution and intensity of the air flow’s energy input, which in turn governs the intra-bed hydrodynamics, heat and mass transfer efficiency, and ultimately, the fluidization quality. Nie and Liu [7] introduced an innovative method based on pressure analysis during the collapse of fluidized beds to investigate their dynamic characteristics. This approach was successfully applied in simulating low-frequency pulsating fluidized beds. The central focus of this research centered around the development of a three-phase mathematical model comprising bubble, emulsion, and wake phases. By measuring the pressure changes occurring during the collapse process, key hydrodynamic parameters were deduced, thereby providing a significant tool and theoretical framework for understanding and quantifying the behavior of pulsating fluidized beds. Furthermore, Ali et al. [8] compellingly demonstrated that pulsation parameters serve as powerful instruments for regulating the performance of nanoparticle fluidized beds. Optimizing these parameters can facilitate multiple targeted objectives such as reducing minimum fluidization velocity, enhancing bed expansion, suppressing non-uniform fluidization, and enabling controlled bubbling.

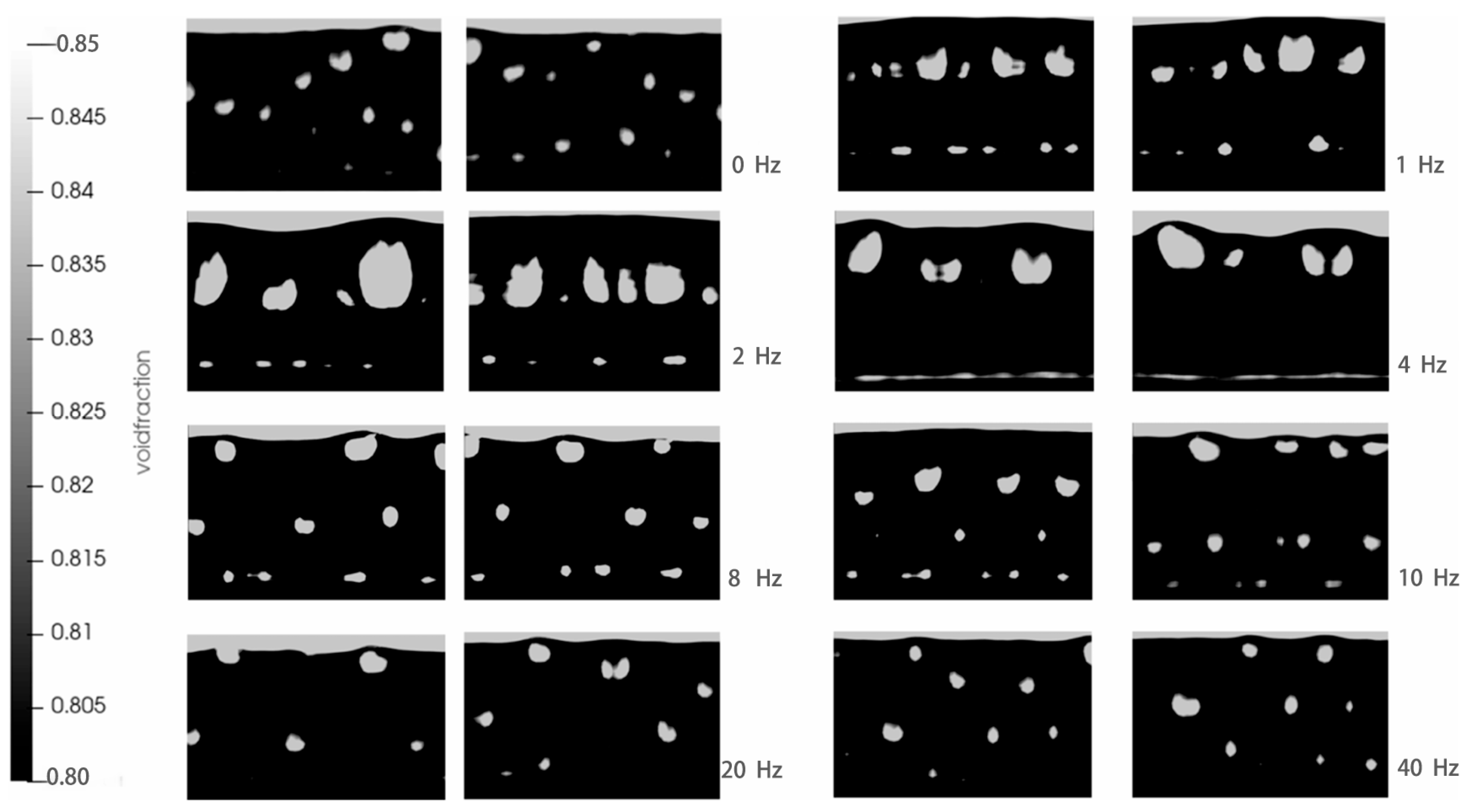
3.1. Pulsation Frequency

The pulsation frequency refers to the number of periodic changes in airflow within a unit time, and it is one of the critical parameters influencing the response behavior of particles/agglomerates. The pulsation frequency dictates the rhythm of energy input. Research by Ali and Asif [9] indicates that for the fluidization of nanopowders, introducing airflow pulsation itself is key to enhancing the process, as it generates instantaneous high shear forces that are central to improving fluidization quality. Within the specified low-frequency range, pulsation frequency does not act as a sensitive parameter, thus providing flexible optimization opportunities for industrial operations. This study strongly supports utilizing airflow pulsation as a simple, efficient, and scalable auxiliary technique for processing highly challenging nanopowder materials.

Bizhaem and Tabrizi [1] conducted an experimental study to systematically investigate the impact of pulsation frequency (1–10 Hz) on the fluid dynamic characteristics of gas-solid pulsed fluidized beds. The study clearly indicated that pulsation frequency serves as a key lever for regulating the performance of pulsed fluidized beds. The effects observed at lower frequencies were found to be more pronounced, leading to significant dynamic changes within the bed; conversely, higher frequency effects were characterized by milder responses, enabling simulations of quasi-continuous flow supplemented by particle vibrations. This approach results in improved fluidization quality, reduced bubble formation, lower startup energy consumption, and substantial enhancements in processing difficult-to-fluidize fine particles. These findings provide essential experimental support for selecting and optimizing operating frequencies in subsequent research efforts.

Some researchers have found that when the pulsation frequency approaches the inherent characteristic frequencies within the bed (such as the natural vibration frequency of agglomerates and the bubble generation frequency), a ‘resonance’ effect may occur. This phenomenon enables optimal fluidization with minimal energy input. The complexity of the inherent frequency in pulsating fluidized beds arises from their multiphase flow nature. It cannot be calculated directly using simple formulas, but rather represents a comprehensive reflection of operating conditions, particle characteristics, and bed structure. To understand its physical essence, one classical theoretical model simplifies the system into a damped mass-spring system; under this model, the undamped natural frequency $f_n$ of the system can be expressed as:

$$f_n={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}$$

(1)

The core challenge of this expression lies in the accurate quantification of the equivalent stiffness $k$ and the equivalent mass $m$. In practical applications, it is exceedingly difficult to use this formula for precise calculations. However, it provides a valuable theoretical framework for understanding the influencing factors. Furthermore, there exists a theoretical estimation method based on a mass-spring model, through which researchers have developed several semi-empirical formulas for preliminary approximations. A widely recognized rule indicates that the system’s dimensionless natural frequency $f_n\sqrt{H_0/g}$ typically stabilizes within a specific range (e.g., 0.4 to 0.8). Consequently, the natural frequency can be approximately estimated as follows:

$$f_n\approx \left(0.4~0.8\right)\times {\displaystyle \frac{\sqrt{\raisebox{1ex}{$g$}\!\left/ \!\raisebox{-1ex}{$H_0$}\right.}}{2\pi }}$$

(2)

The parameter $H_0$ represents the height of the stationary bed, while $g$ denotes the acceleration due to gravity. This equation clearly indicates that the height of the bed is one of the primary factors determining the natural frequency; as the bed height increases, inertia becomes larger and consequently, the natural frequency decreases. Due to limitations inherent in theoretical models, determining natural frequency through experimental signal analysis has emerged as one of the most reliable and widely accepted methods. The core focus lies in analyzing the dynamic response of the bed under perturbations. In engineering practice, it is recommended to initially estimate theoretical values to establish a preliminary range, followed by precise calibration through experimental measurements. Finally, fine-tuning optimizations should be conducted near the determined natural frequency to maximize the effectiveness of pulsating fluidized bed processes. Barletta et al. [10] conducted an analysis using Bode plots in conjunction with an elastic continuum model to clarify the quantitative relationship between the resonance frequency of vibrating fluidized beds, bed height, and wave speed. The equation $f_{\mathrm{n}} = (2n + 1)c/4H$ illustrates this relationship. Additionally, it was confirmed that the wave speed could be accurately predicted by Roy et al. [11] pseudo-homogeneous model, providing a crucial basis for both theoretical calculations and experimental identifications of resonance frequencies. Li et al. [12] established a model based on the theory of spring oscillators, successfully controlling the prediction error of the natural frequency within 15% by simultaneously considering particle characteristics and bed height. Their research reveals that resonant operation not only maximizes amplitude but also leads to an increase in system damping and a decrease in quality factor, resulting in accelerated energy dissipation and elevated energy consumption. Moreover, this operation is highly sensitive to minor variations in parameters, posing risks of operational instability and increased equipment wear.

In his work, Dong Liang [13] pointed out that introducing pulsating air flow into a separation fluidized bed revealed a significant influence of air pulsation frequency on the bed density of a dense-phase pulsating fluidized bed. Based on the relationship between bed density fluctuation and air pulsation frequency, the frequency was categorized into three ranges: a low-frequency range, f ∈ (0, 2.5], a medium-frequency range, f ∈ (2.5, 4.1], and a high-frequency range, f ∈ (4.1, +∞]. In the low-frequency range, both the air-on and air-off durations are relatively long, leading to intense bed fluctuations and maximum density variation. Within the medium-frequency range, the bed density gradually increases from top to bottom, with relatively small density fluctuations, making it suitable for the gravity separation of coal. In the high-frequency range, the density of the middle layer in the fluidized bed becomes significantly greater than that of the upper and lower layers, resulting in a density distribution characteristic unsuitable for coal separation. The optimal operational range for the air velocity ratio is N ∈ [1.1, 1.3], and the optimal operational range for the air pulsation frequency is f ∈ [3.5, 4.5]. The research conducted by Dong et al. [14] clearly demonstrates that in a pulsating fluidized bed, the pulsation frequency is a crucial parameter characterized by distinct partition effects. An optimal mid-frequency window for achieving effective separation exists, ranging from approximately 2.5 to 4.1 Hz. Additionally, the full potential of the pulsation effect is strongly dependent on the operational gas velocity; optimal synergy with pulsation can only be attained at moderate to low gas velocities (N ≈ 1.2). This work provides significant theoretical guidance and experimental evidence for precisely optimizing pulsation parameters in industrial separation processes, thereby maximizing bed stability and process efficiency.

The study conducted by Liu et al. [15] focuses on the utilization of pulsating fluidized beds to process particles with high moisture content, a wide particle size distribution, and a tendency to agglomerate (such as lignite and biomass). Through both experimental investigations and theoretical modeling, the research elucidates the critical role of pulsation frequency (1–6 Hz) in mitigating particle agglomeration and promoting particle separation. Furthermore, it introduces the innovative concept of “critical bubble number” to optimize frequency selection. The findings clearly indicate that for easily agglomerating wet particles with a broad size distribution, pulsation frequency serves as a crucial operational parameter. Low frequencies (1–3 Hz) are advantageous for generating large bubbles that disrupt strong cohesive forces; meanwhile, utilizing the “critical bubble number” model allows for identifying an optimal theoretical frequency tailored to specific materials, thus achieving optimal prevention of agglomeration and promotion of separation. This approach transcends simple empirical judgments regarding high, medium, or low frequencies and provides robust theoretical and experimental support for precise design and operational optimization of pulsating fluidized beds.

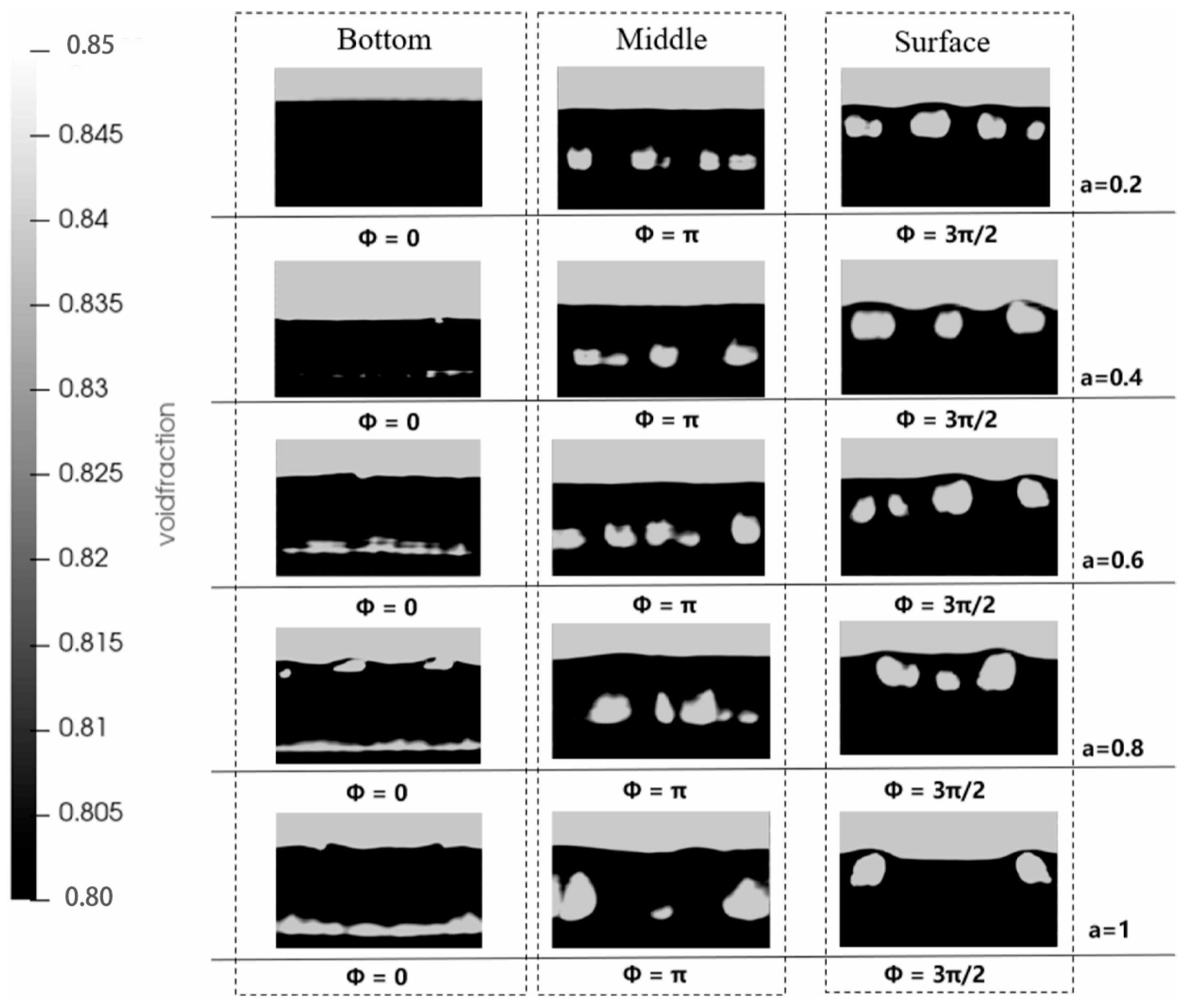
3.2. Pulsation Amplitude and Air Distribution Ratio

Pulsation amplitude (or the associated air distribution ratio) determines the intensity of a single pulsation, i.e., the “mechanical impulse” imparted by the gas flow onto the bed. The amplitude is directly related to the pulsations in drag force and the turbulent kinetic energy acting on the particles/agglomerates. A larger amplitude implies stronger shear forces, which are more conducive to breaking stable force chains and disrupting large agglomerates. If the pulsation amplitude is too small, it may be insufficient to overcome the cohesive forces between particles, failing to effectively disrupt channels and slugs, thereby limiting the improvement in fluidization. Conversely, if the pulsation amplitude is moderate or large, it can provide sufficient energy to break up agglomerates and disrupt bubbles, significantly enhancing fluidization uniformity. Wang and Rhodes [16] conducted a simulation study of pulsating fluidized beds using the discrete element method. This research primarily highlights the critical roles played by pulsation amplitude and baseline gas velocity in facilitating the transition from chaotic to ordered states, as well as in the formation of regular bubble patterns. The study elucidates, at a microscopic level, how these parameters influence bed structure. The DEM simulations provided mechanistic validation that pulsation amplitude and air distribution ratio are core parameters that function synergistically. To achieve a regular fluidization state, two conditions must be satisfied:

• Suitable base airflow: It is essential to precisely control the base airflow within the homogeneous fluidization region, approaching the minimum fluidization velocity, in order to create initial conditions conducive to the generation of regular bubbles.
• Optimized Pulsation Amplitude: Building upon this foundation, an adequately large yet non-excessive pulsation amplitude is applied to effectively drive the periodic formation of channel-like structures, thereby “seeding” a regular sequence of bubbles. This provides crucial theoretical guidance for the precise regulation of airflow combinations in practical applications, aimed at achieving specific fluidization patterns (such as orderly bubbling to enhance reaction selectivity).

Ma in his study on nanoparticles, observed that “as the air distribution ratio increases, more agglomerates move upward, shifting the center of gravity of the agglomerates within the bed higher.” [17]. This indicates that increasing the peak air velocity of the pulsation can effectively enhance bed expansion and promote particle circulation. This provides crucial guidance for accurately adjusting the air supply ratio in practical operations to achieve effective particle circulation.

3.3. Waveform

The waveform describes the functional form of how the air velocity changes with time over a single pulsation cycle (e.g., square wave, sine wave, triangular wave). Different waveforms represent distinct methods of energy application. A square wave delivers the maximum energy instantaneously, resulting in a strong impact effect, whereas a sine wave provides a smooth transition with a relatively gentler action. Current research primarily focuses on square and sine waves. The square wave is more widely used, largely because it generally demonstrates superior performance in breaking up agglomerates and promoting mixing. However, for fragile or easily abraded materials, the gentler sine wave may be more appropriate. In a pulsating fluidized bed, the waveform of the airflow (such as a sine wave) is intricately coupled with the mechanical response of the particle bed due to its continuous variation characteristics, leading to a regular bubble arrangement pattern. This phenomenon not only presents opportunities for optimizing the structure of fluidized beds but also serves as an ideal benchmark for validating multiphase flow models. The alternating nucleation mechanism of bubbles under sine wave conditions underscores the critical role of the dynamic equilibrium between particle frictional stress and gas pulsation in pattern formation [18]. Systematic studies on the influence of waveform are relatively scarce, representing a valuable direction for future in-depth investigation.

3.4. Base Flow Gas Velocity

The base flow gas velocity is the minimum or average gas velocity within the pulsating gas flow, which determines the fundamental fluidization state of the bed. It sets the “background” fluidization level. If the base flow gas velocity is lower than the minimum fluidization velocity, the bed may revert to a fixed-bed state during the pulsation intervals. If the base flow gas velocity is close to or slightly above the minimum fluidization velocity, the effect of the pulsating airflow is to “add refinement to an already good situation,” further optimizing the system on top of the background fluidization. The base flow gas velocity needs to be optimized synergistically with the pulsation amplitude and frequency. A common strategy is to use a lower base flow gas velocity combined with moderate pulsation parameters to achieve high-quality fluidization under energy-efficient and highly effective conditions. In a pulsating fluidized bed, the base flow gas velocity and the pulsation frequency jointly determine the quality of fluidization and drying efficiency. A reasonable matching of these two factors can achieve efficient operation at lower gas velocities, particularly when the operating frequency approaches the system’s inherent frequency (approximately 0.75–1.5 Hz). Under conditions where $U<U_{mf}$, comparable drying performance to that of traditional fluidized beds can still be attained, showcasing significant energy-saving potential [19]. In pulsating fluidized bed drying, a notable synergistic effect exists between base flow gas velocity and pulsing operations. Pulsation not only allows effective drying at lower average gas velocities but also serves as an alternative to conventional high initial gas velocity strategies, thereby enhancing both energy efficiency and uniformity in drying. Additionally, pulsing operations significantly improve particulate mixing states—preventing agglomeration and channeling—and bring the drying process closer to ideal gas-solid contact condition [20]. Chang et al. [21] conducted separation experiments on binary solid mixtures within a pulse fluidized bed, clearly revealing key interactions between apparent gas velocity and pulsing operations affecting separation behavior. The core findings provide important insights into understanding the role of base flow gas velocity in pulsating fluidized beds: In pulse-fluidized systems, base flow gas velocity ($U_g$) is not only a fundamental parameter for maintaining bed fluidization but also acts as a “regulating valve” that determines whether pulsation energy can be effectively utilized to enhance processes such as separation. An optimal window for base flow gas velocity exists relative to the minimum bubbling velocity ($U_{mb}$), being close but not excessively higher than $U_{mb}$. Within this window, the beneficial effects of pulsing parameters—such as frequency and amplitude—can be fully realized, leading to process intensification.

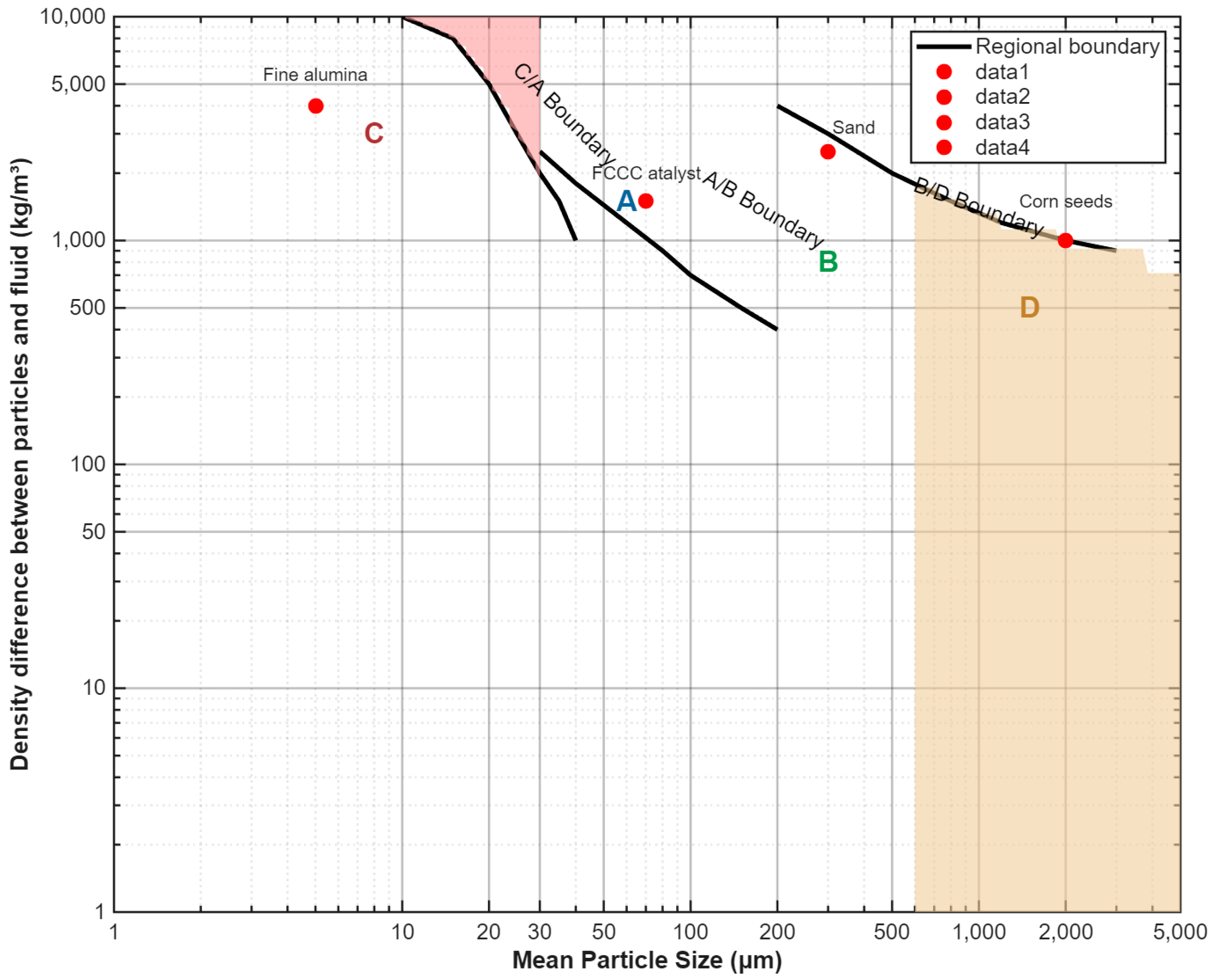
3.5. Particle Size

In a pulsating fluidized bed, particle size is a critical parameter influencing the fluidization characteristics and the efficacy of pulsation effects. For coarse particles (Geldart Group D), pulsation primarily serves to disturb the bed layer, disrupt fixed flow patterns, and enhance mixing. However, the greatest advantage of pulsating fluidization technology lies in its ability to handle difficult-to-fluidize fine powders and ultrafine powders (Geldart Groups C and A/C). These types of particles, typically less than 100 μm in size, are prone to channeling and agglomeration under conventional fluidization due to strong interparticle forces such as van der Waals forces, resulting in poor gas-solid contact efficiency [22]. Figure 1 effectively illustrates Geldart’s classification scheme.

After the introduction of gas pulsation, periodic peaks in gas velocity can exert instantaneous and powerful shear forces, effectively fragmenting the initial agglomerate network and breaking stable channel flows. During phases of lower gas velocities, partial collapse of the bed facilitates particle rearrangement and mixing. This cyclical process of “breaking” and “rebuilding” enables powders that are originally highly cohesive due to their small size to achieve uniform and stable fluidization. As particle sizes diminish to micro- or nano-scale levels, interparticle forces (such as van der Waals forces) increasingly dominate fluidization behavior, leading to pronounced agglomeration and channel flow phenomena. Fluidization of nanoparticles is fundamentally about the fluidization of agglomerates with sizes on the order of hundreds of micrometers [23]. Nanoparticles achieve fluidization through the formation of multi-level agglomerates, which can be categorized into Aggregated Particle Flow (APF) and Aggregate Bed Flow (ABF) modes [24]. The size of these agglomerates is closely related to their fluidization behavior (APF/ABF), providing a means for classifying different types of fluidization processes [23]. To improve the quality of fluidization, it is often necessary to introduce external auxiliary fields. Agglomerate sizes can be estimated using various methods such as image analysis, R-Z equations, and force balance models [23,24]. Understanding the interplay between particle size and interparticle forces is crucial for achieving efficient fluidization applications involving fine powders and nanoparticles [24].

3.6. Flow Patterns of Pulsating Fluidized Bed

In a pulsed fluidized bed system, in addition to the two core parameters of pulse amplitude and frequency, the resulting flow patterns represent another critical evaluation criterion that must be discussed in detail. Pulsation does not merely enhance mixing; rather, it fundamentally alters the hydrodynamic structure within the bed, creating distinct flow patterns. These patterns directly influence the contact efficiency between particles and fluids, as well as heat and mass transfer rates, ultimately affecting process outcomes. Ali et al. [25] investigated three different exhaust strategies through bed collapse experiments. These strategies essentially correspond to various pulsed flow patterns: Single Drainage (SD), Dual Drainage (DD), and Modified Dual Drainage (MDD).

• In the SD mode, residual gases are expelled solely from the top of the bed. This phenomenon results in a dominant upward drag force that delays the collapse of the bed and facilitates the accumulation of fine particles in the upper region, thereby exacerbating size segregation among agglomerates.
• In the DD mode, gas can be discharged simultaneously from both the top and bottom, which reduces airflow resistance and accelerates the collapse rate of the bed. However, due to the presence of initial flow peaks, a pronounced phenomenon of agglomerate layering still occurs, with agglomerate sizes in the lower region being significantly larger than those in the middle and upper regions.
• The MDD pattern utilizes a four-way valve to redirect the inlet gas flow to the atmosphere during collapse, thereby eliminating initial flow spikes and significantly suppressing the size-based separation of agglomerates. Under this pattern, bed collapse occurs more rapidly and smoothly. Frequency domain analysis reveals a substantial reduction in pressure fluctuation amplitude, indicating an enhancement in bed stability.

Research indicates that the MDD mode effectively enhances the fluidization quality of ultrafine particles in a pulsating fluidized bed by optimizing airflow paths and employing multidirectional exhaust strategies. This finding underscores the pivotal role of pulsating mode design in regulating the uniformity and dynamic behavior of fluidized beds.

As elucidated by Brandani [26,27,28] and his collaborators from the University of Edinburgh in their theoretical models and experimental studies, there are distinct critical conditions governing the transitions between these flow regimes. The work of Asif et al. [29,30,31,32] further illustrates, through experimental visualization and data analysis, the dynamic evolution process across various combinations of pulsation parameters, transitioning from unidirectional flow to bidirectional flow, and ultimately leading to complex turbulent patterns. Therefore, when defining and optimizing the operational parameters of a pulsating fluidized bed, it is essential to consider the target flow regime as a core design criterion since it serves as a vital link between operational parameters and system performance.

4. Research Progress

4.1. Hydrodynamics

4.1.1. Granule

The behavior of particles in a pulsating fluidized bed is influenced by several factors, including gravity, buoyancy, and drag force. When equilibrium of forces is disrupted, the particles transition into a fluidized state. Li et al. [4] investigated the fluidization characteristics of Geldart A and Geldart B within a pulsating fluidized bed. Their findings demonstrated that Geldart A achieve Minimum fluidization velocity at lower frequencies compared to their Geldart B counterparts, with a significantly reduced value for the Minimum fluidization velocity. Consequently, Geldart A exhibit superior performance in terms of fluidization relative to Geldart B.

Saidi et al. [33] experimentally investigated the enhancement mechanisms of separation efficiency in binary particle fluidized beds subjected to pulsating airflow. The results indicated that pulsating fluidization significantly improved both the separation efficiency and rate by increasing peak gas velocity, eliminating dead zones, and mitigating channeling effects within the bed. Notably, the pure pulsation mode achieved the most substantial improvement in separation efficiency under fixed flow conditions, thereby validating the effective regulation of particle flow characteristics through pulsating airflow. Zhang performed a simulation analysis on the separation of two-component particles in a pulsating fluidized bed based on the two-fluid model [34]. The simulation outcomes demonstrated an excellent correlation with experimental data reported by Saidi et al. [33]. Furthermore, Particle separation behavior under continuous and pulsating airflow conditions in fluidized beds was compared by Zhang [34]. They concluded that pulsating airflow markedly enhances particle separation efficiency; however, an increase in particle size tends to diminish this separating effect.

However, the rapid advancement of nanotechnology has necessitated a deeper understanding of the physical characteristics of nanoparticles. Nanoparticles exhibit significant application potential across multiple cutting-edge fields due to their unique physical and chemical properties. However, because of strong interparticle cohesive forces, such as van der Waals forces, they do not fluidize as individual particles but rather as larger agglomerates during the fluidization process. This often leads to abnormal fluidization phenomena like channeling and slugging, which limits the full utilization of their excellent physicochemical properties and the efficiency of large-scale processing. To overcome this challenge, pulsating gas flow has been introduced as an effective assisted fluidization technique. By imparting periodic energy input to the gas flow, it can significantly improve the fluidization quality of nanoparticle agglomerates. To deeply reveal the mechanism of pulsating gas flow, researchers have developed advanced numerical models. For instance, Ma Zhikai [17] stated in their work: “First, considering the simultaneous aggregation and breakage processes of nanoparticle agglomerates within the fluidized bed... comparisons between simulation results and experimental data validated the model’s accuracy.” This study employed a method combining the Eulerian-Eulerian Two-Fluid Model with the Population Balance Model (PBM), and improved the aggregation and breakage kernel functions specifically for nanoparticle characteristics, providing a reliable tool for quantitatively studying the dynamic evolution of agglomerates. The same study, by comparing normal gas inflow with pulsating gas inflow, clarified the advantages of pulsating flow. The results indicated: “Under normal gas inflow, agglomerates are densely packed at the bottom of the fluidized bed... Pulsating gas inflow weakened both these correlations.” This demonstrates that pulsating gas flow not only enhances intra-bed mixing, thereby mitigating wall effects and agglomerate segregation, but also alters the coupling relationship between agglomerate size and local hydrodynamic parameters (such as turbulent dissipation rate), thus promoting a more uniform and stable fluidization state.

The work by Du et al. [35] (2023) systematically revealed the nonlinear evolution of the flow characteristics of alumina powder as the particle size decreased from the micron scale (27 μm) to the nanoscale (30 nm), demonstrating a transition from “particle-dominated” to “agglomerate-dominated” behavior. The study indicated that nano-powders, due to extremely strong interparticle forces, exhibit very high compressibility (with a compressibility index as high as 110.36%) and very low packing density, resulting in extremely poor static flowability. However, dynamic flow energy tests showed that the fluidization energy required for nano-powders was actually lower, highlighting the complexity of their flowability assessment: low density promotes flow, while strong cohesive forces inhibit it. The interplay of these factors results in a non-linear relationship between flowability and particle size. This research provided crucial insights into the fundamental properties explaining the root cause of channeling, slugging, and other non-uniform phenomena frequently observed in pulsating fluidized beds involving nanoparticles. It underscores that the successful application of any external field-assisted fluidization technique, such as pulsating fluidization, must overcome these unique and often contradictory flow characteristics inherent to nanoparticles.

The study by Ali et al. [36] (2023), while emphasizing the importance of gas inlet strategies in pulsating fluidized beds for nano-powders and proposing a Modified Dual-Drainage (MDD) strategy to suppress the initial flow spike, leaves the general applicability of its conclusions in question. The validation was conducted only at two extremely low frequencies (0.05 and 0.25 Hz), which is hardly representative of the broader frequency ranges potentially employed in practical industrial operations. Their results clearly indicated that the advantages of the MDD strategy diminish at higher frequencies, highlighting the limitations of this approach under different operating conditions, rather than presenting a universal solution. Furthermore, although the study confirmed that MDD improves bed homogeneity, the investigation into the underlying microscopic mechanisms—such as the specific dynamics of agglomerate breakage—remains insufficient, relying overly on the analysis of macroscopic pressure signals. Consequently, this study primarily elucidates when and under which conditions the MDD strategy is effective, without fully resolving the complex interplay between pulsation parameters and particle characteristics. It serves as a reminder to subsequent researchers that while optimizing the gas inlet configuration is crucial, it must be considered synergistically with pulsation parameters, and its effectiveness is highly dependent on the specific operational window.

4.1.2. Pressure Drop and the Minimum Fluidization Velocity

The relationship between bed pressure drop and superficial velocity in fixed beds and during the initial fluidization stage is often theoretically grounded in the Ergun equation. This equation clearly elucidates the physical reality that pressure drop arises from the combined contributions of viscous losses and inertial losses. It not only successfully predicts flow resistance in fixed beds but also provides a theoretical basis for determining the minimum fluidization velocity ($U_{mf}$) through the force balance criterion. As such, it serves as a core theoretical model for analyzing the transition from a fixed bed to a fluidized bed in gas-solid two-phase flow [37,38], The complete form of the Ergun equation is given as follows:

$${\displaystyle \frac{\Delta P}{\Delta L}}={\displaystyle \frac{150\mu {(1-ϵ)}^2}{D_p^2{ϵ}^3}}U+{\displaystyle \frac{1.75p_f(1-ϵ)}{D_p{ϵ}^3}}{U}^2$$

(3)

In Equation (1): $\Delta P$ is the pressure difference across the material layer, $Pa$; $\Delta L$ is the height of the material layer, $\mathrm{m}$; $ϵ$ is the bed voidage; $\mu$ is the dynamic viscosity of the gas flow, $\mathrm{P}\mathrm{a}·\mathrm{s}$; $U$ is the superficial velocity of the gas flow through the packed bed, $\mathrm{m}/\mathrm{s}$; $D_p$ is the average particle diameter, $\mathrm{m}$; $p_f$ is the density of the gas flow, $\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$.

It has been consistently observed that, in comparison to traditional fluidized beds, the implementation of pulsating airflow can significantly reduce the Minimum fluidization velocity ($U_{mf}$) and alleviate pressure drop fluctuations within the fluidized bed. For instance, Hamed et al. [1] conducted a study on the hydrodynamics of pulsating fluidized beds using three types of particles with average diameters of 196 μm for silica, 95 μm for alumina, and 10 μm for alumina. A square wave with a pulsation frequency ranging from 1 Hz to 10 Hz was employed to generate the pulsating airflow. The results indicated that as the pulsation frequency increased, the bed pressure drop rose progressively until it reached its maximum value at the highest pulsation frequency. At this point, the average pressure drop approached that of continuous airflow. Under conditions of high-frequency pulsating airflow, the Minimum fluidization velocity of silica/alumina particles was found to be significantly lower than that observed in traditional fluidized beds. The results indicate that as the pulsation frequency increases, the pressure drop across the bed progressively rises until it reaches its peak value at the maximum pulsation frequency, where the average pressure drop approximates that observed in continuous airflow. Under high-frequency pulsating airflow conditions, the Minimum fluidization velocity of silica/alumina particles is significantly lower than that observed in traditional fluidized beds. Both ordinary and pulsating fluidized beds were simulated using the Euler-Euler method by Su [39]. Their findings demonstrate that pulsating airflow facilitates a more rapid achievement of fluidization compared to conventional fluidized beds, thereby leading to a reduction in Minimum fluidization velocity. However, within pulsating airflow contexts, continuous variations in airflow are more beneficial for accelerating the fluidization process. Specifically, a rectangular wave decreases the fluidization time by approximately 0.5 s, while a sawtooth wave further accelerates this process by an additional 1.5 s. Furthermore, Li et al. [40] established that for Geldart A, the Minimum fluidization velocity reaches its lowest value (5.68 cm/s) at a pulsation frequency of 3.49 Hz; conversely, Geldart B necessitate a higher frequency (5.24 Hz) to attain stable fluidization (10.0 cm/s).

Additionally, Dong et al. [41] experimentally demonstrated that the introduction of pulsating airflow to induce forced oscillations in a conventional fluidized bed leads to an enhancement in collisions and friction among heavy particles, a reduction in interlocking effects between particles, and a decrease or even complete elimination of peak pressure drops within the bed during critical fluidization conditions. This phenomenon significantly contributes to improving the overall quality of fluidization within the fluidized bed. During their experiments, when the duration of pulsating airflow was set at 200 m/s with an interval of 200 m/s, it resulted in smaller fluctuations in pressure drop and markedly improved stability of pressure drop compared to traditional fluidized beds. Such findings are critically important for achieving uniform and stable quasi-dispersed fluidized beds. Under experimental conditions, density stability measured at the center point of the pulsating fluidized bed was considerably greater than that observed for traditional systems; moreover, at equivalent levels of fluidization number, the pulsating system could sustain a lower-density layer within the bed. Furthermore, That under stable airflow conditions, fluctuations in pressure drop across the fluidized bed predominantly arise from bubble dynamics was found by Su [39]. However, under resonance frequency scenarios, both pronounced influences from pulsating airflows and bubble movement behavior contribute to variations in pressure fluctuations. The fluctuation patterns observed for pressure drops within these systems result from a complex interplay involving factors such as gas velocity, bubble behavior, and alterations in bed height making it inherently complicated phenomena to analyze. Consequently, reliable predictions concerning fluctuations in pressure drop across fluidized beds cannot be solely derived through analysis limited exclusively to bubble behavior present within such systems.

4.1.3. Characteristics of Bubbles

Bubbles are commonly observed in most fluidized beds. As airflows through the spaces between particles, local coalescence occurs, leading to bubble formation. While bubbles can decrease the surface area of gas solid contact, they may also facilitate particle mixing. The characteristics of the particles employed and the processing conditions will influence both the size of the generated bubbles and whether pulsation is advantageous or detrimental to the process, which ultimately depends on the specific application involved.

To enhance gas-solid contact, it is often essential to modify bubble size. Huang et al. [42] conducted a two-dimensional cold-state simulation experiment to investigate the characteristics of bubbles in fluidized beds. They employed a camera to capture the instantaneous flow state of gas and solid within the fluidized bed, analyzing images to compare bubble sizes between pulsating and traditional fluidized beds. Furthermore, they examined the effects of pulsation parameters and material properties on both the average rising speed and size of bubbles. Experimental findings indicated that bubble sizes in pulsating fluidized beds were smaller than those observed in continuous fluidized beds. The presence of pulsating airflow can inhibit bubble growth and diminish surging occurrences. In non-material sand beds, such airflow is more prone to forming larger bubbles within the bed. Moreover, in pulsating fluidized beds, there exists a tendency for the average rising speed of bubbles to decrease as pulsation frequency increases. For mustard seed beds, the relationship between the average rising speed of bubbles, bubble size, and gas velocity is:

$$v_b=0.7197\left(v-v_{mf}\right)+6.530\sqrt{g{d}_b}-1.256$$

(4)

In the formula, v represents the gas velocity (m/s), $v_b$ is the bubble rising velocity (m/s), $v_{mf}$ is the initial fluidization velocity (m/s), $g$ is the gravitational acceleration ($\mathrm{m}/{\mathrm{s}}^2$), and $d_b$ is the average bubble diameter at the bed height H (mm).

Compared with traditional fluidized bed, pulsating fluidized beds exhibit; superior control over bubble size. Li et al. [40] employed a high-speed dynamic camera to perform statistical and image analysis on the evolution of bubbles in a two-dimensional pulsed gas-solid fluidized bed. The results demonstrated that as the fluctuation frequency increased, the expansion height of the bubbles grew, their adhesion to the bed wall diminished, the leading diameter and rising velocity decreased, and the degree of bubble deformation became more pronounced; these trends were particularly evident for Geldart A particles. These findings suggest that high-density pulsating gas-solid fluidized beds can effectively integrate gas and solid phases, thereby generating uniform and stable mixtures. A lower aspect ratio (approaching spherical) reduces the likelihood of bubble coalescence into large slugs, enhancing the uniformity of bed density distribution. Although bubbles with a low aspect ratio possess a relatively smaller surface area, the pulsating disturbances enhance the surface renewal rate, compensating for the reduced area and promoting gas-solid mass transfer. Spherical bubbles (aspect ratio ≈ 1) ascend at a slower rate, extending the contact time between reactants and catalyst particles, which improves reaction conversion efficiency.

Compared to traditional fluidized beds, pulsating fluidized beds offer superior control over bubble size. Li et al. [40] employed a high-speed dynamic camera to conduct statistical and image analysis on the evolution of bubbles in a two-dimensional pulsed gas-solid fluidized bed. The results demonstrated that as the fluctuation frequency increased, the expansion height of the bubbles grew, their adhesion to the bed wall diminished, while both the leading diameter and rising velocity decreased; furthermore, the degree of bubble deformation became more pronounced. These trends were particularly evident for Geldart A. These findings indicate that high-density pulsating gas-solid fluidized beds can effectively integrate gas and solid phases, thereby producing uniform and stable mixtures. A lower aspect ratio (approaching spherical) reduces the likelihood of bubble coalescence into large slugs, which enhances the uniformity of bed density distribution. Although bubbles with a low aspect ratio possess a relatively smaller surface area, pulsating disturbances increase the rate of surface renewal—this compensates for reduced surface area while promoting gas-solid mass transfer. Spherical bubbles (with an aspect ratio close to 1) ascend at a slower rate, which extends contact time between reactants and catalyst particles, consequently improving reaction conversion efficiency.

The behavior of bubbles in a pulsating fluidized bed is influenced by multiple factors. Jia et al. [43] conducted a systematic investigation into the effects of operational parameters, including pulse frequency, amplitude, and bed structure, on bubble dynamics within pulsating fluidized beds. The experimental findings indicate that the formation or bursting of bubbles was not directly correlated with pulse frequency. However, when the pulse frequency approached the natural frequency of the bed, resonance between the pulsating airflow and the system facilitated the generation of organized bubbles (Figure 2). Furthermore, modulating the pulse amplitude effectively constrained bubble growth; specifically, a pulse amplitude within an intermediate range of 0.4u_mf to 0.8u_mf promoted an orderly distribution of bubbles (Figure 3).

4.2. Bed Layer Expansion and Falling Bed Phenomenon

Bed expansion can be observed in both pulsating fluidized beds and conventional fluidized beds. The bed expansion ratio (the maximum bed height divided by the static bed height) is a function of the pulsating gas velocity. Due to the formation and collapse of bubbles at the surface of fluidized beds, accurately measuring bed expansion poses significant challenges. Wan found that, under the same gas velocity, the bed expansion ratio in a pulsating fluidized bed is higher than that in a conventional fluidized bed [44].

The bed expansion ratio is a characteristic feature of flow instability in an aggregative Fluidized Bed. Its formation mechanism is attributed to the intense energy fluctuations that occur when bubbles burst or break at the surface of the bed. As a crucial parameter for characterizing the fluidization state, the bed expansion ratio effectively reflects the intensity of particle movement within the bed. From the perspective of fluidization engineering, a larger bed expansion ratio typically signifies significant bubble coalescence and breakage within the system, which may lead to reduced gas-solid contact efficiency and compromised fluidization uniformity. Consequently, a higher bed expansion ratio indicates lower gas-solid contact efficiency and inferior fluidization quality in the fluidized bed, providing an essential quantitative basis for optimizing its operational parameters. Hu et al. [45] conducted a comparative simulation study using the Euler-Euler method to analyze stable gas inlet and sawtooth waveform pulsating gas inlet in fluidized beds, with a focus on bed expansion ratio and bed expansion rate as research parameters. The results indicated that the variation in bed height over time showed significant fluctuations and instability under stable gas inlet conditions, whereas under sawtooth waveform pulsating gas inlet conditions, the bed expansion exhibited a linear growth trend, indicating a gradual increase in expansion degree. This behavior contributes to an enhancement in fluidization quality.

In traditional steady-state fluidization, nanoparticles are prone to forming channels and cracks, leading to gas short-circuiting that results in bed instability. During the gas shut-off phase (such as low-frequency pulsation), the bed has sufficient time for complete settling, resulting in a dense structure that hinders re-fluidization. This phenomenon is known as bed collapse. However, pulsation demonstrates a significant inhibiting effect on bed collapse. For instance, Ali et al. [8] proposed in his study that gas pulsation can effectively mitigate the occurrence of falling bed phenomenon in nanoparticle fluidized beds through the following mechanisms:

• To shorten the settlement time of the bed layer and prevent complete collapse;
• Enhanced particle movement and bed elasticity, while maintaining partial expansion;
• Third item. Significantly reduce the minimum fluidization velocity and enhance the quality of fluidization at low gas velocities;
• It is particularly suited for nanoparticles that exhibit high cohesion and a tendency to aggregate, such as hydrophilic ABF-type particles.

4.3. Mixing and Segregation

Most industrial fluidized bed depend heavily on effective particle mixing; thus, particle mixing represents a significant area of research. Investigations into pulsating fluidization frequently highlight that, under identical gas-solid ratio conditions, the mixing time associated with pulsating fluidization is shorter than that observed in continuous fluidized beds. For instance, Li et al. [46] conducted experimental studies to evaluate the mixing effects of two different particle systems—one with identical densities but varying sizes and another with similar sizes but differing densities—within a pulsating-assisted fluidized bed. They compared these results to those obtained from conventional fluidized beds. The authors noted that for the two-component system featuring particles of the same density, the mixing index during pulsating-assisted fluidization was marginally superior to that observed in conventional fluidization. While there was an enhancement of the buoyant component at the top of the bed, overall bed mixing remained relatively uniform. The influence of pulse width ratio on mixing effectiveness appeared minimal; conversely, for the two-component particle system distinguished by varying densities, they found that the particle mixing index in pulsating-assisted conditions was somewhat lower than in traditional configurations. Notably, separation by density occurred at both ends—the top and bottom—of the bed. The impact of pulsating airflow on particle mixing remains ambiguous; indeed, during actual operations, a given particle system may either exhibit rapid and thorough mixing or experience instantaneous separation.

Huang et al. [47] conducted cold-state simulation experiments to investigate the mixing characteristics of a pulsating fluidized bed using materials such as millet, silica gel, and mung beans as experimental particles. The findings indicated that for particles with significant differences in particle size or density, the pulsating gas fluidized bed had a minimal effect on the mixing of various particles. It was only at relatively high pulsating airflow velocities (e.g., u = 1.26 m/s) that an improved degree of particle mixing was observed. Within a certain range, higher pulsating frequencies were more favorable for mixing; beyond this frequency range, however, separation became more pronounced. For particles exhibiting minor differences in size or density, increased gas velocity facilitated more uniform mixing. Conversely, under these conditions, higher pulsating frequencies contributed more effectively to particle separation. In cases involving particles with similar sizes or densities, variations in frequency had minimal impact on material mixing outcomes. For equal-density particles specifically, greater gas velocities resulted in enhanced uniformity of the mix. Hu further explored the mixing characteristics of a pulsating fluidized bed by employing silica gel of varying particle sizes alongside glass beads of consistent diameter and millet as experimental materials [48]. Their results reaffirmed that within an equal-density system at constant frequency conditions: a larger pulse width ratio between two-component particles yielded superior mixing efficacy; conversely, in non-equal-density systems under identical pulse width ratios—higher frequencies correlated with improved mixing effectiveness; likewise noted was that under identical open intervals—a lower frequency produced better overall mixing results.

Computational fluid dynamics software was employed to analyze the movement behavior of particles in a rectangular wave pulsating fluidized bed by Peng [49] focusing on both equal-density systems (silica gels with varying particle sizes) and unequal-density systems (glass beads and millet of identical particle size). They utilized the Eulerian two-fluid model for numerical simulations. Their findings were consistent; however, Peng [49] further investigated the pulsating airflow at resonant frequency and discovered that, in comparison to high and low frequencies, the resonant frequency more effectively facilitated the fluidization and mixing of both types of particles. This led to a more uniform average particle size distribution along the height of the bed and contributed to a stable mixing process.

Yang et al. [50] developed a three-dimensional hybrid pulsating fluidized bed model that integrates computational fluid dynamics with the discrete element method to investigate the fluidization and mixing behaviors of green bean particles under four distinct pulsating inlet air velocities of 1, 2, 4, and 8 Hz. The simulation results demonstrated that the pulsating fluidized bed significantly improved the mixing of green bean particles. Notably, axial mixing was found to be more pronounced than radial mixing, with the smallest standard deviation value of particle distribution observed at a frequency of 4 Hz. When the frequency of the inlet gas velocity approached the natural vibrational frequency of the particles, bed expansion was most evident, exhibiting characteristics akin to “resonance.” At a frequency of 2 Hz, both radial and axial mixing effects were optimized for particle behavior. Frequencies that deviated from this optimal range either too high or too low did not show significant enhancements in fluidization performance. Simulation studies have indicated that pulsating airflow at resonant frequencies can induce more uniform particle distributions while markedly improving their mixing indices.

4.4. Heat Transfer and Mass Transfer

In a pulsating fluidized bed, the motion state of particles can be regarded as the superposition of translational, vibrational and rotational motions. Pulsating fluidized beds enhance heat transfer efficiency by increasing the gas-solid contact area and improving flow dynamics. Wang Xiangyou et al. [51] discovered that at specific pulsating airflow velocities, materials in rotational motion exhibited superior heat transfer performance compared to those in vibrational motion, while the impact of pulsation frequency on temperature distribution was relatively minor. Various factors influence heat transfer efficiency. Liu et al. [52] developed a horizontal tube bundle pulsating-assisted fluidized bed to investigate heat transfer within brown coal particles. Their findings demonstrated that the introduction of pulsating airflow could improve the heat transfer rate by 50% to 100% at maximum levels. As the velocity of the pulsating gas increased, so did its effect on enhancing heat transfer rates; notably, 3 Hz and 5 Hz pulsating airflows outperformed 1 Hz flows in terms of heat transfer efficacy.

The pulsation frequency plays a crucial role in determining the heat transfer efficiency of a pulsating fluidized bed. Emily et al. [53] conducted a computational study on the heat transfer performance of submerged tubes within a pulsating fluidized bed, employing the Eulerian-Eulerian method. Their findings indicated that at lower pulsation frequency, the bubbling behavior within the fluidized bed exhibited greater orderliness, resulting in more uniform heat transfer efficiency across all tubes. Conversely, an increase in pulsation frequency was observed to induce fluctuations in the heat transfer efficiency of the fluidized bed.

Research on drying characteristics in a pulsating fluidized bed was conducted by Guo [54]. The author observed that at a lower pulsating gas velocity, a low-frequency pulsating airflow of 0.25 Hz was suitable for heat and mass transfer within the fluidized bed, while at a higher pulsating gas velocity, a high-frequency pulsating airflow of 3.3 Hz was more suitable. Moreover, the addition of pulsating airflow enhanced heat and mass transfer between the gas and solid phases, but the advantage weakened when the frequency increased to a certain level. Summarizing the observations made by the authors, in terms of gas inlet ratio, the size of the gas inlet ratio has a certain influence. When the gas velocity is small, the pulsating gas velocity should be increased, while when the flow rate is large, the stable airflow should be maintained near the Minimum fluidization velocity rate. However, Wang constructed a CFD-DEM parallel numerical simulation method and platform for gas-solid systems and studied a quasi-two-dimensional hybrid pulsating fluidized bed [55]. The authors found that at the particle scale, when the pulsating frequency approaches the natural main frequency of the bed pressure fluctuation, it promotes the internal circulation movement between particles, enhances heat transfer, and thereby improves the drying efficiency.

Guo conducted a study on the drying characteristics in a pulsating fluidized bed [54]. The author observed that at lower pulsating gas velocity, a low-frequency pulsating airflow of 0.25 Hz was optimal for heat and mass transfer within the fluidized bed. Conversely, at higher pulsating gas velocity, a high-frequency pulsating airflow of 3.3 Hz proved to be more effective. Furthermore, the introduction of pulsating airflow significantly enhanced heat and mass transfer between the gas and solid phases; however, this benefit diminished when the frequency exceeded a certain threshold. In summarizing their observations regarding the influence of gas inlet ratio, it was found that varying sizes of the gas inlet ratio have discernible effects on performance. Specifically, when the gas velocity is low, an increase in pulsating gas velocity is advisable; Whereas, when the flow rate becomes significant, it is essential to maintain a stable airflow at or above the minimum fluidization wind speed. Moreover, Wang developed a parallel numerical simulation method and platform utilizing CFD-DEM for analyzing gas-solid systems while investigating a quasi-two-dimensional hybrid pulsating fluidized bed [55]. Her findings revealed that at the particle scale level, when the pulsating frequency approaches the natural dominant frequency associated with bed pressure fluctuations, internal circulation movement among particles is promoted. This enhancement leads to improved heat transfer efficiency and subsequently increases drying efficiency.

4.5. Comparison of Main Numerical Models for Pulsating Fluidized Beds

The complex dynamic behavior of pulsating fluidized beds involves critical microscopic mechanisms such as particle agglomeration, fragmentation, and momentum exchange between the gas-solid phases. Currently, no single model can perfectly simulate phenomena across all scales; the main models exhibit significant differences in core assumptions, applicability, and computational costs.

Table 1. A Specialized Comparison of Three Mainstream Models.

Comparison Criteria	CFD-DEM	Eulerian-Granular	PBM-Coupled
Core Philosophy and Scale	Micro/meso: Fluid as a continuous phase (Euler), tracking the motion of each particle individually (Lagrangian).	Macro perspective: Both fluid and particulate phases are regarded as mutually permeable continuous media	Mesoscopic/Macroscopic: Within the framework of Euler or Euler-Lagrange, we introduce a statistical evolution of particle size distribution.
The Applicability of Pulsating Flow	The method is highly suitable for directly analyzing the transient response of a single particle under periodic external forces, as well as the processes of formation and disintegration of particle aggregates.	The method demonstrates high computational efficiency; however, its resolution is limited. It is capable of capturing the overall periodic expansion and collapse of the bed layers but struggles to directly elucidate the micro-dynamics of particle agglomeration.	Core value lies in describing the dynamic evolution of particle size distribution over time/space under pulsating conditions (e.g., fine powder coalescence leading to increased average particle size).
Key Model Assumptions and Differences	Collision Model: Specify the restitution coefficient and friction coefficient, which are crucial for energy dissipation. Cohesive force model: The accuracy of the liquid bridge and van der Waals force models directly determines the success or failure of aggregation simulations. Momentum exchange (drag force model).	Granular Dynamics Theory: Analogizes particle collisions to gas molecular motion, introducing “granular temperature. Solid-phase constitutive relation: Empirical closure for particle viscosity and pressure. Momentum exchange (towing model)	Aggregation kernel function: Describes the probability of aggregation following particle collisions and represents the main source of uncertainty in the model. Fragmentation kernel: Describes the probability of a cluster fracturing under fluid action and the distribution of its resulting sub-particles. Internal coordinates (usually particle size).
Refine costs	Extremely high	Low	Moderate
Primary Advantages	The physical mechanism is clear and reveals the microscopic principles. Provide detailed particle-scale information (trajectory, force). No need for extensive constitutive assumptions on granular phase behavior.	High computational efficiency, suitable for large-scale engineering calculations. Can effectively predict macro fluidization characteristics (e.g., pressure drop, bed height).	Directly predict key industrial parameter—particle size distribution. Can couple complex particle dynamics processes (growth, aggregation, fragmentation, nucleation)
Min Limitations	Cost constraints make it difficult to simulate full-size devices. Micro parameters (e.g., cohesion) are difficult to measure and calibrate accurately.	Severely reliant on empirical constitutive relationships. The inability to analyze mesoscopic structures such as particle aggregation may result in the loss of key features of fluidized beds.	The aggregation/breaking kernel function is highly empirical and lacks universality. Typically, transient in-formation at the particle scale is not provided.

provides a specialized comparison of three mainstream models.

High-speed imaging and particle tracking technology represent the most direct tools for revealing microscopic dynamics [56]. Through the use of high-speed cameras, one can visually capture the processes of bubble generation, movement, merging, and rupture, as well as the evolution of particle agglomeration. By integrating digital image analysis or particle tracking velocimetry methods, it is possible to quantitatively extract instantaneous velocity fields of particles, their temperature distributions, as well as the size and lifetime distributions of aggregates [57]. These data provide direct evidence for validating the dynamic behavior of particles in CFD-DEM and for assessing the validity of coagulation/breakup kernel functions in population balance models (PBM).

Time-resolved particle image velocimetry (TR-PIV) enables non-intrusive measurement of the instantaneous velocity field in a pulsating fluidized bed. This capability is crucial for validating turbulence models of the fluid phase within Eulerian-Granular methods, as well as for assessing predictions of time-varying gas-solid slip velocities across all models [58]. By comparing vorticity fields and instantaneous velocity fluctuations derived from simulations with experimental data, we can evaluate the ability of models to capture dynamic structures of flow fields—such as vortices and jets—that are essential for driving particle mixing and pulsating behavior.

The wall-force sensors of a pulsating fluidized bed exhibit a characteristic feature: the dynamic stress fluctuations generated at the wall interface. High-frequency response wall force sensors and pressure sensors can accurately measure these transient loads. Comparing simulated time-series data of wall stresses against experimental measurements serves as a rigorous validation method with significant engineering practicality. This approach effectively assesses whether the model accurately reproduces the transfer of momentum and energy among particles, as well as the effects of macroscopic pulsating phenomena (such as slugging oscillations) on the walls.

The choice of model depends on the research objectives [7]. If the aim is to elucidate microscopic mechanisms, CFD-DEM is preferred; however, it incurs significant computational costs. In contrast, for reactor-scale design and optimization, Euler-Euler models or models coupled with Population Balance Modeling (PBM) are more practical. The crux of these approaches lies in the precise description and calibration of coalescence/breakage kernel functions. Regardless of the path chosen, integrating the aforementioned experimental techniques for multi-scale and multi-variable validation remains an indispensable part of the process.

5. Engineering Challenges and Scale-Up Considerations

Although the fundamental principles of Pulsed Fluidized Bed (PFB) and successful experimental results on a laboratory scale are quite promising, their application in industrial settings poses a series of unique engineering challenges. Transitioning from a small-scale, highly controllable experimental setup to a large-scale, continuous industrial system necessitates careful consideration of factors that are often negligible at the research scale. This section will discuss the key practical limitations and obstacles to achieving commercialization of PFB technology.

5.1. Energy Consumption and Pulsation Generation

The primary challenge faced in industrial applications is the additional energy input required to generate and sustain these pulsations. In a laboratory setting, the energy needed to drive small speakers or pneumatic valves is negligible. However, when dealing with large equipment that handles substantial quantities of materials, achieving effective and uniform pulsations across extensive distribution panels necessitates a significant amount of power. This unnecessary energy consumption must be justified by commensurately improving process efficiency—such as increasing drying/coating rates and reducing entrapment phenomena—to ensure economic feasibility. Future research should focus on optimizing pulsation parameters (frequency, amplitude, waveform) to achieve minimal energy input while maximizing process benefits, as well as designing highly efficient pulsing generators with low pressure drop [59].

5.2. Actuator and Mechanical System Reliability

The industrial production process typically spans several months or even years. Therefore, the reliability of pulsating generation systems is paramount. Whether utilizing mechanical pistons, high-frequency valves, or acoustic speakers, the driving components are subject to wear and fatigue. A failure in this system can result in a complete shutdown of the production line. Robust engineering design, selection of industrial-grade components, and implementation of redundant systems or easily maintainable modules are essential. It is imperative to establish a maintenance plan for actuators and demonstrate their long-term durability under harsh conditions such as dust exposure, vibrations, and temperature fluctuations [60,61].

5.3. Distributor Design for Uniform Pulsation

In any fluidized bed, the design of the gas distribution plate is crucial [6], and this importance is particularly pronounced in pulsed fluidized beds (PFBs). At a laboratory scale, achieving uniform gas and pulsation distribution is relatively straightforward. However, as the scale increases, ensuring that the pulsation waves distribute uniformly across a cross-section that may extend several meters in diameter presents significant challenges. Non-uniform distribution can lead to dead zones, channeling effects, and inconsistencies in solid handling. The distribution plate must be meticulously designed to withstand periodic stresses generated by pulsations without experiencing fatigue while also maintaining optimal aerodynamic characteristics. This often necessitates complex design trade-offs among pulsing uniformity, pressure drop, and mechanical strength.

5.4. Particle Attrition and Erosion

The introduction of pulsation introduces alternating stresses, which accelerates collisions between particles as well as between particles and the wall surfaces. This phenomenon may lead to particle wear (resulting in fragmentation into fine powders) and erosion of internal components (such as distributors, container walls, and cyclones). Wear can alter the size distribution of the particles, potentially adversely affecting product quality (for instance, in pharmaceutical or catalyst particles) while increasing material loss due to centrifugal effects. Erosion may compromise the structural integrity of equipment, resulting in unplanned downtime and significant maintenance costs. For fragile materials (such as agricultural products or certain crystalline or coated particles), a careful assessment of the aggressiveness associated with pulsating beds is essential. Strategies to mitigate these impacts include optimizing pulsation parameters to achieve smooth fluidization and reduce bubble generation, as well as employing wear-resistant linings in high-impact areas.

5.5. Scale-Up Methodology and Modeling

Unlike traditional fluidized beds, there is currently no comprehensive method for scaling up the packed bed of particles (PFB). Simply increasing the geometric dimensions while maintaining similar pulsation conditions may not yield equivalent hydrodynamic effects. The critical parameters involved in scale-up remain under investigation—should frequency, dimensionless Strouhal number, or minimum fluidization velocity ratio be kept constant? Advanced computational fluid dynamics (CFD) and discrete element models (DEM) serve as powerful tools for predicting the behavior during scale-up; however, they require substantial computational resources and must be validated against large-scale experimental data. Pilot testing at an intermediate scale is highly recommended to mitigate risks associated with full-scale design and to optimize operational parameters [7].

6. Conclusions and Outlooks

Despite extensive literature highlighting the significant potential of pulsated fluidization technology in reducing minimum fluidization velocity, suppressing bubble generation, and enhancing mass transfer, there remain substantial gaps in understanding the underlying microscopic mechanisms and macroscopic regulation principles behind these advantages. Current research primarily focuses on observational phenomena and has yet to provide accurate answers to: (i) How do pulsation parameters quantitatively affect the dynamic balance between particle agglomeration and fragmentation? (ii) What operational windows can achieve global optimization for specific materials? To overcome this bottleneck, future studies must urgently integrate advanced measurement techniques such as high-speed imaging and particle velocity (PV) with high-fidelity computational fluid dynamics-discrete element method (CFD-DEM) numerical simulations. This integration aims to reveal dynamic mechanisms at the particle scale and establish predictive intelligent control models, thereby advancing this technology from experimental advantages towards precise industrial applications. With the rapid development of artificial intelligence, it is imperative that researchers combine machine learning or AI algorithms to create dynamic control systems based on sensor data. By continuously monitoring bed pressure drop, temperature fluctuations, or particle distribution in real-time, these systems could automatically adjust pulsation parameters to maintain stable fluidized states.

Table 2. The Influence of Operating Parameters of the Pulsating Fluidized Bed on System Performance.

Parameters	${\mathit{U}}_{\mathit{m}\mathit{f}}$	Bubble Dynamics	Mixing Quality	Segregation Tendency	Heat Transfer	Energy Cost
Frequency ↑	↓ Then—/↑	Bubble Size ↓ Quantity ↑	↑ Then ↓	↓	↑	↑
Amplitude ↑	↓↓	Bubble Size ↓↓ Quantity ↑↑	↑↑	↓↓	↑↑	↑↑
Baseline flow ↑	—	Bubble Size ↑↑ Quantity ↓	↑ Then ↓	↑	Gas-Solid ↑	↑↑
Duty cycle ↑	↑	Bubble Size ↑ Quantity ↓	↑ Then ↓	↑	Heat Transfer: Floor to Wall ↓	↑

organizes the variations in pulse parameters, illustrating how each parameter changes.

It is evident from the above chart that there exists an optimal frequency that minimizes $U_{mf}$, while mixing quality demonstrates a peak at a specific frequency, exhibiting an inverted U-shaped relationship. Moderate baseline wind speed can enhance mixing quality; however, excessively high speeds may lead to uneven mixing due to large bubbles and gas short-circuiting. When the duty cycle is within a moderate range, the sustained airflow enhances performance; conversely, excessive duty cycles may result in mixing deterioration due to large bubble formation and stable fluidization.