Dynamics and Mutual Influence of Droplets in a Rotating Liquid Under Centrifugal Forces

Abstract

The article presents the results of experimental studies of the velocity of liquid droplets in a chain under the action of centrifugal forces in a uniformly rotating liquid continuous phase. The aim of the work is to study the mutual influence of droplets on each other through the analysis of entrainment, simplified to plane motion. An experimental setup was developed based on a cylindrical vessel with adjustable angular velocity, a droplet-forming device, and stroboscopic photography to record trajectories. The methodology includes phase saturation, adjustment of the dispersed phase flow rate, and two shooting modes to minimize errors. The dependencies of the satellite trail velocity ($V_{sp}$) on the radial distance (R) and the drop frequency (f) were obtained for three liquid systems; based on regression analysis, a generalized formula $V_{sp}=k·R^a·f^b$ was proposed, providing satisfactory agreement between the calculated and experimental data (deviation < 10%). The results confirm the increase in $V_{sp}$ with increasing R and f, which allows optimizing the extraction and mass transfer processes in centrifugal devices.

1. Introduction

Mass transfer processes in liquid-liquid systems depend to a large extent on the size of the droplets: the smaller the particle size, the greater the specific contact surface area and the more intense the mass transfer. At the same time, increasing the degree of dispersion complicates the subsequent separation of phases, which necessitates the use of effective separation methods, for example, in the field of centrifugal forces [1,2], which greatly exceed the forces of gravity and ensure effective separation even with small differences in phase densities [3]. Well-known analytical dependencies describing the motion of a single droplet in a centrifugal field are available in the literature [4].

However, real dispersed flows cannot be represented as a collection of isolated droplets, since they consist of ensembles [5] where neighboring droplets interact with each other through the velocity field and vortices formed in their wake [6]. In the work [7], the hydrodynamic interaction and deformation of two or more droplets in various configurations, including tandem and off-axis, are studied in detail, illustrating the influence of the mutual arrangement of droplets on their kinematics and coalescence. This phenomenon affects the radial component of the droplet velocity and, as a result, the efficiency of separation. To evaluate this effect, experimental studies of the velocity of a “chain” of droplets—a sequence of droplets moving in each other’s wake—were conducted—in order to establish how the distance between the droplets, determined by the frequency of their separation from the disperser nozzle, and the distance to the axis of rotation affect the kinematics compared to a single droplet.

Thus, it seems relevant to refine approaches to the quantitative description of the kinematics of dispersed flows in centrifugal fields: existing analytical models describe the motion of a single drop well, but do not take into account the interactions in ensembles of successive drops (chains), which are characteristic of many practical processes [8]. This work is aimed at experimentally investigating the kinetics of droplets moving radially in a “chain” in a centrifugal field to establish the conditions under which inter-drop interactions can lead to significant deviations from the predictions of the theory for a single drop, and to determine the dependencies that allow the specified influence of drops on each other to be taken into account.

2. Materials and Methods

As shown in classical works on hydrodynamics, when a body moves in a liquid, a wake (trail) forms behind it, which, depending on the flow regime, can be laminar or turbulent. The velocity of the fluid near the central axis of the wake is proportional to the velocity at the axis itself [9], its value gradually decreases with increasing distance from the body, and the nature of the attenuation of perturbations is described by the same laws as in the case of a single body moving in a stationary fluid. The approach under consideration is based on the assumption that the velocity of a particle in a chain is equal to the sum of the velocities of the drop’s own motion (V_dr) relative to this flow and the accompanying flow relative to the medium (V_sp), which can be formally written as $V_{ch}=V_{sp}+V_{dr}$.

This approach allows us to break down a complex hydrodynamic phenomenon into separate components. The modern literature widely presents generalized dependencies for determining the relative velocity of a single drop in a uniformly rotating fluid, covering the entire spectrum of modes—from the low Reynolds number region (Stokes mode) to transitional and inertial modes, for example [10]:

$$V_{dr}=1.74\cdot {\displaystyle \frac{{∆\rho }^{0.29}\cdot {\sigma }^{0.32}\cdot {\omega }^{0.36}}{{\rho }_c^{0.62}\cdot d^{0.14}}}\cdot R^{0.18}.$$

Since the velocity (V_dr) of a drop in a rotating system is determined by the radius, the assumption considered is also applicable to the case of a chain of drops moving in a centrifugal field. In this case, the deposition of droplets can be described as a steady-state process, since changes in velocity associated with acceleration or inertial transitional effects when R changes do not have a significant effect [11,12]. The conditions for conducting the experiment were selected so that the characteristic values of the Rossby and Ekman numbers remained high enough that the contribution of two-dimensional effects to the flow under consideration was insignificant and could also be excluded from further analysis. Analysis of the experimental results showed that the value of the satellite trail velocity (V_sp) under the action of centrifugal forces can be expressed through a functional dependence, the arguments of which are the inter-drop distance (determined by the frequency of drop arrival) and the radial coordinate characterizing the distance of the drop from the axis of rotation, which is the subject of this study.

Description of the Experimental Setup

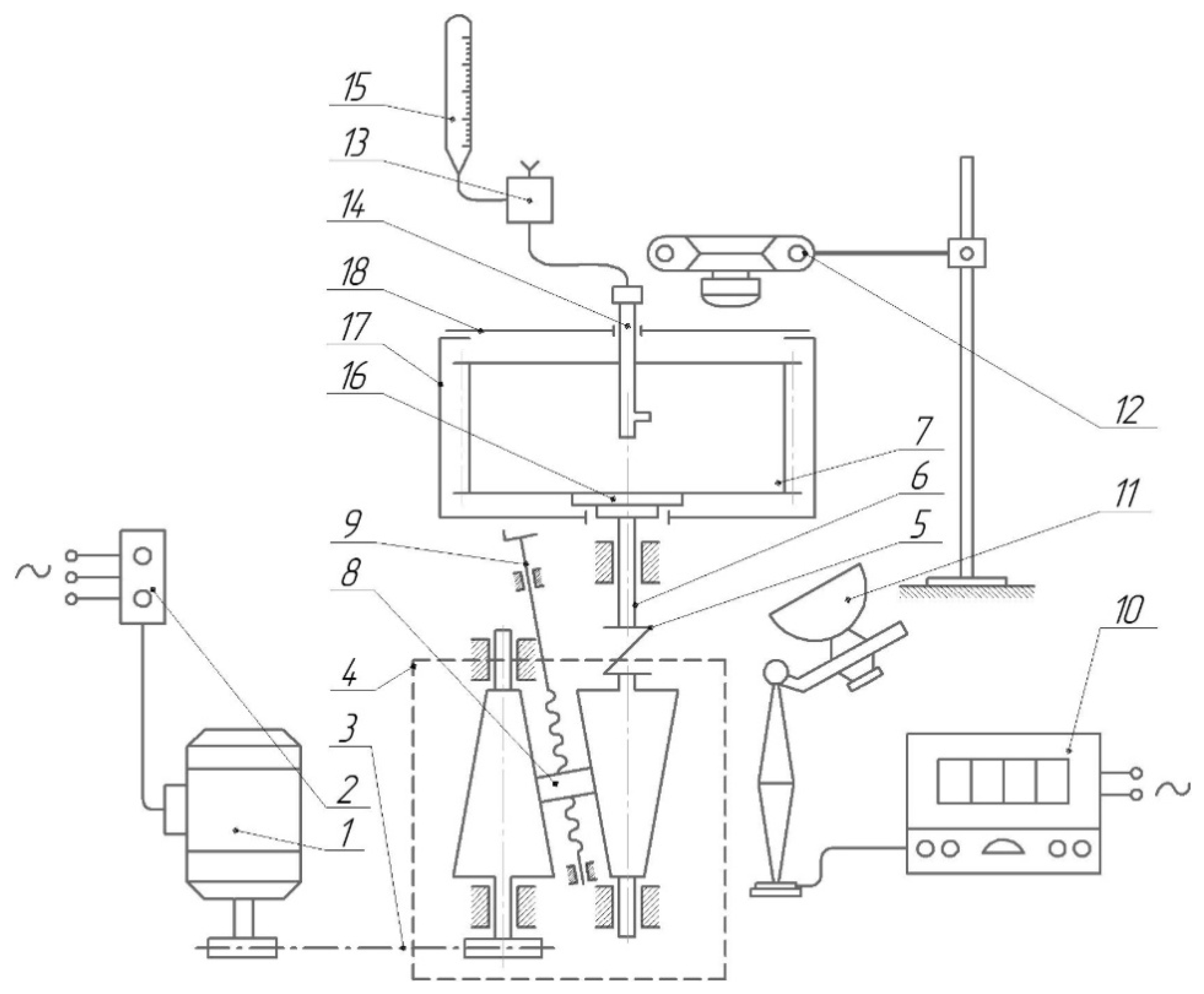
The experimental setup (Figure 1) for studying the motion of liquid droplets under the action of centrifugal forces in a uniformly rotating liquid medium consists of a removable cylindrical vessel (item 7) driven by an electric motor (item 1) with a power of 0.6 kW at a nominal frequency of 1410 rpm with a magnetic starter (item 2).

The angular velocity of the vessel is adjusted in the range of 250–2500 rpm by rotating the flywheel (item 9) and moving the roller (item 8) of the conical friction variator (item 4). The latter is connected to an electric motor via a V-belt drive (item 3) and to the vessel shaft via a sleeve-finger coupling (item 5). A stroboscopic tachometer (item 10) with a pulse lamp (item 11) and a camera (item 12) are used to observe and record the processes inside the vessel. The dispersed phase is dosed through an adjustable valve (item 13) of the droplet-forming device (item 14), and the liquid flow rate is controlled by a measuring tank (item 15). The temperature of the air and liquids before and after the experiment is monitored using a thermometer with a scale of 0.5 °C. The experimental vessel is secured to the working shaft with a cap nut (item 16) and equipped with a protective cover (item 17), the upper part of which is closed with a lid (item 18) with a transparent window for observation and photography. The entire drive of the installation with the bearing assembly (item 6) is mounted on a massive frame, ensuring stable rotation and accurate positioning of the vessel.

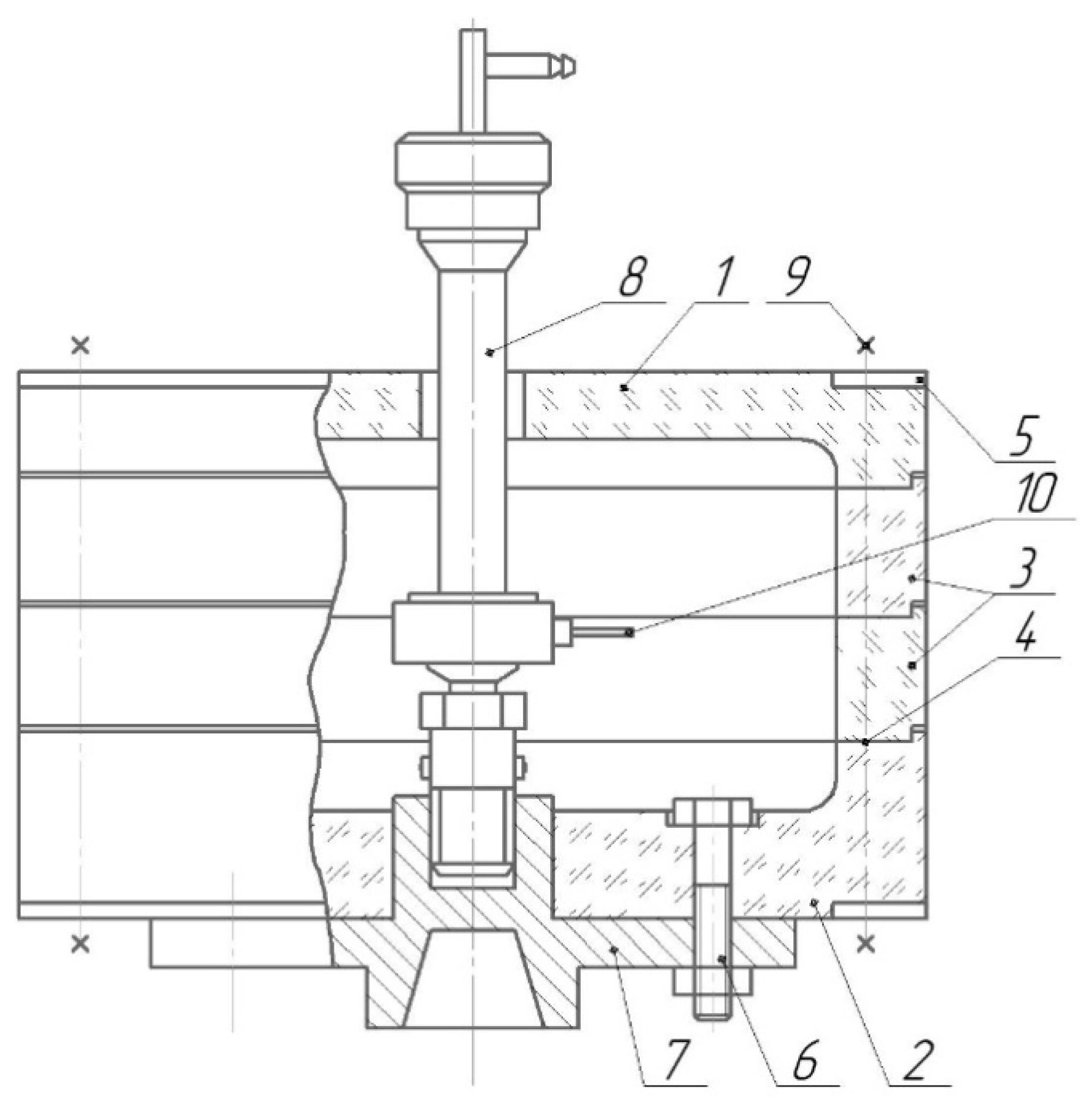
The experimental vessel (Figure 2) consists of a top cover and a bottom (items 1 and 2) made of transparent plexiglass, as well as a set of interchangeable rings (item 3) with gaskets (item 4) for adjusting the distance between the cover and the bottom depending on the requirements of the experiment. To ensure strength, metal rings (item 5) are installed on the lid and bottom, and the entire set of elements is fastened with pins (item 9) located around the periphery of the vessel. The bottom is connected by bolts (item 6) to a crosspiece (item 7), which has a conical hole at the bottom for attaching the vessel to the shaft of the installation, and at the top, in the center of the crosspiece, there is a mounting seat for the droplet-forming device (item 8). The latter is designed to ensure uniform separation of droplets from the nozzles (item 10) as a result of shaking. To ensure the tightness of the dispersing device, fluoroplastic bushings are inserted into the center of the body, allowing the feeder needle to rotate freely and, at the same time, retain the dispersed phase. A set of nozzles of various lengths and diameters allows droplets of widely varying sizes to be obtained. Inside the vessel, in the plane of the nozzles, there is a scale ruler used to calibrate images and determine the magnification scale when processing photographic materials, as well as for correct centering of images.

3. Experimental Methodology

To exclude the influence of mass transfer on the parameters of droplet motion, both liquids under study (droplet and continuous phases) were preliminarily subjected to mutual saturation. For this purpose, the required volumes of both liquids were placed in a glass container, intensively mixed, and allowed to settle until complete phase separation. After separation, the physicochemical characteristics of the phases necessary for further data processing were determined experimentally using the platinum ring break method and a capillary viscometer: density, viscosity, and interfacial tension. The light (continuous) phase was poured into a vessel fixed on a shaft, and the heavy phase (droplets) was poured into the measuring tank of the droplet-forming device. The flow rate of the dispersed phase and the frequency of droplet separation were regulated by a metering valve, so that the design of the disperser allowed the frequency of droplet formation to be changed during the experiment without stopping the rotation of the vessel. The camera was positioned so that the center of the vessel, the scale ruler, and the peripheral area of the vessel were in the field of view (for subsequent calibration and image centering).

The vessel was rotated using a friction variator, smoothly increasing the angular velocity to the required value. Under stroboscopic lighting, the vessel appeared visually stationary, which made it possible to observe and photograph the movement of droplets in stable visual coordinates [13]. The exposure of the frame began at the moment the drop detached from the nozzle and continued until the drop reached the periphery of the vessel; as a result, a single photograph contained a multiple-exposure image of the vessel and separate single-exposure images of the drops in various positions along the entire trajectory of movement. To capture the sequential positions of the droplets, two main shooting modes were used [14], differing in the ratio of the stroboscope flash frequency f_strob and the vessel rotation frequency f_rot:

• f_strob = n∙f_rot, where n is an integer. In this variant, multiple exposures are made, which allows maximum information to be collected in a single frame, but leads to a deterioration in image quality due to the superimposition of traces and increased exposure density.
• f_strob > f_rot, where the flash frequency is higher than the rotor rotation frequency. This mode is free from the losses associated with multiple exposures and produces clear single droplet prints, but as the particle path between fixed positions decreases, the relative error in velocity determination increases.

Each mode has its advantages and limitations; in each case, the choice of mode was determined by the required informativeness of the frame and the permissible error in speed measurement. To eliminate the disadvantages of multiple exposure, a double stroboscopic effect was used when necessary: the frequency of the droplets’ movement was made a multiple of the number of revolutions of the vessel under stroboscopic illumination, as a result of which the droplets were visually fixed at the same points of the trajectory (Figure 3). This made it possible to obtain a single-exposure image with an information capacity comparable to multiple exposures, but with higher image quality.

To study the phases of motion occurring within the time of one rotation of the vessel, a shooting mode was used with a flash frequency several times greater than the number of rotations. In terms of information content, such a frame is equivalent to a video recording, with individual phases of motion being unfolded in the direction of rotation. To reduce the effect of multiple exposures, we used a transparent slit in the vessel casing for shooting, which allowed us to capture a continuous stream of frames without image overlap and improve their quality [15,16,17,18].

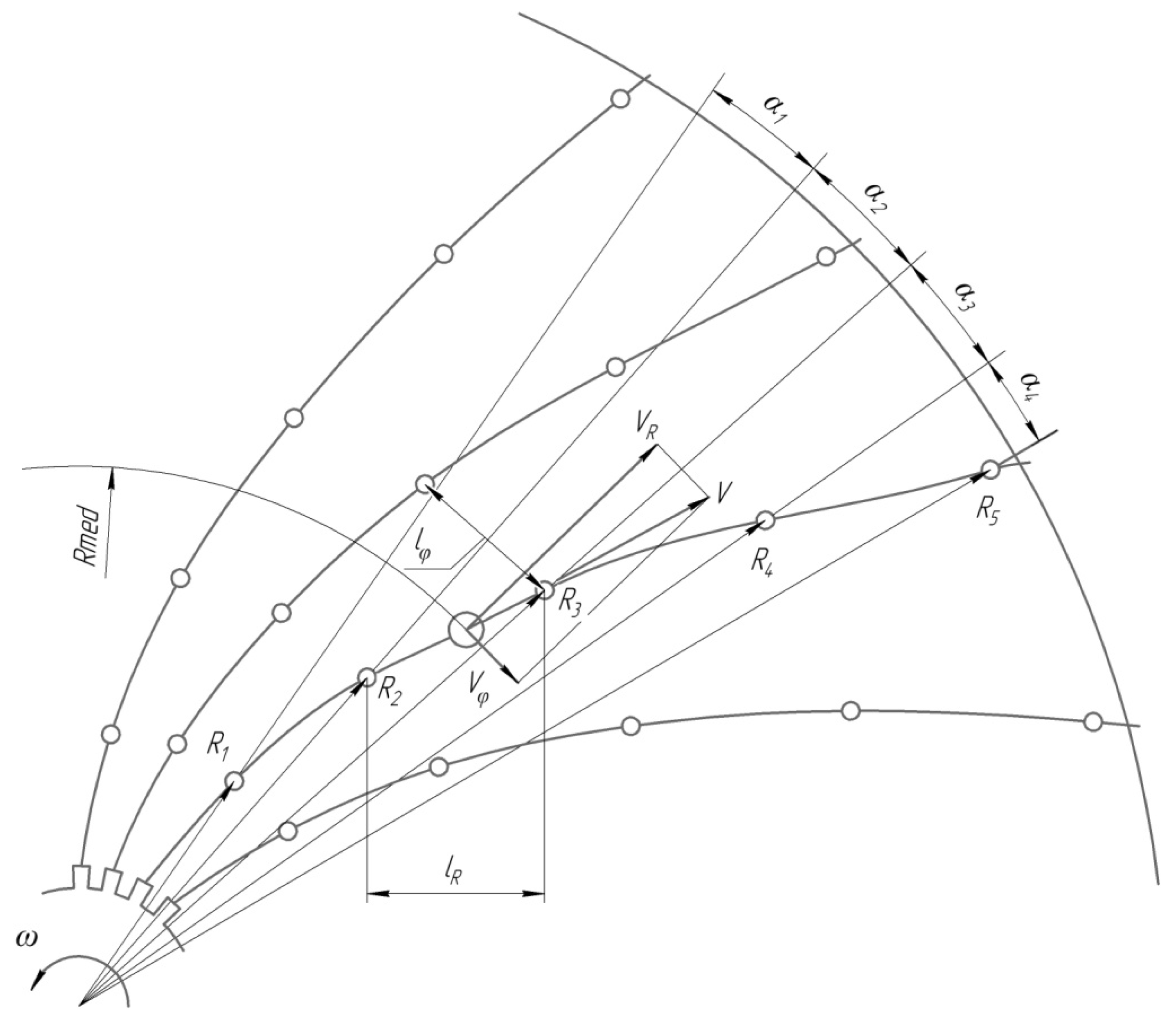
To calculate the speed of the droplets in the images obtained, taking into account the scale per frame, the following dimensions were determined: R_i—distance from the axis of rotation to the center of the droplet; l_Ri and l_φi—the distance between two adjacent images of the drop in the direction of the R axis and the φ axis, respectively; α_i—the angle of deviation of the drop after 60/n seconds (in radians). The relative velocity and its components were calculated using the following formulas:

$$R_{med}=(R_i+{\displaystyle \frac{R_{i+1}-R_i}{2}})·{\displaystyle \frac{1}{M}}, V_i={\displaystyle \frac{l_{Ri}}{t·M}}, V_{Ri}={\displaystyle \frac{R_{i+1}-R_i}{t·M}}, V_{\phi i}={\displaystyle \frac{R_i·{\alpha }_i}{t}},t={\displaystyle \frac{60}{n}}{k}_p.$$

where n is the number of revolutions per minute and k_p is the frequency of the strobe meter lamp flash. It was assumed that the average drop velocity at each section is true in the middle of the section under consideration.

4. Results

During the experiment, the speeds of the drops in the chain were determined for various conditions of motion and systems specified in

Table 1. Experimental Parameters.

System	Rotor Rotation Frequency, 1/s	Drop Diameter, m	Surface Tension, N/m	Density, kg/m3			No.
				Continuous Medium	Dispersed Medium	∆
8	7	6	5	4	3	2	1
Kerosene—water	104.67	0.00124	0.0327	777	1000	223	1
CCl4—water with glycerin (20%)	41.87	0.00167	0.026247	1048	1589	541	2
CCl4—water with glycerin (60%)	83.73	0.0009	0.02479	1150	1589	439	3

, which lists all liquid pairs used in the experiments.

During the experiment, droplets were detached from the spray nozzle using a droplet-forming device by striking the feed needle, which, together with the nozzle, dropped sharply downward, thereby releasing the droplets. The return of the nozzle to its original position by a spring ensures identical conditions for the formation and separation of droplets, as a result of which the latter moved one after another, forming the studied “chain” of droplets. The experimental data were obtained by multiple exposure photography using a double stroboscopic effect, based on which the mutual influence of particles moving in a chain was evaluated for the above-mentioned systems. It should be noted that the experimental conditions considered the turbulent flow regime of the wake, so during the subsequent mathematical processing of the data, it was decided not to take into account the influence of the viscosity of the medium on the wake velocity, and the radial distance from the axis and the frequency of arrival of dispersed particles in the centrifugal field were taken as independent variables.

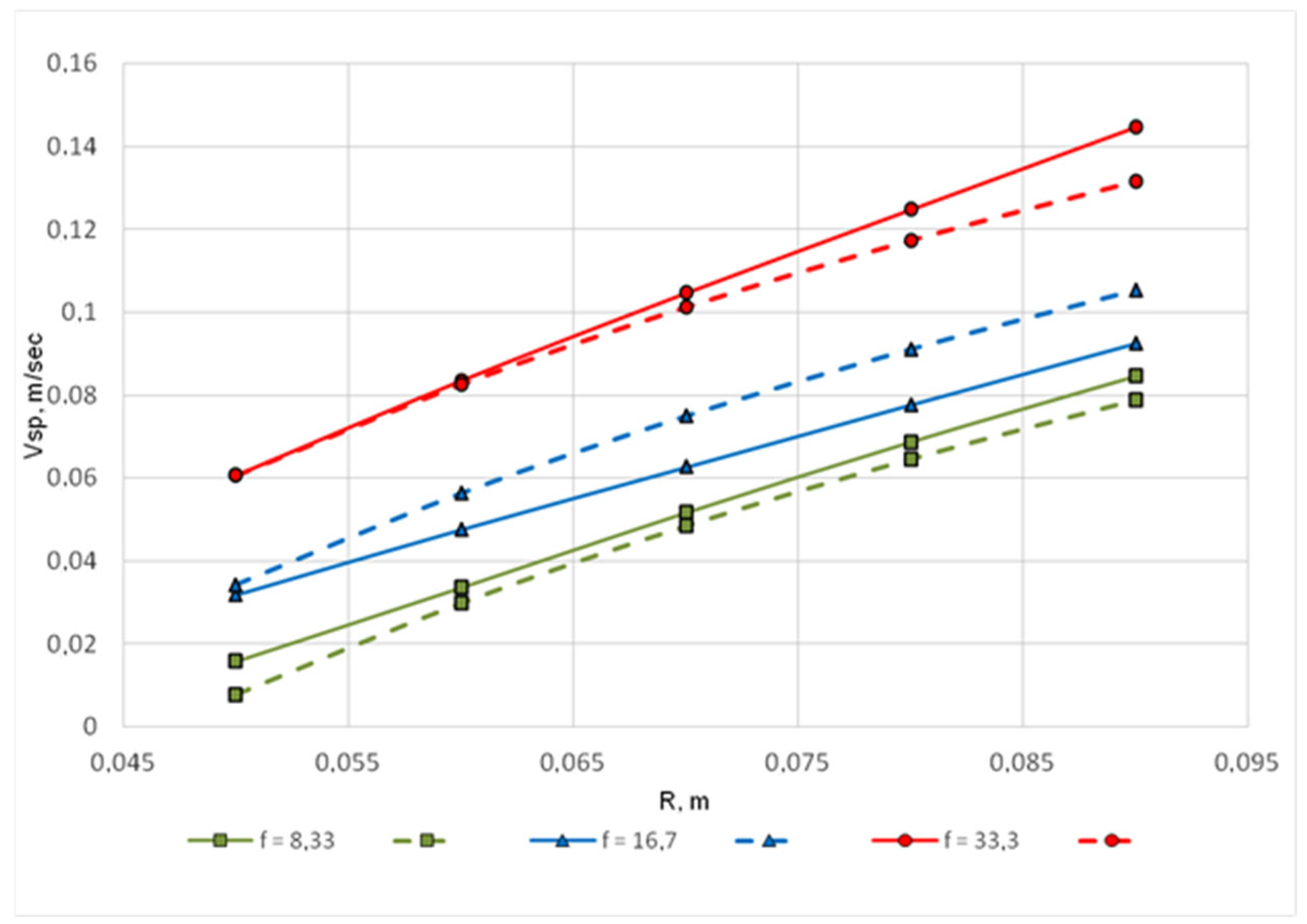
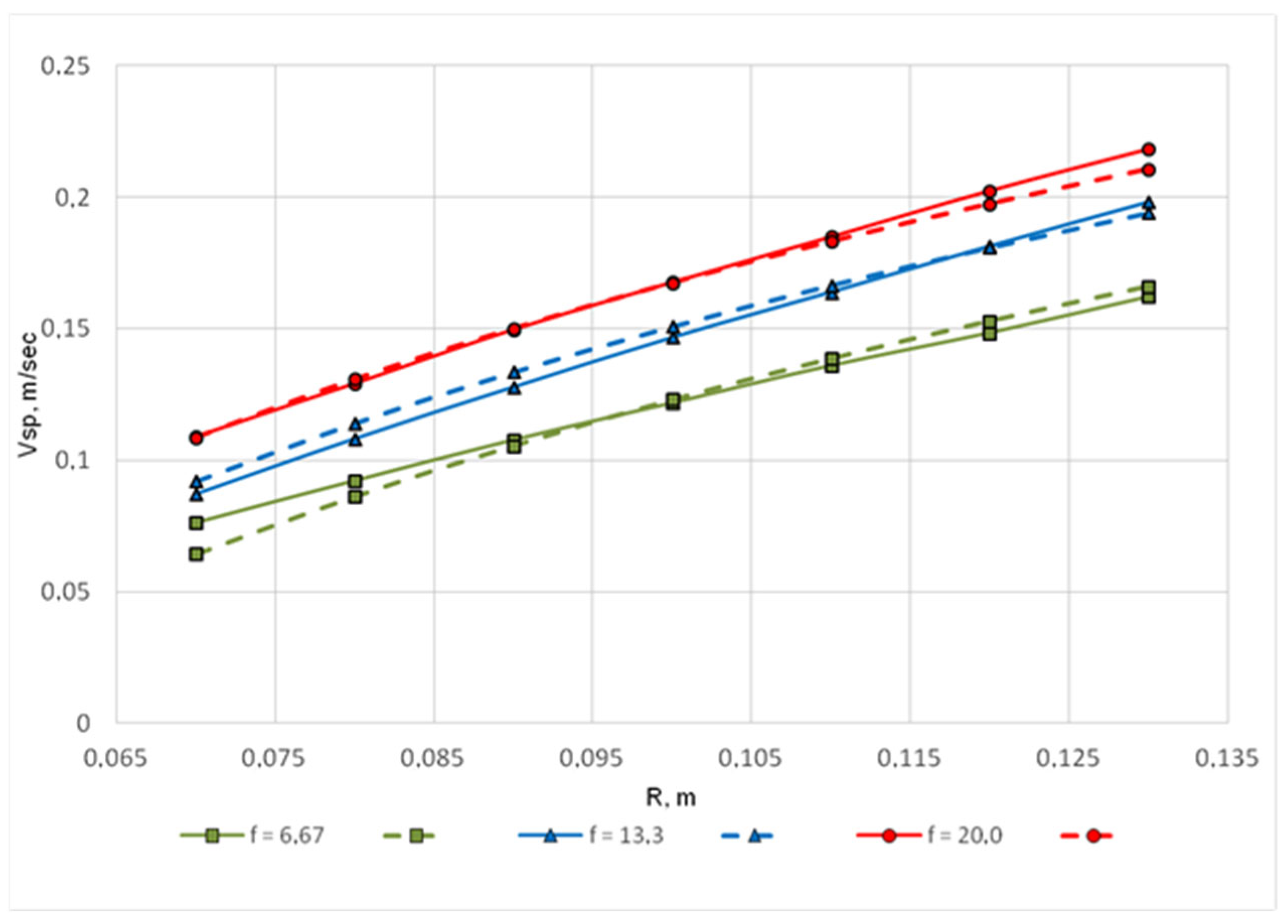
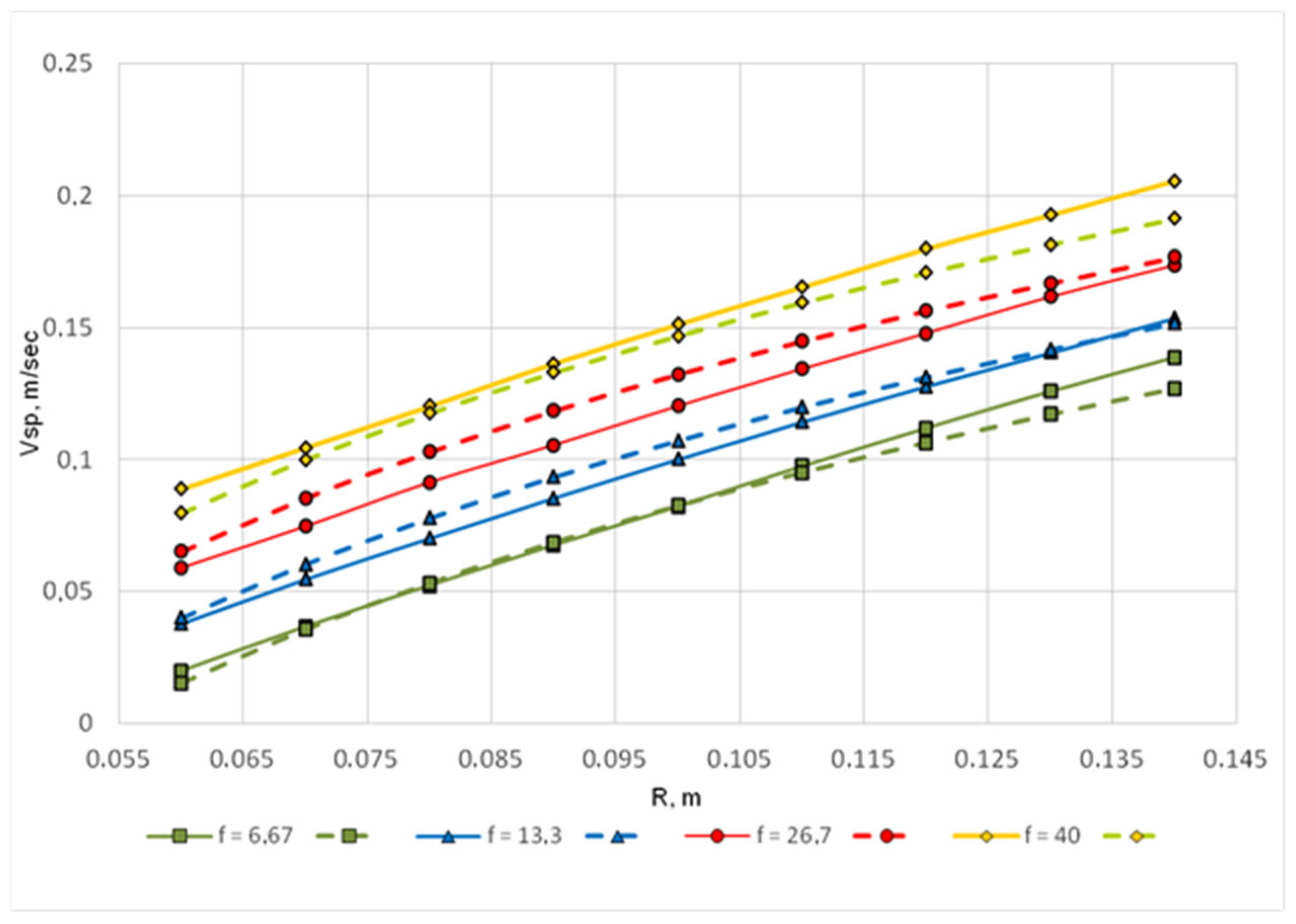
In Figure 4, Figure 5 and Figure 6, the solid line represents the experimental values of the satellite flow velocity V_sp = V_ch − V_dr, where V_ch is the experimentally determined value of the drop velocity in the chain, and V_dr is the velocity of a single drop, determined by the equation above. Based on the results of logarithmic regression analysis, equations were obtained to approximate the experimental data. The dotted line on the graphs (Figure 4, Figure 5 and Figure 6) shows the calculated values according to the specified equations, depending on the velocity of the accompanying flow from the radial distance to the axis of rotation (R) and the frequency of droplet supply from the feeder (f) for the corresponding systems under study: ${{ V}^{\prime }}_{sp1}=0.2891+0.03808·ln\left(f\right)+0.12084·ln\left(R\right)$, ${V^{\prime }}_{sp2}=0.4252+0.04058·ln\left(f\right)+0.16473·ln\left(R\right)$, ${V^{\prime }}_{sp3}=0.3173+0.0360·ln\left(f\right)+0.1317·ln\left(R\right)$.

The above dependencies show that there is a common trend for all the systems under consideration: the satellite trail velocity increases as the particle chain moves in a centrifugal field with an increase in the frequency of droplet arrival, as well as with the distance of the droplets from the axis of rotation. The values of the coefficient of determination R² confirm the adequacy of the obtained equations in the studied range of values (0.945 for system 1; 0.985 for system 2; 0.977 for system 3).

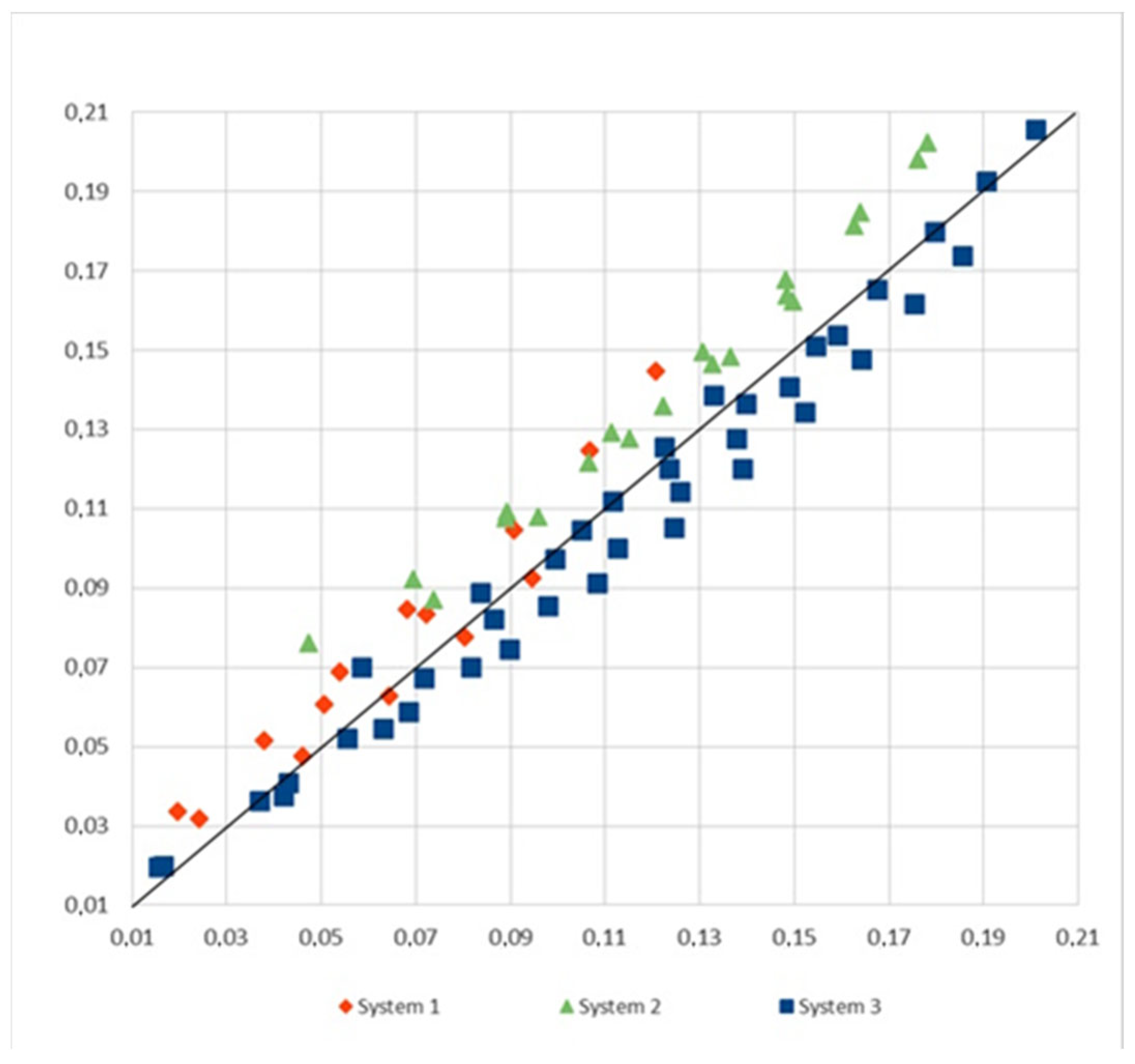
Thus, it becomes possible to determine the general functional dependence of velocity on radius and frequency, which is valid for the range of values studied in this experiment. Applying mathematical processing methods to the experimental data allows us to determine a generalized dependence for the three systems studied: ${V^{\prime }}_{sp}=0.1+ln({1.84}^{{\displaystyle \frac{\rho }{∆\rho }}}{·f}^{0.038}·R^{0.062}·R^{{\displaystyle \frac{0.2·\rho }{∆\rho }}})$.

The calculated values of the velocity of the satellite trail for all the systems under consideration, obtained from equation (V’_sp), are in satisfactory agreement with the experimental data, as can be seen from Figure 7 and confirmed by the coefficient of determination of the obtained regression models, which is close to unity, and the value of MAPE (Mean Absolute Percentage Error), which does not exceed 10%.

5. Conclusions

The experiments demonstrate a significant influence of inter-drop interaction on the dynamics of sedimentation in a centrifugal field, where the velocity of drops in a chain exceeds the velocity of an isolated particle due to slipstreaming. It has been established that in turbulent mode, the viscosity of the medium is insignificant, and the key factors are the radial distance and the frequency of arrival, which is reflected in the generalized dependence V’_sp. The proposed model is consistent with classical hydrodynamic approaches and experimental data for various liquid systems, opening up avenues for predicting the behavior of dispersed systems in centrifugal devices. Further research may be directed toward accounting for the polydispersity of the spray plume during phase interaction during extraction in a liquid-liquid system for industrial application in chemical technology.