Lightweight Design of Screw Rotors via an Enhanced Newton–Raphson-Based Surrogate-Assisted Multi-Objective Optimization Framework
Abstract
1. Introduction
2. Methods
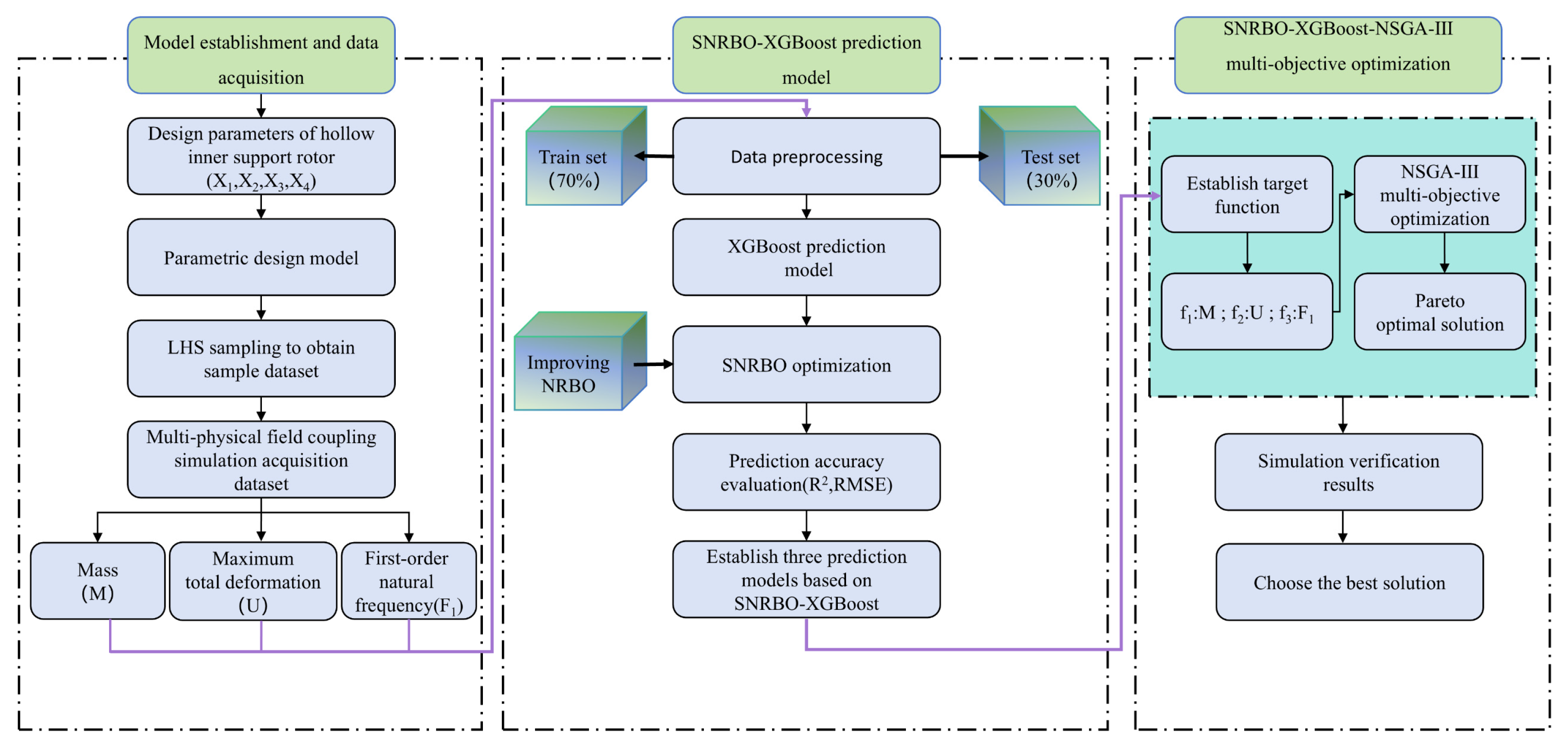
2.1. Study Framework
2.2. Simulation Framework and Performance Indicators
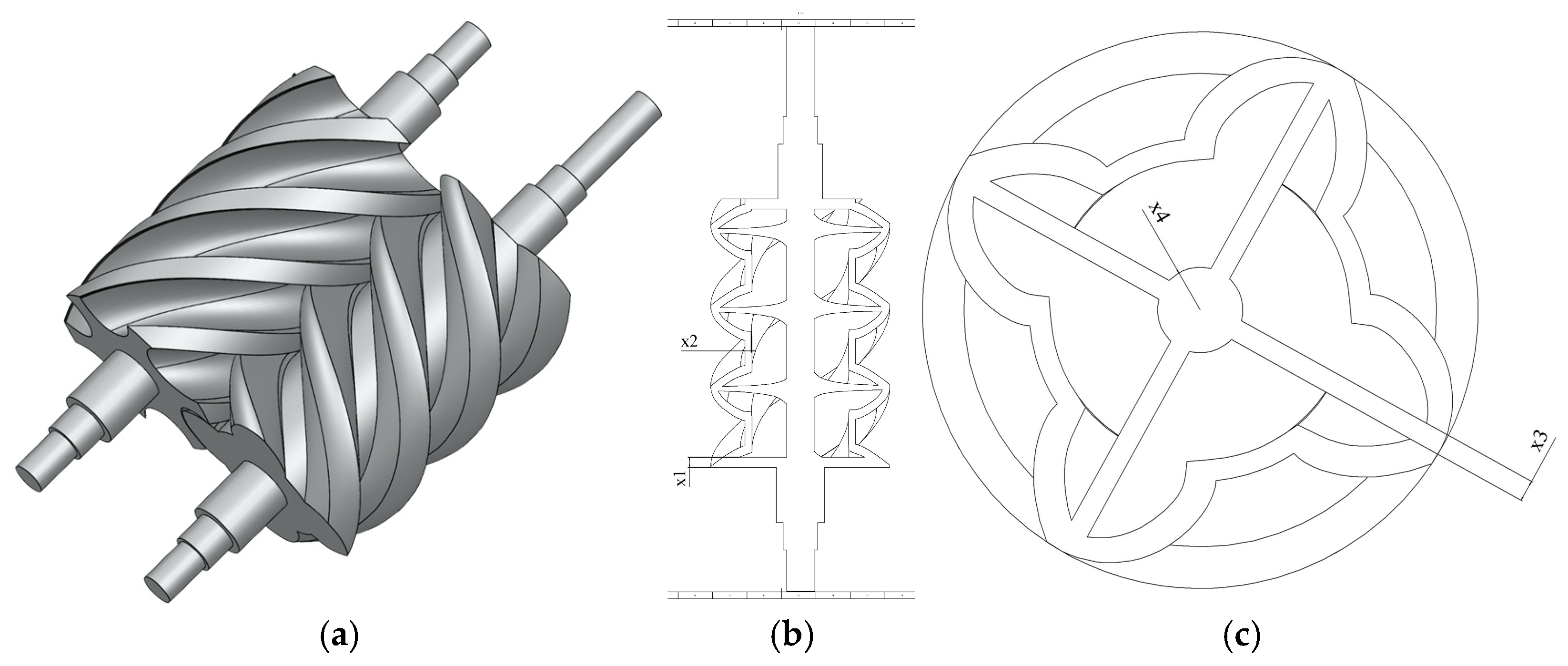
2.2.1. Selection of Design Variables
2.2.2. Multi-Physical Field Coupling Mechanism and Theoretical Characterization of Performance Indicators
- Multi-physical Field Coupling Mechanism: Fluid–structure interaction: The aerodynamic load on the rotor surface induces dynamic deformation. Thermo-structural coupling effect: The steady-state temperature gradient causes thermal stress, which combines with mechanical loads to form a composite stress field. Mass–dynamics correlation: Changes in mass distribution directly affect structural stiffness and modal characteristics.
- Definitions of Key Performance Indicators: Maximum total deformation (U): Indicates the reduction in overall stiffness under thermomechanical loads. Mass (M): Reflects the lightweighting effect, calculated as the product of geometric topological volume and material density. First-order natural frequency (F1): Represents dynamic stability. A larger F1 reduces resonance risk by increasing the gap between the natural frequency and the operational base frequency.
- Necessity of Surrogate Models: The aforementioned indicators exhibit strong nonlinear coupling, and the high-dimensional design space renders analytical solutions impractical. To address this, parametric simulations are used to generate high-dimensional datasets, and surrogate models are constructed to facilitate efficient multi-objective optimization. Implementation details regarding the platform (ANSYS 2022R1), material (316L stainless steel), and boundary conditions are provided in Section 3.2.
2.2.3. Acquisition of Sample Dataset
2.3. SNRBO Algorithm
2.3.1. Fundamentals and Procedure of the NRBO Algorithm
- Algorithm Initialization:
- 2.
- Newton–Raphson Search Rule (NRSR):
- 3.
- Trap Avoidance Operator (TAO):
- 4.
- Update and Iteration Control:
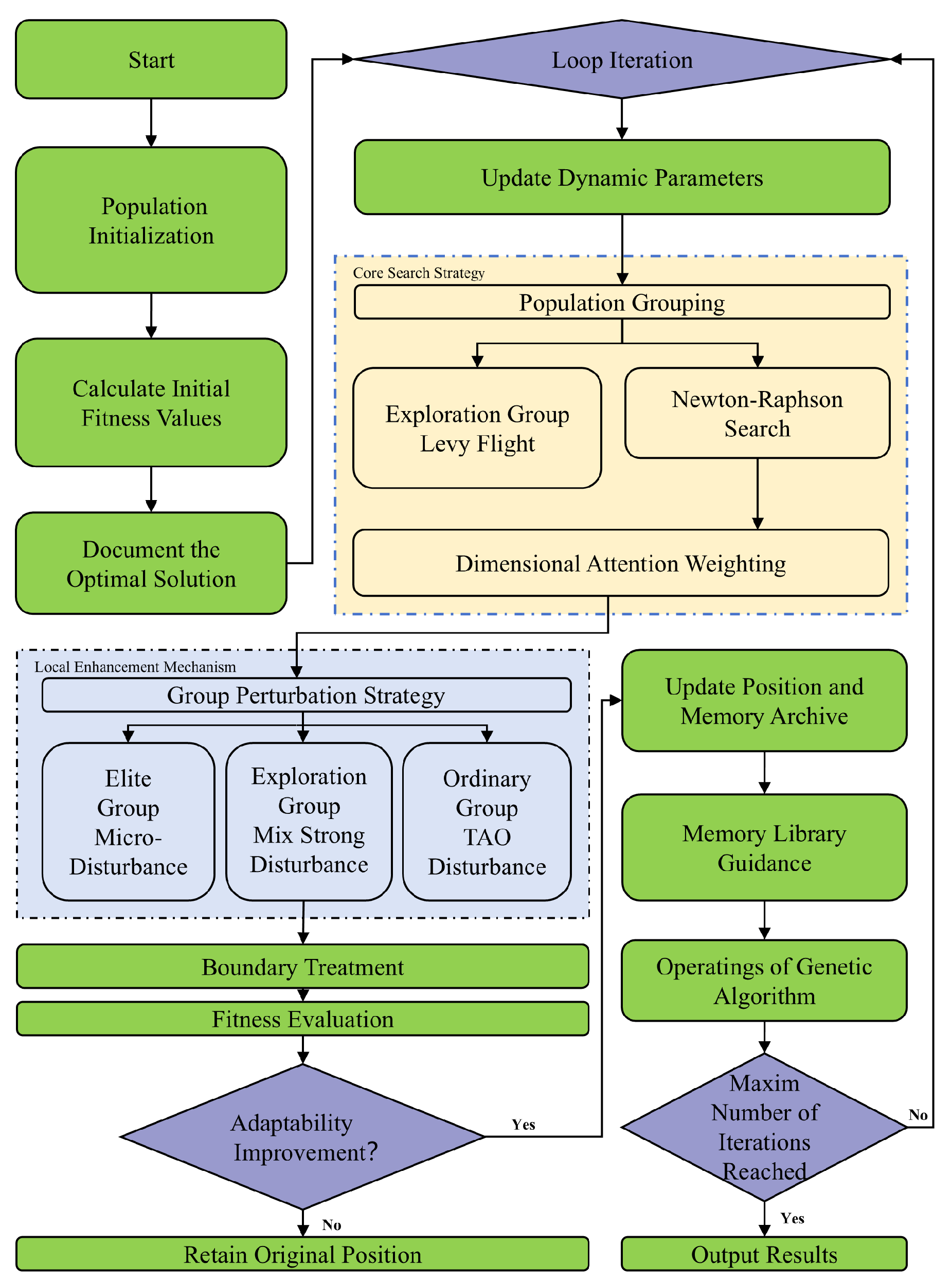
2.3.2. Design of the SNRBO Algorithm
- Dimensional Attention Mechanism:
- 2.
- Adaptive Regulation Mechanism of Dynamic Disturbance Triggering Factor DF:
- 3.
- Lévy Flight Strategy:
- 4.
- Hierarchical Population Structure and Differential Behavior Strategy:
- 5.
- Memory Repository Collaborative Fine-Tuning Mechanism:
- 6.
- GA-based Information Reconfiguration and Population Co-evolution Strategy:
2.3.3. Design and Verification of Ablation Experiment
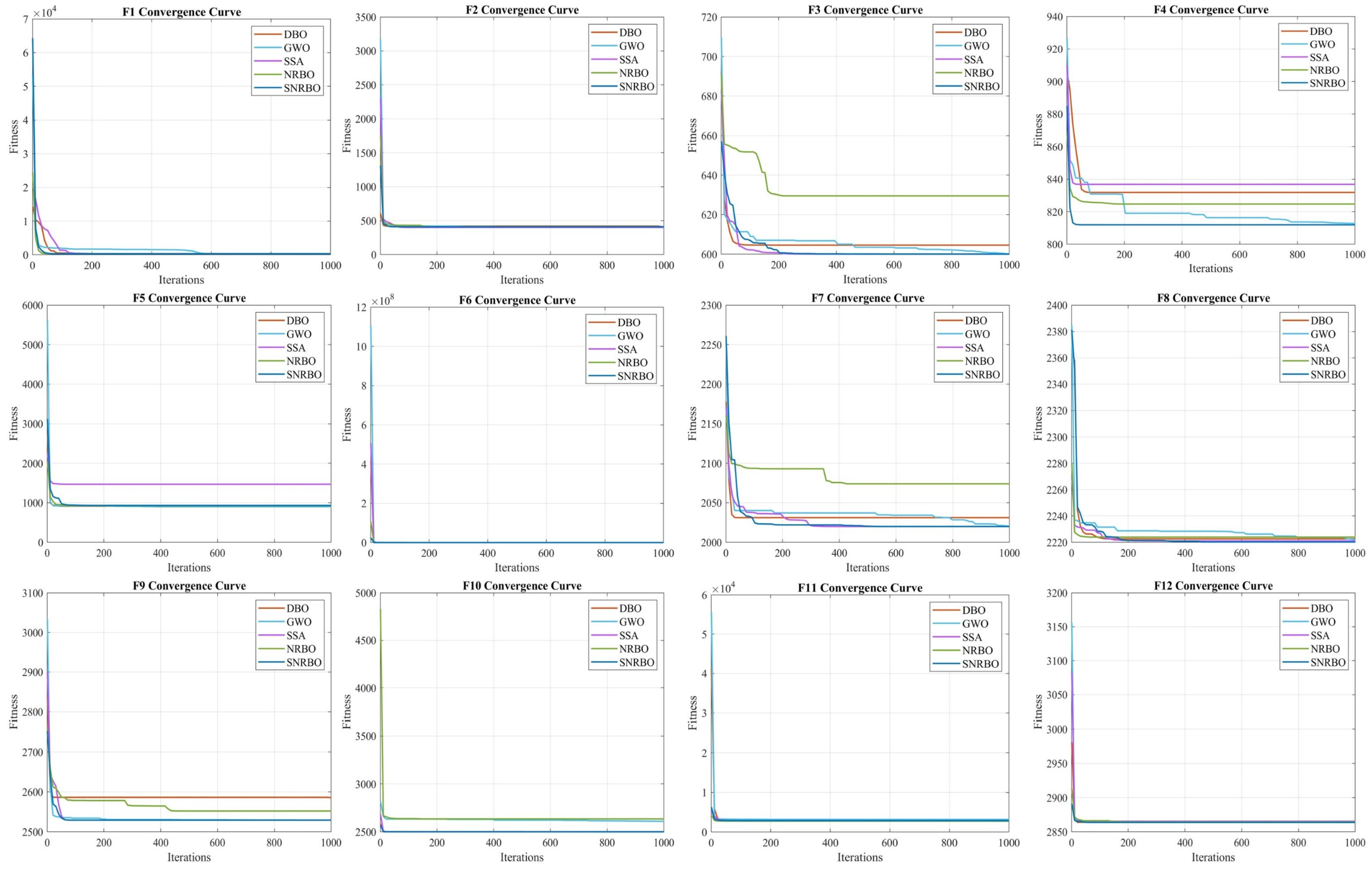
2.3.4. Analysis of the Optimization Effects of Multi-Strategy Integration
2.4. Construction of SNRBO-Optimized XGBoost Surrogate Model
2.4.1. XGBoost Model
2.4.2. Evaluation Metrics for Regression Models
2.5. NSGA-III-Based Multi-Objective Optimization
2.5.1. Objective Functions and Constraints
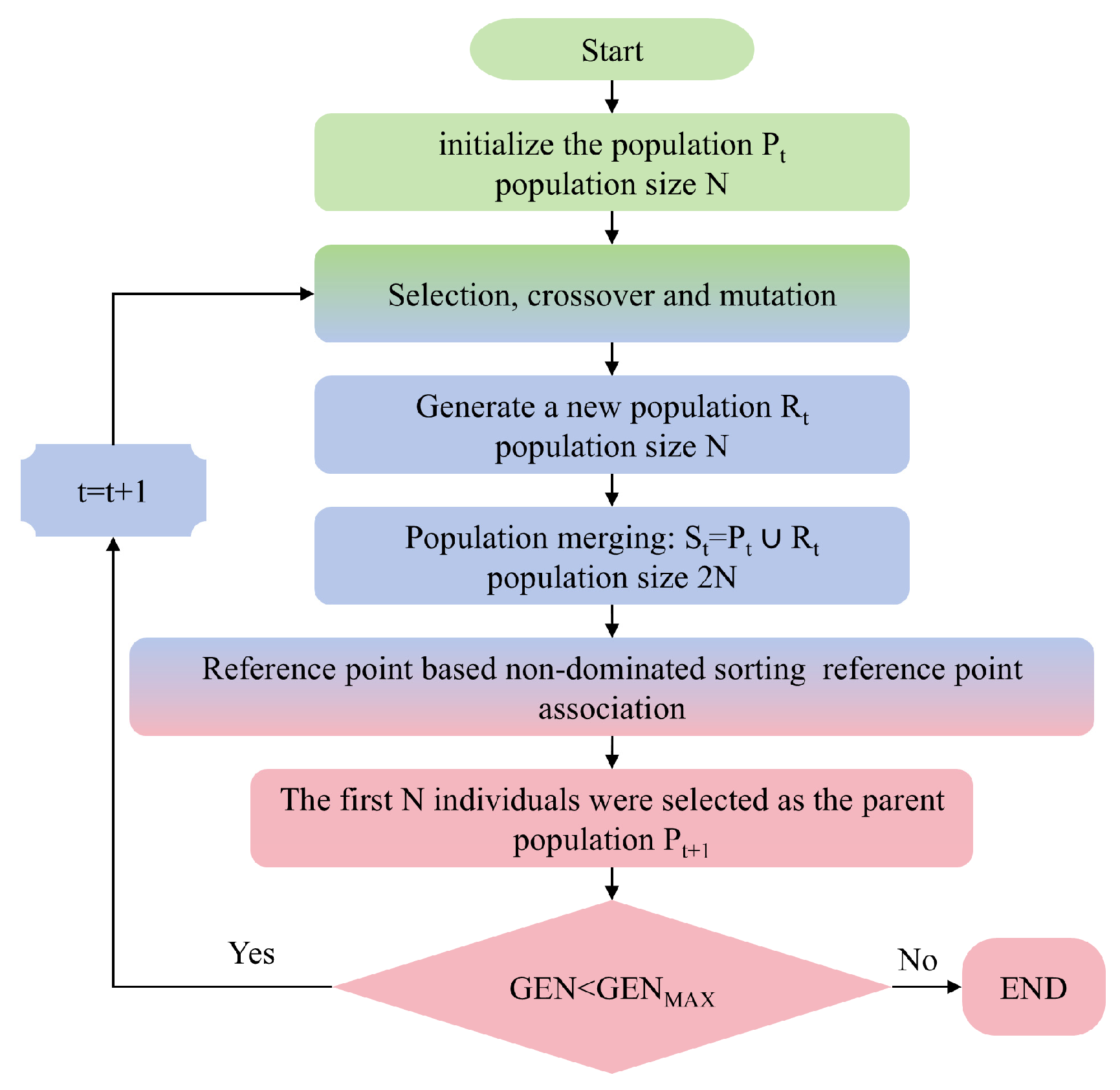
2.5.2. NSGA-III Optimization Procedure
2.5.3. Pareto Optimal Solutions
3. Case Study on the Optimization of Hollow Internally Supported Screw Rotors
3.1. Case Description
3.2. Rotor Structural Performance Simulation
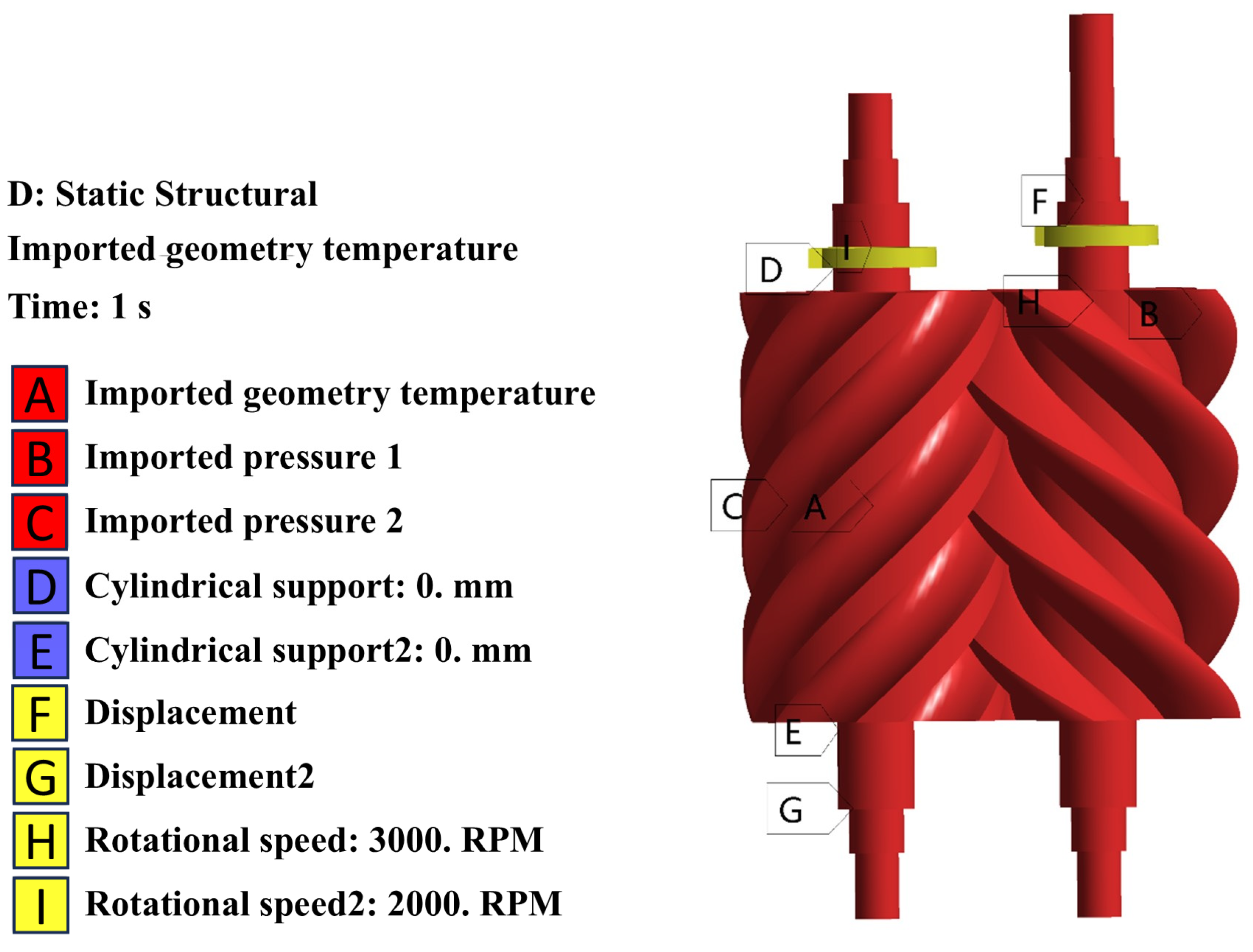
3.2.1. Simulation Settings
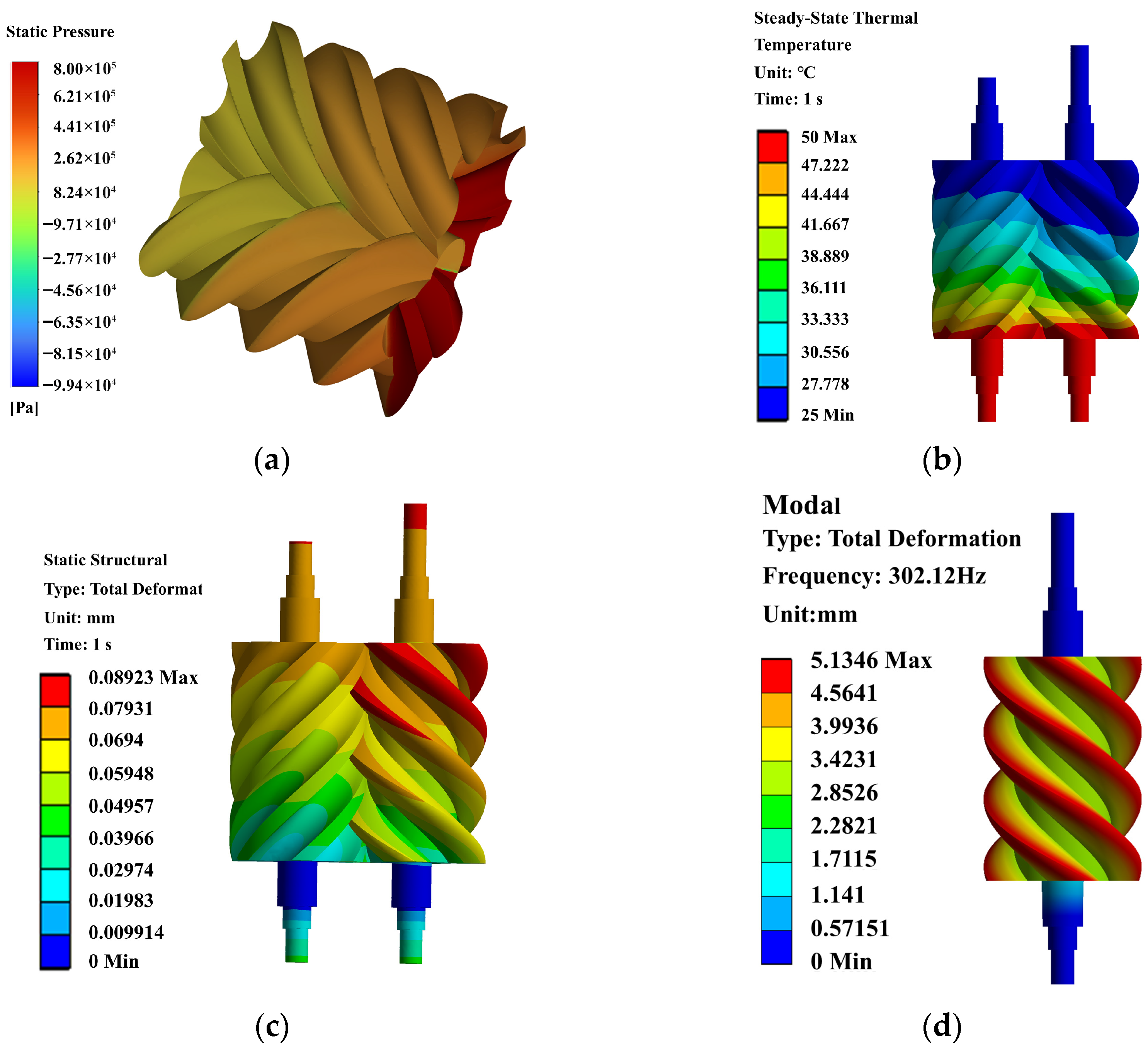
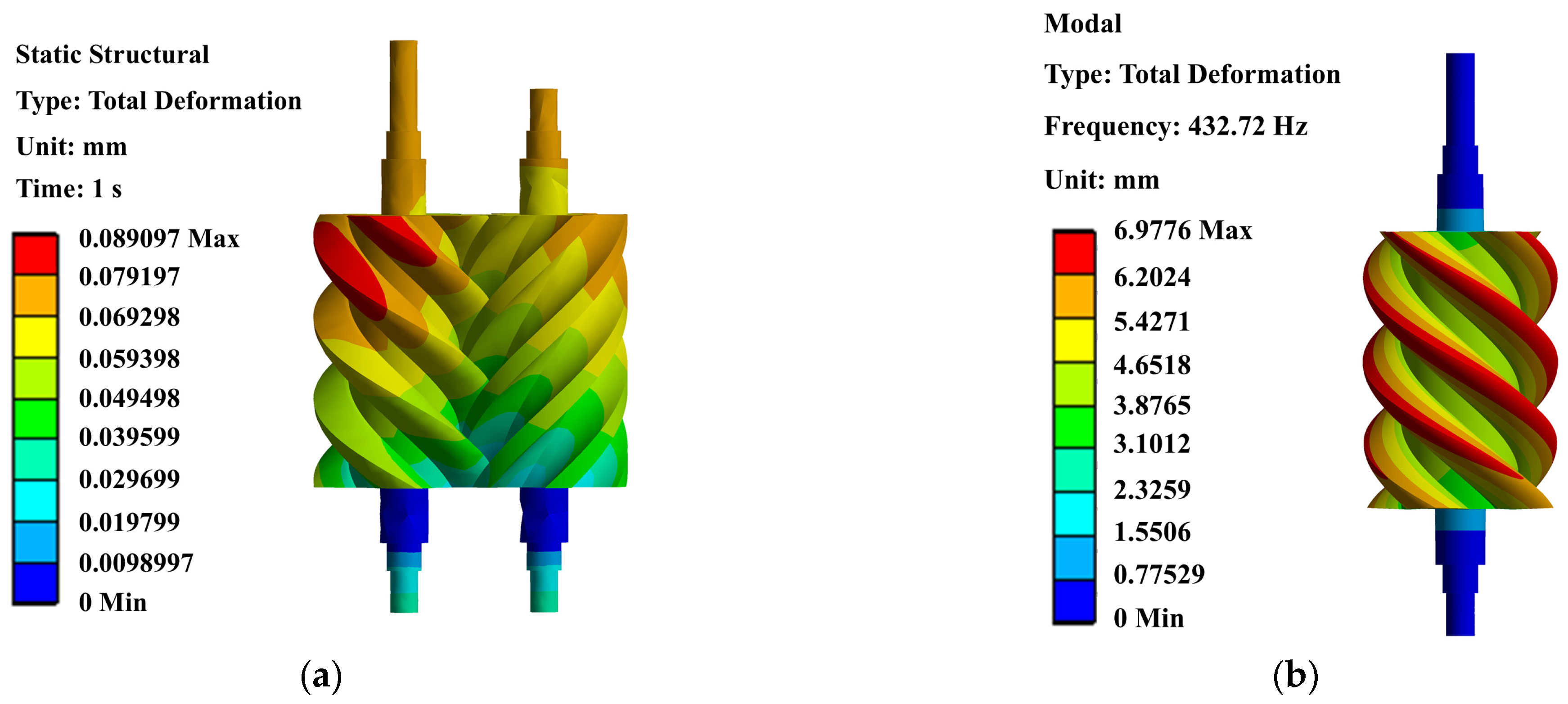
3.2.2. Multi-Physics Coupling Analysis Results and Performance Extraction
3.3. Performance Prediction and Validation Based on the SNRBO-XGBoost Model
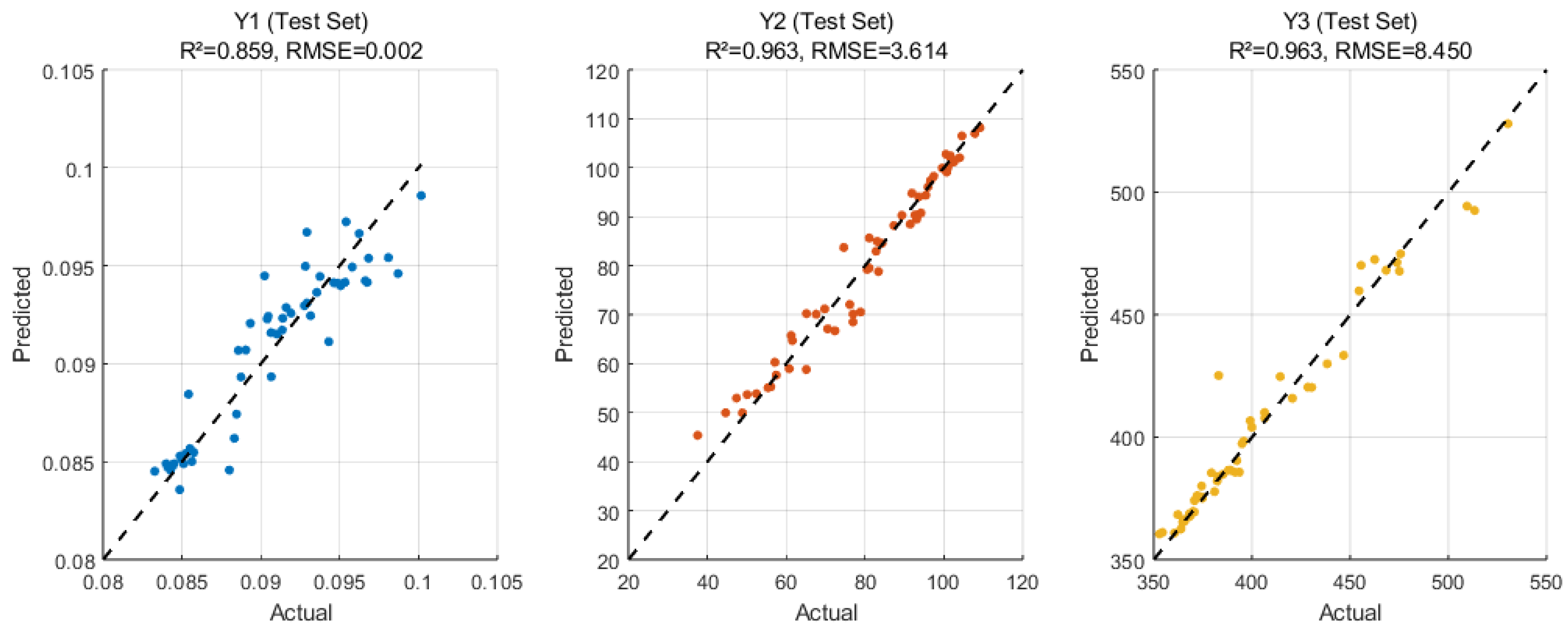
3.3.1. Constructing XGBoost Prediction Model
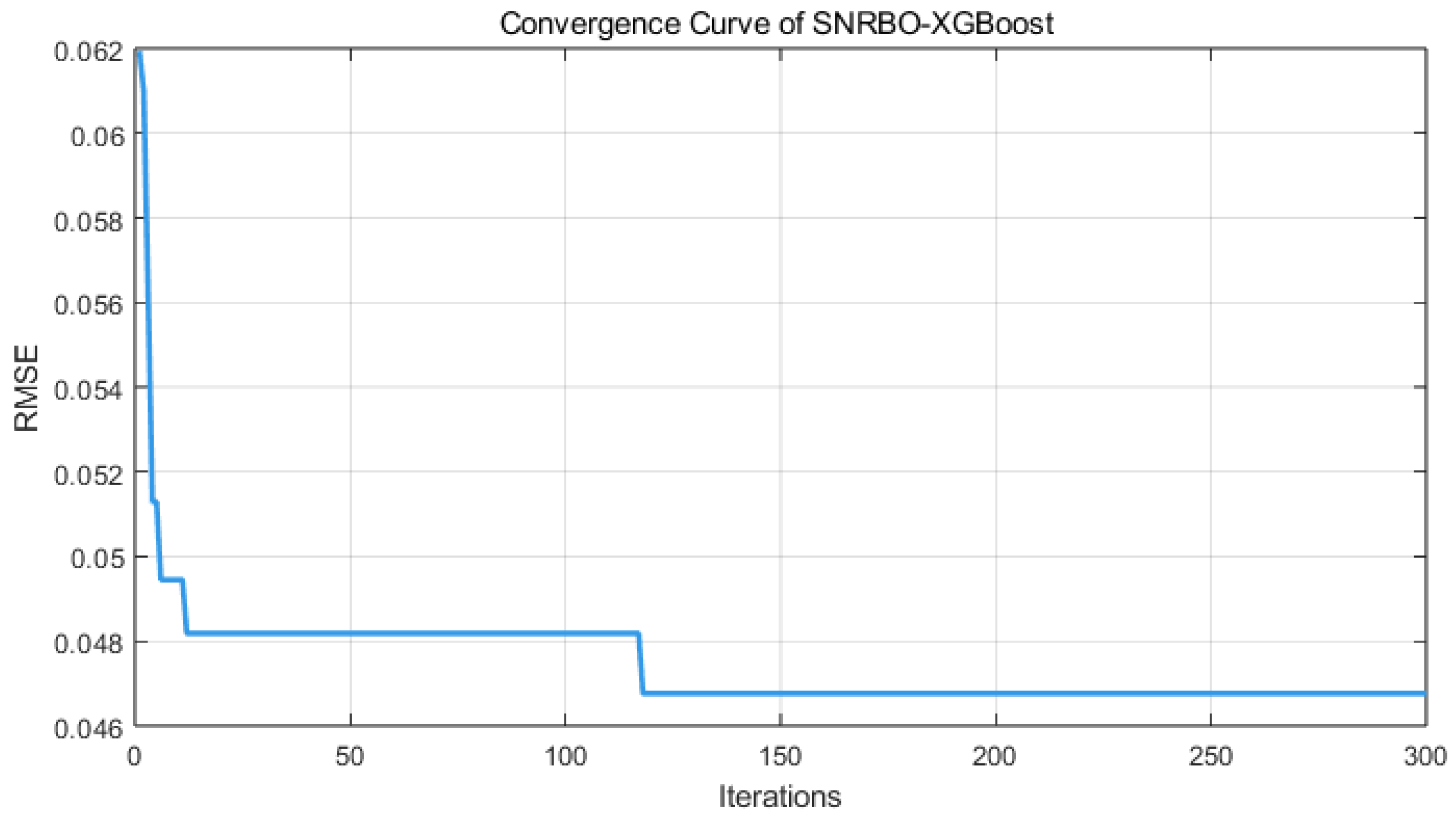
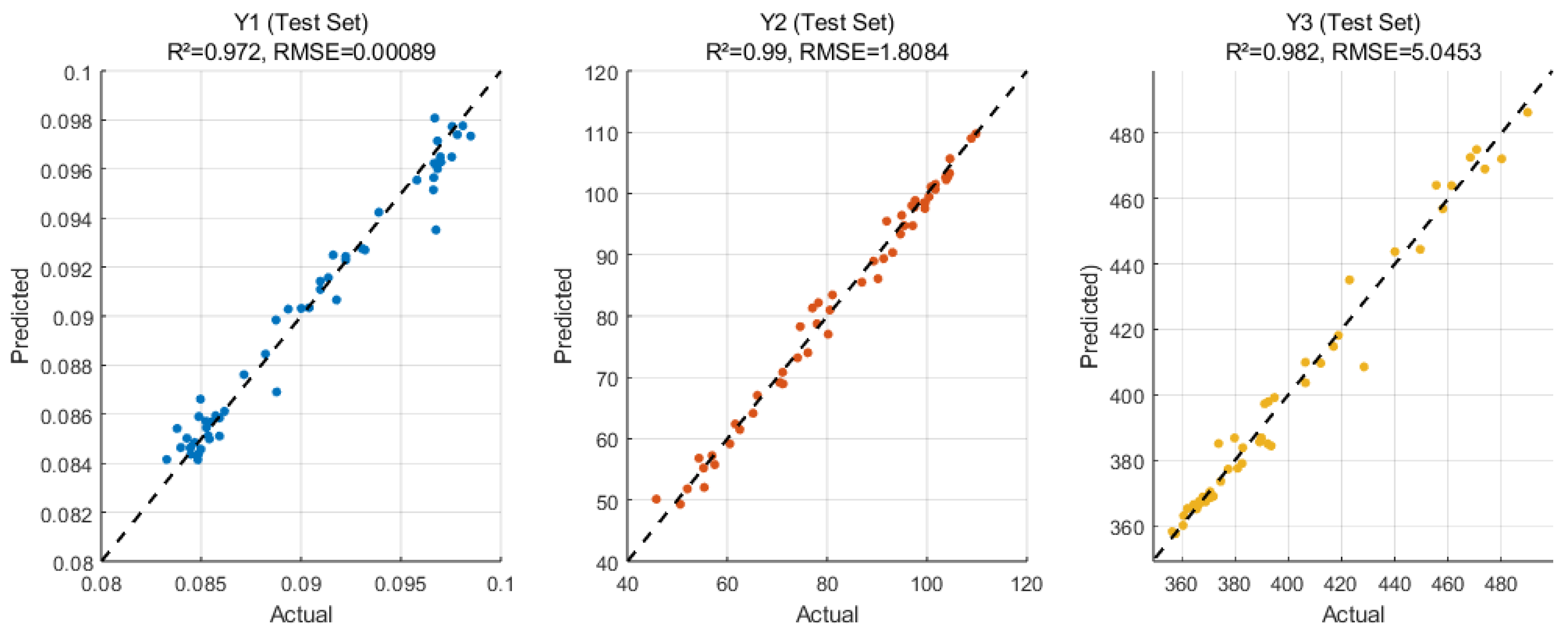
3.3.2. Hyperparameter Optimization of XGBoost Model Based on SNRBO
- Y1: R2 increases by 12.9%, RMSE decreases by 5.6%.
- Y2: R2 increases by 2.8%, RMSE decreases by 49.96%.
- Y3: R2 increases by 1.97%, RMSE decreases by 40.29%.
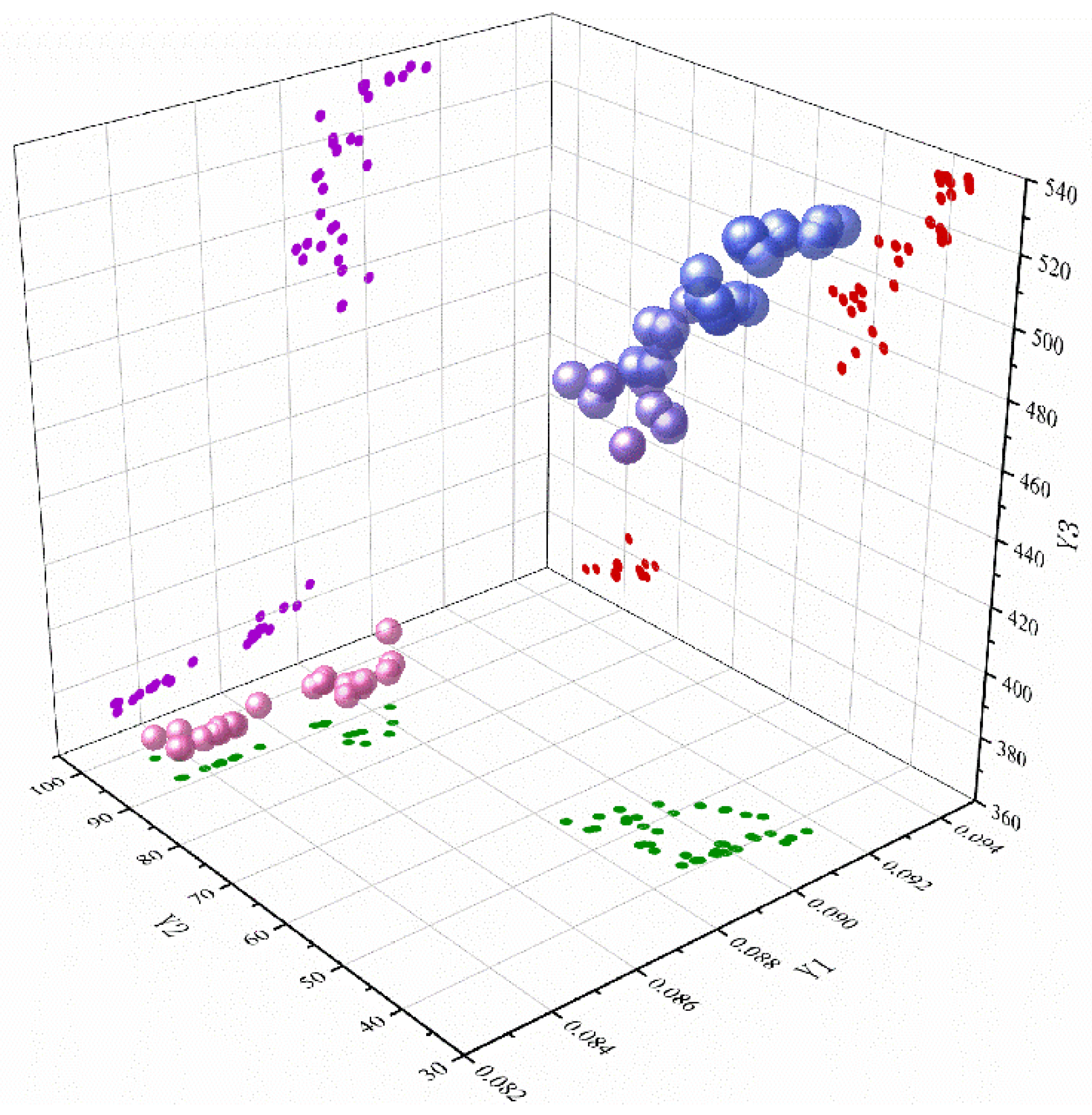
3.3.3. Multi-Objective Optimization of Hollow Internally Supported Screw Rotors Based on NSGA-III
4. Discussion
4.1. Limitations
4.1.1. Additive Manufacturing Dependency
4.1.2. Experimental Verification Is Restricted by Practical Operational Conditions
4.1.3. The Optimization Objectives Have Not Covered All the Performance Requirements
4.2. Performance Comparison of Prediction Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SNRBO | enhanced Newton–Raphson-based optimization algorithm |
| NRBO | Newton–Raphson-based optimization algorithm |
| XGBoost | extreme gradient boosting regression model |
| SHAP | SHapley Additive exPlanations |
| NSGA-Ⅲ | non-dominated sorting genetic algorithm III |
| NSGA-II | non-dominated sorting genetic algorithm II |
| R2 | Coefficient of determination |
| RMSE | Root Mean Square Error |
| BO | Bayesian Optimization |
| SMOTE | Synthetic Minority Over-sampling Technique |
| RSM | Response Surface Methodology |
| GA | Genetic Algorithm |
| FE | Finite Element |
| RVEA | Reference Vector Guided Evolutionary Algorithm |
| HHO | Harris Hawks Optimization |
| CNN | Convolutional Neural Network |
| LSSVM | Least Squares Support Vector Machine |
| DBO | Dung Beetle Optimizer |
| GWO | Grey Wolf Optimizer |
| SSA | Salp Swarm Algorithm |
Appendix A
| Algorithm A1 SNRBO Algorithm Pseudo-Code |
| Input: N, T, DFmin, DFmax, γ, t0 Output: Xb, f(Xb), 1: Initialize population, evaluate fitness 2: Xb = best solution, M = empty set 3: for t = 1 to T do 4: DF = DFmin + (DFmax − DFmin)/(1 + exp(γ(t − t0))) 5: δ = (1 − 2t/T)^5, p_levy = 0.5 + 0.4*DF 6: Rank population, divide into elite E and exploration P groups 7: for each Xi in P do 8: if rand < p_levy then 9: Xi = Levy-Flight (Xi, Xb) 10: Update if improved 11: end 12: for i = 1 to N do 13: if (Xi in P and rand < p_levy) then continue 14: ρ = rand*(Xb − Xi) + rand*(Xr1 − Xr2) 15: X1 = Xi − α*NRSR + ρ, X2 = Xb − α*NRSR + ρ 16: att_weights = normalized dimension variances 17: Xupdate = attention_weighted_combination(X1, X2, att_weights) 18: if Xi in E then DFi = 0.3*DF 19: else if Xi in P then DFi = min(2*DF, 0.95) 20: else DFi = DF 21: if rand < DFi then 22: Xnew = TAO_operator(Xupdate, Xb, mean(X)) 23: else 24: Xnew = Xupdate 25: if t > 0.3T and rand < 0.4 then 26: Xnew = tangent_perturbation(Xnew) 27: end 28: if f(Xnew) < f(Xi) then 29: Xi = Xnew, update Xb and M 30: end 31: if t > 0.4T and mod(t,5) = 0 then 32: replace_worst_solution(M) 33: end if 34: apply_GA_operations() 35: if t > 0.7T then perturb_elite(E) 36: end for 37: return Xb, f(Xb) |
| Fun. | Indicator | NRBO | SNRBO1 | SNRBO2 | SNRBO3 | SNRBO4 | SNRBO5 |
|---|---|---|---|---|---|---|---|
| F1 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F2 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F3 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F4 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F5 | min | 25.7137 | 27.8527 | 28.4447 | 21.4724 | 21.7689 | 9.7922 |
| avg | 28.8771 | 28.5851 | 28.3361 | 22.6339 | 22.1963 | 12.7850 | |
| std | 1.0529 | 0.2999 | 0.1610 | 0.9606 | 0.6451 | 1.4854 | |
| F6 | min | 1.6494 | 1.4600 | 1.1386 | 1.815 × 10−5 | 1.836 × 10−5 | 6.512 × 10−23 |
| avg | 2.3334 | 2.2199 | 1.5224 | 1.432 × 10−4 | 1.949 × 10−4 | 5.138 × 10−18 | |
| std | 0.7418 | 0.6544 | 0.5155 | 1.629 × 10−4 | 2.679 × 10−4 | 1.178 × 10−17 | |
| F7 | min | 5.654 × 10−6 | 2.522 × 10−7 | 1.074 × 10−7 | 6.652 × 10−7 | 5.367 × 10−7 | 1.882 × 10−7 |
| avg | 1.688 × 10−5 | 4.191 × 10−6 | 3.691 × 10−6 | 3.478 × 10−6 | 2.504 × 10−6 | 2.431 × 10−6 | |
| std | 9.616 × 10−6 | 3.304 × 10−6 | 3.551 × 10−6 | 2.922 × 10−6 | 2.421 × 10−6 | 2.253 × 10−6 | |
| F8 | min | −12,568.90 | 12,550.975 | −12,358.18 | −12,214.164 | −12,451.031 | −12,569.486 |
| avg | −11,973.12 | −11,157.92 | −11,003.45 | −11,714.179 | −11,784.138 | −11,977.295 | |
| std | 617.5375 | 1372.6429 | 1072.1951 | 434.0522 | 521.7963 | 611.6129 | |
| F9 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F10 | min | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 |
| avg | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F11 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F12 | min | 0.09233 | 0.03057 | 0.019306 | 2.273 × 10−6 | 5.987 × 10−7 | 6.572 × 10−24 |
| avg | 0.153102 | 0.056847 | 0.032247 | 6.185 × 10−6 | 4.492 × 10−6 | 1.234 × 10−18 | |
| std | 0.054765 | 0.025349 | 0.022736 | 4.491 × 10−6 | 3.871 × 10−6 | 3.489 × 10−18 | |
| F13 | min | 1.189616 | 0.758649 | 0.941598 | 0.022144 | 0.011323 | 4.351 × 10−23 |
| avg | 1.673366 | 1.144747 | 2.02854 | 1.054652 | 0.428257 | 1.829 × 10−9 | |
| std | 0.497172 | 0.226336 | 0.739845 | 1.140854 | 0.449570 | 5.783 × 10−9 | |
| F14 | min | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 |
| avg | 0.998004 | 1.196414 | 1.196809 | 1.196414 | 1.394824 | 0.998004 | |
| std | 0 | 0.627428 | 0.419119 | 0.627428 | 0.836571 | 0 | |
| F15 | min | 0.000307 | 0.000307 | 0.000307 | 0.000307 | 0.000307 | 0.000307 |
| avg | 0.000582 | 0.000582 | 0.002445 | 0.000307 | 0.000410 | 0.000307 | |
| std | 0.000442 | 0.000442 | 0.004310 | 1.7332 × 10−19 | 0.000288 | 2.0284 × 10−19 | |
| F16 | min | −1.03163 | −1.031628 | −1.031628 | −1.031628 | −1.031628 | −1.031628 |
| avg | −1.031629 | −1.031629 | −1.031629 | −1.031629 | −1.031629 | −1.031629 | |
| std | 1.282 × 10−16 | 7.402 × 10−17 | 1.047 × 10−16 | 0 | 7.402 × 10−17 | 7.402 × 10−17 | |
| F17 | min | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 |
| avg | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | 0.397887 | |
| std | 0 | 0 | 0 | 0 | 0 | 2.5173 × 10−12 | |
| F18 | min | 3 | 3 | 3 | 3 | 3 | 3 |
| avg | 3 | 3 | 3 | 3 | 3 | 3 | |
| std | 7.972 × 10−16 | 3.310 × 10−16 | 1.412 × 10−15 | 0 | 1.099 × 10−15 | 7.402 × 10−16 | |
| F19 | min | −3.862782 | −3.862782 | −3.862782 | −3.862782 | −3.862782 | −3.862782 |
| avg | −3.862782 | −3.862782 | −3.862782 | −3.862782 | −3.862782 | −3.862782 | |
| std | 9.004 × 10−16 | 9.362 × 10−16 | 9.004 × 10−16 | 9.362 × 10−16 | 9.004 × 10−16 | 9.362 × 10−16 | |
| F20 | min | −3.321995 | −3.321995 | −3.321995 | −3.321995 | −3.321995 | −3.321995 |
| avg | −3.250659 | −3.274431 | −3.274434 | −3.262549 | −3.2744379 | −3.278761 | |
| std | 0.061396 | 0.061396 | 0.061402 | 0.062662 | 0.061396 | 0.057431 | |
| F21 | min | −10.15311 | −10.15311 | −10.15311 | −10.15311 | −10.15311 | −10.15311 |
| avg | −10.15311 | −10.15311 | −10.15311 | −10.15311 | −10.15311 | −10.15311 | |
| std | 1.184 × 10−15 | 1.324 × 10−15 | 1.675 × 10−15 | 1.324 × 10−15 | 1.026 × 10−15 | 5.921 × 10−16 | |
| F22 | min | −10.40294 | −10.40294 | −10.40294 | −10.40294 | −10.40294 | −10.40294 |
| avg | −10.40294 | −10.40294 | −10.40294 | −10.40294 | −10.40294 | −10.40294 | |
| std | 1.872 × 10−15 | 1.324 × 10−15 | 1.184 × 10−15 | 1.675 × 10−15 | 1.184 × 10−15 | 2.581 × 10−15 | |
| F23 | min | −10.53641 | −10.53641 | −10.53641 | −10.53641 | −10.53641 | −10.53641 |
| avg | −10.53641 | −10.53641 | −10.53641 | −10.53641 | −10.53641 | −10.53641 | |
| std | 1.450 × 10−15 | 1.450 × 10−15 | 1.324 × 10−15 | 1.675 × 10−15 | 2.777 × 10−15 | 1.776 × 10−15 |
| Fun. | Indicator | SNRBO | NRBO | SSA | GWO | DBO |
|---|---|---|---|---|---|---|
| F1 | min | 100 | 124,176.0025 | 100 | 817.51846 | 173.12119 |
| F1 | std | 336.44854 | 52,396,364.03 | 3556.1416 | 62,984,131.2639 | 4475.46590 |
| F1 | avg | 186.27925 | 33,293,989.09 | 3337.8741 | 14,147,219.2599 | 5858.13815 |
| F3 | min | 300 | 313.9677 | 300 | 300.13304 | 300 |
| F3 | std | 0 | 91.04806 | 0 | 1071.63855 | 0 |
| F3 | avg | 300 | 475.57855 | 300 | 852.53363 | 300 |
| F4 | min | 400 | 402.19641 | 400.00000 | 403.14014 | 400.07016 |
| F4 | std | 0 | 31.14973 | 0 | 15.43142 | 13.38114 |
| F4 | avg | 400 | 430.56487 | 400.3674 | 412.35204 | 406.94101 |
| F5 | min | 504.9748 | 516.57792 | 503.97984 | 504.05717 | 504.97479 |
| F5 | std | 8.84329 | 9.96965 | 11.48416 | 5.95447 | 6.66001 |
| F5 | avg | 518.97102 | 533.57897 | 525.30341 | 511.03369 | 522.70239 |
| F6 | min | 600 | 607.12295 | 600.00000 | 600.00891 | 600.00000 |
| F6 | std | 0.00206 | 7.80463 | 1.59585 | 0.35555 | 2.27558 |
| F6 | avg | 600.00152 | 619.90204 | 601.10083 | 600.15725 | 602.33398 |
| F7 | min | 713.91117 | 730.24737 | 731.59653 | 712.33565 | 708.97840 |
| F7 | std | 7.21851 | 21.07161 | 23.75471 | 7.64913 | 7.46474 |
| F7 | avg | 726.19065 | 758.93307 | 783.39142 | 722.16173 | 725.91688 |
| F8 | min | 806.96471 | 813.43160 | 812.93446 | 807.97522 | 808.95463 |
| F8 | std | 6.40387 | 8.96927 | 8.98823 | 3.17468 | 8.82478 |
| F8 | avg | 818.34038 | 827.06885 | 823.92535 | 809.62024 | 822.93602 |
| F9 | min | 900.00000 | 905.84990 | 900.00000 | 900.01313 | 900.00000 |
| F9 | std | 5.65447 | 67.08529 | 354.26517 | 2.82068 | 3.68053 |
| F9 | avg | 905.42374 | 984.95043 | 1145.74665 | 901.14792 | 901.29885 |
| F10 | min | 1133.81242 | 1421.27755 | 1280.61180 | 1015.42557 | 1147.38275 |
| F10 | std | 270.04951 | 250.57236 | 240.40111 | 251.58968 | 253.89499 |
| F10 | avg | 1711.60906 | 2006.60409 | 1683.82157 | 1400.52767 | 1606.67873 |
| F11 | min | 1101.98992 | 1119.55790 | 1102.98524 | 1102.95127 | 1104.97934 |
| F11 | std | 11.51121 | 40.10057 | 25.73050 | 11.73251 | 29.66915 |
| F11 | avg | 1119.06204 | 1166.71162 | 1128.69244 | 1117.48381 | 1132.33242 |
| F12 | min | 1451.38590 | 2897.21761 | 1982.23961 | 6897.36608 | 2508.87278 |
| F12 | std | 2694.83596 | 10,265.77734 | 15,364.86967 | 328,359.1615 | 2,110,737.0396 |
| F12 | avg | 4216.89183 | 14,370.96598 | 15,577.15813 | 177,246.9490 | 70,3962.56377 |
| F13 | min | 1302.98414 | 1405.03686 | 1327.09764 | 2022.79046 | 1443.23262 |
| F13 | std | 12.58360 | 1982.94961 | 5687.09723 | 4092.65220 | 5864.18388 |
| F13 | avg | 1316.87656 | 2504.87980 | 6217.54535 | 8182.66088 | 5145.97250 |
| F14 | min | 1406.96774 | 1440.78368 | 1420.97355 | 1434.10057 | 1422.13311 |
| F14 | std | 14.38608 | 35.93665 | 46.26779 | 931.88763 | 38.43662 |
| F14 | avg | 1430.25107 | 1495.49276 | 1478.91879 | 1709.67369 | 1469.24885 |
| F15 | min | 1501.02371 | 1533.72143 | 1505.59184 | 1502.62578 | 1503.52932 |
| F15 | std | 4.80121 | 75.06641 | 57.04805 | 889.74214 | 113.36744 |
| F15 | avg | 1506.69320 | 1635.57594 | 1557.51709 | 1913.93949 | 1635.95996 |
| F16 | min | 1600.22931 | 1605.90206 | 1601.20917 | 1608.01391 | 1601.65460 |
| F16 | std | 102.02903 | 131.97874 | 111.26928 | 75.50711 | 77.53228 |
| F16 | avg | 1693.02966 | 1748.41829 | 1742.96138 | 1689.35298 | 1686.18223 |
| F17 | min | 1700.33190 | 1730.06691 | 1704.30192 | 1721.33517 | 1716.85587 |
| F17 | std | 21.38372 | 30.73677 | 51.79666 | 32.94601 | 15.16309 |
| F17 | avg | 1725.70295 | 1769.44433 | 1769.23866 | 1746.26028 | 1739.29766 |
| F18 | min | 1800.51291 | 1838.39242 | 1826.82200 | 2255.44064 | 1838.56018 |
| F18 | std | 196.36508 | 1867.81389 | 3151.60955 | 13687.36607 | 16810.86183 |
| F18 | avg | 1897.60093 | 2360.41053 | 4057.23803 | 28533.32891 | 16812.07757 |
| F19 | min | 1900.02737 | 1911.92055 | 1903.43185 | 1909.46430 | 1902.56311 |
| F19 | std | 1.31352 | 63.11017 | 53.67761 | 3485.08861 | 173.65993 |
| F19 | avg | 1901.74850 | 1973.05750 | 1957.93204 | 3062.91461 | 2002.41438 |
| F20 | min | 2000 | 2055.74524 | 2004.60418 | 2020.10918 | 2000.62435 |
| F20 | std | 9.65600 | 50.86268 | 47.55108 | 35.31542 | 42.25531 |
| F20 | avg | 2016.35479 | 2129.97355 | 2054.97615 | 2045.31473 | 2052.15641 |
| F21 | min | 2200 | 2202.67230 | 2200.00000 | 2200.90834 | 2200.00000 |
| F21 | std | 63.08986 | 66.70043 | 63.22422 | 41.31547 | 1.49200 |
| F21 | avg | 2281.36301 | 2270.73246 | 2301.77345 | 2293.25695 | 2203.48697 |
| F22 | min | 2217.52084 | 2250.91451 | 2235.39825 | 2215.19046 | 2237.05251 |
| F22 | std | 17.74511 | 14.76760 | 20.04195 | 17.62704 | 20.43483 |
| F22 | avg | 2301.39941 | 2320.00699 | 2302.31216 | 2302.58202 | 2297.86689 |
| F23 | min | 2610.69861 | 2610.80379 | 2607.44724 | 2600.00272 | 2613.17756 |
| F23 | std | 12.92772 | 13.19294 | 12.36620 | 6.76735 | 10.01144 |
| F23 | avg | 2632.23310 | 2633.03974 | 2635.55692 | 2611.95198 | 2626.76312 |
| F24 | min | 2500 | 2512.01483 | 2742.20024 | 2512.70708 | 2500.00000 |
| F24 | std | 70.62642 | 76.96254 | 16.21712 | 42.94487 | 132.10737 |
| F24 | avg | 2749.04379 | 2738.78077 | 2769.67451 | 2732.94629 | 2631.45750 |
| F25 | min | 2897.83753 | 2900.37786 | 2600.11883 | 2897.97838 | 2897.99141 |
| F25 | std | 37.25321 | 27.22098 | 64.29866 | 18.79091 | 24.45282 |
| F25 | avg | 2937.27896 | 2939.77535 | 2916.72363 | 2925.10783 | 2933.46772 |
| F26 | min | 2600 | 2776.19216 | 2815.56254 | 2900.03202 | 2900.00000 |
| F26 | std | 250.89507 | 233.66277 | 346.84593 | 185.68980 | 53.65751 |
| F26 | avg | 3023.63974 | 3069.35543 | 3164.22478 | 2942.26237 | 3016.90388 |
| F27 | min | 3092.51952 | 3091.43432 | 3089.30808 | 3089.51819 | 3089.54597 |
| F27 | std | 29.52312 | 19.57435 | 11.35292 | 16.15390 | 2.94698 |
| F27 | avg | 3112.32235 | 3100.39465 | 3099.40017 | 3096.15172 | 3095.25721 |
| F28 | min | 3100.00000 | 3135.70347 | 3100.00000 | 3100.05392 | 3100.00000 |
| F28 | std | 148.53881 | 124.59793 | 133.97350 | 112.45144 | 120.61598 |
| F28 | avg | 3339.64232 | 3339.14228 | 3312.58679 | 3335.65132 | 3280.41282 |
| F29 | min | 3159.13411 | 3159.77030 | 3130.64420 | 3132.32337 | 3133.24937 |
| F29 | std | 51.42653 | 60.40935 | 70.04303 | 27.56341 | 65.29587 |
| F29 | avg | 3231.41020 | 3228.67191 | 3253.31266 | 3162.52871 | 3222.27078 |
| F30 | min | 3461.49845 | 3957.63263 | 3875.68595 | 5716.62950 | 3861.09668 |
| F30 | std | 490,258.8057 | 471,382.8663 | 383,885.7759 | 640,575.4247 | 347,806.93168 |
| F30 | avg | 333,555.0316 | 396,657.6868 | 210,909.85553 | 518,213.5952 | 241,165.22062 |
References
- Ulu, E.; Huang, R.; Kara, L.B.; Whitefoot, K.S. Concurrent Structure and Process Optimization for Minimum Cost Metal Additive Manufacturing. ASME J. Mech. Des. 2019, 141, 061701. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Liu, S.; Wang, C.; Shen, S.; Guo, Y. Review and Prospects of Numerical Simulation Research on Internal Flow and Performance Optimization of Twin-Screw Compressors. Energies 2025, 18, 2608. [Google Scholar] [CrossRef]
- Aydın, A.; Engin, T.; Kovacevic, A. Design optimisation of a screw compressor with a focus on rotor depth: A computational fluid dynamics approach. Int. J. Refrig. 2025, 170, 385–397. [Google Scholar] [CrossRef]
- Dhayanandh, K.K.; Rameshkumar, K.; Sumesh, A.; Lakshmanan, N. Influence of oil injection parameters on the performance of diesel powered screw air compressor for water well application. Measurement 2019, 152, 107323. [Google Scholar] [CrossRef]
- Kaufmann, F.; Irrgang, L.; Schifflechner, C.; Spliethoff, H. Fast and accurate modelling of twin-screw compressors: A generalised low-order approach. Appl. Therm. Eng. 2024, 257, 124238. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, H.; Gao, D.; Xu, L.; Zhang, Y. Heat transfer simulation in cavity of twin screw compressor under coupling of clearance leakage-heat by utilizing fuzzy beamlet finite element model. J. Therm. Anal. Calorim. 2021, 143, 3221–3232. [Google Scholar] [CrossRef]
- Tian, Z.Y.; Zhao, Y.Q.; Li, Z.H.; Liu, S.; Wang, D.H. Optimization and characteristic analysis of screw rotor of a twin-screw pump. J. Vibroeng. 2023, 25, 171–188. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q.; Zhang, L.; Fu, Z. Data driven NARMAX modeling for PEMFC air compressor. Int. J. Hydrogen Energy 2019, 45, 20321–20328. [Google Scholar] [CrossRef]
- Kumar, A.; Patil, S.; Kovacevic, A.; Ponnusami, S.A. Performance prediction and Bayesian optimization of screw compressors using Gaussian Process Regression. Eng. Appl. Artif. Intell. 2024, 133, 108270. [Google Scholar] [CrossRef]
- Wang, T.; Qi, Q.; Zhang, W.; Zhan, D. Research on Optimization of Profile Parameters in Screw Compressor Based on BP Neural Network and Genetic Algorithm. Energies 2023, 16, 3632. [Google Scholar] [CrossRef]
- Tran, V.Q.; Wu, Y.R. Uniform-design-based multi-objective optimization for twin-screw rotor profiles generated by sealing line. Mech. Mach. Theory 2025, 209, 105985. [Google Scholar] [CrossRef]
- Saravana, A.; Liu, H.; Able, N.; Collins, J.; Groll, E.A.; Ziviani, D. Conjugate heat transfer analysis of a twin-screw compressor with 4–6 configuration and internal cooling channels. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2022; Volume 1267, p. 012014. [Google Scholar] [CrossRef]
- Zhang, Y.; Huan, C.; Chao, R.; Wan, Z.; Zhi, M.; Wan, X. Design and Analysis of New Screw Rotor Structure Based on the 3D Printing Technology. Mech. Res. Appl. 2020, 33, 19–22. [Google Scholar] [CrossRef]
- Chao, R. Research on Structural Design and Processing Method of Hollow Screw Rotor. Master’s Thesis, Shanxi University of Technology, Shanxi, China, 2021. [Google Scholar] [CrossRef]
- Wan, Z. Design and Optimization of Lightweight Screw Rotor with Hollow Inner Support. Master’s Thesis, Shanxi University of Technology, Shanxi, China, 2021. [Google Scholar] [CrossRef]
- Zh, M. Research on Lightweight Design and Additive Manufacturing Technology of Screw Rotor of Air Compressor. Master’s Thesis, Shanxi University of Technology, Shanxi, China, 2022. [Google Scholar] [CrossRef]
- Bandini, A.; Cascino, A.; Meli, E.; Pinelli, L.; Marconcini, M. Improving Aeromechanical Performance of Compressor Rotor Blisk with Topology Optimization. Energies 2024, 17, 1883. [Google Scholar] [CrossRef]
- Wu, C.; Pan, H.; Luo, Z.; Liu, C.; Huang, H. Multi-objective optimization of residential building energy consumption, daylighting, and thermal comfort based on BO-XGBoost-NSGA-II. Build. Environ. 2024, 254, 111386. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, Z.; Wang, M.; Liu, B.; Tian, W. A machine learning proxy based multi-objective optimization method for low-carbon hydrogen production. J. Clean. Prod. 2024, 445, 141377. [Google Scholar] [CrossRef]
- Han, Y.; Wei, Z.; Huang, G. An imbalance data quality monitoring based on SMOTE-XGBOOST supported by edge computing. Sci. Rep. 2024, 14, 10151. [Google Scholar] [CrossRef] [PubMed]
- Mao, F.; Chen, M.; Zhong, K.; Zeng, J.; Liang, Z. An XGBoost-assisted evolutionary algorithm for expensive multiobjective optimization problems. Inf. Sci. 2024, 666, 120449. [Google Scholar] [CrossRef]
- Mehdary, A.; Chehri, A.; Jakimi, A.; Saadane, R. Hyperparameter optimization with genetic algorithms and XGBoost: A step forward in smart grid fraud detection. Sensors 2024, 24, 1230. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Wang, H.; Sun, X.; Bao, H.; Wang, X.; Liu, J. Multi-objective optimization for impeller structure parameters of fuel cell air compressor using linear-based boosting model and reference vector guided evolutionary algorithm. Appl. Energy 2024, 363, 123057. [Google Scholar] [CrossRef]
- Zivkovic, M.; Tair, M.; Bacanin, N.; Hubálovský, Š.; Trojovský, P. Novel hybrid firefly algorithm: An application to enhance XGBoost tuning for intrusion detection classification. PeerJ Comput. Sci. 2022, 8, e956. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, H.; Chen, Y. Research on SAR image quality evaluation method based on improved harris hawk optimization algorithm and XGBoost. Sci. Rep. 2024, 14, 28364. [Google Scholar] [CrossRef]
- Lima Marinho, T.; do Nascimento, D.C.; Pimentel, B.A. Optimization on selecting XGBoost hyperparameters using meta-learning. Expert Syst. 2024, 41, e13611. [Google Scholar] [CrossRef]
- Li, Q.; Chu, W.; Ji, T.; Wang, H.; Guo, Z. SHAP-XGBoost Enabled Aerodynamic-Structural Balance in Transonic Compressors: T-shaped Groove Casing Treatment Design with Data-Driven Parameter Decoupling. Aerosp. Sci. Technol. 2025, 164, 110391. [Google Scholar] [CrossRef]
- Wang, J.; Chen, B.; Wang, Y.; Pu, D.; Jia, X. Research on four-bar linkage trajectory synthesis using extreme gradient boosting and genetic algorithm. J. Comput. Des. Eng. 2024, 11, 1–21. [Google Scholar] [CrossRef]
- Sowmya, R.; Premkumar, M.; Jangir, P. Newton-Raphson-based optimizer: A new population-based metaheuristic algorithm for continuous optimization problems. Eng. Appl. Artif. Intell. 2023, 128, 107532. [Google Scholar] [CrossRef]
- Huan, B.; Li, X.; Wang, J.; Hu, T.; Tao, Z. An interpretable deep learning model for the accurate prediction of mean fragmentation size in blasting operations. Sci. Rep. 2025, 15, 11515. [Google Scholar] [CrossRef]
- Li, Z.; Wang, M.; Xu, R.; Jiang, J.; Li, J.; Zhang, Z.; Yang, A. Prediction of viscosity of blast furnace slag based on NRBO-DNN model. Alex. Eng. J. 2025, 119, 124–137. [Google Scholar] [CrossRef]
- Li, Y.; Ni, L.; Chen, G.; Zhang, L.; Yao, N.; Wang, G. Neuro-enhanced fractional hysteresis modeling and identification by modified Newton-Raphson optimizer. Appl. Math. Model. 2025, 140, 115865. [Google Scholar] [CrossRef]
- AbouOmar, M.S.; Eltayeb, A.; Al-Quraishi, M.S.; El Ferik, S. Parameter Estimation of Proton Exchange Membrane Fuel Cells Using Chaotic Newton-Raphson-Based Optimizer. Results Eng. 2024, 24, 103369. [Google Scholar] [CrossRef]
- Shi, W.; Liang, Q.; Sun, L. Path Planning for Yarn Changing Robots Based on NRBO and Dynamic Obstacle Avoidance Strategy. Appl. Sci. 2024, 14, 11086. [Google Scholar] [CrossRef]
- Ni, Y.; Song, K.; Pei, L.; Li, X.; Wang, T.; Zhang, H.; Xu, J. State-of-health estimation and knee point identification of lithium-ion battery based on data-driven and mechanism model. Appl. Energy 2025, 385, 125539. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, J.; Shao, Z.; Ma, Q.; Liu, W. Machine Learning Innovations in Renewable Energy Systems with Integrated NRBO-TXAD for Enhanced Wind Speed Forecasting Accuracy. Electronics 2025, 14, 2329. [Google Scholar] [CrossRef]
- Zeng, H.; Wu, B.; Fang, H.; Lin, J. Interpretable wind speed forecasting through two-stage decomposition with comprehensive relative importance analysis. Appl. Energy 2025, 392, 126015. [Google Scholar] [CrossRef]
- Abazine, I.; Elyaqouti, M.; Saadaoui, D.; Hmamou, D.B.; Elhammoudy, A.; Lidaighbi, S.; Ydir, B. Accurate parameter extraction for photovoltaic systems using an improved and stable hybrid Analytical-NRBO algorithm. Int. J. Hydrogen Energy 2025, 139, 564–593. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization. KanGAL Rep. 2005, 341–357. Available online: https://www.academia.edu/download/33925834/Tech-Report-May-30-05.pdf (accessed on 10 October 2025).
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report 9; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Ahrari, A.; Elsayed, S.; Sarker, R.; Essam, D.; Coello, C.A.C. Problem definition and evaluation criteria for the CEC 2022 competition on dynamic multimodal optimization. In Proceedings of the IEEE World Congress on Computational Intelligence (IEEE WCCI 2022), Padua, Italy, 18–23 July 2022. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]


| Study | Structural | Optimization Method | Optimization Results | Comparative Analysis |
|---|---|---|---|---|
| Chao [13] | Equal wall thickness hollow rotor | Finite element static and modal analysis comparing wall thickness designs; prioritize mass reduction while ensuring strength and modal safety. | Mass reduction of 39.75%, 35.82%, and 21.04% for the three wall thickness configurations; corresponding modal frequency decreases of 7.1%, 5.8%, and 0.6% | Focused on manufacturability and weight reduction; lacks systematic optimization and multi-objective strategies, limiting complex design application |
| Wang [14] | Equal wall thickness with internal support structure | RSM with FE static, modal, and FSI analysis; sequential design optimization to reduce mass first, then minimize deformation within parameter limits. | Mass reduced by 27.09%, deformation increased by 2.86% | Sequential optimization, single-point solution; response surface dependent, unsuitable for global multi-objective |
| Zhi [15] | Shell–internal framework structure design integrated with additive manufacturing | Orthogonal design with FE static, FSI, and thermal analysis; reduce mass first, then control deformation; emphasizes manufacturability. | Mass reduced by 25.43%, static deformation increased by 7.4% | Focuses on manufacturability; lacks global exploration, with analysis confined to a limited parameter range and reliant on orthogonal design, reducing optimization depth and trade-off exploration. |
| Present Method | Parameterized modeling with internal support framework for lightweight design | SNRBO surrogate modeling + NSGA-III multi-objective optimization with thermal–fluid–solid coupling; simultaneously minimize mass and deformation, maximize natural frequency. | Mass reduced by 64.43%, deformation reduced by 4.41%, first natural frequency increased by 82.14% | Global multi-objective framework and high-fidelity model; efficient trade-off exploration, strong engineering applicability |
| Design Parameter | Variable Name | Unit | Value Range |
|---|---|---|---|
| Thickness of Both End Faces | X1 | mm | [5,35] |
| Thickness of Working Gear Face | X2 | mm | [4–40] |
| Width of Internal Support Rod | X3 | mm | [4–16] |
| Diameter of Internal Support Column | X4 | mm | [20–78] |
| X1 | X2 | X3 | X4 |
|---|---|---|---|
| 31.70 | 28.40 | 5.10 | 41.30 |
| 14.80 | 8.80 | 8.20 | 45.80 |
| 13.80 | 23.70 | 9.30 | 32.50 |
| 6.90 | 36.10 | 10.30 | 60.60 |
| 6.50 | 12.70 | 7.50 | 75.20 |
| NO. | Name | Dim | Range | fmin |
|---|---|---|---|---|
| F01 | Sphere Function | 30 | [−100,100] | 0 |
| F02 | Schwefel’s Problem 2.22 | 30 | [−10,10] | 0 |
| F03 | Schwefel’s Problem 1.2 | 30 | [−100,100] | 0 |
| F04 | Schwefel’s Problem 2.21 | 30 | [−100,100] | 0 |
| F05 | Generalized Rosenbrock’s Function | 30 | [−30,30] | 0 |
| F06 | Step Function | 30 | [−100,100] | 0 |
| F07 | Quartic Function, i.e., Noise | 30 | [−1.28,1.28] | 0 |
| F08 | Shifted and rotated Levy function | 30 | [−500,500] | −12,569.5 |
| F9 | Shifted and rotated Schwefel’s function | 30 | [−5.12,5.12] | 0 |
| F10 | Hybrid function 1 (N = 3) | 30 | [−32,32] | 0 |
| F11 | Hybrid function 2 (N = 3) | 30 | [−600,600] | 0 |
| F12 | Hybrid function 3 (N = 3) | 30 | [−50,50] | 0 |
| F13 | Hybrid function 4 (N = 4) | 30 | [−50,50] | 0 |
| F14 | Hybrid function 5 (N = 4) | 30 | [−65.536,65.536] | 0.99800383 |
| F15 | Hybrid function 6 (N = 4) | 30 | [−5,5] | 0.0003075 |
| F16 | Hybrid function 7 (N = 5) | 30 | [−5,5] | −1.0316285 |
| F17 | Hybrid function 8 (N = 5) | 30 | [−5,10–5,10] | 0.39788735 |
| F18 | Hybrid function 9 (N = 5) | 30 | [−2,2] | 2.999999 |
| F19 | Hybrid function 10 (N = 6) | 30 | [0,1] | −3.8627821 |
| F20 | Composition function 1 (N = 3) | 30 | [0,1] | −3.3219952 |
| F21 | Composition function 2 (N = 3) | 30 | [0,10] | −10 |
| F22 | Composition function 3 (N = 4) | 30 | [0,10] | −10 |
| F23 | Composition function 4 (N = 4) | 30 | [0,10] | −10 |
| Fun. | Indicator | NRBO | SNRBO1 | SNRBO2 | SNRBO3 | SNRBO4 | SNRBO5 |
|---|---|---|---|---|---|---|---|
| F1 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F2 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F3 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F4 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F5 | min | 25.7137 | 27.8527 | 28.4447 | 21.4724 | 21.7689 | 9.7922 |
| avg | 28.8771 | 28.5851 | 28.3361 | 22.6339 | 22.1963 | 12.7850 | |
| std | 1.0529 | 0.2999 | 0.1610 | 0.9606 | 0.6451 | 1.4854 | |
| F6 | min | 1.6494 | 1.4600 | 1.1386 | 1.815 × 10−5 | 1.836 × 10−5 | 6.512 × 10−23 |
| avg | 2.3334 | 2.2199 | 1.5224 | 1.432 × 10−4 | 1.949 × 10−4 | 5.138 × 10−18 | |
| std | 0.7418 | 0.6544 | 0.5155 | 1.629 × 10−4 | 2.679 × 10−4 | 1.178 × 10−17 | |
| F7 | min | 5.654 × 10−6 | 2.522 × 10−7 | 1.074 × 10−7 | 6.652 × 10−7 | 5.367 × 10−7 | 1.882 × 10−7 |
| avg | 1.688 × 10−5 | 4.191 × 10−6 | 3.691 × 10−6 | 3.478 × 10−6 | 2.504 × 10−6 | 2.431 × 10−6 | |
| std | 9.616 × 10−6 | 3.304 × 10−6 | 3.551 × 10−6 | 2.922 × 10−6 | 2.421 × 10−6 | 2.253 × 10−6 | |
| F8 | min | −12,568.90 | 12,550.975 | −12,358.18 | −12,214.164 | −12,451.031 | −12,569.486 |
| avg | −11,973.12 | −11,157.92 | −11,003.45 | −11,714.179 | −11,784.138 | −11,977.295 | |
| std | 617.5375 | 1372.6429 | 1072.1951 | 434.0522 | 521.7963 | 611.6129 | |
| F9 | min | 0 | 0 | 0 | 0 | 0 | 0 |
| avg | 0 | 0 | 0 | 0 | 0 | 0 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 | |
| F10 | min | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 |
| avg | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | 4.441 × 10−16 | |
| std | 0 | 0 | 0 | 0 | 0 | 0 |
| NO. | Name | Dim | Range | fmin |
|---|---|---|---|---|
| F01 | Shifted and rotated bent cigar function | 10 | [−100,100] | 100 |
| F03 | Shifted and rotated Zakharov function | 10 | [−100,100] | 300 |
| F04 | Shifted and rotated Rosenbrock’s function | 10 | [−100,100] | 400 |
| F05 | Shifted and rotated Rastrigin’s function | 10 | [−100,100] | 500 |
| F06 | Shifted and rotated expanded Scaffer’s F6 function | 10 | [−100,100] | 600 |
| F07 | Shifted and rotated Lunacek bi_Rastrigin function | 10 | [−100,100] | 700 |
| F08 | Shifted and rotated non-continuous Rastrigin’s function | 10 | [−100,100] | 800 |
| F09 | Shifted and rotated Levy function | 10 | [−100,100] | 900 |
| F10 | Shifted and rotated Schwefel’s function | 10 | [−100,100] | 1000 |
| F11 | Hybrid function 1 (N = 3) | 10 | [−100,100] | 1100 |
| F12 | Hybrid function 2 (N = 3) | 10 | [−100,100] | 1200 |
| F13 | Hybrid function 3 (N = 3) | 10 | [−100,100] | 1300 |
| F14 | Hybrid function 4 (N = 4) | 10 | [−100,100] | 1400 |
| F15 | Hybrid function 5 (N = 4) | 10 | [−100,100] | 1500 |
| F16 | Hybrid function 6 (N = 4) | 10 | [−100,100] | 1600 |
| F17 | Hybrid function 7 (N = 5) | 10 | [−100,100] | 1700 |
| F18 | Hybrid function 8 (N = 5) | 10 | [−100,100] | 1800 |
| F19 | Hybrid function 9 (N = 5) | 10 | [−100,100] | 1900 |
| F20 | Hybrid function 10 (N = 6) | 10 | [−100,100] | 2000 |
| F21 | Composition function 1 (N = 3) | 10 | [−100,100] | 2100 |
| F22 | Composition function 2 (N = 3) | 10 | [−100,100] | 2200 |
| F23 | Composition function 3 (N = 4) | 10 | [−100,100] | 2300 |
| F24 | Composition function 4 (N = 4) | 10 | [−100,100] | 2400 |
| F25 | Composition function 5 (N = 5) | 10 | [−100,100] | 2500 |
| F26 | Composition function 6 (N = 5 | 10 | [−100,100] | 2600 |
| F27 | Composition function 7 (N = 6) | 10 | [−100,100] | 2700 |
| F28 | Composition function 8 (N = 6) | 10 | [−100,100] | 2800 |
| F29 | Composition function 9 (N = 3) | 10 | [−100,100] | 2900 |
| F30 | Composition function 10 (N = 3) | 10 | [−100,100] | 3000 |
| Algorithm | Parameter |
|---|---|
| NRBO | |
| SSA | |
| GWO | |
| DBO |
| Fun. | Indicator | SNRBO | NRBO | SSA | GWO | DBO |
|---|---|---|---|---|---|---|
| F1 | min | 100 | 124,176.0025 | 100 | 817.51846 | 173.12119 |
| F1 | std | 336.44854 | 52,396,364.03 | 3556.1416 | 62,984,131.2639 | 4475.46590 |
| F1 | avg | 186.27925 | 33,293,989.09 | 3337.8741 | 14,147,219.2599 | 5858.13815 |
| F3 | min | 300 | 313.9677 | 300 | 300.13304 | 300 |
| F3 | std | 0 | 91.04806 | 0 | 1071.63855 | 0 |
| F3 | avg | 300 | 475.57855 | 300 | 852.53363 | 300 |
| F4 | min | 400 | 402.19641 | 400.00000 | 403.14014 | 400.07016 |
| F4 | std | 0 | 31.14973 | 0 | 15.43142 | 13.38114 |
| F4 | avg | 400 | 430.56487 | 400.3674 | 412.35204 | 406.94101 |
| F5 | min | 504.9748 | 516.57792 | 503.97984 | 504.05717 | 504.97479 |
| F5 | std | 8.84329 | 9.96965 | 11.48416 | 5.95447 | 6.66001 |
| F5 | avg | 518.97102 | 533.57897 | 525.30341 | 511.03369 | 522.70239 |
| F6 | min | 600 | 607.12295 | 600.00000 | 600.00891 | 600.00000 |
| F6 | std | 0.00206 | 7.80463 | 1.59585 | 0.35555 | 2.27558 |
| F6 | avg | 600.00152 | 619.90204 | 601.10083 | 600.15725 | 602.33398 |
| F7 | min | 713.91117 | 730.24737 | 731.59653 | 712.33565 | 708.97840 |
| F7 | std | 7.21851 | 21.07161 | 23.75471 | 7.64913 | 7.46474 |
| F7 | avg | 726.19065 | 758.93307 | 783.39142 | 722.16173 | 725.91688 |
| F8 | min | 806.96471 | 813.43160 | 812.93446 | 807.97522 | 808.95463 |
| F8 | std | 6.40387 | 8.96927 | 8.98823 | 3.17468 | 8.82478 |
| F8 | avg | 818.34038 | 827.06885 | 823.92535 | 809.62024 | 822.93602 |
| F9 | min | 900.00000 | 905.84990 | 900.00000 | 900.01313 | 900.00000 |
| F9 | std | 5.65447 | 67.08529 | 354.26517 | 2.82068 | 3.68053 |
| F9 | avg | 905.42374 | 984.95043 | 1145.74665 | 901.14792 | 901.29885 |
| F10 | min | 1133.81242 | 1421.27755 | 1280.61180 | 1015.42557 | 1147.38275 |
| F10 | std | 270.04951 | 250.57236 | 240.40111 | 251.58968 | 253.89499 |
| F10 | avg | 1711.60906 | 2006.60409 | 1683.82157 | 1400.52767 | 1606.67873 |
| Name | Symbol | Range | Description |
|---|---|---|---|
| num_trees | X1 | [30,500] | Number of decision trees: Too few cause less fitting; too many increase complexity and computational cost. |
| max_depth | X2 | [3,10] | Maximum tree depth: Controls model complexity. Greater depth boosts fitting ability but may cause overfitting. |
| eta | X3 | [0.0001,0.1] | Learning rate: Controls the weight update step size per tree. Smaller values require more iterations but yield a more robust model. |
| Density | Poisson Ratio | Thermal Expansion Coefficient | Thermal Conductivity | Yield Strength |
| 7.95 | 0.3 | 17.3 | 14 | 177 |
| Design Parameter | Optimized Value | Unit |
|---|---|---|
| Thickness of Both End Faces | 27.34 | mm |
| Thickness of Working Gear Face | 4.11 | mm |
| Width of Internal Support Rod | 4.72 | mm |
| Diameter of Internal Support Column | 24.16 | mm |
| Optimization Object | Initialization Value | Optimal Values | Variable Quantity |
|---|---|---|---|
| Maximum total deformation (Mm) | 0.08923 | 0.08896 | −0.3% |
| Mass (kg) | 113.14 | 44.46 | −60.7% |
| First-order Natural Frequency (Hz) | 302.12 | 517.11 | +71.16% |
| Regression Model | R2 | RMSE |
|---|---|---|
| Kriging | 0.943, 0.990, 0.955 | 0.0013, 2.3522, 8.0353 |
| RBF | 0.819, 0.951, 0.839 | 0.0020, 4.0443, 14.326 |
| SNRBO-XGBoost | 0.978, 0.990, 0.982 | 0.0008, 1.8084, 5.0453 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Zhou, J.; Zhou, B.; Zhu, H.; Zhao, Y.; Wang, J. Lightweight Design of Screw Rotors via an Enhanced Newton–Raphson-Based Surrogate-Assisted Multi-Objective Optimization Framework. Processes 2025, 13, 3779. https://doi.org/10.3390/pr13123779
Song J, Zhou J, Zhou B, Zhu H, Zhao Y, Wang J. Lightweight Design of Screw Rotors via an Enhanced Newton–Raphson-Based Surrogate-Assisted Multi-Objective Optimization Framework. Processes. 2025; 13(12):3779. https://doi.org/10.3390/pr13123779
Chicago/Turabian StyleSong, Jiahui, Jianqiang Zhou, Botao Zhou, Hehuai Zhu, Yanwei Zhao, and Junyi Wang. 2025. "Lightweight Design of Screw Rotors via an Enhanced Newton–Raphson-Based Surrogate-Assisted Multi-Objective Optimization Framework" Processes 13, no. 12: 3779. https://doi.org/10.3390/pr13123779
APA StyleSong, J., Zhou, J., Zhou, B., Zhu, H., Zhao, Y., & Wang, J. (2025). Lightweight Design of Screw Rotors via an Enhanced Newton–Raphson-Based Surrogate-Assisted Multi-Objective Optimization Framework. Processes, 13(12), 3779. https://doi.org/10.3390/pr13123779






