Experimental and Modeling Study of Acetonitrile Separation from Water with Ionic Liquids: VLE Data for Binary and Ternary Systems

Abstract

The vapor–liquid equilibrium (VLE) data of the binary acetonitrile + water system and three ternary systems containing ionic liquids (ILs): acetonitrile + water + 1-butyl-3-methylimidazolium chloride ([C₄mim][Cl]), + 1-butyl-3-methylimidazolium tetrafluoroborate ([C₄mim][BF₄]), and + 1-hexyl-3-methylimidazolium chloride ([C₆mim][Cl]) were experimentally measured at low pressures. In addition, the literature VLE data for the binary systems acetonitrile + [C₄mim][Cl], acetonitrile + [C₄mim][BF₄], and acetonitrile + [C₆mim][Cl] were adopted for model correlation. The NRTL and e-NRTL models were employed to correlate the binary data. The experimental results demonstrate that the presence of ILs causes a pronounced salting-out effect on acetonitrile, significantly increasing its relative volatility with respect to water. The separation performance of the three ILs for the acetonitrile + water mixture decreases in the order: [C₄mim][Cl] > [C₆mim][Cl] > [C₄mim][BF₄].

1. Introduction

Acetonitrile is an important chemical raw material [1] that is widely used as an extraction solvent in organic synthesis [2], the petroleum industry, and pharmaceuticals [3]. To ensure the purity of acetonitrile, during the process, the separation of acetonitrile–water mixtures is required. However, acetonitrile–water mixtures form a typical azeotropic system, with an azeotropic temperature of approximately 76 °C at atmospheric pressure and an azeotropic composition of 16% water and 84% acetonitrile by mass [4]. Conventional distillation methods cannot effectively separate them [4,5,6], necessitating specialized techniques. To address this, various separation methods have been developed, including heterogeneous azeotropic distillation, extractive distillation, pervaporation, and extractive distillation [7,8,9]. Among these, extractive distillation is widely applied due to its high energy efficiency and operational flexibility.

In the extractive distillation process, selecting an appropriate entrainer is crucial for the design. Traditional organic entrainers, such as ethylene glycol (EG) [10,11], dimethyl sulfoxide (DMSO) [10,12], and glycerol [1], are commonly used for the separation of acetonitrile and water. For example, DMSO can effectively disrupt the key hydrogen bonding interactions in the acetonitrile–water azeotropic system, thereby increasing the relative volatility of acetonitrile and breaking the azeotropic behavior. However, the practical application of these entrainers is limited by their volatility, high toxicity, and difficulties in recovery.

In the acetonitrile and water system, the addition of salt-based extractants can improve the separation of an azeotropic mixture through the salt effect [13]. However, in practical operations, using solid salts as extractants alone presents challenges such as solid salt handling, corrosion of metals, and crystallization, which may lead to pipeline blockages. As a novel type of solvent, ionic liquids (ILs) possess unique properties, including negligible volatility, near-zero vapor pressure, and the ability to form various combinations of asymmetric organic cations with organic or inorganic anions [14,15,16,17,18]. These features make ILs particularly attractive as entrainers in separation processes, as they can enhance selectivity and efficiency in systems such as acetonitrile + water [16,18,19,20,21].

Li et al. [22] validated through COSMO-RS calculations and experimental measurements that [Emim][OAc] and [Emim][Pro] are effective entrainers for the separation of acetonitrile and water. Fang et al. [19] and Li et al. [20] measured the isobaric VLE data for the ternary system of acetonitrile + water + [C₄mim][BF₄] at atmospheric pressure to investigate the influence of ILs on the phase behavior of the mixture. Their results showed that [C₄mim][BF₄] has a limited effect on enhancing the relative volatility of acetonitrile. But its aqueous solution exhibits lower viscosity [23,24] and surface tension [25], which can improve mass transfer performance and enhance operational efficiency in industrial applications. Meanwhile, another study by Li et al. [16] demonstrated that [C₄mim][Cl] and [C₆mim][Cl] exhibit superior separation performance for acetonitrile, effectively eliminating the azeotrope of the acetonitrile + water system.

However, most previous studies have focused on atmospheric pressure systems, while the VLE behavior of acetonitrile + water + ILs under reduced pressures remains largely unexplored. Theoretically, operating under reduced pressure can further improve the separation efficiency of acetonitrile and even eliminate the azeotropic behavior, offering a new pathway for more efficient industrial separations. Moreover, existing research has primarily centered on ternary systems, with limited data available for binary systems such as acetonitrile + ILs, which are essential for understanding the fundamental interactions between acetonitrile and ILs.

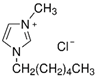
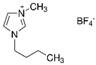
In this work, three ILs ([C₄mim][Cl], [C₆mim][Cl], and [C₄mim][BF₄]) were selected as entrainers. Chloride and tetrafluoroborate anions were chosen because Cl⁻ exhibits stronger hydrophilicity and hydrogen-bonding ability than BF₄⁻ [26], allowing the evaluation of anion effects on phase behavior and selectivity. The [C₄mim]⁺ and [C₆mim]⁺ cations were selected as representative imidazolium cations with medium-length alkyl chains, providing a balance between polarity and viscosity. Previous studies have shown that for the acetonitrile + water system, [Emim]⁺ exhibits a stronger salting-out effect than [Bmim]⁺ [18], motivating us to further investigate the performance of [C₄mim]⁺ and [C₆mim]⁺.

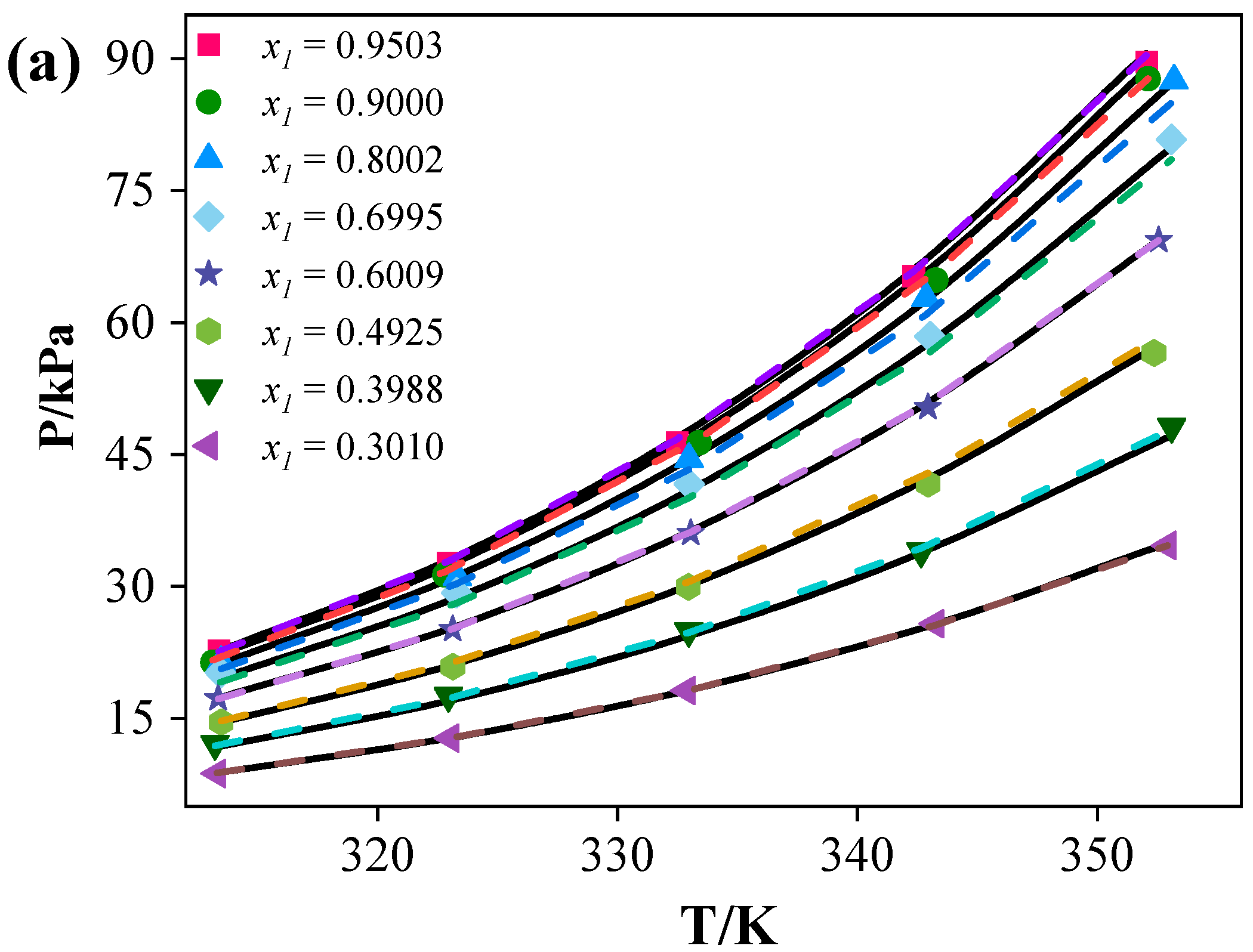
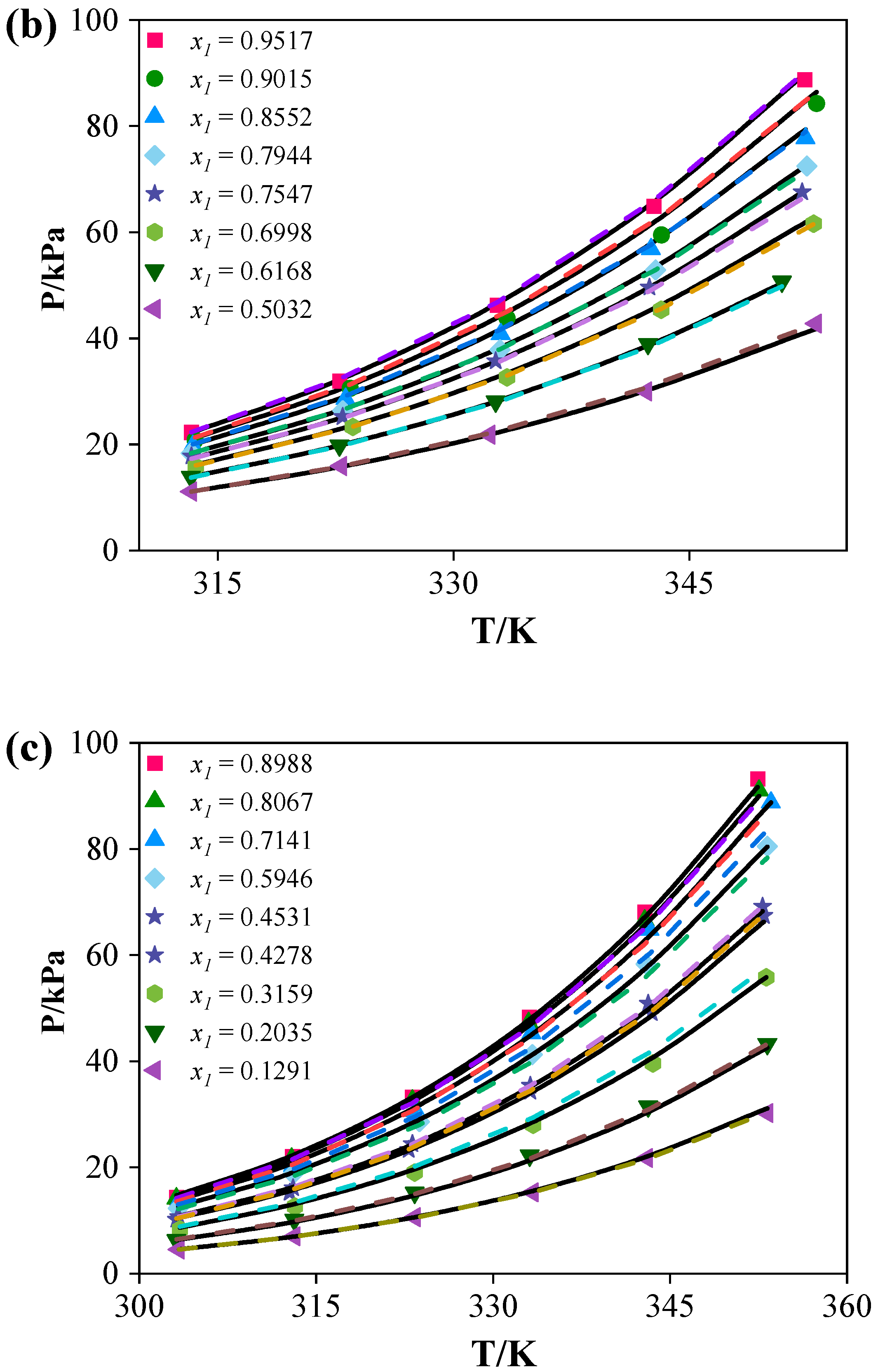
The VLE data of the binary systems (acetonitrile + ILs) were adopted from the literature [27] to explore the interaction mechanisms between ILs and acetonitrile. Meanwhile, the VLE data of the ternary systems (acetonitrile + water + ILs) were determined under different reduced pressures. The combination of these three ILs allows comparison of the effects of cation alkyl chain length and anion type on separation performance, enriching the available literature data, particularly for VLE behavior under reduced pressure. Furthermore, the NRTL model [16,18,19,20] and e-NRTL model [28,29,30], whose accuracy and applicability have been validated in many previous studies, were employed to correlate and predict the experimental data, providing a quantitative description of the thermodynamic behavior of the acetonitrile–water–ILs systems. The results of this study are significant for understanding the separation behavior of binary and ternary systems under reduced pressure, elucidating the effect of pressure on relative volatility, and providing valuable insights for the design of industrial separation processes.

2. Experimental Section

2.1. Chemicals

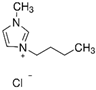
The chemical reagents used in this work included water, acetonitrile, and three ILs. The chemical structures and basic properties of the used ILs are presented in

Table 1. Chemical structures and basic properties of the used ILs.

Structure	Name (Abbreviation)	Molecular Formule	M/g·mol−1	Tb (K)
	1-butyl-3-methylimidazolium chloride ([C4mim][Cl])	C8H15ClN2	174.67	558.0 [31]
	1-hexyl-3-methylimidazolium chloride ([C6mim][Cl])	C10H19ClN2	202.73	603.8 [31]
	1-butyl-3-methylimidazolium tetrafluoroborate ([C4mim][BF4])	C8H15BF4N2	226.03	495.2 [31]

.

Ultrapure water (conductivity < 0.06 μS/cm, resistivity 18.2 $\mathrm{M}\mathsf{\Omega }\cdot \mathrm{c}\mathrm{m}$ at 25 °C) was used without further purification. Acetonitrile (mass fraction ≥ 0.999) was analyzed by gas chromatography (A91 Pro, Panna, Changzhou, China), and no significant impurities were detected, so it was used without further purification. The ILs (mass fraction > 0.990) were degassed using a rotary evaporator (DZFY-1, Kexingyiqi, Shanghai, China) and dehydrated in a vacuum drying oven (DHG-9023A, Jinghongsh, Shanghai, China; pressure 0–5 kPa) at 353.15 K for at least 24 h [20] before use. The water content in the chemical reagents and ILs was determined using a coulometric Karl Fischer titrator (Model KF 831, Metrohm AG, Herisau, Switzerland). The basic specifications of the chemicals used in the experiment are listed in

Table 2. Specifications of chemicals used in the experiment.

Chemicals	Cas No.	Mass Fraction Purity	Mass Fraction Water	Purification Method	Supplier
CH3CN	75-05-8	>0.999 a	<0.0005 c	none	Yonghua Chemical Co., Ltd., Suzhou, Jiangsu, China
H2O	7732-18-5	Resistivity = 18.2 $\mathrm{M}\mathsf{\Omega }\cdot \mathrm{c}\mathrm{m}$	none	Ultrapure filtration	Self-prepared (own source), Changzhou, Jiangsu, China
[C4mim]Cl	79917-90-1	>0.990 b	<0.004 c	Vacuum desiccation	Chengjie Chemical Co., Ltd., Shanghai, China
[C6mim]Cl	171058-17-6	>0.990 b	<0.004 c	Vacuum desiccation	Chengjie Chemical Co., Ltd., Shanghai, China
[C4mim]BF4	174501-65-6	>0.990 b	<0.003 c	Vacuum desiccation	Chengjie Chemical Co., Ltd., Shanghai, China

Note: ^a = Gas chromatography; ^b = Provided by the supplier; ^c = Karl Fischer titrator.

.

2.2. Apparatus and Procedure

The VLE data for binary and ternary mixtures were measured using a glass equilibrium apparatus (self-designed and constructed in-house), as described in the literature [32]. A schematic diagram of the apparatus is provided in Figure S1 of the Supplementary Material (SI). The setup consisted of a vacuum system, a thermostatic bath, and a measurement system. Prior to each experiment, the equilibrium cell was prepared and loaded, and temperature and pressure measurements were calibrated and corrected to ensure reliable VLE data (see Supplementary Material for details).

A liquid sample with a known total amount n_T and the total mole fraction z_i of each component was injected into the equilibrium cell (volume 45 cm³). Typically, about 18 cm³ of liquid was injected, leaving a vapor phase volume of approximately 27 cm³. To remove dissolved gases and volatile impurities, the liquid sample was subjected to freeze–degas–thaw cycles. The sample was rapidly frozen in a liquid nitrogen bath, after which the gases in the equilibrium system were evacuated until the pressure dropped below 7 Pa. The frozen sample was then thawed in a warm water bath. This procedure was typically repeated three times to ensure effective removal of residual gases. The total mass and composition of the sample were checked before and after degassing, showing negligible changes, indicating that the procedure did not affect the final VLE measurements. The equilibrium cell was subsequently immersed in a thermostatted water bath, where the temperature was maintained within a tolerance of ±0.05 K using a precision temperature controller. Equilibrium was deemed reached when the temperature (T) and pressure (P) remained stable for a predefined duration (typically 1 h). The equilibrium T, P, n_T, z_i, liquid phase volume $V^L$ were recorded. The vapor-phase volume $V^G$ was obtained as the difference between the total cell volume and the equilibrium liquid volume ($V^G=45-V^L$). For each temperature, measurements were repeated three times to ensure reliability. The quality of the experimental data was rigorously validated through three key checks: (1) equilibrium confirmation: temperature and pressure were monitored continuously, with readings considered stable if their fluctuations were within ±1.0% over a 5 min interval; (2) reproducibility assessment: triplicate measurements at each temperature yielded standard deviations of <0.5% for pressure and <0.02 K for temperature, confirming data consistency; (3) degassing effectiveness: repeated freeze–thaw cycles were confirmed to remove virtually all dissolved gases and volatile impurities, as evidenced by negligible changes in sample mass and composition (<0.1% relative deviation) before and after degassing. Collectively, these validation steps ensured the accuracy and reliability of the collected VLE data. The compositions of the liquid and vapor phases, and other properties, were determined using a thermodynamic model.

For each component i, mass-balance requires that

$$n_T{z}_i=n_G{y}_i+n_L{x}_i$$

(1)

where $n_G$ and $n_L$ are the vapor and liquid phase mole numbers, and $y_i$ and $x_i$ are the corresponding mole fractions in the vapor and liquid phases, respectively. The moles in liquid and vapor phases, and liquid phase composition can be calculated by Equation (2), Equation (3), and Equation (4), respectively.

$$n_G=f·n_{T }$$

(2)

$$n_L=n_{T }-n_G$$

(3)

$$x_i={\displaystyle \frac{z_i-f{y}_i}{1-f}}$$

(4)

where $f$ is the vapor-phase fraction, defined by

$$f={\displaystyle \frac{V^G}{V_m^G·n_T}}$$

(5)

where $V_m^G$ is the molar volume of the vapor phase, the experiments were conducted at low pressures. Under these conditions, the $V_m^G$ was calculated using the ideal gas law ($V_m^G={\displaystyle \frac{RT}{P}}$). The initial compositions were calculated using mass-balance and phase-fraction relations and then iteratively updated via the NRTL model to satisfy VLE conditions (see Figure S2 for details).

For acetonitrile + IL systems, the volatility of the IL was negligible, and thus the vapor phase was essentially composed entirely of acetonitrile, which simplified the calculations. The ILs used in the experiment were recovered at the end using a rotary evaporator for cost-saving purposes.

The reliability of the apparatus was validated using both pure component and acetonitrile (1) + H₂O (2) binary system. The saturated vapor pressure data of the acetonitrile was measured and compared with literature data [33,34,35,36]. The results are in excellent agreement with literature data. Subsequently, the binary mixture experimental VLE data were compared to literature values [37]. As shown in Figure S3, the experimental and literature data exhibit excellent agreement in both the total pressure–liquid phase composition (P − x) and pressure-vapor-phase composition (P − y) correlations, confirming the accuracy and reliability of the present measurements. More details can be found in Tables S1 and S2, and Figure S4 in the Supplementary Material.

2.3. Uncertainty in Experiment

The uncertainties are primarily determined by the recorded data of the temperature, pressure, and composition (T, P, and x₁). The calculation method of the uncertainties is based on the literature [38,39]. The deviation in the liquid phase composition is mainly from the uncertainty of the balance and the molar fraction values used in the calculation process. The electronic balance had a precision of ±0.1 mg. The deviation in the vapor phase composition primarily results from errors in the measured temperature, pressure, and liquid composition.

The temperature fluctuations of the thermostatic water bath were measured as $\pm$0.05 K. The standard uncertainty for the water bath temperature ($u_{T1}$) is calculated as $u_{T1}=0.05/\sqrt{3}=0.0289 \mathrm{K}$. The accuracy of the mercury thermometer is ±0.02 K, and the standard uncertainty of the thermometer ($u_{T2}$) is calculated as $u_{T2}=0.02/\sqrt{3}=0.0115 \mathrm{K}.$ The standard deviation (s) of temperature measurements over three repetitions was included, with a typical value of s = 0.02 K. Therefore, the standard uncertainty of the temperature measurement is

$$u_T=\sqrt{u_{T1}^2+u_{T2}^2+s^2}=0.037 \mathrm{K}$$

(6)

The uncertainty in the measurement of the mercury column height is ±0.02 mm, and the pressure corresponding to each mm of the mercury column is 1.36 kPa. Therefore, the uncertainty in pressure is

$$u_P=0.02 \mathrm{m}\mathrm{m}\times {\displaystyle \frac{1.36 \mathrm{k}\mathrm{P}\mathrm{a}}{\mathrm{m}\mathrm{m}}}=0.027 \mathrm{k}\mathrm{P}\mathrm{a}$$

(7)

In addition to the instrument uncertainty, the overall pressure uncertainty also includes contributions from variations in the sample composition (mole fractions), temperature fluctuations, and other experimental factors. The combined standard uncertainties were used in the calculation of all reported thermodynamic properties and are consistently reported in the table footnotes.

3. Results and Discussion

3.1. Modeling

The phase equilibrium data were correlated using an activity coefficient model. When the experiment is conducted under low-pressure conditions, the vapor–liquid phase equilibrium criterion can be rewritten as follows:

$$P{y}_i{\phi }_i^v=x_i{\gamma }_i{P}_i^s\exp \left({\displaystyle \frac{V_i^L\left(P-P_i^s\right)}{RT}}\right)$$

(8)

where T and P are the equilibrium temperature and pressure of the mixture; $x_i$ and $y_i$ the mole fractions of component i in the liquid and vapor phases. ${\phi }_i$ the fugacity coefficient in vapor phase and ${\gamma }_i$ the activity coefficient of component i in liquid phase, respectively. At low pressure (<10 bar), the vapor phase can be treated as an ideal gas, so ${\phi }_i$ and $\exp \left({\displaystyle \frac{V_i^L\left(P-P_i^s\right)}{RT}}\right)$ are both close to 1. Equation (8) can be rewritten as follows:

$$y_i={\gamma }_i{x}_i{P}_i^s$$

(9)

$${\gamma }_i={\displaystyle \frac{P{y}_i}{x_i{P}_i^s}}$$

(10)

$${\alpha }_{12}={\displaystyle \frac{y_1/x_1}{y_2/x_2}}$$

(11)

where $P_i^s$ is the saturated vapor pressure, which can be calculated with the Antoine equation as

$$\mathit{ln}\left(P_i^s/kPa\right)=A-{\displaystyle \frac{B}{T/K+C}}$$

(12)

where the parameters of acetonitrile (A = 15.1096, B = 3522.624, C = −18.758) were obtained by fitting experimental data, and those of water (A = 16.287, B = 3821.520, C = −45.663) were taken from the literature [40].

3.1.1. NRTL Model

In this work, two thermodynamic models were considered to calculate the activity coefficients of the solvents. In the first model, it is assumed that the ILs do not dissociate in the solvents and remain as neutral molecular species. In this case, the VLE data were correlated with the non-random two-phase (NRTL) model [41,42] due to its excellent applicability for IL-containing systems [43,44,45]. The general equation for ${\gamma }_i$ of species i in a mixture is

$$ln{\gamma }_i={\displaystyle \frac{\sum _{j=1}^n{x}_i{\tau }_{ji}{G}_{ji}}{\sum _{k=1}^n{x}_k{G}_{ki}}}+\sum _{j=1}^n{\displaystyle \frac{x_j{G}_{ij}}{\sum _{k=1}^n{x}_k{G}_{kj}}}\left({\tau }_{ij}-{\displaystyle \frac{\sum _{m=1}^n{x}_m{\tau }_{mj}{G}_{mj}}{\sum _{k=1}^n{x}_k{G}_{kj}}}\right)$$

(13)

With

$$G_{ji}=exp\left(-{\alpha }_{ji}{\tau }_{ji}\right), {\tau }_{ij}={\mathrm{A}}_{ij}+{\displaystyle \frac{B_{ij}}{T}}$$

(14)

where ${\tau }_{ij}$ is the dimensionless interaction parameter between component i and j, ${\alpha }_{ji}$ is the non-random parameter for the mixture system. For the binary system, there are 5 adjustable parameters (${\alpha }_{12}={\alpha }_{21}, {\mathrm{A}}_{12}, {\mathrm{A}}_{21}, {\mathrm{B}}_{12}, {\mathrm{B}}_{21}$), and for the ternary system, other 10 parameters (${\alpha }_{13, }{\alpha }_{23,} {\mathrm{A}}_{13}, {\mathrm{A}}_{23}, {\mathrm{A}}_{31},{\mathrm{A}}_{32}, {\mathrm{B}}_{13}, {\mathrm{B}}_{23}, {\mathrm{B}}_{31},{\mathrm{B}}_{32}$) are included. The parameters were obtained from VLE data and used Simplex method with the following objective function:

$$OF=\sum _{i=1}^n{\left({\displaystyle \frac{P_i^{exp}-P_i^{cal}}{P_i^{exp}}}\right)}^2$$

(15)

where n is the number of experimental points, the superscripts of ‘exp’ and ‘cal’ severally represent the theoretical and experimental results.

3.1.2. e-NRTL Model

The e-NRTL model is the second thermodynamic model employed in this work, which assumes that the ILs are fully dissociated in aqueous solutions. In this case, the ILs + solvent system is treated as a multicomponent mixture consisting of solvent molecules, cations, and anions. In the e-NRTL model, the excess Gibbs free energy is expressed as the sum of two contributions: the long-range electrostatic term, represented by the Pitzer–Debye–Hückel (PDH) equation ($G^{*E,PDH}$), and the short-range local composition term ($G^{*E,lc}$), described by the NRTL equation. The PDH term [28,29] is expressed as

$${\displaystyle \frac{G^{*E,PDH}}{RT}}=-\left({\displaystyle \sum _i}{x}_i\right){\left({\displaystyle \frac{1000}{M_s}}\right)}^{{\displaystyle \frac{1}{2}}}\left({\displaystyle \frac{4A_{\phi }{I}_x}{\rho }}\right)\ln \left(1+\rho {I_x}^{{\displaystyle \frac{1}{2}}}\right)$$

(16)

where

$$I_x={\displaystyle \frac{1}{2}}\sum _i{x}_i{z}_i^2$$

(17)

where $x_i$ is the mole fraction of ionic species i (i = cation, anion), $M_s$ is the molecular weight of the solvent, and $\rho$ is the “closest approach” parameter, fixed at 14.9. $A_{\phi }$ denotes the Debye–Hückel constant [40]. $I_x$ represents the ionic strength on the mole fraction scale, and $z_i$ is the charge number of ion i. In the case of a solvent + salt system, the short-range (local composition) term [28,29] is expressed as follows:

$$\begin{gathered} {\displaystyle \frac{G^{*E,\mathit{lc}}}{\mathit{RT}}}={ X}_s\left(X_{\mathit{cs}}+X_{\mathit{as}}\right){\tau }_{\mathit{ca},s}+X_c{X}_{\mathit{sc}}{\tau }_{s,\mathit{ca}}+X_a{X}_{\mathit{sa}}{\tau }_{s,\mathit{ca}}-X_c\left({\tau }_{s,\mathit{ca}}+G_{\mathit{cs}}{\tau }_{\mathit{ca},s}\right) \\ -X_a\left({\tau }_{s,\mathit{ca}}+G_{\mathit{as}}{\tau }_{\mathit{ca},s}\right) \end{gathered}$$

(18)

where

$$G_{ij}=\left(-\alpha {\tau }_{ij}\right), G_{ji,ki}=\left(-\alpha {\tau }_{ji,ki}\right)$$

(19)

$$X_i=c_i{x}_i,X_{\mathit{is}}={\displaystyle \frac{X_i{G}_{\mathit{is}}}{X_a{G}_{\mathit{as}}+X_c{G}_{\mathit{cs}}+{ X}_s}}, i=s, c, a$$

(20)

$X_i$ is the effective local mole fraction of species i: for ions ${ c}_i$=|$z_i$|, and for molecules ${ c}_i=1$. The parameter $\alpha$ is the non-randomness factor. The parameters ${\tau }_{ij}$ and ${\tau }_{ji,ki}$ are expressed as

$${\tau }_{ca,s}=A_{12}+{\displaystyle \frac{B_{12}}{T}}$$

(21)

$${\tau }_{s,ca}=A_{21}+{\displaystyle \frac{B_{21}}{T}}$$

(22)

and ${\tau }_{as}={\tau }_{cs}={\tau }_{ca,s}$, ${\tau }_{sc,ac}={\tau }_{sa,ca}={\tau }_{s,ca}$. Further details on the e-NRTL model, especially the expressions of the activity coefficients, can be found elsewhere [28,29,30]. The parameters were obtained by fitting the VLE data using the downhill simplex method, with the same objective function as that employed for the NRTL model.

3.2. Binary Systems

3.2.1. Acetonitrile + Water

The VLE data for the binary mixture of acetonitrile (1) + water (2) were determined at different temperatures ranging from 313.15 to 353.15 K. The experimental data are summarized in Table S1. The observed phase behavior is in good agreement with previously reported for the acetonitrile + water system, including VLE data at low acetonitrile mole fractions [46], as well as data measured at atmospheric pressure [16,47]. Moreover, a comparison with the literature VLE data at 303.13 K [48] shows excellent consistency with our results, demonstrating that both the trends and quantitative values are well captured. These comparisons further confirm the reliability and accuracy of our measurements across a range of experimental conditions.

As illustrated in Figure 1, the acetonitrile + water system exhibits a distinct azeotropic point, and the azeotropic composition shifts towards lower mole fractions of acetonitrile with increasing temperature. This behavior arises from the weakening of hydrogen bonding (between the nitrogen atom of acetonitrile and the hydrogen atom of water) and dipole–dipole interactions as temperature increases. These interactions originally constrain water molecules and suppress their volatility. When they weaken at higher temperatures, the volatility of water increases more significantly than that of acetonitrile, leading to an azeotropic composition richer in water. From a thermodynamic viewpoint, the azeotropic composition can shift with temperature but cannot be eliminated under conventional distillation conditions. Therefore, even under reduced pressure, the acetonitrile–water mixture remains difficult to separate completely. ILs, as promising separation agents, possess unique tunable intermolecular interactions that can significantly modify the volatility and phase equilibrium of such systems [19,20]. Therefore, ILs may overcome the limitations of traditional separation processes and eliminate the azeotrope of the acetonitrile + water system.

3.2.2. Binary Acetonitrile + IL Systems

To evaluate the influence of ILs on the phase behavior of acetonitrile, the VLE data of the binary systems acetonitrile (1) + [C₄mim][Cl] (2), acetonitrile (1) + [C₄mim][BF₄] (2), and acetonitrile (1) + [C₆mim][Cl] (2) were compiled from literature sources. These data were employed to correlate the systems using the NRTL and e-NRTL models. The resulting analysis provides a consistent foundation for assessing the effects of cationic alkyl chain length and anion type on the volatility of acetonitrile under reduced pressure conditions. The corresponding data are presented in

Table 3. Experimental and calculated VLE data of acetonitrile (1) + [C₄mim][Cl] (2).

T/K	${\mathit{P}}_{\mathit{e}\mathit{x}\mathit{p}}$/kPa	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	$\mathit{d}\mathit{e}\mathit{v}/\mathbf{\%}$a	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{e}-\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	$\mathit{d}\mathit{e}\mathit{v}/\mathbf{\%}$a
x1 = 0.9503
313.39	22.709	22.646	0.278	22.572	0.605
322.93	32.681	32.947	0.815	32.846	0.503
332.48	46.396	46.871	1.024	46.735	0.731
342.34	65.322	65.990	1.022	65.813	0.752
352.05	89.634	90.614	1.093	90.392	0.846
x1 = 0.9000
313.14	21.367	21.966	2.802	21.633	1.244
322.82	31.332	32.142	2.587	31.669	1.075
333.41	46.354	47.457	2.379	46.781	0.921
343.27	64.830	66.668	2.836	65.751	1.421
352.12	87.732	88.916	1.350	87.735	0.003
x1 = 0.8002
313.49	21.375	21.238	0.642	20.620	3.534
323.33	31.010	31.211	0.649	30.332	2.186
332.99	44.489	44.489	0.000	43.280	2.718
342.86	62.789	62.524	0.422	60.892	3.021
353.20	87.521	87.399	0.139	85.224	2.625
x1 = 0.6995
313.45	20.186	19.553	3.138	19.098	5.390
323.30	29.261	28.708	1.889	28.079	4.038
332.99	41.620	40.914	1.697	40.076	3.710
343.02	58.412	57.732	1.164	56.641	3.032
353.09	80.837	79.893	1.168	78.520	2.867
x1 = 0.6009
313.36	17.264	17.308	0.253	17.196	0.392
323.13	25.106	25.299	0.767	25.170	0.257
333.05	36.039	36.304	0.736	36.177	0.382
342.94	50.376	50.904	1.048	50.811	0.864
352.56	69.367	69.367	0.000	69.367	0.000
x1 = 0.4925
313.49	14.562	14.527	0.237	14.699	0.938
323.15	20.871	21.096	1.079	21.359	2.339
332.96	29.961	30.095	0.446	30.498	1.792
342.95	41.660	42.263	1.447	42.880	2.929
352.36	56.534	57.115	1.027	58.026	2.640
x1 = 0.3988
313.23	12.114	11.683	3.555	11.881	1.921
322.96	17.557	16.989	3.237	17.264	1.668
332.97	24.947	24.370	2.311	24.756	0.764
342.65	33.977	33.817	0.470	34.351	1.101
353.10	48.155	47.144	2.098	47.903	0.523
x1 = 0.3010
313.31	8.721	8.790	0.790	8.817	1.106
323.04	12.752	12.752	0.000	12.752	0.000
332.89	18.134	18.151	0.096	18.103	0.172
343.25	25.748	25.709	0.153	25.580	0.652
352.93	34.664	34.899	0.678	34.664	0.000

Standard uncertainties: u(T) = 0.037 K, u(P) = 0.70 kPa, u(x₁) = 0.002; u(x₂) = 0.002. u(x₁) and u(x₂) were calculated considering both weighing precision and water content of the IL. ^a: dev = $100\times \left|P_{exp}-P_{cal}^{model}\right|/P_{exp}$; AARD = $\sum _{i=1}^n\sum dev/n.$ AARD ($P_{cal}^{NRTL}$) = 1.19%; AARD ($P_{cal}^{e-NRTL}$) = 1.54%$P_{exp}$—Experimental pressure (kPa); $P_{cal}^{NRTL}$—Calculated pressure by NRTL (kPa); $P_{cal}^{e-NRTL}$—Calculated pressure by e-NRTL (kPa).

,

Table 4. Experimental and calculated VLE data of acetonitrile (1) + [C₄mim][BF₄] (2).

T/K	${\mathit{P}}_{\mathit{e}\mathit{x}\mathit{p}}$/kPa	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	$\mathit{d}\mathit{e}\mathit{v}/\mathbf{\%}$a	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{e}-\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	$\mathit{d}\mathit{e}\mathit{v}/\mathbf{\%}$a
x1 = 0.9517
313.31	22.285	22.201	0.377	22.329	0.197
322.74	31.950	32.159	0.653	32.331	1.193
332.78	46.233	46.558	0.702	46.787	1.199
342.72	64.896	65.652	1.166	65.948	1.621
352.33	88.784	89.759	1.098	90.127	1.513
x1 = 0.9015
313.56	20.826	21.199	1.789	21.341	2.475
323.43	30.580	31.163	1.906	31.325	2.437
333.40	43.810	44.868	2.415	45.032	2.788
343.23	59.484	62.866	5.686	62.999	5.909
353.09	84.244	86.422	2.585	86.474	2.647
x1 = 0.8052
313.42	19.714	19.934	1.118	20.027	1.589
323.13	28.590	29.087	1.738	29.148	1.950
333.00	40.778	41.684	2.221	41.662	2.168
342.56	56.812	57.826	1.784	57.650	1.476
352.39	77.683	79.374	2.176	78.931	1.607
x1 = 0.7944
313.30	18.350	18.326	0.129	18.327	0.126
322.94	26.380	26.600	0.836	26.509	0.490
332.96	37.842	38.223	1.008	37.955	0.299
342.85	52.890	53.452	1.063	52.890	0.000
352.48	72.483	72.660	0.244	71.652	1.146
x1 = 0.7547
313.33	17.794	17.354	2.472	17.300	2.777
322.94	25.211	25.105	0.422	24.936	1.090
332.68	35.699	35.644	0.154	35.275	1.187
342.46	49.587	49.587	0.000	48.895	1.395
352.18	67.565	67.500	0.097	66.321	1.842
x1 = 0.6988
313.60	15.840	16.148	1.947	16.041	1.269
323.59	23.308	23.596	1.237	23.364	0.242
333.40	32.630	33.424	2.434	32.991	1.105
343.20	45.385	46.310	2.039	45.564	0.395
352.91	61.618	62.736	1.814	61.534	0.137
x1 = 0.6168
313.29	13.886	13.885	0.007	13.773	0.815
322.74	19.809	19.805	0.023	19.635	0.878
332.68	28.111	28.089	0.080	27.829	1.004
342.37	38.961	38.647	0.805	38.258	1.804
350.89	50.688	50.351	0.665	49.805	1.743
x1 = 0.5032
313.31	11.109	11.110	0.010	11.109	0.000
322.84	15.935	15.778	0.985	15.881	0.339
332.28	21.846	21.846	0.000	22.118	1.245
342.24	29.983	30.137	0.514	30.683	2.336
353.05	42.763	41.772	2.317	42.763	0.000

Standard uncertainties: u(T) = 0.037 K, u(P) = 0.70 kPa, u(x₁) = 0.002; u(x₂) = 0.002. u(x₁) and u(x₂) were calculated considering both weighing precision and water content of the IL ^a: dev = $100\times \left|P_{exp}-P_{cal}^{NRTL}\right|/P_{exp}$; AARD = $\sum _{i=1}^n\sum dev/n.$ AARD ($P_{cal}^{NRTL}$) = 1.22%; AARD ($P_{cal}^{e-NRTL}$) = 1.36%. $P_{exp}$—Experimental pressure (kPa); $P_{cal}^{NRTL}$—Calculated pressure by NRTL (kPa); $P_{cal}^{e-NRTL}$—Calculated pressure by e-NRTL (kPa).

and

Table 5. Experimental and calculated VLE data of acetonitrile (1) + [C₆mim][Cl] (2).

T/K	${\mathit{P}}_{\mathit{e}\mathit{x}\mathit{p}}$/kPa	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	$\mathit{d}\mathit{e}\mathit{v}/\mathbf{\%}$a	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{e}-\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	$\mathit{d}\mathit{e}\mathit{v}/\mathbf{\%}$a
x1 = 0.8988
303.15	14.377	14.713	2.339	14.221	1.085
312.95	22.055	22.229	0.791	21.495	2.537
323.13	33.294	33.180	0.344	32.100	3.586
333.05	48.332	47.811	1.078	46.279	4.247
342.85	68.132	67.101	1.514	64.986	4.618
352.43	93.271	91.678	1.708	88.836	4.755
x1 = 0.8067
303.15	14.144	14.381	1.675	13.544	4.244
312.91	21.640	21.693	0.246	20.452	5.490
323.15	32.616	32.458	0.485	30.636	6.070
333.01	47.220	46.670	1.165	44.101	6.605
342.85	66.510	65.593	1.379	62.057	6.695
352.55	91.009	89.958	1.155	85.213	6.369
x1 = 0.7141
303.29	13.251	13.829	4.362	13.005	1.859
313.05	20.285	20.856	2.813	19.646	3.148
323.45	30.581	31.387	2.635	29.624	3.130
333.25	45.283	45.005	0.613	42.557	6.020
343.25	64.792	63.564	1.895	60.225	7.049
353.55	88.737	88.772	0.040	84.286	5.016
x1 = 0.5946
303.31	12.295	12.634	2.759	12.140	1.261
313.05	18.822	19.048	1.201	18.348	2.517
323.75	28.615	29.009	1.377	28.024	2.066
333.33	41.262	41.257	0.012	39.964	3.147
342.95	58.350	57.540	1.388	55.892	4.212
353.25	80.520	80.428	0.115	78.368	2.673
x1 = 0.4531
303.35	10.698	10.812	1.063	10.782	0.784
313.05	16.133	16.299	1.030	16.298	1.024
323.15	24.414	24.300	0.468	24.374	0.164
333.15	35.401	35.176	0.635	35.401	0.000
343.15	50.884	49.762	2.204	50.258	1.229
352.85	69.179	68.289	1.286	69.220	0.060
x1 = 0.4278
303.15	10.183	10.348	1.624	10.383	1.966
312.75	15.255	15.553	1.956	15.646	2.561
322.85	23.324	23.217	0.458	23.426	0.437
333.15	34.313	34.010	0.882	34.433	0.348
343.45	49.095	48.618	0.972	49.401	0.624
352.95	67.418	66.278	1.690	67.588	0.252
x1 = 0.3159
303.45	8.314	8.657	4.121	8.857	6.534
313.20	12.642	13.121	3.792	13.443	6.332
323.35	19.040	19.659	3.250	20.178	5.979
333.40	28.038	28.582	1.941	29.407	4.883
343.55	39.591	40.729	2.875	42.023	6.143
353.15	55.806	55.806	0.000	57.754	3.491
x1 = 0.2035
303.15	6.326	6.332	0.102	6.464	2.186
313.15	10.133	9.763	3.648	9.943	1.879
323.35	15.251	14.739	3.358	14.986	1.735
333.10	22.265	21.302	4.325	21.644	2.789
343.15	31.487	30.415	3.406	30.901	1.860
353.25	43.267	42.561	1.633	43.267	0.000
x1 = 0.1291
303.35	4.548	4.548	0.000	4.548	0.000
313.15	7.031	6.991	0.572	6.944	1.242
323.35	10.615	10.615	0.000	10.482	1.257
333.35	15.309	15.566	1.680	15.298	0.073
343.05	21.769	22.056	1.318	21.595	0.799
353.25	30.263	31.123	2.840	30.379	0.384

Standard uncertainties: u(T) = 0.037 K, u(P) = 0.70 kPa, u(x₁) = 0.002; u(x₂) = 0.002. u(x₁) and u(x₂) were calculated considering both weighing precision and water content of the IL ^a: dev = $100\times \left|P_{exp}-P_{cal}^{NRTL}\right|/P_{exp}$; AARD = $\sum _{i=1}^{n}dev/n.$ AARD ($P_{cal}^{NRTL}$) = 1.60%; AARD ($P_{cal}^{e-NRTL}$) = 2.88%. $P_{exp}$—Experimental pressure (kPa); $P_{cal}^{NRTL}$—Calculated pressure by NRTL (kPa); $P_{cal}^{e-NRTL}$—Calculated pressure by e-NRTL (kPa).

.

3.2.3. Modeling and Discussion

In this work, both the NRTL and e-NRTL models were employed to correlate the VLE data. For each binary system, a five-parameter regression was performed for each model to optimize the correlation and ensure accurate representation of the phase behavior. The optimized model parameters are summarized in

Table 6. Model parameters for VLE data fitting.

System	${\mathit{\alpha }}_{12}$	A12	B12	A21	B21	Deviation
NRTL model
Acetonitrile + H2O	0.24	−3.906	1451.04	4.438	−823.011	1.09%
Acetonitrile + [C4mim][Cl]	0.69	−0.868	171.828	69.000	−25.724	1.19%
Acetonitrile + [C4mim][BF4]	0.69	−2.280	534.027	0.631	−1.272	1.22%
Acetonitrile + [C6mim][Cl]	0.72	1.793	−337.092	2.581	−10.356	1.60%
e-NRTL model
Acetonitrile + [C4mim][Cl]	0.20	1.443	−26.198	−1.197	162.130	1.54%
Acetonitrile + [C4mim][BF4]	0.20	−4.375	1204.548	2.909	−838.138	1.36%
Acetonitrile + [C6mim][Cl]	0.20	0.497	4.956	0.401	−63.754	2.88%

.

In this work, as shown in Figure 2a–c, it is found that both models (NRTL and e-NRTL) lead to a satisfactory description of the data. In the binary acetonitrile–IL systems, the equilibrium pressure decreases with increasing IL mole fraction at the same temperature. This is due to stronger solvation and network formation by IL molecules in the liquid phase, which reduces the activity coefficient of acetonitrile. For the two chloride-based ILs ([C₄mim][Cl] and [C₆mim][Cl]), at similar composition and temperature, [C₄mim][Cl] exhibits lower equilibrium pressure than [C₆mim][Cl], indicating that the shorter alkyl chain enhances the interaction between the cation and acetonitrile. For systems with the same cation ([C₄mim][Cl] and [C₄mim][BF₄]), [C₄mim][Cl] shows higher equilibrium pressure. Although BF₄− is larger, less polarizable, and loosely associated with the cation, it can form a specific ion–dipole or $F-C\equiv N$ interactions with acetonitrile, which more strongly restricts its volatility. In contrast, the smaller Cl⁻ forms a tighter local ionic network but interacts less directly with acetonitrile, resulting in a higher activity coefficient and thus higher equilibrium pressure for [C₄mim][Cl]. In summary, the equilibrium pressure trends reflect a balance between ionic network structure, specific ion–solvent interactions, and alkyl chain effects.

To further understand the trends observed in Figure 2, the activity coefficients of acetonitrile were analyzed, as shown in Figure 3. The activity coefficient decreases with increasing IL concentration for all three ILs, indicating a negative deviation from ideality. This behavior is consistent with the pressure trends: as the activity coefficient decreases, the equilibrium pressure correspondingly drops. The influence of IL type on acetonitrile activity follows the order: [C₄mim][BF₄] > [C₄mim][Cl] > [C₆mim][Cl]. For ILs with the same cation, the effect of the anion follows [Cl]₋ < [BF₄]₋, as the larger, more polarizable [BF₄]⁻ interacts more strongly with acetonitrile. For ILs with the same anion, the effect of the cation follows the order [C₄mim]⁺ > [C₆mim]⁺, due to increased steric repulsion from longer alkyl chains. At the molecular level, these trends reflect hydrogen bonding, ion–dipole interactions, and steric effects, which collectively govern acetonitrile activity and volatility. Similar behavior is observed at other temperatures, emphasizing the role of IL structure in modulating acetonitrile volatility. These findings suggest that selecting ILs with tailored intermolecular interactions can enhance acetonitrile–water separation. Note that these effects pertain only to binary systems; ternary systems with water require comprehensive consideration of all component interactions to determine the most effective IL.

3.3. Ternary Systems

3.3.1. Ternary Acetonitrile + Water + ILs Systems

The ternary VLE data of acetonitrile (1) + H₂O (2) + [C₄mim][Cl] (3), + [C₄mim][BF₄] (3), and + [C₆mim][Cl] (3) were experimentally measured under different pressures, with the mole fraction of IL approximately 0.20. The measured data are summarized in

Table 7. Experimental and calculated VLE data of acetonitrile (1) + H₂O (2) + [C₄mim][Cl] (3) ternary system.

T/K	${\mathit{P}}_{\mathit{e}\mathit{x}\mathit{p}}$/kPa	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	${\mathit{\gamma }}_{\mathit{c}\mathit{a}\mathit{l},1}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{\gamma }}_{\mathit{c}\mathit{a}\mathit{l},2}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{y}}_{\mathit{c}\mathit{a}\mathit{l},1}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{\alpha }}_{12}$
x1 = 0.0392; x2 = 0.7648
313.52	9.254	9.620	7.3788	0.5231	0.6880	43.02
323.23	13.858	15.005	7.4045	0.5438	0.6570	37.37
333.18	20.576	23.004	7.4242	0.5637	0.6262	32.68
342.85	29.908	33.984	7.4372	0.5818	0.5973	28.94
352.68	42.953	49.397	7.4447	0.599	0.5692	25.78
x1 = 0.1600; x2 = 0.6400
313.39	15.485	17.220	4.0714	0.5017	0.8611	24.80
323.32	23.976	26.761	4.1403	0.5255	0.8438	21.61
333.38	36.663	40.599	4.2046	0.5481	0.8261	19.00
343.24	54.446	59.526	4.2622	0.5689	0.8086	16.90
353.20	78.422	85.521	4.3152	0.5886	0.7910	15.14
x1 = 0.3201; x2 = 0.4799
313.59	18.681	20.367	2.5453	0.4581	0.9187	16.94
323.35	28.571	31.280	2.5967	0.4861	0.9071	14.64
333.18	43.057	46.827	2.6453	0.5132	0.8951	12.79
342.90	62.238	68.059	2.6902	0.5387	0.8829	11.30
352.87	91.409	97.511	2.7329	0.5637	0.8701	10.04
x1 = 0.4002; x2 = 0.3988
313.41	18.981	20.958	2.1632	0.4116	0.9414	16.01
323.23	28.971	32.170	2.2053	0.442	0.9320	13.66
333.18	43.856	48.239	2.2453	0.4719	0.9220	11.78
342.93	64.735	69.939	2.2817	0.5003	0.9117	10.29
353.39	92.907	101.585	2.3179	0.5298	0.9003	9.00
x1 = 0.4797; x2 = 0.3203
313.40	20.080	21.519	1.8935	0.3469	0.9615	16.68
322.94	29.371	32.506	1.9259	0.3775	0.9546	14.04
332.89	43.556	48.574	1.9573	0.4091	0.9469	11.91
342.87	63.437	70.759	1.9865	0.4404	0.9386	10.21
352.54	90.110	99.596	2.0124	0.4702	0.9301	8.88
x1 = 0.5621; x2 = 0.2389
313.11	20.480	21.708	1.6801	0.2642	0.9787	19.53
322.71	29.570	32.740	1.7044	0.2939	0.9741	15.98
332.71	43.856	48.779	1.7278	0.3255	0.9689	13.24
343.04	64.036	71.608	1.7497	0.3586	0.9629	11.03
352.43	89.910	99.269	1.7676	0.389	0.9569	9.44
x1 = 0.6453; x2 = 0.1577
313.32	21.179	22.213	1.5023	0.1721	0.9909	26.61
323.21	30.969	33.664	1.519	0.1984	0.9885	21.01
333.18	45.954	49.716	1.534	0.2265	0.9857	16.85
342.97	65.135	71.080	1.5471	0.2556	0.9825	13.72
352.81	90.210	99.446	1.5587	0.2862	0.9788	11.28
x1 = 0.7249; x2 = 0.0771
313.37	20.979	22.081	1.3362	0.0783	0.9980	53.07
323.43	30.869	33.469	1.3446	0.0956	0.9972	37.88
333.19	45.954	48.704	1.3516	0.1146	0.9964	29.44
343.01	63.936	69.220	1.3573	0.1359	0.9953	22.52
352.65	86.014	95.632	1.3619	0.159	0.9940	17.62
x1 = 0.7596; x2 = 0.0414
313.42	20.779	21.824	1.2597	0.0452	0.9994	90.78
323.21	29.670	32.624	1.264	0.0571	0.9991	60.50
332.97	44.955	47.350	1.2675	0.0709	0.9988	45.36
342.70	62.937	66.963	1.2700	0.0869	0.9984	34.01
352.30	87.912	92.172	1.2718	0.1049	0.9978	24.72

Standard uncertainties: u(T) = 0.037 K, u(P) = 0.70 kPa, u(x₁) = 0.002, u(x₂) = 0.002, u(x₃) = 0.002. Standard uncertainties were calculated considering both weighing precision and water content of the IL; AARD = ${\displaystyle \frac{100}{n}}\sum _{i=1}^n\left|P_{exp,i}-P_{cal,i}\right|/P_{exp,i}.$ AARD (P) = 9.11%; $P_{exp}$—Experimental pressure (kPa); $P_{cal}^{NRTL}$—Calculated pressure by NRTL (kPa); ${\gamma }_{cal,1}^{NRTL}$, ${\gamma }_{cal,2}^{NRTL}$—Calculated activity coefficients of components 1 and 2; $y_{cal,1}^{NRTL}$—Calculated vapor-phase mole fraction of component 1; ${\alpha }_{12}$—Non-randomness parameter in the NRTL model.

,

Table 8. Experimental and calculated VLE data of acetonitrile (1) + H₂O (2) + [C₄mim][BF₄] (3) ternary system.

T/K	${\mathit{P}}_{\mathit{e}\mathit{x}\mathit{p}}$/kPa	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	${\mathit{\gamma }}_{\mathit{c}\mathit{a}\mathit{l},1}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{\gamma }}_{\mathit{c}\mathit{a}\mathit{l},2}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{y}}_{\mathit{c}\mathit{a}\mathit{l},1}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{\alpha }}_{12}$
x1 = 0.0872; x2 = 0.7188
313.58	11.506	10.012	1.7383	1.2072	0.3475	4.39
323.41	17.633	16.085	1.7630	1.2060	0.3270	4.01
333.40	26.674	25.214	1.7851	1.2044	0.3081	3.67
343.29	38.867	38.223	1.8041	1.2023	0.2910	3.38
352.17	55.808	54.307	1.8191	1.2001	0.2770	3.16
x1 = 0.1690; x2 = 0.6299
313.58	13.656	12.336	1.5962	1.2956	0.5019	3.76
323.43	20.308	19.520	1.6083	1.2971	0.4768	3.40
333.28	30.664	29.974	1.6187	1.2976	0.4535	3.09
343.16	44.239	44.844	1.6276	1.2972	0.4318	2.83
352.86	63.119	65.007	1.6349	1.2962	0.4120	2.61
x1 = 0.2356; x2 = 0.5693
313.94	15.644	14.424	1.5404	1.3655	0.5863	3.42
323.89	23.467	22.666	1.5460	1.3690	0.5603	3.08
333.85	34.799	34.594	1.5505	1.3712	0.5357	2.79
343.58	50.215	50.948	1.5538	1.3722	0.5131	2.55
353.04	69.773	72.590	1.5562	1.3723	0.4924	2.34
x1 = 0.3205; x2 = 0.4724
313.26	16.107	15.319	1.4135	1.4470	0.6697	2.99
322.94	24.066	23.621	1.4142	1.4569	0.6446	2.67
332.69	34.989	35.537	1.4144	1.4648	0.6203	2.41
342.77	50.583	52.788	1.4140	1.4711	0.5963	2.18
352.11	69.467	74.514	1.4132	1.4755	0.5752	2.00
x1 = 0.4085; x2 = 0.3884
313.26	17.699	16.779	1.3341	1.5438	0.7355	2.64
323.02	26.255	25.752	1.3319	1.5596	0.7119	2.35
332.79	38.028	38.472	1.3294	1.5728	0.6889	2.11
342.87	54.259	56.716	1.3265	1.5840	0.6659	1.90
352.94	76.424	81.602	1.3235	1.5929	0.6439	1.72
x1 = 0.4717; x2 = 0.3312
312.34	18.492	16.963	1.2821	1.6250	0.7765	2.44
321.74	27.062	25.585	1.2789	1.6450	0.7554	2.17
332.29	40.075	39.370	1.2751	1.6640	0.7321	1.92
343.29	58.843	59.843	1.2711	1.6802	0.7084	1.71
352.01	78.353	81.740	1.2678	1.6908	0.6902	1.56
x1 = 0.6469; x2 = 0.1580
313.29	19.747	18.622	1.1176	1.9030	0.8803	1.80
322.82	28.710	27.837	1.1149	1.9436	0.8662	1.58
332.97	41.409	41.528	1.1121	1.9815	0.8511	1.40
343.35	59.433	60.851	1.1092	2.0150	0.8355	1.24
353.19	81.971	85.441	1.1066	2.0424	0.8208	1.12
x1 = 0.7204; x2 = 0.0795
313.29	20.010	18.291	1.0462	2.0395	0.9343	1.57
323.04	28.911	27.431	1.0451	2.0954	0.9255	1.37
333.07	41.275	40.467	1.0439	2.1463	0.9163	1.21
342.67	57.532	57.317	1.0428	2.1893	0.9073	1.08
352.21	77.912	79.318	1.0417	2.2268	0.8982	0.97
x1 = 0.7605; x2 = 0.0364
313.41	18.711	18.052	1.0083	2.1258	0.9680	1.45
323.23	27.143	27.039	1.0083	2.1916	0.9635	1.26
333.18	38.973	39.592	1.0082	2.2509	0.9587	1.11
343.53	55.336	57.310	1.0081	2.3054	0.9536	0.98
353.20	75.330	79.179	1.0080	2.3500	0.9487	0.89

Standard uncertainties: u(T) = 0.037 K, u(P) = 0.70 kPa, u(x₁) = 0.002, u(x₂) = 0.002, u(x₃) = 0.002. Standard uncertainties were calculated considering both weighing precision and water content of the IL; AARD = ${\displaystyle \frac{100}{n}}\sum _{i=1}^n\left|P_{exp,i}-P_{cal,i}\right|/P_{exp,i}.$ AARD (P) = 3.95%; $P_{exp}$—Experimental pressure (kPa); $P_{cal}^{NRTL}$—Calculated pressure by NRTL (kPa); ${\gamma }_{cal,1}^{NRTL}$, ${\gamma }_{cal,2}^{NRTL}$—Calculated activity coefficients of components 1 and 2; $y_{cal,1}^{NRTL}$—Calculated vapor-phase mole fraction of component 1; ${\alpha }_{12}$—Non-randomness parameter in the NRTL model.

and

Table 9. Experimental and calculated VLE data of acetonitrile (1) + H₂O (2) + [C₆mim][Cl] (3) ternary system.

T/K	${\mathit{P}}_{\mathit{e}\mathit{x}\mathit{p}}$/kPa	${\mathit{P}}_{\mathit{c}\mathit{a}\mathit{l}}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$/kPa	${\mathit{\gamma }}_{\mathit{c}\mathit{a}\mathit{l},1}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{\gamma }}_{\mathit{c}\mathit{a}\mathit{l},2}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{y}}_{\mathit{c}\mathit{a}\mathit{l},1}^{\mathit{N}\mathit{R}\mathit{T}\mathit{L}}$	${\mathit{\alpha }}_{12}$
x1 = 0.2411; x2 = 0.5589
313.50	17.795	19.199	2.9567	0.6899	0.8494	13.07
323.30	26.011	29.613	3.0015	0.7142	0.8326	11.53
333.40	37.633	44.947	3.0451	0.7374	0.8152	10.23
343.00	52.760	65.176	3.0839	0.7578	0.7987	9.20
352.90	73.128	93.422	3.1214	0.7772	0.7820	8.32
x1 = 0.3213; x2 = 0.4797
313.40	19.365	19.381	2.2979	0.7167	0.8677	9.79
323.40	28.477	30.173	2.3403	0.7445	0.8523	8.62
333.40	40.997	45.618	2.3807	0.7704	0.8367	7.65
343.30	57.880	66.915	2.4187	0.7942	0.8214	6.87
352.70	78.624	94.191	2.4528	0.8152	0.8069	6.24
x1 = 0.3907; x2 = 0.4143
313.30	19.269	19.588	1.9535	0.7409	0.8838	8.07
322.00	27.636	28.817	1.9860	0.7681	0.8715	7.19
331.50	38.896	42.815	2.0201	0.7960	0.8579	6.40
341.00	53.646	62.085	2.0527	0.8222	0.8443	5.75
351.80	76.452	92.220	2.0880	0.8498	0.8288	5.13
x1 = 0.4832; x2 = 0.3178
313.10	20.290	19.470	1.6407	0.7021	0.9159	7.16
322.70	29.537	29.654	1.6690	0.7354	0.9050	6.27
332.80	42.294	44.843	1.6977	0.7688	0.8932	5.50
342.70	58.836	65.525	1.7247	0.7998	0.8814	4.89
351.90	77.949	91.266	1.7486	0.8272	0.8703	4.41
x1 = 0.5596; x2 = 0.2394
313.20	20.727	19.711	1.4731	0.6175	0.9447	7.31
322.90	30.015	29.983	1.4964	0.6514	0.9367	6.33
332.50	42.641	44.203	1.5186	0.6840	0.9284	5.55
342.40	58.319	64.308	1.5405	0.7166	0.9195	4.89
352.30	75.177	91.394	1.5614	0.7481	0.9103	4.34
x1 = 0.6411; x2 = 0.1599
313.30	21.180	20.207	1.3527	0.4514	0.9735	9.16
322.90	30.298	30.411	1.3709	0.4805	0.9692	7.85
332.90	43.081	45.244	1.3889	0.5109	0.9644	6.76
342.80	59.897	65.331	1.4059	0.5410	0.9593	5.88
351.30	78.057	87.904	1.4197	0.5669	0.9547	5.26
x1 = 0.7136; x2 = 0.0874
313.30	20.659	20.864	1.2818	0.1775	0.9945	22.15
322.80	29.969	31.081	1.2952	0.1939	0.9934	18.43
332.70	42.495	45.771	1.3081	0.2122	0.9921	15.38
343.00	60.031	66.603	1.3205	0.2326	0.9905	12.77
351.60	78.902	89.334	1.3300	0.2506	0.9891	11.11

Standard uncertainties: u(T) = 0.037 K, u(P) = 0.70 kPa, u(x₁) = 0.002, u(x₂) = 0.002, u(x₃) = 0.002. Standard uncertainties were calculated considering both weighing precision and water content of the IL; AARD = ${\displaystyle \frac{100}{n}}\sum _{i=1}^n\left|P_{exp,i}-P_{cal,i}\right|/P_{exp,i}.$ AARD (P) = 9.86%; $P_{exp}$—Experimental pressure (kPa); $P_{cal}^{NRTL}$—Calculated pressure by NRTL (kPa); ${\gamma }_{cal,1}^{NRTL}$, ${\gamma }_{cal,2}^{NRTL}$—Calculated activity coefficients of components 1 and 2; $y_{cal,1}^{NRTL}$—Calculated vapor-phase mole fraction of component 1; ${\alpha }_{12}$—Non-randomness parameter in the NRTL model.

, where $\alpha$ represents the relative volatility. These datasets provide a consistent basis for analyzing the effect of ILs on the VLE behavior of acetonitrile and its mixtures with water. The ternary VLE data were correlated using the MRTL model, and the model parameters were taken from the literature [27].

3.3.2. Acetonitrile + Water + ILs Systems Discussion

Since the vapor phase composition was not directly measured, the NRTL model performance was evaluated by comparing calculated pressures with experimental values. The predictions showed that the total average relative deviation of pressure for the acetonitrile (1) + H₂O (2) + [C₄mim][Cl] (3)/[C₄mim][BF₄] (3)/[C₆mim][Cl] (3) was 9.11%, 3.95%, 9.86%, respectively. Compared to binary systems, the deviations for ternary systems were slightly larger, but these results obtained purely from predictions are still satisfactory. The calculated values can be found in Table 7, Table 8 and Table 9.

Adding ILs to the acetonitrile–water system markedly alters the liquid phase molecular interactions. In the binary acetonitrile–IL mixtures, strong specific interactions such as hydrogen bonding between the acetonitrile molecules and the imidazolium cations, anions result in decreased activity coefficients of acetonitrile. However, in the ternary systems, the introduction of water changes the interaction balance: water, being a stronger hydrogen bond donor and acceptor, preferentially interacts with both the cation and the anion of the IL, thereby weakening the acetonitrile–IL interactions and increasing the relative volatility of acetonitrile.

This trend is quantitatively reflected in the activity coefficients. For [C₄mim][Cl] and [C₆mim][Cl], acetonitrile exhibits $\gamma >1$ while water exhibits $\gamma <1$, indicating that acetonitrile is relatively less stabilized in the liquid phase, favoring its transfer to the vapor phase. Moreover, the $\gamma$ value of acetonitrile in the [C₄mim][Cl] system is larger than that in the [C₆mim][Cl] system (within the same order of magnitude), suggesting that a shorter butyl chain enhances the polar–polar interactions between the IL and water while reducing the hydrophobic association with acetonitrile. Conversely, water in [C₄mim][Cl] shows a smaller $\gamma$ value than in [C₆mim][Cl], confirming that a shorter alkyl chain strengthens the solvation of water by the IL when the anion (Cl₋) is held constant.

In contrast, for [C₄mim][BF₄], both acetonitrile and water show $\gamma >1$ and their activity coefficients are close in magnitude, implying weaker selective interactions and limited capacity for preferential solvation. This behavior arises from the lower hydrogen-bond basicity and reduced hydrophilicity of the BF₄₋ anion compared with Cl₋. Additionally, the highly symmetric and weakly polar nature of BF₄₋ diminishes its ability to form directional hydrogen bonds with polar solutes, thereby reducing its capacity to perturb the acetonitrile–water hydrogen-bond network. As a result, [C₄mim][BF₄] provides minimal selectivity between acetonitrile and water, leading to weaker separation performance [19,20].

This conclusion is further supported by the observed relative volatilities: $\alpha$ values for the [C₄mim][Cl] system are significantly higher than those for [C₆mim][Cl] and [C₄mim][BF₄]. The much lower $\alpha$ observed in the [C₄mim][BF₄] system confirms its limited capacity to amplify volatility differences between acetonitrile and water, demonstrating that weaker ion–dipole interactions and reduced polarity directly lead to poorer separation efficiency.

Overall, the separation efficiency of the studied ILs follows the order [C₄mim][Cl] > [C₆mim][Cl] > [C₄mim][BF₄]. This trend underscores that both anion type (governed by hydrophilicity and hydrogen-bond basicity) and cation alkyl chain length (modulating hydrophobicity and steric effects) play decisive roles in tuning molecular interactions and phase equilibrium behavior in the acetonitrile–water system.

To visually illustrate how different ILs influence phase equilibrium, Figure 4 shows x-y diagrams for the ternary systems at 323.15 K, where x^*₁ denotes the normalized mole fraction of acetonitrile in the liquid phase (calculated under the assumption x₃ = 0, mimicking the IL-free binary mixture). This normalization enables direct comparison of IL effects across systems. Under the tested conditions, all ILs eliminated the azeotropic point, with their separation efficiency for the acetonitrile–water system following the same order: [C₄mim][Cl] > [C₆mim][Cl] > [C₄mim][BF₄]. This aligns with our earlier findings, reinforcing that ILs with chloride anions outperform those with BF₄₋ for this separation, and among chloride-based ILs, shorter cation alkyl chains are more effective.

In previous studies, the VLE behavior of acetonitrile + water mixtures in the presence of different ILs, such as [C₄mim][Cl] [16,19], [C₆mim][Cl] [16], [C₄mim][BF₄] [19], [AMIM][Cl] [16], and [C₄mim][DBP] [19], has been reported under atmospheric pressure (101.3 kPa).

As shown in Figure 5, we compared the x-y diagrams of the acetonitrile + water + [C₄mim][Cl]/[C₆mim][Cl] systems under different conditions [16]. The experimental data selected in this work were measured at 352 K. The results consistently demonstrated that IL addition could eliminate or significantly reduce the azeotrope, thereby enhancing the separation of acetonitrile from water. Although the operating pressures and IL loadings differ between our work, the overall trend is consistent: the addition of ILs disrupts the strong interactions between acetonitrile and water, effectively eliminating or significantly reducing the azeotrope and enhancing the separation of acetonitrile from water. Moreover, our measurements under low-pressure conditions with higher IL concentrations further strengthen this effect, resulting in a more complete suppression of the azeotropic behavior.

4. Conclusions

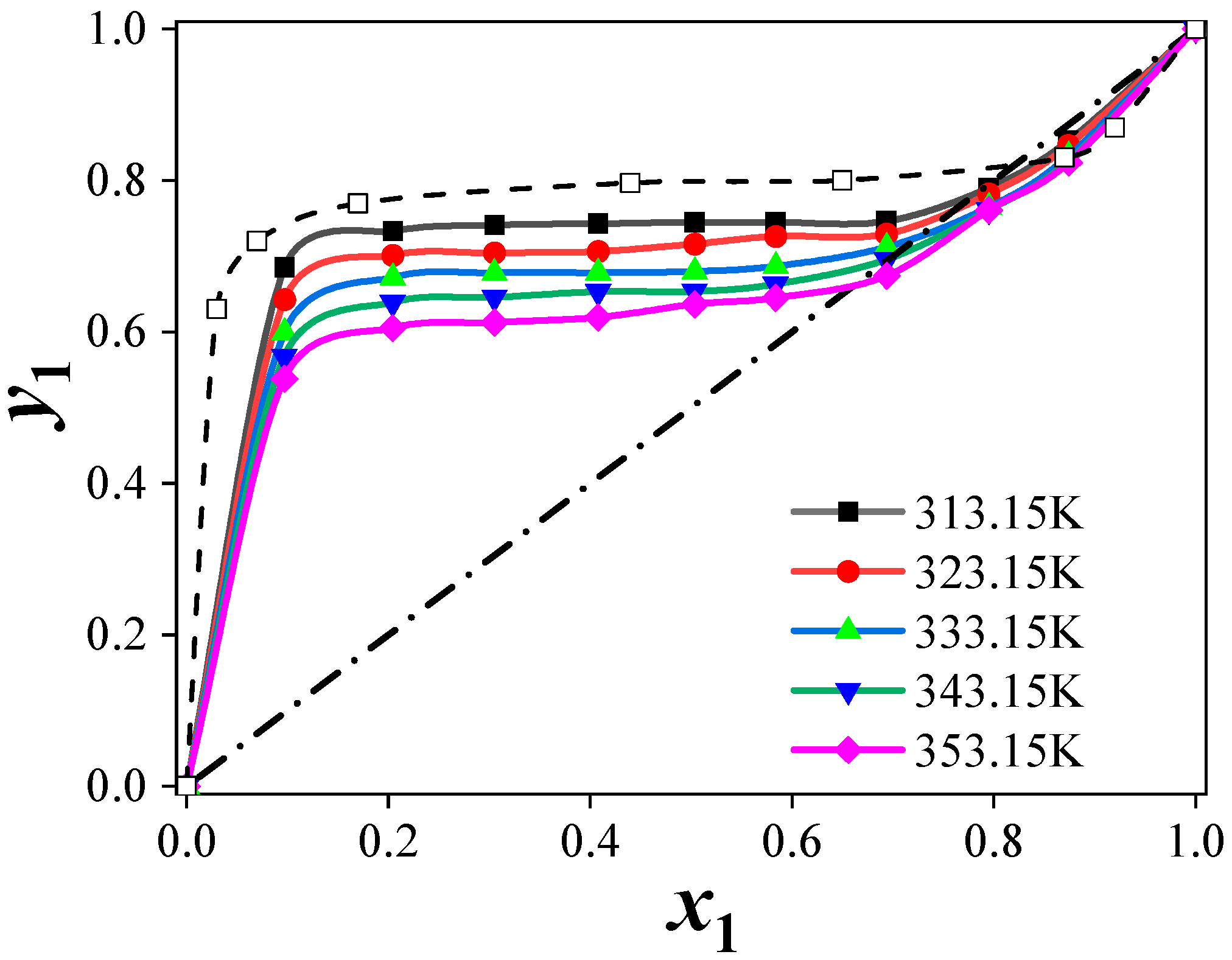
This study analyzed VLE data for three binary systems and three ternary systems (acetonitrile + water + IL), which were experimentally measured using a static isothermal VLE apparatus. The data were correlated and predicted using the NRTL and e-NRTL models. The main findings are summarized as follows:

(1) For the binary systems, the vapor pressure data exhibited negative deviations, with [C₄mim][BF₄] exerting the strongest influence on acetonitrile. Both the NRTL and e-NRTL models provided good correlations of the binary data. The NRTL model yielded average relative pressure deviations of 1.19% ([C₄mim][Cl]), 1.22% ([C₄mim][BF₄]), and 1.60% ([C₆mim][Cl]), whereas the e-NRTL model resulted in deviations of 1.54% ([C₄mim][Cl]), 1.36% ([C₄mim][BF₄]), and 2.88% ([C₆mim][Cl]).

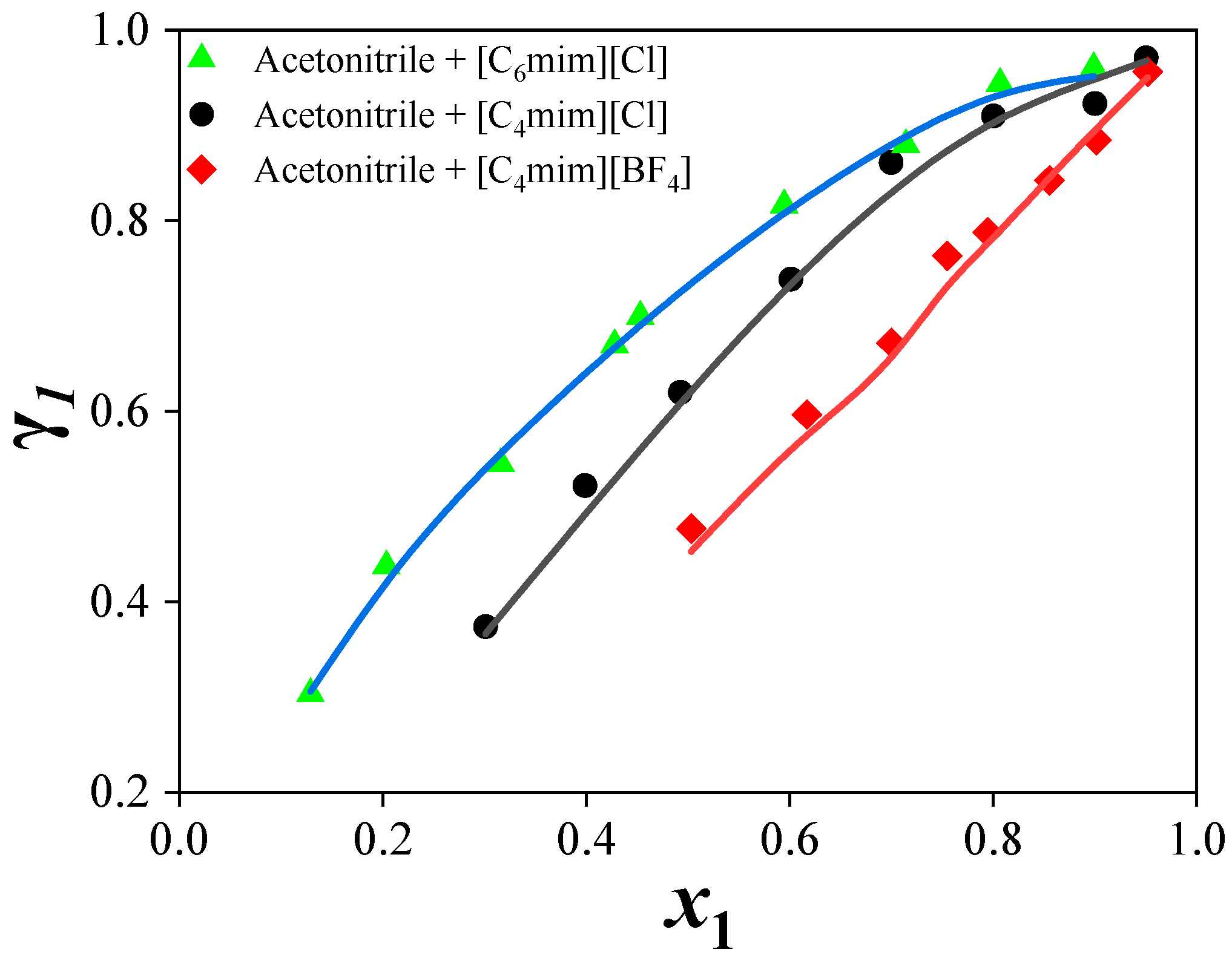
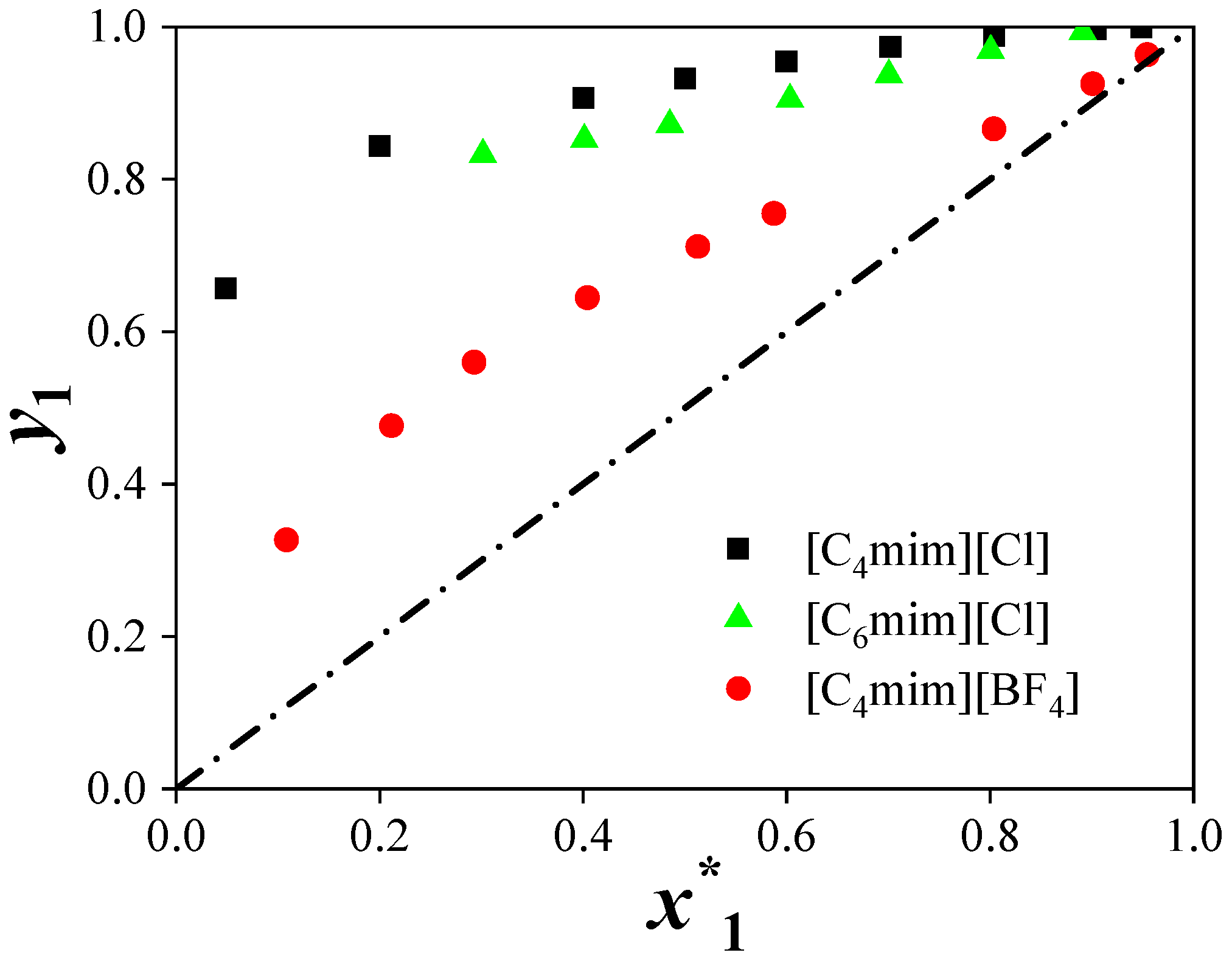
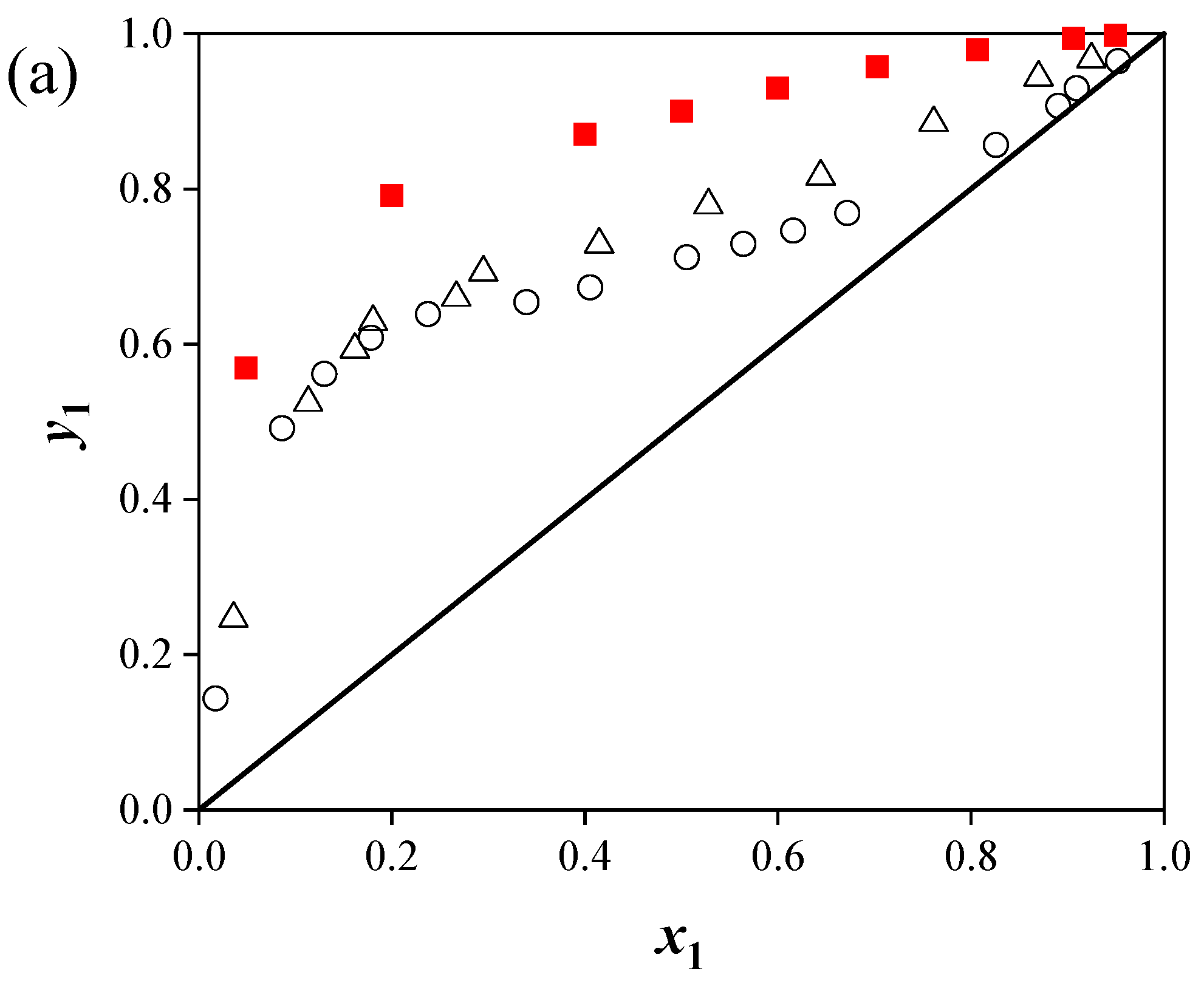
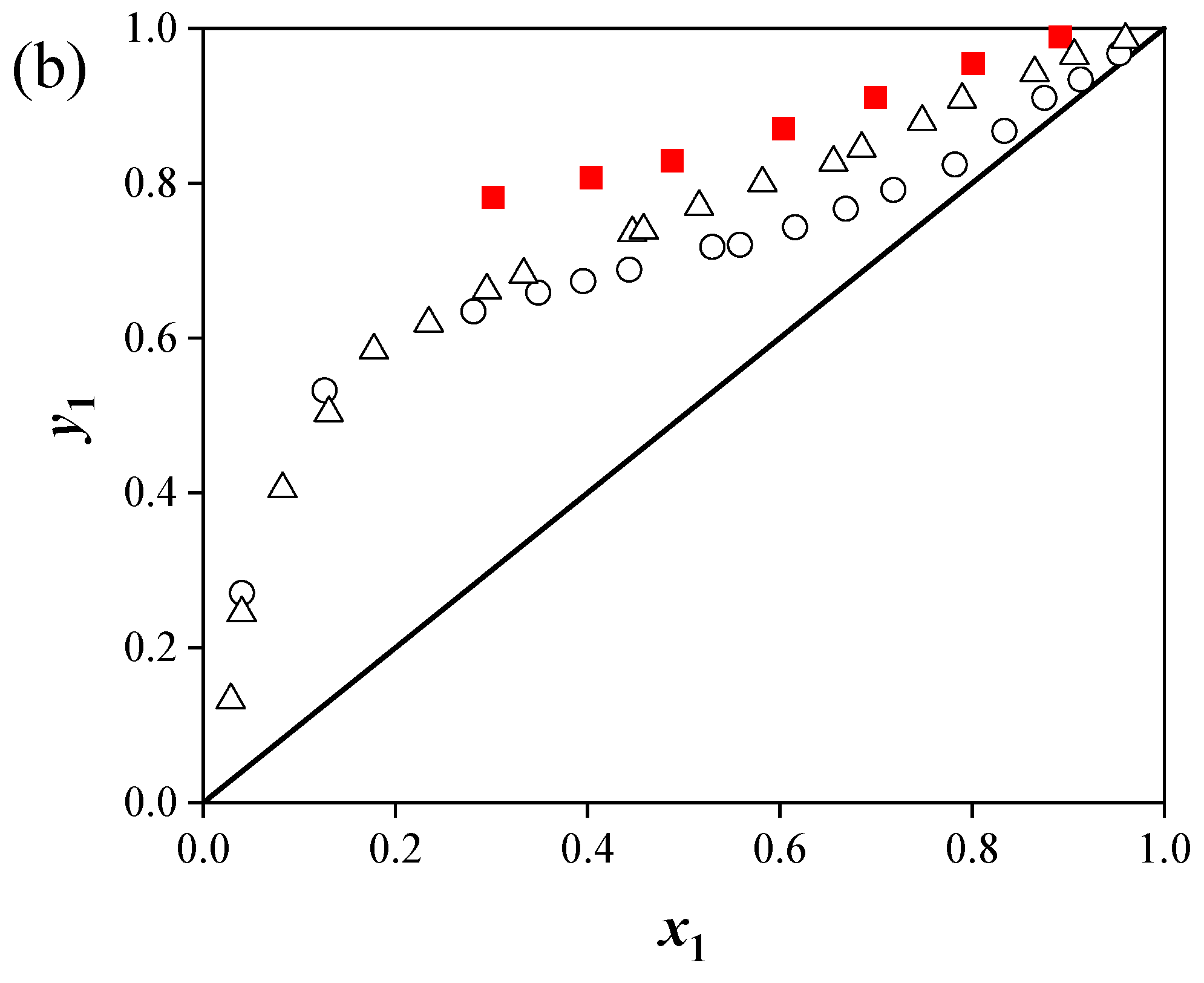
(2) Predictions for the ternary systems showed average relative pressure deviations of 9.11% ([C₄mim][Cl]), 8.85% ([C₄mim][BF₄]), and 9.86% ([C₆mim][Cl]). The addition of ILs increased the relative volatility of acetonitrile by disrupting the strong interactions between acetonitrile and water, thereby enhancing separation efficiency. The separation performance of the ILs followed the order: [C₄mim][Cl] > [C₆mim][Cl] > [C₄mim][BF₄].

(3) The effect of ILs on acetonitrile activity coefficients and phase behavior depended on both cation and anion structures. Chloride-based ILs with shorter alkyl chains provided higher separation efficiency.

These results provide valuable guidance for selecting ILs for acetonitrile + water separation and offer a theoretical basis for designing IL-based separation processes.