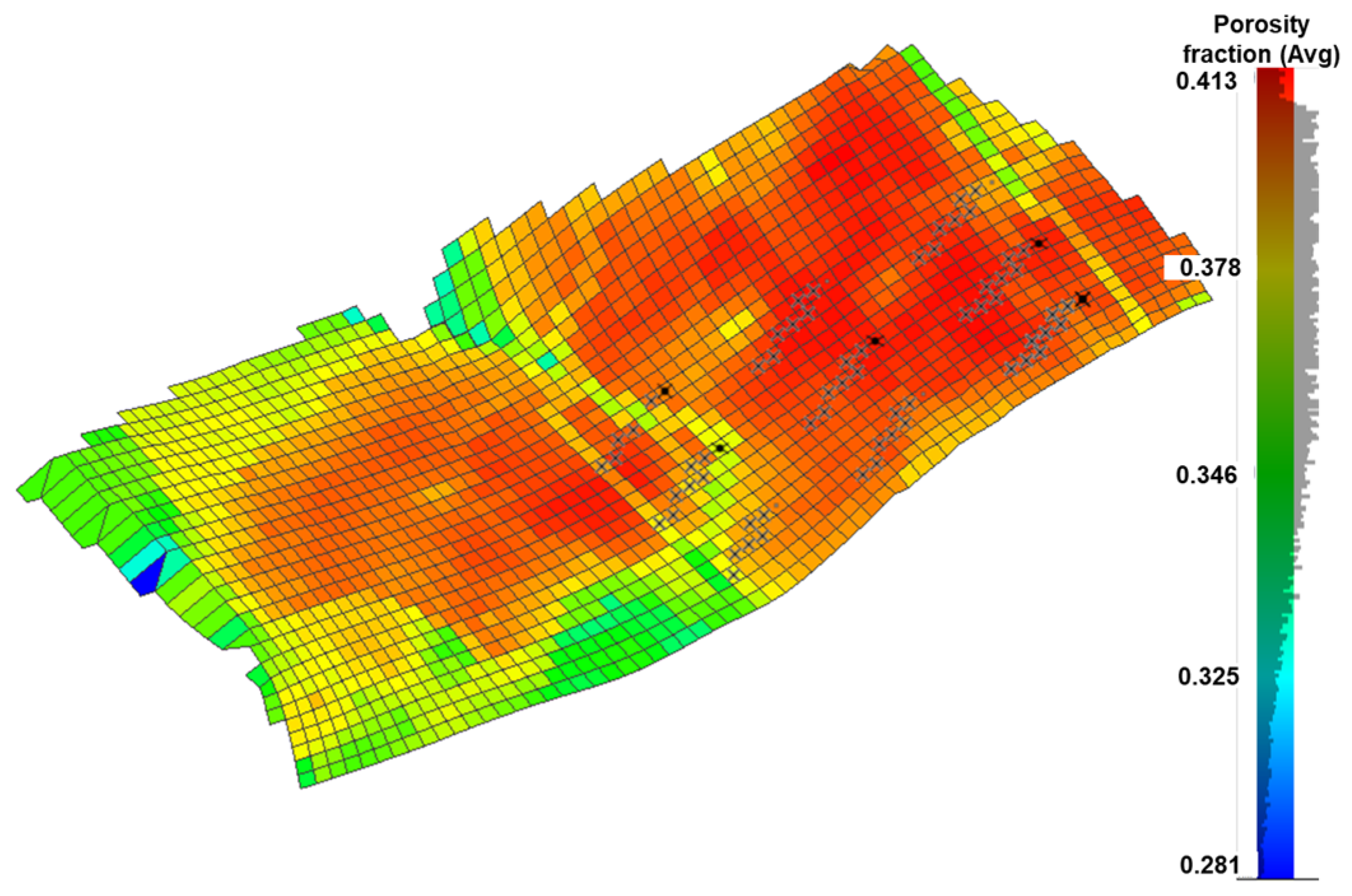
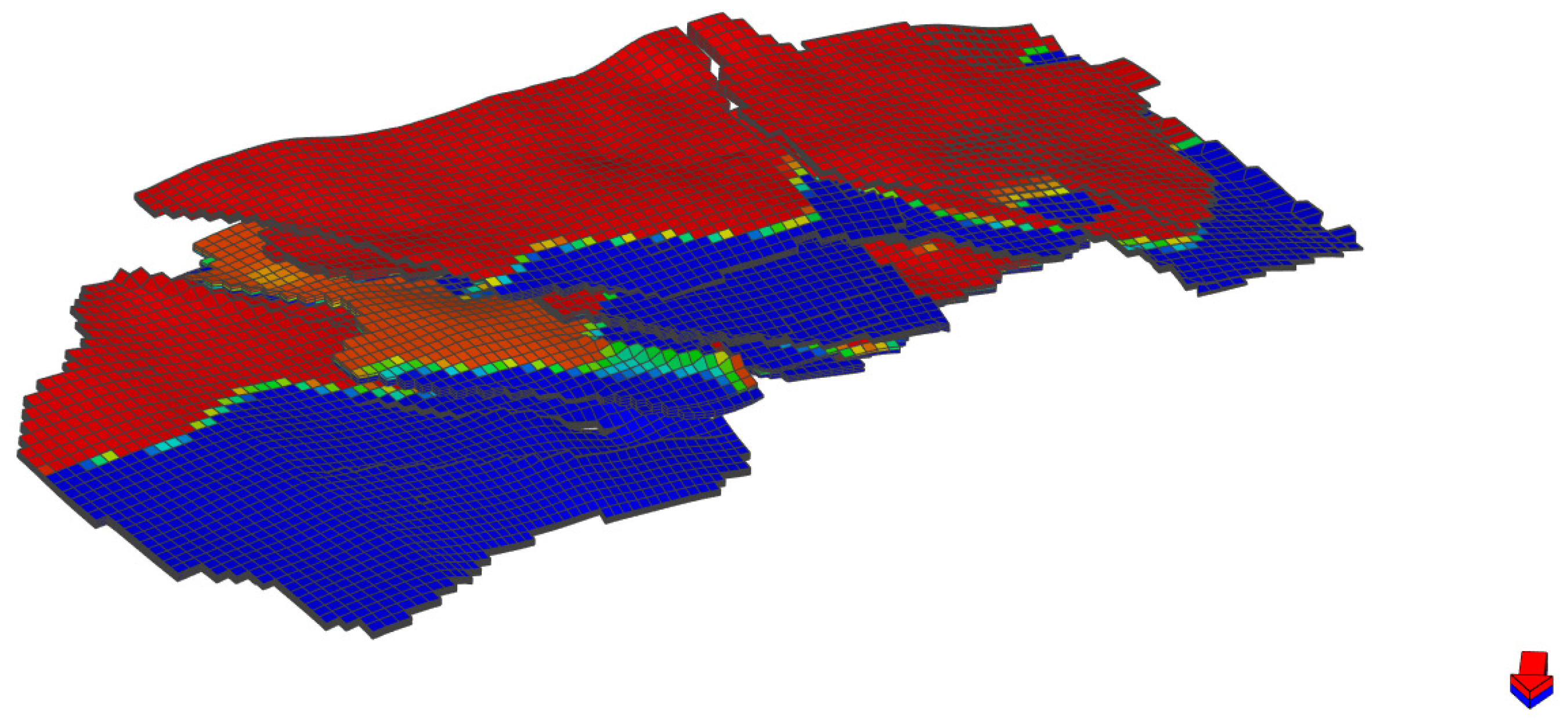
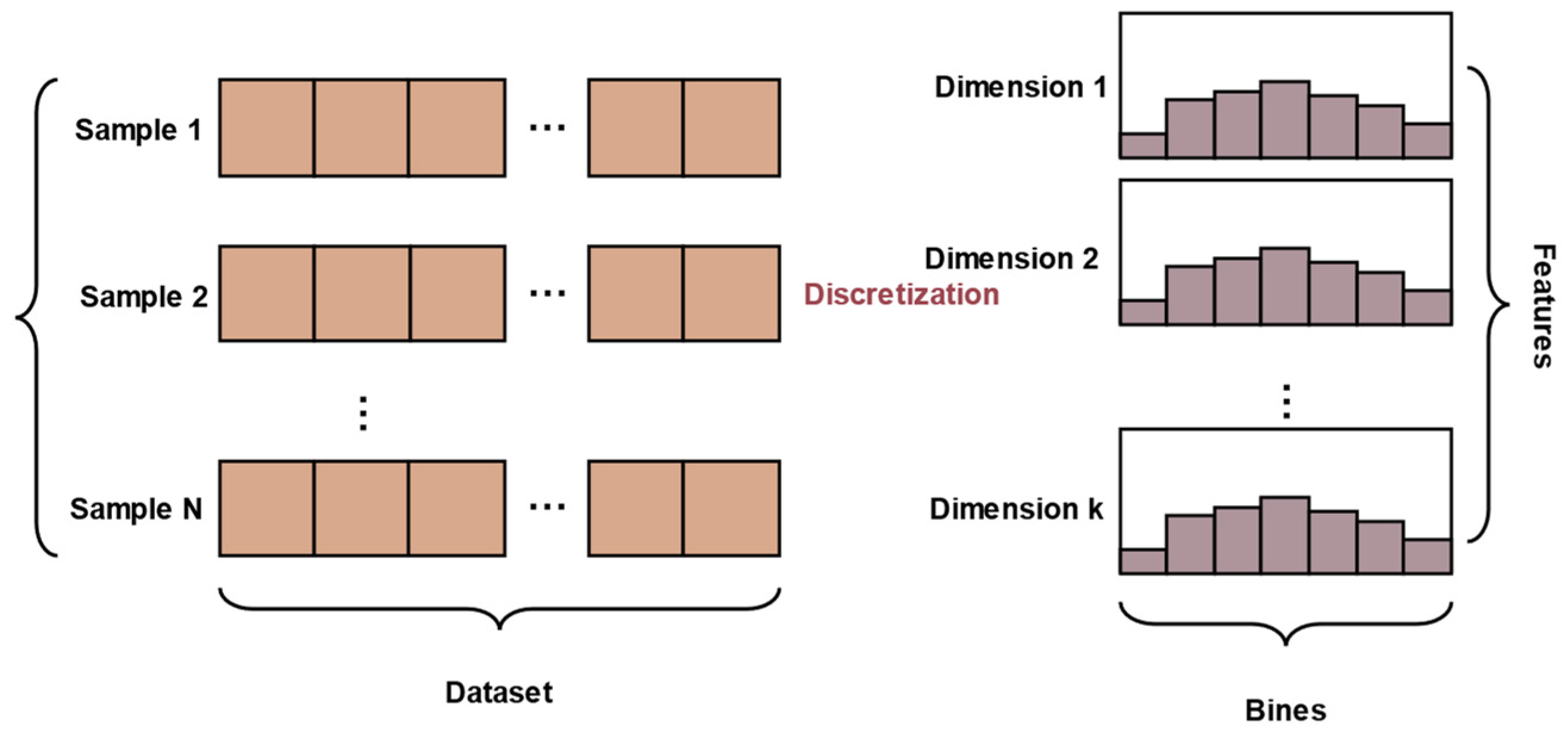
Figure 1.
3D geological model of the N reservoir.
Figure 1.
3D geological model of the N reservoir.
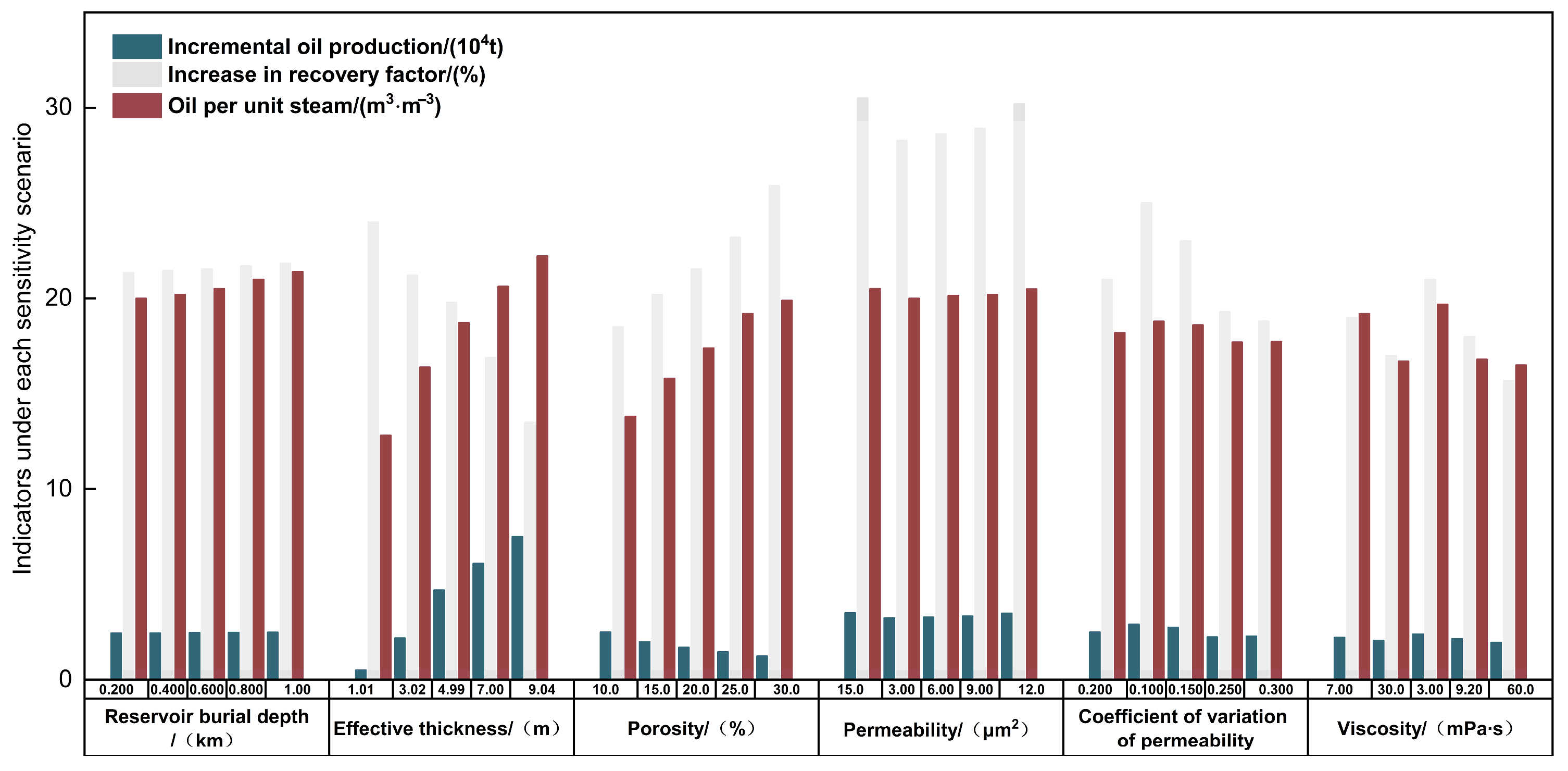
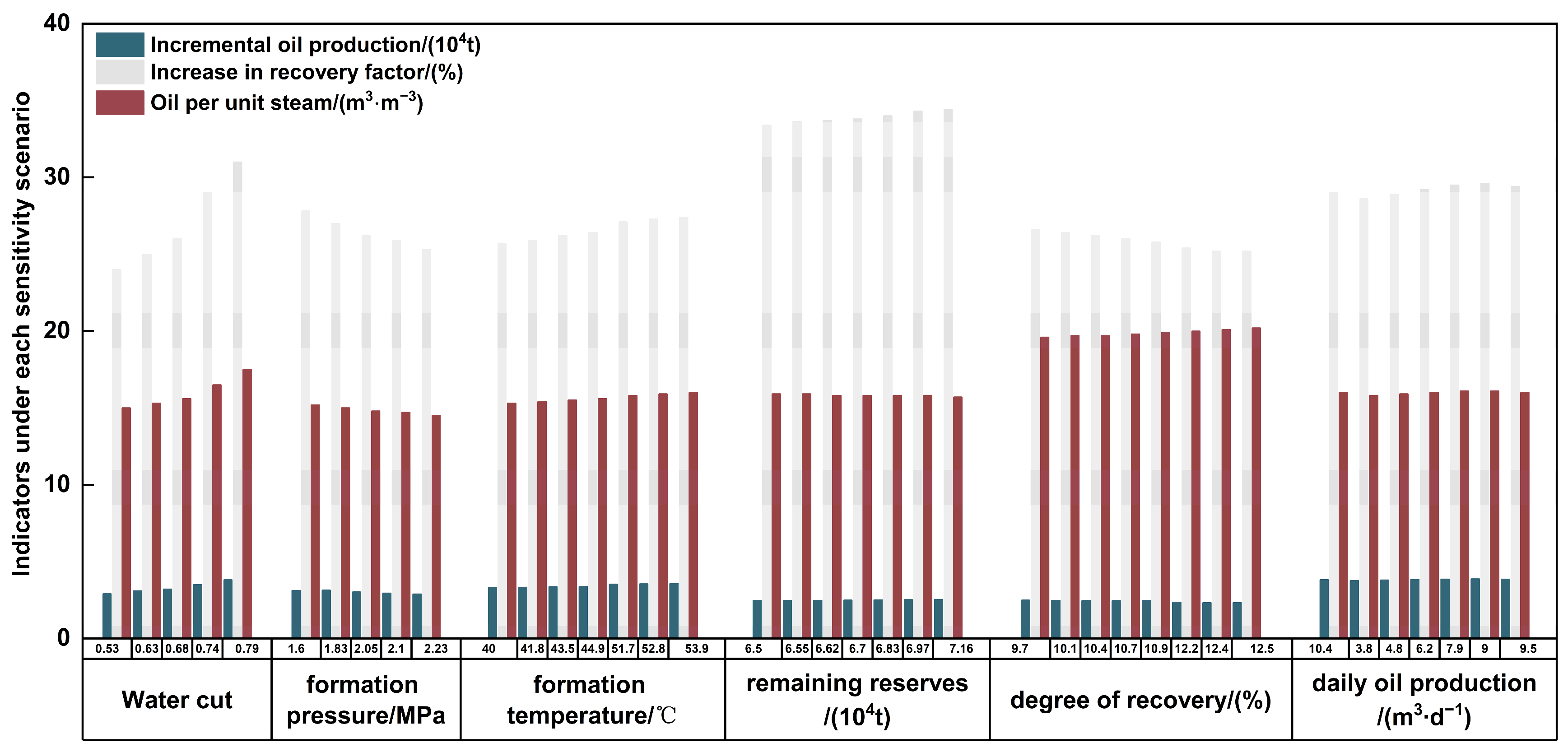
Figure 4.
Influence of geological factors on steam flood potential.
Figure 4.
Influence of geological factors on steam flood potential.
Figure 5.
Influence of development factors on steam flood potential.
Figure 5.
Influence of development factors on steam flood potential.
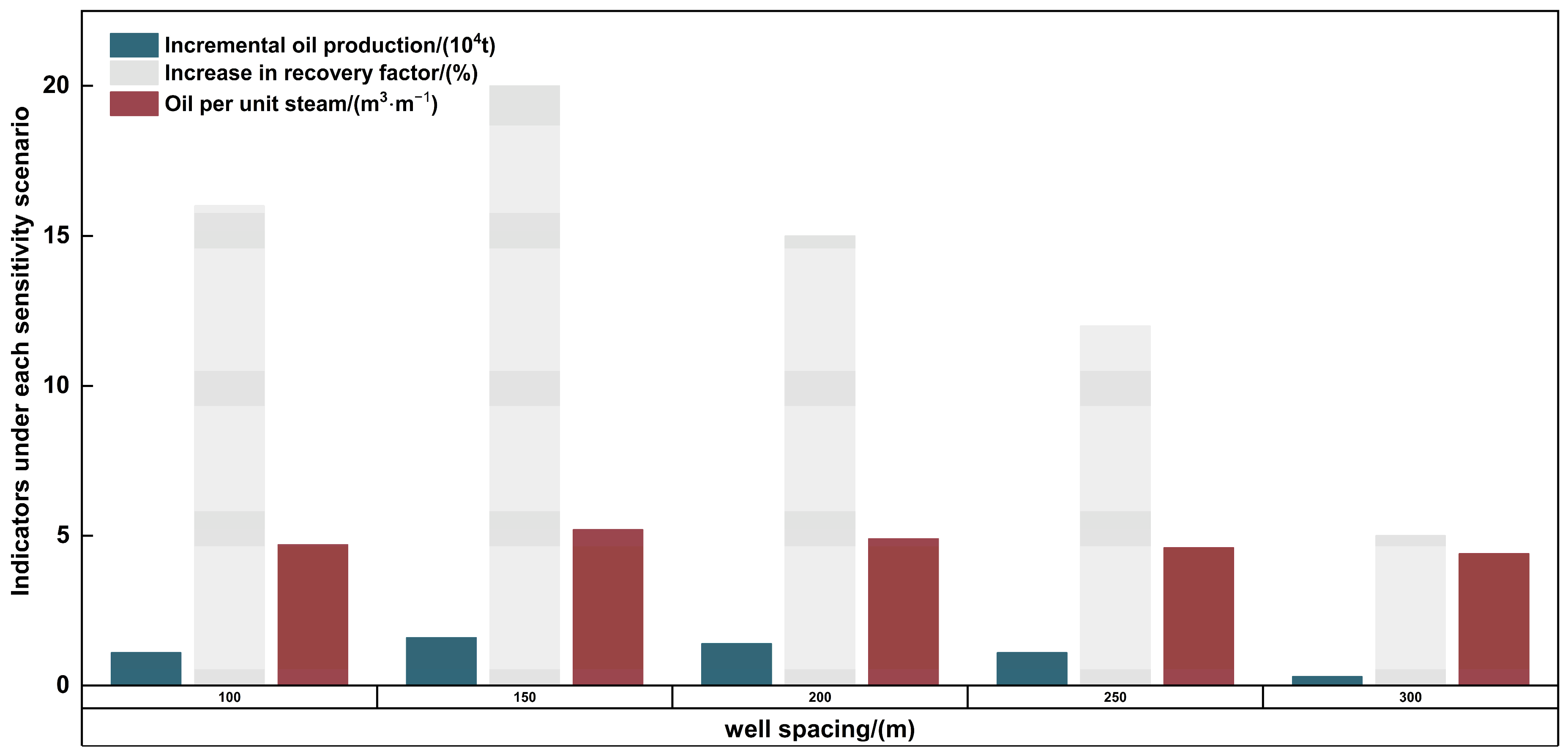
Figure 6.
Effect of process factor (well spacing) on steam flood potential.
Figure 6.
Effect of process factor (well spacing) on steam flood potential.
Figure 7.
Incremental steam flood recovery and influencing factors.
Figure 7.
Incremental steam flood recovery and influencing factors.
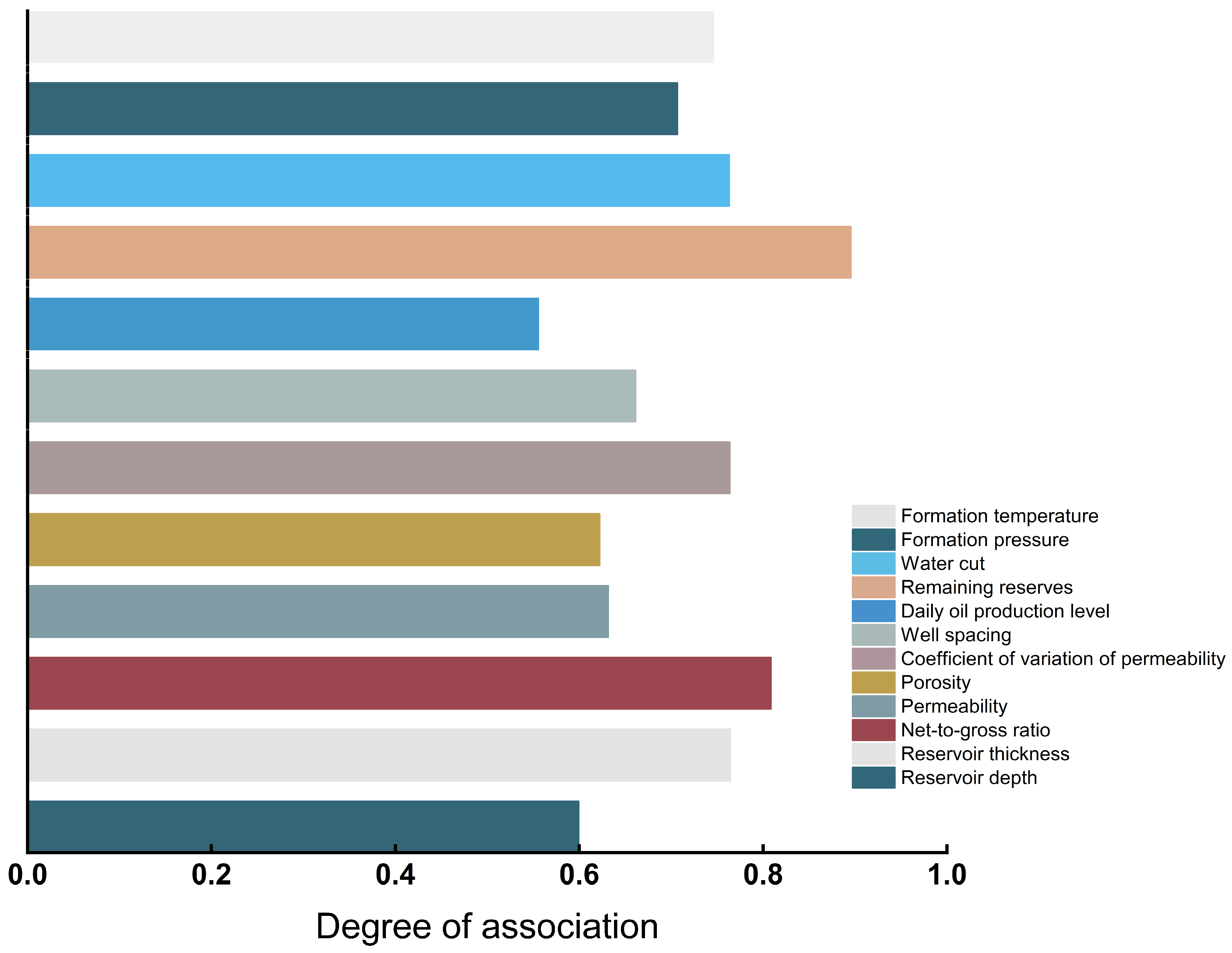
Figure 8.
Degrees of association and ranking.
Figure 8.
Degrees of association and ranking.
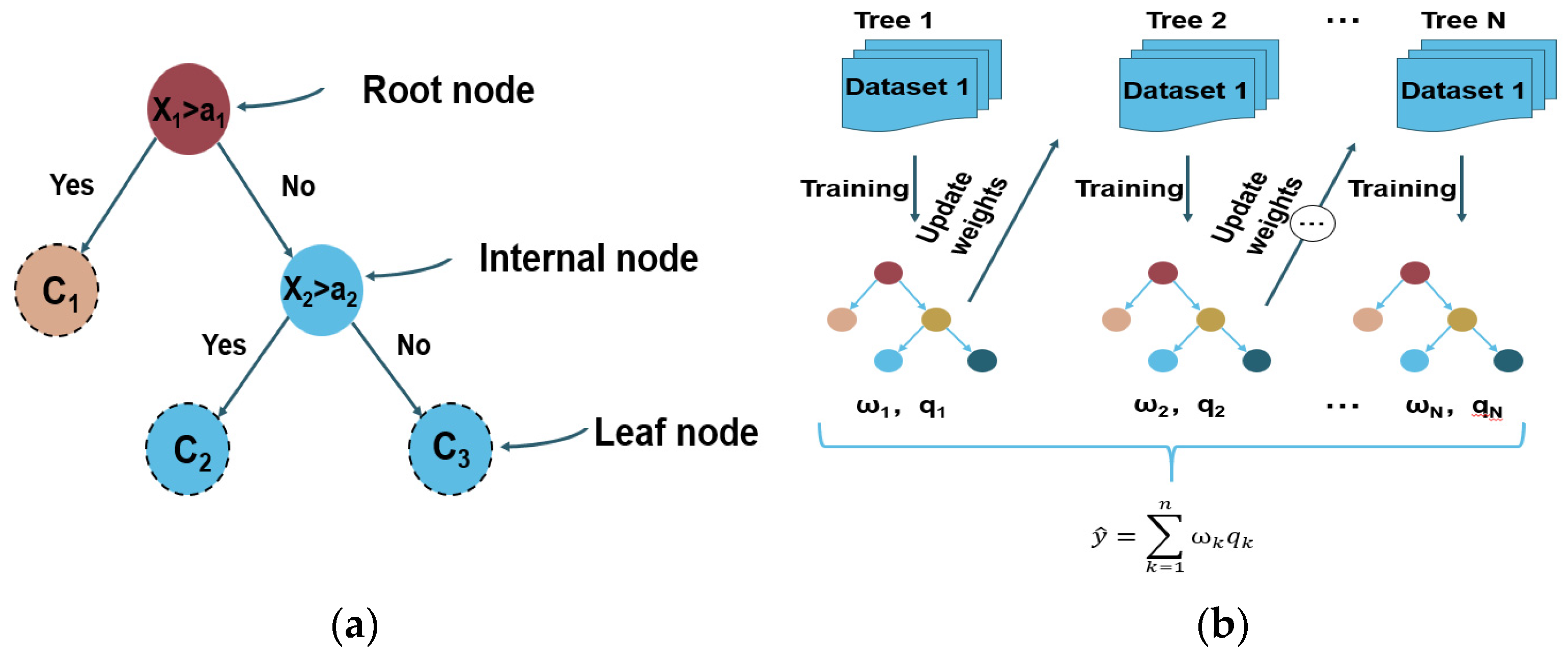
Figure 9.
Schematic of the decision tree models. (a) Schematic of the CART mode; (b) schematic of the XGBoost prediction model.
Figure 9.
Schematic of the decision tree models. (a) Schematic of the CART mode; (b) schematic of the XGBoost prediction model.
Figure 10.
Schematic of LightGBM histogram optimization.
Figure 10.
Schematic of LightGBM histogram optimization.
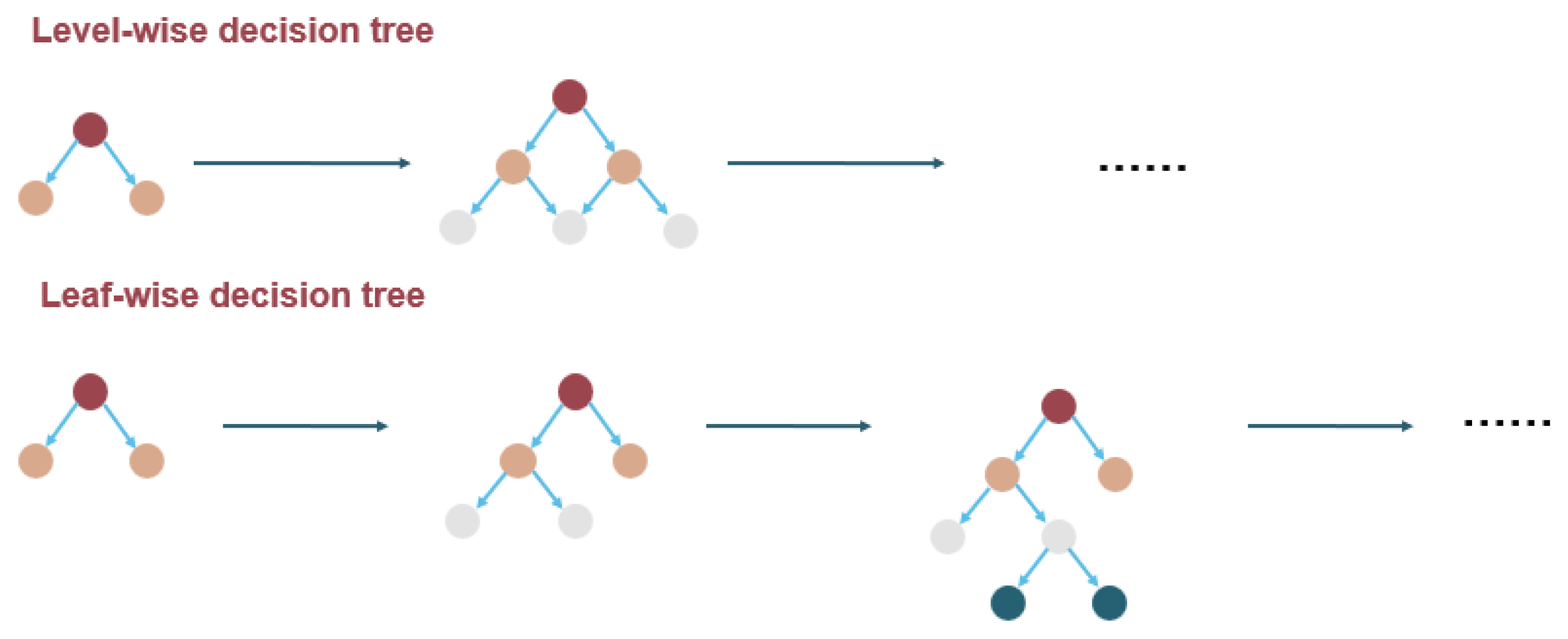
Figure 11.
Comparison of different decision tree growth modes.
Figure 11.
Comparison of different decision tree growth modes.
Figure 12.
Scatter plot of ANN-predicted vs. actual steam-drive potential. (a) Training set; (b) prediction set.
Figure 12.
Scatter plot of ANN-predicted vs. actual steam-drive potential. (a) Training set; (b) prediction set.
Figure 13.
Scatter plot of GBDT-predicted vs. actual steam-drive potential. (a) Training set; (b) prediction set.
Figure 13.
Scatter plot of GBDT-predicted vs. actual steam-drive potential. (a) Training set; (b) prediction set.
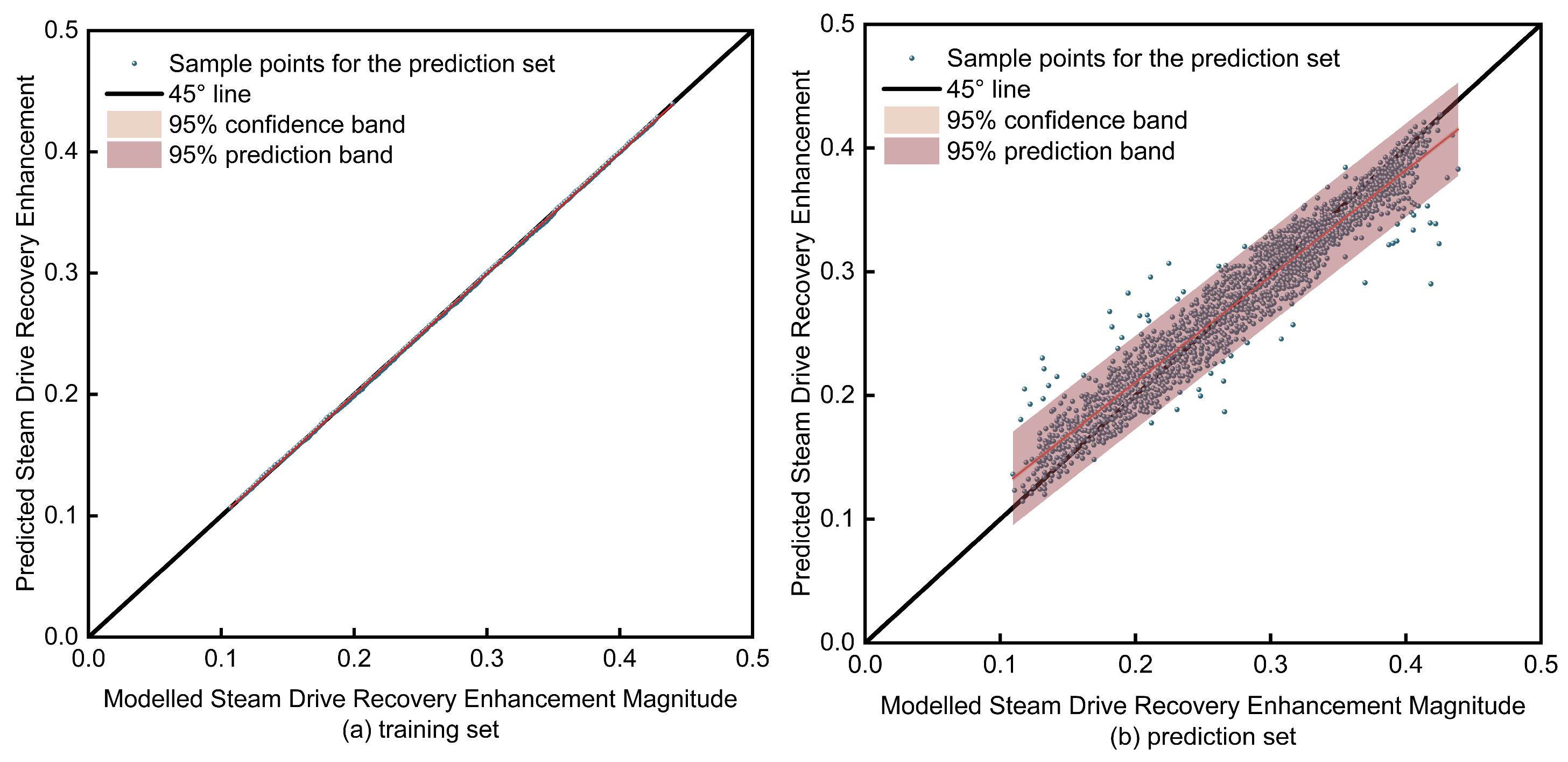
Figure 14.
Scatter plot of XGBoost-predicted vs. actual steam-drive potential. (a) Training set; (b) prediction set.
Figure 14.
Scatter plot of XGBoost-predicted vs. actual steam-drive potential. (a) Training set; (b) prediction set.
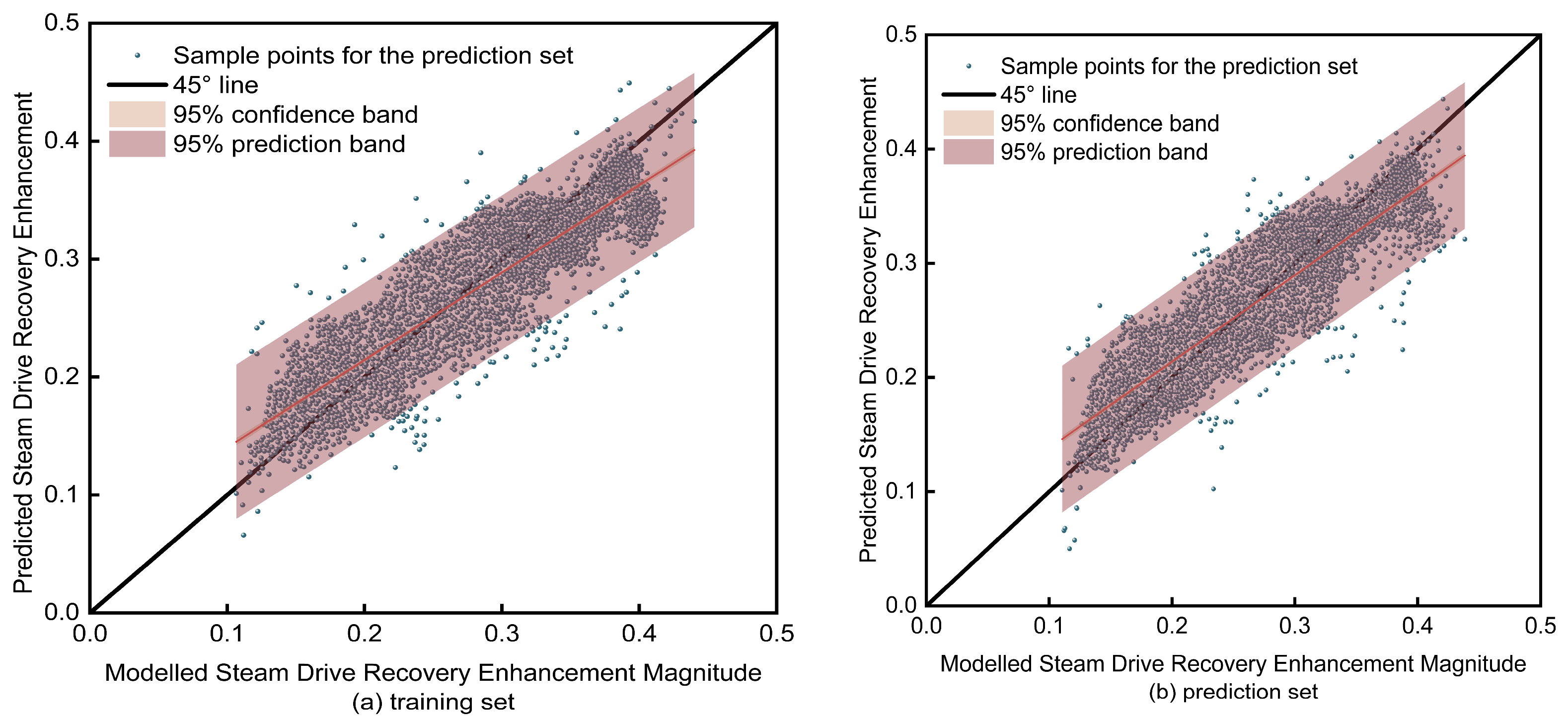
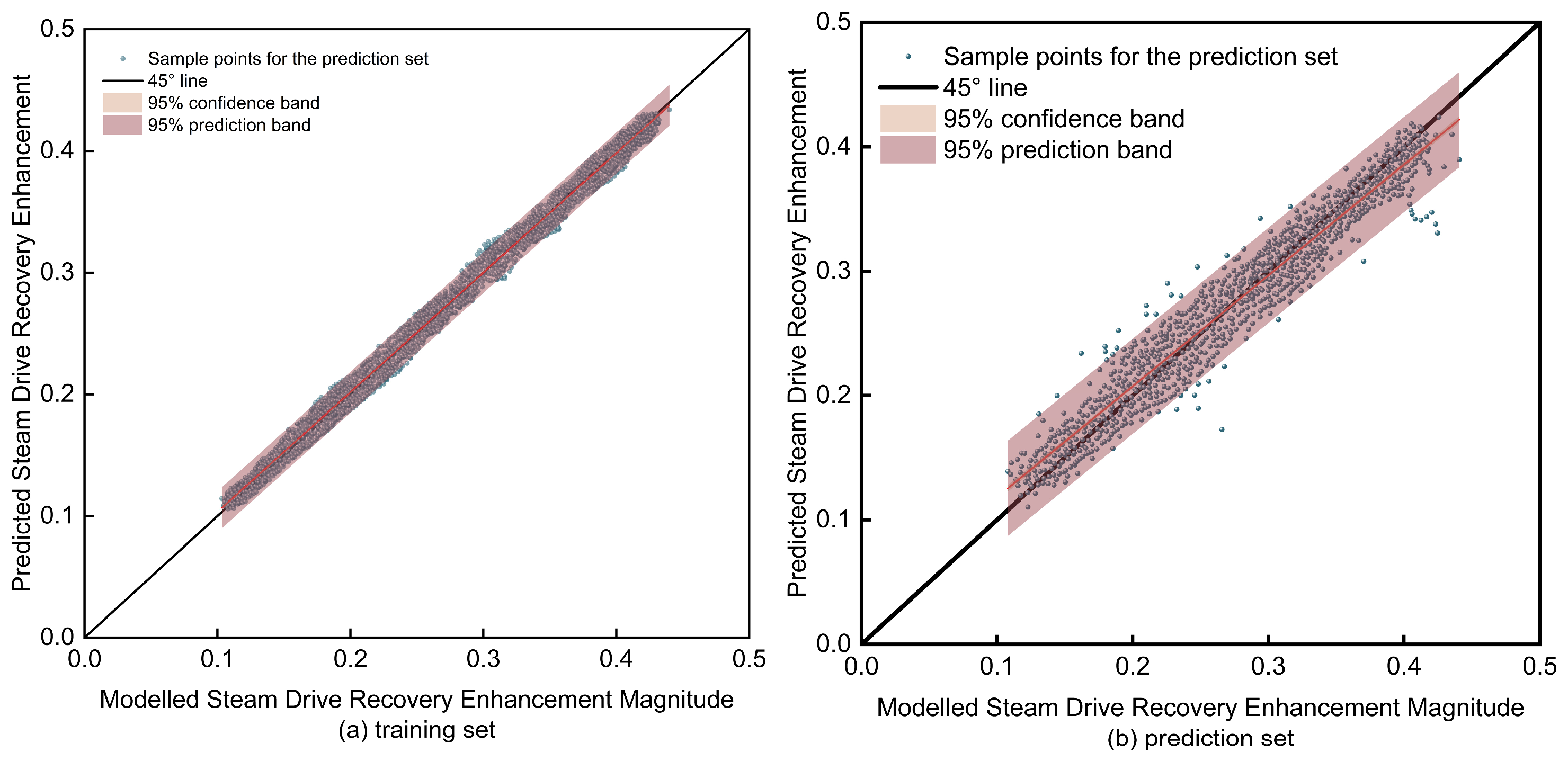
Figure 15.
Scatter plot of LightGBM-predicted vs. actual steam-drive potential: (a) training set; (b) prediction set.
Figure 15.
Scatter plot of LightGBM-predicted vs. actual steam-drive potential: (a) training set; (b) prediction set.
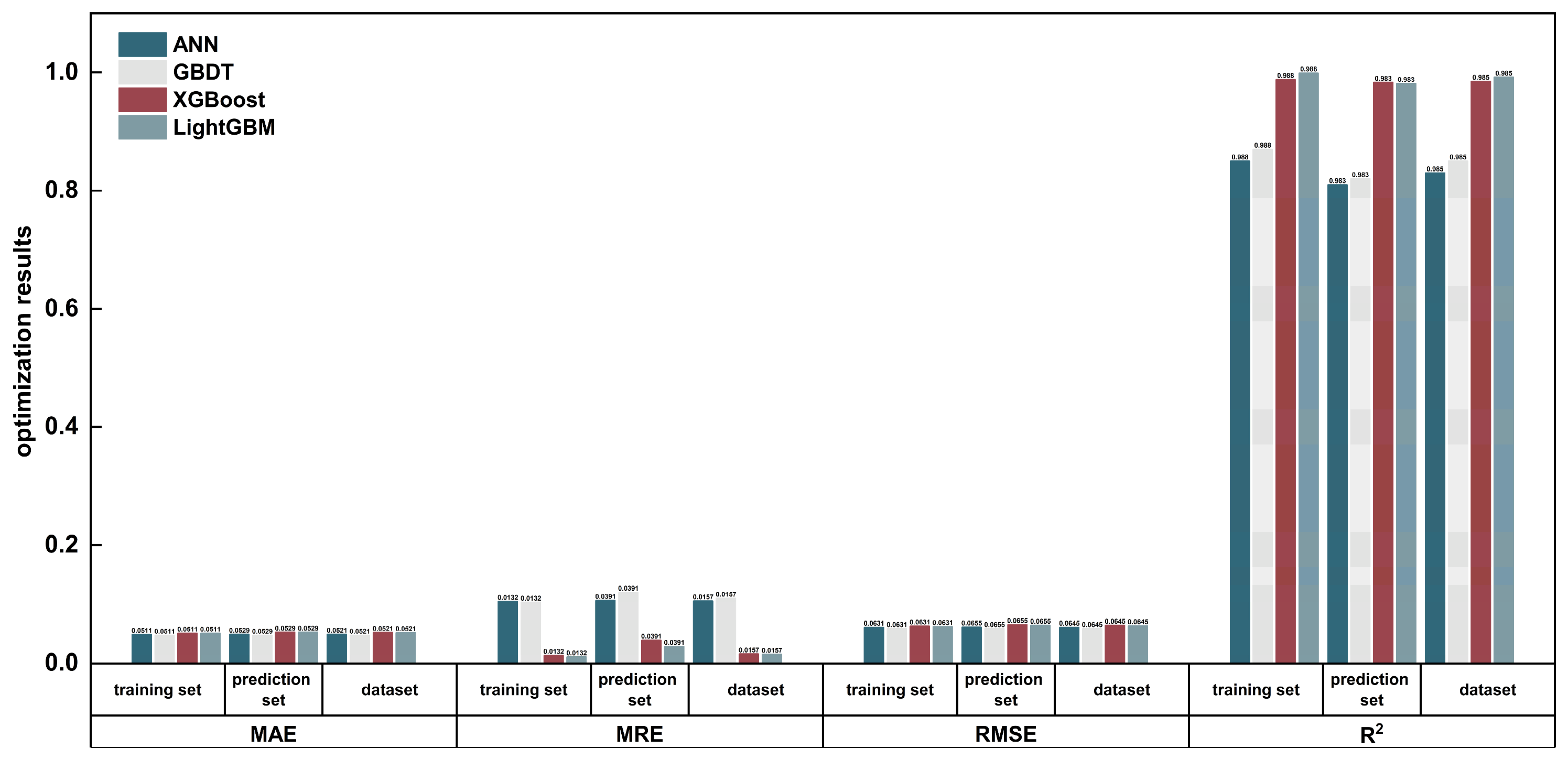
Figure 16.
Summary of evaluations of different artificial intelligence methods.
Figure 16.
Summary of evaluations of different artificial intelligence methods.
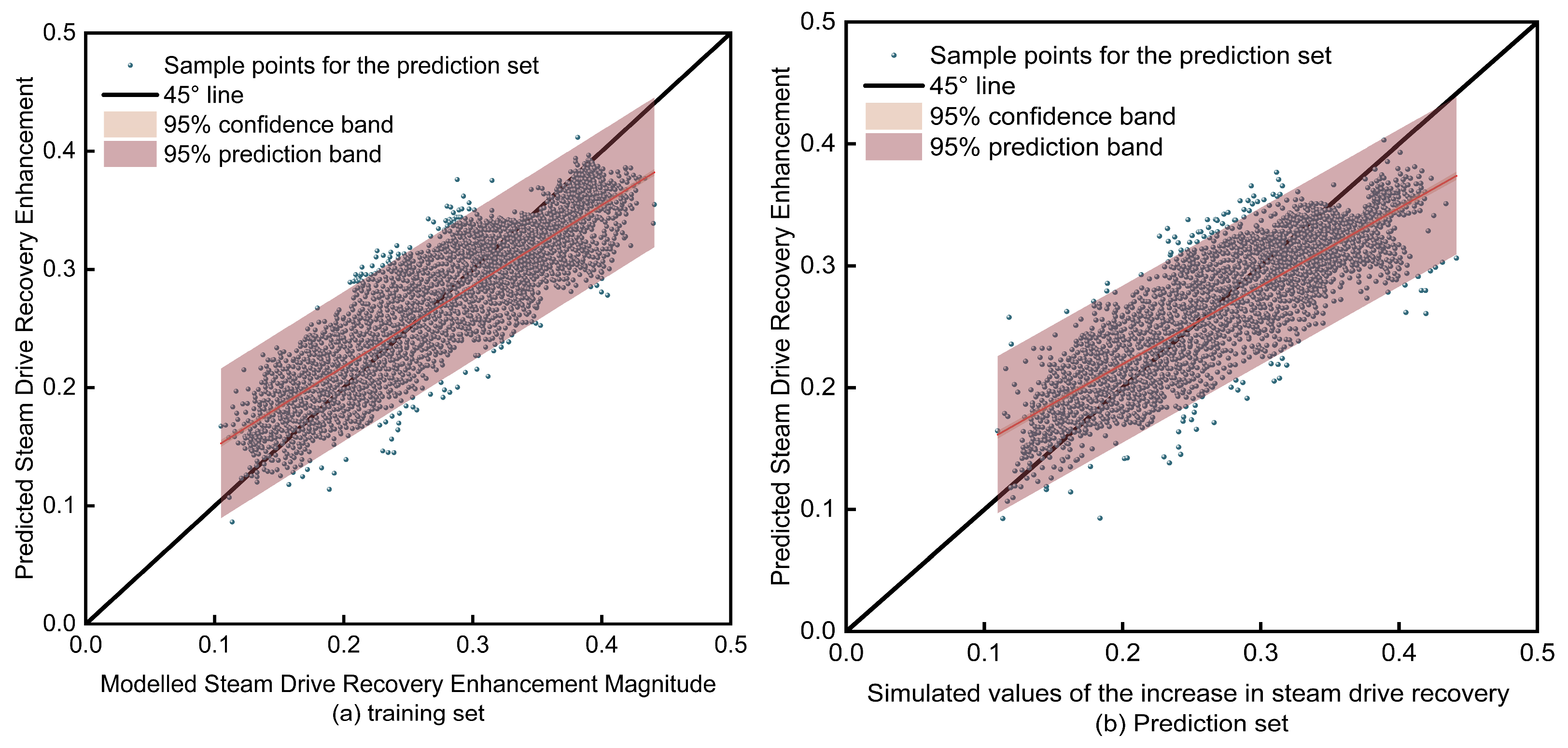
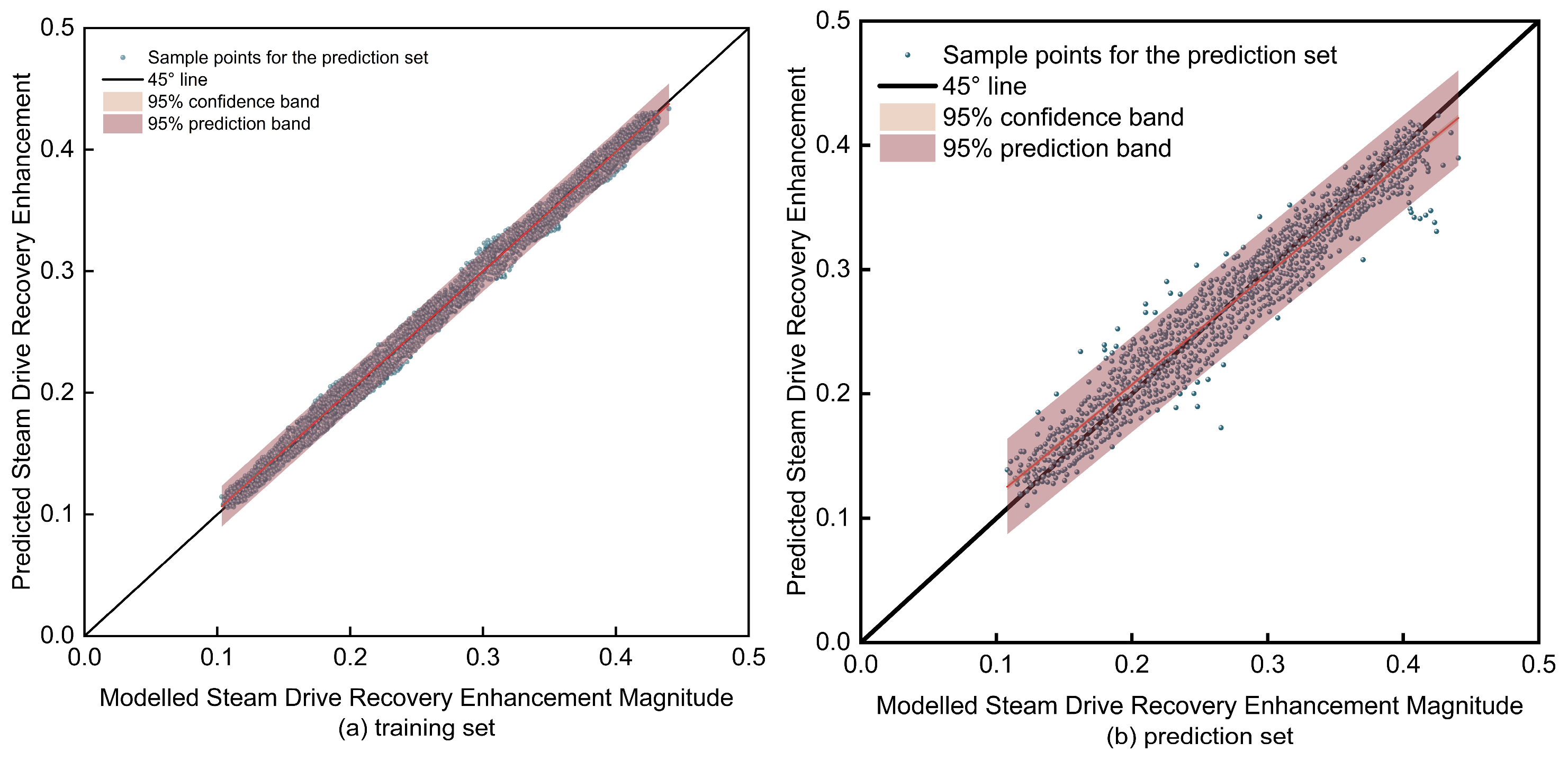
Figure 17.
Scatter plots of the tuned LightGBM predicted vs. actual steam-drive potential: (a) training set; (b) test set.
Figure 17.
Scatter plots of the tuned LightGBM predicted vs. actual steam-drive potential: (a) training set; (b) test set.
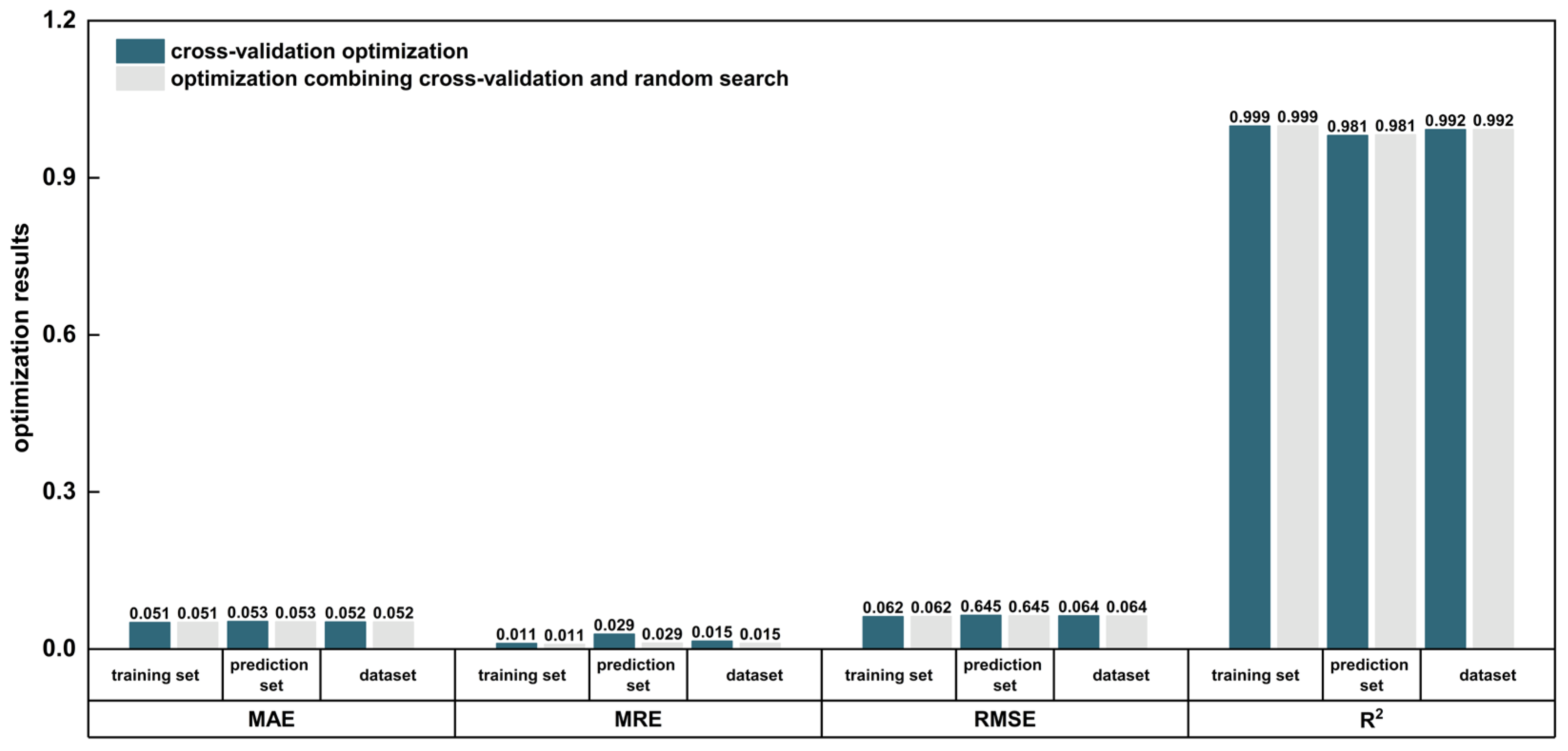
Figure 18.
Evaluation of cross-validation and of cross-validation combined with random search.
Figure 18.
Evaluation of cross-validation and of cross-validation combined with random search.
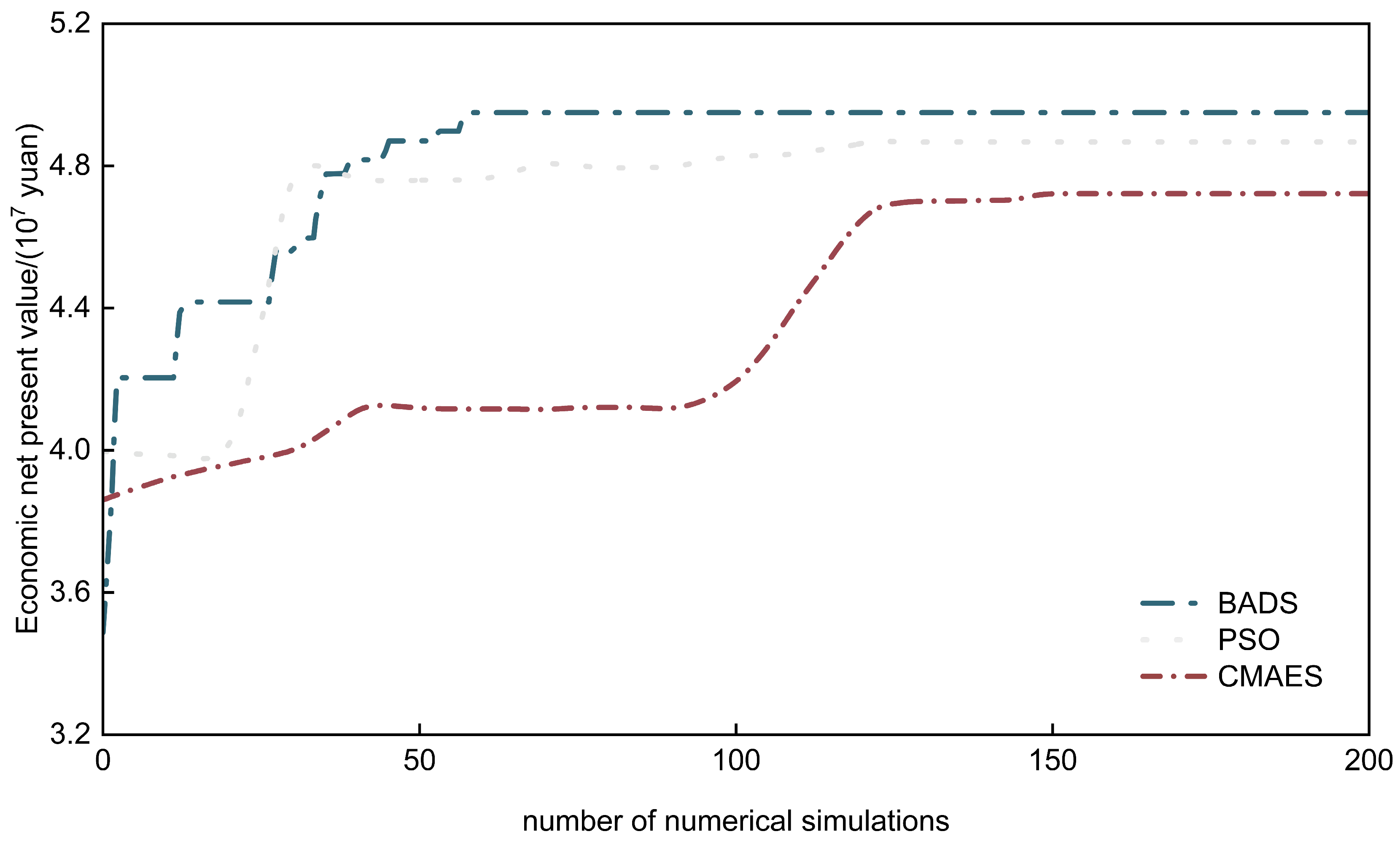
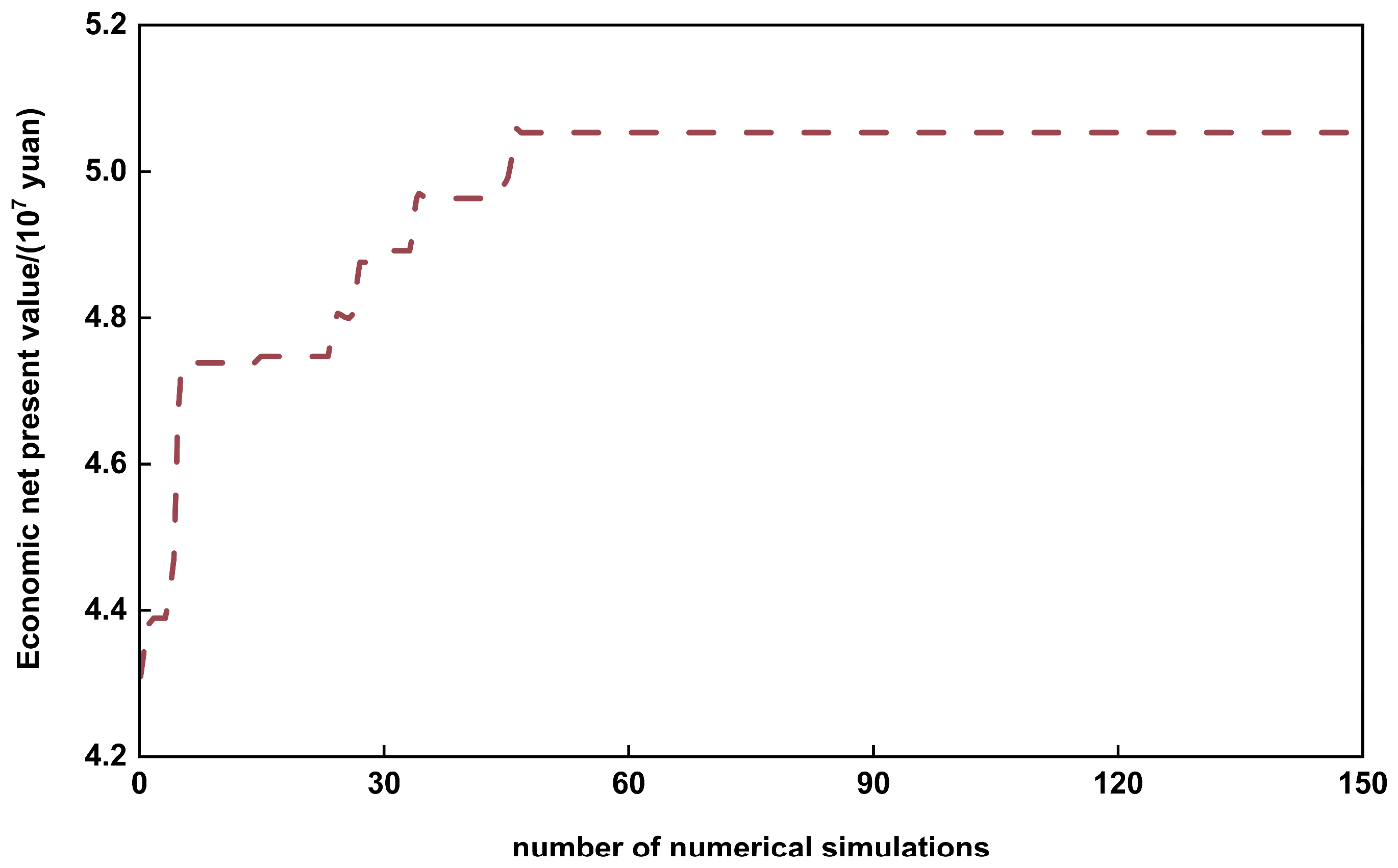
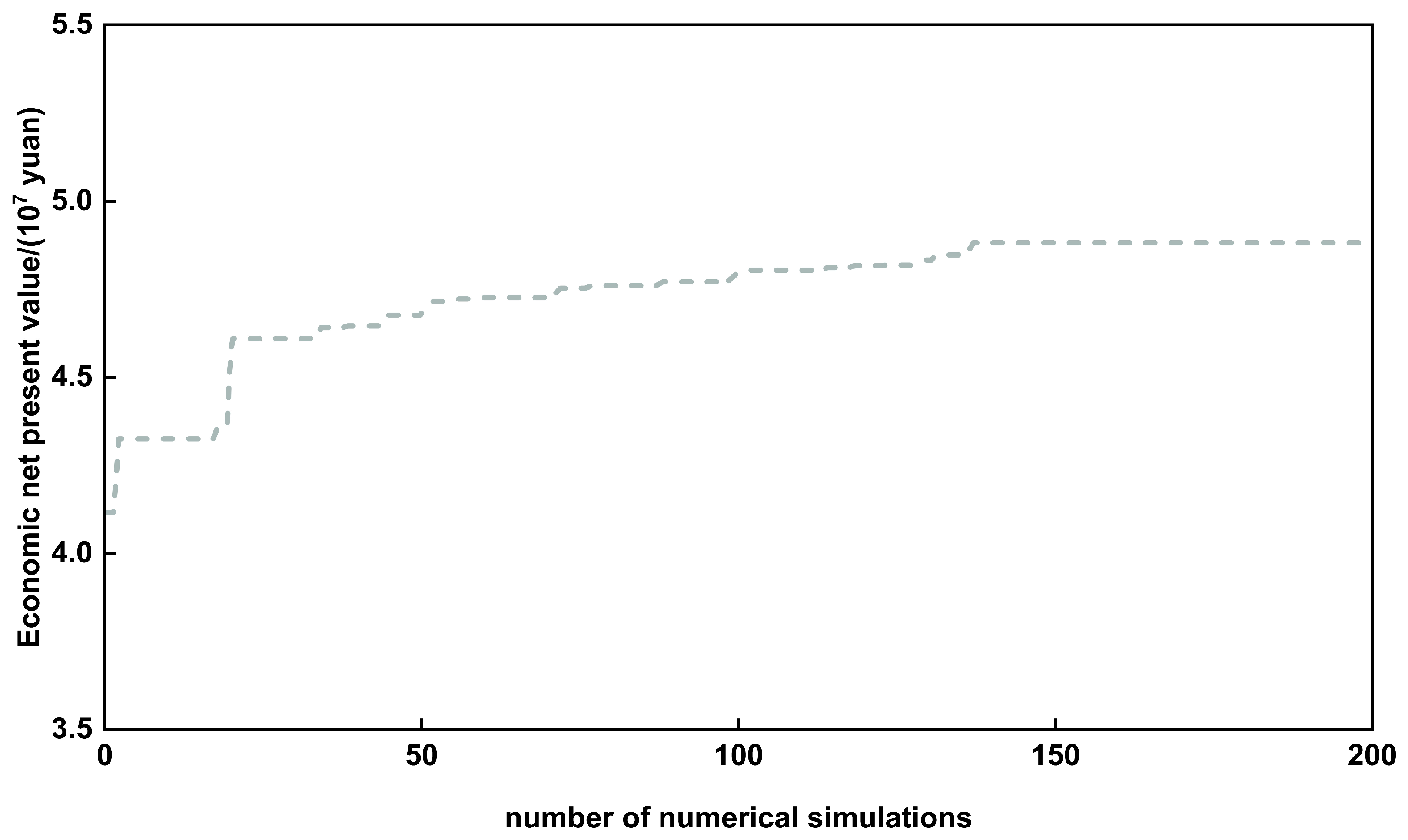
Figure 19.
Optimization dynamics of continuous injection.
Figure 19.
Optimization dynamics of continuous injection.
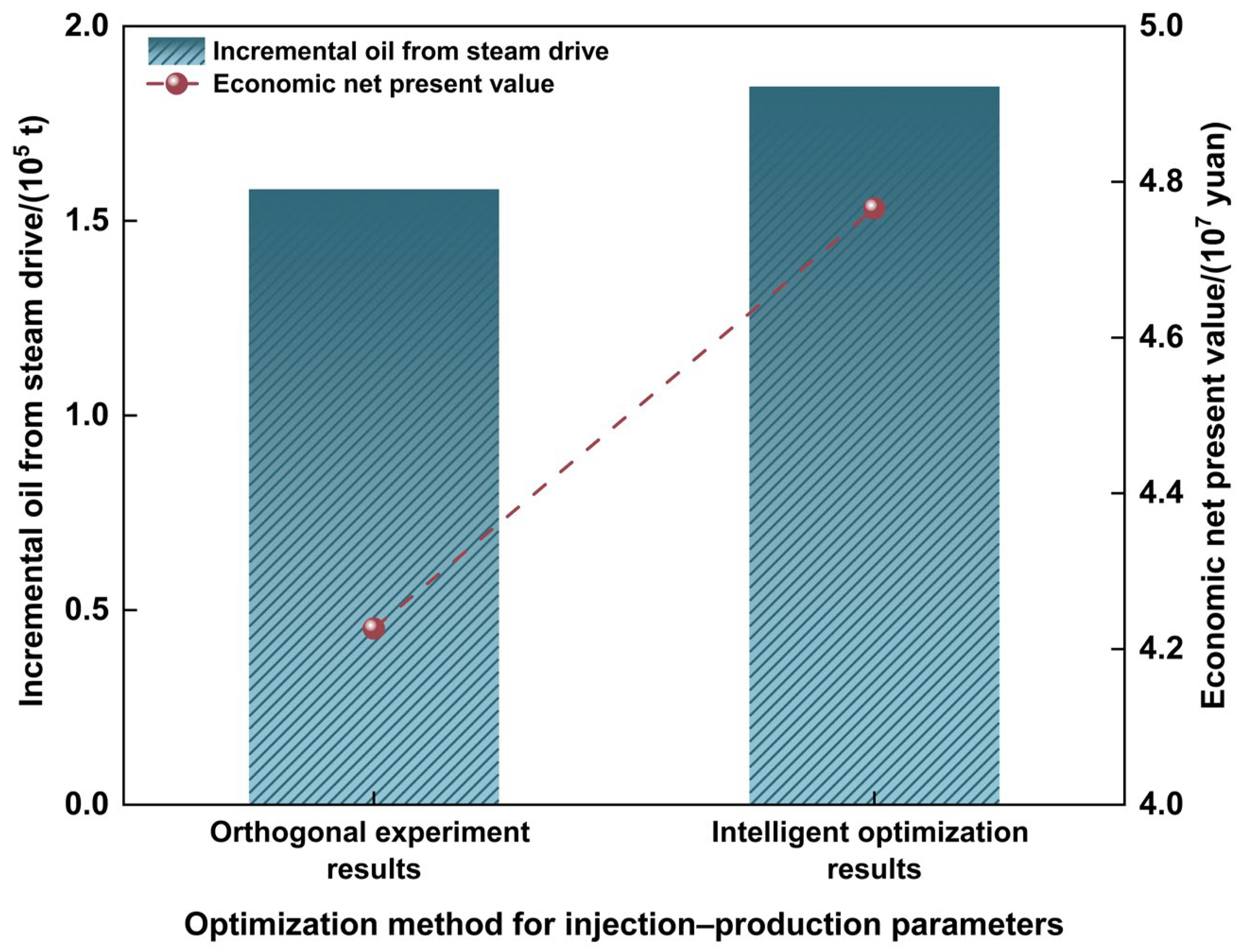
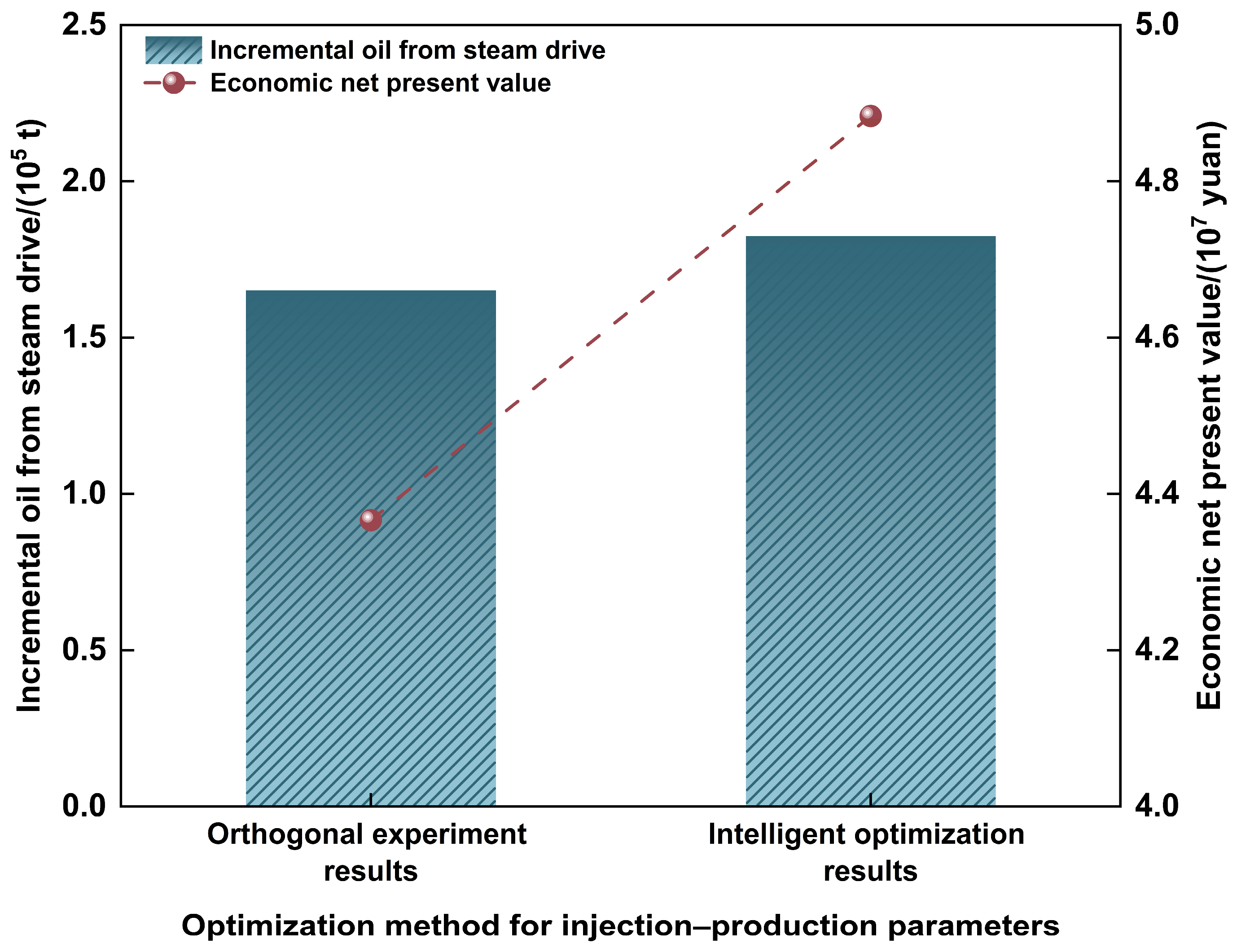
Figure 20.
Comparison of orthogonal experimental design and intelligent optimization results for continuous injection.
Figure 20.
Comparison of orthogonal experimental design and intelligent optimization results for continuous injection.
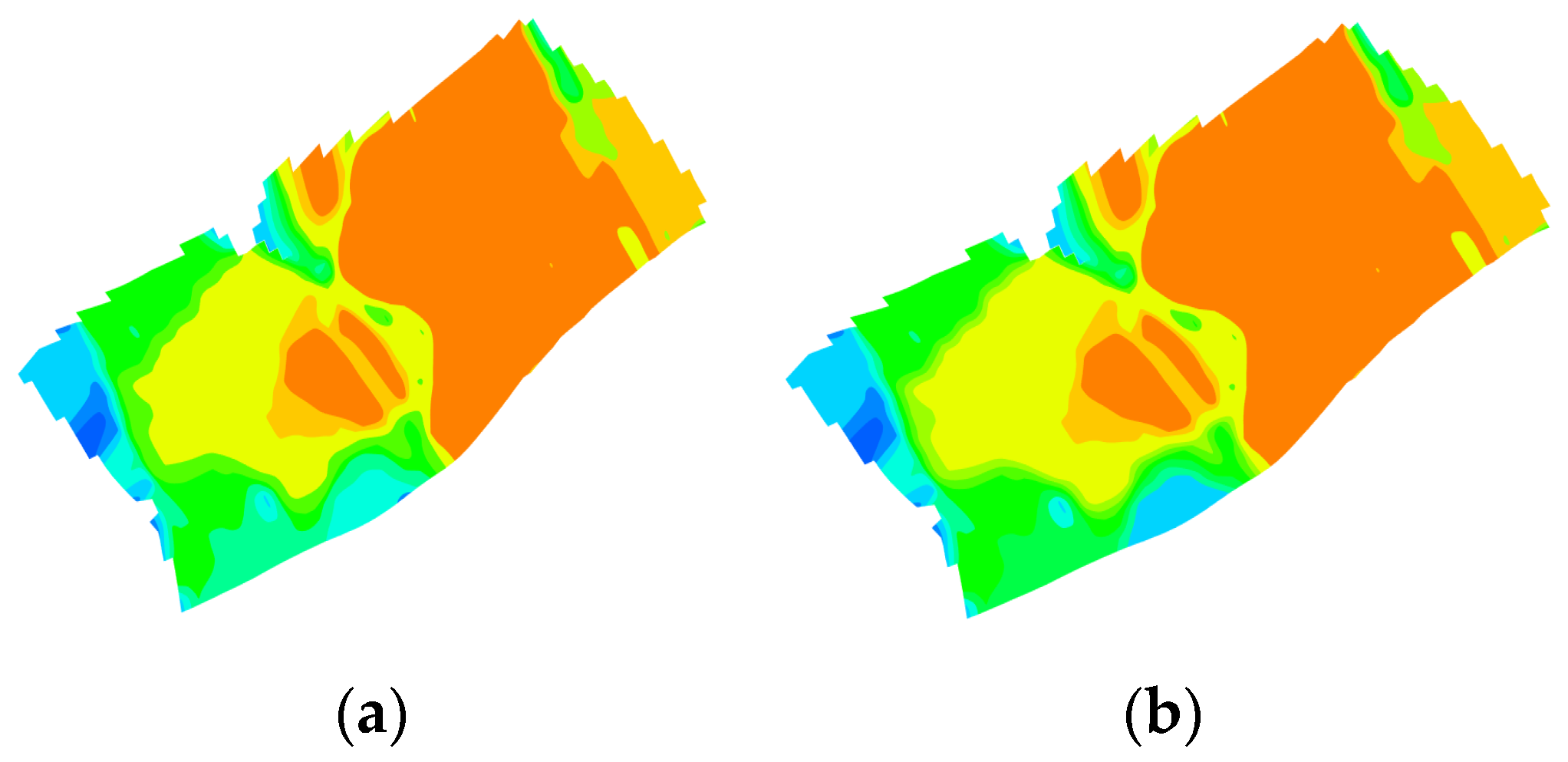
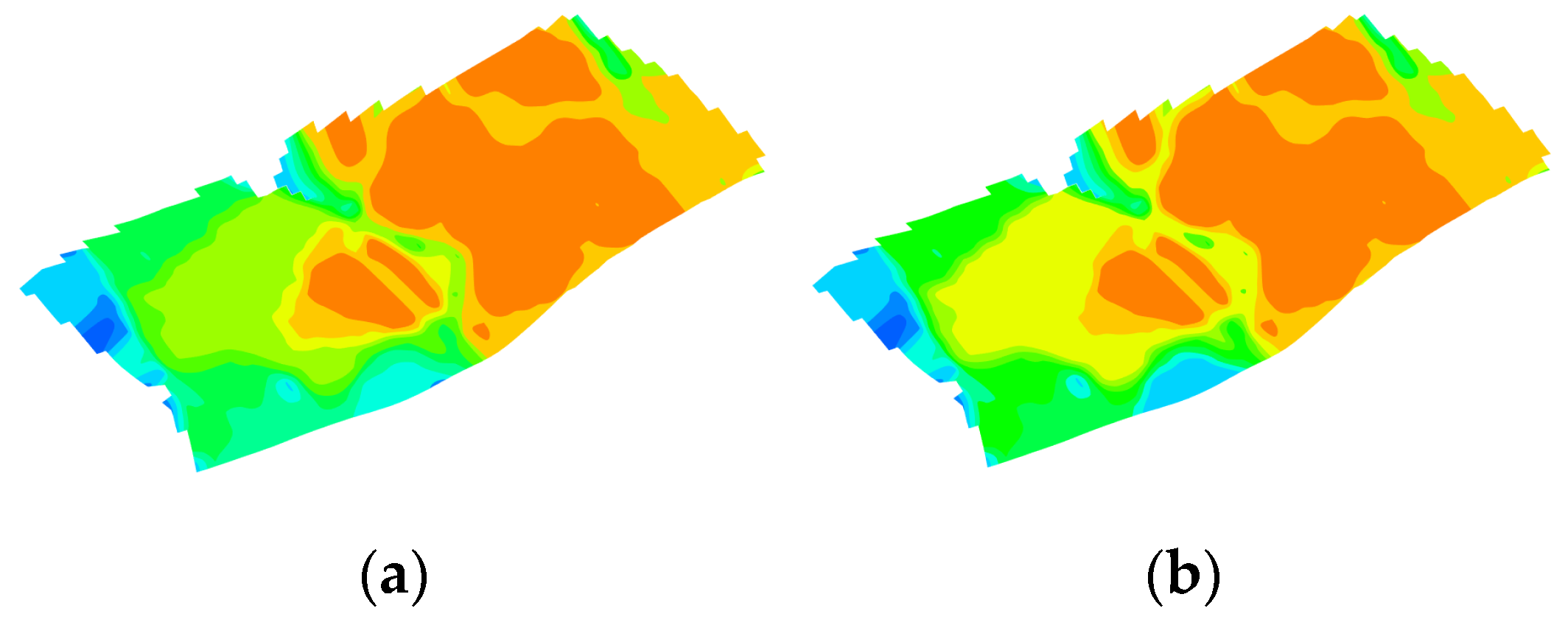
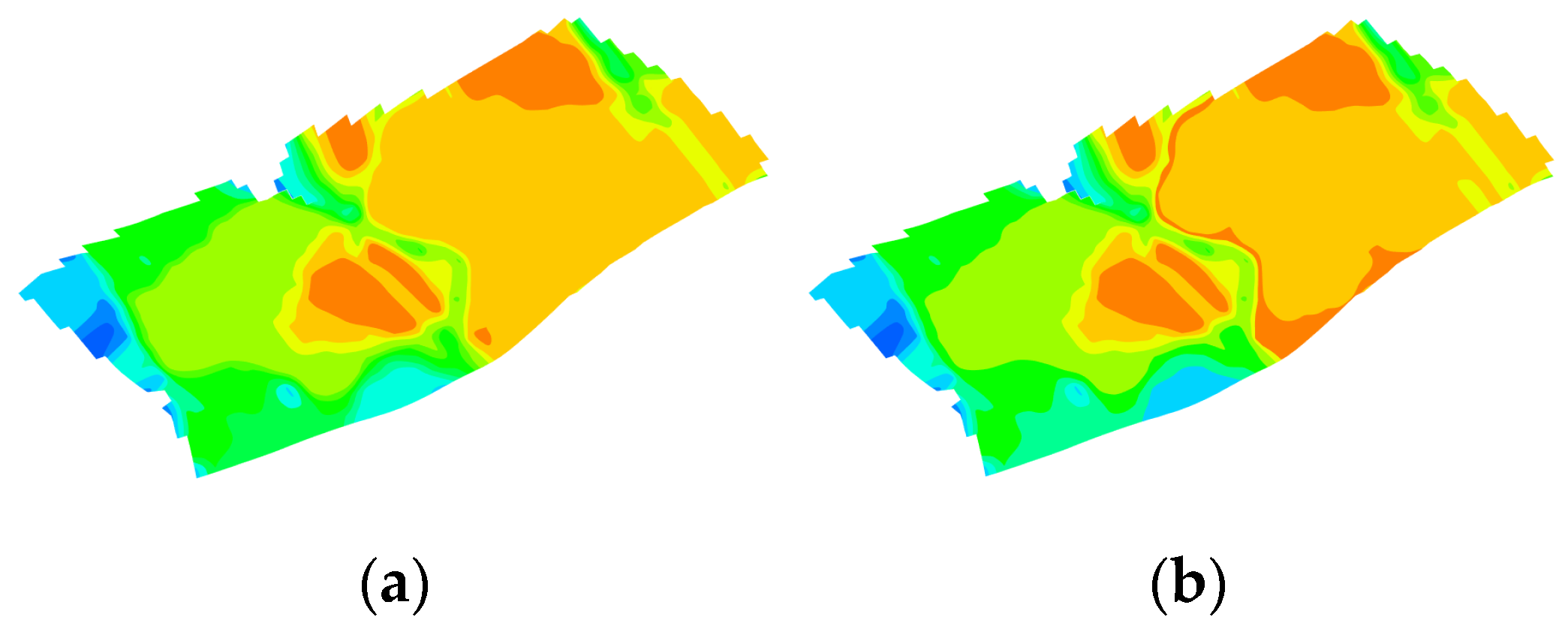
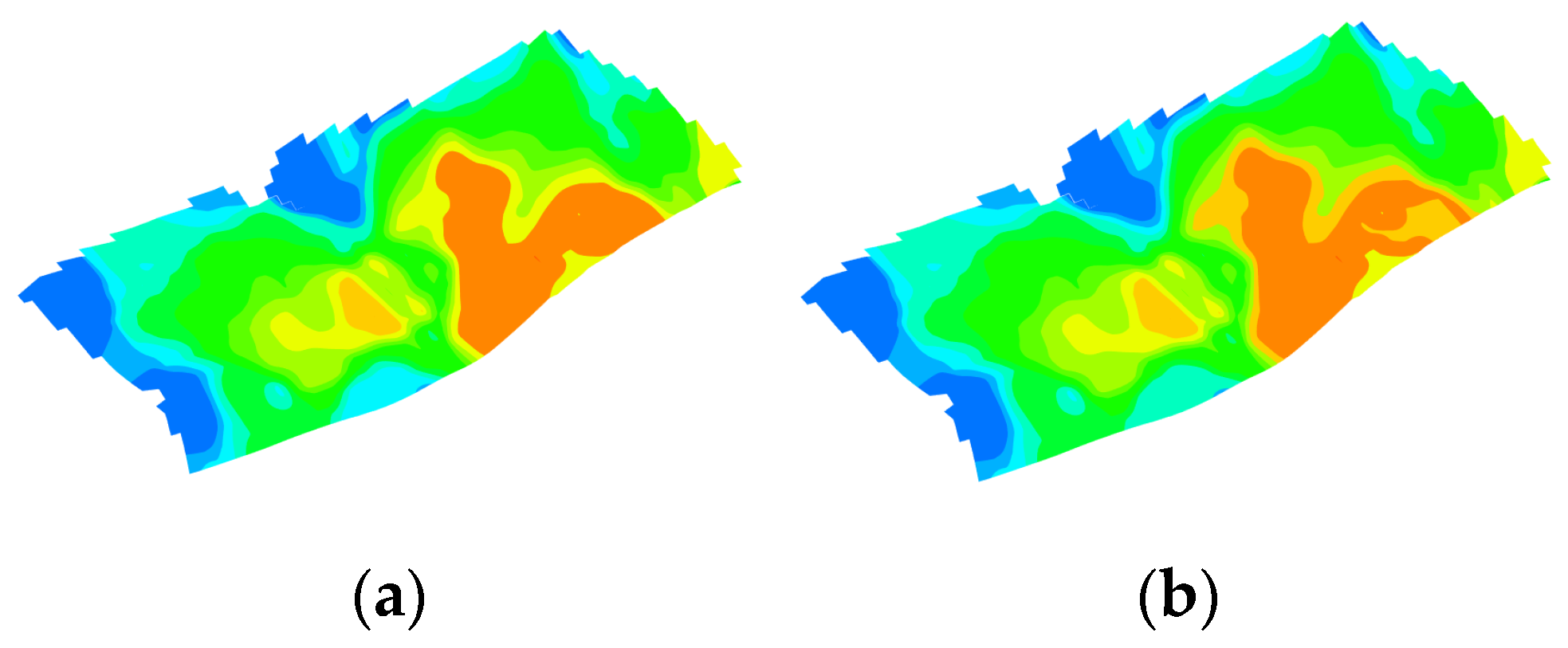
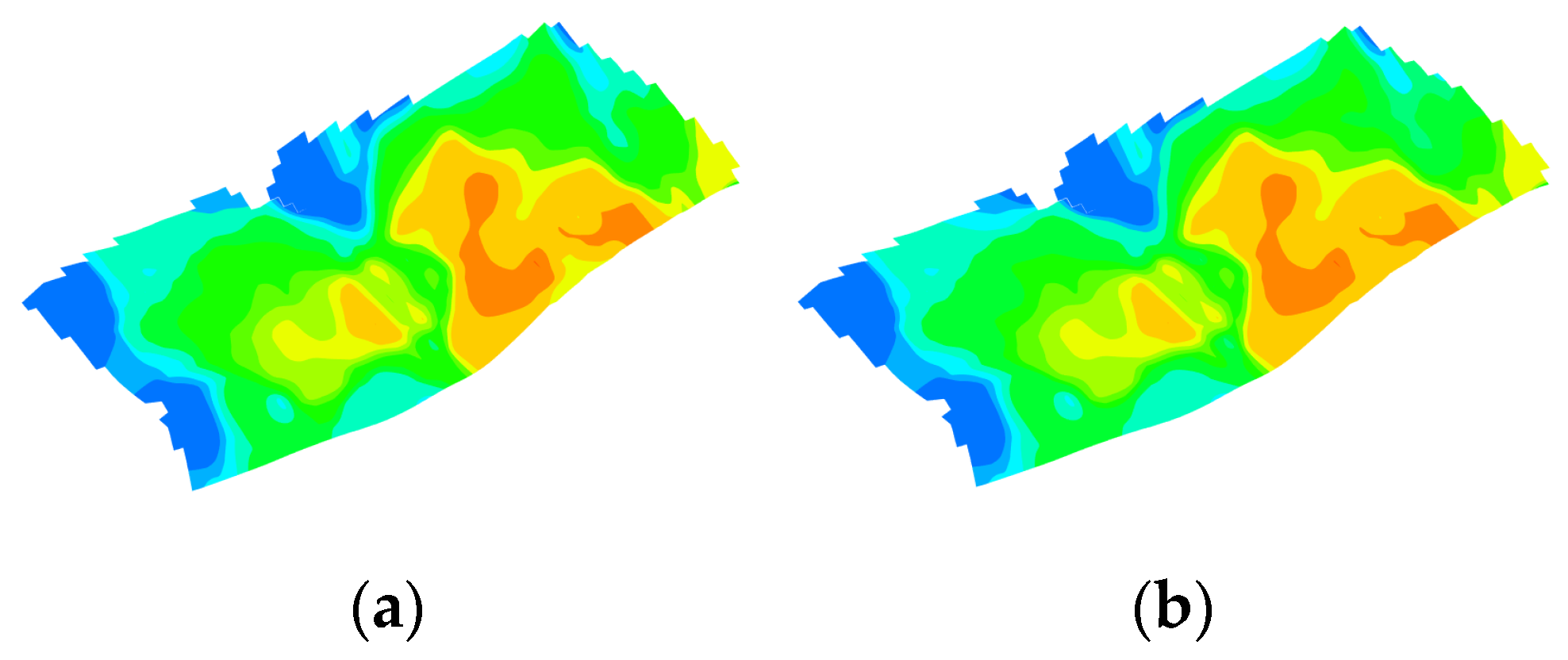
Figure 21.
Comparison of temperature fields of the optimal schemes from orthogonal experimental design and the intelligent optimization method for continuous injection. They should be listed as: (a) Orthogonal experimental design optimization; (b) intelligent optimization method optimization.
Figure 21.
Comparison of temperature fields of the optimal schemes from orthogonal experimental design and the intelligent optimization method for continuous injection. They should be listed as: (a) Orthogonal experimental design optimization; (b) intelligent optimization method optimization.
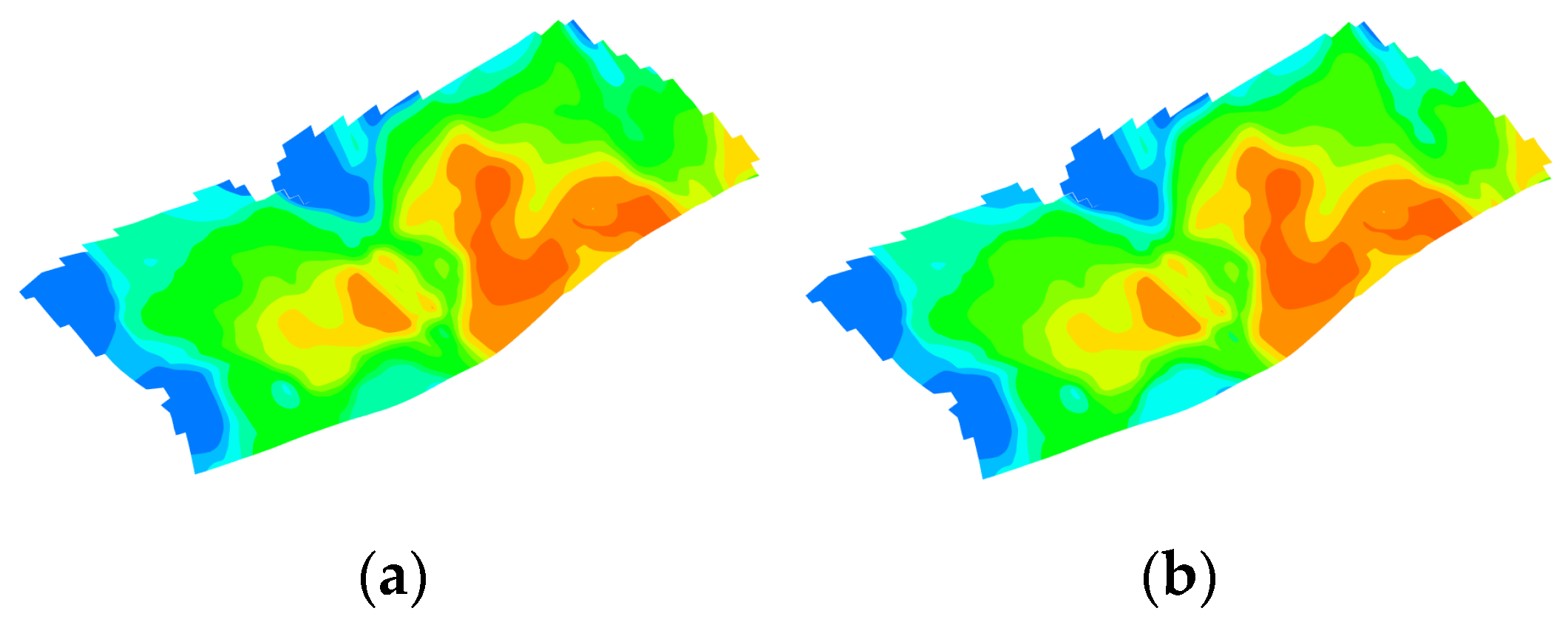
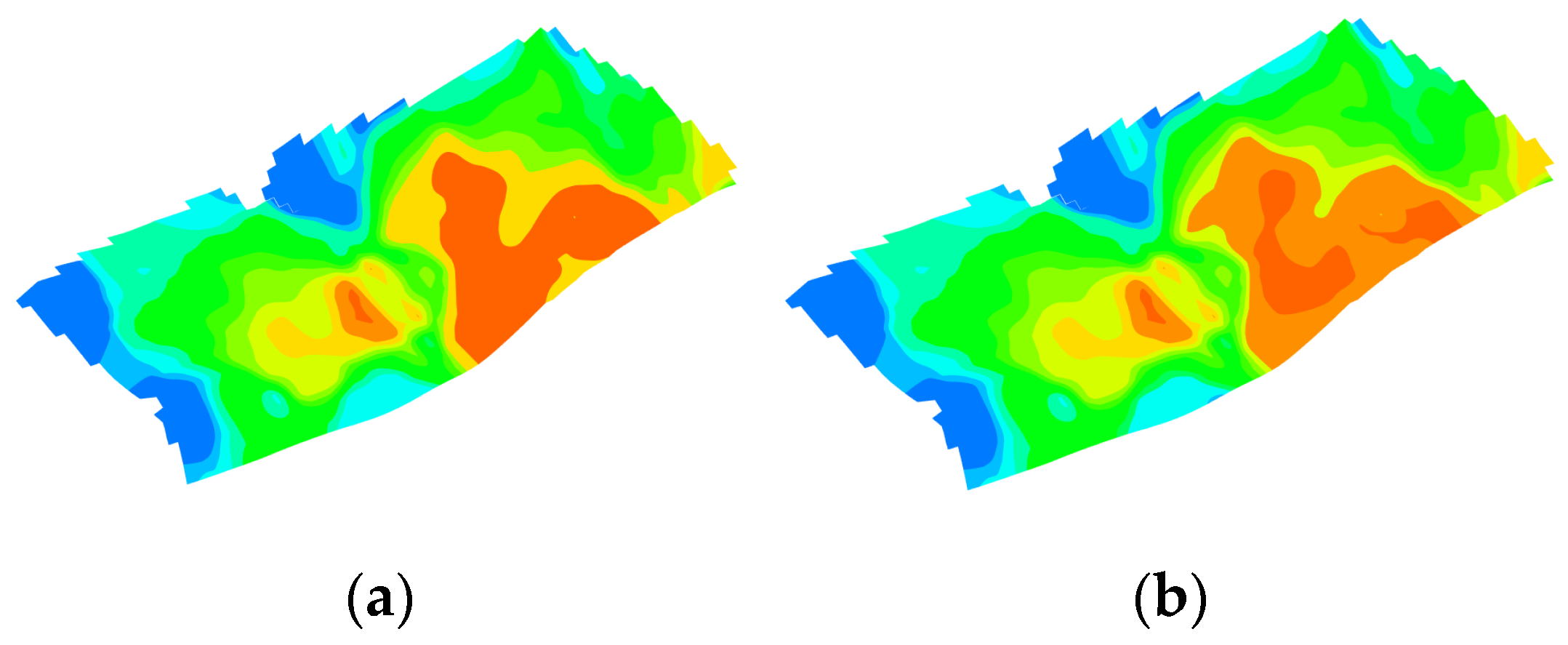
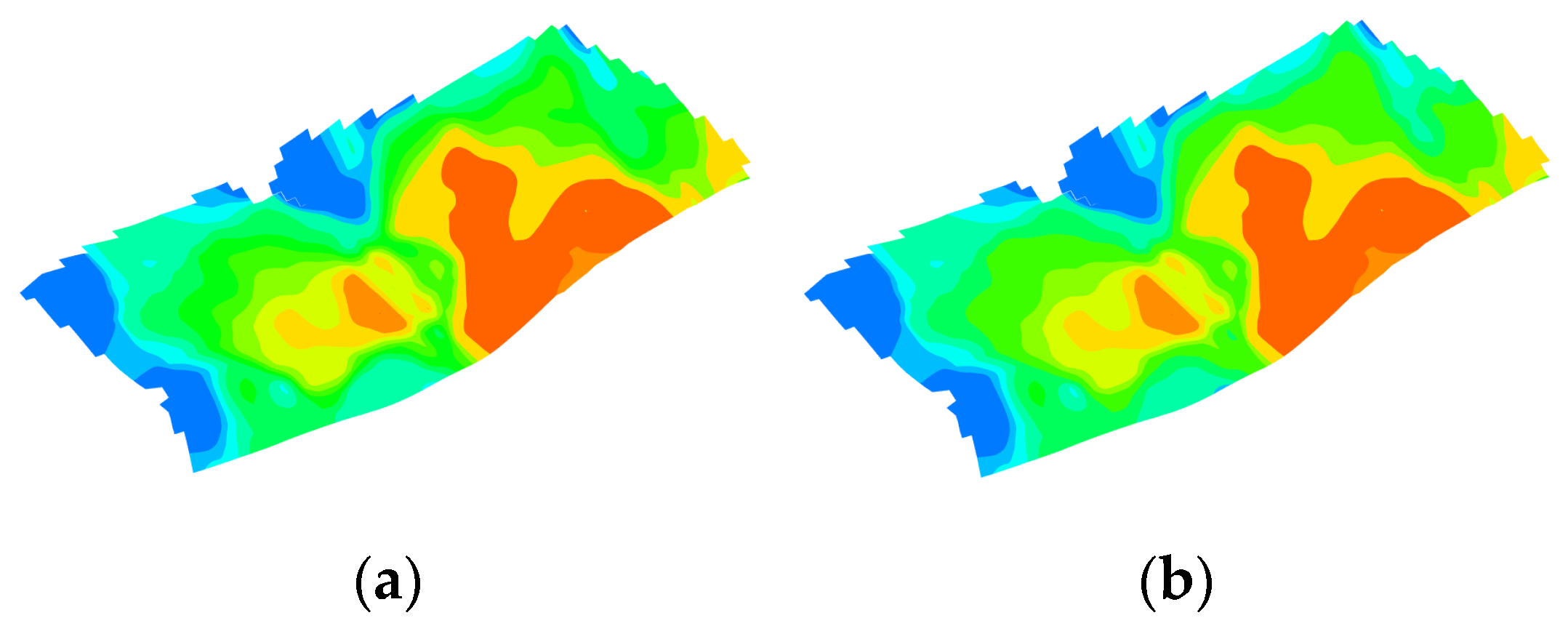
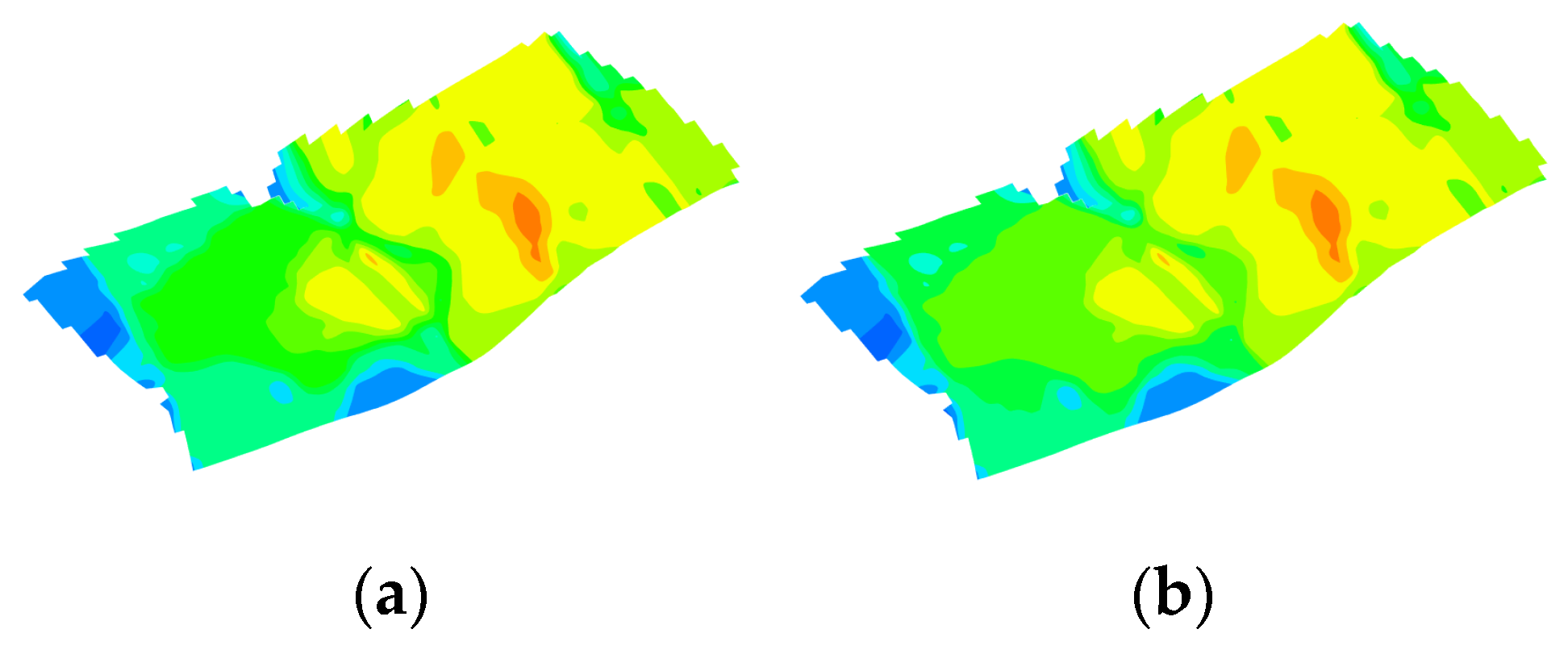
Figure 22.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection. They should be listed as: (a) Orthogonal experimental design optimization; (b) intelligent optimization method optimization.
Figure 22.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection. They should be listed as: (a) Orthogonal experimental design optimization; (b) intelligent optimization method optimization.
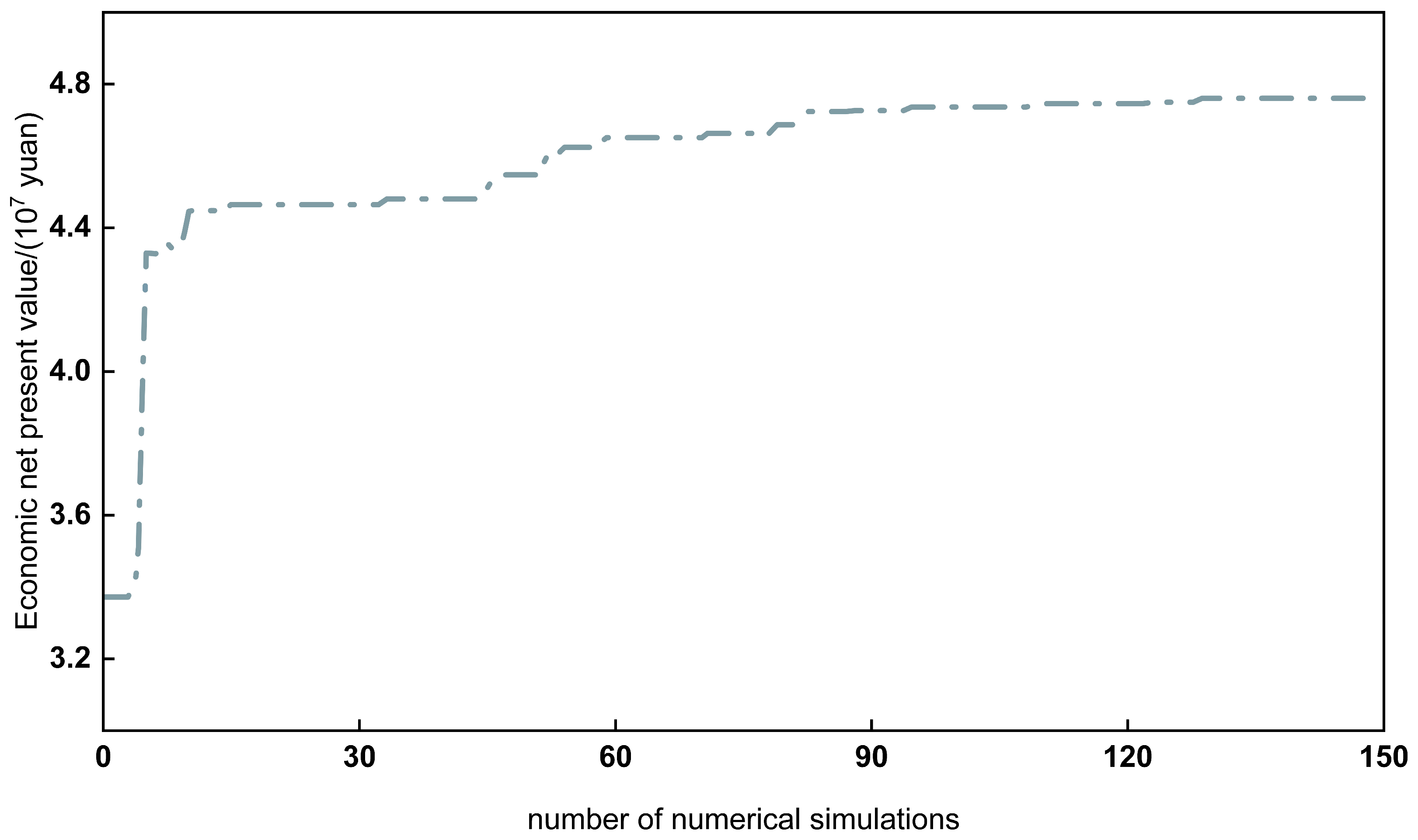
Figure 23.
Optimization dynamics of intermittent injection.
Figure 23.
Optimization dynamics of intermittent injection.
Figure 24.
Comparison of orthogonal experimental design and intelligent optimization results for intermittent steam injection.
Figure 24.
Comparison of orthogonal experimental design and intelligent optimization results for intermittent steam injection.
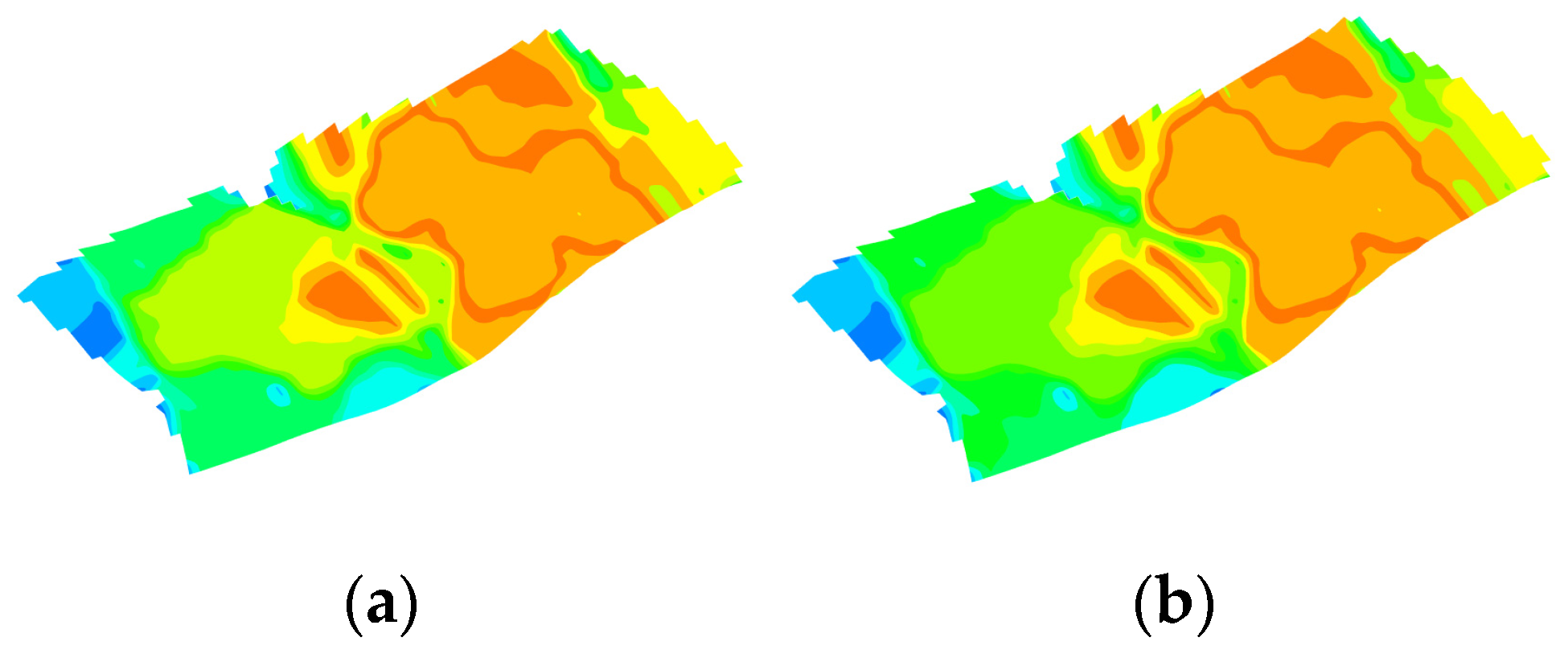
Figure 25.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for intermittent steam injection, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 25.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for intermittent steam injection, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 26.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for intermittent steam injection, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 26.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for intermittent steam injection, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 27.
Optimization dynamics of asynchronous injection–production.
Figure 27.
Optimization dynamics of asynchronous injection–production.
Figure 28.
Comparison of orthogonal experimental design and intelligent optimization results for asynchronous injection production.
Figure 28.
Comparison of orthogonal experimental design and intelligent optimization results for asynchronous injection production.
Figure 29.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for asynchronous injection production, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 29.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for asynchronous injection production, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 30.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for asynchronous injection production, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 30.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for asynchronous injection production, which should be listed as: (a) optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 31.
Optimization dynamics of switching from continuous injection to intermittent injection.
Figure 31.
Optimization dynamics of switching from continuous injection to intermittent injection.
Figure 32.
Comparison of orthogonal experimental design and intelligent optimization results.
Figure 32.
Comparison of orthogonal experimental design and intelligent optimization results.
Figure 33.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by intermittent injection. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 33.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by intermittent injection. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 34.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by intermittent injection. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 34.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by intermittent injection. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 35.
Optimization dynamics of switching from continuous injection to asynchronous injection production.
Figure 35.
Optimization dynamics of switching from continuous injection to asynchronous injection production.
Figure 36.
Comparison of orthogonal experimental design and intelligent optimization results for continuous injection followed by asynchronous injection production.
Figure 36.
Comparison of orthogonal experimental design and intelligent optimization results for continuous injection followed by asynchronous injection production.
Figure 37.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by asynchronous injection production. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 37.
Comparison of temperature fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by asynchronous injection production. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 38.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by asynchronous injection–production. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Figure 38.
Comparison of saturation fields of the optimal schemes from the orthogonal experimental design and the intelligent optimization method for continuous injection followed by asynchronous injection–production. (a) Optimization results of the orthogonal experimental design; (b) optimization results of the intelligent optimization method.
Table 1.
Basic parameters.
Table 1.
Basic parameters.
| Parameters | Values |
|---|
| Average formation permeability (mD) | 500 |
| Average porosity (%) | 37.8 |
| Average oil-layer thickness (m) | 8 |
| Average oil saturation (%) | 65 |
| Reservoir temperature (°C) | 56 |
| Crude oil viscosity (mPa·s) | 56,000 |
| Average reservoir top depth (m) | 1100 |
Table 2.
Schematic of LightGBM histogram optimization.
Table 2.
Schematic of LightGBM histogram optimization.
| Parameter Types | Parameter Name | Minimum Value | Maximum Value |
|---|
| Geological parameters | Average effective thickness/m | 4.94 | 11.55 |
| Permeability coefficient of variation | 0.03 | 0.34 |
| Water cut at time of intervention/% | 4.31 | 98.93 |
| Formation temperature at time of intervention/°C | 33.95 | 62.23 |
| Development parameters | Formation pressure at time of intervention/MPa | 0.85 | 7.45 |
| Degree of production/% | 1.51 | 21.06 |
| Remaining reserves at time of intervention/104 t | 3.84 | 16.60 |
| Process parameters | Well spacing/m | 120 | 240 |
Table 3.
Hyperparameters for different machine learning models.
Table 3.
Hyperparameters for different machine learning models.
| Machine Learning Methods | Hyperparameters | Cross-Validation Range | Optimal Value |
|---|
| ANN | Number of hidden layers | 1 | 1 |
| Number of nodes in hidden layers | 30, 50, 70, 90, 110, 130 | 90 |
| Hidden-layer activation function type | Tanh, ReLu, Logistic | ReLu |
| GBDT | Maximum iterations for weak learners | 1000, 2000, 3000 | 5000 |
| Maximum depth of decision tree | 2, 4, 6, 8, 10 | 2 |
| minimum samples per leaf | 1, 3, 5, 7, 9 | 3 |
| learning rate | 0.05, 0.1, 0.15, 0.2, 0.25, 0.3 | 0.3 |
| Maximum tree depth | 2, 3, 4, 5, 6, 7, 8, 9 | 9 |
| XGBoost | Learning rate | 0.01, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 0.10 |
| Minimum sample weight for a child node | 1, 3, 5, 7, 9 | 5 |
| Number of trees in the ensemble | 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000 | 2000 |
| LightGBM | Learning rate | 0.01, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30 | 0.15 |
| Maximum depth of decision tree | 2, 3, 4, 5, 6, 7, 8, 9 | 3 |
| Maximum iterations for weak learners | 500, 1000, 1500, 2000, 2500, 3000, 3500, 4000 | 4000 |
Table 4.
The five LightGBM hyperparameter combinations with the highest R2 predictive accuracy selected via five-fold cross-validation and random search.
Table 4.
The five LightGBM hyperparameter combinations with the highest R2 predictive accuracy selected via five-fold cross-validation and random search.
| Number | Maximum Depth of the Decision Tree | Learning Rate | Number of Decision Trees | R2 |
|---|
| 1 | 3 | 0.046416 | 4000 | 0.97682 |
| 2 | 3 | 0.046416 | 3500 | 0.97679 |
| 3 | 3 | 0.046416 | 3000 | 0.97673 |
| 4 | 3 | 0.046416 | 2500 | 0.97664 |
| 5 | 3 | 0.1 | 4000 | 0.97653 |
Table 5.
The five hyperparameter combinations that yielded the highest R2 after tuning selected via five-fold cross-validation and random search.
Table 5.
The five hyperparameter combinations that yielded the highest R2 after tuning selected via five-fold cross-validation and random search.
| Number | Maximum Depth of the Decision Tree | Learning Rate | Number of Decision Trees | R2 |
|---|
| 1 | 3 | 0.046416 | 4000 | 0.97682 |
| 2 | 3 | 0.046416 | 3500 | 0.97679 |
| 3 | 3 | 0.046416 | 3000 | 0.97673 |
| 4 | 3 | 0.046416 | 2500 | 0.97664 |
Table 6.
Table of parameter values for economic net present value calculations.
Table 6.
Table of parameter values for economic net present value calculations.
| Parameter Name | Parameter Values |
|---|
| Steam injection cost/(CNY·m−3) | 260 |
| Water treatment cost/(CNY·m−3) | 3.5 |
| Crude oil selling price/(CNY·t−1) | 3000 |
| Discount rate | 10 |
Table 7.
Parameters of the continuous steam-injection optimization model and their values.
Table 7.
Parameters of the continuous steam-injection optimization model and their values.
| Modeling Parameters | Values |
|---|
| Injection rate/(m3·d−1) | 125, 175, 225 |
| Liquid production rate/(t·d−1) | 131.25, 201.25, 270 |
| Injection dryness | 0.65, 0.75, 0.85 |
| Injection temperature/°C | 225, 275, 325 |
Table 8.
Orthogonal experimental design table for continuous steam-injection optimization.
Table 8.
Orthogonal experimental design table for continuous steam-injection optimization.
| Plan | Factor Level |
|---|
| Injection Rate/(m3·d−1) | Injection Dryness | Injection Temperature/°C | Liquid Production Rate
/(t·d−1) | Incremental Oil Recovery from Steam Drive/t | ENPV/104 Yuan |
|---|
| Plan 1 | 125 | 0.65 | 225 | 131.25 | 116,889 | 3677.08 |
| Plan 2 | 125 | 0.75 | 275 | 201.25 | 171,004 | 3936.13 |
| Plan 3 | 125 | 0.85 | 325 | 270 | 170,129 | 3825.62 |
| Plan 4 | 175 | 0.75 | 325 | 131.25 | 120,676 | 3372.56 |
| Plan 5 | 175 | 0.85 | 225 | 201.25 | 176,854 | 4354.68 |
| Plan 6 | 175 | 0.65 | 275 | 270 | 167,954 | 3777.22 |
| Plan 7 | 225 | 0.85 | 275 | 131.25 | 179,035 | 3900.77 |
| Plan 8 | 225 | 0.65 | 325 | 201.25 | 170,865 | 3445.55 |
| Plan 9 | 225 | 0.75 | 325 | 270 | 170,486 | 3376.44 |
Table 9.
Parameters of the intermittent steam-injection optimization model and their values.
Table 9.
Parameters of the intermittent steam-injection optimization model and their values.
| Modeling Parameters | Values |
|---|
| Injection rate/(m3·d−1) | 100, 125, 150, 175, 225 |
| Liquid production rate/(t·d−1) | 115, 143.75, 172.5, 201.25, 258.75 |
| Injection dryness | 0.6, 0.7, 0.8, 0.9, 0.95 |
| Injection time/d | 10, 20, 30, 40, 50 |
| Injection stop time/d | 10, 20, 30, 40, 50 |
| Injection temperature/°C | 200, 225, 250, 300, 350 |
Table 10.
Orthogonal experimental design table for intermittent steam-injection optimization.
Table 10.
Orthogonal experimental design table for intermittent steam-injection optimization.
| Plan | Factor Level |
|---|
| Injection Rate/(m3·d−1) | Injection Dryness | Injection Temperature/°C | Liquid Production Rate/(t·d−1) | Injection Time/d | Injection Stop Time/d | Incremental Oil Recovery from Steam Drive/t | ENPV/104 Yuan |
|---|
| Plan 1 | 100 | 0.6 | 200 | 115 | 10 | 10 | 129,203 | 4378.27 |
| Plan 2 | 100 | 0.7 | 225 | 143.75 | 20 | 20 | 138,109 | 4391.49 |
| Plan 3 | 100 | 0.8 | 250 | 172.5 | 30 | 30 | 148,254 | 4466.28 |
| Plan 4 | 100 | 0.9 | 300 | 201.25 | 40 | 40 | 157,499 | 4506.25 |
| Plan 5 | 100 | 0.95 | 350 | 258.75 | 50 | 50 | 162,752 | 4585.25 |
| Plan 6 | 125 | 0.7 | 250 | 115 | 40 | 50 | 139,581 | 4164.88 |
| Plan 7 | 125 | 0.8 | 300 | 143.75 | 50 | 10 | 173,796 | 4583.46 |
| Plan 8 | 125 | 0.9 | 350 | 172.5 | 10 | 20 | 143,306 | 3987.72 |
| Plan 9 | 125 | 0.95 | 200 | 201.25 | 20 | 30 | 161,079 | 4427.61 |
| Plan 10 | 125 | 0.6 | 225 | 258.75 | 30 | 40 | 127,592 | 4068.31 |
| Plan 11 | 150 | 0.8 | 350 | 115 | 20 | 40 | 141,036 | 4417.92 |
| Plan 12 | 150 | 0.9 | 200 | 143.75 | 30 | 50 | 157,705 | 4389.34 |
| Plan 13 | 150 | 0.95 | 225 | 172.5 | 40 | 10 | 195,348 | 4548.12 |
| Plan 14 | 150 | 0.6 | 250 | 201.25 | 50 | 20 | 146,129 | 4475.28 |
| Plan 15 | 150 | 0.7 | 300 | 258.75 | 10 | 30 | 129,203 | 4077.65 |
| Plan 16 | 175 | 0.9 | 225 | 115 | 50 | 50 | 173,821 | 4545.48 |
| Plan 17 | 175 | 0.95 | 250 | 143.75 | 10 | 40 | 143,484 | 4417.92 |
| Plan 18 | 175 | 0.6 | 300 | 172.5 | 20 | 50 | 130,436 | 4321.17 |
| Plan 19 | 175 | 0.7 | 350 | 201.25 | 30 | 10 | 166,838 | 4542.78 |
| Plan 20 | 175 | 0.8 | 200 | 258.75 | 40 | 50 | 154,471 | 4476.72 |
| Plan 21 | 225 | 0.95 | 300 | 115 | 30 | 20 | 183,263 | 4621.19 |
| Plan 22 | 225 | 0.6 | 350 | 143.75 | 40 | 50 | 148,753 | 4440.92 |
| Plan 23 | 225 | 0.7 | 200 | 172.5 | 50 | 40 | 153,275 | 4476.68 |
| Plan 24 | 225 | 0.8 | 225 | 201.25 | 10 | 50 | 127,961 | 3730.17 |
| Plan 25 | 225 | 0.9 | 250 | 258.75 | 20 | 10 | 184,373 | 4644.25 |
Table 11.
Modeling parameters and their values for asynchronous injection/production optimization.
Table 11.
Modeling parameters and their values for asynchronous injection/production optimization.
| Modeling Parameters | Values |
|---|
| Injection rate/(m3·d−1) | 125, 175, 225 |
| Liquid production rate/(t·d−1) | 131.25, 201.25, 270 |
| Injection dryness | 0.65, 0.75, 0.85 |
| Injection temperature/°C | 225, 275, 325 |
| Injection time/d | 25, 35, 45 |
| Shut-in time/d | 3, 5, 7 |
| Production time/d | 35, 45, 55 |
Table 12.
Orthogonal experimental design table for asynchronous injection/production optimization.
Table 12.
Orthogonal experimental design table for asynchronous injection/production optimization.
| Plan | Factor Level |
|---|
| Injection Rate/m3·d−1 | Injection Dryness | Injection Temperature/°C | Liquid Production Rate/t·d−1 | Injection Time/d | Shut-In Time /d | Production Time/d | Incremental Oil/t | ENPV/104 CNY |
|---|
| Plan 1 | 250 | 110 | 0.7 | 100 | 30 | 3 | 40 | 0.15 | 155,145 |
| Plan 2 | 250 | 110 | 0.8 | 150 | 40 | 5 | 50 | 0.25 | 165,125 |
| Plan 3 | 250 | 110 | 0.9 | 200 | 50 | 7 | 60 | 0.35 | 168,532 |
| Plan 4 | 250 | 172.5 | 0.7 | 100 | 40 | 5 | 60 | 0.35 | 102,421 |
| Plan 5 | 250 | 172.5 | 0.8 | 150 | 50 | 7 | 40 | 0.15 | 180,161 |
| Plan 6 | 250 | 172.5 | 0.9 | 200 | 30 | 3 | 50 | 0.25 | 134,361 |
| Plan 7 | 250 | 240 | 0.7 | 150 | 30 | 7 | 50 | 0.35 | 131,617 |
| Plan 8 | 250 | 240 | 0.8 | 200 | 40 | 3 | 60 | 0.15 | 183,658 |
| Plan 9 | 250 | 240 | 0.9 | 100 | 50 | 5 | 40 | 0.25 | 149,162 |
| Plan 10 | 350 | 110 | 0.7 | 200 | 50 | 5 | 50 | 0.15 | 164,265 |
| Plan 11 | 350 | 110 | 0.8 | 100 | 30 | 7 | 60 | 0.25 | 162,141 |
| Plan 12 | 350 | 110 | 0.9 | 150 | 40 | 3 | 40 | 0.35 | 103,958 |
| Plan 13 | 350 | 172.5 | 0.7 | 150 | 50 | 3 | 60 | 0.25 | 160,880 |
| Plan 14 | 350 | 172.5 | 0.8 | 200 | 30 | 5 | 40 | 0.35 | 84,760 |
| Plan 15 | 350 | 172.5 | 0.9 | 100 | 40 | 7 | 50 | 0.15 | 148,765 |
| Plan 16 | 350 | 240 | 0.7 | 200 | 40 | 7 | 40 | 0.25 | 166,906 |
| Plan 17 | 350 | 240 | 0.8 | 100 | 50 | 3 | 50 | 0.35 | 95,209 |
| Plan 18 | 350 | 240 | 0.9 | 150 | 30 | 5 | 60 | 0.15 | 183,525 |
Table 13.
Parameters and their values for the optimization model of continuous injection followed by intermittent injection.
Table 13.
Parameters and their values for the optimization model of continuous injection followed by intermittent injection.
| Modeling Parameters | Values |
|---|
| Injection rate/(m3·d−1) | 125, 175, 225 |
| Liquid production rate/(t·d−1) | 131.25, 201.25, 270 |
| Injection dryness | 0.65, 0.75, 0.85 |
| Gas–oil ratio timing | 0.15, 0.25, 0.35 |
| Injection time/d | 25, 35, 45 |
| Injection stop time/d | 35, 45, 55 |
| Injection temperature/°C | 225, 275, 325 |
Table 14.
Orthogonal experimental design table for optimization of continuous injection followed by intermittent steam injection.
Table 14.
Orthogonal experimental design table for optimization of continuous injection followed by intermittent steam injection.
| Plan | Factor Level |
|---|
| Injection Rate/(m3·d−1) | Injection Dryness | Injection Temperature/°C | Liquid Production Rate/t·d−1 | Injection Time/d | Gas-Oil Ratio Timing/d | Injection Stop Time/d | Incremental Oil/t | ENPV/104 CNY |
|---|
| Plan 1 | 125 | 0.65 | 225 | 131.25 | 25 | 0.15 | 35 | 226,914 | 4098.95 |
| Plan 2 | 125 | 0.75 | 275 | 201.25 | 35 | 0.25 | 45 | 223,003 | 3871.15 |
| Plan 3 | 125 | 0.85 | 325 | 270 | 45 | 0.35 | 55 | 262,883 | 3729.88 |
| Plan 4 | 175 | 0.65 | 275 | 131.25 | 35 | 0.35 | 55 | 210,460 | 4222.50 |
| Plan 5 | 175 | 0.75 | 325 | 201.25 | 45 | 0.15 | 35 | 246,116 | 4433.58 |
| Plan 6 | 175 | 0.85 | 225 | 270 | 25 | 0.25 | 45 | 216,176 | 4277.84 |
| Plan 7 | 225 | 0.75 | 225 | 131.25 | 45 | 0.25 | 55 | 239,545 | 3056.89 |
| Plan 8 | 225 | 0.85 | 275 | 201.25 | 25 | 0.35 | 35 | 271,159 | 4005.07 |
| Plan 9 | 225 | 0.65 | 325 | 270 | 35 | 0.15 | 45 | 257,766 | 4283.02 |
| Plan 10 | 125 | 0.85 | 325 | 131.25 | 35 | 0.25 | 35 | 242,457 | 2611.28 |
| Plan 11 | 125 | 0.65 | 225 | 201.25 | 45 | 0.35 | 45 | 208,308 | 3874.03 |
| Plan 12 | 125 | 0.75 | 275 | 270 | 25 | 0.15 | 55 | 258,640 | 4135.66 |
| Plan 13 | 175 | 0.75 | 325 | 131.25 | 25 | 0.35 | 45 | 256,025 | 3977.56 |
| Plan 14 | 175 | 0.85 | 225 | 201.25 | 35 | 0.15 | 55 | 276,830 | 3881.96 |
| Plan 15 | 175 | 0.65 | 275 | 270 | 45 | 0.25 | 35 | 229,970 | 3740.99 |
| Plan 16 | 225 | 0.85 | 275 | 131.25 | 45 | 0.15 | 45 | 243,656 | 4165.45 |
| Plan 17 | 225 | 0.65 | 325 | 201.25 | 25 | 0.25 | 55 | 236,237 | 4256.42 |
| Plan 18 | 225 | 0.75 | 225 | 270 | 25 | 0.35 | 35 | 244,496 | 4263.31 |
Table 15.
Parameters and their values for the optimization model of continuous injection followed by asynchronous injection/production.
Table 15.
Parameters and their values for the optimization model of continuous injection followed by asynchronous injection/production.
| Modeling Parameters | Values |
|---|
| Injection temperature/°C | 250, 350 |
| Liquid production rate/(t·d−1) | 110, 172.5, 240 |
| Injection rate/(m3·d−1) | 100, 150, 200 |
| Injection dryness | 0.7, 0.8, 0.9 |
| Gas–oil ratio timing | 0.1, 0.2, 0.3 |
| Injection time/d | 30, 40, 50 |
| Shut-in time/d | 3, 5, 7 |
| Production time/d | 40, 50, 60 |
Table 16.
Orthogonal experimental design table for optimization of continuous injection followed by asynchronous injection/production.
Table 16.
Orthogonal experimental design table for optimization of continuous injection followed by asynchronous injection/production.
| Plan | Factor Level |
|---|
| Injection Temperature/°C | Liquid Production Rate/t·d−1 | Injection Dryness | Injection Rate/(m3·d−1) | Injection Time/d | Shut-In Time/d | Production Time/d | Gas-Oil Ratio Timing | Incremental Oil/t | ENPV/104 CNY |
|---|
| Plan 1 | 250 | 110 | 0.7 | 100 | 30 | 3 | 40 | 0.15 | 155,145 | 4218.67 |
| Plan 2 | 250 | 110 | 0.8 | 150 | 40 | 5 | 50 | 0.25 | 165,125 | 4366.5 |
| Plan 3 | 250 | 110 | 0.9 | 200 | 50 | 7 | 60 | 0.35 | 168,532 | 4235.07 |
| Plan 4 | 250 | 172.5 | 0.7 | 100 | 40 | 5 | 60 | 0.35 | 102,421 | 4176.38 |
| Plan 5 | 250 | 172.5 | 0.8 | 150 | 50 | 7 | 40 | 0.15 | 180,161 | 4086.36 |
| Plan 6 | 250 | 172.5 | 0.9 | 200 | 30 | 3 | 50 | 0.25 | 134,361 | 3605.93 |
| Plan 7 | 250 | 240 | 0.7 | 150 | 30 | 7 | 50 | 0.35 | 131,617 | 3958.98 |
| Plan 8 | 250 | 240 | 0.8 | 200 | 40 | 3 | 60 | 0.15 | 183,658 | 3976.55 |
| Plan 9 | 250 | 240 | 0.9 | 100 | 50 | 5 | 40 | 0.25 | 149,162 | 3266.89 |
| Plan 10 | 350 | 110 | 0.7 | 200 | 50 | 5 | 50 | 0.15 | 164,265 | 3917.74 |
| Plan 11 | 350 | 110 | 0.8 | 100 | 30 | 7 | 60 | 0.25 | 162,141 | 4055.34 |
| Plan 12 | 350 | 110 | 0.9 | 150 | 40 | 3 | 40 | 0.35 | 103,958 | 3028.32 |
| Plan 13 | 350 | 172.5 | 0.7 | 150 | 50 | 3 | 60 | 0.25 | 160,880 | 4364.54 |
| Plan 14 | 350 | 172.5 | 0.8 | 200 | 30 | 5 | 40 | 0.35 | 84,760 | 3180.15 |
| Plan 15 | 350 | 172.5 | 0.9 | 100 | 40 | 7 | 50 | 0.15 | 148,765 | 3201.05 |
| Plan 16 | 350 | 240 | 0.7 | 200 | 40 | 7 | 40 | 0.25 | 166,906 | 4128.34 |
| Plan 17 | 350 | 240 | 0.8 | 100 | 50 | 3 | 50 | 0.35 | 95,209 | 3876.38 |
| Plan 18 | 350 | 240 | 0.9 | 150 | 30 | 5 | 60 | 0.15 | 183,525 | 4045.13 |