Artificial Intelligence-Guided Pulsed Synthesis of Zinc Oxide Nanostructures on Thin Metal Shells
Abstract
1. Introduction
2. Technological Implementation of Pulsed Synthesis of ZnO on Thin Metallic Substrates
2.1. Pulsed Synthesis and Morphology Control of ZnO on Thin Metallic Substrates
2.2. Overview of Pulsed Synthesis Techniques
2.3. Pulse Parameters and Energy Sources
2.4. Reproducibility and Experimental Control
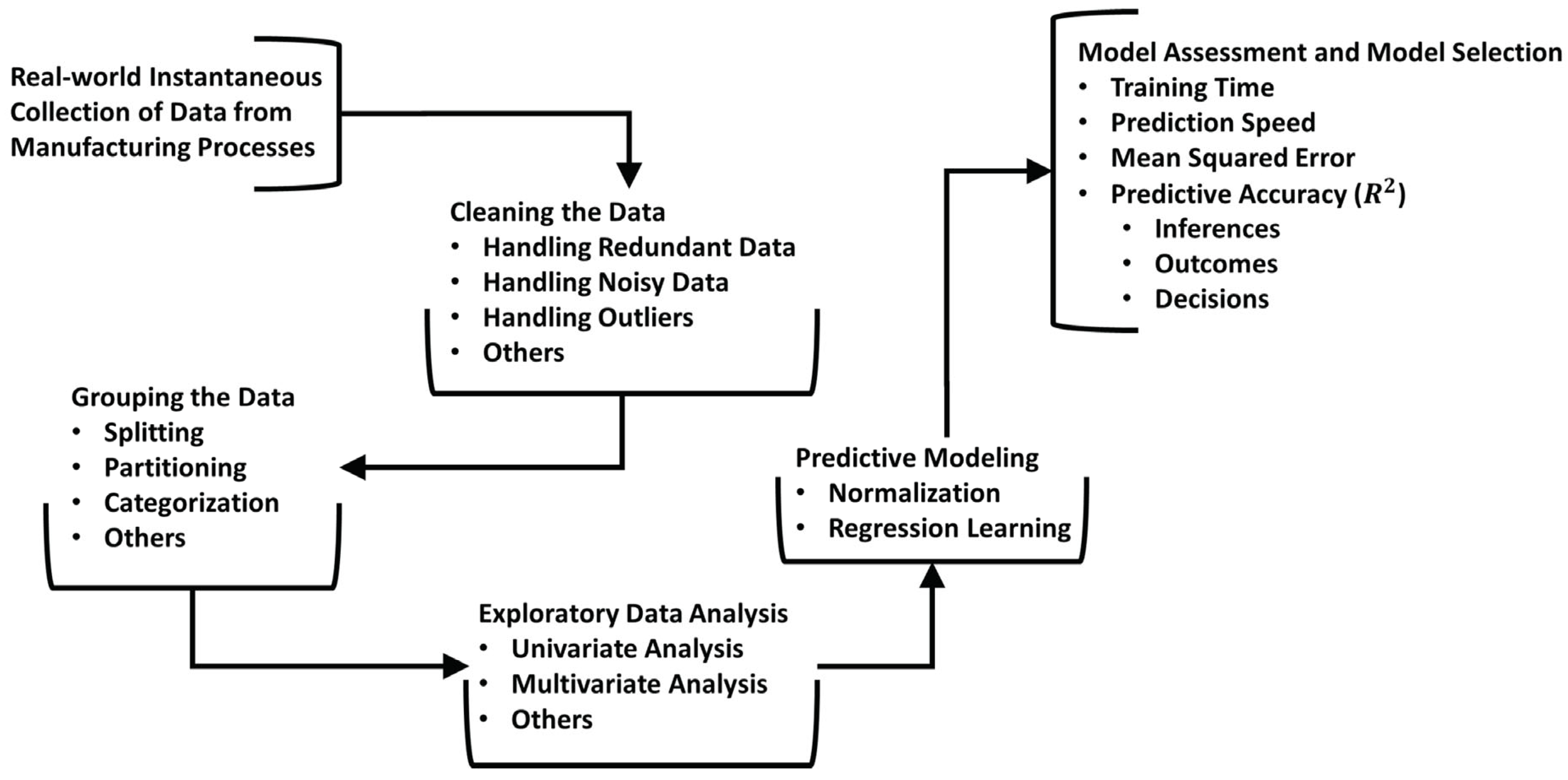
3. Preparation and Reporting of Experimental Data for AI Optimization
3.1. Principles of Experimental Data Preparation in Pulsed Synthesis of ZnO
3.2. Standards for Data Recording and Metadata Representation
3.3. Representativeness and Scalability of Experimental Data
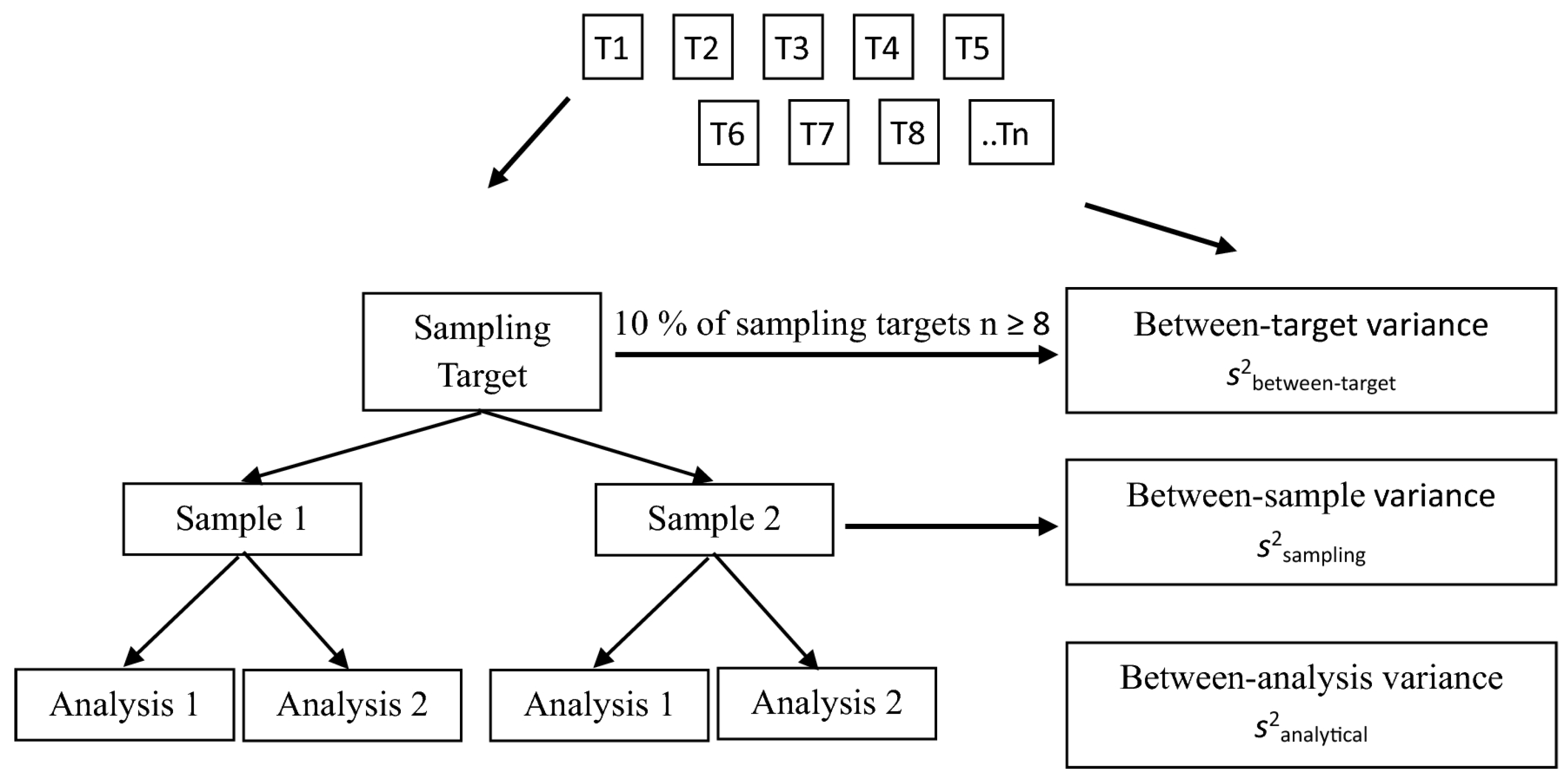
3.4. Quality Control and Measurement Accuracy
3.5. FAIR Principles and Open Data Repositories
4. Artificial Intelligence Methods for Process Optimization and Control
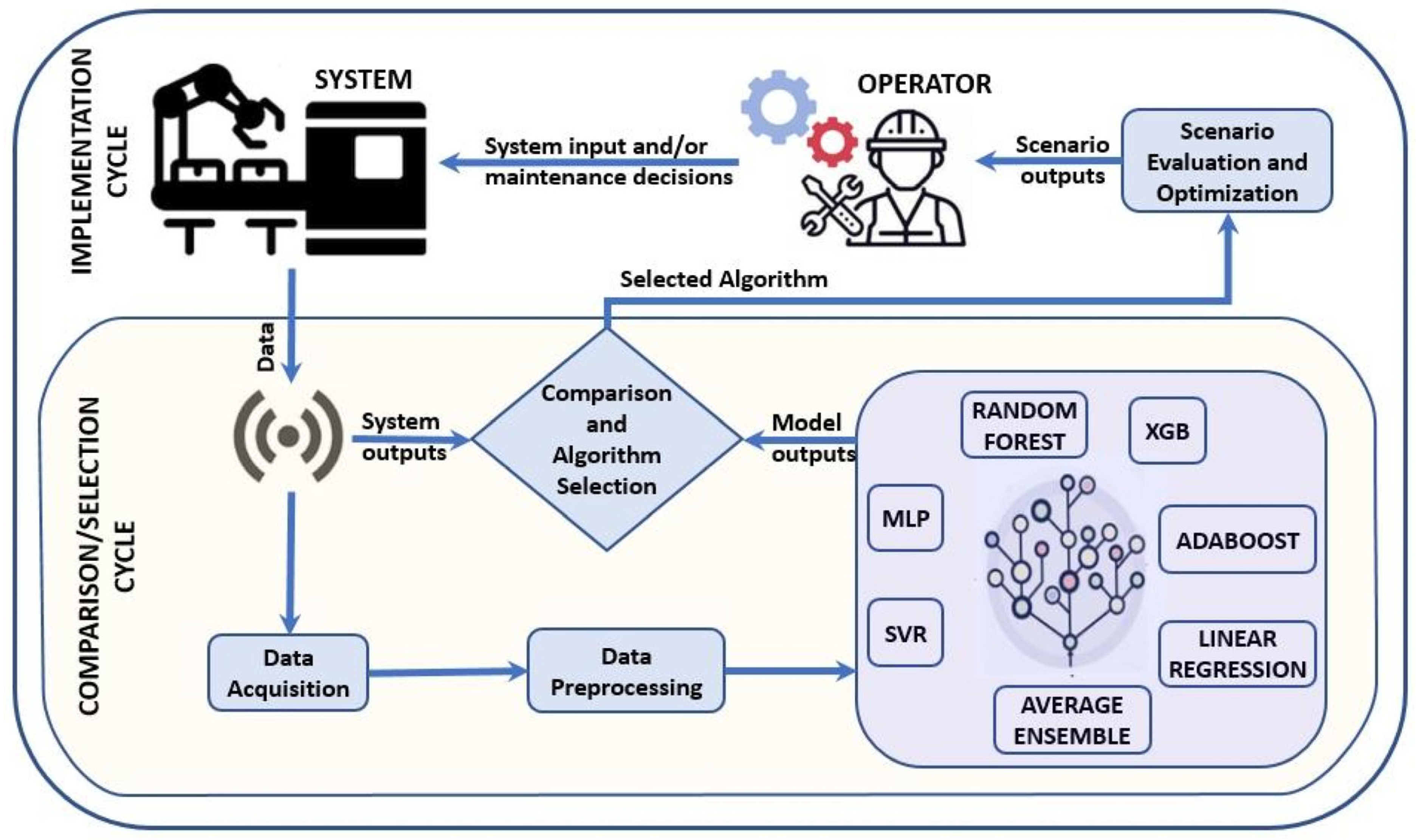
4.1. Active Learning and Adaptive Sampling
4.2. Physics-Informed Neural Networks (PINNs)
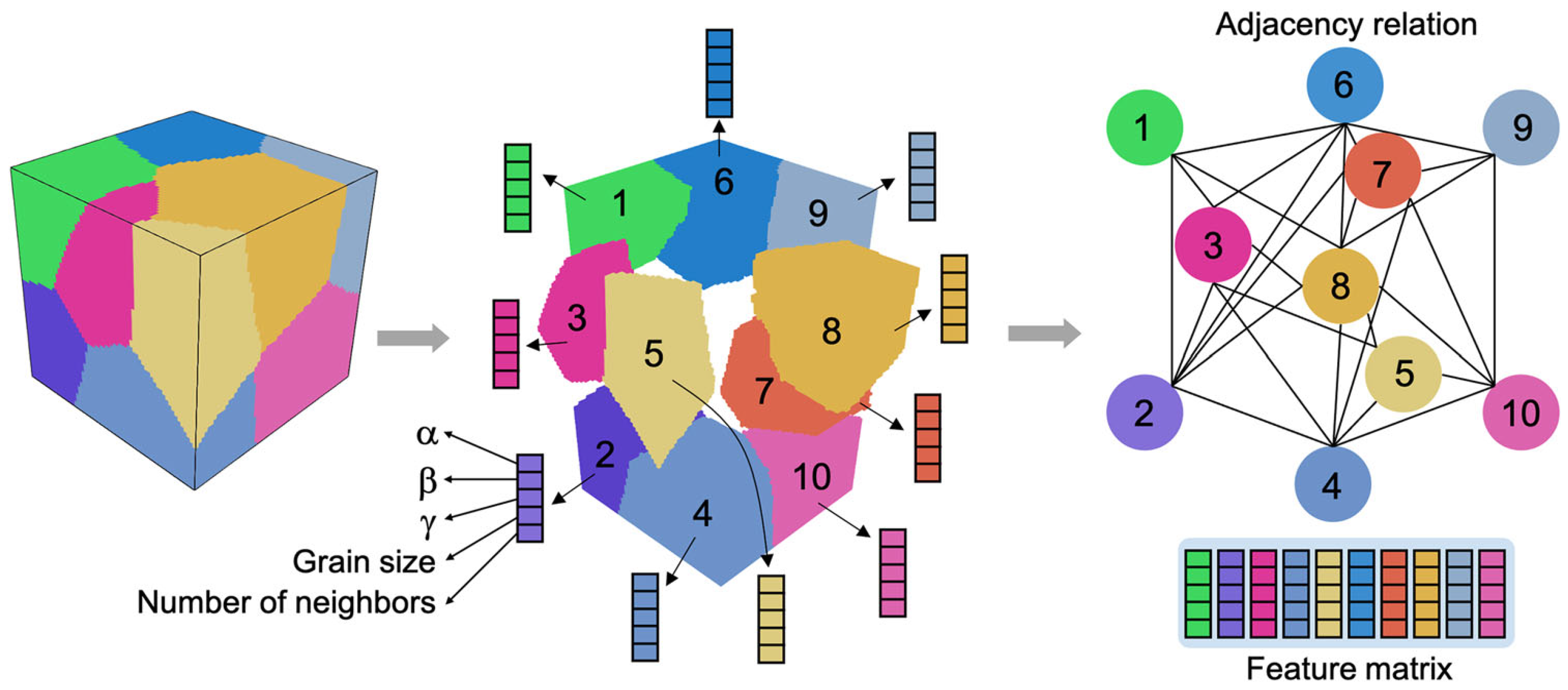
4.3. Graph Neural Networks (GNNs) for Microstructure and Properties
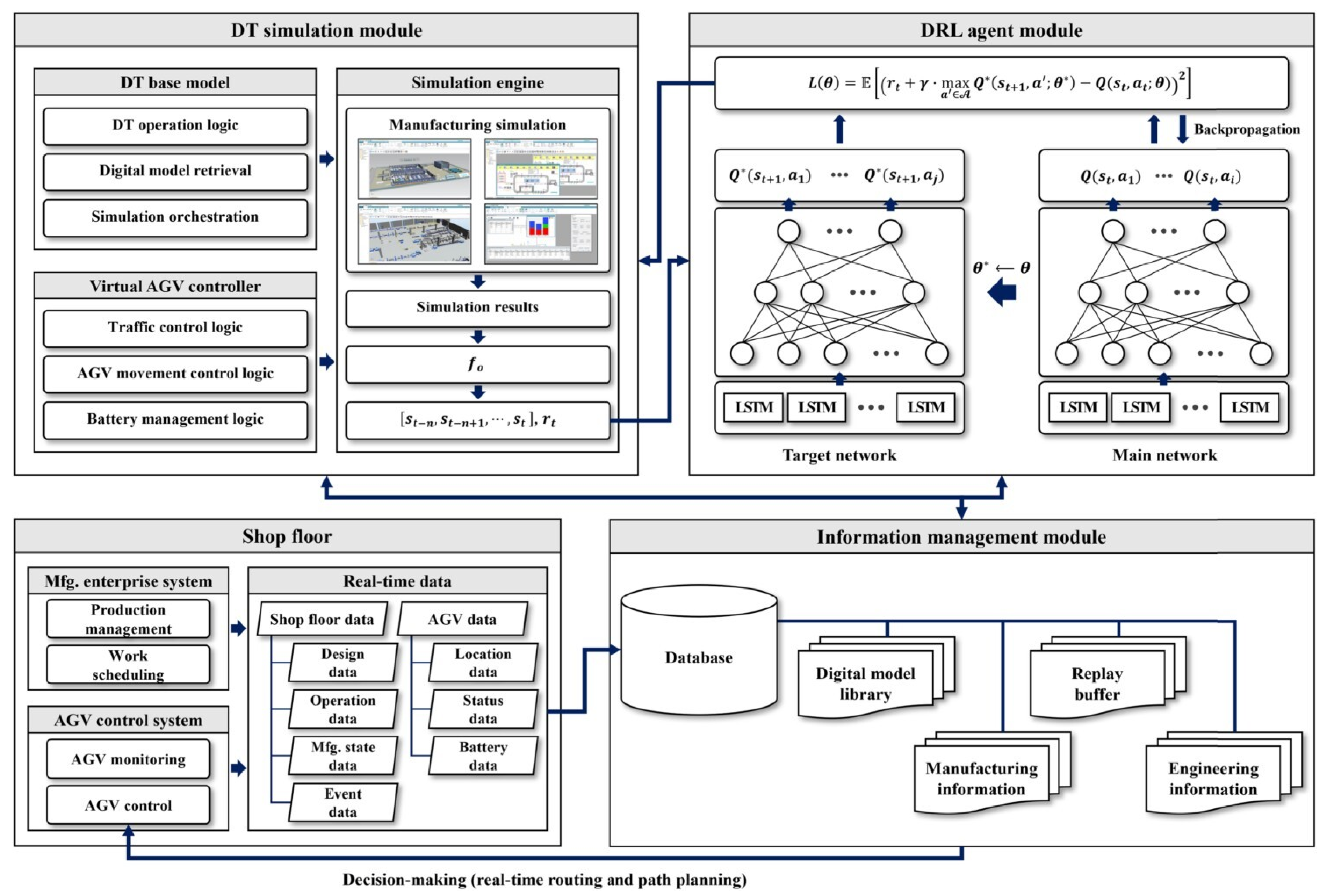
4.4. Self-Driving Laboratories and Reinforcement Learning
4.5. Digital Loop and AI-Guided Workflow for ZnO Nanostructure Synthesis
5. Synthesis and Applications of ZnO Nanostructures
5.1. Pulsed Deposition Strategies for ZnO Nanostructures
5.2. Morphology-Controlled Functional Performance of ZnO Nanostructures Synthesized by Pulsed Techniques
5.3. Technological Advantages and Design Flexibility in Pulsed Synthesis of ZnO Nanostructures
5.4. Scaling and Doping Strategies for ZnO in Pulsed Processing
6. Discussion and Perspectives
6.1. AI Control and Experimental Challenges in Pulsed ZnO Synthesis
6.2. Proposed Experimental Workflow for AI-Guided Pulsed ZnO Synthesis
6.3. AI-Driven Tools and Autonomous Process Control
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Borysiewicz, M.A. ZnO as a functional material, a review. Crystals 2019, 9, 505. [Google Scholar] [CrossRef]
- Raha, S.; Ahmaruzzaman, M. ZnO nanostructured materials and their potential applications: Progress, challenges and perspectives. Nanoscale Adv. 2022, 4, 1868–1925. [Google Scholar] [CrossRef]
- Forsythe, R.C.; Cox, C.P.; Wilsey, M.K.; Müller, A.M. Pulsed laser in liquids made nanomaterials for catalysis. Chem. Rev. 2021, 121, 7568–7637. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xiao, L.; Zheng, Z.; Yan, J.; Sun, L.; Huang, Z.; Li, X. A review on pulsed laser fabrication of nanomaterials in liquids for (photo)catalytic degradation of organic pollutants in the water system. Nanomaterials 2023, 13, 2628. [Google Scholar] [CrossRef]
- Primc, G.; Brenčič, K.; Mozetič, M.; Gorjanc, M. Recent advances in the plasma-assisted synthesis of zinc oxide nanoparticles. Nanomaterials 2021, 11, 1191. [Google Scholar] [CrossRef] [PubMed]
- Issa, M.A.; Aadim, K.A. Study the structural and optical properties of zinc oxide prepared by pulse laser deposition. J. Opt. 2024, 13, 1–6. [Google Scholar] [CrossRef]
- Widyastuti, E.; Hsu, J.-L.; Lee, Y.-C. Insight on photocatalytic and photoinduced antimicrobial properties of ZnO thin films deposited by HiPIMS through thermal oxidation. Nanomaterials 2022, 12, 463. [Google Scholar] [CrossRef]
- Campos, A.C.; Paes, S.C.; Correa, B.S.; Cabrera-Pasca, G.A.; Costa, M.S.; Costa, C.S.; Otubo, L.; Carbonari, A.W. Growth of long ZnO nanowires with high density on the ZnO surface for gas sensors. ACS Appl. Nano Mater. 2019, 3, 175–185. [Google Scholar] [CrossRef]
- Sánchez-Dena, O.; Hernández-López, S.; Camacho-López, M.A.; Acuña-Ávila, P.E.; Reyes-Esqueda, J.A.; Vigueras-Santiago, E. ZnO films from thermal oxidation of zn films: Effect of the thickness of the precursor films on the structural, morphological, and optical properties of the products. Crystals 2022, 12, 528. [Google Scholar] [CrossRef]
- Murzin, S.P. Laser irradiation for enhancing mass transfer in the solid phase of metallic materials. Metals 2021, 11, 1359. [Google Scholar] [CrossRef]
- Sledevskis, E.; Krasovska, M.; Gerbreders, V.; Mihailova, I.; Keviss, J.; Mizers, V.; Bulanovs, A. Impact of ZnO nanostructure morphology on electrochemical sensing performance for lead ion detection in real water samples. Chemosensors 2025, 13, 62. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, X. Nanomaterial ZnO synthesis and its photocatalytic applications: A review. Nanomaterials 2025, 15, 682. [Google Scholar] [CrossRef]
- Kusne, A.G.; Yu, H.S.; Wu, C.M.; Zhang, H.R.; Hattrick-Simpers, J.; DeCost, B.; Sarker, S.; Oses, C.; Toher, C.; Curtarolo, S.; et al. On-the-fly closed-loop materials discovery via Bayesian active learning. Nat. Commun. 2020, 11, 5966. [Google Scholar] [CrossRef]
- Tian, Y.; Li, T.; Pang, J.; Zhou, Y.; Xue, D.; Ding, X.; Lookman, T. Materials design with target-oriented Bayesian optimization. npj Comput. Mater. 2025, 11, 209. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Reiser, P.; Neubert, M.; Eberhard, A.; Torresi, L.; Zhou, C.; Shao, C.; Metni, H.; van Hoesel, C.; Schopmans, H.; Sommer, T.; et al. Graph neural networks for materials science and chemistry. Commun. Mater. 2022, 3, 93. [Google Scholar] [CrossRef] [PubMed]
- Faria, R.d.R.; Capron, B.D.O.; Secchi, A.R.; de Souza, M.B., Jr. Where reinforcement learning meets process control: Review and guidelines. Processes 2022, 10, 2311. [Google Scholar] [CrossRef]
- Vergara, D.; Lampropoulos, G.; Fernández-Arias, P.; Antón-Sancho, Á. Artificial intelligence reinventing materials engineering: A bibliometric review. Appl. Sci. 2024, 14, 8143. [Google Scholar] [CrossRef]
- Opatz, T.; Feldhoff, K.; Wiemer, H.; Ihlenfeldt, S. Sharing research data in collaborative material science and engineering projects. Data 2025, 10, 53. [Google Scholar] [CrossRef]
- Lombaers, P.; de Bruin, J.; van de Schoot, R. Reproducibility and data storage for active learning-aided systematic reviews. Appl. Sci. 2024, 14, 3842. [Google Scholar] [CrossRef]
- Toma, F.T.Z.; Rahman, M.S.; Maria, K.H. A review of recent advances in ZnO nanostructured thin films by various deposition techniques. Discov. Mater. 2025, 5, 60. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Wu, W.; Liu, C.R. The mechanism of controlled integration of ZnO nanowires using pulsed-laser-induced chemical deposition. Nanoscale 2019, 11, 2617–2623. [Google Scholar] [CrossRef]
- Abdalla, A.; Bereznev, S.; Spalatu, N.; Volobujeva, O.; Sleptsuk, N.; Danilson, M. Pulsed laser deposition of Zn(O,Se) layers in nitrogen background pressure. Sci. Rep. 2019, 9, 17443. [Google Scholar] [CrossRef]
- Ciolan, M.A.; Motrescu, I. Pulsed laser ablation: A facile and low-temperature fabrication of highly oriented n-type zinc oxide thin films. Appl. Sci. 2022, 12, 917. [Google Scholar] [CrossRef]
- Li, B.; Ding, L.; Gui, P.; Liu, N.; Yue, Y.; Chen, Z.; Song, Z.; Wen, J.; Lei, H.; Zhu, Z.; et al. Pulsed laser deposition assisted van der waals epitaxial large area quasi-2D ZnO single-crystal plates on fluorophlogopite mica. Adv. Mater. Interfaces 2019, 6, 1901156. [Google Scholar] [CrossRef]
- Fasquelle, D.; Députier, S.; Bouquet, V.; Guilloux-Viry, M. Effect of the microstructure of ZnO thin films prepared by PLD on their performance as toxic gas sensors. Chemosensors 2022, 10, 285. [Google Scholar] [CrossRef]
- Luo, C.-Q.; Ling, F.C.-C.; Rahman, M.A.; Phillips, M.; Ton-That, C.; Liao, C.; Shih, K.; Lin, J.; Tam, H.W.; Djurišić, A.B.; et al. Surface polarity control in ZnO films deposited by pulsed laser deposition. Appl. Surf. Sci. 2019, 483, 1129–1135. [Google Scholar] [CrossRef]
- Kirscher, Q.; Hajjar-Garreau, S.; Grasset, F.; Berling, D.; Soppera, O. Deep-UV laser direct writing of photoluminescent ZnO submicron patterns: An example of nanoarchitectonics concept. Sci. Technol. Adv. Mater. 2022, 23, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Medlin, W.; Uprety, S.; Isaacs-Smith, T.; Olsson, T.; Davis, J.; Burrows, S.; Chumley, S.; Park, M.; Laurent, G.M. Nanosecond-laser annealing of zinc oxide thin-films: The effect of the laser wavelength and fluence. Thin Solid Film. 2024, 791, 140236. [Google Scholar] [CrossRef]
- Nistor, M.G.; Dobrin, D.; Gherendi, F.; Perrière, J. Impact of high oxygen deficiency on the photoluminescence and electrical properties of ZnO thin films produced by pulsed electron beam deposition. Nanoscale 2025, 17, 23000–23009. [Google Scholar] [CrossRef]
- Long, J.; Xiong, W.; Wei, C.Y.R.; Lu, C.C.F.; Wang, R.Q.; Deng, C.S.; Liu, H.; Fan, X.H.; Jiao, B.Z.; Gao, S.; et al. Directional assembly of ZnO nanowires via three-dimensional laser direct writing. Nano Lett. 2020, 20, 5159. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.R. Morphology control by pulsed laser in chemical deposition illustrated in ZnO crystal growth. Cryst. Growth Des. 2019, 19, 2912–2918. [Google Scholar] [CrossRef]
- Frechilla, A.; Frechilla, J.; Angurel, L.A.; Toldrá-Reig, F.; Balas, F.; Martínez, E.; de La Fuente, G.F.; Muñoz-Rojas, D. Laser annealing of transparent ZnO thin films: A route to improve electrical conductivity and oxygen sensing capabilities. RSC Appl. Interfaces 2025, 2, 1607–1620. [Google Scholar] [CrossRef]
- Guerrero de León, J.A.; Pérez-Centeno, A.; Gómez-Rosas, G.; Mariscal, A.; Serna, R.; Santana-Aranda, M.A.; Quiñones-Galván, J.G. Influence of the Zn plasma kinetics on the structural and optical properties of ZnO thin films grown by PLD. SN Appl. Sci. 2019, 1, 475. [Google Scholar] [CrossRef]
- Barbillon, G. Oxygen vacancy dynamics in highly crystalline zinc oxide film investigated by PIERS effect. Materials 2021, 14, 4423. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zou, X.; Wei, H.; Li, Q.; Gao, Q.; Liu, Q.; Zhang, J. SiO2 coated on ZnO nanorod arrays with UV-durable superhydrophobicity and highly transmittance on glass. Front. Chem. 2020, 8, 101. [Google Scholar] [CrossRef] [PubMed]
- Steurer, M.; Somers, P.; Kraft, K.; Grünewald, L.; Kraus, S.; Feist, F.; Weinert, B.; Müller, E.; Dehnen, S.; Feldmann, C.; et al. Photothermal laser printing of sub-micrometer crystalline ZnO structures. Adv. Sci. 2024, 12, e2410771. [Google Scholar] [CrossRef] [PubMed]
- Rajkumar, C.; Arulraj, A. Enhanced photoconductive response of ZnO thin films with the impact of annealing temperatures on structural and optical properties. Sci. Rep. 2025, 15, 28851. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, B.; Liu, W.; Zhu, H.; Zhang, B.; Lu, Q.; Ren, Y.; Chen, F. Femtosecond laser writing of waveguides in zinc oxide crystals: Fabrication and mode modulation. Optics Express 2022, 30, 27694–27703. [Google Scholar] [CrossRef]
- Sahoo, A.; Dixit, T.; Kumari, A.; Gupta, S.; Kothandaraman, R.; Rajeev, P.P.; Rao, M.S.R.; Krishnan, S. Facile control of giant green-emission in multifunctional ZnO quantum dots produced in a single-step process: Femtosecond pulse ablation. Nanoscale Adv. 2024, 7, 524–535. [Google Scholar] [CrossRef]
- Kermiche, F.; Taabouche, A.; Bouabellou, A.; Hanini, F.; Bouachiba, Y. Behavior study of ZnO thin films grown by PLD for several applications. Crystallogr. Rep. 2022, 67, 1239–1245. [Google Scholar] [CrossRef]
- Ou, S.L.; Yu, F.P.; Wuu, D.S. Transformation from film to nanorod via a sacrifical layer: Pulsed laser deposition of ZnO for enhancing photodetector performance. Sci. Rep. 2017, 7, 14251. [Google Scholar] [CrossRef] [PubMed]
- ElZein, B.; Yao, Y.; Barham, A.S.; Dogheche, E.; Jabbour, G.E. Toward the growth of self-catalyzed ZnO nanowires perpendicular to the surface of silicon and glass substrates, by pulsed laser deposition. Materials 2020, 13, 4427. [Google Scholar] [CrossRef]
- Nath, A.; Mishra, M.; Chakrabarti, S. Impact of high substrate temperature on pulsed laser deposited ZnO pillars: A technological route to investigate the structural, optical and superhydrophilic properties. Appl. Surf. Sci. 2024, 646, 158907. [Google Scholar] [CrossRef]
- Murzin, S.P.; Kazanskiy, N.L. Arrays formation of zinc oxide nano-objects with varying morphology for sensor applications. Sensors 2020, 20, 5575. [Google Scholar] [CrossRef] [PubMed]
- Tseng, K.-H.; Lin, Y.-S.; Ku, H.-C.; Lee, H.-L. Study on the characteristics of zinc oxide nanocolloid prepared using electrical spark discharge method. J. Clust. Sci. 2022, 33, 145–150. [Google Scholar] [CrossRef]
- Bishwakarma, H.; Das, A.K. Synthesis of zinc oxide nanoparticles through hybrid machining process and their application in supercapacitors. J. Electron. Mater. 2020, 49, 1541–1549. [Google Scholar] [CrossRef]
- Wen, X.; Liu, Y.; Xi, F.; Zhang, X.; Kang, Y. Micro-arc oxidation (MAO) and its potential for improving the performance of titanium implants in biomedical applications. Front. Bioeng. Biotechnol. 2023, 11, 1282590. [Google Scholar] [CrossRef]
- Rezek, J.; Novák, P.; Houška, J.; Pajdarová, A.D.; Kozák, T. High-rate reactive high-power impulse magnetron sputtering of transparent conductive Al-doped ZnO thin films prepared at ambient temperature. Thin Solid Film. 2019, 679, 35–41. [Google Scholar] [CrossRef]
- Gurbandurdyyev, G.; Mistry, K.; Delumeau, L.-V.; Loke, J.Y.; Teoh, C.H.; Cheon, J.; Ye, F.; Tam, K.C.; Musselman, K.P. Robust, Conformal ZnO coatings on fabrics via atmospheric-pressure spatial atomic layer deposition with in-situ thickness control. ChemNanoMat 2023, 9, e202200498. [Google Scholar] [CrossRef]
- Shahzad, S.; Javed, S.; Usman, M. A review on synthesis and optoelectronic applications of nanostructured ZnO. Front. Mater. 2021, 8, 613825. [Google Scholar] [CrossRef]
- Abdel-Fattah, E.; Elsayed, I.A.; Fahmy, T. Substrate temperature and laser fluence effects on properties of ZnO thin films deposited by pulsed laser deposition. J. Mater. Sci. Mater. Electron. 2018, 29, 19942–19950. [Google Scholar] [CrossRef]
- Khudiar, A.I.; Ofui, A.M. Effect of pulsed laser deposition on the physical properties of ZnO nanocrystalline gas sensors. Opt. Mater. 2021, 115, 111010. [Google Scholar] [CrossRef]
- Jeckell, Z.; Barlaz, D.E.; Houlahan, T.; Huber, W.; Haehnlein, I.; Jurczyk, B.; Ruzic, D.N. Time-resolved ion energy distribution functions during a HiPIMS discharge with cathode voltage reversal. Phys. Scr. 2023, 98, 015605. [Google Scholar] [CrossRef]
- Senegačnik, M.; Kunimoto, K.; Yamaguchi, S.; Kimura, K.; Sakka, T.; Gregorčič, P. Dynamics of laser-induced cavitation bubble during expansion over sharp-edge geometry submerged in liquid—An inside view by diffuse illumination. Ultrason. Sonochem. 2021, 73, 105460. [Google Scholar] [CrossRef] [PubMed]
- Okeil, S.; Rabet, S.; Valadez Huerta, G.; Raabe, G.; Garnweitner, G. Understanding the role of solvent on the growth of zinc oxide: Insight from experiment and molecular dynamics simulations. Langmuir 2024, 40, 19343–19356. [Google Scholar] [CrossRef]
- Murzin, S.P. Improvement of thermochemical processes of laser-matter interaction and optical systems for wavefront shaping. Appl. Sci. 2022, 12, 12133. [Google Scholar] [CrossRef]
- Carlomagno, I.; Lucarini, I.; Secchi, V.; Maita, F.; Polese, D.; Mirabella, S.; Franzò, G.; Notargiacomo, A.; Di Santo, G.; Gonzalez, S.; et al. Surface Zn enrichment induced by excimer laser annealing in ZnO nanorods. Appl. Surf. Sci. 2022, 587, 152313. [Google Scholar] [CrossRef]
- Li, Q.; Hou, X.; Xu, Z.; Li, K.; Wei, Z.; Zhang, L.; Liu, Y. Femtosecond-laser-induced suprawavelength two-dimensional ZnO microstructures for multi-wavelength photodetector devices. Opt. Lett. 2024, 49, 6313. [Google Scholar] [CrossRef] [PubMed]
- Remeš, Z.; Hubička, Z.; Hubík, P. Optical and transport properties of ZnO thin films prepared by reactive pulsed mid-frequency sputtering combined with RF ECWR Plasma. Nanomaterials 2025, 15, 590. [Google Scholar] [CrossRef]
- Brunčko, J.; Šůtta, P.; Netrvalová, M.; Michalka, M.; Vincze, A. Pulsed laser deposition of Ga-doped ZnO films—Influence of deposition temperature and laser pulse frequency on structural, optical and electrical properties. Vacuum 2019, 159, 134–140. [Google Scholar] [CrossRef]
- Nagarjuna, Y.; Hsiao, Y.-J.; Wang, S.-C.; Shao, C.-Y.; Huang, Y.-C. Nanoporous ZnO structure prepared by HiPIMS sputtering for enhanced ozone gas detection. Mater. Today Commun. 2023, 35, 106024. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Yuan, Y.; Yang, L.; Zhang, H.; Liu, Z.; Ouyang, J.; Chen, Q. Reactive high power impulse magnetron sputtering of N-doped ZnO thin films: Structural and optical properties. AIP Adv. 2020, 10, 035320. [Google Scholar]
- Depablos-Rivera, O.; Sánchez-Ake, C.; Álvarez-Mendoza, R.; García-Fernández, T.; Muhl, S.; Villagrán-Muñiz, M. Hybrid magnetron sputtering and pulsed laser ablation for the deposition of composite ZnO–Au films. Thin Solid Film. 2019, 685, 66–74. [Google Scholar] [CrossRef]
- Labis, J.P.; Albrithen, H.A.; Hezam, M.; Ali Shar, M.; Algarni, A.; Alhazaa, A.N.; El-Toni, A.M.; Alduraibi, M.A. Optimization of pulsed laser ablation and radio-frequency sputtering tandem system for synthesis of 2D/3D Al2O3-ZnO nanostructures: A hybrid approach to synthesis of nanostructures for gas sensing applications. Nanomaterials 2023, 13, 1345. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Lechuga, M.; Grojo, D. Simple and robust method for determination of laser fluence thresholds for material modifications: An extension of Liu’s approach to imperfect beams. Open Res. Eur. 2021, 1, 7. [Google Scholar] [CrossRef]
- Hubička, Z.; Čada, M.; Kapran, A.; Olejníček, J.; Kšírová, P.; Zanáška, M.; Adámek, P.; Tichý, M. Plasma diagnostics in reactive high-power impulse magnetron sputtering system working in Ar + H2S gas mixture. Coatings 2020, 10, 246. [Google Scholar] [CrossRef]
- Kolesnikov, A.; Kryukov, Y.; Gafurov, M.; Bodnarchuk, V. Prediction of target erosion for planar magnetron sputtering systems. Coatings 2022, 12, 1807. [Google Scholar] [CrossRef]
- Shepelin, N.A.; Tehrani, Z.P.; Ohannessian, N.; Schneider, C.W.; Pergolesi, D.; Lippert, T. A practical guide to pulsed laser deposition. Chem. Soc. Rev. 2023, 52, 2294–2321. [Google Scholar] [CrossRef]
- Zaplotnik, R.; Primc, G.; Vesel, A. Optical emission spectroscopy as a diagnostic tool for characterization of atmospheric plasma jets. Appl. Sci. 2021, 11, 2275. [Google Scholar] [CrossRef]
- Ayoub, I.; Kumar, V.; Abolhassani, R.; Sehgal, R.; Sharma, V.; Sehgal, R.; Swart, H.C.; Mishra, Y.K. Advances in ZnO: Manipulation of defects for enhancing their technological potentials. Nanotechnol. Rev. 2022, 11, 575–619. [Google Scholar] [CrossRef]
- Mo, G.; Cui, Y.; Yin, J.; Gao, P. Influence of ZnO Film deposition parameters on piezoelectric properties and film-to-substrate adhesion on a GH4169 superalloy steel substrate. Micromachines 2022, 13, 639. [Google Scholar] [CrossRef] [PubMed]
- Kaim, P.; Łukaszkowicz, K.; Szindler, M.; Szindler, M.M.; Basiaga, M.; Hajduk, B. The influence of magnetron sputtering process temperature on ZnO thin-film properties. Coatings 2021, 11, 1507. [Google Scholar] [CrossRef]
- Muthusamy, S.; Bharatan, S.; Sivaprakasam, S.; Mohanam, R. Effect of deposition temperature on Zn interstitials and oxygen vacancies in RF-sputtered ZnO thin films and thin film-transistors. Materials 2024, 17, 5153. [Google Scholar] [CrossRef]
- Danilov, V.A. Laser technology and nanotechnology applying diffractive optical elements. Nanobiotechnol. Rep. 2022, 17, 747–757. [Google Scholar] [CrossRef]
- Volk, A.A.; Abolhasani, M. Performance metrics to unleash the power of self-driving labs in chemistry and materials science. Nat. Commun. 2024, 15, 1378. [Google Scholar] [CrossRef]
- Canty, R.B.; Koscher, B.A.; McDonald, M.A.; Jensen, K.F. Integrating autonomy into automated research platforms. Digit. Discov. 2023, 2, 1259–1268. [Google Scholar] [CrossRef]
- Vescovi, R.; Ginsburg, T.; Hippe, K.; Ozgulbas, D.; Stone, C.; Stroka, A.; Butler, R.; Blaiszik, B.; Brettin, T.; Chard, K.; et al. Towards a modular architecture for science factories. Digit. Discov. 2023, 2, 1980–1998. [Google Scholar] [CrossRef]
- Guevarra, D.; Kan, K.; Lai, Y.; Jones, R.J.R.; Zhou, L.; Donnelly, P.; Richter, M.; Stein, H.S.; Gregoire, J.M. Orchestrating nimble experiments across interconnected labs. Digit. Discov. 2023, 2, 1806–1812. [Google Scholar] [CrossRef]
- Bai, J.; Mosbach, S.; Taylor, C.J.; Karan, D.; Lee, K.F.; Rihm, S.D.; Akroyd, J.; Lapkin, A.A.; Kraft, M. A Dynamic knowledge graph approach to distributed self-driving laboratories. Nat. Commun. 2024, 15, 462. [Google Scholar] [CrossRef]
- Maffettone, P.M.; Friederich, P.; Baird, S.G.; Blaiszik, B.; Brown, K.A.; Campbell, S.I.; Cohen, O.; Davis, R.L.; Foster, I.T.; Haghmoradi, N.; et al. What is missing in autonomous discovery: Open challenges for the community. Digit. Discov. 2023, 2, 1644–1659. [Google Scholar] [CrossRef]
- Tobias, A.V.; Wahab, A. Autonomous ‘self-driving’ laboratories: A review of technology and policy implications. R. Soc. Open Sci. 2025, 12, 250646. [Google Scholar] [CrossRef] [PubMed]
- ISO/IEC Guide 98-1:2024; Uncertainty of Measurement—Part 1: Introduction. International Organization for Standardization: Geneva, Switzerland, 2024. Available online: https://www.iso.org/standard/82708.html (accessed on 10 November 2025).
- ISO/IEC Guide 98-6:2021; Uncertainty of Measurement—Part 6: Developing and Using Measurement Models. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/81374.html (accessed on 10 November 2025).
- Gabriel, V.; Kocán, P.; Holý, V. Effective algorithm for simulations of layer-by-layer growth during pulsed-laser deposition. Phys. Rev. E 2020, 102, 063305. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.W.; Lippert, T. PLD plasma plume analysis: A summary of the PSI contribution. Appl. Phys. A 2023, 129, 138. [Google Scholar] [CrossRef]
- Maculotti, G.; Marschall, M.; Kok, G.; Chekh, B.A.; van Dijk, M.; Flores, J.; Genta, G.; Puerto, P.; Galetto, M.; Schmelter, S. A Shared metrological framework for trustworthy virtual experiments and digital twins. Metrology 2024, 4, 337–363. [Google Scholar] [CrossRef]
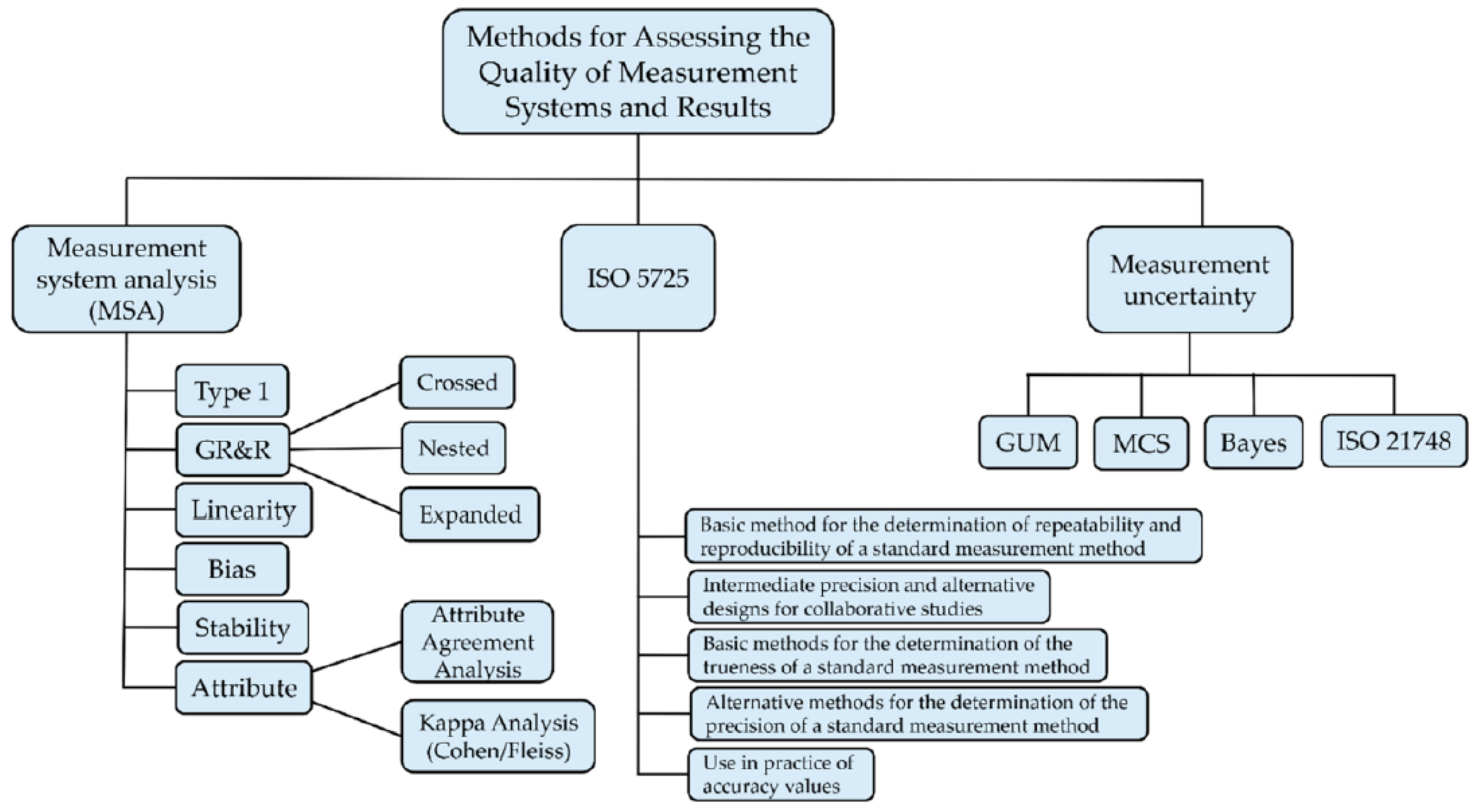
- Razumić, A.; Runje, B.; Alar, V.; Štrbac, B.; Trzun, Z. A Review of methods for assessing the quality of measurement systems and results. Appl. Sci. 2025, 15, 9393. [Google Scholar] [CrossRef]
- Cachoncinlle, C.; Millon, E.; Portier, X.; Hebert, C.; Perrière, J.; Nistor, M. Anisotropy of physical properties in pulsed laser-deposited ZnO films. Appl. Phys. A 2022, 128, 530. [Google Scholar] [CrossRef]
- Ramsey, M.H.; Rostron, P.D. Measurement uncertainty from sampling and its role in validation of measurement procedures. Accred. Qual. Assur. 2024, 29, 153–162. [Google Scholar] [CrossRef]
- Salicone, S. New frontiers in measurement uncertainty. Metrology 2022, 2, 495–498. [Google Scholar] [CrossRef]
- Kumar, R.; Joshi, A.; Khan, S.A.; Misra, S. Automated extraction of synthesis parameters of pulsed laser-deposited materials from scientific literature. Digit. Discov. 2024, 3, 944–953. [Google Scholar] [CrossRef]
- Neykova, N.; Paušová, Š.; Bouzek, K. Dataset of “Optical, Electrical and Surface Properties of Bare and Doped Nanocrystalline ZnO Thin Films on Interdigital Electrodes”. Zenodo 2025. [Google Scholar] [CrossRef]
- Greenberg, J.; Bóveda-Aguirre, P.; Allison, J.; Asinari, P.; Chan, M.; Chandrasekaran, A.; Ertekin, E.; Garoufallou, E.; Galli, G.; Giannozzi, P.; et al. Towards MatCore: A unified metadata standard for materials science. Commun. Comput. Inf. Sci. 2025, 2331, 3–14. [Google Scholar]
- Smirnov, Y.; Schmengler, L.; Kuik, R.; Repecaud, P.-A.; Najafi, M.; Zhang, D.; Theelen, M.; Aydin, E.; Veenstra, S.; De Wolf, S.; et al. Scalable pulsed laser deposition of transparent rear electrode for perovskite solar cells. Adv. Mater. Technol. 2021, 6, 2000856. [Google Scholar] [CrossRef]
- Haider, A.J.; Alawsi, T.; Haider, M.J.; Taha, B.A.; Marhoon, H.A. A comprehensive review on pulsed laser deposition technique to effective nanostructure production: Trends and challenges. Opt. Quantum Electron. 2022, 54, 488. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, X.; Chen, H.; Yang, T.; He, Y. Exploring multi-fidelity data in materials science: Challenges, applications, and optimized learning strategies. Appl. Sci. 2023, 13, 13176. [Google Scholar] [CrossRef]
- Harris, S.B.; Biswas, A.; Yun, S.J.; Roccapriore, K.M.; Rouleau, C.M.; Puretzky, A.A.; Vasudevan, R.K.; Geohegan, D.B.; Xiao, K. Autonomous synthesis of thin film materials with pulsed laser deposition enabled by in situ spectroscopy and automation. Small Methods 2024, 8, 2301763. [Google Scholar] [CrossRef]
- Talirz, L.; Kumbhar, S.; Passaro, E.; Yakutovich, A.V.; Granata, V.; Gargiulo, F.; Borelli, M.; Uhrin, M.; Huber, S.P.; Zoupanos, S.; et al. Materials Cloud, a platform for open computational science. Sci. Data 2020, 7, 299. [Google Scholar] [CrossRef]
- Marschall, M.; Hughes, F.; Wübbeler, G.; Kok, G.; van Dijk, M.; Elster, C. Using a multivariate virtual experiment for uncertainty evaluation with unknown variance. Metrology 2024, 4, 534–546. [Google Scholar] [CrossRef]
- Orvis, T.; Kumarasubramanian, H.; Surendran, M.; Kutagulla, S.; Cunniff, A.; Ravichandran, J. In situ monitoring of composition and sensitivity to growth parameters of pulsed laser deposition. ACS Appl. Electron. Mater. 2021, 3, 1422–1428. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G. A Review of predictive uncertainty estimation with machine learning. Artif. Intell. Rev. 2024, 57, 94. [Google Scholar] [CrossRef]
- Wilkinson, M.D.; Dumontier, M.; Sansone, S.-A.; Bonino da Silva Santos, L.O.; Prieto, M.; Batista, D.; McQuilton, P.; Kuhn, T.; Rocca-Serra, P.; Crosas, M.; et al. Evaluating FAIR maturity through a scalable, automated, community-governed framework. Sci. Data 2019, 6, 174. [Google Scholar] [CrossRef]
- Draxl, C.; Scheffler, M. The NOMAD laboratory: From data sharing to artificial intelligence. J. Phys. Mater. 2019, 2, 036001. [Google Scholar] [CrossRef]
- Scheffler, M.; Aeschlimann, M.; Albrecht, M.; Bereau, T.; Bungartz, H.-J.; Felser, C.; Greiner, M.; Groß, A.; Koch, C.T.; Kremer, K.; et al. FAIR data enabling new horizons for materials research. Nature 2022, 604, 635–642. [Google Scholar] [CrossRef]
- Soiland-Reyes, S.; Sefton, P.; Crosas, M.; Castro, L.J.; Coppens, F.; Fernández, J.M.; Garijo, D.; Grüning, B.; La Rosa, M.; Leo, S.; et al. Implementing the RO-Crate metadata specification. Data Sci. 2022, 5, 97–138. [Google Scholar] [CrossRef]
- Dudarev, V.; Banko, L.; Ludwig, A. An extensible open-source solution for research digitalisation in materials science. npj Comput. Mater. 2025, 11, 116. [Google Scholar] [CrossRef]
- Himanen, L.; Geurts, A.; Foster, A.S.; Rinke, P. Data-driven materials science: Status, challenges, and perspectives. Adv. Sci. 2019, 6, 1900808. [Google Scholar] [CrossRef] [PubMed]
- Lookman, T.; Balachandran, P.V.; Xue, D.; Yuan, R. Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design. npj Comput. Mater. 2019, 5, 21. [Google Scholar] [CrossRef]
- Häse, F.; Roch, L.M.; Aspuru-Guzik, A. Next-generation experimentation with self-driving laboratories. Trends Chem. 2019, 1, 282–291. [Google Scholar] [CrossRef]
- Jinnouchi, R.; Karsai, F.; Kresse, G. On-the-fly active learning of interatomic potentials for large-scale atomistic simulations. J. Chem. Phys. 2020, 152, 234102. [Google Scholar] [CrossRef] [PubMed]
- Karnati, P.; Haque, A.; Taufique, M.F.N.; Ghosh, K. A Systematic study on the structural and optical properties of vertically aligned zinc oxide nanorods grown by high pressure assisted pulsed laser deposition technique. Nanomaterials 2018, 8, 62. [Google Scholar] [CrossRef]
- Wu, E.; Dai, S.; Xuan, X.; He, J.; Liu, Y.; Tan, Y.; Mo, Z.; Yu, J. Picosecond pulsed laser deposition technique to fabricate zinc-oxide thin films through burst mode. Chin. J. Lasers 2022, 49, 0603003. [Google Scholar] [CrossRef]
- Patra, S.P.; Agrawal, R.; Sahlot, P.; Wankhede, V.A. Adoption of cyber-physical systems in manufacturing industries. AIP Conf. Proc. 2024, 2960, 030009. [Google Scholar] [CrossRef]
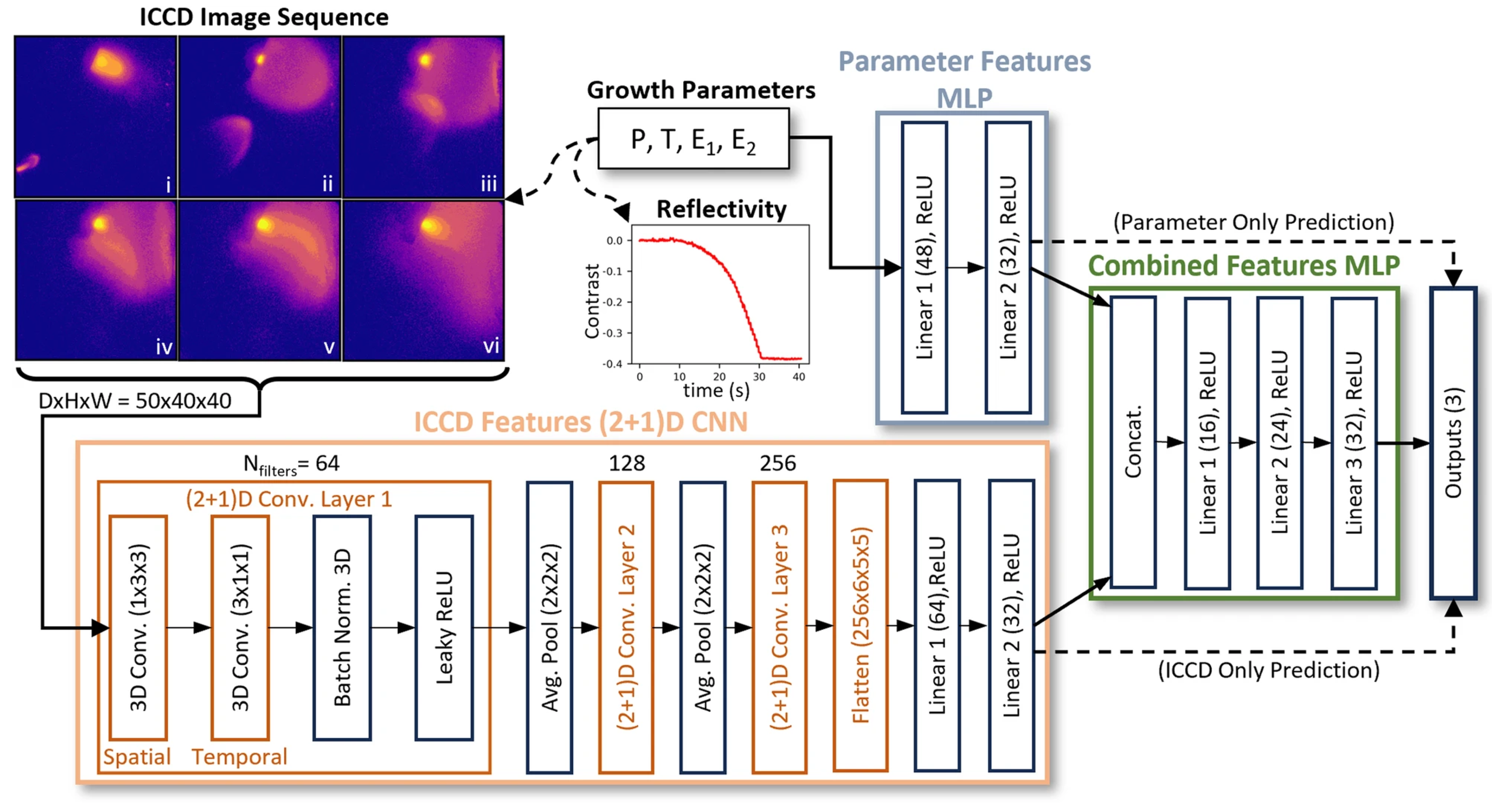
- Harris, S.B.; Rouleau, C.M.; Xiao, K.; Vasudevan, R.K. Deep learning with plasma plume image sequences for anomaly detection and prediction of growth kinetics during pulsed laser deposition. npj Comput. Mater. 2024, 10, 105. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine learning through physics-informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Zhong, L.; Wu, B.; Wang, Y. Low-temperature plasma simulation based on physics-informed neural networks: Frameworks and preliminary applications. Phys. Fluids 2022, 34, 087116. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Di, Y.; Wang, L.; Wang, H.; Zhou, Q. A physics-informed neural network framework to predict 3D temperature field without labeled data in process of laser metal deposition. Eng. Appl. Artif. Intell. 2023, 120, 105908. [Google Scholar] [CrossRef]
- Akinsolu, M.O.; Zribi, K. A generalized framework for adopting regression-based predictive modeling in manufacturing environments. Inventions 2023, 8, 32. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. A Survey of ensemble learning: Concepts, algorithms, applications, and prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef]
- Qin, Y.; DeWitt, S.; Radhakrishnan, B.; Biros, G. GrainNN: A neighbor-aware long short-term memory network for predicting microstructure evolution during polycrystalline grain formation. Comput. Mater. Sci. 2023, 218, 111927. [Google Scholar] [CrossRef]
- Qin, Y.; DeWitt, S.; Radhakrishnan, B.; Biros, G. GrainGNN: A dynamic graph neural network for predicting 3D grain microstructure. J. Comput. Phys. 2024, 510, 113061. [Google Scholar] [CrossRef]
- Dai, M.; Demirel, M.F.; Liang, Y.; Hu, J.-M. Graph neural networks for an accurate and interpretable embedding of polycrystalline microstructure. npj Comput. Mater. 2021, 7, 103. [Google Scholar] [CrossRef]
- Patidar, J.; Pshyk, O.; Thorwarth, K.; Sommerhäuser, L.; Siol, S. Low temperature deposition of functional thin films on insulating substrates enabled by selective ion acceleration using synchronized floating potential HiPIMS. Nat. Commun. 2025, 16, 4719. [Google Scholar] [CrossRef]
- Gao, R.X.; Krüger, J.; Merklein, M.; Möhring, H.-C.; Váncza, J. Artificial intelligence in manufacturing: State of the art, perspectives, and future directions. CIRP Ann. 2024, 73, 723–749. [Google Scholar] [CrossRef]
- Plathottam, S.J.; Rzonca, A.; Lakhnori, R.; Iloeje, C.O. A review of artificial intelligence applications in manufacturing operations. J. Adv. Manuf. Process. 2023, 5, e10159. [Google Scholar] [CrossRef]
- Shi, X.; Zhou, L.; Huang, Y.; Wu, Y.; Hong, Z. A review on the applications of graph neural networks in materials science at the atomic scale. Mater. Genome Eng. Adv. 2024, 2, e50. [Google Scholar] [CrossRef]
- Kuprikov, E.; Kokhanovskiy, A.; Serebrennikov, K.; Turitsyn, S. Deep reinforcement learning for self-tuning laser source of dissipative solitons. Sci. Rep. 2022, 12, 7185. [Google Scholar] [CrossRef]
- Yan, Q.; Deng, Q.; Zhang, J.; Zhu, Y.; Yin, K.; Li, T.; Wu, D.; Jiang, T. Low-latency deep-reinforcement learning algorithm for ultrafast fiber lasers. Photonics Res. 2021, 9, 1493–1501. [Google Scholar] [CrossRef]
- Reuer, K.; Landgraf, J.; Fösel, T.; O’Sullivan, J.; Beltrán, L.; Akin, A.; Norris, G.J.; Remm, A.; Kerschbaum, M.; Besse, J.-C.; et al. Realizing a deep reinforcement learning agent for real-time feedback control of a quantum system. Nat. Commun. 2023, 14, 7138. [Google Scholar] [CrossRef]
- Ogoke, F.; Farimani, A.B. Thermal control of laser powder bed fusion using deep reinforcement learning. Addit. Manuf. 2021, 46, 102033. [Google Scholar] [CrossRef]
- Kuo, H.-A.; Hong, T.-Y.; Chien, C.-F. A Deep reinforcement learning based digital twin framework for resilient production planning under demand uncertainty and an empirical study in semiconductor wafer fabrication. Comput. Ind. Eng. 2025, 208, 111389. [Google Scholar] [CrossRef]
- Schena, L.; Marques, P.A.; Poletti, R.; Ahizi, S.; Van den Berghe, J.; Mendez, M.A. Reinforcement twinning: From digital twins to model-based reinforcement learning. J. Comput. Sci. 2024, 82, 102421. [Google Scholar] [CrossRef]
- Lee, D.; Kang, Y.S.; Noh, S.D. Digital twin-driven deep reinforcement learning for real-time optimisation in dynamic AGV systems. Int. J. Prod. Res. 2025; in press. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q.; Liu, A.; Kusiak, A. Data-driven smart manufacturing. J. Manuf. Syst. 2018, 48, 157–169. [Google Scholar] [CrossRef]
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the digital twin: A systematic literature review. CIRP J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital twin in industry: State-of-the-art. IEEE Trans. Ind. Inf. 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Khan, T.; Khan, U.; Khan, A.; Mollan, C.; Morkvenaite-Vilkonciene, I.; Pandey, V. Data-driven digital twin framework for predictive maintenance of smart manufacturing systems. Machines 2025, 13, 481. [Google Scholar] [CrossRef]
- Xu, Y.; Qamsane, Y.; Puchala, S.; Januszczak, A.; Tilbury, D.M.; Barton, K. A data-driven approach toward a machine- and system-level performance monitoring digital twin for production lines. Comput. Ind. 2024, 157, 104086. [Google Scholar] [CrossRef]
- Kessels, B.M.; Fey, R.H.; van de Wouw, N. Real-time parameter updating for nonlinear digital twins using inverse mapping models and transient-based features. Nonlinear Dyn. 2023, 111, 10255–10285. [Google Scholar] [CrossRef]
- Theerthagiri, J.; Karuppasamy, K.; Lee, S.J.; Shwetharani, R.; Kim, H.-S.; Pasha, S.K.K.; Ashokkumar, M.; Choi, M.Y. Fundamentals and comprehensive insights on pulsed laser synthesis of advanced materials for diverse photo- and electrocatalytic applications. Light Sci. Appl. 2022, 11, 250. [Google Scholar] [CrossRef] [PubMed]
- Ariza, R.; Urbieta, A.; Ferreiro, A.; Rabanal, M.E.; Fernández, P.; Solis, J. Selective growth of ZnO micro- and nano-structures on fs-laser processed metallic Zn substrates for large area applications. J. Alloys Compd. 2025, 1010, 177797. [Google Scholar] [CrossRef]
- Rajkumar, P.; Barman, D.; Kashyap, A.; Sarma, B.K. Realization of ZnO microrods and Ag nanoparticles on glass and Si substrates by magnetron sputtering and near band edge photoluminescence enhancement from the exciton-plasmon system. Mater. Lett. 2022, 325, 132898. [Google Scholar]
- Oga, T.; Kai, R.; Kaneko, N.; Miyazaki, H.; Kaneko, S.; Matsuda, A.; Yoshimoto, M.; Sato, S.; Shirasawa, T. Crystallinity improvement of room-temperature PLD-deposited ZnO thin films on cyclo-olefin polymer substrates subject to surface-pretreatment with vacuum-UV-light irradiation. J. Cryst. Growth 2022, 603, 127012. [Google Scholar] [CrossRef]
- Masuda, T.; Sato, T.; Lippmaa, M.; Dazai, T.; Sekine, N.; Hosako, I.; Koinuma, H.; Takahashi, R. Polarity of homoepitaxial ZnO films grown by Nd:YAG pulsed laser deposition. J. Appl. Phys. 2024, 136, 095303. [Google Scholar] [CrossRef]
- Hadi, A.J.; Nayef, U.M.; Mutlak, F.A.H.; Jabir, M.S. High-efficiency photodetectors based on zinc oxide nanostructures on porous silicon grown by pulsed laser deposition. Plasmonics 2024, 19, 577–593. [Google Scholar] [CrossRef]
- Nistor, M.; Gherendi, F.; Dobrin, D.; Perrière, J. From transparent to black amorphous zinc oxide thin films through oxygen deficiency control. J. Appl. Phys. 2022, 132, 225705. [Google Scholar] [CrossRef]
- Hong, N.H.; Pham, N.S.; Murakami, T.; Meduna, M.; Caha, O.; Miháliková, I.; Friák, M. ZnO thin films made by sputtering: Room temperature ferromagnetism due to Zn defects/vacancies? RSC Adv. 2025, 15, 8830–8838. [Google Scholar] [CrossRef]
- Hippler, R.; Kapran, A.; Wulff, H.; Nepomniashchaia, N.; Remes, Z.; Olejnicek, J.; Cada, M.; Hubicka, Z. Energy distribution of positively and negatively charged plasma ions of a pulsed magnetron sputtering discharge in an argon/oxygen gas mixture and deposition of functional ZnO films. J. Vac. Sci. Technol. A 2025, 43, 053002. [Google Scholar] [CrossRef]
- Krysova, H.; Mansfeldova, V.; Tarabkova, H.; Pisarikova, A.; Hubicka, Z.; Kavan, L. High-quality dense ZnO thin films: Work function and photo/electrochemical properties. J. Solid State Electrochem. 2024, 28, 123–136. [Google Scholar] [CrossRef]
- Tarasov, A.P.; Muslimov, A.E.; Kanevsky, V.M. Stimulated emission in vertically aligned hexagonal ZnO microcrystals synthesized by magnetron sputtering method. Photonics 2022, 9, 871. [Google Scholar] [CrossRef]
- Syed, K.; Krstulović, N.; Casanova-Cháfer, J.; Llobet, E.; Güell, F.; Martínez-Alanis, P.R.; Marciuš, M.; Shagieva, E.; Ristić, D.; Gebavi, H.; et al. The role of the pulsed laser deposition in different growth atmospheres on the gas-sensing properties of ZnO films. Sens. Actuators B Chem. 2023, 382, 133454. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Yuan, Y.; Yang, L.; Zhang, H.; Liu, Z.; Ouyang, J.; Chen, Q. N-doped ZnO (N:ZnO) film prepared by reactive HiPIMS deposition technique. AIP Adv. 2020, 10, 035122. [Google Scholar] [CrossRef]
- Liu, S.; Ou, C.Y.; Liu, C.R. Temporal and spatial temperature modelling for understanding pulsed laser-induced solution-based nanomanufacturing. Nanotechnology 2020, 31, 325601. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, S.; Xu, Y.; Long, J.; Jiao, B.; Gao, H.; Fan, X.; Liu, Y.; Deng, L.; Xiong, W. Glycerol-assisted grain modulation in femtosecond-laser-induced photochemical synthesis of patterned ZnO nanomaterials. Light Adv. Manuf. 2025, 6, 7. [Google Scholar] [CrossRef]
- Ohshima, T. Sputtering Deposition with Low-Cost Multi-Element Powder Targets. IEEE Open J. Nanotechnol. 2023, 4, 172–180. [Google Scholar] [CrossRef]
- Vakulov, Z.; Khakhulin, D.; Zamburg, E.; Mikhaylichenko, A.; Smirnov, V.A.; Tominov, R.; Klimin, V.S.; Ageev, O.A. Towards scalable large-area pulsed laser deposition. Materials 2021, 14, 4854. [Google Scholar] [CrossRef]
- Yu, J.; Han, W.; Suleiman, A.A.; Han, S.; Miao, N.; Ling, F.C.C. Recent advances on pulsed laser deposition of large-scale thin films. Small Methods 2024, 8, e2301282. [Google Scholar] [CrossRef]
- Lorenz, M.; Hochmuth, H.; von Wenckstern, H.; Grundmann, M. Flexible hardware concept of pulsed laser deposition for large areas and combinatorial composition spreads. Rev. Sci. Instrum. 2023, 94, 083905. [Google Scholar] [PubMed]
- Wang, Z.; Luo, C.; Anwand, W.; Wagner, A.; Butterling, M.; Rahman, M.A.; Phillips, M.R.; Ton-That, C.; Younas, M.; Su, S.; et al. Vacancy cluster in ZnO films grown by pulsed laser deposition. Sci. Rep. 2019, 9, 3534. [Google Scholar] [CrossRef] [PubMed]
- Havlová, Š.; Novotný, M.; Fitl, P.; More-Chevalier, J.; Remsa, J.; Kiisk, V.; Kodu, M.; Jaaniso, R.; Hruška, P.; Lukáč, F.; et al. Effect of pulsed laser annealing on optical and structural properties of ZnO:Eu thin film. J. Mater. Sci. 2021, 56, 11414–11425. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Zhou, M.; Zhang, S.; Cao, S.; Lei, G.; Lou, C.; Zhang, J. Plasma-induced oxygen vacancies enabled ultrathin ZnO films for highly sensitive detection of triethylamine. J. Hazard. Mater. 2021, 415, 125757. [Google Scholar] [CrossRef] [PubMed]
- Mandal, A.; Banpurkar, A.G.; Shinde, S.D.; Jejurikar, S.M. Impact of oxygen vacancy on luminescence properties of dysprosium-doped zinc oxide thin films. J. Appl. Phys. 2024, 136, 025302. [Google Scholar] [CrossRef]
- Karakaya, S.; Kaba, L. Effect of fluorine doping on the improvement of electrical and photocatalytic properties of ZnO films. Appl. Phys. A 2024, 130, 167. [Google Scholar] [CrossRef]
- Badgujar, A.C.; Yadav, B.S.; Jha, G.K.; Dhage, S.R. Room-temperature sputtered aluminum-doped ZnO thin films with high figure of merit on large-area glass substrates. ACS Omega 2022, 7, 14203–14210. [Google Scholar] [CrossRef]
- Zubkins, M.; Arslan, H.; Bikse, L.; Purans, J. High power impulse magnetron sputtering of Zn/Al target in an Ar and Ar/O2 atmosphere: The study of sputtering process and AZO films. Surf. Coat. Technol. 2019, 369, 156–164. [Google Scholar] [CrossRef]
- Phelps, J.R.; Saikumar, A.K.; Abdolvand, R.; Sundaram, K.B. Comparison of RF and high impulse magnetron sputtered gallium-doped zinc oxide thin films. Coatings 2023, 13, 71. [Google Scholar]
- Regalado-Contreras, A.; Farías, M.H.; De la Cruz, W. Room-temperature deposition of stable p-type ZnO:N thin films through chemical-species modulation using reactive pulsed laser deposition. Appl. Surf. Sci. 2023, 640, 158393. [Google Scholar] [CrossRef]
- Mickan, M.; Helmersson, U.; Horwat, D. Effect of substrate temperature on the deposition of Al-doped ZnO thin films using high power impulse magnetron sputtering. Surf. Coat. Tech. 2018, 347, 245–251. [Google Scholar] [CrossRef]
- Abbas, Z.M.; Abbas, Q.A. Aluminum-doped ZnO nano-laminar structures by pulsed laser ablation for gas sensing application. J. Opt. 2024, 53, 544–557. [Google Scholar] [CrossRef]
- Chen, X.; Cui, F.; Liu, M.; Lu, Y.; Yu, L. Femtosecond laser spatial shaping of ZnO-PVDF microstructures for interfacial charge regulation enhancing solid–liquid triboelectric energy conversion. J. Colloid. Interface Sci. 2026, 702, 138900. [Google Scholar] [CrossRef] [PubMed]
- Rajendiran, S.; Meehan, D.; Wagenaars, E. Plasma-enhanced pulsed laser deposition of copper oxide and zinc oxide thin films. AIP Adv. 2020, 10, 065323. [Google Scholar] [CrossRef]
- Zhang, Y.; He, T.; Qian, Z.; Wang, Q.; Xu, Y.; Lu, W. Deposition of fluorescent ZnO thin film by radio frequency atmospheric pressure plasma. Eur. Phys. J. Appl. Phys. 2025, 100, 17. [Google Scholar] [CrossRef]
- Park, S.Y.; Choi, Y.; Seo, Y.H.; Kim, H.; Lee, D.H.; Truong, P.L.; Jeon, Y.; Yoo, H.; Kwon, S.J.; Lee, D.; et al. 355 nm nanosecond ultraviolet pulsed laser annealing effects on amorphous In-Ga-ZnO thin film transistors. Micromachines 2024, 15, 103. [Google Scholar] [CrossRef]
- Dikovska, A.O.; Nikov, R.G.; Avdeev, G.V.; Atanasova, G.B.; Dilova, T.; Karashanova, D.B.; Nedyalkov, N.N. ZnO/Zn2TiO4 composite nanostructures produced by laser ablation in air. Physica E 2023, 150, 115707. [Google Scholar] [CrossRef]
- Gündoğdu, Y.; Dursun, S.; Gezgin, S.Y.; Kiliç, H.Ş. Femtosecond laser-induced production of ZnO@Ag nanocomposites for an improvement in photocatalytic efficiency in the degradation of organic pollutants. Opt. Laser Technol. 2024, 170, 110291. [Google Scholar] [CrossRef]

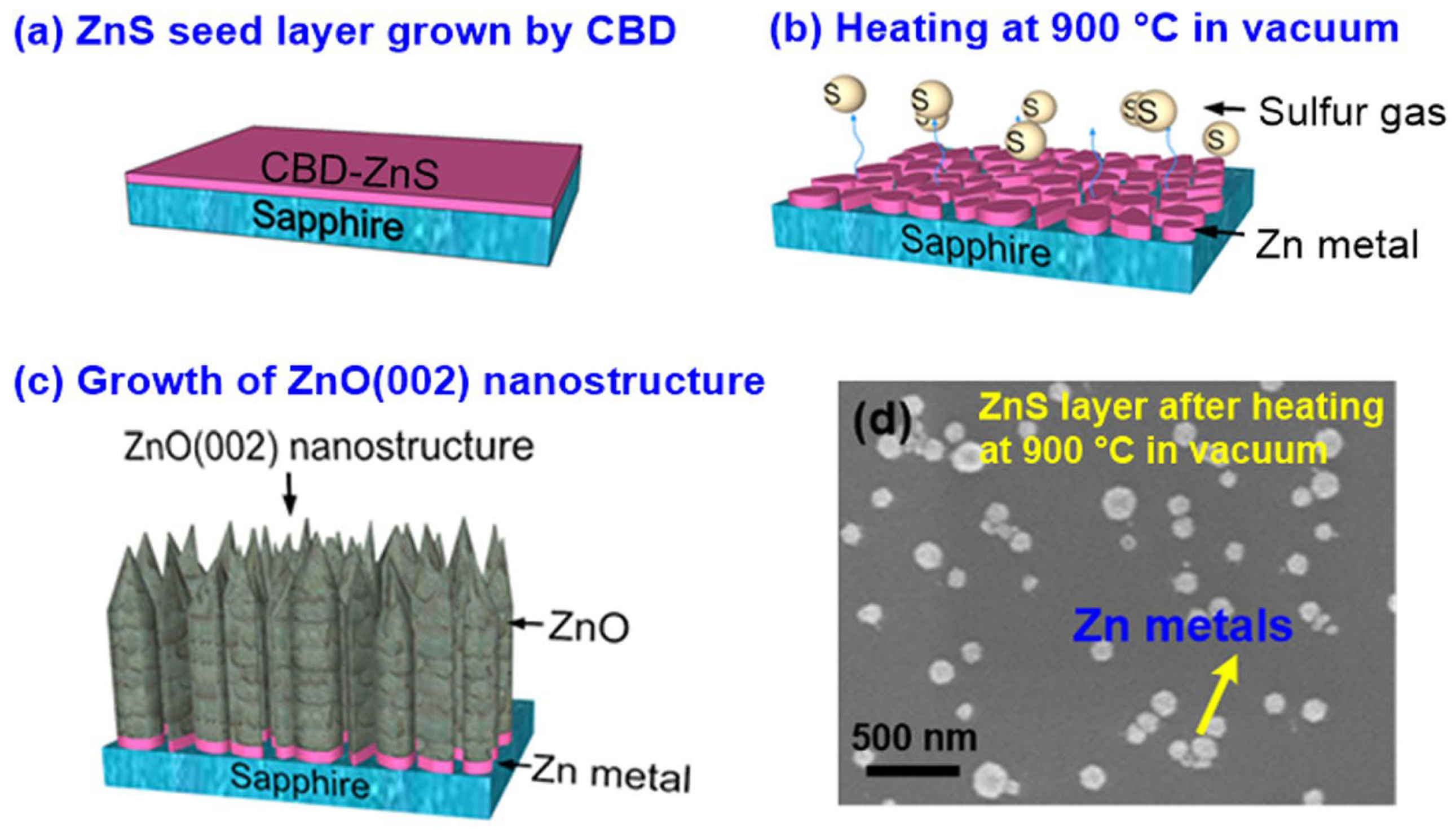


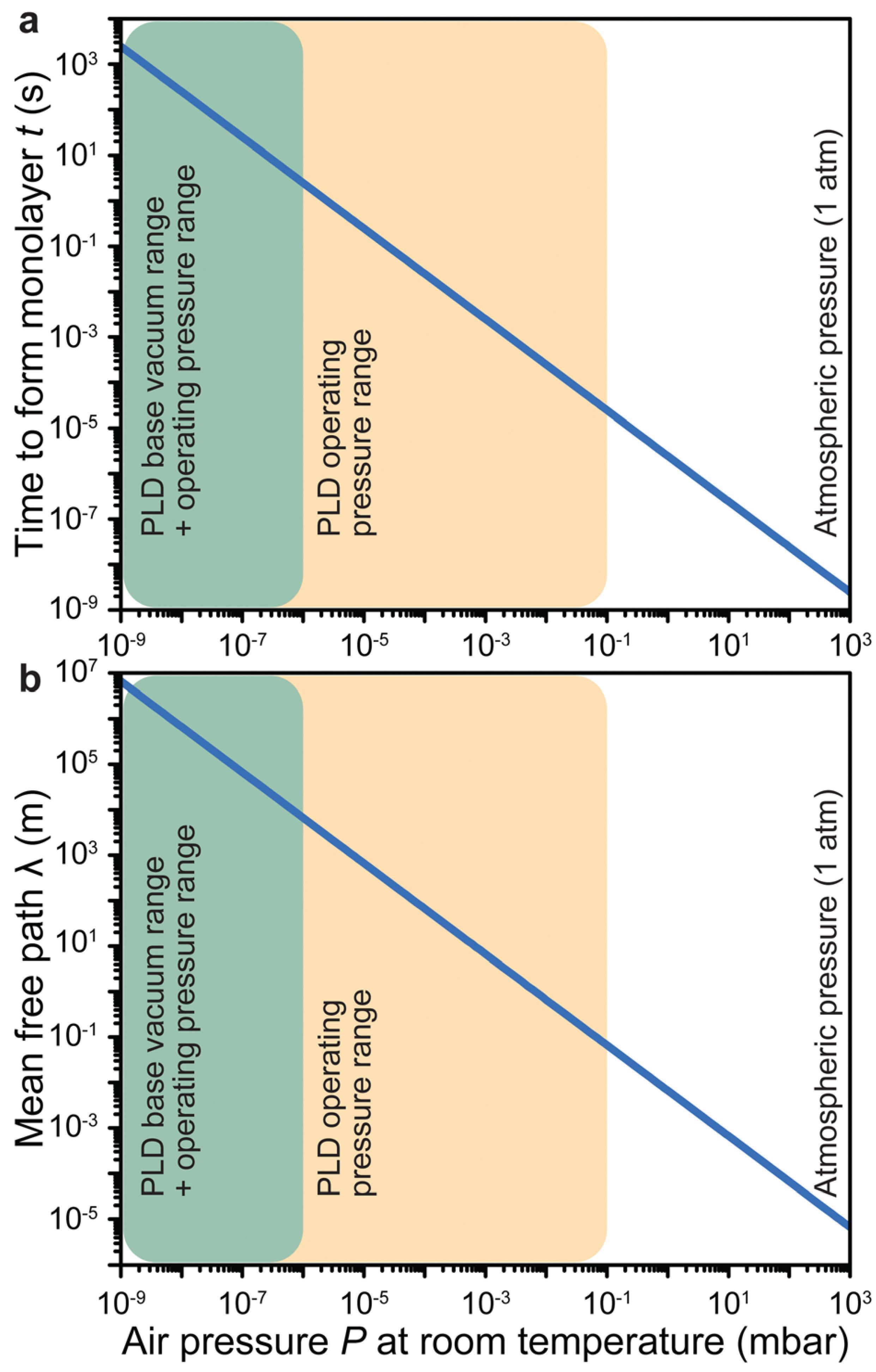

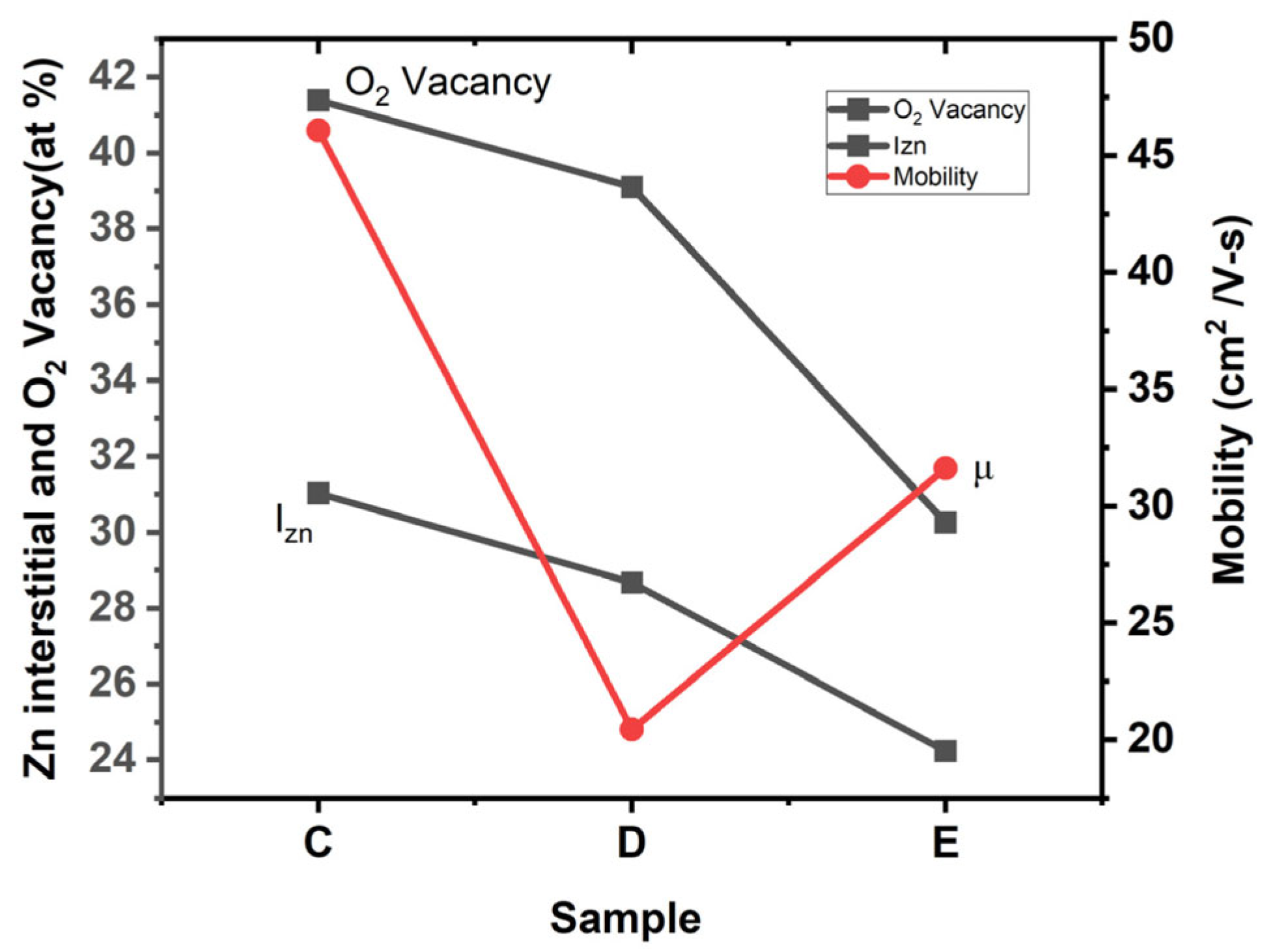
| Method | Operating Parameters | Substrate Temperature * | Growth Rate/Throughput | Morphology Control | Defect Characteristics | References |
|---|---|---|---|---|---|---|
| PLD | Fluence 1–4 J/cm2, p(O2) 10−5–10−1 mbar, 1–10 Hz | RT–700 | 2–9 nm/min | Nanocolumns, c-axis films, thin films, nanorods | Vₒ tunable | [23,24,25,27,40] |
| HiPIMS | Peak current > 1 A/cm2; Ar/O2 mix | RT–500 | 5–20 nm/min | Compact films, textured layers, columnar growth | Controlled Vₒ | [9,49,62,63] |
| Spark/Laser in Liquid | 0.5–3 kV or 1–3 J/cm2 laser, single-pulse | Ambient | 109–1011 part./min | Nanorods, nanosheets, nanowires, clusters | High defect density | [3,4,46,47] |
| MAO | 100–300 V, pulsed discharge | <200 | Variable | Porous oxide layers | High Vₒ, good adhesion | [5,48] |
| Selective Laser Oxidation | Pulsed-periodic laser, Cu–Zn target, air | <700 | 1–4 µm/min (1D nanowires) | Nanowires, nanosheets, 2D patterns | Diffusion-driven Vₒ | [10,45,57] |
| Hybrid (PLD + RFMS/PLD + HiPIMS) | Dual-source; plasma tuning | RT–650 | Tunable | Doped/architectured nanostructures | Complex control | [64,65] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murzin, S.P. Artificial Intelligence-Guided Pulsed Synthesis of Zinc Oxide Nanostructures on Thin Metal Shells. Processes 2025, 13, 3755. https://doi.org/10.3390/pr13113755
Murzin SP. Artificial Intelligence-Guided Pulsed Synthesis of Zinc Oxide Nanostructures on Thin Metal Shells. Processes. 2025; 13(11):3755. https://doi.org/10.3390/pr13113755
Chicago/Turabian StyleMurzin, Serguei P. 2025. "Artificial Intelligence-Guided Pulsed Synthesis of Zinc Oxide Nanostructures on Thin Metal Shells" Processes 13, no. 11: 3755. https://doi.org/10.3390/pr13113755
APA StyleMurzin, S. P. (2025). Artificial Intelligence-Guided Pulsed Synthesis of Zinc Oxide Nanostructures on Thin Metal Shells. Processes, 13(11), 3755. https://doi.org/10.3390/pr13113755






