Data-Driven High-Temperature Superheater Wall Temperature Prediction Using Polar Lights Optimized Kolmogorov–Arnold Networks
Abstract
1. Introduction
1.1. Literature Review
1.2. Contributions of This Work
2. Experiment
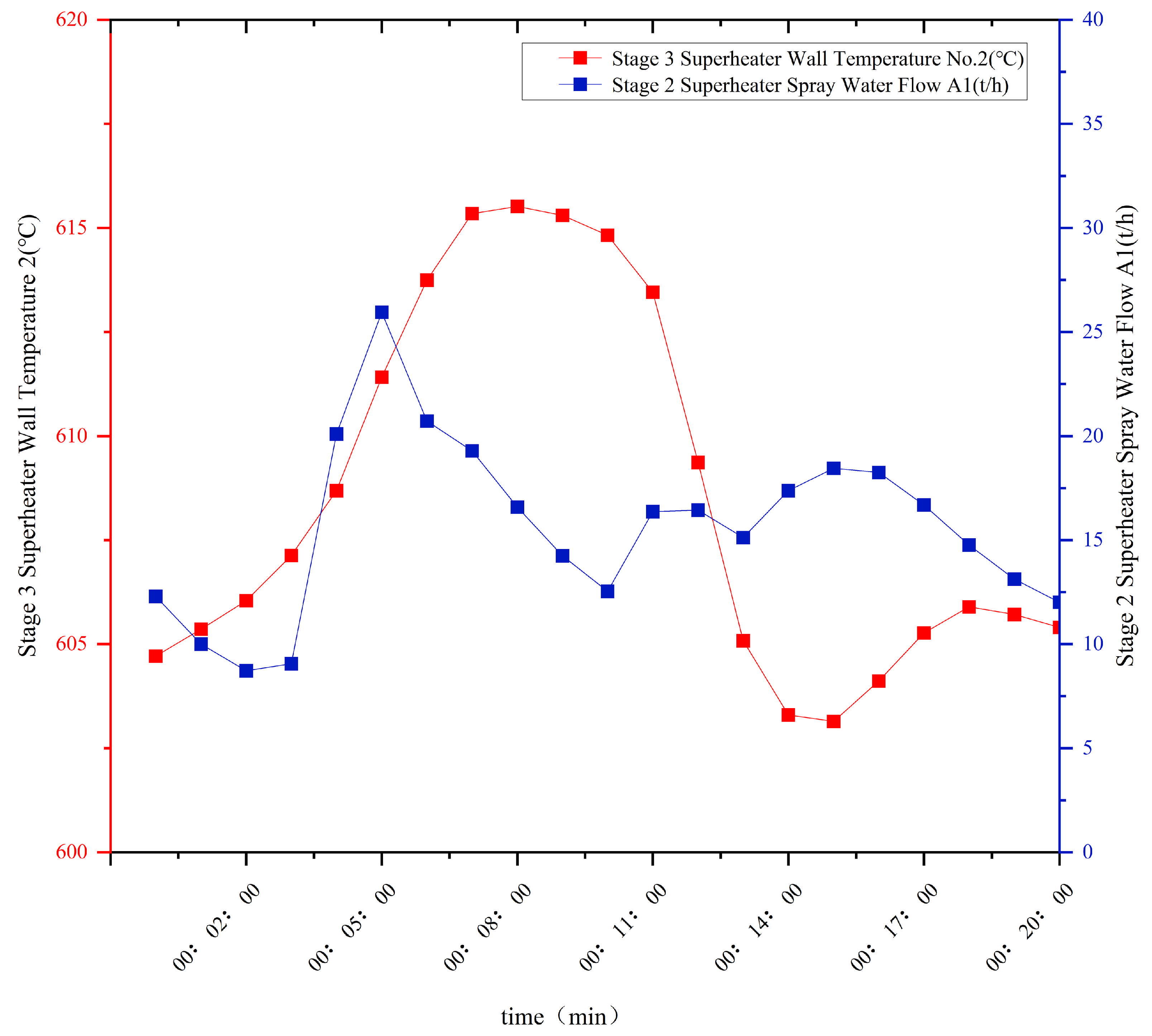
2.1. Data Description
2.2. Data Samples and Pre-Processing
3. Methodology
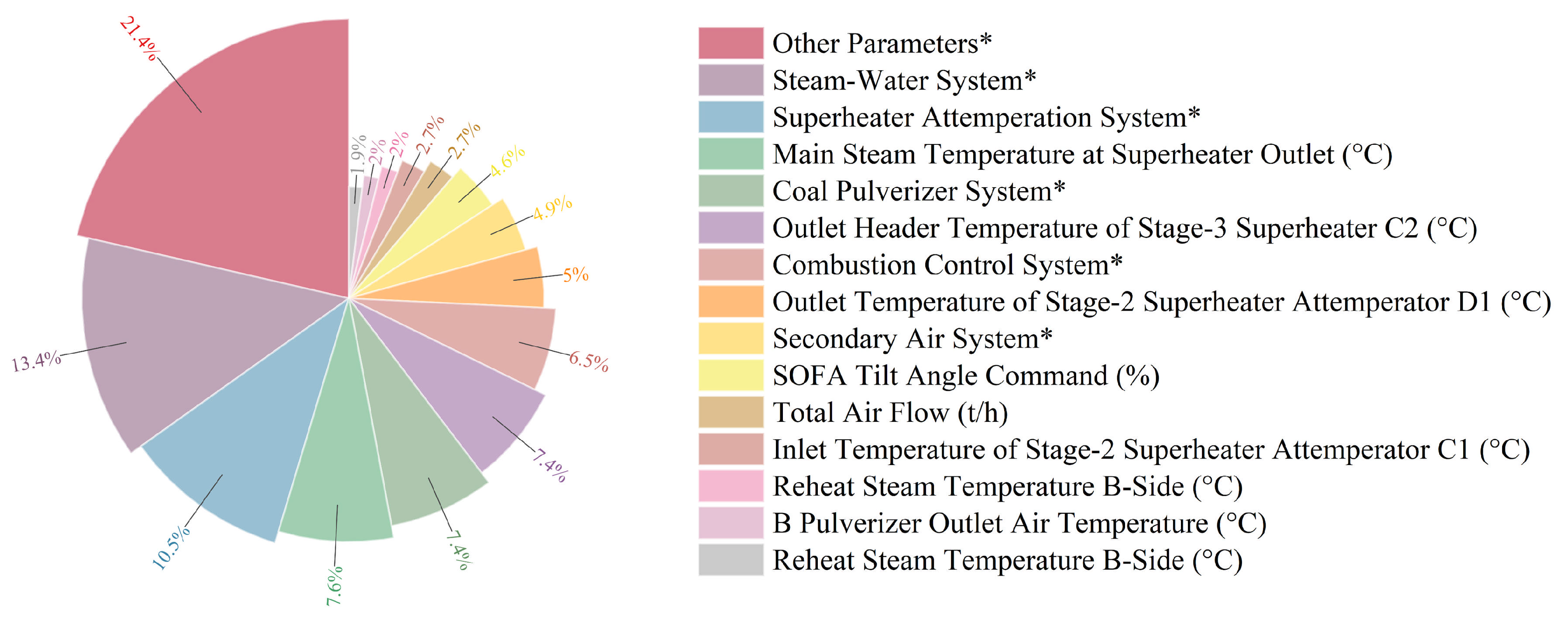
3.1. Random Forest-Based Data Dimension Reduction
3.2. Sliding Window Extraction
3.3. MLPs
3.4. Kolmogorov Arnold Networks
3.5. PLO
- Step 1. Initialization phase
- Step 2. Gyration motion:
- Step 3. Aurora oval walk:
- Step 4. Particle collision:
3.6. KAN Model Hyperparameter Optimization
- Step 1. Define the hyperparameter space
- Step 2. Initialize the auroral particles.
- Step 3. Define the fitness function.
- Step 4. Update the particle positions.
- Step 5. Calculate the light intensities of the particles.
- Step 6. Particle collision.
- Step 7. Update the individual and global optimal positions.
- Step 8. Check the iteration termination condition.
- Step 9. Train the model.
- Step 10. Test the model performance.
3.7. Research Framework
4. Analysis of Experimental Process and Results
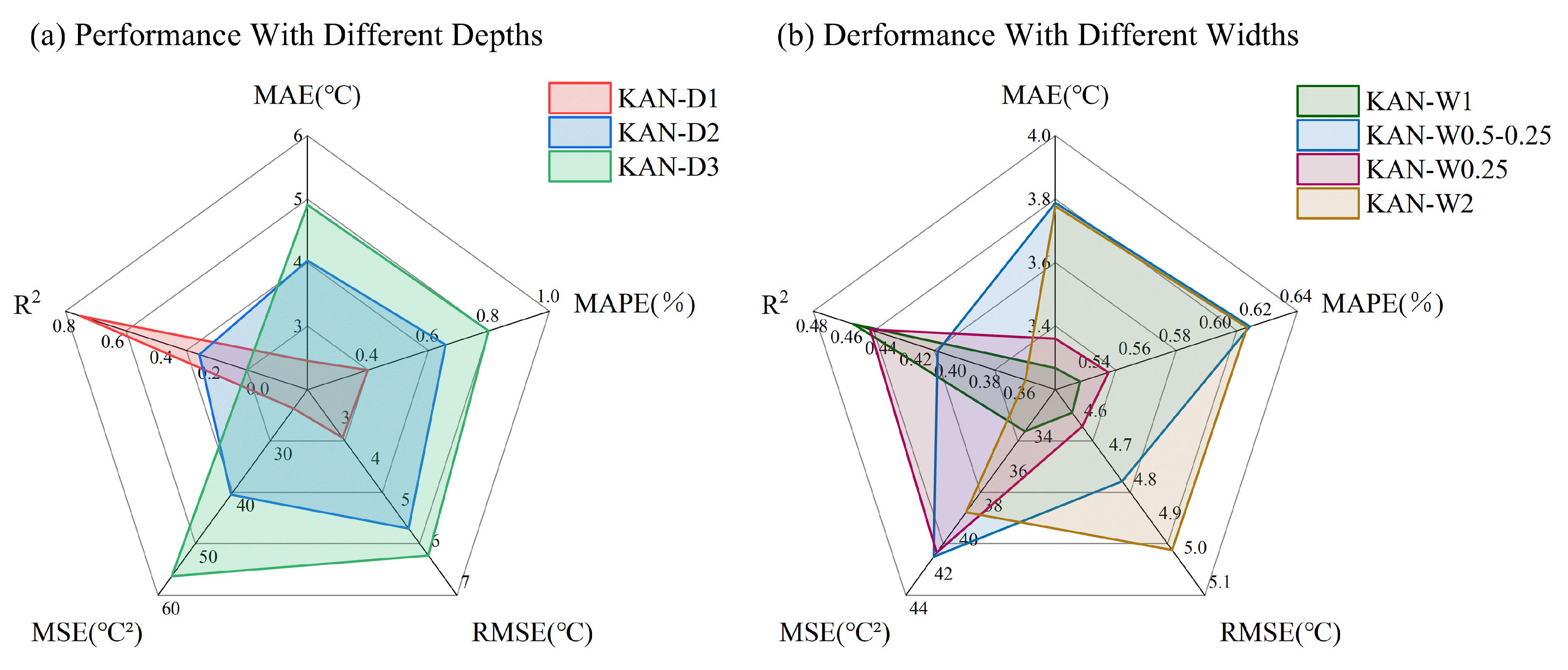
4.1. Structural Analysis: The Effect of Width and Depth on Model Performance
4.1.1. Consistent Hyperparameter Configuration
4.1.2. Canonical KAN Structure and Its Generalization
4.1.3. Experimental Design: Varying Width and Depth
- (1)
- Depth d = 1: Minimal Configuration Without Hidden Layer
- (2)
- Depth d = 2 or 3: With Intermediate Composite Layers
- ➀
- :
- ➁
- , increasing:
- ➂
- , decreasing:
4.1.4. Results and Structural Sensitivity Analysis
4.1.5. Summary and Insights
- (1)
- The depth-1 configuration offers the best trade-off between simplicity and predictive accuracy, especially when the input features are already informative and temporally structured.
- (2)
- The canonical 2n + 1 width remains a stable and effective design choice when used as the final composite layer, validating theoretical expectations.
- (3)
- In deeper networks, progressive expansion of hidden layer widths yields better performance than decreasing-width strategies, though the marginal benefit is limited.
- (4)
- Overall, feature quality and preprocessing outweigh the gains from deeper or wider KAN architectures. Complexity should be introduced only when warranted by the data’s representational demands.
4.2. Hyperparameter Optimization—Polar Lights Optimizer
4.3. Results and Discussions
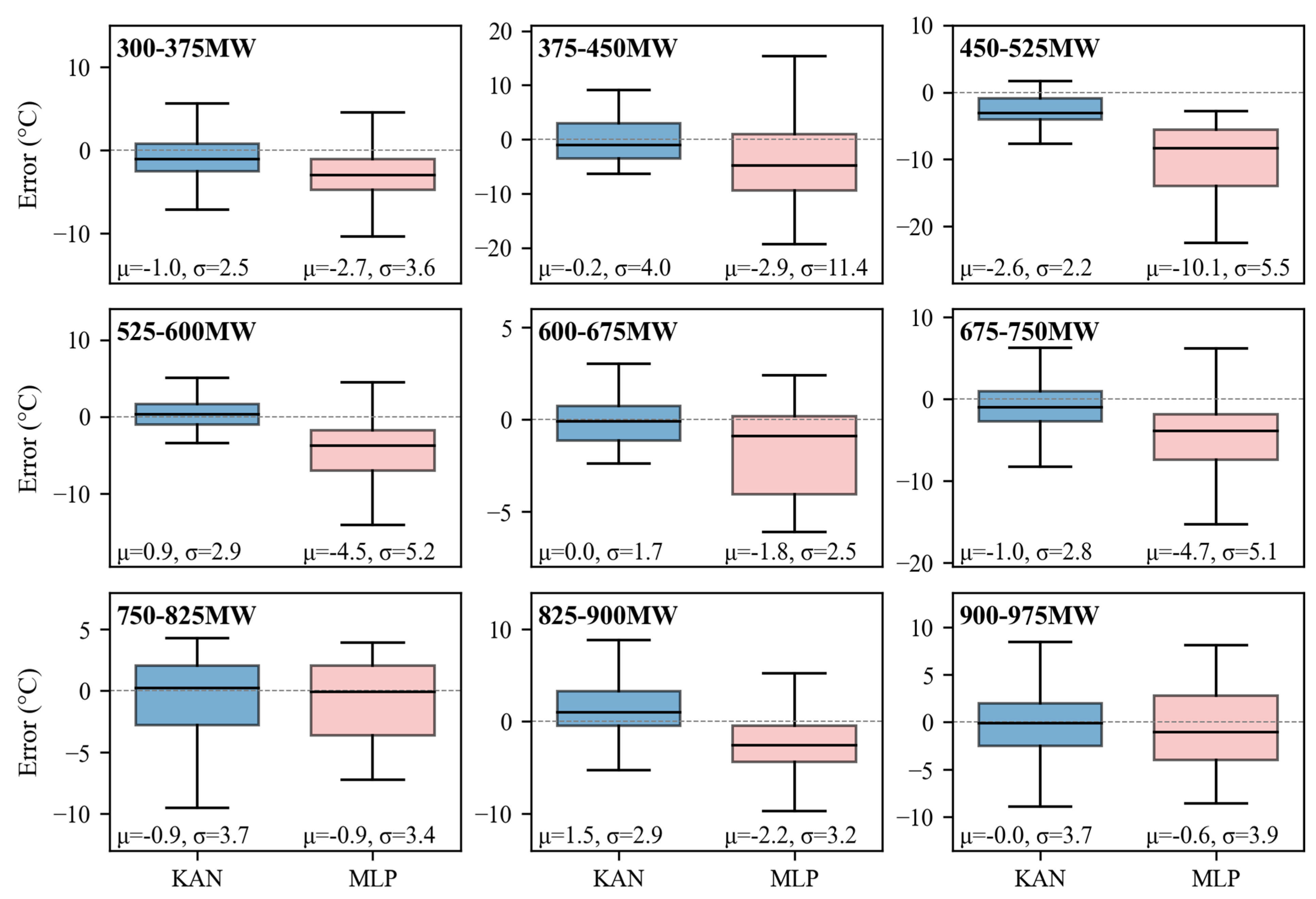
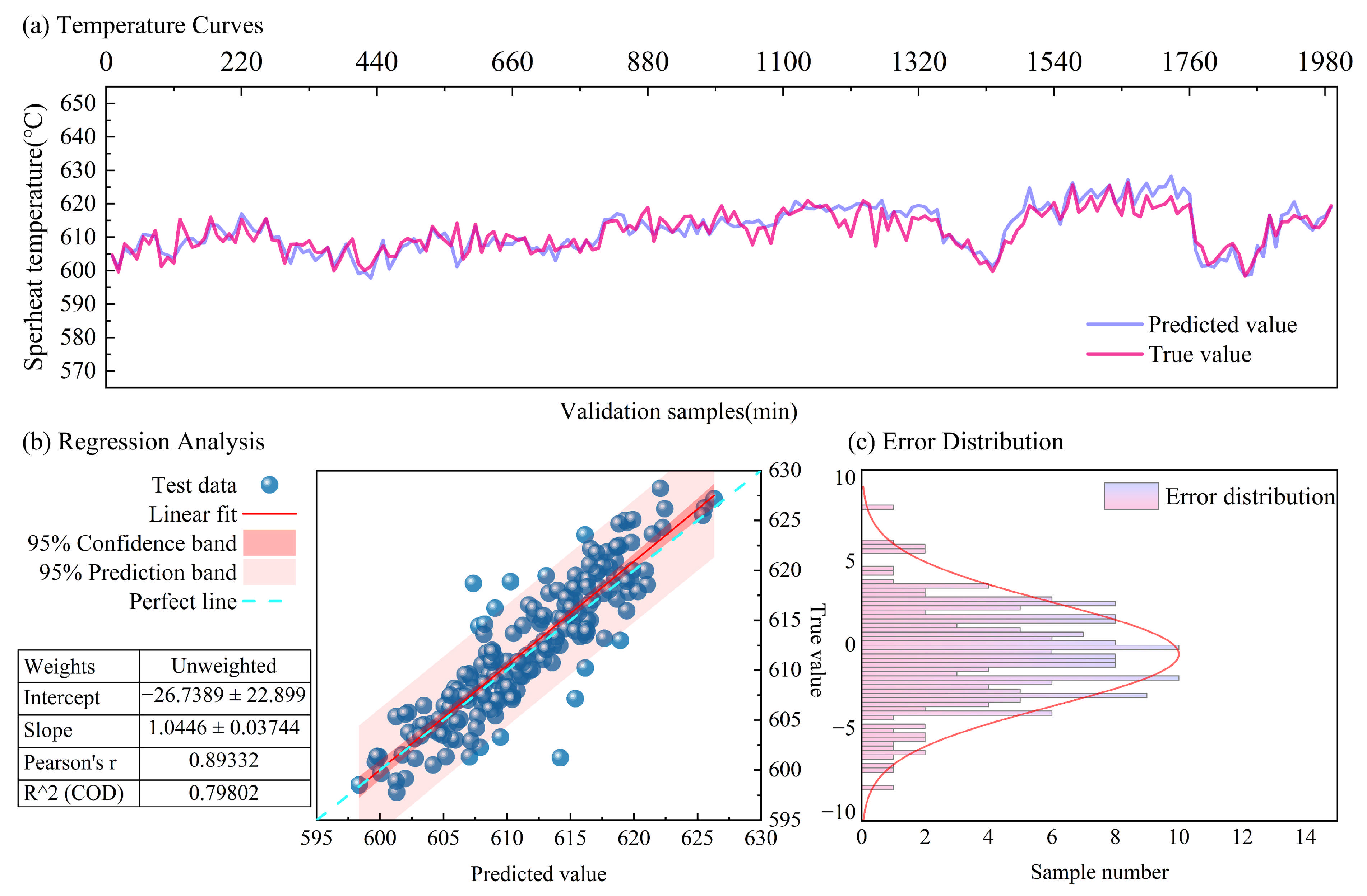
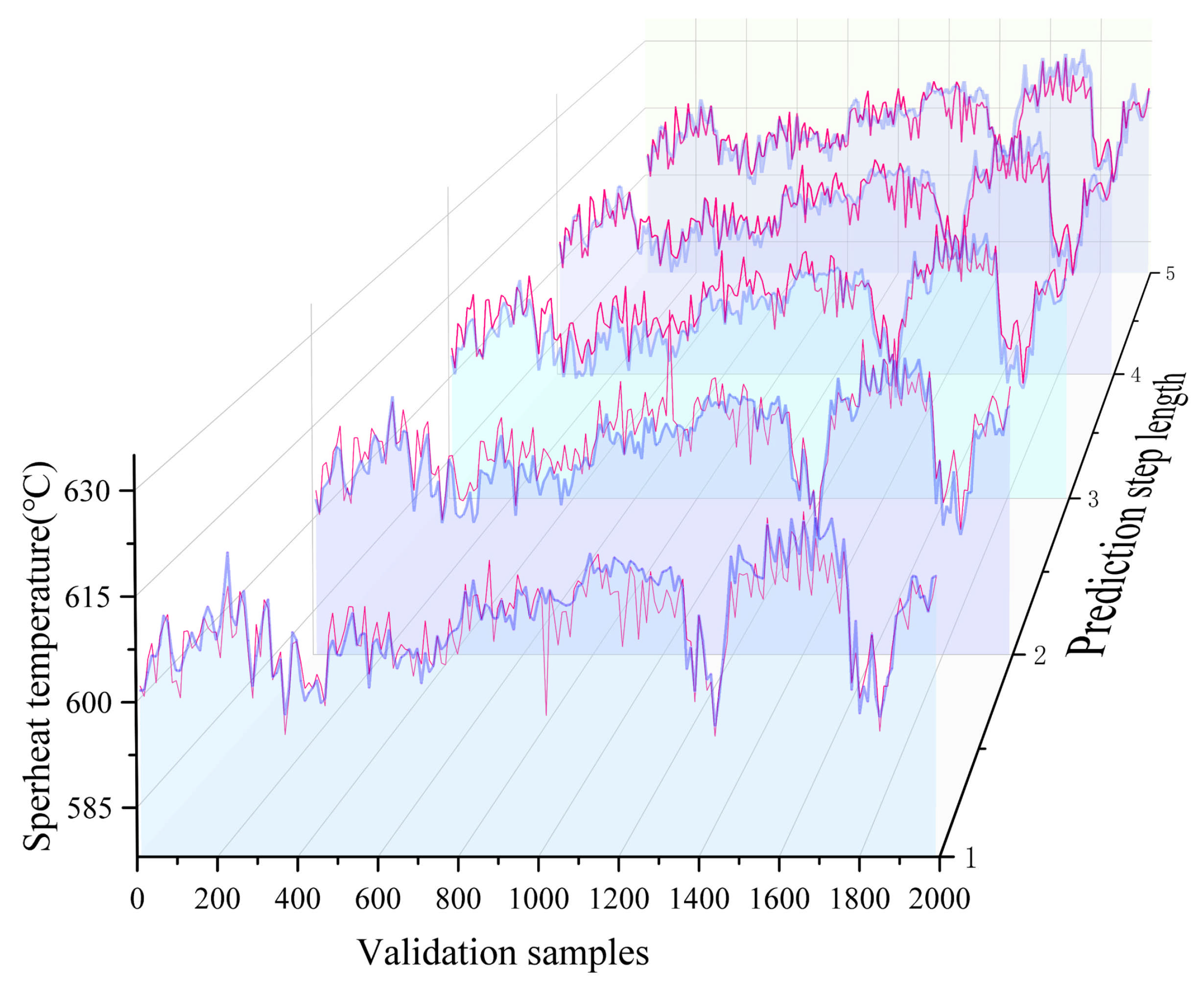
4.3.1. Comparative Analysis of Superheater Wall Temperature Prediction Performance Under Different Load Conditions
4.3.2. Industrial Application
4.3.3. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, S.; Tadge, P.; Mondal, A.; Hussain, N.; Ray, S.; Saha, A. Boiler tube failures in thermal power plant: Two case studies. Mater. Today Proc. 2022, 66, 3847–3852. [Google Scholar] [CrossRef]
- Yin, L.F.; Xie, J.X. Multi-feature-scale fusion temporal convolution networks for metal temperature forecasting of ultra-supercritical coal-fired power plant reheater tubes. Energy 2022, 238, 121657. [Google Scholar] [CrossRef]
- Yan, J.W.; Liu, X.; Huang, S.Y.; Yue, L.; Li, C.; Li, X.Y.; Wei, J.; Fu, J.; Li, W.J.; Wang, H.Y. Coupled model for prediction of water wall tube temperature of supercritical boiler. Therm. Power Gener. 2022, 51, 100–108. [Google Scholar] [CrossRef]
- Zhu, B.W.; Si, F.Q.; Dong, Y.S. Study on Tube Metal Temperature Distribution Characteristics of Final Superheater of Coal-Fired Boiler Based on CFD. Boil. Technol. 2024, 55, 13–20. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, T.; Lu, J.; Wu, Y.; Zhang, T.; Ma, Y. Numerical simulation research on heat transfer characteristics of platen superheater of 660 MW coal-fired boiler. Meitan Xuebao/J. China Coal Soc. 2022, 47, 3860–3869. [Google Scholar] [CrossRef]
- Yu, Y.X.; Liao, H.K.; Wu, Y.L.; Zhong, W. Study on Tube Wall Temperature of Power Plant Boilers Based on Coupled Thermal Hydraulic Analysis. J. Chin. Soc. Power Eng. 2015, 35, 1–7. [Google Scholar] [CrossRef]
- Yu, C.; Si, F.Q.; Li, M.; Wu, H.L. Study on Overtemperature of Boiler Steam Tube base on Coupling Model of Combustion and Hydrodynamic. J. Eng. Therm. Energy Power 2021, 36, 92–98. [Google Scholar] [CrossRef]
- Jin, D.H.; Liu, X.; Zhang, X.Y.; Shen, Y.; Wang, T.; Li, C.; Li, X.Y.; Wei, J.; Fu, J.; Wang, H.Y. A Coupled Model for Predicting the Tube Temperature of Platen Superheater of Coal-fired Boiler. Proc. CSEE 2022, 42, 8951–8961. [Google Scholar] [CrossRef]
- Madejski, P.; Taler, D.; Taler, J. Thermal and flow calculations of platen superheater in large scale CFB boiler. Energy 2022, 258, 124841. [Google Scholar] [CrossRef]
- Cui, Z.P.; Xu, J.; Liu, W.H.; Zhao, G.J.; Ma, S.X. Data-driven modeling-based digital twin of supercritical coal-fired boiler for metal temperature anomaly detection. Energy 2023, 278, 127959. [Google Scholar] [CrossRef]
- Cao, Y.Y.; Mao, D.J.; Chen, S.Q. Boiler Heating Surface Wall Temperature Prediction based on TCN-Attention-BiGRU. Comput. Simul. 2025, 42, 91–98. Available online: https://link.cnki.net/urlid/11.3724.tp.20240328.1028.008 (accessed on 1 September 2025).
- Lu, B.; Liu, X.; Gao, L.; Zhao, X.L. Prediction model of boiler platen superheater tube wall temperature based on NARX neural network. Therm. Power Gener. 2019, 48, 35–40. [Google Scholar] [CrossRef]
- Laubscher, R. Time-series forecasting of coal-fired power plant reheater metal temperatures using encoder-decoder recurrent neural networks. Energy 2019, 189, 116187. [Google Scholar] [CrossRef]
- Wei, X.B.; Cui, Z.P.; Xu, J.; Ma, S.X. Data-driven method for predicting the wall temperature of heating surface of supercritical boilers. Therm. Power Gener. 2023, 52, 106–112. [Google Scholar] [CrossRef]
- Fan, Y.C.; Zhou, Y.Q.; Wei, C.; Liu, X.; Wang, H.Y. Data-driven Modeling for Over-temperature Prediction of Platen Superheater in Coal-fired Boiler. Proc. CSEE 2025, 1–11. [Google Scholar] [CrossRef]
- Yan, X.C.; Cao, H.; Hua, Y.P. Prediction on tube wall temperatures of boiler heating surfaces based on artificial intelligence. Integr. Intell. Energy 2022, 44, 58–62. [Google Scholar] [CrossRef]
- Sha, X.; Huang, Q.; Liu, G.Q.; Li, S.Q. Time Series Analysis of Monitored Heating Surface Wall Temperature of Coal-Fired Boiler. J. Combust. Sci. Technol. 2021, 27, 475–481. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. Comput. Sci. 2014, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, W.Y.; Li, K.Y.; Tang, Z.H.; Liu, Y.; Zhang, F.; Cao, S.X.; Peng, X.Y.; Wu, E.Q.; Zhou, H.C. Dynamic combustion optimization of a pulverized coal boiler considering the wall temperature constraints: A deep reinforcement learning-based framework. Appl. Therm. Eng. 2025, 259, 124923. [Google Scholar] [CrossRef]
- Chen, W.H.; Zhai, C.H.; Wang, X.; Li, J.; Lv, P.B.; Liu, C. GCN- and GRU-Based Intelligent Model for Temperature Prediction of Local Heating Surfaces. IEEE Trans. Ind. Inform. 2023, 19, 5517–5529. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljacic, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2025, arXiv:2404.19756. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H.L. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
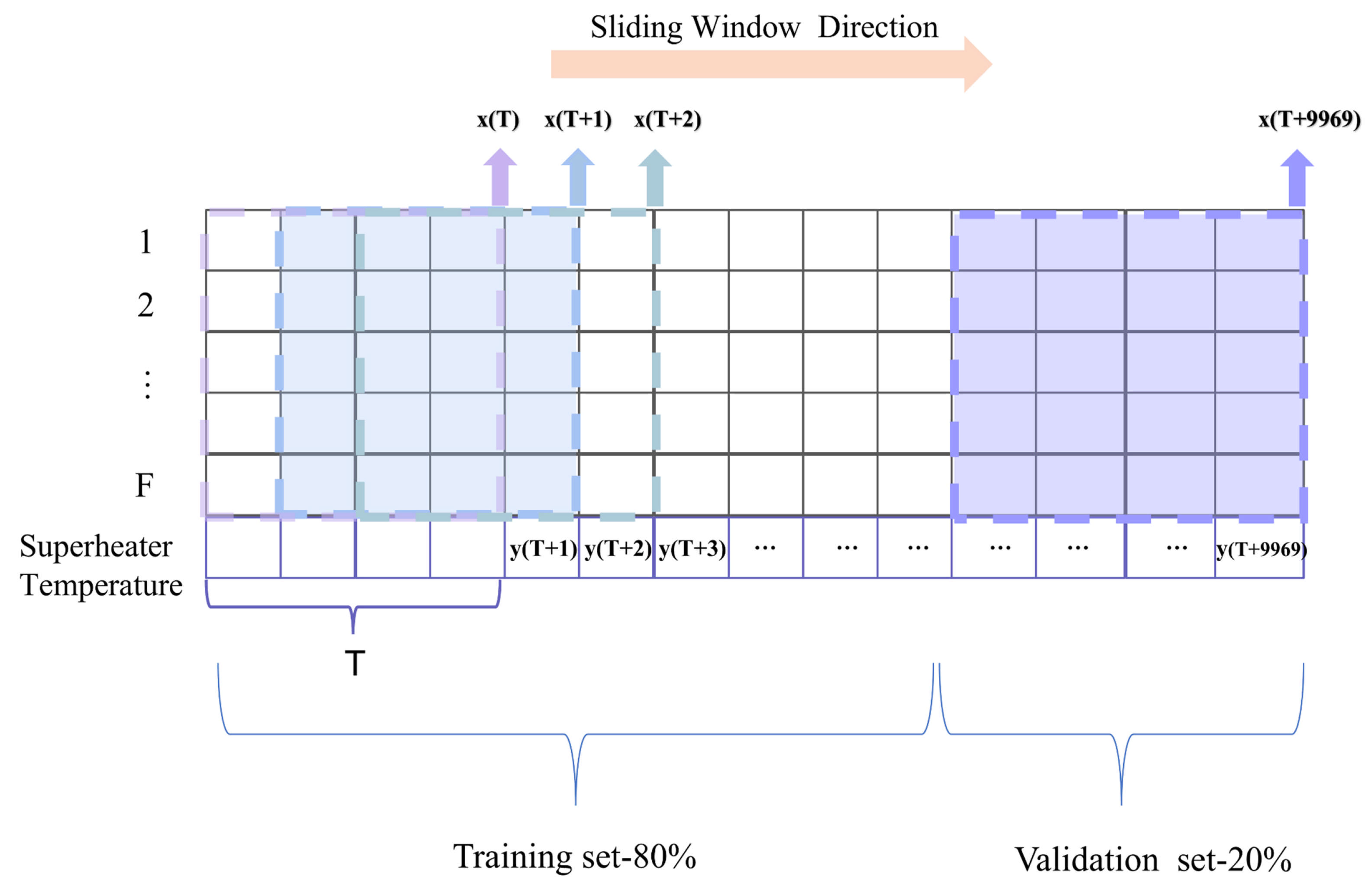
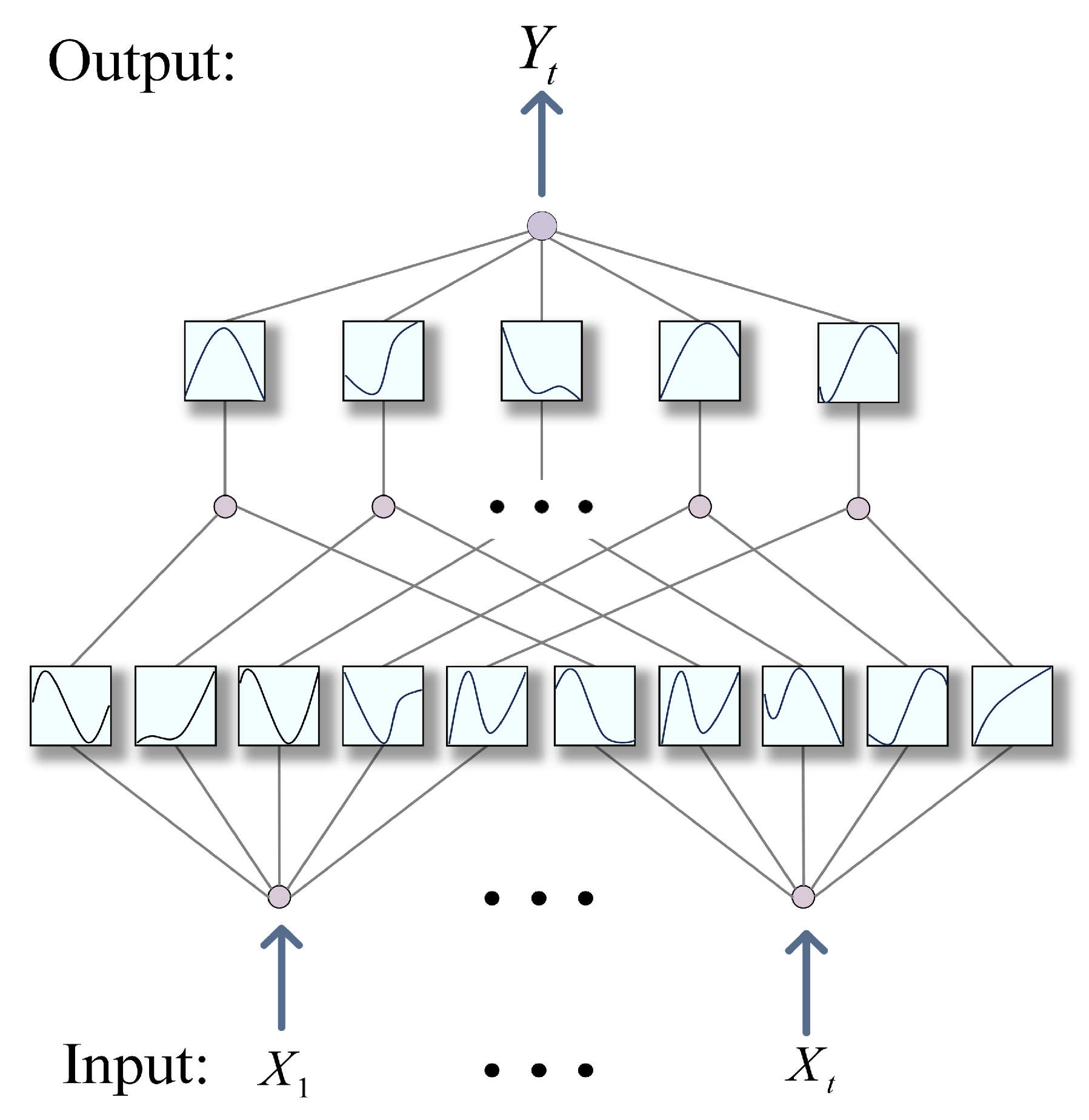
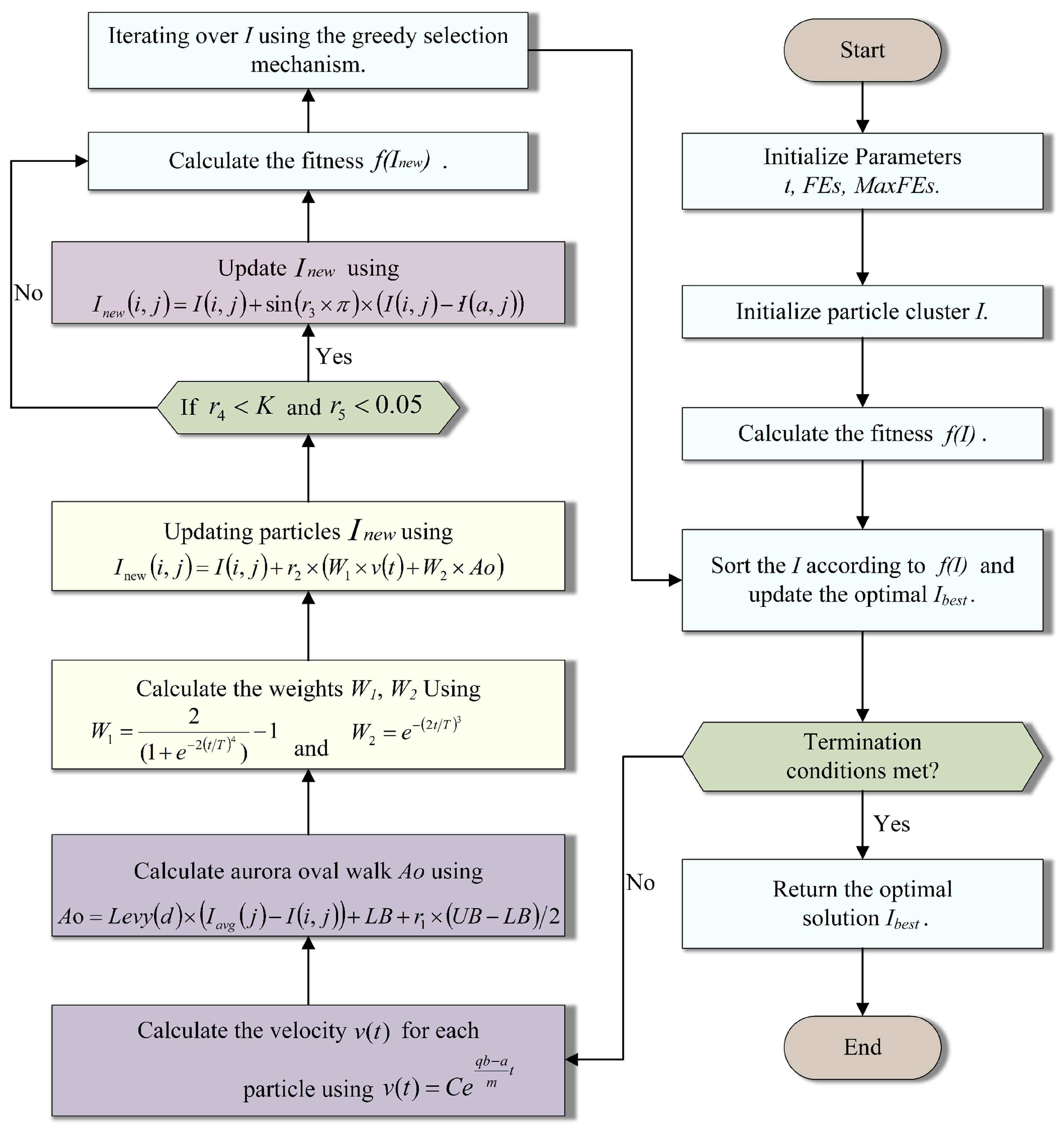
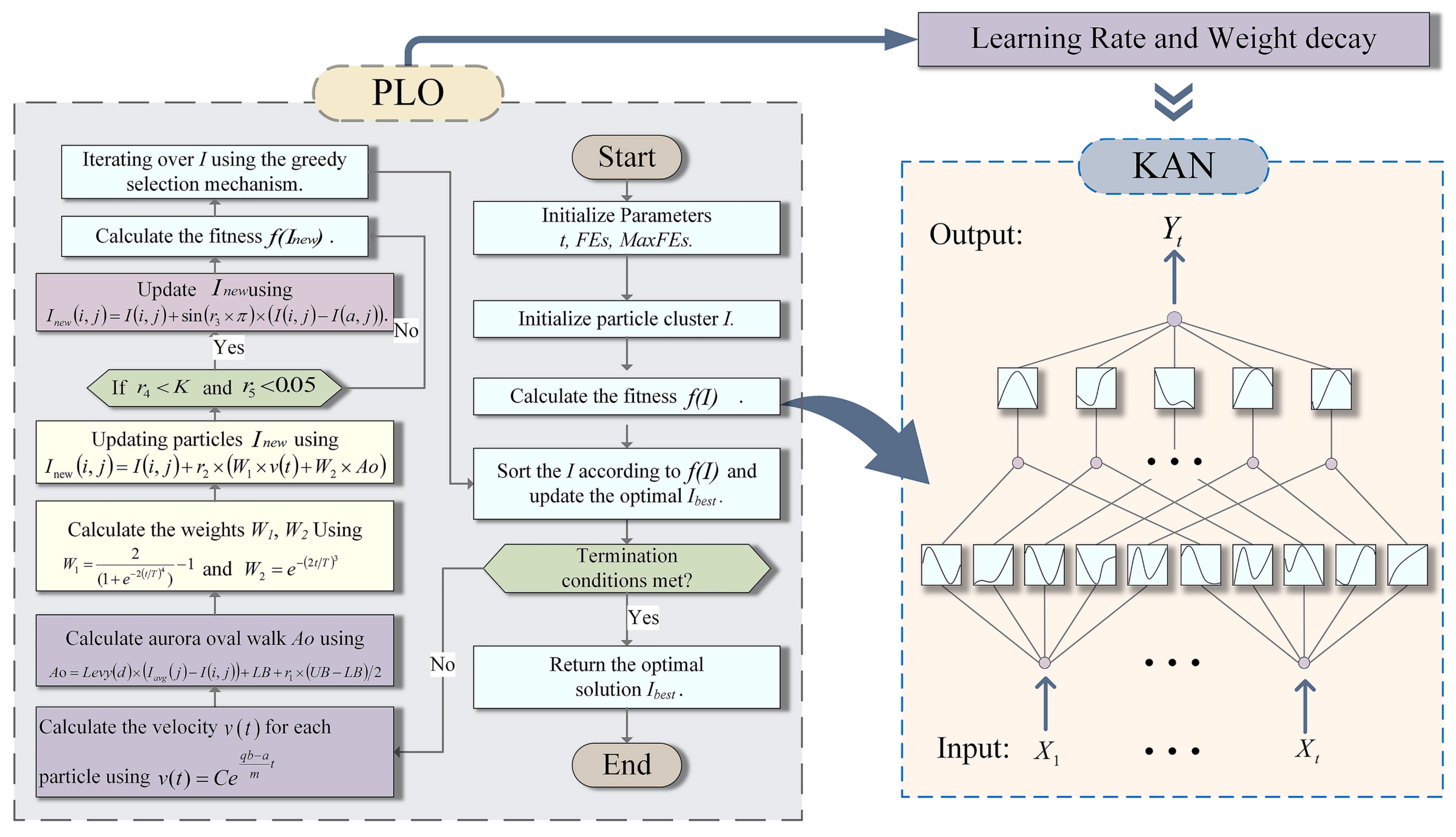
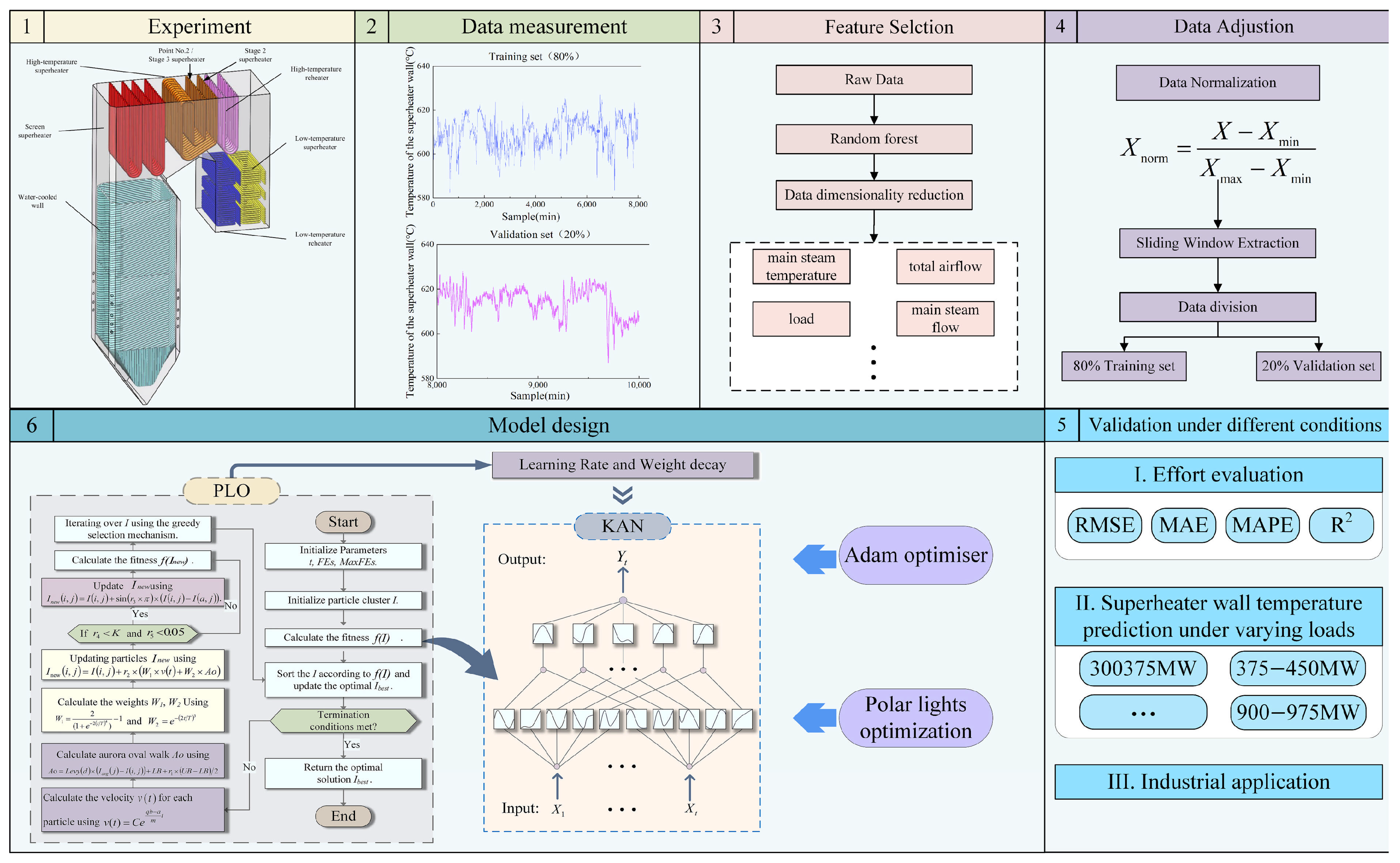
| Steps | Sliding Window (X, T, S): |
|---|---|
| 1 | Initialize the set of subsequences |
| 2 | Window list = Empty list |
| 3 | Calculate the number of subsequences |
| 4 | P = (L − T)/S + 1 |
| 5 | Sliding window to extract subsequences |
| 6 | Do this for i from 0 to (L − T) per stride S: |
| 7 | Extract the segment in the current window |
| 8 | subsequences = X[i : i + T, :] |
| 9 | list add(subsequences) |
| 10 | Return all subsequences |
| 11 | Return list |
| No. | Particle ID | Learning Rate | Weight Decay | MSELoss |
|---|---|---|---|---|
| 1 | 148 | 0.01 | 0.0001 | 23.6846 |
| 2 | 75 | 0.052254 | 0.001 | 58.0932 |
| 3 | 25 | 0.1 | 0.00001 | 61.7773 |
| 4 | 32 | 0.045572 | 0.001 | 64.2408 |
| 5 | 3 | 0.041683 | 0.000954 | 66.2496 |
| 6 | 33 | 0.050921 | 0.000204 | 66.7475 |
| 7 | 31 | 0.093318 | 0.000597 | 68.8121 |
| 8 | 29 | 0.029949 | 0.00001 | 67.3473 |
| 9 | 4 | 0.026770 | 0.000684 | 67.9020 |
| 10 | 1 | 0.025603 | 0.000193 | 68.2937 |
| 11 | 125 | 0.1 | 0.001 | 69.0940 |
| 12 | 138 | 0.1 | 0.001 | 69.8976 |
| 13 | 28 | 0.039075 | 0.000716 | 74.3549 |
| 14 | 83 | 0.033189 | 0.001 | 73.3565 |
| 15 | 17 | 0.023591 | 0.00069 | 73.2457 |
| 16 | 26 | 0.028786 | 0.001 | 73.6511 |
| 17 | 50 | 0.051736 | 0.001 | 74.5700 |
| 18 | 44 | 0.014410 | 0.001 | 74.0408 |
| 19 | 41 | 0.081173 | 0.001 | 74.4267 |
| 20 | 10 | 0.085660 | 0.00001 | 73.5209 |
| 21 | 146 | 0.041680 | 0.001 | 76.8735 |
| 22 | 22 | 0.015276 | 0.000967 | 76.4326 |
| 23 | 18 | 0.065241 | 0.000123 | 76.6444 |
| 24 | 45 | 0.059852 | 0.00001 | 77.7496 |
| 25 | 77 | 0.036008 | 0.001 | 78.8363 |
| 26 | 15 | 0.065748 | 0.000273 | 79.0833 |
| 27 | 37 | 0.046156 | 0.001 | 79.5514 |
| 28 | 30 | 0.038632 | 0.000443 | 79.6732 |
| 29 | 5 | 0.087169 | 0.000492 | 78.5241 |
| 30 | 20 | 0.086154 | 0.00001 | 82.9460 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wang, Y.; Yang, G.; Han, C.; Gao, J.; Xu, S.; Yin, G.; Tian, X.; Wang, Z.; Peng, X. Data-Driven High-Temperature Superheater Wall Temperature Prediction Using Polar Lights Optimized Kolmogorov–Arnold Networks. Processes 2025, 13, 3741. https://doi.org/10.3390/pr13113741
He Z, Wang Y, Yang G, Han C, Gao J, Xu S, Yin G, Tian X, Wang Z, Peng X. Data-Driven High-Temperature Superheater Wall Temperature Prediction Using Polar Lights Optimized Kolmogorov–Arnold Networks. Processes. 2025; 13(11):3741. https://doi.org/10.3390/pr13113741
Chicago/Turabian StyleHe, Zhiqian, Yuhan Wang, Guangmin Yang, Chen Han, Jia Gao, Shiming Xu, Ge Yin, Xuefeng Tian, Zhi Wang, and Xianyong Peng. 2025. "Data-Driven High-Temperature Superheater Wall Temperature Prediction Using Polar Lights Optimized Kolmogorov–Arnold Networks" Processes 13, no. 11: 3741. https://doi.org/10.3390/pr13113741
APA StyleHe, Z., Wang, Y., Yang, G., Han, C., Gao, J., Xu, S., Yin, G., Tian, X., Wang, Z., & Peng, X. (2025). Data-Driven High-Temperature Superheater Wall Temperature Prediction Using Polar Lights Optimized Kolmogorov–Arnold Networks. Processes, 13(11), 3741. https://doi.org/10.3390/pr13113741






