Abstract
Cis-1,1,1,4,4,4-hexafluoro-2-butene (R1336mzz(Z)) is a highly promising alternative refrigerant, particularly in heat pumps with large temperature lifts. To meet the superheat requirement of R1336mzz(Z), the heat pump system typically requires the installation of an internal heat exchanger, which renders system performance more sensitive to the solubility of the refrigerant in lubricant. Dipentaerythritol ester (DiPEC) is one of the main components of POE lubricants. In this study, the solubilities of R1336mzz(Z) in two DiPECs, dipentaerythritol hexaheptanoate (DiPEC7) and dipentaerythritol isononanoate (DiPEiC9), were measured in the temperature range of 293.15 K–343.15 K. The solubility data were correlated using the non-random two-liquid (NRTL) model; the average absolute relative deviation between this work and values from NRTL model is lower than 2%. In addition, the Henry’s constants of R1336mzz(Z) in DiPEC7 and DiPEiC9 were calculated, and the dissolution potential was compared. Moreover, the mixing thermodynamic properties (such as mixing enthalpy change, mixing entropy change, and mixing Gibbs free energy change) of R1336mzz(Z) dissolving in DiPECs were analyzed.
1. Introduction
The Kigali Amendment to the Montreal Protocol has provided significant guidance for global environmental governance and has currently been endorsed by 197 parties. Since the amendment entered into force on 1 January 2019, the clear timetable has accelerated the phase-out of refrigerants with high global warming potential (GWP) [1,2,3,4]. In the field of industrial heat pumps, traditional refrigerants, represented by R245fa (GWP = 1030), are required to be gradually phased out due to their high environmental impact. Hydrofluoroolefin (HFO) refrigerants, relying on their low GWP, have become the primary alternative solution [5]. Among them, cis-1,1,1,4,4,4-hexafluoro-2-butene (R1336mzz(Z), GWP = 2) is a highly promising alternative refrigerant for heat pumps and organic Rankine cycles [6,7,8]. R1336mzz(Z) features a critical temperature of 444.5 K, which enables it to fully meet the operational requirements of high-temperature heat pumps, thus demonstrating considerable application potential in the food drying and chemical processing industries. Furthermore, its A1 safety classification and excellent high-temperature chemical stability ensure the safety of R1336mzz(Z) in practical applications. At present, comprehensive research has been conducted on the basic thermophysical properties of R1336mzz(Z), including critical parameters [7], saturated vapor pressure [9], specific heat capacity [10], viscosity [11], and thermal conductivity [12,13].
For vapor compression heat pumps, the effect of compressor lubricants deserves attention. Elevated operating temperatures may cause lubricant carbonization or a significant decrease in viscosity. Polyol ester (POE) lubricants are suitable for high-temperature heat pumps, as their core component exhibits high thermal stability and a wide viscosity range [14]. Pentaerythritol ester (PEC) and dipentaerythritol ester (DiPEC) are the main components of POE lubricants. Generally speaking, the increase in the number of ester groups in PEC or DiPEC leads to an increase in viscosity [15]. PECs typically have a kinematic viscosity of 10–30 mPa·s at 40 °C [16], while DiPECs exceed 50 mPa·s at 40 °C [17]. The introduction of branched structures can also significantly increase the viscosity of polyol esters. As an example, the kinematic viscosity of dipentaerythritol isononanoate (one of the branched esters) at 40 °C exceeds 390 mPa·s [18,19]. Beyond the intrinsic properties of lubricants, the miscibility between R1336mzz(Z) and polyol esters is also of importance because the miscibility not only drastically alters the lubricant viscosity [20,21] but also degrades the heat transfer capability of R1336mzz(Z) [22]. In addition, understanding the solubility of R1336mzz(Z) in polyol esters enables the optimization of heat pumps. However, to the best of our knowledge, only Brocus et al. measured the solubility of R1336mzz(Z) in POE SE220 [23]; no other measurements have been reported yet.
To fill the gap, in this work, the solubility of R1336mzz(Z) in dipentaerythritol hexaheptanoate (DiPEC7) and dipentaerythritol isononanoate (DiPEiC9) was measured using the isochoric saturation method from 293.15 K to 343.15 K. Based on the solubility data, the deviations of the two mixtures from Raoult’s law were calculated. The non-random two-liquid (NRTL) model was employed to calculate the mole fraction of R1336mzz(Z) in DiPECs. The mixing thermodynamic properties of the mixtures were calculated and analyzed.
2. Experimental Method
2.1. Experimental Samples
The refrigerant (R1336mzz(Z)) was provided by Honeywell, and the DiPEC7 and DiPEiC9 used in present work were supplied by MingKT Corporation. Table 1 presents the basic information of the materials. Figure 1 and Figure 2 show the molecular structures of R1336mzz(Z) and the DiPECs.

Table 1.
Basic information on the materials.
Figure 1.
Molecular structure of R1336mzz(Z).
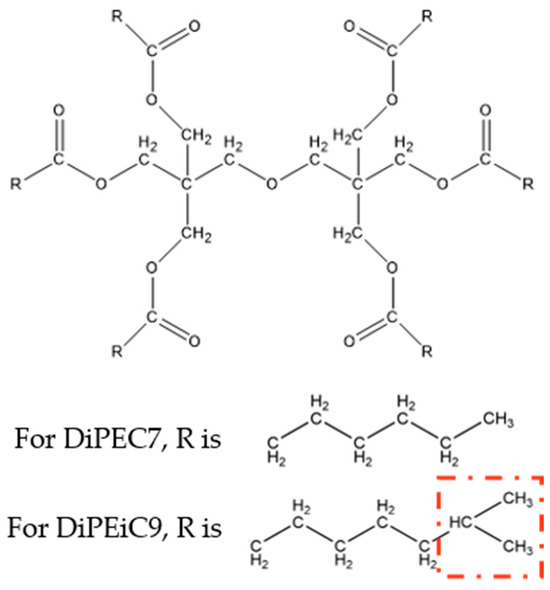
Figure 2.
Molecular structures of DiPEC7 and DiPEiC9.
2.2. Experimental Setup
García et al. measured the saturated vapor pressures of DiPEC7 and DiPEiC9 [15], and their values are almost negligible compared with those of refrigerants. Therefore, the isochoric saturation method was used to measure the solubility of R1336mzz(Z) in DiPEC7 and DiPEiC9. Figure 3 presents the schematic diagram of the experimental system. As the experimental apparatus and procedures have been described in detail in our previous reports [24,25], only a brief introduction is provided here.
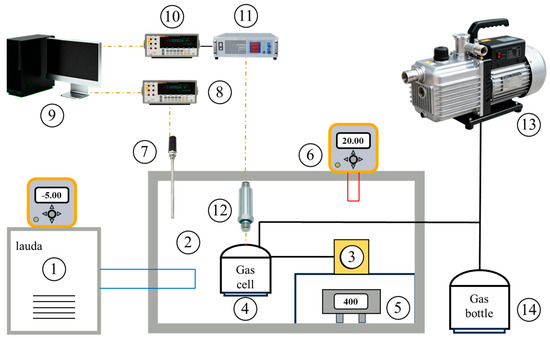
Figure 3.
Schematic diagram of the solubility experimental system. ① Cooling bath, ② thermostat bath, ③ equilibrium cell, ④ gas cell, ⑤ magnetic stirrer, ⑥ temperature controller, ⑦ thermometer, ⑧ digital multimeter, ⑨ data acquisition computer, ⑩ multimeter, ⑪ DC power, ⑫ pressure transducer, ⑬ vacuum pump, ⑭ gas bottle.
Preceding the experiment, the refrigerant R1336mzz(Z) was introduced into the gas cell. A precision balance (Mettler Toledo, Zurich, Switzerland; Model: ME204, accuracy: ±0.0002 g) was used to weigh the DiPEC lubricant, which was then placed into the equilibrium cell. The calibrated volumes of the gas cell and equilibrium cell were determined to be 103.60 ± 0.02 cm3 and 33.37 ± 0.02 cm3, respectively. Upon opening the valve connecting the gas cell and equilibrium cell, the R1336mzz(Z) flowed into the equilibrium cell and dissolved in the lubricant. The system pressure exhibited a gradual decrease due to gas dissolution, and the pressure drop was utilized to compute the solubility of the R1336mzz(Z) in DiPECs. Temperature measurements were performed with a platinum resistance thermometer (Fluke, Everett, USA; Model: 5608,accuracy: 0.01 K), while pressure was measured using a pressure transducer (Keller, Winterthur, Switzerland; Model: 33X, accuracy: 0.03% FS, range: 0–3 MPa). In this work, the expanded uncertainties for temperature and pressure measurements were less than 0.02 K and 2.0 kPa (k = 2), respectively.
The solubility of R1336mzz(Z) in DiPECs is expressed in two forms in this work: mole fraction (x1) and mass fraction (w1). Equations (1) and (2) are used to calculate x1 and w1, respectively:
In all formulas used in this work, the subscripts “1” and “2” denote R1336mzz(Z) and DiPECs, respectively. n and M represent the number of moles and molar mass. n2 can be directly calculated using n2 = m2/M2, while n1 is obtained by solving Equations (3) and (4) simultaneously:
and
In Equations (3) and (4), superscripts “0” and “1” denote the initial and equilibrium states. Vgc and Vec represent the volumes of the gas cell and the equilibrium cell, respectively. V2 is the volume of the DiPECs and is calculated by V2 = m2/ρ2; ρ2 is obtained from Ref. [19]. represents the liquid density of R1336mzz(Z), which has been reported by Sun et al. [26].
In accordance with the principle of uncertainty propagation [27], the experimental uncertainty of solubility measurement Uexp(x1) can be calculated. Equation (5) shows the expression for uncertainty propagation:
where k is the coverage factor (k = 2). Table 2 lists the uncertainty associated with each parameter in Equation (5).

Table 2.
Uncertainties of various parameters.
In Equation (3), the volume change of DiPECs in an equilibrium cell after absorption is only considered as the volume of dissolved saturated liquid R1336mzz(Z), and the excess molar volume (VE) of the R1336mzz(Z)/DiPECs mixture is not included. According to the results reported by Goharshadi et al. [28] and Comuñas et al. [29], the excess molar volume of refrigerants dissolved in organic solvents is typically less than 10 cm3/mol. Considering the VE, Equation (3) can be rewritten as follows:
By comparing the calculated mole fraction using Equations (3) and (6), the uncertainty induced by the excess molar volume UVE(x1) can be determined. Subsequently, the combined expanded uncertainty of the mole fraction U(x1) can be calculated:
Calculated results show that the values for the combined expanded relative uncertainty of the mole fraction Ur(x1) are 2.72% for the R1336mzz(Z)/DiPEC7 mixture and 2.85% for the R1336mzz(Z)/DiPEiC9 mixture, respectively.
2.3. NRTL Model
In this work, the experimental solubility data of R1336mzz(Z) in DiPEC7 and DiPEiC9 were correlated based on the non-random two-liquid (NRTL) activity coefficient model. For the studied systems, the refrigerant R1336mzz(Z) at the equilibrium state can be described by the following equation [30]:
where is the vapor pressure of R1336mzz(Z), which was reported by Sacoda et al. [10]. y represents the mole fraction in gas phase. E is the enhancement factor, which is calculated using Equation (9):
In Equation (9), ζ1 is the Poynting correction factor. and are the fugacity coefficients of R1336mzz(Z) at the equilibrium state and at the saturated state, which can be calculated as follows:
and
where R is the universal gas constant, with a value of 8.31446 J·mol−1·K−1. B is the second virial coefficient of the mixture, which is calculated as follows [31]:
where B11 and B22 are the second virial coefficients of R1336mzz(Z) and DiPECs, respectively. B12 is the second virial coefficient resulting from the mixing process. Because y1 = 1 and y2 = 0, B = B11. B11 was obtained from REFPROP 10.0 [32].
In the NRTL model, γ1 can be calculated as follows [33]:
In Equation (13), α is the non-randomness parameter, which is considered to be 0.2 here. τ12 and τ21 are the binary interaction parameters which are considered as a function of temperature T:
and
where τ12,0, τ12,1, τ12,2, τ21,0 τ21,1, and τ21,2 are the adjustable parameters and can be obtained via the regression of the experimental solubility data.
3. Experimental Results and Discussion
3.1. Experimental Data and Correlation
Table 3 and Table 4 list the mole fraction (x1) values of R1336mzz(Z) in DiPEC7 and DiPEiC9 over the temperature range of 293.15 to 343.15 K. For practical application purpose, the mass fractions (w1) of R1336mzz(Z) in DiPECs are also given in Table 3 and Table 4. Figure 4 and Figure 5 show the effects of temperature and pressure on the mole fraction x1. As expected, the mole fractions of R1336mzz(Z) in DiPEC7 and DiPEiC9 increase with decreasing temperature and increasing pressure.

Table 3.
p-T-x (w) data of R1336mzz(Z) (1) in DiPEC7 (2) a.

Table 4.
p-T-x (w) data of R1336mzz(Z) (1) in DiPEiC9 (2) a.
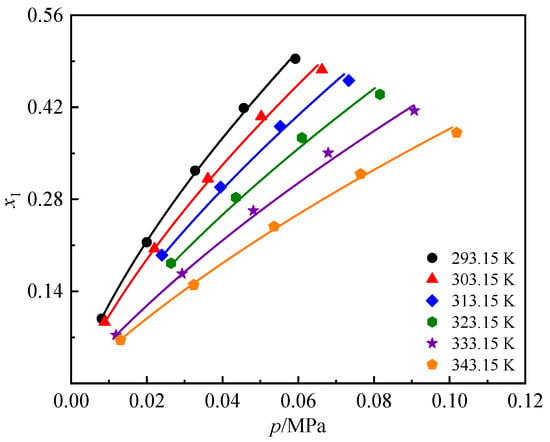
Figure 4.
p-T-x diagram of R1336mzz(Z) in DiPEC7. The solid line represents the calculated results from the NRTL model.
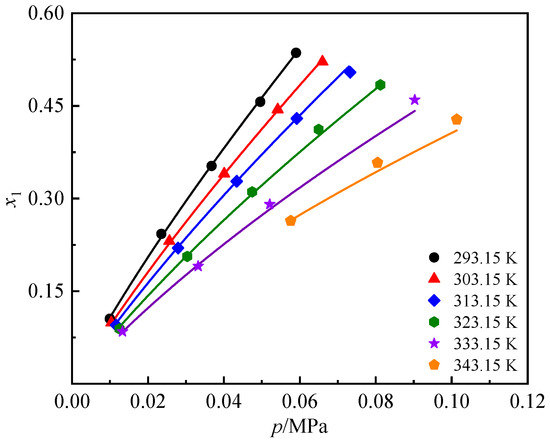
Figure 5.
p-T-x diagram of R1336mzz(Z) in DiPEiC9. The solid line represents the calculated results from the NRTL model.
Table 5 lists the regressed parameters in the NRTL model. Figure 6 and Figure 7 show the deviation distributions between each set of experimental data and the calculated values from the NRTL model. It is obvious that the average absolute relative deviation (AARD) and maximum absolute relative deviation (MARD) between the experimental mole fractions and the calculated values from NRTL model are 1.88% and 3.93% for R1336mzz(Z)/DiPEC7 system, and 1.46% and 4.17% for R1336mzz(Z)/DiPEiC9 system. The NRTL model can represent the experimental solubility data with good accuracy.

Table 5.
Parameters in NRTL model for R1336mzz(Z)/DiPEC7 and R1336mzz(Z)/DiPEiC9 systems.
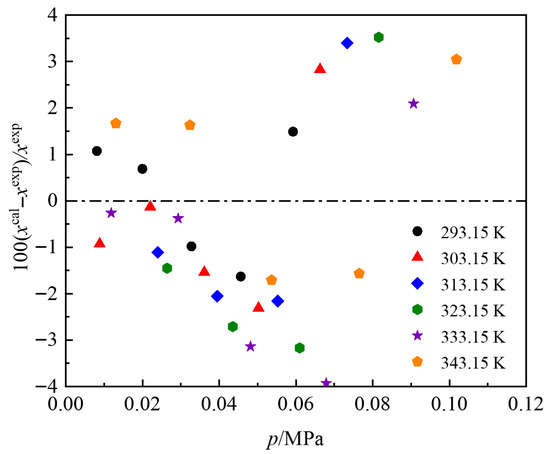
Figure 6.
Deviations between experimental and calculated values for R1336mzz(Z)/DiPEC7.
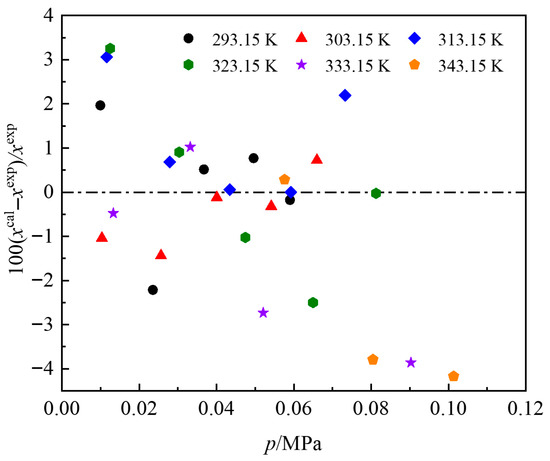
Figure 7.
Deviations between experimental and calculated values for R1336mzz(Z)/DiPEiC9.
The deviation of a mixture from Raoult’s law reflects the non-ideality of the solution. According to Raoult’s law [34], the total vapor pressure of an ideal system can be calculated using the following equation:
where p* represents the total vapor pressure of the ideal solution. and represent the saturated vapor pressures of R1336mzz(Z) and the DiPECs. Because the saturated vapor pressure of the DiPECs is negligible [24], p* = x1. The deviation between the actual pressure p and the ideal pressure p* reflects the deviation of the R1336mzz(Z)/DiPECs system from Raoult’s law, as indicated in Figure 8 and Figure 9. As the temperature increases, the binary mixtures gradually shift from positive deviation to negative deviation from Raoult’s law. This indicates that, as temperature increases, the intermolecular forces between R1336mzz(Z) and DiPECs gradually become stronger than those among R1336mzz(Z) molecules. The conclusion can provide support for analyzing the solubility at higher temperatures.
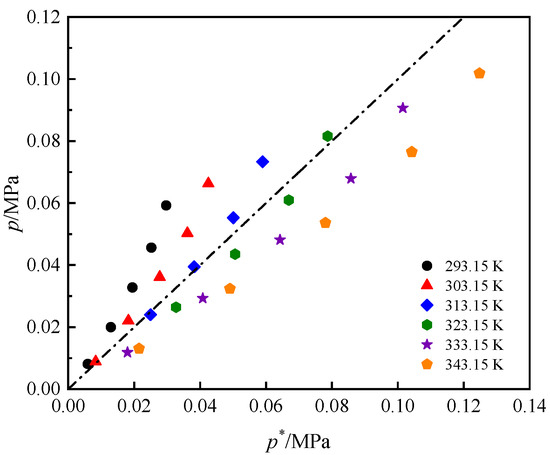
Figure 8.
Deviation of R1336mzz(Z)/DiPEC7 system from Raoult’s law.
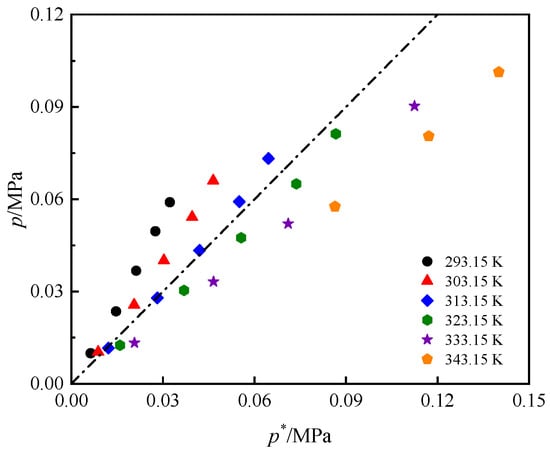
Figure 9.
Deviation of R1336mzz(Z)/DiPEiC9 system from Raoult’s law.
3.2. Solubility Comparison
The Henry’s constant (He) can reflect the dissolution potential of a solute in a solvent [35]. The calculation formula for He is as follows [36]:
Figure 10 compares the Henry’s constants of R1336mzz(Z)/DiPEC7 and R1336mzz(Z)/DiPEiC9 mixtures within the temperature range of 293.15 K–343.15 K. The results show that when the temperature is lower than 328.15 K, the He of R1336mzz(Z)/DiPEC7 is smaller than that of R1336mzz(Z)/DiPEiC9. However, when the temperature is higher than 328.15 K, the He of R1336mzz(Z)/DiPEC7 is larger than that of R1336mzz(Z)/DiPEiC9. This indicates that the R1336mzz(Z)/DiPEiC9 system is less sensitive to temperature. The reason may lie in the branched-chain structure of DiPEiC9, as indicated in Figure 3. The three-dimensional structure formed by the branched chains provides a relatively fixed accommodation space for refrigerant molecules, preventing them from easily detaching due to thermal motion and weakening the influence of temperature on solubility.
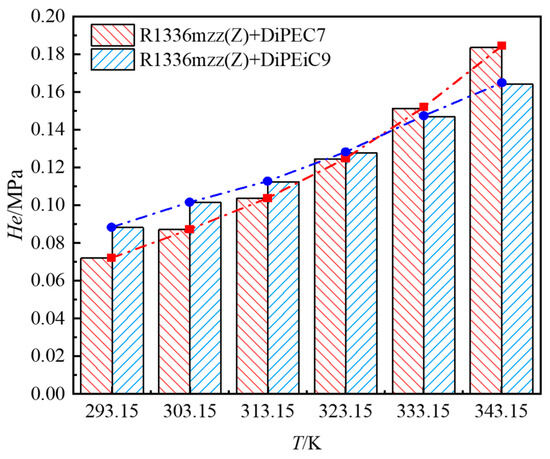
Figure 10.
Comparison of the Henry’s constants of R1336mzz(Z)/DiPEC7 and R1336mzz(Z)/DiPEiC9 systems.
Figure 11 shows the comparison of the solubilities of R1336mzz(Z) in DiPEC7, DiPEiC9, and POE SE220 at 333.15 K [23]. The solubility of R1336mzz(Z) in dipentaerythritol esters is higher than that in the commercial POE SE220 oil. Due to the complex composition of POE oils, each pure component can affect the solubility of R1336mzz(Z). Therefore, a comprehensive and systematic investigation on the solubility behavior of R1336mzz(Z) in the individual pure components of POE oils is essential.
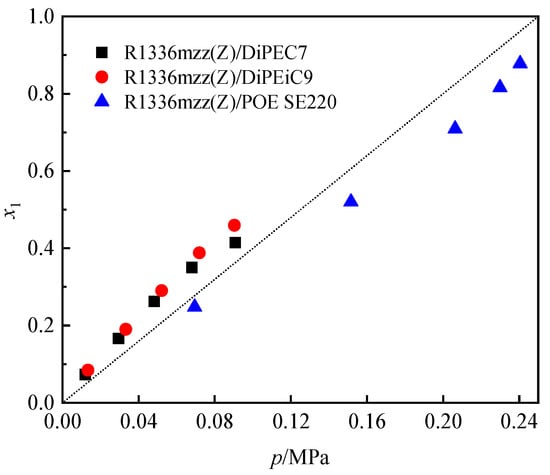
Figure 11.
Comparison of the solubilities of R1336mzz(Z) in DiPEC7, DiPEiC9, and POE SE220 at 333.15 K [23].
3.3. Mixing Thermodynamic Properties
Studying the dissolution behavior of R1336mzz(Z) in DiPECs allows for better understanding the intermolecular interactions. In this work, the mixing thermodynamic properties including the enthalpy change ΔHmix, entropy change ΔSmix, and Gibbs free energy change ΔGmix in the mixing process were calculated based on the solubility data. The calculated formulas are follows [37]:
For an ideal solution, ΔHid = 0. ΔSid, ΔGid, HE, SE, and GE are calculated by:
In Equations (18) to (25), the superscripts “id” and “E” mean the ideal solution and the excess properties of the mixtures. The calculated results of ΔHmix, ΔSmix, and ΔGmix for R1336mzz(Z)/DiPEC7 and R1336mzz(Z)/DiPEiC9 are presented in Table 6 and Table 7, respectively. Both the mixing enthalpy change and mixing entropy change are positive, which proves that the dissolution process is an exothermic and irreversible process. In addition, the change in Gibbs free energy during the mixing process is negative, which is consistent with general thermodynamic laws.

Table 6.
The mixing enthalpy, entropy, and Gibbs free energy of R1336mzz(Z) dissolving in DiPEC7.

Table 7.
The mixing enthalpy, entropy, and Gibbs free energy of R1336mzz(Z) dissolving in DiPEiC9.
4. Conclusions
To address the lack of solubility data for R1336mzz(Z) in POE lubricants, the solubilities of R1336mzz(Z) in DiPEC7 and DiPEiC9 were reported within the temperature range of 293.15 K–343.15 K in this work. The solubility data were correlated using the NRTL model. The AARD between the experimental mole fractions and calculated values from the NRTL model are 1.88% and 1.46% for the R1336mzz(Z)/DiPEC7 and R1336mzz(Z)/DiPEiC9 mixtures, respectively. In addition, the deviation between the mixtures and the ideal system was calculated according to Raoult’s law. The calculated results show that as temperature increases, the deviation of the binary mixtures from Raoult’s law gradually shifts from positive to negative. This phenomenon indicates that with increasing temperature, the intermolecular forces between the refrigerant and lubricant molecules gradually become stronger than those among refrigerant molecules. Furthermore, by calculating the Henry’s constants (He), the dissolution potential of R1336mzz(Z) in DiPEC7 and DiPEiC9 was compared. The results show that for temperatures below 328.15 K, the He of R1336mzz(Z) in DiPEC7 is lower than that in DiPEiC9; conversely, at temperatures exceeding 328.15 K, the He of R1336mzz(Z) in DiPEC7 becomes higher than that in DiPEiC9. The mixing thermodynamic properties of R1336mzz(Z) dissolving in DiPECs, such as the mixing enthalpy change, mixing entropy change, and mixing Gibbs free energy change, were analyzed. The mixing enthalpy change and mixing entropy change are positive, indicating that the dissolution process is an exothermic and irreversible process.
Author Contributions
C.L.: writing—resources, data curation, formal analysis, methodology, and original draft. W.D.—visualization and validation. X.W.—project administration, conceptualization, and review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Key Research and Development Program of China (Grant No. 2022YFE0210200).
Data Availability Statement
All data are available from the corresponding author by request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Vuppaladadiyam, A.K.; Antunes, E.; Vuppaladadiyam, S.S.V.; Baig, Z.T.; Subiantoro, A.; Lei, G.Y.; Leu, S.Y.; Sarmah, A.K.; Duan, H.B. Progress in the development and use of refrigerants and unintended environmental consequences. Sci. Total Environ. 2022, 823, 153670. [Google Scholar] [CrossRef]
- Perry, C.; Nickson, T.; Starr, C.; Grabiel, T.; Geoghegan, S.; Porter, B.; Mahapatra, A.; Walravens, F. More to offer from the Montreal protocol: How the ozone treaty can secure further significant greenhouse gas emission reductions in the future. J. Integr. Environ. Sci. 2024, 21, 2362124. [Google Scholar] [CrossRef]
- Liu, H.P.; Duan, H.B.; Zhang, N.; Ma, Y.; Liu, G.; Miller, T.R.; Mao, R.C.; Xu, M.; Li, J.H.; Yang, J.K. Rethinking time-lagged emissions and abatement potential of fluorocarbons in the post-Kigali Amendment era. Nat. Commun. 2024, 15, 6687. [Google Scholar] [CrossRef]
- Heath, E.A. Amendment to the Montreal Protocol on substances that deplete the ozone layer (Kigali Amendment). Int. Leg. Mater. 2017, 56, 193–205. [Google Scholar] [CrossRef]
- Nair, V. HFO refrigerants: A review of present status and future prospects. Int. J. Refrig. 2021, 122, 156–170. [Google Scholar] [CrossRef]
- Molés, F.; Navarro-Esbrí, J.; Peris, B.; Mota-Babiloni, A.; Barragán-Cervera, Á.; Kontomaris, K. Low GWP alternatives to HFC-245fa in Organic Rankine Cycles for low temperature heat recovery: HCFO-1233zd-E and HFO-1336mzz-Z. Appl. Therm. Eng. 2014, 71, 204–212. [Google Scholar] [CrossRef]
- Tanaka, K.; Akasaka, R.; Sakaue, E.; Ishikawa, J.; Kontomaris, K.K. Measurements of the critical parameters for cis-1,1,1,4,4,4-Hexafluoro-2-butene. J. Chem. Eng. Data 2017, 62, 1135–1138. [Google Scholar] [CrossRef]
- Arpagaus, C.; Bless, F.; Uhlmann, M.; Schiffmann, J.; Bertsch, S.S. High temperature heat pumps: Market overview, state of the art, research status, refrigerants, and application potentials. Energy 2018, 152, 985–1010. [Google Scholar] [CrossRef]
- Sakoda, N.; Higashi, Y.; Akasaka, R. Measurements of vapor pressures for trans-1-Chloro-3,3,3-trifluoropropene (R1233zd(E)) and cis-1,1,1,4,4,4-hexafluoro-2-butene (R1336mzz(Z)). J. Chem. Eng. Data 2020, 65, 4285–4289. [Google Scholar] [CrossRef]
- Kano, Y. Thermophysical properties evaluation for a polar fluid on the basis of the experimentally determined heat capacity and dipole moment in the ideal gas states. J. Therm. Anal. Calorim. 2023, 148, 5573–5587. [Google Scholar] [CrossRef]
- Alam, M.J.; Miyara, A.; Kariya, K.; Kontomaris, K.K. Measurement of viscosity of cis-1,1,1,4,4,4-Hexafluoro-2-butene (R-1336mzz(Z)) by Tandem capillary tubes method. J. Chem. Eng. Data 2018, 63, 1706–1712. [Google Scholar] [CrossRef]
- Alam, M.J.; Islam, M.A.; Kariya, K.; Miyara, A. Measurement of thermal conductivity of cis-1,1,1,4,4,4-hexafluoro-2-butene (R-1336mzz(Z)) by the transient hot-wire method. Int. J. Refrig. 2017, 84, 220–227. [Google Scholar] [CrossRef]
- Perkins, R.A.; Huber, M.L. Measurement and correlation of the thermal conductivity of cis-1,1,1,4,4,4-hexafluoro-2-butene. Int. J. Thermophys. 2020, 41, 103. [Google Scholar] [CrossRef]
- Tijani, M.E.H.; Otero Rodriguez, G.J.; Ramirez, M.; Poulsen, J.L.; Spoelstra, S. Selection of lubricant oils for high temperature heat pumps: A review and selection methodology guidelines. Appl. Therm. Eng. 2025, 273, 126483. [Google Scholar] [CrossRef]
- García, J.; Abou Naccoul, R.; Fernández, J.; Razzouk, A.; Mokbel, I. Vapor-pressure measurements and modeling of dipentaerythritol ester lubricants. Ind. Eng. Chem. Res. 2011, 50, 4231–4237. [Google Scholar] [CrossRef]
- Emel’ianov, V.V.; Krasnykh, E.L.; Sokolov, A.B. Synthetic oils based on pentaerythritol esters. Kinematic viscosity. Fluid Phase Equilib. 2024, 581, 114074. [Google Scholar] [CrossRef]
- Paredes, X.; Pensado, A.S.; Comuñas, M.J.P.; Fernández, J. Experimental dynamic viscosities of dipentaerythritol ester lubricants at high pressure. J. Chem. Eng. Data 2010, 55, 3216–3223. [Google Scholar] [CrossRef]
- Harris, K.R. Temperature and pressure dependence of the viscosities of Krytox GPL102 Oil and di(pentaerythritol) hexa(isononanoate). J. Chem. Eng. Data 2015, 60, 1510–1519. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Y.J.; Wang, X.P. Density, viscosity, and R1234yf solubility in dipentaerythritol esters. J. Chem. Eng. Data 2025, 70, 2057–2067. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E.; Wallin, H.H.; Hauleitner, R.; Arvidsson, M. Progress in rolling bearing technology for refrigerant compressors. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2017, 232, 2948–2961. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, X.D.; Wang, S.B.; Meng, X.Z. Viscosity measurement and correlation of saturated solutions of R-290 with three lubricants. Int. J. Refrig. 2023, 155, 1–6. [Google Scholar] [CrossRef]
- Wang, C.C.; Hafner, A.; Kuo, C.S.; Hsieh, W.D. An overview of the effect of lubricant on the heat transfer performance on conventional refrigerants and natural refrigerant R-744. Renew. Sustain. Energy Rev. 2012, 16, 5071–5086. [Google Scholar] [CrossRef]
- Brocus, J.; Valtz, A.; Coquelet, C.; De Carlan, F. Solubility measurements of refrigerants in polyolesters lubricants at temperature from 323 K to 383 K. Int. J. Refrig. 2022, 134, 278–292. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, Z.; Lu, C.; Wang, X.P. Vapor-liquid equilibrium measurements of 3, 3, 3-trifluoropropene with pentaerythritol tetraheptanoate and pentaerythritol tetranonanoate. J. Chem. Thermodyn. 2022, 174, 106874. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Y.J.; Wang, X.P. Solubility measurements of R1234ze(E), R1243zf, and R1234yf in POE46 at temperatures from 283.15 to 343.15 K. J. Chem. Eng. Data 2024, 69, 1677–1684. [Google Scholar] [CrossRef]
- Sun, Y.J.; Li, X.J.; Meng, X.Y.; Wu, J.T. Measurement and correlation of the liquid density and viscosity of HFO-1336mzz(Z) (cis-1,1,1,4,4,4-hexafluoro-2-butene) at high pressure. J. Chem. Eng. Data 2019, 64, 395–403. [Google Scholar] [CrossRef]
- Bich, W.; Cox, M.G.; Dybkaer, R.; Elster, C.; Estler, W.T.; Hibbert, B.; Imai, H.; Kool, W.; Michotte, C.; Nielsen, L.; et al. Revision of the ‘Guide to the Expression of Uncertainty in Measurement’. Metrologia 2012, 49, 702. [Google Scholar] [CrossRef]
- Goharshadi, E.K.; Moosavi, M.; Abareshi, M. Calculation of thermodynamic properties of lubricant + refrigerant mixtures using GMA equation of state. Int. J. Therm. Sci. 2007, 46, 944–952. [Google Scholar] [CrossRef]
- Comuñas, M.J.P.; Baylaucq, A.; Boned, C.; Canet, X.; Fernández, J. High-pressure volumetric behavior of x 1,1,1,2-tetrafluoroethane + (1 − x) 2,5,8,11,14-pentaoxapentadecane (TEGDME) mixtures. J. Chem. Eng. Data 2002, 47, 233–238. [Google Scholar] [CrossRef]
- Saggion, A.; Faraldo, R.; Pierno, M. Thermodynamics: Fundamental Principles and Applications; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Beattie, J.A.; Stockmayer, W.H. The Second Virial Coefficient for Gas Mixtures. J. Chem. Phys. 1942, 10, 473–476. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermo-Dynamic and Transport Properties-REFPROP, Version 10.0.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. [Google Scholar]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 2004, 14, 135–144. [Google Scholar] [CrossRef]
- Masuku, C.M.; Ma, W.; Hildebrandt, D.; Glasser, D.; Davis, B.H. A vapor–liquid equilibrium thermodynamic model for a Fischer–Tropsch reactor. Fluid Phase Equilibr. 2012, 314, 38–45. [Google Scholar] [CrossRef]
- Gunn, R.D.; Yamada, T.; Whitman, D. Corresponding states. III. Henry’constants for nonpolar binary mixtures. AIChE J. 1974, 20, 906–915. [Google Scholar] [CrossRef]
- Sun, Y.J.; Di, G.L.; Wang, J.; Wang, X.P.; He, M.G. Phase behavior of R1234yf and R600a in pentaerythritol tetranonanoate. Int. J. Refrig. 2020, 109, 135–142. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid Phase Equilibria, 3rd ed.; Prentice Hall PTR: Hoboken, NJ, USA, 1999. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).