An Efficient Control Strategy for Denitrification Systems Using a Hybrid Model and CSGA to Enhance Performance

Abstract

Flue gas denitrification is a critical process in industrial pollution control, essential for achieving environmental sustainability. The central objective of denitrification system control is to precisely regulate the ammonia flow rate while ensuring consistent compliance with nitrogen oxide (NO_x) emission standards, thereby achieving a balance between environmental benefits and economic operational efficiency. However, industrial flue gas treatment is characterized by complex operating conditions, strong nonlinearity, and multivariable coupling, which complicates precise and cost-effective control. To address these challenges, this study proposes an optimized control strategy for denitrification systems based on a hybrid modeling approach and an enhanced genetic algorithm. We developed a Multidimensional Spatiotemporal Convolutional Attention Network (MSCA-Net) to tackle the nonlinear, multivariable, and high-dimensional data characteristics of the system, enabling accurate prediction of NO_x emissions. Furthermore, we implemented a Constraint-aware Genetic Algorithm with Smoothing (CSGA) for global optimization, integrating an Extreme Gradient Boosting (XGBoost) model to generate initial ammonia flow settings, achieving a coefficient of determination (R²) of 0.951. Following optimization, the NO_x compliance rate increased to 94.23%, average ammonia consumption decreased by 33.56 L/h, and the rate of threshold exceedance fell by 8.39%. These results demonstrate that the proposed approach effectively resolves multi-objective optimization challenges, achieving coordinated optimization of NO_x emissions and ammonia flow. The method enhances system stability while simultaneously improving environmental and economic performance.

1. Introduction

With rapid global economic growth and accelerated industrialization, air pollution has become a widespread environmental challenge. It poses a severe threat to human health and the sustainable development of ecosystems. The glass manufacturing industry is a high-energy, high-pollution sector. It emits harmful gases such as nitrogen oxides (NO_x) and sulfur dioxide during the furnace firing process, while consuming large amounts of fossil fuels [1]. NO_x is a key pollutant in atmospheric contamination. Its emissions worsen acid rain, photochemical smog, and haze, and increase the risk of respiratory and cardiovascular diseases in humans [2,3]. Effective control and reduction of NO_x emissions are vital for better air quality, ecological sustainability, and public health protection [4].

Currently, industrial denitrification systems predominantly employ Selective Catalytic Reduction (SCR) as the core technology for flue gas purification [5]. SCR converts NO_x into harmless nitrogen and water in the presence of a catalyst, enabling highly efficient NO_x abatement [6,7]. Since its emergence in the 1980s, SCR has become the mainstream solution for industrial denitrification, relying on ammonia as a reducing agent to achieve efficient NO_x reduction on catalysts such as V₂O₅-WO₃/TiO₂ [8,9,10]. With denitrification efficiencies exceeding 90% and broad operational adaptability, SCR has substantially reduced industrial NO_x emissions worldwide, establishing itself as a pivotal technology for achieving clean emissions in modern denitrification systems [11,12]. Moreover, SCR exhibits favorable low-temperature activity and compatibility with existing industrial infrastructure, offering significant cost-effectiveness and ease of integration in retrofit applications [13].

Despite the significant success of SCR technology in industrial applications, numerous issues and challenges persist in its practical operation. As the operation time extends and operating conditions become more complex, the performance of SCR systems is constrained by various factors, including catalyst aging, reduced activity, and the accumulation of impurities such as SO₂ and ash in the flue gas [14,15]. These changes make precise control of ammonia water flow extremely difficult [16,17]. Improper ammonia flow control may lead to ammonia slip, reduce denitrification efficiency, and cause secondary pollution, while excessive ammonia usage increases operational costs [18]. Furthermore, with increasingly stringent environmental regulations, both domestic and international standards for NO_x emissions in the glass industry have become progressively more demanding. In key regions of China, such as the Beijing–Tianjin–Hebei area, NO_x concentration limits for flat glass plants have been reduced to below 100 mg/m³, with some areas requiring levels under 50 mg/m³. European Union standards are even more rigorous, mandating emissions not exceeding 20 mg/Nm³. Against this backdrop, achieving efficient and precise ammonia flow control under dynamically changing operating conditions has emerged as a critical challenge for industrial denitrification systems.

To address these issues, researchers have proposed various methods. Bonfils et al. [19] proposed a closed-loop control strategy based on NO_x sensors, optimizing the ammonia injection of the SCR system by leveraging the sensors’ cross-sensitivity to NH₃. Chen et al. [20] developed a mathematical model and optimization design method, which reduced NO_x emissions by simulating the performance of the SCR reactor. Li et al. [21] introduced a two-stage SCR control strategy that, combined with dynamic condition adjustments, met the ultra-low NO_x emission requirements for heavy-duty diesel engines. However, these approaches predominantly rely on conventional sensors or mechanistic models, making it difficult to accurately capture and represent the intrinsic nonlinearities and temporal dependencies within SCR system data. This limitation undermines the model’s ability to maintain predictive accuracy and adaptability when confronted with the system’s complex dynamic behaviors, ultimately impeding robust and consistent performance optimization.

In recent years, data-driven approaches have demonstrated remarkable potential for optimizing industrial denitrification systems. Machine learning techniques—represented by artificial neural networks (ANNs), support vector machines (SVMs), long short-term memory (LSTM) networks, and their variants such as Seq2Seq LSTM—have achieved steady advances in predicting NO_x emission concentrations. Meanwhile, evolutionary algorithms, particle swarm optimization, and surrogate-based optimization strategies have offered diverse pathways for parameter tuning in the denitrification process. Despite these advancements, current methodologies still face fundamental limitations in achieving the coordinated optimization of ultra-low NO_x emissions and economic operation. The overall evolution of this research field thus reveals a distinct gap, transitioning from isolated perception to shallow optimization without a truly integrated framework.

Specifically, early studies predominantly focused on improving the predictive accuracy of NO_x concentration models, yet a fundamental paradigm gap persisted—namely, the disconnection between prediction and optimization. For instance, the evolutionary neural network proposed by Azzam et al. [22], the Auto-encoder–ELM model developed by Tang et al. [23], and the Seq2Seq-LSTM network employed by Xie et al. [24] all aimed to enhance prediction accuracy through architectural optimization or advanced feature extraction. More recently, the CS-CNN model introduced by Wang et al. [25] further strengthened dynamic modeling capability. Nevertheless, these efforts have largely treated high-precision prediction as the ultimate goal, without integrating it into a closed-loop control framework. As a result, the prediction models function merely as isolated perceptual units, unable to directly guide real-time ammonia injection strategies, thereby forming an inherently open-loop system architecture.

As research has progressed, several studies have incorporated optimization into the denitrification process. However, significant limitations remain in both how objectives are formulated and how optimization mechanisms are designed. These often result in narrow objectives or low computational efficiency. For example, Wang et al. [26] used a Gaussian process with a genetic algorithm to optimize the combustion process for NO_x reduction. Yet, their framework did not consider key economic indicators such as ammonia consumption, resulting in an incomplete assessment of system benefits. Similarly, this research—together with Liu et al.’s [27] feedforward control strategy—typically uses static or highly simplified surrogate models for optimization. The optimization algorithms themselves also have issues, including random initialization and poor search guidance. These make them poorly suited for the strongly nonlinear, multivariable-coupled dynamics of SCR systems. Such deficiencies constrain both convergence speed and adaptability under different operating conditions.

Notably, recent advances in collaborative optimization have highlighted the frontier challenges of this field. These advances have also provided a more precise benchmark for positioning the present work. Li et al. [28] proposed a synergistic framework based on an SAE–Bi-LSTM model integrated with an improved particle swarm optimization (PSO) algorithm. Xu et al. [29] developed a DNN–MPC structure that achieved notable progress in coupling prediction and control. However, these approaches still have limited capacity to capture the system’s intricate spatiotemporal dynamics. Their optimization modules also generally lack the capability to intelligently extract informative priors from historical data. As a result, they struggle to generate high-quality initial solutions, which reduces overall optimization efficiency and control stability under fluctuating operating conditions. These analyses collectively reveal that the central bottleneck of current research lies in constructing an integrated optimization framework. All components should be deeply coupled to achieve both high-precision dynamic perception and efficient directional search.

In summary, existing data-driven approaches for denitrification systems face three fundamental challenges: (1) insufficient capability of model architectures to capture multivariate spatiotemporal coupling dynamics; (2) a disconnection between the prediction and optimization stages, leading to open-loop decision-making; and (3) a lack of intelligent guidance in the optimization process, resulting in inefficient search strategies.

To address these challenges, this study suggests a new way to control and optimize SCR systems by combining two modeling methods with an improved genetic algorithm. A new network, called a multidimensional spatiotemporal convolutional attention network (MSCA-Net), is created to help the model better understand the system’s complex behaviors. Building on this, a Constraint-aware Genetic Algorithm with Smoothing (CSGA) is introduced to optimize both NO_x emissions and ammonia use, creating a decision-making loop. In addition, an Extreme Gradient Boosting (XGBoost) initializer is used to quickly find good starting solutions, making the process faster and more stable.

The core innovations of this work are summarized as follows:

• To achieve a unified optimization of control precision and economic efficiency in denitrification systems, a hybrid modeling and CSGA-based co-optimization strategy was proposed, ensuring stable compliance with NO_x emission standards while reducing ammonia consumption.
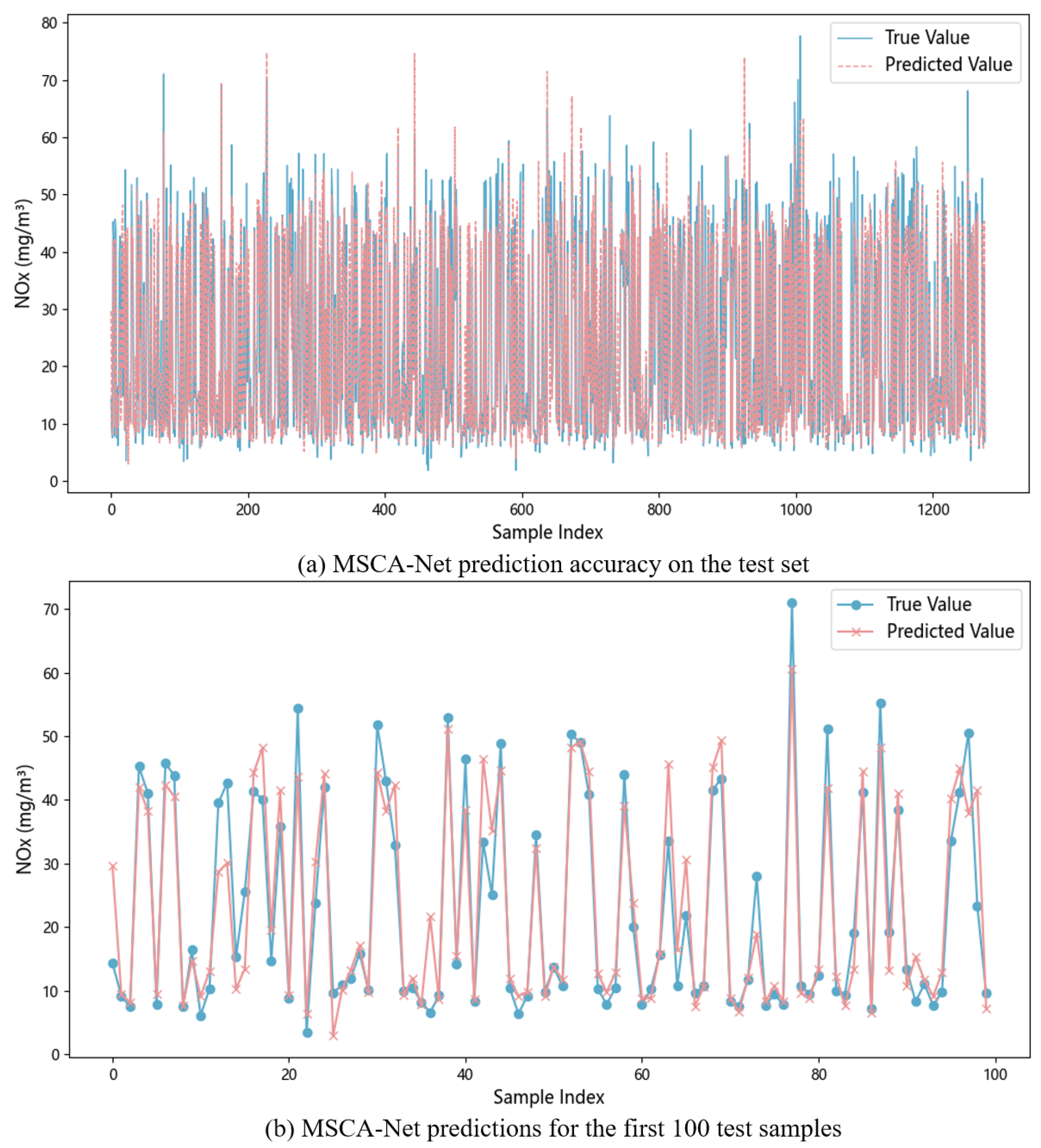
• To address the challenges of multivariable coupling, strong nonlinearity, and complex operating conditions in industrial flue gas treatment, the MSCA-Net was developed, significantly enhancing the accuracy and robustness of NO_x concentration predictions at the system outlet.
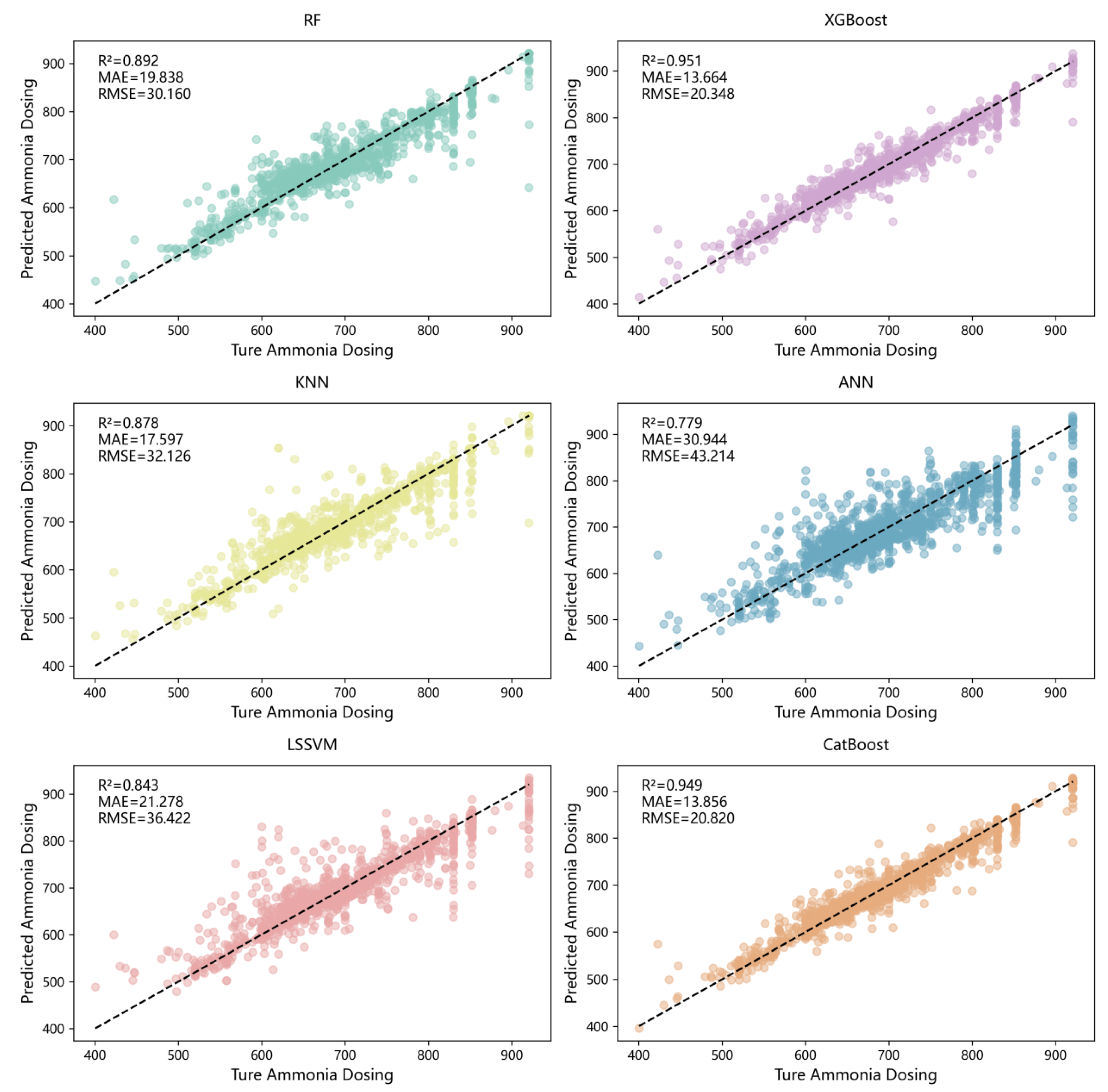
• An XGBoost model was introduced to provide high-quality initial solutions for the optimization process, narrowing the search space and mitigating the randomness of algorithm initialization. Furthermore, a comparative analysis with five baseline models confirmed the superior performance of XGBoost in predicting ammonia flow, achieving an R² of 0.951.
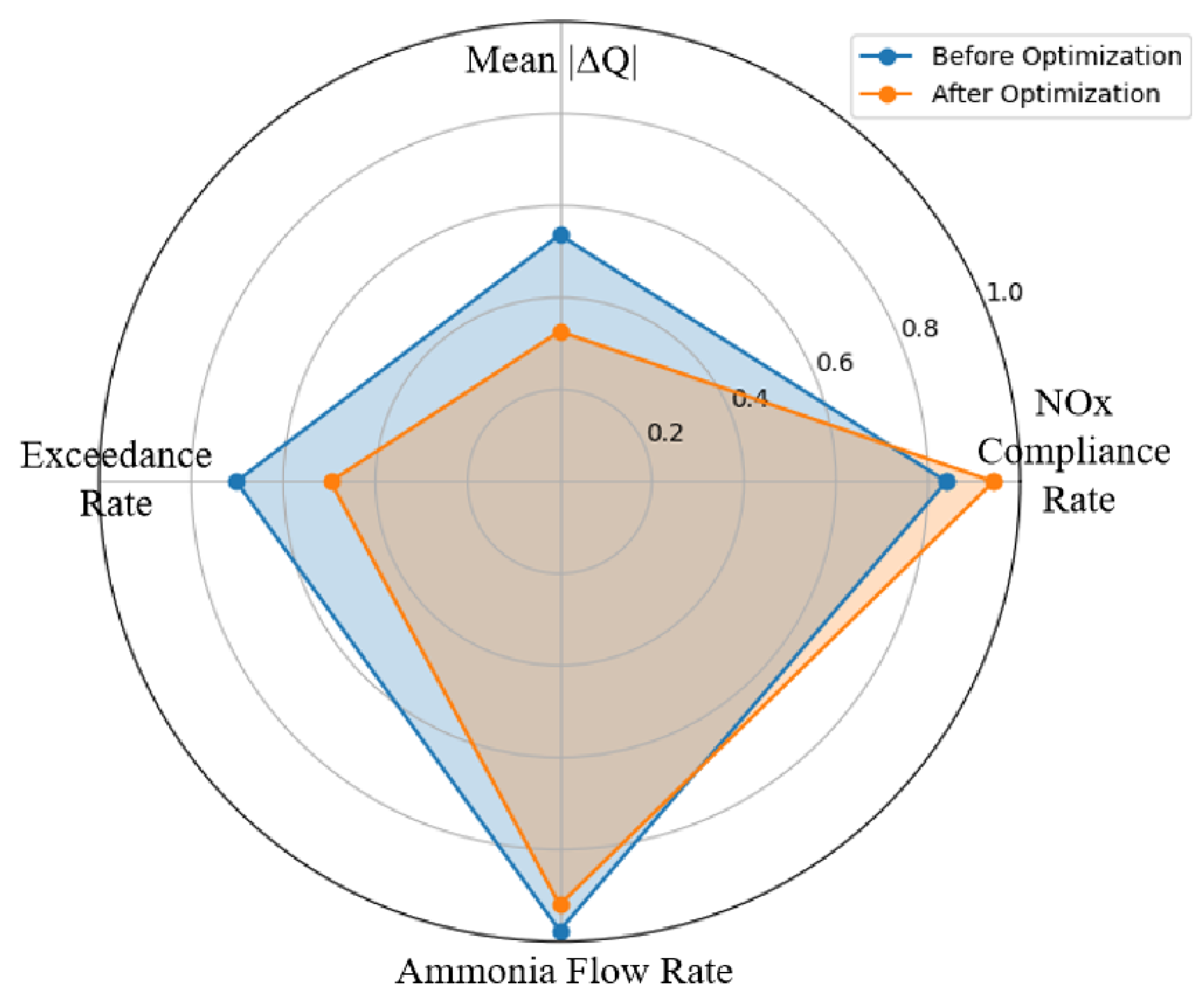
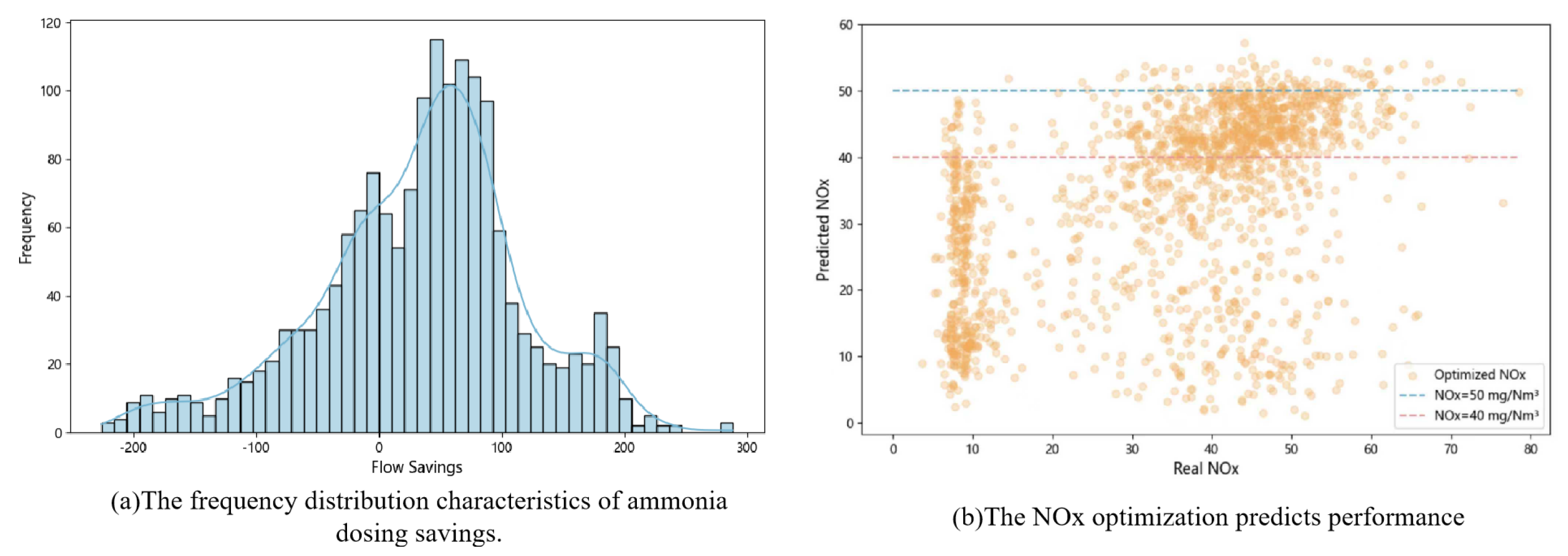
• Global optimization was performed using the CSGA, enabling multi-objective co-optimization of NO_x emissions and ammonia flow, effectively balancing environmental performance with operational cost. Experimental results demonstrate that the proposed strategy increased the NO_x compliance rate by 10.26%, reduced average ammonia consumption by 33.56 L/h, and decreased the rate of threshold exceedance by 8.39%. These improvements not only significantly lower operational costs but also further enhance the stability of the denitrification system.

The remainder of this paper is organized as follows. Section 2 presents the materials and methods. Section 3 reports the results and discussion. Section 4 concludes the study.

2. Materials and Methods

In this section, we propose an optimization strategy for denitrification systems that integrates MSCA-Net, XGBoost, and CSGA. Section 2.1 describes the procedures for data collection and preprocessing. Section 2.2 details the overall framework architecture, including NO_x concentration prediction using MSCA-Net, initial ammonia flow estimation with XGBoost, and the collaborative optimization process enabled by CSGA. Section 2.3 specifies the evaluation metrics employed for model assessment.

2.1. Data Collection and Preprocessing

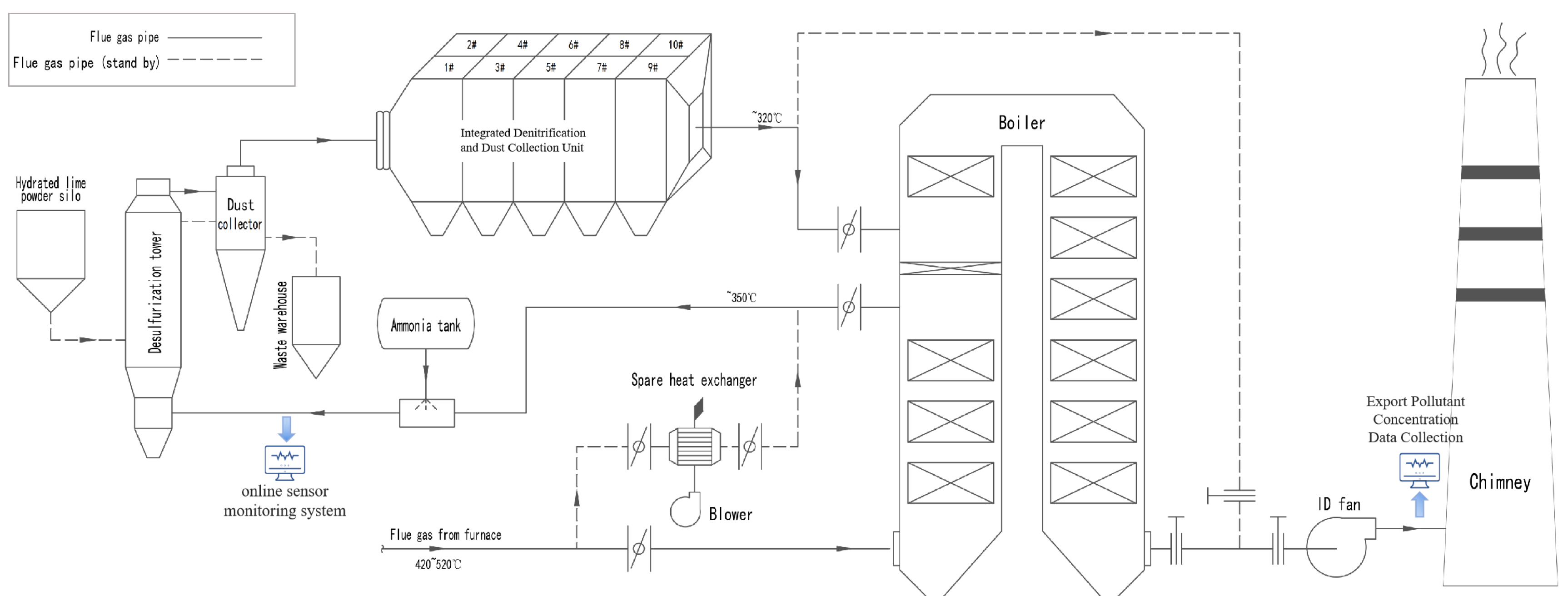
In this study, the experimental data were obtained from a flue gas treatment plant serving a glass-melting furnace located in Guangdong Province, China. The plant employs a comprehensive high-temperature flue gas purification process, as illustrated in Figure 1, which primarily consists of waste heat recovery, desulfurization, denitrification, and dust removal stages. Specifically, the high-temperature flue gas emitted from the glass-melting furnace first enters a boiler unit for waste heat recovery, where its temperature is reduced to approximately 350 °C before proceeding to the conditioning and desulfurization stage. In this stage, the flue gas is thoroughly mixed with ammonia solution injected from an ammonia tank and then directed into the desulfurization tower. Simultaneously, hydrated lime powder from the lime silo is fed into the tower to participate in the desulfurization reaction. Subsequently, the flue gas passes through a dust collector, where separated particulate matter is conveyed to a waste silo. The preliminarily purified flue gas is then introduced into an integrated denitrification–dust-removal unit. Within this unit, NO_x and ammonia undergo selective catalytic reduction on the catalyst surface of the unit’s modular cells, producing nitrogen and water. Meanwhile, alkaline particulates in the gas stream form a filter cake layer that enhances desulfurization, and captured particles are collected through the ash-cleaning system. After completing this high-temperature desulfurization–denitrification–dust-removal process, the purified flue gas is drawn by an induced draft fan and finally discharged through the chimney.

The plant is equipped with an online sensor monitoring system that continuously records key operational parameters. The collected data consist of two frequency categories:

1.

Daily data—furnace temperature (°C): This parameter is measured at four monitoring points positioned inside the glass-melting furnace, and the average value is recorded. As a core process control variable, the furnace temperature exhibits minimal intra-day fluctuations and typically changes only during process adjustments. Therefore, it can be regarded as constant within a single operational day.

2.

Data collected at 1 min intervals: kiln opening signal (%), flue gas temperature (°C), pressure (Pa), flue gas flow rate (Nm³/h), SO₂ concentration (mg/m³), O₂ concentration (%), humidity (%), and ammonia water flow rate (L/h).

In addition to the online sensor monitoring data, the dataset also includes pollutant concentration analyses. Specifically, the NO_x concentration (mg/m³) was measured at the chimney outlet with a one-minute sampling frequency, providing high-resolution monitoring of exhaust gas emissions. The data collection period spanned from 9 April 2024, to 30 March 2025 (356 days in total), yielding approximately 512,640 data samples. The data encompasses various operating conditions of the glass melting furnace, providing a reliable data foundation for the subsequent optimization of ammonia water flow to achieve low NO_x emissions (<50 mg/Nm³).

To ensure data quality and model reliability, a rigorous data preprocessing procedure was implemented. First, all data were resampled to a uniform temporal resolution to generate daily and hourly datasets [30]. The daily dataset was constructed by averaging the one-minute data collected within the same day. The hourly dataset was generated based on the characteristics of each parameter: for the furnace temperature, which remains stable throughout the day, a constant value was used, whereas for dynamic variables, the hourly data were obtained by averaging all minute-level samples within each hour [31]. Second, missing values caused by sensor malfunctions were filled using linear interpolation to preserve temporal continuity [32]. Finally, a multi-level outlier detection and correction strategy was applied to remove anomalous observations.

A multi-level data quality control protocol was implemented using specific parameter thresholds:

1.

Static threshold filtering: measurement values violating operational limits (O₂ > 16%, pressure < −1750 Pa, or humidity > 20%) were marked as invalid and estimated using piecewise linear interpolation [33].

2.

Dynamic outlier detection: a 168 h (7 day) sliding window was used to identify dynamic anomalies. Values deviating more than $\pm 3\sigma$ from the mean within the window were replaced using linear interpolation [34].

After completing the data preprocessing, a preliminary comparison analysis was conducted between the daily and hourly datasets to evaluate the accuracy of NO_x emission prediction. The hourly dataset, which showed better performance, was ultimately selected, with a total of 8522 data points.

2.2. Overall Framework

The workflow of the proposed framework is illustrated in Figure 2. We introduce a three-tier synergistic architecture that integrates MSCA-Net, XGBoost, and CSGA to optimize ammonia flow and regulate NO_x emissions in denitrification systems. MSCA-Net, composed of convolutional neural networks (CNN), convolutional block attention modules (CBAM), and long short-term memory networks (LSTM), enables accurate prediction of NO_x concentrations under highly dynamic and nonlinear operating conditions. XGBoost, leveraging efficient feature selection and regression analysis, generates high-quality initial ammonia flow estimates for CSGA, thereby substantially reducing the optimization search space and enhancing computational efficiency. Finally, CSGA functions as the global optimization engine, employing iterative search strategies to minimize ammonia consumption while ensuring full compliance with emission standards.

To validate the effectiveness of the proposed framework, we evaluated multiple key performance indicators, including NO_x compliance rate, average ammonia consumption, and exceedance ratio. Experimental results demonstrate that the integrated optimization framework significantly outperforms existing benchmark methods in both NO_x concentration prediction accuracy and multi-objective dynamic optimization. These findings confirm the superiority, adaptability, and practical utility of the proposed strategy for denitrification in complex industrial flue gas environments.

2.2.1. MSCA-Net

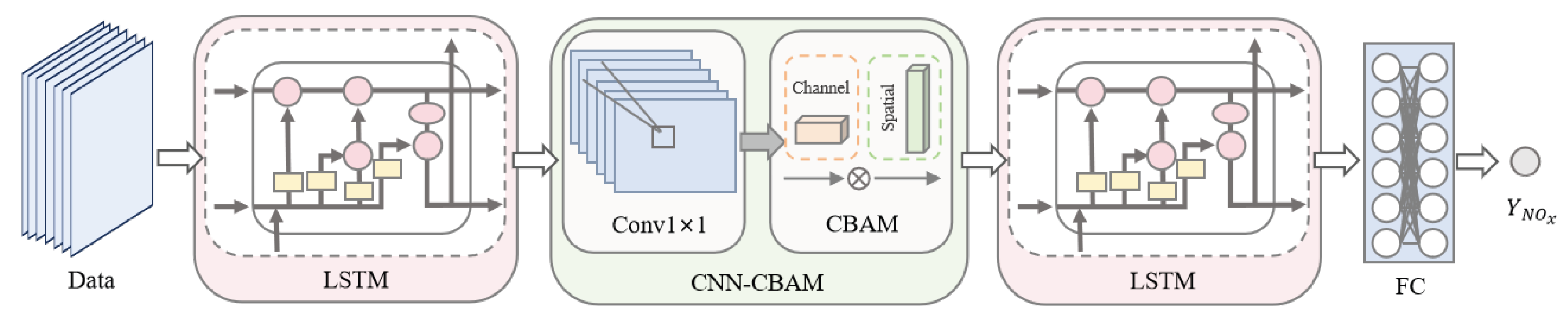
The MSCA-Net is a hybrid deep learning architecture that integrates LSTM, CNN, and CBAM. Its design concept emulates the cognitive reasoning process of engineers in analyzing complex industrial systems: first capturing the overall dynamic evolution of the system, then extracting critical local patterns, and finally focusing on salient information to enhance discriminative capability. The model is built upon a hierarchical feature-processing paradigm, forming a multilayer feature learning framework that jointly leverages temporal modeling, spatial pattern recognition, and attention-based feature refinement. By sequentially incorporating temporal dependency capture, local pattern extraction, and adaptive feature optimization, MSCA-Net enables a progressive information-processing flow—from macro-level dynamic modeling to micro-level feature enhancement. Unlike conventional single-structure networks, MSCA-Net emphasizes the collaborative modeling of global and local representations and the hierarchical optimization of information flow. This design endows the model with memory capability, discriminative power, and robustness when handling the nonlinear and multivariable coupling characteristics of combustion processes, providing an interpretable and generalizable solution for NO_x emission prediction.

The model architecture is shown in Figure 3. The MSCA-Net adopts a strictly sequential, end-to-end architecture, with the data flow designed to capture both global and local temporal–spatial dependencies. Specifically, the input multivariate time-series data are first processed by an initial LSTM layer, which captures long-term temporal dependencies and provides rich global contextual information for subsequent modules. Next, a one-dimensional convolutional layer extracts local spatial patterns from the LSTM outputs, strengthening the model’s ability to perceive correlations among neighboring feature points. The CBAM attention module is then applied to the convolutional feature maps to adaptively reweight channels and spatial locations, highlighting features that are highly correlated with NO_x emission dynamics while suppressing irrelevant noise. After that, a second LSTM layer functions as a contextual aggregator, deeply integrating the refined feature sequences to achieve fine-grained modeling of global temporal patterns—significantly enhancing the model’s representational capacity for complex dynamic processes. Finally, the extracted features are regularized via a Dropout layer and passed through a fully connected layer to perform regression-based NO_x concentration prediction.

LSTM, an enhanced variant of the Recurrent Neural Network (RNN), addresses the vanishing gradient problem commonly encountered in traditional RNNs when processing long sequential data through the introduction of a gating mechanism [35]. The core structure of an LSTM unit consists of three essential gates—the forget gate, input gate, and output gate—which control the retention, updating, and output of information, respectively [36].

$$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f)$$

(1)

$$i_t=\sigma (W_i·[h_{t-1},x_t]+b_i)$$

(2)

$$o_t=\sigma (W_o·[h_{t-1},x_t]+b_o)$$

(3)

where $W_f$ is the weight matrix of the forgetting gate, $[h_{t-1},x_t]$ denotes the concatenation of the previous hidden state $h_{t-1}$ and the current input $x_t$ into a single vector, $b_f$ is the bias term, $W_i$ and $W_o$ are the weight matrices of the input gate and output gate, respectively, with corresponding bias terms $b_i$ and $b_o$, and $\sigma$ represents the sigmoid activation function. Specifically, the forgetting gate governs the retention of information from the previous cell state, determining which components should be discarded. The input gate regulates the extent to which the current candidate state influences the update process, while the output gate controls the degree to which the current cell state contributes to the final hidden state. The ultimate output of the LSTM unit is jointly determined by the output gate and the cell state:

$${\tilde{c}}_t=tanh(W_c·[h_{t-1},x_t]+b_c)$$

(4)

$$c_t=f_t\odot c_{t-1}+i_t\odot {\tilde{c}}_t$$

(5)

$$h_t=o_t\odot tanh\left(c_t\right)$$

(6)

where ${\tilde{c}}_t$ is the input cell state, $c_t$ is the cell state at the current moment, and the symbol ⊙ denotes element-wise multiplication. This design allows the LSTM to effectively capture long-term dependencies in complex time series.

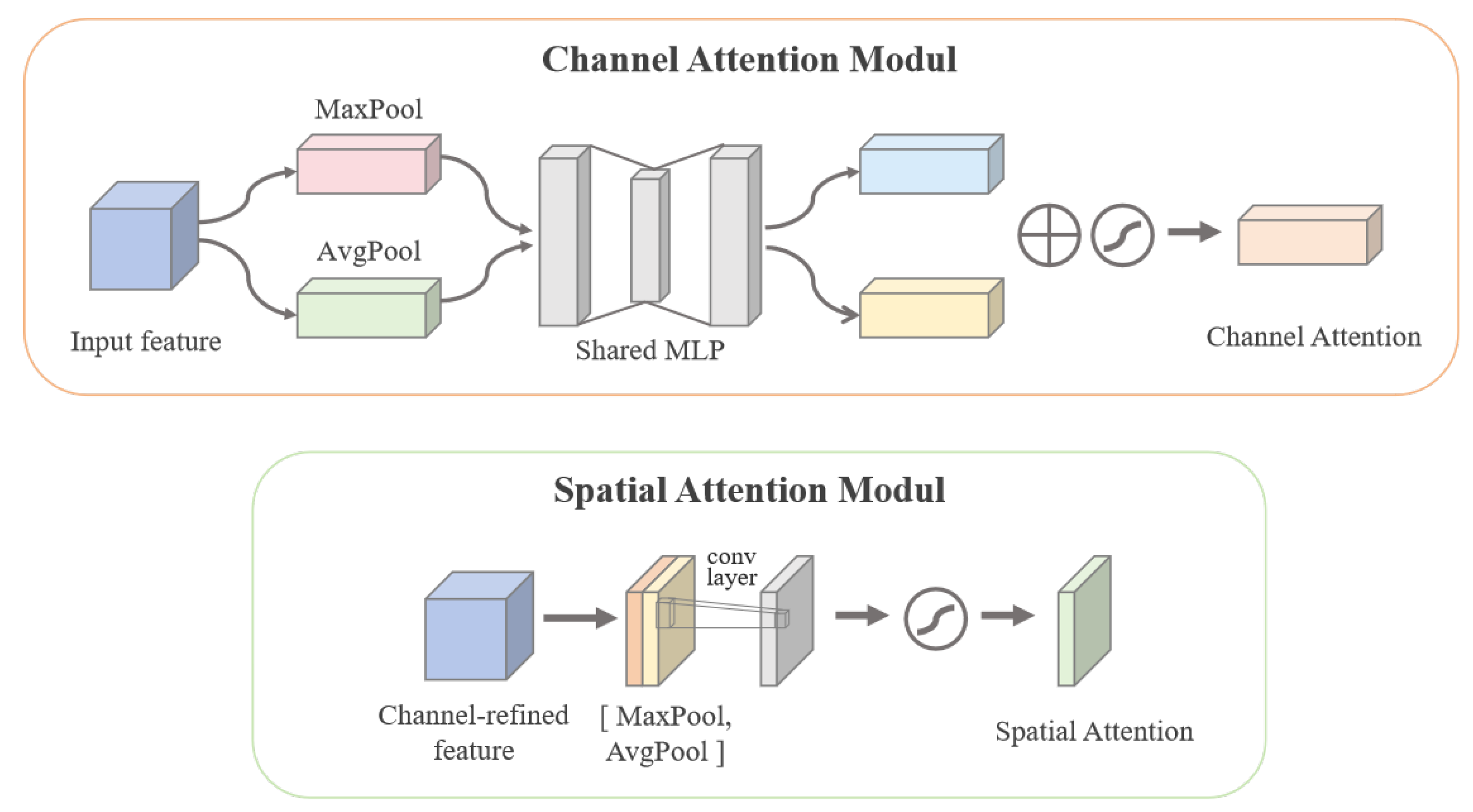
However, standard LSTM networks often struggle to adaptively focus on salient features when processing high-dimensional input data. To overcome this limitation, a CNN module is introduced to extract local high-dimensional representations. Through one-dimensional convolution operations, the CNN captures local dependencies along the temporal axis, effectively identifying high-level patterns between adjacent time steps and compensating for the LSTM’s limitations in local feature modeling. Additionally, the CBAM adaptively recalibrates features along both channel and spatial dimensions, strengthening the representation of important channels and key spatial locations. This mechanism effectively selects and amplifies relevant input features while suppressing noise interference, substantially improving the model’s attention allocation to critical information. CBAM is a lightweight and general-purpose attention module designed to enhance convolutional neural networks’ sensitivity to salient features [37]. The module consists of two submodules: a channel attention module and a spatial attention module. These submodules refine the feature maps by adaptively learning importance weights along the channel and spatial dimensions. The channel attention module first aggregates global spatial information through global average pooling (GAP) and global maximum pooling (GMP). Then it computes channel-wise importance weights using a multilayer perceptron (MLP).

$$M_c\left(F\right)=\sigma \left(MLP\left(AvgPool\right(F\left)\right)+MLP\left(MaxPool\right(F\left)\right)\right)$$

(7)

where $M_c$ is the channel attention feature, F is the input feature, $\sigma$ is the sigmoid function, and MLP is the shared fully connected layer with shared weights. The spatial attention module, on the other hand, generates an attention map over spatial locations by compressing the channel dimensions to emphasize key regions and suppress noise [38]:

$$M_s\left(F\right)=\sigma \left(f^{7\times 7}\left(\left[AvgPool\right(F);MaxPool(F\left)\right]\right)\right)$$

(8)

where $M_s$ is the spatial attention feature. F is the feature after the spatial attention module. $\sigma$ is the sigmoid function, and 7 × 7 denotes the size of the convolution kernel. By integrating CBAM into the CNN layer, the model is able to further enhance the feature responses that have a significant impact on the NO_x concentration prediction on the basis of local high-dimensional features, thus improving the overall prediction accuracy and robustness. The structure of the CBAM is shown in Figure 4.

In this study, CBAM is effectively integrated into the deep neural network architecture to enhance the model’s selective attention to critical features. Based on this design principle, the workflow of MSCA-Net is as follows: first, LSTM functions as a macroscopic temporal feature extractor, capturing long-term dependencies in the input data and grasping overall system dynamics. Subsequently, CNN is introduced to focus on local detailed feature extraction; through multiple convolutional and pooling layers, the model’s ability to perceive complex spatiotemporal patterns is strengthened. Building on this, CBAM adaptively recalibrates feature weights through both channel and spatial attention mechanisms, highlighting the contributions of important channels and key time steps. This enables selective feature enhancement and noise suppression, substantially improving discriminative capability. Finally, the optimized and weighted features are fed into an LSTM unit for fine-grained temporal modeling, generating robust time-series representations that accurately capture the complex dynamic variations of NO_x concentrations in denitrification systems, thereby significantly improving prediction accuracy.

2.2.2. XGBoost

XGBoost is an efficient gradient boosting decision tree algorithm widely used for its high accuracy and computational efficiency in regression tasks [39]. It optimizes the loss function containing L1 and L2 regularization by integrating multiple decision trees to improve model generalization [40]. The objective function is defined as:

$$\mathcal{L}=\sum _{i=1}^{n}l(y_i,{\widehat{y}}_i)+\sum _{k=1}^K\Omega \left(f_k\right)$$

(9)

$$\Omega \left(f_k\right)=\gamma T+{\displaystyle \frac{1}{2}}\lambda \sum _{j=1}^T{w}_j^2$$

(10)

where $y_i$ is the actual value. ${\widehat{y}}_i$ is the predicted value. l is the loss function. $\Omega \left(f_k\right)$ is the regularization term of the tree. T is the number of leaf nodes. $w_j$ is the leaf node weights, and $\gamma$, $\lambda$ are the regularization parameters.XGBoost approximates loss using second-order gradient information:

$${\mathcal{L}}^{\left(t\right)}\approx \sum _{i=1}^n\left[g_i{\widehat{y}}_i^{\left(t\right)}+{\displaystyle \frac{1}{2}}{h}_i{\left({\widehat{y}}_i^{\left(t\right)}\right)}^2\right]+\Omega \left(f_t\right)$$

(11)

where $g_i={\displaystyle \frac{\partial l}{\partial {\dot{y}}_i}}\mathrm{and}{h}_i={\displaystyle \frac{{\partial }^{2}l}{\partial {\dot{y}}_i^2}}$ and are the first and second order derivatives, respectively. Tree construction maximizes the gain by selecting the optimal features through greedy splitting:

$$\mathrm{Gain}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{{\left({\sum }_{i\in I_L}{g}_i\right)}^2}{{\sum }_{i\in I_L}{h}_i+\lambda }}+{\displaystyle \frac{{\left({\sum }_{i\in I_R}{g}_i\right)}^2}{{\sum }_{i\in I_R}{h}_i+\lambda }}-{\displaystyle \frac{{\left({\sum }_{i\in I}{g}_i\right)}^2}{{\sum }_{i\in I}{h}_i+\lambda }}\right]-\gamma$$

(12)

where $I_L$, $I_R$ are the left and right child node sample sets, and I is the parent node sample set. XGBoost utilizes second-order gradient information and parallel computation to efficiently process high-dimensional features and large-scale datasets.

In the proposed framework, the XGBoost model estimates the initial ammonia water flow based on preprocessed input features, including flue gas flow, temperature, O₂ concentration, pressure, and humidity. During the training process, XGBoost employs an additive model structure and optimizes the loss function using gradient descent. In each iteration, the model generates a new decision tree by fitting the current residuals and incorporates second-order derivative information to accelerate the convergence process. Additionally, the use of column subsampling and row subsampling strategies further improves the model’s computational efficiency and generalization ability. The high-precision initial prediction output by the model effectively narrows the search space for CSGA, reducing the overall computational cost of the optimization process. This enables efficient optimization and control of ammonia water flow, ensuring that NO_x emission concentrations remain below 50 mg/Nm³.

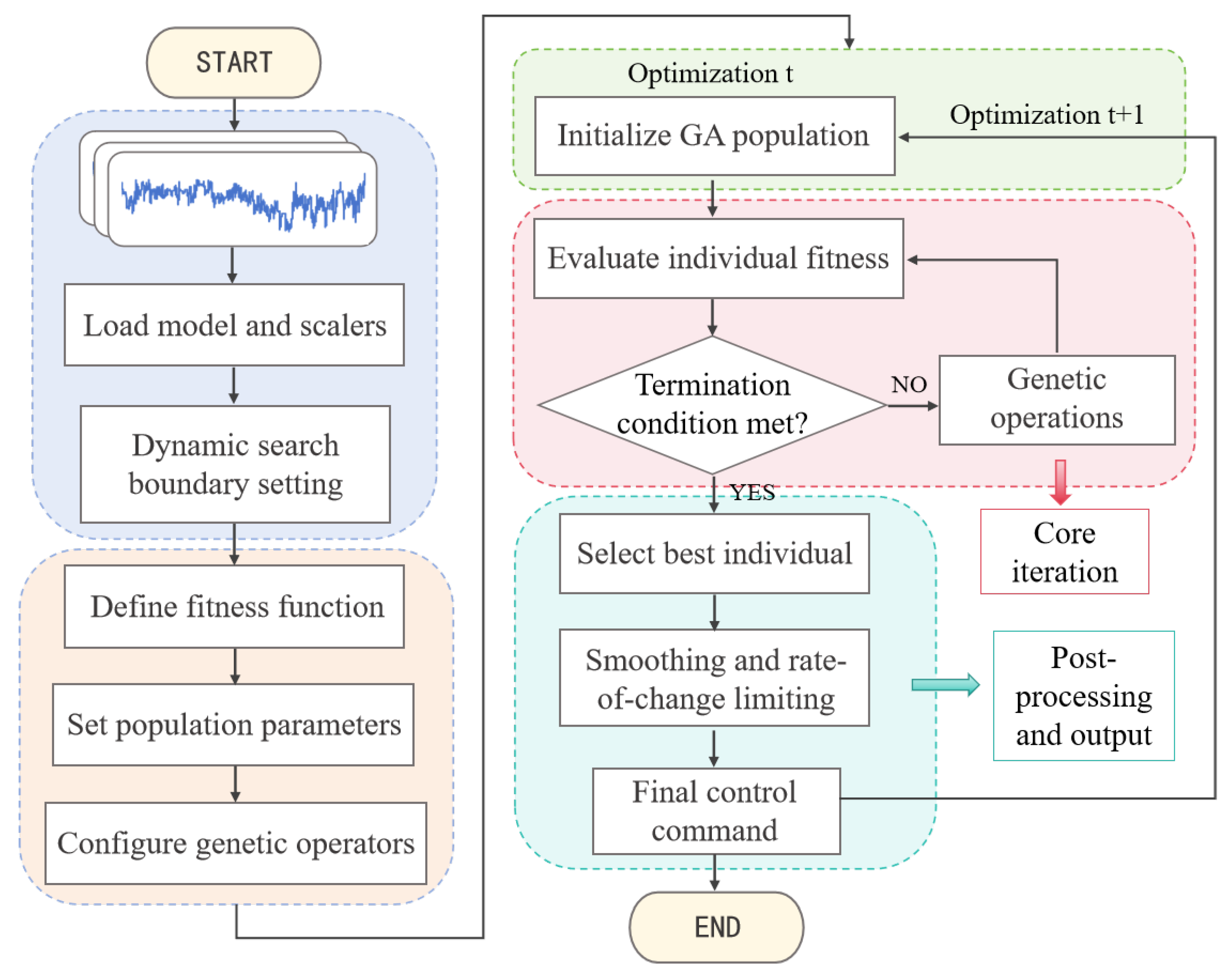
2.2.3. CSGA

Genetic algorithms (GA) are optimization techniques inspired by natural selection and genetic mechanisms, widely applied to solve complex nonlinear optimization problems [41]. The algorithm evolves a population of candidate solutions, with each individual representing a set of ammonia flow parameters, through iterative selection, crossover, and mutation operations to approach the global optimum. In this study, we propose a CSGA, which incorporates several deep modifications tailored for industrial denitrification systems. By introducing a weighted aggregation fitness function and a dynamic search space optimization mechanism, CSGA significantly improves convergence speed and solution quality in the co-optimization of ammonia flow and NO_x emissions, effectively overcoming the premature convergence and low search efficiency limitations often encountered by conventional GA in high-dimensional, strongly constrained problems. The optimization workflow of CSGA is illustrated in Figure 5.

The fitness function is designed to evaluate the performance of each individual solution. In the CSGA algorithm, a weighted aggregate fitness function is formulated to transform the multi-objective optimization problem into a single-objective one through a combination of weighting coefficients and a penalty mechanism. Specifically, the weight coefficient $w_1$ regulates the contribution of ammonia consumption $N{H}_3\left(x\right)$ to the overall objective, reflecting the consideration of economic operating costs. The weight coefficient $w_2$, combined with a nonlinear penalty term $max(0,N{O}_x\left(x\right)-50)$, constitutes the environmental constraint mechanism. When the predicted NO_x emission exceeds the threshold of 50 mg/m³, the penalty term becomes positive and increases proportionally with the degree of violation, thereby guiding the algorithm to search for solutions that comply with environmental regulations.This design ensures that the algorithm achieves multi-objective collaborative optimization of the denitrification system by maintaining an appropriate balance among environmental compliance, economic efficiency, and operational stability. The weighted aggregate fitness function is expressed as follows:

$$\mathrm{Fitness}\left(x\right)=w_1·Q_{{\mathrm{NH}}_3}\left(x\right)+w_2·max(0,{\mathrm{NO}}_x\left(x\right)-50)$$

(13)

where x denotes the ammonia dosing parameter, $Q_{{\mathrm{NH}}_3}$ is the ammonia consumption (L/h), ${\mathrm{NO}}_x$ is the concentration (mg/Nm³) predicted by MSCA-Net, and $w_1$, $w_2$ are the weights balancing cost and emission constraints.

The assignment of weight coefficients is crucial for guiding the search direction of the algorithm. In this study, the final values of the weighting parameters were determined based on an analysis of the typical fluctuation range of ammonia consumption in historical operation data (standard deviation $\approx 78.6$ L/h), combined with a series of preliminary trade-off experiments. The core principle was to strictly ensure environmental compliance while considering economic operating costs. To guarantee that even a slight NO_x exceedance (e.g., 1 mg/Nm³) would produce a penalty large enough to outweigh any potential fitness gain from ammonia savings, the following condition must be satisfied: $w_2\gg w_1$. Experimental results demonstrated that when the weight ratio satisfies approximately ${\displaystyle \frac{w_2}{w_1}}\approx 500$ the optimization achieves an optimal balance between maintaining a high NO_x compliance rate (>94%) and effectively reducing ammonia consumption. Based on this analysis, the final coefficients were set as $w_1$ = 1, $w_2$ = 500.

The individual with higher adaptation is selected by the mechanism with selection probability:

$$P_i={\displaystyle \frac{{\mathrm{Fitness}}_i}{{\sum }_{j=1}^N{\mathrm{Fitness}}_j}}$$

(14)

where N is the population size. Crossover (probability P, usually taken as 0.6–0.9) and mutation (probability $P_m$, usually taken as 0.01–0.1) operations generate new individuals to ensure population diversity.

A data-driven search space optimization mechanism is employed to enhance both the efficiency and practicality of the algorithm. This mechanism dynamically narrows the search boundaries based on historical operational data and incorporates a post-processing control layer. By applying smoothing filters, the theoretically optimal solutions are converted into stable commands that can be safely executed by physical equipment, thereby enabling engineering-ready optimization. Specifically:

1.

Dynamic Search Boundaries: rather than using traditional fixed boundaries, the upper and lower limits are determined dynamically based on the 10th and 90th percentiles of historical data. This guides the algorithm to focus on regions most likely to contain high-quality solutions, improving search efficiency while ensuring the spatial plausibility of the results.

2.

Smoothing and Rate-of-Change Constraints: a moving average filter is applied to the optimized instruction sequence, and the maximum allowable change in ammonia flow between consecutive time steps is enforced. Smooth flow variations are critical for maintaining stable temperature, pressure, and concentration within denitrification systems. This control effectively prevents system disturbances caused by abrupt fluctuations in optimization commands, ensuring physical feasibility and overall system stability while achieving the optimization objectives.

Compared with optimization methods such as gradient descent and particle swarm optimization, GA offers strong global search capabilities, relaxed assumptions on problem structure, and robust adaptability to complex nonlinear constraints, demonstrating clear advantages in high-dimensional and multimodal industrial optimization problems. Accordingly, this study adopts GA as the foundational framework to develop CSGA, further integrating problem-specific knowledge and data-driven strategies. Building on GA’s global exploration capability, CSGA incorporates dynamic boundary adjustment, a weighted aggregation fitness function, and smoothing post-processing to effectively enhance convergence speed, solution quality, and engineering feasibility in denitrification system control. This enables the synergistic optimization of NO_x emission control and economic operation.

2.3. Model Evaluation

To comprehensively validate the overall effectiveness of the proposed framework and the predictive performance of its key components, an evaluation system was established at two levels: system control performance and model prediction accuracy. At the system control level, three key performance indicators were employed: NO_x compliance rate, average ammonia consumption, and exceedance ratio, providing a holistic assessment of the denitrification system in terms of environmental compliance, economic efficiency, and operational reliability. At the predictive model level, MSCA-Net and XGBoost were quantitatively evaluated using three commonly adopted metrics: coefficient of determination (R²), mean absolute error (MAE), and root mean square error (RMSE). R² measures the proportion of variance in the data explained by the model, with values closer to 1 indicating a better fit. MAE quantifies the average absolute deviation between predicted and observed values; it is robust to outliers and provides a reliable measure of error. RMSE emphasizes larger deviations by squaring the residuals, making it sensitive to outliers. Together, MAE and RMSE provide a comprehensive evaluation of model performance across different error characteristics, with smaller values indicating higher predictive accuracy. The specific formulas for each evaluation metric are presented below.

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^N{(y_i-\overline{y})}^2}}$$

(15)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{({\widehat{y}}_i-y_i)}^2}$$

(16)

$$MAE={\displaystyle \frac{1}{N}}\sum _{i=1}^N|{\widehat{y}}_i-y_i|$$

(17)

where N is the total number of samples. $y_i$ is the actual value of the ith sample. ${\widehat{y}}_i$ is the predicted value of the ith sample. And y is the mean of the sample.

3. Results and Discussion

To validate the effectiveness of the proposed method in NO_x reduction and ammonia water flow optimization, a series of experiments were conducted. Firstly, based on the actual operational data of the industrial denitrification system, NO_x prediction and ammonia water flow prediction models were developed and compared with traditional machine learning methods. To ensure the reliability of the experiments, all models were trained and tested under the same data split and hyperparameter settings. Additionally, feature correlation analysis and ablation experiments were performed to explore the relationships between different input variables and the contribution of key model components, providing a comprehensive evaluation of prediction accuracy and optimization performance.

3.1. Variable Correlation and Feature Selection

Considering the numerical characteristics of the dataset and the validity of the input signals, eight variables were initially selected as input features: kiln valve opening, kiln temperature, flue gas temperature and pressure at the system inlet, flue gas flow rate, SO₂ concentration, O₂ concentration, and humidity. The ammonia flow rate was defined as the output variable. For the NO_x prediction model, ammonia flow rate was incorporated as an additional input feature, with outlet NO_x concentration serving as the target output. Ensuring the independence of input features is critical for constructing a robust predictive model. High correlations among features (i.e., multicollinearity) can lead to unstable parameter estimates and adversely affect the model’s generalization capability. Therefore, in this study, Pearson correlation analysis was employed to assess the linear dependencies among all input features. The resulting feature correlations are shown in Figure 6.

Among the input features, kiln temperature exhibited a strong positive correlation with flue gas humidity at the system inlet (p = 0.71). Kiln temperature was therefore selected as the training input, as it contained fewer missing values in the raw data and offered higher data completeness. In addition, kiln temperature showed a significant positive correlation with ammonia flow rate (r = 0.68), indicating that higher kiln temperatures are generally associated with increased ammonia consumption. This further highlights the informative value of kiln temperature in characterizing system operating conditions. The remaining features displayed only weak correlations, suggesting a high degree of mutual independence and suitability as independent variables for model construction.

3.2. Experimental Setup

To comprehensively assess the efficacy of the proposed data-driven framework, the dataset was partitioned into two distinct subsets: a primary subset comprising 6866 samples for model training and testing, and a secondary validation subset containing 1656 samples specifically reserved for evaluating ammonia dosing-optimization performance. All experiments were performed on a single NVIDIA A40 GPU to ensure consistency of computational resources. Both model training and inference were executed under a CUDA 12.2 environment, which provided stable and efficient GPU acceleration. This controlled setup not only guaranteed reproducible results but also minimized potential variability arising from heterogeneous hardware or software configurations.

3.3. Model Performance Evaluation

3.3.1. NO_x Prediction Model Evaluation

To ensure model performance and reproducibility, we systematically configured and optimized the key hyperparameters of MSCA-Net. The detailed hyperparameter settings are summarized in

Table 1. Detailed hyperparameter setting table.

Hyperparameter	Value
Hidden Size	128
Dropout Rate	0.3
Convolutional Filters	64
Kernel Size	3
Optimizer	AdamW
Learning Rate	0.01
Batch Size	64

.

Figure 7 illustrates the predictive performance of the MSCA-Net model on the test dataset for NO_x concentration. Panel (a) compares predicted and observed NO_x concentrations across the full test range. The results demonstrate that the model effectively captures the overall temporal evolution of NO_x concentrations and maintains strong predictive consistency even under complex operating conditions. Although slight deviations appear at a few peak values (e.g., near sample indices 800 and 1200), the model nonetheless exhibits robust performance when handling large-scale data.

Panel (b) provides a magnified view of the first 100 test samples, where observed values are marked with blue circles and predictions with red crosses, connected by lines to highlight correspondence. Compared with the global trend in panel (a), this localized analysis underscores the model’s capability at a fine-grained level. Most predictions align closely with the ground truth, with only minor discrepancies observed around indices 20, 60, and 80. These results indicate that MSCA-Net preserves high predictive accuracy even under strongly nonlinear and multivariate coupling conditions.

Taken together, panels (a) and (b) validate the reliability and practical potential of MSCA-Net in forecasting outlet NO_x concentrations in denitrification systems. The model demonstrates not only large-scale robustness but also superior fine-grained predictive fidelity, reflecting its optimization for the complex dynamics of industrial flue gas treatment.

To evaluate the contribution of each module within MSCA-Net, ablation studies were performed on the dataset. In these experiments, key modules were incrementally incorporated, and their respective impacts on model performance were systematically assessed. The outcomes of these ablation experiments are presented in

Table 2. Ablation study results of MSCA-Net.

LSTM	CNN	CBAM	${\mathit{R}}^2$	MAE	RMSE
✓			0.894	4.033	5.665
✓	✓		0.899	3.818	5.514
✓	✓	✓	0.912	3.540	5.136

Note: The symbol ✓ indicates that the corresponding module is included in the model.

.

The experimental results show that the performance of MSCA-Net improves with the gradual introduction of key modules. When using only LSTM, the model achieved an R² of 0.894, MAE of 4.033, and RMSE of 5.665. After incorporating CNN, R² increased to 0.899, with MAE and RMSE reduced to 3.818 and 5.514, respectively, indicating that CNN enhanced the ability to extract spatial features. Further integration of CBAM increased R² to 0.912, with MAE reduced to 3.540 and RMSE dropping to 5.136, demonstrating that the attention mechanism effectively improved feature representation. In summary, LSTM provides the foundation for temporal modeling, CNN enhances spatial features, and CBAM optimizes feature representation. The collaborative effect of all modules significantly improved the model’s performance.

To assess the reliability of the model performance improvements, five independent repeated experiments were conducted for three different network architectures, and paired t-tests were performed to evaluate statistical significance. The results are summarized in

Table 3. Average R² and standard deviation of model performance under ablation settings (n = 5).

LSTM	CNN	CBAM	Mean ${\mathit{R}}^2$	Standard Deviation
✓			0.8944	0.0011
✓	✓		0.8992	0.0014
✓	✓	✓	0.9094	0.0016

Note: The symbol ✓ indicates that the corresponding module is included in the model.

. The mean R² values for LSTM, LSTM + CNN, and MSCA-Net were 0.8944, 0.8992, and 0.9094, respectively, with corresponding standard deviations of 0.0011, 0.0014, and 0.0016. Compared with the LSTM baseline, the addition of the CNN module led to a significant improvement in model performance (p < 0.01), and the subsequent incorporation of the CBAM module further enhanced performance (p < 0.001). These results indicate that the performance gains of MSCA-Net are not due to chance, but arise from the effective synergistic interactions among its constituent modules, resulting in a stable and robust improvement.

3.3.2. Initial Ammonia Dosing Prediction Model Evaluation

In order to verify the effectiveness of XGBoost for initial ammonia water flow prediction, comparative experiments were conducted using five other models: ANN, RF, KNN, LSSVM, and categorical boosting (CatBoost). Since the performance of machine learning (ML) models can vary with different combinations of hyperparameters, Bayesian Optimization was used to fine-tune the hyperparameters, assessing the performance of each combination to identify the optimal hyperparameter settings for the best model performance.

Table 4. Experimental hyperparameter setting table.

Model	Hyperparameters
ANN	hidden_layer_sizes = (100, 50), max_iter = 1000
RF	n_estimators = 300, max_depth = 10, min_samples_split = 8, min_samples_leaf = 4
KNN	n_neighbors = 3
LSSVM	C = 100, gamma = 1, kernel = ‘rbf’
CatBoost	learning_rate = 0.1, l2_leaf_reg = 1, iterations = 1000, depth = 8, bagging_temperature = 0.2
XGBoost	n_estimators = 351, max_depth = 7, min_child_weight = 4, learning_rate = 0.05, reg_alpha = 0.8, reg_lambda = 0.7

presents the hyperparameter settings for all models.

The predictive performance of the models was comprehensively evaluated through a combination of visual comparison between predicted and observed values, and quantitative metrics including R², MAE, and RMSE. The results indicate that XGBoost achieved the best performance in predicting ammonia flow rates. As shown in Figure 8, the R² values of the six models were as follows: XGBoost (0.951), CatBoost (0.949), RF (0.892), KNN (0.878), LSSVM (0.843), and ANN (0.779), with MAE and RMSE showing consistent trends.From the scatter plots of predicted versus observed values, the predictions of XGBoost and CatBoost lie closest to the diagonal line, indicating minimal prediction errors. In contrast, the prediction points of the ANN model are more widely dispersed, reflecting its relatively poor prediction stability.

The superior performance of XGBoost can be attributed to the strong alignment between its algorithmic mechanisms and the characteristics of the industrial data considered in this study. First, industrial process parameters often exhibit complex nonlinear interactions, and the gradient-boosted tree ensemble structure of XGBoost effectively captures higher-order variable interactions through its recursive partitioning strategy. Second, to address inherent noise and fluctuations in industrial sensor data, XGBoost incorporates L1 and L2 regularization terms in its objective function, which penalize model complexity and enhance generalization, thereby mitigating overfitting to noisy signals. Furthermore, its use of a second-order Taylor expansion for optimization enables more accurate estimation of gradient directions and step sizes, improving both convergence efficiency and overall predictive performance.

In contrast, alternative models demonstrate certain limitations when applied to this task. Although CatBoost also employs a gradient-boosting framework, its ordered boosting mechanism, designed primarily for categorical features, is less effective in this study, where the dataset predominantly consists of numerical variables. Its regularization flexibility is also slightly inferior to that of XGBoost. Random Forest (RF), as a bagging-based ensemble method, generally achieves lower predictive accuracy compared with gradient-boosted architectures. KNN and LSSVM have limited capacity to model high-dimensional nonlinear relationships, while ANN models may be constrained by the size of the training data and the difficulty of hyperparameter tuning, preventing them from fully realizing their theoretical potential.

Taken together, XGBoost consistently exhibits the best performance across multiple evaluation metrics, demonstrating both high accuracy and robustness for predicting ammonia flow rates in industrial processes. These characteristics make it a reliable predictive model for subsequent control strategy development.

3.3.3. Ammonia Dosing Optimization

This study employed a CSGA-based global optimization strategy to simultaneously achieve low NO_x emissions and fine-grained control of ammonia flow rate. Experimental results demonstrate that the NO_x compliance rate increased from 83.97% to 94.23%, representing a 10.26% improvement. The mean ammonia flow rate decreased from 585.69 L/h to 552.14 L/h, yielding an average saving of 33.56 L/h, while the exceedance rate declined by 8.39%. These findings indicate that global optimization not only effectively reduces operational costs but also significantly enhances system stability and control precision.

Figure 9 further illustrates the comparison of key performance indicators before and after CSGA optimization. The pre-optimization performance corresponds to historical operational data collected under the conventional PID control strategy in the plant, serving as a baseline to evaluate the effectiveness of the proposed CSGA optimization framework. In the radar chart, the blue line represents pre-optimization performance, while the orange line corresponds to post-optimization results. For the NO_x compliance rate, the optimized line approaches 1, highlighting a marked improvement in emission control. In terms of ammonia flow rate, the post-optimization values are substantially lower, indicating an effective reduction in ammonia consumption. The exceedance rate similarly decreases, reflecting better management of limit violations. For the mean absolute change in ammonia flow rate (Mean |$\Delta Q$|), a declining trend is also observed after optimization. Collectively, the consistent improvements across all dimensions of the radar chart demonstrate that CSGA global optimization can simultaneously reduce NO_x emissions and precisely regulate ammonia flow, thereby lowering operational costs while enhancing system stability and control accuracy.

Figure 10 presents the overall performance evaluation of the denitrification system optimization strategy. Panel (a) shows the frequency distribution of ammonia savings. The distribution exhibits a unimodal shape, with the peak centered near zero, indicating that ammonia savings fluctuate around zero under most operating conditions. Frequencies gradually decrease toward both tails, with low occurrences in the negative region and at high positive values (e.g., >100 L/h), suggesting that extreme ammonia reductions or increases are rare. Overall, the distribution demonstrates a clear concentration around typical values. Panel (b) illustrates the predictive performance of NO_x optimization. Orange scatter points represent the distribution of optimized NO_x values, while reference lines indicate the target optimization values. The degree of alignment between scatter points and reference lines provides a visual assessment of the model’s accuracy and stability in controlling NO_x emissions.

3.3.4. Computational Cost and Deployment Feasibility Analysis

To evaluate the practical applicability of the proposed approach in industrial settings, the computational performance of the MSCA-Net model and the CSGA optimizer was systematically assessed. The results indicate that MSCA-Net comprises a total of 194,330 parameters, with an average training time of 3.78 min per epoch, demonstrating satisfactory training efficiency. During online inference, the forward prediction time for a single sample remains consistently at the millisecond level (<10 ms), while the CSGA optimizer exhibits an average execution time of 54.47 s per sample, with a standard deviation of 6.67 s, indicating stable convergence characteristics.

From an industrial deployment perspective, the constructed optimization framework aligns well with the operational requirements of process plants. Although the training of MSCA-Net requires certain computational resources, its exceptional inference speed, combined with the stable optimization performance of CSGA, fully satisfies the temporal requirements of an hourly control strategy in denitrification systems. The minute-level optimization time provides sufficient computational margin relative to the hourly control cycle, enabling the completion of all optimization calculations at the beginning of each control period and supplying timely setpoint guidance for on-site operations.

4. Conclusions

This study proposes a control optimization strategy for denitrification systems based on a hybrid modeling framework and an improved genetic algorithm, enabling the efficient, low-cost, and sustainable operation of flue gas denitrification systems using real-time sensor data. Under the ultra-low NO_x emission requirement of maintaining concentrations below 50 mg/Nm³, the strategy significantly reduces ammonia consumption and mitigates secondary environmental impacts, promoting sustainable use of both environmental and material resources. Specifically:

• Proposed an innovative collaborative optimization framework: by integrating the high-precision NO_x prediction model MSCA-Net, XGBoost-guided initialization, and the multi-objective global optimization of CSGA, the framework achieves an effective synergy that simultaneously optimizes environmental and economic performance.
• Validated the superior performance of the strategy: experimental results demonstrate that, compared with conventional methods, the proposed approach significantly improves key performance indicators, including NO_x compliance rate, ammonia consumption reduction, and the control of exceedance ratios.
• Demonstrated the feasibility of industrial deployment: computational cost analysis indicates that the proposed strategy is practically applicable. MSCA-Net achieves millisecond-level forward inference, while the CSGA optimizer requires an average of approximately 54 s per sample, satisfying the real-time requirements of industrial denitrification system control and demonstrating strong deployment potential.

Despite the excellent predictive accuracy and optimization performance, it should be noted that the dataset used in this study is limited to a single plant. The model’s generalization capability across different operating conditions and industrial sites remains to be validated in future work. Based on the outcomes and limitations of the current study, future research will focus on the following directions:

• Enhancing model robustness and generalization: combining transfer learning and domain adaptation techniques to improve the model’s cross-plant generalization and robustness.
• Developing a real-time closed-loop control system: designing a specific edge–cloud collaborative control architecture, in which lightweight models are deployed at the edge for high-frequency real-time optimization, while complex model updates and performance monitoring are handled in the cloud, ultimately enabling the transition from “open-loop optimization” to “closed-loop control”.