Abstract
The accurate detection of high-impedance faults (HIFs) in distribution systems is fundamentally dependent on the extraction of weak fault signatures. However, these features are often obscured by complex and high-level noise present in current transformer (CT) measurement data. To address this challenge, an energy-proportion-guided channel-wise attention stacked denoising autoencoder (EPGCA-SDAE) model is proposed. In this model, wavelet decomposition is employed to transform the signal into informative frequency band components. A channel attention mechanism is utilized to adaptively assign weights to each component, thereby enhancing model interpretability. Furthermore, a physics-informed prior, based on energy distribution, is introduced to guide the loss function and regulate the attention learning process. Extensive simulations using both synthetic and real-world distribution network data are conducted. The superiority of the EPGCA-SDAE over traditional wavelet-based methods, stacked denoising autoencoders (SDAE), denoising convolutional neural network (DnCNN), and Transformer-based networks across various noise conditions is demonstrated. The lowest average mean squared error (MSE) is achieved by the proposed model (simulated: ; real: ), along with enhanced noise robustness, generalization capability, and physical interpretability. These results verify the method’s feasibility within the tested 10 kV distribution system, providing a reliable data recovery framework for fault diagnosis in noise-contaminated distribution network environments.
1. Introduction
With the development of the socio-economy, higher requirements have been imposed on the operational reliability of distribution networks [1,2]. Among various types of faults in distribution networks, single-phase-to-ground faults have been identified as the most prevalent, with the detection of High-Impedance Faults (HIFs) considered particularly challenging. HIFs are typically caused by broken conductors making contact with utility poles, the ground, or tree branches that touch power lines. These faults are often accompanied by arc discharge and are characterized by a time-varying transition resistance, typically ranging from several hundred to several thousand ohms. Due to the nonlinear nature of the transition resistance, repeated extinction and re-ignition of the arc are observed during an HIF event. A pronounced distortion in the zero-sequence current waveform near the zero-crossing point is manifested, which is regarded as a key distinguishing feature of HIFs compared to HIF-like non-fault conditions. In practical scenarios, signals acquired through current transformers (CTs) are prone to distortion, which can obscure essential signal features, thereby rendering the detection of HIFs extremely difficult.
HIF detection methods are generally classified into deterministic and heuristic approaches, signal processing-based techniques, and artificial intelligence (AI)-based methods. In deterministic and heuristic approaches, fault detection is typically carried out based on system knowledge, predefined electrical rules, or empirical features such as current sequence morphology, current or voltage imbalance, or energy variation trends [3,4,5,6]. Although simple architectures and fast computational efficiency are exhibited by these methods, substantial degradation in stability and reliability is often observed under noisy conditions in practical environments. On the other hand, signal processing-based methods are employed to extract discriminative patterns of HIF features through techniques such as time–frequency analysis, wavelet transformation, empirical mode decomposition, or sparse coding. Discrimination is subsequently performed through the application of thresholding strategies or template matching [7,8,9,10,11]. However, the thresholds adopted in these methods are typically determined based on expert knowledge and the availability of high-quality data. Although a certain level of noise immunity is maintained, detection performance is significantly degraded when the noise distribution approximates the characteristic distribution. Finally, AI-based methods are primarily employed through machine learning (ML). These approaches are either used to directly perform end-to-end feature extraction and fault classification by means of models such as variational autoencoders, sparse encoders, or long short-term memory (LSTM) networks, or are developed by combining traditional feature engineering with machine learning models to form hybrid architectures [12,13,14,15]. AI methods are capable of autonomously learning complex fault characteristics and patterns from large volumes of data, demonstrating strong robustness to noise and environmental variations. However, the performance of such models is highly dependent on the scale and quality of the training data, and poor interpretability is generally exhibited due to the presence of the “black box” problem [16,17,18].
However, data obtained in practice are inevitably corrupted by noise ranging in degree. Utilizing effective measures to restore noisy data is very important, as it is a prerequisite and indispensable assurance to obtain accurate distribution network fault diagnosis. Towards this goal, numerous noised counteracting technologies have been designed by researchers. In Bai et al. [19], background noise was suppressed and HIF features were extracted through the integration of the frequency band energy curve with Gaussian smoothing techniques. In Yeh et al. [20], discrete wavelet transform (DWT) was utilized to decompose distribution system signals, and the effective extraction of high-frequency characteristics from high-impedance grounding faults was accomplished through adaptive soft-threshold denoising. In Shahrtash and Sarlak [21], a harmonics energy decision tree algorithm was proposed for high-impedance fault detection, in which fault conditions were identified by analyzing the energy distribution of harmonic components and applying decision tree rules. In Dai et al. [22], a data cleaning method based on a stacked denoising autoencoder (SDAE) was introduced to rectify outliers and missing values in distribution network equipment monitoring data. In Zhang et al. [23], a denoising method based on a deep convolutional neural network (DnCNN) and residual learning was proposed, which effectively removed Gaussian noise. In Pan et al. [24], 1D convolutions were combined with Transformer encoders to enhance global temporal modeling capabilities while preserving local feature extraction. Superior performance was demonstrated by this approach in denoising transient electromagnetic signals, along with improved data interpretation accuracy being achieved. Various approaches for distribution network data denoising are proposed by the aforementioned methods, yet inherent limitations are retained by each. A certain degree of interpretability is provided by traditional techniques such as frequency band energy analysis and wavelet thresholding; however, their performance is constrained by manually defined parameters, and limited adaptability is exhibited in complex noise environments. In contrast, improved denoising effectiveness is demonstrated by deep learning-based methods; nevertheless, clear physical interpretation is not offered by their internal mechanisms, and adequate preservation of critical fault characteristics during the denoising process cannot be readily verified. Consequently, an effective balance between interpretability and denoising performance remains unachieved, and a new approach is urgently required by which denoising capability can be maintained while explicit physical interpretability is simultaneously ensured.
To address this challenge, an energy-proportion-guided channel-wise attention stacked denoising autoencoder (EPGCA-SDAE) is proposed in this paper. The principal contributions of this model comprise two core aspects:
- An energy prior-guided attention training mechanism is introduced, which utilizes physical priors to constrain the attention learning, ensuring that the model purposively preserves critical signal characteristics.
- A channel-wise attention module dedicated to multi-channel wavelet is designed. With the support of the energy proportion guidance mechanism, the importance of different frequency bands is adaptively learned, leading to enhanced denoising performance and improved model interpretability.
The primary advantage of the proposed EPGCA-SDAE framework is considered to lie in its integration of physical interpretability and data-driven learning. Through the embedded energy-proportion guidance within the channel attention mechanism, an explicit alignment between the learned feature weights and the physical energy distribution of the signal is established. By this design, robust noise suppression is achieved. Compared with traditional denoising autoencoders or purely data-driven networks, higher reconstruction accuracy, stronger generalization capability under varying noise conditions, and improved interpretability of internal feature representations are demonstrated.
Nevertheless, a practical limitation is recognized in the acquisition of representative denoising datasets in real-world power distribution systems. The collection of high-quality, labeled HIF data under diverse noise conditions is hindered by safety restrictions, the low frequency of actual fault events, and the variability of field measurement environments. Consequently, the diversity and scale of available datasets are limited, which may restrict the generalization capability of the proposed framework when applied to different system conditions.
2. EPGCA-SDAE for Data Denoising
2.1. Noise’s Impact on Distribution Fault Detection
The accurate identification of HIFs in distribution networks is critically dependent on the capture of their subtle fault characteristics. However, measurement errors introduced by CTs contaminate the signals with noise, causing the already weak fault signatures to be submerged and presenting significant challenges for detection. Figure 1 shows the current waveform after experiencing an actual occurrence of the HIF during the time on a power grid. In Medium 1 (illustrated as the black curve), noticeable oscillations appear around 0.01 s, where the distortion characteristic phenomenon is clearly visible. Conversely, Medium 2 (illustrated as the red curve) experiences stronger noise interference, which nearly fully engulfs the distortion characteristics in the first part. Multiple disorderly and haphazard oscillations are also presented as waveform as that of Medium 2. The fundamental nature of an HIF involves non-linear distortion of the current waveform caused by arcing at the fault point. Consequently, the initial cycles following fault inception are contaminated by strong noise, which severely impedes the accurate extraction and interpretation of the essential fault characteristics.
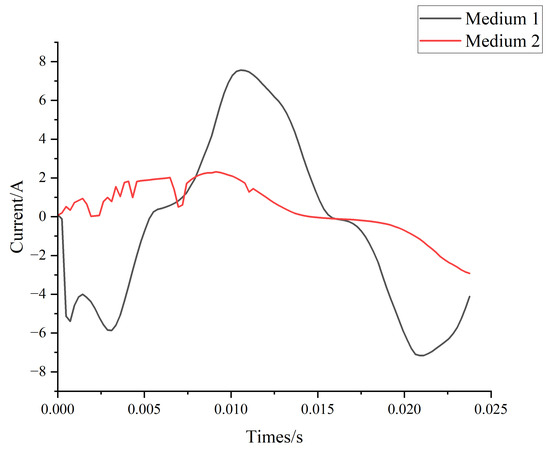
Figure 1.
Waveform of HIF.
Measurement data from CTs are often contaminated by various types of noise [25,26]. This includes internal noise induced by sensor non-linearity, temperature drift, saturation effects, and sampling quantization; responses caused by magnetic core deformation due to mechanical vibration; and external electromagnetic interference introduced during signal transmission. These noise components can submerge subtle fault characteristics. Therefore, effective denoising processing is regarded as a critical step for enhancing the accuracy of distribution network fault diagnosis.
2.2. Fitting of Real Noise Distribution
To evaluate the robustness of the fault identification algorithm under noisy conditions, the simulation signals were contaminated with White Gaussian Noise (WGN) of varying intensities [27,28,29,30]. The noise intensity was controlled by the Signal-to-Noise Ratio (SNR), which is defined as the ratio of the power of the output signal to the power of the noise signal . A smaller SNR value indicates a greater proportion of noise within the total signal, leading to a more significant impact on system performance. The calculation can be expressed as follows:
To achieve a preset SNR level, the required noise power is first calculated based on the power of the original signal , from which the standard deviation of the noise can subsequently be derived.
Subsequently, Gaussian white noise is generated using a normally distributed random variable with a mean of zero and a variance of :
Finally, the contaminated signal is obtained by superimposing the noise signal onto the original simulated signal :
This process can be employed to simulate electrical measurement data from distribution networks under varying noise intensities, thereby enabling the systematic evaluation of the robustness of fault identification methods against noise interference.
2.3. EPGCA-SDAE Model
The proposed EPGCA-SDAE model is composed of four key components: a wavelet decomposition module, a channel-wise attention module, an energy proportion guidance module, and an SDAE denoising module. In the wavelet decomposition module, the raw time-domain signal is first decomposed through multi-level discrete wavelet transform, separating it into several detail coefficients and one approximation coefficient, thereby obtaining a physically meaningful multi-channel feature representation. The purpose of this step is to distinctly separate the energy characteristics of the signal in the time–frequency domain, facilitating differentiated processing by the model in subsequent stages (Figure 2).
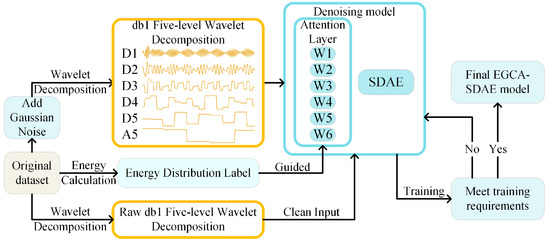
Figure 2.
Framework of EPGCA-SDAE.
Upon acquiring the multi-channel input, the wavelet components are processed by the channel-wise attention module, where they are adaptively weighted. The resulting attention distribution is capable of reflecting the model’s focus on features across different frequency bands, thereby intuitively characterizing the contribution of each channel to both the denoising and decision-making processes. When a specific frequency band exhibits more pronounced distortion characteristics amidst the noise, the weight assigned to that corresponding channel is adaptively increased, thereby ensuring both the accuracy and interpretability of the denoising results.
During the training phase, the energy proportion guidance module is employed to introduce the energy distribution from the original domain as a physical prior. By constructing a target distribution and incorporating it into the loss function, the learning process of the attention mechanism is effectively constrained. This energy proportion guidance enables the model to correct irrational weight assignments. The module ensures that stable denoising performance and high robustness are maintained by the model under various noise conditions.
3. Modules of EPGCA-SDAE
3.1. Wavelet Decomposition Module
The Multilevel Discrete Wavelet Transform (MLDWT) is utilized to progressively decompose a signal into low-frequency and high-frequency components across different scales [31,32,33]. Let the original discrete signal be represented as:
The approximation coefficients and detail coefficients at the j-th level can be expressed as:
where is defined, and h and g are designated as the low-pass and high-pass filters, respectively. After J levels of decomposition, the signal is represented in the coefficient space as:
The structure of the multilevel decomposition is illustrated in Figure 3. The original signal is progressively decomposed into sub-signals with non-overlapping frequency bands through MLDWT, achieving a joint time–frequency representation.
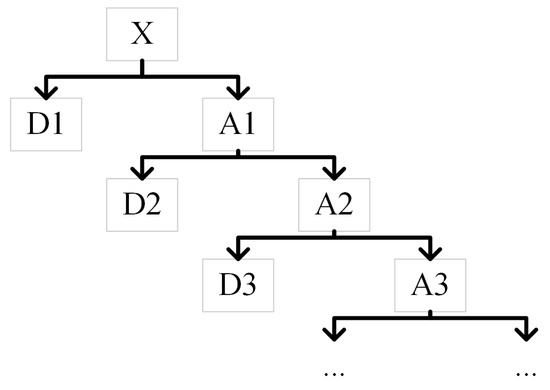
Figure 3.
Analysis tree structure diagram of Multilevel Discrete Wavelet Transform.
For time-domain comparative analysis, a sub-band-wise Inverse Discrete Wavelet Transform (IDWT) is employed: during reconstruction, only the coefficients of the target sub-band are retained, while all others are set to zero, denoted as and . The final signal is reconstructed in the form:
where represents the reconstructed waveform of the approximation component at the J-th level, and represents the reconstructed waveform of the detail component at the j-th level.
The reconstructed signal components not only reflect the proportion of each frequency band but also reveal the temporal distribution of these components, thereby comprehensively characterizing the time–frequency properties of the original signal.
3.2. Channel-Wise Attention Module
After obtaining the various components from the multilevel wavelet decomposition, a channel-wise attention mechanism is introduced in the proposed model to achieve adaptive weighting of different wavelet components. Attention mechanisms have been widely applied in HIF diagnosis [34,35].
Let the channel set obtained after the inverse wavelet transform be denoted as:
First, average pooling is performed along the temporal dimension for each channel to obtain channel-wise features:
where represents the total number of channels.
Subsequently, channel attention logits are obtained through a two-layer nonlinear mapping function:
where , , , , are defined as trainable parameters, and is designated as the activation function.
Next, the channel attention distribution is derived using a tempered softmax function:
where is defined as the temperature coefficient that controls the sparsity of the distribution. The attention weight vector satisfies . Finally, the channel features are weighted using the attention weights:
The weighted multi-channel input is thus obtained and subsequently fed into the encoder–decoder network for further processing.
Through this approach, the contribution of different wavelet channels can be adaptively adjusted by the model, thereby emphasizing key frequency bands while suppressing interference components. More importantly, the attention distribution itself possesses interpretability, intuitively reflecting the decision-making basis of the model during the denoising process.
3.3. Energy Proportion Guidance Module
The original signal is first decomposed by the MLDWT into multiple sub-signals, which are then reconstructed through sub-band-wise IDWT into sub-band components of equal length to the original signal. Since the db1 (Haar) wavelet basis with orthogonality is adopted in this paper, the sub-band components satisfy the orthogonal condition. According to Parseval’s theorem, the sum of squared energies of all sub-band components equals the total energy of the original signal. This energy conservation property enables the sub-band energy distribution to serve as prior information with clear physical significance. In Bai et al. [19], Varghese et al. [36], Zhang et al. [37], Wang et al. [38], energy features are extracted through wavelet or time–frequency analysis, and indicators such as differential energy, frequency band energy curves, and energy proportions are constructed. These derived metrics are utilized for accurate identification of high-impedance grounding faults in distribution networks, thereby enhancing the accuracy and robustness of fault detection. Based on this, the proposed energy proportion guidance module utilizes this prior to constrain the distribution of attention weights. For the c-th channel signal , the following calculations are performed:
where represents the mean of the c-th channel, is the zero-mean channel signal, is the channel energy, is the temperature parameter for energy shaping, is a constant to prevent division by zero, is the normalized energy distribution, is the attention distribution, and denotes the KL divergence.
The final loss function is defined as:
where is the model output, is the target signal, and is the weight of the guidance term.
Through energy proportion guidance, the attention distribution is aligned with the wavelet energy pattern, thereby enhancing the model’s controllability, robustness, and interpretability.
3.4. SDAE Denoising Module
The SDAE is employed as the fundamental reconstruction model in this work. The SDAE architecture is constructed by stacking multiple encoder and decoder layers, enabling the extraction of robust features in a high-dimensional space and the reconstruction of denoised signals during the decoding phase. The fundamental concept involves corrupting the input signal with noise during training, while setting the clean, original signal as the reconstruction target, thereby forcing the network to learn representations that are invariant to noise.
4. Evaluation Metrics
4.1. Average Mean Square Error (MSE)
4.2. Accuracy (ACC)
5. Case Study
5.1. HIF Simulation System
The model performance was validated through simulations conducted using PSCAD/EMTDC 4.6.2 software. The simulation model is shown in Figure 4.
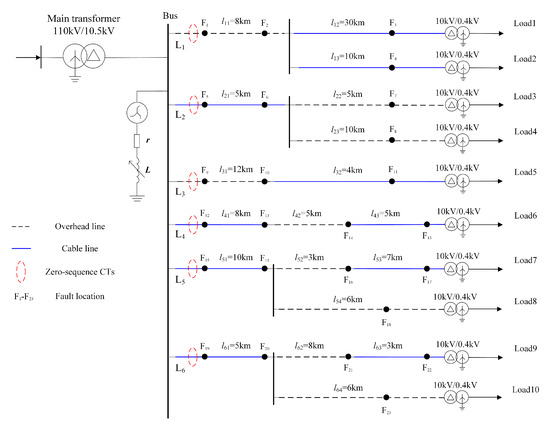
Figure 4.
Network structure of the simulation model.
In the figure, solid lines are used to represent cable lines, while dashed lines are employed to denote overhead lines. The parameter l is defined as the length of the overhead line. F1–F23 represent the predefined fault locations. Zero-sequence current transformers (CTs) are installed at the beginning of each feeder.
The Emanuel model [39], whose structure is depicted in Figure 5, was utilized as the HIF model in this study. The model is composed of two anti-parallel branches, each consisting of a diode, a voltage source, and a resistor. To simulate the random fluctuation characteristics of arc voltage and arc resistance observed in real faults, the parameters , , , and were set to fluctuate randomly over time within a range of of their predefined central values. Different grounding medium scenarios can be simulated by adjusting these parameters.
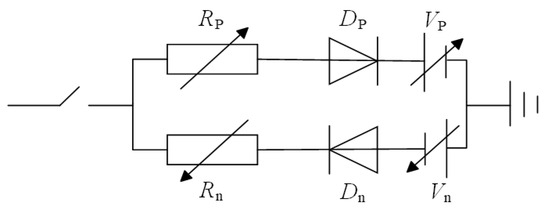
Figure 5.
Emanuel model.
For the dataset generation, the sampling rate was set to 2133 Hz. Fault incidents were simulated across a phase angle range of 0–180 degrees and a resistance range of 500–1500 . High-impedance grounding faults, inrush currents, capacitor switching events, and load switching events were configured at fault points F1–F23. A total of 8000 samples were generated, with a 1:1 ratio between fault data and non-fault data. The dataset was partitioned into 3000 samples for the training set, 3000 samples for the validation set, and 2000 samples for the test set. The first 150 sampling points from each signal were used as the raw input.
5.1.1. Validation of Wavelet Decomposition Effectiveness
The wavelet decomposition module serves as the first component of the model and holds significant importance. To validate its effectiveness, a comparative analysis was conducted between using the original time-domain signals directly as input and utilizing signals processed by the MLDWT. The performance differences between these two input representation methods were systematically evaluated.
In terms of network architecture, a symmetric encoder–decoder structure with two hidden layers has been adopted for all SDAEs. The encoder consists of two fully connected layers with 128 and 64 hidden units, respectively. The decoder mirrors the encoder’s architecture, with the output dimensionality maintained consistent with that of the input. During the training phase, white WGN with a SNR of 15 dB is added to the input data to construct noisy samples.
To compare the effectiveness of different input features, two input modalities have been defined:
- Wavelet Transform: A 5-level decomposition is performed on the raw signal using the db1 wavelet basis, resulting in six sub-band components (D1–D5 and A5). Each component is reconstructed via inverse transformation into sequences matching the length of the original signal, and these are then used as multi-channel inputs.
- Raw Input: The original one-dimensional time-series signal is directly used as the input.
To ensure fairness in the comparative experiments, an identical min–max normalization strategy is applied at both the sample level and the channel level for both input modalities. The loss function for all models is defined as the MSE, and the Adam optimizer is employed for training, with an initial learning rate set to 0.001. The training and validation batch sizes are set to 256 and 512, respectively. The maximum number of training epochs is fixed at 1000, with early stopping enabled (patience = 100). All training hyperparameters, including network initialization, random seed, and learning rate scheduling, were strictly maintained at identical settings across all models, with the exception of the input modality.
A comparative analysis of the denoising performance was conducted between the standard SDAE with raw signal input and the Channel-wise SDAE (C-SDAE) with wavelet-transformed input. The comparative results of the MSE for the two methods under different SNR levels are presented in Figure 6. Furthermore, the training loss curves for both approaches are shown in Figure 7.
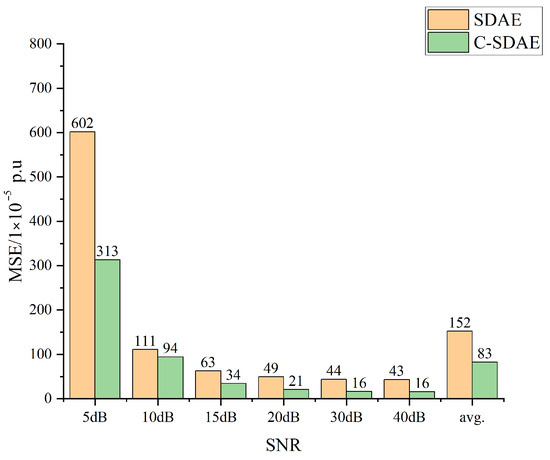
Figure 6.
MSE Performance Comparison Across SNR Levels.
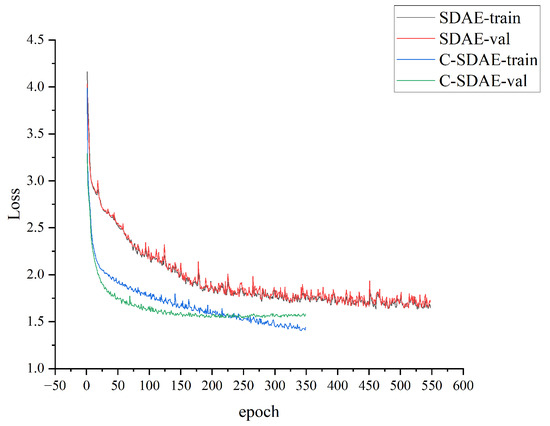
Figure 7.
Training Loss.
The results demonstrate that the C-SDAE achieves significantly lower MSE values across all signal-to-noise ratio (SNR) conditions compared to the conventional SDAE. Specifically, the average MSE is reduced from p.u. to p.u., representing a decrease of approximately , which indicates a substantial performance improvement. This enhancement is most pronounced under high-noise conditions (), where the MSE decreases from p.u. to p.u. Meanwhile, the C-SDAE maintains a consistent performance advantage in the medium-to-low-noise conditions (15–). The training loss curves further reveal that the C-SDAE surpasses the conventional SDAE in both convergence speed and final loss level. On both the training and validation sets, the C-SDAE exhibits faster loss reduction and stabilizes at a lower value. These observations indicate that the multi-scale time–frequency information provided by the MLDWT effectively enhances the time–frequency resolution during feature extraction. This enables the network to better distinguish between useful signal components and noise, thereby significantly improving the overall denoising performance and enhancing the model’s robustness and feature representation capability. Consequently, the necessity of the wavelet decomposition module within the overall framework is successfully validated.
5.1.2. Interpretability of the Attention Mechanism
To validate the adaptive capability and interpretability of the cross-channel attention mechanism under different noise levels, the attention weight distributions across wavelet channels of the channel-wise attention stacked denoising autoencoder (CA-SDAE) model were statistically analyzed at three specific SNRs: , , and . The resulting distributions are illustrated in Figure 8, Figure 9 and Figure 10, with the corresponding average distribution values provided in Table 1. The analysis indicates that the attention weights undergo adaptive redistribution in response to varying noise intensities, and the observed variation pattern demonstrates clear physical significance.
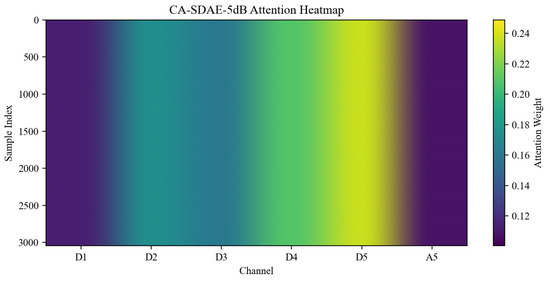
Figure 8.
CA-SDAE 5dB Attention Heatmap.
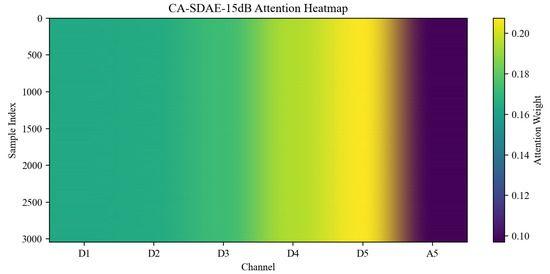
Figure 9.
CA-SDAE 15dB Attention Heatmap.
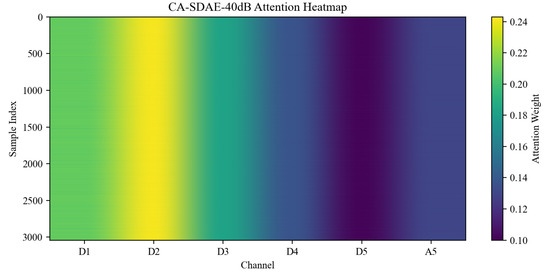
Figure 10.
CA-SDAE 40dB Attention Heatmap.

Table 1.
Average attention weight distribution across wavelet channels under different SNR conditions.
Under high-noise conditions (), the attention is predominantly focused on the low-frequency detail channels D5 (0.237) and D4 (0.209), whereas substantially reduced weights are allocated to the high-frequency channel D1 (0.113) and the approximation component A5 (0.108). This distribution pattern demonstrates that under significant noise interference, strategic emphasis is placed by the model on low-frequency components where signal energy is concentrated and less vulnerable to noise contamination, thereby ensuring reconstruction stability, while high-frequency components that are easily corrupted by noise are effectively suppressed.
Under medium-noise conditions (), a sustained preference is maintained by the model for the low-frequency channels D5 (0.207) and D4 (0.194), while the weights assigned to the medium- and high-frequency channels D3 (0.173), D2 (0.165), and D1 (0.164) are significantly increased. This redistribution reflects that as noise interference diminishes, finer-grained high-frequency features are increasingly leveraged by the model to enhance reconstruction quality, demonstrating a transitional trend from “robustness-first” to “detail-recovery” prioritization.
Under low-noise conditions (), the attention distribution is fundamentally shifted, with weights being significantly tilted toward the high-frequency detail channels D2 (0.241) and D1 (0.209). Compared to the high-noise conditions (), increases of and are observed for D1 and D2, respectively, whereas decreases of and are recorded for D5 and D4. This distribution confirms that under low-noise conditions, high-frequency details can be fully utilized by the model to recover the fine-grained structure of the signal.
The above analysis demonstrates that the proposed channel-wise attention mechanism can adaptively adjust the weight allocation according to the noise level. Its behavioral pattern, which shows reliance on low-frequency components under strong noise conditions and utilization of high-frequency components under weak noise conditions, is shown to align with physical intuition, thereby validating both the interpretability and adaptability of the attention mechanism.
5.1.3. Validation of Energy Proportion Guidance Effectiveness
Although the previously described data-driven attention mechanism demonstrates a promising adaptive trend, its fully data-driven learning approach may lead to distributional biases in certain complex noise scenarios, resulting in a misalignment between the model’s focus and the actual energy characteristics of the signal. To address this limitation, an energy proportion guidance module is introduced in this work, which utilizes the energy distribution from the original domain as a physical prior to constrain the attention weights. By incorporating an energy target distribution term into the loss function, the energy-proportion-based Channel-wise attention stacked denoising autoencoder (EPCA-SDAE) model can automatically rectify unreasonable weight biases during training, thereby ensuring that the allocation results better conform to physical principles.
In this section, four categories of methods were compared:
- C-SDAE: The conventional SDAE without any attention or energy guidance mechanisms, serving as the baseline model
- CA-SDAE: The cross-channel attention is driven solely by data, autonomously learning the weights
- EPCA-SDAE: The global average relative energy is directly adopted as fixed channel weights, with specific values provided in Table 2
 Table 2. Global average relative energy across wavelet channels.
Table 2. Global average relative energy across wavelet channels. - EPGCA-SDAE: The wavelet channel energy distribution is estimated in the original domain for each sample, serving as a guidance term for attention learning, thereby achieving sample-wise dynamic constraints that preserve self-learning capability while preventing deviation from physical priors.
The denoising performance of the four methods is compared in Table 3 using the test set contaminated with noise levels ranging from 5–, where the MSE () p.u. is employed as the evaluation metric. The baseline C-SDAE, which directly processes multi-level wavelet-decomposed signals without any attention or energy guidance, shows limited denoising capability, particularly under low-SNR conditions, while maintaining reasonable performance as the noise level decreases. The purely data-driven CA-SDAE performs poorly under low-SNR conditions, with an MSE of 282.28 recorded at and an overall average MSE of 75.82, indicating that the unconstrained attention mechanism is prone to deviation. By introducing a fixed energy prior, the EPCA-SDAE establishes a physical basis for weight allocation, resulting in a significant reduction of the average MSE to 52.85. In contrast, the proposed EPGCA-SDAE achieves the best performance under all tested conditions, with the average MSE further reduced to 50.60. This corresponds to reductions of , , and over the C-SDAE, CA-SDAE, and EPCA-SDAE, respectively. Notably, the advantage of the EPGCA-SDAE is particularly pronounced in high-noise scenarios, demonstrating that the sample-wise energy-proportion guidance mechanism can substantially enhance model robustness in complex noise environments.

Table 3.
Comparison of denoising performance in terms of MSE under different SNR conditions.
Further analysis from the perspective of ACC provides clearer insight into model performance across different noise levels. For the detection task, an LSTM model [40,41] is employed, which is configured with a single LSTM layer containing 50 hidden units. The tanh activation function is utilized in the LSTM layer, while the output layer is implemented as a fully connected layer with a sigmoid activation function. During the training process, the Adam optimizer is adopted with a learning rate of 0.001, and the binary cross-entropy is chosen as the loss function. The batch size is set to 1024, and the number of iterations is specified as 300. An early stopping strategy is applied with a patience of 50. The dataset is partitioned into training, validation, and test sets according to a 3:4:3 ratio. As shown in Table 4, the accuracy of the original noisy signal under high-noise conditions () is only , indicating that strong noise severely corrupts signal characteristics. After applying different denoising methods, the baseline C-SDAE, which directly processes wavelet-decomposed signals without attention or energy guidance, achieves accuracy, already providing a substantial improvement over the raw noisy input. The purely data-driven CA-SDAE and fixed-prior EPCA-SDAE further improve accuracies to and , respectively, while the proposed EPGCA-SDAE attains the highest accuracy of . As the SNR ratio increases, the accuracy of all methods gradually approaches , with EPGCA-SDAE consistently maintaining the best performance across all test points. For instance, under low-noise conditions (), EPGCA-SDAE achieves an accuracy of , outperforming C-SDAE (), CA-SDAE (), and EPCA-SDAE (). Similarly, at , EPGCA-SDAE again attains the highest accuracy of . Overall, average accuracies of , , and are recorded for C-SDAE, CA-SDAE, and EPCA-SDAE, respectively. Although EPCA-SDAE incorporates a fixed energy prior to ensure physical consistency in weight distribution, its lack of sample-wise adaptation results in slightly lower overall accuracy. In contrast, EPGCA-SDAE further improves the average accuracy to , representing increases of , , and percentage points over C-SDAE, CA-SDAE, and EPCA-SDAE, respectively. This demonstrates that the sample-wise energy proportion guidance mechanism not only ensures physical consistency but also preserves adaptive capability in complex noise scenarios, thereby significantly enhancing both accuracy and stability of classification.

Table 4.
ACC of the LSTM algorithm under varying noise levels (after denoising by different models).
The distributions of attention weights are shown in Figure 11, Figure 12 and Figure 13. The weight distribution of CA-SDAE is characterized by strong randomness and near-uniformity, with insignificant differences observed among channels, making it difficult to highlight dominant channels. Furthermore, only a weak correlation is found with the physical characteristics of the signal, indicating the lack of a clear physical basis for its weight allocation. Although EPCA-SDAE employs a fixed global energy distribution as attention weights, introducing a degree of physical consistency, its adaptive capability is completely lost when dealing with different sample characteristics. In contrast, the proposed EPGCA-SDAE introduces a sample-wise dynamic correction mechanism while respecting the prior ordering of channel energy. This approach not only avoids the tendency toward complete equalization but also breaks through the limitations of fixed templates, thereby achieving a balance between global constraints and local adaptation.
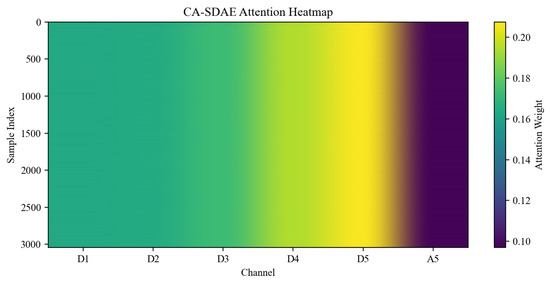
Figure 11.
CA-SDAE Attention Heatmap.
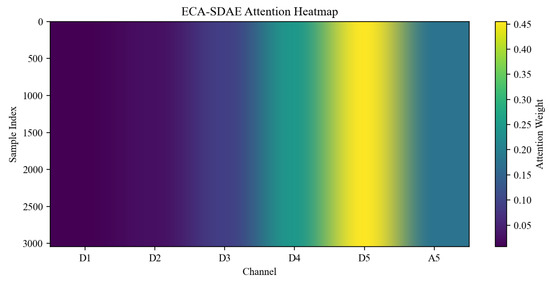
Figure 12.
EPCA-SDAE Attention Heatmap.
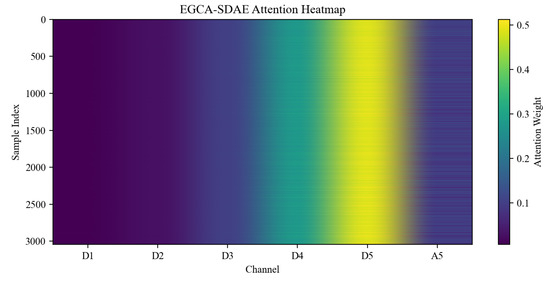
Figure 13.
EPGCA-SDAE Attention Heatmap.
5.1.4. Performance of Denoising Models
To comprehensively evaluate the performance of the proposed EPGCA-SDAE, it is compared in this section with traditional wavelet denoising, the classical SDAE, the DnCNN, and a Transformer-based method. The parameter settings for each method are configured as follows: the wavelet method employs the soft-thresholding strategy proposed by [20]; the SDAE structure remains consistent with that described in Section 5.1.1; the DnCNN adopts a one-dimensional convolutional residual learning framework with a depth of 17 layers, 64 channels per layer, a kernel size of 3, and a batch size of 256; the Transformer denoiser utilizes a 4-layer TransformerEncoder with a hidden dimension of 64, four attention heads, a feed-forward layer dimension of 256, and a batch size of 1024. All models in this section are trained using noise and tested at SNR levels of 5, 10, 15, 20, 30, and , with the MSE () p.u. employed as the evaluation metric.
As can be observed from Table 5, significant differences in performance are demonstrated among the various methods.

Table 5.
Performance comparison of different denoising methods (values are MSE , and the corresponding SNR in dB is shown in parentheses).
The traditional wavelet soft-thresholding approach is shown to provide moderate noise suppression under high-noise conditions and satisfactory performance under low-noise conditions. However, an overall elevated error level is maintained, with an average MSE of 179.76.
The SDAE is observed to perform adequately near its training noise level, but severe performance degradation is exhibited at higher noise levels, while performance saturation is encountered at lower noise levels. This indicates that the feature representations learned by the SDAE are rendered overly sensitive to noise variations, resulting in limited generalization capability and poor robustness.
The DnCNN demonstrates a strong preference for local features, achieving optimal performance at and . However, when the test noise levels deviate from the training distribution, its limited receptive field is found inadequate for modeling global noise structures, leading to significant performance deterioration. Complete failure is observed under high-noise conditions, confirming its inability to effectively extrapolate to unseen noise distributions.
The Transformer method excels at global dependency modeling. Consequently, superior robustness compared to DnCNN is demonstrated, particularly under high-noise conditions not encountered during training, where global information is required for effective noise suppression. However, under low-noise conditions where the primary task shifts to recovering fine local details, potential limitations in capturing such localized information efficiently are revealed, leading to performance plateaus.
The proposed EPGCA-SDAE, under identical training conditions, exhibits exceptional robustness and generalization capability. Across all SNR levels, significantly lower MSE values are achieved compared to all baseline models. A smooth, monotonically improving performance curve is observed as the noise level decreases, indicating that the true physical distribution is effectively learned by the model rather than merely memorizing the training distribution. Ultimately, its average MSE of 50.60 is substantially lower than those of other methods, providing compelling evidence for the superior and stable denoising effectiveness of the proposed architecture in unknown noise environments.
In addition to denoising effectiveness, the computational efficiency and real-time feasibility of the proposed framework were quantitatively evaluated. All experiments were conducted on a workstation equipped with an Intel® Core™ i9-13900HX CPU, 96 GB DDR5 5200 MHz RAM (Intel Corp., Santa Clara, CA, USA), and an NVIDIA® GeForce RTX 4090 Laptop GPU (16 GB VRAM) (NVIDIA, Santa Clara, CA, USA).
Under this configuration, the MLDWT module was observed to require an average processing latency of ms per sample, whereas the subsequent multi-channel attention and SDAE inference pipeline required 0.041 ms per sample. Consequently, an overall end-to-end inference latency of ms per sample was achieved, confirming that the proposed EPGCA-SDAE can operate well within real-time constraints.
To ensure fair comparison, identical batch sizes and data settings were applied to all baseline models. As presented in Table 6, the inference efficiency of the proposed EPGCA-SDAE was found to be comparable to that of the conventional SDAE (0.070 ms/sample) and DnCNN (0.154 ms/sample), slightly higher than the traditional wavelet thresholding method (0.084 ms/sample), while remaining significantly faster than the Transformer-based denoiser (0.435 ms/sample). These results demonstrate that, despite the inclusion of multi-stage physical–data fusion mechanisms, the overall architecture remains computationally lightweight and well suited for real-time deployment in distribution-network fault-detection systems.

Table 6.
Inference speed comparison among denoising models.
5.2. Realistic System
HIF experiments were conducted in a distribution network laboratory, from which measured data were obtained. The laboratory equipment is shown in Figure 14, and the line topology is illustrated in Figure 15. A CT sampler was installed at the beginning of each line. Multiple short-circuit points were introduced during the experiments to ensure data diversity. A total of 600 experimental samples were collected, with high-impedance grounding media including turf, cement brick, red brick, and sand. Additionally, normal scenarios with waveforms similar to HIFs—such as inrush current, capacitor switching, and load switching—were incorporated. The dataset therefore consisted of 600 samples with a 1:1 ratio between fault and non-fault data, which were split into 200 samples for training, 200 for validation, and 200 for testing. The first 150 sampling points were used as the raw input. The EPGCA-SDAE architecture remained consistent with that described in Section 5.1.1. To further examine the model’s stability and generalization under limited real-world data, a five-fold cross-validation accompanied by a guidance strength sensitivity analysis was additionally performed. The guidance strength was determined by the approximate ratio between the energy-guided loss and the reconstruction MSE loss within the total objective, corresponding roughly to no guidance (=0%), weak guidance (≈1%), moderate guidance (≈10%), and strong guidance (≈90%). The results, summarized in Table 7, demonstrate that the model remains stable across folds and achieves optimal denoising performance under moderate guidance, confirming that the proposed physically guided attention mechanism maintains robustness even under small-sample conditions.

Figure 14.
Laboratory measurement setup.
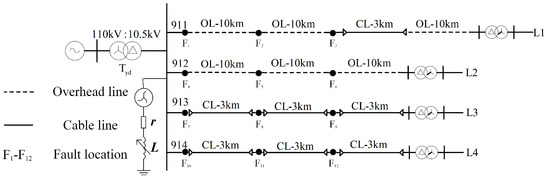
Figure 15.
Laboratory network topology.

Table 7.
Five-fold sensitivity analysis of denoising performance under different guidance strengths (values are MSE ).
A fundamental difference in distribution patterns between the two mechanisms can be clearly observed through the comparison of Figure 16 and Figure 17. The attention distribution of CA-SDAE is characterized by near-equal weighting across channels, with no dominant channels identified. This indicates that when relying solely on data-driven learning, only an “averaged” pattern is acquired by the model, failing to capture the physical imbalance in energy distribution. In contrast, the heatmap of EPGCA-SDAE demonstrates highly consistent and focused characteristics, with significantly elevated weights in channels D5 and D6 stably maintained across all samples. This cross-sample stability confirms that the physical prior has been successfully injected into the model through the energy-proportion-guidance mechanism, providing a clear physical basis and enhanced robustness for attention allocation. Consequently, the “defocused” attention problem inherent in purely data-driven models is fundamentally resolved, transforming the model into a signal processor capable of precisely focusing on critical information according to physical principles. This improvement is directly reflected in the performance metrics: the average MSE is reduced from 113.51 in CA-SDAE to 76.45 in EPGCA-SDAE.
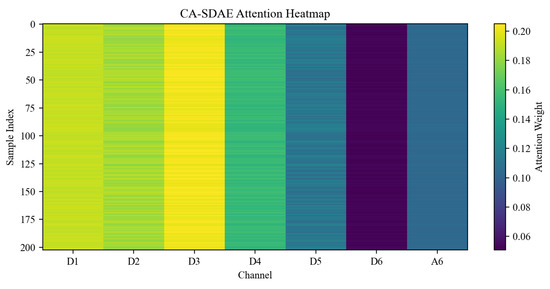
Figure 16.
CA-SDAE Attention Heatmap in the Realistic System.
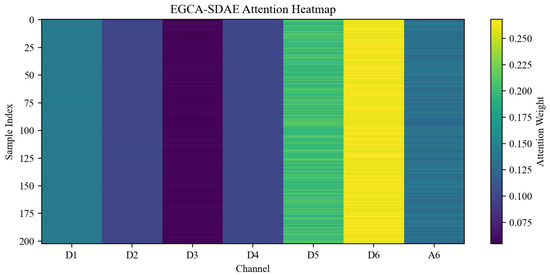
Figure 17.
EPGCA-SDAE Attention Heatmap in the Realistic System.
6. Conclusions
In practical CT data acquisition and transmission processes, various noise interferences are inevitably introduced. The proposed EPGCA-SDAE framework, composed of a wavelet decomposition module, a channel-wise attention module, an energy proportion guidance module, and a foundational SDAE model, effectively addresses data recovery tasks under complex noise distributions.
- The wavelet decomposition module processes the original signal into multiple channels, forming a multi-scale representation suitable for modeling while explicitly preserving energy distribution characteristics across different frequency bands.
- The channel-wise attention module adaptively allocates weights among multi-channel features, enabling dynamic focus on key frequency bands, thereby enhancing the model’s capability to capture dominant signal components.
- The energy proportion guidance module provides channel attention with guidance terms based on sample-wise wavelet energy distributions from the original domain. This approach avoids the averaging problem inherent in purely data-driven methods while ensuring alignment between attention distribution and physical energy characteristics, thereby enhancing model stability and interpretability.
- The foundational SDAE model utilizes stacked autoencoders to achieve multi-channel feature fusion and reconstruction, accomplishing denoising tasks while ensuring the output signal closely approximates the true noise-free signal across various noise levels.
Experimental results demonstrate that the data recovery error was significantly reduced by the EPGCA-SDAE in both the simulation system and the practical system. In the real-world system, the average MSE was decreased from 113.51 (CA-SDAE) to 76.45. Across the cross-SNR test range, an average MSE of 50.60 was achieved, which was found to be substantially lower than those obtained by wavelet thresholding, SDAE, DnCNN, and Transformer methods. This indicates that robust performance can be maintained by the EPGCA-SDAE under high-noise conditions, while fine local details are adequately recovered under low-noise conditions, thereby achieving stable adaptation to diverse noise environments.
In summary, the EPGCA-SDAE framework organically integrates wavelet decomposition, channel-wise attention, energy proportion guidance, and the foundational SDAE model. This integration effectively mitigates the attention averaging problem inherent in purely data-driven models while overcoming the adaptability limitations of fixed-template approaches. Through the collaborative integration of physical priors and deep learning, the model achieves lower recovery errors and enhanced interpretability, demonstrating both its application value and engineering feasibility in practical noisy scenarios within power systems.
It should be noted that the current validation was conducted on a single 10 kV distribution system. Although the proposed model demonstrates strong robustness to varying noise levels, further studies across different network configurations and voltage levels are necessary to verify its general applicability.
Author Contributions
Conceptualization, X.W.; Methodology, X.W.; Software, X.W.; Validation, X.W.; Formal analysis, X.W.; Investigation, X.W.; Data curation, X.W.; Writing—original draft preparation, X.W.; Writing—review and editing, X.W.; Visualization, X.W.; Resources, J.L. and H.W.; Supervision, J.L. and H.W.; Project administration, J.L. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are not publicly available due to institutional restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SNR | signal-to-noise ratio |
| MSE | mean square error |
| SDAE | stacked denoising autoencoder |
| CA-SDAE | channel-wise attention stacked denoising autoencoder |
| EPCA-SDAE | energy-proportion-based channel-wise attention stacked denoising autoencoder |
| EPGCA-SDAE | energy-proportion-guided channel-wise attention stacked denoising autoencoder |
| CT | current transformer |
| HIF | high-impedance fault |
References
- Li, J.; Liu, Y.; Li, C.; Zeng, D.; Li, H.; Wang, G. An FTU-Based Method for Locating Single-Phase High-Impedance Faults Using Transient Zero-Sequence Admittance in Resonant Grounding Systems. IEEE Trans. Power Deliv. 2022, 37, 913–922. [Google Scholar] [CrossRef]
- Aljohani, A.; Habiballah, I. High-Impedance Fault Diagnosis: A Review. Energies 2020, 13, 6447. [Google Scholar] [CrossRef]
- Lien, K.; Chen, S.L.; Liao, C.; Guo, T.; Lin, T.M.; Shen, J.S. Energy variance criterion and threshold tuning scheme for high impedance fault detection. In Proceedings of the IEEE Power Engineering Society—1999 Winter Meeting (Cat. No.99CH36233), New York, NY, USA, 1 January–4 February 1999; Volume 2, p. 957. [Google Scholar] [CrossRef]
- Balser, S.; Clements, K.; Kallaur, E. Detection of High-Impedance Faults; Final Report; Power Technologies Inc.: Schenectady, NY, USA, 1982. [Google Scholar] [CrossRef]
- Sarwagya, K.; De, S.; Nayak, P.K. High-impedance fault detection in electrical power distribution systems using moving sum approach. Iet Sci. Meas. Technol. 2018, 12, 1–8. [Google Scholar] [CrossRef]
- Gao, J.Y.; Wang, X.; Wang, X.; Yang, A.; Yuan, H.; Wei, X. A High-Impedance Fault Detection Method for Distribution Systems Based on Empirical Wavelet Transform and Differential Faulty Energy. IEEE Trans. Smart Grid 2022, 13, 900–912. [Google Scholar] [CrossRef]
- Yeh, H.; Tran, D.H.; Yinger, R. High impedance fault detection using orthogonal transforms. In Proceedings of the 2014 IEEE Green Energy and Systems Conference (IGESC), Tianjin, China, 25–28 May 2014; pp. 67–72. [Google Scholar] [CrossRef]
- Dubey, K.; Jena, P. A Novel High-Impedance Fault Detection Technique in Smart Active Distribution Systems. IEEE Trans. Ind. Electron. 2024, 71, 4861–4872. [Google Scholar] [CrossRef]
- Wei, M.; Shi, F.; Zhang, H.; Chen, W.; Xu, B. Detection and Feeder Identification of the High Impedance Fault at Distribution Networks Based on Synchronous Waveform Distortions. arXiv 2020, arXiv:2005.03411. [Google Scholar] [CrossRef]
- Zhu, X.; Lin, S.; Zhang, S.; He, Z. High-impedance grounding fault detection based on wavelet energy moment. Electr. Power Autom. Equip. 2016, 36, 161–168. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Wei, X.; Song, G.; Wu, L.; Liu, J.; Zeng, Z.; Kheshti, M. High Impedance Fault Detection Method Based on Variational Mode Decomposition and Teager–Kaiser Energy Operators for Distribution Network. IEEE Trans. Smart Grid 2019, 10, 6041–6054. [Google Scholar] [CrossRef]
- Xiao, Q.; Guo, M.; Chen, D.Y. High-Impedance Fault Detection Method Based on One-Dimensional Variational Prototyping-Encoder for Distribution Networks. IEEE Syst. J. 2022, 16, 966–976. [Google Scholar] [CrossRef]
- Gomes, D.P.S.; Ozansoy, C.; Ul-Haq, A. Vegetation High-Impedance Faults’ High-Frequency Signatures via Sparse Coding. IEEE Trans. Instrum. Meas. 2020, 69, 5233–5242. [Google Scholar] [CrossRef]
- Skovajsová, L. Long short-term memory description and its application in text processing. In 2017 Communication and Information Technologies (KIT); IEEE: New York, NY, USA, 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, H.; Lin, N. Imbalance Correction Based on the Ratio of Loss Function Values for Transient Stability Assessment. CSEE J. Power Energy Syst. 2025, 11, 838–849. [Google Scholar] [CrossRef]
- Eikeland, O.F.; Holmstrand, I.S.; Bakkejord, S.; Chiesa, M.; Bianchi, F. Detecting and Interpreting Faults in Vulnerable Power Grids With Machine Learning. IEEE Access 2021, 9, 150686–150699. [Google Scholar] [CrossRef]
- Joga, S.R.K.; Sinha, P.; Maharana, M.K. A novel graph search and machine learning method to detect and locate high impedance fault zone in distribution system. Eng. Rep. 2022, 5, e12556. [Google Scholar] [CrossRef]
- Lopes, G.N.; Silva, M.P.D.; Vieira, J.C.M. Comparison of Machine Learning-Based Methods for High Impedance Fault Detection in Distribution Systems. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE), Grenoble, France, 23–26 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Bai, H.; Gao, J.; Li, W.; Wang, K.; Guo, M. Detection of High-Impedance Fault in Distribution Networks Using Frequency-Band Energy Curve. IEEE Sens. J. 2024, 24, 427–436. [Google Scholar] [CrossRef]
- Yeh, H.; Sim, S.; Bravo, R. Wavelet and Denoising Techniques for Real-Time HIF Detection in 12-kV Distribution Circuits. IEEE Syst. J. 2019, 13, 4365–4373. [Google Scholar] [CrossRef]
- Shahrtash, S.M.; Sarlak, M. High Impedance Fault Detection Using Harmonics Energy Decision Tree Algorithm. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Dai, J.; Song, H.; Sheng, G.; Jiang, X. Cleaning Method for Status Monitoring Data of Power Equipment Based on Stacked Denoising Autoencoders. IEEE Access 2017, 5, 22863–22870. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2016, 26, 3142–3155. [Google Scholar] [CrossRef]
- Pan, D.; Qi, T.; Feng, G.; Wang, H.; Zhang, Z.; Wei, X. TEM1Dformer: A Novel 1-D Time Series Deep Denoising Network for TEM Signals. IEEE Sens. J. 2024, 24, 414–426. [Google Scholar] [CrossRef]
- Lu, B.; Sihao, C.; Li, G.; Xiao, L.; Surname, G.N. Simulation and Experimental Verification on Vibration and Noise of Current Transformer. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 716–721. [Google Scholar] [CrossRef]
- Schettino, B.; Duque, C.; Silveira, P.; Ribeiro, P.; Cerqueira, A. A New Method of Current-Transformer Saturation Detection in the Presence of Noise. IEEE Trans. Power Deliv. 2014, 29, 1760–1767. [Google Scholar] [CrossRef]
- May, Z.; Alam, M.K.; Rahman, N.A.A.; Mahmud, M.S.; Nayan, N.A. Denoising of Hydrogen Evolution Acoustic Emission Signal Based on Non-Decimated Stationary Wavelet Transform. Processes 2020, 8, 1460. [Google Scholar] [CrossRef]
- Geng, Y.; Ji, Y.; Wang, D.; Zhang, H.; Lu, Z.; Xing, A.; Gao, M.; Chen, M. Strength prediction of recycled concrete using hybrid artificial intelligence models with Gaussian noise addition. Eng. Appl. Artif. Intell. 2025, 149, 110566. [Google Scholar] [CrossRef]
- Wang, H.; Ouyang, Y. Adaptive Data Recovery Model for PMU Data Based on SDAE in Transient Stability Assessment. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, S.; Liu, B. Hybrid Physical-Data Driven Model for Denoising of Generator State Measurements. IEEE Trans. Instrum. Meas. 2025, 74, 2509912. [Google Scholar] [CrossRef]
- Ali, M.S.; Bakar, A.A.A.; Tan, C.; Arof, H.; Mokhlis, H.; Talip, M.S.A. High Impedance Fault Localization Using Discrete Wavelet Transform for Single Line to Ground Fault. Arab. J. Sci. Eng. 2017, 42, 5031–5044. [Google Scholar] [CrossRef]
- Silva, S.; Costa, P.; Gouvêa, M.; Lacerda, A.; Alves, F.; Leite, D.F. High impedance fault detection in power distribution systems using wavelet transform and evolving neural network. Electr. Power Syst. Res. 2018, 154, 474–483. [Google Scholar] [CrossRef]
- Biswal, T.; Parida, S. A novel high impedance fault detection in the micro-grid system by the summation of accumulated difference of residual voltage method and fault event classification using discrete wavelet transforms and a decision tree approach. Electric Power Syst. Res. 2022, 209, 108042. [Google Scholar] [CrossRef]
- Thomas, J.B.; Chaudhari, S.G.; Shihabudheen, K.V.; Verma, N.K. CNN-Based Transformer Model for Fault Detection in Power System Networks. IEEE Trans. Instrum. Meas. 2023, 72, 2504210. [Google Scholar] [CrossRef]
- Zhang, Q.; Qi, Z.; Cui, P.; Xie, M.; Din, J. Detection of single-phase-to-ground faults in distribution networks based on Gramian Angular Field and Improved Convolutional Neural Networks. Electr. Power Syst. Res. 2023, 221, 109501. [Google Scholar] [CrossRef]
- Varghese, P.R.; Subathra, M.; Peter, G.; Stonier, A.A.; Kuppusamy, R.; Teekaraman, Y. A novel MODWT–local pattern transformation feature fusion approach for high-impedance fault detection in medium voltage power distribution networks. Neural Comput. Appl. 2024, 37, 17457–17471. [Google Scholar] [CrossRef]
- Zhang, H.; Su, X.; Long, C.; Ren, J. High Impedance Arc Fault Detection in Distribution Networks Based on Instantaneous Parameters Characteristic in Time-frequency Domain. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 23–30 April 2023; pp. 555–561. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Liu, W.; Gao, J.; Wei, X. Faulty Feeder Detection Under High-Impedance Fault for Active Distribution Networks in Resonant Grounding Mode. IEEE Trans. Instrum. Meas. 2024, 73, 3530811. [Google Scholar] [CrossRef]
- Lin, J.; Lin, X.; Wang, H.; Guo, M. Time-adaptive High Impedance Fault Detection Model Based on Cost-sensitive Method. Electr. Power Syst. Res. 2025, 247, 111752. [Google Scholar] [CrossRef]
- Wang, H.; Gao, F.; Chen, Q.; Bu, S.; Lei, C. Instability Pattern-Guided Model Updating Method for Data-Driven Transient Stability Assessment. IEEE Trans. Power Syst. 2025, 40, 1214–1227. [Google Scholar] [CrossRef]
- Chen, Q.; Bu, S.; Wang, H.; Lei, C. Real-Time Multi-Stability Risk Assessment and Visualization of Power Systems: A Graph Neural Network-Based Method. IEEE Trans. Power Syst. 2025, 40, 2955–2968. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).